Synthetic Battery Data Generation and Validation for Capacity Estimation

Abstract

Simple parameter-based models are typically unable to function in all situations due to the rapidly tightening margins for error in the use of contemporary estimation techniques. The development of data-driven models as a result has made the availability of trustworthy battery data essential. The generation of such data from battery systems necessitates prolonged cycling tests that can last for months, which makes data collection challenging. In this article, a combination of approaches is presented that uses measured operational data from battery packs to generate synthetic data utilizing Markov chains and neural networks in order to ultimately estimate the capacity fade based on operational drive cycle data. The experimental data used for this study are generated using scaled operational cycles with multiple charge/discharge pulses applied repetitively on a commercially available battery pack. The synthetically generated data have the flexibility of matching user-imposed conditions, and have potential for a variety of applications in the analysis and safety of commercial battery systems. Finally, capacity estimation results present the outcome of a comprehensive study into capacity fade estimation in battery packs.

1. Introduction

Over the last two decades, energy storage technologies and especially lithium-ion battery technology have worked their way to the forefront of the automotive industry. Electric Vehicle (EV) battery technology continually pushes the bounds of lithium-ion batteries’ ability to provide ample power, longevity, and safety. While the demand for such batteries has grown, the need for better observation and control of the overall system’s state of health has gained momentum as well.

The state of health (SoH) of a battery refers to the current operating ability to hold energy without an applied external load. Generally speaking, SoH is calculated or estimated in contrast to its beginning-of-life state or to its designed performance characteristics. SoH is a critical diagnostic parameter for system assessment not only for the overall health in terms of holding energy, but also in terms of the remaining life of the battery. Hence, SoH provides an important indicator regarding the functioning capabilities. To determine the change in SoH of a battery over its lifetime, several important factors become critical. The first factor to note is the natural capacity loss with time due to self-discharge, where the battery loses its reversible reaction ability to hold charge. Second is internal resistance, which tends to increase with constant cycling and utilization, which in turn makes the battery itself heat up significantly more during charge or discharge pulses. This increased heating results in a drop in efficiency as the battery losses increase. That is, the operating temperature of batteries can have a detrimental effect on SoH and performance if the batteries are operated in extremes of cold or hot ambient temperatures. Another factor concerns the designed cycle life of the battery. Batteries are developed to sustain a limited number of charge–discharge cycles in an effective manner before critical degradation in performance occurs. Such a design philosophy is aimed at ensuring that batteries are optimized from a cost as well as performance perspective. Lastly, the depth of discharge of the battery, as well as how frequently the battery is overcharged or over-discharged, have a considerable and irreversible impact on the any battery’s ability to sustainably hold energy and perform consistently [1]. All these factors point to SoH evaluation as being very fundamental in the diversified application of batteries, as evidenced in prevalent applications such as EVs and electronics, as well as specialized and high-precision applications such as medical devices and satellites.

As was discussed in [2], the role of data and its analysis has become increasingly crucial as the operational conditions faced by batteries and packs have resulted in higher demands. The generation of reliable and useful data requires lengthy cycling tests, often over many months, making the collection of data cumbersome. Hence, this article ties together the topics of battery health and data analysis with the generation and utilization of meaningful synthetic data.

In the transportation domain, there has been a significant upsurge in the demand for clean energy-based energy solutions [3], with significant annual growth [4] and growth in global sales, along with multiple automakers also making the transition to primarily battery-based vehicle offerings. This shift has brought about a significant interest in the reliability associated with the battery packs in EVs because a major portion of the manufacturing cost is associated with these packs. Along the same lines, therefore, the battery SoH has increased the capability of battery management systems to address safety concerns.

The reliability of a battery pack will not be as high as the quoted reliability of a single cell. Additionally, interactions between cells can also cause small production variations between the cells to be magnified, resulting in excessive stress and an increase in failure rates, which result in premature failures, often representing hazards and leading to safety concerns. The failures which take the most precedence are generally due to the gradual deterioration of, or reduction in, the active chemicals, resulting in reduced cell capacity. Cell lifetime is defined as the age when the capacity reduction, or the increase in internal impedance, reaches pre-determined, unacceptable levels [5,6]. As was mentioned in [2], the costs associated with pack replacement are daunting and undesirable.

Coupled with the boost in demand, legislative directives requiring automakers to produce larger volumes of EVs have created a requirement for battery technology to be pushed further as researchers strive to expand from traditional methods to exceed present performance standards. This has led the scientific community to look beyond the boundaries of traditional statistical as well electro-chemical approaches for interpreting and analyzing the fade in capacity of batteries [7,8]. Predominantly, the approaches adopted for evaluating the capacity fade or SoH of batteries can be classified into three categories: (a) experimental methods, which rely upon specific experimental measurements of impedance [9,10], internal resistance [11], and energy levels [12], as well as other measurements such as incremental capacity and differential voltages [13]; (b) model-based methods, in which internal parameter estimations are conducted using indicators which are measured directly—some such models are Kalman filters [14,15], observers [16], and simplified electro-chemical models [17]; (c) machine learning-based methods, in which statistical as well as deep learning models are used in conjunction with large volumes of data in order to predict SOH—popular approaches use support vector regression algorithms [18], fuzzy logic [19], and neural networks [20].

The use of machine learning in these applications has gained significant traction in recent times and specialized methods have been developed, particularly some using cloud storage and computing. Some deep learning applications involve time-series analysis where recurrent neural networks and long short-term memory networks are used to acquire temporal relationships in the data, facilitating robust SoH forecasts [21]. Another application is in feature extraction, where convolutional networks are utilized for identifying important features in an automated manner without manual intervention, especially in utilizing multi-dimensional data from sensors [22]. Data fusion approaches can often provide a more holistic image of the the health of a battery, wherein various types of data, such as current, voltage, and temperature measurements, along with impedance spectrography data, are fused together. Another approach that finds use in not only estimation but also in other systems associated with batteries is anomaly detection methods where unusual or unexpected behaviors in the operation of batteries are identified early in the hopes of preventing early degradation or damage with proactive maintenance. Finally, approaches have recently emerged out of transfer learning [23], where pre-trained deep learning models trained on test datasets generated in laboratory conditions, as well as operational data gathered from real-world applications in related fields, are used to refine the estimation tasks performed on batteries, notably when data availability is bounded and finite.

All of these factors have led to important studies in estimating the battery SoH, especially in terms of capacity and capacity fade. In battery capacity fade studies, the most significant barrier is simply the availability of test data, typically addressed by extensive data gathering through round-the-clock experimentation with specialized test facilities. With the rapid improvements in data science, the idea of augmenting experimental data with synthetically generated data has become very promising. In the broader domains of computer vision, natural language processing, self-supervised learning, reliability engineering [24], and energy studies [25], the utility of synthetic data has shown its effectiveness. As was highlighted in [2], synthetic data provide a statistically proven methodology to validate aging models with less dependency on experimental data.

The work was conducted in response to the necessity for validation of estimating methodologies on diverse sets of test data. Following the recent developments in the use of synthetic data in the research community, this article demonstrates the generation of synthetic battery data utilizing Markov chains in conjunction with experimental battery data collected from batteries employed in EVs. With the availability of high-fidelity battery data being limited and requirements for performance thresholds of estimation methodologies becoming more and more stringent, this work provides a bridging mechanism to reduce the disparity in battery data. This opens avenues for better prediction and estimation of key parameters such as the correlation between capacity fade or state of health and the open circuit voltage of individual cells and packs. Also, as has been talked about in [2], such frameworks of large-scale data simulation provide the analytical capability to subject systems to edge cases that would otherwise be unachievable in real-world circumstances. Another benefit of such a framework is the ability to re-train or reinitialize the Markov chains with new data collected over time.

This article is divided into five primary sections. First, an overview is provided about the experimental data and the methodology of synthetic data generation. Following this, a discussion is provided regarding the prediction of capacity fade using neural networks. Following a presentation of the synthetic data generation results, validation results are presented which make use of synthetic data as well as the prediction algorithm. Prior to the Conclusions section, application to functional safety systems is also discussed.

2. Synthetic Data Generation Methodology

The benefits of having a large dataset are multi-faceted. Having ample data not only helps reduce bias and over-fitting, but also facilitates training of models to enhance robustness. In the domain of battery testing and modeling, the availability of drive data through real-world testing involves significant resources. Thus, the idea of generating synthetic data is very appealing.

In the methodology of this study, the generation of synthetic data consists of two parts. First, EV pack data are used to generate synthetic current profiles using Markov chains. Then, a neural network structure is used where the input is the synthetic current profile generated using the EV pack and the output is the synthetic voltage behavior. Here, the pack used for training uses a three-cell pack whose output is in the form of voltage centroids; the reader is referred to [26,27] for supporting development.

2.1. Current Profile Generation

For the generation of synthetic current profiles, data obtained from the telemetry on-board an EV were utilized along with a stochastic Markov chain approach. In the following, the methodology is detailed, and a summary is provided at the end.

2.1.1. EV Pack

The EV data were obtained from a Renault Twizy, which was subjected to extensive real-world driving with an average driving speed of 8.03 km/hr, with the maximum being 66.79 km/hr [28].

The pack under observation consists of 96 cells, where the variation in voltage and SoC during a sample drive cycle is depicted in Figure 1. In the cycle shown, the lowest SoC reached is 60.44% and the voltage variation ranges between 398 V and 348.5 V.

2.1.2. Synthetic Current Profile Approach

For generating the current pulses, a Markov chain approach is adopted. This modeling approach is appropriate because EV drive cycle data have stochastic tendencies due to the fact that charge/discharge current pulses experienced by a battery pack can be arbitrary, where each pulse is dependent on the previous state.

Using the current data from multiple drive cycles obtained from the automotive pack, a transition probability matrix $P_A$ of current transitions is constructed as follows:

$$P_A=\left[\begin{array}{ccc}{a}_{1,1}& \cdots & a_{1,j}\\ ⋮& \ddots & ⋮\\ a_{i-1,1}& \cdots & a_{i-1,j}\\ a_{i,1}& \cdots & a_{i,j}\end{array}\right]$$

(1)

where $a_{i,j}$ is the number of times the current pulses change from i to state j in the test data.

A second probability matrix $P_C$ can be calculated where each element is

$$c_{i,j}=\sum _{k=1}^j{b}_{i,k},$$

(2)

where $b_{i,j}={\displaystyle \frac{a_{i,j}}{{\sum }_{k=1}^n{a}_{i,k}}}$, representing the transition probability from state i to j.

After both the transition matrices are generated, the following steps are followed:

• An initial state is chosen randomly.
• A uniform random number between 0 and 1 is selected.
• The upper bound of the interval in which this random number is greater than the transition probability of the following state is selected as the next current state.

Specific details considered while generating the current profiles are as follows:

• A total of 50 states have been used between 0 and 200 A (the EV pack data have a maximum discharge current pulse of 193.4 A and a minimum of 0.2 A).
• The duration of each discharge pulse and rest period following each pulse has been set to vary randomly between 1 and 5 min.
• In certain cases, the same state transition can be repeated several times; the effects of this situation are avoided by re-initiating the sequence after three repetitions.

2.2. Voltage Profile Generation

Characterizing the voltage behavior of the pack is considered next. For this purpose, a three-cell pack manufactured by Turnigy Power Systems, rated at 2200 mAh, was utilized for generating the voltage test data.

In order to generate profiles that are synthetic characterizations of voltage behavior, but based on experimentally obtained data, a neural network structure is employed, taking the current profiles as input to produce voltage “centroids” as output. Because reduction in data volumes is desirable, the neural network model is trained on cluster centroids rather than on raw data.

2.2.1. Three-Cell Pack

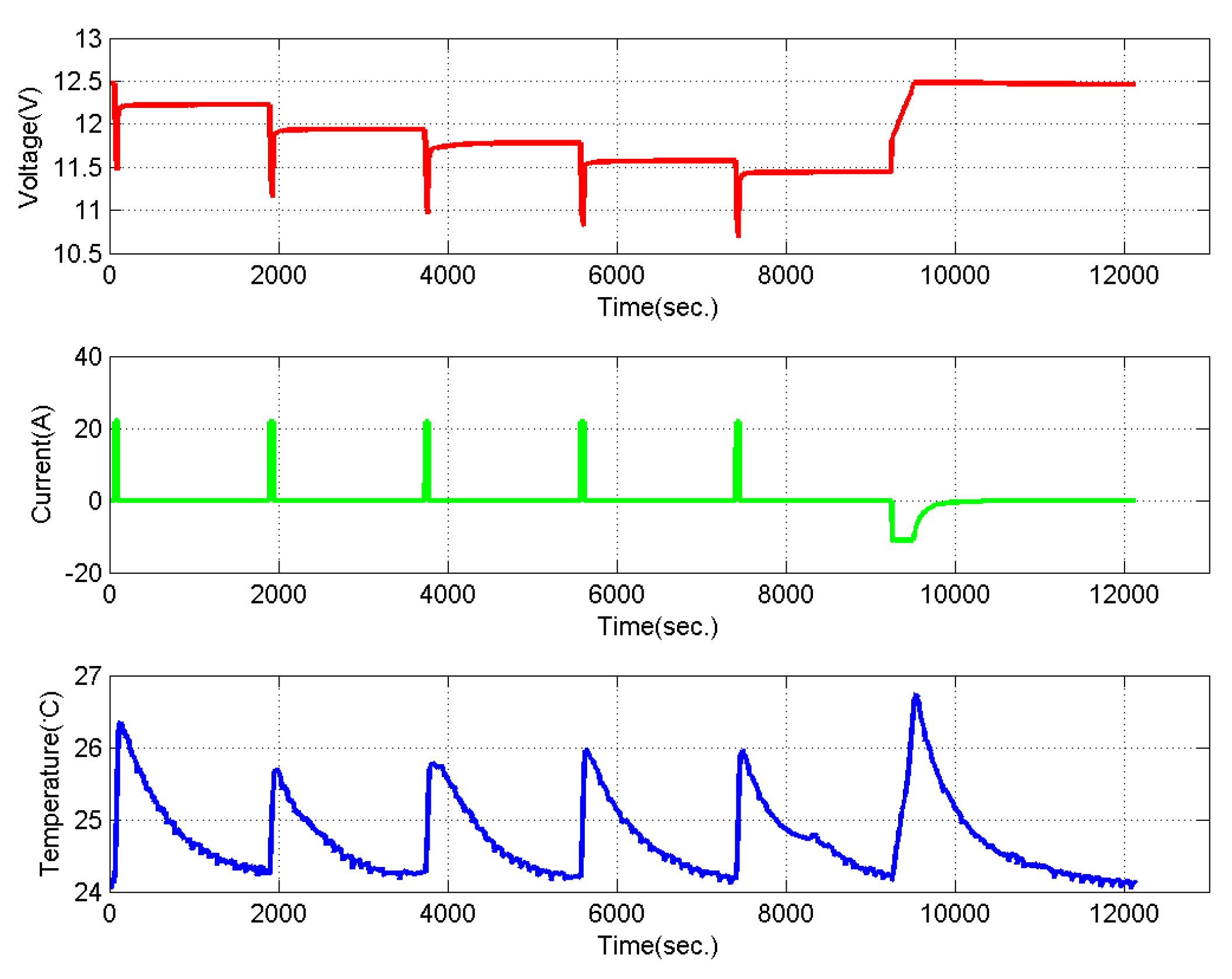
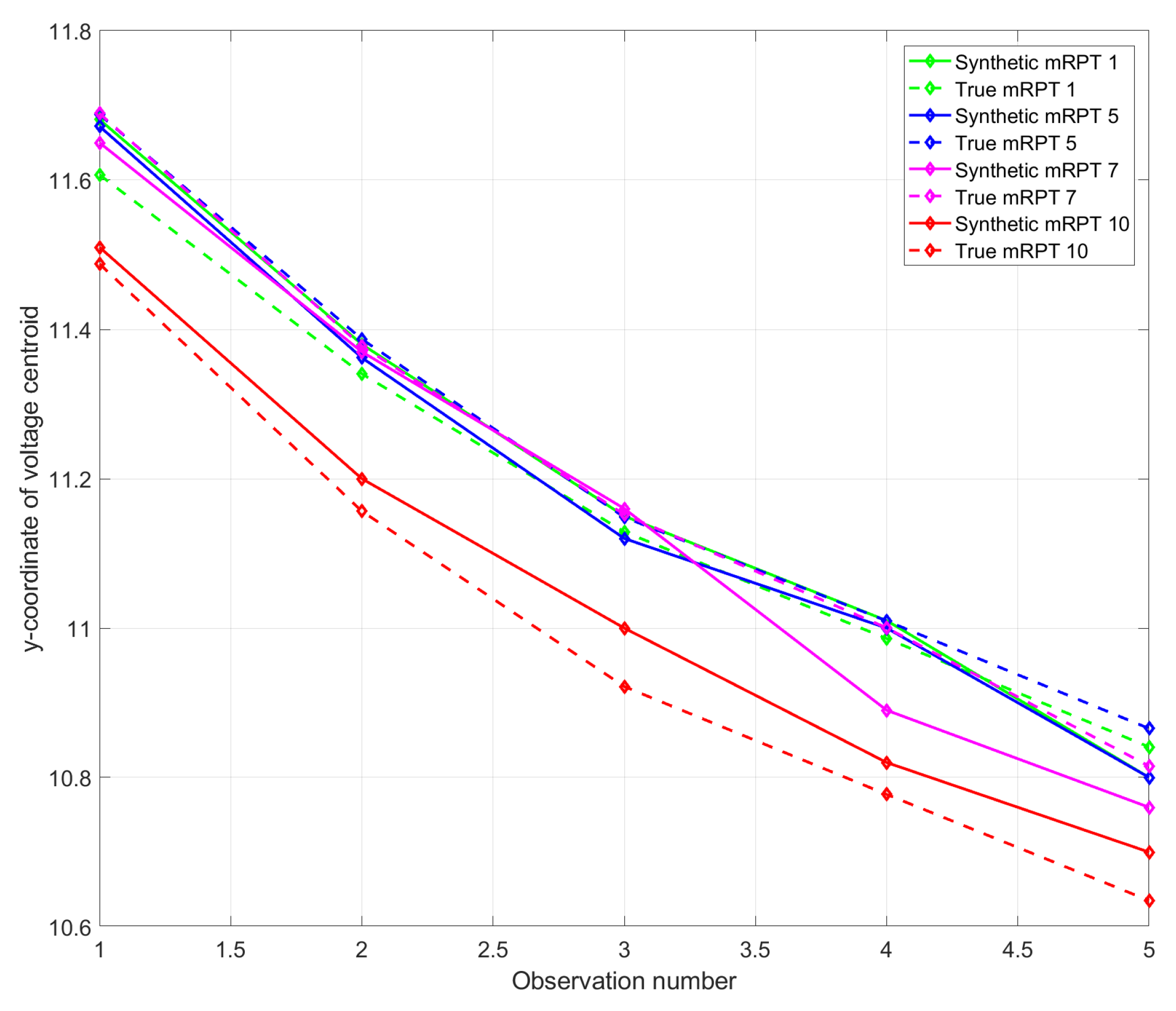
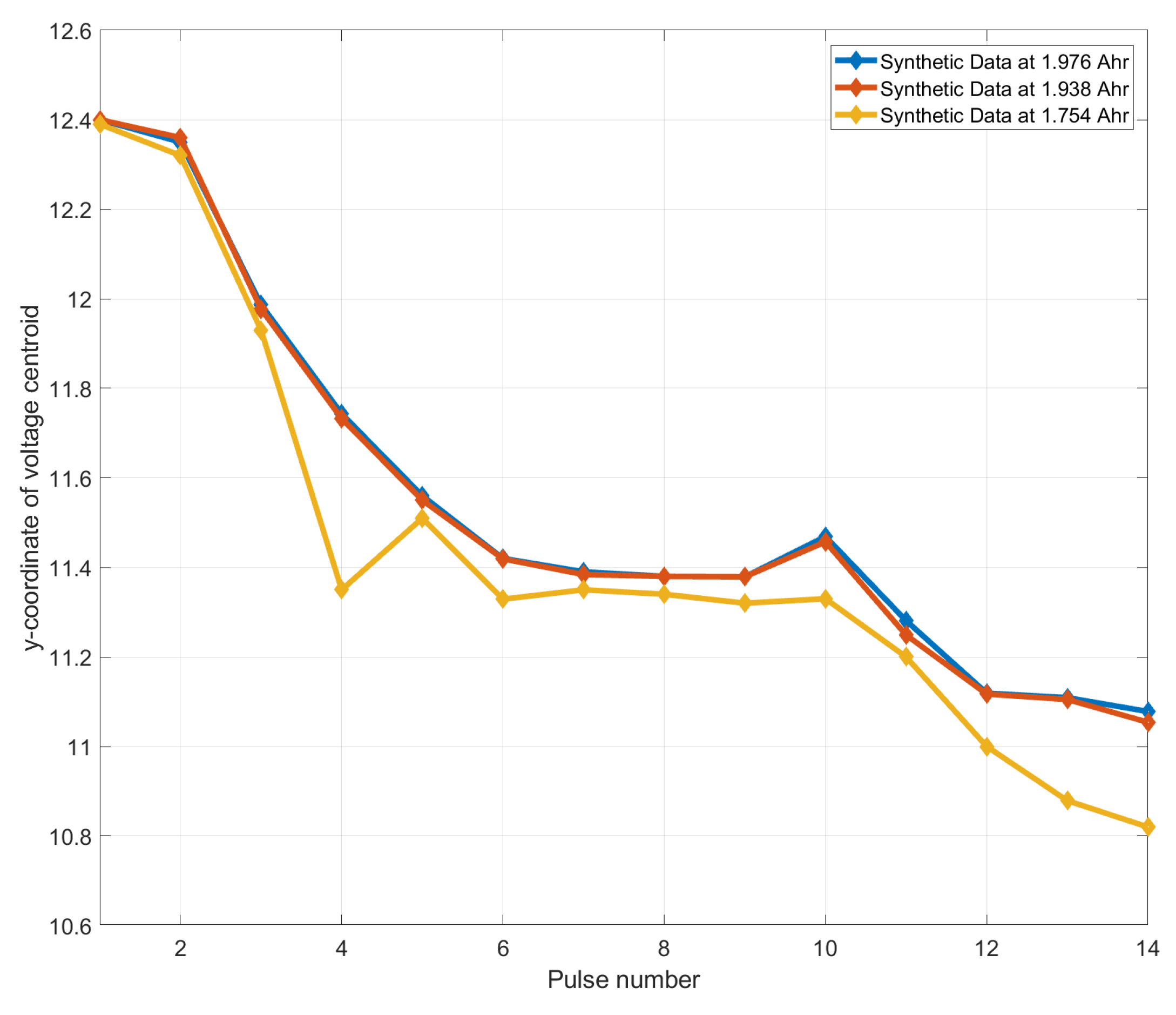
As a brief summary of the process described in [2,27,28], we note that the three-cell Turnigy packs are subjected to three separate testing profiles. First, a characterization profile $Q_i$ (where i is the number of the test) is used, constructed to capture the capacity of the pack. Second, a mini-reference performance test (mRPT), as shown in Figure 2, is used. 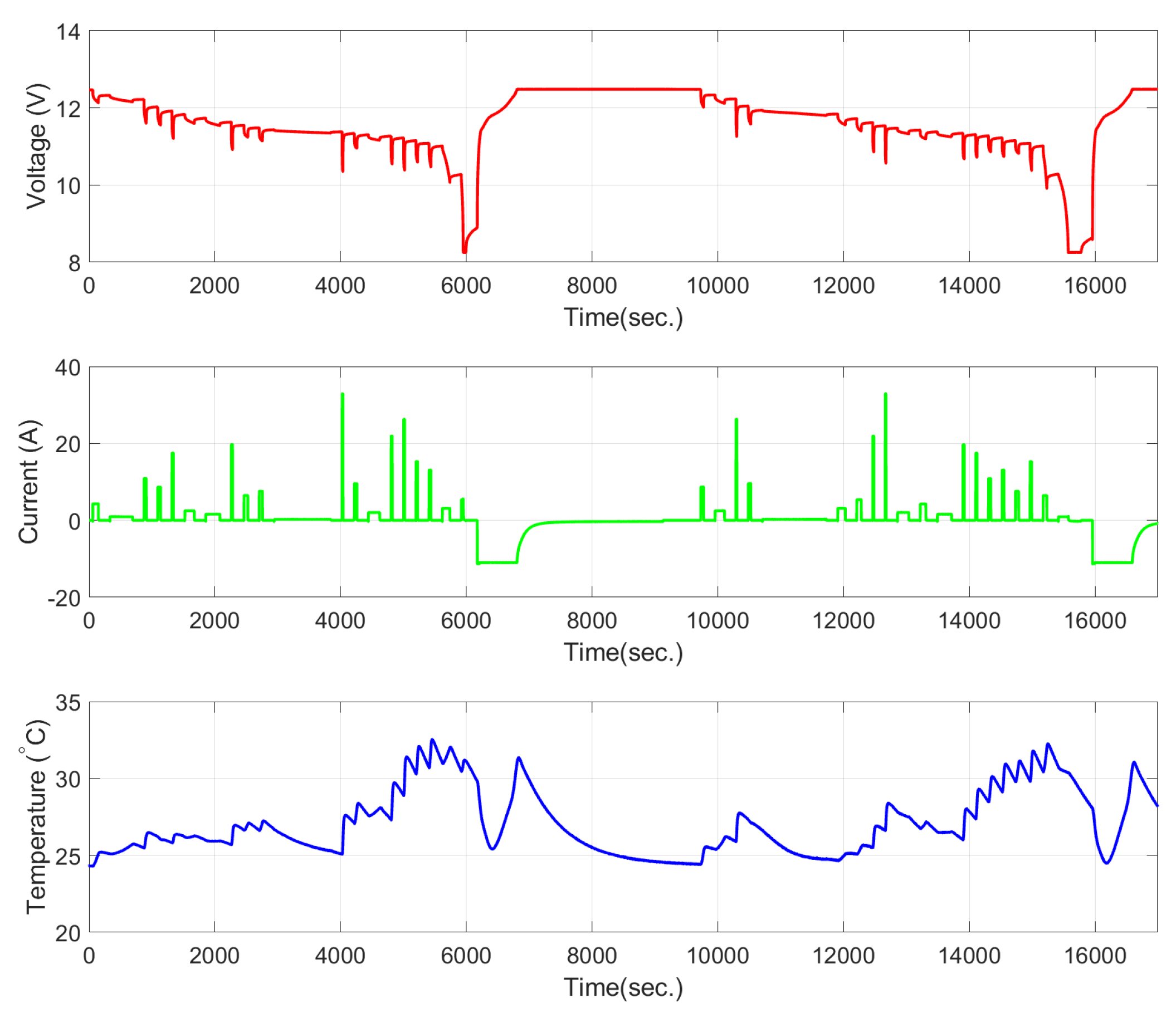Finally, a representative drive cycle profile consisting of multiple discharge pulses is used, shown in Figure 3. Each drive cycle consists of twenty discharge pulses, wherein each discharges the pack by 5% SoC.

All three tests are designed to discharge the pack from over its full range, from 100% SoC down to 0% SoC. This is performed either in one single discharge pulse or in multiple pulses. The sequence of tests is ordered such that ten drive cycle tests are followed by one mRPT and one characterization profile. Although this process has been executed in the laboratory for several packs at multiple temperatures, the pack tested at 25 ${}^{°}$C is used for the results presented here.

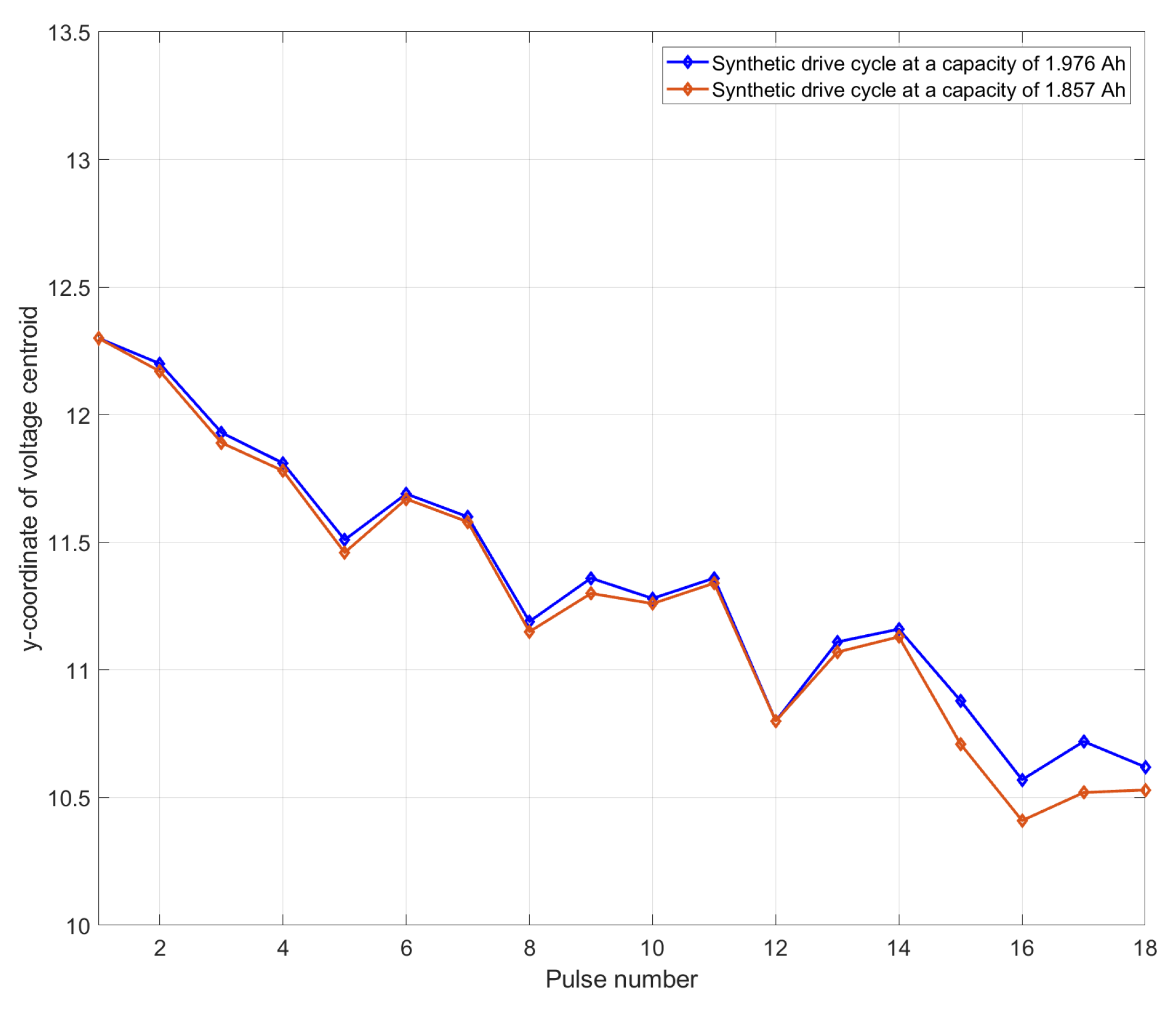
The capacity variation in this pack tested at 25 ${}^{°}$C was initially at 1.976 Ah and the pack was cycled until the capacity dropped to 1.576 Ah.

2.2.2. Clustering

The observations discussed in [27] highlighted how mPRT data can be clustered and utilized with a polynomial fit function as an input to a neural network for estimating the present capacity of a battery pack. While the mRPT data used possess some structure, the error margins below 2% served as the base for further development. The K-means clustering approach used here divides n-observations into $k\le n$ sets by minimizing the variance according to

$$\underset{S}{arg\; min}\sum _{i=1}^k\sum _{x\in S_i}\parallel {x-{\mu }_i\parallel }^2=\underset{S}{arg\; min}\sum _{i=1}^k\left|S_i\right|Var{S}_i,$$

(3)

where ${\mu }_i$ is the mean of the points in $S_i$ with $S_i$ being the set number. Because there are twenty discharge pulses in each drive cycle, k was set to 20, thus generating 20 centroids each time.

2.2.3. Neural Network Structure

With the training data being structured in centroids, the final step is to develop a neural network which can be trained on the experimental data and is used to generate synthetic voltage centroids based on the synthetic current profiles. The network used has three hidden layers with 10, 100, and 10 neurons individually, trained for 1000 epochs with a learning rate of 0.001. The optimizer used is the (ADAM) optimizer [29].

The training and synthetic data generation steps are as follows:

• In the training phase, the input data comprise current and SoC values at the beginning of each discharge pulse, rendering the corresponding capacity value. The target data comprise the centroids generated by clustering the voltage response. Both input and target are from the three-cell pack.
• The dataset is split, using 90% for training and 10% for validation and testing.
• For generating the synthetic voltage data, the input data comprise synthetically generated current profiles, where the SoC is calculated using Coulomb Counting [2], as well as a desired capacity value.

2.3. Summary of Methodology

Before moving to application discussion, results, and validation, in this section we provide a succinct summary of the methodology.

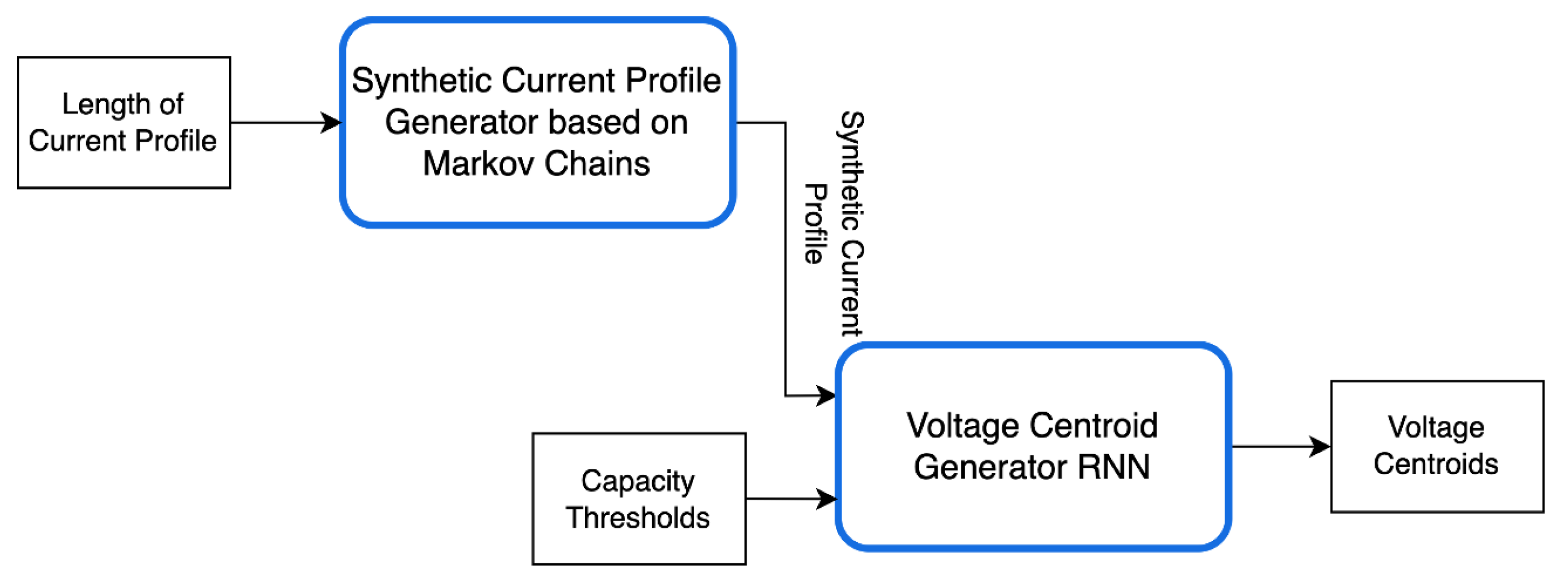
The synthetic data generation process consists of two distinct steps, as highlighted in Figure 4. In the first step, the current profile is generated, where historical profiles using real-world data are utilized; in this case, that is data from EVs in typical driving cycles. These current profiles are used to develop a transition probability matrix, and this matrix in turn is used in a Markov chain generation algorithm to generate synthetic current profiles. Thus, depending on time and computing resources, an arbitrarily large set of synthetically generated current profiles can be obtained.

In the second step of the process, the aforementioned synthetic current profile is fed into a recurrent neural network that has been trained using current profiles and observed capacity value as inputs, and using voltage centroids as outputs. The end result of the process, using these two steps, is the generated set of synthetic current and voltage data.

3. Synthetic Data Results

A sample synthetic voltage profile is highlighted in Figure 5, where the same 18-pulse current and SoC profiles were given as inputs at two different capacity points, 1.976 Ah and 1.857 Ah [2].

4. Synthetic Data Validation

An inherent challenge with using synthetic data generation is in validating the process. Several approaches are possible; here, we use the mRPT test data generated from experimentation on the three-cell pack, leading to a synthetic drive cycle profile used for capacity estimation.

4.1. mRPT-Based Validation

In Figure 6, a comparison is shown between experimental (true) and synthetically generated voltage cluster points corresponding to mRPTs 1, 5, 7, and 10. This provides the first metric for a level of confidence in utilization of the synthetic cluster points.

In

Table 1. mRPT mean square error comparison.

Test	1	5	7	10
MSE (%)	1.924	1.210	2.489	3.987

, the mean square error is shown between the true mRPT voltage cluster values and the synthetically generated cluster values. As has been the case with estimation results in our investigation into predicting capacity fade, as the capacity of the battery fades, estimation errors tend to increase (as seen in the case of test 10). Although this typically happens when the battery is entering a failure mode, and not during typical operation ranges, these error margins are deemed tolerable.

4.2. Capacity Estimation Using Synthetic Data

The final step in using the synthetically generated data utilizes the methodology outlined in [28], where drive cycle data are given as input to a network to predict features aligning with what an mRPT test would depict. Following this, the predicted features are fed to a network which is trained on the mRPT features and SoC behavior based on designed characteristics, or the beginning-of-life data. This approach provides a method to go from a drive cycle to a predicted capacity number.

As shown in Figure 7, the behavior of voltage centroids for one drive cycle is generated at three capacity points using a randomized current profile generated using the Markov process. The current profile is such that each pulse can discharge the battery by 3% SoC to 5% SoC, with some pulses having no discharge at all. The nature of the three plots depicts that when there is marginal capacity change (1.976 Ahr to 1.938 Ahr), relatively little variation results. But with a large drop (1.938 Ahr to 1.754 Ahr), significant and visible changes are observed, especially in the lower ranges of SoC.

In the next step, the three profiles generated are then fed to the feature generator [28], which generates the voltage centroids for an mRPT data structure. The output of this network is fed to a second network and capacity predictions are obtained. The results obtained are shown in

Table 2. Capacity estimation results in the SoC range of 50% to 10%.

Test No.	Estimated Capacity (Ahr)	True Capacity (Ahr)	% Error
1	1.981	1.976	0.25
5	1.967	1.938	1.49
10	1.645	1.754	6.21

.

The predictions related to the 10th test show a relatively large error of 6.21%, but this prediction is in a range where the battery pack has lost around 22% of its rated capacity. As has been discussed in [27], as a battery starts losing its capacity, its behavior starts becoming increasingly erratic, especially in terms of its open circuit voltage. This deterioration causes the battery to shift away from the patterns observed in RPT and mRPTs and consequently makes it challenging for neural networks to make predictions accurately. In order to reduce this error margin, the next step was to try and remove the large variations in the data observed after the 15th pulse and observe the estimation numbers. The results of this step are shown in

Table 3. Capacity estimation results in the SoC range of 50% to 10% with truncated data.

Test No.	Estimated Capacity (Ahr)	True Capacity (Ahr)	% Error
1	1.951	1.976	1.26
5	1.947	1.938	0.46
10	1.832	1.754	4.46

.

Reducing the data range did show some reduction in error margins for the tenth test without much effect on the first and fifth tests.

5. Application Discussion

Neglecting the SOH of a lithium-ion battery, or failure to monitor and maintain a reliable SOH, can have serious consequences. As the battery degrades over time, not only is capacity reduced, but the risk of failure increases, possibly leading to incidents such as thermal runaways and fire. Additionally, neglecting SOH can also result in a reduction in the overall performance and efficiency of the battery, reducing its usable life and leading to early replacement.

As a particular application area for this work, functional safety has emerged as a crucial concern in the utilization of second-life batteries, particularly in the EV automobile industry where partially used battery packs are available to be reused. Second-life lithium-ion batteries that can no longer be used as EV batteries are typically disqualified from use if they fall below 80% of the total usable capacity. However, a growing industry is focused on re-purposing lithium-ion batteries for less-demanding applications. For example, second-life batteries can be used for material handling vocations such as forklifts and golf carts, after a process of disassembly (of used packs) and reassembly (of repurposed packs).

The available data for such repurposed battery pack systems are inherently limited due to many factors, and ultimately must be appended. Such updating leads to the use of synthetically generating a candidate profile set for typical operation (such as in forklift use). For example, this would include one or more years of synthetically generated cycles where each cycle is defined as one charge and one discharge dataset of the forklift battery pack. In generating these synthetic profiles, the introduction of trends in reduced capacity and increased internal resistance can be easily accommodated. Doing this introduces an important aspect of expected aging.

Once a hazard and risk analysis is completed, and a failure mode evaluation follows, the process for synthetic data generation discussed in this article is very useful in estimating the SoH of second-life batteries. That is, synthetic data become crucial in utilizing mathematical models built from a combination of first principles and available data to characterize and ultimately predict system behavior in the presence of degradation and system faults. Such simulation allows for model performance evaluation and improvement based on available parameter sets. However, for simulations to be effective, the use of aging data through many cycles of use (charging and discharging) must be employed. The results of these simulations lead to quantifiable confidence levels and, ultimately, a formulation of algorithms for the prediction of system health. The outcome can be described as a framework for model-based functional safety system characterization.

6. Conclusions

As a method to address the issue of quality data availability, probabilistic and synthetic data generation is a concept with much promise. For this purpose, by the use of Markov chains, a concept has been demonstrated which can be used to combine multiple datasets in order to gain larger datasets which are beneficial to a multitude of machine learning implementations. Even with a large number of assumptions, the datasets generated can provide reproducible baseline testing datasets with potential on-board as well as cloud applications in battery applications.

Finally, the research reported in [2,26,27,28], culminating in this article, features a set of useful and promising results from a group of methodologies whereby simple ideas from machine learning and data science are used to not only reduce the amount of data required in the prediction of capacity fade, but also to shift reliance to more accessible data.

The research following this work is focused on several important off-shoots where packs can be looked at for fault detection and isolation, observation and estimation of other fade parameters such as impedance, exploration of simpler micro-controller implementations, incorporating cloud connectivity, and so on. The ultimate goal in capacity fade estimation and prediction of general SoH for battery packs is to be able to use typical drive cycle data for learning and prediction in automotive-grade packs on-board a battery management system in an EV. Moreover, current research by the authors utilizing the methodologies discussed in this article in the area of functional safety for second-life battery systems has led to an innovative model-based approach.