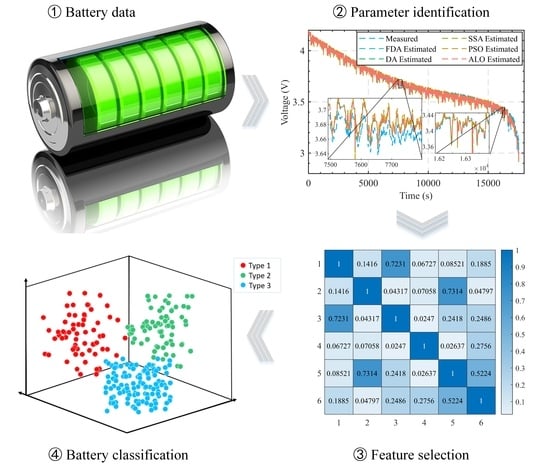
Classification of Lithium-Ion Batteries Based on Impedance Spectrum Features and an Improved K-Means Algorithm
Abstract
:1. Introduction
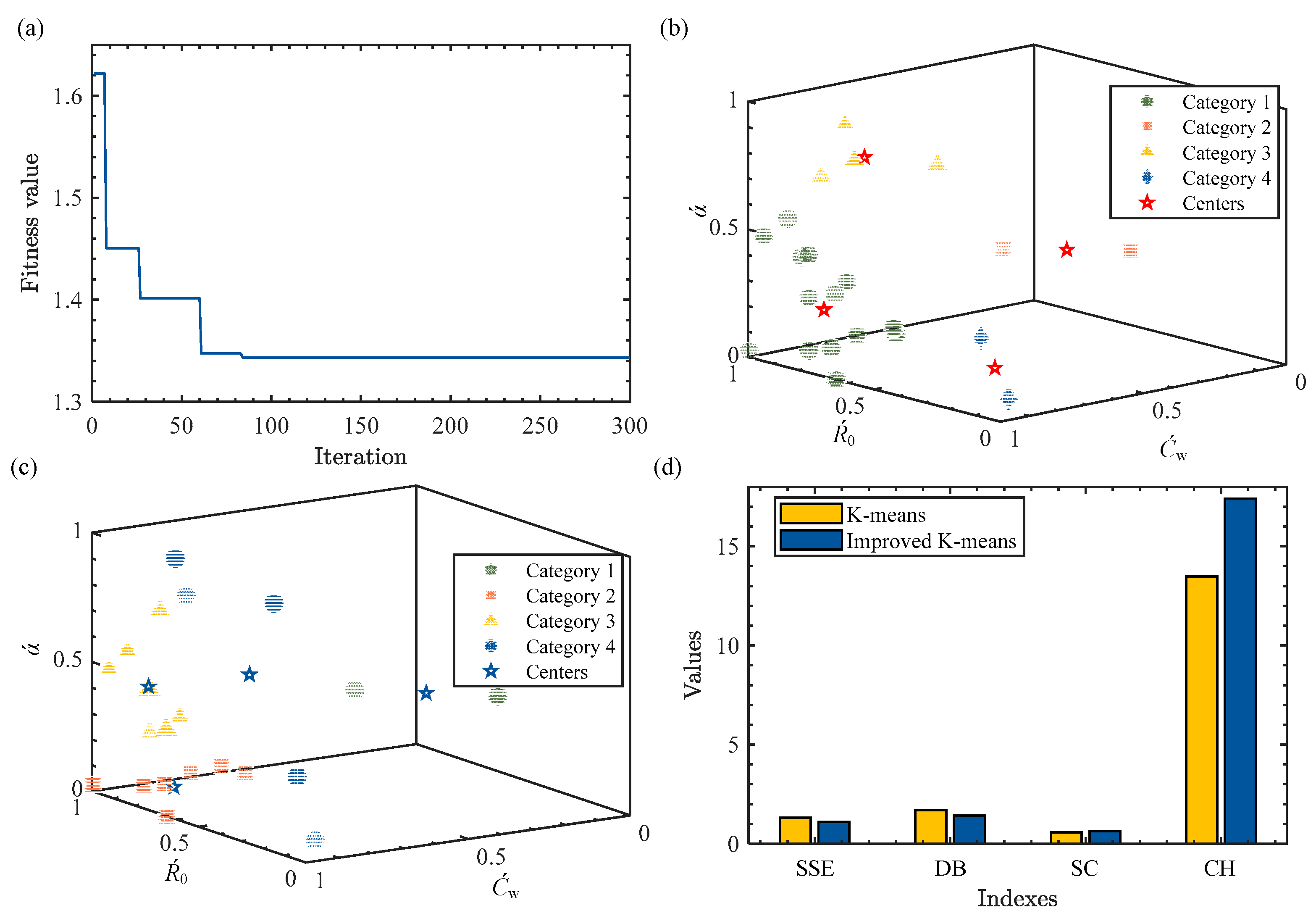
- (a)
- A parameter identification method for battery fractional order models is proposed, utilizing the FDA and compared with other optimization algorithms such as the dragonfly algorithm (DA), salp swarm algorithm (SSA), ant lion optimizer (ALO), and particle swarm optimization (PSO) algorithm. This method aims to effectively identify the parameters of fractional order models.
- (b)
- The correlation between battery model parameters is analyzed using Pearson correlation coefficients. These coefficients are then presented as thermodynamic diagrams to guide feature dimensionality reduction. This analysis helps to understand the relationships between different battery model parameters.
- (c)
- An improved K-means algorithm is introduced for battery classification. It employs the GWO algorithm to optimize the cluster centers. This adaptation addresses the issue of traditional K-means algorithms being highly sensitive to the initial cluster center selection.
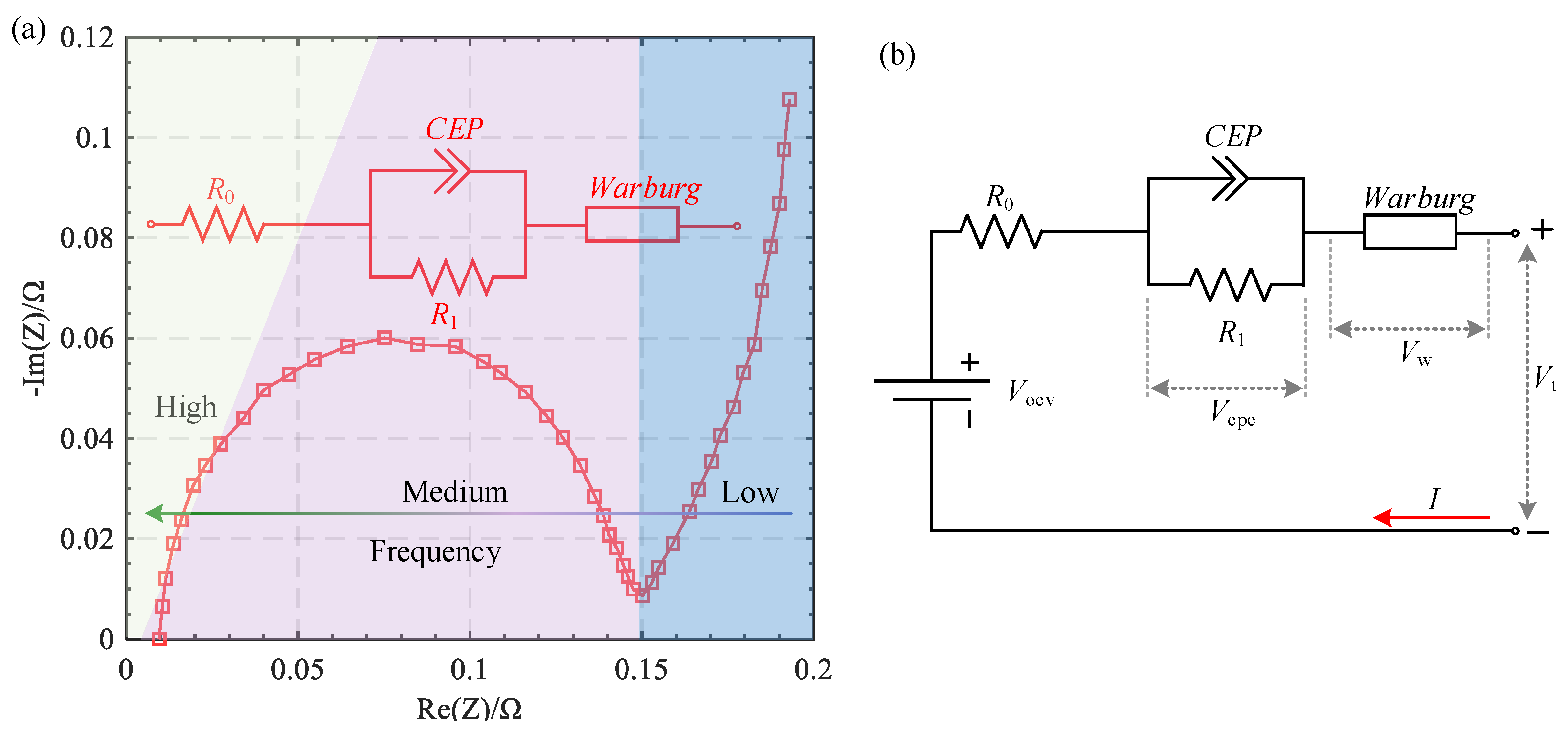
2. Battery Modeling
3. Parameter Identification
4. Experiments and Discussions
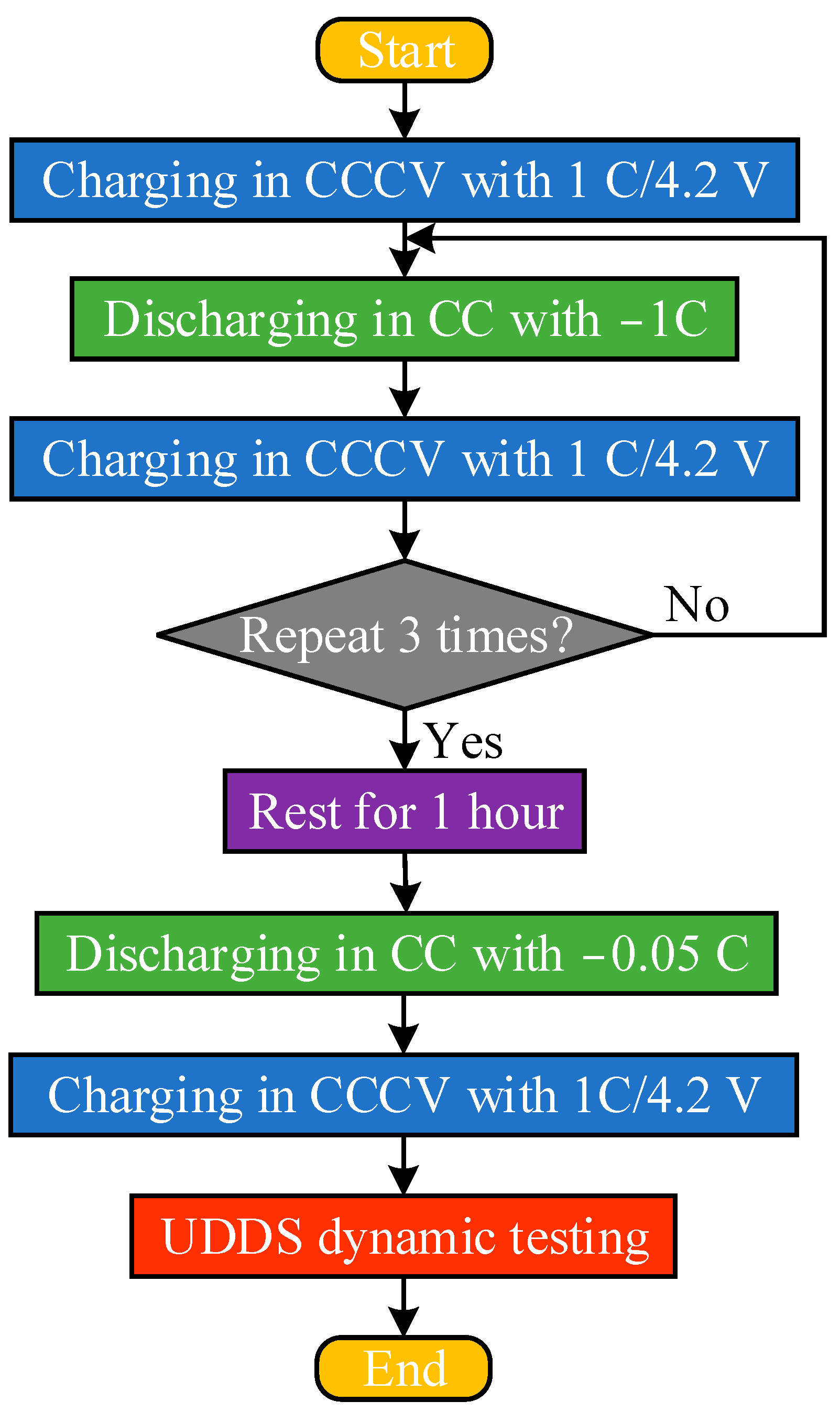
4.1. Experimental Platforms and Schemes
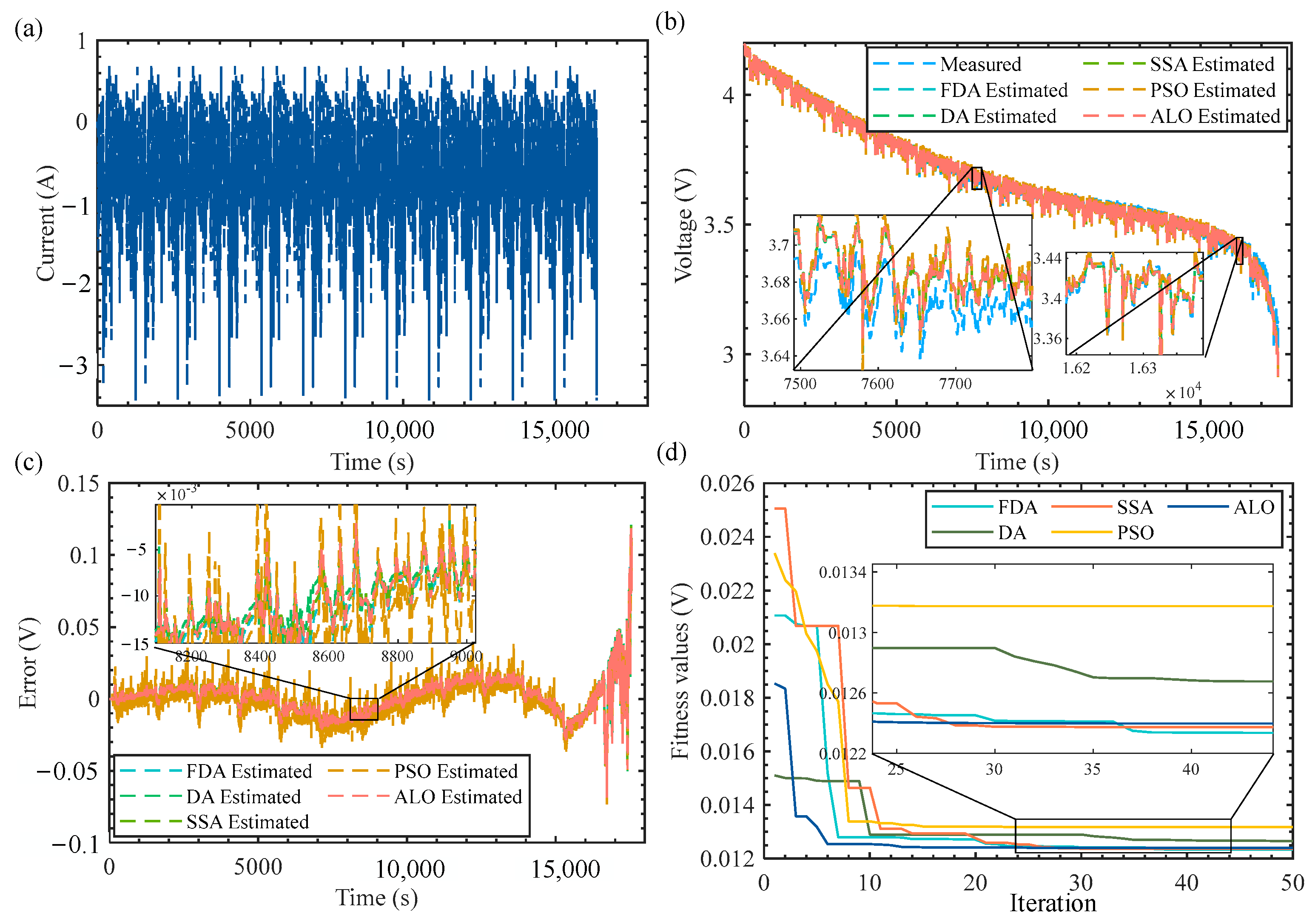
4.2. Parameter Identification and Validation
4.3. Clustering-Based Battery Classification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lyu, Z.; Zhang, Y.; Wang, G.; Gao, R. A semiparametric clustering method for the screening of retired Li-ion batteries from electric vehicles. J. Energy Storage 2023, 63, 107030. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, Y.; Li, D.; Cui, X.; Wang, L.; Li, L.; Wang, K. Electrochemical impedance spectroscopy: A new chapter in the fast and accurate estimation of the state of health for lithium-ion batteries. Energies 2023, 16, 1599. [Google Scholar] [CrossRef]
- Liu, X.; Chang, G.; Tian, J.; Wei, Z.; Zhang, X.; Wang, P. Flexible path planning-based reconfiguration strategy for maximum capacity utilization of battery pack. J. Energy Chem. 2023, 86, 362–372. [Google Scholar] [CrossRef]
- Lai, X.; Deng, C.; Tang, X.; Gao, F.; Han, X.; Zheng, Y. Soft clustering of retired lithium-ion batteries for the secondary utilization using Gaussian mixture model based on electrochemical impedance spectroscopy. J. Clean. Prod. 2022, 339, 130786. [Google Scholar] [CrossRef]
- Zhou, P.; He, Z.; Han, T.; Li, X.; Lai, X.; Yan, L.; Lv, T.; Xie, J.; Zheng, Y. A rapid classification method of the retired LiCoxNiyMn1−x−yO2 batteries for electric vehicles. Energy Rep. 2020, 6, 672–683. [Google Scholar] [CrossRef]
- Liu, C.; Tan, J.; Shi, H.; Wang, X. Lithium-ion cell screening with convolutional neural networks based on two-step time-series clustering and hybrid resampling for imbalanced data. IEEE Access 2018, 6, 59001–59014. [Google Scholar] [CrossRef]
- Liu, K.; Hu, X.; Zhou, H.; Tong, L.; Widanage, W.; Marco, J. Feature analyses and modeling of lithium-ion battery manufacturing based on random forest classification. IEEE/ASME Trans. Mechatron. 2021, 26, 2944–2955. [Google Scholar] [CrossRef]
- Marchetti, F.; Perracchione, E. Local-to-global support vector machines (LGSVMs). Pattern Recognit. 2022, 132, 108920. [Google Scholar] [CrossRef]
- Zhou, Z.; Duan, B.; Kang, Y.; Shang, Y.; Cui, N.; Chang, L.; Zhang, C. An efficient screening method for retired lithium-ion batteries based on support vector machine. J. Clean. Prod. 2020, 267, 121882. [Google Scholar] [CrossRef]
- Lai, X.; Huang, Y.; Deng, C.; Gu, H.; Han, X.; Zheng, Y.; Ouyang, M. Sorting, regrouping, and echelon utilization of the large-scale retired lithium batteries: A critical review. Renew. Sustain. Energy Rev. 2021, 146, 111162. [Google Scholar] [CrossRef]
- Tian, J.; Wang, Y.; Liu, C.; Chen, Z. Consistency evaluation and cluster analysis for lithium-ion battery pack in electric vehicles. Energy 2020, 194, 116944. [Google Scholar] [CrossRef]
- Tian, J.; Liu, X.; Chen, C.; Xiao, G.; Wang, Y.; Kang, Y.; Wang, P. Feature fusion-based inconsistency evaluation for battery pack: Improved gaussian mixture model. IEEE Trans. Intell. Transp. Syst. 2023, 24, 446–458. [Google Scholar] [CrossRef]
- Lai, X.; Deng, C.; Li, J.; Zhu, Z.; Han, X.; Zheng, Y. Rapid sorting and regrouping of retired lithium-ion battery modules for echelon utilization based on partial charging curves. IEEE Trans. Veh. Technol. 2021, 70, 1246–1254. [Google Scholar] [CrossRef]
- Zhou, Z.; Ran, A.; Chen, S.; Zhang, X.; Wei, G.; Li, B.; Kang, F.; Zhou, X.; Sun, H. A fast screening framework for second-life batteries based on an improved bisecting K-means algorithm combined with fast pulse test. J. Energy Storage 2020, 31, 101739. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, X.; Xiang, Y. An inconsistency assessment method for backup battery packs based on time-series clustering. J. Energy Storage 2020, 31, 101666. [Google Scholar] [CrossRef]
- Wang, L.; Ke, J.; Zhan, M.; Aina, T. Efficient and fast active equalization method for retired battery pack using wide voltage range bidirectional converter and DBSCAN clustering algorithm. IEEE Trans. Power Electron. 2022, 37, 13824–13833. [Google Scholar]
- Li, M.; Wang, L.; Wang, Y.; Chen, X.; Chen, Z. A framework for states co-estimation of hybrid energy storage systems based on fractional-order theory. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 224–233. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhu, J.; Jiang, B.; Wang, X.; Wei, X.; Dai, H. Insights on the degradation mechanism for large format prismatic graphite/LiFePO4 battery cycled under elevated temperature. J. Energy Storage 2023, 60, 106624. [Google Scholar] [CrossRef]
- Yu, Q.; Dai, L.; Xiong, R.; Chen, Z.; Zhang, X.; Sheng, W. Current sensor fault diagnosis method based on an improved equivalent circuit battery model. Appl. Energy 2022, 310, 118588. [Google Scholar] [CrossRef]
- Xiong, R.; Tian, J.; Shen, W.; Lu, J.; Sun, F. Semi-supervised estimation of capacity degradation for lithium ion batteries with electrochemical impedance spectroscopy. J. Energy Chem. 2023, 76, 404–413. [Google Scholar] [CrossRef]
- Singh, A.; Kim, M.; Meena, A.; Wi, T.; Lee, H.; Kim, K. Na/Al Codoped layered cathode with defects as bifunctional electrocatalyst for high-performance Li-ion battery and oxygen evolution reaction. Small 2021, 17, 2005605. [Google Scholar] [CrossRef]
- Du, X.; Meng, J.; Peng, J.; Peng, Q.; Wu, J.; Lin, M. A two-stage optimization framework for fast Lithium-ion battery impedance measurement. IEEE Trans. Power Electron. 2023, 38, 5659–5664. [Google Scholar] [CrossRef]
- Tang, X.; Lai, X.; Liu, Q.; Zheng, Y.; Zhou, Y.; Ma, Y.; Gao, F. Predicting battery impedance spectra from 10-second pulse tests under 10 Hz sampling rate. IScience 2023, 26, 106821. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, G.; Li, X.; Chen, Z. A fractional-order model-based state estimation approach for lithium-ion battery and ultra-capacitor hybrid power source system considering load trajectory. J. Power Sources 2020, 449, 227543. [Google Scholar] [CrossRef]
- Karami, H.; Anaraki, M.; Farzin, S.; Mirjalili, S. Flow direction algorithm (FDA): A novel optimizer approach for solving optimization problems. Comput. Ind. Eng. 2021, 156, 107224. [Google Scholar] [CrossRef]
- Liu, X.; Li, Y.; Kang, Y.; Zhao, G.; Dun, B.; Zhang, C. An accurate co-estimation of core temperature and state of charge for Lithium-ion batteries with electro-thermal model. IEEE J. Emerg. Sel. Top. Power Electron. 2023. [Google Scholar] [CrossRef]
- Wu, L.; Liu, K.; Liu, J.; Pang, H. Evaluating the heat generation characteristics of cylindrical lithium-ion battery considering the discharge rates and N/P ratio. J. Energy Storage 2023, 64, 107182. [Google Scholar] [CrossRef]
- Feng, F.; Song, B.; Xu, J.; Na, W.; Zhang, K.; Chai, Y. Multiple time scale state-of-charge and capacity-based equalisation strategy for lithium-ion battery pack with passive equalizer. J. Energy Storage 2022, 53, 105196. [Google Scholar] [CrossRef]
- Tang, X.; Zhou, Y.; Gao, F.; Lai, X. Joint estimation of state-of-charge and state-of-health for all cells in the battery pack using “leader-follower” strategy. Etransportation 2023, 15, 100213. [Google Scholar] [CrossRef]
- Lin, M.; You, Y.; Meng, J.; Wang, W.e.i.; Wu, J.; Stroe, D. Lithium-ion batteries SOH estimation with multimodal multilinear feature fusion. IEEE Trans. Energy Convers. 2023. [Google Scholar] [CrossRef]


| Require: The number of flows N, the maximum number of iterations Nmax, upper and lower bounds of decision variables bu, bl, etc. |
| 1. Initialize the positions of flows: |
| 2. Xf = [X1, X2, …, XN]T, Xi = [, , …, ] |
| 3. Calculate the fitness function for each flow. |
| 4. Ffit = [ffit,1, ffit,2, …, ffit,N] |
| 5. Sort the results and select the best result. |
| 6. Initialize the velocity of flows. |
| 7. Vmax = 0.1 × (bu − bl), Vmin = −0.1 × (bu − bl) |
| 8. For (niter = 1 to Nmax) do |
| 9. Update the nonlinear weight as Equation (18). |
| 10. For (i = 1 to α) do |
| 11. For (j = 1 to β) do |
| 12. Calculate the location of the ith flow as Equation (14). |
| 13. Calculate the neighborhood radius as Equation (15). |
| 14. Calculate the fitness value of neighbor flow Ffin,n(j). |
| 15. End for |
| 16. Sort position of neighborhoods as [~,indx] = sort(Ffin,n). |
| 17. If Ffin,n(indx(1)) < Ffin,f(i) |
| 18. Calculate the slope to the neighborhood as Equation (20). |
| 19. Update the velocity of each flow as Equation (19). |
| 20. If V < Vmin than |
| 21. V = −Vmin |
| 22. else V > Vmax than |
| 23. V = −Vmax |
| 24. End if |
| 25. Flow moves to the best neighborhood as Equation (21). |
| 26. Flow moves to rth flow as Equation (22). |
| 27. End for |
| 28. Calculate the fitness function of new flow Ffit,f,new(i). |
| 29. If Ffit,f,new(i) < Ffit,f(i) |
| 30. Xf(i) = Xf,new(i) |
| 31. Ffit,l(i) = Ffit,f,new(i) |
| 32. End if |
| 33. If Ffit,l(i) < Ffit,best |
| 34. Xbest = Xfit,l(i) |
| 35. Ffit,best = Ffit,l(i) |
| 36. End if |
| 37. End for |
| Parameters | Values | Units |
|---|---|---|
| Nominal capacity | 2500 | mAh |
| Nominal voltage | 3.6 | V |
| Maximum charge voltage | 4.2 | V |
| Minimum discharge voltage | 3.0 | V |
| Operating temperature | −20~+60 | °C |
| Cathode material | Nickel-cobalt-manganese | - |
| Anode material | Graphite | - |
| Coefficients | k0 | k1 | k2 | k3 | k4 |
|---|---|---|---|---|---|
| Values | 3.9194 | −0.8259 | 1.1141 | 0.1656 | 0.0062 |
| Boundary | R0 (Ω) | R1 (Ω) | Ccpe (F/sα) | Cw (F/sβ) | α | β |
|---|---|---|---|---|---|---|
| Lower | 0.05 | 0.05 | 50 | 50 | 0.3 | 0.3 |
| Upper | 0.5 | 0.7 | 120 | 4000 | 1.0 | 1.0 |
| Algorithms | R0 (Ω) | R1 (Ω) | Ccpe (F/sα) | Cw (F/sβ) | α | β | RMSE/V | MAE/V |
|---|---|---|---|---|---|---|---|---|
| FDA | 0.0186 | 0.0215 | 97.12 | 3801.34 | 0.539 | 0.303 | 0.0123 | 0.0087 |
| DA | 0.0230 | 0.0201 | 19.37 | 1039.32 | 0.302 | 0.430 | 0.0126 | 0.0091 |
| SSA | 0.0141 | 0.0246 | 51.40 | 1407.23 | 0.415 | 0.320 | 0.0123 | 0.0088 |
| PSO | 0.0350 | 0.2054 | 100.94 | 3901.52 | 0.301 | 0.308 | 0.0131 | 0.0093 |
| ALO | 0.0072 | 0.0252 | 20.020 | 630.90 | 0.470 | 0.322 | 0.0124 | 0.0088 |
| Cell | R0 (Ω) | R1 (Ω) | Ccpe (F/sα) | Cw (F/sβ) | α | β |
|---|---|---|---|---|---|---|
| 1# | 0.0198 | 0.0198 | 99.75 | 3986.39 | 0.362 | 0.769 |
| 2# | 0.0186 | 0.0215 | 97.12 | 3801.34 | 0.5393 | 0.3026 |
| 3# | 0.0181 | 0.0245 | 95.98 | 1924.54 | 0.5561 | 0.3049 |
| 4# | 0.0165 | 0.0276 | 89.21 | 3716.70 | 0.4473 | 0.3130 |
| 5# | 0.0183 | 0.0239 | 90.52 | 3999.86 | 0.3072 | 0.7709 |
| 6# | 0.0229 | 0.0284 | 95.99 | 3989.25 | 0.3223 | 0.7604 |
| 7# | 0.0184 | 0.0241 | 96.68 | 3994.72 | 0.3066 | 0.7596 |
| 8# | 0.0098 | 0.0303 | 32.23 | 3894.95 | 0.3602 | 0.3040 |
| 9# | 0.0122 | 0.0261 | 40.00 | 3655.87 | 0.4752 | 0.3254 |
| 10# | 0.0185 | 0.0261 | 92.83 | 3971.76 | 0.5183 | 0.3387 |
| 11# | 0.0181 | 0.0134 | 61.37 | 3823.72 | 0.8489 | 0.3053 |
| 12# | 0.0190 | 0.0360 | 94.36 | 3899.55 | 0.3749 | 0.3019 |
| 13# | 0.0212 | 0.0153 | 94.04 | 3912.60 | 0.6721 | 0.3142 |
| 14# | 0.0179 | 0.0185 | 90.08 | 351.67 | 0.4921 | 0.3047 |
| 15# | 0.0203 | 0.0463 | 85.69 | 2754.04 | 0.3486 | 0.3128 |
| 16# | 0.0203 | 0.0151 | 94.36 | 3709.59 | 0.7767 | 0.3103 |
| 17# | 0.0181 | 0.0022 | 86.21 | 3943.02 | 0.9457 | 0.3004 |
| 18# | 0.0217 | 0.0245 | 93.80 | 3605.42 | 0.5573 | 0.3099 |
| 19# | 0.0209 | 0.0267 | 96.61 | 3718.61 | 0.4681 | 0.3188 |
| 20# | 0.0210 | 0.0209 | 94.63 | 3702.66 | 0.5748 | 0.3053 |
| 21# | 0.0184 | 0.0278 | 98.47 | 3717.06 | 0.4050 | 0.3028 |
| 22# | 0.0228 | 0.0125 | 93.51 | 3825.61 | 0.6030 | 0.3327 |
| 23# | 0.0170 | 0.0217 | 22.88 | 3037.73 | 0.8204 | 0.3013 |
| 1: Initialize the number of cluster centers K, generate K grey wolves (cluster centers) randomly, and calculate initial fitness. |
| 2: Determine the current optimal Alpha Grey Wolves, suboptimal Beta Grey Wolves, and third-best Delta Grey Wolves based on their fitness. |
| 3: The positions of other wolves are updated based on the positions of Alpha, Beta, and Delta Grey Wolves. |
| 4: Recalculate the fitness of each grey wolf based on its new location. |
| 5: If the termination condition is met (reaching the maximum number of iterations or fitness reaching a threshold), the algorithm ends. Otherwise, return to Step 3. |
| 6: The output result shows that the final Alpha Grey Wolf position is the optimized K-means clustering center. |
| Algorithms | SSE | DB | SC | CH |
|---|---|---|---|---|
| K-means | 1.3186 | 1.6985 | 0.5642 | 13.4763 |
| Improved K-means | 1.1002 | 1.4187 | 0.6314 | 17.4081 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Tian, J.; Yan, Z.; Li, X.; Pan, T. Classification of Lithium-Ion Batteries Based on Impedance Spectrum Features and an Improved K-Means Algorithm. Batteries 2023, 9, 491. https://doi.org/10.3390/batteries9100491
Zhang Q, Tian J, Yan Z, Li X, Pan T. Classification of Lithium-Ion Batteries Based on Impedance Spectrum Features and an Improved K-Means Algorithm. Batteries. 2023; 9(10):491. https://doi.org/10.3390/batteries9100491
Chicago/Turabian StyleZhang, Qingping, Jiaqiang Tian, Zhenhua Yan, Xiuguang Li, and Tianhong Pan. 2023. "Classification of Lithium-Ion Batteries Based on Impedance Spectrum Features and an Improved K-Means Algorithm" Batteries 9, no. 10: 491. https://doi.org/10.3390/batteries9100491
APA StyleZhang, Q., Tian, J., Yan, Z., Li, X., & Pan, T. (2023). Classification of Lithium-Ion Batteries Based on Impedance Spectrum Features and an Improved K-Means Algorithm. Batteries, 9(10), 491. https://doi.org/10.3390/batteries9100491