Abstract
Quinones are one of the most promising and widely investigated classes of redox active materials for organic aqueous redox flow batteries. However, quinone-based flow batteries still lack the necessary performance in terms of metrics, such as specific capacity, power density, and long-term stability, to achieve mass market adoption. These performance metrics are directly related to the physicochemical properties of the quinone molecules, including their equilibrium redox potential, aqueous solubility, and chemical stability. Given the enormous chemical and configurational space of possible quinones and the high tunability of their properties, there has been a recent surge in the use of high-throughput virtual screening (HTVS) for the rational design and discovery of new high-performing molecules. In this review article, HTVS efforts for the computational design and discovery of quinones are reviewed with a special focus on the enumerated space of core quinone motif, the methods and approximations used for the estimation of performance descriptors, and the emergent structure-property relationships. The knowledge and methodological gaps in conventional HTVS efforts are discussed, and strategies for improvement are suggested.
1. Introduction
The ever-increasing energy requirements caused by global population growth and economic growth have resulted in high consumption of fossil fuels, environmental damage, and subsequent climate change. Although the costs of renewable solar and wind energy have decreased over the last decade, their intermittent nature remains a significant issue, especially when combined with the fact that energy demand fluctuates both temporally and regionally. This has prompted the development of grid-scale energy storage systems to balance the fluctuating supply of energy and user demands.
Due to their scalability and distinctive design, which allows for the decoupling of their power and energy output [,,], aqueous redox flow batteries (ARFBs) are among the most promising next-generation grid-scale energy storage devices. The chemical energy in ARFBs is provided by redox active materials dissolved in water and stored in external tanks, as shown schematically in Figure 1 below (adapted from ref. []), so a continuous circulation of the redox active materials using pumps is necessary to sustain the chemical reaction, similar to a fuel cell. Similar to a battery, the system can be charged and discharged because the related redox reactions are reversible.
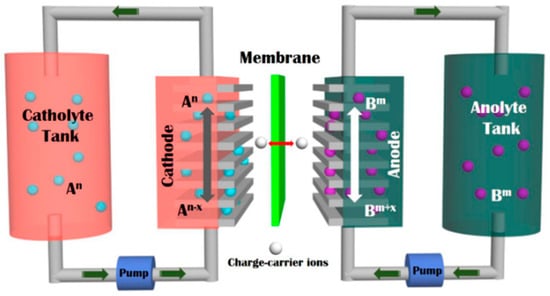
Figure 1.
Schematic showing a typical redox flow battery with the tanks containing the dissolved catholyte (also known as posolyte) and the anolyte (also known as negolyte) materials. The electrolytes at each electrode are circulated using pumps. Reprinted with permission from Ref. []. 2022, Elsevier.
The development of next-generation ARFBs with high cell voltage, energy density, power density, and long life depends on finding redox active materials (RAMs) with high redox potential, high aqueous solubility, high stability, and rapid redox kinetics [,,]. Satisfying these fundamental material requirements will form the foundation on which further cell- and pack-level optimization can be performed to bring ARFBs from the lab to the market. While vanadium ARFBs have taken the lead in commercialization among available technologies, they are still prohibitively expensive [] and suffer from low rate kinetics and long-term stability issues []. Inorganic alternatives based on iron [] and zinc [] offer potentially much lower costs; however, the increased complexity of these storage concepts (e.g., in hybrid flow batteries and metal-air systems) [] due to the involvement of gas-phase active species and the propensity of metal deposition decreases the efficiency and operating lifetime significantly when compared to vanadium ARFBs.
In this regard, organic molecules have emerged [,,] as an attractive alternate class of RAMs for ARFBs because: (I) They are composed of only earth-abundant elements, which implies potentially much lower costs. (II) They allow a high degree of tunability of their physicochemical properties, which implies an immense potential to achieve high theoretical capacities, energy and power densities, and long-term stability. (III) They offer a huge amount of flexibility in the use of multielectron-transfer RAMs without the complications that are typically associated with inorganic multivalent ions []. Various ARFB performance metrics, such as energy and power density, energy and charge capacity, efficiency (voltaic, coulombic), and capacity fade rate, are controlled by the physicochemical properties of organic RAMs, membranes, and electrodes. The physicochemical properties that influence these performance metrics are listed below in Table 1. A more detailed account of these relations can be found in recent review articles by Fisher et al. [], Ding et al. [], and Cao et al. [].

Table 1.
List of key physicochemical properties of redox active materials and the aqueous redox flow battery performance metrics that depend on them. Information obtained from Fisher et al. [], Ding et al. [], and Cao et al. [].
The molecular structure of organic RAMs has a decisive influence on these properties, including redox potential, aqueous solubility, stability, electrochemical kinetics, synthesizability, and toxicity. This degree of freedom has been extensively utilized in both experimental and theoretical investigations of organic RAMs [,,] by making systematic modifications to the molecular structures and analyzing their effects on ARFB performance.
Significant strides in organic ARFBs have been made in recent years, yet they must still undergo substantial research and development to achieve large-scale commercialization. There are several problems in employing organic RAMs in redox flow batteries, which include low energy density, low stability, insufficient rate kinetics, and high permeation through membranes, leading to irreversible capacity fade. Some of these problems are highly intrinsic to the molecular structure of organic RAMs and must be addressed at the molecular scale. According to the recent review by Fischer et al. [], the first such problem with using organic RAMs is their comparably low energy density [], which hardly exceeds 13 Wh/L compared to the state-of-the-art vanadium ARFBs (≈25–35 Wh/L) and zinc-bromine ARFBs (≈70 Wh/L). The reason for this has been pointed out to be the typically higher concentration of the inorganic RAMs and the battery voltage [,]. The second problem with using organic RAMs (arguably far more critical in the long-term than the first problem) is their instability, which has several aspects ranging from chemical and electrochemical [,] to calendar-life [] stability. For the majority of mechanisms that cause instability, the degradation of the organic molecule leads to irreversible capacity losses. In this regard, the reader is pointed to some excellent reviews published in the last few years, which cover a lot of ground in describing the underlying mechanisms of degradation [,,].
Given the vast chemical space of possible organic molecules, many different classes have been proposed and investigated [,,], including carbonyls (quinones, fluorenone, and indigo carmine), nitroxide radicals (TEMPO), viologens, aza-aromatics (phenazine, alloxazine, and phenothiazine), and metallocene complexes. Among these, classes, such as carbonyls [,,,,,,,,,] and aza-aromatics [,,,,,] have aromatic π systems that offer much higher stability and electrochemical reversibility compared to others because they can delocalize the radical ionic states during the redox reactions.
Among all the tested classes of organic molecules, quinones are one of the most widely investigated because they have shown great promise in ARFBs [] due to the tuneability of their properties as both low-potential electrolytes (negolytes) and high-potential electrolytes (catholytes). Quinones are found in fungi, algae, bacteria, plants, and animals in various forms depending on the aromatic ring structure, size, sidechain (substituent) groups, etc. The chemical motif common to all quinones is the 6-membered ring system, in which carbonyl groups (–C=O) can be placed in para or ortho positions, depending on where the carbon atom belongs in the ring.
The chemical space of possible quinones (~106) offers a huge potential for the discovery and rational design of high-performing candidates that can eventually enable ARFB commercialization. Even the most advanced experimental screening techniques cannot screen such a large chemical space for the best candidates. However, the inherently parallel nature of the material screening problem coupled with recent advances in parallel computing and distribution techniques have given rise to the idea of high-throughput virtual screening (HTVS) []. The central idea of HTVS is to screen out a large number of different materials enumerated in a virtual library as rapidly (and time efficient) as possible, with maximally autonomous workflows for screening the best candidates. HTVS involves the use of “funnels”, such that each funnel is typically associated with a performance descriptor, which is related to one or more ARFB performance metrics. As screening proceeds, some candidate materials are eliminated at each level of the hierarchy in the funnel, depending on a descriptor screening criterion. The effectiveness of any HTVS effort in finding new material candidates that beat the state-of-the-art depends on a few crucial factors: (1) the size and diversity of the starting virtual library of candidates, (2) the accuracy and rapidity with which the performance descriptors can be calculated, and (3) the extraction of principles for the rational design of new candidates that emerge from structure–property and property–property correlations.
The HTVS approach for quinones is shown schematically in Figure 2. It begins with the creation of a comprehensive virtual library of candidate molecules. This is typically performed by substituting hydrogen positions on core “backbone” rings with various substituent (or functional) groups and/or by substituting the carbon atoms in the rings with heterocyclic atoms. The candidates in the virtual library are then screened based on the values of their performance descriptors (redox potentials, aqueous solubility, chemical, and electrochemical stability, rate kinetics, synthetic accessibility, etc.), each of which is directly related to one or more ARFB performance metrics (volumetric capacity, energy and power density, capacity fade rate, etc.). The final set of screened molecules at the end of the funnel represents the “best” candidates that are worthy of further experimental validation. HTVS efforts for quinones for ARFBs [,,,,,,,,] have not only led to the discovery of new high-performing candidates but also have elucidated several molecular design principles that are not intuitive, and which can be used to aid future rational design and discovery efforts.
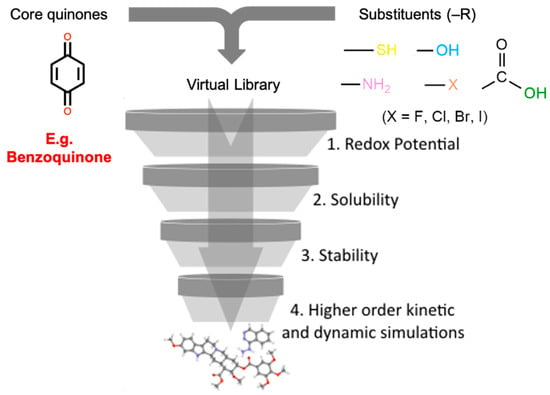
Figure 2.
Schematic diagram of the typical implementation of an HTVS of quinones with sequential funnels associated with performance descriptors.
As is evident from the aforementioned literature references, there are already a huge number of review articles on the performance and status of organic RAMs. In this article, HTVS efforts for the computational design and discovery of quinones are reviewed with a special focus on the enumerated space of core quinone motifs, the methods used for the estimation of performance descriptors, and the emergent structure-property relationships. The main objective of this article is to inform researchers who are new to this field about the choice of available methods for quinone HTVS and their effectiveness, and to point out specific ways in which the overall HTVS strategy needs to be improved. Another objective is to summarize the discovered structure-property relationships and design principles for researchers who may use them to optimize the performance of quinones in experiments. This article does not address the general topic of high-throughput and machine learning-based prediction of redox potentials, aqueous solubility, or other physicochemical properties of organic compounds, which can be found elsewhere [,,,,,,,]. As will be evident in the following, a majority of current HTVS efforts for quinones focus on the first problem of low nominal voltage and concentration of quinone ARFBs. In this regard, the applied methods for theoretical predictions of the redox potential and aqueous solubility are reviewed in greater detail. A list of all the abbreviations and mathematical symbols used in this article is given in Table 2.

Table 2.
List of abbreviations and mathematical symbols and their meanings.
2. Redox Potential
The cell voltage is a metric of utmost importance as it is directly proportional to the energy density and energy capacity of the ARFB [,,]. The cell voltage is related to the equilibrium redox potential of the RAM. From a theoretical standpoint, the redox potential is arguably the most extensively investigated property of quinones. This is in part due to their versatility as the RAM in both aqueous [,,,,,,] and nonaqueous [,,,,,] flow batteries, as well as the electrode [] in organic Li-ion batteries. The redox potential of quinones can be tuned by structural functionalization, i.e., by substituting electron-withdrawing groups (EWGs) and electron-donating groups (EDGs) into the core structure. In general, adding electron-donating groups shifts the redox potential in the negative direction, and vice versa [].
Another decisive factor that influences the redox potential is the electrolyte’s value during operation. Depending on the , the production or transport of either hydronium () or hydroxy () ions can change their concentrations by a large amount. As a result, the equilibrium voltage might shift significantly during the redox reaction, or charge accumulation can occur, which can change the redox chemistry in an undesirable way [].
Theoretical predictions: Redox potentials are defined in the context of reversible redox reactions at equilibrium and are related to the Gibbs free energy of change of the reaction through the Nernst Equation []. The redox reactions of quinones proceed via the change in the formal oxidation state of oxygen atoms in the carbonyl groups that get protonated. Depending on the of the solution and the type of solvent, quinones can undergo either a two- reduction, a two-/one- reduction, or a two-/two- reduction, which is also called proton-coupled-electron-transfer (PCET) mechanism []. For purposes of computational chemistry-based predictions, however, the PCET mechanism for quinones is widely accepted in the literature, especially in acidic aqueous environments. For the reduction of a solvated quinone molecule to upon transfer of electrons () and protons (), the redox reaction is given as:
The Gibbs free energy change in the reaction, , at temperature, , can be expressed as:
where the terms represent the standard (Gibbs) free energies of formation, the terms in square brackets represent activities, is the Faraday constant, and the free energy of the electron at the electrode, which is at equilibrium redox potential , has been expressed in terms of its electrochemical potential . At equilibrium, , therefore:
This general form of the redox potential does not take into account any kinetic phenomena or the order of transfer. It assumes that the reduced and oxidized forms are thermodynamically stable, and do not involve radicals and open-shell calculations. In addition, this form assumes a single-step transfer of all and . In a more general, multi-step scheme, the second term in Equation (3) is often reported in terms of the acid dissociation constants () of the reaction intermediates [,,]. The general / transfer scheme (adopted from []) is depicted in Figure 3a, which also shows a typical Pourbaix diagram (Figure 3b) of the quinone redox potential as a function of the .
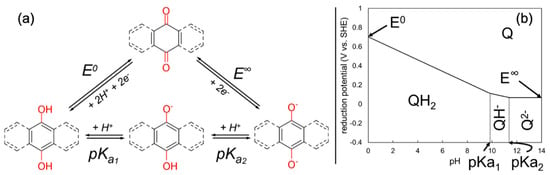
Figure 3.
(a) Redox and acid−base equilibria between benzoquinone () and hydroquinone in acid ( ), along with their monodeprotonated ( ) or dideprotonated ( ) forms. (b) Typical Pourbaix diagram of the redox couple, where the regions are marked by the thermodynamically most stable acido−basic forms in the entire pH range. Figure adapted from Gaudin et al. [] (under Creative Commons Attribution 4.0).
At standard conditions (), this general form reduces to the well-known form of the Nernst equation:
Using techniques from computational chemistry and statistical thermodynamics, it is possible to theoretically estimate the standard free energy change during the redox reaction . Many models are now available in the literature that allow for quantitative predictions of reduction potentials [] by treating the effect of the solvent either implicitly (as a continuum dielectric) or explicitly (e.g., by including water molecules in the solvation shell).
In practice, the calculated redox potentials are often reported not in absolute terms but rather with reference to a known standard reference electrode. An additional benefit of using a reference is that it enables the use of isodesmic reaction schemes. As the experimental value of the reference electrode is known, the difference between the experimental and calculated values for the reference species yields correction terms, which can be then added to the predicted value of the molecule of interest. For the case of quinones in ARFBs, the standard hydrogen electrode (SHE: ) is the most popular choice for the standard reference electrode. The standard redox potential relative to SHE, , can be understood in a straightforward manner as follows:
For a typical two-/two- (PCET) reduction in quinones in water, . Therefore, Equation (5) takes a form that lends itself very suitably to calculations, given by:
where the explicit calculation of is avoided and all the other free energies of formation can be calculated using any one of the numerous modern computational chemistry codes. Nevertheless, predicting the free energies of the formation of the molecules in aqueous media is not entirely free of error. Commonly used computational chemistry models have well-known limitations of either ignoring or not accurately accounting for contributions from explicit solvation and reorganization, entropic, zero-point, and nonelectrostatic effects. Often in practice, either the solvation (electrostatic, reorganization, cavitation, etc.) or thermal (entropic, zero-point) contributions or both are added separately as correction terms () to the internal energy (), both of which can be calculated using DFT. In this way, the Gibbs formation energy terms are approximated as . This results in a less accurate yet highly effective way to rapidly estimate redox potentials given by:
This formulation works rather well in practice because of the serendipitous cancellation of errors in the correction terms in Equation (7). As will be discussed in the following, various studies have assigned different degrees of importance to the factors influencing the correction terms. While some ignore it entirely, others take into account both the solvation and the thermal contributions. However, there exist disagreements in the literature about the relative importance of these contributions. A natural strategy that has been adopted to overcome these limitations, while maintaining predictability, is to use experimental redox potential data for fitting the parameters of a simplified linear equation:
where and are simply the slope and intercept of the linear calibration model. Ideally, and should be determined by fitting experimental data obtained under consistent conditions with respect to the type of electrode, supporting electrolyte, concentration, temperature, scan rate, etc. Lastly, an even simpler set of descriptors are the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energy levels for direct prediction of the redox potentials []. From a mechanistic standpoint, it is clear to understand that the reduction in indicates transfer from the Fermi level at the electrode to its LUMO level, and the oxidation in indicates transfer from its HOMO level to the Fermi level at the electrode. The limiting Fermi level is determined by the redox potential. Similar to Equation (8), the HOMO/LUMO levels can be approximately related to the redox potential as:
where the constants are obtained by fitting experimental data. Irrespective of the chosen level of approximation, the inherent accuracy of predicting redox potential is significantly affected by the chosen method for calculating internal and free energies.
Some theoretically rigorous approaches for predicting free energies of the reactants and products in the aqueous phase are: (a) performing molecular dynamics (MD) simulations over a long enough simulation time, followed by thermodynamic integration [,] to obtain , or (b) sampling the system over a large number of microstates and performing ensemble averaging to predict the []. The accuracy of this approach is also affected by the choice of the interatomic potentials for energy calculations and the algorithms used for sampling. However, by design, this approach includes the contributions of explicit solvation, entropic, nonelectrostatic, and ion-pairing effects [] without necessarily resorting to fitting or heuristics.
Liu et al. [] predicted the redox potential of three quinone molecules using first-principles MD and then performed an integration of the vertical energy gap [,]. The first-principles MD simulations were performed using the BLYP exchange-correlation functional and the computationally expensive hybrid HSE06 functional. They found that the BLYP-driven MD simulations produced much higher errors (0.2–0.7 V) compared to the HSE06-driven MD simulations, which were an order of magnitude lower (0.02–0.09 V) with respect to experiments. It must be noted that their production simulations were run for only a small timespan of 6.0 ps after equilibration for 2.0 ps, which was likely due to computing time limitations associated with first-principles MD. While the appropriate MD simulation time depends on the characteristic relaxation time for a given system, 6.0 ps is not a large time window to get robust statistics, which could explain these relatively high errors despite using first-principles MD.
Kim et al. [] created one of the earliest attempts to include explicit solvation effects in the prediction of redox potentials of quinones using quantum mechanics/molecular mechanics (QM/MM) simulations and compared their predictions to those of DFT calculations with the polarizable continuum model (PCM) of implicit solvation. They found that the DFT (PCM) model predicts the redox potentials of 16 out of 19 anthraquinones with a low mean absolute deviation (MAD) of 0.037 V. However, it is highly erroneous (MAD of 0.194 V) for three redox couples that have either group positioned for intramolecular hydrogen bonding that are not balanced with the intermolecular H-bonding of the solvent. The QM/MM simulations, which include explicit water molecules, were found to account for these imbalances, thereby reducing the MAD to 0.033 V. The best linear fit between their theoretical predictions and experiments was found to have an R2 = 0.835. This accuracy has been improved by later prediction models that do not use computationally expensive QM/MM simulations.
A more recent study by Yu et al. [] also used first-principles MD followed by thermodynamic integration to calculate the redox potentials of quinones and their derivatives. They used a multistep scheme in which the MD trajectories were first generated using the relatively cheaper functional BLYP, and then the configurations from the trajectories were computed with higher-level functional HSE06 and Grimme’s D3 van der Waals corrections for subsequent use in thermodynamic integration. Their scheme yielded quite a low MAD (0.028 V) for 12 quinones. They also used a gas phase model akin to Equation (7) and fit the constants of the linear equation to their first-principles MD results and found an overall MAD of 0.097 V, which is over three times that of the MD results versus the experiments. Nevertheless, this deviation is within typical DFT errors (0.1 V), which explains very well why the linear model has been used extensively and effectively in the literature by fitting it to experimental data. Interestingly, the authors also used only 5 ps of MD sampling time, but with added van der Waals corrections, higher energy cutoffs, and better thermostats compared to that of Liu et al. []. The first-principles MD approach has not found much traction in practice, not only because it is several orders of magnitude more computationally expensive than other approaches but also because simple linear models are already quite effective within the range of acceptable errors, as is discussed in the following.
Zhang et al. [] performed a systematic comparison of several computational chemistry methods to point out strategies that balance the trade-offs between prediction accuracy and computational cost. They employed nine (AM1, MNDO, MNDOD, PM3, PM6, PM6-D3, PM6-D3H4X, PM7, and RM1) semiempirical quantum mechanics (SEQM) methods, two (GFN1-xTB, DFTB-D3) density functional-based tight binding (DFTB) methods, and seven (LDA, PBE, BLYP, B3LYP, PBE0, HSE06, and M08-HX) DFT functionals for performing calculations as various levels of approximations corresponding to Equations (7) and (8), as also shown schematically in Figure 4a. They performed geometry optimization and predicted formation energies at different levels of theory (SEQM, DFTB, and DFT) both with and without the effect of implicit solvation. By fitting the coefficients of Equation (8) to experimental data on 43 quinones that have been studied experimentally in ARFBs, Zhang et al. [] inferred the following: (I) the inclusion of implicit solvation effects within the Poisson Boltzmann Formalism (PBF) reduced the root mean squared error (RMSE) across all levels of theory by 0.02 V, (II) while (I) is hardly surprising, it was also found that molecular geometry optimization with implicit solvation consistently leads to higher errors and a better strategy is needed to perform geometry optimization in the gas phase followed by single point formation energy calculations of with implicit solvation, (III) there is no significant effect of using zero-point and or dispersion corrections on the prediction accuracy at any DFT level of theory. Their work showed that at the DFT level, the PBE functional, which has little to no empiricism in its design, offers the best compromise between prediction accuracy (RMSE = 0.051 V) and computational cost. Notably, the computationally more demanding functional M08-HX performs best (RMSE = 0.044 V) among the selected functionals, as it is heavily parametrized to show good performance for thermochemistry. Most importantly, a comparison across all methods and approaches showed that DFTB-D3, which is at least three orders of magnitude computationally cheaper than DFT (PBE), can offer reasonable accuracy (RMSE = 0.072 V) and is most suitable for HTVS.
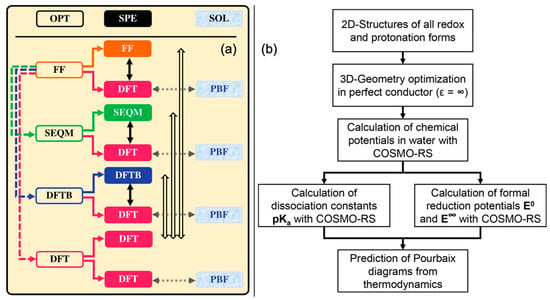
Figure 4.
(a) Schematic diagram showing the workflow for geometry optimization (OPT) and single point energy (SPE) calculations at various levels of theory used by Zhang et al. [] (Figure adapted from Ref. [] under Creative Commons Attribution 4.0). The hollow arrows denote the differences between gas-phase reaction energies obtained at different levels of theory. The solid black arrows denote the differences between energy computed using DFT on a fixed geometry obtained from a lower-level preceding theory and the geometry computed at that lower-level preceding theory. The dotted gray arrows represent the solvation effect from gas-phase SPE to solution-phase SPE when the implicit solvation model is considered. (b) Methodology of prediction of Pourbaix diagrams from COSMO-RS employed in the work of Gaudin et al. []. (Figure adapted from Ref. [] under Creative Commons Attribution 4.0).
A recent effort by Fornari et al. [] also performed extensive analyses of the various factors affecting the accuracy of redox potential predictions, with a special focus on the treatment of the deprotonated state of quinones at high . They chose B3LYP as their standard method for the calculation of formation energies along with the COSMO implicit solvation method, and their results had both similarities and dissimilarities with previous reports. Notably, they found that B3LYP performed even better than the composite G4MP2, the double hybrid rev-DOD-BLYP-D4, and the meta-hybrid M06-2X-D3 functionals by a significant amount (0.1 V). They compared COSMO-based predictions to the predictions from the SM12 solvation model and found only systematic differences in the order of 0.1 V, which could be removed by recalibrating the linear fit. To understand the deficiencies across implicit solvation models, they employed a cluster continuum approach with explicit water molecules to account for solvation. Using this approach, they were able to reduce the error for an outlier molecule from 0.43 V to as much as 0.15 V by adding 18 explicit water molecules. These findings are in agreement with the previous investigation by Kim et al. [], who found that treatment of aqueous solvation using explicit water molecules leads to a significant reduction in prediction errors. In overall agreement with Zhang et al. [], they also found that the inclusion of solvation effects lowers the prediction errors significantly and that geometry optimization with a solvation model provides only slightly better results than in the gas phase. However, they observed that it is the addition of the thermochemical contributions that causes the largest reduction in the mean absolute errors from (MAE) 0.308 V to 0.074 V. It must be noted that the prediction models from Fornari et al. [] and Zhang et al. [] cannot be directly compared because the latter used experimental data to fit the linear model’s (Equation (8)) slope and intercept. Nevertheless, from the survey of these studies [,,,,], it is quite clear that using less parametrized DFT functionals (PBE and B3LYP) can account for most of the contributions to the free energy changes during electron transfer that remain after error cancellation. The use of expensive higher-order DFT functionals offers no significant improvement in accuracy when predicting quinone redox potentials.
To include the effect of on redox potential predictions, especially at higher values, Fornari et al. [] used the Alberty-Legendre transform, which is similar to Equation (3). Algebraically, the use of Equation (3) only comes into play only when (under the assumption of simultaneous / transfers) the number of transferred and are not the same. However, at higher both the oxidized and the reduced form undergo deprotonation. In this case, the free energy terms and in Equation (3) must be updated to account for this change in state. Fornari et al. [] used the acid dissociation constants () of the reactant and product molecules predicted from the ChemAxon cheminformatics software to account for deprotonations of both redox forms at higher . With this new protocol, which combined both DFT calculations and cheminformatics-based predictions, the MAE with respect to experimental potentials was found to be 0.121 V at pH = 7 and 0.144 V at pH = 13.
The problem of predicting redox potentials across the entire scale was treated rigorously by Gaudin et al. [] As shown in Figure 4b, they evaluated the chemical potentials of reaction intermediates () with different oxidation and protonation states (see also Figure 3) using the COSMO model, which yielded Gibbs free energies in an ideal conductor. These were then used as inputs in a COSMO-RS model to obtain their Gibbs free energies in water, which, summed together with the Gibbs free energy in the conductor, provided the total free energy of the reaction intermediates. These Gibbs free energies were plugged into energy balance equations akin to Equation (7), which provided the equilibrium redox potentials for (at ) and (at ). Furthermore, the limiting values for and were calculated using the same COSMO-based geometry optimization and solvation models (as for the Gibbs free energies). Furthermore, they used material balance equations, redox potentials, and values of the intermediates to develop a self-consistent model for finding the number of transferred protons at any given . With the help of this formalism, they were able to calculate Pourbaix diagrams that were in good quantitative and qualitative agreement with reported data on four different anthraquinones. Expectedly, the predictive power of this approach is dependent on the accuracy with which the Gibbs free energies of formation and can be predicted. The prediction of using first-principle simulations is a wide-open research area in itself, and some excellent reviews have already been published [,,].
3. Aqueous Solubility
The aqueous solubility of quinones is the next important property that has been widely investigated because it is directly proportional to the energy capacity, energy density, and power density of the ARFB. The amount of quinone that can be dissolved in water is decided by the thermodynamics of aqueous solvation, which competes with the thermodynamics of crystallization. The aqueous solvation of quinones, and organic molecules in general, is a complex function of polar electrostatic interactions with water, solvent reorganization and entropic contributions, inter- and intramolecular H-bonding, and the delocalized charge density in the aromatic rings. Water is a polar solvent with a high Gutmann donor number, a high acceptor number, and a high polarizability. As a consequence, the presence of substituent groups and the size of the quinone molecule have an enormous influence on its solubility. Hydrophilic substituents, including −SO3H, −PO3H2, −COOH, and −OH, can increase the solubility of the core quinone by a few orders of magnitude [,,,]. In general, negatively charged substituents (−SO3−, −PO3H−, −COO−, etc.) have the most enhancing effect on solubility, followed by positively charged substituents (−C5H6N+, −C3H5N2+, −N(CH3)4+, etc.) and then neutral substituents (−CN, −OH, −OCH3, etc.) []. Apart from the molecule itself, the of the solution and the accompanying counter-ions in the solution have an enormous effect on the solubility [,]. However, these effects have not been taken into account when making theoretical predictions of quinone solubility, as is evident in the published literature.
Theoretical predictions: Intrinsic aqueous solubility is defined as the maximum amount of a nonionized compound that can get dissolved in 1 L of water and is commonly measured in LogS (S in mol/L) units []. Predictions of aqueous solubility are often very inaccurate, even though the solubility of a compound can be related rigorously to its other structural and physicochemical properties [,,]. This decades-old challenge has been tackled with broadly four types of approaches: (1) empirical methods, such as the generalized solubility equation (GSE) and its variants that use property-property relationships [], (2) statistical methods that use quantitative structure-property relationships (QSPR) and cheminformatic descriptors [,], (3) physics-based methods that use Monte Carlo, MD or first-principles simulations to predict the free energy of the dissolution reaction [,] and (4) data-driven, machine learning, and other high-dimensional regression methods [,,].
Multiple efforts have attempted to combine the strengths of various approaches, for instance, by combining first-principles calculated energies with physicochemical and cheminformatic descriptors as inputs in a data-driven machine learning model [,]. However, it has proven very difficult to achieve error values below 0.3 LogS units on datasets of appreciable size (1000 points), which indicates a huge real error of 100.3 2 times in solubility. Remarkably, current models do not improve even when trained on standardized data with much lower measurement RMSE values [] (0.05 LogS) than usually available [,] (0.6–0.7 LogS). This suggests that there is little complementarity between the chemical information provided by the available methods, and more importantly, that an accurate method that captures the underlying thermochemistry of dissolution is still missing. Excellent reviews on these issues are already available in the published literature [,].
As will be evident in the next section, most HTVS studies ignore the important effect of coordinating ions [,,] and [] when predicting the aqueous solubility of quinones using first-principles methods. The solubility (in mol/L) can be predicted from the Gibbs free energy of the dissolution of the organic molecule from its crystalline form to its solvated aqueous form. At equilibrium, the free energy balance is given as:
where and represent the Gibbs free energies of formation for the crystalline and aqueous phases, represents the activity of the molecule at equilibrium, and the * indicates the Ben-Naim standard states [] (i.e., at 1 mol/L). The free energy balances for dissolution are depicted schematically in Figure 5. The activity can be expressed simply as the product of solubility, , and molar volume, . The definition of the dissolution Gibbs free energy is . Substituting these in Equation (10) yields:
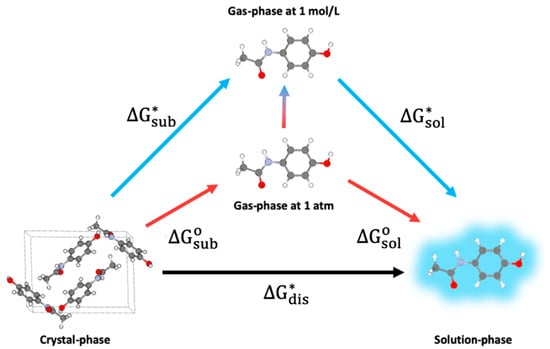
Figure 5.
Thermodynamic cycle linking Gibbs free energy of dissolution of an organic molecule to its sublimation and solvation-free energies. The linking requires a change in the standard state of the gas-phase molecule (shown in the center).
This equation is valid for the dissolution of a molecule in neutral water, without considering its ionic dissociation () or acidity of the solution (). In practice, one uses a thermodynamic cycle for dissolution in which the crystalline phase first gets sublimated to the gas phase, followed by aqueous solvation of the gaseous molecule, as shown in Figure 5 below.
One of the reasons for using such a cycle is that the Gibbs free energies for sublimation () and solvation () are more straightforward to calculate than those for dissolution. This thermodynamic cycle can take two paths, via the Ben-Naim (i.e., at 1 mol/L) or the standard (i.e., gas at 1 atm) states. As the Gibbs free energies for sublimation are typically referred to as the gas at standard conditions, one can rewrite as:
where is the standard Gibbs free energy of sublimation, , and . Combining Equations (11) and (12) yields:
As is evident from Equation (13), the accurate first-principles calculations of solubility necessitate full computational characterization of both the crystal and solution phases. While the prediction of the solvation free energy () has matured significantly over the last decade [,], there is ample evidence that the most erroneous contribution to the calculation of the dissolution free energy originates in the incorrect estimation of the sublimation free energy (), which relates to the solute’s crystal structure [,]. The algorithms for crystal structure prediction of organic crystals typically require extensive searches over space groups, unit cell dimensions, and atomic coordinates using a large number of randomized simulations in a Monte Carlo scheme []. Such an approach for predicting the sublimation-free energy is computationally prohibitive and does not even guarantee high prediction accuracy. This is simply because of the exponential scaling in Equation (13) such that an error of 1 kcal/mol (which is the “heaven of chemical accuracy” for thermochemical calculations) in the prediction of the sublimation free energy implies an error of 6.4 times in the prediction of solubility in mol/L.
Therefore, it is hardly surprising that all known HTVS efforts to date, which use first-principles simulations for predicting quinones’ solubility, routinely ignore the sublimation free energy and use the free energy of solvation () as a descriptor for the overall solubility. Using only is not entirely without merit because it is loosely correlated with experimental and cheminformatics-predicted solubility []. Unlike the extensive work on redox potentials, there are no known studies that have systematically tried to identify rapidly calculable descriptors [] for predicting the aqueous solubility of quinones exclusively, either using first-principles simulations or other methods. The standard method for calculation of solvation-free energies using first-principles methods is to use an implicit solvation method. Implicit solvation is a coarse-grained yet highly effective approach in atomistic simulations to account for a surrounding liquid electrolyte on the level of a continuous polarizable medium, for which the readers are pointed to an extensive recent review in ref. []. However, this approach is not free of errors and is often corrected by using explicit water molecules as conducted in the cluster-continuum approach [,], or the use of QM/MM approaches [,].
The use of cheminformatics (e.g., in the software ChemAxon) and statistics-based methods is quite prevalent in the literature for HTVS of quinones based on solubility, as will be evident in the next section. These methods are dependent on simple and rapidly calculable descriptors and physicochemical properties of molecules (in their gaseous or solvated phases). In principle, such methods can be systematically tuned by fitting them to more available experimental data on aqueous solubility. It must be noted that the currently available amount of open-source data on aqueous solubility is neither large nor diverse enough [] for building data-driven models that are applicable across all classes of molecules and that can predict solubility within 0.3 LogS units. The best models to date use careful data selection to maximize accuracy [,], but this strategy offers no guarantees on the accuracy of molecules “out of set”. The availability of consistently produced experimental data specifically for quinones is even more scarce and scattered, with only a few tens [,,,] of available data points.
4. High-Throughput Virtual Screening: Status and Challenges
For organic ARFBs, a majority of HTVS efforts have been invested in discovering new quinones as negolytes, while discovering quinones as posolytes has served as a much greater challenge to achieve. A summary of the HTVS efforts for quinone discovery from published literature is presented in Table 3. The table lists the core quinone structures that were used as backbones for functionalization along with the literature reference under the column name “Total cores/[Ref]”, the substituent groups are listed under “Substituents”, and the total number of redox couples enumerated in the library under “Library”. It must be noted that some of these reviewed studies are simply high-throughput efforts without the screening aspect.

Table 3.
Summary of the virtual libraries enumerated in HTVS literature for quinones.
The HTVS of quinones begins with the creation of a virtual library in which the candidate quinones are systematically enumerated. As shown schematically in Figure 6, the enumeration can be conducted along various structural and configurational degrees of freedom, which can be broadly classified into two categories under core variations (Figure 6a) and substituent variations (Figure 6b). Core variations indicate modifications to the core molecules based on the extent and type of conjugation in the structure, the total number and position of the carbonyl groups, and the type of heteroatom substitutions. Analogously, substituent variations indicate modifications based on their type and mix of substituents, their positions relative to each other and relative to the carbonyl groups, and their total number and tendency to form intramolecular H-bonds.
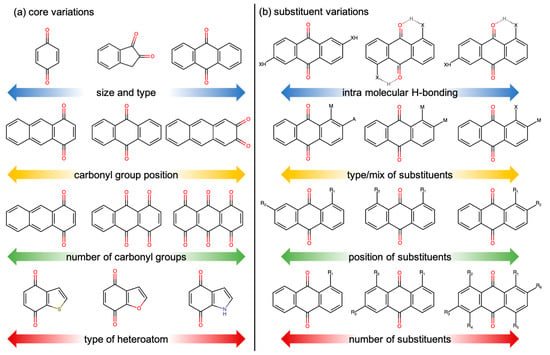
Figure 6.
Schematic showing examples of the various structural and configurational degrees of freedom that are modified when creating a virtual library: (a) core variations and (b) substituent variations.
One of the seminal efforts to use HTVS to discover benzo-, naphtho-, and anthraquinones for ARFBs was performed by Er et al. []. They considered two limiting conditions in the design of their virtual library for understanding the effects of the incorporated substituents on the redox potential of the quinone couples, i.e., with a single position substituted and with all positions substituted. Based on their analysis of the structure-property relationships, Er et al. [] found that groups, which enable new intramolecular hydrogen bonds due to their positioning, strongly influence the calculated total free energies of the molecules. The quinones with carbonyl pairs in para positions were found to have a redox potential suited for the anode (i.e., close to 0 V vs SHE), whereas the groups in the ortho positions were found to be appropriate for the cathode (closer to 1.23 V vs. SHE). Irrespective of the number of aromatic rings in the core quinone structures, functionalization with EDGs (−OH, −NH2) resulted in lower potential values and vice versa. Similarly, irrespective of the number of aromatic rings, incorporating the −OH, −NH2, −COOH, −SO3H, and −PO3H2 groups decreased the solvation energy, thereby likely increasing their solubility. They found that substituting all positions was more effective at decreasing solvation energy than just one, however, at the likely cost of lower synthetic accessibility.
Huynh et al. [] performed one of the most systematic analyses of the quinone redox mechanism by conducting a broad set of experiments for 25 core quinones under consistent conditions, accompanied by extensive theoretical calculations. They compared the one- reduction potential in acetonitrile and the two-/two- redox potential in water and found no overall linear correlation. However, they did find trends between the two redox potentials within sub-groups based on the type of substituent groups, which has major implications on rational design strategies for ARFBs. To explore this aspect further, they predicted the redox potentials of several benzoquinones with numerous EDGs and EWGs using DFT calculations and found that it is the effects of the functional groups on the values of the reaction intermediates that play a decisive role in tuning the two-/two- redox potentials. Their results also confirmed that using functional groups with H-bonding (−CHO, −COCH3, −CO2CH3, −CO2H) or negative charge could shift the redox potentials to more positive values, whereas using sterically bulky groups (−C(CH3)3) could shift the redox potentials in the negative direction. Additionally, they found that the strong electronic withdrawing inductive effect of halogens only significantly influences the one- redox potential and not so much the two-/two- potentials. The reason for this observation was argued to be a net “redox leveling”, which implies that stabilization available for is canceled by . Nevertheless, the overall magnitude of the effect of using halogens was found to be strong enough to significantly influence the two-/two- redox potentials.
The HTVS by Er et al. [] was extended in the recent work of Schwan et al. [], who attempted to close the gap between singly and fully substituted quinone derivatives by considering a large variational space of possible numbers and positions of functionalization. The authors also looked at the effects of explicit water, intramolecular H-bonding, steric hindrances, and inductive and resonance effects. While the effects of the EDG and EWG substituent groups were in agreement with previous reports, the effect of the number of substituents was not linear. For both benzoquinone and naphthoquinone derivatives, this effect strongly depended on the kind of substituent and its position relative to the carbonyl groups, such that larger cumulative effects on redox potentials were observed for substituents with major resonance effects than for substituents with major inductive effects. For anthraquinone derivatives, the authors found that the substituent −OCH3 both increased and decreased the redox potential depending on the number and positioning of the functional groups owing to steric effects. They also estimated the influence of (three) explicit water molecules on the calculation of redox potential for all benzoquinone derivatives. Interestingly, this led to a lowering of the redox potential in several cases because of spontaneous Michael addition, which provides strong evidence that the experimental data on benzoquinones may be significantly affected by side reactions. Otherwise, the addition of water molecules generally led to positive shifts in the redox potentials by 90 meV compared to using just the implicit solvation model. The authors also performed a systematic analysis of the effect of intra-molecular H-bonding by varying the orientation of the hydrogens on the hydroxyl groups—an effect that is ignored routinely in the published literature (except for first-principles MD and QM/MM investigations). As shown in Figure 7, the comparison between various orientations of the hydrogens on hydroxyl groups revealed drastic differences in the relative energies of the conformers for benzoquinones (120 meV), naphthoquinones (310 meV), and anthraquinones (500 meV).
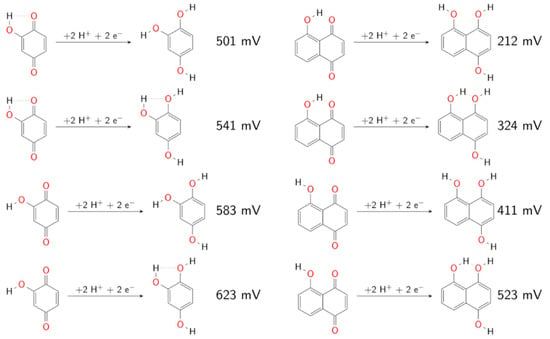
Figure 7.
Comparison between various orientations of the hydrogens on hydroxyl groups that result in drastic differences in the relative energies of the conformers for benzoquinones (left) and naphthoquinones (right). Reprinted with permission from Ref. []. 2022, John Wiley and Sons.
Additionally, Schwan et al. [] also addressed the issue of stability in terms of geometric structure. Substitution of groups can lead to distortions and strain in the ideally “ring-plane” structures [], which results in a reduced overlap between the π orbitals, reduced aromaticity, and thus, reduced stability. For all core structures considered, the authors found the distortion effect to be proportional to the number of substituent groups. It is interesting to note that the −OCH3 and −SO3− groups were found to cause very large distortions and form unphysical structures. However, these groups also allow a very high degree of tunability of both redox potentials and solubility. The existence of such a correlation implies that the success in designing novel high-performance molecules by using the cumulative effect of adding more substituent groups is probably going to be limited not only by their synthetic accessibility but also by their inherent structural stability.
Flores et al. [] considered a combinatorial library of bioinspired benzothiophenoquinones that possess structural similarities with indolequinones for HTVS. Using the data generated from DFT-calculated redox potentials, they also developed a cheminformatics model that predicts redox potentials to within ±0.09 V based solely on molecular connectivity. In contrast to Er et al. [], they considered all possible numbers (2–4) and configurations of substitutions. Although the general trends for EDGs and EWGs were found to agree with previous reports, there were notable exceptions for trends in the opposite direction for both EDGs and EWGs when comparing single and double substitutions. They also found that, generally, the change in redox potential in either direction is higher when substitutions are made in rings opposite each other as compared to the same ring. This nonlinear dependence was not found to be true for solubility, where increasing the number of solubilizing functional groups decreased the solvation energy. They identified several new molecules both for the anode ( 0.25 V) and cathode ( 0.95 V) with solubility > 2 mol/L, that are worthy of further investigation.
Han et al. [] considered three different indolequinones as core structures. Their findings on the effect of substituent groups on redox potentials and solubility were quite similar to previous reports. In addition, they showed that indolequinones with carbonyl pairs in ortho positions are not suitable as negolytes and tend to have lower solubilities than the ones with carbonyl pairs at the para positions. From the 180 enumerated indolequinone derivatives, they found ten molecules suitable as negolytes (< 0.2 V) and nine molecules as posolytes ( > 0.9 V). Among these 19 molecules, only three molecules were identified as having an aqueous solubility > 2 mol/L.
Tabor et al. [] performed one of the very few HTVS investigations of a variety of quinones with a special focus on their chemical stability in water and its relationship to the redox potential. As electrophiles, quinones can undergo nucleophilic attack by water, thus, resulting in the loss of RAMs. The authors studied two mechanisms of nucleophilic addition of water that limit quinone performance in practical ARFBs, one reversible (Gem-diol formation) and one irreversible (Michael addition), as shown in Figure 8. As descriptors of stability, they considered the equilibrium constant for hydration () and the change in energy for gem-diol formation and Michael addition/substitution (). The criteria for stability were: (1) , which implies that at equilibrium the Gem-diol form of a molecule is less than 10 times as abundant than the oxidized form of the molecule, which is not a very strict criterion because the gem-diol formation is still more favored, and (2) , which implies that the molecule is less susceptible to Michael addition than a known quinone alizarin red S for which .
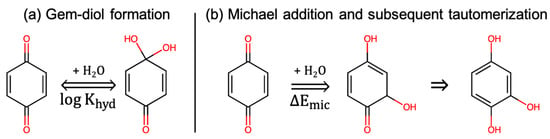
Figure 8.
The mechanisms of chemical instability considered by Tabor et al. []. (a) Gem-diol formation, which is reversible but hampers kinetics. (b) Michael addition on the molecule in which a single vulnerable site of attack and subsequent tautomerization is shown.
Notably, the redox potentials and descriptors for stability were calculated at the calibrated PM7/COSMO level of theory, and the authors demonstrated excellent parity between the PM7/COSMO results and the DFT results for all of the properties of the molecules within the considered chemical space. The structure-property relationships from their work on the effect of positioning of substituent groups and carbonyls on redox potentials were in agreement with previous reports. Notably, the closer the substituent groups were to the carbonyl redox sites, the more pronounced the effect on the redox potential was. The effect was found to occur at different positions for benzo- and naphthoquinones compared to anthraquinones and phenanthrenes, owing to the number and arrangement of rings.
To understand the correlation between redox potential and water stability, the authors first divided their molecules into two groups, one with only a single pair of carbonyls and the other with two pairs of carbonyls. Expectedly, EWGs that make the molecule more electron-deficient will increase the redox potential as well as the propensity towards nucleophilic attack. This general correlation was found to hold well for molecules with a single pair of carbonyls, however, it was substantially less pronounced for molecules with two pairs of carbonyls. Generally speaking, the existence of such a correlation is desirable for negolytes because the lower the redox potential, the lower the propensity toward nucleophilic attack. However, for the same reason, this correlation is undesirable for prospective posolytes. Screening even with very benign stability criteria, the authors were able to provide reasons as to why very few quinones were successful as posolytes (>0.9 V vs. SHE) in full cell cycling tests. Based on their investigation, the authors provided recommendations for designing quinones that can overcome water stability issues. For the mitigation of the Michael addition kinetics, bulky functional groups that provide steric hindrance can be added to the molecules, presumably at the cost of synthetic accessibility. Especially for quinones with multiple carbonyl pairs, the authors suggested tuning the of the reduced intermediates in such a way that the potential is “flattened out” at lower values, which would allow otherwise unpromising molecules at to become viable at higher values. This proposition alludes to the same effect at higher (>12) which is known from both experimental and computational investigations [].
For organic ARFBs, there is growing interest in developing single molecules with three distinct, well-separated (>1.0 V) redox states that could potentially serve as both the negolyte and the posolyte. In principle, such a molecule can be used at both electrodes, which minimizes irreversible loss of active material via membrane crossover. These “symmetric” organic ARFBs are potentially an inexpensive, durable, and safe energy storage technology. The strategy of having multiple redox pairs by fusing quinones with aza-aromatic [,] motifs in the same molecule was explored by Fornari et al. []. The authors investigated the viability of having multiple redox moieties on a compact molecular core. They performed a systematic investigation of such three-ring molecules with multiple moieties by comparing the results with a reference system composed of two molecules, each with just one redox moiety. The prototypical moieties used by them included 1,2-quinone, 1,4-quinone, pyrazine, and pyridazine. Their analysis of structure-property relations demonstrated that the electronic interaction between the two different moieties can be exploited to tune the difference between the redox potentials. Their work also confirmed that intramolecular hydrogen bonding between adjacent units has a major effect on tuning the redox potentials. Notably, their results also show that multiple moieties often improve solubility in comparison to molecules with a single moiety. While it is not clear if these molecules will be stable in water or easily react with themselves, another problem that is directly apparent is that molecules with multiple moieties are more difficult to synthesize than their single counterparts.
While many of these studies have looked at the systematic design of virtual libraries, Kristensen et al. [] investigated a large set of entirely naturally occurring quinones, primarily derived from bacteria and fungi. Remarkably, the distribution of redox potentials spanned a wide range from −1.38 V to 1.49 V vs. SHE. While this range is well beyond the potential limits of hydrogen evolution ( < 0 V) and oxygen evolution ( > 1.23 V) reactions, this work offers a choice from a wide variety of core structures and unconventional functional groups that can be used to design new quinones. It is not entirely inconceivable that such quinones, which would be typically synthetically inaccessible in a chemical lab, could be mass-produced using biotechnological harvesting methods.
Inspired by the excellent performance of quinone moieties typically used as food-coloring agents and organic dyes [], Zhang et al. [] enumerated the space of small quinones with carbonyl pairs on 5-membered rings (3-Cyclopentene-1,2-dione, 4-Cyclopentene-1,3-dione) and heterocyclic substitutions with sulfur, oxygen, and nitrogen atoms. In addition to the DFT calculation of redox potentials, the authors also predicted aqueous solubility using a machine learning model developed in their group [] and explored the commercial availability of the library molecules on the ZINC database [] by developing vendor data-mining codes. To quantify the overall effect of substituent groups on the energy density of the core structures as negolytes, they proposed as a metric for the volumetric energy density that is expressed as a product of solubility and cell voltage. It was found that the effects of functional groups on both redox potentials and solubility were in significant contrast to previous findings. For instance, except for -OH, all other functional groups (−F, −SO3H, −COOH, −NH2) led to a decrease in solubility for molecules with a single 5-membered ring. Furthermore, heteroatom substitutions led to drastic shifts in the properties of both cyclopentenediones and benzoquinones. Except for a few cases of −OH and −SO3H substitution, most derivatives of these motifs were found to have worse predicted energy density than their respective core quinones. However, this was not found to be the case for cyclopentenediones fused with benzene rings, which led to the prediction of several substituted molecules with better energy density compared to their respective core quinones. The authors found 16 (out of 3257) molecules to be commercially available, out of which, only seven had enough solubility to allow for experimental characterization. As an important result of their HTVS, the authors identified and experimentally validated Indigo-3(SO3H) as a new negolyte, whose electrochemical performance and solubility were found to be competitive to that standard quinone AQDS. This molecule was recommended for further testing and characterization in symmetric ARFBs to reduce irreversible capacity losses due to membrane crossover.
In analogy to Table 3, Table 4 provides a summary of the types of approximations and methods used for calculating equilibrium redox potentials under “Redox Potential”, the method/model for estimating aqueous solubility under “Solubility”, and specific molecule recommendations based on screening criteria under “Candidates”. A glance at this information reveals several interesting aspects about the status of HTVS in quinones. Firstly, the methods for predicting redox potentials are approaching a level of maturity that is quite sufficient for purposes of rapid screening. This is evident from the fact that all surveyed studies use simple linear models to predict the redox potentials within an error of 0.1 V vs. SHE. For an intended ARFB of cell voltage = 1 V, this represents a 10 % error and can be considered small given that the screening is typically conducted in the space of thousands of candidate molecules. It is especially encouraging to see the use of semiempirical methods, which have accuracy on par with DFT but require 10−3 times the compute time.

Table 4.
Summary of the methods used for redox potential and solubility prediction in available HTVS literature, along with the number of screened candidates and their respective criteria.
On the contrary, a proper assessment of methods for predicting the aqueous solubility of quinones cannot be done because of the dearth of consistently generated experimental solubility data for a large and diverse set of quinones. Aqueous solubility prediction is a difficult task irrespective of the adopted approach, and the lack of data specific to quinones hinders the development of surrogate prediction models. As argued earlier, an error of 0.3 LogS units in solubility implies an error of 100.32 times the actual solubility in mol/L. Given that solubility is directly proportional to the energy and power density, this error is too high even from the standpoint of HTVS. In this regard, better solubility prediction models for quinones need to be developed that are both rapidly executable and have significantly lower prediction errors. Another missing gap in the HTVS of quinones is the chemical space of quinones with a mixture of different substituent groups on the same core molecule. Enumeration of such a virtual library will be a much more demanding task, both combinatorically and computationally, as compared to enumerating a library of quinones with a single type of functional group on each core. However, this is an effort worthy of pursuing further because it can lead to the discovery of quinones that are able to overcome the performance-limiting trade-offs and correlations between various competing performance metrics.
The next major improvement needed in the HTVS of quinones is the inclusion of descriptors for stability. With a few exceptions, all known HTVS efforts for quinone discovery have focused exclusively on the first major problem of low cell voltage and RAM concentration. While the synthetic accessibility, viscosity, ionic conductivity, toxicity, etc., of quinones are also important to the overall ARFB performance, addressing the second major problem of low stability is of critical importance for any chance of long-term operation and high rechargeability for the ARFB. Typical mechanisms of degradation of quinones include nucleophilic substitution/addition [,,,,], disproportionation [], tautomerization [], protodesulfonation [], anthrone formation [,], and dimerization [,,]. Typically, nucleophilic substitution/addition is the dominant mechanism for quinone posolytes (e.g., benzoquinone derivatives with high redox potentials) due to the electron deficiency of their oxidized form []. For quinone negolytes, the typical decomposition reaction involves disproportionation of the reduced form, leading to the formation of an electrochemically inactive compound, such as anthrone [,].
In an analogy to using experimental redox potential data for accurately predicting redox potentials, new first-principles calculable stability descriptors corresponding to each of these decomposition pathways must be identified from spectroscopic and electrochemical data, which may include information on the type of decomposition products. Understandably, the calculated stability descriptor may not be directly comparable with the available experimental data. For instance, the free energy of disproportionation is not an experimentally accessible quantity under normal circumstances. However, it can be compared directly to the capacity fade rate. The existence of a correlation between the two quantities for a set of quinones will provide a basis for employing the descriptor for HTVS. In addition, the comparison of free energy-based stability descriptors to one another may provide information on the dominance of one decomposition pathway over another.
5. Summary and Outlook
Driven by advancements in computing power, data analysis, and workflow automation techniques in the digital age, HTVS is a highly effective approach for accelerating the rational design and discovery of high-performance materials. HTVS efforts for quinone discovery have significantly narrowed down the space of potentially high-performing candidates of various sizes, moieties, and substituent groups. Additionally, these studies have provided broadly applicable design principles that have found solid validation in experiments. Nevertheless, wide gaps in the prediction of solubility and stability still need to be bridged to increase the “success rate” of such efforts and the chance of finding candidate quinones that exhibit disruptive performance in ARFBs. From a methodological standpoint, performing HTVS along a hierarchical pipeline, i.e., sequentially down-selecting RAMs by evaluating the redox potential, solubility, and stability, may not necessarily be the most efficient approach. The challenge of material discovery is a multi-objective optimization problem, as high cell voltage, high concentrations of active species, and high stability are all desired simultaneously for any ARFB. However, the performance descriptors are often correlated to each other in such a way that optimizing one makes the other worse, which implies the existence of unavoidable, inherent trade-offs. Unless one can design an overall ‘performance rating’ of candidates that simultaneously takes into account the contributions of all the performance descriptors, the conventional HTVS approach eliminates potentially high-performing candidates at each sequential step. This could happen, for instance, when a candidate scores well on two out of three performance metrics but scores rather averagely on the third, or when the method used to estimate the performance descriptor has an error large enough that the candidate fails to meet the screening criteria and is unnecessarily eliminated. To avoid such a scenario, an improved approach that goes beyond sequential HTVS is needed.
One way to improve the conventional approach would be to find the pareto-optimal hypersurface [,], which essentially represents the set of candidates that are equally “fit” for achieving the desired objective. As a simple example, the volumetric energy density of an ARFB is a product of the cell voltage and the RAM concentration. In this regard, the pareto-optimal boundary curve could represent all candidates for whom the product of their redox potential and solubility satisfies some minimum value, irrespective of the individual redox potential or solubility values. Such an analysis will not only make the screening more robust (i.e., less sensitive to prediction errors), but it will also help set theoretical limits on the ARFB’s performance. Further, the knowledge of this boundary can be used to extract structure-property relationships, which can in turn inspire the search for new candidates that are outliers to those structure-property relationships by using powerful methods, such as reinforcement learning [,].
Funding
A.K. thanks the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) for funding this research effort under the Germany’s Excellence Strategy—Exzellenzcluster 2186 “The Fuel Science Center” ID: 390919832.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Li, Z.; Lu, Y.-C. Material Design of Aqueous Redox Flow Batteries: Fundamental Challenges and Mitigation Strategies. Adv. Mater. 2020, 32, 2002132. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Díez, E.; Ventosa, E.; Guarnieri, M.; Trovò, A.; Flox, C.; Marcilla, R.; Soavi, F.; Mazur, P.; Aranzabe, E.; Ferret, R. Redox flow batteries: Status and perspective towards sustainable stationary energy storage. J. Power Sources 2021, 481, 228804. [Google Scholar] [CrossRef]
- Narayan, S.R.; Nirmalchandar, A.; Murali, A.; Yang, B.; Hoober-Burkhardt, L.; Krishnamoorthy, S.; Prakash, G.K.S. Next-generation aqueous flow battery chemistries. Curr. Opin. Electrochem. 2019, 18, 72–80. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, T.; Ali, M.; Wu, C.; Chen, W. Recent Progress in Organic Species for Redox Flow Batteries. Energy Storage Mater. 2022, 50, 105–138. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, C. Cost-effective iron-based aqueous redox flow batteries for large-scale energy storage application: A review. J. Power Sources 2021, 493, 229445. [Google Scholar] [CrossRef]
- Wang, G.; Zou, H.; Zhu, X.; Ding, M.; Jia, C. Recent progress in zinc-based redox flow batteries: A review. J. Phys. D Appl. Phys. 2021, 55, 163001. [Google Scholar] [CrossRef]
- Khor, A.; Leung, P.; Mohamed, M.R.; Flox, C.; Xu, Q.; An, L.; Wills, R.G.A.; Morante, J.R.; Shah, A.A. Review of zinc-based hybrid flow batteries: From fundamentals to applications. Mater. Today Energy 2018, 8, 80–108. [Google Scholar] [CrossRef]
- Fischer, P.; Mazúr, P.; Krakowiak, J. Family Tree for Aqueous Organic Redox Couples for Redox Flow Battery Electrolytes: A Conceptual Review. Molecules 2022, 27, 560. [Google Scholar] [CrossRef]
- Zhong, F.; Yang, M.; Ding, M.; Jia, C. Organic Electroactive Molecule-Based Electrolytes for Redox Flow Batteries: Status and Challenges of Molecular Design. Front. Chem. 2020, 8. Available online: https://www.frontiersin.org/articles/10.3389/fchem.2020.00451 (accessed on 4 November 2022). [CrossRef]
- Zhao, Z.; Zhang, C.; Li, X. Opportunities and challenges of organic flow battery for electrochemical energy storage technology. J. Energy Chem. 2022, 67, 621–639. [Google Scholar] [CrossRef]
- Fang, X.; Li, Z.; Zhao, Y.; Yue, D.; Zhang, L.; Wei, X. Multielectron Organic Redoxmers for Energy-Dense Redox Flow Batteries. ACS Mater. Lett. 2022, 4, 277–306. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, C.; Zhang, L.; Zhou, Y.; Yu, G. Molecular engineering of organic electroactive materials for redox flow batteries. Chem. Soc. Rev. 2018, 47, 69–103. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Tian, J.; Xu, J.; Wang, Y. Organic Flow Batteries: Recent Progress and Perspectives. Energy Fuels 2020, 34, 13384–13411. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Q.; Zhang, X.; Ran, J.; Han, X.; Yang, Z.; Xu, T. Degradation of electrochemical active compounds in aqueous organic redox flow batteries. Curr. Opin. Electrochem. 2022, 32, 100895. [Google Scholar] [CrossRef]
- Kwabi, D.G.; Ji, Y.; Aziz, M.J. Electrolyte Lifetime in Aqueous Organic Redox Flow Batteries: A Critical Review. Chem. Rev. 2020, 120, 6467–6489. [Google Scholar] [CrossRef]
- Brushett, F.R.; Aziz, M.J.; Rodby, K.E. On Lifetime and Cost of Redox-Active Organics for Aqueous Flow Batteries. ACS Energy Lett. 2020, 5, 879–884. [Google Scholar] [CrossRef]
- Huskinson, B.; Marshak, M.P.; Suh, C.; Er, S.; Gerhardt, M.R.; Galvin, C.J.; Chen, X.; Aspuru-Guzik, A.; Gordon, R.G.; Aziz, M.J. A metal-free organic–inorganic aqueous flow battery. Nature 2014, 505, 195–198. [Google Scholar] [CrossRef]
- Wu, M.; Jing, Y.; Wong, A.A.; Fell, E.M.; Jin, S.; Tang, Z.; Gordon, R.G.; Aziz, M.J. Extremely Stable Anthraquinone Negolytes Synthesized from Common Precursors. Chem 2020, 6, 1432–1442. [Google Scholar] [CrossRef]
- Guiheneuf, S.; Godet-Bar, T.; Fontmorin, J.-M.; Jourdin, C.; Floner, D.; Geneste, F. A new hydroxyanthraquinone derivative with a low and reversible capacity fading process as negolyte in alkaline aqueous redox flow batteries. J. Power Sources 2022, 539, 231600. [Google Scholar] [CrossRef]
- Kwabi, D.G.; Lin, K.; Ji, Y.; Kerr, E.F.; Goulet, M.-A.; De Porcellinis, D.; Tabor, D.P.; Pollack, D.A.; Aspuru-Guzik, A.; Gordon, R.G.; et al. Alkaline Quinone Flow Battery with Long Lifetime at pH 12. Joule 2018, 2, 1894–1906. [Google Scholar] [CrossRef]
- Wedege, K.; Dražević, E.; Konya, D.; Bentien, A. Organic Redox Species in Aqueous Flow Batteries: Redox Potentials, Chemical Stability and Solubility. Sci Rep 2016, 6, 39101. [Google Scholar] [CrossRef] [PubMed]
- Hoober-Burkhardt, L.; Krishnamoorthy, S.; Yang, B.; Murali, A.; Nirmalchandar, A.; Prakash, G.K.S.; Narayanan, S.R. A New Michael-Reaction-Resistant Benzoquinone for Aqueous Organic Redox Flow Batteries. J. Electrochem. Soc. 2017, 164, A600. [Google Scholar] [CrossRef]
- Ji, Y.; Goulet, M.-A.; Pollack, D.A.; Kwabi, D.G.; Jin, S.; De Porcellinis, D.; Kerr, E.F.; Gordon, R.G.; Aziz, M.J. A Phosphonate-Functionalized Quinone Redox Flow Battery at Near-Neutral pH with Record Capacity Retention Rate. Adv. Energy Mater. 2019, 9, 1900039. [Google Scholar] [CrossRef]
- Feng, R.; Zhang, X.; Murugesan, V.; Hollas, A.; Chen, Y.; Shao, Y.; Walter, E.; Wellala, N.P.N.; Yan, L.; Rosso, K.M.; et al. Reversible ketone hydrogenation and dehydrogenation for aqueous organic redox flow batteries. Science 2021, 372, 836–840. [Google Scholar] [CrossRef]
- Yang, X.; Garcia, S.N.; Janoschka, T.; Kónya, D.; Hager, M.D.; Schubert, U.S. Novel, Stable Catholyte for Aqueous Organic Redox Flow Batteries: Symmetric Cell Study of Hydroquinones with High Accessible Capacity. Molecules 2021, 26, 3823. [Google Scholar] [CrossRef]
- Wang, C.; Yu, B.; Liu, Y.; Wang, H.; Zhang, Z.; Xie, C.; Li, X.; Zhang, H.; Jin, Z. N-alkyl-carboxylate-functionalized anthraquinone for long-cycling aqueous redox flow batteries. Energy Storage Mater. 2021, 36, 417–426. [Google Scholar] [CrossRef]
- Hollas, A.; Wei, X.; Murugesan, V.; Nie, Z.; Li, B.; Reed, D.; Liu, J.; Sprenkle, V.; Wang, W. A biomimetic high-capacity phenazine-based anolyte for aqueous organic redox flow batteries. Nat Energy 2018, 3, 508–514. [Google Scholar] [CrossRef]
- Pang, S.; Wang, X.; Wang, P.; Ji, Y. Biomimetic Amino Acid Functionalized Phenazine Flow Batteries with Long Lifetime at Near-Neutral pH. Angew. Chem. Int. Ed. 2021, 60, 5289–5298. [Google Scholar] [CrossRef]
- Lin, K.; Gómez-Bombarelli, R.; Beh, E.S.; Tong, L.; Chen, Q.; Valle, A.; Aspuru-Guzik, A.; Aziz, M.J.; Gordon, R.G. A redox-flow battery with an alloxazine-based organic electrolyte. Nat. Energy 2016, 1, 16102. [Google Scholar] [CrossRef]
- Li, X.-L.; Fu, Y. Theoretical study of reduction potentials of substituted flavins. J. Mol. Struct. THEOCHEM 2008, 856, 112–118. [Google Scholar] [CrossRef]
- Orita, A.; Verde, M.G.; Sakai, M.; Meng, Y.S. A biomimetic redox flow battery based on flavin mononucleotide. Nat. Commun. 2016, 7, 13230. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Pang, S.; Wang, X.; Wang, P.; Ji, Y. Ultrastable aqueous phenazine flow batteries with high capacity operated at elevated temperatures. Joule 2021, 5, 2437–2449. [Google Scholar] [CrossRef]
- Symons, P. Quinones for redox flow batteries. Curr. Opin. Electrochem. 2021, 29, 100759. [Google Scholar] [CrossRef]
- Pyzer-Knapp, E.O.; Suh, C.; Gómez-Bombarelli, R.; Aguilera-Iparraguirre, J.; Aspuru-Guzik, A. What Is High-Throughput Virtual Screening? A Perspective from Organic Materials Discovery. Annu. Rev. Mater. Res. 2015, 45, 195–216. Available online: https://www.annualreviews.org/doi/10.1146/annurev-matsci-070214-020823 (accessed on 20 September 2022). [CrossRef]
- Er, S.; Suh, C.; Marshak, M.P.; Aspuru-Guzik, A. Computational design of molecules for an all-quinone redox flow battery. Chem. Sci. 2015, 6, 885–893. [Google Scholar] [CrossRef]
- Pineda Flores, S.D.; Martin-Noble, G.C.; Phillips, R.L.; Schrier, J. Bio-Inspired Electroactive Organic Molecules for Aqueous Redox Flow Batteries. 1. Thiophenoquinones. J. Phys. Chem. C 2015, 119, 21800–21809. [Google Scholar] [CrossRef]
- Huynh, M.T.; Anson, C.W.; Cavell, A.C.; Stahl, S.S.; Hammes-Schiffer, S. Quinone 1 e− and 2 e−/2 H+ Reduction Potentials: Identification and Analysis of Deviations from Systematic Scaling Relationships. J. Am. Chem. Soc. 2016, 138, 15903–15910. [Google Scholar] [CrossRef]
- Han, Y.-K.; Jin, C.-S. Computational screening of electroactive indolequinone derivatives as high-performance active materials for aqueous redox flow batteries. Curr. Appl. Phys. 2018, 18, 1507–1512. [Google Scholar] [CrossRef]
- Tabor, D.P.; Gómez-Bombarelli, R.; Tong, L.; Gordon, R.G.; Aziz, M.J.; Aspuru-Guzik, A. Mapping the frontiers of quinone stability in aqueous media: Implications for organic aqueous redox flow batteries. J. Mater. Chem. A 2019, 7, 12833–12841. [Google Scholar] [CrossRef]
- Fornari, R.P.; Mesta, M.; Hjelm, J.; Vegge, T.; de Silva, P. Molecular Engineering Strategies for Symmetric Aqueous Organic Redox Flow Batteries. ACS Mater. Lett. 2020, 2, 239–246. [Google Scholar] [CrossRef]
- Kristensen, S.B.; van Mourik, T.; Pedersen, T.B.; Sørensen, J.L.; Muff, J. Simulation of electrochemical properties of naturally occurring quinones. Sci. Rep. 2020, 10, 13571. [Google Scholar] [CrossRef] [PubMed]
- Schwan, S.; Schröder, D.; Wegner, H.A.; Janek, J.; Mollenhauer, D. Substituent Pattern Effects on the Redox Potentials of Quinone-Based Active Materials for Aqueous Redox Flow Batteries. ChemSusChem 2020, 13, 5480–5488. [Google Scholar] [CrossRef]
- Zhang, Q.; Khetan, A.; Sorkun, E.; Niu, F.; Loss, A.; Pucher, I.; Er, S. Data-driven discovery of small electroactive molecules for energy storage in aqueous redox flow batteries. Energy Storage Mater. 2022, 47, 167–177. [Google Scholar] [CrossRef]
- Li, T.; Zhang, C.; Li, X. Machine learning for flow batteries: Opportunities and challenges. Chem. Sci. 2022, 13, 4740–4752. [Google Scholar] [CrossRef] [PubMed]
- Frey, D.; Shin, J.H.; Musco, C.; Modestino, M.A. Chemically-informed data-driven optimization (ChIDDO): Leveraging physical models and Bayesian learning to accelerate chemical research. React. Chem. Eng. 2022, 7, 855–865. [Google Scholar] [CrossRef]
- Wang, F.; Cheng, J. Automated workflow for computation of redox potentials, acidity constants, and solvation free energies accelerated by machine learning. J. Chem. Phys. 2022, 157, 024103. [Google Scholar] [CrossRef] [PubMed]
- Boobier, S.; Hose, D.R.J.; Blacker, A.J.; Nguyen, B.N. Machine learning with physicochemical relationships: Solubility prediction in organic solvents and water. Nat. Commun. 2020, 11, 5753. [Google Scholar] [CrossRef] [PubMed]
- Ward, L.; Dandu, N.; Blaiszik, B.; Narayanan, B.; Assary, R.S.; Redfern, P.C.; Foster, I.; Curtiss, L.A. Graph-Based Approaches for Predicting Solvation Energy in Multiple Solvents: Open Datasets and Machine Learning Models. J. Phys. Chem. A 2021, 125, 5990–5998. [Google Scholar] [CrossRef] [PubMed]
- Gao, P.; Yang, X.; Tang, Y.-H.; Zheng, M.; Andersen, A.; Murugesan, V.; Hollas, A.; Wang, W. Graphical Gaussian process regression model for aqueous solvation free energy prediction of organic molecules in redox flow batteries. Phys. Chem. Chem. Phys. 2021, 23, 24892–24904. [Google Scholar] [CrossRef]
- Jinich, A.; Sanchez-Lengeling, B.; Ren, H.; Harman, R.; Aspuru-Guzik, A. A Mixed Quantum Chemistry/Machine Learning Approach for the Fast and Accurate Prediction of Biochemical Redox Potentials and Its Large-Scale Application to 315 000 Redox Reactions. ACS Cent. Sci. 2019, 5, 1199–1210. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Jinich, A.; Aspuru-Guzik, A. MultiDK: A Multiple Descriptor Multiple Kernel Approach for Molecular Discovery and Its Application to Organic Flow Battery Electrolytes. J. Chem. Inf. Model. 2017, 57, 657–668. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Cheng, J.; Lu, X.; He, M.; Wang, R. Redox potentials of aryl derivatives from hybrid functional based first principles molecular dynamics. Phys. Chem. Chem. Phys. 2016, 18, 14911–14917. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Goodson, T.; Zimmerman, P.M. Achieving Accurate Reduction Potential Predictions for Anthraquinones in Water and Aprotic Solvents: Effects of Inter- and Intramolecular H-Bonding and Ion Pairing. J. Phys. Chem. C 2016, 120, 22235–22247. [Google Scholar] [CrossRef]
- Yu, J.; Zhao, T.-S.; Pan, D. Tuning the Performance of Aqueous Organic Redox Flow Batteries via First-Principles Calculations. J. Phys. Chem. Lett. 2020, 11, 10433–10438. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Khetan, A.; Er, S. Comparison of computational chemistry methods for the discovery of quinone-based electroactive compounds for energy storage. Sci. Rep. 2020, 10, 22149. [Google Scholar] [CrossRef] [PubMed]
- Fornari, R.P.; de Silva, P. A Computational Protocol Combining DFT and Cheminformatics for Prediction of pH-Dependent Redox Potentials. Molecules 2021, 26, 3978. [Google Scholar] [CrossRef]
- Gaudin, T.; Aubry, J.-M. Prediction of Pourbaix diagrams of quinones for redox flow battery by COSMO-RS. J. Energy Storage 2022, 49, 104152. [Google Scholar] [CrossRef]
- Guo, C.; Wang, W.; Feng, W.; Li, P. Insights into the one-electron reduction behavior of tetrachloro-o-benzoquinone: A DFT and molecular dynamics study. RSC Adv. 2017, 7, 12775–12782. [Google Scholar] [CrossRef]
- Cheng, L.; Assary, R.S.; Qu, X.; Jain, A.; Ong, S.P.; Rajput, N.N.; Persson, K.; Curtiss, L.A. Accelerating Electrolyte Discovery for Energy Storage with High-Throughput Screening. J. Phys. Chem. Lett. 2015, 6, 283–291. [Google Scholar] [CrossRef]
- Assary, R.S.; Zhang, L.; Huang, J.; Curtiss, L.A. Molecular Level Understanding of the Factors Affecting the Stability of Dimethoxy Benzene Catholyte Candidates from First-Principles Investigations. J. Phys. Chem. C 2016, 120, 14531–14538. [Google Scholar] [CrossRef]
- Ding, Y.; Li, Y.; Yu, G. Exploring Bio-inspired Quinone-Based Organic Redox Flow Batteries: A Combined Experimental and Computational Study. Chem 2016, 1, 790–801. [Google Scholar] [CrossRef]
- Pelzer, K.M.; Cheng, L.; Curtiss, L.A. Effects of Functional Groups in Redox-Active Organic Molecules: A High-Throughput Screening Approach. J. Phys. Chem. C 2017, 121, 237–245. [Google Scholar] [CrossRef]
- Lambert, F.; Danten, Y.; Gatti, C.; Frayret, C. A tool for deciphering the redox potential ranking of organic compounds: A case study of biomass-extracted quinones for sustainable energy. Phys. Chem. Chem. Phys. 2020, 22, 20212–20226. [Google Scholar] [CrossRef] [PubMed]
- McNeill, A.R.; Bodman, S.E.; Burney, A.M.; Hughes, C.D.; Crittenden, D.L. Experimental Validation of a Computational Screening Approach to Predict Redox Potentials for a Diverse Variety of Redox-Active Organic Molecules. J. Phys. Chem. C 2020, 124, 24105–24114. [Google Scholar] [CrossRef]
- Zhou, X.; Khetan, A.; Er, S. Evaluation of Computational Chemistry Methods for Predicting Redox Potentials of Quinone-Based Cathodes for Li-Ion Batteries. Batteries 2021, 7, 71. [Google Scholar] [CrossRef]
- Fenini, F.; Drazevic, E.; Bentien, A. Impact of pH management on utilization and performance of anthraquinone/ ferrocyanide flow batteries. J. Power Sources 2022, 540, 231641. [Google Scholar] [CrossRef]
- Marenich, A.V.; Ho, J.; Coote, M.L.; Cramer, C.J.; Truhlar, D.G. Computational electrochemistry: Prediction of liquid-phase reduction potentials. Phys. Chem. Chem. Phys. 2014, 16, 15068–15106. [Google Scholar] [CrossRef]
- Méndez-Hernández, D.D.; Tarakeshwar, P.; Gust, D.; Moore, T.A.; Moore, A.L.; Mujica, V. Simple and accurate correlation of experimental redox potentials and DFT-calculated HOMO/LUMO energies of polycyclic aromatic hydrocarbons. J. Mol. Model. 2013, 19, 2845–2848. [Google Scholar] [CrossRef]
- Qu, X.; Persson, K.A. Toward Accurate Modeling of the Effect of Ion-Pair Formation on Solute Redox Potential. J. Chem. Theory Comput. 2016, 12, 4501–4508. [Google Scholar] [CrossRef]
- Costanzo, F.; Sulpizi, M.; Valle, R.G.D.; Sprik, M. The oxidation of tyrosine and tryptophan studied by a molecular dynamics normal hydrogen electrode. J. Chem. Phys. 2011, 134, 244508. [Google Scholar] [CrossRef]
- Ghosh, D.; Roy, A.; Seidel, R.; Winter, B.; Bradforth, S.; Krylov, A.I. First-Principle Protocol for Calculating Ionization Energies and Redox Potentials of Solvated Molecules and Ions: Theory and Application to Aqueous Phenol and Phenolate. J. Phys. Chem. B 2012, 116, 7269–7280. [Google Scholar] [CrossRef] [PubMed]
- Fujiki, R.; Matsui, T.; Shigeta, Y.; Nakano, H.; Yoshida, N. Recent Developments of Computational Methods for pKa Prediction Based on Electronic Structure Theory with Solvation Models. J 2021, 4, 849–864. [Google Scholar] [CrossRef]
- Ho, J. Are thermodynamic cycles necessary for continuum solvent calculation of pKas and reduction potentials? Phys. Chem. Chem. Phys. 2014, 17, 2859–2868. [Google Scholar] [CrossRef]
- Navo, C.D.; Jiménez-Osés, G. Computer Prediction of pKa Values in Small Molecules and Proteins. ACS Med. Chem. Lett. 2021, 12, 1624–1628. [Google Scholar] [CrossRef]
- Bauer, S.; Namyslo, J.C.; Kaufmann, D.E.; Turek, T. Evaluation of Options and Limits of Aqueous All-Quinone-Based Organic Redox Flow Batteries. J. Electrochem. Soc. 2020, 167, 110522. [Google Scholar] [CrossRef]
- Mao, J.; Ruan, W.; Chen, Q. Understanding the Aqueous Solubility of Anthraquinone Sulfonate Salts: The Quest for High Capacity Electrolytes of Redox Flow Batteries. J. Electrochem. Soc. 2020, 167, 070522. [Google Scholar] [CrossRef]
- Huang, Z.; Lee, J.; Henkensmeier, D.; Hempelmann, R.; Kim, S.; Chen, R. Effect of Molecular Structure and Coordinating Ions on the Solubility and Electrochemical Behavior of Quinone Derivatives for Aqueous Redox Flow Batteries. J. Electrochem. Soc. 2020, 167, 160502. [Google Scholar] [CrossRef]
- Raevsky, O.A.; Grigorev, V.Y.; Polianczyk, D.E.; Raevskaja, O.E.; Dearden, J.C. Aqueous Drug Solubility: What Do We Measure, Calculate and QSPR Predict? Mini-Rev. Med. Chem. 2019, 19, 362–372. Available online: https://www.eurekaselect.com/article/92000 (accessed on 4 November 2022). [CrossRef] [PubMed]
- Duarte Ramos Matos, G.; Mobley, D.L. Challenges in the use of atomistic simulations to predict solubilities of drug-like molecules. F1000Research 2019, 7, 686. [Google Scholar] [CrossRef]
- Bergström, C.A.S.; Larsson, P. Computational prediction of drug solubility in water-based systems: Qualitative and quantitative approaches used in the current drug discovery and development setting. Int. J. Pharm. 2018, 540, 185–193. [Google Scholar] [CrossRef]
- Skyner, R.E.; McDonagh, J.L.; Groom, C.R.; van Mourik, T.; Mitchell, J.B.O. A review of methods for the calculation of solution free energies and the modelling of systems in solution. Phys. Chem. Chem. Phys. 2015, 17, 6174–6191. [Google Scholar] [CrossRef] [PubMed]
- Ali, J.; Camilleri, P.; Brown, M.B.; Hutt, A.J.; Kirton, S.B. Revisiting the General Solubility Equation: In Silico Prediction of Aqueous Solubility Incorporating the Effect of Topographical Polar Surface Area. J. Chem. Inf. Model. 2012, 52, 420–428. [Google Scholar] [CrossRef] [PubMed]
- Chevillard, F.; Lagorce, D.; Reynès, C.; Villoutreix, B.O.; Vayer, P.; Miteva, M.A. In Silico Prediction of Aqueous Solubility: A Multimodel Protocol Based on Chemical Similarity. Mol. Pharm. 2012, 9, 3127–3135. [Google Scholar] [CrossRef] [PubMed]
- McDonagh, J.L.; Nath, N.; De Ferrari, L.; van Mourik, T.; Mitchell, J.B.O. Uniting Cheminformatics and Chemical Theory To Predict the Intrinsic Aqueous Solubility of Crystalline Druglike Molecules. J. Chem. Inf. Model. 2014, 54, 844–856. [Google Scholar] [CrossRef]
- Boothroyd, S.; Kerridge, A.; Broo, A.; Buttar, D.; Anwar, J. Solubility prediction from first principles: A density of states approach. Phys. Chem. Chem. Phys. 2018, 20, 20981–20987. [Google Scholar] [CrossRef]
- Fowles, D.J.; Palmer, D.S.; Guo, R.; Price, S.L.; Mitchell, J.B.O. Toward Physics-Based Solubility Computation for Pharmaceuticals to Rival Informatics. J. Chem. Theory Comput. 2021, 17, 3700–3709. [Google Scholar] [CrossRef]
- Sorkun, M.C.; Koelman, J.M.V.A.; Er, S. Pushing the limits of solubility prediction via quality-oriented data selection. iScience 2021, 24, 101961. [Google Scholar] [CrossRef]
- Panapitiya, G.; Girard, M.; Hollas, A.; Sepulveda, J.; Murugesan, V.; Wang, W.; Saldanha, E. Evaluation of Deep Learning Architectures for Aqueous Solubility Prediction. ACS Omega 2022, 7, 15695–15710. [Google Scholar] [CrossRef]
- Oja, M.; Sild, S.; Piir, G.; Maran, U. Intrinsic Aqueous Solubility: Mechanistically Transparent Data-Driven Modeling of Drug Substances. Pharmaceutics 2022, 14, 2248. [Google Scholar] [CrossRef]
- Llinas, A.; Avdeef, A. Solubility Challenge Revisited after Ten Years, with Multilab Shake-Flask Data, Using Tight (SD ∼ 0.17 log) and Loose (SD ∼ 0.62 log) Test Sets. J. Chem. Inf. Model. 2019, 59, 3036–3040. [Google Scholar] [CrossRef]
- Palmer, D.S.; Mitchell, J.B.O. Is Experimental Data Quality the Limiting Factor in Predicting the Aqueous Solubility of Druglike Molecules? Mol. Pharm. 2014, 11, 2962–2972. [Google Scholar] [CrossRef] [PubMed]
- Llinàs, A.; Glen, R.C.; Goodman, J.M. Solubility Challenge: Can You Predict Solubilities of 32 Molecules Using a Database of 100 Reliable Measurements? J. Chem. Inf. Model. 2008, 48, 1289–1303. [Google Scholar] [CrossRef] [PubMed]
- Ye, R.; Henkensmeier, D.; Chen, R. Imidazolium cation enabled reversibility of a hydroquinone derivative for designing aqueous redox electrolytes. Sustain. Energy Fuels 2020, 4, 2998–3005. [Google Scholar] [CrossRef]
- McDonagh, J.L.; Palmer, D.S.; van Mourik, T.; Mitchell, J.B.O. Are the Sublimation Thermodynamics of Organic Molecules Predictable? J. Chem. Inf. Model. 2016, 56, 2162–2179. [Google Scholar] [CrossRef] [PubMed]
- Emami, S.; Jouyban, A.; Valizadeh, H.; Shayanfar, A. Are Crystallinity Parameters Critical for Drug Solubility Prediction? J. Solut. Chem. 2015, 44, 2297–2315. [Google Scholar] [CrossRef]
- Reilly, A.M.; Cooper, R.I.; Adjiman, C.S.; Bhattacharya, S.; Boese, A.D.; Brandenburg, J.G.; Bygrave, P.J.; Bylsma, R.; Campbell, J.E.; Car, R.; et al. Report on the sixth blind test of organic crystal structure prediction methods. Acta Cryst. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 439–459. [Google Scholar] [CrossRef]
- Li, J.; Xu, H.; Wang, J.; Wang, Y.; Lu, D.; Liu, J.; Wu, J. Theoretical insights on the hydration of quinones as catholytes in aqueous redox flow batteries. Chin. J. Chem. Eng. 2021, 37, 72–78. [Google Scholar] [CrossRef]
- Ringe, S.; Hormann, N.G.; Oberhofer, H.; Reuter, K. Implicit Solvation Methods for Catalysis at Electrified Interfaces. Chem. Rev. 2022, 122, 10777–10820. Available online: https://pubs.acs.org/doi/10.1021/acs.chemrev.1c00675 (accessed on 4 November 2022). [CrossRef]
- Zhang, J.; Zhang, H.; Wu, T.; Wang, Q.; van der Spoel, D. Comparison of Implicit and Explicit Solvent Models for the Calculation of Solvation Free Energy in Organic Solvents. J. Chem. Theory Comput. 2017, 13, 1034–1043. [Google Scholar] [CrossRef]
- Sadowsky, D.; Arey, J.S. Prediction of aqueous free energies of solvation using coupled QM and MM explicit solvent simulations. Phys. Chem. Chem. Phys. 2020, 22, 8021–8034. [Google Scholar] [CrossRef]
- Sorkun, M.C.; Khetan, A.; Er, S. AqSolDB, a curated reference set of aqueous solubility and 2D descriptors for a diverse set of compounds. Sci. Data 2019, 6, 143. [Google Scholar] [CrossRef] [PubMed]
- Zhigalko, M.V.; Shishkin, O.V.; Gorb, L.; Leszczynski, J. Out-of-plane deformability of aromatic systems in naphthalene, anthracene and phenanthrene. J. Mol. Struct. 2004, 693, 153–159. [Google Scholar] [CrossRef]
- de la Cruz, C.; Molina, A.; Patil, N.; Ventosa, E.; Marcilla, R.; Mavrandonakis, A. New insights into phenazine-based organic redox flow batteries by using high-throughput DFT modelling. Sustain. Energy Fuels 2020, 4, 5513–5521. [Google Scholar] [CrossRef]
- Zhang, Q.; Khetan, A.; Er, S. A quantitative evaluation of computational methods to accelerate the study of alloxazine-derived electroactive compounds for energy storage. Sci. Rep. 2021, 11, 4089. [Google Scholar] [CrossRef] [PubMed]
- Carretero-González, J.; Castillo-Martínez, E.; Armand, M. Highly water-soluble three-redox state organic dyes as bifunctional analytes. Energy Environ. Sci. 2016, 9, 3521–3530. [Google Scholar] [CrossRef]
- Irwin, J.J.; Shoichet, B.K. ZINC—A Free Database of Commercially Available Compounds for Virtual Screening. J. Chem. Inf. Model. 2005, 45, 177–182. Available online: https://pubs.acs.org/doi/10.1021/ci049714%2B (accessed on 3 November 2022). [CrossRef]
- Wu, M.; Bahari, M.; Jing, Y.; Amini, K.; Fell, E.M.; George, T.Y.; Gordon, R.G.; Aziz, M.J. Highly Stable, Low Redox Potential Quinone for Aqueous Flow Batteries. Batter. Supercaps 2022, 5, e202200009. [Google Scholar] [CrossRef]
- Murali, A.; Nirmalchandar, A.; Krishnamoorthy, S.; Hoober-Burkhardt, L.; Yang, B.; Soloveichik, G.; Prakash, G.K.S.; Narayanan, S.R. Understanding and Mitigating Capacity Fade in Aqueous Organic Redox Flow Batteries. J. Electrochem. Soc. 2018, 165, A1193. [Google Scholar] [CrossRef]
- Jing, Y.; Zhao, E.W.; Goulet, M.-A.; Bahari, M.; Fell, E.M.; Jin, S.; Davoodi, A.; Jónsson, E.; Wu, M.; Grey, C.P.; et al. In situ electrochemical recomposition of decomposed redox-active species in aqueous organic flow batteries. Nat. Chem. 2022, 14, 1103–1109. [Google Scholar] [CrossRef]
- Zhao, E.W.; Liu, T.; Jónsson, E.; Lee, J.; Temprano, I.; Jethwa, R.B.; Wang, A.; Smith, H.; Carretero-González, J.; Song, Q.; et al. In situ NMR metrology reveals reaction mechanisms in redox flow batteries. Nature 2020, 579, 224–228. [Google Scholar] [CrossRef]
- Carney, T.J.; Collins, S.J.; Moore, J.S.; Brushett, F.R. Concentration-Dependent Dimerization of Anthraquinone Disulfonic Acid and Its Impact on Charge Storage. Chem. Mater. 2017, 29, 4801–4810. [Google Scholar] [CrossRef]
- Deb, K.; Gupta, H. Searching for Robust Pareto-Optimal Solutions in Multi-objective Optimization. In Evolutionary Multi-Criterion Optimization; Springer: Berlin/Heidelberg, Germany, 2005; pp. 150–164. [Google Scholar]
- Wang, Z.; Rangaiah, G.P. Application and Analysis of Methods for Selecting an Optimal Solution from the Pareto-Optimal Front obtained by Multiobjective Optimization. Ind. Eng. Chem. Res. 2017, 56, 560–574. [Google Scholar] [CrossRef]
- Popova, M.; Isayev, O.; Tropsha, A. Deep reinforcement learning for de novo drug design. Sci. Adv. 2018, 4, eaap7885. [Google Scholar] [CrossRef] [PubMed]
- Pereira, T.; Abbasi, M.; Ribeiro, B.; Arrais, J.P. Diversity oriented Deep Reinforcement Learning for targeted molecule generation. J. Cheminformatics 2021, 13, 21. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).