Development of a Fusion Framework for Lithium-Ion Battery Capacity Estimation in Electric Vehicles
Abstract
1. Introduction
1.1. Review of Existing Battery Capacity Estimation Approaches
1.2. Existing Challenges and Original Contributions
1.3. Outline of the Paper
2. Multi-Dimensional Capacity Estimation and Fusion
2.1. Development of the Adaptive Fusion Framework
2.2. Revisiting Capacity Estimation at Different Working Conditions
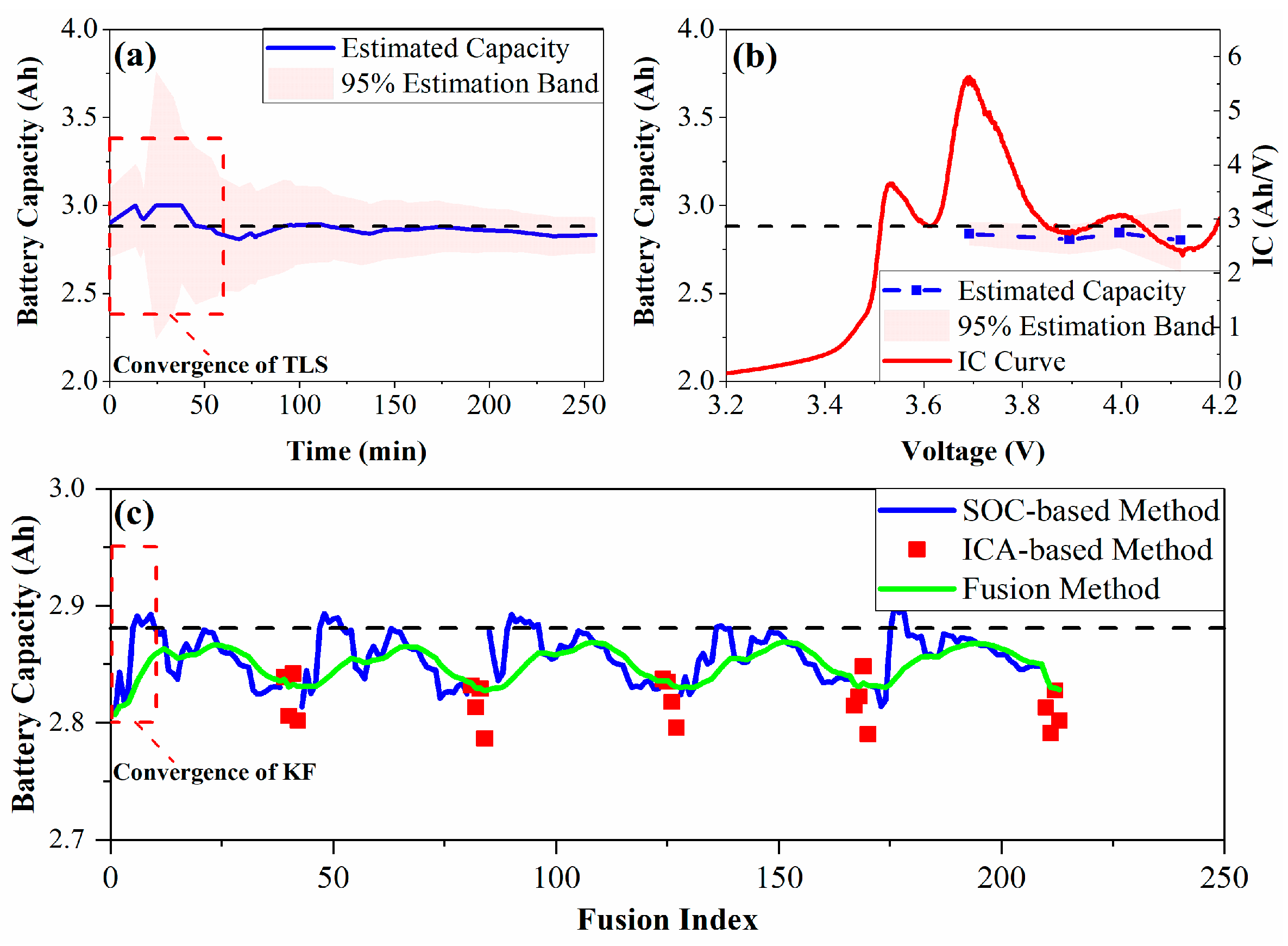
2.2.1. SOC-Based Estimation during the Discharging Condition
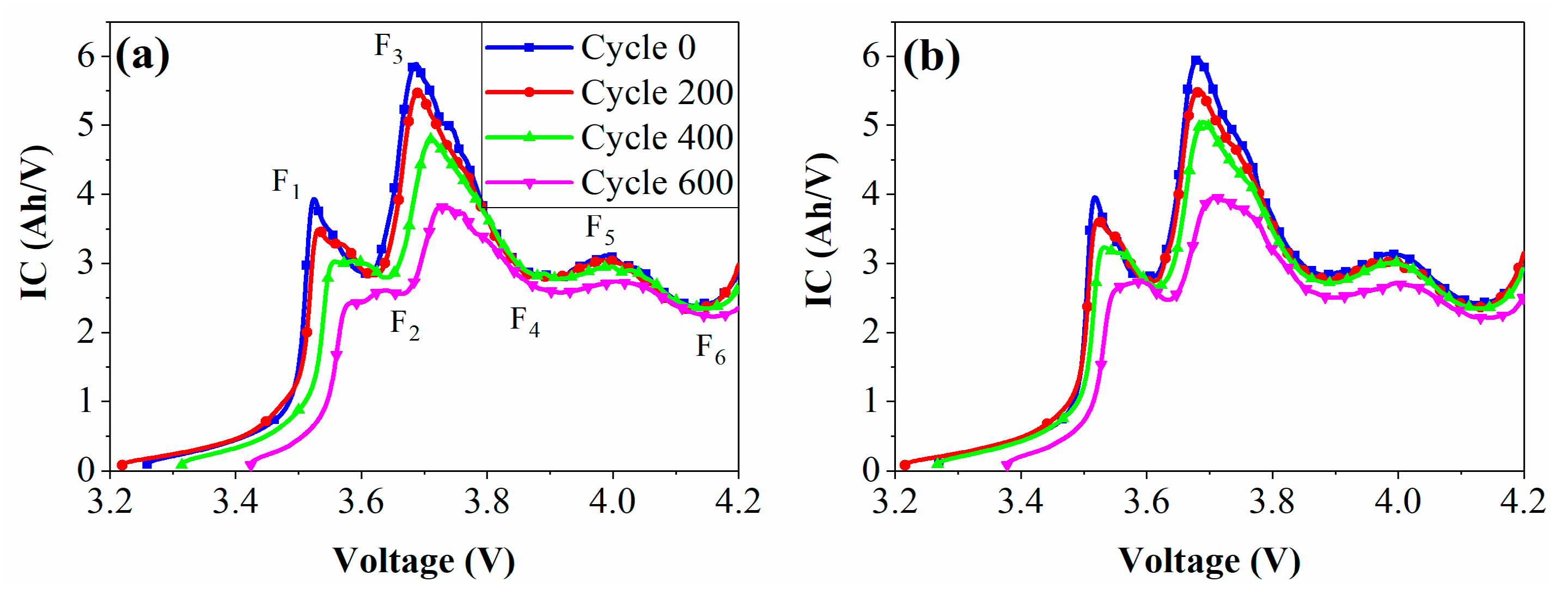
2.2.2. ICA-Based Estimation during the Charging Condition
2.3. Adaptive Capacity Fusion during Complete Operating Conditions
3. Experimental Setups and Design
4. Results and Discussion
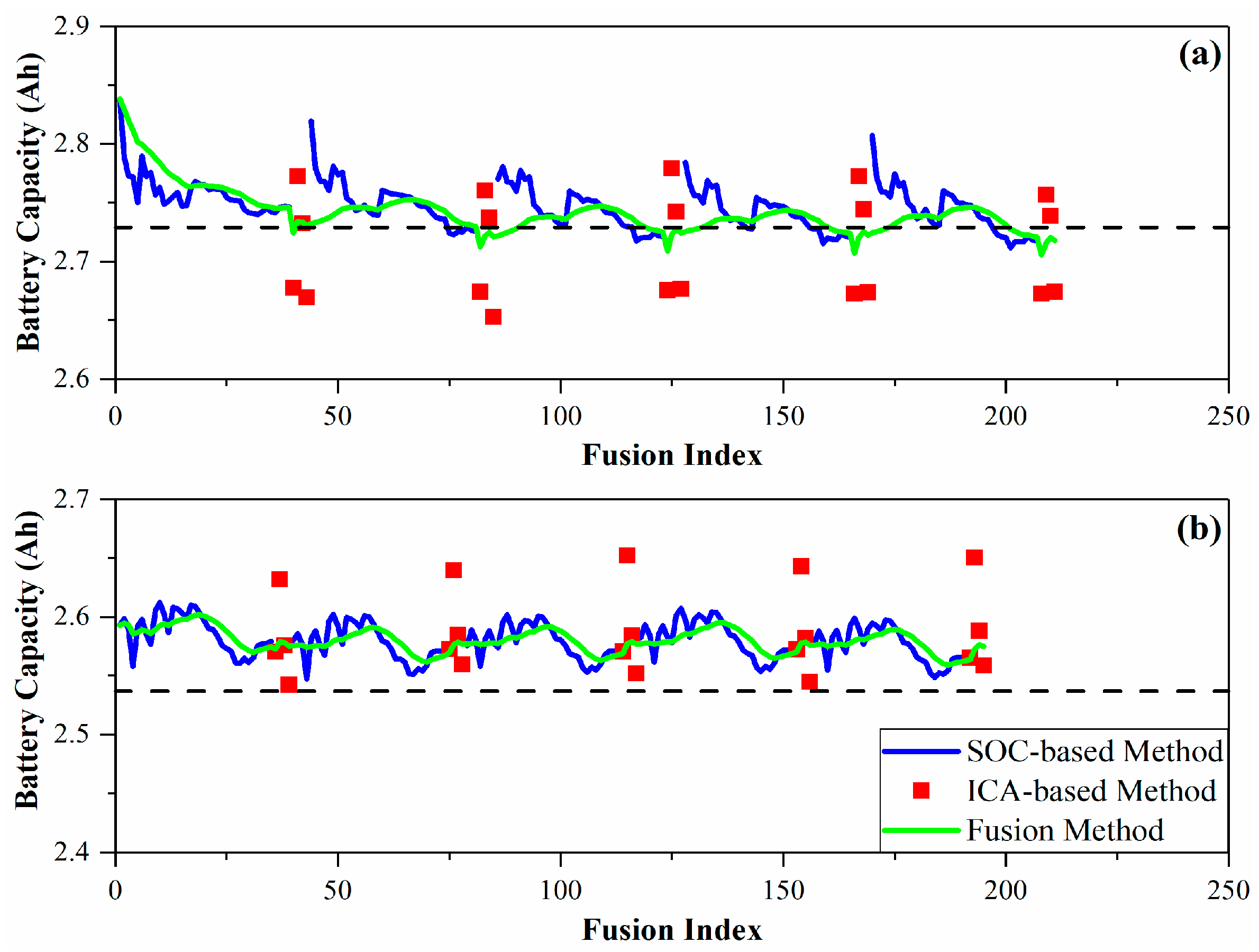
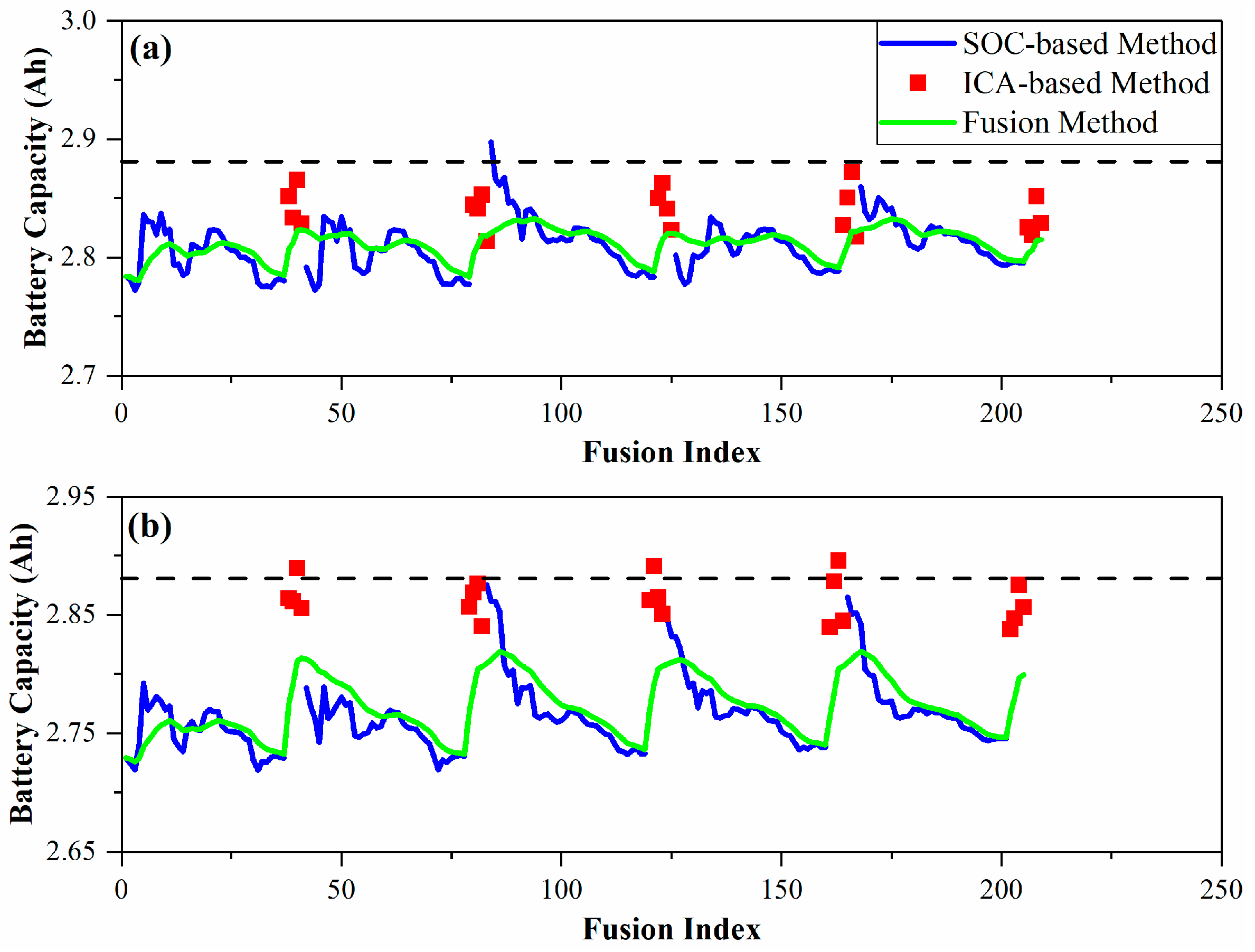
4.1. Effectiveness of the Proposed Capacity Fusion
4.2. Adaptability to Different Aging Statuses
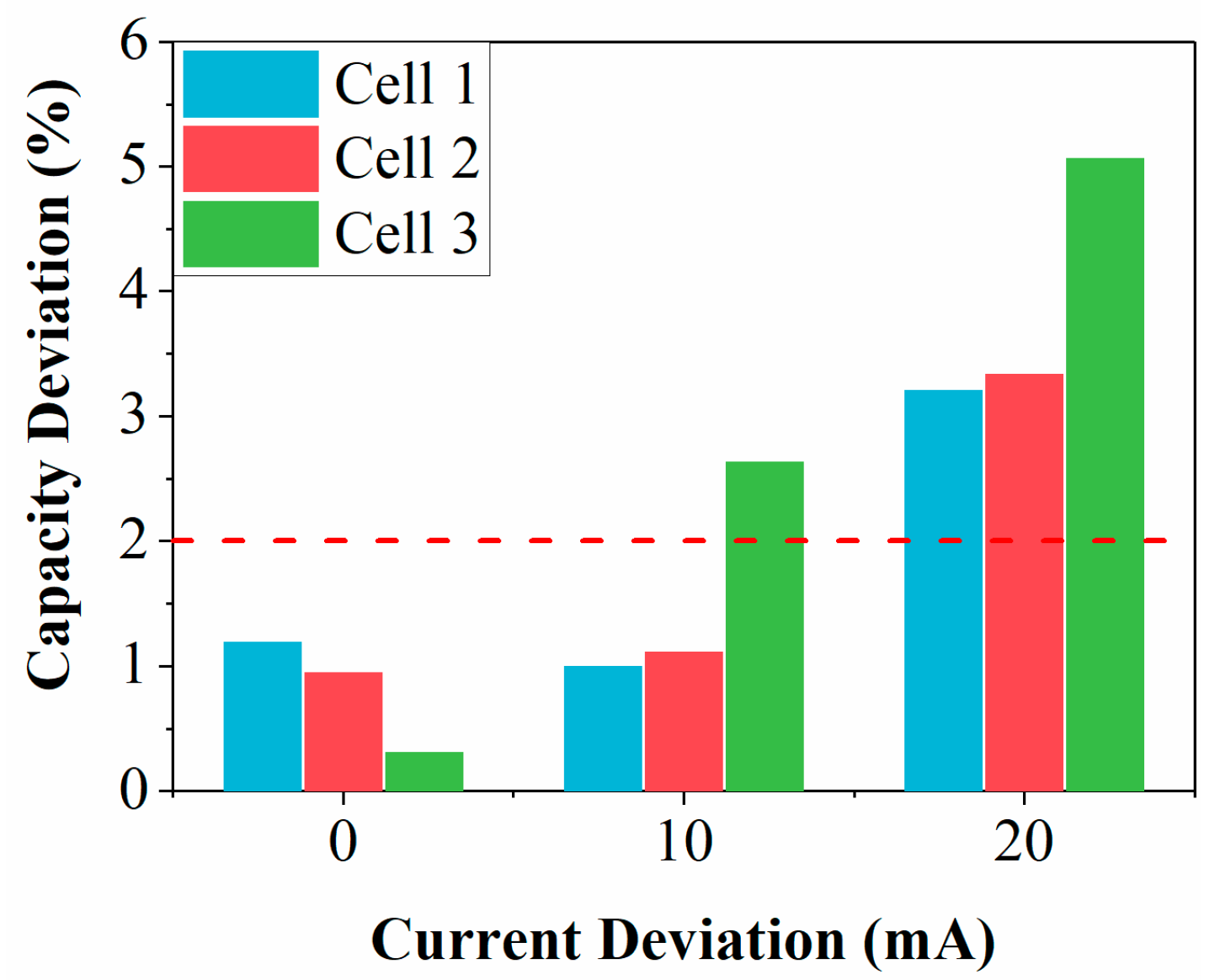
4.3. Application with Inaccurate Battery Current Information
5. Conclusion and Future Research Trends
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dai, H.; Jiang, B.; Hu, X.; Lin, X.; Wei, X.; Pecht, M. Advanced battery management strategies for a sustainable energy future: Multilayer design concepts and research trends. Renew. Sustain. Energy Rev. 2021, 138, 110480. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Zhu, J.; Dai, H.; Zheng, Y.; Xu, X.; Chen, Q. A review of modeling, acquisition, and application of lithium-ion battery impedance for onboard battery management. eTransportation 2021, 7, 100093. [Google Scholar] [CrossRef]
- Fasahat, M.; Manthouri, M. State of charge estimation of lithium-ion batteries using hybrid autoencoder and Long Short Term Memory neural networks. J. Power Sources 2020, 469, 228375. [Google Scholar] [CrossRef]
- Moustafa, M.G.; Sanad, M.M.S. Green fabrication of ZnAl2O4-coated LiFePO4 nanoparticles for enhanced electrochemical performance in Li-ion batteries. J. Alloys Compd. 2022, 903, 163910. [Google Scholar] [CrossRef]
- Sanad, M.M.S.; Toghan, A. Unveiling the role of trivalent cation incorporation in Li-rich Mn-based layered cathode materials for low-cost lithium-ion batteries. Appl. Phys. A 2021, 127, 1–15. [Google Scholar] [CrossRef]
- Hu, X.; Che, Y.; Lin, X.; Deng, Z. Health Prognosis for Electric Vehicle Battery Packs: A Data-Driven Approach. IEEE/ASME Trans. Mechatron. 2020, 25, 2622–2632. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Dai, H. Estimation of state of health of lithium-ion batteries based on charge transfer resistance considering different temperature and state of charge. J. Energy Storage 2019, 21, 618–631. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Zhang, L. Co-estimation of capacity and state-of-charge for lithium-ion batteries in electric vehicles. Energy 2019, 174, 33–44. [Google Scholar] [CrossRef]
- Jiang, B.; Dai, H.; Wei, X.; Jiang, Z. Multi-kernel Relevance Vector Machine with Parameter Optimization for Cycling Aging Prediction of Lithium-ion Batteries. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 1–12. [Google Scholar] [CrossRef]
- Goh, T.; Park, M.; Seo, M.; Kim, J.G.; Kim, S.W. Successive-approximation algorithm for estimating capacity of Li-ion batteries. Energy 2018, 159, 61–73. [Google Scholar] [CrossRef]
- Farmann, A.; Waag, W.; Marongiu, A.; Sauer, D.U. Critical review of on-board capacity estimation techniques for lithium-ion batteries in electric and hybrid electric vehicles. J. Power Sources 2015, 281, 114–130. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; Van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.; Tian, J. Towards a smarter battery management system: A critical review on battery state of health monitoring methods. J. Power Sources 2018, 405, 18–29. [Google Scholar] [CrossRef]
- Schwunk, S.; Armbruster, N.; Straub, S.; Kehl, J.; Vetter, M. Particle filter for state of charge and state of health estimation for lithium–iron phosphate batteries. J. Power Sources 2013, 239, 705–710. [Google Scholar] [CrossRef]
- Einhorn, M.; Conte, F.V.; Kral, C.; Fleig, J. A method for online capacity estimation of lithium ion battery cells using the state of charge and the transferred charge. IEEE Trans. Ind. Appl. 2012, 48, 736–741. [Google Scholar] [CrossRef]
- Zhou, Z.; Cui, Y.; Kong, X.; Li, J.; Zheng, Y. A fast capacity estimation method based on open circuit voltage estimation for LiNixCoyMn1-x-y battery assessing in electric vehicles. J. Energy Storage 2020, 32, 101830. [Google Scholar] [CrossRef]
- Zou, Y.; Hu, X.; Ma, H.; Li, S.E. Combined state of charge and state of health estimation over lithium-ion battery cell cycle lifespan for electric vehicles. J. Power Sources 2015, 273, 793–803. [Google Scholar] [CrossRef]
- Wei, Z.; Leng, F.; He, Z.; Zhang, W.; Li, K. Online state of charge and state of health estimation for a lithium-ion battery based on a data–model fusion method. Energies 2018, 11, 1810. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; Chen, Z.; He, H. A data-driven multi-scale extended Kalman filtering based parameter and state estimation approach of lithium-ion polymer battery in electric vehicles. Appl. Energy 2014, 113, 463–476. [Google Scholar] [CrossRef]
- Kim, I.L.S. A technique for estimating the state of health of lithium batteries through a dual-sliding-mode observer. IEEE Trans. Power Electron. 2010, 25, 1013–1022. [Google Scholar] [CrossRef]
- Hua, Y.; Cordoba-Arenas, A.; Warner, N.; Rizzoni, G. A multi time-scale state-of-charge and state-of-health estimation framework using nonlinear predictive filter for lithium-ion battery pack with passive balance control. J. Power Sources 2015, 280, 293–312. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, J.; Ji, D.; Tseng, K.J. A multi-timescale estimator for battery state of charge and capacity dual estimation based on an online identified model. Appl. Energy 2017, 204, 1264–1274. [Google Scholar] [CrossRef]
- Jiang, B.; Dai, H.; Wei, X. A Cell-to-Pack State Estimation Extension Method Based on a Multilayer Difference Model for Series-Connected Battery Packs. IEEE Trans. Transp. Electrif. 2022, 8, 2037–2049. [Google Scholar] [CrossRef]
- Li, Y.; Abdel-Monem, M.; Gopalakrishnan, R.; Berecibar, M.; Nanini-Maury, E.; Omar, N.; van den Bossche, P.; Van Mierlo, J. A quick on-line state of health estimation method for Li-ion battery with incremental capacity curves processed by Gaussian filter. J. Power Sources 2018, 373, 40–53. [Google Scholar] [CrossRef]
- He, J.; Bian, X.; Liu, L.; Wei, Z.; Yan, F. Comparative study of curve determination methods for incremental capacity analysis and state of health estimation of lithium-ion battery. J. Energy Storage 2020, 29, 101400. [Google Scholar] [CrossRef]
- Bian, X.; Liu, L.; Yan, J. A model for state-of-health estimation of lithium ion batteries based on charging profiles. Energy 2019, 177, 57–65. [Google Scholar] [CrossRef]
- Zhang, S.; Zhai, B.; Guo, X.; Wang, K.; Peng, N.; Zhang, X. Synchronous estimation of state of health and remaining useful lifetime for lithium-ion battery using the incremental capacity and artificial neural networks. J. Energy Storage 2019, 26, 100951. [Google Scholar] [CrossRef]
- Shen, S.; Sadoughi, M.; Chen, X.; Hong, M.; Hu, C. A deep learning method for online capacity estimation of lithium-ion batteries. J. Energy Storage 2019, 25, 100817. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, X.; Lin, X.; Xu, L.; Che, Y.; Hu, L. General Discharge Voltage Information Enabled Health Evaluation for Lithium-Ion Batteries. IEEE/ASME Trans. Mechatron. 2020, 26, 1295–1306. [Google Scholar] [CrossRef]
- Hu, C.; Jain, G.; Zhang, P.; Schmidt, C.; Gomadam, P.; Gorka, T. Data-driven method based on particle swarm optimization and k-nearest neighbor regression for estimating capacity of lithium-ion battery. Appl. Energy 2014, 129, 49–55. [Google Scholar] [CrossRef]
- Deng, Z.; Yang, L.; Cai, Y.; Deng, H.; Sun, L. Online available capacity prediction and state of charge estimation based on advanced data-driven algorithms for lithium iron phosphate battery. Energy 2016, 112, 469–480. [Google Scholar] [CrossRef]
- Jiang, B.; Zhu, J.; Wang, X.; Wei, X.; Shang, W.; Dai, H. A comparative study of different features extracted from electrochemical impedance spectroscopy in state of health estimation for lithium-ion batteries. Appl. Energy 2022, 322, 119502. [Google Scholar] [CrossRef]
- Tan, Y.; Zhao, G. Transfer learning with long short-term memory network for state-of-health prediction of lithium-ion batteries. IEEE Trans. Ind. Electron. 2020, 67, 8723–8731. [Google Scholar] [CrossRef]
- Zheng, Y.; Qin, C.; Lai, X.; Han, X.; Xie, Y. A novel capacity estimation method for lithium-ion batteries using fusion estimation of charging curve sections and discrete Arrhenius aging model. Appl. Energy 2019, 251, 113327. [Google Scholar] [CrossRef]
- Xiong, R.; Wang, J.; Shen, W.; Tian, J.; Mu, H. Co-Estimation of State of Charge and Capacity for Lithium-ion Batteries with Multi-Stage Model Fusion Method. Engineering 2021, 7, 1469–1482. [Google Scholar] [CrossRef]
- Balasingam, B.; Avvari, G.V.; Pattipati, B.; Pattipati, K.R.; Bar-Shalom, Y. A robust approach to battery fuel gauging, part II: Real time capacity estimation. J. Power Sources 2014, 269, 949–961. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, C.; Yue, B.; Wan, J.; Guizani, M. Information fusion for edge intelligence: A survey. Inf. Fusion 2022, 81, 171–186. [Google Scholar] [CrossRef]
- Qiao, D.; Wei, X.; Fan, W.; Jiang, B.; Lai, X.; Zheng, Y.; Tang, X.; Dai, H. Toward safe carbon–neutral transportation: Battery internal short circuit diagnosis based on cloud data for electric vehicles. Appl. Energy 2022, 317, 119168. [Google Scholar] [CrossRef]
- Qiao, D.; Wang, X.; Lai, X.; Zheng, Y.; Wei, X.; Dai, H. Online quantitative diagnosis of internal short circuit for lithium-ion batteries using incremental capacity method. Energy 2021, 243, 123082. [Google Scholar] [CrossRef]
- Jiang, B.; Dai, H.; Jiang, W.; Pei, F. A novel framework of multi-dimension capacity estimation and fusion for lithium-ion battery. In Proceedings of the 2020 IEEE Vehicle Power and Propulsion Conference (VPPC), Gijón, Spain, 26–29 October 2020. [Google Scholar]
- Han, C.; Zhu, H.; Duan, Z. Estimation fusion. In Multi-Source Information Fusion, 2nd ed.; Tsinghua University Press: Beijing, China, 2010; pp. 250–319. [Google Scholar]
- Jiang, B.; Dai, H.; Wei, X. Incremental capacity analysis based adaptive capacity estimation for lithium-ion battery considering charging condition. Appl. Energy 2020, 269, 115074. [Google Scholar] [CrossRef]
- Jiang, B.; Dai, H.; Wei, X.; Xu, T. Joint estimation of lithium-ion battery state of charge and capacity within an adaptive variable multi-timescale framework considering current measurement offset. Appl. Energy 2019, 253, 13619. [Google Scholar] [CrossRef]
- Wei, Z.; Zou, C.; Leng, F.; Soong, B.H.; Tseng, K.-J. Online model identification and state-of-charge estimate for lithium-ion battery with a recursive total least squares-based observer. IEEE Trans. Ind. Electron. 2018, 65, 1336–1346. [Google Scholar] [CrossRef]
- Kim, T.; Wang, Y.; Sahinoglu, Z.; Wada, T.; Hara, S.; Qiao, W. A Rayleigh Quotient-based recursive total-least-squares online maximum capacity estimation for lithium-ion batteries. IEEE Trans. Energy Convers. 2015, 30, 842–851. [Google Scholar] [CrossRef]
- Pastor-Fernández, C.; Uddin, K.; Chouchelamane, G.H.; Widanage, W.D.; Marco, J. A comparison between electrochemical impedance spectroscopy and incremental capacity-differential voltage as li-ion diagnostic techniques to identify and quantify the effects of degradation modes within battery management systems. J. Power Sources 2017, 360, 301–318. [Google Scholar] [CrossRef]
- Dubarry, M.; Beck, D. Analysis of Synthetic Voltage vs. Capacity Datasets for Big Data Li-ion Diagnosis and Prognosis. Energies 2021, 14, 2371. [Google Scholar] [CrossRef]
- Dubarry, M.; Berecibar, M.; Devie, A.; Anseán, D.; Omar, N.; Villarreal, I. State of health battery estimator enabling degradation diagnosis: Model and algorithm description. J. Power Sources 2017, 360, 59–69. [Google Scholar] [CrossRef]
- Crassidis, J.L.; Cheng, Y. Error-covariance analysis of the total least-squares problem. J. Guid. Control. Dyn. 2014, 37, 1053–1063. [Google Scholar] [CrossRef][Green Version]
- Ramachandran, K.M.; Tsokos, C.P. Linear regression models. In Mathematical Statistics with Applications in R, 3rd ed.; Academic Press: Cambridge, MA, USA, 2021; pp. 301–341. [Google Scholar]
- Fang, Q.; Wei, X.; Dai, H. A Remaining Discharge Energy Prediction Method for Lithium-Ion Battery Pack Considering SOC and Parameter Inconsistency. Energies 2019, 12, 987. [Google Scholar] [CrossRef]
- You, H.; Zhu, J.; Wang, X.; Jiang, B.; Sun, H.; Liu, X.; Wei, X.; Han, G.; Ding, S.; Yu, H.; et al. Nonlinear health evaluation for lithium-ion battery within full-lifespan. J. Energy Chem. 2022, 72, 333–341. [Google Scholar] [CrossRef]



| Cell No. | Capacity | SOH | DDC |
| Cell 1 | 2.881 Ah | 99.34% | NEDC |
| Cell 2 | 2.729 Ah | 94.11% | NEDC |
| Cell 3 | 2.537 Ah | 87.48% | UDDS |
| Method | Criterion | Cell 1 | Cell 2 | Cell 3 |
|---|---|---|---|---|
| SOC-based method | MaxAPE (%) | 2.328 | 3.298 | 2.876 |
| RMSE (%) | 1.061 | 0.882 | 1.780 | |
| ICA-based method | MaxAPE (%) | 3.278 | 2.805 | 4.542 |
| RMSE (%) | 2.300 | 1.675 | 2.401 | |
| Fusion method: Kalman filter | MaxAPE (%) | 1.862 | 1.820 | 2.547 |
| RMSE (%) | 1.144 | 0.575 | 1.703 | |
| Fusion method: Moving average | MaxAPE (%) | 2.239 | 1.823 | 2.698 |
| RMSE (%) | 1.141 | 0.751 | 1.788 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, B.; Wei, X.; Dai, H. Development of a Fusion Framework for Lithium-Ion Battery Capacity Estimation in Electric Vehicles. Batteries 2022, 8, 112. https://doi.org/10.3390/batteries8090112
Jiang B, Wei X, Dai H. Development of a Fusion Framework for Lithium-Ion Battery Capacity Estimation in Electric Vehicles. Batteries. 2022; 8(9):112. https://doi.org/10.3390/batteries8090112
Chicago/Turabian StyleJiang, Bo, Xuezhe Wei, and Haifeng Dai. 2022. "Development of a Fusion Framework for Lithium-Ion Battery Capacity Estimation in Electric Vehicles" Batteries 8, no. 9: 112. https://doi.org/10.3390/batteries8090112
APA StyleJiang, B., Wei, X., & Dai, H. (2022). Development of a Fusion Framework for Lithium-Ion Battery Capacity Estimation in Electric Vehicles. Batteries, 8(9), 112. https://doi.org/10.3390/batteries8090112







