Temperature Dependence of Hard Carbon Performance in Sodium Half-Cells with 1 M NaClO4 in EC/DEC Electrolyte
Abstract
:1. Introduction
2. Experimental
2.1. Synthesis of Hard Carbon
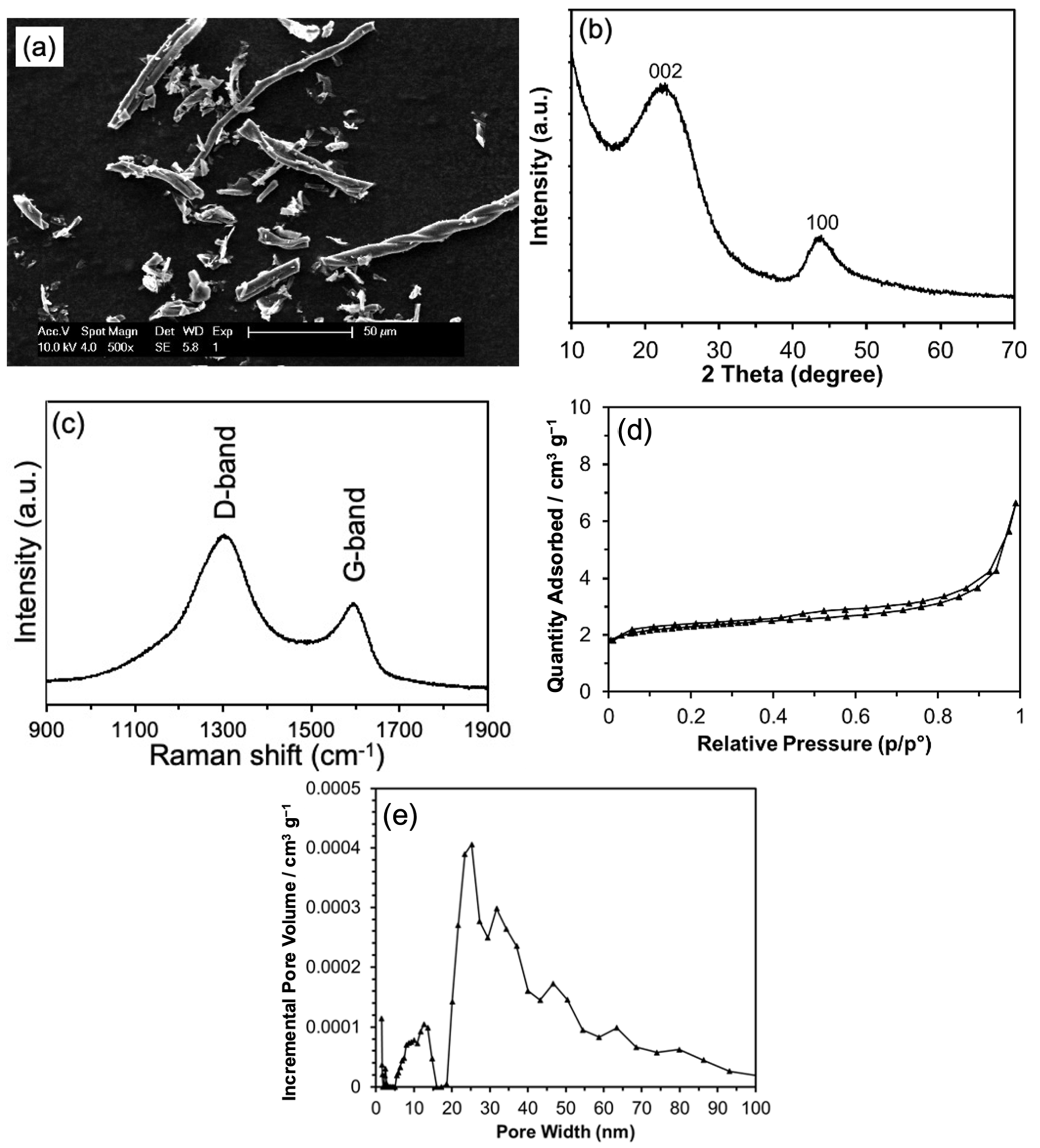
2.2. Material Characterisation
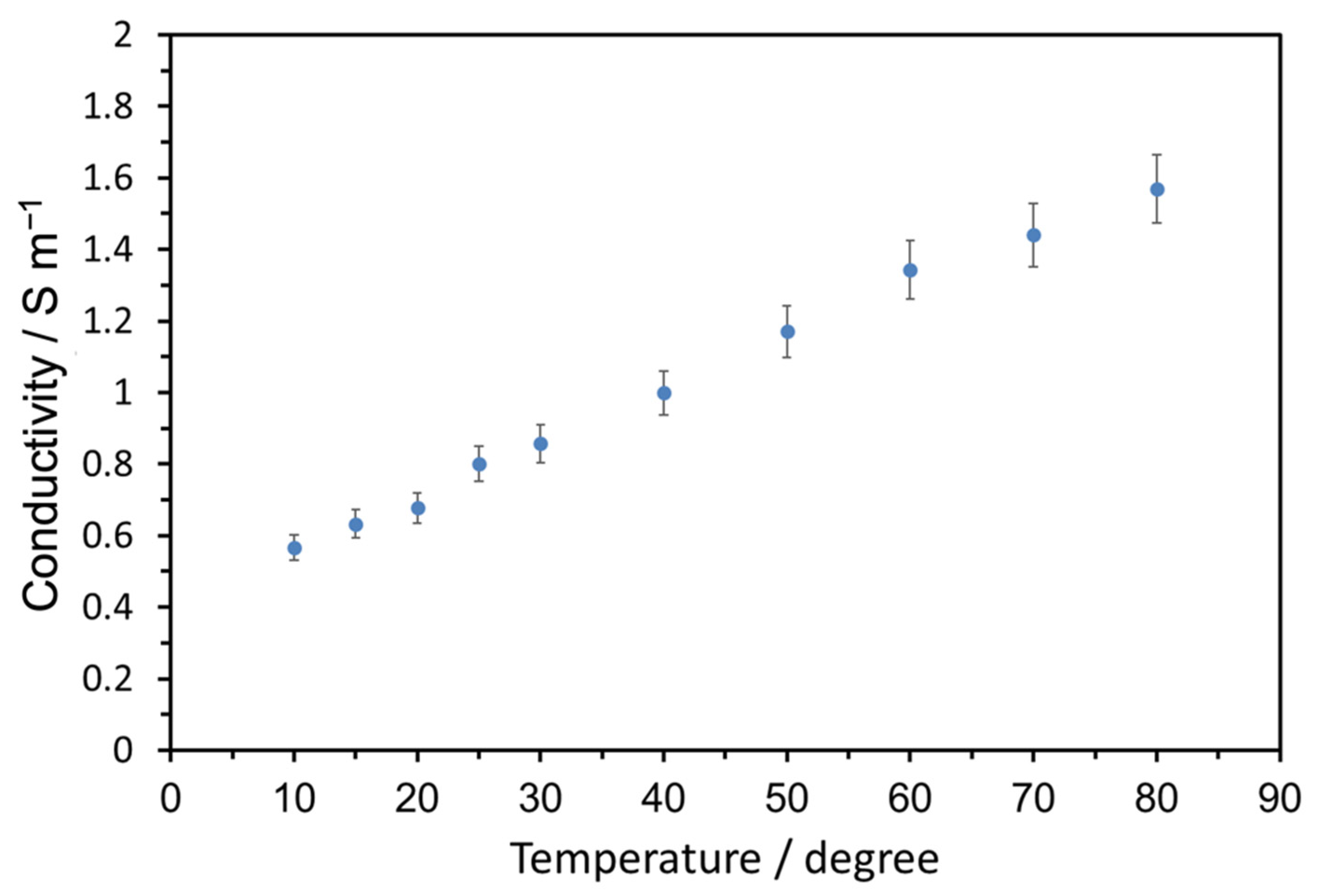
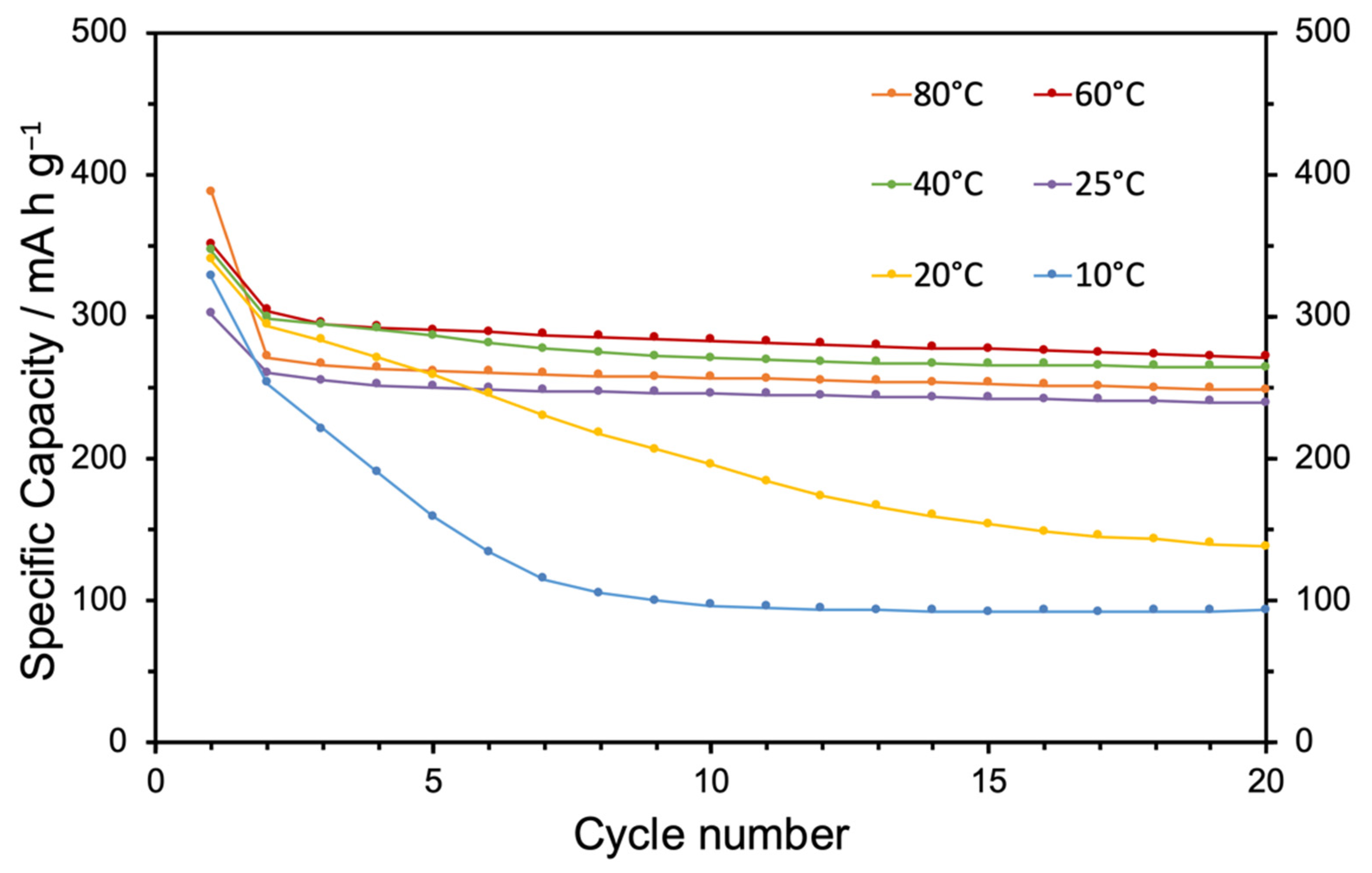
2.3. Electrochemistry Evaluation
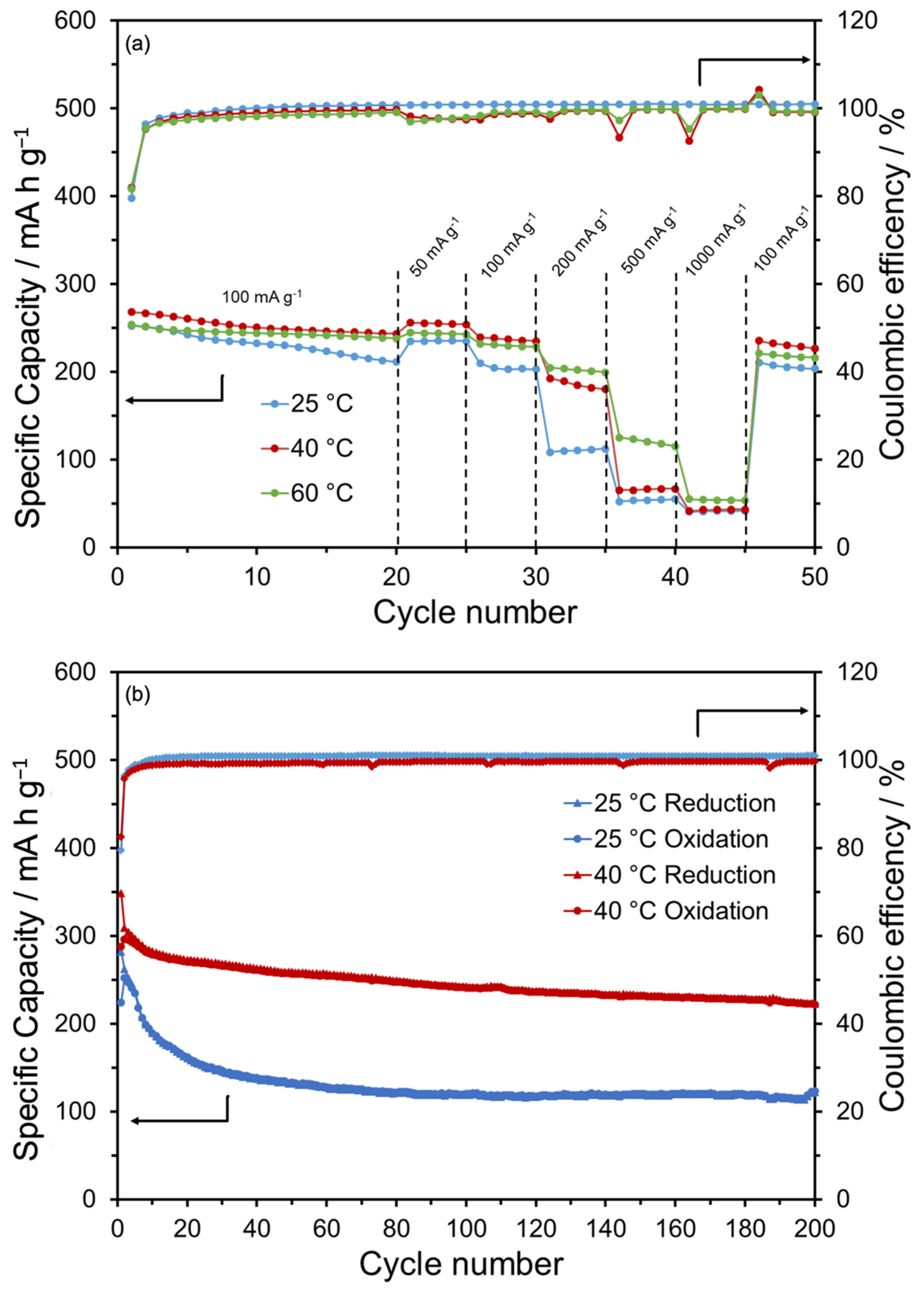
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Slater, M.D.; Kim, D.; Lee, E.; Johnson, C.S. Sodium-Ion Batteries. Adv. Funct. Mater. 2013, 23, 947–958. [Google Scholar] [CrossRef]
- Nayak, P.K.; Yang, L.; Brehm, W.; Adelhelm, P. From Lithium-Ion to Sodium-Ion Batteries: Advantages, Challenges, and Surprises. Angew. Chem. Int. Ed. 2018, 57, 102–120. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.; Song, W.; Son, D.Y.; Ono, L.K.; Qi, Y. Lithium-Ion Batteries: Outlook on Present, Future, and Hybridized Technologies. J. Mater. Chem. A 2019, 7, 2942–2964. [Google Scholar] [CrossRef]
- Li, Y.; Lu, Y.; Adelhelm, P.; Titirici, M.M.; Hu, Y.S. Intercalation Chemistry of Graphite: Alkali Metal Ions and Beyond. Chem. Soc. Rev. 2019, 48, 4655–4687. [Google Scholar] [CrossRef]
- Asher, R.C.; Wilson, S.A. Lamellar Compound of Sodium with Graphite. Nature 1958, 181, 409–410. [Google Scholar] [CrossRef]
- Ge, P.; Fouletier, M. Electrochemical intercalation of sodium in graphite. Solid State Ion. 1988, 28–30, 1172–1175. [Google Scholar] [CrossRef]
- Xiao, B.; Rojo, T.; Li, X. Hard Carbon as Sodium-Ion Battery Anodes: Progress and Challenges. ChemSusChem 2019, 12, 133–144. [Google Scholar] [CrossRef]
- Wang, Q.; Zhu, X.; Liu, Y.; Fang, Y.; Zhou, X.; Bao, J. Rice Husk-Derived Hard Carbons as High-Performance Anode Materials for Sodium-Ion Batteries. Carbon 2018, 127, 658–666. [Google Scholar] [CrossRef]
- Li, Y.; Hu, Y.S.; Titirici, M.M.; Chen, L.; Huang, X. Hard Carbon Microtubes Made from Renewable Cotton as High-Performance Anode Material for Sodium-Ion Batteries. Adv. Energy Mater. 2016, 6, 1600659. [Google Scholar] [CrossRef]
- Yasin, G.; Arif, M.; Mehtab, T.; Shakeel, M.; Mushtaq, M.A.; Kumar, A.; Nguyen, T.A.; Slimani, Y.; Nazir, M.T.; Song, H. A Novel Strategy for the Synthesis of Hard Carbon Spheres Encapsulated with Graphene Networks as a Low-Cost and Large-Scalable Anode Material for Fast Sodium Storage with an Ultralong Cycle Life. Inorg. Chem. Front. 2020, 7, 402–410. [Google Scholar] [CrossRef]
- Yu, Z.E.; Lyu, Y.; Wang, Y.; Xu, S.; Cheng, H.; Mu, X.; Chu, J.; Chen, R.; Liu, Y.; Guo, B. Hard Carbon Micro-Nano Tubes Derived from Kapok Fiber as Anode Materials for Sodium-Ion Batteries and the Sodium-Ion Storage Mechanism. Chem. Commun. 2020, 56, 778–781. [Google Scholar] [CrossRef] [PubMed]
- Kamiyama, A.; Kubota, K.; Nakano, T.; Fujimura, S.; Shiraishi, S.; Tsukada, H.; Komaba, S. High-Capacity Hard Carbon Synthesized from Macroporous Phenolic Resin for Sodium-Ion and Potassium-Ion Battery. ACS Appl. Energy Mater. 2020, 3, 135–140. [Google Scholar] [CrossRef]
- Wang, P.; Yang, B.; Zhang, G.; Zhang, L.; Jiao, H.; Chen, J.; Yan, X. Three-Dimensional Carbon Framework as a Promising Anode Material for High Performance Sodium Ion Storage Devices. Chem. Eng. J. 2018, 353, 453–459. [Google Scholar] [CrossRef]
- Demir, E.; Aydin, M.; Arie, A.A.; Demir-Cakan, R. Apricot Shell Derived Hard Carbons and Their Tin Oxide Composites as Anode Materials for Sodium-Ion Batteries. J. Alloys Compd. 2019, 788, 1093–1102. [Google Scholar] [CrossRef]
- Bandhauer, T.M.; Garimella, S.; Fuller, T.F. A Critical Review of Thermal Issues in Lithium-Ion Batteries. J. Electrochem. Soc. 2011, 158, R1. [Google Scholar] [CrossRef]
- Ma, S.; Jiang, M.; Tao, P.; Song, C.; Wu, J.; Wang, J.; Deng, T.; Shang, W. Temperature Effect and Thermal Impact in Lithium-Ion Batteries: A Review. Prog. Nat. Sci. Mater. Int. 2018, 28, 653–666. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal Runaway Mechanism of Lithium Ion Battery for Electric Vehicles: A Review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Zhao, X.; Chu, G.; Sun, J.; Chen, C. Thermal Runaway Caused Fire and Explosion of Lithium Ion Battery. J. Power Sources 2012, 208, 210–224. [Google Scholar] [CrossRef]
- Ratnakumar, B.V.; Smart, M.C.; Surampudi, S. Effects of SEI on the Kinetics of Lithium Intercalation. J. Power Sources 2001, 97–98, 137–139. [Google Scholar] [CrossRef]
- Zhang, S.S.; Xu, K.; Jow, T.R. The Low Temperature Performance of Li-Ion Batteries. J. Power Sources 2003, 115, 137–140. [Google Scholar] [CrossRef]
- Ding, C.; Nohira, T.; Hagiwara, R.; Fukunaga, A.; Sakai, S.; Nitta, K. Electrochemical Performance of Hard Carbon Negative Electrodes for Ionic Liquid-Based Sodium Ion Batteries over a Wide Temperature Range. Electrochim. Acta 2015, 176, 344–349. [Google Scholar] [CrossRef]
- Lin, X.; Du, X.; Tsui, P.S.; Huang, J.-Q.; Tan, H.; Zhang, B. Exploring Room- and Low-Temperature Performance of Hard Carbon Material in Half and Full Na-Ion Batteries. Electrochim. Acta 2019, 316, 60–68. [Google Scholar] [CrossRef]
- Cao, Y.; Cao, X.; Dong, X.; Zhang, X.; Xu, J.; Wang, N.; Yang, Y.; Wang, C.; Liu, Y.; Xia, Y. All-Climate Iron-Based Sodium-Ion Full Cell for Energy Storage. Adv. Funct. Mater. 2021, 31, 2102856. [Google Scholar] [CrossRef]
- Eshetu, G.G.; Grugeon, S.; Kim, H.; Jeong, S.; Wu, L.; Gachot, G.; Laruelle, S.; Armand, M.; Passerini, S. Comprehensive Insights into the Reactivity of Electrolytes Based on Sodium Ions. ChemSusChem 2016, 9, 462–471. [Google Scholar] [CrossRef]
- Chen, Z.; Duan, H.; Xu, Z.; Chen, C.; Yan, Y.; Wu, S. Fast Sodium Storage with Ultralong Cycle Life for Nitrogen Doped Hollow Carbon Nanofibers Anode at Elevated Temperature. Adv. Mater. Interfaces 2020, 7, 1901922. [Google Scholar] [CrossRef]
- Ponrouch, A.; Palacín, M.R. On the High and Low Temperature Performances of Na-Ion Battery Materials: Hard Carbon as a Case Study. Electrochem. Commun. 2015, 54, 51–54. [Google Scholar] [CrossRef]
- Hou, B.H.; Wang, Y.Y.; Ning, Q.L.; Li, W.H.; Xi, X.T.; Yang, X.; Liang, H.J.; Feng, X.; Wu, X.L. Self-Supporting, Flexible, Additive-Free, and Scalable Hard Carbon Paper Self-Interwoven by 1D Microbelts: Superb Room/Low-Temperature Sodium Storage and Working Mechanism. Adv. Mater. 2019, 31, 1903125. [Google Scholar] [CrossRef]
- Cheng, H.; Garcia-Araez, N.; Hector, A.L.; Soulé, S. Synthesis of Hard Carbon-TiN/TiC Composites by Reacting Cellulose with TiCl 4 Followed by Carbothermal Nitridation/Reduction. Inorg. Chem. 2019, 58, 5776–5786. [Google Scholar] [CrossRef]
- Mei, J.; Liao, T.; Sun, Z. Two-Dimensional Metal Oxide Nanosheets for Rechargeable Batteries. J. Energy Chem. 2018, 27, 117–127. [Google Scholar] [CrossRef]
- Gao, Y.; Qiu, X.; Wang, X.; Chen, X.; Gu, A.; Yu, Z. Nitrogen-Doped Porous Carbon Microspheres for High-Rate Anode Material in Lithium-Ion Batteries. Nanotechnology 2020, 31, 155702. [Google Scholar] [CrossRef]
- Atkins, P.W.; de Paula, J. Motion in Liquids. In Atkins’ Physical Chemistry, 10th ed.; Oxford University Press: Oxford, UK, 2014; p. 799. [Google Scholar]
- Reichstädter, L.; Fischerová, E.; Fischer, O. Conductance of Lithium and Sodium Perchlorates and Tetraphenylborates in 2-Butanone from −35 to 25 °C. J. Solut. Chem. 1999, 28, 35–60. [Google Scholar] [CrossRef]
- Bhide, A.; Hofmann, J.; Katharina Dürr, A.; Janek, J.; Adelhelm, P. Electrochemical Stability of Non-Aqueous Electrolytes for Sodium-Ion Batteries and Their Compatibility with Na0.7CoO2. Phys. Chem. Chem. Phys. 2014, 16, 1987–1998. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Liu, Y.; Li, Y.; Ling, L.; Wu, F.; Wu, C. Mille-Feuille Shaped Hard Carbons Derived from Polyvinylpyrrolidone: Via Environmentally Friendly Electrostatic Spinning for Sodium Ion Battery Anodes. RSC Adv. 2017, 7, 5519–5527. [Google Scholar] [CrossRef]
- Pletcher, D. AC Impedance. In A first Course in Electrode Processes, 2nd ed.; Royal Society of Chemistry: Cambridge, UK, 2009; pp. 211–214. [Google Scholar]
- Bommier, C.; Surta, T.W.; Dolgos, M.; Ji, X. New Mechanistic Insights on Na-Ion Storage in Nongraphitizable Carbon. Nano Lett. 2015, 15, 5888–5892. [Google Scholar] [CrossRef] [PubMed]
- Qiu, S.; Xiao, L.; Sushko, M.L.; Han, K.S.; Shao, Y.; Yan, M.; Liang, X.; Mai, L.; Feng, J.; Cao, Y.; et al. Manipulating Adsorption–Insertion Mechanisms in Nanostructured Carbon Materials for High-Efficiency Sodium Ion Storage. Adv. Energy Mater. 2017, 7, 1700403. [Google Scholar] [CrossRef]
- Sun, N.; Guan, Z.; Liu, Y.; Cao, Y.; Zhu, Q.; Liu, H.; Wang, Z.; Zhang, P.; Xu, B. Extended “Adsorption–Insertion” Model: A New Insight into the Sodium Storage Mechanism of Hard Carbons. Adv. Energy Mater. 2019, 9, 1901351. [Google Scholar] [CrossRef]
- Alvin, S.; Cahyadi, H.S.; Hwang, J.; Chang, W.; Kwak, S.K.; Kim, J. Revealing the Intercalation Mechanisms of Lithium, Sodium, and Potassium in Hard Carbon. Adv. Energy Mater. 2020, 10, 2000283. [Google Scholar] [CrossRef]
- Chen, T.; Liu, Y.; Pan, L.; Lu, T.; Yao, Y.; Sun, Z.; Chua, D.H.C.; Chen, Q. Electrospun Carbon Nanofibers as Anode Materials for Sodium Ion Batteries with Excellent Cycle Performance. J. Mater. Chem. A 2014, 2, 4117–4121. [Google Scholar] [CrossRef]
- Thomas, P.; Ghanbaja, J.; Billaud, D. Electrochemical Insertion of Sodium in Pitch-Based Carbon Fibres in Comparison with Graphite in NaClO4-Ethylene Carbonate Electrolyte. Electrochim. Acta 1999, 45, 423–430. [Google Scholar] [CrossRef]
- Kumar, H.; Detsi, E.; Abraham, D.P.; Shenoy, V.B. Fundamental Mechanisms of Solvent Decomposition Involved in Solid-Electrolyte Interphase Formation in Sodium Ion Batteries. Chem. Mater. 2016, 28, 8930–8941. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R. Impedance. In Electrochemical Methods: Fundamentals and Applications, 2nd ed.; John Wiley: Chichester, UK, 2001; pp. 383–385. [Google Scholar]
- Adams, R.A.; Varma, A.; Pol, V.G. Temperature Dependent Electrochemical Performance of Graphite Anodes for K-Ion and Li-Ion Batteries. J. Power Sources 2019, 410–411, 124–131. [Google Scholar] [CrossRef]
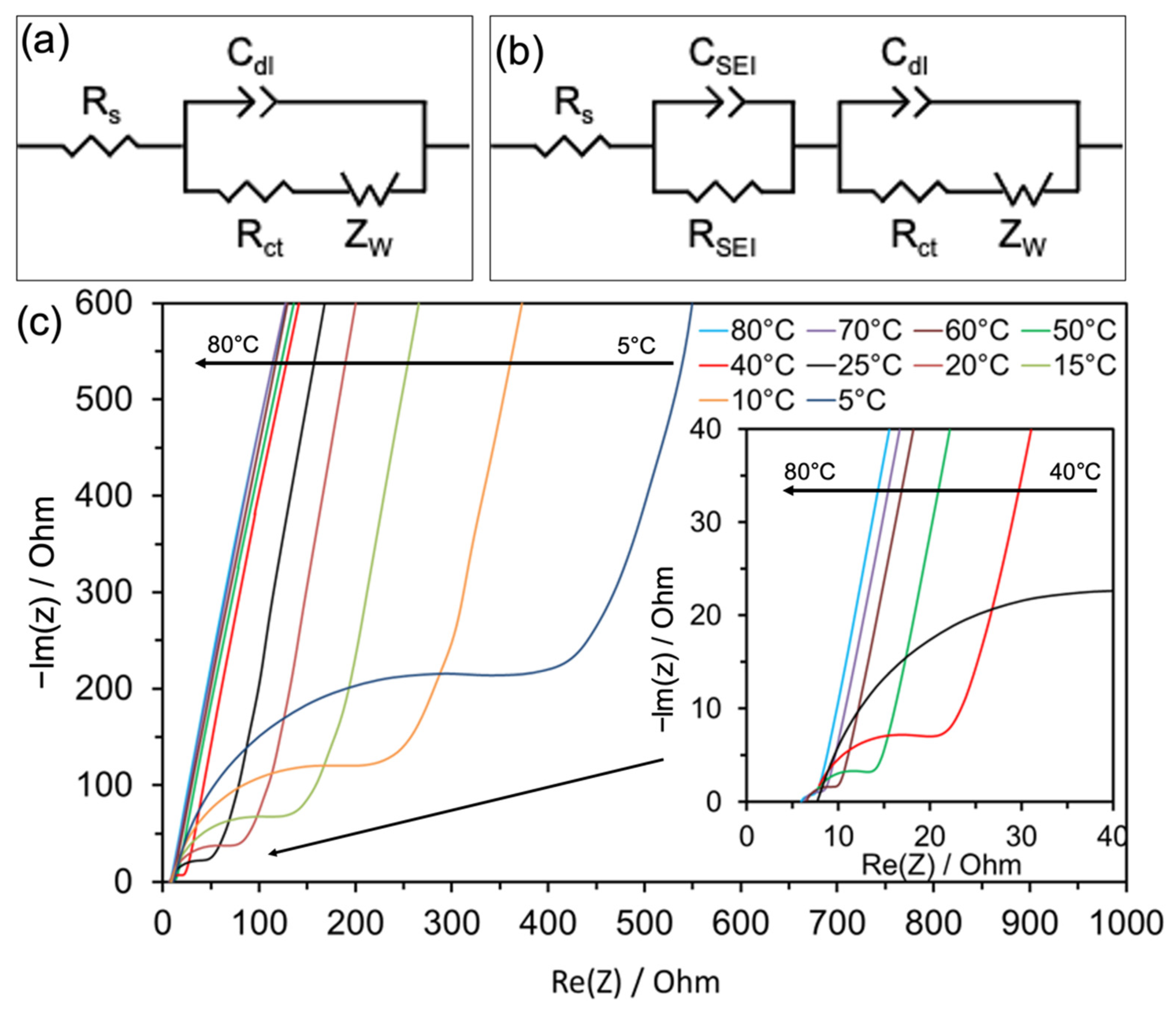
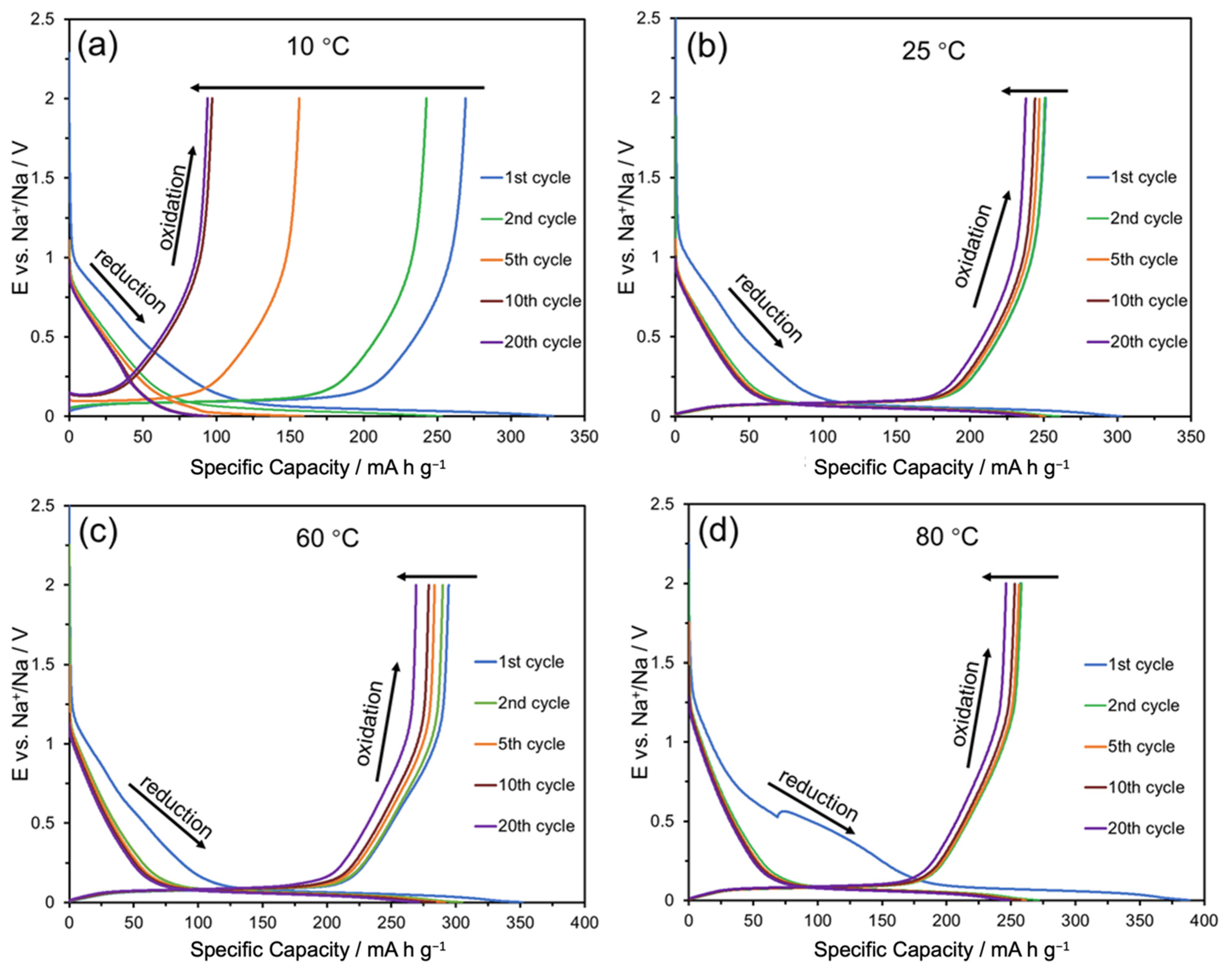
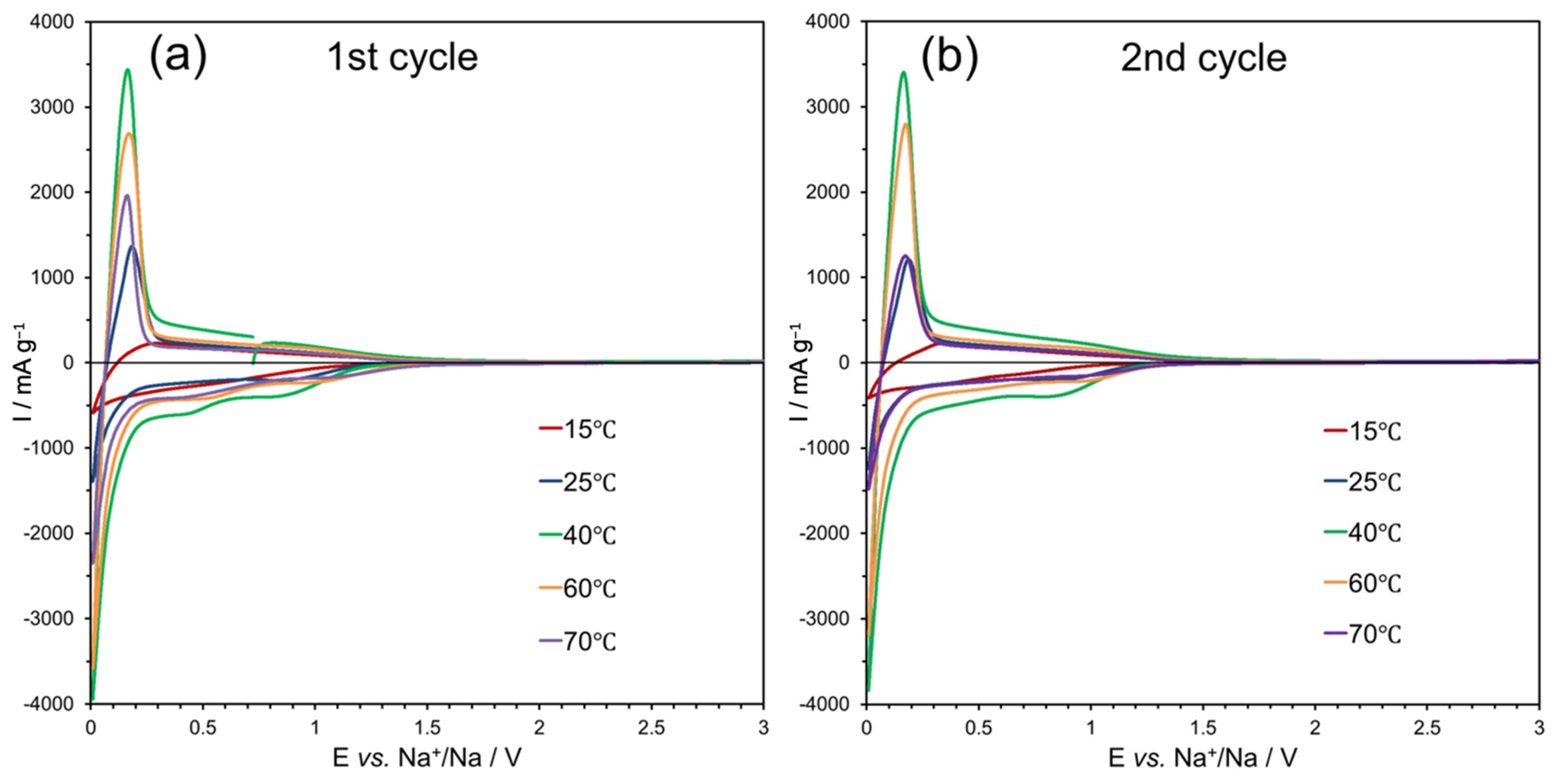
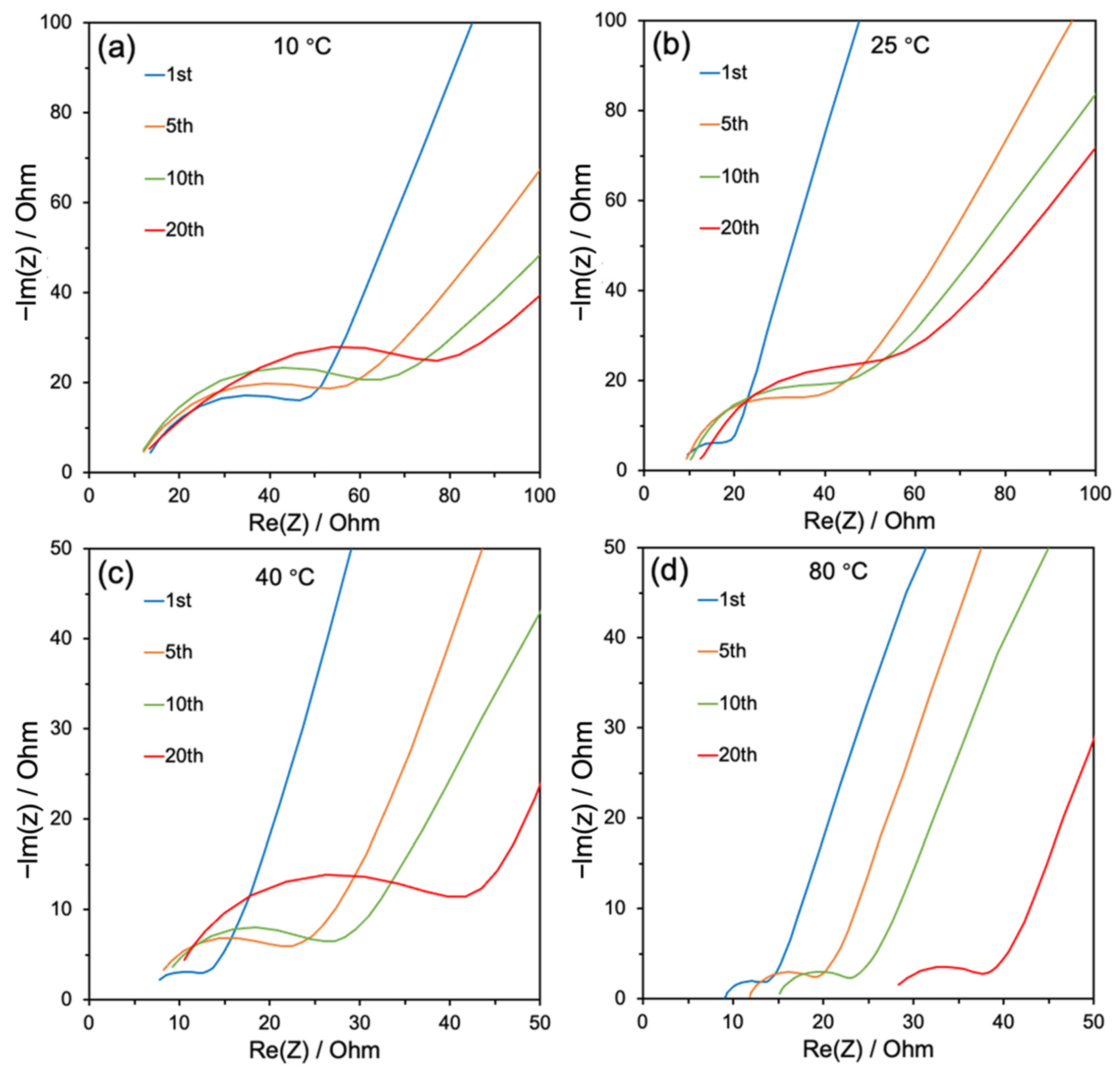
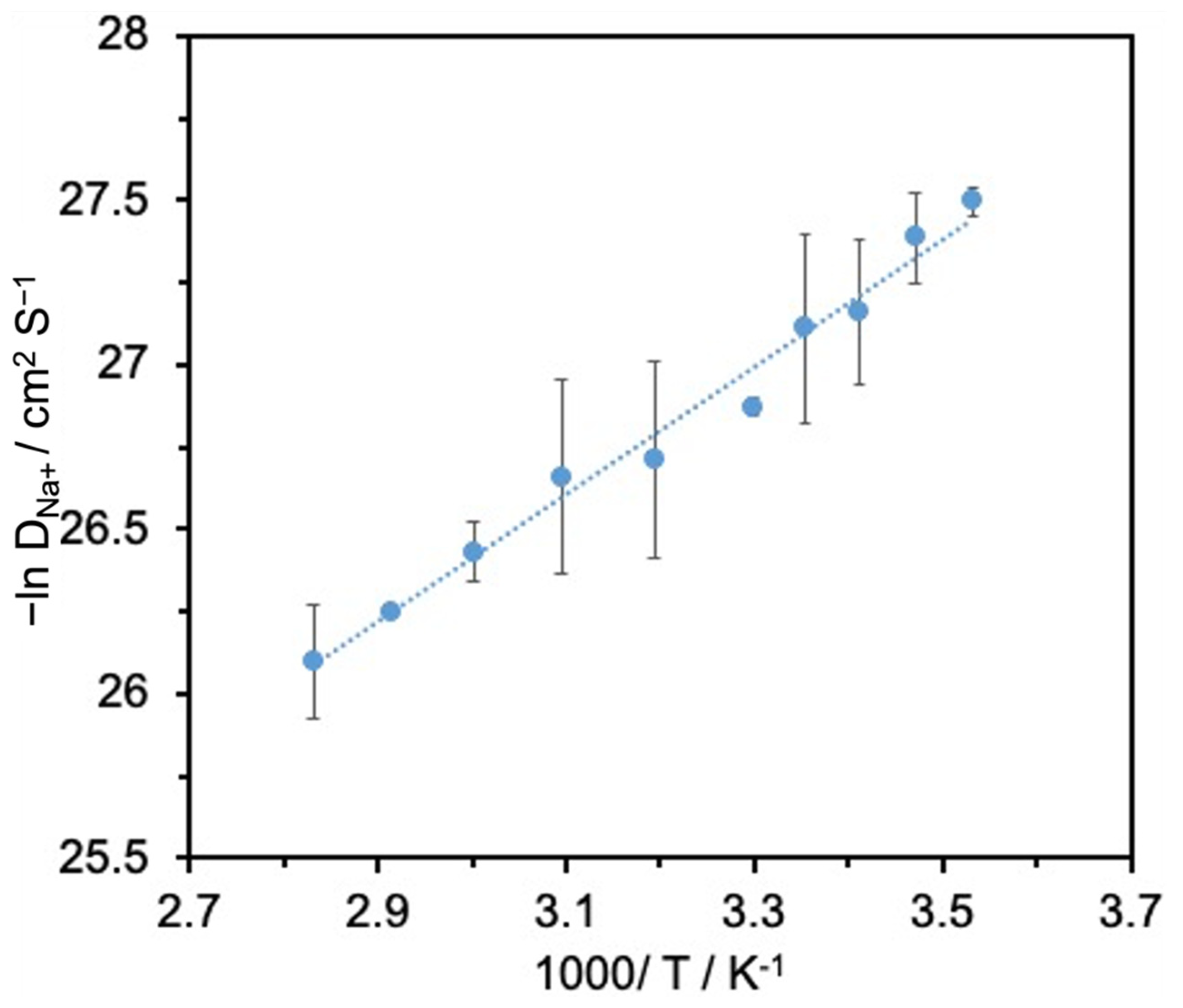
| Temperature (°C) | Rs (Ω) | Rct (Ω) | I0 (μA) | Ks (cm s−1) |
|---|---|---|---|---|
| 5 | 11.2 | 439 | 5.46 × 10−5 | 5.96 × 10−7 |
| 10 | 9.64 | 246 | 9.92 × 10−5 | 1.08 × 10−6 |
| 15 | 8.54 | 142 | 1.75 × 10−4 | 1.91 × 10−6 |
| 20 | 7.63 | 80.9 | 3.12 × 10−4 | 3.41 × 10−6 |
| 25 | 8.51 | 41.9 | 6.13 × 10−4 | 6.69 × 10−6 |
| 40 | 7.25 | 15.7 | 1.72 × 10−3 | 1.88 × 10−5 |
| 50 | 7.24 | 7.27 | 3.83 × 10−3 | 4.18 × 10−5 |
| 60 | 6.55 | 3.26 | 8.81 × 10−3 | 9.61 × 10−5 |
| 70 | 6.18 | 2.48 | 1.19 × 10−2 | 1.30 × 10−4 |
| 80 | 5.92 | 1.94 | 1.57 × 10−2 | 1.71 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Hector, A.L.; Razmus, W.O.; Wills, R.G.A. Temperature Dependence of Hard Carbon Performance in Sodium Half-Cells with 1 M NaClO4 in EC/DEC Electrolyte. Batteries 2022, 8, 108. https://doi.org/10.3390/batteries8090108
Liu B, Hector AL, Razmus WO, Wills RGA. Temperature Dependence of Hard Carbon Performance in Sodium Half-Cells with 1 M NaClO4 in EC/DEC Electrolyte. Batteries. 2022; 8(9):108. https://doi.org/10.3390/batteries8090108
Chicago/Turabian StyleLiu, Bowen, Andrew L. Hector, Weronika O. Razmus, and Richard G. A. Wills. 2022. "Temperature Dependence of Hard Carbon Performance in Sodium Half-Cells with 1 M NaClO4 in EC/DEC Electrolyte" Batteries 8, no. 9: 108. https://doi.org/10.3390/batteries8090108
APA StyleLiu, B., Hector, A. L., Razmus, W. O., & Wills, R. G. A. (2022). Temperature Dependence of Hard Carbon Performance in Sodium Half-Cells with 1 M NaClO4 in EC/DEC Electrolyte. Batteries, 8(9), 108. https://doi.org/10.3390/batteries8090108







