Abstract
The temperature of lithium-ion batteries is crucial in terms of performance, aging, and safety. The internal temperature, which is complicated to measure with conventional temperature sensors, plays an important role here. For this reason, numerous methods exist in the literature for determining the internal cell temperature without sensors, which are usually based on electrochemical impedance spectroscopy. This study presents a method in the time domain, based on the pulse resistance, for determining the internal cell temperature by examining the temperature behavior for the cylindrical formats 18650, 21700, and 26650 in isothermal and transient temperature states for different states of charge (SOCs). A previously validated component-resolved 2D thermal model was used to analyze the location of the calculated temperature within the cell, which is still an unsolved question for pulse resistance-based temperature determination. The model comparison shows that is close to the average jelly roll temperature. The differences between surface temperature and depend on the SOC and cell format and range from to (18650), to (21700), and to (26650). The difference decreases for each cell format with increasing SOC and is linear dependent on the cell diameter.
1. Introduction
Key features of lithium-ion batterys (LIBs), such as performance [1,2,3], aging [1,2,3], and safety [1,2], are heavily influenced by temperature. Therefore, monitoring and controlling the temperature within a battery pack is an essential task for any battery management system (BMS), with various methods for indicating LIB temperatures in existence [4]. Surface-mounted temperature sensors, such as thermistors or thermocouples, are a common method to measure the temperature of LIBs within a battery pack. Although these sensors are assumed to indicate temperatures close to the (average) internal LIB temperature [5], they suffer from heat transfer delay due to the thermal mass and thermal conductivity of batteries, and consequently, give an incomplete and delayed temperature information of the LIB. Particularly in certain operating scenarios, such as fast charging or demanding load conditions, the internal temperature may significantly differ from the surface temperature [4,6]. The resulting internal temperature differences, especially in larger format LIBs, may remain undetected and affect performance, aging, and safety of the LIB in an adverse way [7]. Therefore, several temperature estimation methods have been developed to overcome the limitation of surface temperature measurements and indicate the internal temperature of LIBs. These methods usually utilize a certain impedance feature of the electrochemical impedance spectroscopy (EIS) to determine the LIB’s temperature, whereby the nature of the determined temperature varies from method to method. Table 1 summarizes the statements on the determined temperature from existing methods in the literature, which range from electrode-specific temperatures [8,9], internal/core temperature [2,5,10,11,12,13,14,15,16,17,18,19] to average/integral [20,21,22], and internal temperature distribution [6,23,24,25]. The cells examined in the studies of Table 1 cover a wide variety of chemistries and casing types, including various cylindrical, prismatic, and pouch cells with capacities reaching from 2.3 –90 . Mainly individual cells were studied. Only [5,9,10,18,20] considered interconnected systems. Depending on the thermal boundary conditions, heating scenario, and cell format, the observed differences between internal cell temperature and surface temperature range from about 2 –3 [11,21], over 5 –7 [2,11,23], and up to 10 [24,26].

Table 1.
Overview of impedance-based temperature estimation methods in the literature.
In our previous work [27] we developed a temperature estimation method, which is not dependent on a certain impedance feature from the EIS, but directly relates the pulse resistance or direct current resistance () to the LIB’s temperature. Since the pulse resistance can be calculated from load fluctuations generated by the application itself, the method does not require excitation hardware to generate the specific sinusoidal signal required for an EIS or complex filters and transformations to extract the frequency spectrum from the current and voltage time-domain measurements of the BMS. Thereby, our method reduces the complexity and cost of an online sensorless temperature indication. In our previous studies, we avoided discrepancies between the measured surface and internal LIB temperature, since the focus was placed on method development [27] and aging behavior [28]. This was achieved by applying a controlled surface temperature with Peltier elements to a module of small cylindrical (18650) battery cells and moderate load conditions. For a better understanding and the differentiation of this work, the key results of the two previous publications are briefly summarized below.
The first publication [27] focused on the development and applicability of the method. For this purpose, the influence of different pulse parameters on the and the relation to SOC and temperature for three individual 18650 cells (same type as in Table 2) was examined. The parameters examined were the pulse amplitude, pulse duration, pulse current direction, and pulse shape. The pulse shape was varied by changing the pulse rise and fall time from instant ( 40 ) to . In the next step, a resistance-based temperature estimation method was developed and its accuracy was evaluated for various parametrization and validation scenarios. Subsequently, the transferability of the method from individual cells to a module consisting of six cells connected in series was examined. The cells of the module were of the same type, but different from those used for the original parametrization. To adjust the differences between the individual cells and the module, only an offset correction of the values was necessary. Finally, the applicability of the method was validated. For this purpose, the module was discharged with a dynamic load profile and the temperature was estimated using the developed method. The root mean square error (RMSE) for the validation ranged between and . Since aging has a major impact on the resistance of a cell, this topic was investigated in the second publication [28]. For this purpose, exactly the same module as in [27] was examined and aged with constant current and dynamic load profiles until the first cell in the module reached a state of health (SOH) of 80%. The influence of aging on the accuracy of the method was investigated and an extension of the method to adapt to capacity loss and resistance change was developed. By adapting the method to the effects of aging, the RMSE could be reduced from a maximum of 15 to .

Table 2.
General information and parameters of the investigated cells, including the nominal capacity (), the average capacity () and resistance () as well as the corresponding relative standard deviations and of the five cell batches used for the cell selection.
With cylindrical battery cell formats reaching from 18650, over 21700 to 26650 and even larger formats, such as Tesla’s 4680 cell, internal temperature discrepancies and their influence on LIBs vary significantly [29]. For instance, fast charging poses the risk of severe battery damage [30] if the battery temperature is not controlled correctly by the BMS and/or thermal management system, especially under harsh environmental conditions, such as extreme heat or cold. Therefore, this study focuses on the relation of a LIB’s pulse resistance, which was used for temperature estimation in our previous study [27], and the internal temperature of the three common cylindrical battery cell formats: 18650, 21700, and 26650. The study focuses on analyzing the relationship between the surface and the internal cell temperature in relation to the temperature indicated by the (). The aim is to determine to what extent the pulse resistance from our previous study [27] is suitable for monitoring the internal cell temperature and thus contributes to increasing the safety, performance, and lifetime of LIBs. For this purpose, three representative cylindrical cells are experimentally investigated under isothermal conditions and in a transient temperature state by applying an external temperature change similar to Haussmann and Melbert [21]. A validated 2D thermal model is utilized to analyze the internal temperature behavior of the cells and additionally serves as a reference for comparison with the pulse resistance-based temperature.
The remainder of this study is structured as follows. Section 2 describes the investigated cells, the utilized equipment as well as the test procedures. Section 3 briefly introduces the 2D thermal model used to analyze the relationship between the temperature indicated by the pulse resistance and the internal temperature of the investigated cells. Section 4 presents the results for the to temperature relation under isothermal conditions and the function to relate the to the cell temperature. Subsequently, the results for the temperature indicated by the () under an external temperature change and the surface temperature are compared and discussed. At the end of Section 4, the spatial relation of and the internal temperature simulated by the 2D thermal model are addressed. Section 5 summarizes the results, presents the key conclusions of the study, and gives an outlook on possible future work.
2. Experiment
2.1. Investigated Cells
For this study, the three cylindrical cells listed in Table 2 were selected. The 18650 and the 21700 cells were selected since they represent the latest nickel manganese cobalt oxide (NMC) chemistry with silicon content in the anode composite and a nickel-rich cathode material [33]. Furthermore, the 18650 was investigated in our previous studies [27,28] and the 2D thermal model of both cells (18650 and 21700) was already implemented and validated in the study of Steinhardt et al. [31]. The 26650 cell’s LiMn2O4 (LMO) chemistry [34,35] was chosen to investigate if the relation of the and temperature is altered by different chemistry. To verify the cell chemistries, the open-circuit voltages (OCVs) of the cells were analyzed using differential voltage analysis (DVA). The results are briefly presented in Appendix A. For each cell format, a batch of five sample cells was initially cycled for ten cycles according to the manufacturer’s standard charge and discharge procedure.
Subsequently, a representative cell was selected for this study from each batch, which showed the least deviation in resistance and capacity from the average batch parameters listed in Table 2. The cells were fully charged with a constant current (CC) followed by a constant voltage (CV) protocol until reaching the upper cut-off voltage, with equal to the manufacturer’s standard charging current and . The capacity of each cell in the batches was determined by discharging the fully charged cell with to the lower cut-off voltage. The resistance of each cell was determined with a galvanostatic EIS from 10 to 10 at a state of charge (SOC) of 50%, whereby represents the real part of the impedance at the zero-crossing of the imaginary part.
2.2. Experimental Setup
Figure 1 shows the experimental setup used in this study. Three PT100 temperature sensors were distributed over the cells’ surface: one sensor to measure the temperature at the positive terminal (), one sensor to measure the temperature at the center of the cell (), and one sensor to measure the temperature at the negative terminal (). The temperature sensors were bonded to the cells’ surface with superglue and monitored in a 4-wire connection with a cell measurement unit (CMU) from BaSyTec. An additional negative temperature coefficient (NTC) thermistor connected to a cell test system (CTS) from BaSyTec was used to measure the ambient temperature () close to the cells’ surface. All temperature sensors were initially gain and offset calibrated using a Fluke 1524 reference thermometer and a platinum resistance probe with an accuracy of . A potentiostat (VMP3) from BioLogic was used to electrically characterize the cells, which were connected via clipboards with gold contact pins in a 4-wire connection. Only the data acquisition of CTS and CMU were synchronized by integrating the CMU in the CTS test protocol. To synchronize the electrical measurements of the VMP3 and the temperature data of the CTS and CMU, the unused sense wires of the CTS were connected with the sense wires of the VMP3. Thereby, the pulses generated by the VMP3 were also measured from the CTS and served as a means of data synchronization. The thermal boundary conditions were set with a Binder KT 115 climatic chamber, achieving a temperature fluctuation of less than .
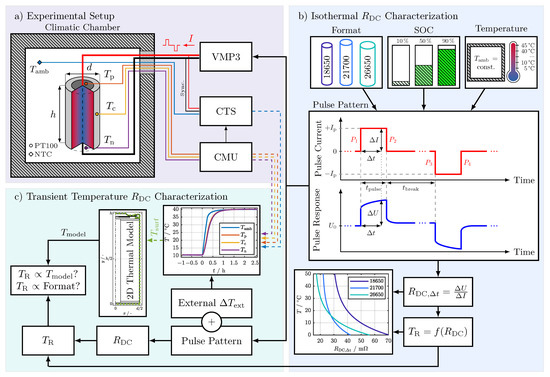
Figure 1.
Study overview. (a) Experimental setup: climatic chamber for temperature control, temperature sensor placement on investigated cells (temperature at the positive terminal (), temperature at the center of the cell (Tc), and temperature at the negative terminal (Tn)), ambient temperature (Tamb), and measurement equipment as follows: Potentiostat (VMP3) from BioLogic, cell test system
(CTS) and cell measurement unit (CMU) from BaSyTec. (b) RDC characterization (flowchart from top to bottom): investigated cell formats, SOCs, and temperature range followed by the pulse pattern used for the characterization of the investigated cells, the equation for the RDC calculation (Equation (1)), and an exemplary result for the temperature estimation function. (c) Internal temperature characterization: flowchart for the investigation of the relation between the internal temperature calculated by the 2D thermal model and the temperature calculated from RDC values during an external change in temperature (ΔText) by increasing the ambient temperature (Tamb) from 10 °C to 40 °C.
2.3. Test Procedures
Two test procedures were conducted in this study. The first one is depicted in Figure 1b, showing the isothermal characterization of the . The second test procedure in Figure 1c shows the transient temperature characterization under an external change in temperature. Both test procedures are presented in detail in the following sections.
2.3.1. Isothermal Characterization
The different cell formats from Table 2 were characterized at a SOC of 10%, 50%, and 90% in the temperature range of 5 –45 in 5 increments to gain the characteristics at isothermal conditions. The resistance of a cell is usually relatively constant over the middle SOC range, but can increase sharply at the edges of the SOC range [27,36]. In order to investigate the influence at the SOC fringe, the SOCs 10% and 10% were chosen, for the middle range a SOC of 50%. The of each cell at each SOC and temperature was calculated from the pulse pattern shown in Figure 1b. The cells rested for at least 6 at each temperature before the pulse pattern was applied to ensure that the cells were thermally and electrically equilibrated. For a continuous temperature estimation, continuous values and therefore continuous pulses were needed. To avoid a change in SOC, the pulse pattern contained one charging pulse followed by an equivalent discharging pulse to maintain an even charge balance. The individual pulse parameters listed in Table 3 were carefully selected to fulfill the following requirements:

- (P.1)
- Our previous analysis in [27] revealed that the optimal evaluation time for the for temperature estimation is in the region of 10 to approximately 100 . To cover this range with margin, the pulse duration () was set to 150 . However, the exact evaluation time () is determined in Section 4.1 with the results listed in Table 4.
- (P.2)
- The continuous pulses may affect each other since LIBs are time-variant systems. The pause between the charging and discharging pulses () was set to 5 , which proved to be long enough to avoid the preceding pulse to affect the following one (see Section 4.1).
- (P.3)
- To analyze the transient temperature behavior (see Section 2.3.2), the cell temperature is changed by externally heating the cell and simultaneously applying current pulses. Internal temperature changes due to heating of the cells through ohmic losses [37] caused by the continuous application of the pulses had to be avoided. Therefore, the pulse current and duration had to be small. The pulse duration with 150 selected in (P.1) is already relatively short. Nevertheless, the current had to be large enough to induce a voltage response with a sufficient signal-to-noise ratio (SNR) to avoid inaccurate measurements. The trade-off resulted in a pulse current of . Taking the resistance values for from Table 2 into account, the resulting heat generation of the applied pulses is less than for each cell.
To test the validity of the properties (P.1) to (P.3), the pulse pattern was repeated for over an hour (360 times) at each temperature, and SOC of the isothermal characterization. The pulses in Figure 1b were used to calculate the according to Equation (1), where is the resistance calculated from the current change and the corresponding voltage change after the time has passed. Only between 1 and 149 were evaluated.
Since the pulse pattern contains four different current changes, marked with to in Figure 1b, four different were calculated from the pattern. The final goal of the isothermal characterization was the derivation, parametrization, and analysis of the temperature estimation function for the different pulse current types ( to ) and evaluation times (), exemplary depicted at the bottom of Figure 1b. The corresponding results are presented and discussed in Section 4.1.
2.3.2. Transient Temperature Characterization
The test procedure for the transient temperature characterization in Figure 1c was realized by simultaneously generating an from 10–40 with the climatic chamber and continuously applying the pulse pattern from Figure 1b to the cells. Before heating the cells with the maximum heating rate to 40 , the cells rested at least for 6 at 10 to ensure that they start from a thermally equilibrated state. The resulting temperature behavior is exemplarily shown in the upper right corner of Figure 1c. The pulses were used to continuously calculate values, which in turn were used to estimate the temperature with the function determined in Section 4.1. The data of , , and was used during the external temperature change to determine the relation between the estimated temperature and the averaged surface temperature () for the different cylindrical cell formats. Here, is the average of , , and . Additionally, the surface temperature served as input for the 2D thermal model [31] for the 18650 and 21700 cells to identify the internal cell temperature distribution () during the external temperature change and investigate the relation between and . The corresponding results are presented and discussed in Section 4.2. The model itself is briefly described in the upcoming section.
3. 2D Thermal Model
A previously validated 2D thermal model was used to relate to the internal temperature distribution for the 18650 and 21700 cells. This model was developed and parameterized by Steinhardt et al. [31] for the same cell types as used in this work. The model is a component-resolved model, which means that components such as the steel case and the current interrupt device in the positive cell pole are resolved separately. Overall, the axisymmetric model geometry in Figure 1c defines seven domains with no heat source term, since the cells are not operated in this study. The dimensions of the geometry were either measured in [31] with a micrometer screw or taken from computed tomography scans of the cell. All simulations were run in COMSOL Multiphysics 5.4 with an adiabatic boundary in the inner core of the cell and a defined temperature for the rest of the boundaries.
Every material parameter in the model is considered isotropic except for thermal conductivity, which is defined by the in-plane and through-plane directions of the cell’s jelly roll. In the study by [31], the thermal conductivity and the specific heat capacity of the electrode-separator stack were measured at three different SOCs. The measured thermal parameters at the lowest, middle, and highest SOC by [31] were used in this work for the SOC of 10%, 50%, and 90%, respectively. Since the dependence of the thermal model parameters on temperature is less than 0.2% , a dependence on temperature in the model is omitted and all parameters were set to their 300 value, which also helped to reduce the model complexity. For example, for the 18650 cell at a SOC of 50%, a specific heat capacity for the jelly roll of 1004 // and a through-plane conductivity of // were taken from [31] and used for the simulation in this work. For all further details, we refer the interested reader to the work of Steinhardt et al. [31].
4. Results & Discussion
4.1. Isothermal Characterization
In our previous works [27,28], we used a general exponential equation, such as [21,22], to describe the relationship between resistance and temperature. However, in the literature, the relation between resistance for different cell internal processes and temperature is frequently described with a (modified) Arrhenius relation [8,10,11,12,14,18,19,20,23]. Since the Arrhenius relation is a more commonly used and physics-based approach, the goal of this chapter is to deduce and parameterize an Arrhenius-based function describing the relation between the values, derived from the characterization pulses, and the cell temperature in thermal equilibrium. First, the processes that make up the overpotential during the 150 pulse need to be identified. Subsequently, a function in the time domain is derived to map the resistance-temperature behavior. The current pulse duration of 150 limits the effects, building up the voltage response to the following processes [36,38,39]:
- (E.1)
- Ohmic losses, due to limiting electronic/ionic conductivity of the current collectors, the electrolyte, the active materials of the electrodes, and additives, such as carbon black.
- (E.2)
- Contact losses, attributed to contact resistance between one of the electrodes and the current collector, as well as from particle-to-particle contacts.
- (E.3)
- Interface losses, related to the charge transfer at the electrodes, as well as the contribution of the solid electrolyte interface (SEI).
The contribution of slower processes, such as diffusion, to the voltage response of the characterization pulses, was assumed to be negligibly small within 150 and is therefore neglected.
After identifying the processes building up the voltage response and consequently the , a functional description of the relation between the processes and cell temperature is needed. The ohmic and contact losses are dominated by the ionic conductivity of the electrolyte [36]. Schmidt et al. [11] used the general Arrhenius relation in Equation (2) to describe the functional relation between temperature and the electrolyte impedance of a LIB from EIS measurements.
To account for the influence of temperature-independent resistances, such as the current collectors and contact resistances, in the impedance spectra Schmidt et al. [11] expanded the general Arrhenius to Equation (3) by adding the temperature-independent term .
Although the electronic resistance of the current collector increases with temperature, the authors assumed the resistance to be almost constant in the investigated temperature region between 0 –30 [11]. The remaining variables are the activation energy , the Boltzmann constant , a pre-exponential factor representing the hypothetical resistance at an infinite temperature, and the absolute temperature . Gantenbein et al. [36] confirmed the results of Schmidt et al. [11] for Equation (3) and additionally used Equation (2) to describe the temperature dependence of the resistance related to the charge transfer and SEI process using EIS measurements and analyzing the distribution of relaxation times. Barai et al. [40] showed that different resistance characterization methodologies, such as and EIS, can be aligned if the time scales match. Therefore, a parametrization of Equations (2) and (3) with values comparable to Schmidt et al. [11] and Gantenbein et al. [36] should be achievable. Since the is calculated in the time domain, it is difficult to assign a particular to an individual process, such as ionic electrolyte conductivity or charge transfer, in contrast to analysis making use of impedance spectra as in [11,36]. Consequently, at least the sum of Equations (2) and (3) would be required to describe the temperature behavior of the , although a meaningful parametrization is hardly feasible, since, as mentioned above, no clear separation of the processes in the time domain is possible. However, the aim of the study is not to describe the temperature dependence of the individual processes (E.1) to (E.3) separately, but to describe them in total. For this reason, the authors assume that a single temperature-independent term () and one temperature-dependent exponential term (), as in Equation (3), are sufficient to represent the overall behavior of the over temperature. For the finally needed description of temperature as a function of resistance, the inverse function of Equation (3) is formed, resulting in Equation (4).
The function of Equation (4) was parameterized for the four current changes to of the pulse pattern in Figure 1b for each cell format and in the range of 1–149. Figure 2 serves as a representative fitting result for to discuss the results of the parametrization. The results of the parameters (see Figure A2), (see Figure A3), and (see Figure A4) for all are depicted in Appendix B. Although a physical interpretation of the parameters is not the aim of this work, it is worth noting that the results for the activation energy in Figure A2 are in a reasonable range of 0.1–0.6 for between 1 and 149. The values for tend towards common literature values for the activation energy related to the ionic conductivity of the electrolyte with [39], [36], and [41]. With increasing the activation energy rises to almost eV, covering common literature values related to the interface processes between the anode, including the SEI, and the electrolyte with 0.35–0.45 [42], [36], 0.55–0.62 [43], and [44], and also related to the charge transfer at the cathode with [36] and 0.64–0.69 [43]. The values for the temperature-independent resistance in Figure A3 are close to the initially measured in Table 2, which was determined with EIS measurements.
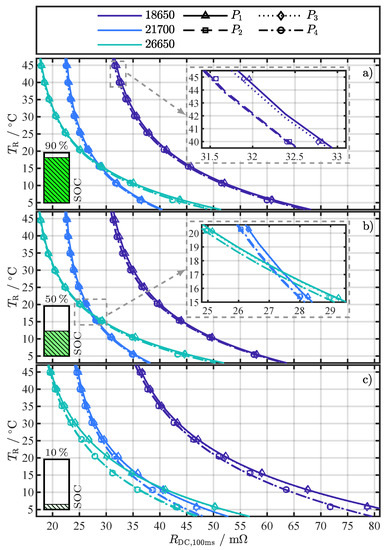
Figure 2.
Exemplary fitting results of Equation (4) for for different cell formats and current changes to (see pulse pattern in Figure 1b) at the investigated SOCs (a) 90%, (b) 50%, and (c) 10%. The marker type represents the averaged value from the repeated pulse pattern (360 values) at each temperature point. The close-ups in (a,b) visualize the minimal difference between current changes and .
Each subfigure in Figure 2 shows one of the investigated SOCs: 90%, 50%, and 10%. The fitting results for different cell formats are distinguished by color and the current changes by line and marker type, whereby the marker type represents the averaged value from the repeated pulse pattern (360 values) at each temperature point. No trend in could be observed over the 360 pulses for a specific temperature. Therefore, the break of 5 between pulses proved to be long enough to prevent the repeating pulses from significantly interfering with each other (P.2) or heating the cells internally (P.3). As assumed, Equation (4) can reflect the temperature behavior of the values, despite the fact that the resistance values represent the superposition of several processes. Similar to [19,22], who used the R-Square () as a criterion for assessing the fitting quality for their temperature estimation method, the adjusted R-Square () [45] was used for a quantitative assessment of the fitting results in this work. The and are statistical measures for the goodness of a curve fitting result, whereby values closer to one indicate a better fit quality. In contrast to the , the number of fitted variables is taken into account with the to avoid over-fitting. As the number of fitted variables increases, will also increase. However, the fitting quality may not improve in a practical sense. To avoid such over-fitting, the statistic can be utilized. The overall above 0.98 for all (see Figure A5), strongly indicates the validity of Equation (4) as the proposed fitting function.
Assessing the fitting results in Figure 2 for any of the three cells over the SOC range, the expected dependency on the SOC can be seen. The dependency becomes apparent by comparing the x-axis values where the fitting function exceeds 45 . For example, this value for the 26650 cell is around 32 at a SOC of 90% in Figure 2a, then drops slightly in Figure 2b at a SOC of 50% to around 31 and rises in Figure 2c at a SOC of 10% to about 35 . These SOC-dependent fluctuations can also be observed in the 18650 and 21700 cell and are consistent with previous studies [27,36]. The difference in the curves, parameterized with and , compared to the curves, parameterized with and , is particularly evident at temperatures below 25 and the SOC of 10% in Figure 2c. At a first glance, there is no difference in the fitting results for the different current changes for the SOCs 90% and 50% in Figure 2a,b. However, the close-ups in Figure 2a,b reveal that there is a difference in the curves, albeit a small one. In our previous study [27], we already noticed this difference in for the 18650 cell for different current changes, which is probably caused by the initial condition of the cells at the start of the pulse. For and the cells start from an almost equilibrated state, where no current is applied. On the other hand, and start from a already polarized state, since current was already flowing for 150 , creating a small Li-ion concentration gradient [46]. With the current changes at and , the system returns to the equilibrium state and the concentration gradients decrease. This difference in Li-ion concentration at the start of compared to results in a small overpotential difference and might be the cause for the difference in [40].
For the determination of the cell temperature behavior during the external temperature change in Section 4.2, a and current change type ( to ) must be selected that is used for the parametrization of Equation (4). Since all have a very high in Figure A5, the RMSE of the fitting is used as the second criterion for the selection. In Figure A6, the RMSE of the individual fit variants is shown as a complement to the in Figure A5. Table 4 summarizes the minimal RMSE for each SOC and cell format together with the corresponding pulse current type () and for the temperature estimation with Equation (4) in Section 4.2, the settings ( and ) for the minimal RMSE from Table 4 as well as all other settings within an error margin of in respect to the minimum error were used. This measure intends to minimize the influence of noise and increase the accuracy of the temperature estimation during the external temperature change, which is discussed in the next section.
4.2. Transient Temperature Characterization
The results for the temperature estimation with Equation (4) and the setting according to Table 4 are presented in Figure 3. The figure only showcases the results for a SOC of 50%. The originally calculated values () in Figure 3a–c all tend to increased noise for increased temperatures, whereby the level of noise differs from cell to cell. By considering the corresponding estimation functions in Figure 3d–f, it is apparent that the different slopes of the estimation functions are responsible for the different noise levels. Schmidt et al. [11] also noticed this for their EIS-based temperature estimation method. The exemplary input deviation of for the nominal value of 10 causes a deviation in temperature below . In contrast, the same input deviation at 40 causes a variation between (Figure 3d) and (Figure 3e). However, the filtered values () emphasize that the noise can be significantly reduced by applying a moving average filter.
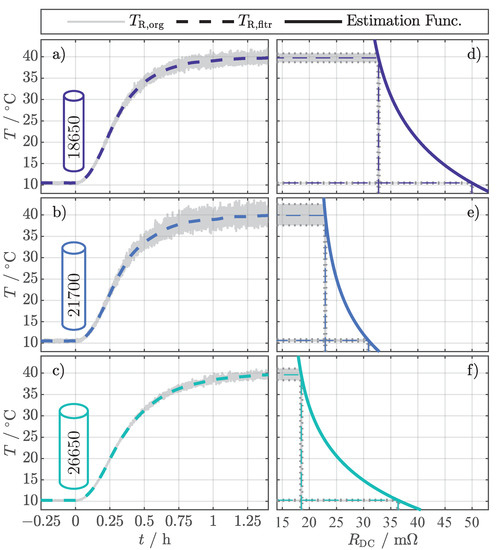
Figure 3.
Exemplary temperature estimation results for the investigated cell formats 18650 (a), 21700 (b), and 26650 (c) at a SOC of 50% evaluated with Equation (4) and the setting according to Table 4. shows the originally calculated values and shows the values filtered with a moving average filter. The different and increased noise can be related to the individual slopes of the estimation functions in (d–f).
Figure 4 relates the sensor temperature data to the filtered . The moment when the setpoint for the climatic chamber temperature () changes from 10–40 was set to zero on the x-axis. The variation of the ambient temperature () for the different cell formats at the different SOCs is negligibly small. However, there is a small difference between cells, probably caused by the positioning of the cells within the climatic chamber. The ambient temperature rises from 10 with a constant heating rate of about 100 / to 35 in about and converges to the final temperature of 40 in about . Since the mean absolute deviation over all cell surface related temperatures (, , ) during each experiment is less than , only the average over the three cell surface temperature sensors () is depicted in Figure 4. The resistance-related temperature always lags behind the average surface temperature for each cell format and SOC, whereby the difference increases with increasing cell size. This already shows that , like the temperatures of the existing EIS-based methods in Table 1, is related to the internal cell temperature and depends on the cell dimensions. For a detailed analysis, the difference between the surface temperature and the is considered and discussed in comparison to the 2D thermal model in the following section.
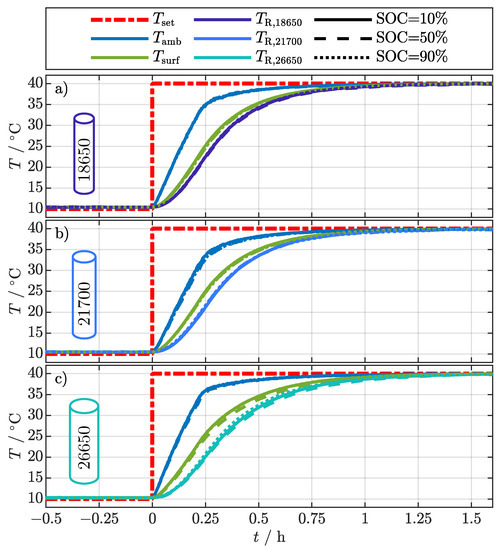
Figure 4.
Temperature development during the external temperature change from 10–40 for the different cell formats 18650 (a), 21700 (b), and 26650 (c) at the investigated SOC of 10%, 50%, and 90%.
4.3. Internal Temperature: Model versus
With the help of the 2D thermal model from Section 3, the internal temperature of the cells, especially the jelly roll, can be broken down in more detail and can be assigned to a corresponding internal temperature. For this purpose, six simulations were run evaluating the core (), the center (), and the average () temperature of the jelly roll. The spatial location of the temperatures is shown in Figure 5j, with the temperature simulated at half of the cell height and at the core of the jelly roll (), the temperature simulated at half of the cell height and at the center of the jelly roll (), and the simulated average jelly roll temperature (). The averaged surface temperature () was used as the temperature boundary condition on the entire surface of the cells, also shown in Figure 5j. The evaluation of the temperature difference between and the jelly roll temperatures (, , ) resulted in the corresponding temperature differences (, , ) for the 18650 and 21700 cell at the three SOC points shown in Figure 5a–f. Additionally, the corresponding differences (, ) between and are depicted. For the 26650 cell, only the differences () between and are depicted in Figure 5g–i, since the model parameters for this cell type were not investigated by Steinhardt et al. [31].
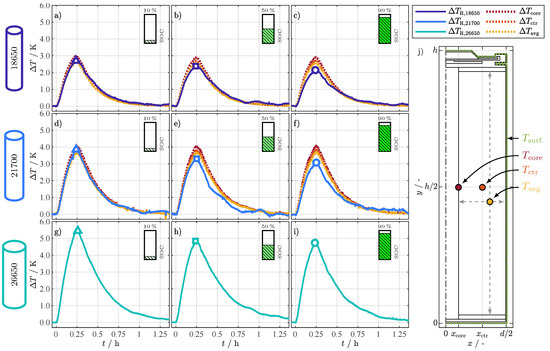
Figure 5.
Temperature differences (a–c), (d–f), and (g–i) between the averaged surface temperature () and the temperature indicated by the () at each SOC point and for each cell format. Additional temperature differences , , and in (a–f) for the three simulated temperature locations of the jelly roll in (j) according to the 2D thermal model simulation results for the 18650 and 21700 format. The differences are again related to the averaged surface temperature. and are simulated at half of the cell height () and at the core (), respectively at the center () of the jelly roll. represents the average simulated jelly roll temperature.
Comparing the differences in Figure 5 over the cell format, it is remarkable that they increase with the cell size and decrease with the SOC. For the 18650 format, in Figure 5a–c the maximal difference for , marked with symbols, ranges between and . For the 21700 format in Figure 5d–f, the range lies between and ; for the 26650 format in Figure 5g–i, between and . There are deviations between simulation- and resistance-related temperature differences for the individual formats depending on the SOC. For a SOC of 10% in Figure 5a,d, the resistance-related differences and are in good accordance with the simulated differences and range between the average and the center temperature, which is in accordance with [20,21,22] from Table 1. This result seems realistic for two reasons: First, maps the temperature dependence of the aggregated processes of the cell (see (E.1) to (E.3)), which corresponds to the concept that also maps the aggregated/average temperature of the jelly roll. Second, assuming that the relationship between resistance and temperature (see Figure 2) is almost linear for the temperature differences considered (), the area-related average temperature () also corresponds to the area-related average value of the resistance. With increasing SOC in Figure 5b,c,e,f and keep decreasing, whereas the simulated temperatures show minor differences between SOCs, although the simulation parameters are adapted to the SOC. For the 18650 format, the maximum simulated difference for decreases only by from at 10% SOC to at 90% SOC, which is in accordance with the increasing through-plane thermal conductivity for this cell [31]. The difference , in contrast, decreases by . The simulation results for the maximum difference of for the 21700 format stay within , whereas decreases by . The deviations between simulated and -based temperature differences are obvious, but stay below and are closest to . The deviations arise from two possible reasons:
- (R.1)
- Although the simulation parameters are for the same pristine cell type, they were not determined for exactly the same cell and thus might slightly differ between the cells used in [31] to parameterize the 2D thermal model and the ones used in this study. Also, the SOC points in the study by Steinhardt et al. [31] do not exactly match the SOC points investigated in this study. Since the thermal conductivity of a LIB is dependent on the SOC [47], the parameter deviation in thermal conductivity might partly cause the deviation between the simulation and .
- (R.2)
- The 2D thermal model does not consider thermal conductivity changes related to mechanical changes. The jelly roll expands when the cell is charged [48] and the contact area and pressure between the layers in the jelly roll and between the jelly roll and the metal casing of the cell increases. Several studies [49,50] showed that increased compression reduces the thermal contact resistance, leading to improved thermal conductivity and therefore reducing the difference between surface and core temperature.
While no specific reason in the previous list can be pinpointed as the decisive one, in sum they explain the deviations between simulated temperature differences and .
4.4. Internal Temperature: Cell Geometry & State of Charge
All cells reach the maximum difference after approximately at the end of the constant heating phase (see Figure 4). The peaks are highlighted with different markers in Figure 5, representing the different SOC, and are used to discuss the dependence on cell geometry and SOC in Figure 6. The dependence of the maximum difference () on the cell diameter is depicted in Figure 6a and on the SOC in Figure 6b.
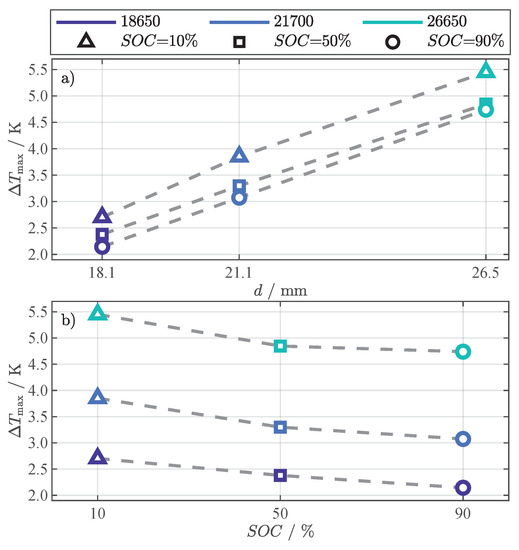
Figure 6.
Relation between the maximum of the -based temperature difference () from Figure 5 and cell diameter d (a), respectively SOC (b).
The correlation with the cells’ diameter, surface, and volume was investigated using the values for height h and diameter d from Table 2 and the general equations for a cylindrical body. All three geometrical values show a high linear correlation to at any SOC, indicated by a Pearson correlation coefficient of at least . In Figure 6a, the relation between and the cell diameters is depicted, which had the highest correlation. As expected, the difference increases with rising cell diameter.
The maximum difference steadily decreases with increasing SOC, as depicted in Figure 6b. As already discussed, this is in contrast to the simulation results in Figure 5a–f, but can be explained with model parameter uncertainties (R.1) and missing mechanical dependencies of the model on pressure and thermal contact resistance (R.2).
5. Summary & Conclusions
Knowing the internal temperature of LIBs is essential for performance, aging, and safety aspects. In the literature various studies exist, which determine different internal cell temperatures with EIS-based methods (see Table 1). In contrast to the existing literature methods, we proposed a time-domain approach based on the pulse resistance in our recent work [27]; however, we did not focus on the cell’s internal location of the temperature determined with the . Therefore, we investigated the relation of the -based temperature and the surface temperature of three different cylindrical LIBs listed in Table 2 and compared the results to a validated 2D thermal model for the 18650 and 21700 format. First, the temperature estimation function (see Equation (4)) was deduced and parameterized under isothermal conditions for the three SOCs: 10%, 50%, and 90%. Subsequently, the estimation functions were used to determine during an external temperature change from 10 to 40 . The different slopes of the estimation functions resulted in different temperature noise levels, especially at elevated temperatures above 30 with up to . The noise was reduced with a moving average filter, which resulted in the necessary measurement accuracy (see Figure 3). Compared to the averaged surface temperature, was found to represent an internal temperature of the cells, whereby the difference to the averaged surface temperature increased with cell dimensions (see Figure 4). In order to establish a more precise relationship between and the internal cell temperature, the surface temperature difference was compared with the corresponding simulation results of the 2D thermal model (see Figure 5). The simulation results for the average/center temperature of the jelly roll and match for a SOC of 10%. For increased SOCs the simulation results show minor changes, whereas steadily decreases, but is still within to the simulation results and closest to . The difference between simulation and could be traced back to two possible reasons: model parameter uncertainties (R.1) and missing mechanical dependencies of the model on pressure and thermal contact resistance (R.2). Correlating the cell diameter to the temperature difference showed an almost perfect linear relation with a Pearson correlation coefficient of above (see Figure 6a). This result shows that the use of resistance-based temperature estimation is more relevant for larger cell formats, as the difference between surface and internal temperature increases and the method determines the average jelly roll temperature. The development of the temperature difference over the SOC showed a decreasing trend (see Figure 6b). This is probably a consequence of the jelly roll expansion, causing a reduced thermal contact resistance between the jelly roll and metal casing and increasing the thermal conductivity.
In conclusion, the following key results of the study can be identified:
- The can be utilized to determine the internal cell temperature for different cell chemistries and cylindrical cell formats.
- The comparison with the 2D thermal model shows that most likely represents the average jelly roll temperature (). Thus, offers an advantage over conventional temperature sensors, which only determine the surface temperature at one point of the cell.
- Consequently, methods as in our previous works [27,28], which are based on the , can contribute to improving the performance, lifetime, and safety of LIBs by detecting internal temperature discrepancies before conventional temperature sensors.
- An important point regarding the applicability is the temperature range, for which -based methods are applicable. As shown in Figure 3, the accuracy of the method strongly depends on the slope of the estimation function (Equation (4)), which steadily increases with rising temperatures. For this reason, correspondingly precise measurement hardware for the current and voltage monitoring of the BMS is a prerequisite to avoid large temperature estimation errors in the elevated temperature range.
Based on the results of this study, new questions arise that are worth investigating. For example, a detailed study on the relationship between jelly roll expansion and would be interesting, especially the question if follows the nonlinear course of the diameter change of cylindrical LIBs over the SOC, such as measured by [48]. The present study only considered homogeneous surface temperature changes. For safety reasons, an investigation into “hot spots”, induced by locally heating the cells, would also be of interest.
Author Contributions
Conceptualization, S.L.; methodology, S.L.; software, S.L. and M.S.; validation, S.L. and M.S.; formal analysis, S.L. and M.S.; investigation, S.L.; data curation, S.L.; writing—original draft preparation, S.L. and M.S.; writing—review and editing, S.L., M.S. and A.J.; visualization, S.L.; supervision, A.J.; project administration, S.L.; funding acquisition, A.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the German Federal Ministry of Education and Research (BMBF) via the research project OSLiB (grant number: 03X90330A). The project was overseen by Project Management Juelich (PtJ).
Data Availability Statement
Not applicable.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| BMS | battery management system |
| CC | constant current |
| CMU | cell measurement unit |
| CTS | cell test system |
| CV | constant voltage |
| DVA | differential voltage analysis |
| EIS | electrochemical impedance spectroscopy |
| FEM | finite element model |
| LIB | lithium-ion battery |
| LMO | LiMnO |
| NMC | nickel manganese cobalt oxide |
| NTC | negative temperature coefficient |
| OCV | open-circuit voltage |
| R-Square | |
| adjusted R-Square | |
| direct current resistance | |
| RMSE | root mean square error |
| SEI | solid electrolyte interface |
| SNR | signal-to-noise ratio |
| SOC | state of charge |
| SOH | state of health |
| SSE | sum of square error |
| SST | total sum of squares |
| ambient temperature | |
| simulated average jelly roll temperature | |
| temperature at the center of the cell | |
| temperature simulated at half of the cell height and at the core of the jelly roll | |
| temperature simulated at half of the cell height and at the center of the jelly roll | |
| external change in temperature | |
| temperature at the negative terminal | |
| temperature at the positive terminal | |
| temperature indicated by the | |
| temperature difference between and the for the 18650 cell | |
| temperature difference between and the for the 21700 cell | |
| temperature difference between and the for the 26650 cell | |
| averaged surface temperature |
Appendix A. Differential Voltage Analysis
Figure A1 shows the DVA of the three investigated cells and the corresponding markers for silicon (Si), graphite (Gr), and NMC. The DVAs were evaluated from OCVs gained from a discharge with between 4.2 to 2.5 with being the discharge capacity. Since the 18650 and 21700 cell have the same chemistry, the markers for silicon, graphite, and NMC in Figure A1a,b are almost identical in SOC and magnitude. The DVA of the 26650 cell in Figure A1c lacks the silicon peaks and only shows the typical graphite peaks, which speaks for a pure graphite anode with no silicon content. The LMO cathode could not be verified by the DVA, but is reported by [34,35].
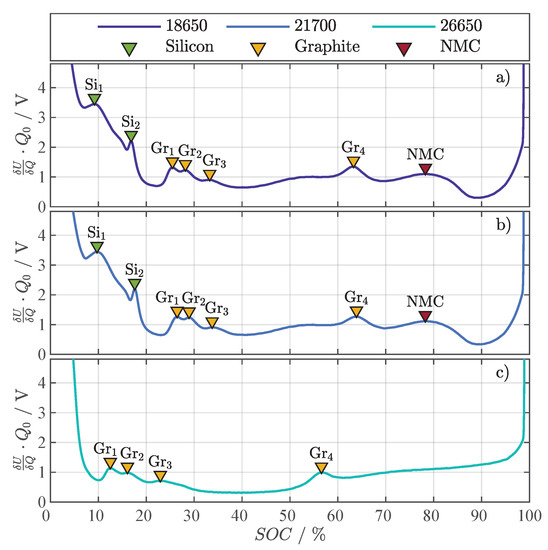
Figure A1.
Differential voltage analysis with representative peak markers for silicon (Si), graphite (Gr), and NMC for the three investigated cell formats: 18650 with NMC | Si/Gr (a), 21700 with NMC | Si/Gr (b), and 26650 with LMO | Gr (c).
Appendix B. Function Parameters
The three fitting parameter , , and for Equation (4) in the range of 1–149 are depicted in Figure A2, Figure A3, and Figure A4, respectively. Each figure shows the parameters for the three investigated cell formats and the four different pulse current types ( to ), with a subplot for the corresponding SOCs 90%, 50%, and 10%.
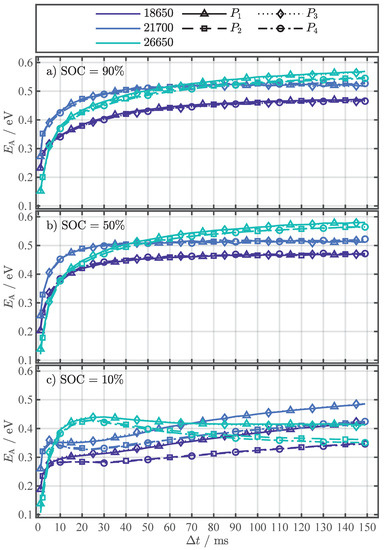
Figure A2.
Fitting results for Equation (4) for the parameter , each investigated cell format, and the four different pulse current types ( to ) at the SOCs 90% (a), 50% (b), and 10% (c).
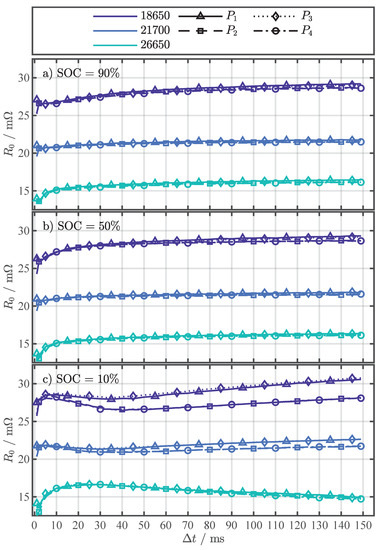
Figure A3.
Fitting results for Equation (4) for the parameter , each investigated cell format, and the four different pulse current types ( to ) at the SOCs 90% (a), 50% (b), and 10% (c).
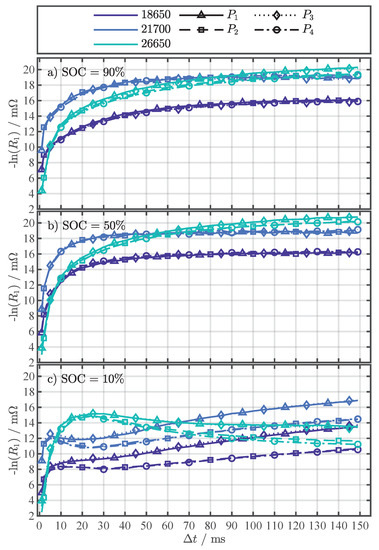
Figure A4.
Fitting results for Equation (4) for the parameter , each investigated cell format, and the four different pulse current types ( to ) at the SOCs 90% (a), 50% (b), and 10% (c).
Appendix C. Fitting Quality & Error
This section briefly introduces the calculation of the as a statistical measure of the goodness of a curve fitting result and the RMSE as measure of the fitting error. The results were generated using MATLAB’s curve fitting toolbox. The can be calculated from Equations (A1)–(A4), where:
- -
- the sum of square error (SSE) in Equation (A1) describes the total deviation of the response values of the fit from the measured response values ,
- -
- the total sum of squares (SST) in Equation (A2) describes the total deviation of the mean from the measured response values ,
- -
- the general in Equation (A3) determines how successful the fit is in explaining the variation of the data,
- -
- and the adjusted R-Square statistic in Equation (A4) considers the number of fitted model variables m in addition to the number of response values n.
A more detailed description on the calculation of can be found in [45]. Figure A5 shows the for in the range of 1 –149 for the investigated cell formats and the four different pulse current types ( to ), with each subplot showing one of the investigated SOCs of 10%, 50%, and 90%. The values close to 1 indicate an almost optimal fitting quality for the parameters of Equation (4).
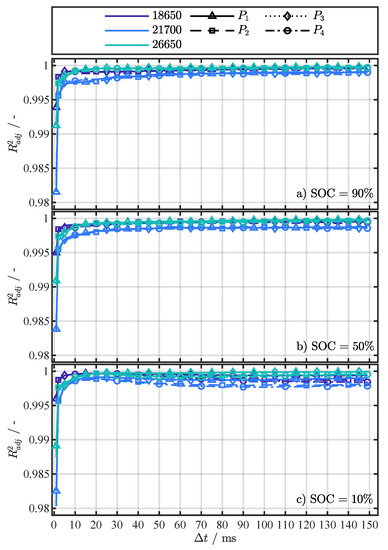
Figure A5.
results for fitting Equation (4) for each investigated cell format and the four different pulse current types ( to ) at the SOCs 90% (a), 50% (b), and 10% (c).
The RMSE in Figure A6a,b steadily decreases with increasing leveling below , whereby the error for and is minimally smaller than for and . This is partially true for a SOC of 10% in Figure A6c as well. In contrast to Figure A6a,b, the RMSE increases again for greater than 25 except for the parametrization with and for the 26650 cell. Again, the error for and is in general smaller than for and .
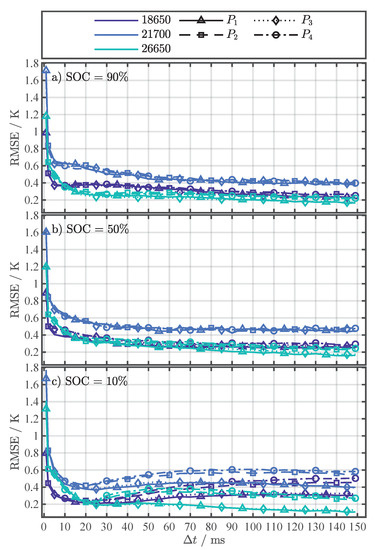
Figure A6.
RMSE results for fitting Equation (4) for each investigated cell format and the four different pulse current types ( to ) at the SOCs 90% (a), 50% (b), and 10% (c).
References
- Ma, S.; Jiang, M.; Tao, P.; Song, C.; Wu, J.; Wang, J.; Deng, T.; Shang, W. Temperature effect and thermal impact in lithium-ion batteries: A review. Prog. Nat. Sci. Mater. Int. 2018, 28, 653–666. [Google Scholar] [CrossRef]
- Morello, R.; Di Rienzo, R.; Roncella, R.; Saletti, R.; Schwarz, R.; Lorentz, V.; Hoedemaekers, E.; Rosca, B.; Baronti, F. Advances in Li-Ion Battery Management for Electric Vehicles. In Proceedings of the IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 4949–4955. [Google Scholar] [CrossRef] [Green Version]
- Alipour, M.; Ziebert, C.; Conte, F.V.; Kizilel, R. A Review on Temperature-Dependent Electrochemical Properties, Aging, and Performance of Lithium-Ion Cells. Batteries 2020, 6, 35. [Google Scholar] [CrossRef]
- Raijmakers, L.; Danilov, D.L.; Eichel, R.A.; Notten, P. A review on various temperature-indication methods for Li-ion batteries. Appl. Energy 2019, 240, 918–945. [Google Scholar] [CrossRef]
- Beelen, H.; Mundaragi Shivakumar, K.; Raijmakers, L.; Donkers, M.; Bergveld, H.J. Towards impedance–based temperature estimation for Li–ion battery packs. Int. J. Energy Res. 2020, 44, 2889–2908. [Google Scholar] [CrossRef]
- Richardson, R.R.; Zhao, S.; Howey, D.A. On-board monitoring of 2-D spatially-resolved temperatures in cylindrical lithium-ion batteries: Part II. State estimation via impedance-based temperature sensing. J. Power Sources 2016, 327, 726–735. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Ai, W.; Naylor Marlow, M.; Patel, Y.; Wu, B. The effect of cell-to-cell variations and thermal gradients on the performance and degradation of lithium-ion battery packs. Appl. Energy 2019, 248, 489–499. [Google Scholar] [CrossRef]
- Srinivasan, R. Monitoring dynamic thermal behavior of the carbon anode in a lithium-ion cell using a four-probe technique. J. Power Sources 2012, 198, 351–358. [Google Scholar] [CrossRef]
- Carkhuff, B.G.; Demirev, P.A.; Srinivasan, R. Impedance-Based Battery Management System for Safety Monitoring of Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2018, 65, 6497–6504. [Google Scholar] [CrossRef]
- Srinivasan, R.; Carkhuff, B.G.; Butler, M.H.; Baisden, A.C. Instantaneous measurement of the internal temperature in lithium-ion rechargeable cells. Electrochim. Acta 2011, 56, 6198–6204. [Google Scholar] [CrossRef]
- Schmidt, J.P.; Arnold, S.; Loges, A.; Werner, D.; Wetzel, T.; Ivers-Tiffée, E. Measurement of the internal cell temperature via impedance: Evaluation and application of a new method. J. Power Sources 2013, 243, 110–117. [Google Scholar] [CrossRef]
- Raijmakers, L.; Danilov, D.L.; van Lammeren, J.; Lammers, M.; Notten, P. Sensorless battery temperature measurements based on electrochemical impedance spectroscopy. J. Power Sources 2014, 247, 539–544. [Google Scholar] [CrossRef]
- Beelen, H.; Raijmakers, L.; Donkers, M.; Notten, P.; Bergveld, H.J. An Improved Impedance-Based Temperature Estimation Method for Li-ion. IFAC-PapersOnLine 2015, 48, 383–388. [Google Scholar] [CrossRef]
- Spinner, N.S.; Love, C.T.; Rose-Pehrsson, S.L.; Tuttle, S.G. Expanding the Operational Limits of the Single-Point Impedance Diagnostic for Internal Temperature Monitoring of Lithium-ion Batteries. Electrochim. Acta 2015, 174, 488–493. [Google Scholar] [CrossRef]
- Sun, J.; Wei, G.; Pei, L.; Lu, R.; Song, K.; Wu, C.; Zhu, C. Online Internal Temperature Estimation for Lithium-Ion Batteries Based on Kalman Filter. Energies 2015, 8, 4400–4415. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.G.; Sun, Z.C.; Wei, X.Z.; Dai, H.F. A new lithium-ion battery internal temperature on-line estimate method based on electrochemical impedance spectroscopy measurement. J. Power Sources 2015, 274, 990–1004. [Google Scholar] [CrossRef]
- Zhu, J.; Sun, Z.; Wei, X.; Dai, H. Battery Internal Temperature Estimation for LiFePO4 Battery Based on Impedance Phase Shift under Operating Conditions. Energies 2017, 10, 60. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, R.; Demirev, P.A.; Carkhuff, B.G. Rapid monitoring of impedance phase shifts in lithium-ion batteries for hazard prevention. J. Power Sources 2018, 405, 30–36. [Google Scholar] [CrossRef]
- Wang, L.; Lu, D.; Song, M.; Zhao, X.; Li, G. Instantaneous estimation of internal temperature in lithium–ion battery by impedance measurement. Int. J. Energy Res. 2020, 44, 3082–3097. [Google Scholar] [CrossRef]
- Raijmakers, L.H.J.; Danilov, D.L.; van Lammeren, J.P.M.; Lammers, T.J.G.; Bergveld, H.J.; Notten, P.H.L. Non-Zero Intercept Frequency: An Accurate Method to Determine the Integral Temperature of Li-Ion Batteries. IEEE Trans. Ind. Electron. 2016, 63, 3168–3178. [Google Scholar] [CrossRef] [Green Version]
- Haussmann, P.; Melbert, J. Internal Cell Temperature Measurement and Thermal Modeling of Lithium Ion Cells for Automotive Applications by Means of Electrochemical Impedance Spectroscopy. SAE Int. J. Altern. Powertrains 2017, 6, 261–270. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Chen, Q.; Zhu, J.; Dai, H. Lithium-ion battery temperature on-line estimation based on fast impedance calculation. J. Energy Storage 2019, 26, 100952. [Google Scholar] [CrossRef]
- Richardson, R.R.; Ireland, P.T.; Howey, D.A. Battery internal temperature estimation by combined impedance and surface temperature measurement. J. Power Sources 2014, 265, 254–261. [Google Scholar] [CrossRef]
- Richardson, R.R.; Howey, D.A. Sensorless Battery Internal Temperature Estimation Using a Kalman Filter With Impedance Measurement. IEEE Trans. Sustain. Energy 2015, 6, 1190–1199. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Li, W.; Hu, X.; Lin, X.; Zhang, Y.; Dan, D.; Feng, F.; Liu, B.; Li, K. An Enhanced Online Temperature Estimation for Lithium-Ion Batteries. IEEE Trans. Transp. Electrif. 2020, 6, 375–390. [Google Scholar] [CrossRef]
- Forgez, C.; Vinh Do, D.; Friedrich, G.; Morcrette, M.; Delacourt, C. Thermal modeling of a cylindrical LiFePO4/graphite lithium-ion battery. J. Power Sources 2010, 195, 2961–2968. [Google Scholar] [CrossRef]
- Ludwig, S.; Zilberman, I.; Horsche, M.F.; Wohlers, T.; Jossen, A. Pulse resistance based online temperature estimation for lithium-ion cells. J. Power Sources 2021, 490, 229523. [Google Scholar] [CrossRef]
- Ludwig, S.; Zilberman, I.; Oberbauer, A.; Rogge, M.; Fischer, M.; Rehm, M.; Jossen, A. Adaptive method for sensorless temperature estimation over the lifetime of lithium-ion batteries. J. Power Sources 2022, 521, 230864. [Google Scholar] [CrossRef]
- Tranter, T.G.; Timms, R.; Shearing, P.R.; Brett, D.J.L. Communication—Prediction of Thermal Issues for Larger Format 4680 Cylindrical Cells and Their Mitigation with Enhanced Current Collection. J. Electrochem. Soc. 2020, 167, 160544. [Google Scholar] [CrossRef]
- Tomaszewska, A.; Chu, Z.; Feng, X.; O’Kane, S.; Liu, X.; Chen, J.; Ji, C.; Endler, E.; Li, R.; Liu, L.; et al. Lithium-ion battery fast charging: A review. eTransportation 2019, 1, 100011. [Google Scholar] [CrossRef]
- Steinhardt, M.; Gillich, E.I.; Rheinfeld, A.; Kraft, L.; Spielbauer, M.; Bohlen, O.; Jossen, A. Low-effort determination of heat capacity and thermal conductivity for cylindrical 18650 and 21700 lithium-ion cells. J. Energy Storage 2021, 42, 103065. [Google Scholar] [CrossRef]
- Shenzhen Fest Technology Co., Ltd. Efest IMR 26650 5000mAh 40A Flat Top Battery. Available online: https://www.efestpower.com/index.php?ac=article&at=read&did=448. (accessed on 18 January 2022).
- Popp, H.; Zhang, N.; Jahn, M.; Arrinda, M.; Ritz, S.; Faber, M.; Sauer, D.U.; Azais, P.; Cendoya, I. Ante-mortem analysis, electrical, thermal, and ageing testing of state-of-the-art cylindrical lithium-ion cells. e & i Elektrotechnik und Informationstechnik 2020, 137, 169–176. [Google Scholar] [CrossRef]
- Wei, Y.; Agelin-Chaab, M. Experimental investigation of a novel hybrid cooling method for lithium-ion batteries. Appl. Therm. Eng. 2018, 136, 375–387. [Google Scholar] [CrossRef]
- Wei, Y.; Agelin-Chaab, M. Development and experimental analysis of a hybrid cooling concept for electric vehicle battery packs. J. Energy Storage 2019, 25, 100906. [Google Scholar] [CrossRef]
- Gantenbein, S.; Weiss, M.; Ivers-Tiffée, E. Impedance based time-domain modeling of lithium-ion batteries: Part I. J. Power Sources 2018, 379, 317–327. [Google Scholar] [CrossRef]
- Bernardi, D. A General Energy Balance for Battery Systems. J. Electrochem. Soc. 1985, 132, 5. [Google Scholar] [CrossRef] [Green Version]
- Illig, J.; Ender, M.; Chrobak, T.; Schmidt, J.P.; Klotz, D.; Ivers-Tiffée, E. Separation of Charge Transfer and Contact Resistance in LiFePO 4 -Cathodes by Impedance Modeling. J. Electrochem. Soc. 2012, 159, A952–A960. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, J.; Pan, Z.; Ouyang, M. Impedance characterization of lithium-ion batteries aging under high-temperature cycling: Importance of electrolyte-phase diffusion. J. Power Sources 2019, 426, 216–222. [Google Scholar] [CrossRef]
- Barai, A.; Uddin, K.; Widanage, W.D.; McGordon, A.; Jennings, P. A study of the influence of measurement timescale on internal resistance characterisation methodologies for lithium-ion cells. Sci. Rep. 2018, 8, 21. [Google Scholar] [CrossRef]
- Song, J.Y.; Wang, Y.Y.; Wan, C.C. Conductivity Study of Porous Plasticized Polymer Electrolytes Based on Poly(vinylidene fluoride) A Comparison with Polypropylene Separators. J. Electrochem. Soc. 2000, 147, 3219. [Google Scholar] [CrossRef]
- Suresh, P.; Shukla, A.K.; Munichandraiah, N. Temperature dependence studies of a.c. impedance of lithium-ion cells. J. Appl. Electrochem. 2002, 32, 267–273. [Google Scholar] [CrossRef]
- Muto, S.; Tatsumi, K.; Kojima, Y.; Oka, H.; Kondo, H.; Horibuchi, K.; Ukyo, Y. Effect of Mg-doping on the degradation of LiNiO2-based cathode materials by combined spectroscopic methods. J. Power Sources 2012, 205, 449–455. [Google Scholar] [CrossRef]
- Schranzhofer, H.; Bugajski, J.; Santner, H.J.; Korepp, C.; Möller, K.C.; Besenhard, J.O.; Winter, M.; Sitte, W. Electrochemical impedance spectroscopy study of the SEI formation on graphite and metal electrodes. J. Power Sources 2006, 153, 391–395. [Google Scholar] [CrossRef]
- Raju, N.S.; Bilgic, R.; Edwards, J.E.; Fleer, P.F. Methodology Review: Estimation of Population Validity and Cross-Validity, and the Use of Equal Weights in Prediction. Appl. Psychol. Meas. 1997, 21, 291–305. [Google Scholar] [CrossRef]
- Fuller, T.F. Relaxation Phenomena in Lithium-Ion-Insertion Cells. J. Electrochem. Soc. 1994, 141, 982. [Google Scholar] [CrossRef] [Green Version]
- Maleki, H.; Hallaj, S.A.; Selman, J.R.; Dinwiddie, R.B.; Wang, H. Thermal Properties of Lithium–Ion Battery and Components. J. Electrochem. Soc. 1999, 146, 947–954. [Google Scholar] [CrossRef]
- Willenberg, L.; Dechent, P.; Fuchs, G.; Teuber, M.; Eckert, M.; Graff, M.; Kürten, N.; Sauer, D.U.; Figgemeier, E. The Development of Jelly Roll Deformation in 18650 Lithium-Ion Batteries at Low State of Charge. J. Electrochem. Soc. 2020, 167, 120502. [Google Scholar] [CrossRef]
- Maleki, H.; Selman, J.; Dinwiddie, R.; Wang, H. High thermal conductivity negative electrode material for lithium-ion batteries. J. Power Sources 2001, 94, 26–35. [Google Scholar] [CrossRef]
- Richter, F.; Kjelstrup, S.; Vie, P.J.; Burheim, O.S. Thermal conductivity and internal temperature profiles of Li-ion secondary batteries. J. Power Sources 2017, 359, 592–600. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).