A Regression-Based Technique for Capacity Estimation of Lithium-Ion Batteries
Abstract
:1. Introduction
- Current measurement error and SOC estimation error are considered in the proposed method.
- The proposed methods are closed-form and recursive. This means they do not need high computational effort and high memory space.
- In addition, a proposed method is fading memory. This gives weight to recent data and fades the effect of early data. This makes proposed methods applicable in online applications and increases capacity estimation during several cycles for SOH estimation.
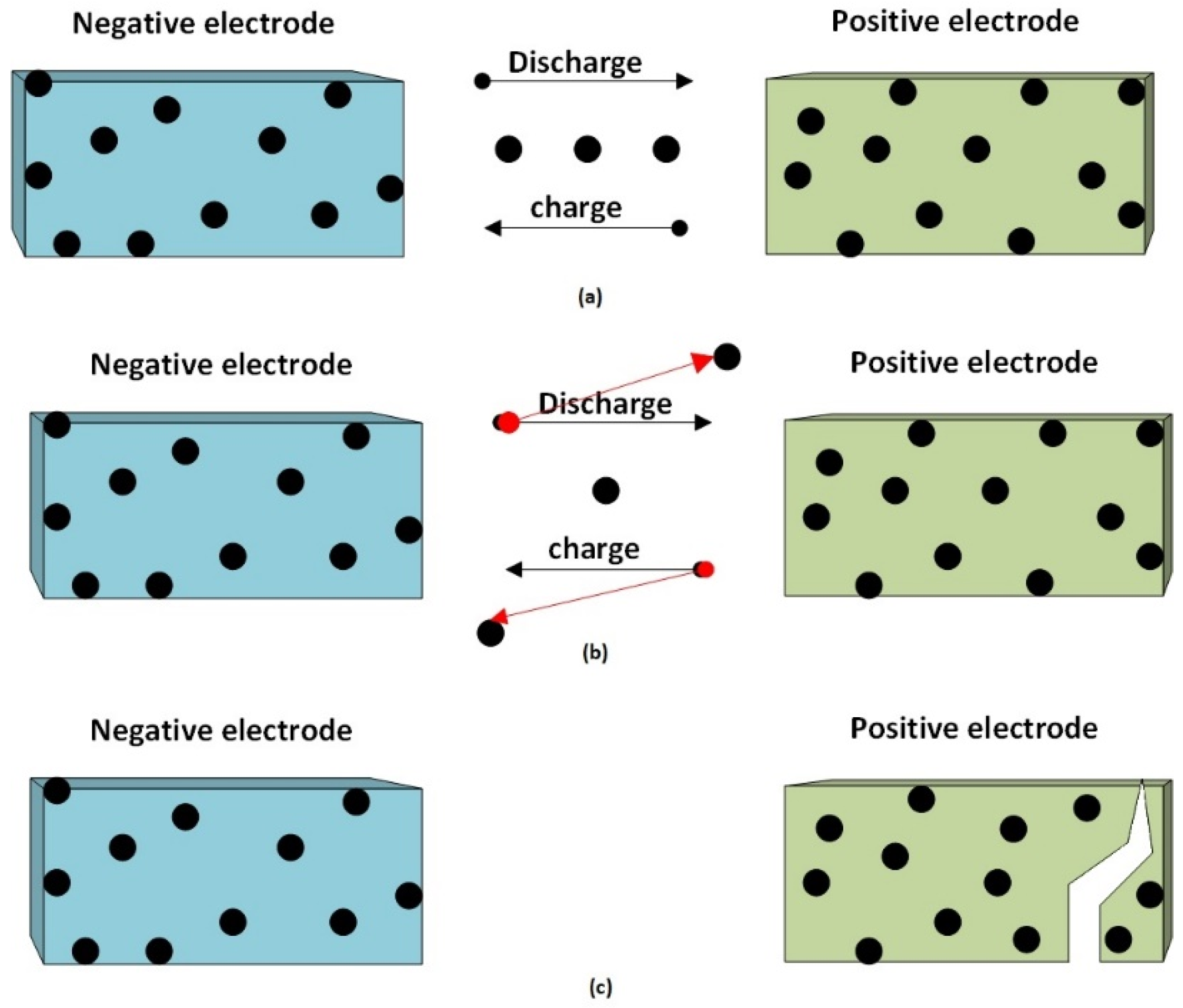
2. Reasons for Lithium-Ion Batteries Ageing
- Interface of electrolyte and electrodes;
- Active material;
- Composite electrode.
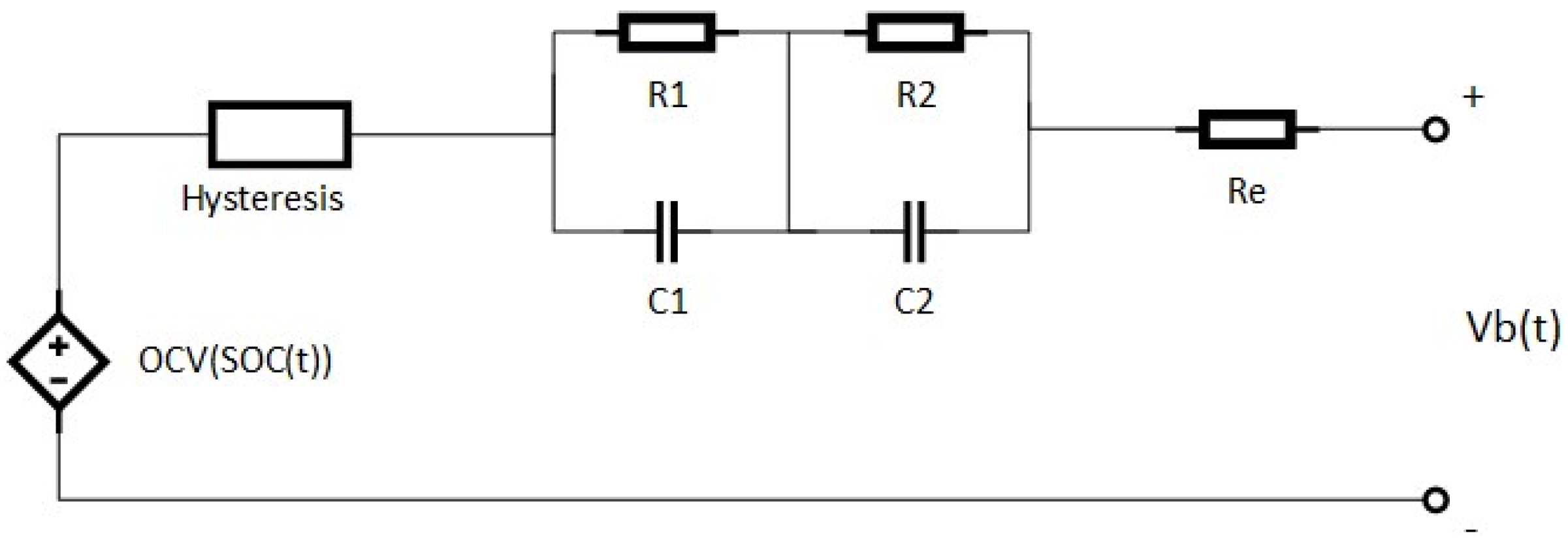
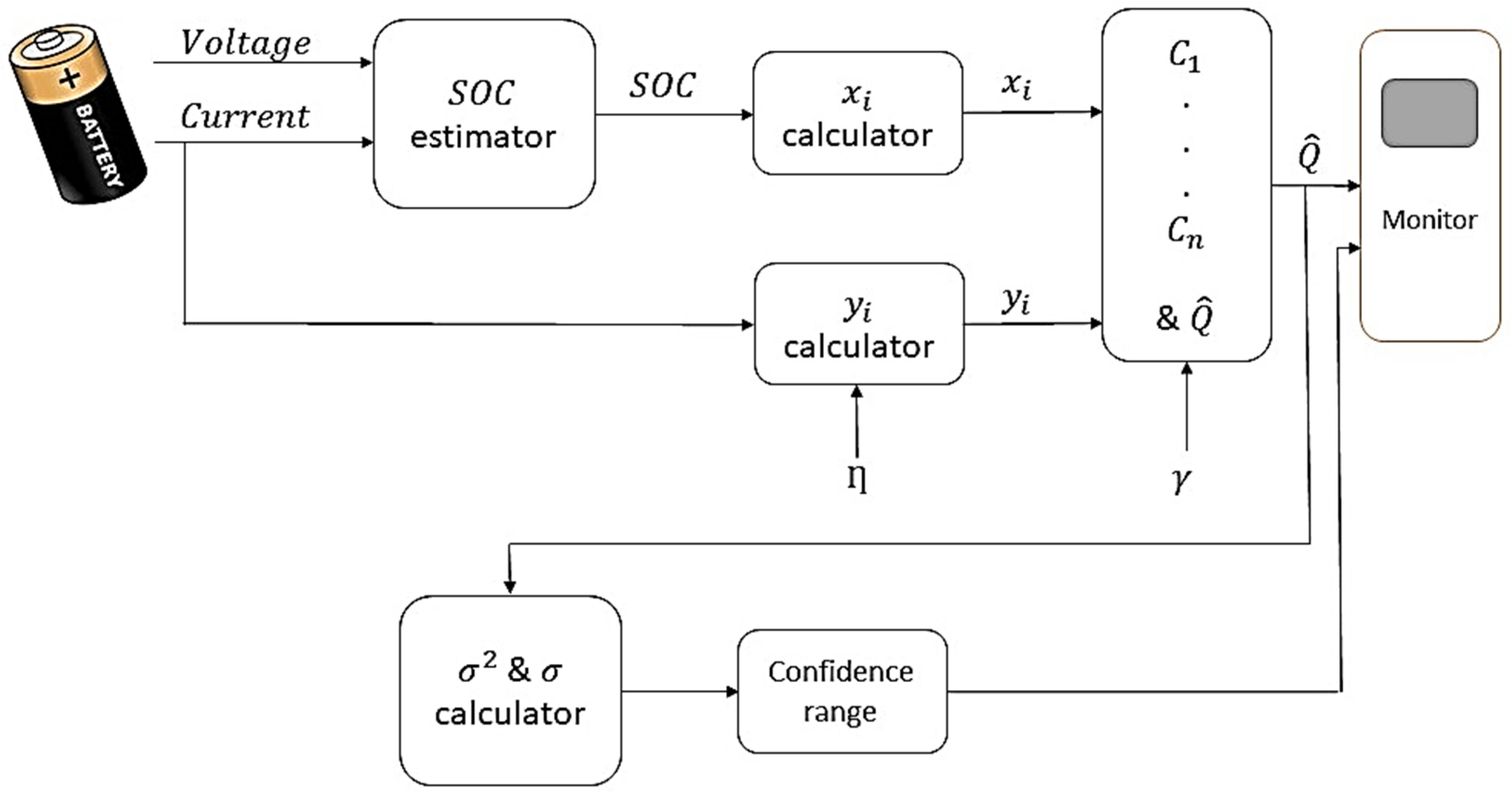
3. Capacity Estimation
3.1. Calculation of
3.2. Proposed Methods to Estimate
3.2.1. The First Type of Least Squares Method
3.2.2. The Second Type of Least Squares Method
3.2.3. The Third Type of Least Squares Method
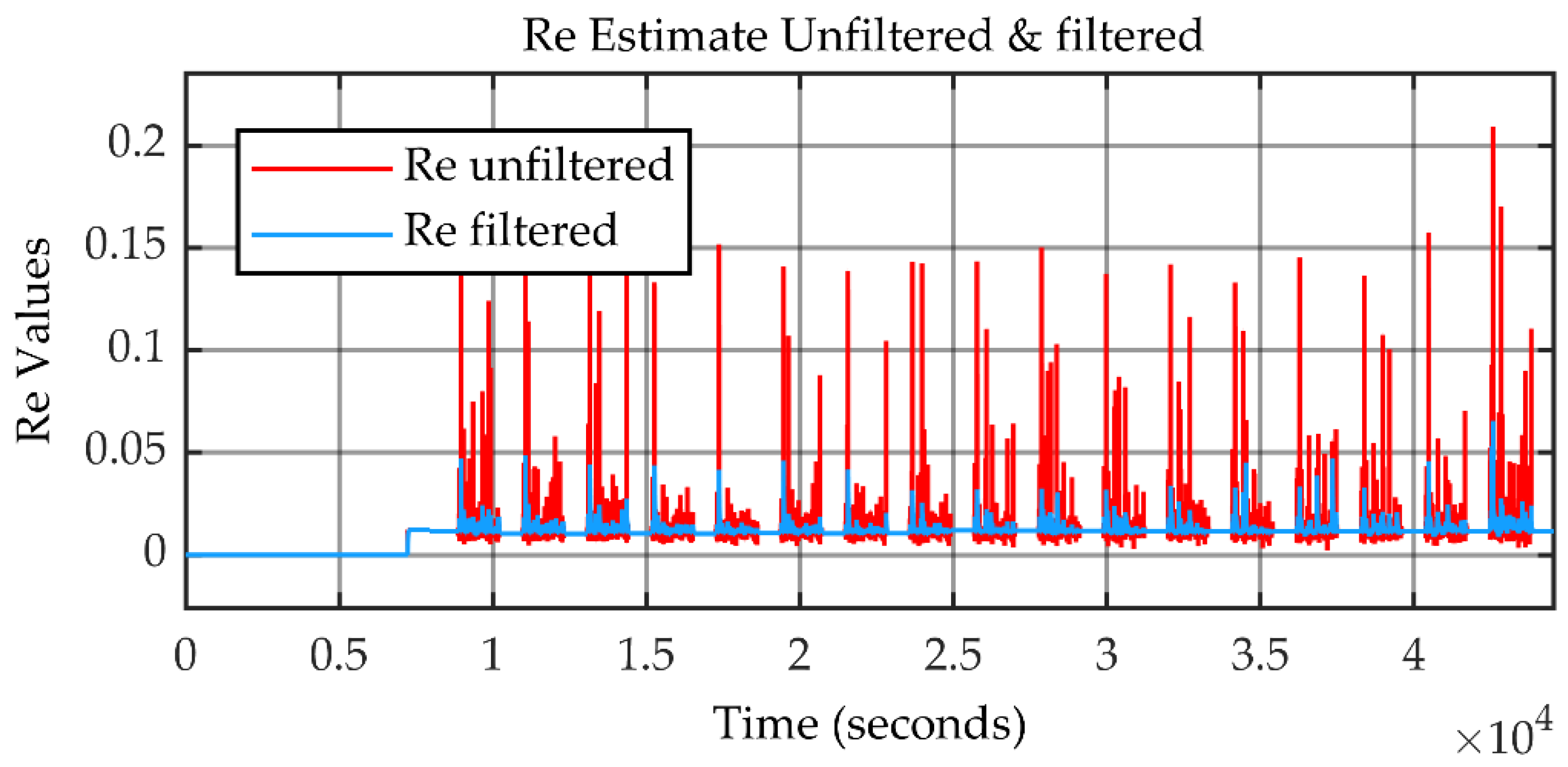
3.2.4. Confidence Intervals
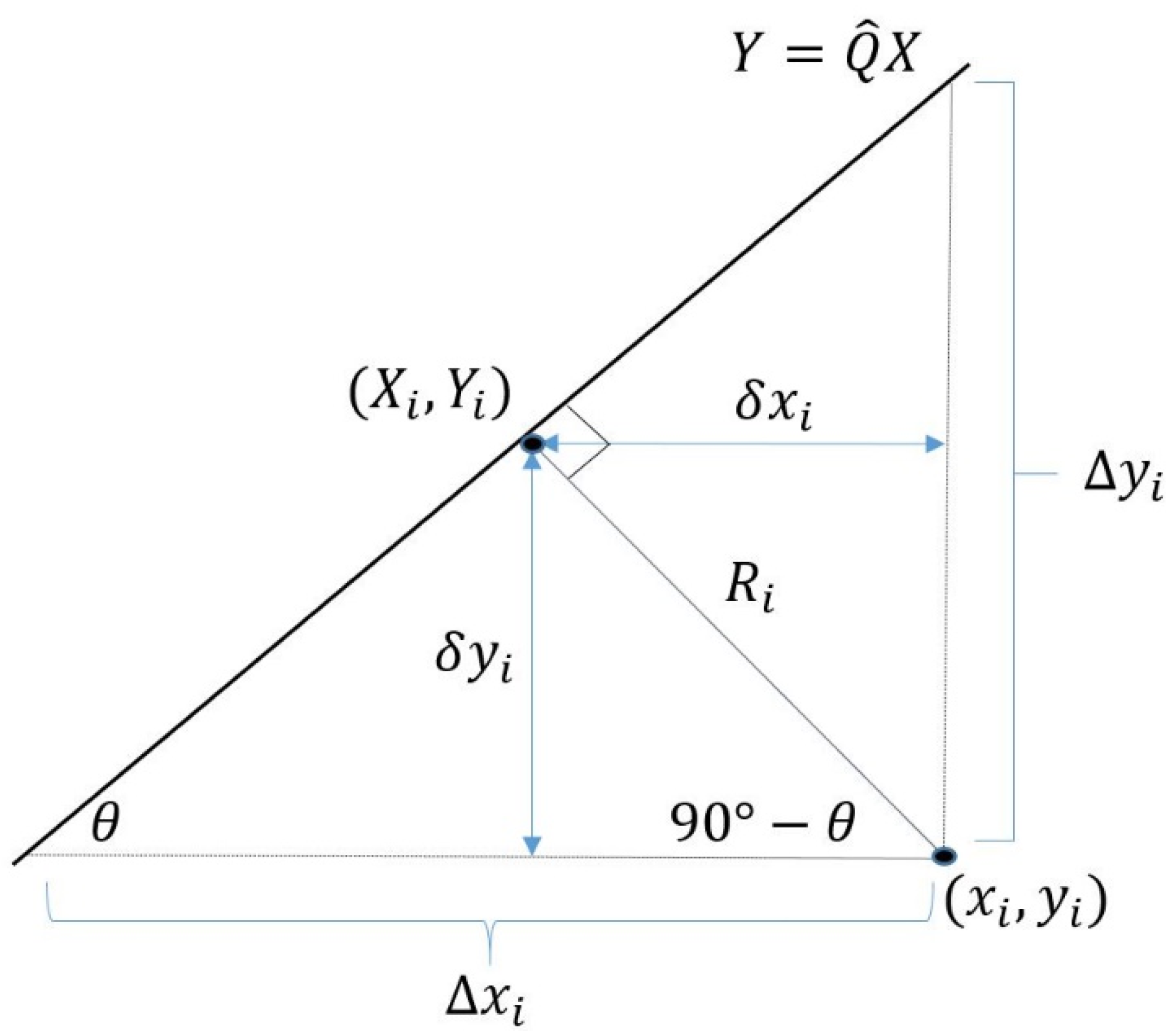
3.2.5. Geometry Method
3.2.6. Total Geometry Method
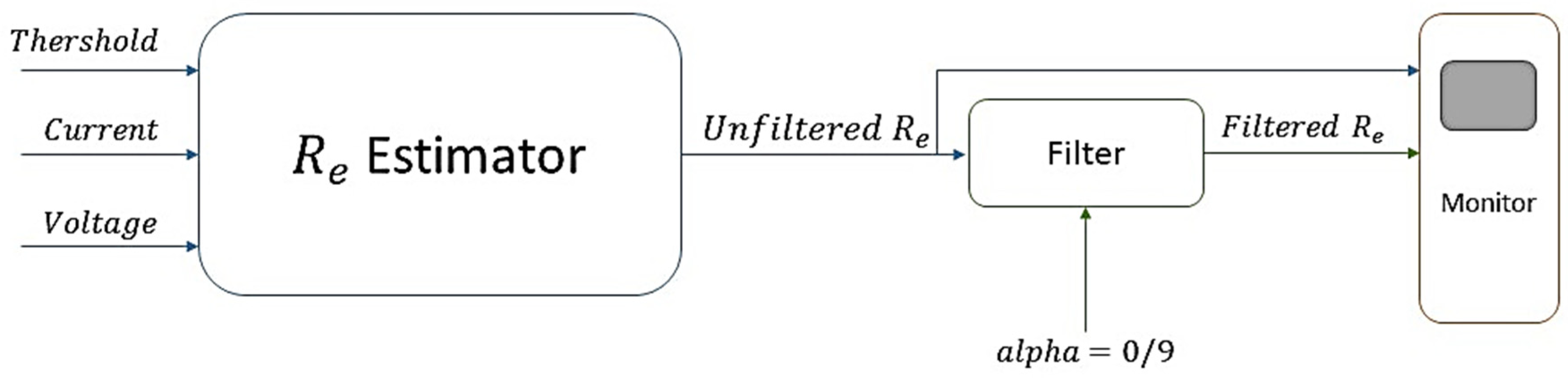
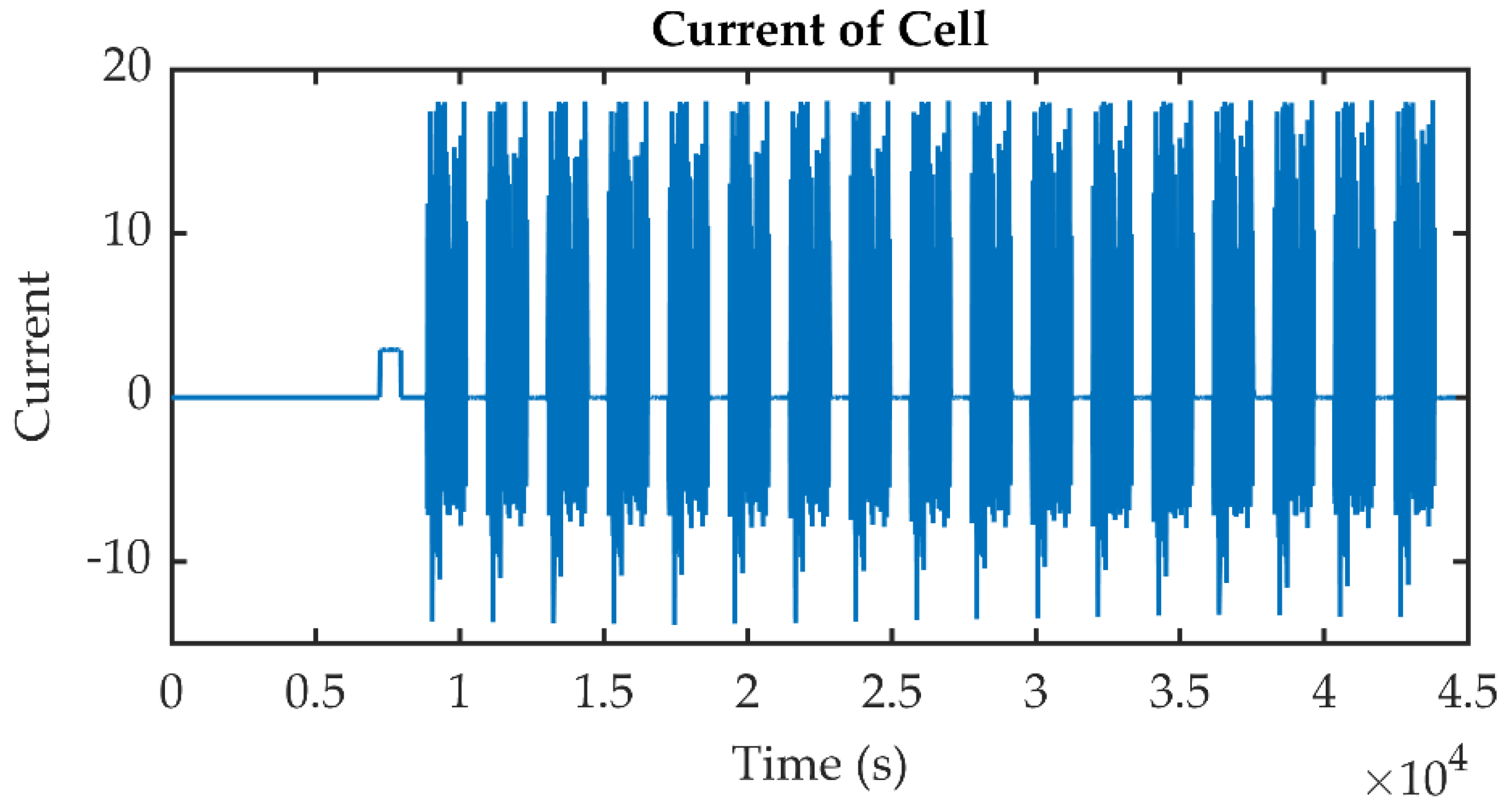
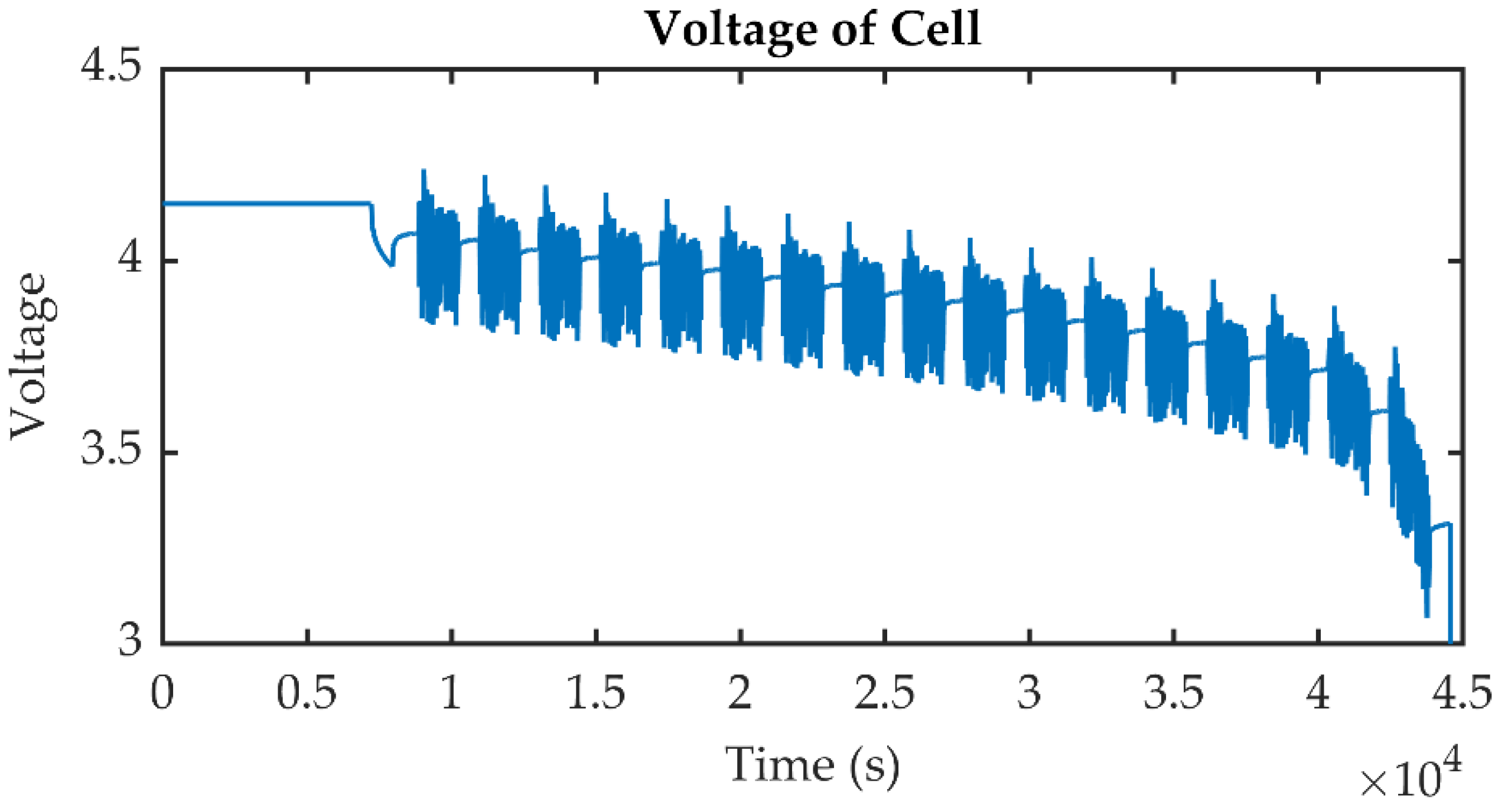
4. Validation by Experimental Data
5. Conclusions
- This method can estimate state of health of the battery in an online condition while the battery is being used in the vehicle (it is not only a method for the laboratory);
- It does not need extensive experiments in the laboratory to obtain charge and discharge curves;
- It does not need a significant number of datasets and learning processes;
- Even if it is better to have a more accurate model of the battery, this method can provide satisfying results without precise knowledge of the model;
- It does not have a high computational load and does not need a large data memory.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Madani, S.S.; Swierczynski, M.J.; Kaer, S.K. A review of thermal management and safety for lithium ion batteries. In Proceedings of the 2017 Twelfth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 11–13 April 2017; pp. 1–20. [Google Scholar]
- Huang, R.-J.; Zhang, Y.; Bozzetti, C.; Ho, K.-F.; Cao, J.-J.; Han, Y.; Daellenbach, K.R.; Slowik, J.G.; Platt, S.M.; Canonaco, F.; et al. High secondary aerosol contribution to particulate pollution during haze events in China. Nature 2014, 514, 218–222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Capasso, C.; Veneri, O. Experimental analysis on the performance of lithium based batteries for road full electric and hybrid vehicles. Appl. Energy 2014, 136, 921–930. [Google Scholar] [CrossRef]
- Madani, S.S.; Schaltz, E.; Kær, S.K. A review of different electric equivalent circuit models and parameter identification methods of lithium-ion batteries. ECS Trans. 2018, 87, 23–37. [Google Scholar] [CrossRef]
- Dunn, B.; Kamath, H.; Tarascon, J.-M. Tarascon, electrical energy storage for the grid: A battery of choices. Science 2011, 334, 928–935. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Liang, J.; Yang, Z.; Li, G. A review of lithium-ion battery for electric vehicle applications and beyond. Energy Procedia 2019, 158, 4363–4368. [Google Scholar] [CrossRef]
- Hu, Y.; Yurkovich, S.; Guezennec, Y.; Yurkovich, B. Electro-thermal battery model identification for automotive applications. J. Power Sources 2011, 196, 449–457. [Google Scholar] [CrossRef]
- Li, Y.; Zou, C.; Berecibar, M.; Nanini-Maury, E.; Chan, J.C.-W.; Bossche, P.V.D.; Van Mierlo, J.; Omar, N. Random forest regression for online capacity estimation of lithium-ion batteries. Appl. Energy 2018, 232, 197–210. [Google Scholar] [CrossRef]
- El Mejdoubi, A.; Oukaour, A.; Chaoui, H.; Gualous, H.; Sabor, J.; Slamani, Y. State-of-charge and state-of-health lithium-ion batteries’ diagnosis according to surface temperature variation. IEEE Trans. Ind. Electron. 2015, 63, 2391–2402. [Google Scholar] [CrossRef]
- Ungurean, L.; Cârstoiu, G.; Micea, M.V.; Groza, V. Battery state of health estimation: A structured review of models, methods and commercial devices. Int. J. Energy Res. 2017, 41, 151–181. [Google Scholar] [CrossRef]
- She, C.; Li, Y.; Zou, C.; Wik, T.; Wang, Z.; Sun, F. Offline and online blended machine learning for lithium-ion battery health state estimation. IEEE Trans. Transp. Electrif. 2021. [Google Scholar] [CrossRef]
- Krupp, A.; Ferg, E.; Schuldt, F.; Derendorf, K.; Agert, C. Incremental capacity analysis as a state of health estimation method for lithium-ion battery modules with series-connected cells. Batteries 2021, 7, 2. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, X.; Dou, X.; Zhang, X. A rapid online calculation method for state of health of lithium-ion battery based on coulomb counting method and differential voltage analysis. J. Power Source 2020, 479, 228740. [Google Scholar] [CrossRef]
- Chen, Z.; Mi, C.C.; Fu, Y.; Xu, J.; Gong, X. Online battery state of health estimation based on Genetic Algorithm for electric and hybrid vehicle applications. J. Power Sources 2013, 240, 184–192. [Google Scholar] [CrossRef]
- Landi, M.; Gross, G. Measurement techniques for online battery state of health estimation in vehicle-to-grid applications. IEEE Trans. Instrum. Meas. 2014, 63, 1224–1234. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Saad, M.H.; Ayob, A. Neural network approach for estimating state of charge of lithium-ion battery using backtracking search algorithm. IEEE Access 2018, 6, 10069–10079. [Google Scholar] [CrossRef]
- Watrin, N.; Blunier, B.; Miraoui, A. Review of adaptive systems for lithium batteries state-of-charge and state-of-health estimation. In Proceedings of the 2012 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 18–20 June 2012; pp. 1–6. [Google Scholar]
- Hu, X.; Li, S.; Jia, Z.; Egardt, B. Enhanced sample entropy-based health management of Li-ion battery for electrified vehicles. Energy 2014, 64, 953–960. [Google Scholar] [CrossRef]
- Kelsey, B.; Hatzell, A.S.; Hosam, K.F. A survey of long-term health modeling, estimation, and control of Lithium-ion batteries: Challenges and opportunities. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012. [Google Scholar]
- Kim, J.; Shin, J.; Chun, C.; Cho, B.H. Stable configuration of a li-ion series battery pack based on a screening process for improved voltage/SOC balancing. IEEE Trans. Power Electron. 2012, 27, 411–424. [Google Scholar] [CrossRef]
- Burgos-Mellado, C.; Orchard, M.E.; Kazerani, M.; Cárdenas, R.; Sáez, D. Particle-filtering-based estimation of maximum available power state in Lithium-Ion batteries. Appl. Energy 2016, 161, 349–363. [Google Scholar] [CrossRef]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.-C.; Besenhard, J.O.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Source 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Groot, J. State-of-Health Estimation of Li-Ion Batteries: Cycle Life Test Methods; Chalmers Tekniska Hogskola: Gothenburg, Sweden, 2012. [Google Scholar]
- Madani, S.S.; Schaltz, E.; Kær, S.K. An electrical equivalent circuit model of a lithium titanate oxide battery. Batteries 2019, 5, 31. [Google Scholar] [CrossRef] [Green Version]
- Sun, T.; Jiang, S.; Li, X.; Cui, Y.; Lai, X.; Wang, X.; Ma, Y.; Zheng, Y. A novel capacity estimation approach for lithium-ion batteries combining three-parameter capacity fade model with constant current charging curves. IEEE Trans. Energy Convers. 2021, 36, 2574–2584. [Google Scholar] [CrossRef]
- Choi, Y.; Ryu, S.; Park, K.; Kim, H. Machine learning-based lithium-ion battery capacity estimation exploiting multi-channel charging profiles. IEEE Access 2019, 7, 75143–75152. [Google Scholar] [CrossRef]
- Li, W.; Sengupta, N.; Dechent, P.; Howey, D.; Annaswamy, A.; Sauer, D.U. Online capacity estimation of lithium-ion batteries with deep long short-term memory networks. J. Power Source 2021, 482, 228863. [Google Scholar] [CrossRef]
- He, Y.; He, R.; Guo, B.; Zhang, Z.; Yang, S.; Liu, X.; Zhao, X.; Pan, Y.; Yan, X.; Li, S. Modeling of Dynamic Hysteresis Characters for the Lithium-Ion Battery. J. Electrochem. Soc. 2020, 167, 090532. [Google Scholar] [CrossRef]
- University of Maryland Website. Available online: https://calce.umd.edu/battery-data (accessed on 1 October 2021).
- Al-Gabalawy, M.; Hosny, N.S.; Dawson, J.A.; Omar, A.I. State of charge estimation of a Li-ion battery based on extended Kalman filtering and sensor bias. Int. J. Energy Res. 2020, 45, 6708–6726. [Google Scholar] [CrossRef]
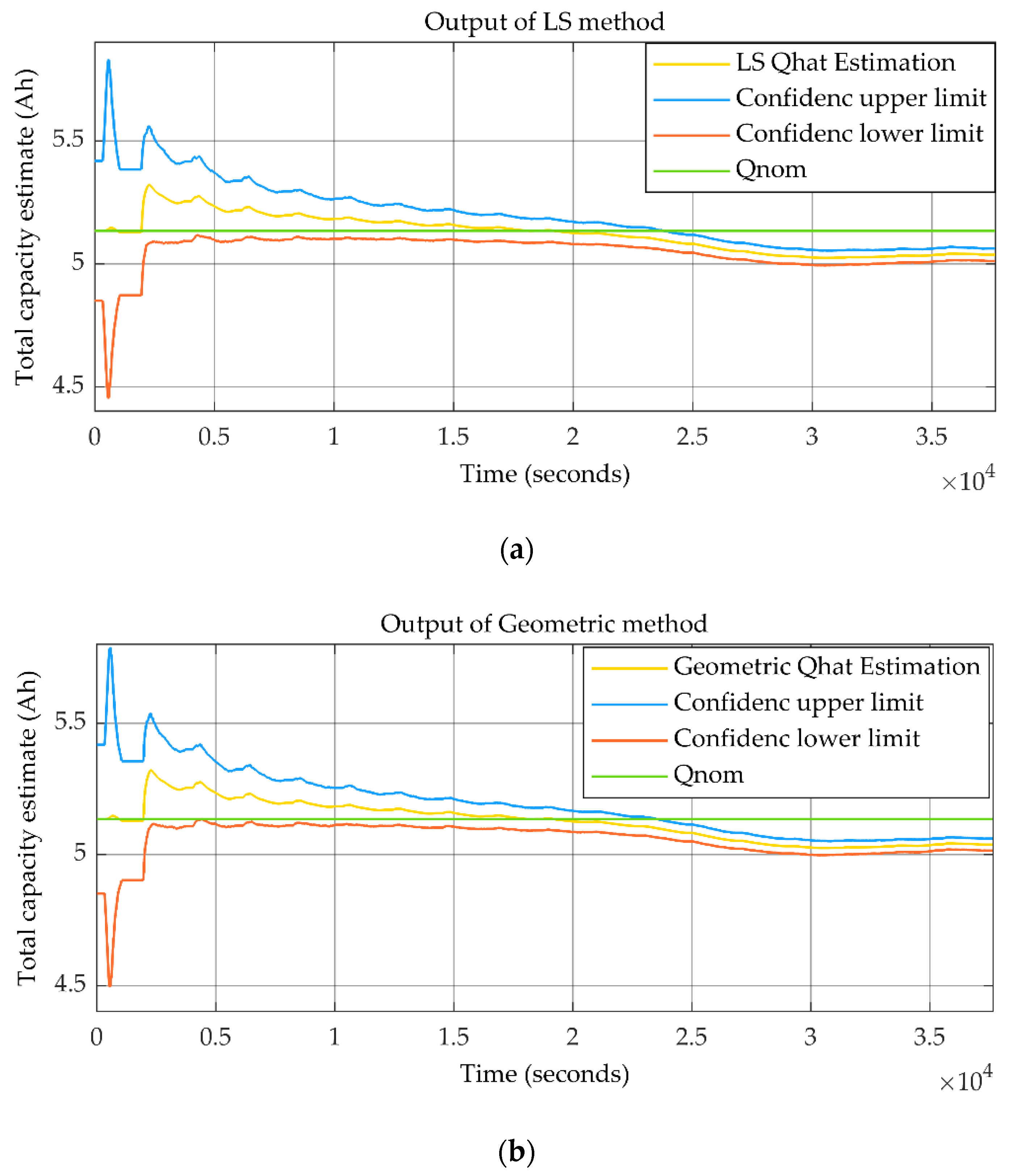
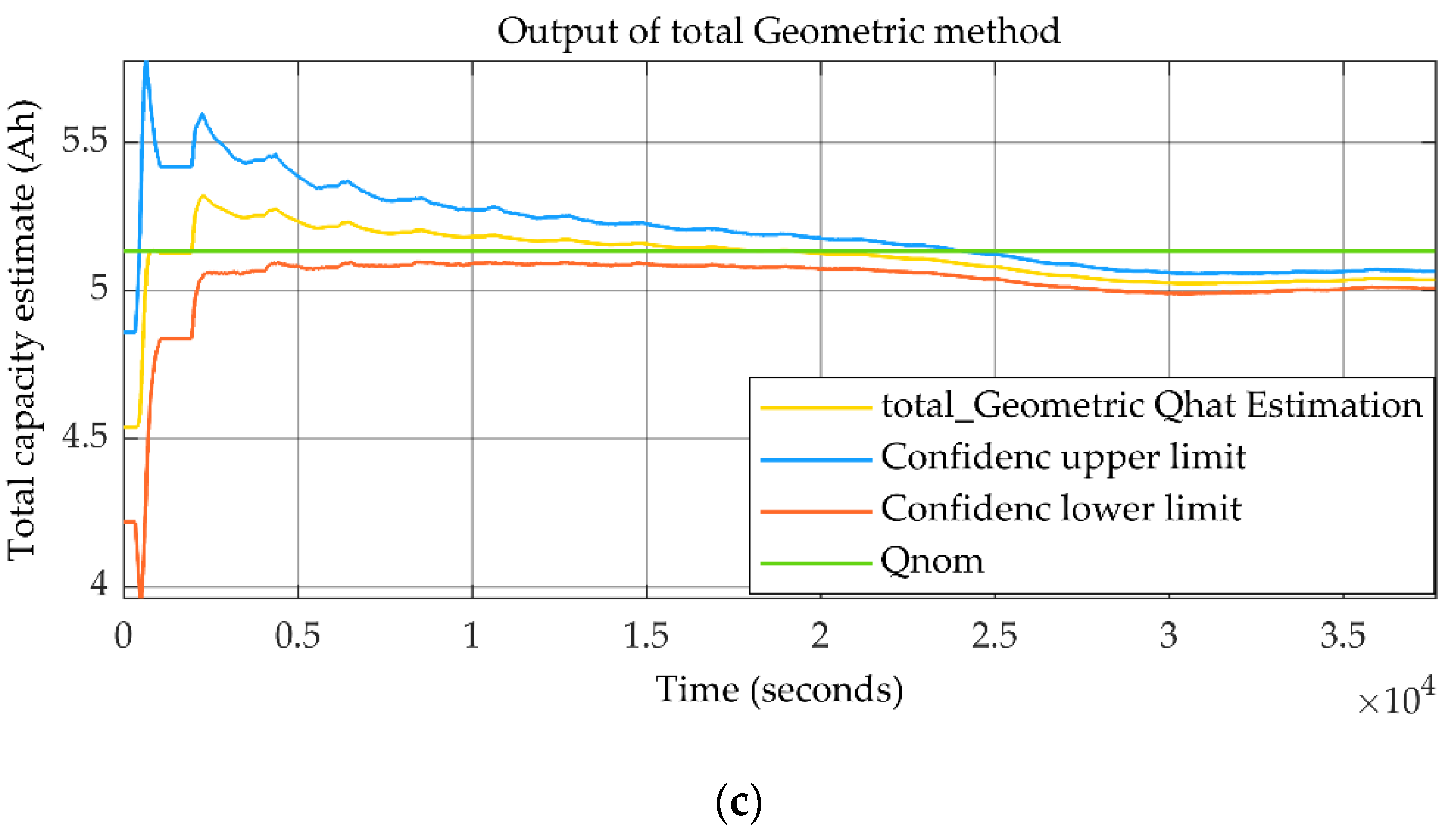
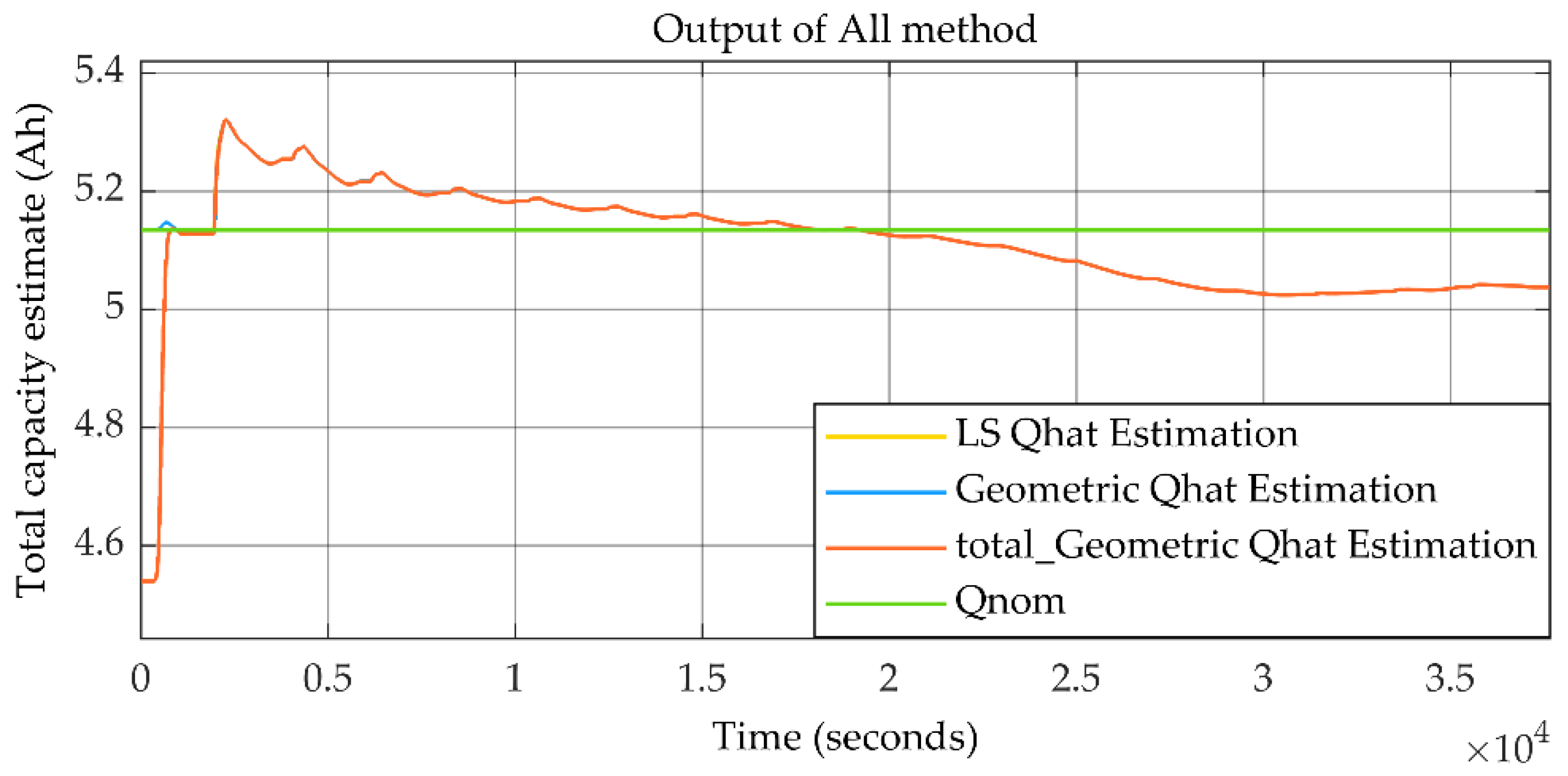
| Description of Parameter | Name of Parameter | Selected Value |
|---|---|---|
| Variance of x data | ||
| Variance of y data | ||
| Coefficient of filtering | 0.99 | |
| Threshold of minimum current | threshold | 2 |
| Coefficient for fading memory | 0.99 | |
| Coefficient of columbic efficiency | 0.9929 (from lab data) | |
| Nominal value of battery capacity | 5.1314 (from lab data) |
| Method | RMSPE | MAPE |
|---|---|---|
| LS3 | ≤0.02 | ≤0.015 |
| Geometry | ≤0.02 | ≤0.015 |
| Total geometry | ≤0.02 | ≤0.015 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madani, S.S.; Soghrati, R.; Ziebert, C. A Regression-Based Technique for Capacity Estimation of Lithium-Ion Batteries. Batteries 2022, 8, 31. https://doi.org/10.3390/batteries8040031
Madani SS, Soghrati R, Ziebert C. A Regression-Based Technique for Capacity Estimation of Lithium-Ion Batteries. Batteries. 2022; 8(4):31. https://doi.org/10.3390/batteries8040031
Chicago/Turabian StyleMadani, Seyed Saeed, Raziye Soghrati, and Carlos Ziebert. 2022. "A Regression-Based Technique for Capacity Estimation of Lithium-Ion Batteries" Batteries 8, no. 4: 31. https://doi.org/10.3390/batteries8040031
APA StyleMadani, S. S., Soghrati, R., & Ziebert, C. (2022). A Regression-Based Technique for Capacity Estimation of Lithium-Ion Batteries. Batteries, 8(4), 31. https://doi.org/10.3390/batteries8040031









