Cycling of Double-Layered Graphite Anodes in Pouch-Cells
Abstract
:1. Introduction
2. Methodology
2.1. Pouch-Cells
2.2. Electrochemical Characterisation
3. Results
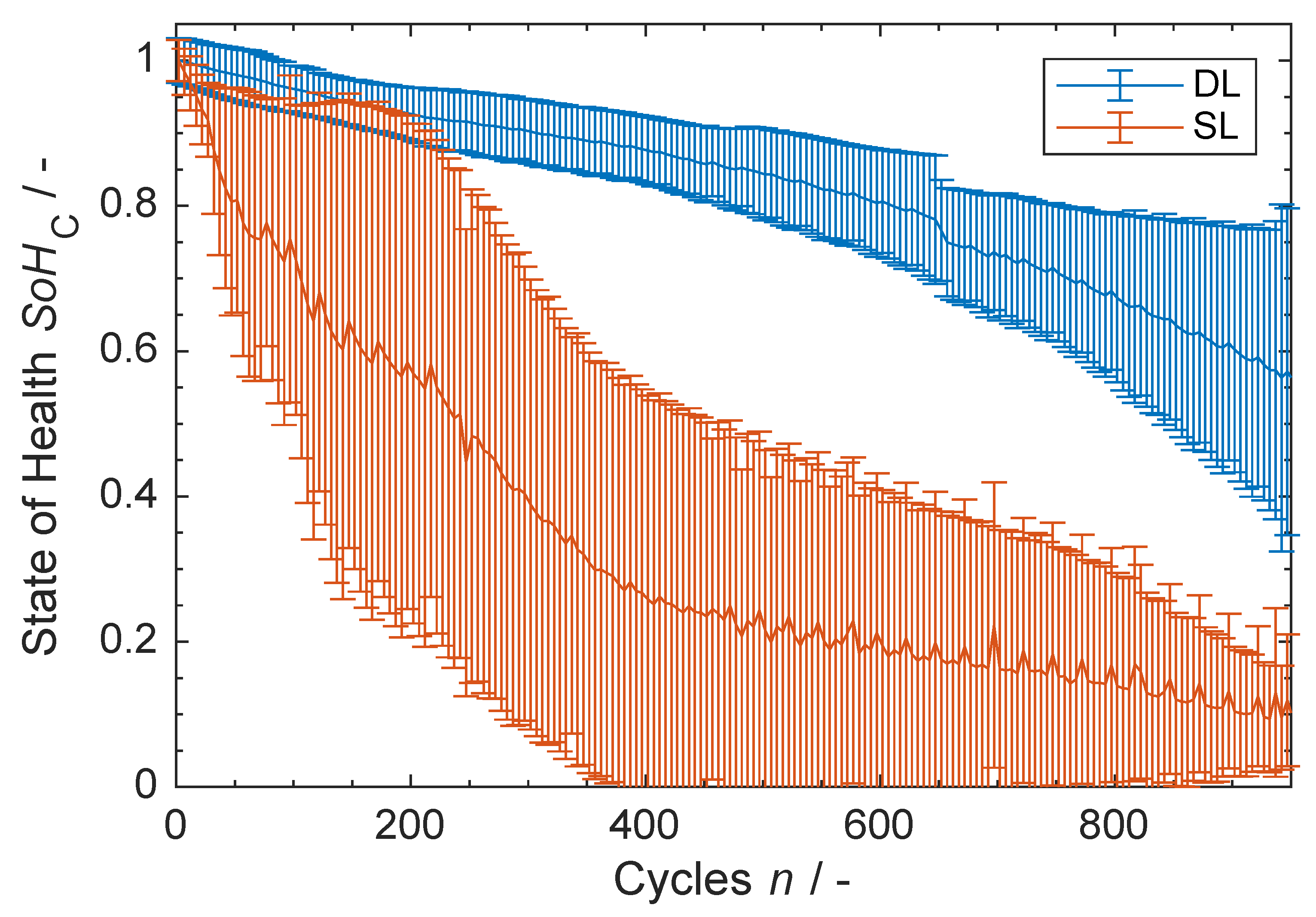
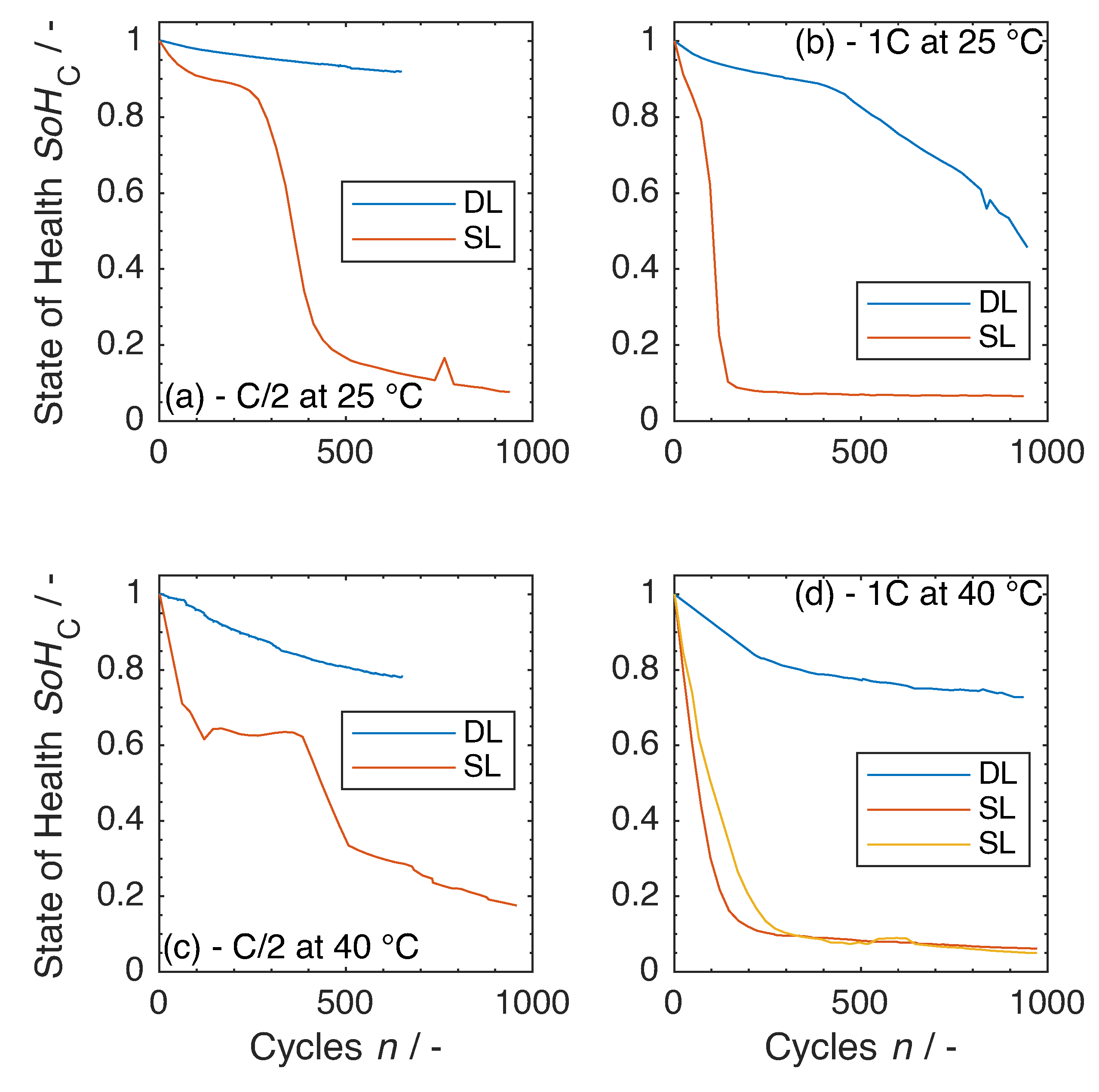
3.1. Discharge Capacity
3.2. Beginning-of-Life
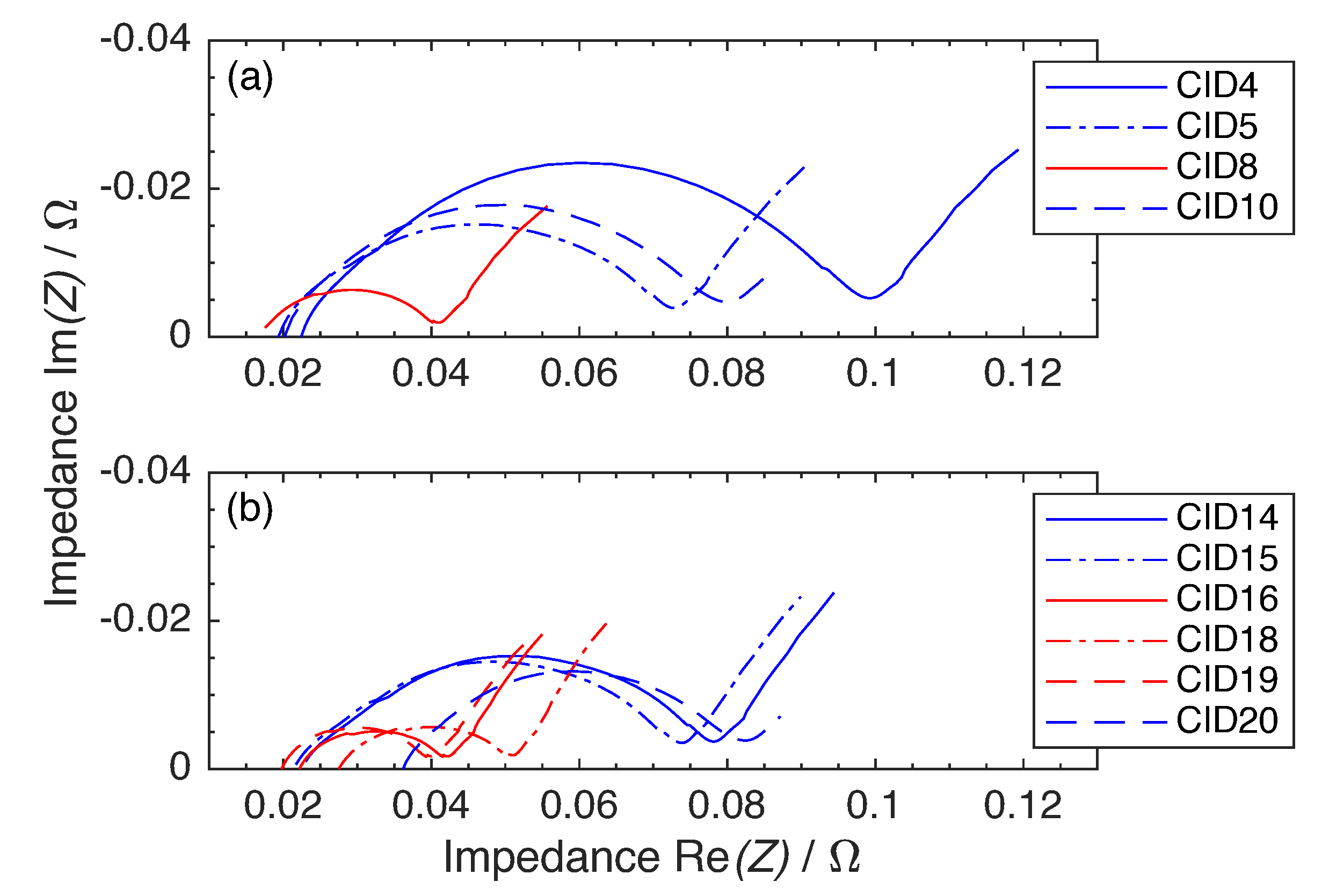
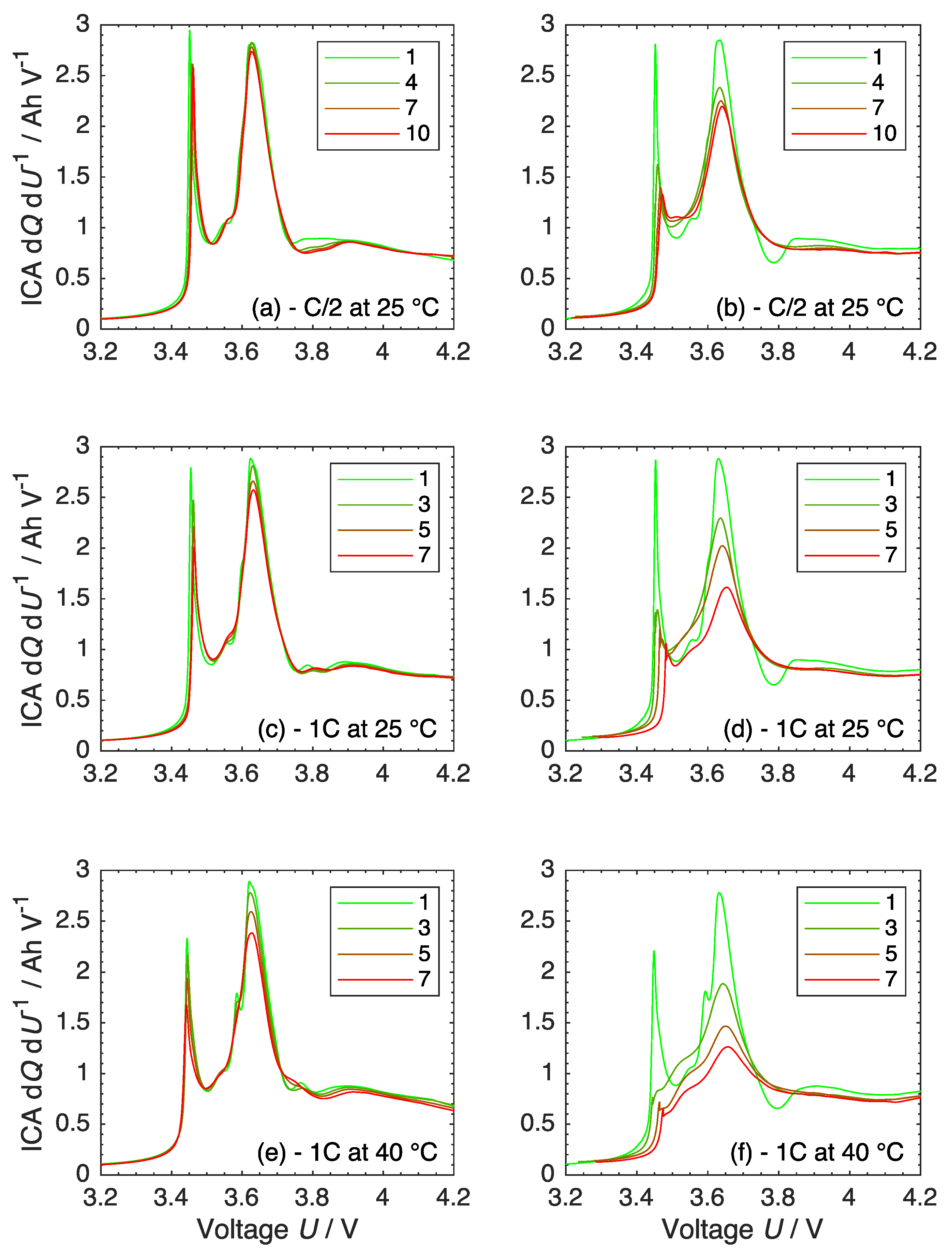
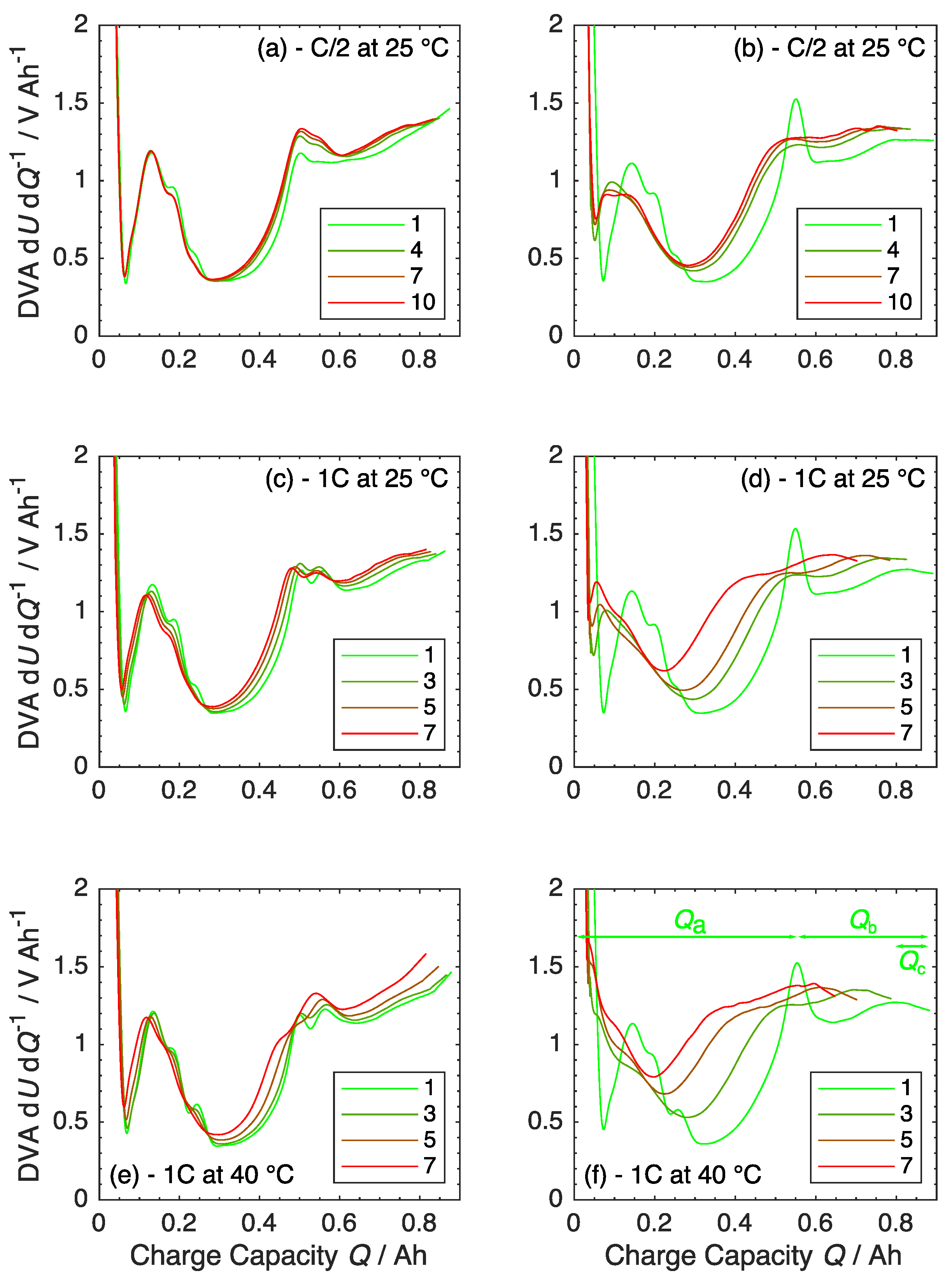
3.3. Ageing
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reddy, M.V.; Julien, C.M.; Mauger, A.; Zaghib, K. Sulfide and oxide inorganic solid electrolytes for all-solid-state Li batteries: A Review. Nanomaterials 2020, 10, 1606. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Huang, S.; Wang, S.; Mizota, I.; Liu, X.; Hou, X. Considering critical factors of silicon/graphite anode materials for practical high-energy lithium-ion battery applications. Energy Fuels 2020, 35, 944–964. [Google Scholar] [CrossRef]
- Yang, J.; Liu, Q.; Pupek, K.Z.; Dzwiniel, T.L.; Dietz Rago, N.L.; Cao, J.; Dandu, N.; Curtiss, L.; Liu, K.; Liao, C.; et al. Molecular Engineering to Enable High-Voltage Lithium-Ion Battery: From Propylene Carbonate to Trifluoropropylene Carbonate. ACS Energy Lett. 2021, 6, 371–378. [Google Scholar] [CrossRef]
- Liang, G.; Peterson, V.K.; See, K.W.; Guo, Z.; Pang, W.K. Developing high-voltage spinel LiNi0.5Mn1.5O4 cathodes for high-energy-density lithium-ion batteries: Current achievements and future prospects. J. Mater. Chem. A 2020, 8, 15373–15398. [Google Scholar] [CrossRef]
- Ji, X.; Hou, S.; Wang, P.; He, X.; Piao, N.; Chen, J.; Fan, X.; Wang, C. Solid-State Electrolyte Design for Lithium Dendrite Suppression. Adv. Mater. 2020, 32, 2002741. [Google Scholar] [CrossRef]
- An, S.J.; Li, J.; Daniel, C.; Mohanty, D.; Nagpure, S.; Wood, D.L., III. The state of understanding of the lithium-ion-battery graphite solid electrolyte interphase (SEI) and its relationship to formation cycling. Carbon 2016, 105, 52–76. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Delacourt, C.; Forgez, C.; Pelissier, S. Study of graphite/NCA Li-ion cell degradation during accelerated aging tests—Data analysis of the SIMSTOCK project. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011. [Google Scholar] [CrossRef]
- Schaltz, E.; Stroe, D.I.; Nørregaard, K.; Ingvardsen, L.S.; Christensen, A. Incremental capacity analysis applied on electric vehicles for battery state-of-health estimation. IEEE Trans. Ind. Appl. 2021, 57, 1810–1817. [Google Scholar] [CrossRef]
- Keil, P.; Jossen, A. Calendar aging of NCA lithium-ion batteries investigated by differential voltage analysis and coulomb tracking. J. Electrochem. Soc. 2016, 164, A6066. [Google Scholar] [CrossRef]
- Waag, W.; Käbitz, S.; Sauer, D.U. Experimental investigation of the lithium-ion battery impedance characteristic at various conditions and aging states and its influence on the application. Appl. Energy 2013, 102, 885–897. [Google Scholar] [CrossRef]
- Qi, Y.; Jang, T.; Ramadesigan, V.; Schwartz, D.T.; Subramanian, V.R. Is there a benefit in employing graded electrodes for lithium-ion batteries? J. Electrochem. Soc. 2017, 164, A3196. [Google Scholar] [CrossRef] [Green Version]
- Hosseinzadeh, E.; Marco, J.; Jennings, P. The impact of multi-layered porosity distribution on the performance of a lithium ion battery. Appl. Math. Model. 2018, 61, 107–123. [Google Scholar] [CrossRef]
- Liu, L.; Guan, P.; Liu, C. Experimental and simulation investigations of porosity graded cathodes in mitigating battery degradation of high voltage lithium-ion batteries. J. Electrochem. Soc. 2017, 164, A3163. [Google Scholar] [CrossRef]
- Diehm, R.; Kumberg, J.; Dörrer, C.; Müller, M.; Bauer, W.; Scharfer, P.; Schabel, W. In Situ Investigations of Simultaneous Two-Layer Slot Die Coating of Component-Graded Anodes for Improved High-Energy Li-Ion Batteries. Energy Technol. 2020, 8, 1901251. [Google Scholar] [CrossRef]
- Wood, M.; Li, J.; Du, Z.; Daniel, C.; Dunlop, A.R.; Polzin, B.J.; Jansen, A.N.; Krumdick, G.K.; Wood Iii, D.L. Impact of secondary particle size and two-layer architectures on the high-rate performance of thick electrodes in lithium-ion battery pouch cells. J. Power Sources 2021, 515, 230429. [Google Scholar] [CrossRef]
- Huang, C.; Young, N.P.; Zhang, J.; Snaith, H.J.; Grant, P.S. A two layer electrode structure for improved Li Ion diffusion and volumetric capacity in Li Ion batteries. Nano Energy 2017, 31, 377–385. [Google Scholar] [CrossRef]
- Müller, D.; Landa-Medrano, I.; Eguia-Barrio, A.; Boyano, I.; Urdampilleta, I.; de Meatza, I.; Fill, A.; Birke, P. Electrochemical characterization of bi-layered graphite anodes combining high and low porosity in lithium-ion cells to improve cell performance. Electrochim. Acta 2021, 391, 138966. [Google Scholar] [CrossRef]
- Keil, P. Aging of Lithium-Ion Batteries in Electric Vehicles. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2017. [Google Scholar]
- Landa-Medrano, I.; Eguia-Barrio, A.; Sananes-Israel, S.; Lijó-Pando, S.; Boyano, I.; Alcaide, F.; Urdampilleta, I.; de Meatza, I. In Situ Analysis of NMC graphite Li-Ion Batteries by Means of Complementary Electrochemical Methods. J. Electrochem. Soc. 2020, 167, 090528. [Google Scholar] [CrossRef]
- Jung, R.; Metzger, M.; Maglia, F.; Stinner, C.; Gasteiger, H.A. Oxygen Evolution and Its Effect on the Cycling Stability of LiNixMnyCozO2 (NMC) Cathode Materials for Li-Ion Batteries; ECS Meeting Abstracts: New Orleans, LA, USA, 2017; Volume MA2017-01. [Google Scholar]
- Keil, P.; Schuster, S.F.; Wilhelm, J.; Travi, J.; Hauser, A.; Karl, R.C.; Jossen, A. Calendar aging of lithium-ion batteries. J. Electrochem. Soc. 2016, 163, A1872. [Google Scholar] [CrossRef]
- Schindler, M.; Sturm, J.; Ludwig, S.; Schmitt, J.; Jossen, A. Evolution of initial cell-to-cell variations during a three-year production cycle. eTransportation 2021, 8, 100102. [Google Scholar] [CrossRef]
- Pastor-Fernández, C.; Widanage, W.D.; Marco, J.; Gama-Valdez, M.Á.; Chouchelamane, G.H. Identification and quantification of ageing mechanisms in Lithium-ion batteries using the EIS technique. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 27–29 June 2016. [Google Scholar]
- Berecibar, M.; Dubarry, M.; Omar, N.; Villarreal, I.; Van Mierlo, J. Degradation mechanism detection for NMC batteries based on Incremental Capacity curves. World Electr. Veh. J. 2016, 8, 350–361. [Google Scholar] [CrossRef] [Green Version]
- Dubarry, M.; Truchot, C.; Liaw, B.Y. Synthesize battery degradation modes via a diagnostic and prognostic model. J. Power Sources 2012, 219, 204–216. [Google Scholar] [CrossRef]
- Li, Y.; Abdel-Monem, M.; Gopalakrishnan, R.; Berecibar, M.; Nanini-Maury, E.; Omar, N.; van den Bossche, P.; Van Mierlo, J. A quick on-line state of health estimation method for Li-ion battery with incremental capacity curves processed by Gaussian filter. J. Power Sources 2018, 373, 40–53. [Google Scholar] [CrossRef]





| Loop | Step | Parameter | Exit | Note |
|---|---|---|---|---|
| CC/CV Ch. | V/mA/ h | initial three cycles | ||
| CC Disch. | V | |||
| Start-1 | Start check-up | |||
| CC Ch. | 450 mA | V/ min | ||
| CC/CV Disch. | 450 mA | V/mA/ h | Disch. before C/20 | |
| Pause | h | |||
| C/20 CC Ch. | 45 mA | V | for ICA and DVA. | |
| CC Disch. | 450 mA | /2 | Discharge to | |
| Pause | h | |||
| EIS | mHz–kHz | mA | ||
| Start-2 | = {1, 2, 3, 4, 5} C | |||
| Pause | 0.5 h | |||
| CC Pulse | V/ s | |||
| Pause | 0.5 h | |||
| DC Pulse | V/ s | |||
| End-2 | End check-up | |||
| Start-3 | 25 times | Cyclic ageing | ||
| CC/CV Ch. | V/mA/ h | |||
| CC Disch. | V | |||
| End-3 | ||||
| End-1 |
| Cell Pair (Cell ID) | Cycling (CC/CV-CC) | at T | EIS | C/20 Charge | Pulse Test |
|---|---|---|---|---|---|
| 1/11 | 300 mA–300 mA | 25 °C | - | - | - |
| 2/12 | 500 mA–500 mA | 25 °C | - | - | - |
| 3/13 | 800 mA–500 mA | 25 °C | - | - | - |
| 4/14 | 450 mA–450 mA | 25 °C | 25 cyc | 25 cyc | 25 cyc |
| 5/15 | 900 mA–900 mA | 25 °C | 25 cyc | 25 cyc | 25 cyc |
| 6/16 | 450 mA–450 mA | 40 °C | 25 cyc | 25 cyc | 25 cyc |
| 7/17 | - | - | - | - | |
| 8/18 | 900 mA–900 mA | 40 °C | 25 cyc | 25 cyc | 25 cyc |
| 9/- | - | - | - | - | |
| -/19 | 900 mA–900 mA | 40 °C | 25 cyc | 25 cyc | 25 cyc |
| 10/20 | 300 mA–300 mA | 25 °C | 10 cyc | - | - |
| n | ||||||
|---|---|---|---|---|---|---|
| x | ||||||
| y | ||||||
| z |
| DL CID 4/5 | SL CID 14/15 | |||
|---|---|---|---|---|
| Measurement | ||||
| II | 26 | 20 | 28 | 34 |
| III | 22 | 29 | 29 | 47 |
| IV | 19 | 36 | 40 | 63 |
| CID 4 | CID 14 | CID 5 | CID 15 | CID 8 | CID 18 | |
|---|---|---|---|---|---|---|
| /% | 0 | −2 | −4 | −16 | −4 | −24 |
| /% | −9 | −21 | −7 | −29 | −12 | −30 |
| /% | 0 | 0 | 0 | −14 | −20 | −25 |
| /% | −3 | −9 | −5 | −21 | −7 | −26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Müller, D.; Fill, A.; Birke, K.P. Cycling of Double-Layered Graphite Anodes in Pouch-Cells. Batteries 2022, 8, 22. https://doi.org/10.3390/batteries8030022
Müller D, Fill A, Birke KP. Cycling of Double-Layered Graphite Anodes in Pouch-Cells. Batteries. 2022; 8(3):22. https://doi.org/10.3390/batteries8030022
Chicago/Turabian StyleMüller, Daniel, Alexander Fill, and Kai Peter Birke. 2022. "Cycling of Double-Layered Graphite Anodes in Pouch-Cells" Batteries 8, no. 3: 22. https://doi.org/10.3390/batteries8030022
APA StyleMüller, D., Fill, A., & Birke, K. P. (2022). Cycling of Double-Layered Graphite Anodes in Pouch-Cells. Batteries, 8(3), 22. https://doi.org/10.3390/batteries8030022








