Abstract
The alkali metal pyroxenes of the AVSi2O6 (A = Li and Na) family have attracted considerable interest as cathode materials for the application in Li and Na batteries. Computer modelling was carried out to determine the dominant intrinsic defects, Li and Na ion diffusion pathways and promising dopants for experimental verification. The results show that the lowest energy intrinsic defect is the V–Si anti-site in both LiVSi2O6 and NaVSi2O6. Li or Na ion migration is slow, with activation energies of 3.31 eV and 3.95 eV, respectively, indicating the necessity of tailoring these materials before application. Here, we suggest that Al on the Si site can increase the amount of Li and Na in LiVSi2O6 and NaVSi2O6, respectively. This strategy can also be applied to create oxygen vacancies in both materials. The most favourable isovalent dopants on the V and Si sites are Ga and Ge, respectively.
1. Introduction
Rechargeable batteries have been the subject of considerable research for many years, to improve energy efficiency and reduce the emission of greenhouse gases [1,2,3]. There is currently much research on Li and Na ion batteries, particularly for use in electric vehicles [4,5]. Materials with a low cost, low hazard risk, high structural and chemical stability and high capacity are of great interest for preparing cathode materials for Li or Na ion batteries. A variety of materials, including phosphate (-, silicate (-, and borate ()-based materials, have been experimentally and theoretically screened for use as cathode materials in batteries [6,7,8,9,10,11,12,13,14,15,16,17]. The search for alternative materials continues.
Silicate-based materials have been considered as candidate cathode materials for both Li and Na ion batteries [6,18,19,20] due to the high abundance of silicon and the lattice stabilisation provided by units. Among them, polyanion orthosilicates such as A2FeSiO4 and A2MnSiO4 (A = Li or Na) have attracted considerable attention due to their strong electrochemical performance [12,13,21,22,23]. Li2FeSiO4 has attracted much interest due to its high theoretical capacity of 332 mAhg−1 [18,24]. However, the performance of this material is hindered by its slow Li-ion diffusion and low electronic conductivity [18]. Many experimental and theoretical studies have focused on the modification of Li2FeSiO4 to improve its properties [25,26,27,28]. Li2MnSiO4, Na2FeSiO4 and Na2MnSiO4 materials have also been studied extensively to assess their performance as cathode materials for batteries [29,30,31,32,33].
Interest in AVSi2O6 (A = Li and Na) materials as cathodes for the application of rechargeable batteries has emerged in recent years due to the existence of variable oxidation states of vanadium, leading to redox reactions [34,35,36]. Li2VSi2O6 was reported to be a potential cathode material for use in Li-ion batteries [34,35]. Two different high capacities of 85 mAhg–1 and 181 mAhg–1 were measured at 30 °C and 60 °C, respectively, due to the introduction of additional 0.42 Li+ ions arising from redox reactions (V3+/V4+ and V2+/V3+) [34]. Very recently, a sol–gel method was used to prepare a high-capacity NaVSi2O6 cathode material yielding a specific capacity of 80 mAhg–1 [36]. Density functional theory simulation was used to examine the stability of Na insertion into NaVSi2O6, and it was concluded that poor cycle stability is directly related to the significant volume change [36]. Although a number of experimental studies have investigated the performance of AVSi2O6 (A = Li and Na), theoretical studies of the defects and ion transport rates are lacking in the literature. Defects are crucial because they strongly influence the performance of electrode materials.
In this study, defect properties, Li (or Na) ion diffusion and solutions of dopants in LiVSi2O6 and NaVSi2O6 are presented with the aid of classical simulations for the first time. In previous simulation studies, we used this methodology to study the defect and diffusion properties in battery materials, fuel-cell materials and minerals [37,38,39,40,41,42,43].
2. Computational Methods
We used the interatomic potential simulation code GULP (General Utility Lattice Program) [44] to examine the intrinsic defect properties, dopant solution and the diffusion of Li (or Na) ions in both LiVSi2O6 and NaVSi2O6. In this method, the interaction between the ions in the lattice is defined as the sum of long-range (Coulomb) and short-range (Pauli repulsion and van der Waals attraction) interactions. Buckingham potentials (Table 1) were used to describe short-range interactions. Full geometry optimisation was performed using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm [45]. The lattice relaxation around point defects and migrating ions was examined using the Mott–Littleton method [46].

Table 1.
Buckingham potential parameters used [30,41,47,48,49].
This methodology divides the lattice into two regions (region I and region II). In region I (inner sphere), ions around the defects are relaxed explicitly. Ions present in region II (outer sphere) are relaxed using a quasi-quantum continuum method. In all defect calculations, there are 684 and 4801 atoms present in region I and region II, respectively. Ion migration calculations were carried out considering two nearest neighbour vacancy sites as initial and final configurations. Seven interstitial positions were selected in a direct linear route, and they were allowed to relax in different directions (x, y, z, xy, yz and xz). Activation energies were calculated considering the energy difference between the local maximum energy and the vacancy formation energy. This methodology assumes that ions are fully charged with a dilute limit. Thus, it is expected that defect energies will be overestimated. However, the relative energy trend will be consistent.
3. Results and Discussion
3.1. Crystal Structures of LiVSi2O6 and NaVSi2O6
Both LiVSi2O6 and NaVSi2O6 crystallized in a monoclinic structure with a space group of C2/c (see Figure 1). An octahedral coordination was found for Al3+ ions. Si4+ ions formed tetrahedral coordination with four nearest-neighbour O2– ions. A SiO4 unit shared its corners with adjacent VO6 and SiO4 units, whereas two adjacent VO6 units share their edges. The experimentally determined lattice parameters of LiVSi2O6 at room temperature are reported to be a = 9.657 Å, b = 8.623 Å, c = 5.287 Å, α = γ = 90.0° and β = 110.15° [50]. In an experimental study, Ohashi et al. [51] used an X-ray diffraction technique to find the lattice constants of NaVSi2O6 [a = 9.634 Å, b = 8.741 Å, c = 5.296 Å, α = γ = 90.0° and β = 106.91°] at 296 K. The choice of pair-wise potentials used in this study was validated by performing full-geometry optimisation calculations on bulk LiVSi2O6 and NaVSi2O6 structures. A good agreement between calculated and experimental lattice parameters was obtained (see Table 2).
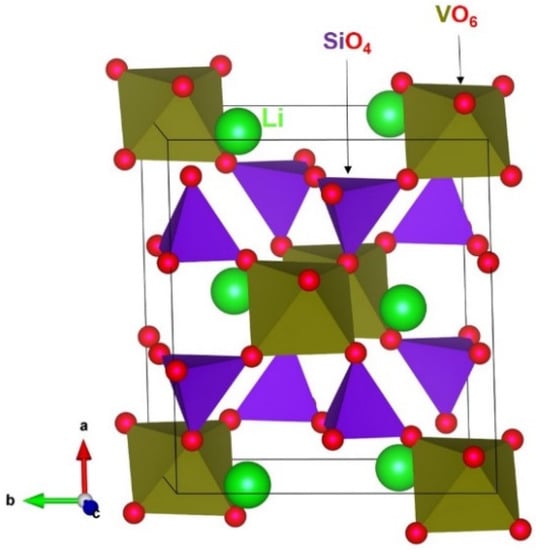
Figure 1.
Crystal structure of LiVSi2O6 (ICSD_CollCode55164.cif) [50] generated using the VESTA (Visualization for Electronic and STructural Analysis) [52] visualisation program.

Table 2.
Calculated and experimental lattice parameters of bulk LiVSi2O6 and NaVSi2O6.
3.2. Defect Properties
Point defects influence the mechanical, electronic and chemical properties of a material. Formation energies of intrinsic point defects (vacancies and interstitials) were first calculated and combined to calculate Frenkel and Schottky defect energies. Cation inter-mixing defects (anti-site defects) were also calculated, because these can govern the diffusion property. Here, we apply the Kröger–Vink notation [53] to write reaction equations to describe the intrinsic defect processes.
Figure 2 shows the calculated reaction energies for LiVSi2O6 and NaVSi2O6. The most dominant defect process was the V–Si anti-site defect cluster in both materials. This indicates that there will be a small concentration of V on the Si site and Si on the V site simultaneously. The isolated form of this defect is higher in energy than its cluster form. This is because of the exothermic binding of isolated defects. Previous experimental and theoretical studies have highlighted the presence of anti-site defects in various oxide materials [54,55,56]. The Li–V and Li–Si anti-defect cluster energies are higher than that of the V–Si anti-site defect cluster. This is due to the higher cation charge mismatch (Li–Si or Li–V). The Li (or Na) Frenkel was found to be the second most favourable defect. This process would expect an increase in the concentration of Li or Na vacancies, which enhances the vacancy-assisted Li or Na diffusion. The Li2O (or Na2O) Schottky defect is the lowest energy process among other Schottky processes. This defect process will degrade the as-prepared material, affecting the performance of batteries. Other Frenkel defects exhibit higher formation energies than the Li (or Na) Frenkel.
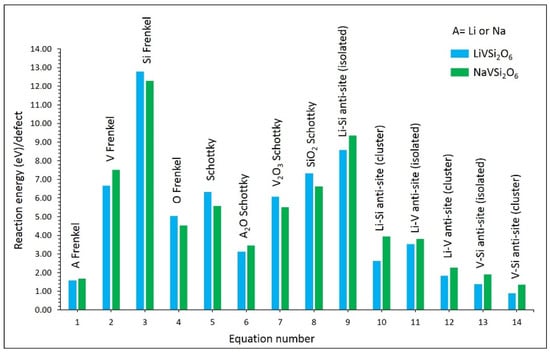
Figure 2.
Intrinsic defect energies in LiVSi2O6 and NaVSi2O6.
3.3. Diffusion of Li and Na Ions
Here, we calculate the diffusion of Li+ and Na+ ions. High ionic conductivity is one of the key features of a cathode material, because it determines the performance of batteries. The current methodology has the ability to determine the diffusion pathways together with activation energies. In previous simulations, many oxide materials have been assessed and the results from those simulations have been supportive in interpreting the experimental data [57,58,59].
Four different possible Li local hops (A, B, C and D) were identified in LiVSi2O6 (see Figure 3a). Local Li hops together with activation energies are provided in Table 3. Hops A and D formed a long-range Li migration pathway (A→ D→ A→ D) with a zig-zag pattern in the ac plane. Activation energies for these hops were 2.47 eV and 4.49 eV, respectively, meaning that long-range migration requires an overall activation energy of 4.49 eV. A long-range Li migration pathway consisting of local hop B (B→ B→ B→ B) is observed in the bc plane. The overall activation energy for this pathway is 6.41 eV. A potential Li–Li hop (C) with a jump distance of 5.02 Å was also identified. This local hop forms a long-range diffusion pathway (C→ C→ C→ C) in the bc plane with a net activation energy of 3.31 eV. Energy profile diagrams plotted to calculate activation energies for Li-local hops are shown in Figure 4. Although this long-range pathway has the lowest overall migration energy, the diffusion of Li-ions in this material is expected to be very slow.
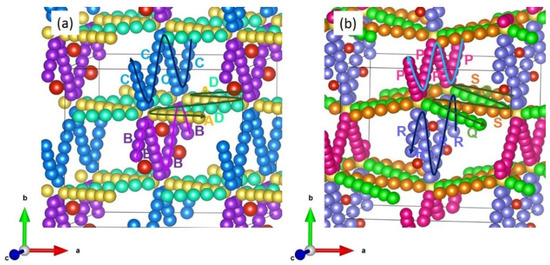
Figure 3.
Migration pathways (a) Long-range Li-ion migration pathways (B→ B→ B→ B, C→ C→ C→ C and A→ D→ A→ D) in LiVSi2O6 and (b) long-range Na-ion migration pathways (P→ P→ P→ P, R→ R→ R→ R and Q→ S→ Q→ S) in NaVSi2O6.

Table 3.
Activation energies for the migration of Li-ions and Na-ions in LiVSi2O6 and NaVSi2O6, respectively.
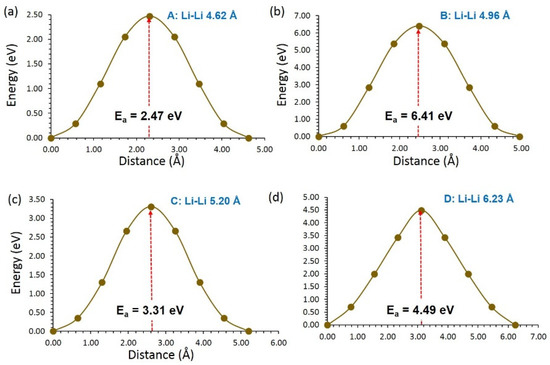
Figure 4.
Energy profile diagrams for the local Li-ion hopping of (a) A, (b) B, (c) C and (d) D in LiVSi2O6.
For Na-ion migration in NaVSi2O6, four local hops (P, Q, R and S) were identified. These hops were then allowed to construct long-range migration pathways, as shown in Figure 3b. In general, activation energies were higher than that calculated for Li-ions in LiVSi2O6 (see Table 3). This can partly be due to the ionic radius of Na+ (1.02 Å) being larger than that of Li+ (0.76 Å) [60]. A long-range Na-ion pathway (P→ P→ P→ P) exhibits an activation energy of 3.95 eV. This pathway can be directly compared with the long-range Li-ion pathway in LiVSi2O6 (C→ C→ C→ C). In both LiVSi2O6 and NaVSi2O6, the lowest ion migration pathway is the same. Although hop Q has the lowest activation energy of 2.88 eV, this hop should be combined with hop S to induce long-range diffusion. The overall activation energy for this diffusion pathway is 7.97 eV (see Table 3). The local hop R exhibits a very large activation energy of 11.78 eV. This can partly be due to the presence of V in that particular zig-zag plane. Figure 5 shows energy profile diagrams calculated for each local Na hop in NaVSi2O6.
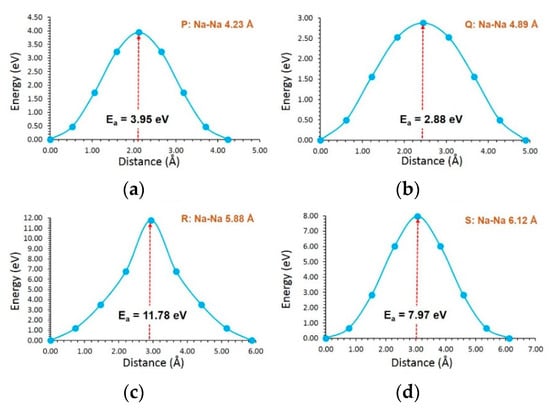
Figure 5.
Energy profile diagrams for the local Na-ion hopping of (a) P, (b) Q, (c) R and (d) S in NaVSi2O6.
Our calculations show that the ionic conductivity in both LiVSi2O6 and NaVSi2O6 is low. A possible way of increasing ion diffusion can be achieved by preparing these materials at nano scales. Appropriate doping strategies (see Section 3.4) can also be introduced to increase the concentration of ions (Li+ or Na+) in the form of interstitial defects.
3.4. Solution of Dopants
Dopants can play a significant role in governing the performance of materials. Here, we consider monovalent (M = Li+, Na+, K+ and Rb+), trivalent (M = Al3+, Ga3+, Sc3+, In3+, Y3+, Gd3+ and La3+) and tetravalent dopants (M = Ge4+, Ti4+, Sn4+, Zr4+ and Ce4+) on the Li (or Na), V (or Si) and Si sites, respectively. The lowest solution energy dopant is predicted for future experimental verification. Necessary charge-compensating defects and energies of lattices were included in the reaction equations. Buckingham potentials used for dopants are given in the electronic supplementary materials (see Table S1).
3.4.1. Monovalent Dopants
Monovalent dopants were considered on the Li site in LiVSi2O6 and the Na site in NaVSi2O6. The defect reaction process used for LiVSi2O6 is given by the following equation:
An exoergic solution energy of –0.35 eV was determined for Na+ in LiVSi2O6 (see Figure 6a). This is partly due to the ionic radius of Li+ (0.76 Å) matching with the ionic radius of Na+ (1.02 Å) [60]. It is possible to synthesise Li1−xVSi2O6 (0.0 < x < 1.0). However, the exact concentration should be verified experimentally. The solution energy increases with the increasing ionic radius. The largest solution energy is calculated for the Rb+. In the case of NaVSi2O6, the most favourable dopant is Li+. The solution energy for this dopant is 0.83 eV. Although this dopant is not thermodynamically feasible, the doping process can be performed at high temperatures. Solution energies for K+ and Rb+ are higher than that calculated for Li+ due to their larger ionic radii than that of Li+.
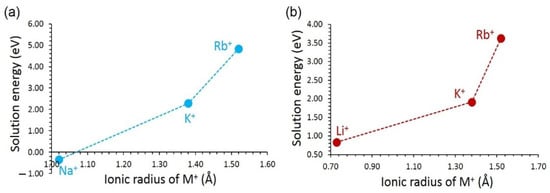
Figure 6.
Solution energy of M2O with respect to the M+ ionic radius in (a) LiVSi2O6 and (b) NaVSi2O6.
3.4.2. Trivalent Dopants
A range of trivalent dopants were substituted on the vanadium site. Vanadium has a charge of +3 in this material; therefore, charge-compensating defects were not necessary. The following reaction equation explains the doping process:
Solution energies are shown in Figure 7. In both LiVSi2O6 and NaVSi2O6, the most favourable dopant is Ga. The preference of Ga in both materials is due to the close ionic radius match between V3+ (0.64 Å) and Ga3+ (0.62 Å) [60]. Al exhibits positive solution energies in both materials, although its ionic radius (0.54 Å) is smaller than that of V3+. The solution energy increases with the increasing ionic radius from Sc to La. A similar trend in the solution energies is noted for both materials, although the solution energies are slightly lower in LiVSi2O6 than in NaVSi2O6. The most unfavourable dopant is La3+.
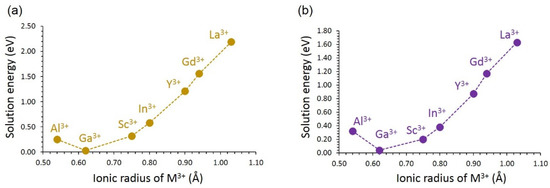
Figure 7.
Solution energy of M2O3 with respect to the M3+ ionic radius in (a) LiVSi2O6 and (b) NaVSi2O6.
In order to create Li interstitials in LiVSi2O6 or Na interstitials in NaVSi2O6, the Si site was substituted by trivalent dopants, as described by defect Equation (17). The incorporation of a trivalent cation onto a tetravalent cation lattice site results in two potential compensating defects (Li+ interstitial ion and a host lattice oxygen vacancy) and a second phase material (SiO2), in contrast to the experiment.
This efficient strategy can improve the capacity of the batteries. Al3+ is a promising dopant for this strategy. In a previous simulation study on Li2MnSiO4 cathode material, Al3+ was identified as a candidate dopant for generating Li interstitials [30]. In general, there is a gradual increase in the solution energy with increasing ionic radii in both materials (see Figure 8). Slightly favourable solution energies were calculated for NaVSi2O6, although the solution process is endoergic. The promising dopant Al3+ can be tested and validated experimentally. The lowest solution energy calculated for Al3+ can partly be due to the small difference between the ionic radii of Al3+ (0.39 Å) and Si4+ (0.26 Å) [60]. Endoergic solution energies are due to the quadruply charged Si being occupied by triply charged dopants.
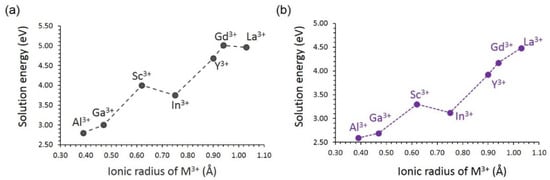
Figure 8.
Solution energy of M2O3 forming interstitials with respect to the M3+ ionic radius in (a) LiVSi2O6 and (b) NaVSi2O6.
As mentioned earlier, trivalent doping on the Si site can also generate oxygen vacancies as charge-compensating defects, as defined by the following equation:
The oxygen vacancies can promote vacancy-assisted Li or Na migration via Li2O or Na2O formation. Al3+ is a suitable dopant for this as well (see Figure 9). The trend in the solution energies is almost the same as that observed for the formation interstitials (see Figure 8). The solution energies are higher by ~1.50 eV for each dopant than that calculated for interstitials, meaning that high temperature should be applied for the oxygen vacancy formation process.
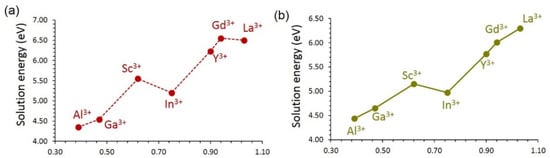
Figure 9.
Solution energy of M2O3 forming oxygen vacancies with respect to the M3+ ionic radius in (a) LiVSi2O6 and (b) NaVSi2O6.
3.4.3. Tetravalent Dopants
Finally, tetravalent cations were doped on the Si site. This doping process produces no charge-compensating defects, as explained by Equation (19):
The results show that the most favourable dopant for this process is Ge4+ (see Figure 10). The favourability of this dopant is due to the smaller ionic radius of Ge4+ (0.39 Å), closer to that of Si4+ (0.26 Å). There is a big jump in the solution energy for Ti4+. Solution energy then increases with the increasing ionic radius. Both LiVSi2O6 and NaVSi2O6 exhibit almost similar solution energies. The possible composition that can be prepared by experiments is LiVSi2-xGexO6 or NaVSi2−xGexO6 (x = 0.0 < x < 1.0). The largest solution energy is calculated for Ce4+, suggesting that this dopant requires high temperatures. The migration of Li-ions was calculated in the presence of Ge4+ dopant. The doping was reflected in the activation energies of local hops. In all cases, there were small reductions in the activation energies (LiVSi2O6: A-4.53 eV, B-4.88 eV, C-5.10 eV and D-4.40 eV; NaVSi2O6: P-3.89 eV, Q-2.80 eV, R-11.67 eV and S-7.90 eV). In all cases, long-range diffusion pathways were unaffected.
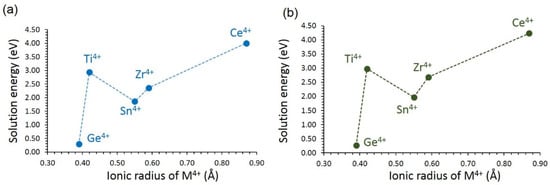
Figure 10.
Solution energy of MO2 with respect to the M4+ ionic radius in (a) LiVSi2O6 and (b) NaVSi2O6.
4. Conclusions
In conclusion, we used atomistic simulation based on the classical pair potentials to examine the defects, diffusion and dopant properties of LiVSi2O6 and NaVSi2O6. The dominant defect in both materials is the V–Si anti-site defect, suggesting that a small amount of cation inter-mixing will be present. The Li or Na ionic conductivity is slow in both materials, indicating that the as-prepared materials should be modified to increase the rate of Li-ion (or Na-ion) diffusion. The doping of Al on the Si site is an efficient strategy to increase the concentration of Li and Na in LiVSi2O6 and NaVSi2O6, respectively. Such doping can also create oxygen vacancies in both materials. The candidate isovalent dopants on the V and Si sites are Ga and Ge, respectively.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/batteries8030020/s1, Table S1: Two body Buckingham potentials used for dopant oxides in LiVSi2O6 and NaVSi2O6.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The high-performance computing centre at Imperial College London is acknowledged for providing computational facilities to run GULP code.
Conflicts of Interest
The author declares no conflict of interest.
References
- Liang, Y.; Zhao, C.-Z.; Yuan, H.; Chen, Y.; Zhang, W.; Huang, J.-Q.; Yu, D.; Liu, Y.; Titirici, M.M.; Chueh, Y.L.; et al. A review of rechargeable batteries for portable electronic devices. InfoMat 2019, 1, 6–32. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Park, K.-S. The Li-Ion Rechargeable Battery: A Perspective. J. Am. Chem. Soc. 2013, 135, 1167–1176. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.; Song, W.; Son, D.-Y.; Ono, L.K.; Qi, Y. Lithium-ion batteries: Outlook on present, future, and hybridized technologies. J. Mater. Chem. A 2019, 7, 2942–2964. [Google Scholar] [CrossRef]
- Chen, W.; Liang, J.; Yang, Z.; Li, G. A Review of Lithium-Ion Battery for Electric Vehicle Applications and Beyond. Energy Procedia 2019, 158, 4363–4368. [Google Scholar] [CrossRef]
- Karabelli, D.; Singh, S.; Kiemel, S.; Koller, J.; Konarov, A.; Stubhan, F.; Miehe, R.; Weeber, M.; Bakenov, Z.; Birke, K.P. Sodium-Based Batteries: In Search of the Best Compromise Between Sustainability and Maximization of Electric Performance. Front. Energy Res. 2020, 8, 349. [Google Scholar] [CrossRef]
- Islam, M.S.; Fisher, C.A.J. Lithium and sodium battery cathode materials: Computational insights into voltage, diffusion and nanostructural properties. Chem. Soc. Rev. 2014, 43, 185–204. [Google Scholar] [CrossRef]
- Bao, L.; Gao, W.; Su, Y.; Wang, Z.; Li, N.; Chen, S.; Wu, F. Progression of the silicate cathode materials used in lithium ion batteries. Chin. Sci. Bull. 2013, 58, 575–584. [Google Scholar] [CrossRef]
- Ling, J.; Karuppiah, C.; Krishnan, S.G.; Reddy, M.V.; Misnon, I.I.; Ab Rahim, M.H.; Yang, C.C.; Jose, R. Phosphate Polyanion Materials as High-Voltage Lithium-Ion Battery Cathode: A Review. Energy Fuels 2021, 35, 10428–10450. [Google Scholar] [CrossRef]
- Niu, Y.; Zhang, Y.; Xu, M. A review on pyrophosphate framework cathode materials for sodium-ion batteries. J. Mater. Chem. A 2019, 7, 15006–15025. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y.; Sun, J.; Chen, A. A Review on Applications of Layered Phosphorus in Energy Storage. Trans. Tianjin Univ. 2020, 26, 104–126. [Google Scholar] [CrossRef]
- Yang, S.-H.; Xue, H.; Guo, S.-P. Borates as promising electrode materials for rechargeable batteries. Coord. Chem. Rev. 2021, 427, 213551. [Google Scholar] [CrossRef]
- Roy, B.; Cherepanov, P.; Nguyen, C.; Forsyth, C.; Pal, U.; Mendes, T.C.; Howlett, P.; Forsyth, M.; MacFarlane, D.; Kar, M. Lithium Borate Ester Salts for Electrolyte Application in Next-Generation High Voltage Lithium Batteries. Adv. Energy Mater. 2021, 11, 2101422. [Google Scholar] [CrossRef]
- Zhang, Q.; Ji, S.; Yan, C.; Wang, X. Insights into the porosity and electrochemical performance of nano Li2FeSiO4 and Li2FeSiO4/C composite cathode materials. Mater. Technol. 2021, 1–10. [Google Scholar] [CrossRef]
- Li, L.; Han, E.; Pei, X.; Fu, C.; Zhang, M. The research on the electrochemical performance of Li2FeSiO4/mgx and Li2FeSiO4/cux. Inorg. Nano-Met. Chem. 2021, 51, 1536–1545. [Google Scholar] [CrossRef]
- Fisher, C.A.J.; Hart Prieto, V.M.; Islam, M.S. Lithium Battery Materials LiMPO4 (M = Mn, Fe, Co, and Ni): Insights into Defect Association, Transport Mechanisms, and Doping Behavior. Chem. Mater. 2008, 20, 5907–5915. [Google Scholar] [CrossRef]
- Clark, J.M.; Barpanda, P.; Yamada, A.; Islam, M.S. Sodium-ion battery cathodes Na2FeP2O7 and Na2MnP2O7: Diffusion behaviour for high rate performance. J. Mater. Chem. A 2014, 2, 11807–11812. [Google Scholar] [CrossRef]
- Kalantarian, M.M.; Hafizi-Barjini, M.; Momeni, M. Ab Initio Study of AMBO3 (A = Li, Na and M = Mn, Fe, Co, Ni) as Cathode Materials for Li-Ion and Na-Ion Batteries. ACS Omega 2020, 5, 8952–8961. [Google Scholar] [CrossRef]
- Nytén, A.; Kamali, S.; Häggström, L.; Gustafsson, T.; Thomas, J.O. The lithium extraction/insertion mechanism in Li2FeSiO4. J. Mater. Chem. 2006, 16, 2266–2272. [Google Scholar] [CrossRef]
- Yang, F.; Xia, Z.; Huang, S.; Zhang, X.; Song, Y.; Xiao, G.; Shao, G.; Liu, Y.; Deng, H.; Jiang, D.; et al. High field phase transition of cathode material Li2MnSiO4 for lithium-ion battery. Mater. Res. Express 2020, 7, 026104. [Google Scholar] [CrossRef]
- Eshetu, G.G.; Zhang, H.; Judez, X.; Adenusi, H.; Armand, M.; Passerini, S.; Figgemeier, E. Production of high-energy Li-ion batteries comprising silicon-containing anodes and insertion-type cathodes. Nat. Commun. 2021, 12, 5459. [Google Scholar] [CrossRef]
- Nishimura, S.-I.; Hayase, S.; Kanno, R.; Yashima, M.; Nakayama, N.; Yamada, A. Structure of Li2FeSiO4. J. Am. Chem. Soc. 2008, 130, 13212–13213. [Google Scholar] [CrossRef] [PubMed]
- Politaev, V.V.; Petrenko, A.A.; Nalbandyan, V.B.; Medvedev, B.S.; Shvetsova, E.S. Crystal structure, phase relations and electrochemical properties of monoclinic Li2MnSiO4. J. Solid State Chem. 2007, 180, 1045–1050. [Google Scholar] [CrossRef]
- Zhang, P.; Xu, Y.; Zheng, F.; Wu, S.Q.; Yang, Y.; Zhu, Z.-Z. Ion diffusion mechanism in Pn NaxLi2-xMnSiO4. CrystEngComm 2015, 17, 2123–2128. [Google Scholar] [CrossRef]
- Li, L.; Han, E.; Qiao, S.; Liu, H.; Shi, Y.; Yuan, W. Synthesis characterization and improved electrochemical performance of Li2FeSiO4/C as cathode for lithium-ion battery by metal doping. Prog. Nat. Sci. Mater. Int. 2019, 29, 111–118. [Google Scholar] [CrossRef]
- Kumar, A.; Jayakumar, O.D.; Bashiri, P.; Nazri, G.A.; Naik, V.M.; Naik, R. Mg doped Li2FeSiO4/C nanocomposites synthesized by the solvothermal method for lithium ion batteries. Dalton Trans. 2017, 46, 12908–12915. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Jia, T.; Liu, C.; Han, E.; Yang, Y.; Qin, Y.; Zhang, M. The modification of Li2FeSiO4 materials by dual doping with Ag and PO43− or BO33−. Ionics 2021, 27, 1887–1898. [Google Scholar] [CrossRef]
- Kim, C.; Yoo, G.W.; Son, J.T. Barium Doped Li2FeSiO4 Cathode Material for Li-Ion Secondary Batteries. J. Nanosci. Nanotechnol. 2015, 15, 8808–8812. [Google Scholar] [CrossRef]
- Li, S.-D.; Gao, K. Insights into manganese and nickel co-doped Li2FeSiO4 cathodes for lithium-ion battery. Ionics 2021, 27, 2345–2352. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Defects, Dopants and Sodium Mobility in Na2MnSiO4. Sci. Rep. 2018, 8, 14669. [Google Scholar] [CrossRef]
- Kuganathan, N.; Islam, M.S. Li2MnSiO4 Lithium Battery Material: Atomic-Scale Study of Defects, Lithium Mobility, and Trivalent Dopants. Chem. Mater. 2009, 21, 5196–5202. [Google Scholar] [CrossRef]
- Zhu, L.; Zeng, Y.-R.; Wen, J.; Li, L.; Cheng, T.-M. Structural and electrochemical properties of Na2FeSiO4 polymorphs for sodium-ion batteries. Electrochim. Acta 2018, 292, 190–198. [Google Scholar] [CrossRef]
- Law, M.; Ramar, V.; Balaya, P. Na2MnSiO4 as an attractive high capacity cathode material for sodium-ion battery. J. Power Sources 2017, 359, 277–284. [Google Scholar] [CrossRef]
- Hou, P.; Feng, J.; Wang, Y.; Wang, L.; Li, S.; Yang, L.; Luo, S.H. Study on the properties of Li2MnSiO4 as cathode material for lithium-ion batteries by sol-gel method. Ionics 2020, 26, 1611–1616. [Google Scholar] [CrossRef]
- Ni, J.; Kawabe, Y.; Morishita, M.; Watada, M.; Takeichi, N.; Sakai, T. Pyroxene LiVSi2O6 as an electrode material for Li-ion batteries. J. Power Sources 2010, 195, 8322–8326. [Google Scholar] [CrossRef]
- Hameed, A.S.; Reddy, M.V.; AlQaradawi, S.Y.; Adams, S. Synthesis, structural and lithium storage studies of graphene-LiVSi2O6 composites. Ionics 2019, 25, 1559–1566. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, Y.; Huang, Y.; Wang, X.; Cheng, W.; Sun, Y.; Jia, D.; Tang, X. Simple synthesis and electrochemical performance of NaVSi2O6 as a new sodium-ion cathode material. Int. J. Energy Res. 2021, 45, 10746–10751. [Google Scholar] [CrossRef]
- Wong, L.L.; Chen, H.; Adams, S. Design of fast ion conducting cathode materials for grid-scale sodium-ion batteries. Phys. Chem. Chem. Phys. 2017, 19, 7506–7523. [Google Scholar] [CrossRef]
- Yeandel, S.R.; Chapman, B.J.; Slater, P.R.; Goddard, P. Structure and Lithium-Ion Dynamics in Fluoride-Doped Cubic Li7La3Zr2O12 (LLZO) Garnet for Li Solid-State Battery Applications. J. Phys. Chem. C 2018, 122, 27811–27819. [Google Scholar] [CrossRef]
- Byrne, E.H.; Raiteri, P.; Gale, J.D. Computational Insight into Calcium–Sulfate Ion Pair Formation. J. Phys. Chem. C 2017, 121, 25956–25966. [Google Scholar] [CrossRef]
- Taylor, F.H.; Buckeridge, J.; Catlow, C.R.A. Defects and Oxide Ion Migration in the Solid Oxide Fuel Cell Cathode Material LaFeO3. Chem. Mater. 2016, 28, 8210–8220. [Google Scholar] [CrossRef]
- Treacher, J.C.; Wood, S.M.; Islam, M.S.; Kendrick, E. Na2CoSiO4 as a cathode material for sodium-ion batteries: Structure, electrochemistry and diffusion pathways. Phys. Chem. Chem. Phys. 2016, 18, 32744–32752. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, R.; Wood, S.M.; Islam, M.S.; Nazar, L.F. Na-ion mobility in layered Na2FePO4F and olivine Na[Fe,Mn]PO4. Energy Environ. Sci. 2013, 6, 2257–2264. [Google Scholar] [CrossRef]
- Panchmatia, P.M.; Orera, A.; Kendrick, E.; Hanna, J.V.; Smith, M.E.; Slater, P.R.; Islam, M.S. Protonic defects and water incorporation in Si and Ge-based apatite ionic conductors. J. Mater. Chem. 2010, 20, 2766–2772. [Google Scholar] [CrossRef][Green Version]
- Gale, J.D.; Rohl, A.L. The General Utility Lattice Program (GULP). Mol. Simul. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Gale, J.D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 1997, 93, 629–637. [Google Scholar] [CrossRef]
- Mott, N.F.; Littleton, M.J. Conduction in polar crystals. I. Electrolytic conduction in solid salts. Trans. Faraday Soc. 1938, 34, 485–499. [Google Scholar] [CrossRef]
- Woodley, S.M.; Catlow, C.R.A.; Piszora, P.; Stempin, K.; Wolska, E. Computer Modeling Study of the Lithium Ion Distribution in Quaternary Li–Mn–Fe–O Spinels. J. Solid State Chem. 2000, 153, 310–316. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Defects and dopant properties of Li3V2(PO4)3. Sci. Rep. 2019, 9, 333. [Google Scholar] [CrossRef]
- Minervini, L.; Grimes, R.W.; Sickafus, K.E. Disorder in Pyrochlore Oxides. J. Am. Ceram. Soc. 2000, 83, 1873–1878. [Google Scholar] [CrossRef]
- Redhammer, G.J.; Roth, G. Structural variation and crystal chemistry of LiMe3+Si2O6 clinopyroxenes Me3+ = Al, Ga, Cr, V.; Fe, Sc and In. Z. Für Krist.—Cryst. Mater. 2004, 219, 278–294. [Google Scholar] [CrossRef]
- Ohashi, H.; Osawa, T.; Sato, A. NaVSi2O6. Acta Crystallogr. Sect. C 1994, 50, 1652–1655. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
- Kröger, F.A.; Vink, H.J. Relations between the Concentrations of Imperfections in Crystalline Solids. In Solid State Physics; Seitz, F., Turnbull, D., Eds.; Academic Press: Cambridge, MA, USA, 1956; Volume 3, pp. 307–435. [Google Scholar]
- Kempaiah Devaraju, M.; Duc Truong, Q.; Hyodo, H.; Sasaki, Y.; Honma, I. Synthesis, characterization and observation of antisite defects in LiNiPO4 nanomaterials. Sci. Rep. 2015, 5, 11041. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Choe, M.J.; Enrique, R.A.; Orvañanos, B.; Zhou, L.; Liu, T.; Thornton, K.; Grey, C.P. Effects of Antisite Defects on Li Diffusion in LiFePO4 Revealed by Li Isotope Exchange. J. Phys. Chem. C 2017, 121, 12025–12036. [Google Scholar] [CrossRef]
- Gardiner, G.R.; Islam, M.S. Anti-Site Defects and Ion Migration in the LiFe0.5Mn0.5PO4 Mixed-Metal Cathode Material. Chem. Mater. 2010, 22, 1242–1248. [Google Scholar] [CrossRef]
- Islam, M.S.; Driscoll, D.J.; Fisher, C.A.J.; Slater, P.R. Atomic-Scale Investigation of Defects, Dopants, and Lithium Transport in the LiFePO4 Olivine-Type Battery Material. Chem. Mater. 2005, 17, 5085–5092. [Google Scholar] [CrossRef]
- Heath, J.; Chen, H.; Islam, M.S. MgFeSiO4 as a potential cathode material for magnesium batteries: Ion diffusion rates and voltage trends. J. Mater. Chem. A 2017, 5, 13161–13167. [Google Scholar] [CrossRef]
- Stokes, S.J.; Islam, M.S. Defect chemistry and proton-dopant association in BaZrO3 and BaPrO3. J. Mater. Chem. 2010, 20, 6258–6264. [Google Scholar] [CrossRef]
- Shannon, R. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).