Comparison of Capacity Fade for the Constant Current and WLTC Drive Cycle Discharge Modes for Commercial LiFeYPO4 Cells Used in xEV Vehicles
Abstract
1. Introduction
1.1. xEV
1.2. LiFeYPO4
1.3. Testing of Cycle Aging
1.4. Simulation of Cycle Aging
1.5. Objectives of This Paper
- (a)
- What is the difference of capacity fade for the CC and DrC discharge mode?
- (b)
- How can be commonly available CC discharging results of capacity fade understood in terms of supposed dynamic WLTC discharging profile representing real performance of the xEV battery?
- CC discharge cycles: this is the usual test mode, when the battery is discharged in CC mode and charged in CC/CV mode.
- Drive cycle discharge cycles: battery is discharged with a current waveform based on drive cycle and it is charged in CC/CV mode.
2. Methods of Comparison
2.1. General Considerations
2.2. Battery Chemistry Selection
2.3. Electric Current Waveform for the Experiment
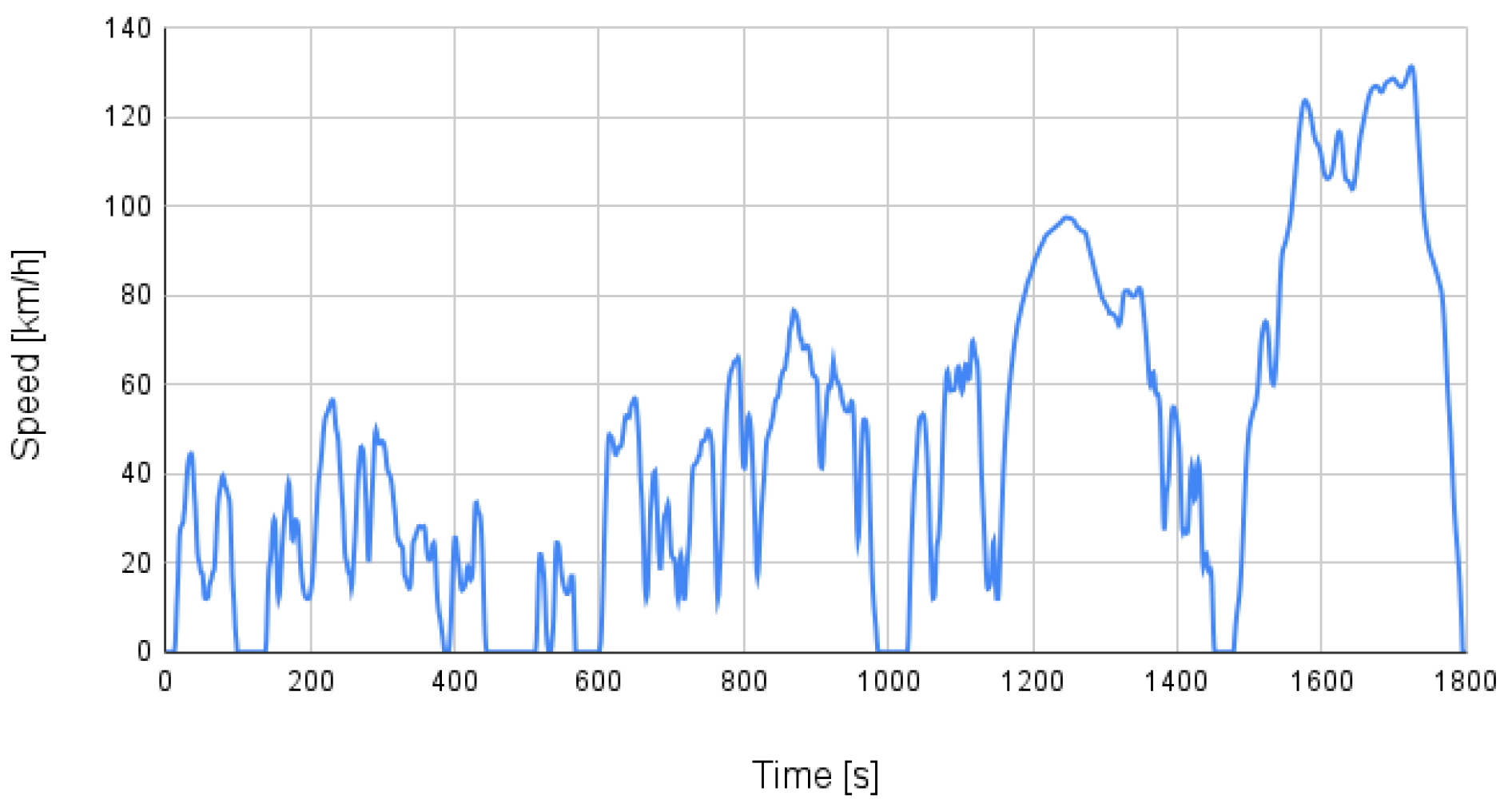
2.3.1. Vehicle Test Cycle
2.3.2. Battery Electric Vehicle Model
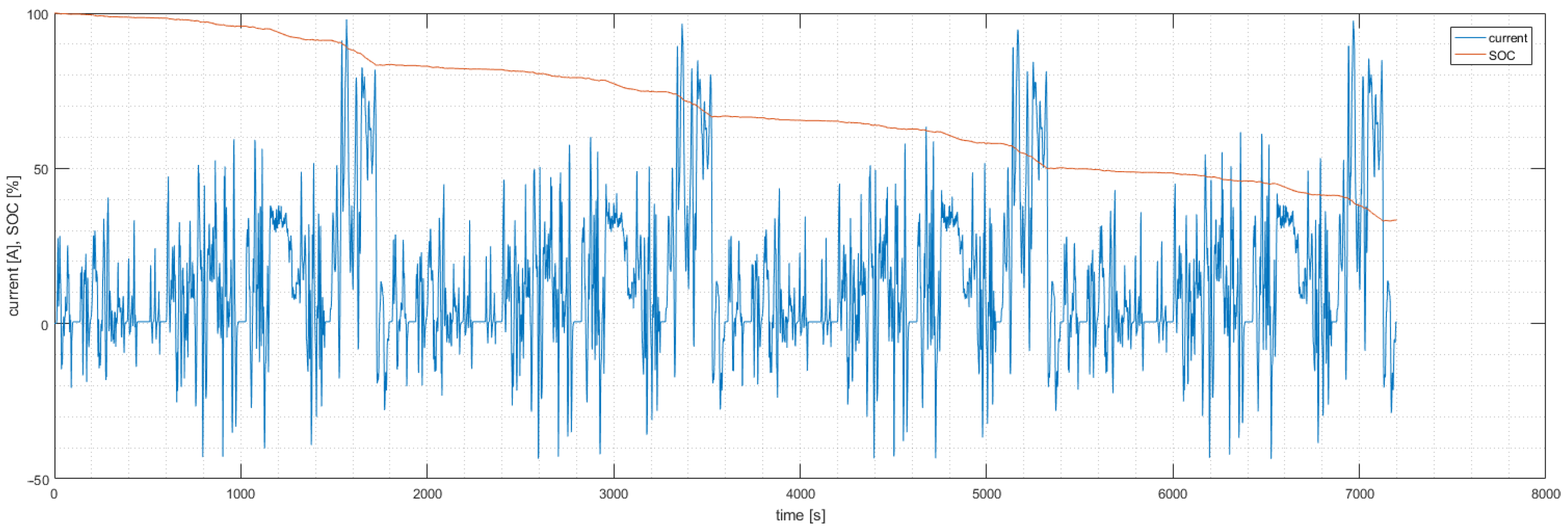
2.4. Drive Cycle Mode
2.5. Continuous Current Mode
2.6. Simulation
3. Experiment Set-Up
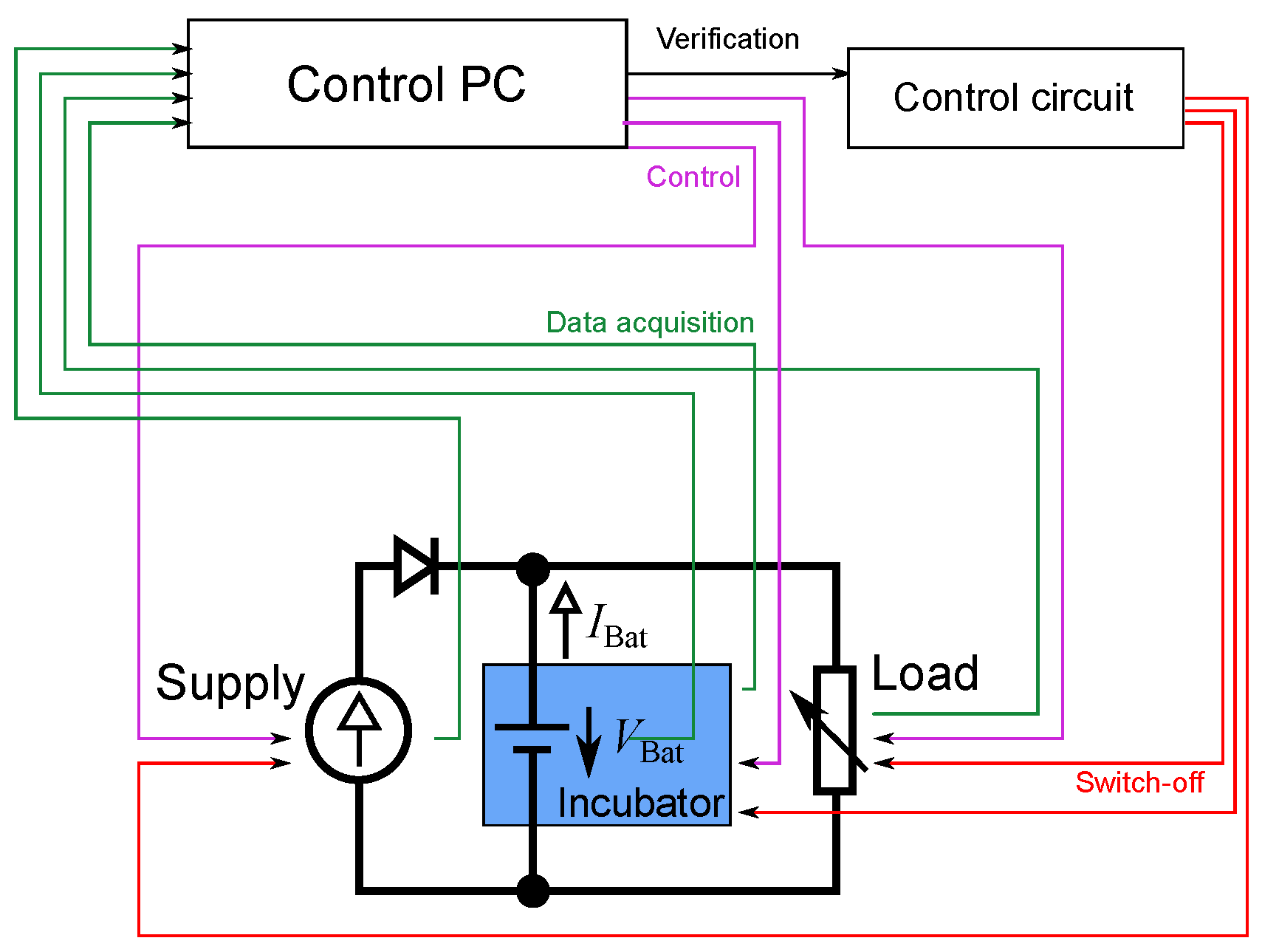
3.1. Equipment
3.2. Cycling Specification
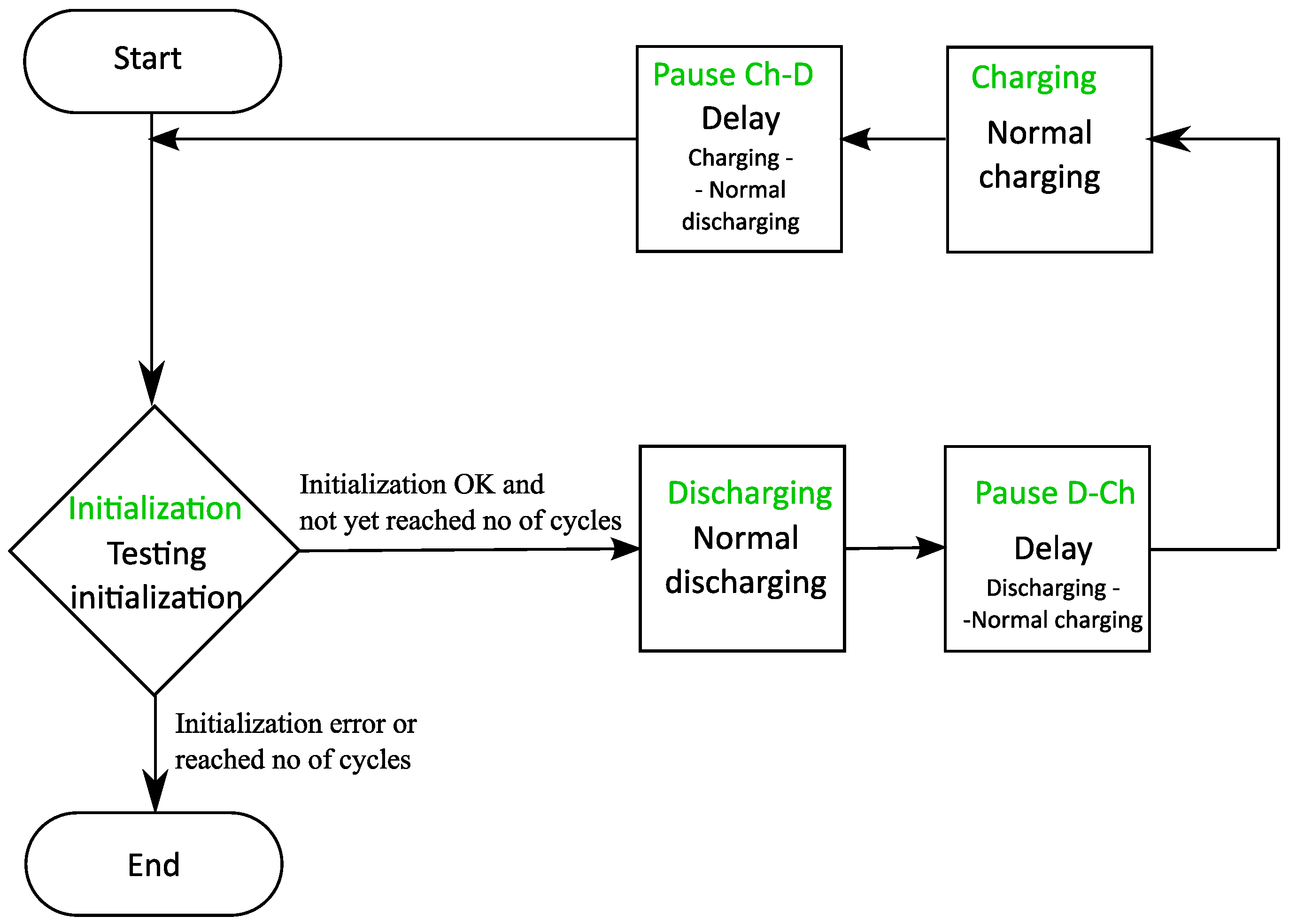
3.2.1. State Machine
3.2.2. Parameters
- CC mode Charging current ;
- charging voltage ;
- CV mode Charging cut-off current ;
- delay between discharging and charging ;
- delay between charging and discharging .
3.3. Cells Samples Used
3.3.1. Cell Types
3.3.2. Sampling
4. Experiment Results
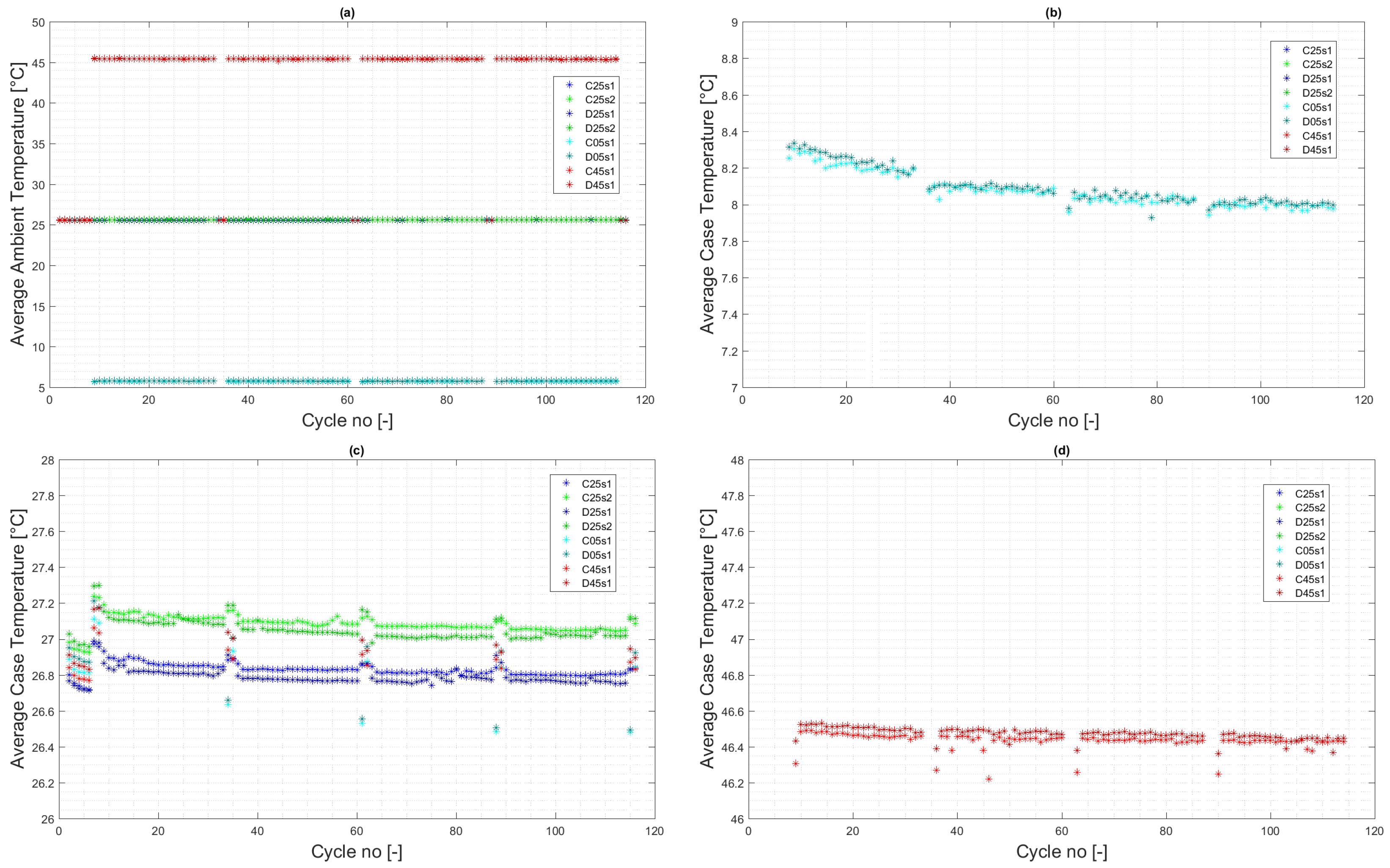
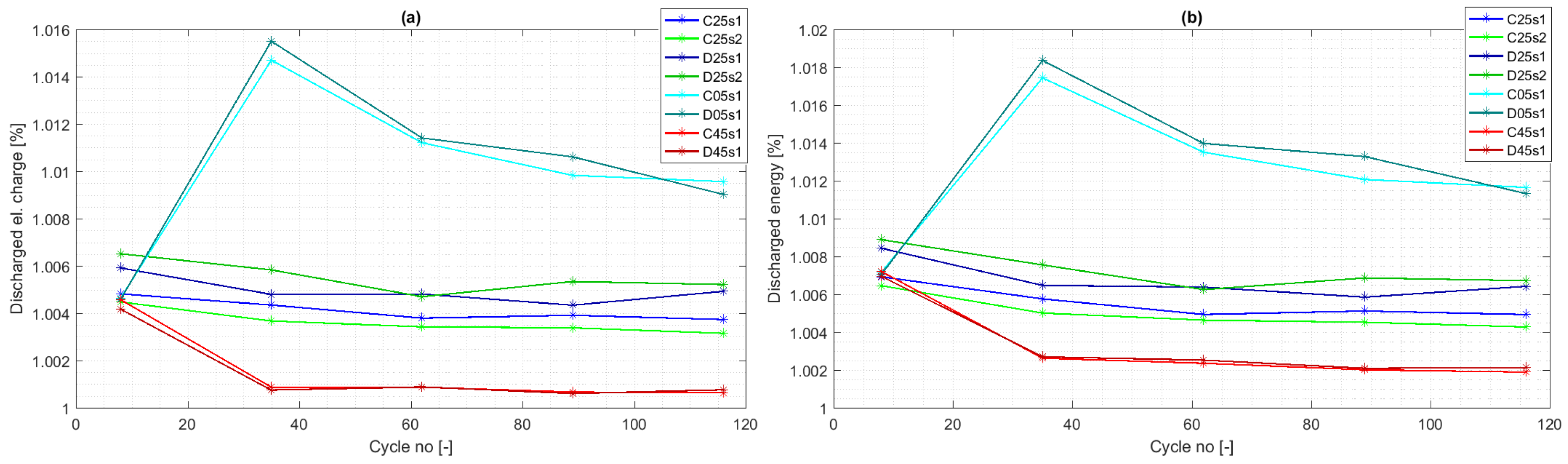
4.1. Experiment Validity Verification
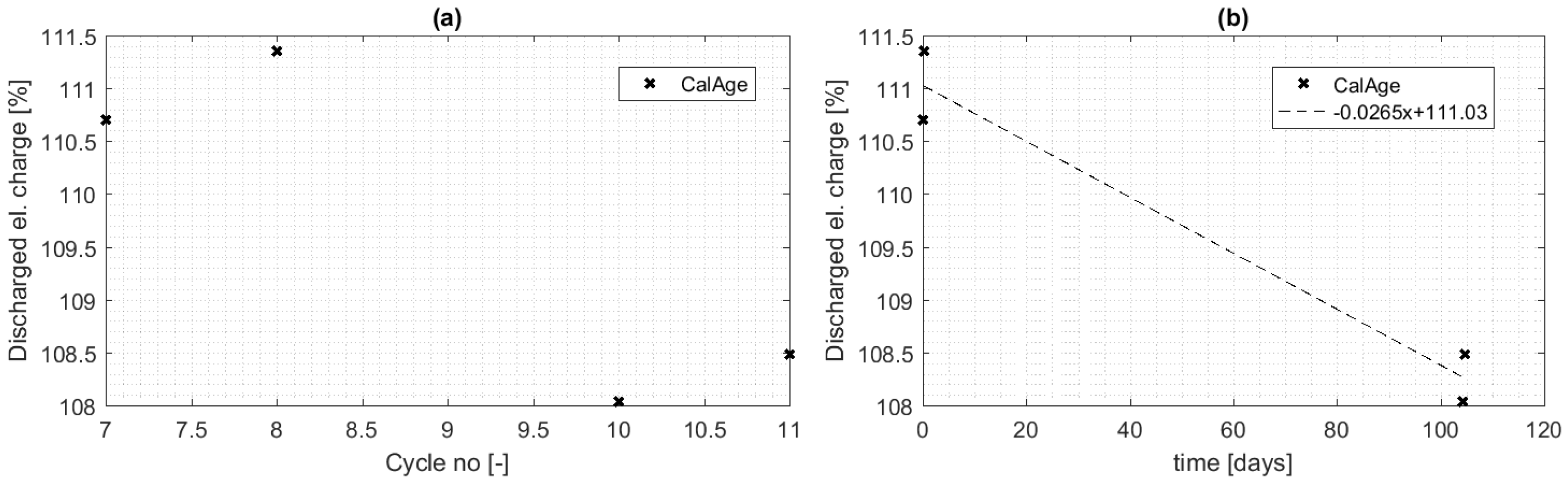
4.2. Calendar Aging
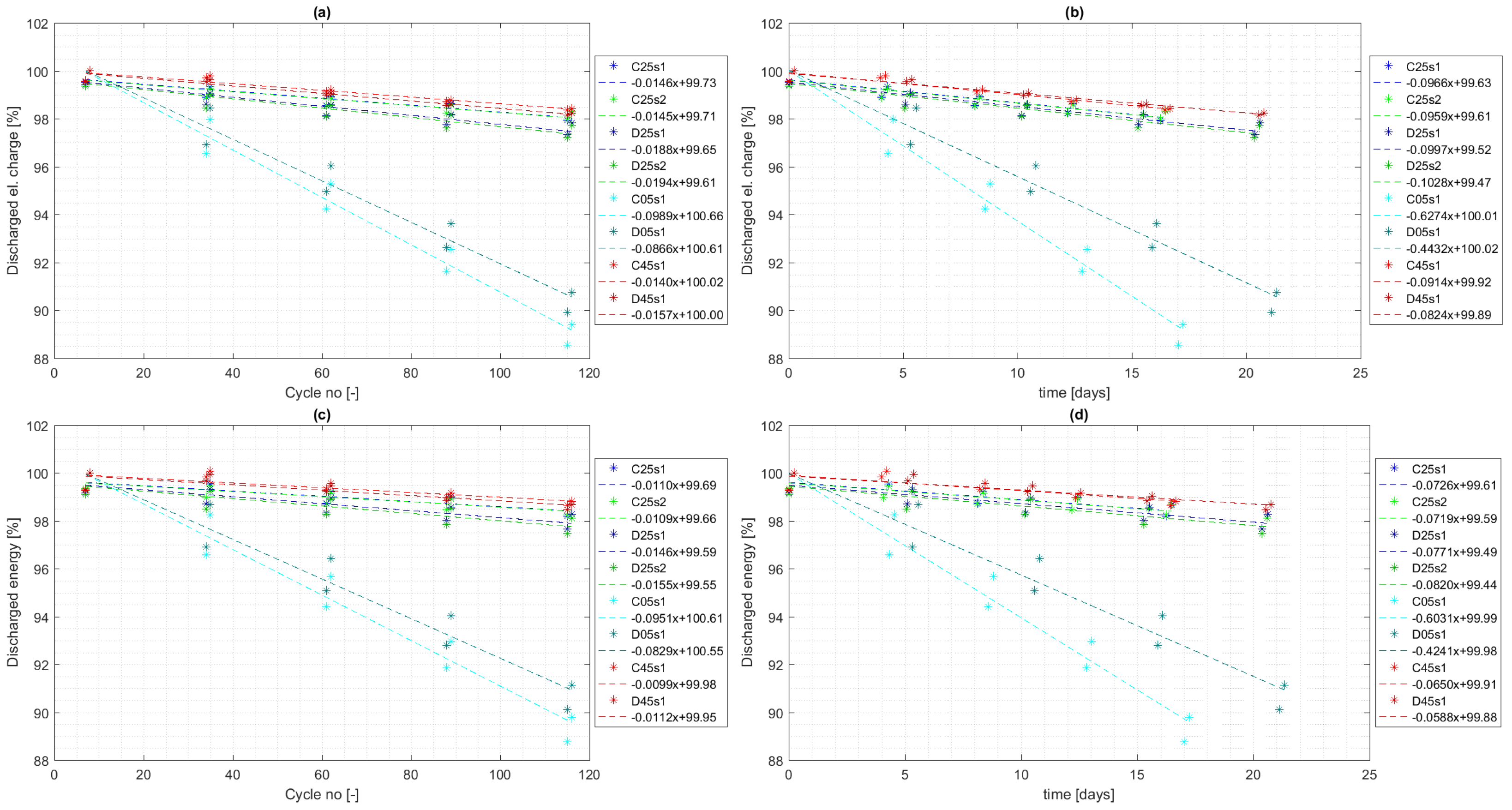
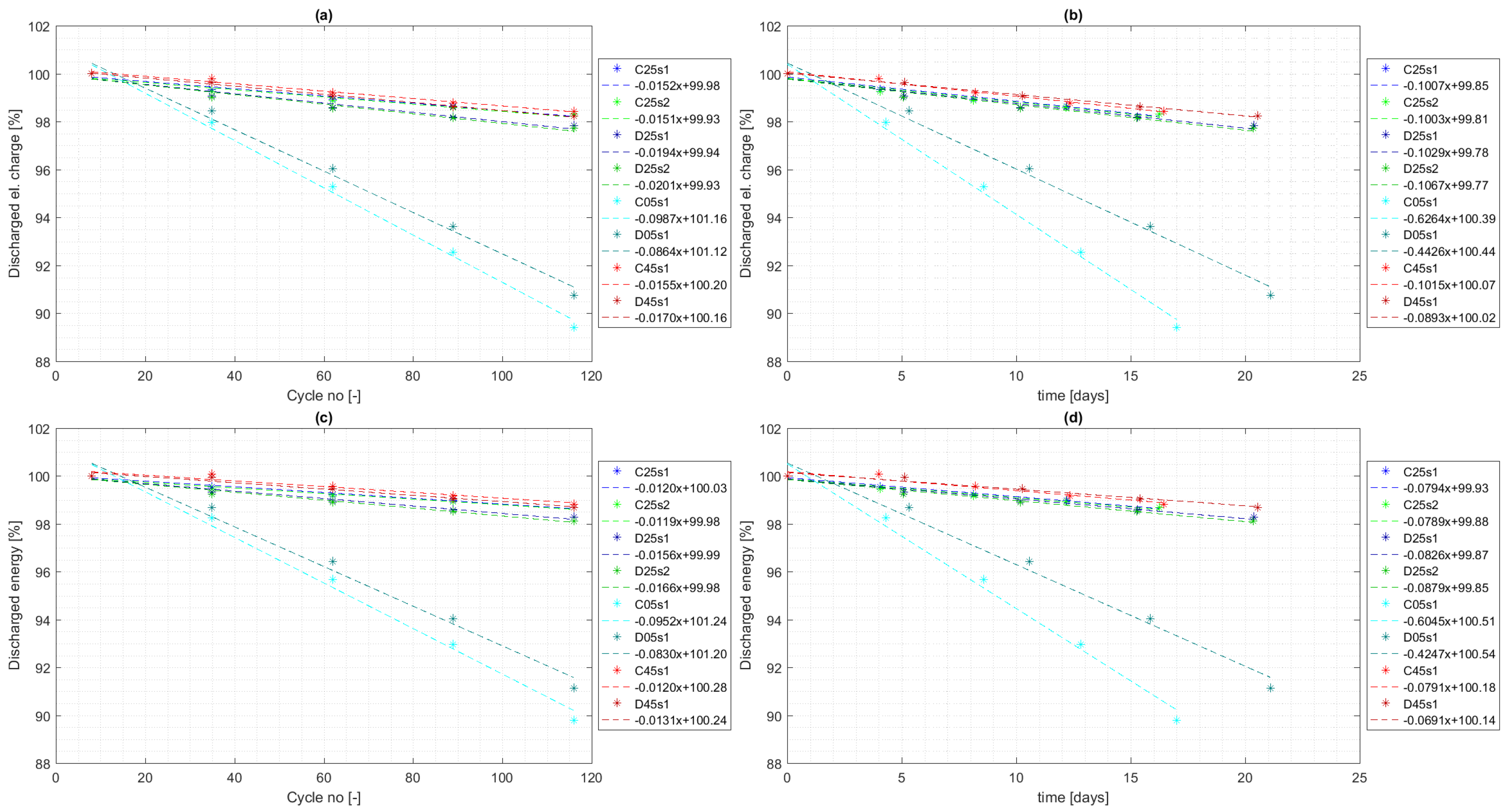
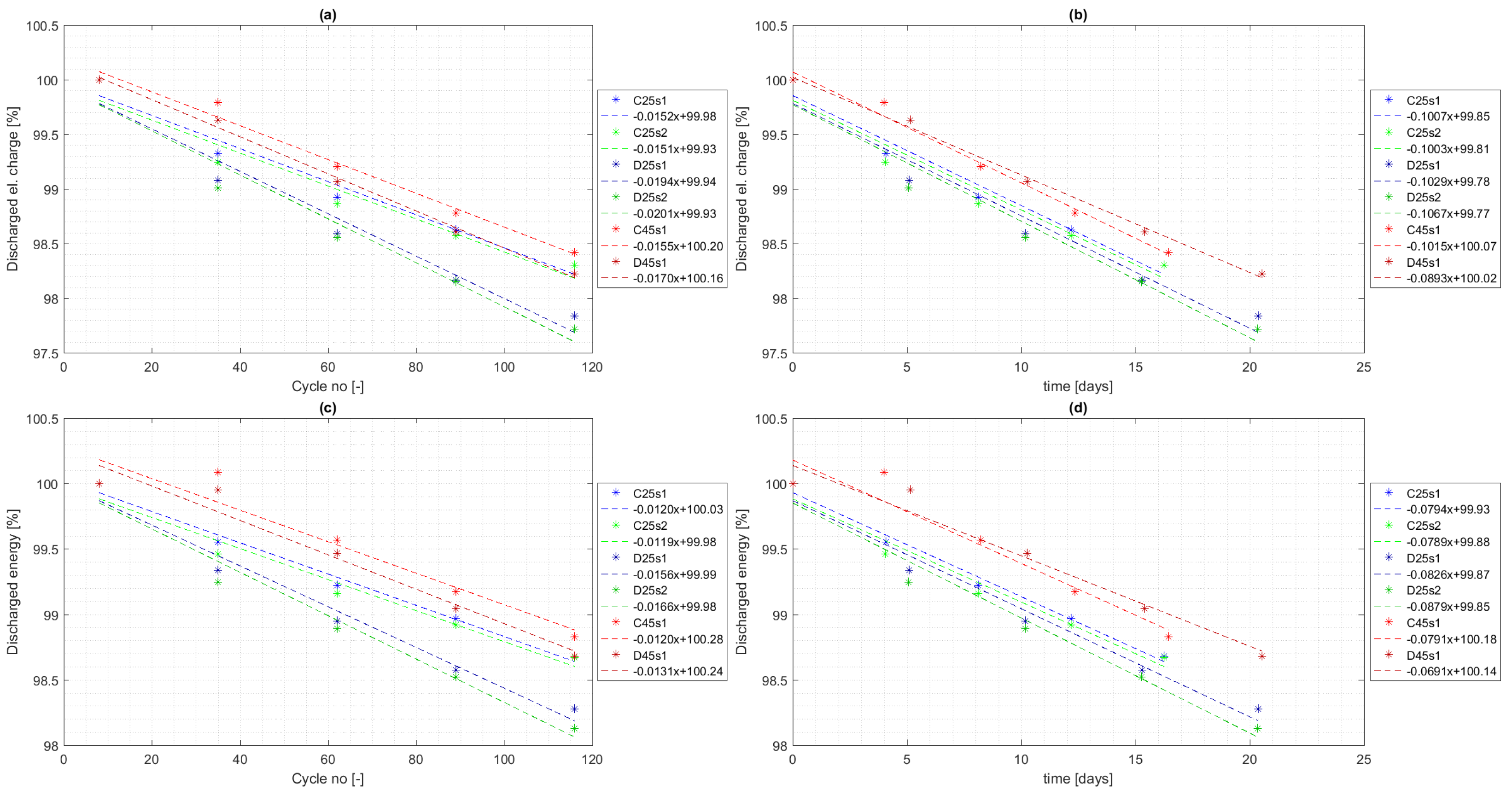
4.3. Cycle Aging
- 30.4% increase in capacity fade at temperature 25 °C ( vs. per cycle);
- 12.5% decrease in capacity fade at temperature 5 °C ( vs. per cycle);
- 9.7% increase in capacity fade at temperature 45 °C ( vs. per cycle).
- 4.3% increase in capacity fade at temperature 25 °C ( vs. per cycle);
- 29.3% decrease in capacity fade at temperature 5 °C ( vs. per cycle);
- 12.0% decrease in capacity fade at temperature 45 °C ( vs. per cycle).
5. Aging Simulation
5.1. Concise Description of P2D Model
5.2. P2D Model Calibration
5.2.1. Calendar Aging
SEI Layer Growth
Governing Equations
Optimization Procedure
5.2.2. Cycle Aging
Active Material Isolation
Governing Equation
Optimization Procedure
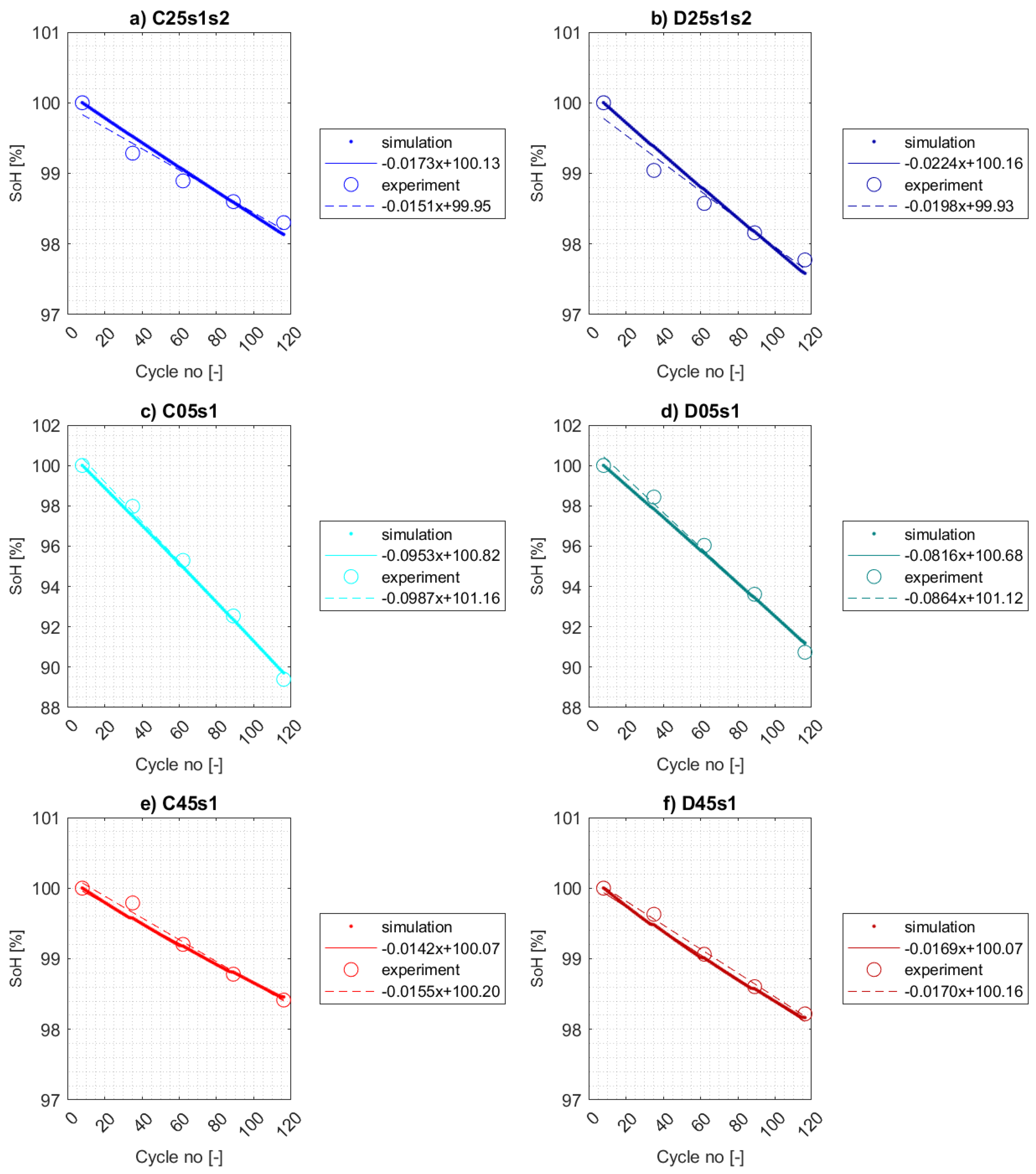
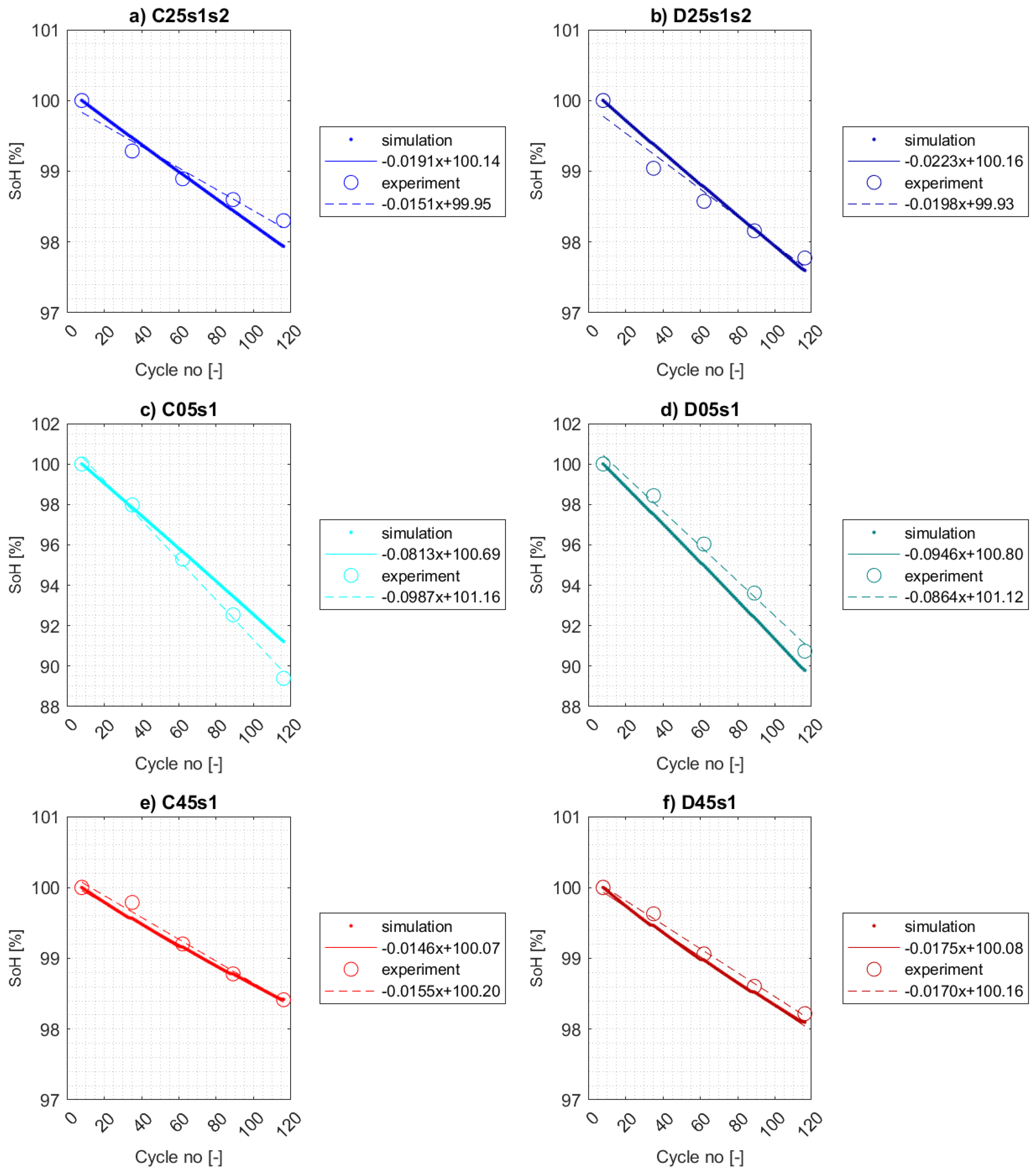
5.3. Simulation Results
5.3.1. Calendar Aging
5.3.2. Cycle aging
- Charge consumed in the side reaction at the anode is not counterbalanced by that consumed at the cathode as reported in [56] due to no side reactions occured at the cathode.
- The effects of cycle aging on capacity fade can be superposed by those of calendar aging. Thus, the calibrated SEI layer growth model using experimental data from calendar aging test for 25 °C may be insufficient for calibrating active material isolation model at temperature 5 °C.
- Different behavior of electrolyte model under low operating temperatures.
6. Conclusions
Possible Results Usage
- Based on any suitable vehicle dynamics model, any feasible number of consecutive WLTC cycles is stated appropriately to the xEV range and its assumed operation.
- RMS value of battery current is computed for the given traction battery and given number of consecutive WLTC cycles during one discharging cycle .
- Depth of discharge is computed for the given traction battery as the total discharged and charged electric charge during the given number of consecutive WLTC cycles (i.e., )
- The estimation of cycle life in real automotive battery operation is based on data about cycle life for given temperature, current and DoD:
- (a)
- temperature is chosen equal for results of capacity fade per cycle and for cycle life specification in a data sheet;
- (b)
- cycle life data are interpolated from the battery current values in a data sheet, such as the current equals the value ;
- (c)
- cycle life data are interpolated from the DoD values in a data sheet, such as that it equals DoD equals the value .
- Interpolated cycle life value is multiplied by reciprocal value of the multiplicative coefficient originating from results of capacity fade per cycle (e.g., for 30.4% increase the coefficient equals 1.304, reciprocal is 0.767). This value is denoted as
- Cycle life can be converted to total distance traveled within battery life as in units of kilometers (as 23.266 km is the distance of one WLTC 3b cycle).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BEV | Battery Electric Vehicle |
| BMS | Battery Management System |
| CalAge | Calendar Aging |
| CC | Constant Current |
| CV | Constant Voltage |
| DAQ | Data Acquisition |
| DoD | Depth of Discharge |
| DrC | Drive Cycle |
| EC | Ethylene Carbonate |
| FCEV | Fuel Cell Electric Vehicles |
| HEV | Hybrid Electric Vehicles |
| LFP | Lithium Iron Phosphate |
| LLI | Loss of Lithium Inventory |
| LYP | Lithium Iron Yttrium Phosphate |
| MAE | Mean Absolute Error |
| NEDC | New European Driving Cycle |
| OCV | Open Circuit Voltage |
| P2D | Pseudo-two-dimensional |
| PC | Personal Computer |
| PHEV | Plug-in Hybrid Electric Vehicles |
| RMSE | Root Mean Square Error |
| SEI | Solid Electrolyte Interphase |
| SoC | State of Charge |
| SoH | State of Health |
| WLTC | Worldwide Harmonized Light Vehicles Test Cycle |
| WLTP | Worldwide Harmonized Light Vehicles Test Procedures |
| xEV | Electric Vehicles in general |
References
- Vetter, J.; Novák, P.; Wagner, M.; Veit, C.; Moller, K.C.; Besenhard, J.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Herrera, F.; Fuenzalida, F.; Marquez, P.; Gautier, J.L. Improvement of the electrochemical performance of LiFePO4 cathode by Y-doping. MRS Commun. 2017, 7, 515–522. [Google Scholar] [CrossRef]
- GWL, a.s. The Difference between the LFP and LFYP. 2009. Available online: https://gwl-power.tumblr.com/post/237080531/faq-the-difference-between-the-lfp-and-lfyp (accessed on 16 October 2022).
- SIG Energy Technology. CALB Battery CA100 Specification. 2022. Available online: https://www.sig-innotech.com/en/products/cell/ca100 (accessed on 16 February 2022).
- Thunder Sky Winston Battery Limited. Thunder Sky Winston Battery TSWB-LYP40AHA Specification. 2022. Available online: https://en.winston-battery.com/?cnxdc/318.html (accessed on 16 February 2022).
- Lewerenz, M.; Munnix, J.; Schmalstieg, J.; Kabitz, S.; Knips, M.; Sauer, D.U. Systematic aging of commercial LiFePO4|Graphite cylindrical cells including a theory explaining rise of capacity during aging. J. Power Sources 2017, 345, 254–263. [Google Scholar] [CrossRef]
- Groot, J.; Swierczynski, M.; Stan, A.I.; Kaer, S.K. On the complex ageing characteristics of high-power LiFePO4/graphite battery cells cycled with high charge and discharge currents. J. Power Sources 2015, 286, 475–487. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, C.Y.; Tang, X. Cycling degradation of an automotive LiFePO4 lithium-ion battery. J. Power Sources 2011, 196, 1513–1520. [Google Scholar] [CrossRef]
- Panchal, S.; Mathew, M.; Dincer, I.; Agelin-Chaab, M.; Fraser, R.; Fowler, M. Thermal and electrical performance assessments of lithium-ion battery modules for an electric vehicle under actual drive cycles. Electr. Power Syst. Res. 2018, 163, 18–27. [Google Scholar] [CrossRef]
- Baure, G.; Dubarry, M. Synthetic vs. Real Driving Cycles: A Comparison of Electric Vehicle Battery Degradation. Batteries 2019, 5, 42. [Google Scholar] [CrossRef]
- Hosseininasab, S.; Lin, C.; Pischinger, S.; Stapelbroek, M.; Vagnoni, G. State-of-health estimation of lithium-ion batteries for electrified vehicles using a reduced-order electrochemical model. J. Energy Storage 2022, 52, 104684. [Google Scholar] [CrossRef]
- Olmos, J.; Gandiaga, I.; de Ibarra, A.S.; Larrea, X.; Nieva, T.; Aizpuru, I. Modelling the cycling degradation of Li-ion batteries: Chemistry influenced stress factors. J. Energy Storage 2021, 40, 102765. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, S.; Han, X.; Lu, L.; Li, W.; Zhang, F.; Ouyang, M. Toward more realistic microgrid optimization: Experiment and high-efficient model of Li-ion battery degradation under dynamic conditions. eTransportation 2022, 14, 100200. [Google Scholar] [CrossRef]
- Wu, L.; Pang, H.; Geng, Y.; Liu, X.; Liu, J.; Liu, K. Low-complexity state of charge and anode potential prediction for lithium-ion batteries using a simplified electrochemical model-based observer under variable load condition. Int. J. Energy Res. 2022, 46, 11834–11848. [Google Scholar] [CrossRef]
- Jenu, S.; Hentunen, A.; Haavisto, J.; Pihlatie, M. State of health estimation of cycle aged large format lithium-ion cells based on partial charging. J. Energy Storage 2022, 46, 103855. [Google Scholar] [CrossRef]
- Tesla, Inc. Q3 2021 Update. 2021. Available online: https://www.sec.gov/Archives/edgar/data/1318605/000156459021051307/tsla-ex991_85.htm (accessed on 5 April 2022).
- Rivian Automotive, Inc. Q4 2021 Shareholder Letter. 2021. Available online: https://assets.rivian.com/2md5qhoeajym/7MVaHLcGevcUKE0QZZjzEZ/e3ac410e5f9676c894389c6bc844f1e7/Rivian-Q4-2021-Shareholder-Letter.pdf (accessed on 5 April 2022).
- XPeng Inc. XPeng Launches New LFP-Battery Powered Vehicles, Expanding Product Offering for Diversified Customer Needs. 2021. Available online: https://en.xiaopeng.com/news/news_info/3807.html (accessed on 5 April 2022).
- Sadil, J.; Kekula, F.; Toman, R.; Doleček, V. Design Assistance Model of Traction Battery. 2020. Available online: http://www.lss.fd.cvut.cz/Members/sadil/hlavni-stranka/2020-design-assistance-model-of-traction-battery-sw-1 (accessed on 6 June 2022).
- United Nations Economic Commission for Europe. ECE/TRANS/180/Add.15, UN Global Technical Regulation No. 15: Worldwide Harmonized Light vehicles Test Procedure. 2019. Available online: https://www.unece.org/fileadmin/DAM/trans/main/wp29/wp29wgs/wp29gen/wp29registry/ECE-TRANS-180a15am5e.pdf (accessed on 31 March 2022).
- Gamma Technologies, LLC. GT-SUITE v2021, Version 2021, Build 2; Computer Software; Gamma Technologies, LLC: Westmont, IL, USA, 2021. [Google Scholar]
- Sui, X.; Świerczyński, M.; Teodorescu, R.; Stroe, D.I. The Degradation Behavior of LiFePO4/C Batteries during Long-Term Calendar Aging. Energies 2021, 14, 1732. [Google Scholar] [CrossRef]
- Broussely, M.; Biensan, P.; Bonhomme, F.; Blanchard, P.; Herreyre, S.; Nechev, K.; Staniewicz, R. Main aging mechanisms in Li ion batteries. J. Power Sources 2005, 146, 90–96. [Google Scholar] [CrossRef]
- GWL, a.s. GWL Important Information for Batteries. 2022. Available online: https://shop.gwl.eu/Important-Information-for-Batteries (accessed on 17 June 2022).
- GWL, a.s. GWL Winston Battery WB-LYP40AHA Description, Parameters and Documents. 2022. Available online: https://shop.gwl.eu/Winston-40Ah-200Ah/WB-LYP40AHA-LiFeYPO4-3-3V-40Ah.html (accessed on 17 February 2022).
- Winston Battery Limited. Operator’s Manual, LYP/LP Winston Rare-Earth Lithium Yttrium Power Battery; Winston Battery Limited: Hong Kong, China, 2011. [Google Scholar]
- GWL. GWL Winston Battery WB-LYP40AHA Individual Cell Data Measured by the Manufacturer and Provided by the Supplier; GWL: Prague, Czech Republic, 2021. [Google Scholar]
- Cao, W.; Li, J.; Wu, Z. Cycle-life and degradation mechanism of LiFePO4-based lithium-ion batteries at room and elevated temperatures. Ionics 2016, 22, 1791–1799. [Google Scholar] [CrossRef]
- Spingler, F.B.; Naumann, M.; Jossen, A. Capacity Recovery Effect in Commercial LiFePO4/Graphite Cells. J. Electrochem. Soc. 2020, 167, 040526. [Google Scholar] [CrossRef]
- Zheng, L.; Zhu, J.; Wang, G.; Lu, D.D.C.; He, T. Differential voltage analysis based state of charge estimation methods for lithium-ion batteries using extended Kalman filter and particle filter. Energy 2018, 158, 1028–1037. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Gamma Technologies. GT-SUITE User Manual; Version 2022 Build 1.000; Gamma Technologies: Westmont, IL, USA, 2022. [Google Scholar]
- An, S.J.; Li, J.; Daniel, C.; Mohanty, D.; Nagpure, S.; Wood, D.L. The state of understanding of the lithium-ion-battery graphite solid electrolyte interphase (SEI) and its relationship to formation cycling. Carbon 2016, 105, 52–76. [Google Scholar] [CrossRef]
- Krupp, A.; Beckmann, R.; Diekmann, T.; Ferg, E.; Schuldt, F.; Agert, C. Calendar aging model for lithium-ion batteries considering the influence of cell characterization. J. Energy Storage 2022, 45, 103506. [Google Scholar] [CrossRef]
- Baghdadi, I.; Briat, O.; Delétage, J.Y.; Gyan, P.; Vinassa, J.M. Lithium battery aging model based on Dakin’s degradation approach. J. Power Sources 2016, 325, 273–285. [Google Scholar] [CrossRef]
- Li, D.; Danilov, D.; Zhang, Z.; Chen, H.; Yang, Y.; Notten, P.H.L. Modeling the SEI-Formation on Graphite Electrodes in LiFePO4 Batteries. J. Electrochem. Soc. 2015, 162, A858–A869. [Google Scholar] [CrossRef]
- Keil, P.; Schuster, S.F.; Wilhelm, J.; Travi, J.; Hauser, A.; Karl, R.C.; Jossen, A. Calendar Aging of Lithium-Ion Batteries. J. Electrochem. Soc. 2016, 163, A1872–A1880. [Google Scholar] [CrossRef]
- Li, D.; Danilov, D.L.; Xie, J.; Raijmakers, L.; Gao, L.; Yang, Y.; Notten, P.H. Degradation Mechanisms of C6/LiFePO4 Batteries: Experimental Analyses of Calendar Aging. Electrochim. Acta 2016, 190, 1124–1133. [Google Scholar] [CrossRef]
- Zheng, Y.; He, Y.B.; Qian, K.; Li, B.; Wang, X.; Li, J.; Miao, C.; Kang, F. Effects of state of charge on the degradation of LiFePO4/graphite batteries during accelerated storage test. J. Alloys Compd. 2015, 639, 406–414. [Google Scholar] [CrossRef]
- Naumann, M.; Schimpe, M.; Keil, P.; Hesse, H.C.; Jossen, A. Analysis and modeling of calendar aging of a commercial LiFePO4/graphite cell. J. Energy Storage 2018, 17, 153–169. [Google Scholar] [CrossRef]
- Ploehn, H.J.; Ramadass, P.; White, R.E. Solvent Diffusion Model for Aging of Lithium-Ion Battery Cells. J. Electrochem. Soc. 2004, 151, A456. [Google Scholar] [CrossRef]
- Kupper, C.; Bessler, W.G. Multi-Scale Thermo-Electrochemical Modeling of Performance and Aging of a LiFePO Graphite Lithium-Ion Cell. J. Electrochem. Soc. 2016, 164, A304–A320. [Google Scholar] [CrossRef]
- Ramadass, P.; Haran, B.; Gomadam, P.M.; White, R.; Popov, B.N. Development of First Principles Capacity Fade Model for Li-Ion Cells. J. Electrochem. Soc. 2004, 151, A196. [Google Scholar] [CrossRef]
- Ramasamy, R.P.; Lee, J.W.; Popov, B.N. Simulation of capacity loss in carbon electrode for lithium-ion cells during storage. J. Power Sources 2007, 166, 266–272. [Google Scholar] [CrossRef]
- Yang, X.G.; Leng, Y.; Zhang, G.; Ge, S.; Wang, C.Y. Modeling of lithium plating induced aging of lithium-ion batteries: Transition from linear to nonlinear aging. J. Power Sources 2017, 360, 28–40. [Google Scholar] [CrossRef]
- Gamma Technologies. AutoLion—Electrochemical Lithium-ion Battery Model; Version 2022; Gamma Technologies: Westmont, IL, USA, 2022. [Google Scholar]
- Gamma Technologies. AutoLion Application Manual and Calibration Procedure; Version 2022; Gamma Technologies: Westmont, IL, USA, 2022. [Google Scholar]
- Gu, W.B.; Wang, C.Y. Thermal-Electrochemical Modeling of Battery Systems. J. Electrochem. Soc. 2000, 147, 2910. [Google Scholar] [CrossRef]
- Sikha, G.; Popov, B.N.; White, R.E. Effect of Porosity on the Capacity Fade of a Lithium-Ion Battery. J. Electrochem. Soc. 2004, 151, A1104. [Google Scholar] [CrossRef]
- Kamyab, N.; Weidner, J.W.; White, R.E. Mixed Mode Growth Model for the Solid Electrolyte Interface (SEI). J. Electrochem. Soc. 2019, 166, A334–A341. [Google Scholar] [CrossRef]
- Safari, M.; Morcrette, M.; Teyssot, A.; Delacourt, C. Multimodal Physics-Based Aging Model for Life Prediction of Li-Ion Batteries. J. Electrochem. Soc. 2009, 156, A145. [Google Scholar] [CrossRef]
- Liu, L.; Park, J.; Lin, X.; Sastry, A.M.; Lu, W. A thermal-electrochemical model that gives spatial-dependent growth of solid electrolyte interphase in a Li-ion battery. J. Power Sources 2014, 268, 482–490. [Google Scholar] [CrossRef]
- Lin, X.; Park, J.; Liu, L.; Lee, Y.; Sastry, A.M.; Lu, W. A Comprehensive Capacity Fade Model and Analysis for Li-Ion Batteries. J. Electrochem. Soc. 2013, 160, A1701–A1710. [Google Scholar] [CrossRef]
- Liu, Q.; Du, C.; Shen, B.; Zuo, P.; Cheng, X.; Ma, Y.; Yin, G.; Gao, Y. Understanding undesirable anode lithium plating issues in lithium-ion batteries. RSC Adv. 2016, 6, 88683–88700. [Google Scholar] [CrossRef]
- Delacourt, C.; Safari, M. Life Simulation of a Graphite/LiFePO4 Cell under Cycling and Storage. J. Electrochem. Soc. 2012, 159, A1283–A1291. [Google Scholar] [CrossRef]
- Safari, M.; Delacourt, C. Simulation-Based Analysis of Aging Phenomena in a Commercial Graphite/LiFePO4 Cell. J. Electrochem. Soc. 2011, 158, A1436. [Google Scholar] [CrossRef]
- Prada, E.; Domenico, D.D.; Creff, Y.; Bernard, J.; Sauvant-Moynot, V.; Huet, F. A Simplified Electrochemical and Thermal Aging Model of LiFePO-Graphite Li-ion Batteries: Power and Capacity Fade Simulations. J. Electrochem. Soc. 2013, 160, A616–A628. [Google Scholar] [CrossRef]
- Jin, X.; Vora, A.; Hoshing, V.; Saha, T.; Shaver, G.; Wasynczuk, O.; Varigonda, S. Applicability of available Li-ion battery degradation models for system and control algorithm design. Control Eng. Pract. 2018, 71, 1–9. [Google Scholar] [CrossRef]
- Safari, M.; Delacourt, C. Aging of a Commercial Graphite/LiFePO4 Cell. J. Electrochem. Soc. 2011, 158, A1123. [Google Scholar] [CrossRef]

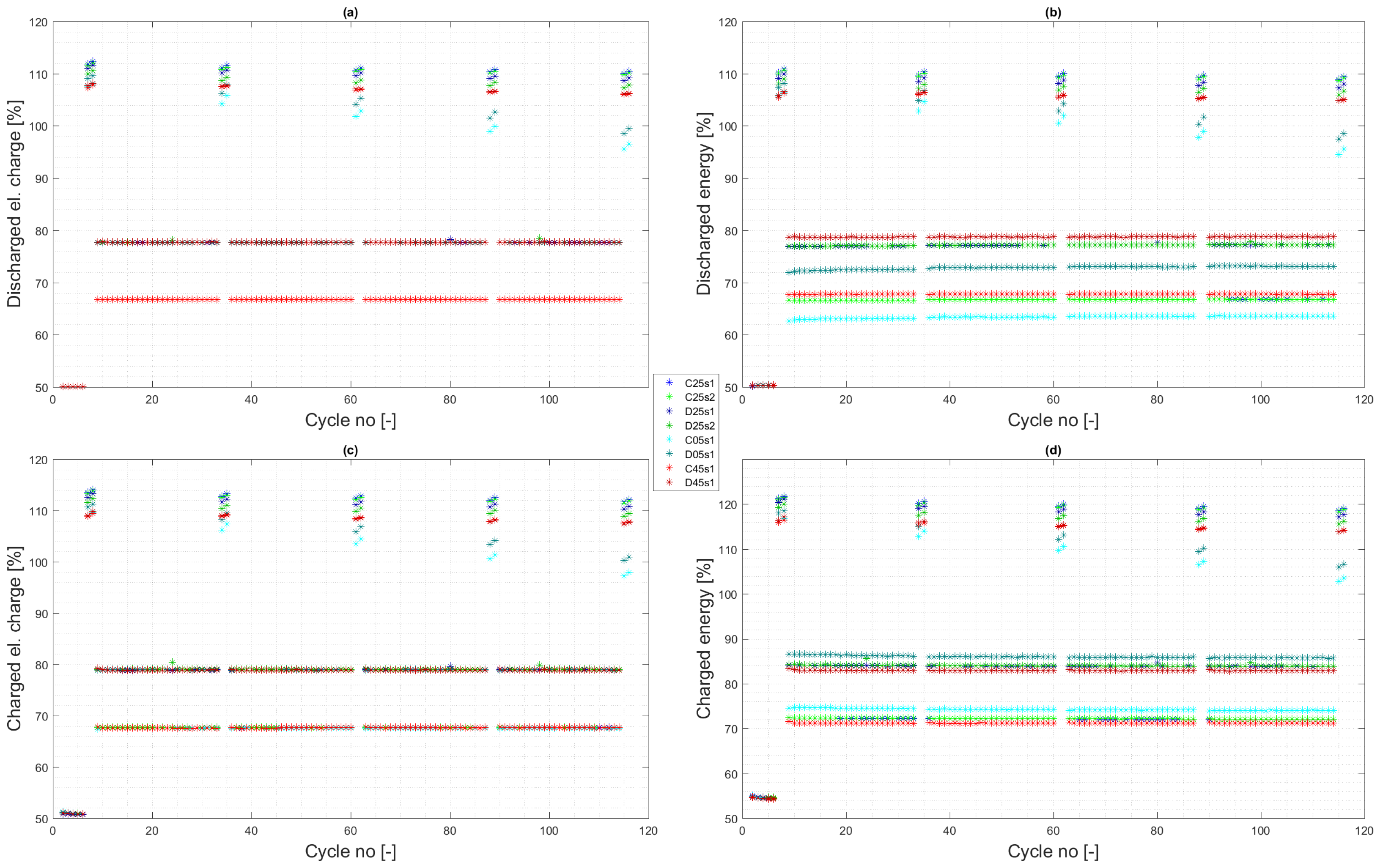
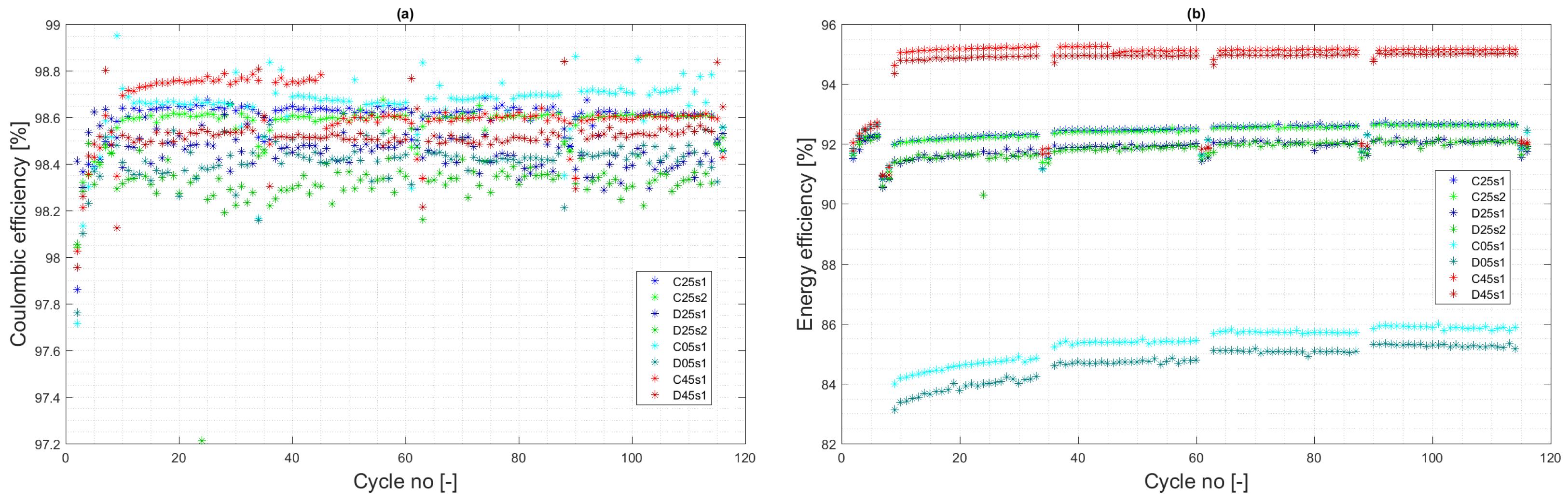
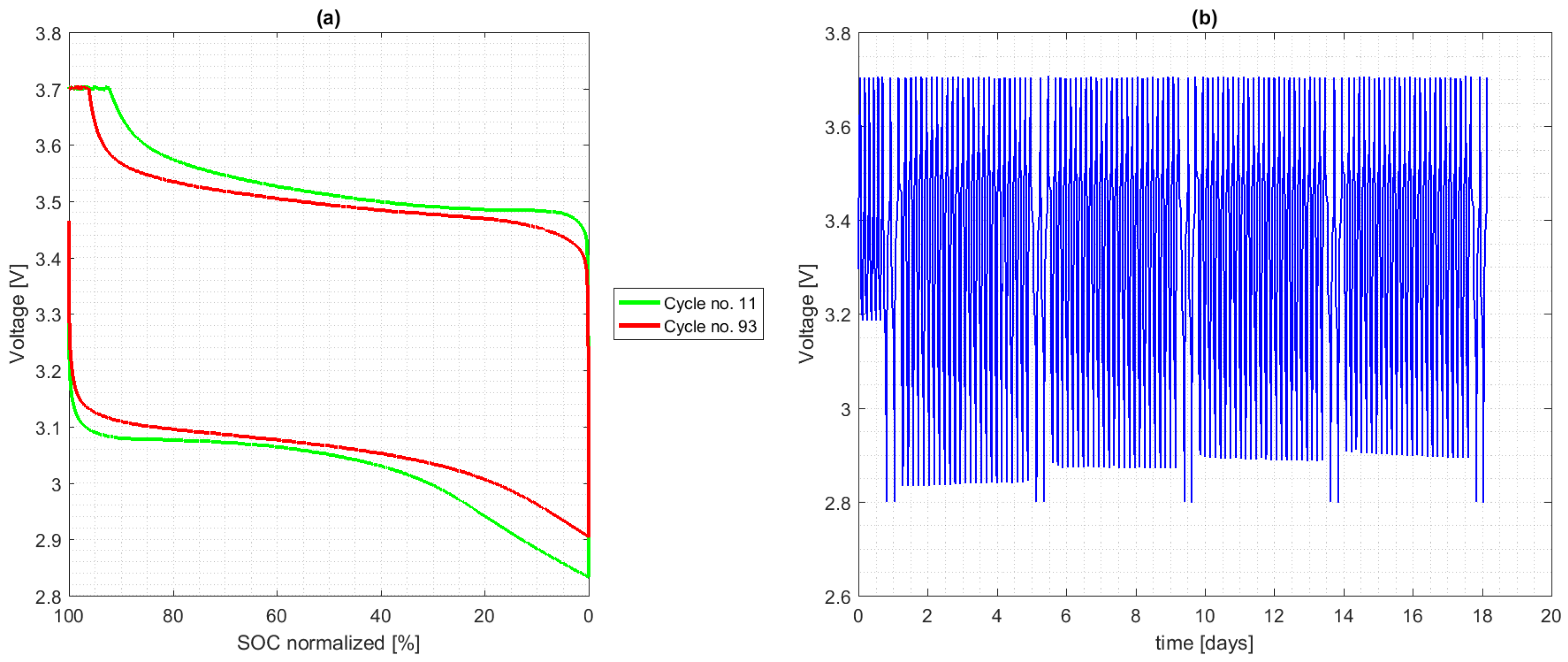
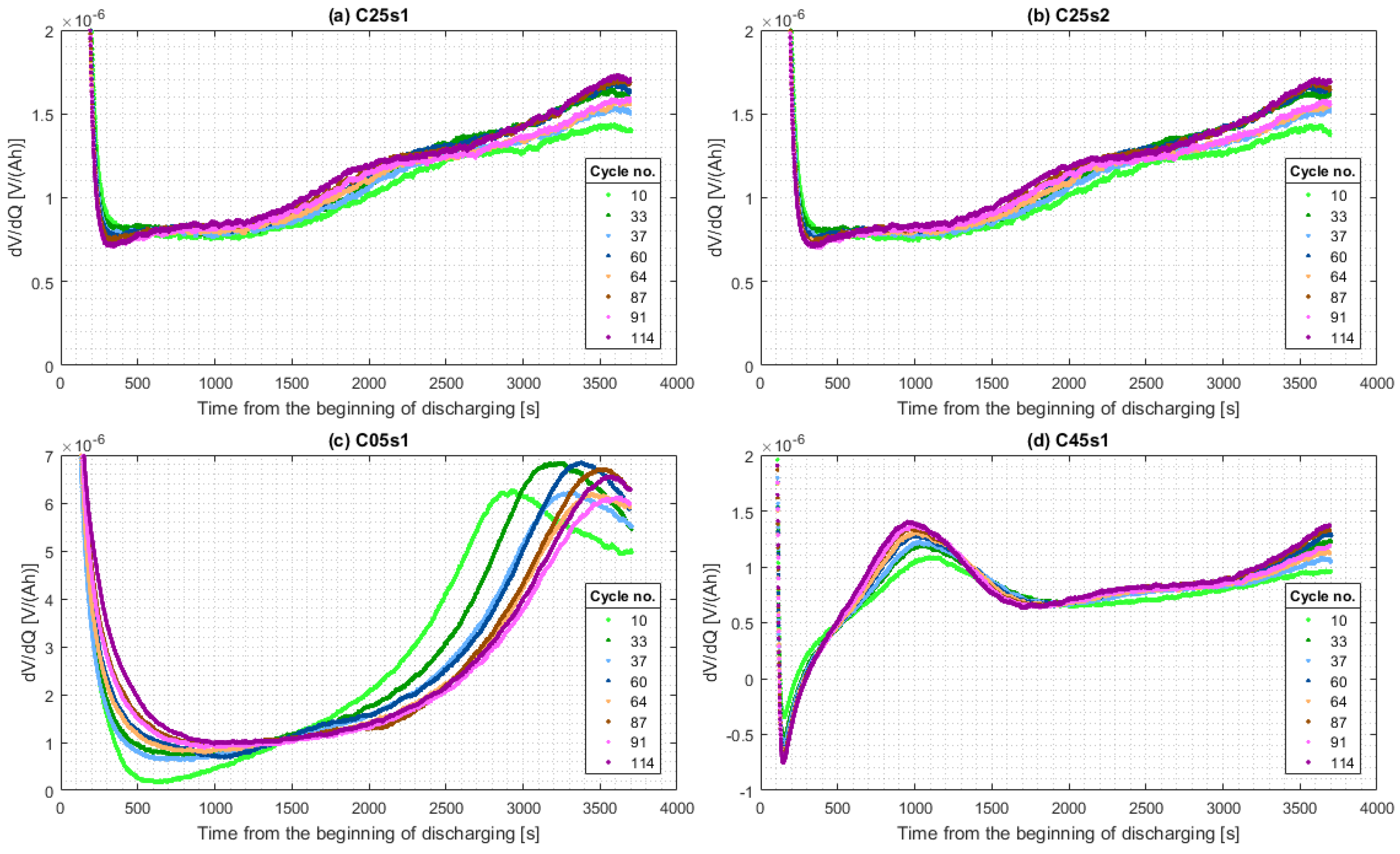



| Component | Variable | Value | Unit |
|---|---|---|---|
| Vehicle | Mass | 1300 | kg |
| Vehicle | Front area | 2.1 | m |
| Vehicle | Drag coefficient | 0.31 | - |
| Tire | Rolling resistance coefficient | 0.015 | - |
| Differential | Final Drive Ratio | 7.05 | - |
| Differential | Efficiency | 0.95 | - |
| Electric motor | Efficiency | original map fcn (rpm. Nm) | - |
| Battery cell | Capacity | 40 | Ah |
| Battery cell | Nominal voltage | 3.3 | V |
| Battery cell | Weight | 1600 | g |
| Battery system | Connection | 82 ser × 2 par | - |
| Battery system | Nominal voltage | 277.2 | V |
| Battery system | Total energy | 22.18 | kWh |
| Boundary condition | Auxiliary power | 300 | W |
| Boundary condition | Passenger and Cargo Mass | 80 | kg |
| Boundary condition | The initial State of Charge | 100 | % |
| Indication | |||||||
|---|---|---|---|---|---|---|---|
| — | |||||||
| 0.5 C charge | 1 | 1 | 0 | 2.8 | 25 | 25 | 0 |
| formatting | 5 | 6 | 0.5 | 2.8 | 25 | 25 | 50 |
| capacity test | 2 | 8 | 0.5 | 2.8 | 25 | 25 | max |
| 25 normal cycles | 25 | 33 | 0.65 | 2.4 | 66.67 | ||
| capacity test | 2 | 35 | 0.5 | 2.8 | 25 | 25 | max |
| 25 normal cycles | 25 | 60 | 0.65 | 2.4 | 66.67 | ||
| capacity test | 2 | 62 | 0.5 | 2.8 | 25 | 25 | max |
| 25 normal cycles | 25 | 87 | 0.65 | 2.4 | 66.67 | ||
| capacity test | 2 | 89 | 0.5 | 2.8 | 25 | 25 | max |
| 25 normal cycles | 25 | 114 | 0.65 | 2.4 | 66.67 | ||
| capacity test | 2 | 116 | 0.5 | 2.8 | 25 | 25 | max |
| Manufacturer SN | C | Denom. | Use for Experiment | ||
|---|---|---|---|---|---|
| - | - | - | |||
| 200803-Y18612 | 0.52 | 3.302 | 46.5 | C25s1 | CC disch 25 °C (1.) |
| 200803-Y18621 | 0.55 | 3.302 | 46.5 | C25s2 | CC disch 25 °C (2.) |
| 200803-Y18613 | 0.53 | 3.302 | 46.5 | D25s1 | DrCy disch 25 °C (1.) |
| 200803-Y18620 | 0.54 | 3.302 | 46.5 | D25s2 | DrCy disch 25 °C (2.) |
| 210412-Y05461 | 0.54 | 3.297 | 46 | C05s1 | CC disch 5 °C |
| 210412-Y05453 | 0.53 | 3.298 | 46 | D05s1 | DrCy disch 5 °C |
| 210412-Y05469 | 0.55 | 3.297 | 46 | C45s1 | CC disch 45 °C |
| 210412-Y05468 | 0.54 | 3.297 | 46 | D45s1 | DrCy disch 45 °C |
| 200803-Y18605 | 0.58 | 3.303 | 46 | CalAge | Calendar aging |
| Sample | Cap/C S | Cap/C A | Cap/T S | Cap/T A |
|---|---|---|---|---|
| C25s1 | ||||
| C25s2 | ||||
| D25s1 | ||||
| D25s2 | ||||
| C05s1 | ||||
| D05s1 | ||||
| C45s1 | ||||
| D45s1 |
| Sample | Ene/C S | Ene/C A | Ene/T S | Ene/T A |
|---|---|---|---|---|
| C25s1 | ||||
| C25s2 | ||||
| D25s1 | ||||
| D25s2 | ||||
| C05s1 | ||||
| D05s1 | ||||
| C45s1 | ||||
| D45s1 |
| Parameter Symbol | ||||
|---|---|---|---|---|
| − | [44,50,51] | − | ||
| − | [44,52,53] | − | ||
| − | 162 [54] | − | ||
| − | [54] | − | ||
| − | [51,52] | − |
| Parameter Symbol | |
|---|---|
| Sample | ||||
|---|---|---|---|---|
| — | ||||
| C25s1s2 | ||||
| D25s1s2 | ||||
| C05s1 | ||||
| D05s1 | ||||
| C45s1 | ||||
| D45s1 |
| Sample | ||||
|---|---|---|---|---|
| — | ||||
| C25s1s2 | ||||
| D25s1s2 | ||||
| C05s1 | ||||
| D05s1 | ||||
| C45s1 | ||||
| D45s1 |
| Sample | ||||
|---|---|---|---|---|
| — | ||||
| C25s1s2 | ||||
| D25s1s2 | ||||
| C05s1 | ||||
| D05s1 | ||||
| C45s1 | ||||
| D45s1 |
| Parameter Symbol | ||
|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadil, J.; Kekula, F.; Majera, J.; Pisharodi, V. Comparison of Capacity Fade for the Constant Current and WLTC Drive Cycle Discharge Modes for Commercial LiFeYPO4 Cells Used in xEV Vehicles. Batteries 2022, 8, 282. https://doi.org/10.3390/batteries8120282
Sadil J, Kekula F, Majera J, Pisharodi V. Comparison of Capacity Fade for the Constant Current and WLTC Drive Cycle Discharge Modes for Commercial LiFeYPO4 Cells Used in xEV Vehicles. Batteries. 2022; 8(12):282. https://doi.org/10.3390/batteries8120282
Chicago/Turabian StyleSadil, Jindřich, František Kekula, Juraj Majera, and Vivek Pisharodi. 2022. "Comparison of Capacity Fade for the Constant Current and WLTC Drive Cycle Discharge Modes for Commercial LiFeYPO4 Cells Used in xEV Vehicles" Batteries 8, no. 12: 282. https://doi.org/10.3390/batteries8120282
APA StyleSadil, J., Kekula, F., Majera, J., & Pisharodi, V. (2022). Comparison of Capacity Fade for the Constant Current and WLTC Drive Cycle Discharge Modes for Commercial LiFeYPO4 Cells Used in xEV Vehicles. Batteries, 8(12), 282. https://doi.org/10.3390/batteries8120282






