Electronic, Optical, Mechanical and Li-Ion Storage Properties of Novel Benzotrithiophene-Based Graphdiyne Monolayers Explored by First Principles and Machine Learning
Abstract
1. Introduction
2. Computational Methods
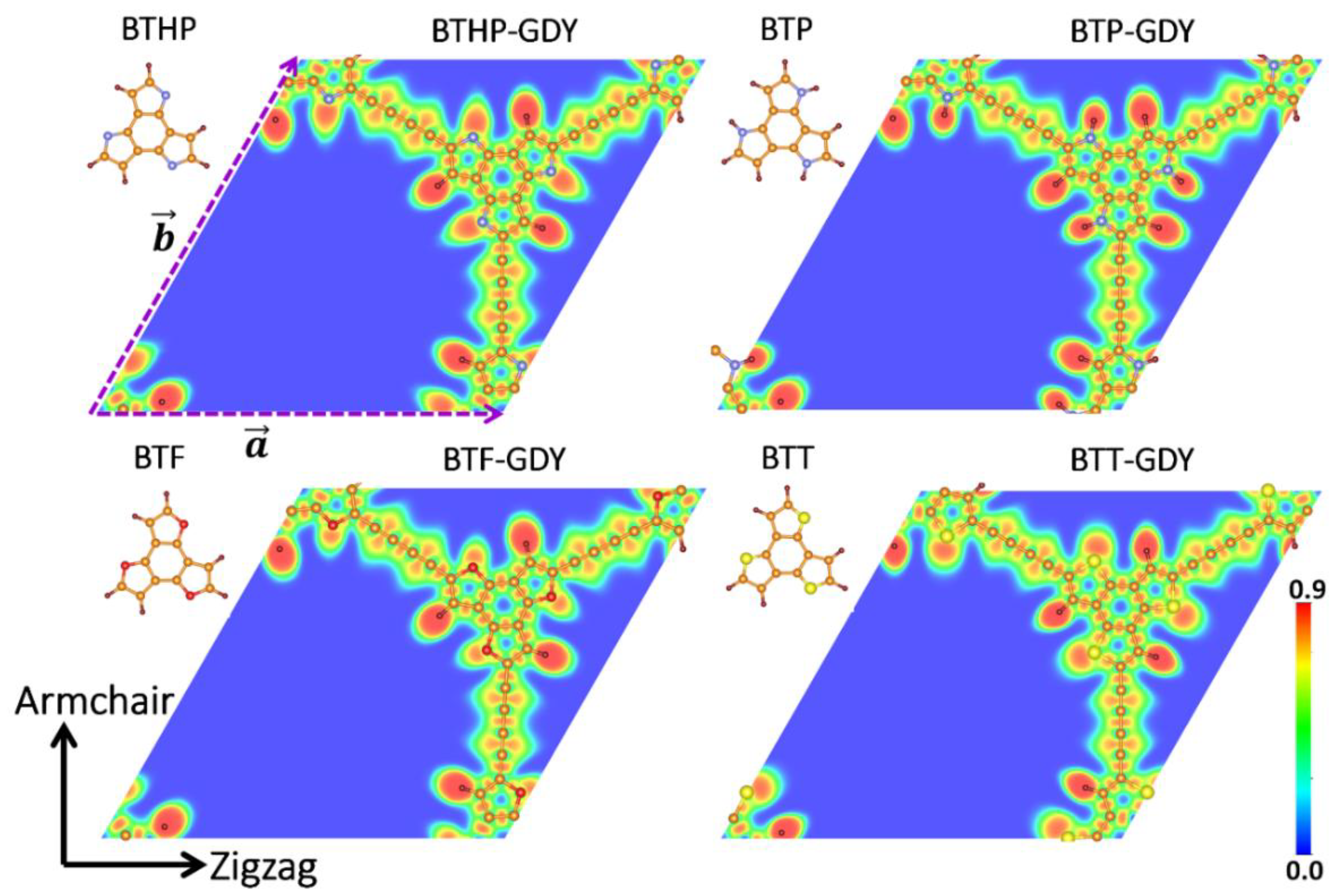
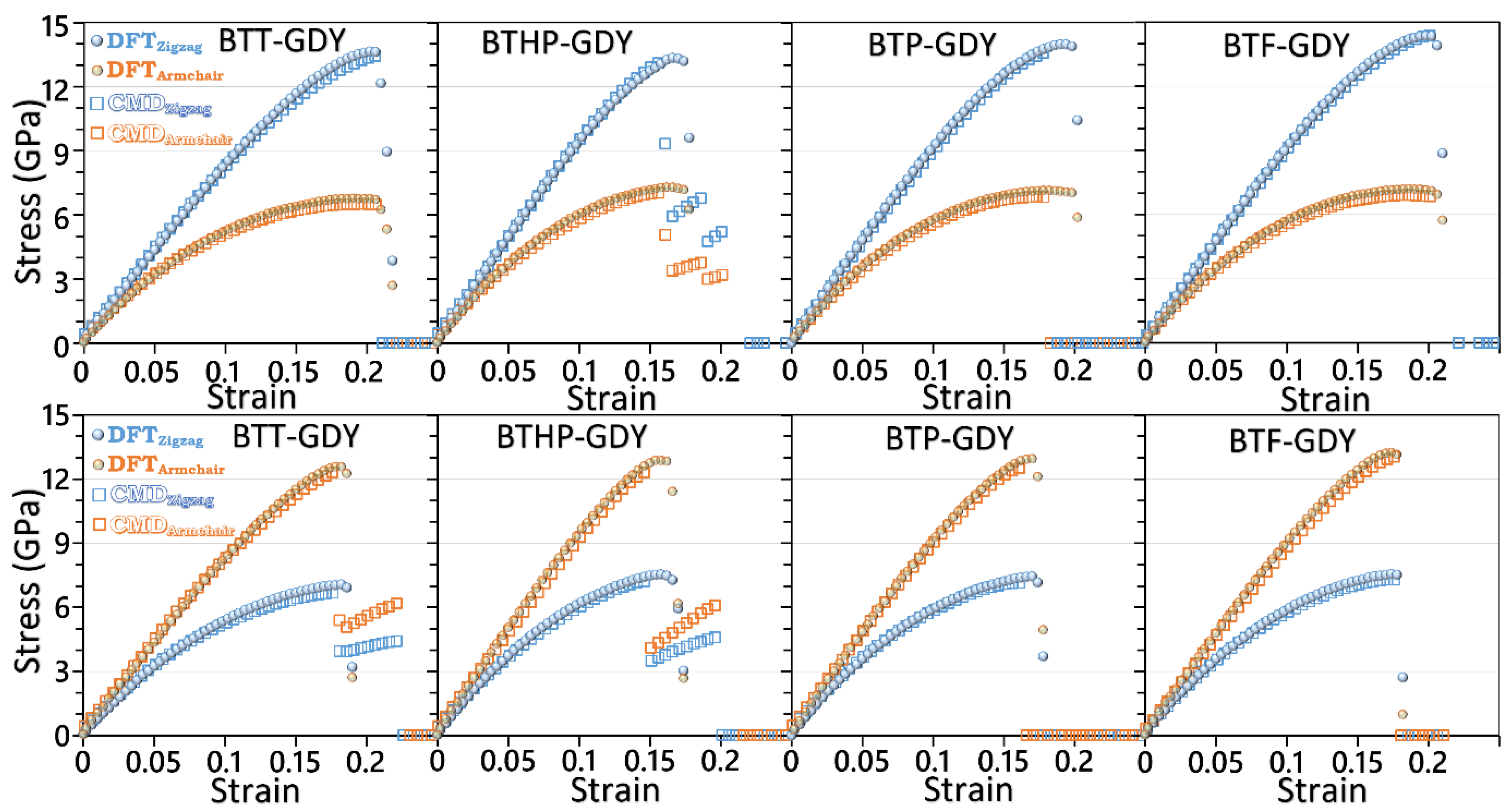
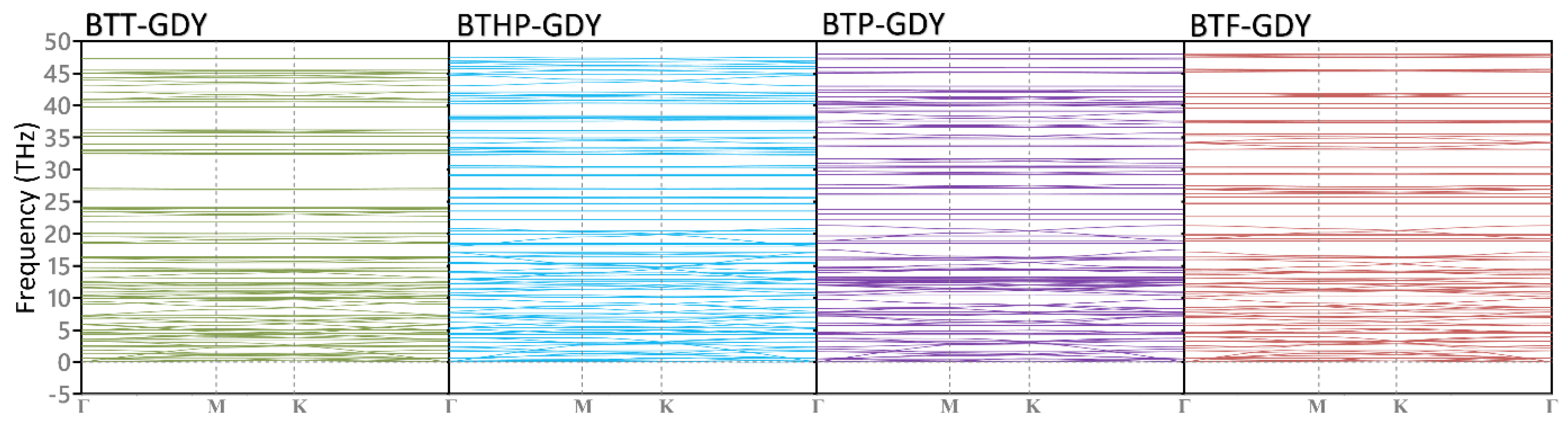
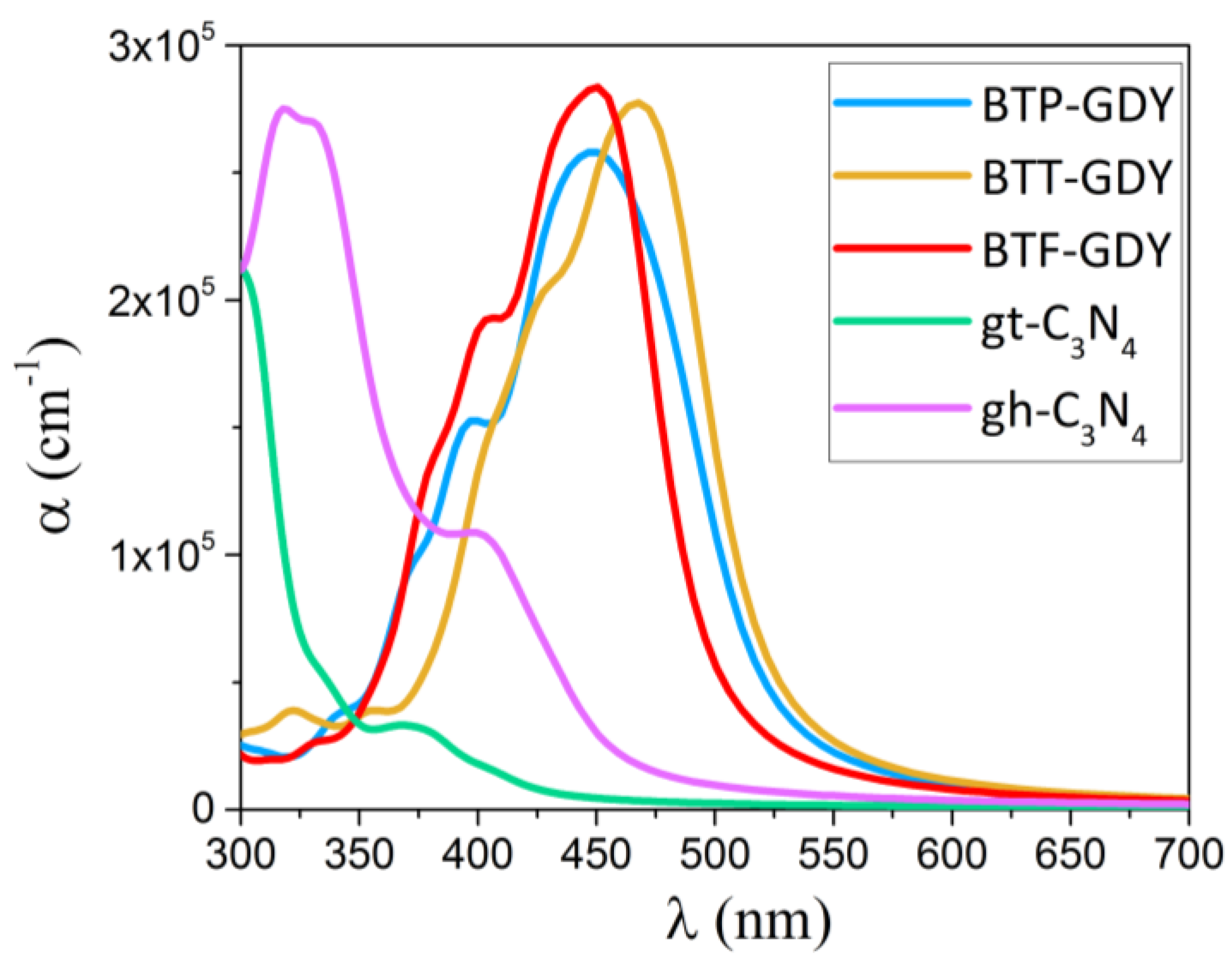
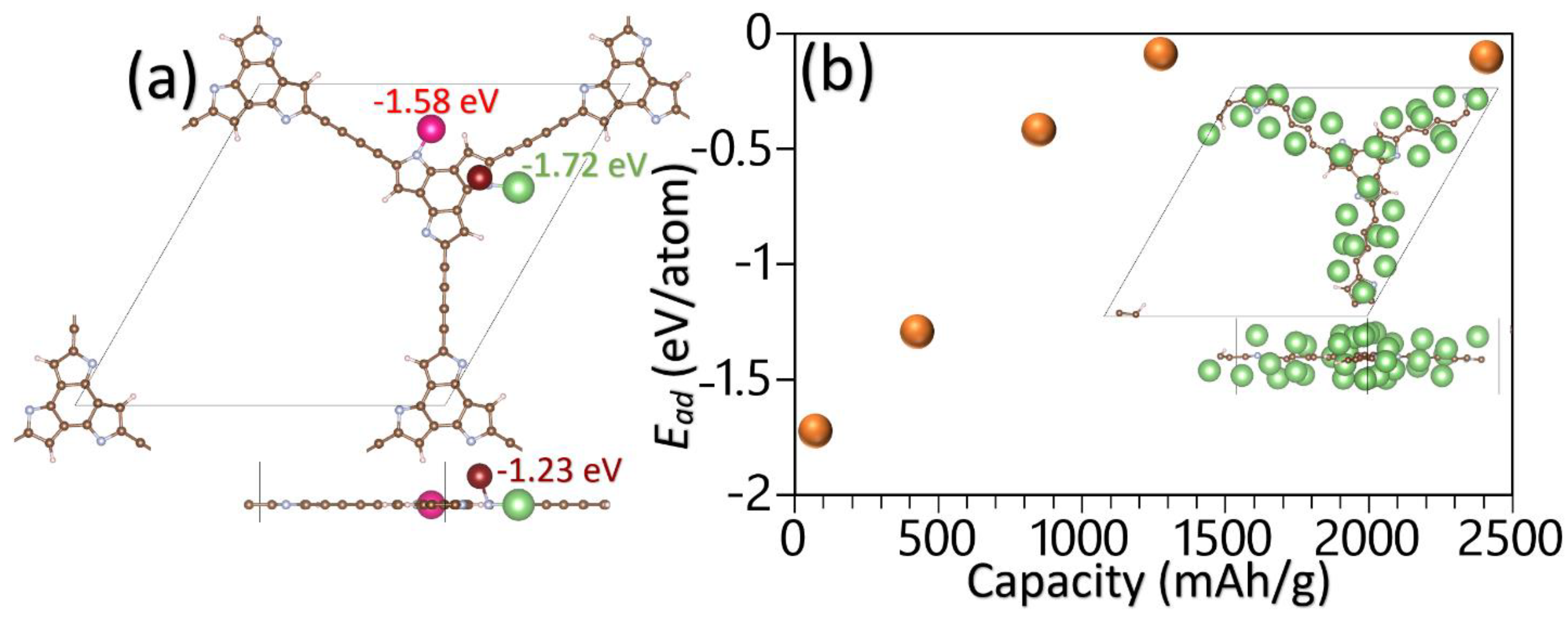
3. Results and Discussions
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baughman, R.H.; Eckhardt, H.; Kertesz, M. Structure-property predictions for new planar forms of carbon: Layered phases containing sp2 and sp atoms. J. Chem. Phys. 1987, 87, 6687. [Google Scholar] [CrossRef]
- Xu, Z.; Lv, X.; Li, J.; Chen, J.; Liu, Q. A promising anode material for sodium-ion battery with high capacity and high diffusion ability: Graphyne and graphdiyne. RSC Adv. 2016, 6, 25594–25600. [Google Scholar] [CrossRef]
- Hussain, T.; Hankel, M.; Searles, D.J. Graphenylene Monolayers Doped with Alkali or Alkaline Earth Metals: Promising Materials for Clean Energy Storage. J. Phys. Chem. C 2017, 121, 14393–14400. [Google Scholar] [CrossRef]
- Bahari, Y.; Mortazavi, B.; Rajabpour, A.; Zhuang, X.; Rabczuk, T. Application of two-dimensional materials as anodes for rechargeable metal-ion batteries: A comprehensive perspective from density functional theory simulations. Energy Storage Mater. 2021, 35, 203–282. [Google Scholar] [CrossRef]
- Lin, Z.Z. Graphdiyne as a promising substrate for stabilizing Pt nanoparticle catalyst. Carbon 2015, 86, 301–309. [Google Scholar] [CrossRef]
- Bartolomei, M.; Carmona-Novillo, E.; Giorgi, G. First principles investigation of hydrogen physical adsorption on graphynes’ layers. Carbon 2015, 95, 1076–1081. [Google Scholar] [CrossRef]
- Autreto, P.A.S.; De Sousa, J.M.; Galvao, D.S. Site-dependent hydrogenation on graphdiyne. Carbon 2014, 77, 829–834. [Google Scholar] [CrossRef]
- Hatam-Lee, S.M.; Rajabpour, A.; Volz, S. Thermal conductivity of graphene polymorphs and compounds: From C3N to graphdiyne lattices. Carbon 2020, 161, 816–826. [Google Scholar] [CrossRef]
- Mortazavi, B.; Shahrokhi, M.; Zhuang, X.; Rabczuk, T. Boron-graphdiyne: A superstretchable semiconductor with low thermal conductivity and ultrahigh capacity for Li, Na and Ca ion storage. J. Mater. Chem. A 2018, 6, 11022–11036. [Google Scholar] [CrossRef]
- Sun, L.; Jiang, P.H.; Liu, H.J.; Fan, D.D.; Liang, J.H.; Wei, J.; Cheng, L.; Zhang, J.; Shi, J. Graphdiyne: A two-dimensional thermoelectric material with high figure of merit. Carbon 2015, 90, 255–259. [Google Scholar] [CrossRef]
- Wang, X.M.; Lu, S.S. Thermoelectric transport in graphyne nanotubes. J. Phys. Chem. C 2013, 117, 19740–19745. [Google Scholar] [CrossRef]
- Li, G.; Li, Y.; Liu, H.; Guo, Y.; Li, Y.; Zhu, D. Architecture of graphdiyne nanoscale films. Chem. Commun. 2010, 46, 3256–3258. [Google Scholar] [CrossRef] [PubMed]
- Matsuoka, R.; Sakamoto, R.; Hoshiko, K.; Sasaki, S.; Masunaga, H.; Nagashio, K.; Nishihara, H. Crystalline Graphdiyne Nanosheets Produced at a Gas/Liquid or Liquid/Liquid Interface. J. Am. Chem. Soc. 2017, 139, 3145–3152. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Li, X.; Tu, Z.; Zhao, F.; He, J.; Guan, Z.; Huang, C.; Yi, Y.; Li, Y. Synthesis, Electronic Structure of Boron-Graphdiyne with an sp-Hybridized Carbon Skeleton and Its Application in Sodium Storage. Angew. Chem. 2018, 130, 4032–4037. [Google Scholar] [CrossRef]
- Kan, X.; Ban, Y.; Wu, C.; Pan, Q.; Liu, H.; Song, J.; Zuo, Z.; Li, Z.; Zhao, Y. Interfacial Synthesis of Conjugated Two-Dimensional N-Graphdiyne. ACS Appl. Mater. Interfaces 2018, 10, 53–58. [Google Scholar] [CrossRef] [PubMed]
- Matsuoka, R.; Toyoda, R.; Shiotsuki, R.; Fukui, N.; Wada, K.; Maeda, H.; Sakamoto, R.; Sasaki, S.; Masunaga, H.; Nagashio, K.; et al. Expansion of the Graphdiyne Family: A Triphenylene-Cored Analogue. ACS Appl. Mater. Interfaces 2018, 11, 2730–2733. [Google Scholar] [CrossRef]
- Wang, X.-H.; Zhang, Z.-C.; Wang, J.-J.; Chen, X.-D.; Yao, B.-W.; Hou, Y.-X.; Yu, M.-X.; Li, Y.; Lu, T.-B. Synthesis of Wafer-Scale Monolayer Pyrenyl Graphdiyne on Ultrathin Hexagonal Boron Nitride for Multibit Optoelectronic Memory. ACS Appl. Mater. Interfaces 2020, 12, 33069–33075. [Google Scholar] [CrossRef]
- Gao, L.; Ge, X.; Zuo, Z.; Wang, F.; Liu, X.; Lv, M.; Shi, S.; Xu, L.; Liu, T.; Zhou, Q.; et al. High Quality Pyrazinoquinoxaline-based Graphdiyne for Efficient Gradient Storage of Lithium Ions. Nano Lett. 2020, 20, 7333–7341. [Google Scholar] [CrossRef]
- Pan, Q.; Chen, X.; Li, H.; Chen, S.; Zheng, X.; Liu, H.; Li, B.; Zhao, Y. Preparation of crystalline benzotrithiophene-based two-dimensional graphdiyne analogue. 2D Mater. 2021, 9, 14001. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.; Pack, J. Special points for Brillouin zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Bardeen, J.; Shockley, W. Deformation potentials and mobilities in non-polar crystals. Phys. Rev. 1950, 80, 72. [Google Scholar] [CrossRef]
- Sander, T.; Maggio, E.; Kresse, G. Beyond the Tamm-Dancoff approximation for extended systems using exact diagonalization. Phys. Rev. B 2015, 92, 45209. [Google Scholar] [CrossRef]
- Shapeev, A.V. Moment tensor potentials: A class of systematically improvable interatomic potentials. Multiscale Model. Simul. 2016, 14, 1153–1173. [Google Scholar] [CrossRef]
- Novikov, I.S.; Gubaev, K.; Podryabinkin, E.V.; Shapeev, A.V. The MLIP package: Moment Tensor Potentials with MPI and Active Learning. Mach. Learn. Sci. Technol. 2021, 2, 025002. [Google Scholar]
- Podryabinkin, E.V.; Shapeev, A.V. Active learning of linearly parametrized interatomic potentials. Comput. Mater. Sci. 2017, 140, 171–180. [Google Scholar] [CrossRef]
- Mortazavi, B.; Novikov, I.S.; Podryabinkin, E.V.; Roche, S.; Rabczuk, T.; Shapeev, A.V.; Zhuang, X. Exploring phononic properties of two-dimensional materials using machine learning interatomic potentials. Appl. Mater. Today 2020, 20, 100685. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Mortazavi, B.; Silani, M.; Podryabinkin, E.V.; Rabczuk, T.; Zhuang, X.; Shapeev, A. V First-Principles Multiscale Modeling of Mechanical Properties in Graphene/Borophene Heterostructures Empowered by Machine-Learning Interatomic Potentials. Adv. Mater. 2021, 33, 2102807. [Google Scholar] [CrossRef] [PubMed]
- Mortazavi, B.; Shahrokhi, M.; Shojaei, F.; Rabczuk, T.; Zhuang, X.; Shapeev, A.V. A first-principles and machine-learning investigation on the electronic, photocatalytic, mechanical and heat conduction properties of nanoporous C5N monolayers. Nanoscale 2022, 14, 4324–4333. [Google Scholar] [CrossRef] [PubMed]
- Silvi, B.; Savin, A. Classification of Chemical-Bonds Based on Topological Analysis of Electron Localization Functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
- Yue, Q.; Chang, S.; Kang, J.; Qin, S.; Li, J. Mechanical and Electronic Properties of Graphyne and Its Family under Elastic Strain: Theoretical Predictions. J. Phys. Chem. C 2013, 117, 14804–14811. [Google Scholar] [CrossRef]
- Rawat, A.; Jena, N.; Dimple, D.; De Sarkar, A. A comprehensive study on carrier mobility and artificial photosynthetic properties in group VI B transition metal dichalcogenide monolayers. J. Mater. Chem. A 2018, 6, 8693–8704. [Google Scholar] [CrossRef]
- Salavati, M.; Rabczuk, T. First-principles investigation of N-triphenylene-graphdiyne nanosheets as an anode material for Na, K, Mg and Ca storage. Comput. Mater. Sci. 2019, 169, 109093. [Google Scholar] [CrossRef]
- Mortazavi, B.; Shahrokhi, M.; Madjet, M.E.; Makaremi, M.; Ahzi, S.; Rabczuk, T. N-, P-, As-triphenylene-graphdiyne: Strong and stable 2D semiconductors with outstanding capacities as anodes for Li-ion batteries. Carbon 2019, 141, 291–303. [Google Scholar] [CrossRef]
- Li, C.; Zhang, X.; Wang, K.; Sun, X.; Ma, Y. High-power and long-life lithium-ion capacitors constructed from N-doped hierarchical carbon nanolayer cathode and mesoporous graphene anode. Carbon 2018, 140, 237–248. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, X.; Chen, J.; Wang, X.; Wang, D.; Mao, Z. PVP-assisted synthesis of g–C3N4–derived N-doped graphene with tunable interplanar spacing as high-performance lithium/sodium ions battery anodes. Carbon 2021, 174, 98–109. [Google Scholar] [CrossRef]
- Wang, Z.; Qie, L.; Yuan, L.; Zhang, W.; Hu, X.; Huang, Y. Functionalized N-doped interconnected carbon nanofibers as an anode material for sodium-ion storage with excellent performance. Carbon 2013, 55, 328–334. [Google Scholar] [CrossRef]


| Polymer | Lattice Constants (Å) | l (Å) a | EgPBE (eV) b | EgHSE06 (eV) c | EVBM, ECBM (eV) d | EWF (eV) e | Molecule | EH-L (eV) f | EH, EL (eV) g |
|---|---|---|---|---|---|---|---|---|---|
| BTHP-GDY | 22.820 | 1.24–1.49 | 0.03 | 0.06 | −6.01, −5.95 | 5.98 | BTHP | 1.38 | −5.94, −4.56 |
| BTP-GDY | 23.101 | 1.23–1.42 | 1.83 | 2.49 | −4.87, −2.38 | 3.63 | BTP | 4.31 | −4.91, −0.60 |
| BTF-GDY | 22.885 | 1.23–1.42 | 1.94 | 2.65 | −5.63, −2.98 | 4.31 | BTF | 4.92 | −5.84, −0.92 |
| BTT-GDY | 23.670 | 1.23–1.76 | 1.88 | 2.53 | −5.62, −3.09 | 4.36 | BTT | 4.39 | −5.82, −1.44 |
| Diacetylene | 5.87 | −7.26, −1.39 |
| Carrier Type | µ (cm2 V−1 s−1) | ||||
|---|---|---|---|---|---|
| BTF-GDY | electron | 38 | 6.50 | 1.69 | 6.70 |
| heavy hole | 38 | 16.67 | 2.65 | 0.42 | |
| light hole | 38 | 0.36 | 2.72 | 855.78 | |
| BTT-GDY | electron | 34 | 5.26 | 2.34 | 4.79 |
| heavy hole | 34 | 62.5 | 3.19 | 0.02 | |
| light hole | 34 | 0.37 | 3.28 | 451.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mortazavi, B.; Shojaei, F.; Shahrokhi, M.; Rabczuk, T.; Shapeev, A.V.; Zhuang, X. Electronic, Optical, Mechanical and Li-Ion Storage Properties of Novel Benzotrithiophene-Based Graphdiyne Monolayers Explored by First Principles and Machine Learning. Batteries 2022, 8, 194. https://doi.org/10.3390/batteries8100194
Mortazavi B, Shojaei F, Shahrokhi M, Rabczuk T, Shapeev AV, Zhuang X. Electronic, Optical, Mechanical and Li-Ion Storage Properties of Novel Benzotrithiophene-Based Graphdiyne Monolayers Explored by First Principles and Machine Learning. Batteries. 2022; 8(10):194. https://doi.org/10.3390/batteries8100194
Chicago/Turabian StyleMortazavi, Bohayra, Fazel Shojaei, Masoud Shahrokhi, Timon Rabczuk, Alexander V. Shapeev, and Xiaoying Zhuang. 2022. "Electronic, Optical, Mechanical and Li-Ion Storage Properties of Novel Benzotrithiophene-Based Graphdiyne Monolayers Explored by First Principles and Machine Learning" Batteries 8, no. 10: 194. https://doi.org/10.3390/batteries8100194
APA StyleMortazavi, B., Shojaei, F., Shahrokhi, M., Rabczuk, T., Shapeev, A. V., & Zhuang, X. (2022). Electronic, Optical, Mechanical and Li-Ion Storage Properties of Novel Benzotrithiophene-Based Graphdiyne Monolayers Explored by First Principles and Machine Learning. Batteries, 8(10), 194. https://doi.org/10.3390/batteries8100194









