Grid-Scale Battery Energy Storage for Arbitrage Purposes: A Colombian Case
Abstract
:1. Introduction
- 1.
- An adequate battery degradation model, based on an upper piecewise linear approximation, is included in the arbitrage strategies to improve the robustness of the results.
- 2.
- A comparison of different arbitrage strategies for the Colombian electricity market to determine which is the most suitable.
- 3.
- An economic evaluation to determine the viability of installing BESS to perform energy arbitrage in the Colombian electricity market.
2. Mathematical Model
2.1. Objective Function
2.2. Constraints
2.2.1. Charge Energy Limit
2.2.2. Discharge Energy Limit
2.2.3. Energy Capacity Limit
2.2.4. Power Capacity Limit
2.2.5. Charge and Discharge Signal
2.2.6. Energy Balance
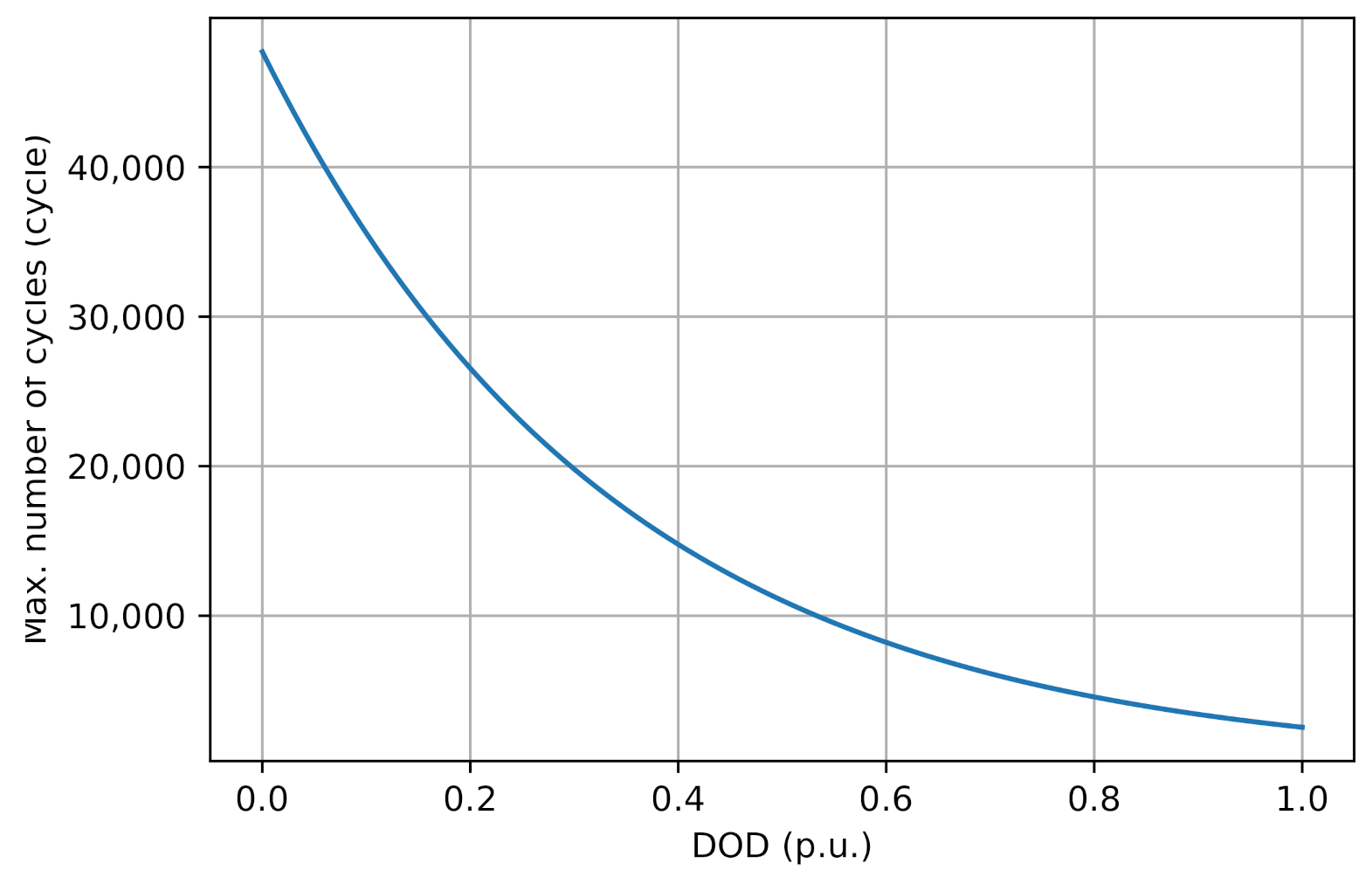
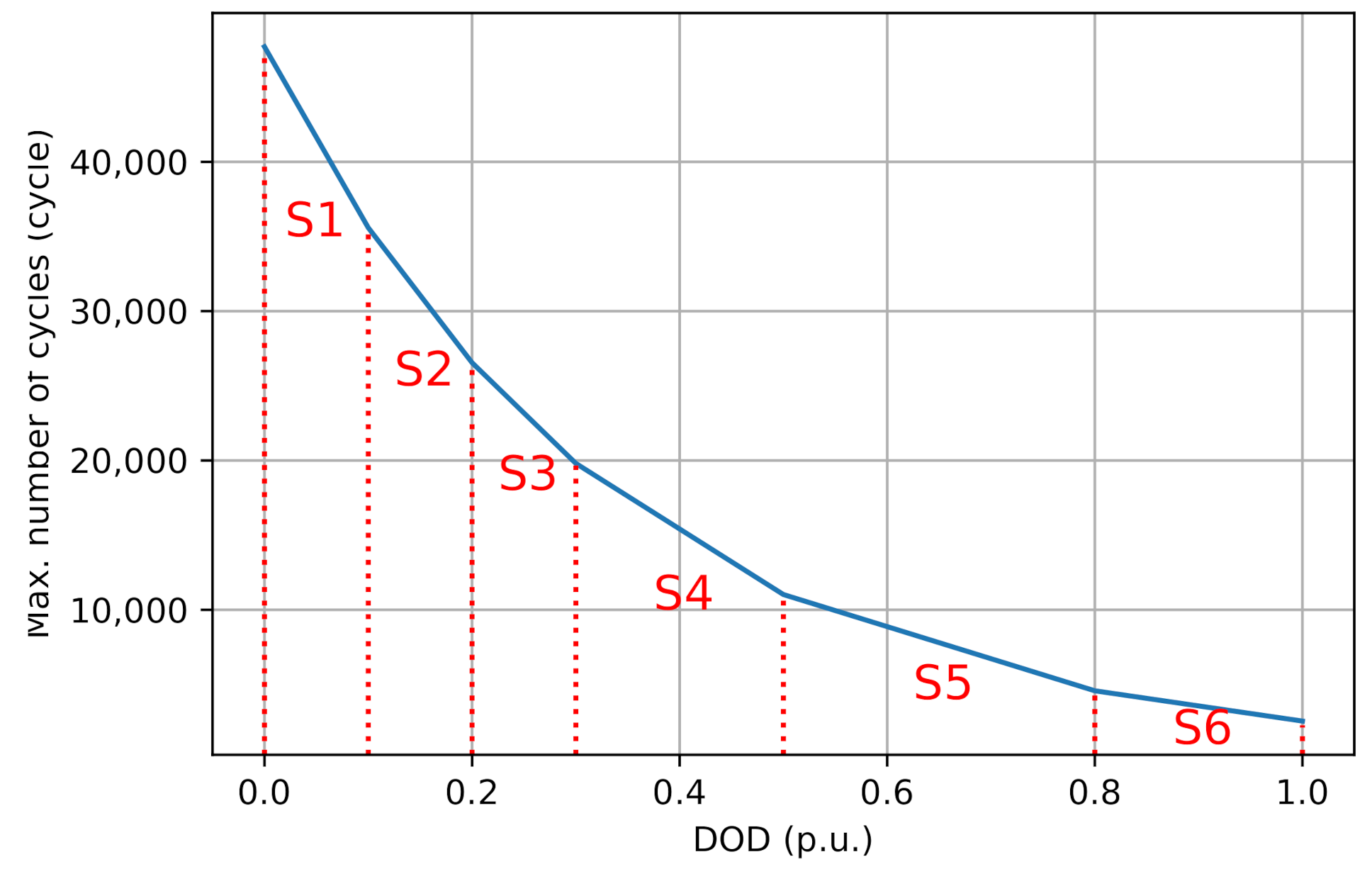
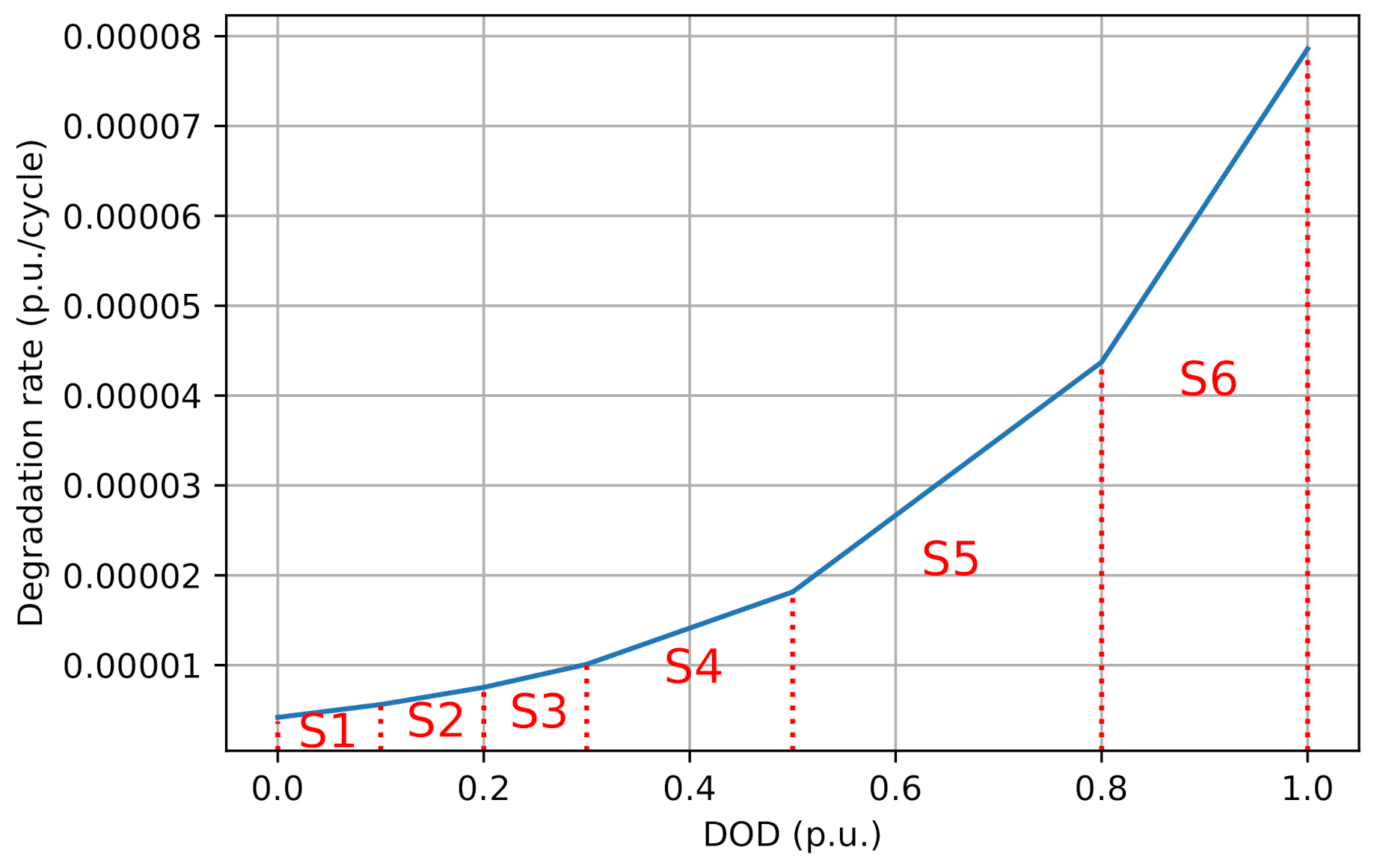
2.3. BESS Degradation
3. Case Studies
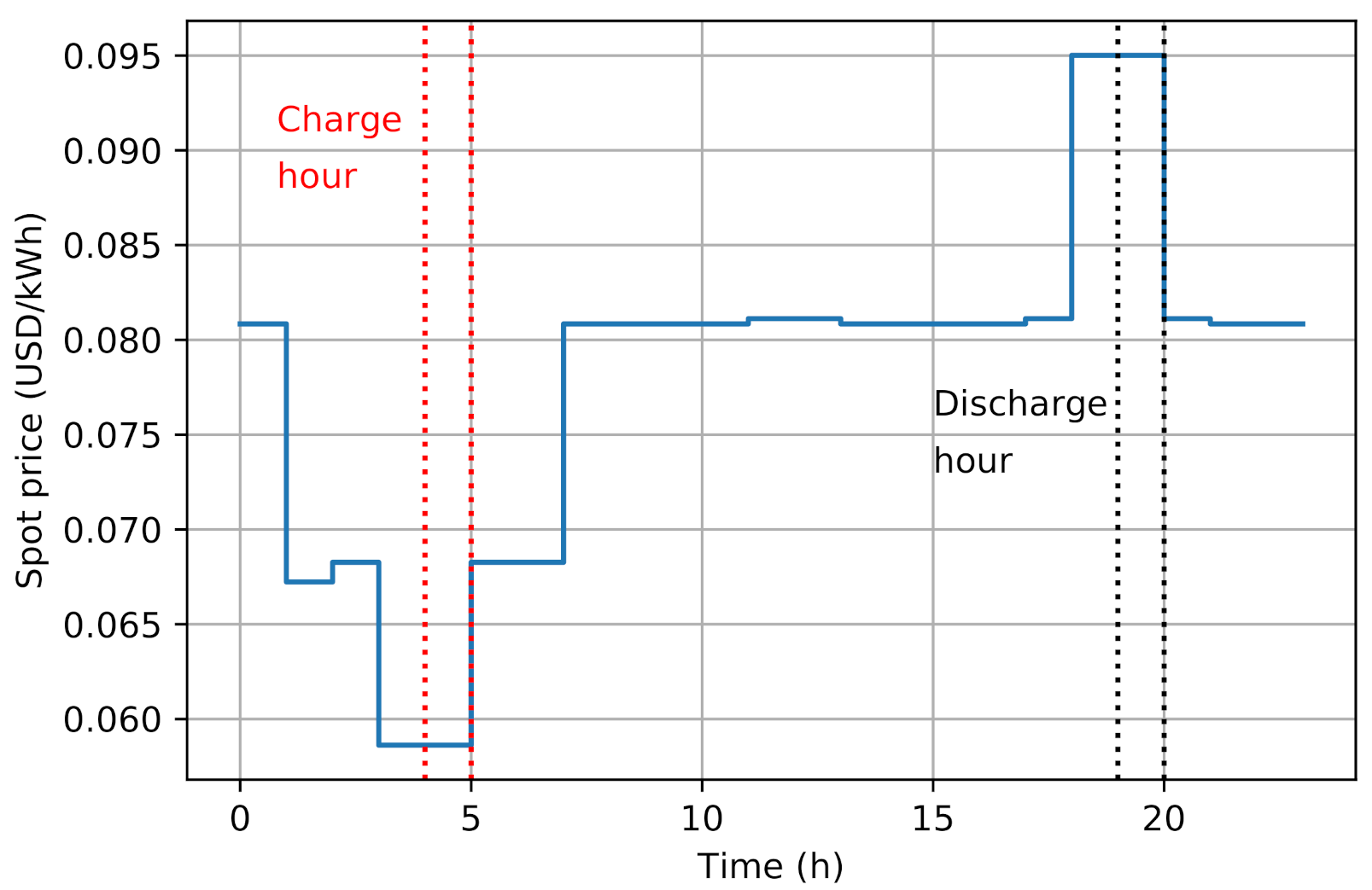
3.1. Optimal Case (Case A)
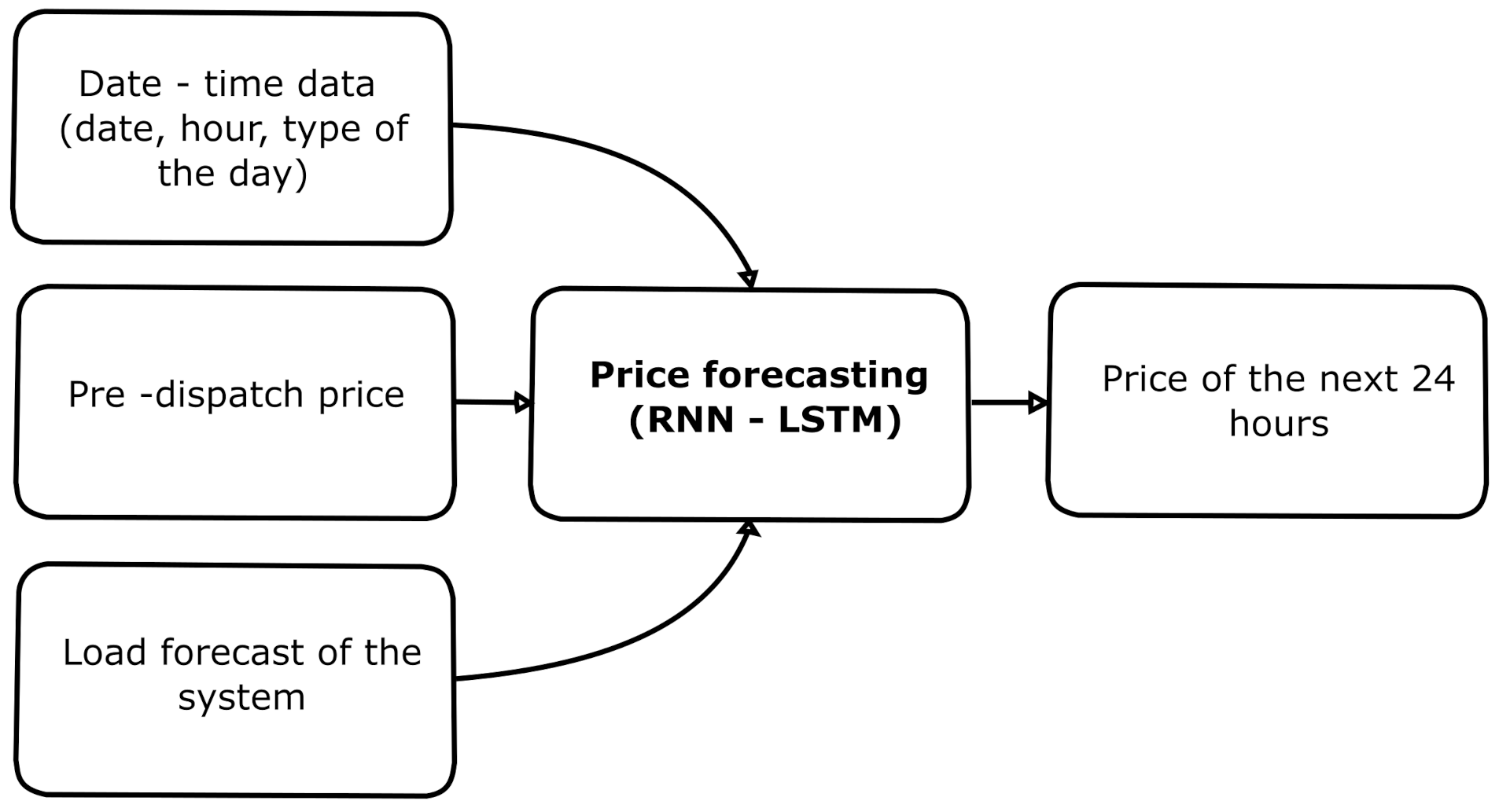
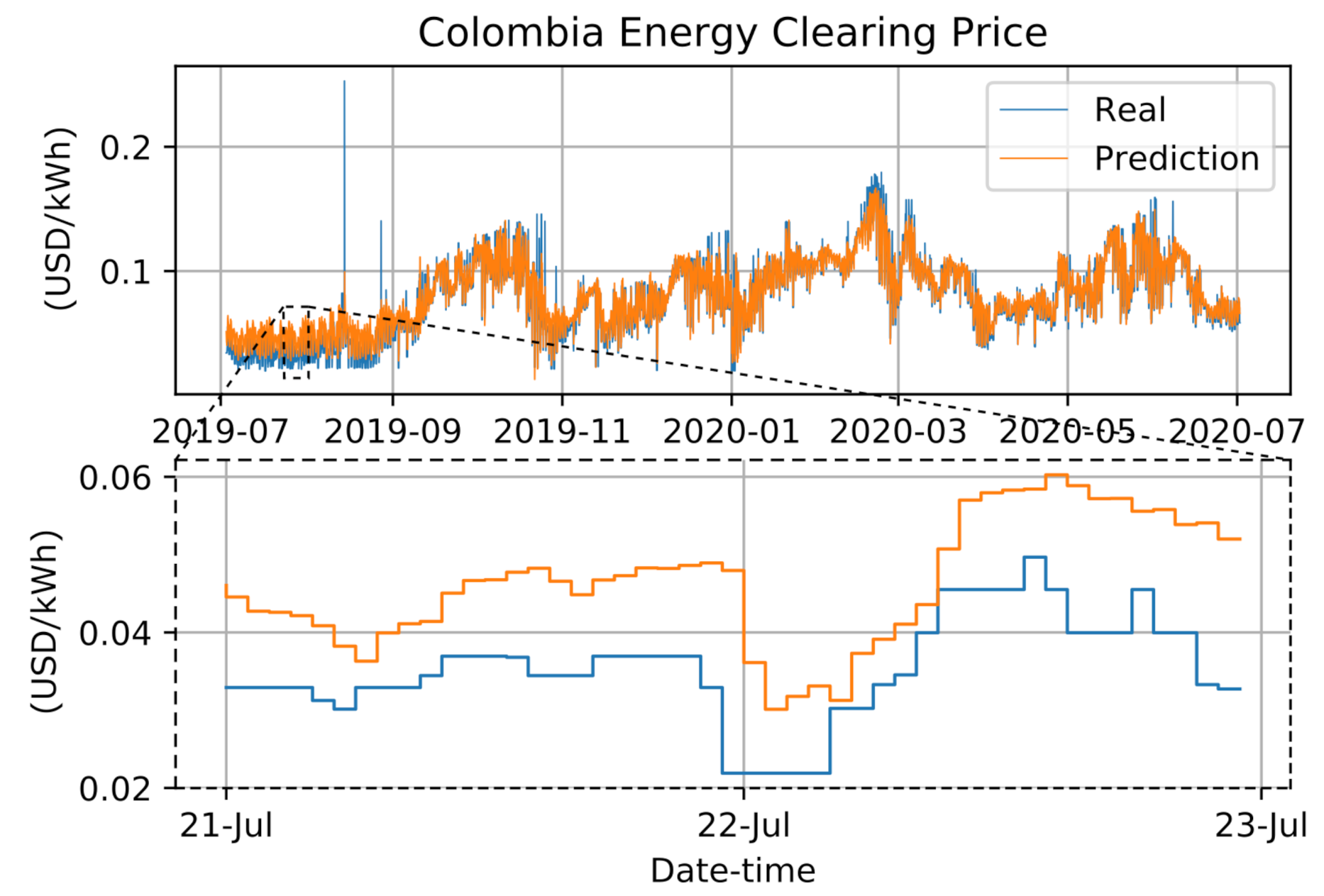
3.2. Day-Ahead Forecast Case (Case B)
3.3. Mirror Arbitrage Case (Case C)
3.4. Back to Back Case (Case D)
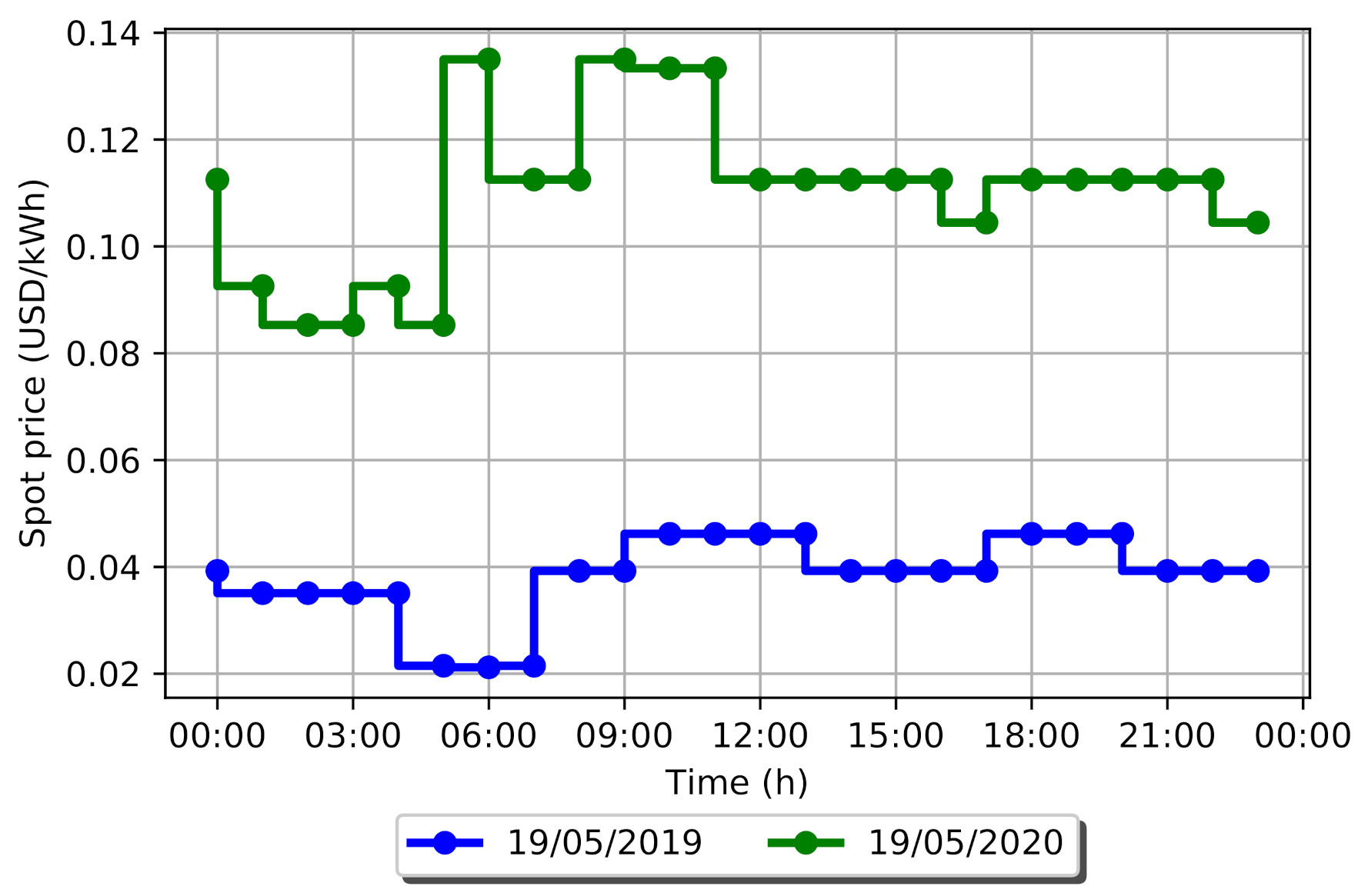
3.5. Statistical-Based Operating Strategy (Case E)
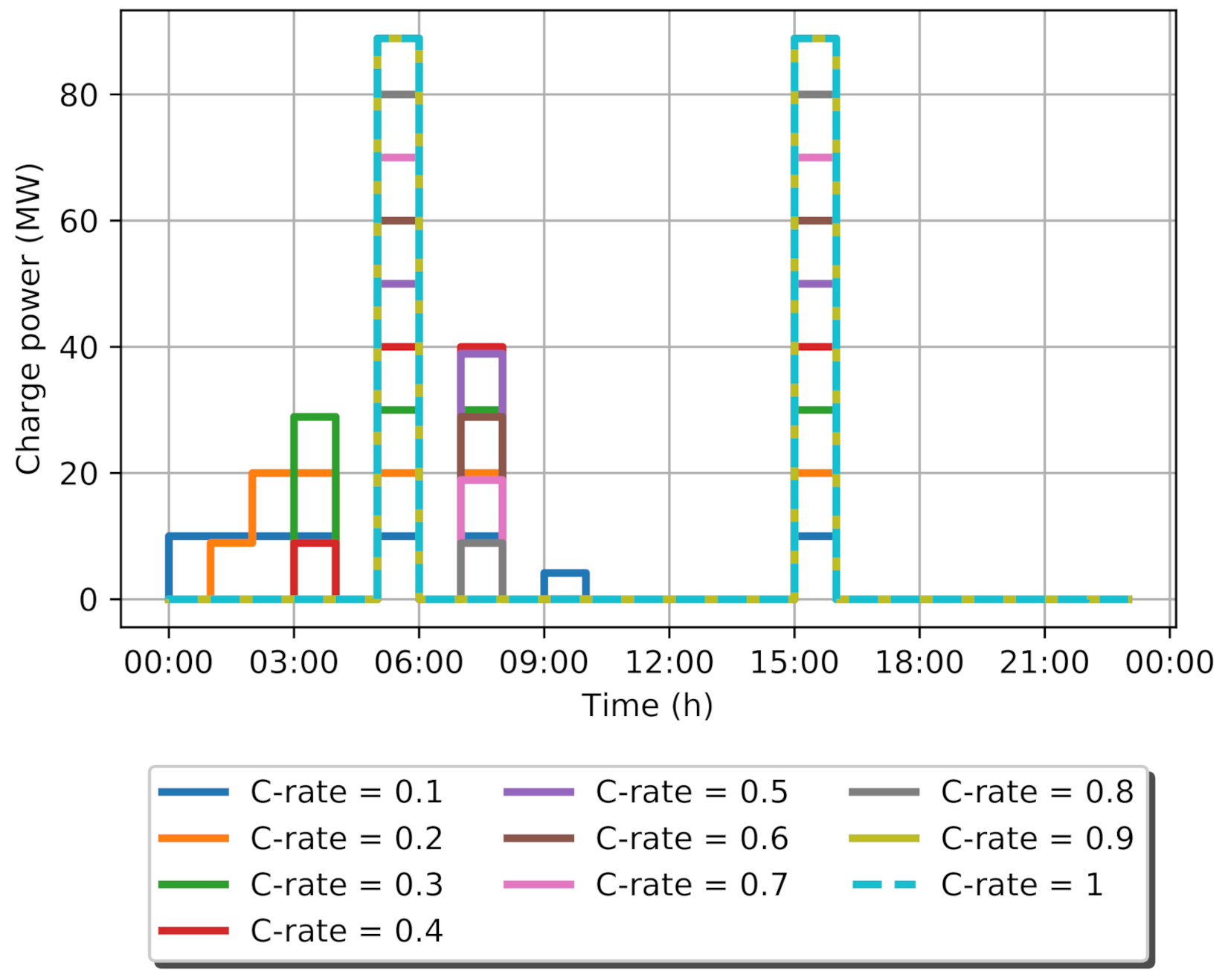
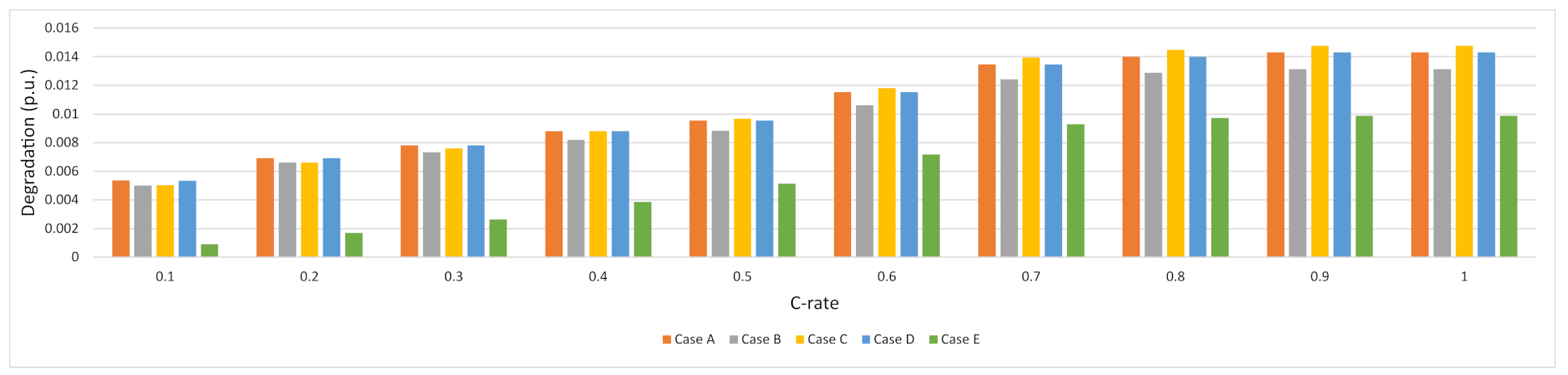
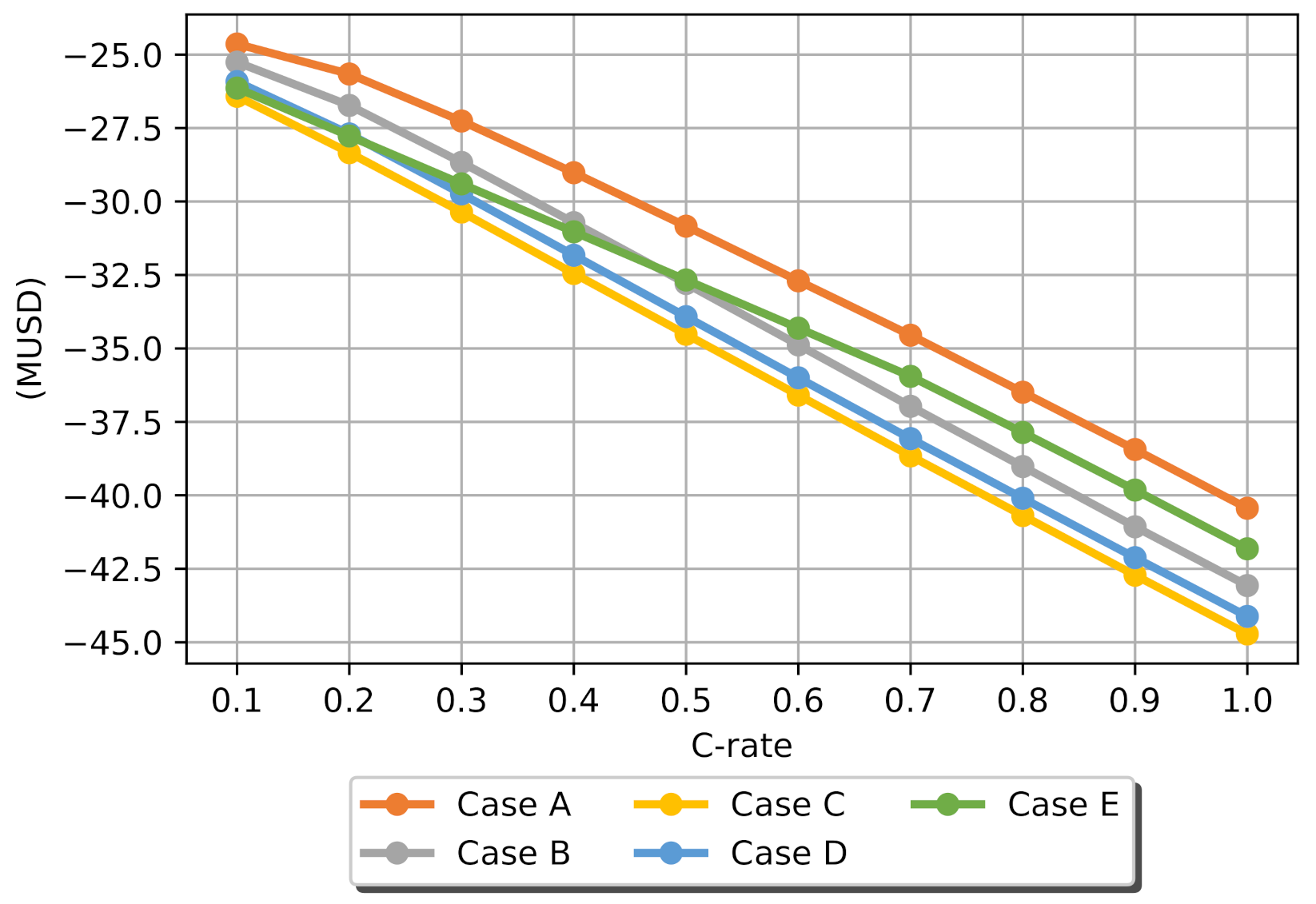
4. Results and Analysis
4.1. Results
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | Description |
| t | Steps of time (h) |
| T | Simulation horizon |
| d | Linear segment of BESS degradation curve |
| D | Group of linear segments of BESS degradation curve: (S1, S2, S3, S4, S5, S6) |
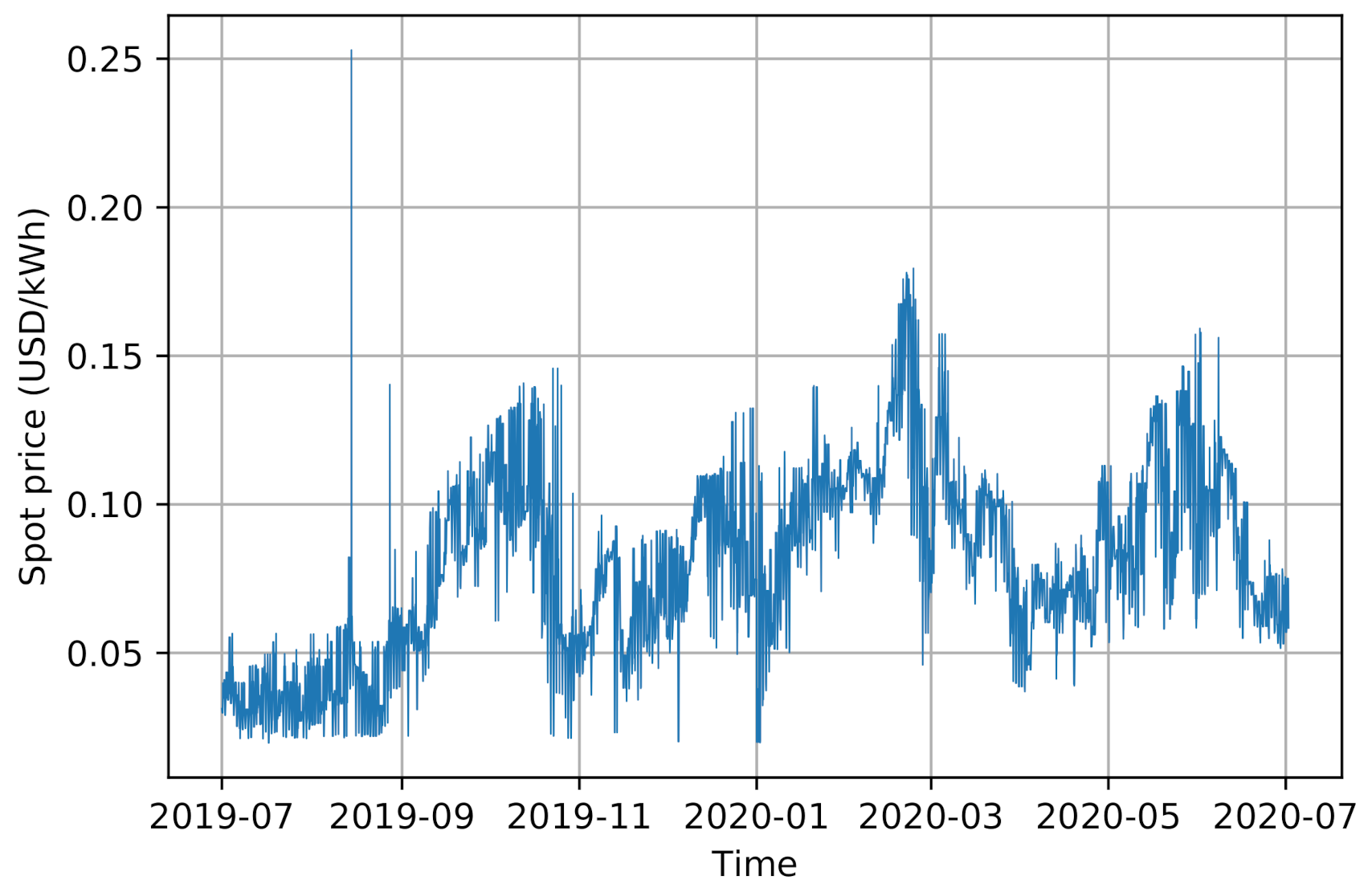
| Price of energy in t ($/MWh) | |
| Amount of power discharged in the system in t (MW) | |
| Amount of power charged for the system in t (MW) | |
| Market operation time segment, for this case is 1 (h) | |
| Power capacity of Energy Storage System (MW) | |
| Energy capacity of Energy Storage System at time t (MWh) | |
| Energy level of Energy Storage System at time t (MWh) | |
| Cost of power capacity in Energy Storage System with n technology ($/MW) | |
| Cost of energy capacity in Energy Storage System with n technology ($/MWh) | |
| Initial State of Charge of the Energy Storage System (p.u.) | |
| Minimum State of Charge of the Energy Storage System (p.u.) | |
| Maximum State of Charge of the Energy Storage System (p.u.) | |
| State of Charge of the Energy Storage System in t (p.u.) | |
| Charge efficiency of power conversion process of n technology of Energy Storage System (p.u.) | |
| Discharge efficiency of power conversion process of n technology of Energy Storage System (p.u.) | |
| Big number | |
| Signal of charge (Binary) | |
| Signal of discharge (Binary) | |
| Self discharge (p.u./h) | |
| Degradation rate of BESS (p.u./cycle) | |
| Degradation rate of BESS for segment d (p.u./cycle) | |
| Slope of linear segment d of BESS degradation curve (p.u./cycle) | |
| Constant of linear segment d of BESS degradation curve (p.u.) | |
| Depth of Discharge (p.u.) | |
| Depth of Discharge minimum of linear segment d (p.u.) | |
| Depth of Discharge maximum of linear segment d (p.u.) | |
| Integral variable signal of linear segment d at time t (Binary) |
References
- Department of Energy of United States of America. DOE Global Energy Storage Database Projects. 17 November 2020. Available online: https://www.sandia.gov/ess-ssl/global-energy-storage-database-home/ (accessed on 2 February 2021).
- BloombergNEF. Energy Storage Investments Boom as Battery Costs Halve the Next, Decade. (n.d.) Available online: https://about.bnef.com/blog-/energy-storage-investments-boom-battery-costs-halve-next-decade/ (accessed on 31 March 2021).
- BloombergNEF; Goldie-Scot, L. A Behind the Scenes Take on Lithium-Ion Battery Prices. BloombergNEF, 2019. Available online: https://about.bnef.com/blog/behind-scenes-take-lithium-ion-battery-prices/ (accessed on 25 April 2021).
- Li, L.; Liu, P.; Li, Z.; Wang, X. A multi-objective optimization approach for selection of energy storage systems. Comput. Chem. Eng. 2018, 115, 213–225. [Google Scholar] [CrossRef]
- Eyer, J.; Corey, G.P.; SANDIA. Energy Storage for the Electricity Grid: Benefits and Market Potential Assessment Guide. In a Study for the DOE Energy Storage Systems Program (Issues SAND2010-0815). 2010. Available online: http://www.ntis.gov/help/ordermethods.asp?loc=7-4-0#online (accessed on 13 May 2021).
- Rampersadh, N.; Davidson, I.E. Grid energy storage devices. In Proceedings of the 2017 IEEE PES-IAS PowerAfrica Conference: Harnessing Energy, Information and Communications Technology (ICT) for Affordable Electrification of Africa, Accra, Ghana, 27–30 June 2017; pp. 121–125. [Google Scholar] [CrossRef]
- Wu, F.-B.; Yang, B.; Ye, J.-L. Chapter 5-Integrated ESS application and economic analysis. In Grid-Scale Energy Storage Systems and Applications; Elsevier: Amsterdam, The Netherlands, 2019; pp. 153–201. [Google Scholar] [CrossRef]
- Zamani-Dehkordi, P.; Chitsaz, H.; Rakai, L.; Zareipour, H. A price signal prediction method for energy arbitrage scheduling of energy storage systems. Int. J. Electr. Power Energy Syst. 2020, 122, 106122. [Google Scholar] [CrossRef]
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.C.; Kim, H.; Yoon, Y.T. Optimal ESS investment strategies for energy arbitrage by market structures and participants. J. Electr. Eng. Technol. 2018, 13, 51–59. [Google Scholar] [CrossRef]
- Byrne, R.H.; Silva-Monroy, C.A. Estimating the Maximum Potential Revenue for Grid Connected Electricity Storage: Arbitrage and Regulation. 2012. Available online: http://www.sandia.gov/ess/publications/SAND2012-3863.pdf (accessed on 15 May 2021).
- Zafirakis, D.; Chalvatzis, K.J.; Baiocchi, G.; Daskalakis, G. The value of arbitrage for energy storage: Evidence from European electricity markets. Appl. Energy 2016, 184, 971–986. [Google Scholar] [CrossRef]
- Akbari-Dibavar, A.; Zare, K.; Nojavan, S. A hybrid stochastic-robust optimization approach for energy storage arbitrage in day-ahead and real-time markets. Sustain. Cities Soc. 2019, 49, 101600. [Google Scholar] [CrossRef]
- Salles, M.B.C.; Huang, J.; Aziz, M.J.; Hogan, W.W. Potential Arbitrage Revenue of Energy Storage Systems in PJM. Energies 2017, 10, 1100. [Google Scholar] [CrossRef] [Green Version]
- Krishnamurthy, D.; Uckun, C.; Zhou, Z.; Thimmapuram, P.R.; Botterud, A. Energy Storage Arbitrage Under Day-Ahead and Real-Time Price Uncertainty. IEEE Trans. Power Syst. 2018, 33, 84–93. [Google Scholar] [CrossRef]
- Fang, X.; Hodge, B.-M.S.; Bai, L.; Cui, H.; Li, F.F. Mean-Variance Optimization-Based Energy Storage Scheduling Considering Day-Ahead and Real-Time LMP Uncertainties. IEEE Trans. Power Syst. 2018, 33, 7292–7295. [Google Scholar] [CrossRef]
- Terlouw, T.; AlSkaif, T.; Bauer, C.; van Sark, W. Multi-objective optimization of energy arbitrage in community energy storage systems using different battery technologies. Appl. Energy 2019, 239, 356–372. [Google Scholar] [CrossRef]
- Martins, J.; Miles, J. A techno-economic assessment of battery business models in the UK electricity market. Energy Policy 2021, 148, 111938. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, B. Energy Storage Arbitrage in Real-Time Markets via Reinforcement Learning. In Proceedings of the IEEE Power and Energy Society General Meeting, Portland, OR, USA, 5–9 August 2018; pp. 1–11. [Google Scholar] [CrossRef] [Green Version]
- Wankmüller, F.; Thimmapuram, P.R.; Gallagher, K.G.; Botterud, A. Impact of battery degradation on energy arbitrage revenue of grid-level energy storage. J. Energy Storage 2017, 10, 56–66. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Zhou, Z.; Botterud, A.; Zhang, K.; Ding, Q. Stochastic coordinated operation of wind and battery energy storage system considering battery degradation. J. Mod. Power Syst. Clean Energy 2016, 4, 581–592. [Google Scholar] [CrossRef] [Green Version]
- Bera, A.; Almasabi, S.; Tian, Y.; Byrne, R.H.; Chalamala, B.; Nguyen, T.A.; Mitra, J. Maximising the investment returns of a grid-connected battery considering degradation cost. IET Gener. Transm. Distrib. 2020, 14, 4711–4718. [Google Scholar] [CrossRef]
- Zhuo, W.; Savkin, A.V. Profit Maximizing Control of a Microgrid with Renewable Generation and BESS Based on a Battery Cycle Life Model and Energy Price Forecasting. Energies 2019, 12, 2904. [Google Scholar] [CrossRef] [Green Version]
- Mallon, K.R.; Assadian, F.; Fu, B. Analysis of On-Board Photovoltaics for a Battery Electric Bus and Their Impact on Battery Lifespan. Energies 2017, 10, 943. [Google Scholar] [CrossRef]
- Xu, Y.; Zhao, T.; Zhao, S.; Zhang, J.; Wang, Y.; Energy Research Institute @ Nanyang Technological University (ERI@N); State Grid Corporation of China. Multi-objective chance-constrained optimal day-ahead scheduling considering BESS degradation. CSEE J. Power Energy Syst. 2018, 4, 316–325. [Google Scholar] [CrossRef]
- Kadri, A.; Mohammadi, F. Energy storage optimization for global adjustment charge reduction in Ontario. J. Energy Storage 2020, 30, 101491. [Google Scholar] [CrossRef]
- Fu, R.; Remo, T.; Margolis, R.; Fu, R.; Remo, T.; Margolis, R. 2018 U.S. Utility-Scale Photovoltaics- Plus-Energy Storage System Costs Benchmark; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2018. Available online: https://www.nrel.gov/docs/fy19osti/71714.pdf (accessed on 28 May 2021).
- Arcos-Vargas, Á.; Canca, D.; Núñez, F. Impact of battery technological progress on electricity arbitrage: An application to the Iberian market. Appl. Energy 2020, 260, 114273. [Google Scholar] [CrossRef]
- Damato, G.; Hoffman, S. Energy Storage Cost Summary for Utility Planning: Executive Summary; Electric Power Research Institute: Washington, DC, USA, 2016; Issue November. [Google Scholar]

| Item | Value |
|---|---|
| Charge efficiency (%) | 90 |
| Discharge efficiency (%) | 90 |
| Self-discharge (%/h) | 0.00625 |
| Minimum State of Charge (p.u.) | 0.2 |
| Maximum State of Charge (p.u.) | 1.0 |
| Item | Value |
|---|---|
| Li-ion Battery (USD/MWh) | 209,000.00 |
| Power conversion system (USD/MW) | 70,000.00 |
| Structural Balance Of System (USD/MW) | 20,000.00 |
| Electrical Balance Of System (USD/MW) | 80,000.00 |
| Engineering, Procurement, and Construction (USD/MWh) | 35,000.00 |
| Land acquisition (USD/MWh) | 1000.00 |
| Interconnection fee (USD/MW) | 30,000.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peñaranda, A.F.; Romero-Quete, D.; Cortés, C.A. Grid-Scale Battery Energy Storage for Arbitrage Purposes: A Colombian Case. Batteries 2021, 7, 59. https://doi.org/10.3390/batteries7030059
Peñaranda AF, Romero-Quete D, Cortés CA. Grid-Scale Battery Energy Storage for Arbitrage Purposes: A Colombian Case. Batteries. 2021; 7(3):59. https://doi.org/10.3390/batteries7030059
Chicago/Turabian StylePeñaranda, Andrés F., David Romero-Quete, and Camilo A. Cortés. 2021. "Grid-Scale Battery Energy Storage for Arbitrage Purposes: A Colombian Case" Batteries 7, no. 3: 59. https://doi.org/10.3390/batteries7030059
APA StylePeñaranda, A. F., Romero-Quete, D., & Cortés, C. A. (2021). Grid-Scale Battery Energy Storage for Arbitrage Purposes: A Colombian Case. Batteries, 7(3), 59. https://doi.org/10.3390/batteries7030059






