Determination of Diffusion Coefficients of Lithium in Solid Electrolyte LiPON

Abstract

A structural model of LiPON solid electrolyte, containing elements that simulate drift conductivity, diffusion conductivity, and leakage current was proposed. The dependence of the impedance of the structural model on frequency was calculated, and the parameters of the model at which the theoretical curve best approximates the experimental Nyquist diagrams were determined. Based on these data, the ion diffusion coefficient and conductivity of LiPON were calculated, which are D₁ = 1.5 × 10⁻¹¹ cm²/s and σ = 1.9 × 10⁻⁶ S/cm, respectively.

1. Introduction

The expansion of the market for miniature and wearable electronic devices, such as smartphones, wrist gadgets, transdermal patches, RFID tags, and smart cards, is driving the demand for solid state Li ion battery (SSLIB). In the overwhelming majority of commercially available batteries, phosphorus-lithium oxynitride (LiPON) is used as a solid electrolyte. It should be noted that the specific capacity of SSLIB is significantly lower than the capacity of batteries with liquid electrolytes. Thus, in the SSLIB of electrochemical system Li_xV₂O₅/LiPON/Si@O@Al [1], the specific capacity is 5.6 µA·h/cm² and 6.5 mA·h/cm³, while the thin-film cells of the same system with a liquid electrolyte have a maximum capacity of 200 µA·h/cm² and 20 mA·h/cm³. The decrease in capacity is due to the lower ionic conductivity of the solid LiPON electrolyte compared to the liquid electrolyte. The conductivity of a solid electrolyte depends on the concentration of free lithium ions and their mobility. In this case, the main reason for the low conductivity is the low mobility of lithium ions, which is related to the diffusion coefficient by the Einstein relation. In addition, in electrolytes, a stationary electric field is screened by charge carriers and charge transfer occurs mainly due to diffusion. It follows that the ionic conductivity of a solid electrolyte is determined by the diffusion of lithium ions; therefore, the diffusion coefficient is as important an electrolyte characteristic as its conductivity.

To determine the diffusion coefficient of lithium ions and calculate the ionic conductivity, a Pt/LiPON/Pt structure was fabricated and studied by impedance spectroscopy method. Below is a description of the Pt/LiPON/Pt manufacturing process, the results of impedance spectroscopy, and their interpretation based on the proposed structural model. By fitting the parameters of the structural model, the Warburg amplitudes for diffusion elements were determined and the diffusion coefficient of lithium ions and LiPON conductivity were calculated.

2. Results

2.1. Experimental Samples

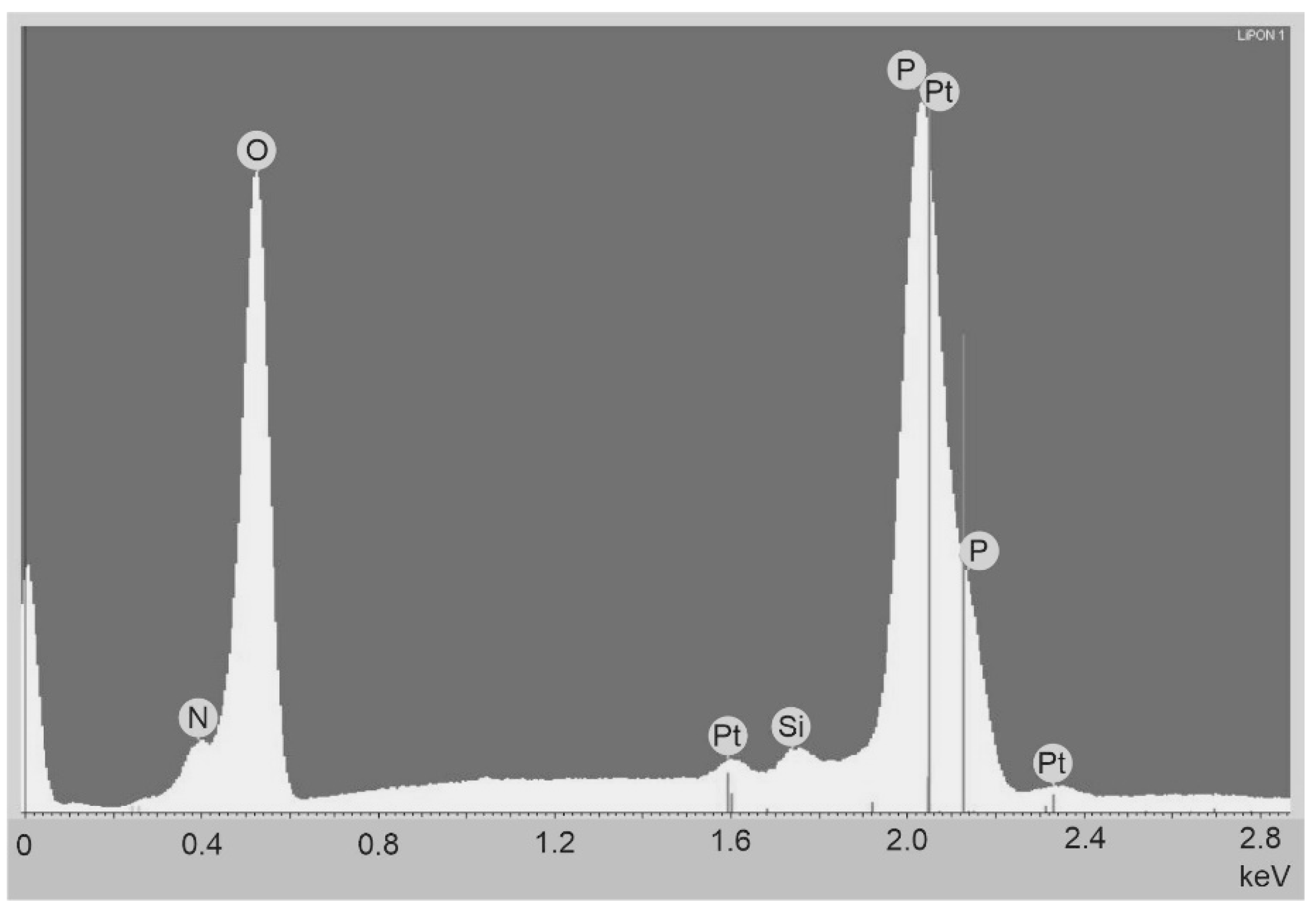
LiPON films (Figure 1) were deposited on the oxidized silicon wafer at a SCR-651 “Tetra” unit by magnetron sputtering of lithium orthophosphate under a nitrogen flow (18.6 standard cubic cm/min) at a residual pressure of 2 μbar. The magnetron power was 150 W, the deposition time was 3 h, and the thickness of the deposited film was 1 μm. The thickness of the platinum electrodes, deposited by magnetron sputtering, was 100 nm. Copper foil strips, attached to platinum electrodes by electroconductive glue, served as down conductors. 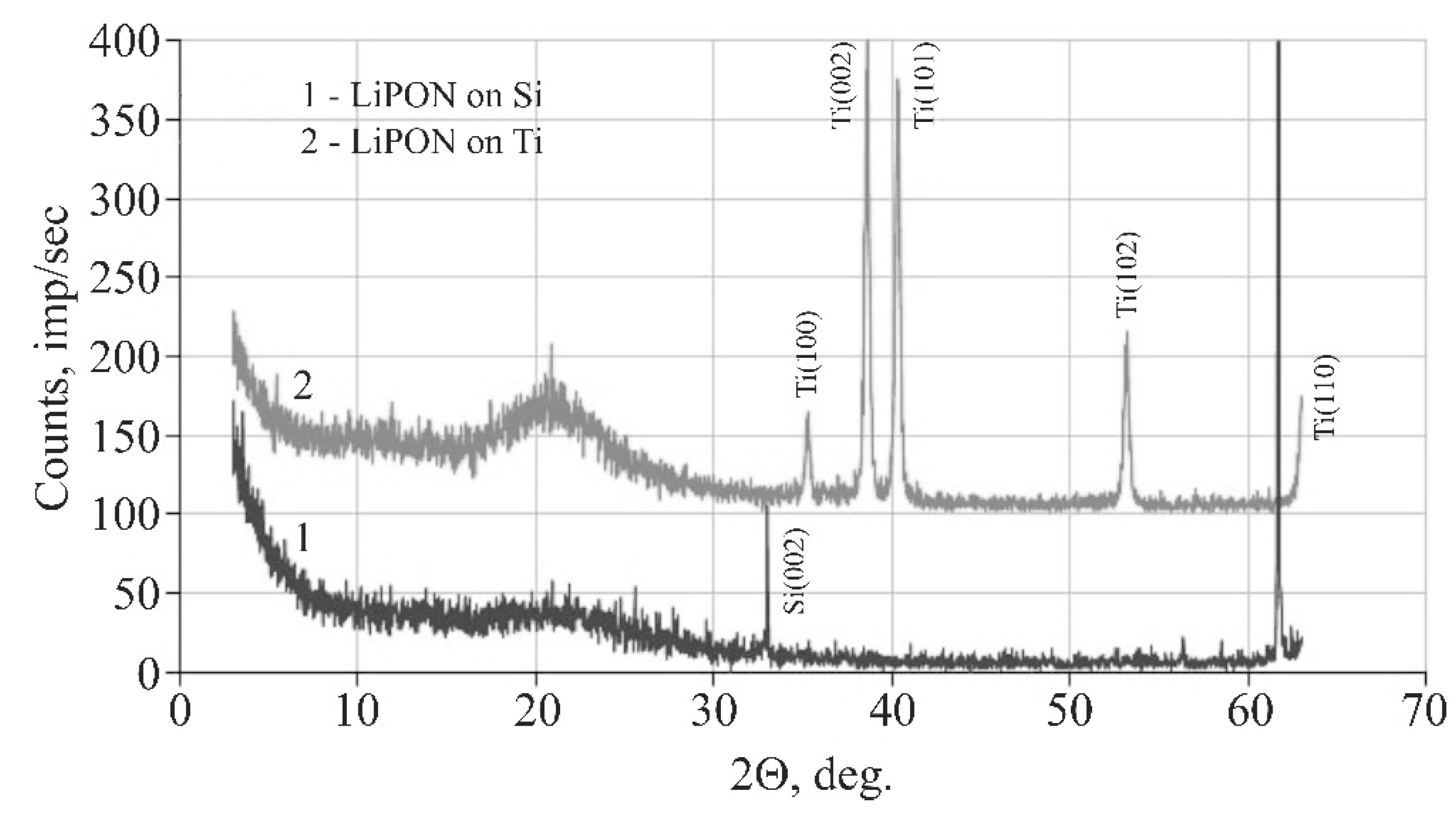The nitrogen concentration in the LiPON films, according to the data of energy dispersive analysis (INCAx-act EDA), was 16.8 at.% at an accelerating voltage of 5 kV and 16.5 at.% at a voltage of 7 kV (Figure 2). According to X-ray phase analysis (ARL X’tra), the LiPON films were amorphous (Figure 3). Figure 4 shows the cleavage of a Pt(100 nm)/LiPON(1 μm)/Pt(100 nm) cell. The inset shows a section of the solid LiPON electrolyte layer. The impedance spectrum obtained on a multichannel potentiostat-galvanostat P-20X8 in the frequency range of 1 Hz to 20 kHz is shown in Figure 5.

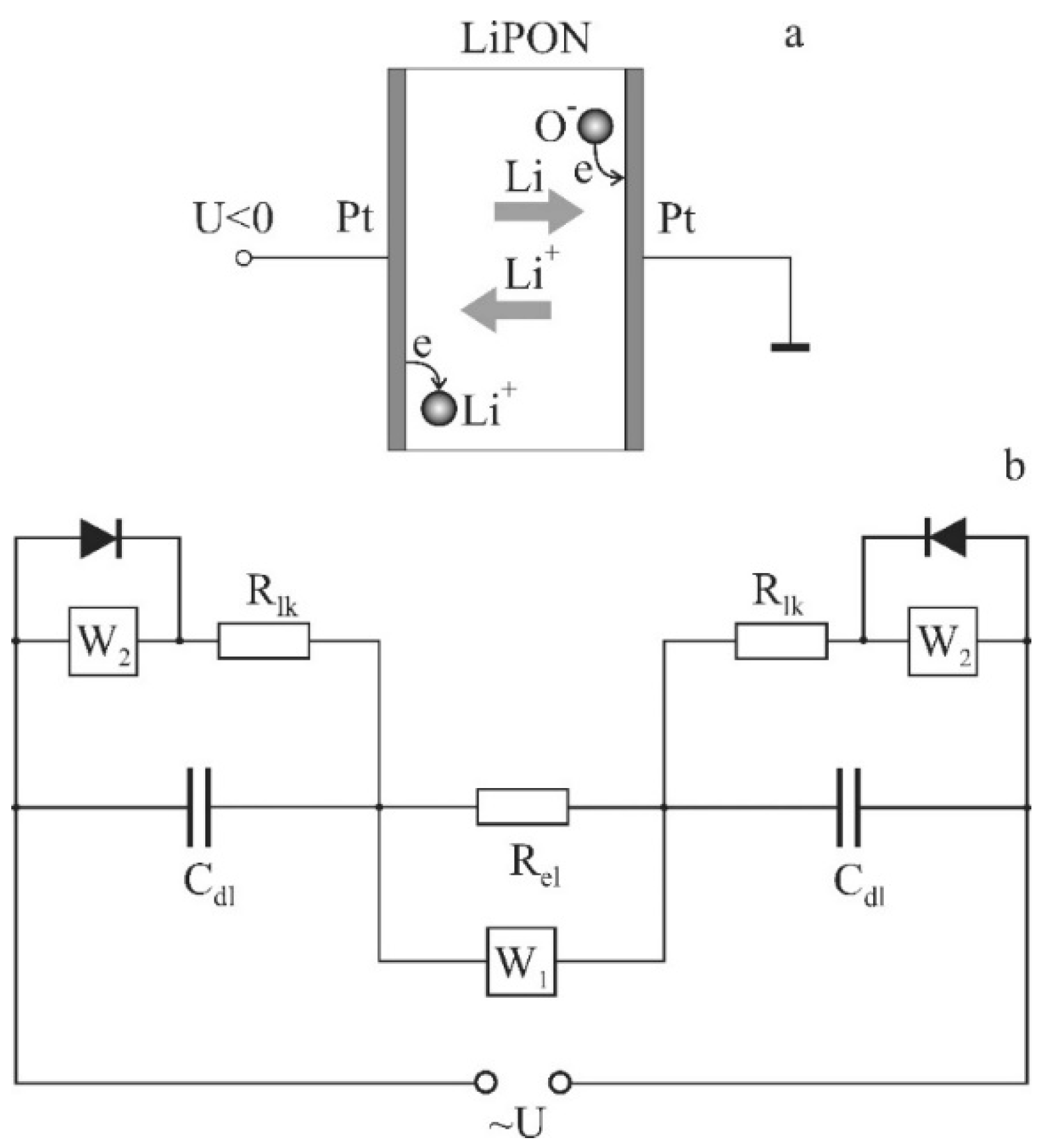
To explain the features of the obtained spectrum, a structural model, shown in Figure 6, was proposed. When choosing a structural model, the following features of the Pt/LiPON/Pt cell were considered. First of all, it was taken into consideration that in the cell, the diffusion mechanism of charge transfer prevails. The lithium concentration gradient required to shield the external field was formed by lithium dissolved in platinum electrodes and the Faraday process. As was shown in [2], platinum electrodes contain a large amount of dissolved lithium and, depending on the polarity, extraction or insertion of lithium occurs. In addition, according to the results of [3], a Faraday process takes place on platinum electrodes, and the leakage current circuit is closed by the flow of the resulting lithium atoms. In other words, there are two oppositely directed diffusion flows: lithium ions and atoms.

The proposed structural model (Figure 6) consists of two capacitors corresponding to the capacitance of an electric double layer (EDL) on platinum electrodes, connected by an active resistance and a Warburg diffusion element. These elements simulate the drift and diffusion components of the polarization current. The Faraday process is simulated by a leakage current circuit connected in parallel to each of the capacitors and consists of an active resistance and a diffusion element. Since neutral lithium atoms are formed only at the cathode, diodes are connected in parallel to the diffusion elements, which shunt the Warburg diffusion element on the electrode, which, in this half-period is, the anode. Since it is not possible to calculate the impedance of a model with such structural elements as a diode, a simplified model is considered below.

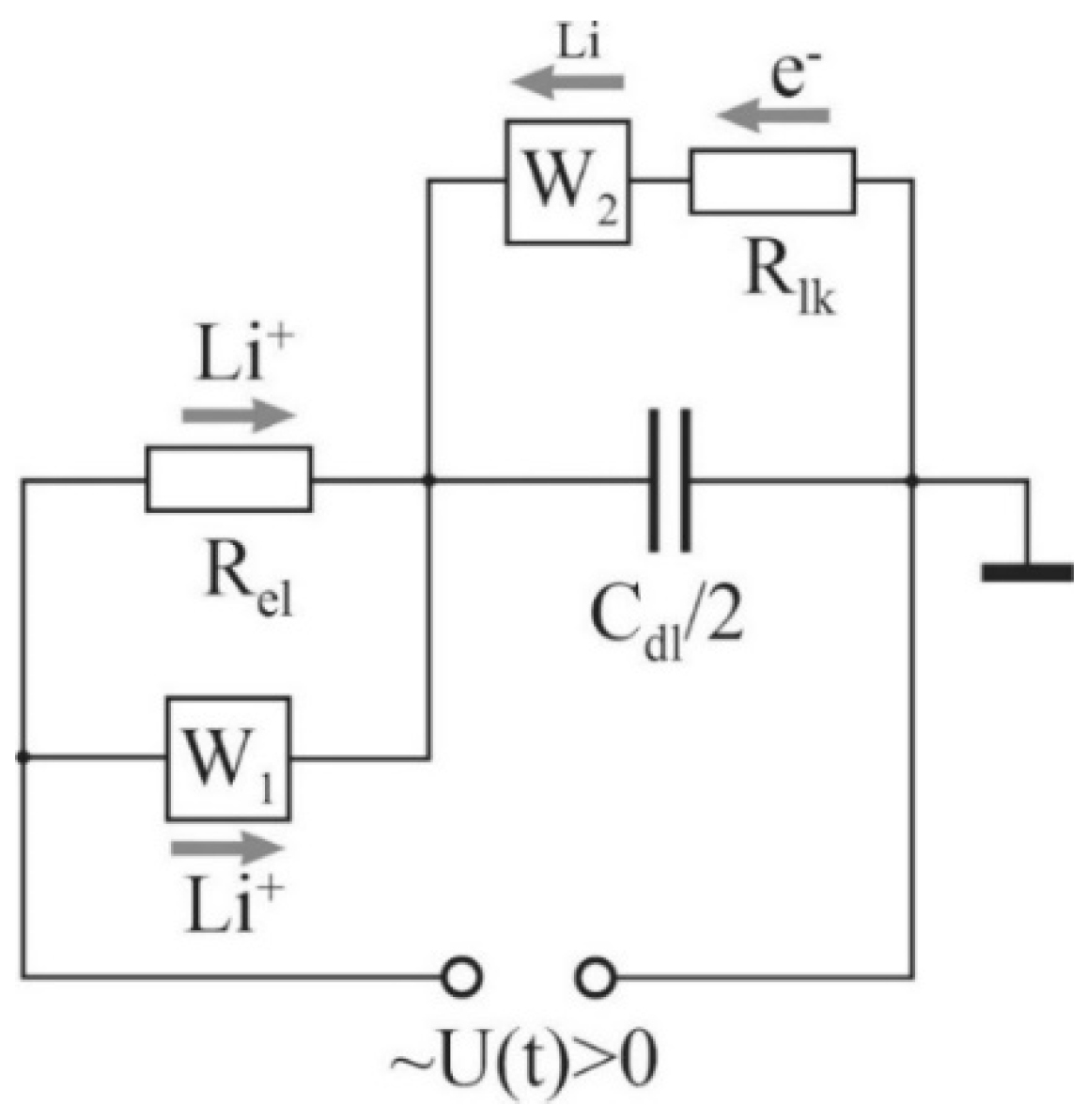
In a simplified model (Figure 7), both EDLs were represented by one capacitor, $C_{dl}/2$, and one leakage circuit. The current through the resistor, $R_{lk}$, simulates the redox reactions at the electrodes, while its value is determined by the rate of these reactions. The leakage current circuit is closed through the Warburg element, W₂, which simulates the resistance to the diffusion flux of lithium atoms moving from the cathode to the anode, where they are oxidized again.

The impedance of the structural model shown in Figure 7, which is calculated in the same way as the resistance of parallel and series-connected conductors, has the form

$$\begin{array}{l}\widehat{Z}=\frac{A_{W1}}{\sqrt{\omega }}{R}_{el}\frac{(1-j)\left(R_{el}+\frac{A_{W1}}{\sqrt{\omega }}+j\frac{A_{W1}}{\sqrt{\omega }}\right)}{{\left(R_{el}+\frac{A_{W1}}{\sqrt{\omega }}\right)}^2+\frac{A_{W1}^2}{\omega }}-\\ -\frac{2}{\omega C_{dl}}\frac{\left[\frac{A_{W2}}{\sqrt{\omega }}+j\left(R_{lk}+\frac{A_{W2}}{\sqrt{\omega }}\right)\right]\left[R_{lk}+\frac{A_{W2}}{\sqrt{\omega }}+j\left(\frac{A_{W2}}{\sqrt{\omega }}+\frac{2}{\omega C_{dl}}\right)\right]}{{\left(R_{lk}+\frac{A_{W2}}{\sqrt{\omega }}\right)}^2+{\left(\frac{A_{W2}}{\sqrt{\omega }}+\frac{2}{\omega C_{dl}}\right)}^2}\end{array}$$

(1)

Separation of the real and imaginary parts of the impedance given by Equation (1) yields in the following expressions:

$$Re\widehat{Z}=R_{el}\frac{2+\frac{\sqrt{\omega }{R}_{el}}{A_{W1}}}{1+{\left(1+\frac{\sqrt{\omega }{R}_{el}}{A_{W1}}\right)}^2}+{\left(\frac{2}{\omega C_{dl}}\right)}^2\frac{R_{lk}+\frac{A_{W2}}{\sqrt{\omega }}}{{\left(R_{lk}+\frac{A_{W2}}{\sqrt{\omega }}\right)}^2+{\left(\frac{A_{W2}}{\sqrt{\omega }}+\frac{2}{\omega C_{dl}}\right)}^2}$$

(2)

$$Im\widehat{Z}=-j\frac{\frac{\sqrt{\omega }{R}_{el}^2}{A_{W1}}}{1+{\left(1+\frac{\sqrt{\omega }{R}_{el}}{A_{W1}}\right)}^2}-j\frac{2}{\omega C_{dl}}\frac{{\left(R_{lk}+\frac{A_{W2}}{\sqrt{\omega }}\right)}^2+\frac{A_{W2}}{\sqrt{\omega }}\left(\frac{A_{W2}}{\sqrt{\omega }}+\frac{2}{\omega C_{dl}}\right)}{{\left(R_{lk}+\frac{A_{W2}}{\sqrt{\omega }}\right)}^2+{\left(\frac{A_{W2}}{\sqrt{\omega }}+\frac{2}{\omega C_{dl}}\right)}^2}$$

(3)

where $A_W=U_0/\sqrt{2D}Sqc$; Ω·s^−1/2 is Warburg coefficient; U₀, V is voltage amplitude across platinum electrodes; D, m²/s is diffusivity coefficient; S, m² is electrode area; q, C is ion charge; c, m⁻³ amplitude of oscillation of the nonequilibrium lithium concentration at the electrode surface.

2.2. Diffusivity and Conductivity Calculation

Equations (2) and (3) represent the parametric equation of a curve referred to as the Nyquist diagram. Figure 2, along with the experimental Nyquist diagram, shows a diagram calculated by Equations (2) and (3) for the following values of the parameters of structural elements: R_el = 180 Ω, R_lk = 11,000 Ω, C_dl = 2.1 × 10⁻⁷ F, A_W1 = 10⁴ Ω·s^−1/2, and A_W2 = 9 × 10⁴ Ω·s^−1/2. 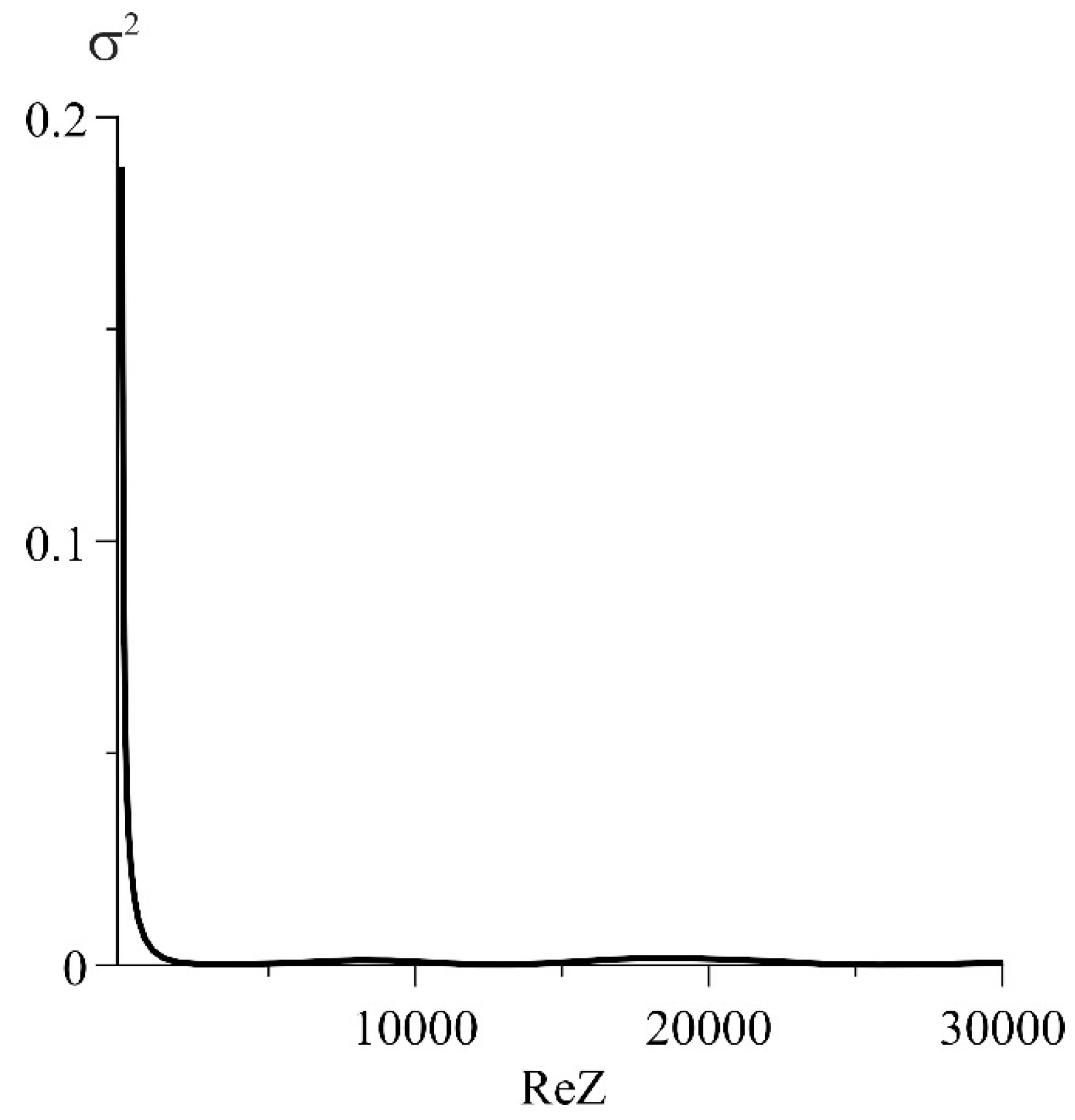The value R_el = 180 Ω was obtained by the method described in [3] and was not used for fitting. The rest of the parameters were selected so that the deviation from the experimental curve, characterized by RSS (residual sum of squares), was minimal. Since the value of RSS itself does not characterize the quality of the approximation, it is expedient to use the normalized squared deviations, ${\sigma }^2(\mathrm{ReZ})={[{\mathrm{ImZ}}^{\exp }\left(\mathrm{ReZ}\right)-{\mathrm{ImZ}}^{\mathrm{ap}}\left(\mathrm{ReZ}\right)]}^2{/[\mathrm{ImZ}}^{\exp }{\left(\mathrm{ReZ}\right)]}^2$, shown in Figure 8.

Note that, at high frequencies, the discrepancy between the experimental curve and its model increases. It is possible to achieve a more accurate coincidence of the experimental and calculated diagrams by introducing a constant phase element (CPE). This is the most commonly used approach. However, the structural models obtained in this case, in spite of the perfect coincidence of appropriate diagrams with the experimental curves, hardly lend themselves to physical interpretation. Therefore, in this work, the choice is made in the favor of the physical meaning, although with some damage to the accuracy of approximation of the experimental curves. For example, in the high-frequency region, according to Figure 7, the capacitor ($C_{dl}/2$) shunts the elements $R_{lk}$ and $W_2$, and their variation does not affect the shape of the Nyquist diagram in any way. Therefore, it makes no sense to achieve full compliance of the model with the experimental curve in this area (Figure 8).

The value of the Warburg amplitude obtained by fitting was related to the diffusion coefficient by the equation

$$A_{W1}=\frac{U_0}{\sqrt{2D_1}Sq{c}_0}$$

(4)

allowing us to find the diffusion coefficient of lithium ions, D₁. For this, it was necessary to know the amplitude of oscillation (c₀) of their non-equilibrium concentration near the electrode. It is usually expressed from the Nernst equation for the electrode potential. In this case, c₀ can be expressed as the potential of a charged plane formed by an electrolyte layer with a thickness of d_Li located in the plane x = 0 and placed in a medium of known dielectric permeability, ε_r. With respect to the grounded electrode located in the plane x = δ, such a potential will be equal to U₀ = Eδ, according to the Gauss theorem $E=d_{\mathrm{Li}}{c}_{0}q/2{\epsilon }_0{\epsilon }_r$. Then $c_0=2{\epsilon }_0{\epsilon }_r{U}_0/d_{\mathrm{Li}}q\delta$, where d_Li is the diameter of the lithium ion, q is the charge of the ion, and δ is the thickness of the LiPON layer. Expressing the diffusion coefficient from Equation (4) and substituting c₀, we obtain the final expression for the diffusion coefficient.

$$D_1=\frac{1}{2}{\left(\frac{d_{\mathrm{Li}}\delta }{A_{W1}2S{\epsilon }_0{\epsilon }_r}\right)}^2$$

(5)

In [3], the relative dielectric permeability of LiPON was estimated as ${\epsilon }_r\approx 250$, and the remaining parameters were d_Li = 1.56 × 10⁻¹⁰ m, δ = 10⁻⁶ m, A_W1 = 10⁴ Ω·s^−1/2, and S = 6.4 × 10⁻⁵ m². Their substitution in Equation (5) gives the value of the diffusion coefficient D₁ = 1.5 × 10⁻¹¹ cm²/s, which is in good agreement with the data of [4,5].

The error in determining the diffusion coefficient can be estimated as follows. Logarithmic derivation of Equation (5) gave the dependence of the error in determining the diffusion coefficient on the Warburg amplitude of ∆D₁/D₁ ≈ 2∆A₁/A₁, since all other parameters were determined more accurately. In the course of fitting, the variation of the normalized $RSS={\displaystyle \sum _{i=1}^N{\sigma }_i^2}$ in a vicinity of its minimum value, $RS{S}_{\min }=0.03345$, was ≈0.5%, which corresponds to $2\Delta A_1/A_1\approx 18\%$. Thus, the final value of the diffusion coefficient will be as follows: D₁ = 1.5 (± 0.3) × 10⁻¹¹ cm²/s.

The obtained value of the diffusion coefficient makes it possible to find the mobility of lithium ions, µ = 5.8 × 10⁻¹⁰ cm²/V·s and calculate the conductivity of LiPON. The value of the concentration of lithium ions, $C_{{\mathrm{Li}}^{+}}$, required for this calculation can be found on the basis of the leakage current, which is related to the concentration by the ratio

$$\frac{C_{{\mathrm{Li}}^{+}}S{d}_{\mathrm{Li}}q}{{\tau }_0}=i_{lk}$$

(6)

where ${\tau }_0$ is the relaxation time of the concentration of lithium ions due to reduction reactions at a cathode. In [3], the relaxation time during the discharge of Pt/LiPON/Pt through 1 MΩ was determined as ${\tau }_0=51.3$ s. In this case, Equation (6) gives the concentration value in the near-cathode layer by $C_{{\mathrm{Li}}^{+}}=2.1\times {10}^{22}$ cm⁻³. For the obtained values of the concentration and mobility of lithium ions, the conductivity was σ =1.9 × 10⁻⁶ S·cm⁻¹. This value agrees with the data of [6], where the conductivity of LiPON was 2.3 (± 0.7) × 10⁻⁶ s·cm⁻¹, as well as with the results of [4,5] and a number of other works. It was noteworthy that the active resistance of LiPON, defined for a similar structure in [3] as 180 Ω, gives the conductivity value of 0.87 × 10⁻⁶ s·cm⁻¹.

The difference in the values of the amplitudes A_W1 and A_W2 was explained by the fact that A_W1 simulates the complex resistance to the diffusion flux of lithium ions, and A_W2—to the diffusion flux of lithium atoms. Indeed, when the lithium ions reached the cathode, they were reduced to atoms, creating a concentration gradient and a diffusion flux directed from the cathode to the anode. Upon reaching the anode, the lithium atoms were oxidized, closing the leakage current circuit, and then moved in the opposite direction under the action of the electric field. The concentrations of lithium ions ($C_{{\mathrm{Li}}^{+}}=2.1\times {10}^{22}$) and atoms ($C_{\mathrm{Li}}\sim {10}^{19}$) at the cathode [3] differ by three orders of magnitude. It can be expected that the amplitudes of the concentration oscillation differ by the same order, while the Warburg amplitudes differ by less than one order of magnitude. Hence, one can conclude that the diffusion coefficients of ions and atoms are also different.

3. Conclusions

A method for calculating the diffusion coefficient of lithium in solid electrolyte LiPON, based on the analysis of impedance spectroscopy data, was proposed. The essence of the method was to approximate the experimental Nyquist diagram by a curve obtained on the basis of the LiPON structural model and to determine the model parameters by the least squares method. One of the fitting parameters is the Warburg amplitude, which was related to the diffusion coefficient in Equation (5). This relationship was used to calculate the diffusion coefficient of lithium. The result obtained is in good agreement with the literature and data. This indicates the adequacy of the structural model of the solid electrolyte LiPON, which can be considered as an equivalent circuit.