1. Introduction
The end of life (EOL) is related to the concept of failure in global terms, which can be defined as the fact of something not working, or no longer working as well as it should. The concept of failure can be assessed by criteria such as performance (performing at an unsatisfactory level), functionality (incapable of performing a specific function) and availability (machine breaks down) [
1]. Nonetheless, the basic concepts of how an EOL event should be specified are not clear [
2], especially in systems with nonlinear degradation behaviours such as lithium ion secondary batteries (LIBs).
Nowadays, LIBs are widely used to propel electric vehicles (EV) because of their outstanding combination of energy density, power density and lifetime. However, even with the lifetime being better than that of other secondary batteries, it is still usually below the life expectancy of an overall vehicle. It is important to accurately define and estimate the EOL event of the LIB, at which a replacement should be considered. Generally, the LIBs integrated in EVs are considered to have reached their EOL when their dischargeable capacity drops to a certain value relative to its initial value [
3]. It is typically fixed at 80% [
4,
5] or at 70% [
6,
7]. There are also some other cases where the EOL is defined by the relative resistance instead of the relative capacity. In those cases, the EOL is typically set to 200% of the initial resistance of the battery [
8,
9]. The relative capacity is commonly linked to high-energy EV applications and the relative resistance threshold is normally related to high-power EV applications [
9]. The use of any of these kinds of fixed EOL threshold values simplifies considerably the EOL calculation. Specially, the use of such simplifications is interesting when analysing the performance level of different electrochemical battery designs [
10] or evaluating the response of prognosis algorithms before using them in an on-board application [
11]. However, lifespan estimations of LIBs integrated in EVs require more complex battery EOL criteria than those simplified values because the battery EOL depends on the nature of the application and the design parameters of the battery [
12].
LIBs are complex electrochemical systems with nonlinear degradation behaviours, which depend on various intrinsic features and external conditions, making the EOL estimation a challenge [
13]. Current literature is inconclusive about the fixed EOL values being too conservative or too progressive. On one hand, numerous studies suggest that the commonly used fixed EOL threshold values are conservative. Wood et al. [
14] demonstrated that the lifespan of an EV operated in a conservative way is beyond the commonly assumed 80% fixed EOL threshold value. Casal et al. [
15] gave empirical evidence for this argument. They saw that the EOL in some of the test cases were lower than those fixed 70–80% EOL values. On the other hand, there are studies that suggest that those fixed values are not conservative. Ziegler et at. [
16] saw that the battery should not go below 70% of its original capacity due to safety issues. In a previous study, Arrinda et al. [
17] saw that the EOL can come at higher relative capacity values than the 80%. The evaluated application specifications, defined mainly by a minimum EV driving range, were not fulfilled at a relative capacity of 85.69%. These studies highlight that it is still notoriously difficult to accurately predict the EOL [
18].
The EOL needs to be clear and unambiguous in order to ensure proper and safe operation of the EV [
12]. In this respect, Yingzhi et al. [
19] defined the EOL of a LIB as the point in time when the selected LIB can no longer provide enough power or energy to accomplish its intended function. However, the applied EOL estimation approach only addresses an application under specific use conditions. It cannot be generalized. In contrast, Goebel et al. [
20] defined a generalizable conceptual EOL approach where the EOL is a Boolean output defined by a multi-dimensional EOL threshold. The EOL threshold is theoretically estimated through repeated application of the inferred state equation and threshold equation, but it can be addressed by using simpler structures. The EOL threshold could be determined based on EOL observations or it can be calculated through the simulation of the states of the system for given input conditions. However, the conceptual proposals were not put into practice.
Inspired by Goebel et al.’s [
20] conceptual EOL approach, this paper develops and puts into practice the methodology behind the EOL threshold calculation through simulations. The generated methodology is generalizable and captures the application and battery characteristics of an EV. The paper is structured as follows:
Section 2 presents the generalizable systematic methodology for estimating the EOL. This section is composed of 3 phases. In the first phase, the health indicators (HIs) used in the literature are introduced and correlated with the condition monitoring variables (behavioural variables). In the second phase, the most common application specifications are analysed. In addition, the application specifications of two typical use cases are down-scaled to cell level: a high-energy EV and a high-power EV. In the third phase, the model-based simulation environment is introduced. Here, the battery testing methodology followed in the EU-funded Horizon 2020 project iModBatt [
21] is applied to construct the battery electric and thermal models. These models are used to simulate the battery performance for a range of operating conditions to map the EOL threshold that describes the EOL event. Afterwards,
Section 3 presents and discusses the results of the proposed two examples.
Section 4 is dedicated to the validation of the stated hypotheses and the obtained EOL threshold of the evaluated high-energy EV application. Finally, the conclusions are drawn in
Section 5.
2. Methodology
The EOL definition for LIBs integrated in EVs is usually a fixed value that neglects the battery and application characteristics. In this context, a generalizable methodology to determine the EOL that also captures the application and battery characteristics of an EV is presented.
The proposed methodology focuses on developing an “M”-dimensional EOL threshold, where M represents the chosen number of HIs that define the EOL event. The proposal consists of an algorithm that searches the combinational value of the selected HIs at which the battery system stops fulfilling the specifications defined by the application. The methodology is divided into the following five steps, which are developed in three different phases:
Select the HIs of interest.
Detect the behavioural variable (electric, thermal, physical, etc.) where the effects of the chosen HIs can be observed.
Define the EOL criteria by addressing the link between the battery behavioural variables of interest and the downscaled application specifications.
Define the values of the chosen HIs that will be evaluated. Generate the evaluation grid composed of the combination of those values.
Find the combinational value of the HIs where the battery system stops fulfilling the EOL criteria.
The first two steps are related to the HIs and are developed in the first phase of the methodology. Firstly, the HIs are selected. There are many different HIs and, depending on the aim and resources of the EOL evaluation, it will be more interesting to use one or another. Nevertheless, there is a selection restriction. The relative pure ohmic resistance increase must be selected because of the design of the proposed approach to estimate the EOL event. Apart from this, the proposed method allows the use of any kind and any number of HIs. Secondly, the behavioural variables in which the effect of the chosen HIs can be observed are detected. It is important to detect properly the measurable variables that influence each HI in order to establish the link between HIs and application restrictions.
The third and fourth steps, which are developed in the second phase of the methodology, consist of merging the chosen HIs and the application specifications in order to run the simulation environment. Firstly, the application specifications are downscaled from system level to cell level. The downscaled application specifications are translated into the battery behavioural variables of interest (the variables linked with the selected HIs). As a result, we obtain (1) the EOL criteria that describe the EOL event and (2) the testing inputs that correspond to each EOL criterion. Secondly, the grid that delimitates the case study is generated with the values of the HIs. For this, vectors are determined. Each vector has the values that each HI but one (the pure ohmic resistance increase) will take in the simulation. The evaluation grid is generated based on the combinations of those vectors.
The fifth step consists of calculating the EOL threshold by integrating the previously built elements in a model-based simulation environment. This simulation environment is developed in the third phase of the methodology. Firstly, the electric-thermal behaviour of the battery system is modelled. Then, the battery electric and thermal behaviour is simulated, where the relative pure ohmic resistance is modified with the aim of finding the exact operating conditions where the battery system stops fulfilling the application specifications. As a result of identifying those operating conditions, an -dimensional EOL threshold map that considers HIs of interest is calculated.
2.1. Phase 1: Health Indicators
The health indicators (HIs) describe the aging behaviour and represent the state of health (SOH) of a battery/cell. The HIs must evolve with time and it is advantageous for them to be measurable quantities [
20]. There are many kinds of variables that can be used as HIs. The most common HI is the relative capacity (relative to the dischargeable capacity measured at the beginning of life), which is often labelled as the SOH itself. It is a direct representation of the energy that the battery can provide. A decrease in the dischargeable capacity of the battery translates to a lower EV driving range.
The relative value of the inner pure ohmic resistance of the battery appears in many studies as well. The pure ohmic resistance limits the applicable power at certain state-of-charge (SOC) levels. The increase of the pure ohmic resistive value increases the effect that the current has on the observed voltage value. As a result, the end-of-charge and end-of-discharge voltage limits are reached at earlier SOC values if the same current is applied. It especially affects the charging time in case of fast charging [
22].
These two HIs are relatively easy to measure/estimate, and their effect on the performance decrease can be directly addressed to application specifications (driving range, charging time, etc.). The increase of the pure ohmic resistance as well as the decrease of the dischargeable capacity affects the voltage vs capacity response of the battery (the increase of the pure ohmic resistance is linked to the power capability of the battery because of the ohmic drop and heat dissipation). Nonetheless, these two HIs are not the only ones that can be used to describe the aging behaviour of the battery. There are some other HIs reported in literature:
- -
The decrease of the end-of-discharge voltage with repetitive operating conditions [
19].
- -
The drift of the open circuit voltage (OCV) of the electrodes [
19].
- -
The increase of the time constant of the transitory response of the battery [
12].
- -
The decrease of the thermal conductivity of the inner components of the battery [
12].
- -
The increase of the effect of the reversible part of the heat generation [
12].
- -
The loss of lithium ion inventory (LLI) [
23].
- -
The loss of active material (LAM) on the electrodes [
23].
- -
The organic reduction of the electrolyte or the pressure inside the battery [
12].
However, it is not common to define the EOL with those HIs. Some of them represent variables with low observability. For example, LLI, LAM or the organic concentration of the electrolyte cannot be measured; they need to be guessed under several assumptions. Some others represent variables with no records of typical aging check-up tests. Thermal performance variations are an example since they are typically dismissed from the aging evaluations. A few represent variables with a lower study interest level compared to the commonly used HIs. If the pure ohmic resistance increase is evaluated, the rest of the impedance aspects are dismissed. This is why we have only used the two most common HIs for the proposed case study: the relative capacity and the relative resistance.
2.2. Phase 2: Application Specifications
The proposed EOL mapping is application-oriented. The application is the main element of the EOL criterion. Among the typical EV applications, the most common restricting specification is the driving range. In general, EVs used to require a minimum driving range that needs to be covered throughout their lifespan. This minimum driving range could be used to define the EOL event. Nonetheless, there could be some other restrictions such as a minimum time of operation, a minimum acceleration specification, a maximum charging time, a maximum heat generation or the assurance of avoiding catastrophic events (safety margin).
In this study, two applications are evaluated: (1) an EV with high-energy application requirements and (2) an EV with high-power application requirements. Taking as example these two applications, we will explain the downscaling of the application specifications from system to cell level and the definition of the EOL criteria.
2.2.1. High-Energy EV Application
The evaluated high-energy EV application consists of an electric public bus that needs to cover a certain bus route without any charging stop during the expected 17 h of operation. The remaining 7 h of the day are used to clean and charge the bus. In consequence, the application has two restrictions: one restriction in terms of driving range (17 h of non-stop operation without reaching the minimum voltage threshold) and a second restriction in terms of charging time (in 7 h the bus needs to be charged to fulfil the next day’s 17 h of non-stop operation). Those restrictions define the EOL criteria. The EOL event will come when the battery system is not able to provide the required amount of energy for the 17 h of operation. Among the different reasons behind the occurrence of the EOL event, we have discarded the charging time and only have considered the driving range as an EOL criterion since the charge is done at 0.5 C and it is expected to always have plenty of time to charge the battery system within the predefined 7 h.
The characteristics of the application led to the selection of a high-energy NMC-C pouch cell. The battery/cell characteristics are shown in
Table 1.
The bus manufacturer did a detailed analysis of the characteristics of the bus route and gave us the expected power profile for the battery system. Based on the design of the battery system, the provided power profile was downscaled by dividing it by the number of cells on the designed battery system. As a result, the most probable power profile at cell level was obtained.
We analysed the battery system and we saw that the liquid-based battery cooling of the bus has a high cooling and heating power and good thermal contact to the cells. Therefore, each cell is assumed to have an independent adiabatic thermal environment. As a result, the room temperature profile is simplified to a constant 25 °C temperature profile.
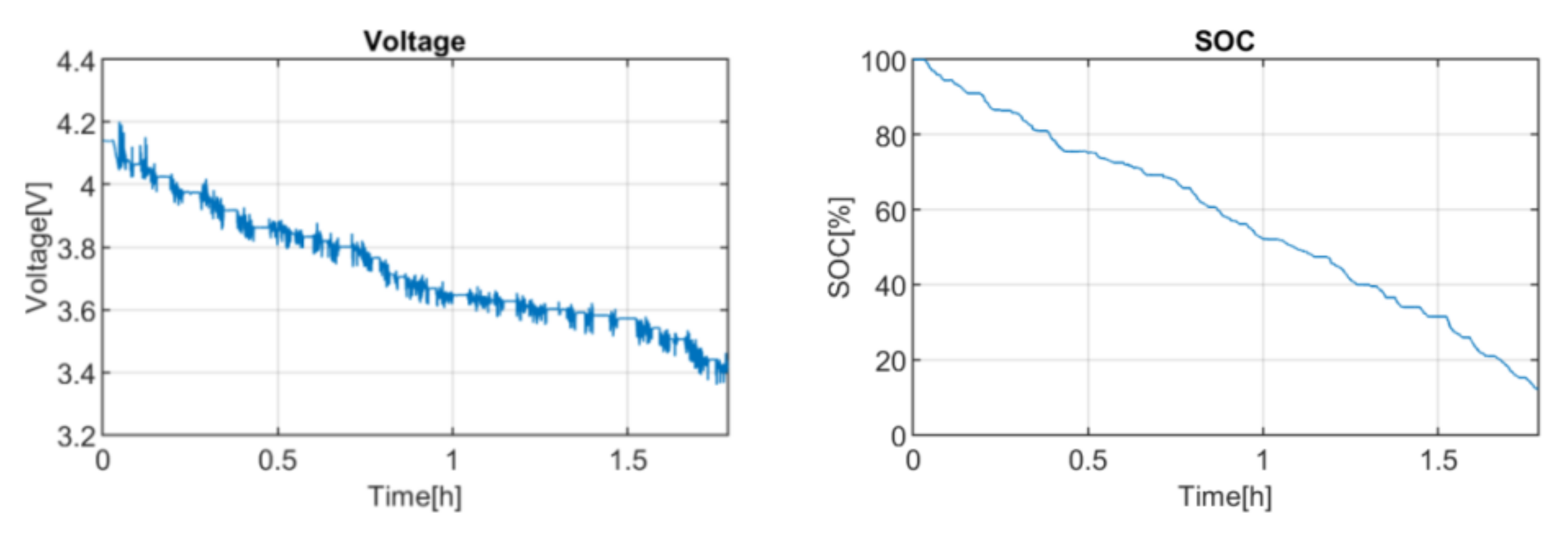
The obtained downscaled power profile was tested on the selected battery in a climatic chamber at 25 °C, thus emulating the real operation of the bus. The battery was previously charged to 100% SOC. The voltage response and SOC evolution are shown in
Figure 1.
Afterwards, the simulation results were exploited. Firstly, the applied current profile was considered as the most probable current profile of the application. This current profile is used as the testing input to calculate the EOL event under the defined EOL criteria. Secondly, we have defined the capacity decrease values that will be studied. The values are selected based on the observed response of the battery. In this case, the values are selected based on the SOC value that the battery reaches at the end of the discharge, which is 12.17%. Taking this into account, the range of the capacity decrease has been limited from 0 to 20%. The jump between points is decided in terms of the desired accuracy level and computational resources. In this case, we selected a jump of 1%.
After defining the values of the first HI, the values of the other HIs, except the one for ohmic resistance, need to be defined too. In this example, only one HI except for the pure ohmic resistance has been selected, so there is no need to calculate the values of any other HI.
2.2.2. High-Power EV Application
The evaluated high-power EV application consists of an electric public bus that needs to cover a certain bus route. The bus works every day for 16 h and it spends the rest of the day (8 h) being cleaned and charged. During application, the bus is fast-charged for 7 min at the start or at the end of the bus route with a constant-current (CC) charge strategy (as safety, the charge can go under a constant-voltage (CV) phase if the conditions are met). In consequence, the application has three restrictions: a restriction in terms of driving range of the line itself (the bus route needs to be operated without reaching the minimum voltage threshold); a second restriction in terms of charging time (in 8 h the bus has to be charged enough to fulfil the 16 h of operation of the next day); and a third restriction related to the driving range needed for the whole day, that takes into account the first driving range restriction, but also the charge opportunities at the beginning and at the end of the bus route (the bus needs to be able to fulfil the 16 h of daily operation without reaching the minimum voltage threshold thanks to the charging opportunities of 7 min at the beginning and at the end of the line). Those restrictions define the EOL criteria. The EOL event will come when the battery system is not able to provide the required amount of energy to complete the bus route throughout the 16 h of operation. Among the different reasons behind the occurrence of the EOL event, the slow charging time as an EOL criterion was discarded since the charge is done at 1C and therefore it is expected to always have plenty of time to charge the battery system within the predefined 8 h. Besides, since the first restriction is part of the third restriction, the EOL criterion is built only based on the third restriction: the driving range of the 16 h of daily operation.
The characteristics of the application led to the selection of a high-power NMC-LTO prismatic cell. The battery/cell characteristics are shown in
Table 2.
The bus manufacturer gave us the power profile of the battery system and the maximum current values of the fast charging station. Based on this data, we downscaled the power profile from battery system level to cell level and we determined that the maximum fast-charge current is 4C.
The downscaled power profile is repeated 12 times each day with stops of 7 min in between each repetition in order to charge the battery system. The power profile of the bus route is invariant, notwithstanding the evolution of the battery condition. The battery has to deliver the demanded power at the demanded time irrespective of the battery state. Nonetheless, the charging process of 7 min can change from a constant power to a CV phase depending on the battery state (voltage). The testing input that represents this charge cannot be defined as a constant current profile since the applied charging power depends on the voltage of the battery. Therefore, the testing input related with the opportunistic charging process (fast charge) consists of a constant current value that the charging manager will adjust if the requirements are met (if the battery reaches the end-of-charge voltage, the charging manager will change the charging strategy from CC to CV, reducing the charge current accordingly).
Both high-energy EV application and high-power EV application have the same liquid based heating–cooling system. Therefore, the room temperature profile is simplified to a constant 25 °C temperature profile as well.
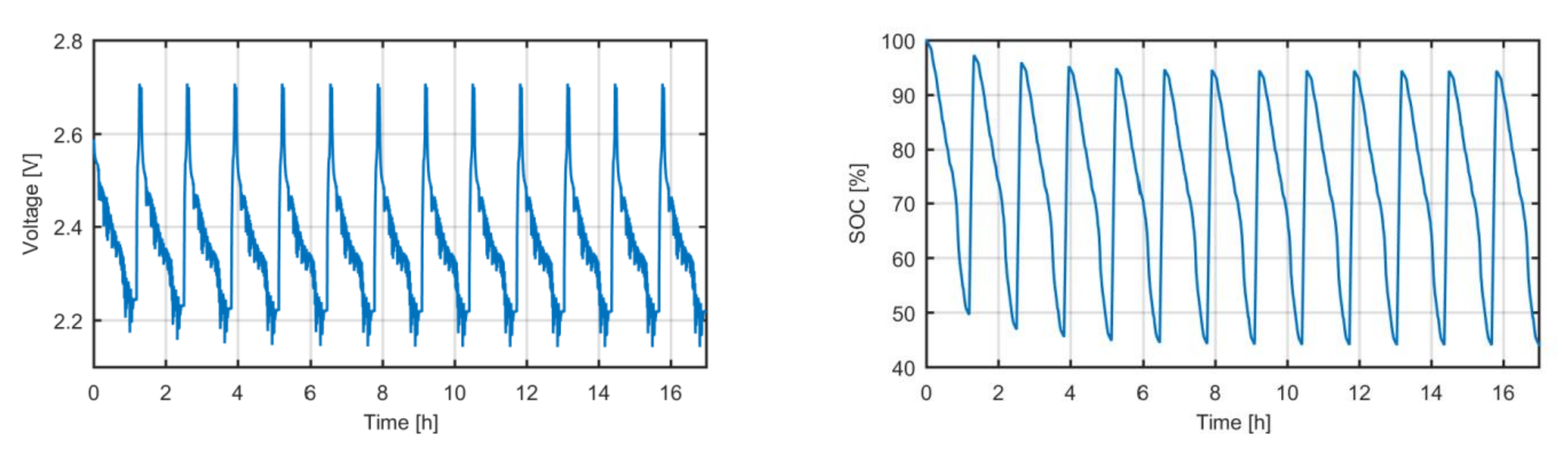
The resultant testing input was run on the selected cell in a climatic chamber at 25 °C, thus emulating the real operation of the high-power electric bus. As for the initial condition, the battery was charged to 100% SOC. The voltage response and SOC evolution is shown in
Figure 2.
After finishing the test, we defined the most probable current profile that represents the bus route. We merged this current profile with the constant current value on the opportunistic charging process to generate the testing input that will be used in the EOL event definition. Then, we defined the capacity decrease values that will be studied. The minimum SOC was 49.61% after applying the bus route operation profile and 44.05% after applying the daily operation profile. As consequence, the range of the capacity decrease was limited from 0 to 60%. The jump between points was decided to be 1%.
Finally, the values of the other HIs, except the one for ohmic resistance, need to be defined too. In this example, as in the high-energy EV application, only one HI except for the pure ohmic resistance has been selected, so there is no need to calculate the values of any other HI.
2.3. Phase 3: Simulation
The developed algorithm estimates the “M”-dimensional EOL threshold (recall that “M” is the number of selected HIs) by calculating the values of the selected battery HIs that define the EOL event. The proposal simulates the electric and thermal behaviour of the battery under the downscaled operation profiles at the defined health conditions to estimate the value of the pure ohmic resistance that defines the EOL event. For this purpose, the electric and thermal behaviour of the selected battery was modelled. In those developed models, the selected HIs were set as free variables (variables that can be modified from the outside).
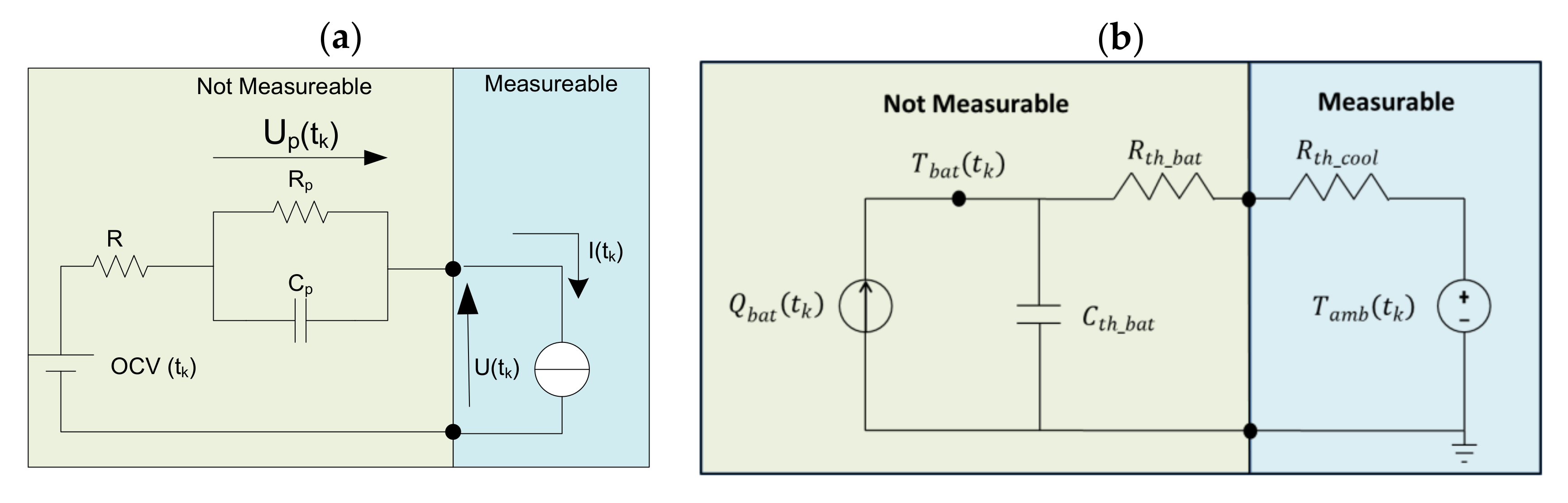
2.3.1. Battery Model
The applied battery model describes the electric and thermal behaviour of the chosen battery. It is assumed that the scale up from the battery/cell level to the battery system is trivial and that the interactions between cells are negligible. The developed electric [
24] and thermal models [
25] are shown in
Figure 3.
The proposed electric model is a first order resistor-capacitor (RC) equivalent electric circuit that employs the thermodynamically stable open circuit voltage OCV, the ohmic resistance of the battery, and a RC circuit that describes the polarization of the battery caused by transfer, diffusion and other factors, see Equations (1) and (2) [
26].
This electric circuit is one of the most common equivalent circuit models applied in battery modelling [
27], which includes an OCV, a resistor and a RC network in series to forecast battery response at a particular SOC [
28]. However, since in real (LIB) applications all parameters vary as functions of working conditions (temperature, current rate) and battery usage history (degradation) [
28], multi-value parameters are usually applied such as in this case. For this purpose, an array of the values of the parameters at different conditions are saved, allowing a posterior lookup from a table, finding the appropriate value for each parameter and interpolating them at different conditions. For the parametrization of the resistor and the RC network, a pulse characterization test is performed at six different current rates (2 C, 1 C and 0.5 C at charge and discharge) as well as at three different room temperatures (10 °C, 25 °C and 45 °C), see
Table 3. The OCV values are also taken at those three different temperatures, profiting from the rest times between different pulses of the applied pulse characterization test.
On the other hand, the proposed thermal model is a 1D RCR equivalent thermal circuit that employs the thermal behaviour of the battery as a first-order impedance (
) [
29] and the cooling as a thermal resistance (
) (Equations (4)–(6)). The capacitive response (
) is linked to the specific heat capacity of the battery and the resistive response (
) is linked to the inner thermal conductivity of the battery. This model is built under the following simplifications and assumptions [
30]:
- -
The heat is generated at just one point (1D).
- -
The thermal properties of the battery are completely homogeneous all along the battery.
- -
All the cells have the same temperature (no heat transfer between cells).
- -
The physical properties of the battery are independent of the temperature.
- -
The battery experiences only convection cooling.
The parameters of the model are calculated by applying three specific thermal tests. Firstly, the specific heat capacity is calculated using the energy conservation Equation (7) on the Thermal Hazard Technology (THT) heat capacity protocol defined in
Table 4. Then, the entropic factor of the battery, which represents the evolution of the OCV at different temperatures considering different SOC, is modelled with the test described in
Table 5. Finally, the remaining thermal variables of the equivalent thermal circuit are obtained by fitting the equivalent thermal circuit equations on any performance test. In this case, the first part of the Hybrid Power Pulse Characterization [
4] test is taken: the 1C charge discharge.
2.3.2. Algorithm
The proposed EOL mapping algorithm is presented in Algorithm 1. It consists of searching the values of each of the selected HI that define the EOL event. In other words, it is designed to find the HIs that make the battery reach the EOL criterion. For that, the described electric-thermal model is simulated under certain use conditions related to the EOL criteria (under certain testing input).
| Algorithm 1. Top view algorithm of the proposed EOL mapping approach.
|
1:
2: for to do
3: for u to do
4:
5: end for
6:
7: end for |
Where
= Number of threshold points or evaluation points on the EOL map.
= () evaluation point or combination of the HI values under evaluation.
= End of Life threshold value at () evaluation point.
= Value vector of () Health Indicator.
= Generator of the evaluated numerical grid.
= Battery electric-thermal model adapted to the EOL criteria and the HIs.
= () End of Life criterion imposed by the application specifications.
= Number of HIs.
= Number of End of Life criteria.
= Test input of the model that allows the test of each EOL criterion. |
The selected use cases are both EV applications with a driving range as EOL criteria. Both have the same two HIs under evaluation: the capacity decrease and the resistance increase. Both algorithms perform the evaluation loop times, where is the number of combinations between the defined values of the selected HIs except for the pure ohmic resistance. In this case, only represents the number of capacity decrease values under evaluation ( in high-energy EV application and in high-power EV application).
Once is defined, the value of the pure ohmic resistance (the free parameter) is calculated. In order to simplify the proposed approach to calculate the pure ohmic resistance that defines the EOL event, we have stated the following hypotheses for the high-energy EV application:
- -
The polarization voltage and OCV do not change significantly with the increase of the pure ohmic resistance and thus are neglected.
- -
The pure ohmic resistance increases uniformly over the whole SOC range.
- -
The change in the heating of the cell due to the pure ohmic resistance increase does not significantly affect the voltage response of the cell and, thus, is neglected.
Considering these three hypotheses, the required resistance increase (
) that leads to overcome the minimum voltage threshold (
) is calculated at each loop iteration based on the electric equivalent circuit equations, see Equation (8).
Nonetheless, the third hypothesis cannot be assumed for a high-power EV application due to the effect the resistance has on the fast charge. In this scenario, firstly, the CC charge strategy (with CV phase if the requirements are met) is emulated in the simulation, and secondly, a way of finding iteratively the real EOL threshold is generated when integrating those fast charges.
For the first issue, a proportional integral (PI) controller that emulates the CC and CV (if the requirements are met) charge strategy is implemented, see pseudo-code in Algorithm 2. The PI controller’s parameters are adjusted manually, where the integral controller’s parameter is left dependent on the estimated pure ohmic resistance increase (
). The previous integral value (
) in the first iteration is made equal to Equation (9).
| Algorithm 2. PI controller algorithm used to control the CV phase on the fast charging process.
|
1:
2:
3:
4: if
5:
6: else if
7:
8: end if |
Where
= Charge current at Constant-Current (CC) phase.
= End of charge voltage, which is also the consign voltage.
= Estimated voltage with the model.
= Integral controller’s gain.
= Proportional controller’s gain.
= Charging current consign.
= Integral gain of the PI controller.
= Previous integral gain of the PI controller.
= Voltage difference between the estimated and the consign voltages.
|
For the second issue, firstly, it is assumed that the real resistance increase (
) is below a certain resistance increase (
). This resistance increase (
) is calculated based on the two stated hypotheses and by neglecting the effect of the resistance increase on the battery response, see Equation (8). Afterwards, a bisection method (a numerical method) is applied with a limit of iterations (
), see Algorithm 3.
| Algorithm 3. Bisection method used on the resistance increase calculation with fast charges.
|
1:
2: for to do
3:
4:
5: if
6:
7: else
8:
9: end if
10: end for
11: |
Where
= Number of iterations on the bisection method.
= Resistance increase value under study.
= Obtained SOC response of the battery under the I current profile.
|
3. Results and Discussion
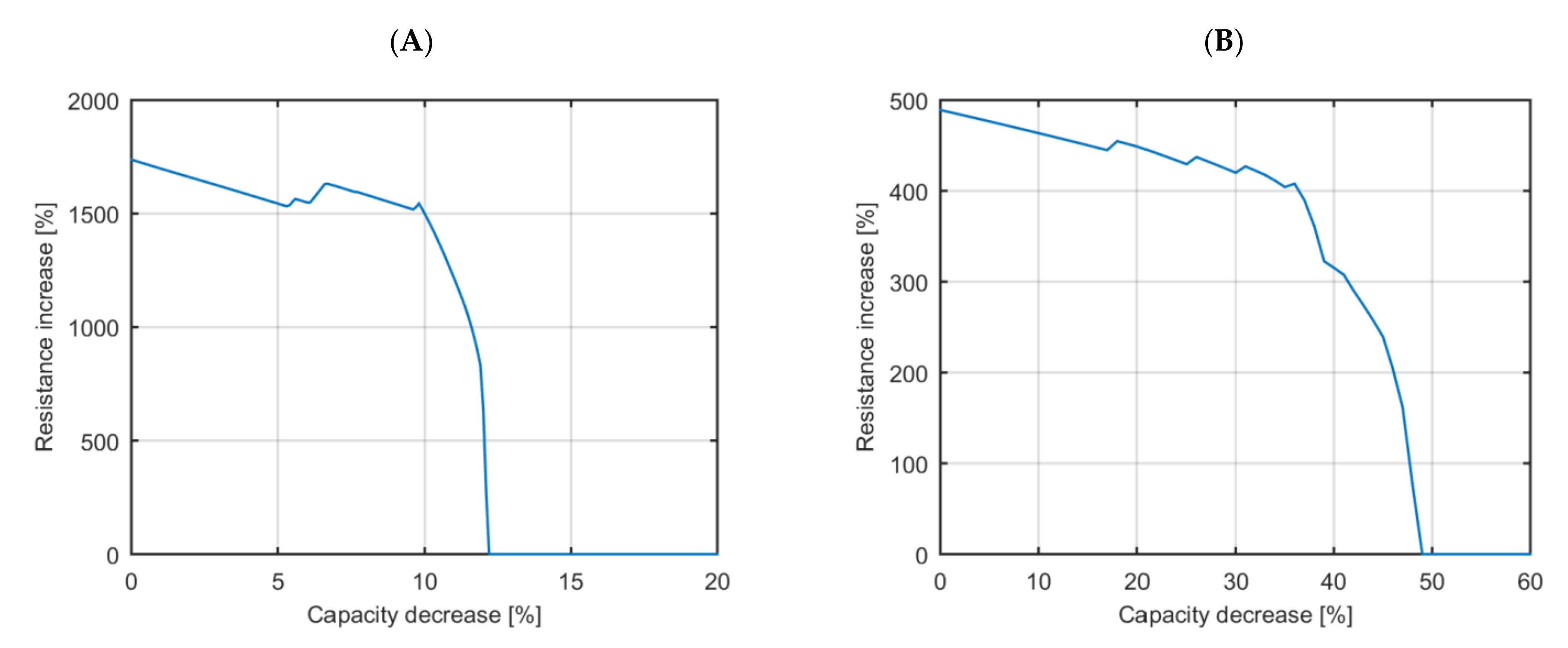
The EOL mapping algorithm has been applied to both use cases. The EOL map for the application with a high-energy requirement is displayed in
Figure 4A and the EOL map for the application with a high-power requirement is displayed in
Figure 4B.
The observed results in
Figure 4A show that the EOL event of the high-energy EV application is not reached with a capacity decrease up to 10% unless there is a resistance increase higher than 1500% (a 16 times bigger resistance than the initial one). Between capacity decrease values from 10 to 12.2%, the resistance increase that describes the EOL event decreases drastically from 1400 to 0% (to the resistance at the beginning of life). Batteries with capacity decrease values from 12.2% onwards cannot be used for this application.
The observed results in
Figure 4B show that the EOL event is not reached with a capacity decrease up to 41% unless there is a resistance increase higher than 200% (triple the value at the beginning of life). Between capacity decrease values of 41 to 49%, the required resistance to reach the EOL decreases to the value at the beginning of life (a resistance increase value of 0%). Batteries with capacity decrease values from 49% onwards cannot be used for this application.
The high-energy EV application applies a relatively small discharge current rate to the battery system (the mean current rate is around 0.2 C and there are current peaks of 1 C at most). In consequence, the voltage drop due to the pure ohmic resistance is small, even at relatively huge resistance increases, while 100% increase in resistance is considered already as the EOL threshold in current literature [
8,
9]. Besides, the selected high-energy LIB has a huge voltage difference between the minimum value and its nominal value, which is almost maintained until 5% SOC. In this case, the difference between these two voltages is more than 1V, which is a comparatively high margin to overcome with the voltage drop due to the battery’s pure ohmic resistance. Based on this, it is stated that the resistance does not significantly affect the EOL event of the evaluated high-energy application.
The EOL event of the high-power EV application is reached with significantly lower relative pure ohmic resistance values than in the high-energy application. The EOL event of the high-power EV application is reached with resistance increase values below 500% from the start (from the beginning of life) no matter the capacity decrease. In contrast, the EOL event of the high-energy EV application is reached with resistance increases below 500% at a significantly advanced state of degradation (with a capacity decrease of 12%).
The required resistance increase to reach the EOL drops drastically from a certain capacity decrease onwards. This phenomenon is especially evident in the high-energy EV application, where the EOL becomes defined from a combined 12% capacity decrease and 500% resistance increase to a combined 12.2% capacity decrease and 0% resistance increase (for a difference of 0.2% capacity decrease, there is a change of 500% of the required resistance increase to reach the EOL).
The high-power EV application applies relatively high discharge current rates (maximum discharge current peaks of 5 C) with repeated 7 min ultra-fast charges (the battery is charged at 4 C [
32]). The ultra-fast charge with a short duration is especially sensitive to the resistance increase. Besides, the voltage window of this high-power LIB is significantly smaller than that of the high-energy LIB as it requires lower voltage drops to reach the maximum and minimum voltage threshold. Based on this, it is stated that the EOL event on high-power EV applications must consider both the capacity decrease and the resistance increase.
Finally, it should be highlighted that these results are obtained neglecting any energy losses (additional or increased consumptions by EV components such as the battery thermal management system) or resistance increase from the upscaling of the battery to system level (additional resistance contribution from the connections, wires, power electronics, etc.). However, they significantly affect the real EOL threshold of the application. As a consequence, the obtained results are likely to suffer changes in the upscaling process (the form of the EOL threshold map will be the same; what changes is the initial value of each HI). Nonetheless, these results (that neglect the energy losses and resistance increases from the upscaling) can help to define the specifications of the battery system in terms of energy efficiency and total resistance in early battery system design steps.
4. Validation
The three hypotheses used to simplify the algorithm of the simulation environment in
Section 2.3.2 of this paper have been analysed and validated. The first hypothesis states that the polarization voltage and OCV do not change significantly with the increase of the pure ohmic resistance. The second hypothesis states that the resistance is increased uniformly over the whole SOC range. The third hypothesis states that the change in the heating of the cell due to the increase of the resistance increase does not significantly affect the voltage response of the cell. In addition, we have validated the obtained EOL threshold at cell level. The stated three hypotheses and the resultant EOL threshold have been validated only on the selected high-energy lithium ion battery because the high-power batteries have not been aged enough to generate the required data on any of the validations. The high-power battery was tested at accelerated aging conditions for more than 2 years but there is only a 5% performance decrease in the worst case, which is insufficiently low to validate the calculated EOL threshold.
4.1. First Hypothesis
The first hypothesis states that the polarization voltage and OCV does not change significantly with the increase of the pure ohmic resistance. To validate this, firstly, the OCVs of a fresh and of an aged cell were compared (
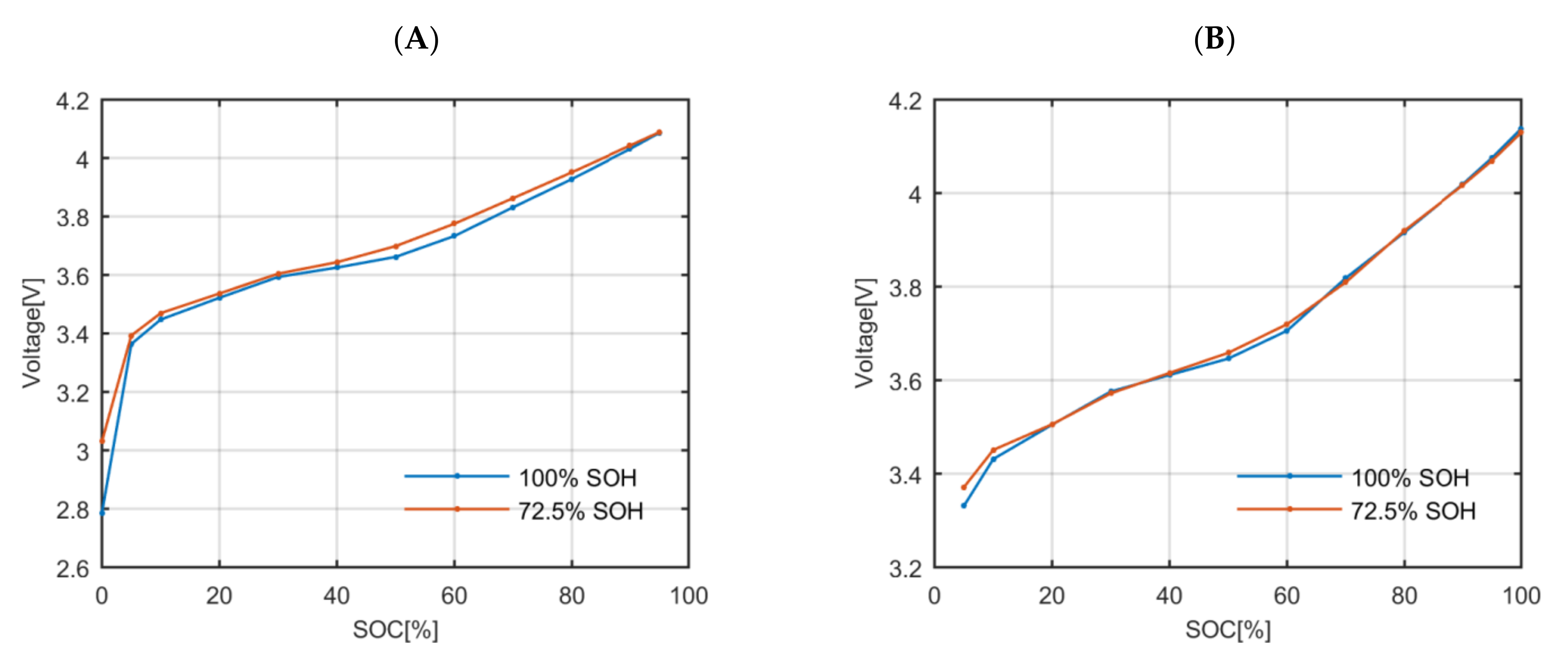
Figure 5). The relative capacity was considered to be the SOH itself. The aged and fresh cell have slightly different OCV profiles.
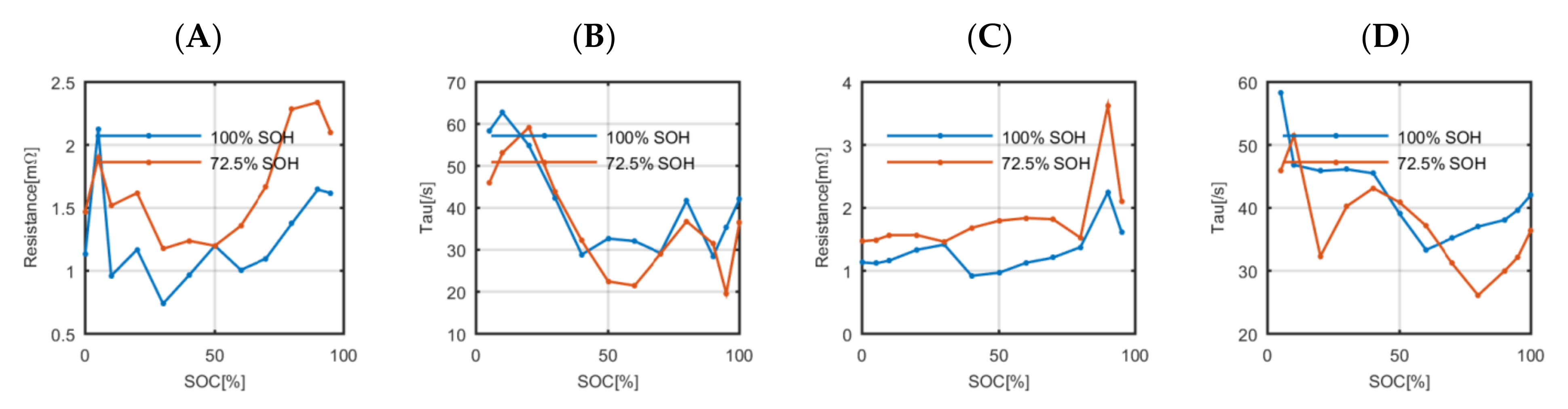
Secondly, the parameters that define the polarization impedance (the polarization resistance and the polarization time constant) of a fresh and an aged cell were compared (
Figure 6). The fresh and the aged polarization impedances have values of the same order. There are significant changes in some specific SOC values due to the degradation but also due to the uncertainty of the applied estimation process. However, all the values are between similar upper and lower boundaries, which suggests that the use of the polarization impedance values estimated on a fresh cell will not have a significant impact when simulating the voltage response of the aged cell using the polarization impedance values estimated at fresh state.
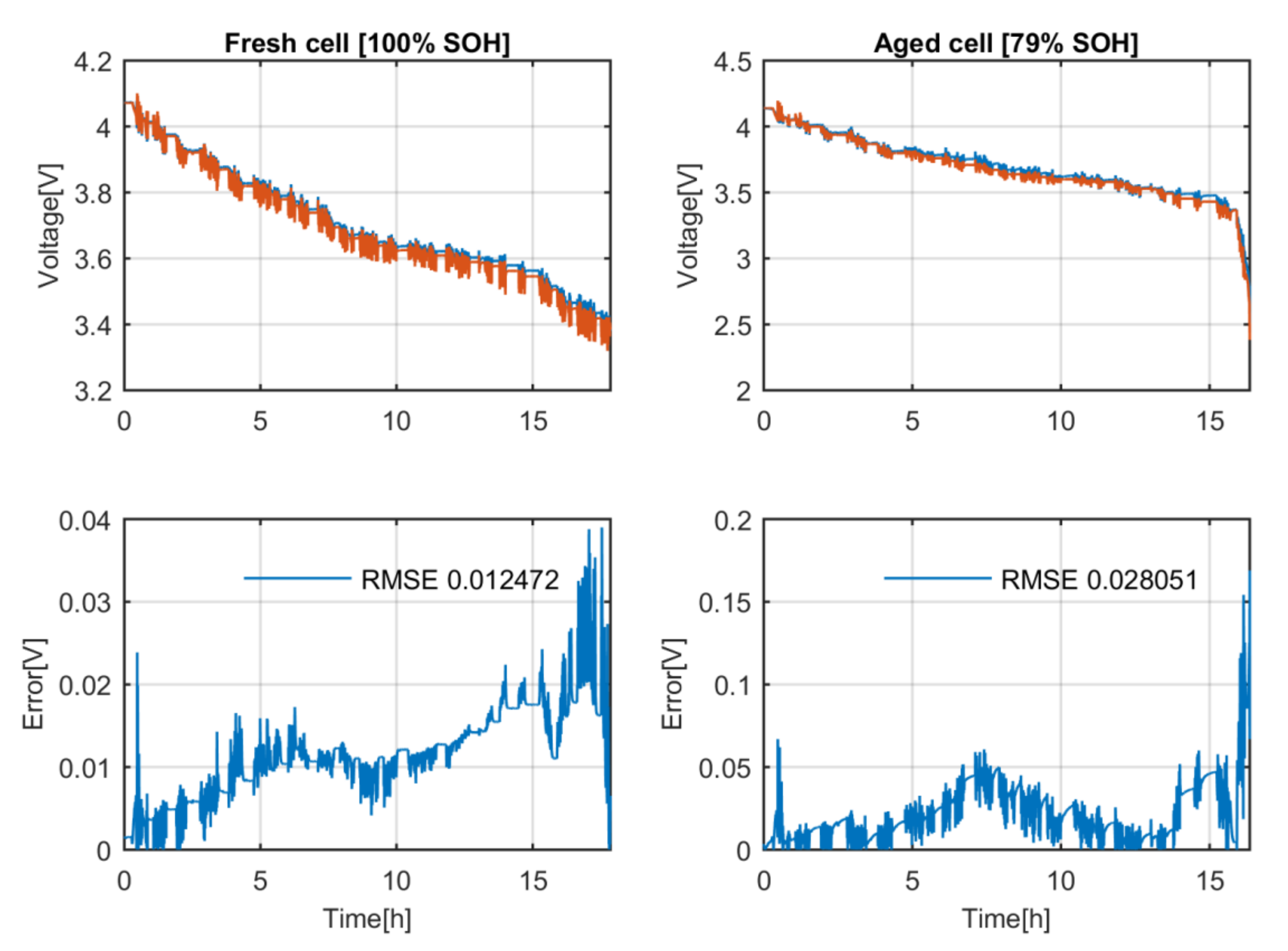
Thirdly, the correctness of the proposed model representing the behaviour of an aged battery with the measured OCV and polarization impedance values at fresh state is tested, see
Figure 7. The simulated aged cell voltage profile has a root mean square error (RMSE) of 0.028 V and the simulated fresh cell voltage profile has a RMSE of 0.012 V. There is a relevant difference in the committed errors, but on both cases the committed RMSE is below 30 mV, which is low enough to consider the proposed model accurate [
24].
To sum up, the model that simulates the behaviour of the battery can describe its voltage response at fresh and aged state with a similar accuracy even though the change in the OCV and polarization impedance due the aging is neglected. Therefore, this hypothesis is correct.
4.2. Second Hypothesis
The second hypothesis states that the resistance increases uniformly over the whole SOC range. In other words, a measured resistance increase at a SOC value is representative of the resistance increase over the whole SOC range. This hypothesis simplifies the integration of the relative resistance as a HI in the simulation.
The simulation calculates the required resistance increase to reach the EOL event. The calculated resistance increase is related with the resistance of the most critical SOC, and this SOC depends on the application specifications and battery characteristics. This SOC level/value can vary.
To validate this hypothesis, we evaluated the differences between the resistance increase for the most critical SOC values of the high-energy EV application (below 20%) and the SOC value that represents the selected HI (50% SOC). The results of three tested batteries with different SOH are shown in
Table 6.
The results show that the resistance does not increase at the same rate. The cell nº 3 shows a difference of 15.55% between the measured resistance increase values at 5% SOC and at 50% SOC. This second hypothesis is not correct. However, the results also show that the resistance increases monotonically over the whole SOC range. The pure ohmic resistance at every SOC increases due to the aging. In consequence, it is proposed to add the uncertainty related to the differences the pure ohmic resistance could have at different SOC values. The proposal consists of adding a confidence range of 20% to the resistance increase of the calculated EOL threshold, see
Section 4.4.
4.3. Third Hypothesis
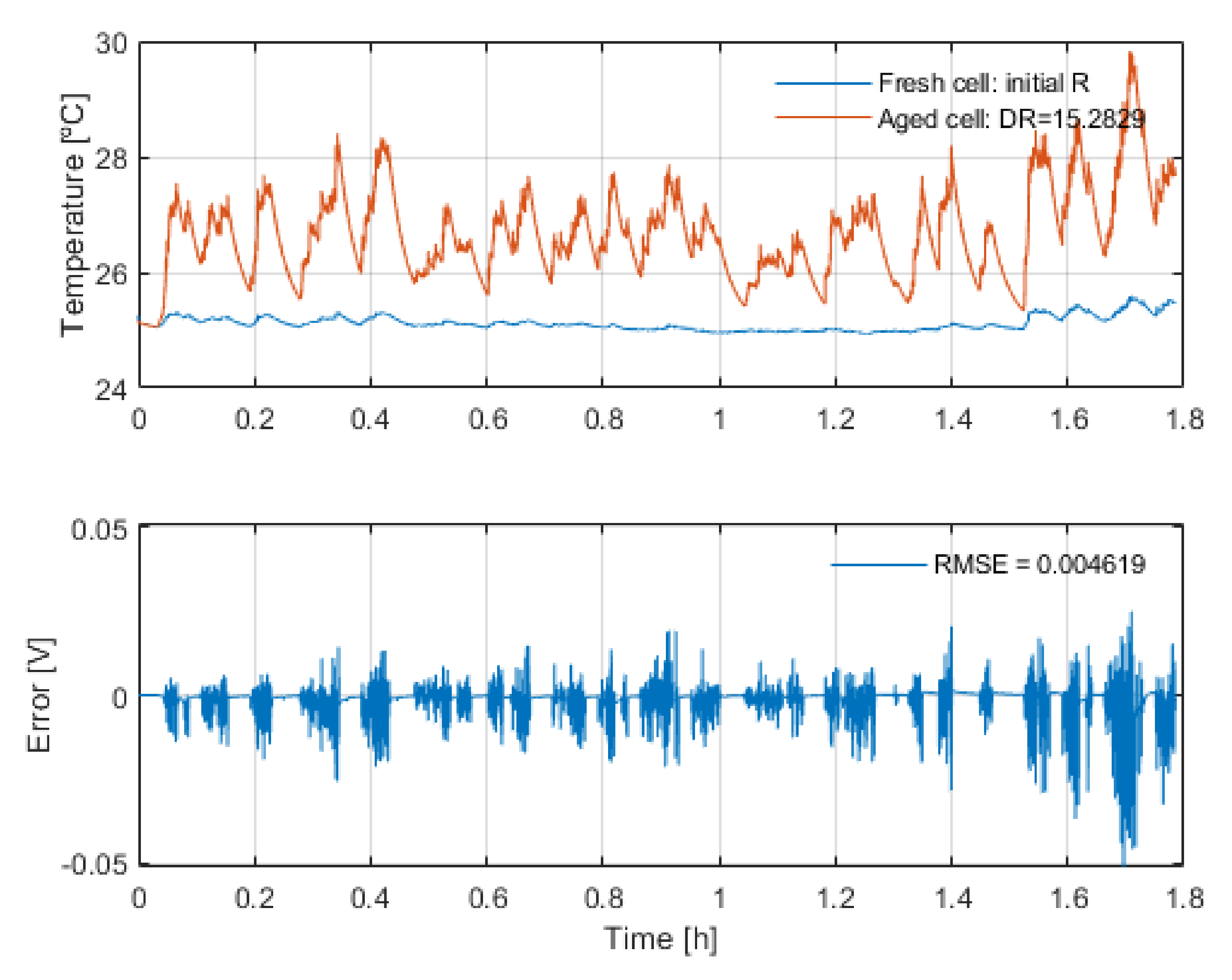
The third hypothesis states that the change in the heating of the cell due to the resistance increase does not significantly affect the voltage response of the cell. This hypothesis is applied only to the high-energy application use case and it is tested by simulations of the thermal and electric response of that high-energy battery with the obtained resistance increase, see
Figure 8.
The results show that even though the temperature increases by almost 5 °C due to the increase in the resistance, the voltage response of the battery remains practically unaffected; there is a maximum drift of 52 mV between both simulations. This voltage error could impact the EOL determination only when the voltage level is 52 mV above the end of discharge voltage. However, this scenario is given at a SOC value lower than 0.5%. This is why this hypothesis is considered correct.
4.4. High-Energy Application
The calculated EOL threshold itself is evaluated. The calculated EOL threshold of the high-energy EV application is validated at battery-cell level. We tested seven batteries with different degradation levels to determine whether they had already experienced the EOL event. The values for resistance increase and capacity decrease are shown for each cell in
Table 7.
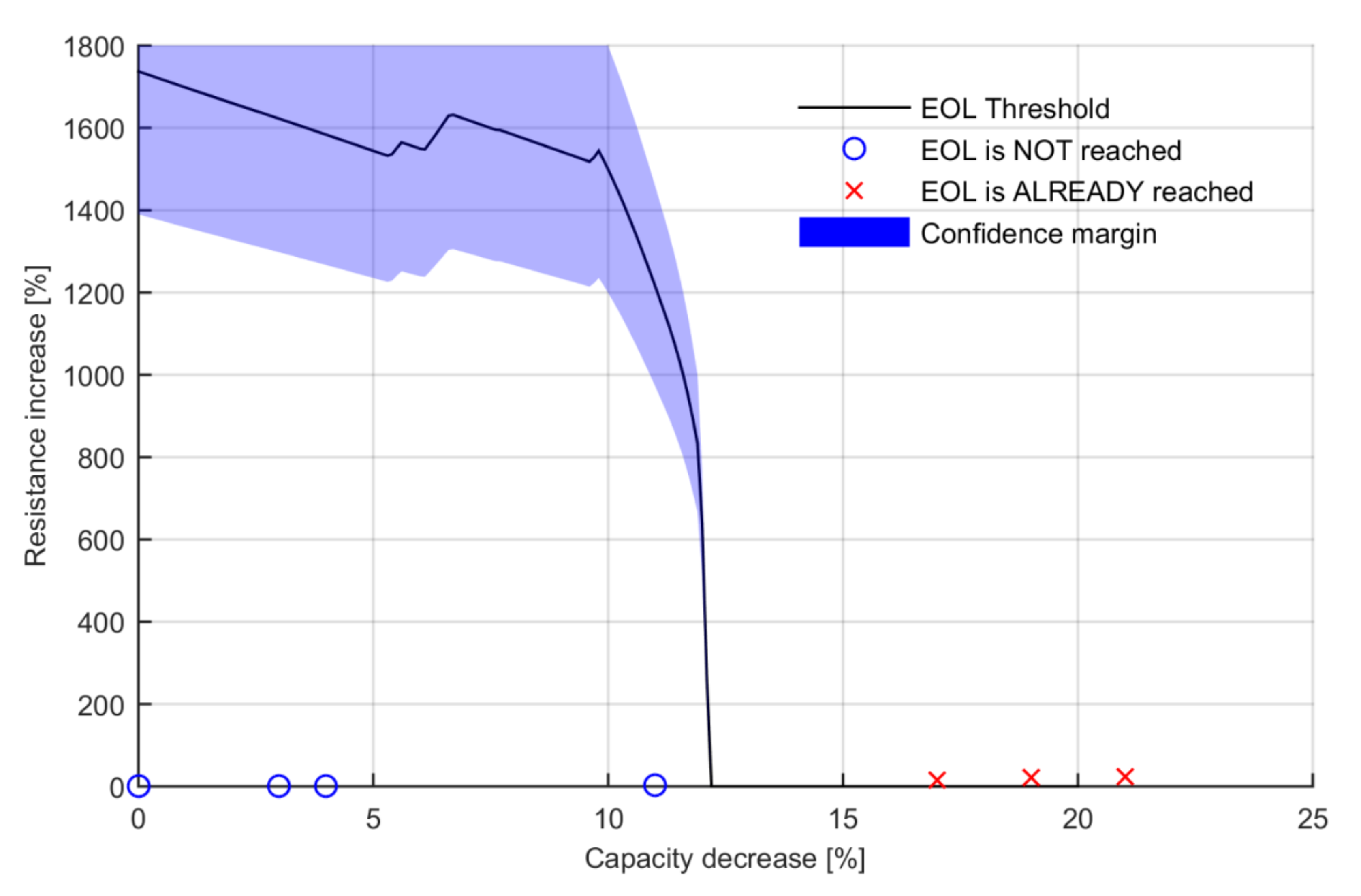
A downscaled power profile was applied to each of those seven batteries at a fully charged state. The test was conducted in a climatic chamber set at 25 °C. The batteries that had already experienced the EOL event were identified by checking that the battery was not able to complete the downscaled power profile without reaching the end of discharge voltage. The observations were added to the calculated EOL threshold, see
Figure 9.
The results show that the batteries that combine relative resistance and relative capacity values lower than the calculated EOL threshold have still not experienced the EOL event (nº 1, 2, 3 and 4) and that those that have higher values have already experienced it (nº 5, 6 and 7). This proves the veracity of the results and the viability of the defined methodology. Nonetheless, it can be observed that the tested batteries show low resistance increases if compared with the resistance increases required to reach the EOL event. In fact, the resistance and capacity evolution change at similar rates under normal operating conditions. The required resistance increase defined by the theoretical EOL threshold above 1000% is not expected to appear during normal degradation of the selected high-energy LIB. It is practically impossible to generate an aging path that leads to a battery with less than 10% capacity decrease and a resistance increase up to 1000%. This means that the relative capacity decrease is the dominating value defining the EOL event.
5. Conclusions
The proposal provides the tools to calculate an EOL threshold that captures the application and battery characteristics. In addition, the methodology allows the integration of different type of HIs in the EOL definition. It is no longer necessary to select between the relative capacity or the relative resistance to define the EOL threshold; we are able to use both or even add some additional ones since we can calculate exactly the combined values of the selected HIs that define the EOL.
The results have shown that the EOL is dependent on the battery characteristics as well as on the application specifications. The ranges of resistance increase and capacity decrease that lead to the EOL vary greatly between applications. We have seen that the commonly assumed fixed EOL threshold values lead to significant errors in defining the EOL event. The commonly assumed 80–70% relative capacity EOL threshold is too optimistic for the high-energy EV application (the EOL event happens before reaching 87%); and both, the 200% relative resistance and 80–70% relative capacity as EOL threshold are still far from defining the real EOL event in the high-power EV application (the EOL event is not reached even at a combination of 400% relative resistance and 60% relative capacity).
The validation of the calculated EOL threshold has shown that the proposed methodology could be used, firstly, to develop application-dependent sensitivity analysis of the different HIs; and secondly, to define battery system specifications in terms of energy efficiency and resistivity. Thanks to the calculated EOL threshold, we can quantify the specification of the maximum resistance and the minimum efficiency of the battery system due to the added wires, connection, electronics, etc.
As for the future, we will add safety considerations to the EOL criteria. The validation of the EOL threshold of the high-energy EV application has shown that its safety threshold is below its EOL threshold. However, it is not clear whether the high-power battery can reach the defined EOL threshold values without crossing the safety threshold; it has not been possible to age the high-power battery enough to cross the EOL threshold.
Author Contributions
Conceptualization, M.A., M.O. and E.M.; methodology, M.A. and M.O.; software, M.A.; validation, M.A.; writing—original draft preparation, M.A.; writing—review and editing, M.A., M.O., E.M., H.P., M.J. and B.G.; supervision, H.M.; project administration, I.C. All authors have read and agreed to the published version of the manuscript.
Funding
The iModBatt project has received funding from the European Union’s Horizon 2020 Programme for research and innovation under Grant Agreement No. 770054.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Zhang, J.; Lee, J. A review on prognostics and health monitoring of Li-ion battery. J. Power Sources 2011, 196, 6007–6014. [Google Scholar] [CrossRef]
- Gorjian, N.; Ma, L.; Mittinty, M.; Yarlagadda, P.; Sun, Y. A review on degradation models in reliability analysis. In Engineering Asset Lifecycle Management; Kiritsis, D., Emmanouilidis, C., Koronios, A., Mathew, J., Eds.; Springer: London, UK, 2009; pp. 369–384. [Google Scholar] [CrossRef]
- Lin, C.; Tang, A.; Wang, W. A Review of SOH Estimation Methods in Lithium-ion Batteries for Electric Vehicle Applications. Energy Procedia 2015, 75, 1920–1925. [Google Scholar] [CrossRef]
- ABC, US. USABC Electric Vehicle Battery Test Procedures Manual. Revision 2; Idaho National Engineering Laboratory: Idaho Falls, ID, USA, 1996. [Google Scholar]
- Groenewald, J.; Grandjean, T.; Marco, J. Accelerated energy capacity measurement of lithium-ion cells to support future circular economy strategies for electric vehicles. Renew. Sustain. Energy Rev. 2017, 69, 98–111. [Google Scholar] [CrossRef]
- Podias, A.; Pfrang, A.; Di Persio, F.; Kriston, A.; Bobba, S.; Mathieux, F.; Messagie, M.; Boon-Brett, L. Sustainability Assessment of Second Use Applications of Automotive Batteries: Ageing of Li-Ion Battery Cells in Automotive and Grid-Scale Applications. World Electr. Veh. J. 2018, 9, 24. [Google Scholar] [CrossRef]
- Kim, E.; Wu, B.; Shin, K.; Lee, J.; He, L. Adaptive Battery Diagnosis/Prognosis for Efficient Operation. In Proceedings of the 10th ACM International Conference on Future Energy Systems, Phoenix, AZ, USA, 25–28 June 2019; ACM: New York, NY, USA, 2019; Volume 10, pp. 150–159. [Google Scholar] [CrossRef]
- Grandjean, T.R.B.; Groenewald, J.; McGordon, A.; Widanage, W.D.; Marco, J. Accelerated Internal Resistance Measurements of Lithium-Ion Cells to Support Future End-of-Life Strategies for Electric Vehicles. Batteries 2018, 4, 49. [Google Scholar] [CrossRef]
- Ecker, M.; Gerschler, J.B.; Vogel, J.; Käbitz, S.; Hust, F.; Dechent, P.; Sauer, D.U. Development of a lifetime prediction model for lithium-ion batteries based on extended accelerated aging test data. J. Power Sources 2012, 215, 248–257. [Google Scholar] [CrossRef]
- Sauer, D.U.; Wenzl, H. Comparison of different approaches for lifetime prediction of electrochemical systems—Using lead-acid batteries as example. J. Power Sources 2008, 176, 534–546. [Google Scholar] [CrossRef]
- Lyu, D.; Niu, G.; Zhang, B.; Chen, G.; Yang, T. Lebesgue-Time–Space-Model-Based Diagnosis and Prognosis for Multiple Mode Systems. IEEE Trans. Ind. Electron. 2021, 68, 1591–1603. [Google Scholar] [CrossRef]
- Wenzl, H.; Baring-Gould, I.; Kaiser, R.; Liaw, B.Y.; Lundsager, P.; Manwell, J.; Ruddell, A.; Svoboda, V. Life prediction of batteries for selecting the technically most suitable and cost effective battery. J. Power Sources 2005, 144, 373–384. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; van Mierlo, J.; van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Wood, E.; Alexander, M.; Bradley, T.H. Investigation of battery end-of-life conditions for plug-in hybrid electric vehicles. J. Power Sources 2011, 196, 5147–5154. [Google Scholar] [CrossRef]
- Casals, L.C.; Rodríguez, M.; Corchero, C.; Carrillo, R.E. Evaluation of the End-of-Life of Electric Vehicle Batteries According to the State-of-Health. World Electr. Veh. J. 2019, 10, 63. [Google Scholar] [CrossRef]
- Ziegler, A.; Oeser, D.; Hein, T.; Montesinos-Miracle, D.; Ackva, A. Run to Failure: Aging of Commercial Battery Cells beyond Their End of Life. Energies 2020, 13, 1858. [Google Scholar] [CrossRef]
- Arrinda, M.; Oyarbide, M.; Macicior, H.; Muxika, E. Prognosis of the Remaining Useful Life of a Lithium Battery Based on a Data-Driven Method and Gaussian Processes. In Proceedings of the 30th International Electric Vehicle Symposium & Exhibition, Stuttgart, Germany, 9–11 October 2017; AVERE: Brussels, Belgium, 2017; pp. 1–12. [Google Scholar]
- Saha, B.; Poll, S.; Goebel, K.; Christophersen, J. An integrated approach to battery health monitoring using bayesian regression and state estimation. In Proceedings of the 2007 IEEE Autotestcon, Baltimore, MD, USA, 17–120 September 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 646–653. [Google Scholar] [CrossRef]
- Cui, Y.; Yang, J.; Du, C.; Zuo, P.; Gao, Y.; Cheng, X.; Ma, Y.; Yin, G. Prediction Model and Principle of End-of-Life Threshold for Lithium Ion Batteries Based on Open Circuit Voltage Drifts. Electrochim. Acta 2017, 255, 83–91. [Google Scholar] [CrossRef]
- Goebel, K.; Daigle, M.; Saxena, A.; Sankararaman, S.; Roychoudhury, I.; Celaya, J. Prognostics: The Science of Prediction; Createspace Independent Publishing Platform: Scotts Valley, CA, USA, 2017. [Google Scholar]
- iModBatt Consortium. Industrial Modular Battery Pack Concept Addressing High Energy Density, Environmental Friendliness, Flexibility and Cost Efficiency for Automotive Applications. 2020. Available online: https://cidetec.es/imodbatt/en/ (accessed on 24 July 2020).
- Popp, H.; Zhang, N.; Jahn, M.; Arrinda, M.; Ritz, S.; Faber, M.; Sauer, D.U.; Azais, P.; Cendoya, I. Ante-mortem analysis, electrical, thermal, and ageing testing of state-of-the-art cylindrical lithium-ion cells. Ante-Mortem-Analyse sowie elektrische, thermische und Alterungstests von State-of-the-Art zylindrischen Lithi-um-Ionen-Zellen. e & i Elektrotechnik Inf. 2020, 137, 169–176. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Liaw, B.; Bor, Y. Cell degradation in commercial LiFePO4 cells with high-power and high-energy designs. J. Power Sources 2014, 258, 408–419. [Google Scholar] [CrossRef]
- Qiu, S.; Chen, Z.; Masrur, M.A.; Murphey, Y.L. Battery hysteresis modeling for state of charge estimation based on Extended Kalman Filter. In Proceedings of the 6th IEEE Conference on Industrial Electronics and Applications, Beijing, China, 21–23 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 184–189. [Google Scholar] [CrossRef]
- Damay, N.; Forgez, C.; Bichat, M.-P.; Friedrich, G. Thermal modeling of large prismatic LiFePO 4 /graphite battery. Coupled thermal and heat generation models for characterization and simulation, version hal-01500605. J. Power Sources 2017, 283, 37–45. [Google Scholar] [CrossRef]
- Shen, P.; Ouyang, M.; Lu, L.; Li, J.; Feng, X. The Co-estimation of State of Charge, State of Health, and State of Function for Lithium-Ion Batteries in Electric Vehicles. IEEE Trans. Veh. Technol. 2018, 67, 92–103. [Google Scholar] [CrossRef]
- Watrin, N.; Blunier, B.; Miraoui, A. Review of adaptive systems for lithium batteries State-of-Charge and State-of-Health estimation. In Proceedings of the 2012 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 18–20 June 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, M.; Rincon-Mora, G. Accurate Electrical Battery Model Capable of Predicting Runtime and I–V Performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Forgez, C.; Do, D.V.; Friedrich, G.; Morcrette, M.; Delacourt, C. Thermal modeling of a cylindrical LiFePO4/graphite lithium-ion battery. J. Power Sources 2010, 195, 2961–2968. [Google Scholar] [CrossRef]
- Maleki, H.; Al Hallaj, S.; Selman, J.R.; Dinwiddie, R.B.; Wang, H. Thermal Properties of Lithium-Ion Battery and Components. J. Electrochem. Soc. 2019, 146, 947–954. [Google Scholar] [CrossRef]
- Thermal Hazard Technology. EV+ Accelerating Rate Calorimeter. Available online: https://www.thermalhazardtechnology.com/battery-products/ev-plus-accelerating-rate-calorimeter (accessed on 26 August 2020).
- Daigle, J.-C.; Asakawa, Y.; Beaupré, M.; Gariépy, V.; Vieillette, R.; Laul, D.; Trudeau, M.; Zaghib, K. Boosting Ultra-Fast Charge Battery Performance: Filling Porous nanoLi4Ti5O12 Particles with 3D Network of N-doped Carbons. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
High-energy application profile: voltage response and the SOC evolution of the battery.
Figure 1.
High-energy application profile: voltage response and the SOC evolution of the battery.
Figure 2.
High-Power application profile: voltage response and the SOC evolution of the battery.
Figure 2.
High-Power application profile: voltage response and the SOC evolution of the battery.
Figure 3.
(a) Equivalent electric model; (b) Equivalent thermal model.
Figure 3.
(a) Equivalent electric model; (b) Equivalent thermal model.
Figure 4.
The obtained EOL map in terms of the resistance increase and the capacity decrease on (A) the high-energy electric vehicle application and (B) the high-power electric vehicle application.
Figure 4.
The obtained EOL map in terms of the resistance increase and the capacity decrease on (A) the high-energy electric vehicle application and (B) the high-power electric vehicle application.
Figure 5.
The OCV values at fresh state and aged state of the high-energy battery. (A) is the charge OCV profile and (B) is the discharge OCV profile.
Figure 5.
The OCV values at fresh state and aged state of the high-energy battery. (A) is the charge OCV profile and (B) is the discharge OCV profile.
Figure 6.
Charge transfer impedance at fresh state and aged state of the high-energy battery at the whole SOC range. (A) is the charge transfer resistance; (B) is the charge Time constant (τ); (C) is the discharge transfer resistance and (D) is the discharge Tau.
Figure 6.
Charge transfer impedance at fresh state and aged state of the high-energy battery at the whole SOC range. (A) is the charge transfer resistance; (B) is the charge Time constant (τ); (C) is the discharge transfer resistance and (D) is the discharge Tau.
Figure 7.
Difference between the estimated voltage and the measured one at fresh state and aged state of the high-energy battery.
Figure 7.
Difference between the estimated voltage and the measured one at fresh state and aged state of the high-energy battery.
Figure 8.
Above, the temperature profiles with the high-energy application initial resistance and EOL resistance are shown. Below, the error generated by those two temperature profiles when simulating the voltage response with the EOL resistance is displayed.
Figure 8.
Above, the temperature profiles with the high-energy application initial resistance and EOL resistance are shown. Below, the error generated by those two temperature profiles when simulating the voltage response with the EOL resistance is displayed.
Figure 9.
Validation of the EOL mapping of the high-energy application. The blue circles represent the batteries that have fulfilled the operation profile and the red x symbols are the ones that have not fulfilled the operation profile.
Figure 9.
Validation of the EOL mapping of the high-energy application. The blue circles represent the batteries that have fulfilled the operation profile and the red x symbols are the ones that have not fulfilled the operation profile.
Table 1.
High-Energy battery specifications.
Table 1.
High-Energy battery specifications.
| Item | Specification |
|---|
| Nominal capacity | 54 [Ah] |
| Maximum voltage | 4.2 [V] |
| Minimum voltage | 2.5 [V] |
| Nominal voltage | 3.65 [V] |
| Standard charge current | 54 [A] |
| Standard discharge current | 54 [A] |
| Nominal resistance | 0.65 [mΩ] |
Table 2.
High-power battery specifications.
Table 2.
High-power battery specifications.
| Item | Specification |
|---|
| Nominal capacity | 23 [Ah] |
| Maximum voltage | 2.7 [V] |
| Minimum voltage | 1.5 [V] |
| Nominal voltage | 2.3 [V] |
| Fast charge current | 115 [A] |
| Fast discharge current | 115 [A] |
| Nominal resistance | 0.6 [mΩ] |
Table 3.
Pulse characterization test used on the parametrization of the equivalent electric circuit at a certain current Ia and at a certain temperature Ta.
Table 3.
Pulse characterization test used on the parametrization of the equivalent electric circuit at a certain current Ia and at a certain temperature Ta.
| Step | Action | Mode | Conditions | Comments | Current | Temp. |
|---|
| 1 | Rest | - | 1 h | | | Ta |
| 2 | Charge | CC-CV | Vmax@0.05C | | Ia |
| 3 | Rest | - | 1 h | | |
| 4 | Discharge | CC-CV | Vmin@0.05C | Capacity measurement | Ia |
| 5 | Rest | - | 1 h | | |
| 6 | Start cycle | | | Pulse test, charge, start | |
| 7 | Rest | - | 1 h | OCV measurement | |
| 8 | Charge | - | 60s@not 100% SoC | Charge Pulse. Resistance estimation | Ia |
| 9 | Rest | - | 10 min | | |
| 10 | Charge | - | 10%SOC | Set SOC: 10,20,…,80,90 | |
| 11 | End cycle | | | | |
| 12 | Charge | CC-CV | Vmax@0.05C | | Ia |
| 13 | Start cycle | | | Pulse test, discharge, start | |
| 14 | Rest | - | 1 h | OCV measurement | |
| 15 | Discharge | - | 60s@not 0% SOC | Discharge Pulse. Resistance estimation | Ia |
| 16 | Rest | - | 10 min | | |
| 17 | Discharge | - | 10%SOC | Set SOC: 90,80,…,20,10 | |
| 18 | End cycle | | | | |
| 19 | Discharge | CC-CV | Vmin@0.05C | | Ia |
| 20 | Rest | - | 1 h | | |
| 21 | Charge | - | 30%SOC | Charge to 30% | Ia |
Table 4.
Specific heat capacity test.
Table 4.
Specific heat capacity test.
| Step | Comments |
|---|
| 1 | Calibration of the Accelerating Rate Calorimeter (ACR) [31] according to mass and battery volume |
| 2 | Joint assembly of sandwich type analysis (battery-thermal blanket-battery) |
| 3 | Heat generation according to THT (5–10 mW/gr and 7.75 W/m2 max.) |
| 4 | Adiabatic environment generation (Heaters ARC) |
| 5 | Measuring dT/dt stable area (30 °C and 50 °C) |
Table 5.
Entropic factor tests.
Table 5.
Entropic factor tests.
| Step | Action | Value | End Conditions | Comments |
|---|
| 1 | Discharge | 1C | Vmin | (* initial 24 h pause at 0% and 100% SOC. The rest SOC rest 2 h) |
| 2 | Charge | 1C | % SOC desired |
| 3 | Pause | - | * 24/2 h |
| 4 | Set temp | −20 °C | - |
| 5 | Pause | - | 2 h |
| 6 | Set temp | −10 °C | - |
| 7 | Pause | - | 2 h |
| 8 | Set temp | 0 °C | - |
| 9 | Pause | - | 2 h |
| 10 | Set temp | 10 °C | - |
| 11 | Pause | - | 2 h |
| 12 | Set temp | 20 °C | - |
| 13 | Pause | - | 2 h |
| 14 | Set temp | 30 °C | - |
| 15 | Pause | - | 2 h |
| 16 | Set temp | 40 °C | - |
| 17 | Pause | - | 2 h |
| 18 | Set temp | 50 °C | - |
| 19 | Pause | - | 2 h |
| 20 | Set temp | 60 °C | - |
| 21 | Pause | - | 2 h |
Table 6.
Pure ohmic resistance homogeneity at different SOH of the High-Energy battery.
Table 6.
Pure ohmic resistance homogeneity at different SOH of the High-Energy battery.
| Cell | ΔSOH | ΔR at 5% SOC | ΔR at 10% SOC | ΔR at 20% SOC | ΔR at 50% SOC |
|---|
| Nº 1 | 11% | 18.38% | 7.74% | 11.47% | 15.84% |
| Nº 2 | 18% | 22.34% | 25.63% | 30.25% | 33.49% |
| Nº 3 | 21% | 24.48% | 25.81% | 33.17% | 40.03% |
Table 7.
Values of Health Indicators of the tested batteries to validate the calculated EOL threshold of the High-Energy electric vehicle application.
Table 7.
Values of Health Indicators of the tested batteries to validate the calculated EOL threshold of the High-Energy electric vehicle application.
| Battery | Nº 1 | Nº 2 | Nº 3 | Nº 4 | Nº 5 | Nº 6 | Nº 7 |
|---|
| Capacity decrease | 0% | 3% | 4% | 11% | 17% | 19% | 21% |
| Resistance increase | 0% | 0% | 0% | 2% | 15% | 21% | 23% |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).