Generalized Distribution of Relaxation Times Analysis for the Characterization of Impedance Spectra
Abstract
1. Introduction
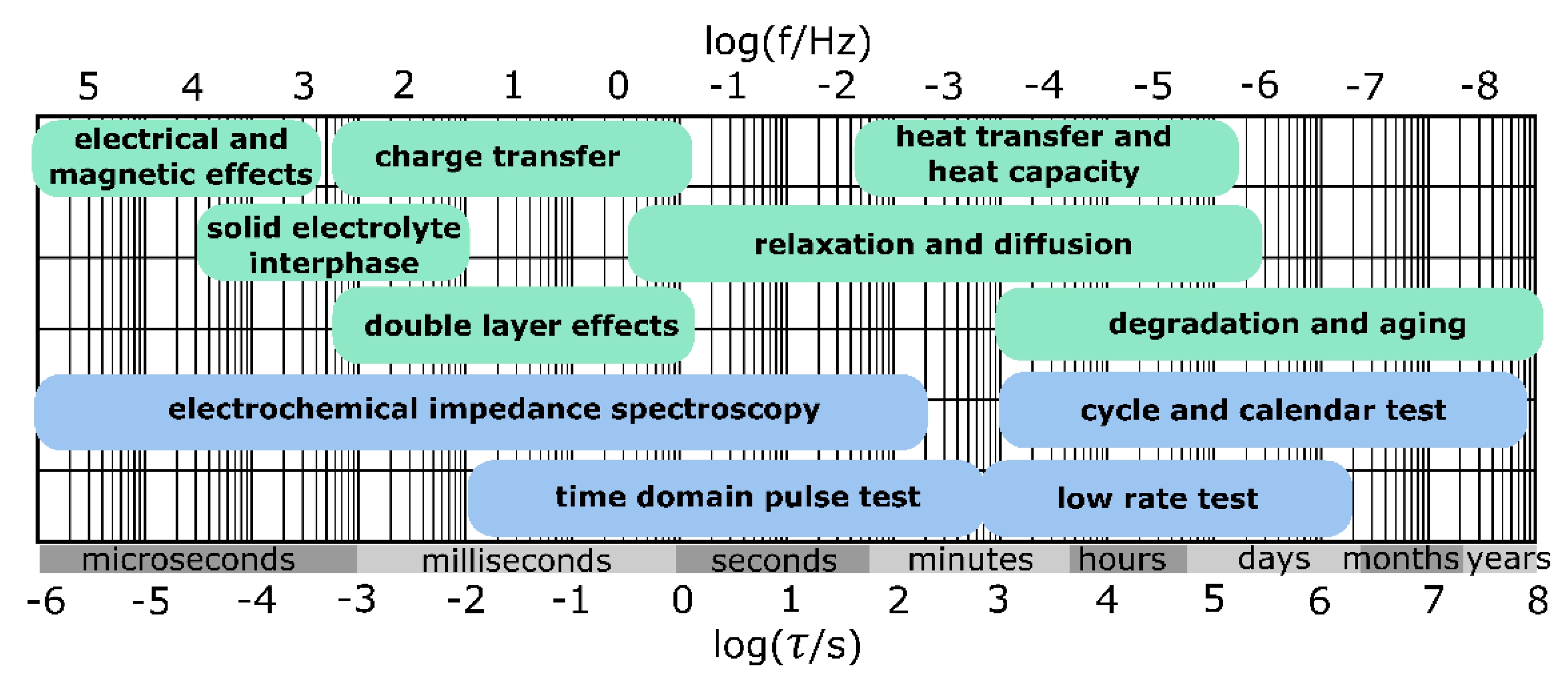
1.1. Generalized Impedance Spectroscopy
1.2. Distribution of Relaxation Times Analysis
1.3. Solving the Optimization Problem of DRT Using Regularization
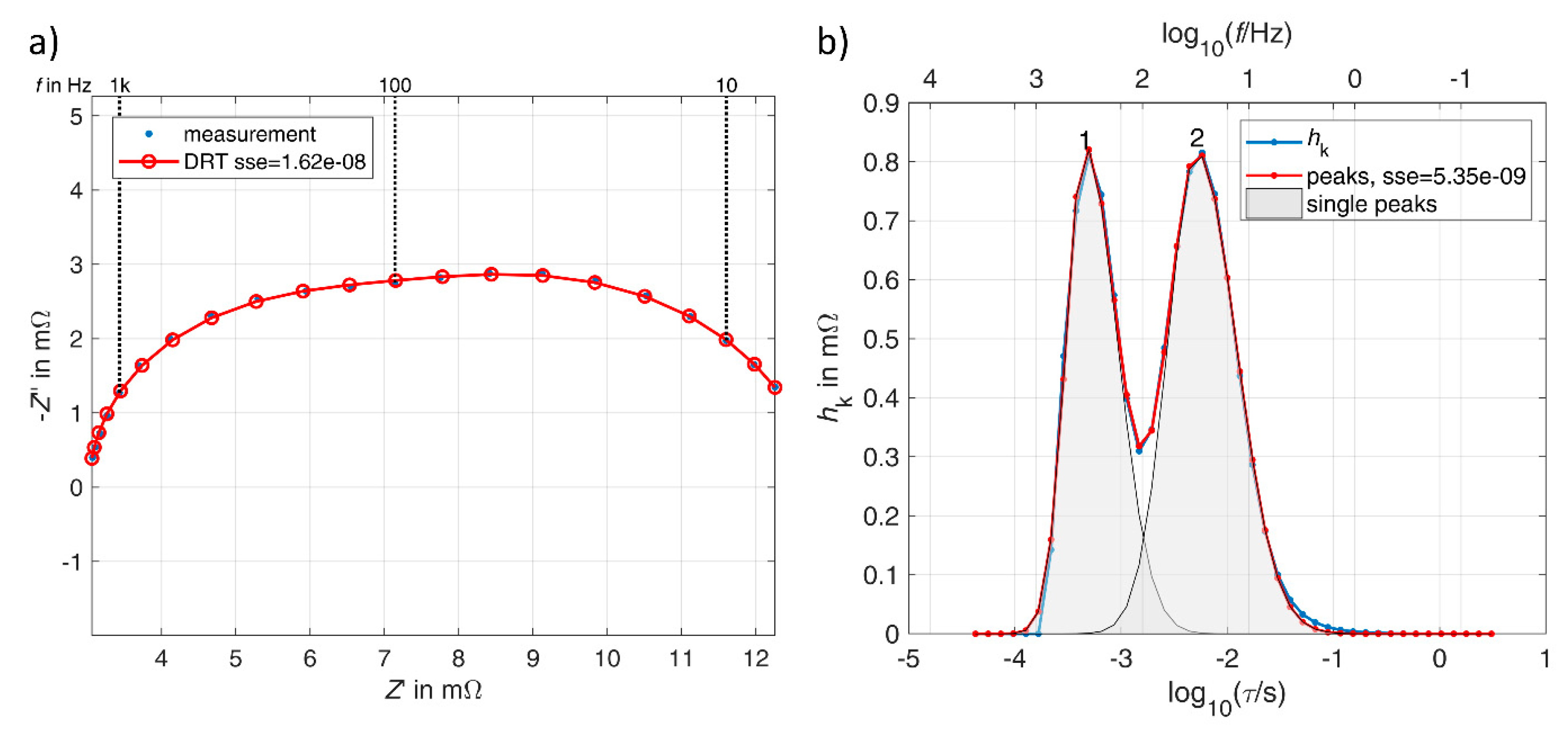
1.4. Analyzing Distribution Functions by Peak Analysis
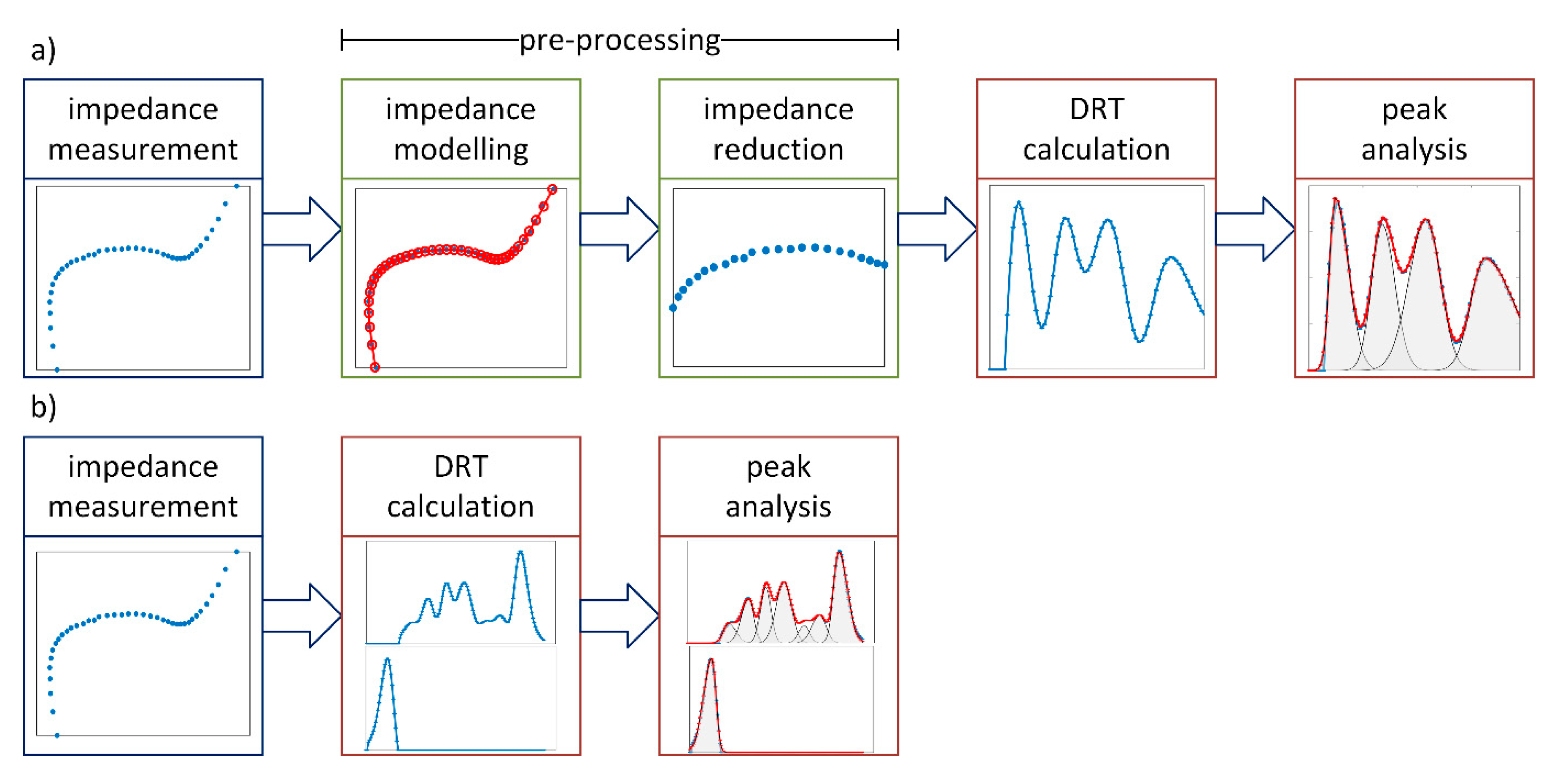
1.5. Discussion of Shortcomings of DRT
2. Generalized Distribution of Relaxation Times Analysis
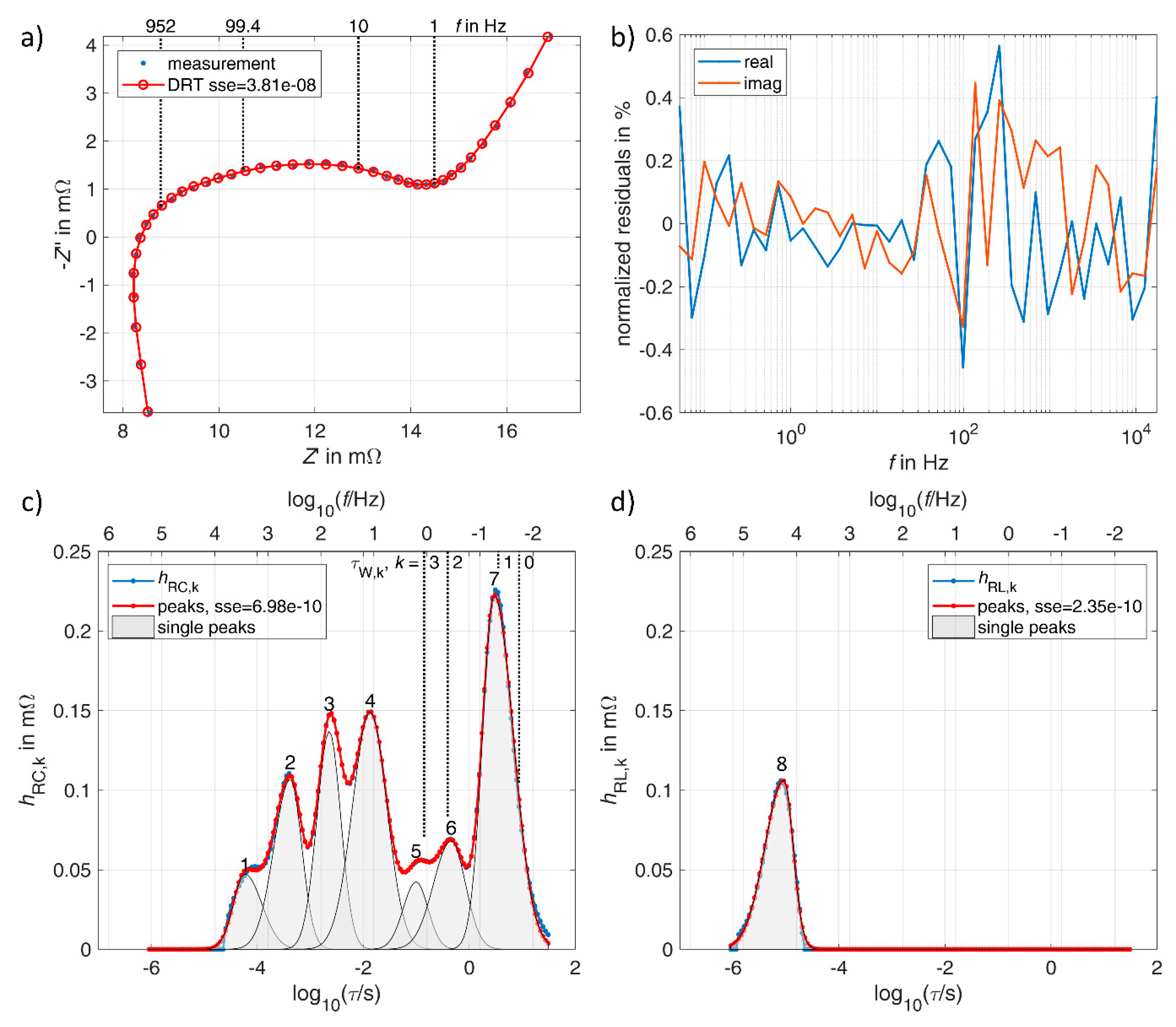
3. Results of GDRT Analysis
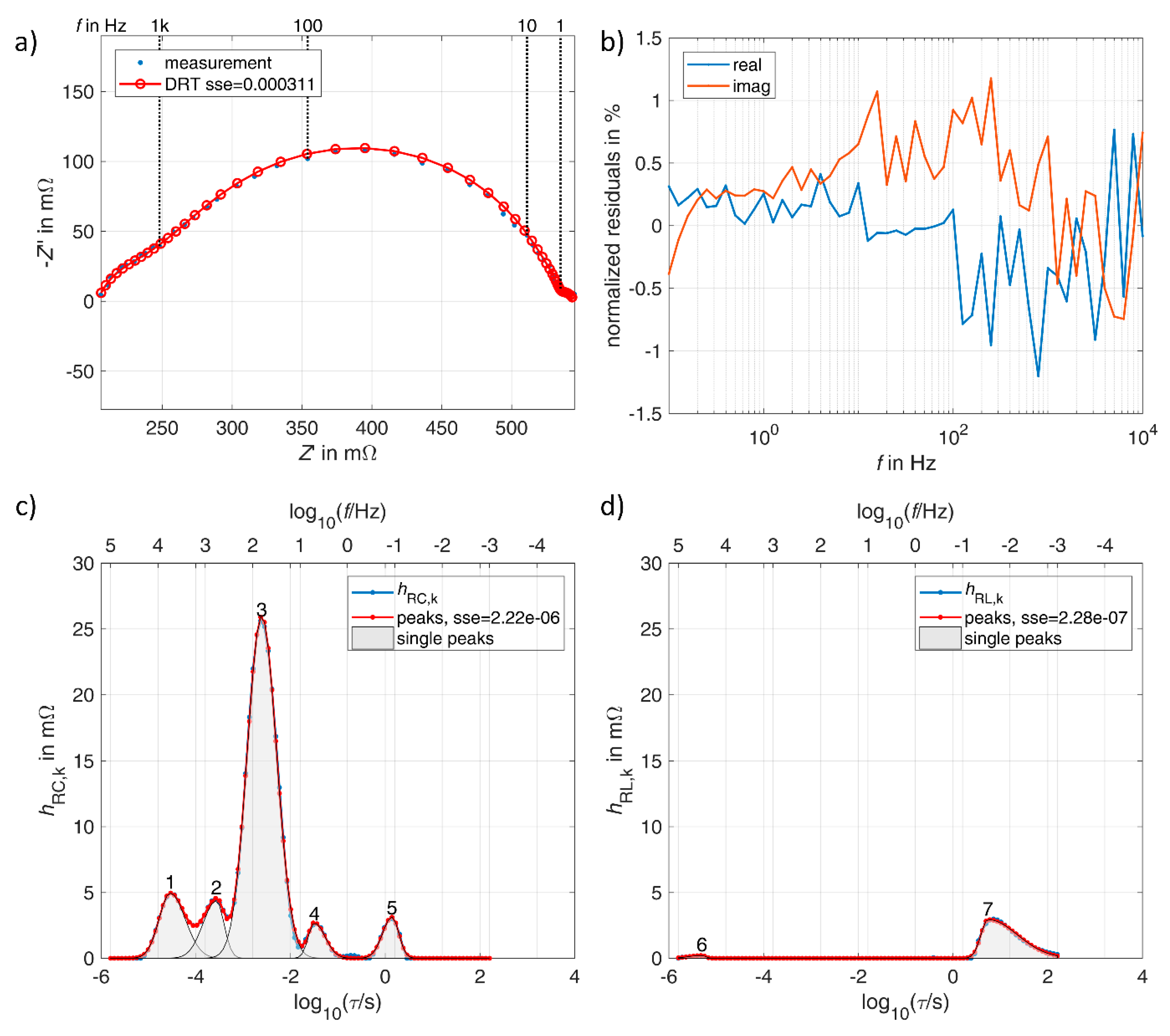
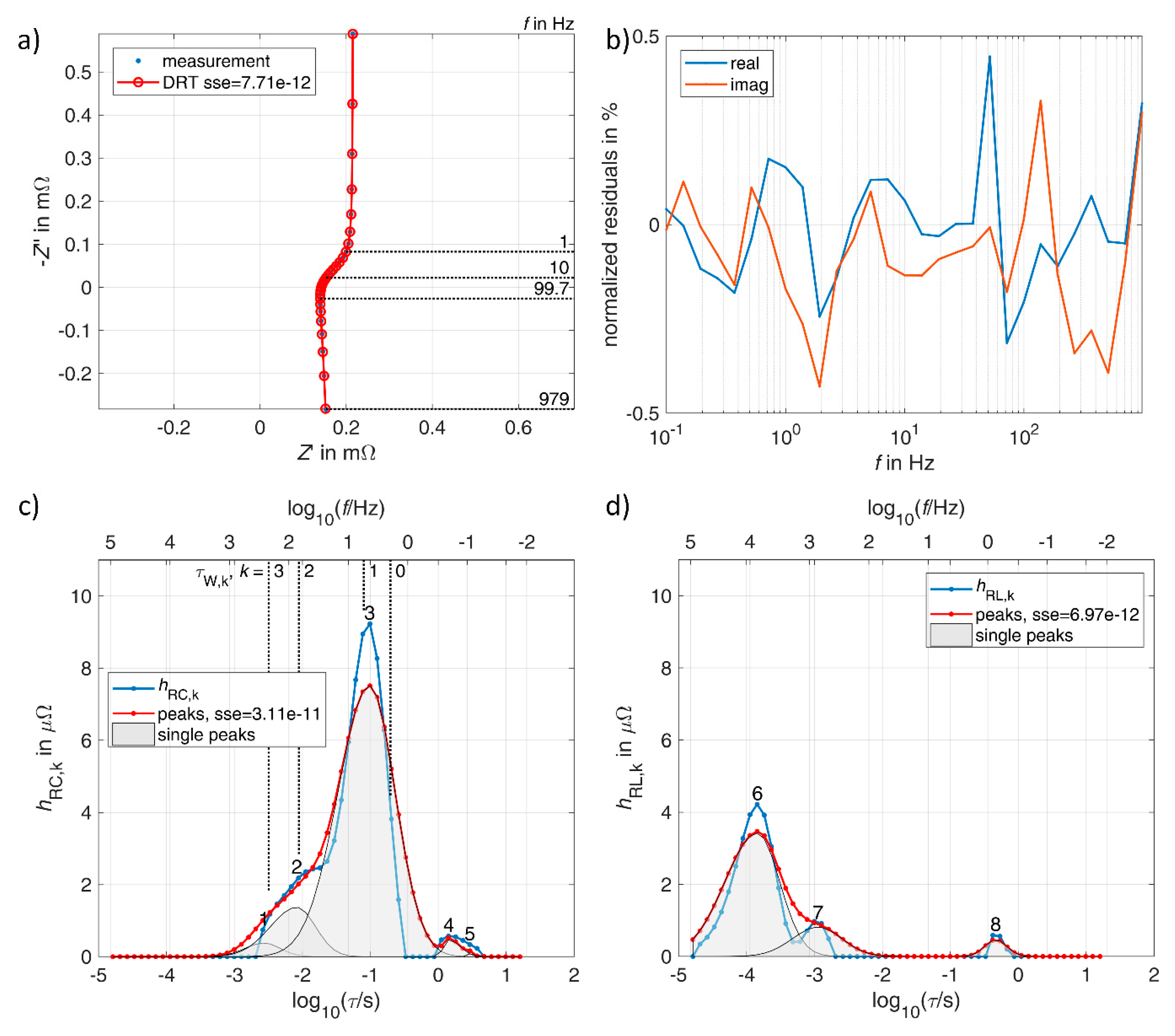
3.1. Lithium-Ion Battery
3.2. Vanadium Redox Flow Battery
3.3. Double Layer Capacitor
4. Summary
Funding
Acknowledgments
Conflicts of Interest
References
- Hagen, G.; Schulz, A.; Knörr, M.; Moos, R. Four-Wire Impedance Spectroscopy on Planar Zeolite/Chromium Oxide Based Hydrocarbon Gas Sensors. Sensors 2007, 7, 2681–2692. [Google Scholar] [CrossRef] [PubMed]
- Andreaus, B.; McEvoy, A.J.; Scherer, G.G. Analysis of performance losses in polymer electrolyte fuel cells at high current densities by impedance spectroscopy. Electrochim. Acta 2002, 47, 2223–2229. [Google Scholar] [CrossRef]
- Danzer, M.A.; Hofer, E.P. Analysis of the electrochemical behaviour of polymer electrolyte fuel cells using simple impedance models. J. Power Sources 2009, 190, 25–33. [Google Scholar] [CrossRef]
- Buller, S.; Thele, M.; De Doncker, R.W.A.A.; Karden, E. Impedance-based simulation models of supercapacitors and Li-ion batteries for power electronic applications. IEEE Trans. Ind. Appl. 2005, 41, 742–747. [Google Scholar] [CrossRef]
- Andre, D.; Meiler, M.; Steiner, K.; Wimmer, C.; Soczka-Guth, T.; Sauer, D.U. Characterization of high-power lithium-ion batteries by electrochemical impedance spectroscopy. I. Experimental investigation. J. Power Sources 2011, 196, 5334–5341. [Google Scholar] [CrossRef]
- Jossen, A. Fundamentals of battery dynamics. J. Power Sources 2006, 154, 530–538. [Google Scholar] [CrossRef]
- Tröltzsch, U.; Kanoun, O.; Tränkler, H.-R. Characterizing aging effects of lithium ion batteries by impedance spectroscopy. Electrochim. Acta 2006, 51, 1664–1672. [Google Scholar] [CrossRef]
- Schindler, S.; Bauer, M.; Petzl, M.; Danzer, M.A. Voltage relaxation and impedance spectroscopy as in-operando methods for the detection of lithium plating on graphitic anodes in commercial lithium-ion cells. J. Power Sources 2016, 304, 170–180. [Google Scholar] [CrossRef]
- Barsoukov, E.; Macdonald, J.R. Impedance Spectroscopy—Theory, Experiment and Applications, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Baumann, F.S.; Fleig, J.; Habermeier, H.-U.; Maier, J. Impedance spectroscopic study on well-defined (La,Sr)(Co,Fe)O3−δ model electrodes. Solid State Ion. 2006, 177, 1071–1081. [Google Scholar] [CrossRef]
- Fleig, J. Solid Oxide Fuel Cell Cathodes: Polarization Mechanisms and Modeling of the Electrochemical Performance. Annu. Rev. Mater. Res. 2003, 33, 361–382. [Google Scholar] [CrossRef]
- Heimerdinger, P.; Rosin, A.; Danzer, M.A.; Gerdes, T. Humidity-dependent through-plane impedance technique for proton conducting polymer membranes. Membranes 2019, 9, 62. [Google Scholar] [CrossRef] [PubMed]
- Fabregat-Santiago, F.; Bisquert, J.; Palomares, E.; Otero, L.; Kuang, D.; Zakeeruddin, S.M.; Grätzel, M. Correlation between Photovoltaic Performance and Impedance Spectroscopy of Dye-Sensitized Solar Cells Based on Ionic Liquids. J. Phys. Chem. C 2007, 111, 6550–6560. [Google Scholar] [CrossRef]
- Garland, J.E.; Crain, D.J.; Zheng, J.P.; Sulyma, C.M.; Roy, D. Electro-analytical characterization of photovoltaic cells by combining voltammetry and impedance spectroscopy: Voltage dependent parameters of a silicon solar cell under controlled illumination and temperature. Energy Env. Sci. 2011, 4, 485–498. [Google Scholar] [CrossRef]
- Bertemes Filho, P. Tissue Characterisation using an Impedance Spectroscopy Probe. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2002. Available online: https://www.researchgate.net/publication/268260305 (accessed on 28 September 2018).
- Kyle, U.G.; Bosaeus, I.; De Lorenzo, A.D.; Deurenberg, P.; Elia, M.; Gómez, J.M.; Lilienthal Heitmann, B.; Kent-Smith, L.; Melchior, J.-C.; Pirlich, M.; et al. Bioelectrical impedance analysis—Part I: Review of principles and methods. Clin. Nutr. 2004, 23, 1226–1243. [Google Scholar] [CrossRef] [PubMed]
- Bohuslavek, Z. Prediction of commercial classification values of beef carcasses by means of the bioelectrical impedance analysis (BIA). Czech J. Anim. Sci. 2003, 48, 243–250. [Google Scholar]
- Gabrielli, C.; Tribollet, B. A Transfer Function Approach for a Generalized Electrochemical Impedance Spectroscopy. J. Electrochem. Soc. 1994, 141, 1147–1157. [Google Scholar] [CrossRef]
- Grübl, D.; Janek, J.; Bessler, W.G. Electrochemical Pressure Impedance Spectroscopy (EPIS) as Diagnostic Method for Electrochemical Cells with Gaseous Reactants: A Model-Based Analysis. J. Electrochem. Soc. 2016, 163, 599–610. [Google Scholar] [CrossRef]
- Engebretsen, E.; Mason, T.J.; Shearing, P.R.; Hinds, G.; Brett, D.J.L. Electrochemical pressure impedance spectroscopy applied to the study of polymer electrolyte fuel cells. Electrochem. Commun. 2017, 75, 60–63. [Google Scholar] [CrossRef]
- Barsoukov, E.; Hwan Jang, J.; Lee, H. Thermal impedance spectroscopy for Li-ion batteries using heat-pulse response analysis. J. Power Sources 2002, 109, 313–320. [Google Scholar] [CrossRef]
- Schmidt, J.P.; Manka, D.; Klotz, D.; Ivers-Tiffée, E. Investigation of the thermal properties of a Li-ion pouch-cell by electrothermal impedance spectroscopy. J. Power Sources 2011, 196, 8140–8146. [Google Scholar] [CrossRef]
- Klotz, D.; Shai Ellis, D.; Dotan, H.; Rothschild, A. Empirical in operando analysis of the charge carrier dynamics in hematite photo anodes by PEIS, IMPS and IMVS. Phys. Chem. Chem. Phys. 2016, 18, 23438–23457. [Google Scholar] [CrossRef] [PubMed]
- Ivers-Tiffée, E.; Weber, A. Evaluation of electrochemical impedance spectra by the distribution of relaxation times. J. Ceram. Soc. Jpn. 2017, 125, 193–201. [Google Scholar] [CrossRef]
- Schichlein, H.; Müller, A.C.; Voigts, M.; Krügel, A.; Ivers-Tiffée, E. Deconvolution of electrochemical impedance spectra for the identification of electrode reaction mechanisms in solid oxide fuel cells. J. Appl. Electrochem. 2002, 32, 875–882. [Google Scholar] [CrossRef]
- Illig, J.; Ender, M.; Chrobak, T.; Schmidt, J.P.; Klotz, D.; Ivers-Tiffée, E. Separation of charge transfer and contact resistance in LiFePO4-cathodes by impedance modeling. J. Electrochem. Soc. 2012, 159, 952–960. [Google Scholar] [CrossRef]
- Schmidt, J.P.; Berg, P.; Schönleber, M.; Weber, A.; Ivers-Tiffée, E. The distribution of relaxation times as basis for generalized time-domain models for Li-ion batteries. J. Power Sources 2013, 221, 70–77. [Google Scholar] [CrossRef]
- Weiß, A.; Schindler, S.; Galbiati, S.; Danzer, M.A.; Zeis, R. Distribution of Relaxation Times Analysis of High-Temperature PEM Fuel Cell Impedance Spectra. Electrochim. Acta 2017, 230, 391–398. [Google Scholar] [CrossRef]
- Rosenbach, D.; Mödl, N.; Hahn, M.; Petry, J.; Danzer, M.A.; Thelakkat, M. Synthesis and Comparative Studies of Solvent-free Brush Polymer Electrolytes for Lithium Batteries. ACS Appl. Energy Mater. 2019. [Google Scholar] [CrossRef]
- Hahn, M.; Schindler, S.; Triebs, L.-C.; Danzer, M.A. Optimized Process Parameters for a Reproducible Distribution of Relaxation Times Analysis of Electrochemical Systems. Batteries 2019, 5, 43. [Google Scholar] [CrossRef]
- Tikhonov, A.N. On the stability of inverse problems. Dokl. Akad. Nauk SSSR 1943, 39, 195–198. [Google Scholar]
- Weese, J. A reliable and fast method for the solution of Fredholm integral equations of the first kind based on Tikhonov regularization. Comput. Phys. Commun. 1992, 69, 99–111. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Goncharsky, A.; Stepanov, V.; Yagola, A.G. Numerical Methods for the Solution of Ill-Posed Problems; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Lawson, C.L.; Hanson, R.J. Solving Least-Squares Problems; Prentice Hall: Upper Saddle River, NJ, USA, 1974; Chapter 23; p. 161. [Google Scholar]
- Boukamp, B.A.; Rolle, A. Analysis and Application of Distribution of Relaxation Times in Solid State Ionics. Solid State Ion. 2017, 302, 12–18. [Google Scholar] [CrossRef]
- Schindler, S.; Danzer, M.A. Influence of cell design on impedance characteristics of cylindrical lithium-ion cells: A model-based assessment from electrode to cell level. J. Energy Storage 2017, 12, 157–166. [Google Scholar] [CrossRef]
- Boukamp, B.A. Derivation of a Distribution Function of Relaxation Times for the (fractal) Finite Length Warburg. Electrochim. Acta 2017, 252, 154–163. [Google Scholar] [CrossRef]
- Schneider, J.; Zeis, R.; Danzer, M.A.; Roth, C. Employing DRT Analysis in VRFB: Towards Online Degradation Monitoring. In Proceedings of the Electrochemistry 2018, Ulm, Germany, 24–26 September 2018. [Google Scholar]
- Itagaki, M.; Suzuki, S.; Shitanda, I.; Watanabe, K.; Nakazawa, H. Impedance analysis on electric double layer capacitor with transmission line model. J. Power Sources 2007, 164, 415–424. [Google Scholar] [CrossRef]
- Yoo, H.D.; Jang, J.H.; Ryu, J.H.; Park, Y.; Oh, S.M. Impedance analysis of porous carbon electrodes to predict rate capability of electric double-layer capacitors. J. Power Sources 2014, 267, 411–420. [Google Scholar] [CrossRef]
- Schönleber, M.; Ivers-Tiffée, E. The Distribution Function of Differential Capacity as a new tool for analyzing the capacitive properties of Lithium-Ion batteries. Electrochem. Commun. 2015, 61, 45–48. [Google Scholar] [CrossRef]
| Physical Domain | Generalized Voltage (Intensive, Across Variable) | Generalized Current (Extensive, Through Variable) | Generalized Impedance (Transfer Function) |
|---|---|---|---|
| Electrical | Voltage | Current | Impedance |
| Electrostatic | Voltage | Dielectric flow | Dielectric impedance |
| Magnetostatic | Magnetic voltage | Magnetic flow | Magnetic resistance |
| Mechanical (translatory) | Force | Velocity | Mass |
| Mechanical (rotatory) | Torque | Angular velocity | Inertia |
| Hydro-mechanical | Pressure | Volume flow , Mass flow | Pneumatic impedance |
| Thermal conductivity | Temperature difference | Heat flow | Thermal impedance |
| Impedance Element | Parameter | Value |
|---|---|---|
| Ohmic resistance | ||
| RC element | ||
| ZARC element | ||
| Degree of Freedom | Variable |
|---|---|
| Definition of error and optimization function | |
| Modelling of impedance spectrum | |
| Exclusion of non-resistive-capacitive elements | |
| Number of time constants | |
| Min/max time constant | |
| Distribution of predefined time constants | |
| Choice of regularization parameter |
| Variable | Value | Variable | Value |
|---|---|---|---|
| Variable | Value | Variable | Value |
|---|---|---|---|
| Variable | Value | Variable | Value |
|---|---|---|---|
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danzer, M.A. Generalized Distribution of Relaxation Times Analysis for the Characterization of Impedance Spectra. Batteries 2019, 5, 53. https://doi.org/10.3390/batteries5030053
Danzer MA. Generalized Distribution of Relaxation Times Analysis for the Characterization of Impedance Spectra. Batteries. 2019; 5(3):53. https://doi.org/10.3390/batteries5030053
Chicago/Turabian StyleDanzer, Michael A. 2019. "Generalized Distribution of Relaxation Times Analysis for the Characterization of Impedance Spectra" Batteries 5, no. 3: 53. https://doi.org/10.3390/batteries5030053
APA StyleDanzer, M. A. (2019). Generalized Distribution of Relaxation Times Analysis for the Characterization of Impedance Spectra. Batteries, 5(3), 53. https://doi.org/10.3390/batteries5030053





