1. Introduction
Electrochemical impedance spectroscopy (EIS) is a well-known method applied since the 1970s [
1] for electrochemical power sources and their components including materials such as commercial battery cells [
2], single electrodes [
3,
4], experimental cells with reference electrodes [
5], solid oxide fuel cells (SOFCs) [
6], polymer membrane fuel cells (PEMFCs) [
7], separators, membranes or electrolytes [
8,
9]. In addition, the technique is used in other scientific fields, e.g., to obtain the bio impedance in medicine [
10] or biology.
The EIS provides the frequency-dependent impedance of an electrochemical system by applying a sinusoidal current, measuring the voltage response (galvanostatic EIS) or vice versa (potentiostatic EIS), and applying Ohm’s law. The impedance spectra are interpreted regarding their high-frequency inductive behavior [
11] caused by geometry, wiring and the test setup, their low-frequency diffusion behavior [
12] and mainly their interphase behavior. Numerous studies focus on battery impedance, e.g., correlating aging to changes in the impedance spectrum [
13] or explaining the relaxation behavior in graphite anodes [
14]. Analyzing the impedance without applying further techniques is complex, though. Effects overlap, processes are non-ideal, causing deviations between the expected and the measured spectra. Even the number of single processes cannot be obtained unambiguously. Therefore, the DRT became of interest in the 1990s [
1] and was applied first for SOFCs [
15,
16]. Later on, the DRT was adapted for the characterization of PEMFC and batteries [
2,
7,
17]. As the result of a mathematical transformation, the polarization contributions at predefined time constants of the investigated system are derived. Exemplary, in
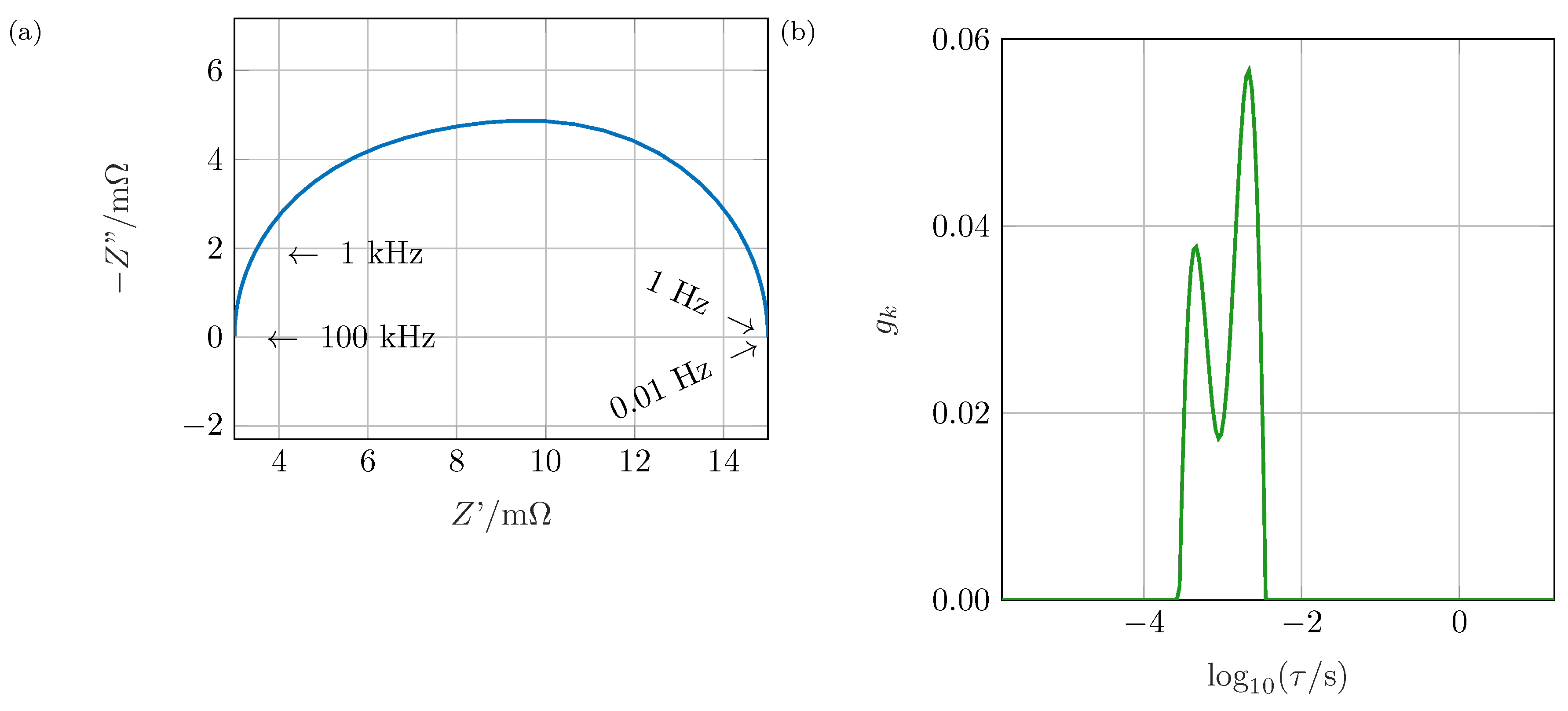
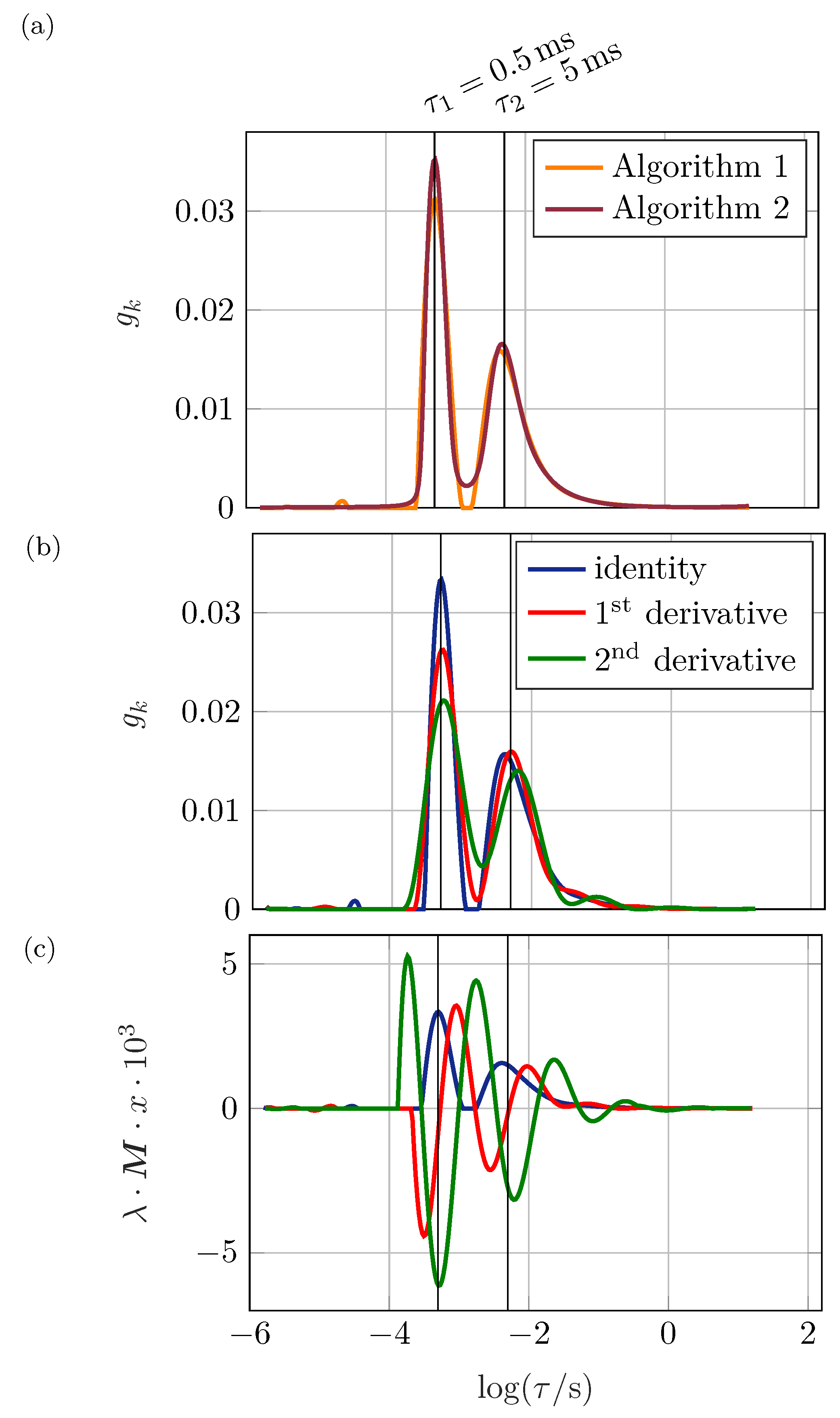
Figure 1a the impedance spectrum of two RC elements (resistor and capacitor in parallel) connected in series is shown: a deformed semi-circle with no distinct maximum of
results. This shape might be caused, e.g., by a non-ideal process due to large inhomogeneities within the electrode or by separate processes. Investigating the impedance spectrum, no further conclusions can be drawn. Applying the DRT algorithm as shown in
Figure 1b, the two involved processes can be separated easily. Therefore, the contribution of single processes to the system’s impedance can be calculated.
The DRT offers a model-free, universal approach for the detailed analysis of electrochemical systems or any other data obtained from impedance measurement. This means that no a-priori assumptions, e.g., electrical, physical or chemical models or knowledge are necessary, which is an essential advantage when dealing with complex or hardly understood specimen such as fuel cell stacks or new materials with novel conducting mechanisms.
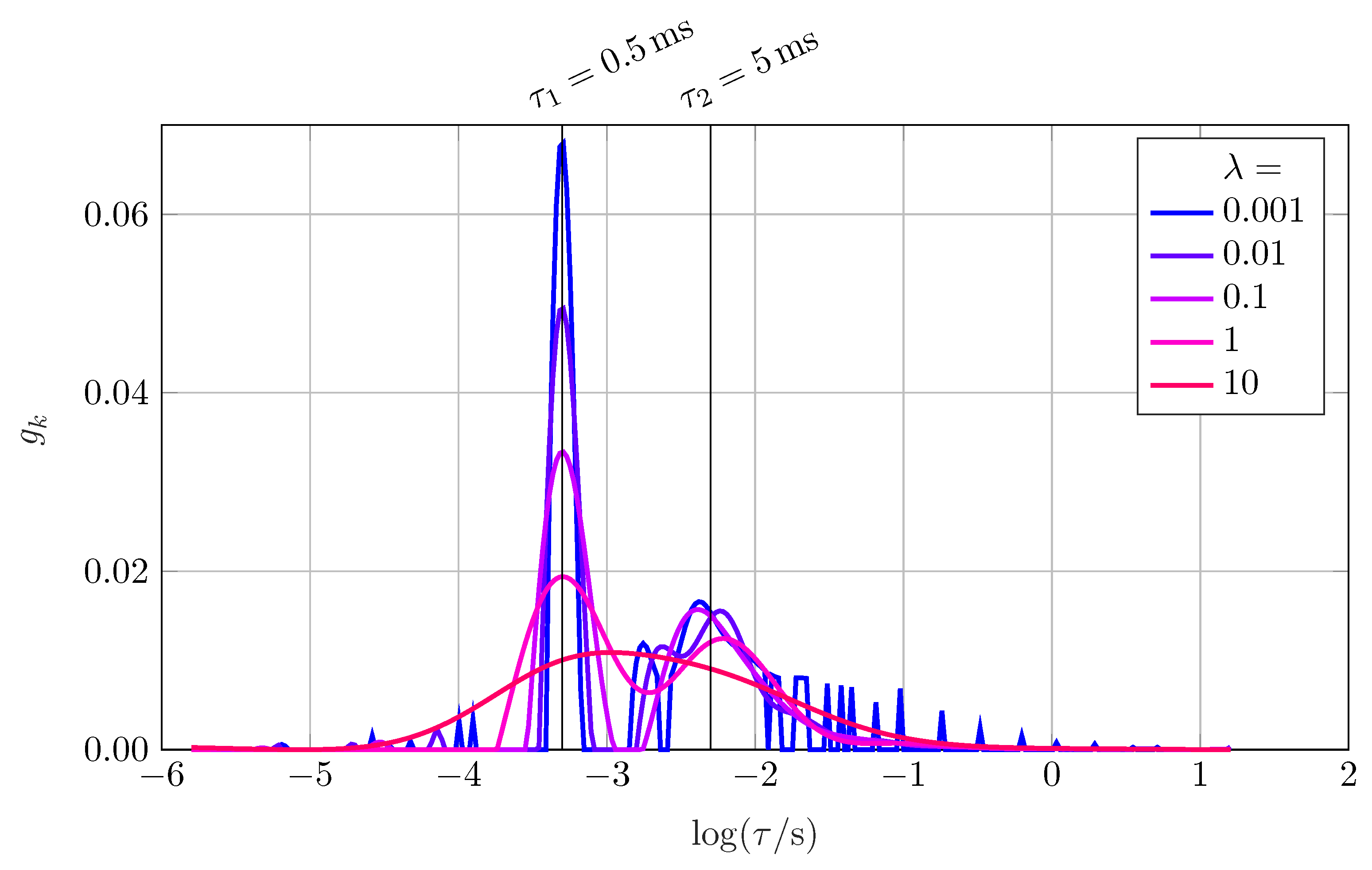
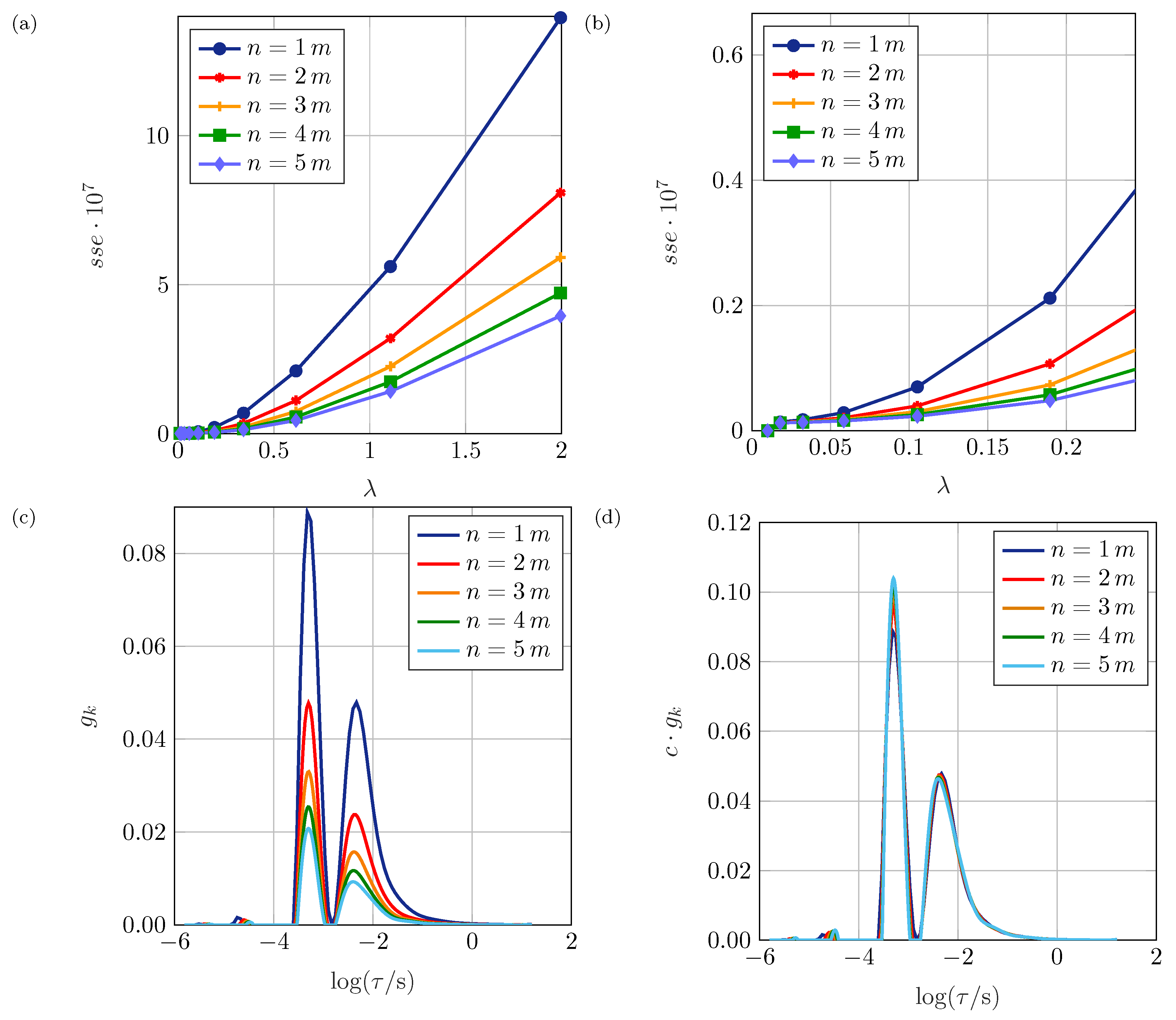
On the other hand, the DRT analysis strongly depends on the choice of its process parameters which are, in many publications, neither revealed nor discussed. Thus, the DRT algorithm containing those parameters is described in detail within this paper. Furthermore, an extensive parameter study is performed to evaluate the impact and correlation of those process parameters on the calculated distribution function. The study includes the optimization of the regularization parameter, the number of predefined discrete time constants as sampling points of the distribution function and the mathematical formulation of the regularization term. It is investigated whether real parts, imaginary parts of the complex impedance or both should be used for the calculation of the DRT. Finally, the impact of the optimization function and optimization algorithm is shown. As an instructive example of a complex impedance spectrum comprising inductive, resistive, capacitive and diffusive overlapping polarization contributions of multiple components within an electrochemical system, the algorithm is applied on impedance data from a commercial Ah Nickel–Manganese–Cobalt–Oxide (NMC) lithium-ion pouch cell by Kokam and the results are discussed in detail. Furthermore, the features of the impedance spectra are assigned to the individual peaks observed in the distribution functions. For more insight into the single peaks within the DRT, a novel post-processing approach is presented, adapting modified Gaussian peaks to the distribution function resulting in a quantification of every single process within the spectrum.
By reporting all relevant information about the used algorithm, the results presented in this publication can be easily reproduced by other researchers. The information includes
the optimization algorithm,
the error function,
the type of data used, i.e., using real or imaginary parts of the complex impedance,
measurement parameters, e.g., current or frequency range,
regularization parameter,
number of time constants,
the pre- and post-processing routine,
the minimum and maximum time constants for the DRT.
2. Deriving DRT from EIS Data
The main idea of the DRT is to express the complex-valued, frequency-dependent impedance of an electrochemical system as an infinite series of differential RC-elements in series with an ohmic resistor
[
7,
15,
17]:
The integral is often normalized by introducing
which leads to
The normalized Equation (
3) has two advantages compared to Equation (
1):
The term corresponds to the relative differential contribution of a single ohmic-capacitive element as and results in , which is the well-known equation for an RC-element.
The function
is computed numerically. Therefore, the integral in Equation (
3) has to be discretized yielding the finite sum
The range of time constants
has to be chosen a priori based on the available frequency range of the impedance data. Usually, the interval of time constant matches the interval of measured frequencies. The number of time constants
n has to be large compared to the expected numbers of processes within the investigated system. The determination of the optimal number is part of our process parameter analysis in
Section 3.
Equation (
4) describes the resistive–capacitive behavior of the impedance spectrum as a sum of RC elements connected in series with predefined time constants. Neither assumptions are made regarding the number of processes involved nor model concepts on electrical, physical or chemical processes are required as in case of the model-based analysis of electrochemical impedance spectroscopy. Hence, the DRT analysis is regarded as a model-free method for the characterization of electrochemical systems. Furthermore, it has to be stated that due to the ohmic-capacitive nature of Equation (
4), the DRT is not valid for inductive systems. Purely capacitive contributions cannot be described neither. Mathematically, these restrictions regarding the examined complex impedance can be expressed as
2.1. Dealing with Artefacts at the Boundaries of the Measured Frequency Range
If the measured impedance spectrum is not converging towards the real axis at the boundaries of the measured frequency range as demanded by Equations (
5) and (
6), as is it the case e.g., for diffusion processes at low frequencies, the DRT analysis will yield artefacts, i.e., singularities or diverging, steep slopes at the boundaries of the interval of time constants corresponding to the extremes of the measured frequencies. To deal with this issue we propose to extend the predefined vector of time constants beyond the minimum or maximum time constant corresponding to the according maximum and minimum frequency. Mathematically this is legitimate since the choice of the predefined time constants does not have to match the measured frequencies compulsorily as can be seen in the definition of the optimization problem later. This approach does not extrapolate the measured spectrum beyond the measured frequency range. Not even new assumptions are made on the behavior of the device under test beyond the measured frequency range. Instead, the optimization problem maps a wider vector of time constants onto the exactly same impedance information in frequency domain and therewith helps to better extract all information contained in the measured frequency spectrum. A back calculation of the identified DRT into frequency domain would be the same as fitting an RC circuit to the measured spectrum. As for fitting an equivalent circuit model to a measured impedance spectrum, the model is only valid for the measured frequency range. Since real systems will never have a limited bandwidth and a measurement system will never be able to measure an unlimited frequency range, we show in the results that broadening the predefined vector of time constants is beneficial for the analysis of electrochemical systems, especially if polarization processes are not abated at the boundaries of the measured frequencies as it the case for the solid state diffusive behavior of lithium-ion batteries.
2.2. Calculation of g()
For the equations above,
has to be calculated from an impedance spectrum. Measured or model-based, computer-generated spectra are limited in their number of frequency points. Typically, the frequency vector of the treated impedance data is logarithmically scaled, with 6 [
14], 7 [
18], 10 [
7,
19] or 16 [
20] steps per decade, respectively. Often, this information is missing in publications [
2,
21,
22]. However, this relatively small amount of
m data points (i.e., the measured data including frequency and impedance values) leads to the issue that there are usually less data points than sampling points for the time constants of the DRT analysis (
).
Therefore, the resulting optimization problem
with the matrix
and the vector
as introduced below is ill-posed and might be ill-conditioned. Therefore, it cannot be solved analytically. One way to overcome the ill-posed optimization problem in Equation (
8) is to apply numerical regularization. Among the regularization techniques commonly used for calculation of DRTs of electrochemical systems, Tikhonov regularization has proven to be a powerful technique [
23,
24]. The optimization function
is extended by a regularization term
where
is the regularization parameter. Its influence on the resulting distribution will be discussed in
Section 3. The parameter
represents the discrete values of the distribution function
.
The parameter can be extended to , where is the regularization matrix. In the simplest case, is defined as , representing the identity matrix.
In addition, the constraint
has to be taken into account, since negative contributions to the impedance are physically not feasible.
The solution of the problem stated in Equation (
9) can be obtained by multiple numeric algorithms. As the optimization problem is ill-posed with no unique solution and as commonly used least-squares algorithms are only able to find local optima, it is crucial to be aware of the used optimization algorithm. Otherwise, the results of the DRT can hardly be reproduced. Ciucci et al. [
25] and Wan et al. [
26] give insight into the optimization problem including a detailed discussion on the regularization matrix. Nevertheless, to the authors’ knowledge there is no publication which gives insight into the used optimization algorithm.
Considering Equation (
4), the matrix
consists of
in
i-th line and
k-th column where
represent normalized RC-elements with a time constant
evaluated at the angular frequency
.
The vector consists of the m measured or generated impedance values. This may happen in various ways:
With both real and imaginary parts used, a number of time constants leads to an under-determined system. With , the problem is overdetermined. Both cases lead to an ill-posed problem as there is no unique solution. If , the system is well-posed. For all three cases, Tikhonov regularization is applicable.
A non-negative least squares (NNLS) solver is used as proposed by Lawson and Hanson ([
29], p. 161). As this algorithm can only deal with matrix-vector-systems, Equation (
9) is re-written according to Kaipio [
30] and Wu [
31]:
The solver returns which turns into after normalization.
2.3. Pre-Processing of Measurement Data
As stated above, the DRT can only deal with resistive–capacitive systems. The frequency- independent
has to be subtracted from the impedance before running the DRT routine. In addition, electrochemical systems are never only resistive–capacitive. There are inductive contributions due to the measurement setup or the specimen itself [
11] as well as diffusive behavior e.g., when investigating batteries. Therefore, it is critical that such influences are removed from the impedance data beforehand.
There are two proper ways to deal with inductive and capacitive branches: the first is to fit an appropriate equivalent circuit (EC) to the measurement data using the model-and-reduce approach. This EC may contain a resistor, an inductor, a capacitor, RL-elements (resistor and inductivity in parallel), RC-elements, ZARC-elements (
), constant phase elements (CPE) (
) and Warburg-elements (planar and spherical diffusion) all connected in series. The contribution of non-resistive–capacitive EC elements is subtracted from the measured spectrum to fulfil the RC-constraint of the DRT (Equations (
5)–(
7))
This pre-processing step is in opposition to the advantage of not needing any a priori knowledge for the DRT at first glance as the EC fit needs to be precise. Only non-RC elements have to be identified and characterized precisely to be subtracted properly while the exact characterization of electrode and interface processes is not essential within this step. Imprecise EC fits lead to peaks without any physical meaning, offering space for misinterpretations. For an appropriate fit, Equations (
5) and (
6) should be fulfilled after subtracting non-inductive-resistive components.
Choosing an EC requires experience by the scientist. A by-inspection analysis of the impedance spectrum while keeping in mind the spectra of the specific elements is beneficial. The EC is then fitted using a trust-region method. The two-dimensional error function to be minimized is given by
with
representing the impedance function of the EC whose parameters are to be optimized.
The second option, called cut-and-shift approach, does not need any a priori assumptions: first, all data points with are cut off the spectrum. As a second step, the ohmic offset is removed by subtracting from the spectrum.
The entire workflow is summarized in
Figure 2. The validity of the measured spectrum is proven by Kramers–Kronig test: in accordance to literature, a spectrum is said to be valid as long as the residual between the measured and the Kramers–Kronig reconstructed impedance is below 1% for every data point. Within the pre-processing step non-resistive–capacitive components are removed. Finally, the DRT is calculated from the reduced spectrum and
is obtained.
Tikhonov regularization is not the only possible approach for calculating the DRT. Fourier transformation is used as well [
15,
17]. A comparison between regularization and Fourier transform is not part of this paper, though a study on benefits and disadvantages of either method might be interesting in the future.
2.4. Post-Processing of Result
In general, once has been calculated, the distribution function can simply be interpreted in a phenomenological manner: the number of processes involved can be identified as well as changes e.g., during ageing or relaxation or differences between used materials, morphologies or cell designs. For a proper quantitative analysis, post-processing is required.
We quantify the polarization of each peak by fitting the numerical distribution to a sum of modified, non-normalized Gaussian probability density functions with adjustable height
H, standard deviation
and skew
s using a logarithmic time constants scale. The introduction of the skew allows asymmetric distributions:
Thus, the area under each specific peak corresponds to the impedance contribution of the underlying process. Furthermore, the standard deviation corresponds to the ideality or uniformity of a process, e.g., a narrow peak indicates a process with a small band width, e.g., a uniform particle size. Wide peaks point to distributed processes, e.g., a wide spread particle size distribution or a geometric influence of a large-scale specimen. The skew indicates the distribution of the non-ideal process, e.g., whether there are more small-sized or large particles within the electrode. Yet, an overall quantification or correlation to the system’s attributes is not easily achievable, but a quantitative comparison between various DRTs can be achieved.
4. Analysis of Measurement Data
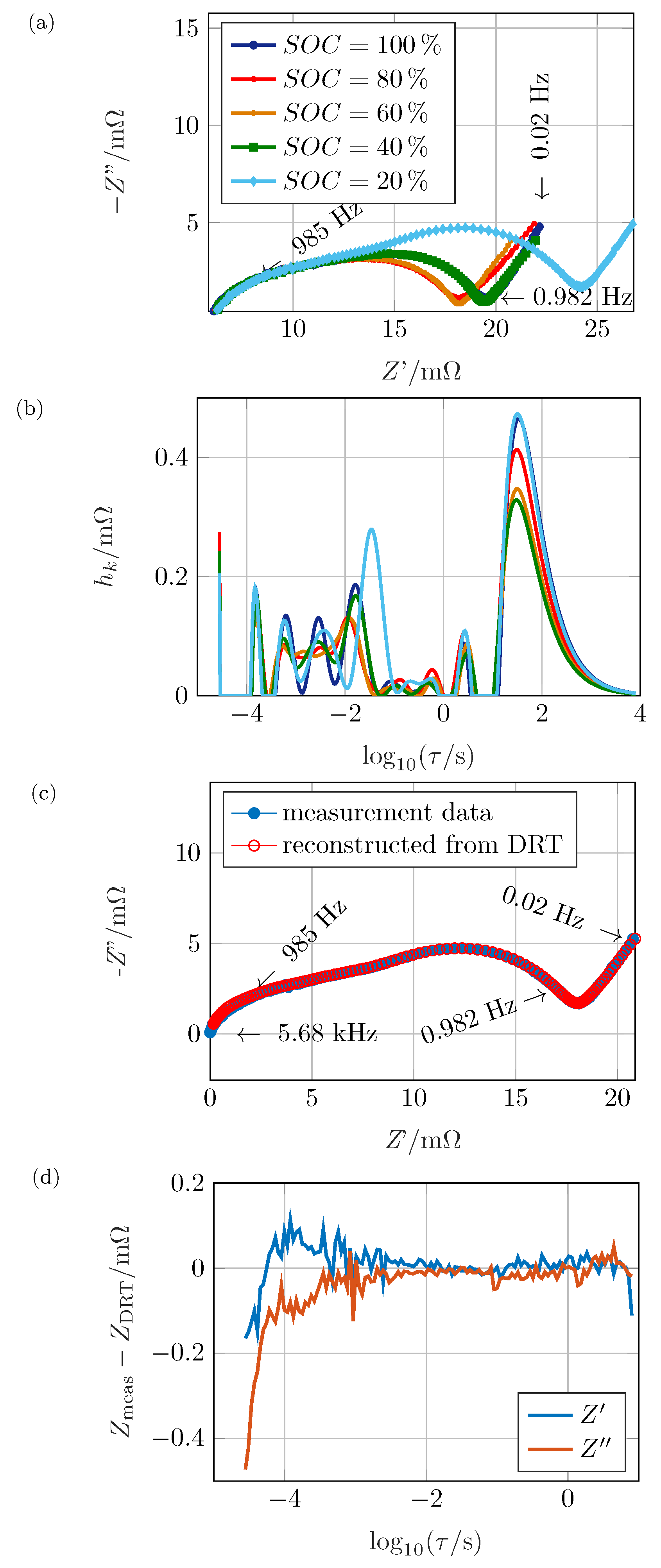
The algorithm was applied on measured impedance spectra to validate the method and to quantify the predominant polarization effects in a real electrochemical system. As specimen, a commercial Li-ion battery, Kokam SLPB526495 with a nominal capacity of
Ah in pouch cell format with a high energy NMC cathode was investigated. The impedance spectrum was measured using a Zahner ZENNIUM pro electrochemical workstation applying galvanostatic EIS at an amplitude of 120
within a frequency range of 20
to 5
with 21 steps per decade. The
(state of charge) was varied between 20% and 100% in 20% steps. For the variation, the cell was charged to 100%
as recommended by the manufacturer. After 3
of relaxation, the impedance was measured. Then, the cell was repeatedly discharged at 0.5C for
. Again, after 3
of relaxation, the impedance was measured. The five resulting spectra are displayed in
Figure 7a. The upper frequency limit was set so that there was no inductive behavior within the spectrum, while interface processes and the diffusion branch were visible. The ohmic resistance increased monotonously from
to
with decreasing
. The high-frequency feature of the impedance spectrum is typically associated with the process at the current collector/active material interface process [
4]. Though, this assignment has to be studied carefully as there might be inductive contributions within that frequency range. The mid-frequency feature was strongly dependent on the
. It can be assumed that the underlying process was related to the charge transfer reaction [
4]. The diffusion, which occurs at low frequencies, did not seem to show an obvious
-dependency within the Nyquist plot. A quantitative comparison is hard due to the offset in Re(
Z) and possibly overlapping electrode processes between the different graphs.
In
Figure 7b, the distribution functions of the spectra in
Figure 7a are shown. The DRT have been obtained by applying the cut-and-shift approach introduced in
Section 2. In addition, the range of time constants has been extended by three decades towards low frequencies compared to the measured range also introduced within
Section 2. The branch itself was fitted to the time constants for the measured frequencies, while semi-circles which were caused by contributions of lower frequencies in
are necessary to bypass the resistive–capacitive restriction. This procedure was proven to be suitable by comparing the reconstructed spectrum to the original data in
Figure 7c as the graphs do not deviate strongly at 20%
. The reconstructions of the other
s have been of equal quality (not shown here). Only for high frequencies, the graphs do not entirely match due to the onset of superimposed inductive contributions. This influence must be neglected for the DRT anyway. For the data point at 20
there was a deviation due to the non-RC restriction which cannot be compensated perfectly, but in a sufficient manner.
Figure 7d shows the absolute residual between measured and reconstructed impedance within the measured frequency range where
. Due to the cut-and-shift approach, the data point for the highest displayed frequency is close to zero. Thus, even a small difference would lead to a huge relative error which, in this case, is of no specific relevance. The good quality of the fit is proven by deviations below
for the entire spectrum, except the very small time constants. As stated above, this was caused by a beginning inductive influence, which can neither be avoided nor subtracted precisely. For the highest time constants, the difference begins to grow as the limitations regarding Equation (
5) begin to impact the reconstructed spectrum.
Analyzing
Figure 7b in more detail, the absolute distribution function
h is used instead of
g, enabling both a quantitative and qualitative analysis as the distribution functions are all within the same magnitude. The value
, representing the contribution of the lowest time constant, is not equal to zero. This is caused by a combination of imperfect subtraction of the purely ohmic resistance and the presence of some minor inductive contributions at high frequencies. The absolute value of
is strongly dependent on the number of measurement points, the regularization parameter and the number of time constants used within the DRT. This peak can be ignored for further investigations as it is not related to an electrode process. At high time constants, the contribution of the solid-state diffusion is dominant. Preliminary studies with constant phase and Warburg elements have shown that the three peaks closest to the main peak are also diffusion-related and necessary for a precise reconstruction. This is in accordance to a recent publication by Boukamp [
38] who also derives a formula for the characteristic time constants of the peaks obtained in relation to the exact time constant calculated from finite length Warburg element formula. The results of our preliminary study are in very good accordance to the formula given as [
38]
where the main diffusion peak is referred to as
and the smaller ones as
,
etc. with decreasing time constant, respectively. With synthetic Warburg data,
calculated from
to
is equal. Increasing the regularization parameter, the calculated
differ increasingly, especially for high indices of
, and shift towards lower time constants. Investigating the battery as a whole, the match of the theoretical and practical peak positions
differs up to a factor of eight between the three small and one large diffusion-related peaks. Furthermore, at 60% there is a small additional peak visible. This non-ideal behavior may be caused by the distributed solid-phase diffusion throughout the porous electrode material and by the simultaneous presence of anode and cathode diffusion process. These result in non-ideal Warburg behavior in combination with the regularization-based effect as mentioned above. Further, the polarization resistances of the four peaks differ from their theoretical values for the same reason.
In contrast to
Figure 7a, a significant change in diffusive behavior becomes visible when investigating the DRT. For intermediate
s, the diffusion shows a smaller peak in the DRT than for high or low
s within the measured frequency range. As previously seen in
Figure 7a, the slowest interface process is strongly dependent on the electrodes’
and therefore on the lithium surface concentration of the particles. Starting with the fully charged cell, the polarization and the characteristic time constant decreases strongly and is almost constant for 80% and 60%. When discharging further, the polarization rises by more than a factor of two and the time constant shifts towards higher values. At around
1 × 10
s there are two more processes visible. Due to their characteristic time constants, it can be assumed that these peaks represent electrode or interface processes. The faster process shows the highest polarization resistance at 20% and 100%, while the value is lower and close to constant for intermediate
SOCs. The fastest process shows a constant shape and height. For further investigations, a quantitative analysis of the three electrode process-related peaks is inevitable.
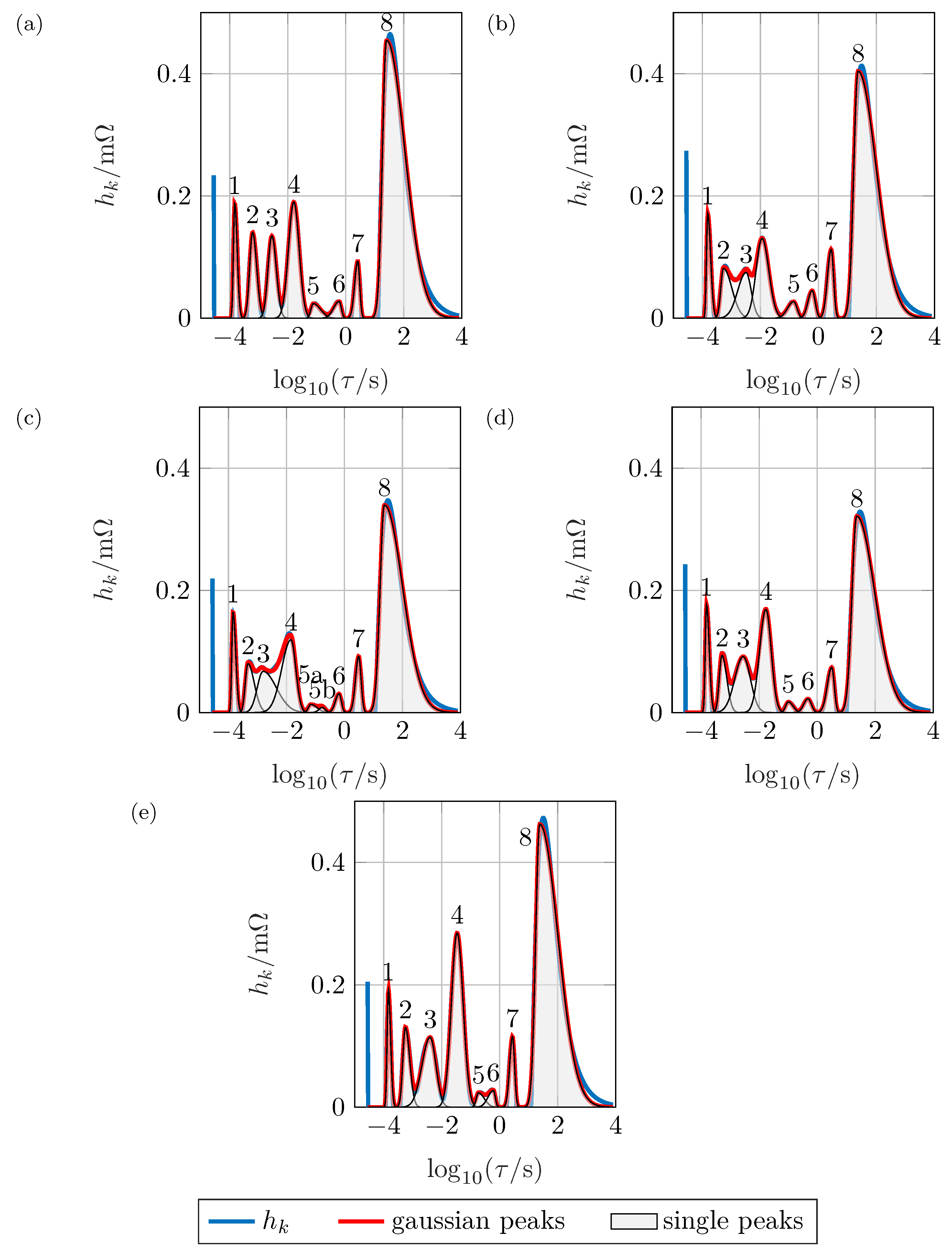
The peak analysis shown in
Figure 8 allows a quantitative analysis of each separate distribution in
Figure 7b. As mentioned above, peak 1 does not show a noteworthy
SOC-dependency and has a polarization resistance of
. It can be assumed that this peak represents the particle-particle or particle-current collector interface [
4].
Peaks 2 and 4 show a similar SOC dependency: For high and low SOCs, the polarization resistance is large, while it is low for intermediate SOCs. The higher the resistance, the higher is furthermore the time constant. The width of the peaks does only change due to the change in height. As there are two charge transfer reactions expected within the battery, it can be assumed that peaks 2 and 4 represent those. Peak 3 behaves differently: it significantly changes its width and the characteristic time constant at 60% is lower than could be expected when compared to the other SOCs. This peak could hence be assigned to the SEI, while the exact reason for this behavior remains unclear. Considering these findings, peak 4 can be assigned to the anodic charge transfer reaction based on the following indicators:
The time constant of the anodic charge transfer is typically higher than that of the SEI [
39,
40]
The resistance increases for high and low values reaching a minimum at medium
s.
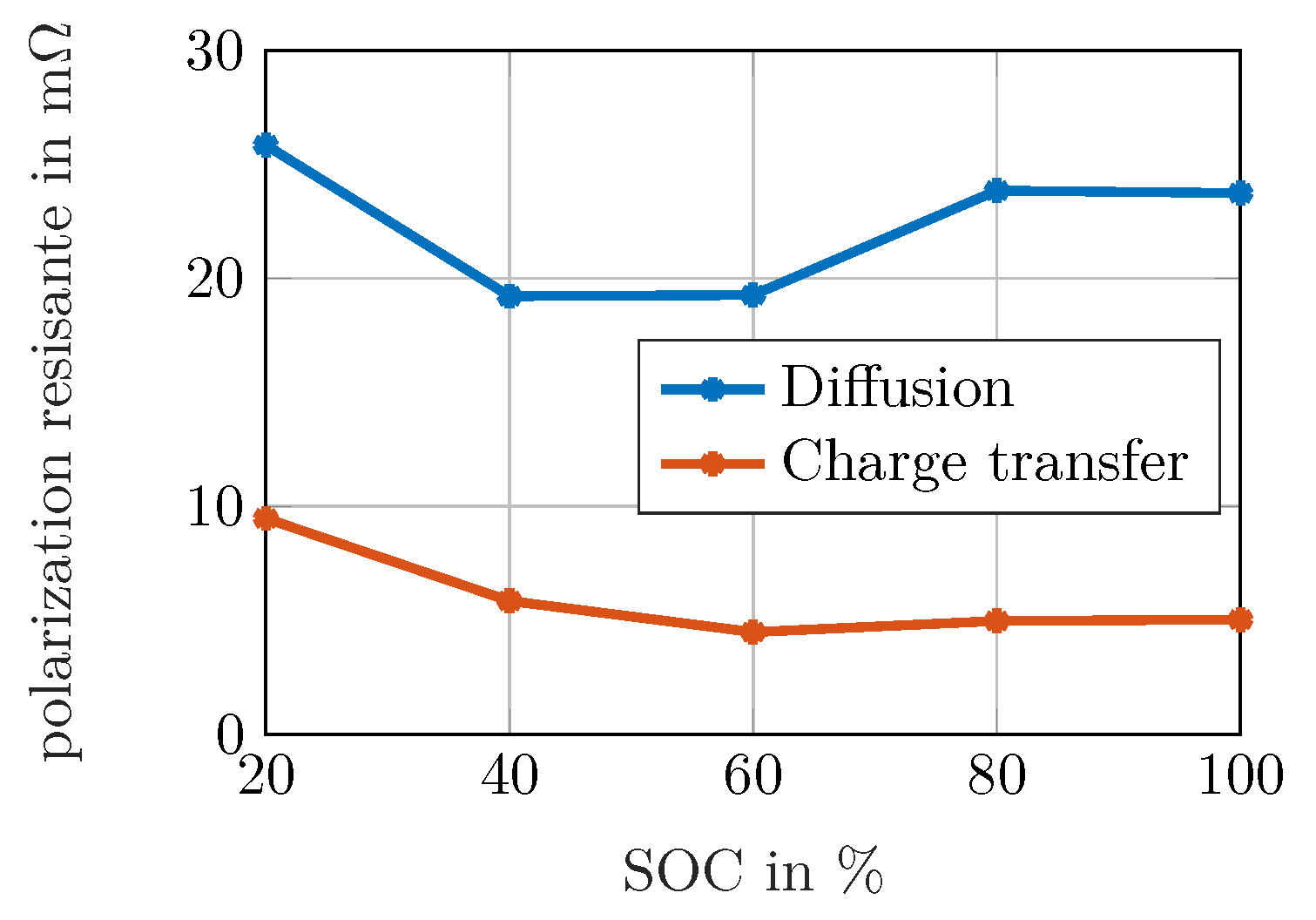
Figure 9 underlines this observation. This is in accordance with the Butler–Volmer kinetics, where the exchange current density is small at high and low
s [
14,
41]. To differentiate the process from the cathodic reaction,
Figure 9 shows that the resistance is highest at low SOCs, whereas the increase is only shallow at 80% and 100%. It has to be considered that in commercial cells, the anode is over-dimensioned so that lithium plating is avoided by restricting high lithium concentrations in the anode. This leads to an disproportionate distribution of the anode’s degree of lithiation. Thus, its SOC is not well-proportionate but shifted towards smaller concentrations. This leads to the conclusion that peak 3 is caused by the anodic charge transfer reaction.
The qualitative investigation of the diffusive process in
Figure 9 is of interest as well. The absolute value is calculated by adding the resistances of peaks 5–8. Summing up the values of charge transfer and diffusion obtained e.g., for 20%
, approx. 37
are achieved. However, the maximum value of
is below 30
in
Figure 7a. As the assumption of convergence towards
for frequencies below the measured range is not necessarily fulfilled, e.g., when a limited reservoir leads to capacitive behavior for very low frequencies, the polarization contribution obtained for the diffusive branch must neither be interpreted as an absolute value for an overall diffusion resistance nor be used to draw conclusions of processes outside the measured frequency range. Instead, the values can be taken into account for a comparison of different spectra to visualize changes in diffusive behavior, if the frequency range and the regularization parameter is equal for the investigated spectra.
The qualitative behavior of the diffusive values can be interpreted in two ways: in a descriptive manner, the diffusion is limited when the concentrations are either close to the maximum while there are still more ions to be intercalated and transported towards the particles’ center or when the concentration is close to zero, but there is a demand of ions from the inner particle to be deintercalated at the surface. Considering electrochemistry, diffusion leads to a high polarization when the differential capacity is small, i.e., a small change of concentration leads to a large change in the open circuit voltage when the surface concentration differs from the average concentration. This is the case at high SOCs, but even stronger at low SOCs for the investigated NMC cell. Both explanations lead to the same result: As the resistance increases for high and for low SOCs in a similar way, it can be assumed that anodic and cathodic solid state diffusion overlap within the diffusion peak showing similar time constants without the possibility of separation.
Analyzing the DRT, we are able to gain significantly more information on the dominant polarization mechanisms. The dependency of solid state diffusion could be assessed quantitatively and the dominating electrode processes could be assigned to peak 2–4.