Electrochemical Impedance Spectroscopy and Determination of the Internal Resistance as a Way to Estimate Lead-Acid Batteries Condition
Abstract
:1. Introduction
- formation of a low-conducting layer at the grid/active mass interface (PCL of type 1). This is probably the most frequent case of the PCL effect caused by the formation of a passivation layer next to a typical corrosive layer at the grid/active mass interface. This tight coating contains PbSO4, and/or PbO1±n compounds,
- PCL of the second type is related to an increase in resistance of the pasted active mass (PAM), which can be observed in case of weak adhesion between a grid and the PAM. The corrosive layer consists mainly of β-PbO2, and the concentration of sulphuric acid is far higher in this area. Thus, the original spatial structure of the plate is distorted, which causes electrochemical insulation of a part of the active mass. However, a decrease in active mass has not yet been observed.
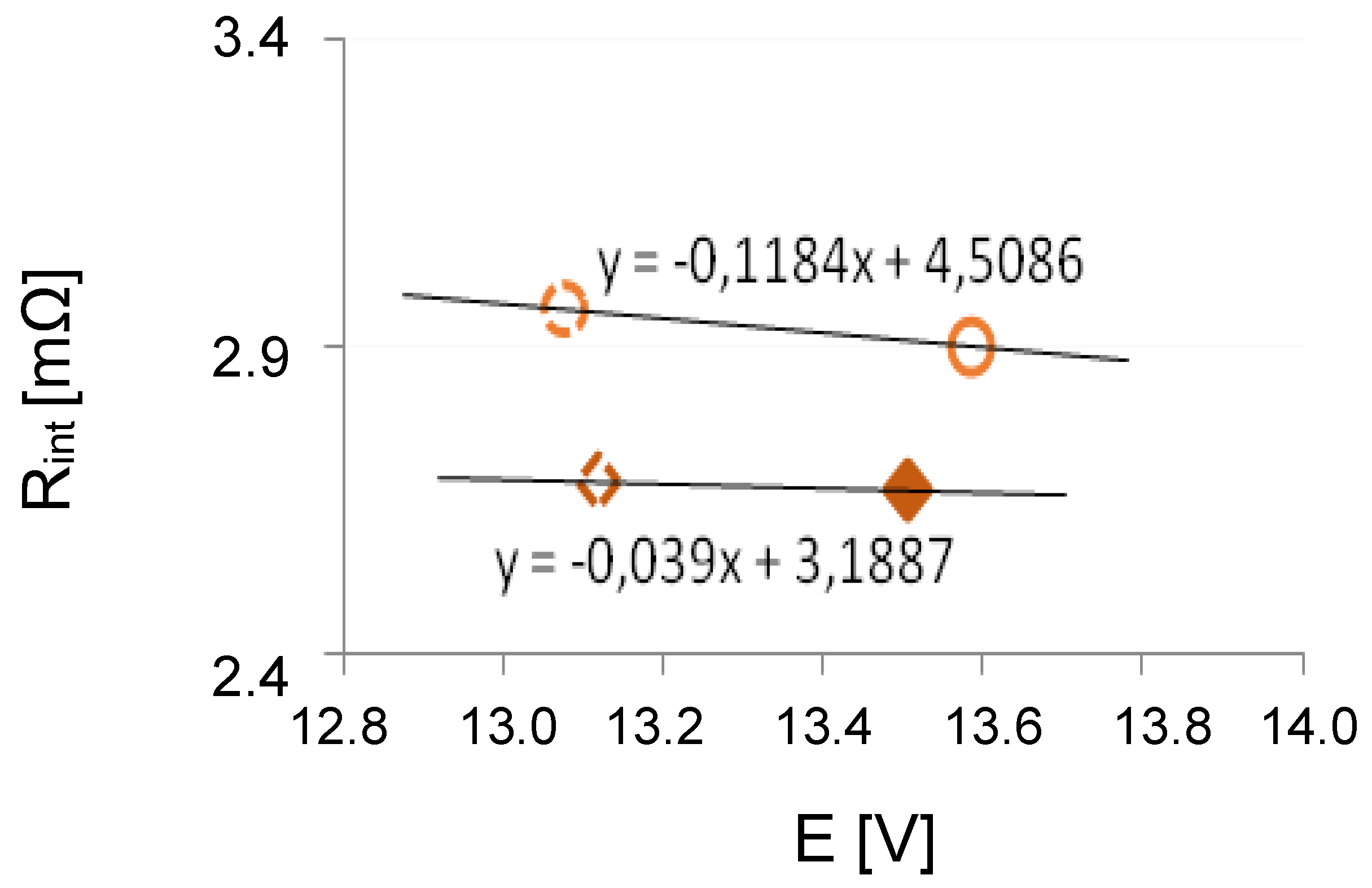
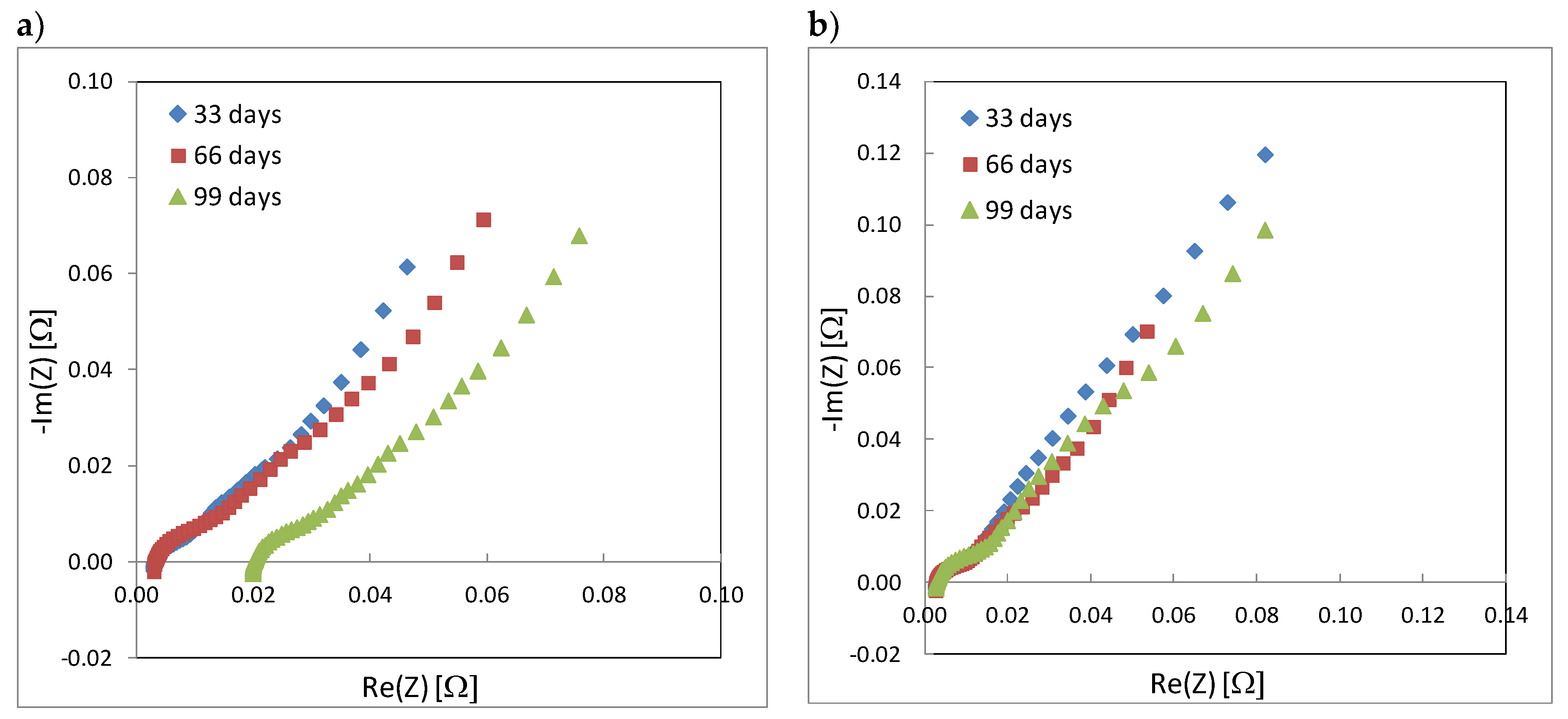
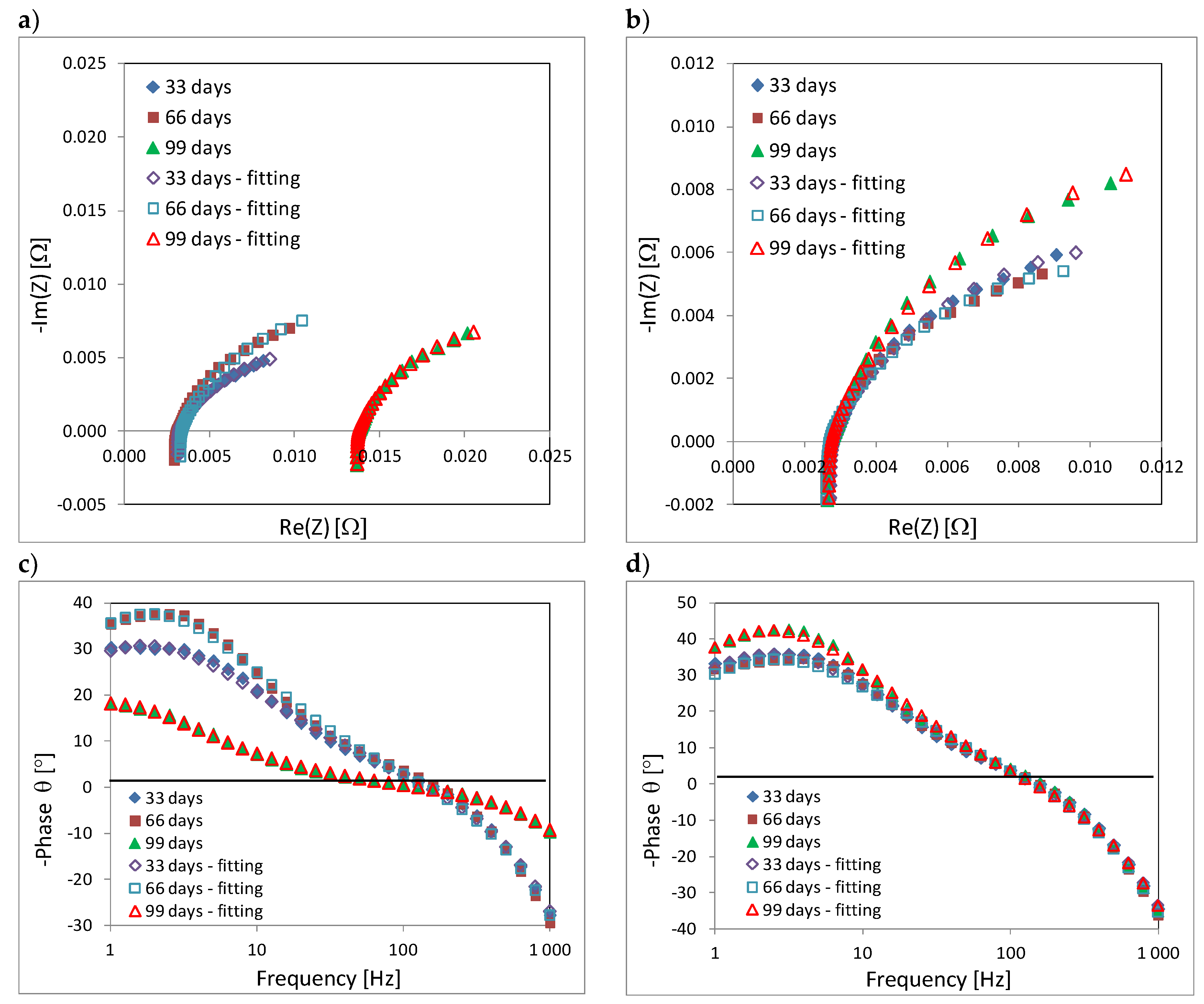
2. Results and Discussion
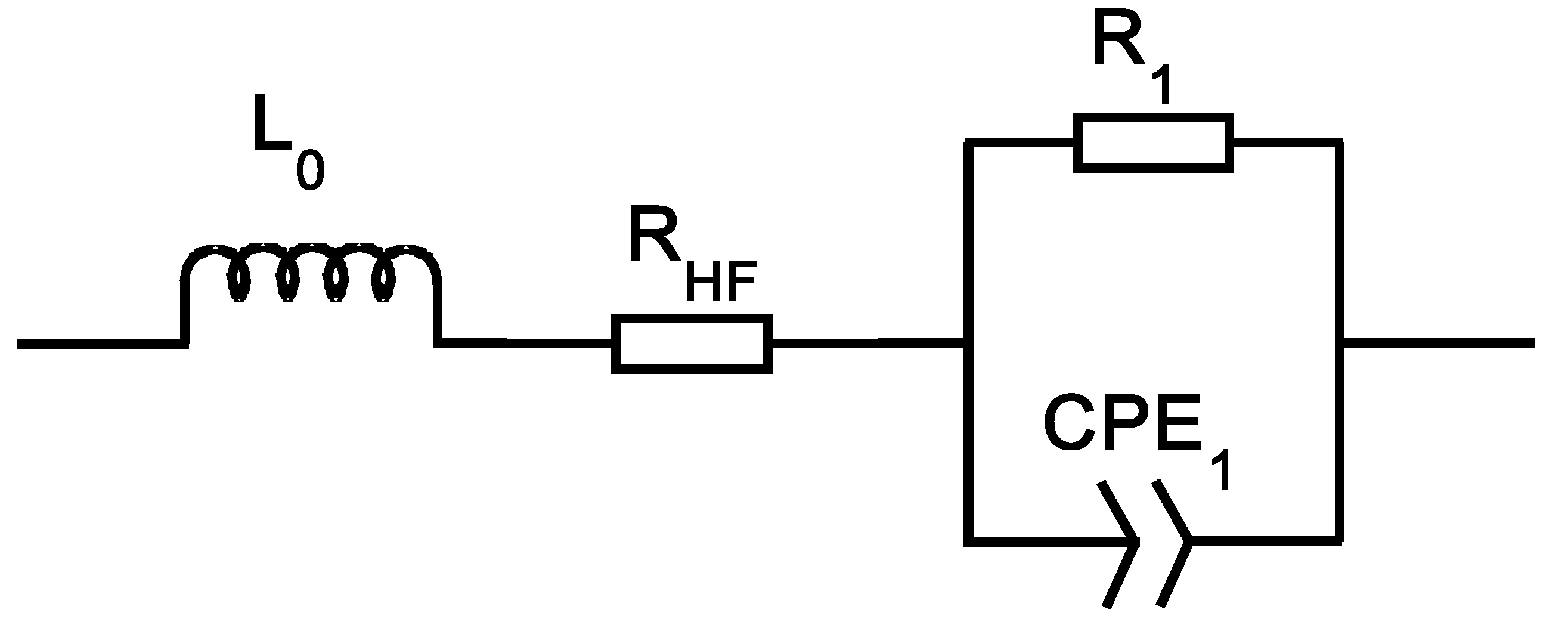
- inductance L0 attributed to electrode geometry and connections inside the cell,
- resistance RHF due to the connections, the separator, the electrolyte resistivity and the surface coverage of the electrodes by crystalline lead sulphate,
- resistance R1 depending on the porosity of the electrodes,
- CPE1 responsible for heterogeneous phenomena.
3. Materials and Methods
- Acquiring already used battery with a known history, in order to increase the probability of detection of the PCL effect,
- The mildness of the initial physicochemical changes accompanying the PCL effect,
- The choice of tests and the testing conditions,
- The appropriate classification of these changes and their assignment to the area of the PCL effect (or other).
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sato, S.; Kawamura, A. A new estimation method of state of charge using terminal voltage and internal resistance for lead acid battery. In Proceedings of the Power Conversion Conference, Osaka, Japan, 2–5 April 2002; Volume 2, pp. 565–570. [Google Scholar]
- Zhendong, Z.; Zihan, L.; Nan, H. The VRLA battery internal resistance on-line measuring device. In Proceedings of the 2012 International Conference on Information Management, Innovation Management and Industrial Engineering (ICIII), Sanya, China, 20–21 October 2012; pp. 404–406. [Google Scholar]
- Baraniak, M.; Jankowska, E.; Budzyński, M.; Lula, M.; Majchrzycki, W. Report IMN-CLAiO No. 6093.01 in Polish; Institute of Non-Ferrous Metals: Poznań, Poland, 2012. [Google Scholar]
- Majchrzycki, W.; Jankowska, E.; Baraniak, M. Report IMN-CLAiO No. 6436.01 in Polish; Institute of Non-Ferrous Metals: Poznań, Poland, 2013. [Google Scholar]
- Abraham, P.; Bača, P.; Vaculík, S. Resistivity and Impedance Changes of Lead-Acid Accumulator. ECS Trans. 2014, 48, 303–308. [Google Scholar] [CrossRef]
- Gençten, M.; Dönmez, K.B.; Şahin, Y.; Pekmez, K.; Suvac, E. Voltammetric and electrochemical impedimetric behavior of silica-based gel electrolyte for valve-regulated lead-acid battery. J. Solid State Electrochem. 2014, 18, 2469–2479. [Google Scholar] [CrossRef]
- Shih, H.; Lo, T.-C. Electrochemical Impedance Spectroscopy for Battery Research and Development Technical Report No 31; Solartron: Farnborough, UK, 1996. [Google Scholar]
- Fasih, A. Modeling and Fault Diagnosis of Automotive Lead-Acid Batteries. Master’s Thesis, The Ohio State University, Columbus, OH, USA, 2 April 2006. [Google Scholar]
- Moseley, P.T.; Garche, J.; Parker, C.D.; Rand, D.A.J. Valve-Regulated Lead-Acid Batteries, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 2004; ISBN 9780080474731. [Google Scholar]
- Pavlov, D. Lead-Acid Batteries: Science and Technology, 2nd ed.; Elsevier Science: Amsterdam, The Netherlands, 2017; ISBN 9780444595607. [Google Scholar]
- Łęgosz, Z. Czy baterie VRLA mogą żyć 20 lat? Przedwczesna utrata pojemności—Fundamentalny problem baterii VRLA. Wiadomości Elektrotechniczne 2001, R. LXIX, 111–115. [Google Scholar]
- Calábek, M.; Micka, K.; Bača, P.; Křivák, P.; Šmarda, V. Resistance changes and premature capacity loss in lead battery plates. J. Power Sources 1996, 62, 161–166. [Google Scholar] [CrossRef]
- Hollenkamp, A.F. Premature capacity loss in lead/acid batteries: A discussion of the antimony-free effect and related phenomena. J. Power Sources 1991, 36, 567–585. [Google Scholar] [CrossRef]
- Kosai, M.; Yasukawa, S.; Osumi, S.; Tsubota, M. Effect of antimony on premature capacity loss of lead/acid batteries. J. Power Sources 1997, 67, 43–48. [Google Scholar] [CrossRef]
- Pavlov, D. Effect of corrosion layer on phenomena that cause premature capacity loss in lead/acid batteries. J. Power Sources 1994, 48, 179–193. [Google Scholar] [CrossRef]
- Pavlov, D.; Petkova, G.; Dimitrov, M.; Shiomi, M.; Tsubota, M. Influence of fast charge on the life cycle of positive lead–acid battery plates. J. Power Sources 2000, 87, 39–56. [Google Scholar] [CrossRef]
- Shiomi, M.; Okada, Y.; Tsuboi, Y.; Osumi, S.; Tsubota, M. Study of PCL mechanism: Influence of grid/PAM state on PCL. J. Power Sources 2003, 113, 271–276. [Google Scholar] [CrossRef]
- Huet, F. A review of impedance measurements for determination of the state-of-charge or state-of-health of secondary batteries. J. Power Sources 1998, 70, 59–69. [Google Scholar] [CrossRef]
- Blanke, H.; Bohlen, O.; Buller, S.; De Doncker, R.W.; Fricke, B.; Hammouche, A.; Linzen, D.; Thele, M.; Uwe Sauer, D. Impedance measurements on lead–acid batteries for state-of-charge, state-of-health and cranking capability prognosis in electric and hybrid electric vehicles. J. Power Sources 2005, 144, 418–425. [Google Scholar] [CrossRef]
- Karden, E.; Buller, S.; De Doncker, R.W. A method for measurement and interpretation of impedance spectra for industrial batteries. J. Power Sources 2000, 85, 72–78. [Google Scholar] [CrossRef]
- Diard, J.-P.; Le Gorrec, B.; Montella, C. EIS study of electrochemical battery discharge on constant load. J. Power Sources 1998, 70, 78–84. [Google Scholar] [CrossRef]
- Karden, E.; Buller, S.; De Doncker, R.W. A frequency-domain approach to dynamical modeling of electrochemical power sources. Electrochim. Acta 2002, 47, 2347–2356. [Google Scholar] [CrossRef]
- Wei, Z.; Tseng, K.J.; Wai, N.; Lim, T.M.; Skyllas-Kazacos, M. Adaptive estimation of state of charge and capacity with online identified battery model for vanadium redox flow battery. J. Power Sources 2016, 332, 389–398. [Google Scholar] [CrossRef]
- Wei, Z.; Bhattarai, A.; Zou, C.; Meng, S.; Lim, T.M.; Skyllas-Kazacos, M. Real-time monitoring of capacity loss for vanadium redox flow battery. J. Power Sources 2018, 390, 261–269. [Google Scholar] [CrossRef]
- Barsoukov, E.; Macdonald, J.R. (Eds.) Impedance Spectroscopy Theory, Experiment, and Applications, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Zhu, W.H.; Zhu, Y.; Tatarchuk, B.J. A simplified equivalent circuit model for simulation of Pb–acid batteries at load for energy storage application. Energy Convers. Manag. 2011, 52, 2794–2799. [Google Scholar] [CrossRef]
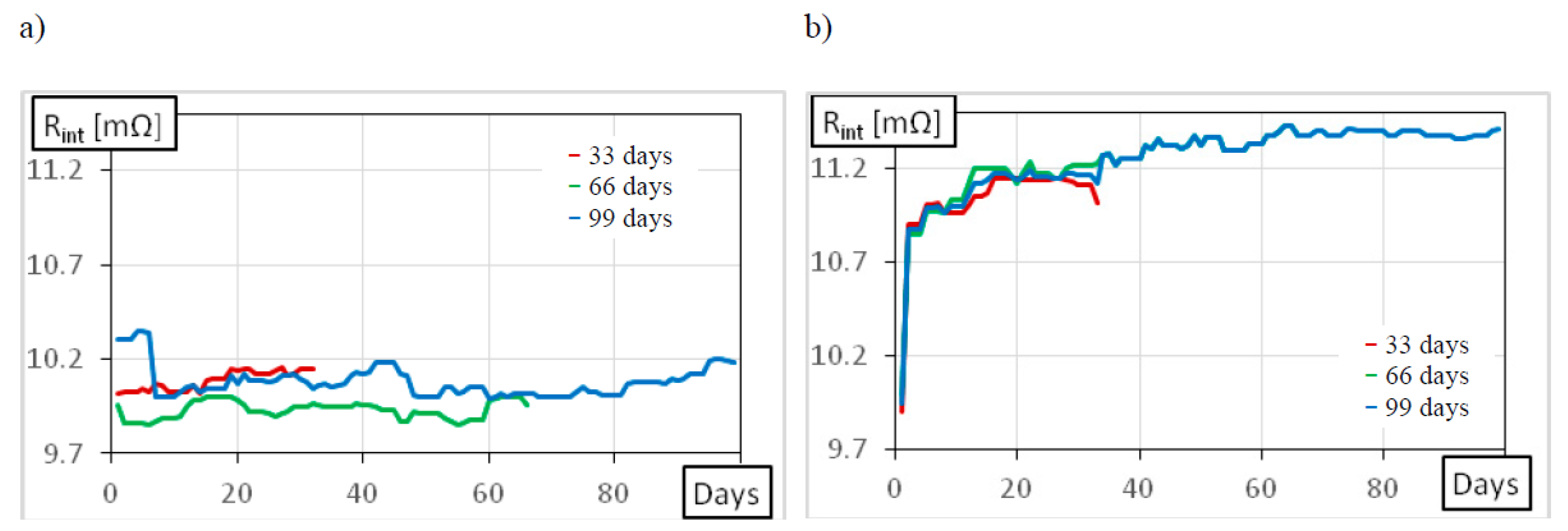
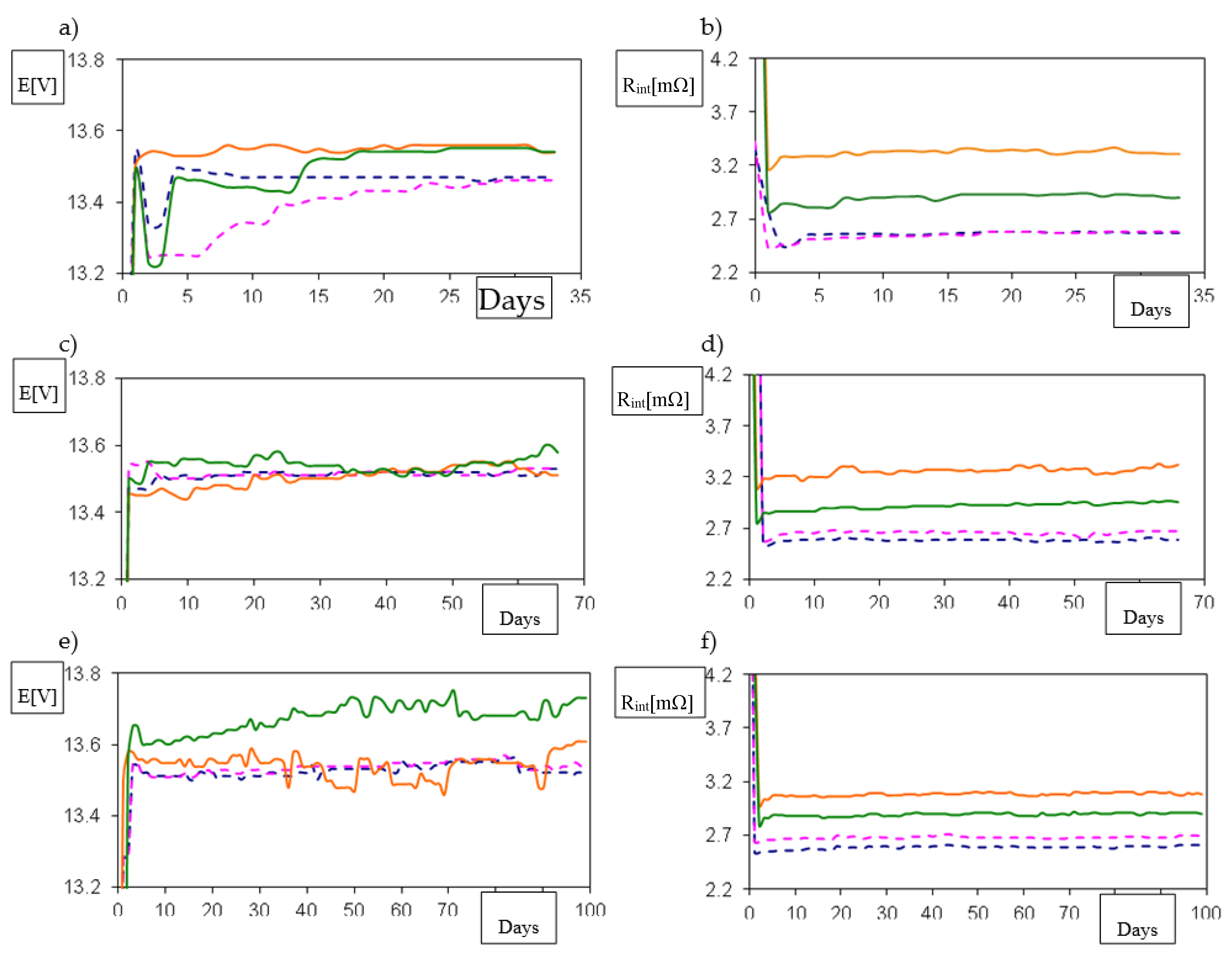
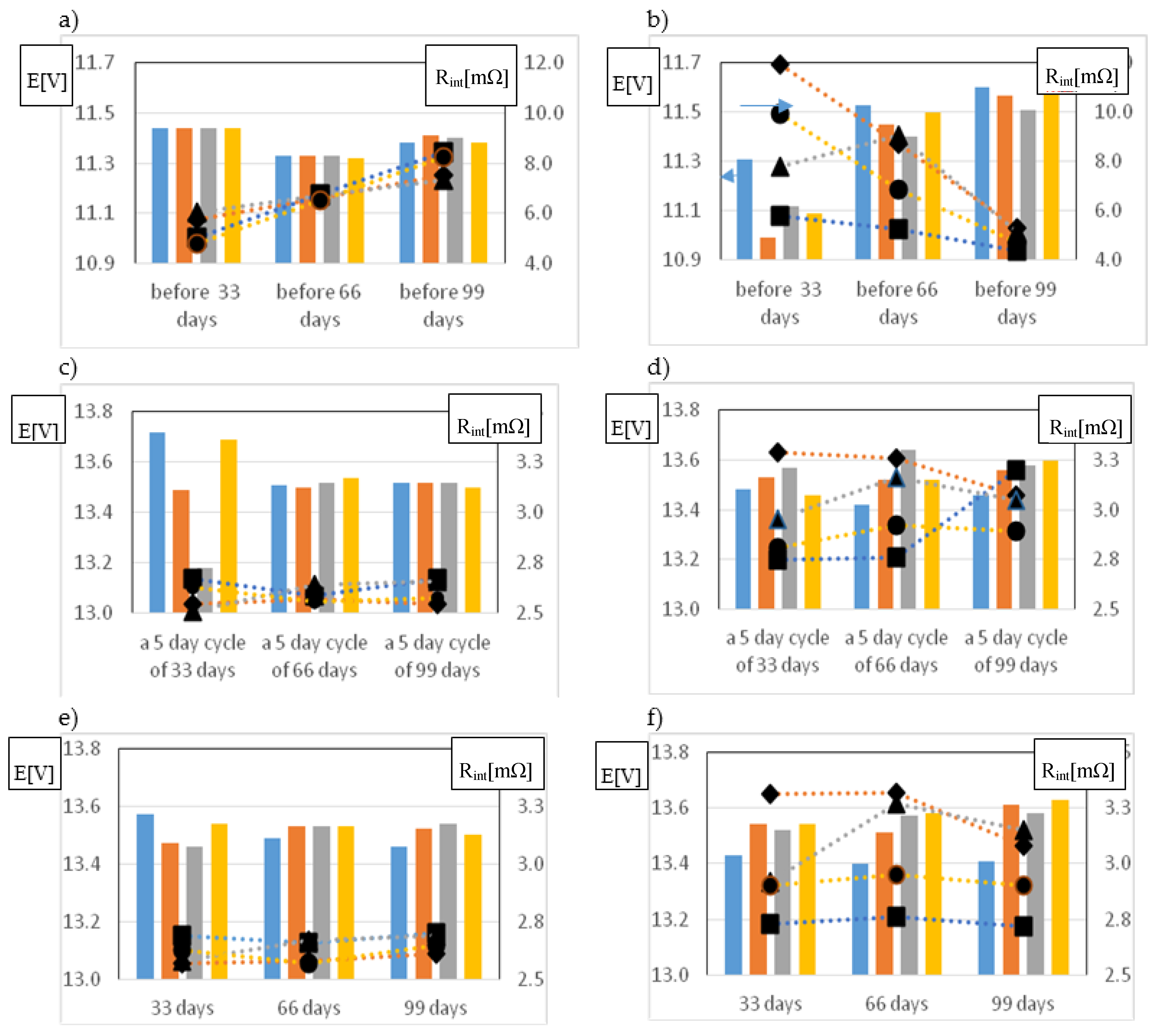
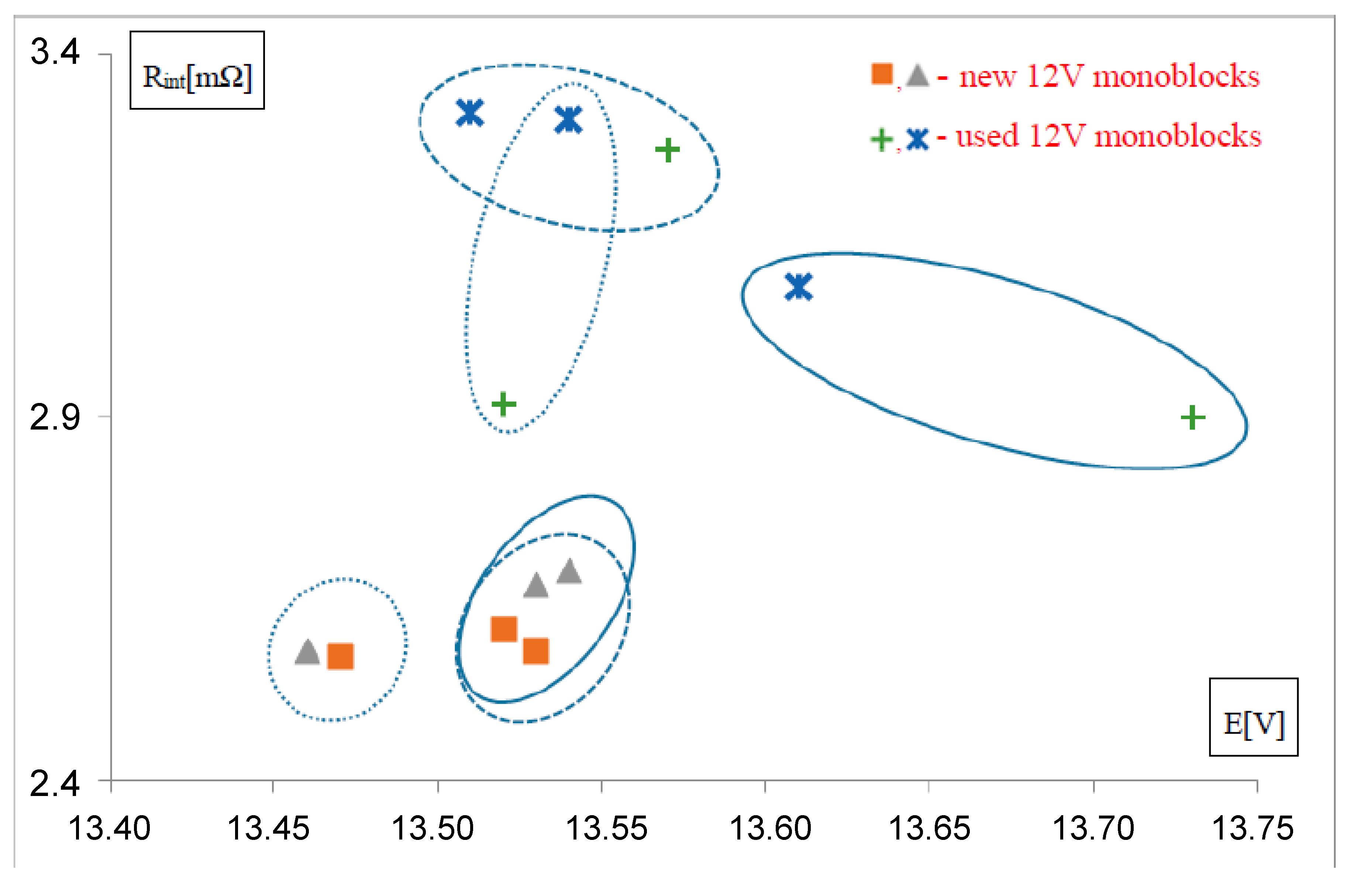



| Time of Float Charge (d) | Capacity of a Brand New 48 V Battery (Ah) | Capacity of a Used 48 V Battery (Ah) |
|---|---|---|
| 0 * | 109 | 109 |
| 33 | 113 | 103 |
| 66 | 114 | 82 |
| 99 | 116 | 76 |
| Test | Brand New (1) (Ω) | Brand New (2) (Ω) | Used (1) (Ω) | Used (2) (Ω) |
|---|---|---|---|---|
| 33 days | 0.0026 | 0.0026 | 0.0033 | 0.0029 |
| 66 days | 0.0026 | 0.0027 | 0.0033 | 0.0029 |
| 99 days | 0.0026 | 0.0027 | 0.0031 | 0.0029 |
| No. of Battery–Days | L0 (H) | RHF (Ω) | R1 (Ω) | QO (S·sn) | n |
|---|---|---|---|---|---|
| U9-33 | 2.83 × 10−7 | 0.00276 | 0.03350 | 22.27 | 0.75 |
| U9-66 | 3.02 × 10−7 | 0.00275 | 0.02449 | 18.38 | 0.78 |
| U9-99 | 3.52 × 10−7 | 0.01950 | 0.01879 | 24.70 | 0.72 |
| U10-33 | 2.68 × 10−7 | 0.00315 | 0.01724 | 27.31 | 0.71 |
| U10-66 | 2.89 × 10−7 | 0.00330 | 0.02405 | 17.67 | 0.78 |
| U10-99 | 3.69 × 10−7 | 0.01370 | 0.02088 | 18.62 | 0.78 |
| U12-33 | 2.89 × 10−7 | 0.00288 | 0.01870 | 28.53 | 0.70 |
| U12-66 | 3.14 × 10−7 | 0.00299 | 0.02335 | 18.34 | 0.77 |
| U12-99 | 3.80 × 10−7 | 0.01990 | 0.02210 | 18.80 | 0.77 |
| N13-33 | 2.97 × 10−7 | 0.00270 | 0.01817 | 18.83 | 0.77 |
| N13-66 | 3.06 × 10−7 | 0.00258 | 0.01664 | 20.05 | 0.75 |
| N13-99 | 2.94 × 10−7 | 0.00267 | 0.02458 | 14.12 | 0.81 |
| N14-33 | 3.27 × 10−7 | 0.00258 | 0.02084 | 16.93 | 0.79 |
| N14-66 | 3.25 × 10−7 | 0.00254 | 0.01569 | 19.12 | 0.76 |
| N14-99 | 2.51 × 10−7 | 0.00260 | 0.02276 | 14.11 | 0.81 |
| N15-33 | 3.01 × 10−7 | 0.00260 | 0.02014 | 17.36 | 0.79 |
| N15-66 | 3.48 × 10−7 | 0.00256 | 0.01606 | 18.63 | 0.76 |
| N15-99 | 2.28 × 10−7 | 0.00261 | 0.02302 | 14.16 | 0.81 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Majchrzycki, W.; Jankowska, E.; Baraniak, M.; Handzlik, P.; Samborski, R. Electrochemical Impedance Spectroscopy and Determination of the Internal Resistance as a Way to Estimate Lead-Acid Batteries Condition. Batteries 2018, 4, 70. https://doi.org/10.3390/batteries4040070
Majchrzycki W, Jankowska E, Baraniak M, Handzlik P, Samborski R. Electrochemical Impedance Spectroscopy and Determination of the Internal Resistance as a Way to Estimate Lead-Acid Batteries Condition. Batteries. 2018; 4(4):70. https://doi.org/10.3390/batteries4040070
Chicago/Turabian StyleMajchrzycki, Włodzimierz, Ewa Jankowska, Marek Baraniak, Piotr Handzlik, and Robert Samborski. 2018. "Electrochemical Impedance Spectroscopy and Determination of the Internal Resistance as a Way to Estimate Lead-Acid Batteries Condition" Batteries 4, no. 4: 70. https://doi.org/10.3390/batteries4040070
APA StyleMajchrzycki, W., Jankowska, E., Baraniak, M., Handzlik, P., & Samborski, R. (2018). Electrochemical Impedance Spectroscopy and Determination of the Internal Resistance as a Way to Estimate Lead-Acid Batteries Condition. Batteries, 4(4), 70. https://doi.org/10.3390/batteries4040070





