Real-Time Implementation of an Extended Kalman Filter and a PI Observer for State Estimation of Rechargeable Li-Ion Batteries in Hybrid Electric Vehicle Applications—A Case Study
Abstract
:1. Introduction
2. Li-Ion Battery: Terminology, Electric Model Circuit and Validation Tests, a Case Study
- (1)
- Battery selection criteria, identify the main disturbance and the factors that affect the battery performance
- (2)
- Battery terminology
- (3)
- BMS functions, hardware and software components
- (4)
- SOC direct measurement methods reported in the literature
- (5)
- Analytic battery models reported in the literature
- (6)
- Li-Ion battery model selection
- (7)
- ADVISOR MATLAB platform model validation, a case study
2.1. Li-Ion Battery Model Selection, Disturbances and the Factors Which Affect the Battery Performance
- Chemical changes: the battery is an electrochemical device which converts chemical energy into electrical energy or vice versa by means of controlled chemical reactions between a set of active chemicals. Typically, the desired chemical reactions inside the battery are usually accompanied by unwanted, parasitic chemical reactions which consume some of the active chemicals or impede their reactions. Even if the battery cell’s active chemicals remain unaffected over time, the battery cells can fail because unwanted chemical or physical changes to the seals keeping the electrolyte in place.
- Depletion of the active chemicals: under different conditions of pressure, temperature, electric field and duration of the reaction, the active chemicals in a battery cell may break down or combine in many different ways.
- Temperature effects: the battery operation has a strongly dependency on temperature, which is a crucial factor for safety consideration. Elevated temperatures during storage or use seriously affect the battery life since the chemical reactions inside the battery are driven by temperature. An increase in battery temperature leads to an increase in chemical reactions speed inside the battery cells. High temperatures provide an increased performance, but the rate of the unwanted chemical reactions will increase also affecting the battery life. The temperature affects both the shelf life and the life cycle of the battery, since the chemical reactions induce failures as a result of parasitic reactions within the battery cells. The thumb rule is that “for every 10 °C increase in temperature the reaction rate doubles”. Thus, an hour at 35 °C is equivalent to two hours at 25 °C in battery life, thus the heat is one of the strongest enemy for the battery; even small increases in temperature have a great impact on battery performance [18].
- Pressure effects: an increased internal pressure within a battery cell is usually the consequence of increased temperature. The “excessive currents or a high ambient temperature will cause the battery cell temperature to rise and the resulting expansion of the active chemicals will in turn cause the internal pressure in the battery cell to rise. Overcharging also causes a rise in temperature, but more seriously, overcharging can also cause the release of gases resulting in an even greater build up in the internal pressure”, as is stated in [18]. An increased pressure tends to magnify the effects of high temperature by increasing the rate of the chemical actions in the battery cell.
- Depth of discharge (DOD): is related to battery SOC as is defined in next Section 2.2 that at a given temperature and discharge rate is proportional with the amount of active chemicals transformed with each charge and discharge cycle. For almost all chemistries “the number of cycles yielded by a battery goes up exponentially the shallower the DOD”.
- Charging level: the life cycle of Lithium-Ion batteries can be increased by reducing the charging cut off voltage, i.e., gives the battery a partial charge instead of fully charging it.
- Charging rate: the battery life is also influenced by the charging rate. Essentially, at high discharge rates the battery capacity decreases since the transformation of the active chemicals are affected by the battery current drawn. The result is incomplete or unwanted chemical reactions, and thus, an associated decrease in capacity. This “may be accompanied by changes in the morphology of the electrode crystals such as cracking or crystal growth which adversely affect the internal impedance” of the battery cell, as is stated in [18]. Similar problems occur during battery charging cycles. There is a limitation as to how quickly the lithium ions can enter into the intercalation layers of the anode. Since the battery input current increases too much during the charging process, a “lithium plating” process takes place, and surplus ions are deposited on the anode in the form of lithium metal that results in an irreversible capacity loss. Conversely, maintaining the higher voltages needed for fast charging can lead to breakdown of the electrolyte which also results in capacity loss. Thus, with each battery charge/discharge cycle the accumulated irreversible capacity loss will increase [18].
- Voltage effects: The practical voltage limits are the consequence of the onset of undesirable chemical reactions which take place beyond the safe operating conditions range. Protection circuits are “designed to keep the battery cell well within its recommended working range with limits set to include a safety margin” [18].
- Cell aging effects: the “passage of current through the battery cell and the heating and cooling the cell is subjected to will cause small changes in the microstructure or morphology of the active chemicals” [18]. A battery “does not have infinite life time due to unwanted chemical reactions, including electrolyte decomposition, physical damage, and the loss of active materials in the battery” [18]. These are irreversible changes that usually cause unrecoverable capacity fade, and deteriorate the battery performance, such as increase of internal resistance and high self-discharge rate [18]. These aging effects of the battery ultimately will result in battery failure. The aging process is caused by complex operating conditions affected by the number of cycling, ambient temperature, DOD, and current rate [18]. Also, in [18] are summarized the following aging effects:
- ○
- High temperature accelerates the aging of the battery in both cycling and calendar modes;
- ○
- Large DOD variance speeds up the aging process;
- ○
- Arduous current cycle profile accelerates the aging process.
- Coulombic efficiency (CE): it is not a standard definition for CE, but we can roughly define it as charge capacity at the end of the discharge cycle with the battery cell fully recharged divided by charge capacity at the beginning of the charge cycle. The CE is also called faradaic efficiency or current efficiency and describes the charge efficiency by which electrons are transferred in batteries. CE can be defined also as the ratio of the total charge extracted from the battery to the total charge put into the battery over a full cycle. Li-Ion battery has one of the highest CE ratings in rechargeable batteries class. It offers an efficiency that exceeds 99 percent. This, however, is only possible when the Li-Ion battery is charged at a moderate input current and at cool temperatures. Conversely, ultra-fast charging lowers the CE because of losses due to charge acceptance and heat, so also does a very slow charge in which self-discharge comes into play. The coulombic efficiency of Li-Ion improves with cycling, some start at 99.5 percent and reached 99.9 percent within 30 cycles [18]. The consistency on repeat tests is high, reflected in a very stable Li-Ion battery system. Unlike Li-Ion batteries, the Lead acid batteries reach a CE of about 90 percent, and nickel-based batteries have a CE lower than 90 percent. With fast charge, NiCad and NiMH may reach 90 percent but a slow charge reduces this to about 70 percent [18]. Lower charge acceptance when above 70 percent SOC and self-discharge that increases when the battery gets warm toward the end of charge are contributing factors for the low CE. Best efficiencies of Li-Ion batteries attain mid-range SOC of 30–70 percent [18]. All battery chemistry systems provide unique CE values that vary with charge rates and temperature. Also, the age has a considerable impact on CE. Precise measurements on Coulombic efficiency provides an excellent method of characterizing the essential aspects of Li-Ion battery cells and performance providing very quick answers with reasonably small samples. It enables technologies to be ranked by their Coulombic efficiency and is particularly useful as a lab tool for comparing the effects of alternative materials on cell performance.
- Loss of electrolyte: any reduction in the volume of the battery cell’s active chemicals will reduce directly the cell’s electrical capacity.
- Internal resistance: the internal resistance of the battery is affected by the following factors: conductor resistance, electrolyte resistance, ionic mobility, separator efficiency, reactive rates at the electrodes, and concentration polarization, temperature effects and changes in SOC. When a battery fails, it is typically since it has built up enough internal resistance that it can no longer supply a useful amount of power to an external load, according to the maximum power transfer between the source and the load, as is stated in [15]. The actual ageing process results in a gradual reduction in Li-Ion battery capacity over time. When a battery cell reaches its specified lifetime it does not stop working suddenly, the ageing process continues at the same rate as before so that a battery cell whose capacity had fallen to 80% after 1000 cycles will probably continue working to perhaps 2000 cycles when its effective capacity will have fallen to 60% of its original capacity [15]. Moreover, an alternative measure of the battery life cycle is related to the battery cell internal resistance. In this case the life cycle is defined as the number of cycles the battery can perform before its internal resistance increases by an agreed amount usually 1.3 times or double its initial value when is new [15].
- Insulation resistance: it is well described in [15]. Also, in [15] the HEV is considered as a “complex production of mechanical-electrical integration”, for which the power supply typically being in the range 100–500 V is obtained by means of several series battery packs. The BMS hardware devices consisting of high voltage components, the traction battery, electrical motor and energy recycle device, the battery charger and its auxiliary device deal with a large current and insulation [15], thus, insulation issues must be under consideration from the design stage. As is stated in [15], the poor working conditions, such as shaking, corrosion, changes in temperature and humidity, “could cause fast aging of the power cable and insulation materials, or even brake the insulation, which would decrease the insulation strength and endanger personnel”. Thus, needs to ensure safety operating conditions for personnel are required to evaluate the insulation conditions for entire HEV’s BMS. The national standard (NS) 18384.3-2001, stipulates several safety requirements for HEVs, especially for insulation resistance state, measurement method, that are shown in [15]. According to NS, the insulation state of an EV is evaluated according to the ground insulation resistance of the DC positive and negative bus. The definition of traction battery insulation resistance in NS “is the relative resistance to maximum leakage current (in the worst condition) where there is a short between the traction battery and ground (electric chassis)”, as is mention in [15]. Thus, to ensure the insulation security of on-board BMS, it is necessary to detect the insulation resistance and raise an alarm in time.
2.2. Li-Ion Battery Terminology
2.3. Battery Management System: Functions, Hardware and Software Components
2.4. Li-Ion Battery SOC Measurement Methods Reported in the Literature
2.4.1. Laboratory Tests and Chemistry Dependent Methods
- A laboratory method for determining SOC consists of completely discharge a cell, recording discharged ampere-hours, to determine its remaining available capacity. This method “is the most accurate SOC measurement technique, but is impractical in HEV as the battery energy is wasted by the test, and the test cannot dynamically estimate SOC”, as is stated in [7].
- Chemistry-dependent methods for other chemistries, e.g., lead-acid batteries, are all inappropriate since our application is using Li-Ion battery.
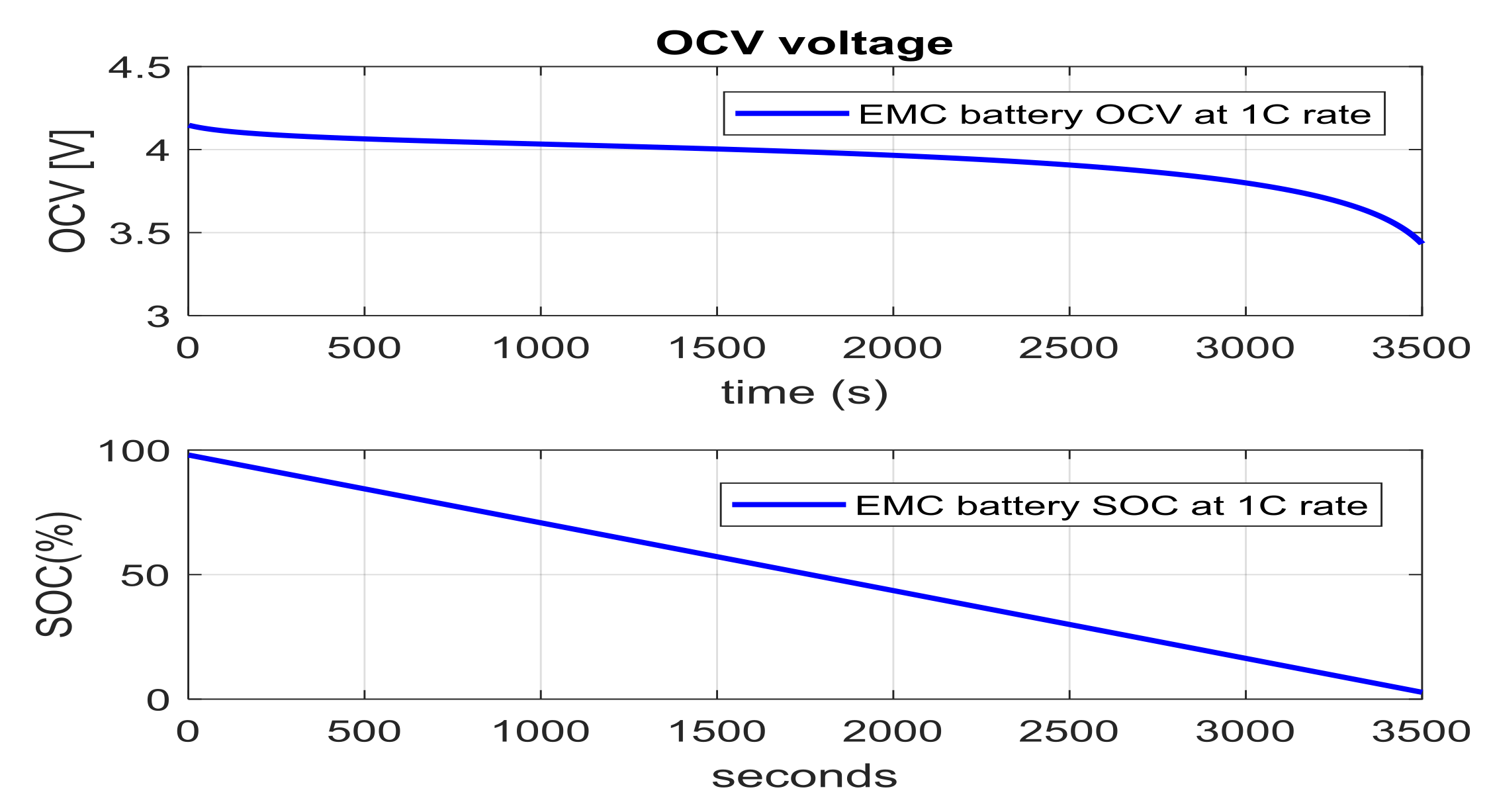
- Open-circuit voltage (OCV) measurements. “If the battery cell is allowed to rest for a long period, its terminal voltage decays to OCV that may be used to infer SOC via a lookup table” [7]. However, long periods of battery inactivity sometimes hours must occur before the terminal voltage approaches OCV. But, the method may not be used for dynamic SOC estimation due to the fact that “long periods of battery inactivity, sometimes hours, must occur before the terminal voltage approaches OCV”, as is stated in [7], and also “this method includes the dependence of OCV on temperature, and presence of terminal voltage hysteresis, especially at low temperatures” [7].
2.4.2. Electro-Chemical Methods
2.4.3. Impedance Spectroscopy
2.4.4. Equivalent Electric Circuit Models
2.4.5. Coulomb Counting
2.4.6. Artificial Neural Networks (ANN)
2.4.7. Model Based State Estimation Techniques
2.5. Linear and Nonlinear Analytic Li-Ion Battery Models in State Space Representation Reported in Literature
2.5.1. Electrochemical Models
2.5.2. Computational Intelligence Based Models
2.5.3. Analytical Models
2.5.4. Stochastic Models
2.5.5. Electric Circuit Models
- model only with SOC as state: is the simplest model capable to estimate the battery terminal voltage in a limited way, but was improved later by adding to the model multiple states
- a combined model that has SOC as a state and predicts the terminal battery voltage as a combination of three nonlinear models, separately or all together, the second one being adopted in our case study [3,7]:
- ○
- Shepherd model:
- ○
- Unnewehr universal model:
- ○
- Nernst model:
- The zero-state hysteresis model, conceived to compensate partially the hysteresis effect, one of the main drawback of a simple model. The cell voltage lags the predicted voltage in some sense [7]; more precisely, it may also be defined as a characteristic of a system in which a change in the direction of the independent variable leads to the dependent variable failing to retrace the path it passed in the forward direction [7]. This model adds no additional states for hysteresis, so it is named the “zero-state hysteresis model”.
- The one-state hysteresis model is an improvement over the simple model where the slow transition in the level of the hysteresis from charging and discharging cycles may be modeled by adding a “hysteresis state”.
- The enhanced self-correcting (ESC) model is conceived to model the “relaxation effect”, implemented as a low-pass filter on input current , since the cell model must accurately predict its behavior in a dynamic HEV environment [7].
- Adding temperature dependence to the model, as is done briefly in [7] that shows how to incorporate temperature dependence into the models. According to [7] a very simple method, can use a table of different models, where each model had parameters optimized for a specific temperature. The second method used in [7] performs a joint optimization over the entire temperature range, where every parameter is represented by a continuous fourth order polynomial of temperature to force nearby models to have similar parameter values. The cell data were collected from UDDS tests can be provided by ADVISOR MATLAB platform described in Section 2.7, and the optimization method performed at 16 controlled temperatures from −30 to 45 °C, in increments of 5 °C. This second method did not result in modeling errors as low as when individually optimized; the generalization performance was much better [7].
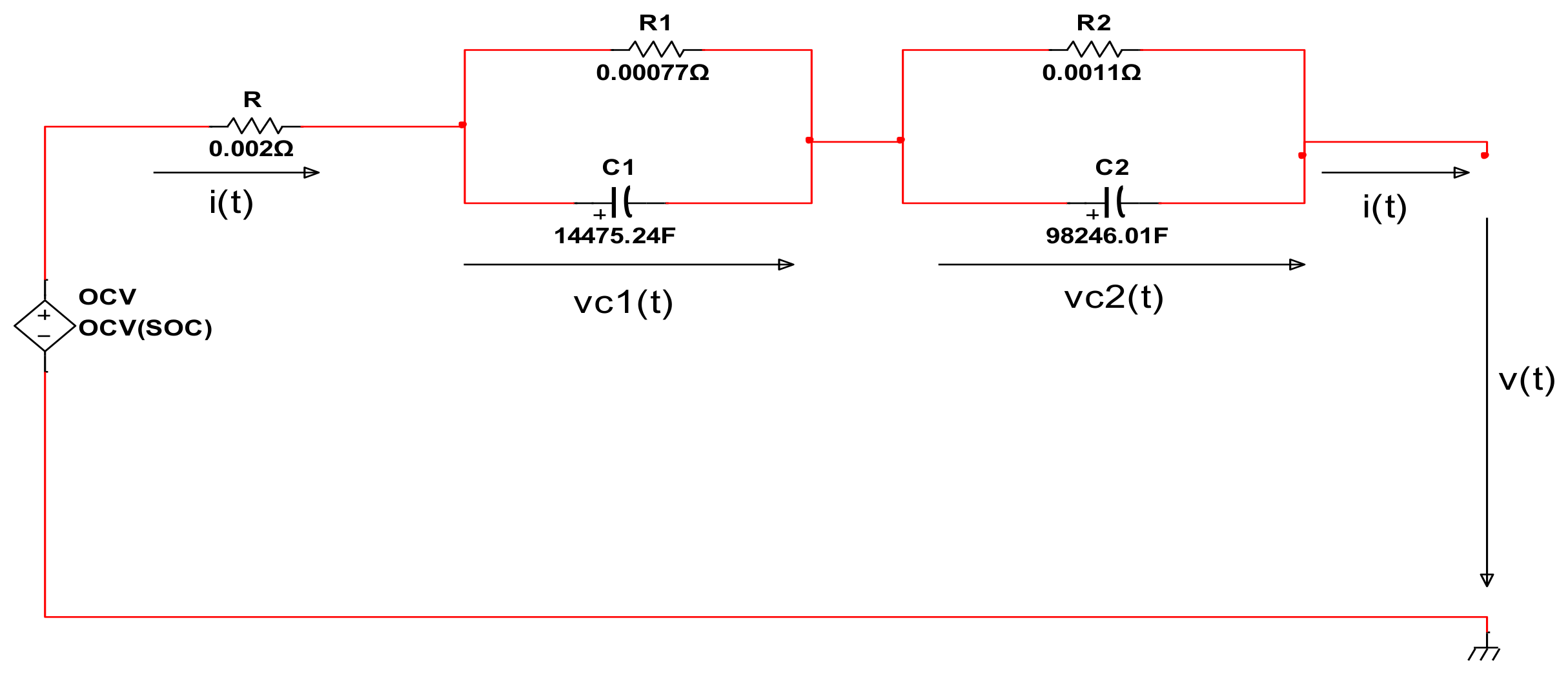
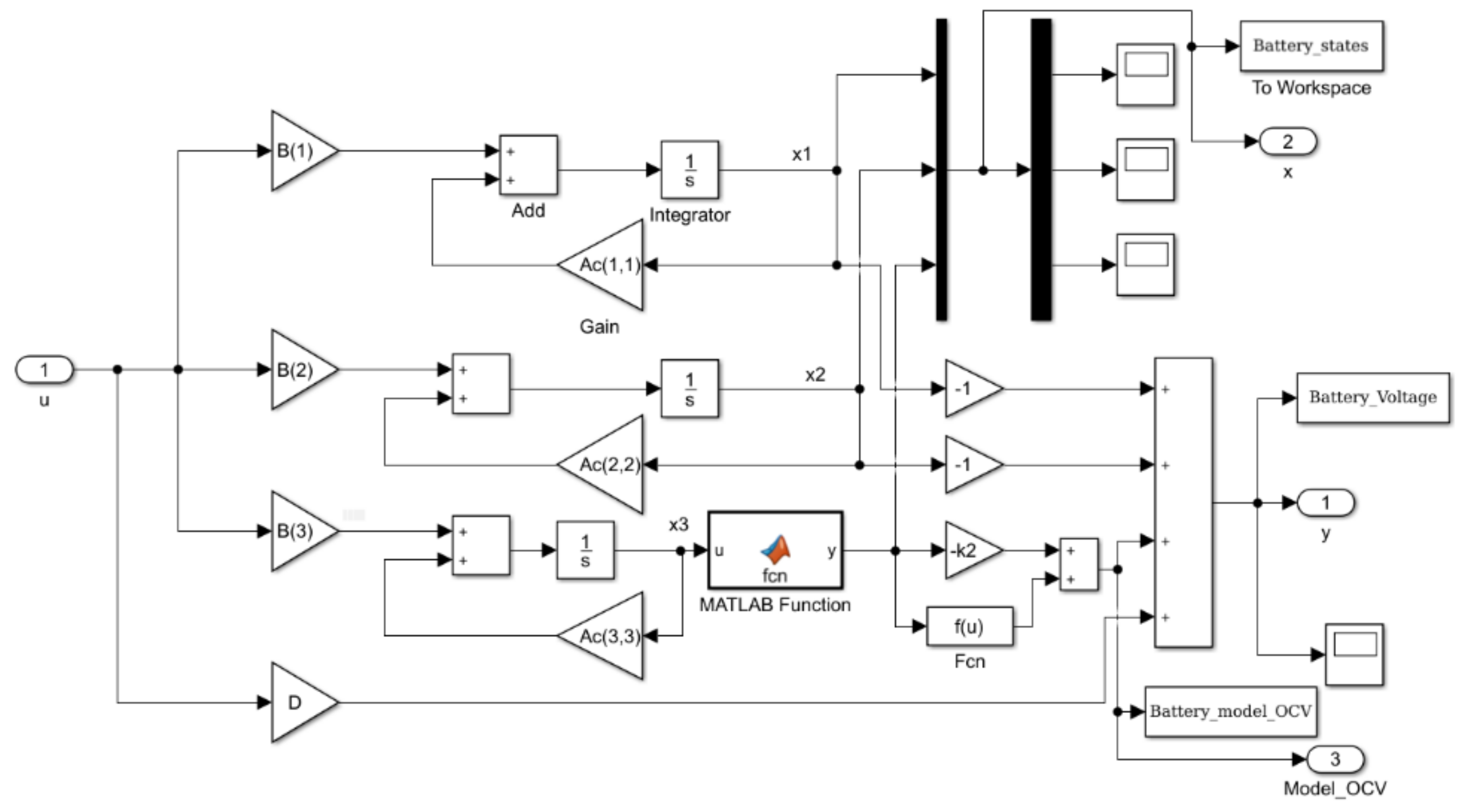
2.6. Li-Ion Battery Equivalent Model Circuit in State Space Representation
2.6.1. Continuous Time State Space Representation
2.6.2. Discrete Time State-Space Representation
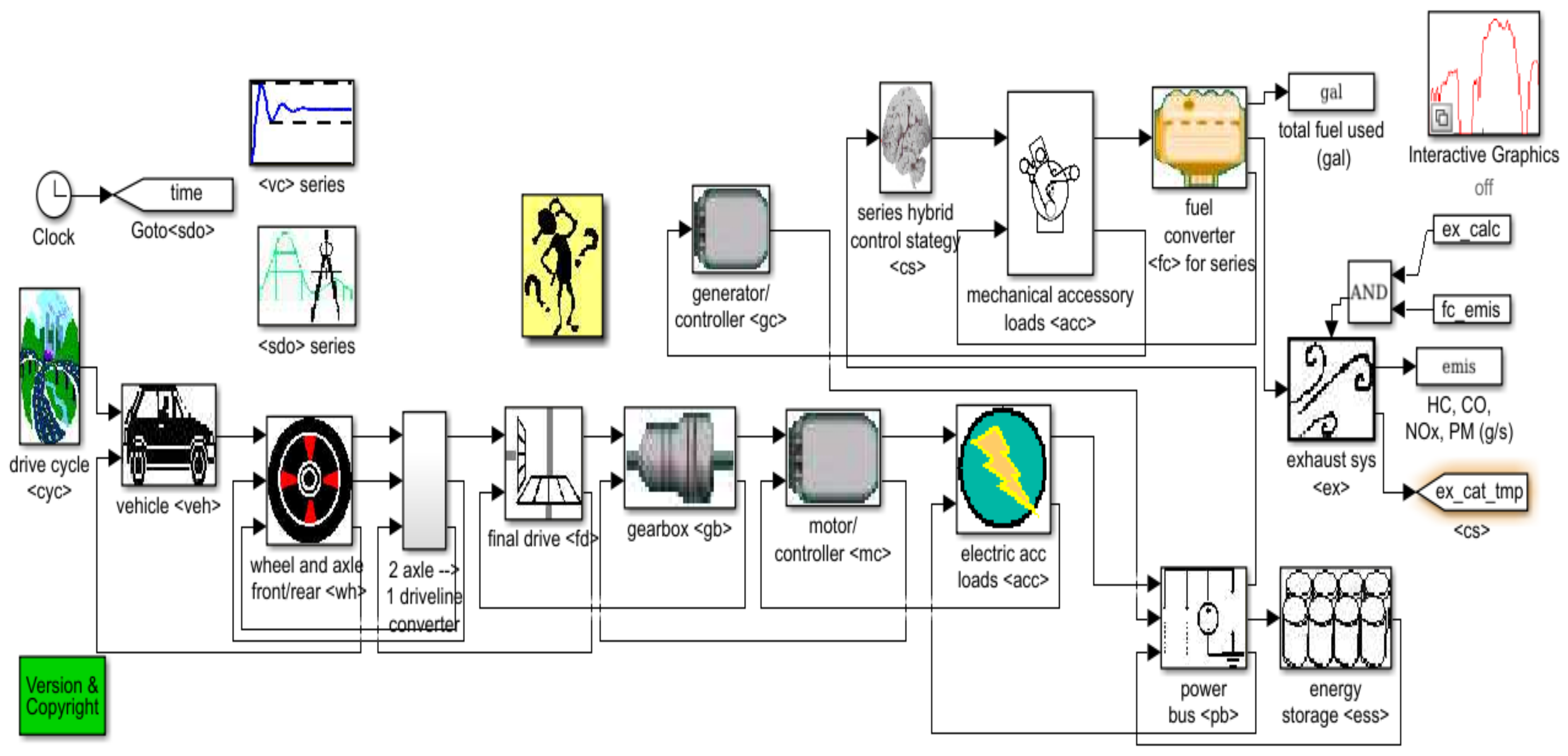
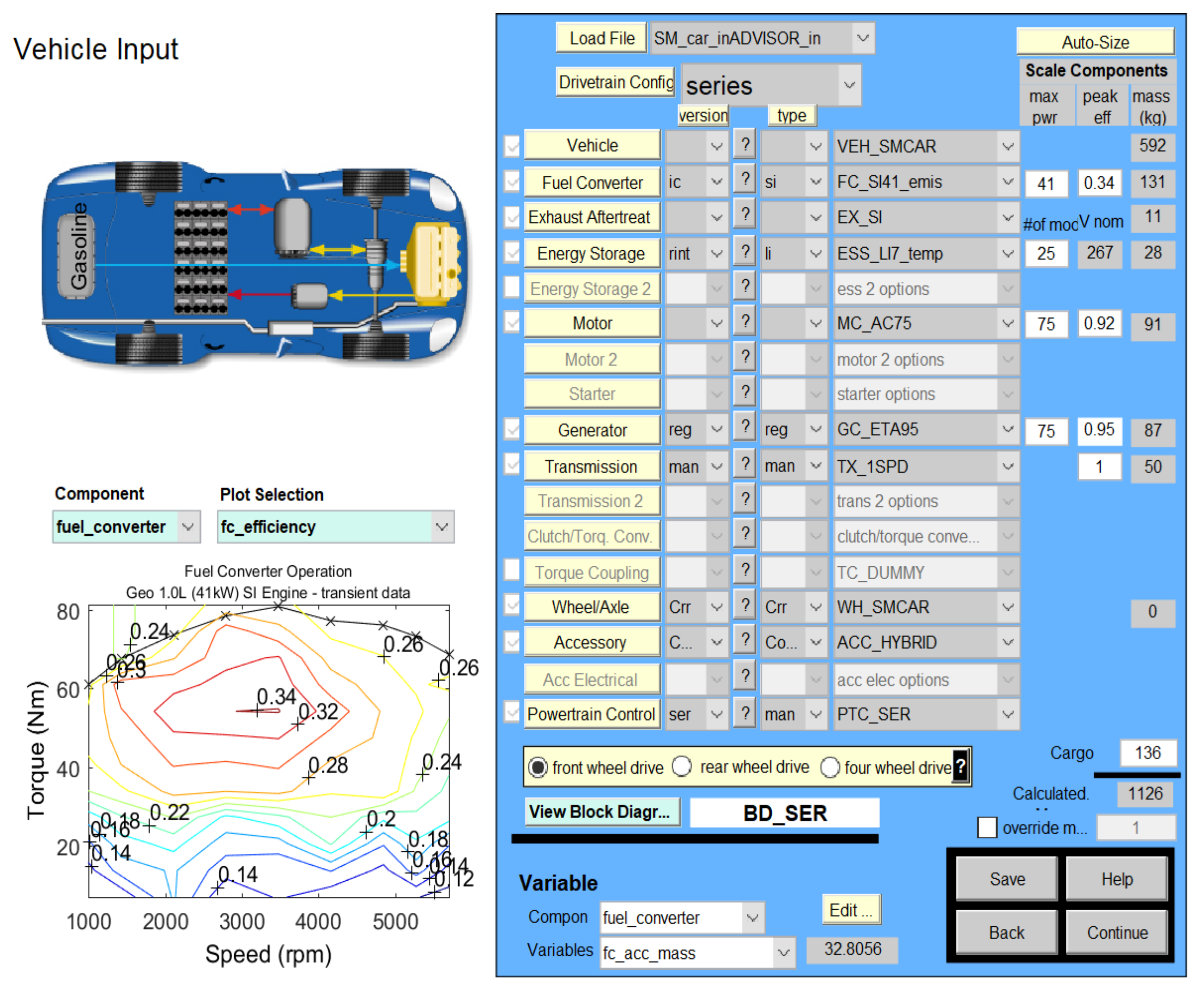
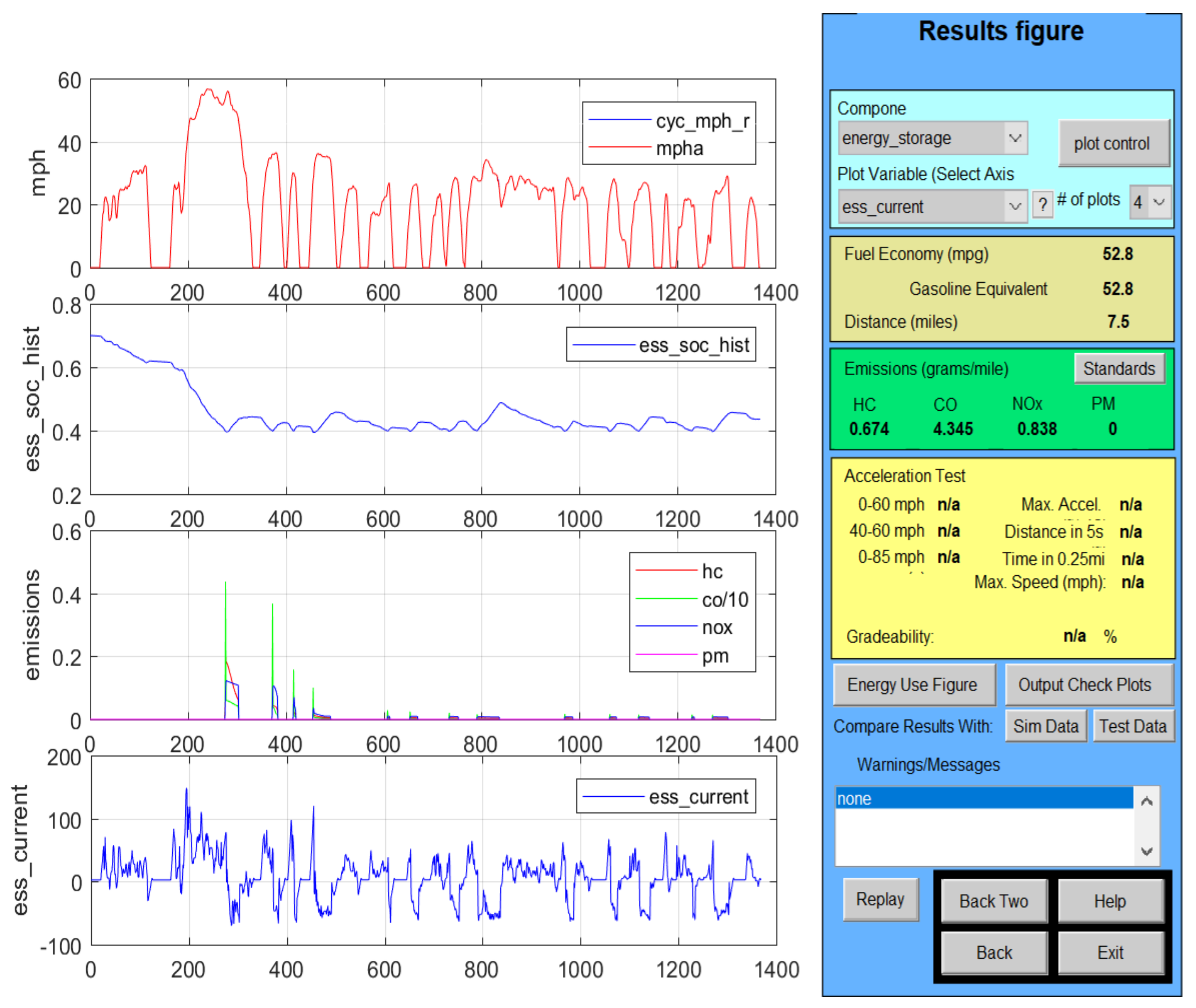
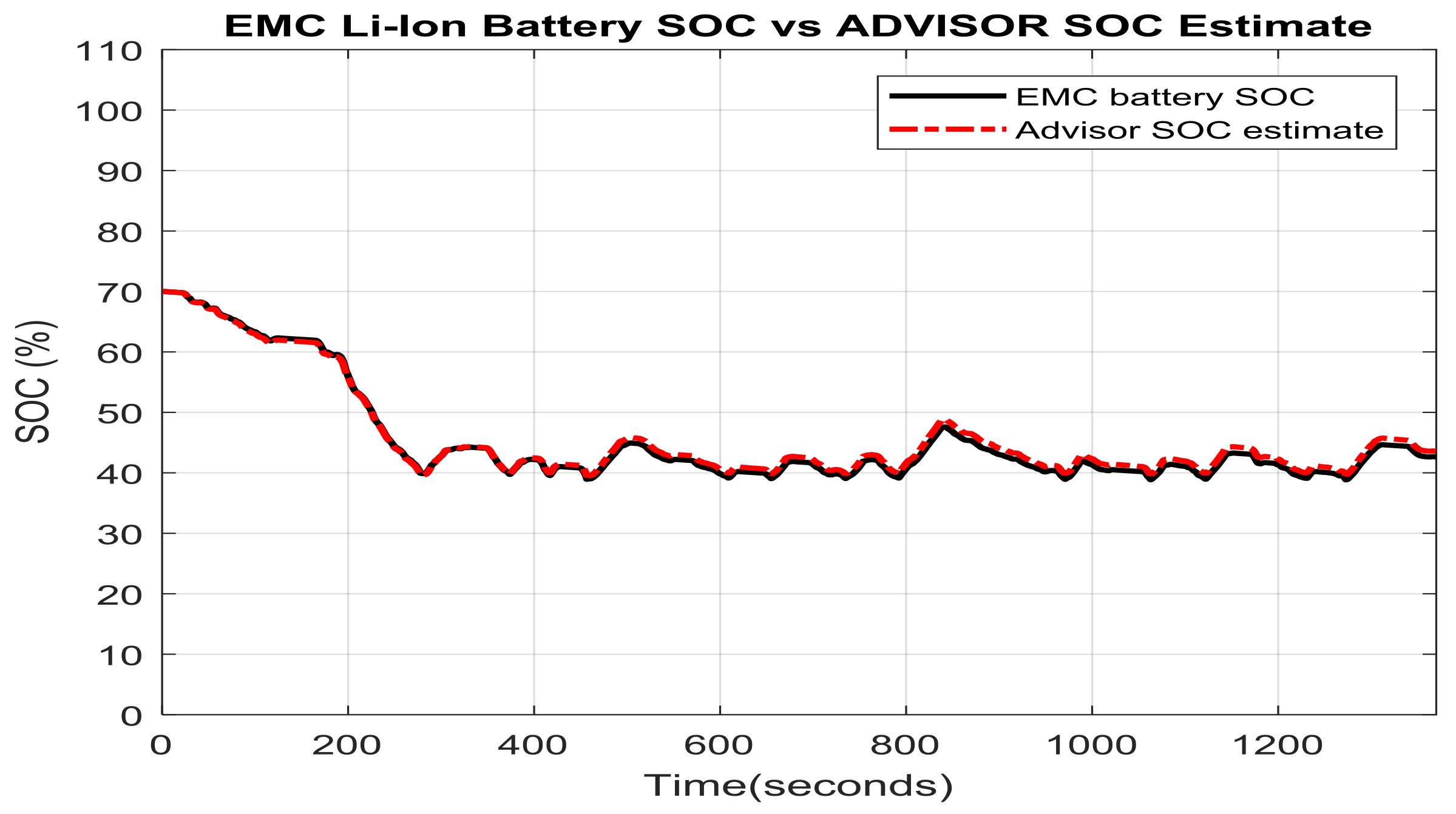
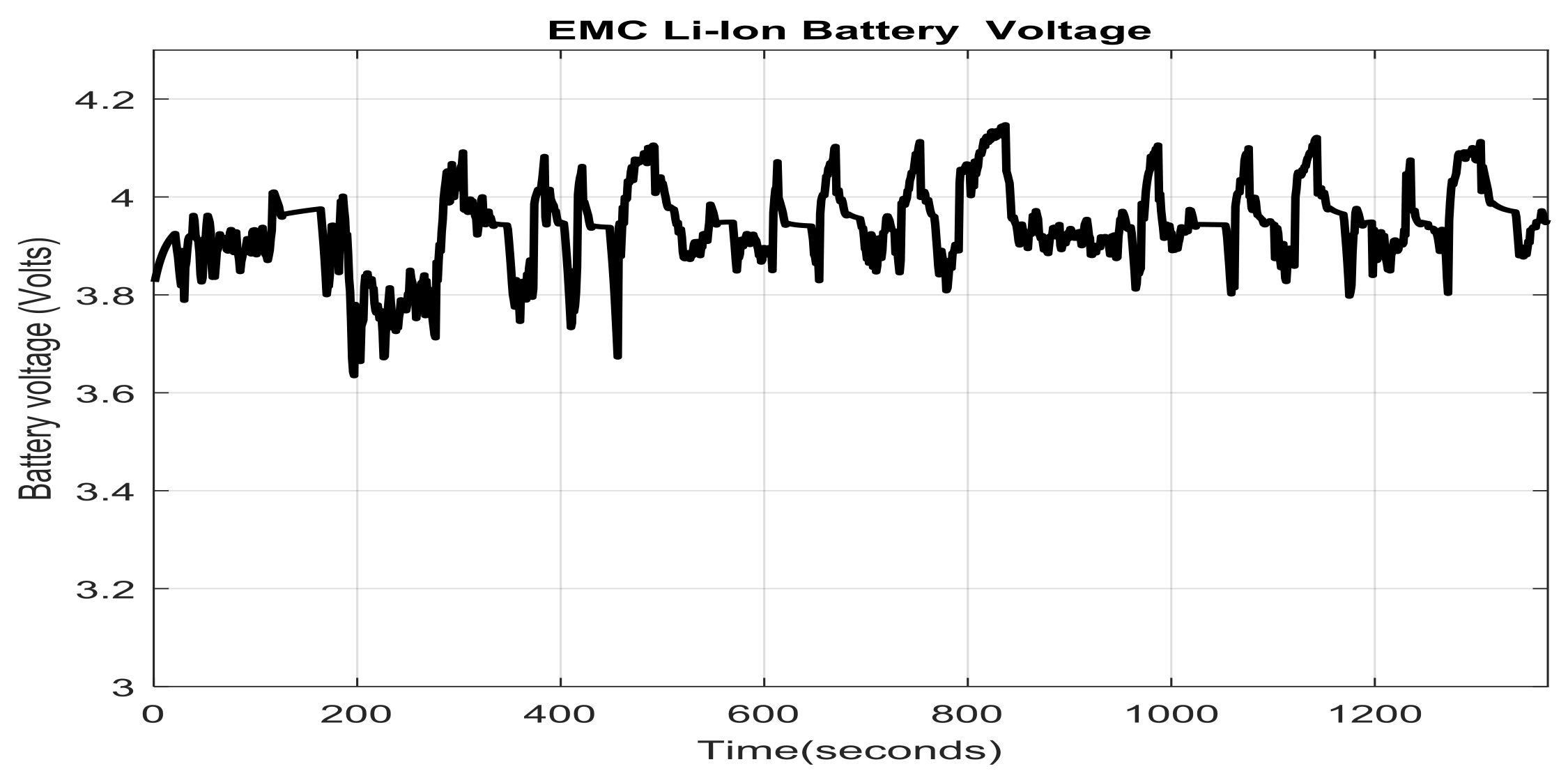
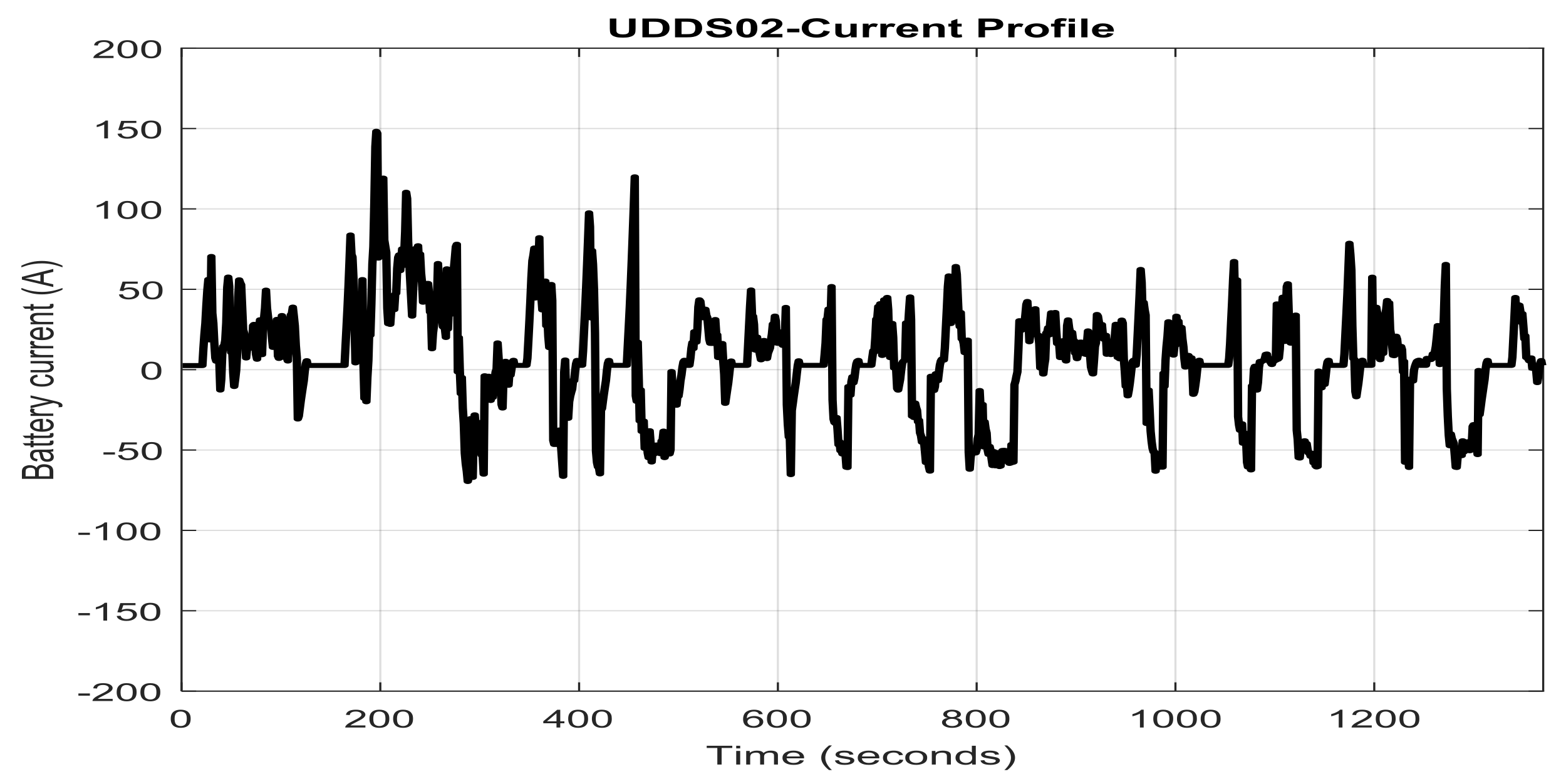
2.7. Li-Ion Battery Equivalent Circuit Model Validation in ADVISOR MATLAB Platform, a Case Study
- an internal resistance model (Rint)
- a resistance–capacitance model (RC)
- a partnership for a new generation of vehicles (PNGV) capacitance model (PNGV model)
- a neural network (nnet) lead acid model (PbA nnet)
- a fundamental lead acid battery model (PbA fund)
- a cold-start phase (505 s) known as bag 1
- a hot-transient (870 s) known as bag 2
- a hot-start (505 s) known as bag 3
3. Extended Kalman Filter and Proportional Integral Observer Real Time SOC Estimators
3.1. Real Time Extended Kalman Filter SOC Estimator Design
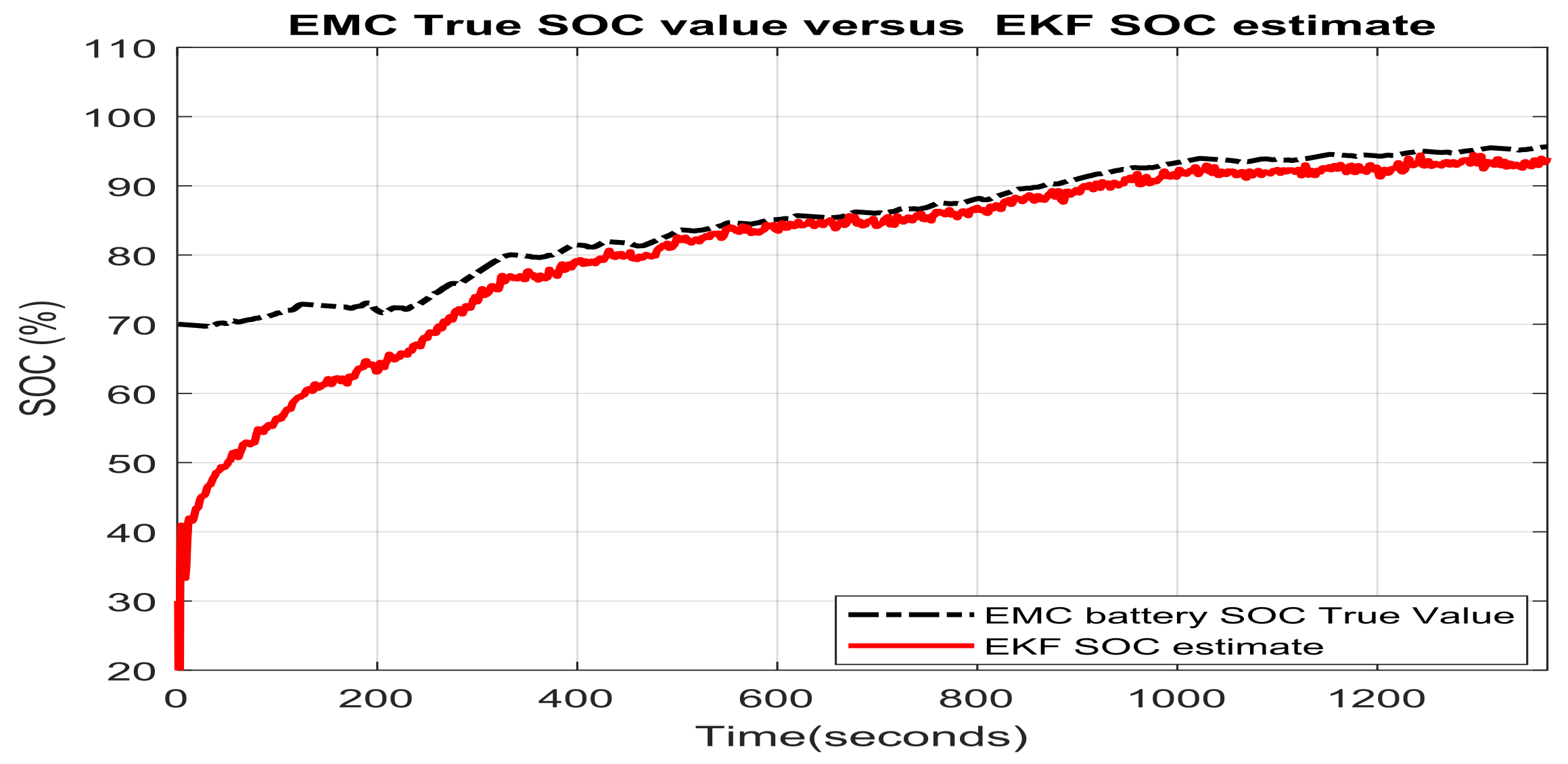
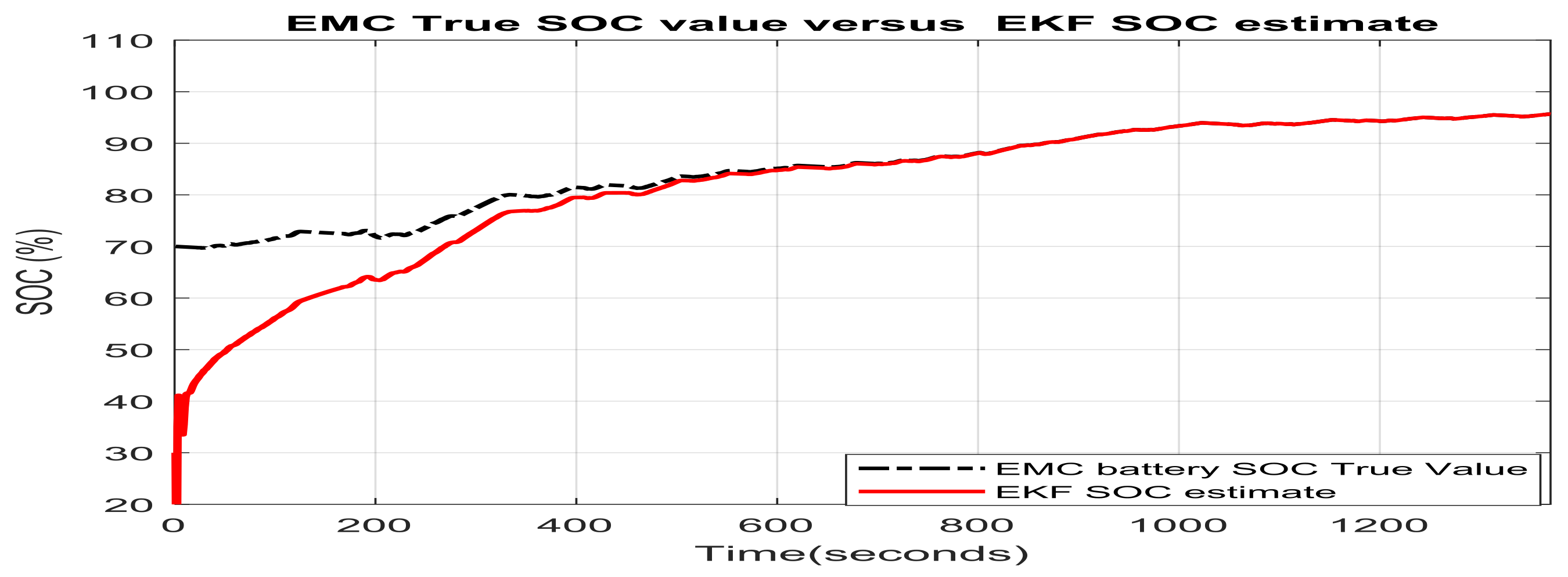
3.1.1. Real Time EKF SOC Estimator Implementation on MATLAB Platform, Simulation Results and Performance Analysis
- changes (increase or decrease) in SOC initial values
- simultaneous changes in SOC initial value and measurement current sensor noise level
- simultaneous changes in SOC initial values and changes in internal resistance of Li-Ion battery 2RC EMC (two time increase of room temperature resistance value given in Table 1) due to the effects mentioned in Section 2.1, especially the changes in temperature effects
- simultaneous changes in SOC initial value and the nominal value of the battery nominal capacity due to aging and/or temperature effects
3.1.2. Temperature Effects on Li-Ion Battery Model Parameters and on Real Time EKF SOC Estimator Implementation, Simulation Results and Performance Analysis on MATLAB Platform
- A simplification is done by separately studying each parameter and its variation with respect to SOC(k) and T.
- The nonlinear equation for the specified parameter is used to generate data for a range of SOC and sometimes for different temperatures (depending on the case).
- These data will be introduced to a curve fitting procedure where an expression of lower order has to be found.
- The output of the high order equations model and the output of the lower order equations model are compared.
- Step 1. Initiate a battery discharging cycle at a nominal discharging current based on a given SOC interval step to obtain the effect of SOC on OCV parameter
- Step 2. Measure the internal impedance:
- Step 3. Apply a curve fitting method to obtain the resistive and capacitive RC battery polarization cell component values based on the measured internal impedance at the various temperature conditions.
- Step 4. Update the battery model parameters dynamically based on the collected data and self-heating, described by the following thermal model equation [22]:where m is the battery mass (kg), is the specific heat (J/(kg·K)), are the RC polarization cells voltages, is the heat transfer coefficient , is cell surface area (), is the cell temperature (K) and is the ambiental temperature (K). This thermal model is easy to be modeled in SIMULINK. In [22], p. 50, Table 3.1 are given the values of the extracted model parameters for four different temperatures: , shown below in Table 2 also:
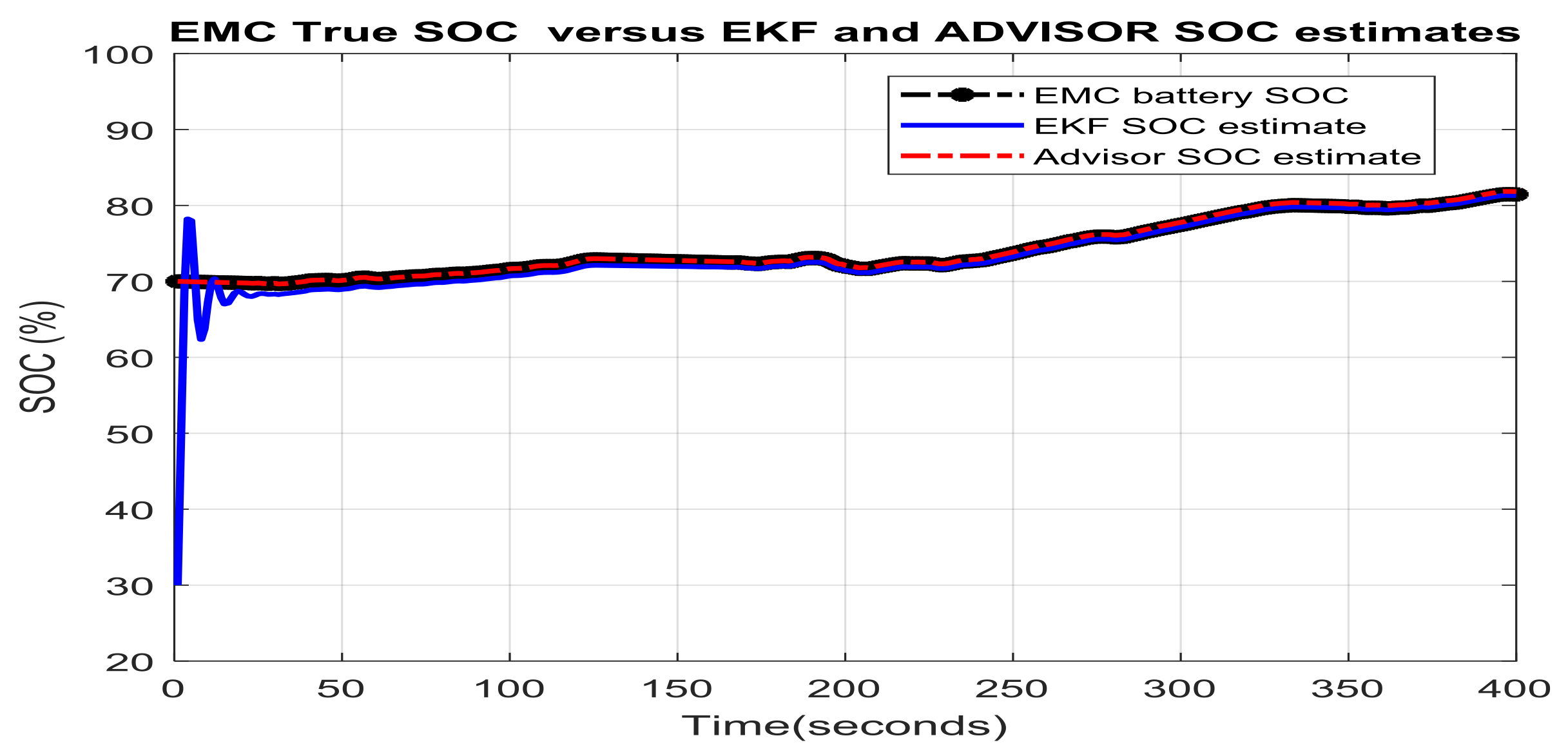
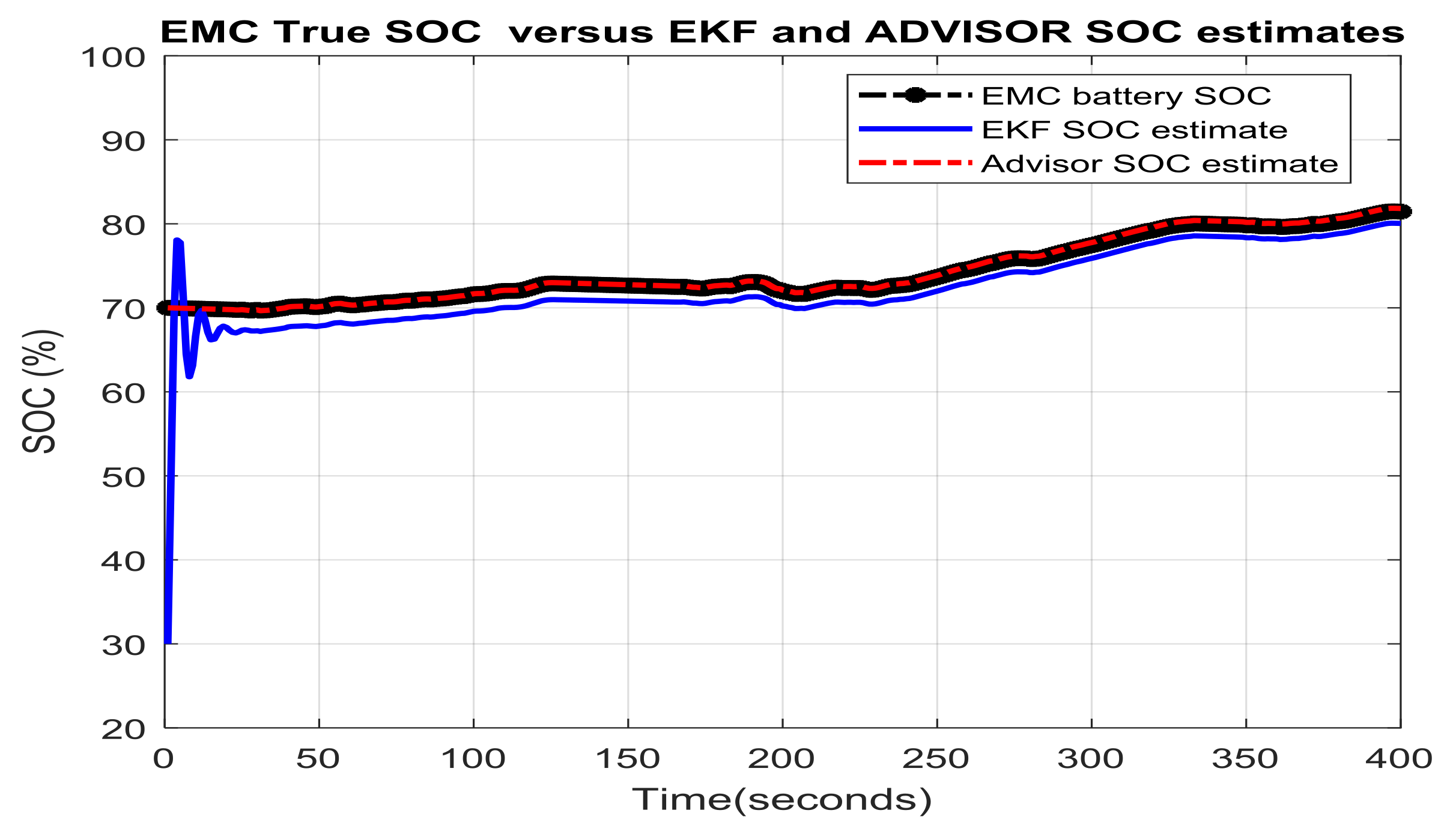
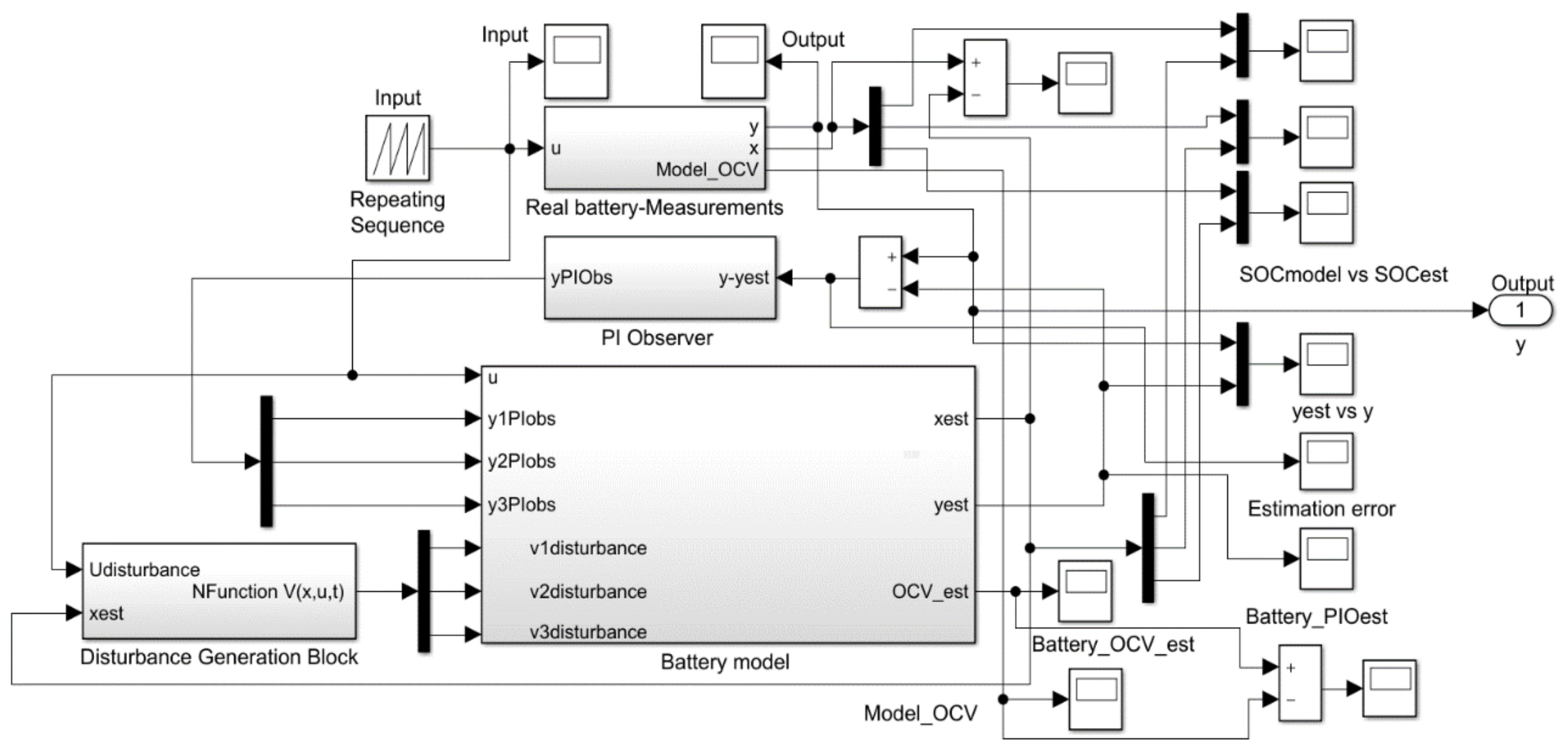
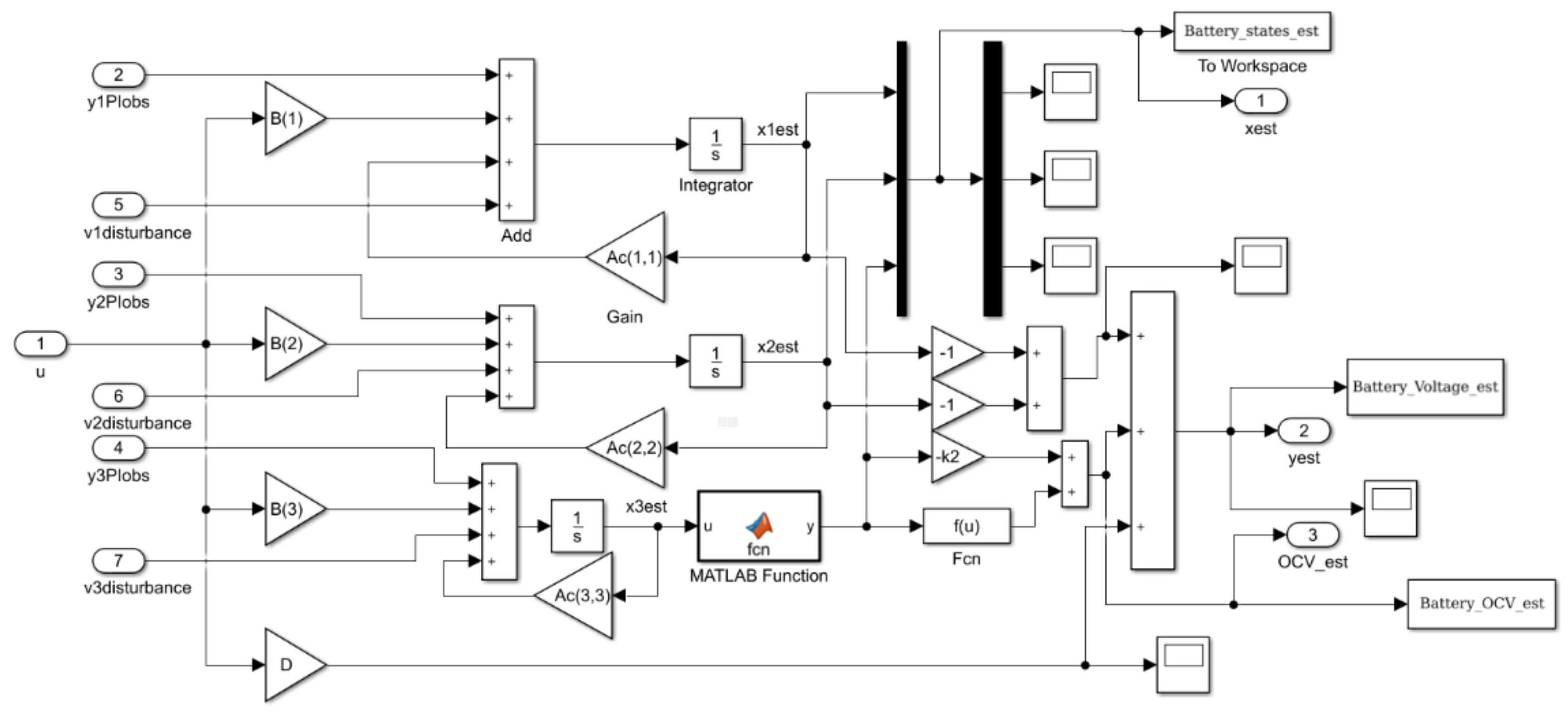
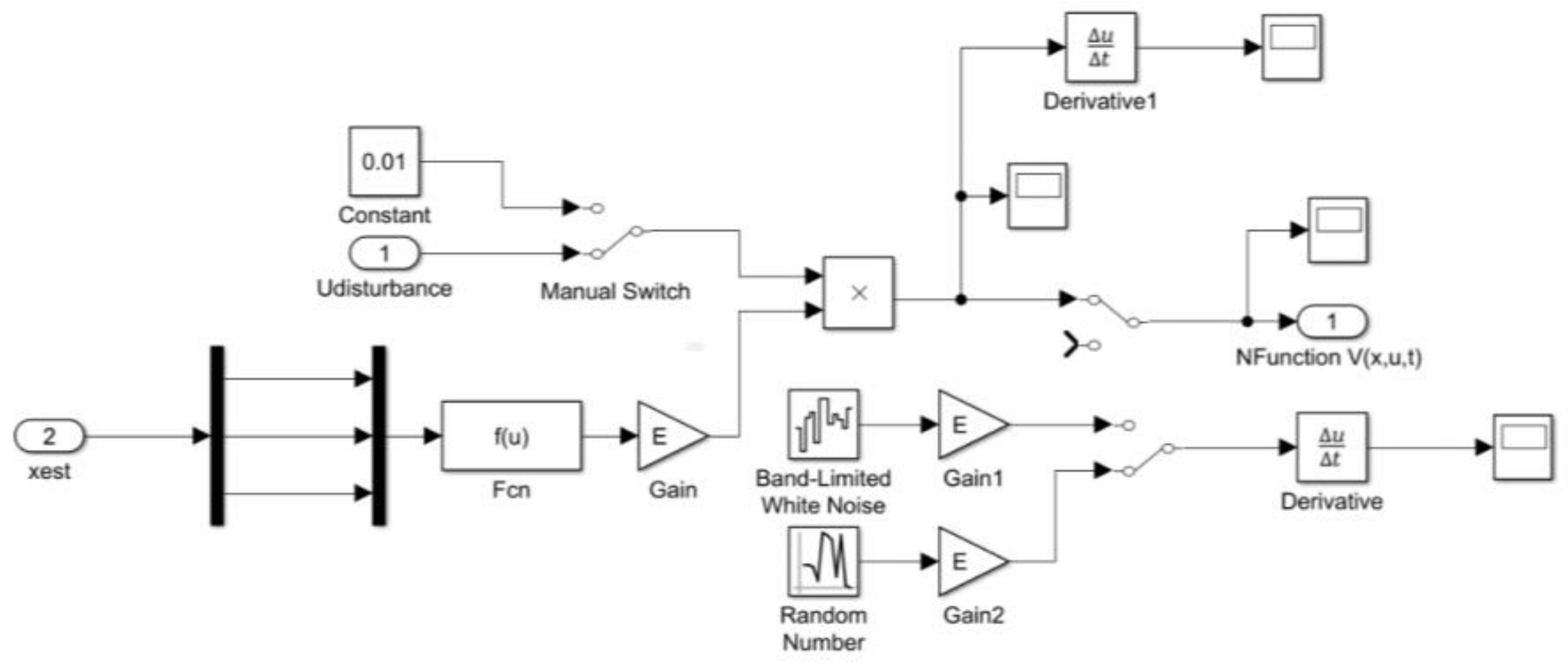
3.2. Real-Time PI Observer SOC Estimator
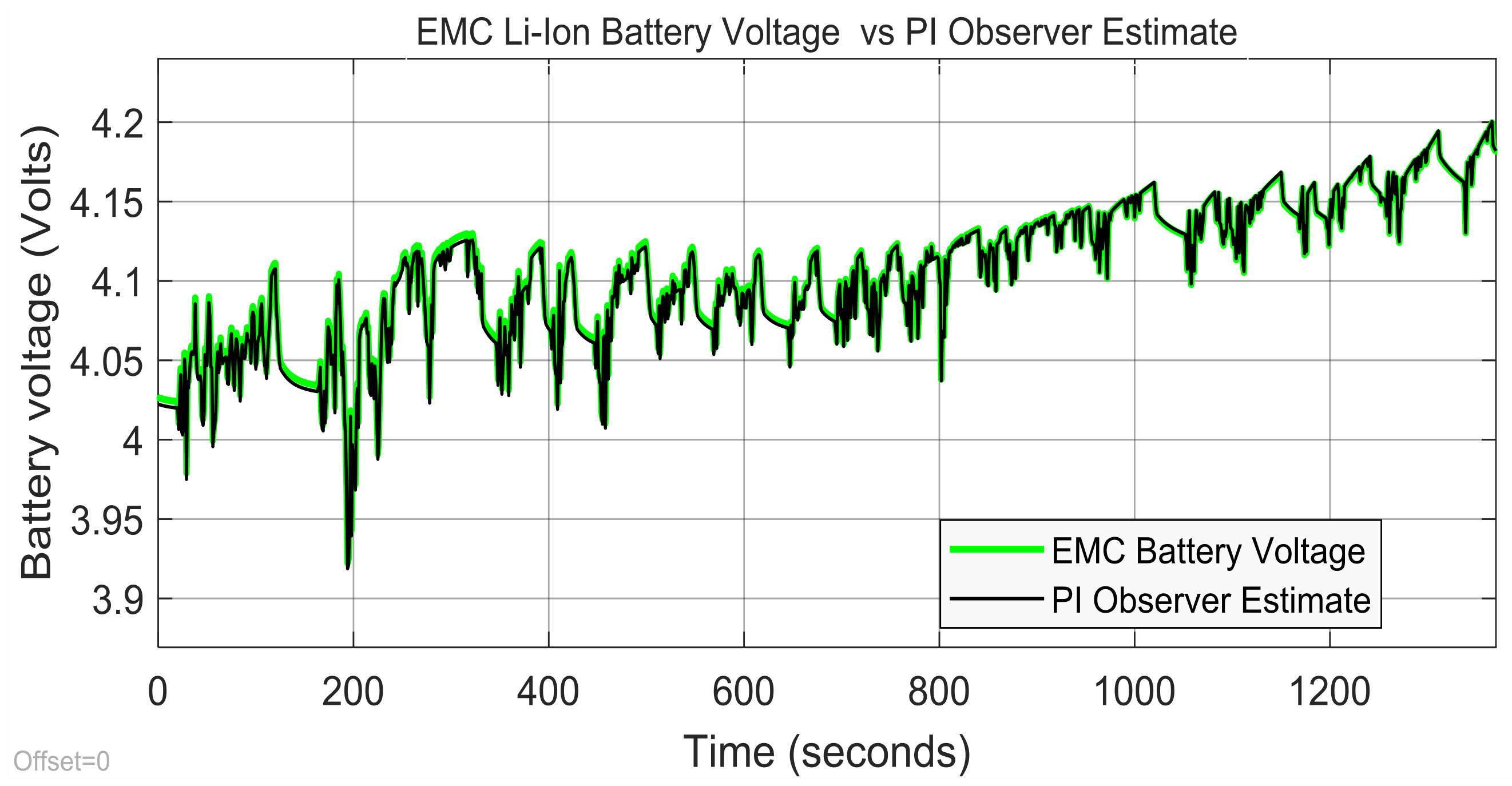
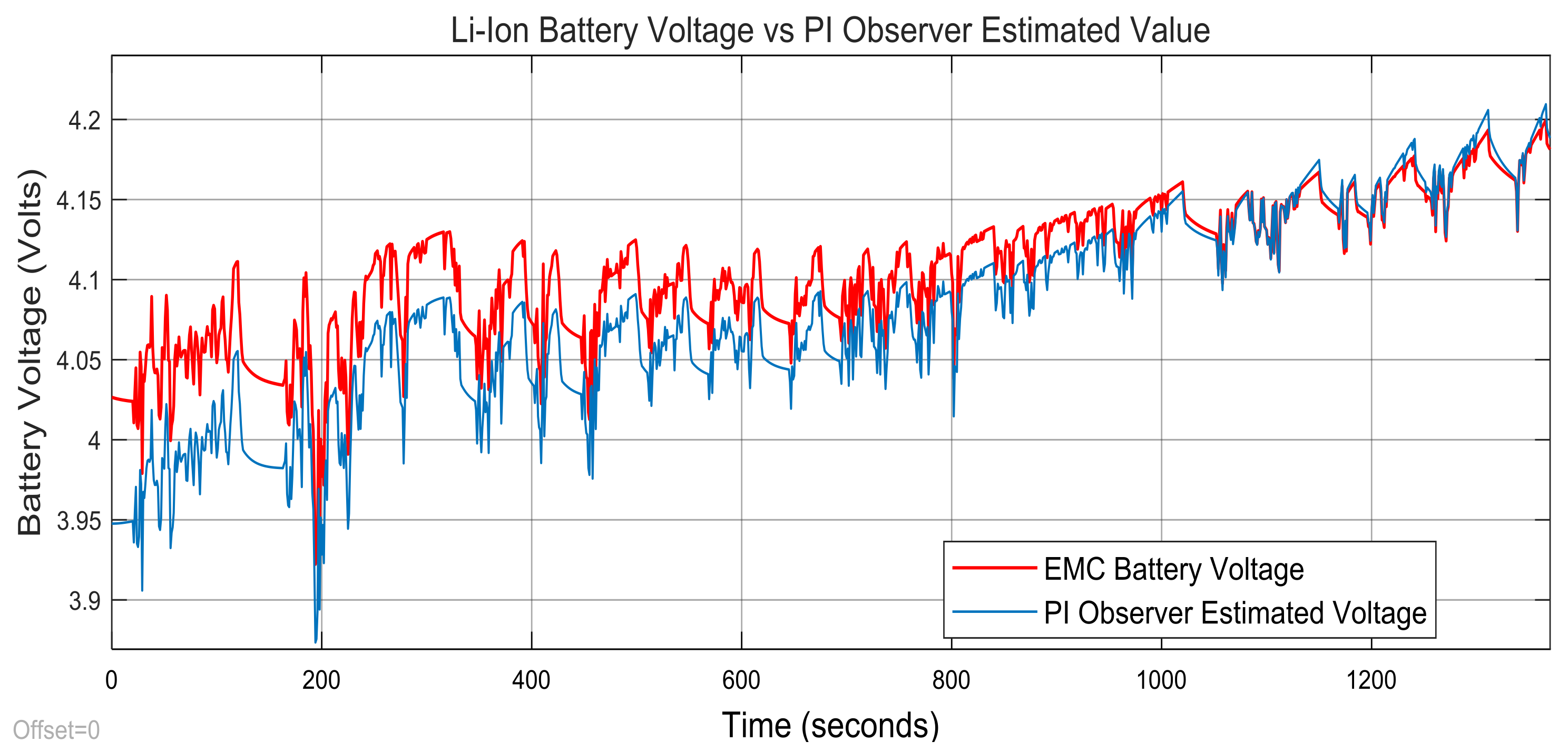
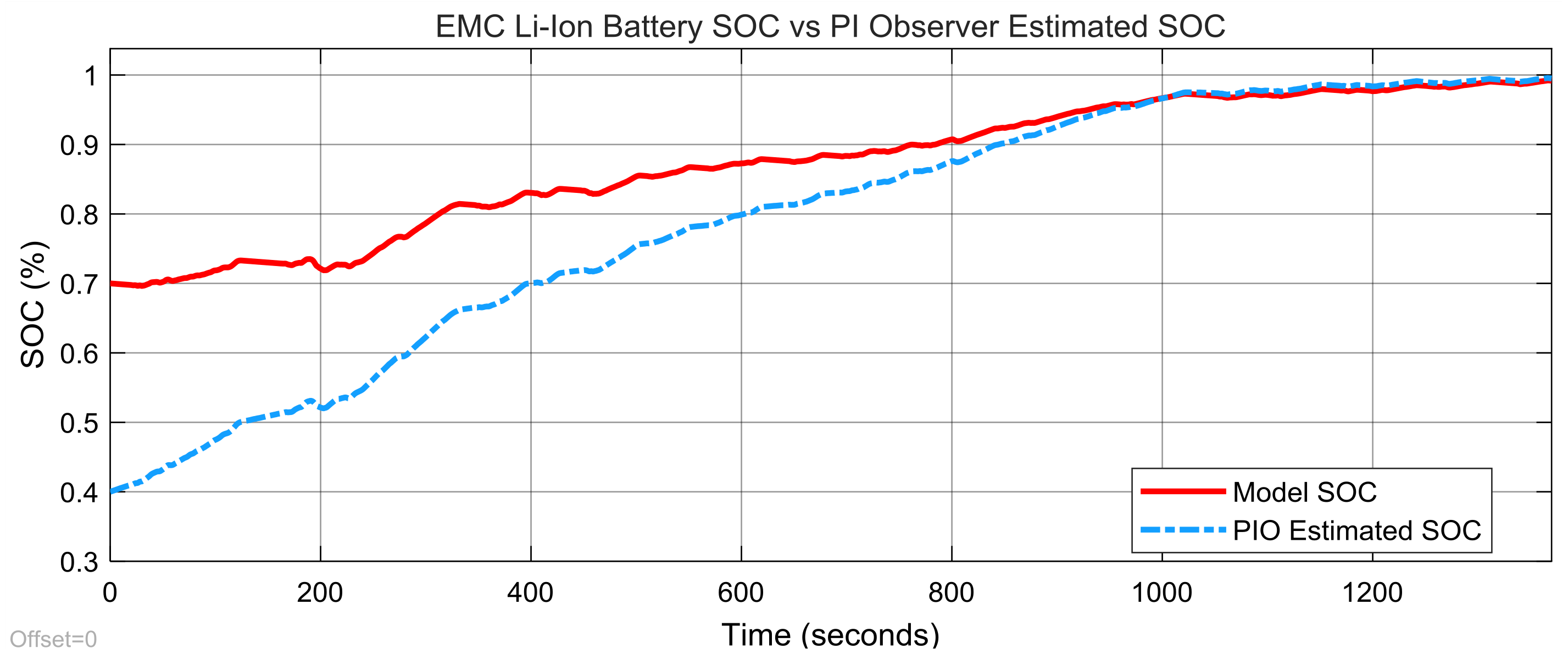
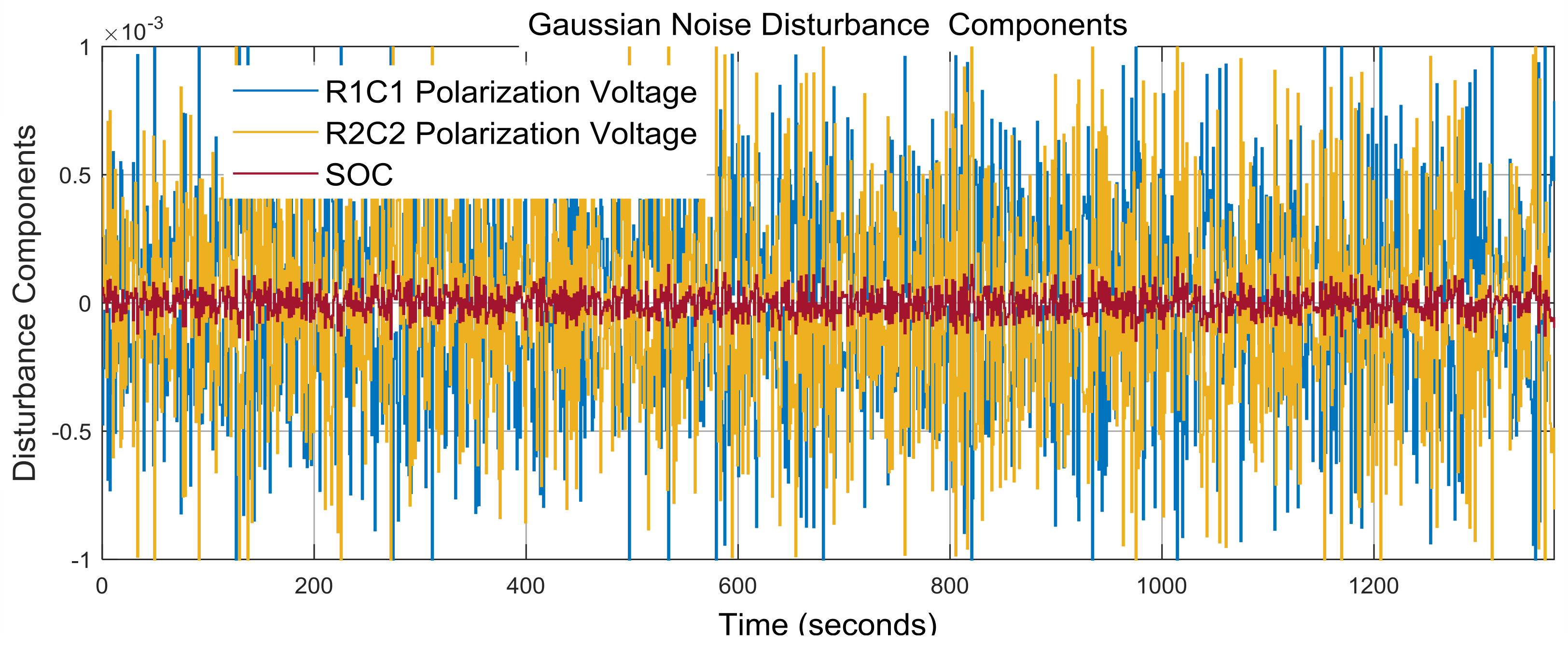
3.3. Real-Time PIO SOC Estimator SIMULINK Simulation Results
4. Conclusions
- changes (increase or decrease) in SOC initial values
- simultaneous changes in SOC initial value and measurement current sensor noise level
- simultaneous changes in SOC initial value and changes in internal resistance of Li-Ion battery due to the effects mentioned in Section 2.1, especially the temperature effects
- simultaneous changes in SOC initial value and the nominal value of the battery capacity due to aging and/or temperature effects
Author Contributions
Conflicts of Interest
Abbreviations
| NiCad | nickel cadmium |
| NiMH | nickel metal hydride |
| Li-Ion | lithium-ion |
| EV | electric vehicle |
| HEV | hybrid electric vehicle |
| BMS | battery management system |
| EMC | equivalent model circuit |
| ADVISOR | advanced vehicle simulator |
| EPA | environmental protection agency |
| UDDS | urban dynamometer driving schedule |
| FTP-75 | federal test procedure at 75 F |
| FE | fuel economy |
| HWFET | highway fuel economy test |
| OCV | open-circuit voltage |
| EKF | extended Kalman filter |
| PIO | proportional-integral observer |
| SOH | state of health |
| DOD | depth of discharge |
| NREL | national renewable energy laboratory |
| UKF | unscented Kalman filter |
| EnKF | ensemble Kalman filter |
| PF | particle filter |
References
- Young, K.; Wang, C.; Wang, L.Y.; Strunz, K. Electric Vehicle Battery Technologies: Chapter 2. In Electric Vehicle Integration into Modern Power Networks, 1st ed.; Garcia-Valle, R., Peças Lopes, J., Eds.; Springer: New York, NY, USA, 2013; pp. 15–26. [Google Scholar] [CrossRef]
- Xia, B.; Zheng, W.; Zhang, R.; Lao, Z.; Sun, Z. A novel observer for Lithium-Ion battery state of charge estimation in electric vehicles based on a second-order equivalent circuit model. Energies 2017, 10, 1150. [Google Scholar] [CrossRef]
- Farag, M. Lithium-Ion Batteries, Modeling and State of Charge Estimation. Master’s Thesis, McMaster University of Hamilton, Hamilton, ON, Canada, 2013. [Google Scholar]
- Cui, X.; Shen, W.; Zhang, Y.; Hu, C. A Novel Active Online State of Charge Based Balancing Approach for Lithium-Ion Battery packs during Fast Charging process in Electric Vehicles. Energies 2017, 10, 1766. [Google Scholar] [CrossRef]
- Lowe, M.; Tokuoka, S.; Trigg, T.; Gereffi, G. Li-Ion Batteries for Electric Vehicles. The US Chain; Research Report; Center on Globalization Governance and Competitiveness: Durham, NC, USA, 2010; pp. 1–68. Available online: https://unstats.un.org/unsd/trade/s_geneva2011/refdocs/RDs/Lithium-Ion%20Batteries%20 (Gereffi%20-%20May%202010).pdf (accessed on 17 March 2018).
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 1. Background. J. Power Sources 2004, 134, 252–261. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Simon, J.J.; Uhlmann, J.K. A New Extension of the Kalman Filter to Nonlinear Systems. In Process of AeroSense, Proceedings of the 11th International Symposium on Aerospace/Defense Sensing, Simulation and Controls, Orlando, FL, USA, 21–24 April 1997; SPIE: Orlando, FL, USA, 1997; Available online: https://people.eecs.berkeley.edu/~pabbeel/cs287-fa09/readings/JulierUhlmann-UKF.pdf (accessed on 21 January 2018).
- Tudoroiu, N.; Radu, S.M.; Tudoroiu, E.-R. Improving Nonlinear State Estimation Techniques by Hybrid Structures, 1st ed.; LAMBERT Academic Publishing: Saarbrucken, Germany, 2017; 56p, ISBN 978-3-330-04418-0. [Google Scholar]
- Xu, J.; Cao, B. Battery Management System for Electric Drive Vehicles-Modeling State Estimation and Balancing—Chapter 4. In New Applications of Electric Drives, 1st ed.; Chomat, M., Ed.; INTECH: Rijeka, Croatia, 2015; pp. 87–113. [Google Scholar] [CrossRef]
- Johnson, V.H. Battery Performance Models in ADVISOR. J. Power Sources 2001, 110, 321–329. [Google Scholar] [CrossRef]
- Tremblay, O.; Dessaint, L.A. A Generic Battery Model for the Dynamic Simulation of Hybrid Electric Vehicles. In Proceedings of the IEEE Vehicle Power and Propulsion Conference VPPC 2007, Arlington, TX, USA, 9–12 September 2007; pp. 284–289. [Google Scholar] [CrossRef]
- Xing, Y.; Ma, E.W.M.; Tsui, K.L.; Pecht, M. Battery Management Systems in Electric and Hybrid Vehicles. Energies 2011, 4, 1840–1857. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, C. Fundamentals and Applications of Lithium-Ion Batteries in Electric Drive Vehicles, 1st ed.; John Wiley & Sons: Singapore, 2015; 300p, ISBN 978-1-118-41478-1. [Google Scholar]
- Wipke, K.B.; Cuddy, R.M. Using an Advanced Vehicle Simulator (ADVISOR) to Guide Hybrid Vehicle Propulsion System Developmen; Research Gate Net; National Renewable Energy Laboratory: Golden, CO, USA, 1996; Available online: https://www.researchgate.net/publication/255260311Using_an_advanced_vehicle_simulator_ADVISOR_to_guide_hybrid_vehicle_propulsion_system_development (accessed on 4 March 2018).
- [Internet]. Evaluation and Adaption of 5-Cycle FE Testing and Calculations for HEV. US Department of Energy, Argonne National Laboratory, 15 May 2012; p. 4. Available online: https://www.energy.gov/sites/prod/files/2014/03/f10/vss065_lohsebusch_2012_o.pdf (accessed on 15 March 2018).
- Lakkis, M.E.; Sename, O.; Corno, M.; Bresch, P.D. Combined battery SOC/SOH estimation using a nonlinear adaptive observer. In Proceedings of the European Control Conference, Linz, Austria, 15–17 July 2015; Available online: https://www.researchgate.net/publication/308863249_Combined_battery_SOCSOH_estimation_using_a_nonlinear_adaptive_observer (accessed on 17 March 2018).
- [Internet]. Battery and Engineering Technologies. Battery Life (and Death). Available online: http://www.mpoweruk.com/life.htm (accessed on 18 March 2018).
- Taesic, K. A Hybrid Battery Model Capable of Capturing Dynamic Circuit Characteristics and Nonlinear Capacity Effects. Master’s Thesis, University of Nebraska, Lincoln, NE, USA, 2012. [Google Scholar]
- Prasanna Mantravadi, S.R. Modeling, Simulation & Implementation of Li-Ion Battery Powered Electric and Plug-In Hybrid Vehicles. Master’s Thesis, University of Akron, Akron, OH, USA, 2011. [Google Scholar]
- Moshirvaziri, A. Lithium-Ion Battery Modeling for Electric Vehicles and Regenerative Cell Testing Platform. Master’s Thesis, University of Toronto, Toronto, ON, Canada, 2013. Available online: https://www.academia.edu/8205872/LITHIUM-ION_BATTERY_MODELING_for_ELECTRIC_VEHICLES_and_REGENERATIVE_CELL_TESTING_PLATFORM (accessed on 18 March 2018).





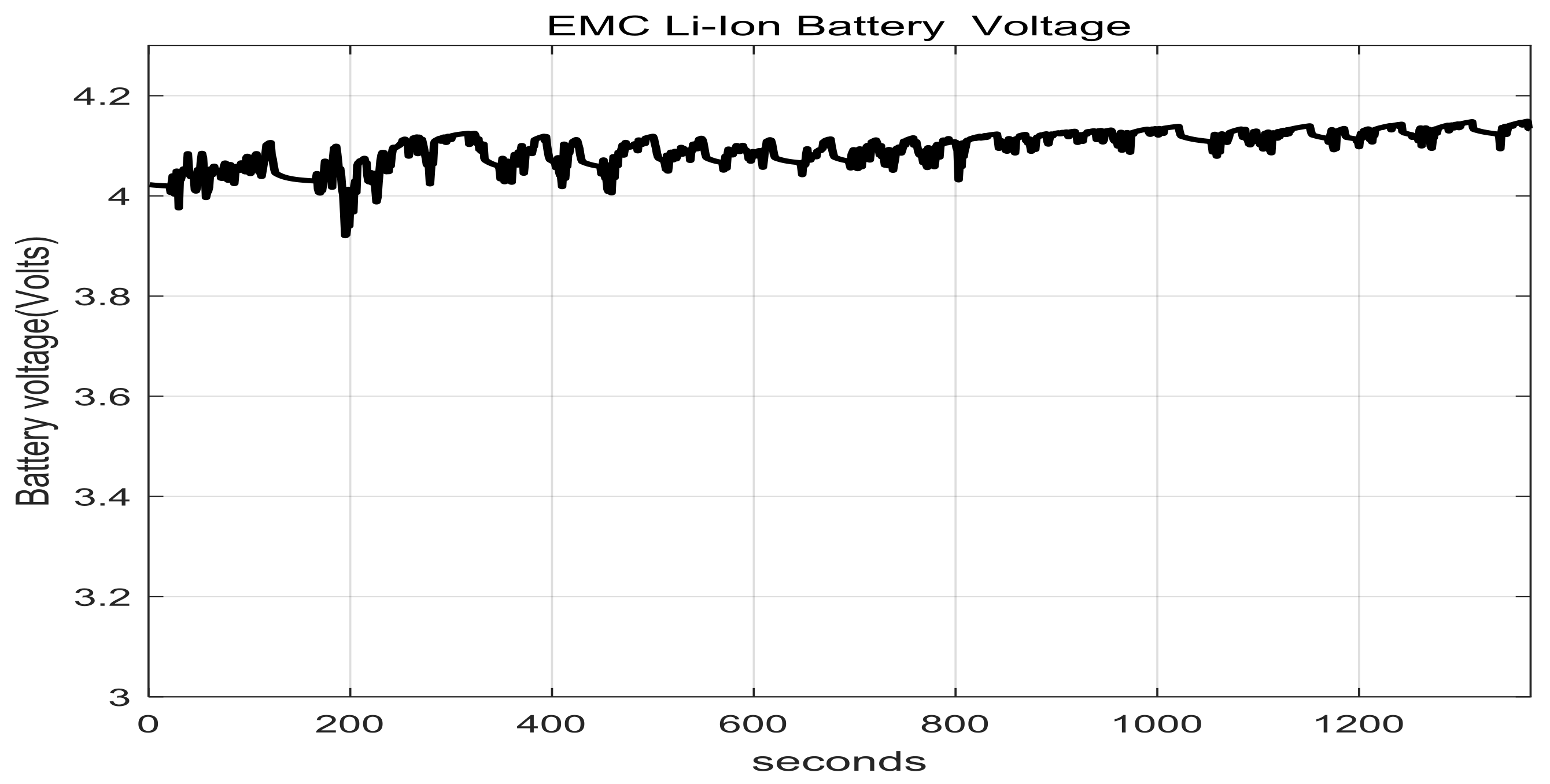


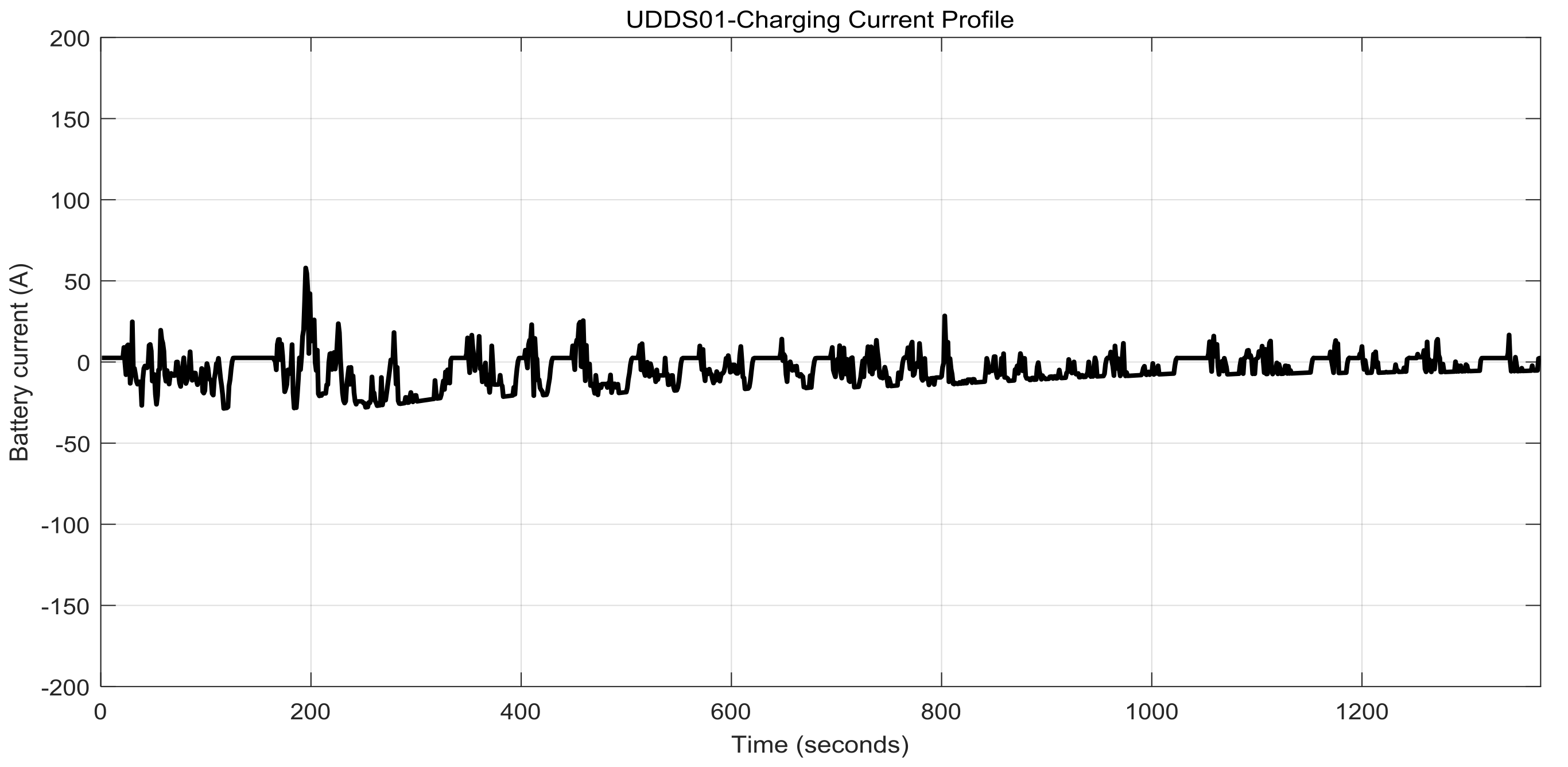
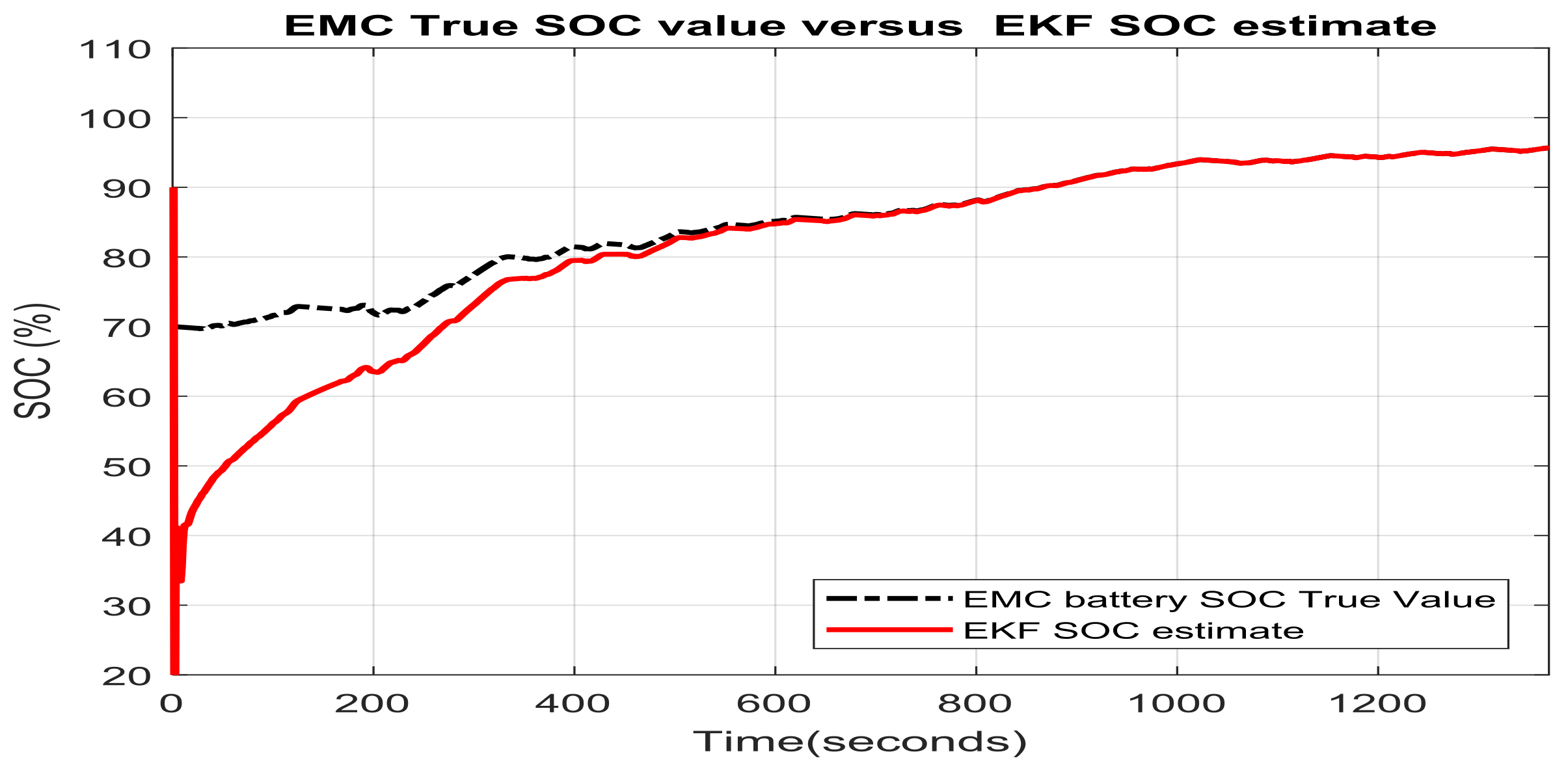








| Item | Parameters/Coefficients | Symbol | Value | Unit Measure |
|---|---|---|---|---|
| 1 | Li-Ion battery EMC parameters: | |||
| 1.1 | The battery internal ohmic resistance (slightly different for charging and discharging cycle) | R | 0.0022 | Ω (ohm) |
| 1.2 | The first cell polarization resistance | R1 | 0.00077 | Ω |
| 1.3 | The second cell polarization resistance | R2 | 0.0011 | Ω |
| 1.4 | The first cell polarization capacitance | C1 | 14,475.24 | F (farad) |
| 1.5 | The second cell polarization resistance | C2 | 98,246.01 | F |
| 2 | Li-Ion battery characteristics: | |||
| 2.1 | The value of the battery nominal capacity | Cnom | 6 | Ah (Amperes hours) |
| 2.2 | The voltage nominal value of the battery | Vnom | 3.6 | V (volt) |
| 2.3 | Coulombic efficiency:
| η | 0.98 0.86 | |
| 3 | The OCV coefficients: | K0 | 4.23 | |
| K1 | 0.0000386 | |||
| K2 | 0.24 | |||
| K3 | 0.22 | |||
| K4 | −0.04 | |||
| Li-Ion Battery Parameter | Temperature (°C) | Unit | |||
|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | mΩ | |
| R | 8 | 8.1 | 7.5 | 7.6 | |
| R1 | 4.3 | 4.1 | 1.9 | 1.0 | mΩ |
| R2 | 5.5 | 3.5 | 2.5 | 1.8 | mΩ |
| R3 | 10 | 7.5 | 5.1 | 3.2 | mΩ |
| C1 | 0.4 | 0.4 | 0.3 | 0.3 | F |
| C2 | 4.3 | 4.1 | 4.1 | 4 | F |
| C3 | 49.8 | 35.3 | 3.9 | 35.1 | F |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tudoroiu, R.-E.; Zaheeruddin, M.; Radu, S.-M.; Tudoroiu, N. Real-Time Implementation of an Extended Kalman Filter and a PI Observer for State Estimation of Rechargeable Li-Ion Batteries in Hybrid Electric Vehicle Applications—A Case Study. Batteries 2018, 4, 19. https://doi.org/10.3390/batteries4020019
Tudoroiu R-E, Zaheeruddin M, Radu S-M, Tudoroiu N. Real-Time Implementation of an Extended Kalman Filter and a PI Observer for State Estimation of Rechargeable Li-Ion Batteries in Hybrid Electric Vehicle Applications—A Case Study. Batteries. 2018; 4(2):19. https://doi.org/10.3390/batteries4020019
Chicago/Turabian StyleTudoroiu, Roxana-Elena, Mohammed Zaheeruddin, Sorin-Mihai Radu, and Nicolae Tudoroiu. 2018. "Real-Time Implementation of an Extended Kalman Filter and a PI Observer for State Estimation of Rechargeable Li-Ion Batteries in Hybrid Electric Vehicle Applications—A Case Study" Batteries 4, no. 2: 19. https://doi.org/10.3390/batteries4020019
APA StyleTudoroiu, R.-E., Zaheeruddin, M., Radu, S.-M., & Tudoroiu, N. (2018). Real-Time Implementation of an Extended Kalman Filter and a PI Observer for State Estimation of Rechargeable Li-Ion Batteries in Hybrid Electric Vehicle Applications—A Case Study. Batteries, 4(2), 19. https://doi.org/10.3390/batteries4020019






