Abstract
The advent of large-scale renewable energy generation and electric mobility is driving a growing need for new electrochemical energy storage systems. Metal-air batteries, particularly zinc-air, are a promising technology that could help address this need. While experimental research is essential, it can also be expensive and time consuming. The utilization of well-developed theory-based models can improve researchers’ understanding of complex electrochemical systems, guide development, and more efficiently utilize experimental resources. In this paper, we review the current state of metal-air batteries and the modeling methods that can be implemented to advance their development. Microscopic and macroscopic modeling methods are discussed with a focus on continuum modeling derived from non-equilibrium thermodynamics. An applied example of zinc-air battery engineering is presented.
1. Introduction
In the ever-growing search for safe and high-performance energy storage technology, development of metal-air batteries is taking on new importance [1]. The promise of these systems is clear: a significant increase in energy density over Li-ion batteries, utilization of abundant materials, and improved safety [2]. While great progress has been made in their development, challenges remain before secondary metal-air batteries can become widely commercially viable.
Metal-air batteries comprise a metal electrode (e.g., Zn, Li, Mg, Al, etc.), electrolyte (aqueous or non-aqueous), and a bi-functional air electrode (BAE). The basic operating principle is to electrochemically reduce O2 from air and oxidize the metal electrode to reversibly form solid metal-oxides. In this way, both the volume and the weight of the battery can be significantly reduced compared to Li-ion systems. Figure 1 compares the theoretical energy density and specific energy of metal-air systems. In some non-ideal cases the precipitation of the solid discharge product can consume active electrolyte components, reducing the achievable energy density [3]. Research into a variety of metal-air chemistries is ongoing. The homogeneous deposition of Mg metal makes Mg-air systems appealing [4,5,6], but aqueous Mg-air batteries are severely limited by the corrosion of the Mg electrode. Ionic liquid electrolytes have been proposed for Mg-air systems, but they also suffer from electrochemical instability, particularly during charging, and the reversibility of the cell is limited [7]. Another interesting contender is Al-air. Al is an abundant and safe material, and Al-air batteries have high theoretical energy density and specific energy values [8,9,10]. However theses systems are susceptible to corrosion and have not demonstrated adequate cycling stability. The natural abundance and safety of sodium combined with its comparable properties with lithium have driven research into Na-air [11,12,13]. These systems are still in a very early stage of research. Si-air batteries have also attracted attention [14]. They have a high theoretical energy density and are stable in aqueous electrolytes. Experimental studies of Si-air systems have been performed in both ionic liquid [15] and alkaline electrolytes [16], but they currently face challenges with the reversibility of the solid discharge product, precipitation, and pore blockage. Among the metal-air systems under development, Li-air and Zn-air are the most promising [17,18,19].

Figure 1.
Overview of the theoretical energy density and specific energy (including oxygen) of commonly researched metal-air batteries. Values are calculated considering the specific mass and volume of the discharge product with the OCV and charge transfered in the cell reaction.
Li-air batteries (LABs) have been researched for decades [20], but have only become a widely-pursued topic since the early 2000s. The electrolyte has proved to be a limiting factor in LAB development. The most common electrolyte configurations of Li-air systems are aprotic (non-aqueous) and aqueous. Mixed electrolyte systems have also been proposed. The beginning of the LAB research wave focused on aprotic electrolytes. The first work on the aprotic Li-air system (LiPF6 in ethylene carbonate (EC)) was performed in 1996 by Abraham, et al. [21], who proposed an overall reaction forming Li2O2 or Li2O. Early aprotic Li-air cells were based on a carbonate solvent, but it has since been shown that carbonate solvents are unstable, producing lithium-carbonates during discharging and evolving CO2 during charing [22,23,24,25]. These days, carbonate electrolytes have been abandoned in favor of ether and ester solvents with lithium salts. A second challenge for LABs in aprotic electrolytes relates to the precipitation of Li2O2. When this solid precipitates in the cathode, it can form a dense layer over the carbon surface and inhibit the transfer of electrons. As precipitation continues, entire pores in the cathode may become blocked, passivating the electrode and limiting the cell capacity. Finally, it has been noted that oxygen transport in aprotic eletrolytes can be a challenging factor in LAB performance, especially at higher current densities [26,27]. This has motivated researches to learn from the success of the gas diffusion electrode in fuel cells and pursue investigations of LABs with aqueous electrolytes.
It is well known that Li metal reacts violently with water, which had previously limited the use of aqueous electrolytes for Li-air systems. Then in 2004, a glass ceramic layer over the Li electrode was successfully proposed to protect the metal electrode while still allowing the electrochemical reaction to proceed [28,29]. In alkaline aqueous electrolytes, the discharge product is LiOH·H2O instead of Li2O2. In these systems, LiOH·H2O tends to precipitate at the separator-anode interface [30], which reduces the risk of pore clogging in the cathode as observed in aprotic LABs. However, when aqueous alkaline electrolytes are exposed to air, dissolved CO2 reacts with OH− to form carbonates, which slowly reduces the conductivity of the electrolyte and limits the lifetime of the cell.
In the recent wave of interest in the development of Li-air batteries, many theoretical studies have highlighted the impressive possibilities of these systems [30,31,32,33,34,35,36] and the company International Business Machines Corporation (IBM) pursued Li-air systems for commercial applications [17]. Although significant challenges remain [37,38,39,40,41], the future of Li-air batteries is promising.
Zn-air batteries (ZABs) stand alone as the only fully mature metal-air system and have been successfully commercialized as primary cells for many years. They are particularly suitable for low-current applications like hearing aids. However, their calendar life and electrical rechargeability is limited [42]. One major advantage of Zn as an electrode material is that, unlike Li, it is stable in water. In an effort to improve the rechargeability of ZABs, alternative near-neutral aqueous [43,44] and ionic liquid electrolytes [45,46,47] have been proposed. Current research continues to focus on material development to address the lifetime limitations and cell engineering to improve the performance of these systems [48]. Although some hurdles remain, the development of secondary ZABs has progressed to the point that they could become feasible for stationary storage applications and some Start-Ups like Eos Energy Storage [49] and Fluidic Energy [50] have begun to commercialize the technology. Zn-air systems offer perhaps the most immediate and reliable pathway to a viable secondary metal-air battery.
In this review, we examine model-based design tools that can be applied to advance development of metal-air systems. The majority of existing models were developed for Zn-air cells, as they are the oldest and most mature system. Therefore our review shall focus mainly on the application of models to ZABs and highlight some important advances unique to LABs. Note that these methods are easily translatable to other metal-air systems.
2. Zinc-Air Batteries
In this section, we present a summary of the working principle of ZABs and discuss the main challenges hindering the development of electrically-rechargeable Zn-air systems.
2.1. Working Principle
In their most common configuration, Zn-air batteries contain a metallic Zn electrode, porous separator, circa 30 wt % aqueous KOH electrolyte, and a bi-functional air electrode (BAE). The BAE consists of a porous substrate and a bi-functional air catalyst (e.g., MnO2) to facilitate the oxygen-reduction and oxygen-evolution reactions (ORR, OER) [51,52,53]. The design of the BAE is similar to gas diffusion layers (GDL) from fuel cell applications. The porous BAE substrate contains carbon fibers and binder with mixed hydrophilic and hydrophobic properties to promote the formation of the so-called three phase boundary, while hindering the electrolyte from flooding out. The Zn electrode is often a paste consisting of zinc metal powder, electrolyte, and binder [54]. The capacity of the cell is determined by the Zn electrode, which is designed in such a way as to include as much active material as possible while minimizing the effects of shape-change and electrolyte concentration gradients. Aqueous KOH is the most common electrolyte for Zn-air batteries due to its high conductivity (circa 600 ).
An operational schematic of a ZAB in alkaline electrolyte is shown in Figure 2. When the cell is discharged, the Zn electrode is electrochemically oxidized to form Zn(OH)42− (zincate) complexes,

Figure 2.
Operational schematic of an alkaline zinc-air battery. The various (electro)chemical reactions are indicated by the colored ovals; white arrows indicated discharging and black arrows indicate charging. Dashed lines show important transport paths.
Oxygen gas enters the cell through the BAE and dissolves into the electrolyte, where it is reduced to form OH− ions,
When the saturation limit of zinc in the electrolyte is exceeded, solid ZnO precipitates mainly in the anode and the battery achieves a stable working point,
When the cell is charged, ZnO dissolves, zinc is redeposited at the Zn electrode and oxygen gas is evolved in the BAE. The overall cell reaction is given by
The open-circuit voltage of a ZAB in 30 wt % KOH is 1.65 V. The high conductivity of the electrolyte, high mobility of OH−, and reasonable kinetics of the ORR give the cell a nominal discharge voltage of 1.2 V at current densities of circa 10 [55]. The molar volume of ZnO is 60% larger than metallic Zn, which causes the cell to expand during discharge. Even so, ZAB button cells demonstrate a practical energy density on the order of 1000 [55].
2.2. Challenges, Progress, and Opportunities
While ZABs have been quite successful as primary cells, there are a number of hurdles that limit their electrical rechargeability and provide opportunities for further research.
The most well-known challenges relate to the aqueous KOH electrolyte. When the ZAB is operated in air, CO2 can dissolve in the electrolyte and react with OH− to form CO32− [56]. This parasitic reaction reduces the conductivity of the electrolyte, slows down the cell reactions, and eventually kills the cell [55]. As such, the lifetime of alkaline ZABs is limited from the moment they are exposed to air. A CO2 filter could be applied to scrub the air [57], but this adds cost and complexity to the system. A second challenge for the electrolyte is the evolution of hydrogen gas. The potential of the Zn electrode reaction is below the potential for hydrogen evolution, which causes the electrolyte to be thermodynamically unstable [58]. However, H2 evolution on the Zn surface can be kinetically suppressed with dopants, such as Hg, In, or Bi [19,59,60,61].
To address these challenges, current research is focused on the development of alternative electrolytes. An ideal electrolyte for Zn-air batteries should be stable in the electrochemical window of the cell, stable in air, conductive, non-corrosive, and thermodynamically favor the reversible precipitation of the desired final discharge product. Alternatives include aqueous alkaline with additives [62], which were recently evaluated by Schröder et al. [63] and Mainar, et al. [64,65]. Near-neutral chloride-based electrolytes have been experimentally evaluated by Zong and co-workers [43,44] with promising initial results. Chloride-based electrolytes address the carbonation issue and could improve the quality of Zn deposition, but they struggle with the precipitation of zinc-chlorides and the strongly oxidative nature of chlorine. Non-aqueous ionic liquid electrolytes [45,46,66,67,68] have been proposed with promising results [69], but the rate of these systems is limited and much work remains to be done.
Metal electrodes offer the possibility of achieving very high energy density. However, the formation of mossy or dendritic metal structures during charging can cause the electrode to change shape [70] and lead to an internal short-circuit [71], killing the cell. With its low surface diffusion characteristics and fast deposition kinetics [72], Zn is specifically vulnerable to electrode shape change. Achieving homogeneous Zn deposition is essential to the development of a secondary ZAB. Electrolyte additives and alternative electrode designs have been proposed to address this challenge [43,73,74,75,76,77], with mixed results.
A further challenge in Zn electrode design is the passivation of the electrode surface due to ZnO precipitation [78]. To achieve a high energy density, the precipitation of ZnO is required. However, when ZnO precipitates on the active surface of the Zn metal, it limits the transport of species to/from the electrolyte. When this ZnO barrier becomes too large, the electrochemical reaction can no longer proceed and the electrode is passivated [62,79]. ZnO passivation can take on two forms [54,80]. Type I ZnO has a porous white morphology. It precipitates near the surface of the Zn particle, but does not block it completely. The formation of type I ZnO is reversible. Type II ZnO forms a black dense layer directly on the surface of the the Zn particle. It is thought that type II ZnO forms on the active sites of the Zn metal, permanently blocking them and creating a passivating avalanche effect [81].
Finally, the development of an active, stable, and cheap bi-functional air catalyst is a hotly pursued topic in material science [44,51,82,83,84]. It is difficult to find a catalyst that is suitable for both the ORR and the OER. The alternating oxidative and reductive environments present in the BAE during cycling further complicates this challenge, and tends to accelerate the degradation of both the BAE carbon substrate and the catalyst. This difficultly is compounded for near-neutral electrolytes, in which the pH of the electrolyte may vary within the buffering range. From a material science perspective, research into new catalyst combinations and non-carbon BAE substrates is on-going. Alternative 3-electrode cell designs have also been proposed [19].
On a system level, the challenges described above have led to creative engineering solutions including mechanically rechargeable Zn-air fuel cells with some niche applications [69]. However, the logistical challenges of these designs prevented them from being adopted on a wide scale. The goal is to develop a high-performance electrically rechargeable Zn-air battery. To achieve this, new ideas and novel designs are needed on every level from material science up through system engineering. In the following section we discuss how numerical modeling and simulation can help in this pursuit and give an overview of recent progress.
3. Numerical Modeling and Simulation
Experimentally-based research can be expensive and time consuming. The development of theory-based models can help guide researchers down the most promising paths, provide a framework for interpreting experimental results, and lead to new breakthroughs in battery design.
Numerical modeling and simulation serve many purposes in metal-air battery research and can span a wide range of space and time-scales [30,85,86]. In the following sections, we review modeling methods commonly used in development of metal-air batteries. We begin on the material level, highlighting methods for studying the electronic properties of catalysts and metal electrodes as well as electrolyte thermodynamics and composition. We then move up to the electrode level, and discuss numerical studies of electrode architecture and what considerations are important in the design process. Finally, we give an overview of cell-level continuum modeling and discuss recent contributions to the literature.
3.1. Material Development
The first step in designing a feasible battery must be the selection of appropriate materials. Anode, cathode, and electrolytes all have their own, sometimes conflicting, requirements for activity and stability. Applied modeling methods can help screen potential materials, identify promising paths for development, and reduce the reliance on trial-and-error approaches.
3.1.1. Electrode Materials
Catalyst development is one of the most expensive and time consuming aspects of material research in metal-air systems. Bi-functional air catalysts can take on a wide range of compositions, often include expensive or toxic metals (e.g., Pt, Ag, Co, etc.), and are labor intensive to produce and test. Atomic-scale modeling methods can be applied early in the design process to screen potential catalysts.
Density functional theory (DFT) uses quantum mechanical calculations to make predictions about the electronic structure of multi-atom systems [87]. This method allows researchers to investigate the properties of materials considering the influence of things like surface structures and local coordination of atoms. The basic approach of DFT is to analyze a multi-atom system as the movement of electrons through a fixed array of atomic nuclei. Using the Born-Oppenheimer approximation, the state of the nuclei and the electrons can be split into separate mathematical expressions [88]. In this way the adiabatic potential energy surface of the atoms can be calculated and used to investigate the characteristics of the material [87]. Due to the complexity of the calculations involved, the method is confined to considering a limited number of atoms. Nonetheless it has been shown to be effective at screening the properties of metal alloys for a variety of applications [89].
Beginning with the work of Norskov, et al. [90], there have been a wealth of DFT studies investigating the reaction pathway, activity, and stability of materials in metal-air systems. Viswanathan et al. have utilized DFT to predict the activity of different pure and alloyed metals [91,92]. This group has also applied DFT calculations to investigate a range of phenomena in Li-air batteries [93,94]. In 2010, Keith and Jacob clarified a multi-pathway electrochemical mechanism for the ORR, which showed good agreement with experimental data. Eberle and Horstmann correlated the change in reaction pathway to an observed change in the Tafel slope [95]. In 2017, Tripkovic and Vegge elucidated the mechanism of the ORR on Pt (111), and used their results to investigate the high activity of Pt-alloys [96]. Non-metallic catalysts, such as nitrogen-doped graphene, are desirable due to their safety and low cost. A multi-scale model featuring DFT of such systems was recently presented by Vazquez-Arenas, et al. [97], and used to investigate the rate-determining step for the ORR in KOH electrolyte.
DFT simulations can also be applied to investigate metal electrode materials and solid precipitants. Siahrostami, et al., modeled the effect of surface structure on zinc dissolution [98]. They applied their model to simulate the dissolution of a Zn kink atom, highlighting the potential steps of the dissolution process and predicting the overpotential of the reaction. For electro-deposition, Jäckle and Groß propose that surface diffusion processes are key to understanding the formation of metallic surface structures [99]. They utilized a DFT model to evaluate a range of metal anode materials for their tendency to form dendrites. In the case of non-aqueous Li-air batteries, the precipitation of Li2O2 can electrically isolate the cathode. DFT simulations have been applied to investigate the growth and electronic structure of Li2O2 [31,100,101,102,103], in an attempt to mitigate the risk of passivation.
3.1.2. Electrolytes
The behavior of liquid electrolytes in electrochemical systems can be quite complex and have a deciding influence on overall cell performance. The first step in determining the suitability of an electrolyte for a given system is to examine its equilibrium thermodynamics.
The speciation of ions, solubility of solids, and equilibrium potential of electrodes in an electrolyte is strongly dependent on pH and solute concentration [80,104,105]. For some systems, such as KOH−ZnO, this behavior is rather straightforward and well-documented [80,106], while for others, such as ZnCl2−NH4Cl, it is very complex and sensitive [3,107]. Figure 3a shows the speciation of the Zn2+ ion in ZnCl2−NH4Cl. Understanding this behavior can be helpful in interpreting battery performance and optimizing system design.
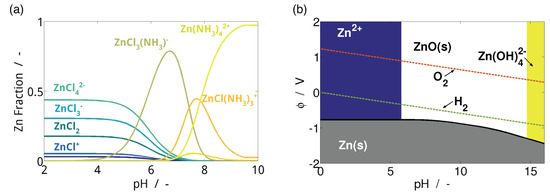
Figure 3.
(a) Zn speciation plot for 0.51 M ZnCl2−2·34 M NH4Cl with pH adjusted by NH4OH reproduced from Clark, et al. [3] with permission from Wiley-VCH and (b) simplified Pourbaix diagram for M.
According to the law of mass action, for a system at equilibrium with a constant temperature, the value of the reaction quotient is constant. For a generic reaction, this concept is expressed as,
The value of the constant, , is referred to as the thermodynamic stability constant (sometimes also called the formation or equilibrium constant). In the 1970s, Smith and co-workers assembled an exhaustive compilation of thermodynamic stability constants of metal-ligand complexes, pKa values of acids, and solubility products of solids for a myriad of both inorganic and organic molecules [108,109,110,111]. By incorporating these equilibrium expressions for every electrolyte reaction into simple equations for the conservation of mass and charge, the equilibrium composition of the electrolyte and the solubility of solids can be predicted as a function of pH and solute concentration. A framework for such a model [112,113] was presented by Limpo, et al., in the 1990s, and was expanded upon in more recent research [106,114]. Clark, et al., recently presented a framework for predicting the discharge characteristics of a Zn-air cell with an aqueous near-neutral electrolyte based on equilibrium thermodynamic considerations [3], and showed how they can be incorporated into a dynamic model.
Models of equilibrium thermodynamics can also be used to generate potential-pH, or Pourbaix, diagrams [115]. Figure 3b shows a simplified example for the aqueous Zn system. The Nernst equation describes the connection between solute concentration and the equilibrium electrode potential [116]. The equilibrium potentials for the electrochemical reactions in Zn-air systems [80] can be expressed as:
Taking this into consideration, researchers can predict the influence of shifts in pH or solute concentration on electrode potential. Aside from describing the voltage of the cell, this is also useful for identifying possible parasitic reactions, such as H2 evolution or redox shuttles.
In addition to thermodynamic models, DFT can be used to screen properties of electrolytes and their suitability for metal-air applications. One of the major challenges in aprotic LABs is the development of a solvent that is stable and facilitates oxygen solubility and transport. In 2015, Husch and Korth presented a study of non-aqueous LAB electrolytes [117]. In a wide-ranging work requiring about 2 million hours of process time, they integrated DFT calculations into a larger framework to screen 927,000 potential electrolyte solvents for high Li+ and O2 solubilities and low viscosity. An illustration of their work is shown in Figure 4. By strategically applying modeling methods, Husch, et al., were able to by pass the trial-and-error approach and directly highlight electrolyte solvents with the highest chances of success.
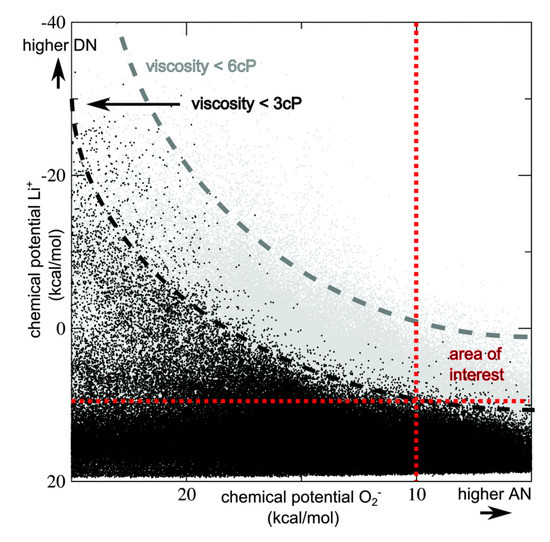
Figure 4.
Chemical potentials for Li+ vs. chemical potentials for O2 in the bulk candidate compound are plotted for all 927,000 compounds. Black dots indicate compounds with a viscosity below 3 cP, grey dots indicate compounds with a viscosity below 6 cP. Reproduced from Husch, et al. [117]—Published by the Physical Chemistry Chemical Physics (PCCP) Owner Societies.
3.2. Electrode Design
The development of active and stable materials is essential to battery design. However, care must be taken to appropriately scale-up materials to the electrode level. In this section, we discuss modeling tools which can help fashion suitable materials into high-performance electrodes.
3.2.1. Bi-Functional Air Electrode (BAE)
The BAE in Zn-air batteries is comprised of a porous structure (usually carbon fibers and binder) with mixed hydrophilic and hydrophobic properties. The idea is to encourage the formation of the so-called three-phase boundary without either over-saturating (flooding) or under-saturating (drying out) the pores. When the cell is cycled, pressure gradients are induced in the battery due to the precipitation and dissolution of solid products, which can change the saturation of the BAE. To simulate this behavior, a method of predicting the pressure-saturation characteristics of the BAE structure is needed.
The Lattice Boltzmann Method (LBM) is useful for simulating multi-phase flow in porous media. This approach uses the Boltzmann equation to simulate the flow of fluids as a combination of collision and streaming events of particles on a discrete lattice [118,119]. Particle positions are confined to the nodes of the lattice and it is assumed that they can move between their current position and adjacent nodes in discrete lattice directions. The probability to find particles at a lattice node with a velocity component in any of the discrete directions is described by a distribution function [120]. If solid boundaries are present in the system, no-slip boundary conditions can be introduced by a simple bounce back scheme. Implementation of the basic LBM equations is straightforward, and there are a variety of open-source codes available [121].
In electrochemical research [122], Lattice Boltzmann models have been applied to investigate the transport of water in the GDL of PEM fuel cells [123,124,125,126]. One significant benefit of LBM is the ability to simulate flow in complex geometries. Using X-ray tomography [127] or focus ion beam scanning electron microscope (FIB-SEM) images [128], real electrode structures can be modeled in 3D and their transport properties evaluated. Recently, Danner, et al., presented a LBM model to predict the pressure-saturation parameters of BAEs in metal-air batteries [128]. Figure 5 shows pressure-saturation curves calculated with LBM for both 2D and 3D simulations of real BAE structures. Their simulations show that the pressure-saturation characteristics of air electrode substrates vary according to whether the electrolyte is draining from the structure (configuration I) or imbibing the structure (configuration II). They proposed this is because the structure contains some pores that can be filled with electrolyte, but are not easily emptied.
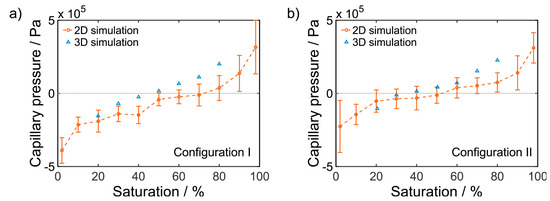
Figure 5.
Pressure-saturation curves for real air electrode structures simulated with 2D and 3D Lattice-Boltzmann models for (a) draining (configuration I) and (b) imbibition (configuration II). Reproduced from Journal of Power Sources, 324, T. Danner, S. Eswara, V.P. Schulz, A. Latz, Characterization of gas diffusion electrodes for metal-air batteries, 646–656, Copyright 2016, with permission from Elsevier [128].
3.2.2. Metal Electrode
The design of the metal electrode is determined mostly by effects linked to passivation and shape change. For Zn-air batteries, the precipitation of ZnO on the electrode surface can isolate it from the electrolyte and slow down the reaction kinetics, eventually killing the electrode. It has been shown that ZnO can take on a porous white morphology (type I) that is reversible, or a dense black morphology (type II) that is irreversible. To model the effects of these precipitants on electrode performance, various models have been developed.
As discussed in Section 2.2, type I ZnO is formed when the dissolved zinc concentration in the electrolyte exceeds the saturation limit, and it precipitates near the electrode surface. This layer of porous ZnO is generally modeled as an additional mass transport barrier [55], slowing diffusion and migration of OH− to the electrode surface. Early models determined the passivation characteristics using the so-called Sand equation, an empirical expression linking current density, i, and passivation time, t, with constants, k and :
In 1981, Liu, et al., expanded this concept taking into account the mechanism for type I ZnO precipitation. They proposed that the passivation due to type I ZnO occurs via a dissolution-saturation-precipitation mechanism. Put simply, the Zn electrode dissolves until the concentration of Zn(OH)42− exceeds the saturation limit for nucleation, and the ZnO phase grows as the precipitation reaction proceeds. In their model, they calculate the time required to saturate the electrolyte with Zn(OH)42− (), the time to precipitate type I ZnO (), and the time to precipitate type II ZnO (), and define the passivation time as [78]. The resulting 0D model is a helpful predictor of Zn electrode performance, but is not suitable for use in continuum modeling.
In the continuum model of Zn electrodes developed by Sunu and Bennion in 1980 [129], they considered passivation by assuming that the precipitation of ZnO reduced the active surface area available for the Zn dissolution reaction. More recently in 2017, Stamm, et al., implemented the effect of type I ZnO passivation in a continuum model by calculating the thickness of the ZnO shell and numerically solving for the species concentration at the surface [55], assuming Nernst-Planck transport across the barrier. These values were then used to calculate the Nernst potential and exchange current density of the Zn dissolution reaction.
While models for passivation due to type I ZnO are rather well developed, there are fewer models for type II ZnO passivation. In 1991, Prentice, et al. [81] proposed that type II ZnO forms directly on the surface of the Zn electrode, and does not follow the dissolution-saturation-precipitation mechanism of type I. By calculating the fractional surface coverage of various zinc-hydroxides as a function of concentration and electrode potential, they were able to simulate rotating disk experiments. Their simulations agreed well with experimental measurements. The model was recreated and the results are shown in Figure 6.
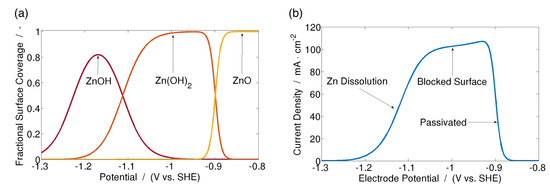
Figure 6.
(a) Fractional surface coverage of species on the Zn electrode surface, and (b) simulated LSV measurement of type II ZnO passivation. Recreated from the model described by Prentice, et al. [81].
While much progress has been made in understanding the mechanisms of Zn passivation, work remains to be done. A more unified theory of type I and type II passivation, along with implementation in a continuum model, could be an area for future research. A dedicated review of experimental and modeling studies of Zn electrode passivation was presented by Bockelman, et al., in 2017 [130].
3.3. Cell Modeling
The modeling methods described above are very useful for evaluating the properties of individual materials or components, but researchers often need to know how these components will interact with each other in a real electrochemical cell.
Continuum models are among the most useful and widely-applied methods for studying the cell-level performance of metal-air batteries. This approach applies the mass and charge continuity equations to describe the transient characteristics of spatially discretized systems [85,131]. A list of important continuum models for metal-air systems from the literature is presented in Table 1. For most applications, a 1D model is sufficient to describe the system. However, 2D and 3D [132,133] finite volume models of batteries can give more in-depth information for detailed analysis. The mass and charge continuity equations can be expressed in generic terms as,
where is the concentration of solute i, is the electrolyte volume fraction, is the diffusion-migration flux, is the convective flux, is the reaction source term, is the electrolyte current density and is the solute charge number. A detailed derivation of these terms based on non-equilibrium thermodynamics and their applicability to metal-air systems can be found in existing works [3,30,55,134]. In their most general form, the continuity equations describe the local conservation of mass and charge due to transport across the boundaries of a control volume and the presence of a source/sink within the bulk of the control volume. To successfully implement these equations physical models for electrolyte transport and (electro)chemical reactions are needed.

Table 1.
Comparison of continuum models for metal-air systems. Transport models listed are concentrated solution theory (CST) or dilute solution theory (DST).
Chemical reaction models feature a term describing the thermodynamic driving force and an expression of the kinetics [143]. In the case of electrochemical reactions, the most widely-used model is the Butler-Volmer approximation [144],
where is the rate constant (linked to the exchange current density), is the symmetry factor, is the surface overpotential, and the other variables take on their usual meaning. While this approximation is sufficient to describe simple electrodes, the precipitation of solid metal-oxides on the surface of the metal electrode forms an insulating layer and can cause the kinetics of the electrode to deviate from idealized models [62,79,145]. Special models of metal-electrode kinetics considering the effects of passivation have been developed [78,81,130] and implemented [55] in continuum simulations.
The Marcus theory of charge transfer reaction kinetics is a more accurate alternative to the Butler-Volmer approximation [146,147,148]. The Marcus model builds on an Arrhenius approach, in that the pre-exponential factor is described by the electronic coupling element, , and the reorganization free energy, , and the exponential term containing the activation energy. In its quantum mechanical form, the Marcus theory is expressed as
Marcus theory results naturally from quantum mechanics, and can be more easily linked to simulations like DFT [149]. While this approach has been applied in some continuum models, it is difficult to parameterize.
Electrolyte transport is modeled using a combination of expressions for diffusion, migration and convective mass flux [116], as well as a source term stemming from the chemical reactions described above [150,151]. While the fundamental components of electrolyte transport models are universal, their exact form can vary based on the ionic strength [116] and pH [3] of the electrolyte. For low ionic strength electrolytes, a simplified dilute solution theory (DST) approach can be applied to model the diffusion and migration transport of solutes [116].
For high ionic strength electrolytes, a more complete concentrated solution theory (CST) is needed. In this case, a coupled expression for diffusion-migration flux can be derived from non-equilibrium thermodynamics [134,152,153]. For strongly acidic or alkaline electrolytes, the concentrations of H+ or OH− are usually so high that concentration gradients do not affect the thermodynamic stability of the solutes. However, for electrolytes in the weakly acidic to weakly alkaline range, the concentrations of solutes in electrolytes can swing by orders of magnitude as pH gradients develop in the cell [80,112,113] and can affect the performance of the cell [3]. A new method for modeling electrolyte transport in near-neutral systems was recently proposed by Clark, et al. [3].
When metal-air batteries are operated, the precipitation and dissolution of solids and the conversion of H2O by the ORR/OER can induce a convective flux of electrolyte in the cell [30]. In general terms, the convective flux can be expressed as
where is the center-of-mass velocity of the electrolyte. This adds an additional level of complexity to metal-air battery models over closed systems, such as Li-ion, which often apply a simpler Nernst-Planck model. A method for considering multi-phase convective flow in continuum models was presented by Horstmann, et al. [30] and is discussed in detail later in the text.
Continuum models of ZABs have been developed intermittently since the 1980s. The first 1D continuum model of a Zn electrode in an alkaline ZAB was developed in 1980 by Sunu and Bennion [129]. It was based on the general 1D model for concentrated transport in porous electrodes outlined by Newman [116]. Their simulations showed the inhomogeneous precipitation of ZnO and investigated the shape change of the Zn electrode during cycling. In 1992, Mao and White [135] developed an extended model that also resolved the separator and air electrode. They found that K2Zn(OH)4 does not precipitate and compared simulated cell voltages with experimental measurements. Ten years later, Deiss, et al. [136] performed ZAB cycling simulations with a 1D model of the Zn electrode and separator based on dilute solution theory. They studied the redistribution of Zn and the development of concentration gradients in the cell.
In recent years, there has been a boom in continuum modeling frameworks for both Zn-air and Li-air systems, with some areas of overlap. In 2012, Neidhardt, et al., presented a flexible continuum modeling framework for multi-phase management, with direct application to a variety of electrochemical systems [131]. In their work, they applied this framework to simulate a range of fuel cells and batteries to demonstrate the versatility of the approach. In their simulations of non-aqueous Li−O2 batteries, they noted that the system is limited by a combination of slow oxygen transport and blockage of cathode pores with Li2O2.
To address the oxygen transport and passivation challenges associated with aprotic LABs, Horstmann, et al., were motivated to examine precipitation in alkaline aqueous LABs [30]. Their model featured two important developments. The first was the introduction of pressure-saturation expression to simulate the electrolyte flooding and drying-out of the BAE. The saturation of porous structures was described with a so-called Leverett approach, which had previously been applied in models of fuel cells. The Leverett function, , uses empirical constants to approximate the saturation of a porous structure as a function of the capillary pressure, ():
In this expression, is the electrolyte permeability, is the porosity of the electrode, is the surface tension, and and are the pressure in the electrolyte and gas phases, respectively. In the expression for the Leverett function, s is the electrode saturation and the remaining variables are constants. These constants can be determined experimentally or predicted numerically by combining 3D structure characterization with LBM simulations [128]. With the pressure of the electrolyte and the saturation of the BAE known, the convective velocity of the electrolyte can be solved using a Darcy model:
where is the viscosity of the electrolyte. Their simulations found that the availability of gas diffusion electrodes for aqueous systems reduces the oxygen transport limitations seen in non-aqueous LAB systems.
The second development was the implementation of a model for LiOH·H2O precipitation based on the classical theory of nucleation and growth. By defining terms for the reaction enthalpy of formation for both the bulk and surface of the nucleus, they identified the critical formation energy and nucleus size. Considering a diffusion limited precipitation mechanism and the supersaturation of Li+ as the driving force for nucleation and growth, they were able to simulate the spatially resolved precipitation of LiOH·H2O. The results, shown in Figure 7, indicate that LiOH·H2O does not block the cathode pores. Rather it precipitates mostly near the separator-anode interface, thereby addressing the passivation challenge in aprotic LABs.
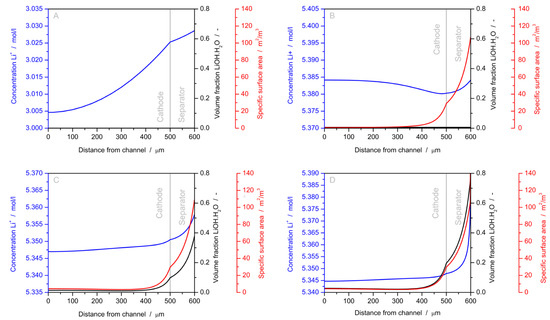
Figure 7.
Spatial profiles of salt concentration, volume fraction of LiOH·H2O, and the specific surface are of precipitation during galvanostatic cell discharge (i = 10 ). Li+ concentration increases before LiOH·H2O nucleates (A) As the discharge progresses, LiOH·H2O nucleates (B) and precipitates (C) until the cell fails due to a solid film forming at the separator-anode interface (D). Precipitation occurs mainly close to the anode due to the small transference number of Li+. Reprinted from Horstmann, et al. [30]—Reproduced by permission of The Royal Society of Chemistry.
In 2015, the model of Horstmann, et al., was extended by Grübl and Bessler to engineer seven variants of aqueous alkaline LAB systems [141]. They identified improvements to the glass separator and the development of lighter electrode materials as areas for further research. While the potential advantages of aqueous LABs are clear, most recent modeling studies have focused on non-aqueous systems.
One of the first continuum models for non-aqueous LABs was presented by Andrei, et al., in 2010 [137]. Their simulations considered the effects of cell architecture and operational conditions on concentration profiles and cell voltage, and provided a solid foundation for further development. Recent multi-scale modeling studies of non-aqueous LABs focus heavily on the nucleation and growth of solids, and their affect on cell performance. A 1D continuum model of a LAB was developed by Albertus, et al., in 2011 [26]. They found that although O2 transport can be limiting for high current densities, the main limitation in LABs relates to the precipitation of solids. For carbonate solvents, the dominant discharge product is Li2CO3, which, along with Li2O2, poses a strong passivation risk to the cathode. The model was based on a CST approach for electrolyte transport. It did not consider the effects of electrolyte convection or cathode saturation, which was identified as an area for future development.
With the shift to non-carbonate electrolytes, the morphology of Li2O2 precipitated during discharge became the subject of research. Knowing that pore blockage was a challenge in LAB performance, Xue, et al., developed a continuum model to investigate Li2O2 precipitation considering the pore size distributions of cathode materials [140]. They later extended their model to determine the effect of both electrolyte solvent and applied current density on Li2O2 morphology [154]. A nano-scale continuum model to study the rate-dependent growth of Li2O2 was presented by Horstmann, et al. [35]. They found that the morphology of Li2O2 shifts from discrete particles at low discharge rates to an electronically insulating film at high current densities. This line of research was then expanded to consider the effects of Li2O2 precipitation on the charging process. Yin, et al., presented a continuum model for non-aqueous LABs that links the size of the Li2O2 particles created during discharging to the two-step voltage profile observed during charging [142]. The effect of the Li2O2 reaction mechanism on the discharge/charge characteristics was investigated by Grübl, et al. [155]. They found that the reaction mechanism is partially irreversible, and considered the effects of adding a redox mediator to the electrolyte. Finally, some researchers have highlighted not only the effects of Li2O2 morphology, but also its electronic properties. Radin, et al. integrated a DFT simulation of Li2O2 with charge carrying dopants into a simple Nernst-Planck continuum model to study ways to promote the OER [103]. They found that dopants, such as Co and Ni could enhance the OER and improve the rechargeability of non-aqueous LABs.
Applying continuum modeling methods to both aqueous and non-aqueous LAB development has illuminated the challenges and the opportunities inherent to these systems. Further research is needed into the effects of solid precipitation and oxygen transport in non-aqueous LABs and the long-term electrolyte stability of aqueous LABs. However, the modeling studies highlighted above have shown promising paths for further investigation.
Zn-air continuum modeling studies provide insight into challenges, such as electrolyte carbonation, Zn electrode passivation, and improved cell design. In 2014, Schröder, et al. published a framework for a 0D ZAB continuum model, which they utilized to study the effect of air composition on cell performance [138]. Examining the effects of the relative humidity (RH) and carbon dioxide content of air, they found that controlling the RH can help reduce electrolyte loss and that the presence of CO2 can dramatically limit the lifetime of the cell. In a separate paper, they combined this model with x-ray tomography measurements of a primary button cell to monitor the state-of-charge during discharge [139].
Experimental tests of ZAB button cells have shown a voltage step in the middle of discharge, particularly at high current densities [55]. In 2017, Stamm, et al., presented a model to clarify the mechanism behind this observation. Concentration profiles from their model are shown in Figure 8. The nucleation of ZnO requires an over-saturation of Zn(OH)42− in the electrolyte. For high current densities, the electrolyte concentration gradients that develop in the cell are strong enough that Zn(OH)42− does not reach the critical super-saturation for nucleation in the anode-separator interface and ZnO does not nucleate. As a result, the surface concentration of OH− in this region is much higher than in areas of the electrode covered by a ZnO film, as shown in Figure 8c. When the uninhibited Zn near the separator is completely utilized, the overpotential of the dissolution reaction increases, causing the observed drop in cell voltage. For this reason, they proposed that Zn electrodes should contain a small amount of ZnO powder. In this way, the effects of inhomogeneous ZnO nucleation can be avoided. Stamm, et al., also considered the effects of CO2 dissolution in the KOH electrolyte. They found that after about 2 months, the carbonation of the electrolyte becomes so severe that the cell can no longer function. To address this issue, they purpose employing either carbon dioxide filters or neutral electrolytes.
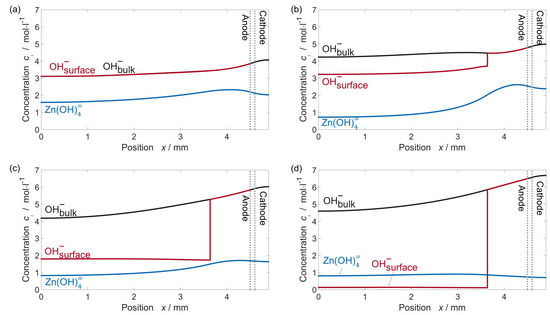
Figure 8.
Various concentration profiles in an alkaline ZAB button cell during galvanostatic discharge at 125 at different times. (a) Before ZnO nucleates, the OH− concentration at the Zn surface and electrolyte bulk are equal and zincate concentration reaches its maximum; (b) ZnO precipitates inhomogeneously in the Zn-electrode, causing the OH− surface concentration to be higher near the separator and fall as the ZnO barrier becomes thicker; (c) OH− concentration continues to fall as ZnO passivation barrier grows; (d) OH− concentration at the Zn-electrode surface is small and limits the further dissolution of Zn. Reproduced from Journal of Power Sources, 360, J. Stamm, A. Varzi, A. Latz, B. Horstmann, Modeling nucleation and growth of zinc oxide during discharge of primary zinc-air batteries, 136–149, Copyright 2017, with permission from Elsevier [55].
ZABs with near-neutral chloride-based electrolytes could address the electrolyte carbonation issue and have been experimentally investigated [43,44]. The initial results are promising, but the composition and behavior of these electrolytes during cell operation is unclear. In 2017, Clark, et al. presented a continuum framework for modeling pH buffered aqueous electrolytes, and applied it to study ZABs with pH adjusted ZnCl2−NH4Cl electrolytes [3]. Utilizing a 0D thermodynamic model of the electrolyte, they determined the pH stability and predicted the conditions under which a range of solids would precipitate. Integrating this method into a 1D continuum model, they simulated the performance of experimental near-neutral ZABs from the literature. Figure 9 shows concentration profiles of in the cell proposed by Goh, et al. [43] during cycling. The Zn electrode is on the left and the BAE is on the right of the domain. To maintain a neutral pH in the BAE, the buffer reaction NH4+ ⇌ NH3 + H+ counteracts the pH shifts inherent in the ORR/OER. As more NH3 is produced, it forms dominant complexes with Zn2+, shown in Figure 9a. Because there is an excess of NH4+ in the electrolyte, the buffer reaction is uninhibited and the pH during discharging is relatively stable (Figure 9e). During charging, the buffer reaction is reversed and NH3 is converted to NH4+. As NH3 is depleted, zinc-chloride complexes dominate in the BAE (Figure 9b). Some of the NH3 that was produced during discharge diffuses into the bulk electrolyte and cannot be quickly recovered. When NH3 is locally depleted, the buffer reaction becomes limited and the pH in the BAE becomes acidic (Figure 9f). Acidic pH values can accelerate catalyst degradation and limit the lifetime of the cell. In their work, Clark, et al., discuss how cell architecture and electrolyte composition can be optimized to avoid this effect and improve performance.
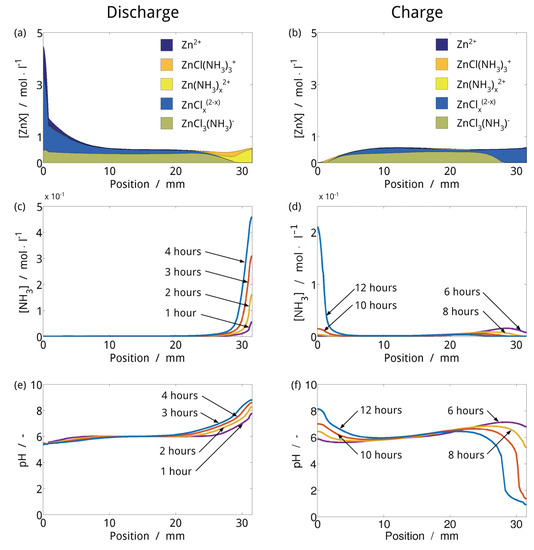
Figure 9.
Electrolyte composition of near-neutral ZAB in during discharging and charging. At the end of discharging (a), zinc in the gas diffusion electrode (GDE) exists as Zn(NH3)42+ . Once the capacity of zinc to take up NH3 is completely utilized, NH3 accumulates in the GDE (c); As the NH4+/NH3 solution approaches its equivalence point, the pH value in the GDE becomes steadily more alkaline (e); At the Zn electrode, the small amount of NH3 present is taken up by excess Zn2+ and the pH value becomes slightly more acidic. When the cell is charged, the production of H+ in the GDE pushes the equilibrium of the ammonium buffer back towards NH4+. The zinc–ammine complexes release NH3 back to the solution as charging progresses, and at the end of charging, zinc in the GDE exists exclusively as zinc–chloride complexes (b); To stabilize the pH value in the GDE, there must be NH3 available for the conversion into NH4+. However, a considerable amount of the NH3 produced during discharging diffuses into the bulk electrolyte and cannot be quickly recovered. This leads to a depletion of NH3 in the GDE (d); At the Zn electrode, the concentration of NH3 increases because of the redeposition of zinc. Without NH3 to stabilize the pH value, the electrolyte in the GDE becomes acidic (f). At the Zn electrode, the loss of aqueous Zn2+ and the relative excess of NH3 cause the pH value to increase. Reproduced from Clark, et al. [3] with permission from Wiley-VCH.
Continuum models can be invaluable for investigating a range of phenomena in electrochemical cells, from the effects of discharge product precipitation to the electrolyte stability. Through the development of theory-based models, side-by-side with experimental investigation and validation, researchers can identify and pursue the most promising paths towards advanced metal-air batteries.
4. Model-Based Battery Engineering
To provide an example of how modeling and simulation can be applied to advance zinc-air battery development, we performed a series of cell-level continuum simulations using existing ZAB models [3,55]. In this analysis, we optimize the thickness of the zinc electrode to maximize the capacity of the cell while avoiding the unwanted effects of passivation. The initial composition of the electrolyte is 7 M KOH, saturated with ZnO. The BAE and separator are both 0.5 mm in length and the Zn-electrode is varied. The cell is galvanostatically discharged at current densities ranging from 0.1 to 50 .
Figure 10a shows the magnitude of the KOH concentration drop across the cell at the end of charging. As the thickness of the Zn electrode and the magnitude of the current density increase, the long transport paths and large source terms induce significant concentration gradients in the cell. This is important because KOH gradients can affect the solubility of ZnO and increase the risk of passivation in the Zn electrode.
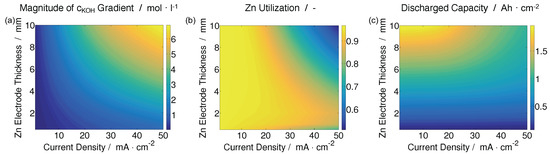
Figure 10.
(a) Magnitude of the KOH concentration gradient across the cell at the end of discharge; (b) Zn utilization; and (c) discharged capacity as a function of Zn electrode thickness and current density.
Figure 10b presents the utilization of zinc metal in the battery. The results show that for current densities less than circa 20 , the active Zn in the electrode is essentially completely utilized (>90%) for all Zn electrode thicknesses. However, for higher current densities, passivation of the electrode occurs due to two competing factors. The ZnO that precipitates in the electrode acts as a barrier to mass transport. For thick Zn electrodes, this barrier to transport is so large that the bulk concentration of KOH in the Zn electrode drops to the point that there is insufficient hydroxide present to form Zn(OH)42− complexes, and Zn utilization drops to circa 50%. For thin electrodes, the ZnO transport barrier remains relatively small and the bulk KOH concentration remains in an acceptable range. However, in these electrodes there is less active surface area available for the reaction, which leads to a higher flux term at the surface of the Zn particles. For current densities over 30 and electrodes less than 2 mm, the magnitude of the flux term is large enough to locally deplete OH− at the electrode surface and passivate the electrode. The Zn utilization drops to circa 80%.
Figure 10c shows the discharged capacity of the battery. Increasing the thickness of the Zn electrode increases the amount of active material in the cell and the theoretically achievable capacity. However, the passivation of thick electrodes at higher current densities limits the amount of Zn that can be utilized, as shown in the previous figure. The result is that a battery with a 5 mm Zn electrode discharged at 10 has roughly the same capacity as a battery with a 10 mm Zn electrode discharged at 50 .
When designing an alkaline ZAB, care should be taken to size the Zn electrode considering the current requirement and the desired capacity. With this information, an informed decision can be taken regarding how much Zn paste should be included in the battery to obtain the optimum performance.
Model-based engineering can also be applied in the testing phase of development to design experiments with the highest chance of success. Because Zn electrodes have a high capacity and can only be discharged at limited rates, it takes a very long time to study their cycling characteristics. Often, the solution is to perform “accelerated” tests with smaller electrodes or at higher current densities, both of which increase the risk of irreversible passivation.
Consider the case in which a researcher wants to cycle a ZAB 200 times in less than 3 months. One cycle is defined as moving between 70% and 30% state-of-charge (SOC), and the electrode consists of a paste that is 50 vol % Zn and 50 vol % electrolyte. Figure 11a shows the time required to complete 200 cycles under these conditions for different combinations of current density and Zn electrode thickness.

Figure 11.
(a) Time required to cycle a ZAB 200 times for various Zn electrode thickness and current density combinations; (b) passivation time; and (c) operational window for a model ZAB.
Figure 11b shows the time required to passivate the Zn electrode. By comparing the passivation time with the cycling time and applying an engineering safety factor of 1.3, we can mark the passivation limitations of the system. This region is shaded in black in Figure 11c. Combinations in the red zone of the figure exceed the time limitation, and we assume that electrodes smaller than 100 microns are impractical to manufacture (orange). With these factors in mind, we define a region of combinations (green) which could fit the researcher’s needs.
When appropriately applied, model-based battery design can be of great value to scientists and engineers. The tools we have reviewed and applied in this analysis give insight into every aspect of battery performance, from the atomic structure of materials to the dynamic performance of whole cells. Embracing an integrated approach to modeling and understanding battery performance can help guide researchers towards achieving the goal of viable and high-performance metal-air batteries.
5. Conclusions
A variety of modeling and simulation methods can be applied to aid the development of zinc-air and other metal-air battery systems. While many metal-air systems are currently under development, Li-air batteries (LABs) and Zn-air batteries (ZABs) are the most promising systems.
On the material level, density functional theory (DFT) can be applied to investigate the electronic properties of catalysts and metals. This could help to screen new catalysts for properties like activity, stability, and selectivity and to elucidate the effect of surface structures on metal dissolution and deposition. Furthermore, equilibrium thermodynamic models can be used to predict the speciation of electrolytes and the solubility of precipitants. This can help determine not only the state of the electrolyte for different pH and concentration mixtures, but also its stability within the electrochemical window of the cell.
When it comes to electrode design, one challenge is to develop a bi-functional air electrode (BAE) that maintains an optimum level of saturation (neither flooding nor drying out) during battery operation. Lattice-Boltzmann-Methods (LBM) can be developed to investigate the pressure-saturation characteristics of real BAE structures in 2D or 3D.
Physics-based continuum modeling is the most useful and widely-utilized method for simulating the cell-level performance of metal-air batteries. Models constructed with this method are able to give researchers insight into a range of phenomena including the coupled effects of electrolyte concentrations, precipitation of solids, electrode kinetics, and cell voltage. The versatility of continuum modeling and the wide array of existing literature on the subject make it a good tool to advance the development of metal-air batteries.
Numerical modeling and simulation studies have shown that the performance LABs with non-aqueous electrolytes is encouraging but limited by slow oxygen transport and pore blockage by Li2O2. DFT simulations have been applied to elucidate the electronic structure and reaction mechanisms of Li2O2 and investigate possible alternative non-aqueous electrolyte solvents. Continuum models have highlighted the cell-level effects of Li2O2 precipitation and O2 transport. The nucleation and growth of Li2O2 particles and films and its effect on the reversibility and performance of non-alkaline LABs is a major topic of research. Aqueous LABs improve oxygen transport in the air electrode and facilitate more favorable precipitation, but the long-term stability of the electrolyte is limited when exposed to CO2. Continuum models developed for aqueous LABs have provided a framework for integrating the multi-phase flow in the air electrode into models of other metal-air systems.
ZABs stand alone as the only successfully commercialized primary metal-air system so far. Modeling studies of these systems highlight the performance of the alkaline electrolyte in air, passivation and shape change of the Zn electrode, and cell-level engineering. Because of its historical dominance, there is a long history of Zn-air continuum models, going back to the 1980s. Recent studies have been provided a scheme for interpreting and understanding experimental results, and a new framework developed to model ZABs with alternative near-neutral electrolytes could find wide application in other electrochemical systems. Implementing these modeling tools in the design process brings researchers closer to the goal of building high-performance and electrically rechargeable zinc-air batteries.
Acknowledgments
This work has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 646186 (ZAS-project). The support of the bwHPC initiative through the use of the JUSTUS HPC facility at Ulm University is acknowledged. The authors wish to thank Timo Danner for the helpful discussion.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gröger, O.; Gasteiger, H.A.; Suchsland, J.P. Review—Electromobility: Batteries or Fuel Cells? J. Electrochem. Soc. 2015, 162, A2605–A2622. [Google Scholar]
- Rahman, M.A.; Wang, X.; Wen, C. High Energy Density Metal-Air Batteries: A Review. J. Electrochem. Soc. 2013, 160, A1759–A1771. [Google Scholar] [CrossRef]
- Clark, S.; Latz, A.; Horstmann, B. Rational Development of Neutral Aqueous Electrolytes for Zinc-Air Batteries. ChemSusChem 2017, 10, 4735–4747. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhang, X.; Li, H.B.; Yoo, H.D.; Chi, X.; An, Q.; Liu, J.; Yu, M.; Wang, W.; Yao, Y. Mixed-phase mullite electrocatalyst for pH-neutral oxygen reduction in magnesium-air batteries. Nano Energy 2016, 27, 8–16. [Google Scholar] [CrossRef]
- Li, C.S.; Sun, Y.; Gebert, F.; Chou, S.L. Current Progress on Rechargeable Magnesium-Air Battery. Adv. Energy Mater. 2017, 7. [Google Scholar] [CrossRef]
- Chen, L.D.; Norskov, J.K.; Luntz, A.C. Theoretical Limits to the Anode Potential in Aqueous Mg-Air Batteries. J. Phys. Chem. C 2015, 119, 19660–19667. [Google Scholar] [CrossRef]
- Vardar, G.; Sleightholme, A.E.S.; Naruse, J.; Hiramatsu, H.; Siegel, D.J.; Monroe, C.W. Electrochemistry of magnesium electrolytes in ionic liquids for secondary batteries. ACS Appl. Mater. Interfaces 2014, 6, 18033–18039. [Google Scholar] [CrossRef] [PubMed]
- Mokhtar, M.; Talib, M.Z.M.; Majlan, E.H.; Tasirin, S.M.; Ramli, W.M.F.W.; Daud, W.R.W.; Sahari, J. Recent developments in materials for aluminum-air batteries: A review. J. Ind. Eng. Chem. 2015, 32, 1–20. [Google Scholar] [CrossRef]
- Zhang, Z.; Zuo, C.; Liu, Z.; Yu, Y.; Zuo, Y.; Song, Y. All-solid-state Al-air batteries with polymer alkaline gel electrolyte. J. Power Sources 2014, 251, 470–475. [Google Scholar] [CrossRef]
- Fu, G.; Chen, Y.; Cui, Z.; Li, Y.; Zhou, W.; Xin, S.; Tang, Y.; Goodenough, J.B. Novel Hydrogel-Derived Bifunctional Oxygen Electrocatalyst for Rechargeable Air Cathodes. Nano Lett. 2016, 16, 6516–6522. [Google Scholar] [CrossRef] [PubMed]
- Adelhelm, P.; Hartmann, P.; Bender, C.L.; Busche, M.; Eufinger, C.; Janek, J. From lithium to sodium: Cell chemistry of room temperature sodium-air and sodium-sulfur batteries. Beilstein J. Nanotechnol. 2015, 6, 1016–1055. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, P.; Bender, C.L.; Vračar, M.; Dürr, A.K.; Garsuch, A.; Janek, J.; Adelhelm, P. A rechargeable room-temperature sodium superoxide (NaO2) battery. Nat. Mater. 2012, 12, 228–232. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Park, H.; Lee, B.; Seong, W.M.; Lim, H.D.; Bae, Y.; Kim, H.; Kim, W.K.; Ryu, K.H.; Kang, K. Dissolution and ionization of sodium superoxide in sodium–oxygen batteries. Nat. Commun. 2016, 7, 10670. [Google Scholar] [CrossRef] [PubMed]
- Durmus, Y.E. Modeling of Silicon Air-Batteries. Master’s Thesis, Ulm University, Ulm, Germany, 2013; p. 106. [Google Scholar]
- Cohn, G.; Ein-Eli, Y. Study and development of non-aqueous silicon-air battery. J. Power Sources 2010, 195, 4963–4970. [Google Scholar] [CrossRef]
- Durmus, Y.E.; Aslanbas, O.; Kayser, S.; Tempel, H.; Hausen, F.; de Haart, L.G.; Granwehr, J.; Ein-Eli, Y.; Eichel, R.A.; Kungl, H. Long run discharge, performance and efficiency of primary Silicon–air cells with alkaline electrolyte. Electrochim. Acta 2017, 225, 215–224. [Google Scholar] [CrossRef]
- Girishkumar, G.; McCloskey, B.; Luntz, A.C.; Swanson, S.; Wilcke, W. Lithium-air battery: Promise and challenges. J. Phys. Chem. Lett. 2010, 1, 2193–2203. [Google Scholar] [CrossRef]
- Lee, J.S.; Kim, S.T.; Cao, R.; Choi, N.S.; Liu, M.; Lee, K.T.; Cho, J. Metal-air batteries with high energy density: Li-air versus Zn-air. Adv. Energy Mater. 2011, 1, 34–50. [Google Scholar] [CrossRef]
- Li, Y.; Dai, H. Recent advances in zinc–air batteries. Chem. Soc. Rev. 2014, 43, 5257–5275. [Google Scholar] [CrossRef] [PubMed]
- Blurton, K.F.; Sammells, A.F. Metal/air batteries: Their status and potential—A review. J. Power Sources 1979, 4, 263–279. [Google Scholar] [CrossRef]
- Abraham, K.M.; Jiang, Z. A Polymer Electrolyte-Based Rechargeable Lithium/Oxygen Battery. J. Electrochem. Soc. 1996, 143, 1–5. [Google Scholar]
- Xu, W.; Xu, K.; Viswanathan, V.V.; Towne, S.A.; Hardy, J.S.; Xiao, J.; Nie, Z.; Hu, D.; Wang, D.; Zhang, J.G. Reaction mechanisms for the limited reversibility of Li-O2 chemistry in organic carbonate electrolytes. J. Power Sources 2011, 196, 9631–9639. [Google Scholar] [CrossRef]
- McCloskey, B.D.; Bethune, D.S.; Shelby, R.M.; Girishkumar, G.; Luntz, A.C. Solvents critical role in nonaqueous Lithium-Oxygen battery electrochemistry. J. Phys. Chem. Lett. 2011, 2, 1161–1166. [Google Scholar] [CrossRef] [PubMed]
- Freunberger, S.A.; Chen, Y.; Peng, Z.; Griffin, J.M.; Hardwick, L.J.; Bardé, F.; Novák, P.; Bruce, P.G. Reactions in the rechargeable lithium-O2 battery with alkyl carbonate electrolytes. J. Am. Chem. Soc. 2011, 133, 8040–8047. [Google Scholar] [CrossRef] [PubMed]
- McCloskey, B.D.; Speidel, A.; Scheffler, R.; Miller, D.C.; Viswanathan, V.; Hummelshøj, J.S.; Nørskov, J.K.; Luntz, A.C. Twin problems of interfacial carbonate formation in nonaqueous Li-O2 batteries. J. Phys. Chem. Lett. 2012, 3, 997–1001. [Google Scholar] [CrossRef] [PubMed]
- Albertus, P.; Girishkumar, G.; McCloskey, B.; Sanchez-Carrera, R.S.; Kozinsky, B.; Christensen, J.; Luntz, A.C. Identifying Capacity Limitations in the Li/Oxygen Battery Using Experiments and Modeling. J. Electrochem. Soc. 2011, 158, A343–A351. [Google Scholar] [CrossRef]
- Monroe, C.W. Does Oxygen Transport Affect the Cell Voltages of Metal/Air Batteries? J. Electrochem. Soc. 2017, 164, E3547–E3551. [Google Scholar] [CrossRef]
- Visco, S.J.; Katz, B.D.; Nimon, Y.S.; De Jonghe, L.C. Protected Active Metal Electrode and Battery Cell Structures with Non-Aqueous Interlayer Architecture. U.S. Patent 7282295 B2, 16 October 2007. [Google Scholar]
- Visco, S.J.; Nimon, Y.S. Active Metal/aqueous Electrochemical Cells and Systems. U.S. Patent 7645543 B2, 12 January 2010. [Google Scholar]
- Horstmann, B.; Danner, T.; Bessler, W.G. Precipitation in aqueous lithium–oxygen batteries: A model-based analysis. Energy Environ. Sci. 2013, 6, 1299–1314. [Google Scholar] [CrossRef]
- Hummelshøj, J.S.; Luntz, A.C.; Norskov, J.K. Theoretical evidence for low kinetic overpotentials in Li-O2 electrochemistry. J. Chem. Phys. 2013, 138, 034703. [Google Scholar] [CrossRef] [PubMed]
- Sandhu, S.S.; Brutchen, G.W.; Fellner, J.P. Lithium/air cell: Preliminary mathematical formulation and analysis. J. Power Sources 2007, 170, 196–209. [Google Scholar] [CrossRef]
- Zheng, J.P.; Liang, R.Y.; Hendrickson, M.; Plichta, E.J. Theoretical Energy Density of Li–Air Batteries. J. Electrochem. Soc. 2008, 155, A432–A437. [Google Scholar] [CrossRef]
- Sahapatsombut, U.; Cheng, H.; Scott, K. Modelling of operation of a lithium-air battery with ambient air and oxygen-selective membrane. J. Power Sources 2014, 249, 418–430. [Google Scholar] [CrossRef]
- Horstmann, B.; Gallant, B.; Mitchell, R.; Bessler, W.G.; Shao-Horn, Y.; Bazant, M.Z. Rate-dependent morphology of Li2O2 growth in Li-O2 batteries. J. Phys. Chem. Lett. 2013, 4, 4217–4222. [Google Scholar] [CrossRef] [PubMed]
- Danner, T.; Horstmann, B.; Wittmaier, D.; Wagner, N.; Bessler, W.G. Reaction and transport in Ag/Ag2O gas diffusion electrodes of aqueous Li-O2 batteries: Experiments and modeling. J. Power Sources 2014, 264, 320–332. [Google Scholar] [CrossRef]
- Lu, J.; Jung Lee, Y.; Luo, X.; Chun Lau, K.; Asadi, M.; Wang, H.H.; Brombosz, S.; Wen, J.; Zhai, D.; Chen, Z.; et al. A lithium–oxygen battery based on lithium superoxide. Nature 2016, 529, 377–382. [Google Scholar] [CrossRef] [PubMed]
- Johnson, L.; Li, C.; Liu, Z.; Chen, Y.; Freunberger, S.A.; Ashok, P.C.; Praveen, B.B.; Dholakia, K.; Tarascon, J.M.; Bruce, P.G. Erratum: The role of LiO2 solubility in O2 reduction in aprotic solvents and its consequences for Li-O2 batteries. Nat. Chem. 2014, 7, 87. [Google Scholar] [CrossRef]
- Gao, X.; Chen, Y.; Johnson, L.; Bruce, P.G. Erratum: Promoting solution phase discharge in Li-O2 batteries containing weakly solvating electrolyte solutions. Nat. Mater. 2016, 15, 918. [Google Scholar] [CrossRef] [PubMed]
- McCloskey, B.D.; Bethune, D.S.; Shelby, R.M.; Mori, T.; Scheffler, R.; Speidel, A.; Sherwood, M.; Luntz, A.C. Limitations in rechargeability of Li-O2 batteries and possible origins. J. Phys. Chem. Lett. 2012, 3, 3043–3047. [Google Scholar] [CrossRef] [PubMed]
- Vegge, T.; Garcia-Lastra, J.M.; Siegel, D.J. Lithium–oxygen batteries: At a crossroads? Curr. Opin. Electrochem. 2017, 6, 100–107. [Google Scholar] [CrossRef]
- Pei, P.; Wang, K.; Ma, Z. Technologies for extending zinc-air battery’s cyclelife: A review. Appl. Energy 2014, 128, 315–324. [Google Scholar] [CrossRef]
- Thomas Goh, F.W.; Liu, Z.; Hor, T.S.A.; Zhang, J.; Ge, X.; Zong, Y.; Yu, A.; Khoo, W. A Near-Neutral Chloride Electrolyte for Electrically Rechargeable Zinc-Air Batteries. J. Electrochem.Soc. 2014, 161, A2080–A2086. [Google Scholar] [CrossRef]
- Sumboja, A.; Ge, X.; Zheng, G.; Goh, F.T.; Hor, T.A.; Zong, Y.; Liu, Z. Durable rechargeable zinc-air batteries with neutral electrolyte and manganese oxide catalyst. J. Power Sources 2016, 332, 330–336. [Google Scholar] [CrossRef]
- MacFarlane, D.R.; Tachikawa, N.; Forsyth, M.; Pringle, J.M.; Howlett, P.C.; Elliott, G.D.; Davis, J.H.; Watanabe, M.; Simon, P.; Angell, C.A. Energy applications of ionic liquids. Energy Environ. Sci. 2014, 7, 232–250. [Google Scholar] [CrossRef]
- Liu, Z.; Abedin, S.Z.E.; Endres, F. Electrodeposition of zinc films from ionic liquids and ionic liquid/water mixtures. Electrochim. Acta 2013, 89, 635–643. [Google Scholar] [CrossRef]
- Liu, Z.; El Abedin, S.Z.; Endres, F. Dissolution of zinc oxide in a protic ionic liquid with the 1-methylimidazolium cation and electrodeposition of zinc from ZnO/ionic liquid and ZnO/ionic liquid-water mixtures. Electrochem. Commun. 2015, 58, 46–50. [Google Scholar] [CrossRef]
- Fu, J.; Cano, Z.P.; Park, M.G.; Yu, A.; Fowler, M.; Chen, Z. Electrically Rechargeable Zinc–Air Batteries: Progress, Challenges, and Perspectives. Adv. Mater. 2017, 29, 1604685. [Google Scholar] [CrossRef] [PubMed]
- Amendola, S.; Binder, M.; Black, P.J.; Sharp-Goldman, S.; Johnson, L.; Kunz, M.; Oster, M.; Chciuk, T.; Johnson, R. Electrically Rechargeable, Metal-Air Battery Systems and Methods. U.S. Patent 2012/0021303 A1, 26 January 2012. [Google Scholar]
- Friesen, C.; Krishnan, R.; Friesen, G. Rechargeable Electrochemical Cell System with a Charging Electrode Charge/discharge Mode Switching in the Cells. U.S. Patent US 2011/0070506 A1, 24 March 2011. [Google Scholar]
- Lee, D.U.; Xu, P.; Cano, Z.P.; Kashkooli, A.G.; Park, M.G.; Chen, Z. Recent progress and perspectives on bi-functional oxygen electrocatalysts for advanced rechargeable metal–air batteries. J. Mater. Chem. A 2016, 4, 7107–7134. [Google Scholar] [CrossRef]
- Neburchilov, V.; Wang, H.; Martin, J.J.; Qu, W. A review on air cathodes for zinc-air fuel cells. J. Power Sources 2010, 195, 1271–1291. [Google Scholar] [CrossRef]
- Stoerzinger, K.a.; Risch, M.; Han, B.; Shao-Horn, Y. Recent Insights into Manganese Oxides in Catalyzing Oxygen Reduction Kinetics. ACS Catal. 2015, 5, 6021–6031. [Google Scholar] [CrossRef]
- Horn, Q.C.; Shao-Horn, Y. Morphology and Spatial Distribution of ZnO Formed in Discharged Alkaline Zn/MnO2 AA Cells. J. Electrochem. Soc. 2003, 150, A652–A658. [Google Scholar] [CrossRef]
- Stamm, J.; Varzi, A.; Latz, A.; Horstmann, B. Modeling nucleation and growth of zinc oxide during discharge of primary zinc-air batteries. J. Power Sources 2017, 360, 136–149. [Google Scholar] [CrossRef]
- Jörissen, L. Bifunctional oxygen/air electrodes. J. Power Sources 2006, 155, 23–32. [Google Scholar] [CrossRef]
- Drillet, J.F.; Holzer, F.; Kallis, T.; Müller, S.; Schmidt, V. Influence of CO2 on the stability of bifunctional oxygen electrodes for rechargeable zinc/air batteries and study of different CO2 filter materials. Phys. Chem. Chem. Phys. 2001, 3, 368–371. [Google Scholar] [CrossRef]
- Hwang, B.; Oh, E.S.; Kim, K. Observation of electrochemical reactions at Zn electrodes in Zn-air secondary batteries. Electrochim. Acta 2016, 216, 484–489. [Google Scholar] [CrossRef]
- Suresh Kannan, A.R.; Muralidharan, S.; Sarangapani, K.B.; Balaramachandran, V.; Kapali, V. Corrosion and anodic behaviour of zinc and its ternary alloys in alkaline battery electrolytes. J. Power Sources 1995, 57, 93–98. [Google Scholar] [CrossRef]
- Vorkapicc, L.Z.; Drazzicc, D.M.; Despic, A.R. Corrosion of Pure and Amalgamated Zinc in Concentrated Alkali Hydroxide Solutions. J. Electrochem. Soc. 1974, 121, 1385–1392. [Google Scholar] [CrossRef]
- Baugh, L.M.; Tye, F.L.; White, N.C. Corrosion and polarization characteristics of zinc in battery electrolyte analogues and the effect of amalgamation. J. Appl. Electrochem. 1983, 13, 623–635. [Google Scholar] [CrossRef]
- Dirkse, T.; Hampson, N. The anodic behaviour of zinc in aqueous solution—-III. Passivation in mixed KF-KOH solutions. Electrochim. Acta 1972, 17, 813–818. [Google Scholar] [CrossRef]
- Schröder, D.; Sinai Borker, N.N.; König, M.; Krewer, U. Performance of zinc air batteries with added K2CO3 in the alkaline electrolyte. J. Appl. Electrochem. 2015, 45, 427–437. [Google Scholar] [CrossRef]
- Mainar, A.R.; Leonet, O.; Bengoechea, M.; Boyano, I.; de Meatza, I.; Kvasha, A.; Guerfi, A.; Blazquez, J.A. Alkaline aqueous electrolytes for secondary zinc-air batteries: An overview. Int. J. Energy Res. 2016, 40, 1032–1049. [Google Scholar] [CrossRef]
- Mainar, A.R.; Iruin, E.; Colmenares, L.C.; Kvasha, A.; de Meatza, I.; Bengoechea, M.; Leonet, O.; Boyano, I.; Zhang, Z.; Blazquez, J.A. An overview of progress in electrolytes for secondary zinc-air batteries and other storage systems based on zinc. J. Energy Storage 2018, 15, 304–328. [Google Scholar] [CrossRef]
- Kar, M.; Winther-Jensen, B.; Forsyth, M.; MacFarlane, D.R. Chelating ionic liquids for reversible zinc electrochemistry. Phys. Chem. Chem. Phys. 2013, 15, 7191–7197. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.S.; Lee, T.; Song, H.K.; Cho, J.; Kim, B.S. Ionic liquid modified graphene nanosheets anchoring manganese oxide nanoparticles as efficient electrocatalysts for Zn–air batteries. Energy Environ. Sci. 2011, 4, 4148–4154. [Google Scholar] [CrossRef]
- Endres, F.; Abbott, A.; MacFarlane, D.R. (Eds.) Electrodeposition from Ionic Liquids, 1st ed.; Wiley-VCH: Weinheim, Germany, 2008; p. 410. [Google Scholar]
- Xu, M.; Ivey, D.G.; Xie, Z.; Qu, W. Rechargeable Zn-air batteries: Progress in electrolyte development and cell configuration advancement. J. Power Sources 2015, 283, 358–371. [Google Scholar] [CrossRef]
- Mclarnon, F.R.; Cairns, E.J. The Secondary Alkaline Zinc Electrode. J. Electrochem. Soc. 1991, 138, 645–664. [Google Scholar] [CrossRef]
- Kim, H.; Jeong, G.; Kim, Y.U.; Kim, J.H.; Park, C.M.; Sohn, H.J. Metallic anodes for next generation secondary batteries. Chem. Soc. Rev. 2013, 42, 9011–9034. [Google Scholar] [CrossRef] [PubMed]
- Bockris, J.O.; Nagy, Z.; Damjanovic, A. On the Deposition and Dissolution of Zinc in Alkaline Solutions. J. Electrochem. Soc. 1972, 119, 285–295. [Google Scholar] [CrossRef]
- Sun, K.E.; Hoang, T.K.; Doan, T.N.L.; Yu, Y.; Zhu, X.; Tian, Y.; Chen, P. Suppression of Dendrite Formation and Corrosion on Zinc Anode of Secondary Aqueous Batteries. ACS Appl. Mater. Interfaces 2017, 9, 9681–9687. [Google Scholar] [CrossRef] [PubMed]
- Banik, S.J.; Akolkar, R. Suppressing Dendritic Growth during Alkaline Zinc Electrodeposition using Polyethylenimine Additive. Electrochim. Acta 2015, 179, 475–481. [Google Scholar] [CrossRef]
- Diggle, J.W.; Damjanovic, A. The inhibition of the dendritic electrocrystallization of zinc from doped alkaline zincate solutions. J. Electrochem. Soc. 1972, 119, 1649–1658. [Google Scholar] [CrossRef]
- Schmid, M.; Willert-Porada, M. Electrochemical behavior of zinc particles with silica based coatings as anode material for zinc air batteries with improved discharge capacity. J. Power Sources 2017, 351, 115–122. [Google Scholar] [CrossRef]
- Zelger, C.; Laumen, J.; Laskos, A.; Gollas, B. Rota-Hull Cell Study on Pulse Current Zinc Electrodeposition from Alkaline Electrolytes. Electrochim. Acta 2016, 213, 208–216. [Google Scholar] [CrossRef]
- Liu, M.B. Passivation of Zinc Anodes in KOH Electrolytes. J. Electrochem. Soc. 1981, 128, 1663–1668. [Google Scholar] [CrossRef]
- Dirkse, T.; Hampson, N. The anodic behaviour of zinc in aqueous KOH solution—II. passivation experiments using linear sweep voltammetry. Electrochim. Acta 1972, 17, 387–394. [Google Scholar] [CrossRef]
- Zhang, X.G. Corrosion and Electrochemistry of Zinc, 1st ed.; Plenum Press: New York, NY, USA, 1996. [Google Scholar]
- Prentice, G. A Model for the Passivation of the Zinc Electrode in Alkaline Electrolyte. J. Electrochem. Soc. 1991, 138, 890–894. [Google Scholar] [CrossRef]
- Jung, J.I.; Risch, M.; Park, S.; Kim, M.G.; Nam, G.; Jeong, H.Y.; Shao-Horn, Y.; Cho, J. Optimizing nanoparticle perovskite for bifunctional oxygen electrocatalysis. Energy Environ. Sci. 2016, 9, 176–183. [Google Scholar] [CrossRef]
- Mainar, A.R.; Colmenares, L.C.; Leonet, O.; Alcaide, F.; Iruin, J.J.; Weinberger, S.; Hacker, V.; Iruin, E.; Urdanpilleta, I.; Blazquez, J.A. Manganese oxide catalysts for secondary zinc air batteries: From electrocatalytic activity to bifunctional air electrode performance. Electrochim. Acta 2016, 217, 80–91. [Google Scholar] [CrossRef]
- Li, Y.; Gong, M.; Liang, Y.; Feng, J.; Kim, J.E.; Wang, H.; Hong, G.; Zhang, B.; Dai, H. Advanced zinc-air batteries based on high-performance hybrid electrocatalysts. Nat. Commun. 2013, 4, 1805. [Google Scholar] [CrossRef] [PubMed]
- Tan, P.; Kong, W.; Shao, Z.; Liu, M.; Ni, M. Advances in modeling and simulation of Li–air batteries. Prog. Energy Combust. Sci. 2017, 62, 155–189. [Google Scholar] [CrossRef]
- Grew, K.N.; Chiu, W.K. A review of modeling and simulation techniques across the length scales for the solid oxide fuel cell. J. Power Sources 2012, 199, 1–13. [Google Scholar] [CrossRef]
- Sholl, D. S.; Steckel, J.A. Density Functional Theory: A Practical Introduction, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Mattsson, A.E.; Schultz, P.A.; Desjarlais, M.P.; Mattsson, T.R.; Leung, K. Designing meaningful density functional theory calculations in materials science—A primer. Model. Simul. Mater. Sci. Eng. 2005, 13, 1–31. [Google Scholar]
- Hörmann, N.G.; Jäckle, M.; Gossenberger, F.; Roman, T.; Forster-Tonigold, K.; Naderian, M.; Sakong, S.; Groß, A. Some challenges in the first-principles modeling of structures and processes in electrochemical energy storage and transfer. J. Power Sources 2015, 275, 531–538. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Rossmeisl, J.; Logadottir, A.; Lindqvist, L.; Kitchin, J.R.; Bligaard, T.; Jónsson, H. Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B 2004, 108, 17886–17892. [Google Scholar] [CrossRef]
- Viswanathan, V.; Hansen, H.A.; Rossmeisl, J.; Nørskov, J.K. Universality in oxygen reduction electrocatalysis on metal surfaces. ACS Catal. 2012, 2, 1654–1660. [Google Scholar] [CrossRef]
- Hansen, H.A.; Viswanathan, V.; Nørskov, J.K. Unifying kinetic and thermodynamic analysis of 2 e- and 4 e-reduction of oxygen on metal surfaces. J. Phys. Chem. C 2014, 118, 6706–6718. [Google Scholar] [CrossRef]
- Viswanathan, V.; Nørskov, J.K.; Speidel, A.; Scheffler, R.; Gowda, S.; Luntz, A.C. Li-O2 kinetic overpotentials: Tafel plots from experiment and first-principles theory. J. Phys. Chem. Lett. 2013, 4, 556–560. [Google Scholar] [CrossRef] [PubMed]
- Aetukuri, N.B.; McCloskey, B.D.; Garcia, J.M.; Krupp, L.E.; Viswanathan, V.; Luntz, A.C. Solvating additives drive solution-mediated electrochemistry and enhance toroid growth in non-aqueous Li-O2 batteries. Nat. Chem. 2015, 7, 50–56. [Google Scholar] [CrossRef] [PubMed]
- Eberle, D.; Horstmann, B. Oxygen Reduction on Pt(111) in Aqueous Electrolyte: Elementary Kinetic Modeling. Electrochim. Acta 2014, 137, 714–720. [Google Scholar] [CrossRef]
- Tripkovic, V.; Vegge, T. Potential and Rate Determining Step for Oxygen Reduction on Pt(111). J. Phys. Chem. C 2017, 121, 26785–26793. [Google Scholar] [CrossRef]
- Vazquez-Arenas, J.; Ramos-Sanchez, G.; Franco, A.A. A multi-scale model of the oxygen reduction reaction on highly active graphene nanosheets in alkaline conditions. J. Power Sources 2016, 328, 492–502. [Google Scholar] [CrossRef]
- Siahrostami, S.; Tripković, V.; Lundgaard, K.T.; Jensen, K.E.; Hansen, H.A.; Hummelshøj, J.S.; Mýrdal, J.S.G.; Vegge, T.; Nørskov, J.K.; Rossmeisl, J. First principles investigation of zinc-anode dissolution in zinc–air batteries. Phys. Chem. Chem. Phys. 2013, 15, 6416–6421. [Google Scholar] [CrossRef] [PubMed]
- Jäckle, M.; Groß, A. Microscopic properties of lithium, sodium, and magnesium battery anode materials related to possible dendrite growth. J. Chem. Phys. 2016, 141. [Google Scholar] [CrossRef] [PubMed]
- Hummelshøj, J.S.; Blomqvist, J.; Datta, S.; Vegge, T.; Rossmeisl, J.; Thygesen, K.S.; Luntz, A.C.; Jacobsen, K.W.; Nørskov, J.K. Communications: Elementary oxygen electrode reactions in the aprotic Li-air battery. J. Chem. Phys. 2010, 132. [Google Scholar] [CrossRef] [PubMed]
- Radin, M.D.; Rodriguez, J.F.; Tian, F.; Siegel, D.J. Lithium peroxide surfaces are metallic, while lithium oxide surfaces are not. J. Am. Chem. Soc. 2012, 134, 1093–1103. [Google Scholar] [CrossRef] [PubMed]
- Radin, M.D.; Siegel, D.J. Charge transport in lithium peroxide: relevance for rechargeable metal–air batteries. Energy Environ. Sci. 2013, 6, 2370. [Google Scholar] [CrossRef]
- Radin, M.D.; Monroe, C.W.; Siegel, D.J. How dopants can enhance charge transport in Li2O2. Chem. Mater. 2015, 27, 839–847. [Google Scholar] [CrossRef]
- Dirkse, T.P. The Nature of the Zinc-Containing Ion in Strongly Alkaline Solutions. J. Electrochem. Soc. 1954, 101, 328. [Google Scholar] [CrossRef]
- Larcin, J.; Maskell, W.C.; Tye, F.L. Leclanche cell investigations I: Zn(NH3)2Cl2 solubility and the formation of ZnCl2·4Zn(OH)2·H2O. Electrochim. Acta 1997, 42, 2649–2658. [Google Scholar] [CrossRef]
- Zhang, Y.; Muhammed, M. Critical evaluation of thermodynamics of complex formation of metal ions in aqueous solutions—VI. Hydrolysis and hydroxo-complexes of Zn2+ at 298.15 K. Hydrometallurgy 2001, 60, 215–236. [Google Scholar] [CrossRef]
- Clark, S.; Latz, A.; Horstmann, B. Cover Feature: Rational Development of Neutral Aqueous Electrolytes for Zinc-Air Batteries. ChemSusChem 2017, 10, 4666. [Google Scholar] [CrossRef]
- Smith, R.; Martell, A. Critical Stability Constants; Springer: New York, NY, USA, 1976; Volume 4. [Google Scholar]
- Martell, A.E.; Smith, R.M. Critical Stability Constants; Springer: New York, NY, USA, 1977; Volume 5. [Google Scholar]
- Martell, A.; Smith, R. Other Organic Ligands, 1st ed.; Springer: New York, NY, USA, 1977. [Google Scholar]
- Dirkse, T. The Solubility Product Constant of ZnO. J. Electrochem. Soc. 1986, 133, 1656–1657. [Google Scholar] [CrossRef]
- Limpo, J.; Luis, A. Solubility of zinc chloride in ammoniacal ammonium chloride solutions. Hydrometallurgy 1993, 32, 247–260. [Google Scholar] [CrossRef]
- Limpo, J.; Luis, A.; Cristina, M. Hydrolysis of zinc chloride in aqueous ammoniacal ammonium chloride solutions. Hydrometallurgy 1995, 38, 235–243. [Google Scholar] [CrossRef]
- Vazquez-Arenas, J.; Sosa-Rodriguez, F.; Lazaro, I.; Cruz, R. Thermodynamic and electrochemistry analysis of the zinc electrodeposition in NH4Cl-NH3 electrolytes on Ti, Glassy Carbon and 316L Stainless Steel. Electrochim. Acta 2012, 79, 109–116. [Google Scholar] [CrossRef]
- Rojas-Hernández, A.; Ramírez, M.T.; Ibáñez, J.G.; González, I. Construction of multicomponent Pourbaix diagrams using generalized species. J. Electrochem. Soc. 1991, 138, 365–371. [Google Scholar] [CrossRef]
- Newman, J.; Thmoas-Alyea, K.E. Electrochemical Systems, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Husch, T.; Korth, M. Charting the known chemical space for non-aqueous lithium–air battery electrolyte solvents. Phys. Chem. Chem. Phys. 2015, 17, 22596–22603. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for Fluid Flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Trouette, B. Lattice Boltzmann simulations of a time-dependent natural convection problem. Comput. Math. Appl. 2013, 66, 1360–1371. [Google Scholar] [CrossRef]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann Method for Complex Flows. Annu. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Sukop, M.C.; Thorne, D.T. Lattice Boltzmann Modeling; Springer: Berlin, Germany, 2006; Volume 79, p. 016702. [Google Scholar]
- He, X.; Li, N. Lattice Boltzmann simulation of electrochemical systems. Comput. Phys. Commun. 2000, 129, 158–166. [Google Scholar] [CrossRef]
- Niu, X.D.; Munekata, T.; Hyodo, S.A.; Suga, K. An investigation of water-gas transport processes in the gas-diffusion-layer of a PEM fuel cell by a multiphase multiple-relaxation-time lattice Boltzmann model. J. Power Sources 2007, 172, 542–552. [Google Scholar] [CrossRef]
- Hao, L.; Cheng, P. Lattice Boltzmann simulations of water transport in gas diffusion layer of a polymer electrolyte membrane fuel cell. J. Power Sources 2010, 195, 3870–3881. [Google Scholar] [CrossRef]
- Molaeimanesh, G.R.; Akbari, M.H. A three-dimensional pore-scale model of the cathode electrode in polymer-electrolyte membrane fuel cell by lattice Boltzmann method. J. Power Sources 2014, 258, 89–97. [Google Scholar] [CrossRef]
- Kim, K.N.; Kang, J.H.; Lee, S.G.; Nam, J.H.; Kim, C.J. Lattice Boltzmann simulation of liquid water transport in microporous and gas diffusion layers of polymer electrolyte membrane fuel cells. J. Power Sources 2015, 278, 703–717. [Google Scholar] [CrossRef]
- Ostadi, H.; Rama, P.; Liu, Y.; Chen, R.; Zhang, X.X.; Jiang, K. 3D reconstruction of a gas diffusion layer and a microporous layer. J. Membr. Sci. 2010, 351, 69–74. [Google Scholar] [CrossRef]
- Danner, T.; Eswara, S.; Schulz, V.P.; Latz, A. Characterization of gas diffusion electrodes for metal-air batteries. J. Power Sources 2016, 324, 646–656. [Google Scholar] [CrossRef]
- Sunu, W.G.; Bennion, D.N. Transient and Failure Analyses of the Porous Zinc Electrode. J. Electrochem. Soc. 1980, 127, 2007–2016. [Google Scholar] [CrossRef]
- Bockelmann, M.; Reining, L.; Kunz, U.; Turek, T. Electrochemical characterization and mathematical modeling of zinc passivation in alkaline solutions: A review. Electrochim. Acta 2017, 237, 276–298. [Google Scholar] [CrossRef]
- Neidhardt, J.P.; Fronczek, D.N.; Jahnke, T.; Danner, T.; Horstmann, B.; Bessler, W.G. A Flexible Framework for Modeling Multiple Solid, Liquid and Gaseous Phases in Batteries and Fuel Cells. J. Electrochem. Soc. 2012, 159, A1528–A1542. [Google Scholar] [CrossRef]
- Hein, S.; Latz, A. Influence of local lithium metal deposition in 3D microstructures on local and global behavior of Lithium-ion batteries. Electrochim. Acta 2016, 201, 354–365. [Google Scholar] [CrossRef]
- Hein, S.; Feinauer, J.; Westhoff, D.; Manke, I.; Schmidt, V.; Latz, A. Stochastic microstructure modeling and electrochemical simulation of lithium-ion cell anodes in 3D. J. Power Sources 2016, 336, 161–171. [Google Scholar] [CrossRef]
- Latz, A.; Zausch, J. Thermodynamic consistent transport theory of Li-ion batteries. J. Power Sources 2011, 196, 3296–3302. [Google Scholar] [CrossRef]
- Mao, Z.; White, R.E. Mathematical modeling of a primary zinc/air battery. J. Electrochem. Soc. 1992, 139, 1105–1114. [Google Scholar] [CrossRef]
- Deiss, E.; Holzer, F.; Haas, O. Modeling of an electrically rechargeable alkaline Zn-air battery. Electrochim. Acta 2002, 47, 3995–4010. [Google Scholar] [CrossRef]
- Andrei, P.; Zheng, J.P.; Hendrickson, M.; Plichta, E.J. Some Possible Approaches for Improving the Energy Density of Li-Air Batteries. J. Electrochem. Soc. 2010, 157, A1287–A1295. [Google Scholar] [CrossRef]
- Schröder, D.; Krewer, U. Model based quantification of air-composition impact on secondary zinc air batteries. Electrochim. Acta 2014, 117, 541–553. [Google Scholar] [CrossRef]
- Arlt, T.; Schröder, D.; Krewer, U.; Manke, I. In operando monitoring of the state of charge and species distribution in zinc air batteries using X-ray tomography and model-based simulations. Phys. Chem. Chem. Phys. 2014, 16, 22273–22280. [Google Scholar] [CrossRef] [PubMed]
- Xue, K.H.; Nguyen, T.K.; Franco, A.A. Impact of the Cathode Microstructure on the Discharge Performance of Lithium Air Batteries: A Multiscale Model. J. Electrochem. Soc. 2014, 161, E3028–E3035. [Google Scholar] [CrossRef]
- Grübl, D.; Bessler, W.G. Cell design concepts for aqueous lithium-oxygen batteries: A model-based assessment. J. Power Sources 2015, 297, 481–491. [Google Scholar] [CrossRef]
- Yin, Y.; Gaya, C.; Torayev, A.; Thangavel, V.; Franco, A.A. Impact of Li2O2 Particle Size on Li-O2 Battery Charge Process: Insights from a Multiscale Modeling Perspective. J. Phys. Chem. Lett. 2016, 7, 3897–3902. [Google Scholar] [CrossRef] [PubMed]
- Bazant, M.Z. Theory of chemical kinetics and charge transfer based on nonequilibrium thermodynamics. Acc. Chem. Res. 2013, 46, 1144–1160. [Google Scholar] [CrossRef] [PubMed]
- Latz, A.; Zausch, J. Thermodynamic derivation of a Butler-Volmer model for intercalation in Li-ion batteries. Electrochim. Acta 2013, 110, 358–362. [Google Scholar] [CrossRef]
- Breiter, M. Dissolution and passivation of vertical porous zinc electrodes in alkaline solution. Electrochim. Acta 1970, 15, 1297–1304. [Google Scholar] [CrossRef]
- Bai, P.; Bazant, M.Z. Charge transfer kinetics at the solid-solid interface in porous electrodes. Nat. Commun. 2014, 5, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.; Smith, R.B.; Bai, P.; Bazant, M.Z. Simple formula for Marcus-Hush-Chidsey kinetics. J. Electroanal. Chem. 2014, 735, 77–83. [Google Scholar] [CrossRef]
- Zeng, Y.; Bai, P.; Smith, R.B.; Bazant, M.Z. Simple formula for asymmetric Marcus-Hush kinetics. J. Electroanal. Chem. 2015, 748, 52–57. [Google Scholar] [CrossRef]
- Melander, M.; Jónsson, E.O.; Mortensen, J.J.; Vegge, T.; García Lastra, J.M. Implementation of Constrained DFT for Computing Charge Transfer Rates within the Projector Augmented Wave Method. J. Chem. Theory Comput. 2016, 12, 5367–5378. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Yu, J.S.; Sunden, B. Review on mechanisms and continuum models of multi-phase transport phenomena in porous structures of non-aqueous Li-Air batteries. J. Power Sources 2015, 278, 352–369. [Google Scholar] [CrossRef]
- Andersen, C.P.; Hu, H.; Qiu, G.; Kalra, V.; Sun, Y. Pore-Scale Transport Resolved Model Incorporating Cathode Microstructure and Peroxide Growth in Lithium-Air Batteries. J. Electrochem. Soc. 2015, 162, A1135–A1145. [Google Scholar] [CrossRef]
- Monroe, C.W.; Delacourt, C. Continuum transport laws for locally non-neutral concentrated electrolytes. Electrochim. Acta 2013, 114, 649–657. [Google Scholar] [CrossRef]
- Latz, A.; Zausch, J. Multiscale modeling of lithium ion batteries: Thermal aspects. Beilstein J. Nanotechnol. 2015, 6, 987–1007. [Google Scholar] [CrossRef] [PubMed]
- Xue, K.H.; McTurk, E.; Johnson, L.; Bruce, P.G.; Franco, A.A. A Comprehensive Model for Non-Aqueous Lithium Air Batteries Involving Different Reaction Mechanisms. J. Electrochem. Soc. 2015, 162, A614–A621. [Google Scholar] [CrossRef]
- Grübl, D.; Bergner, B.; Schröder, D.; Janek, J.; Bessler, W.G. Multistep Reaction Mechanisms in Nonaqueous Lithium-Oxygen Batteries with Redox Mediator: A Model-Based Study. J. Phys. Chem. C 2016, 120, 24623–24636. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).