A Review of Model-Based Design Tools for Metal-Air Batteries
Abstract
1. Introduction
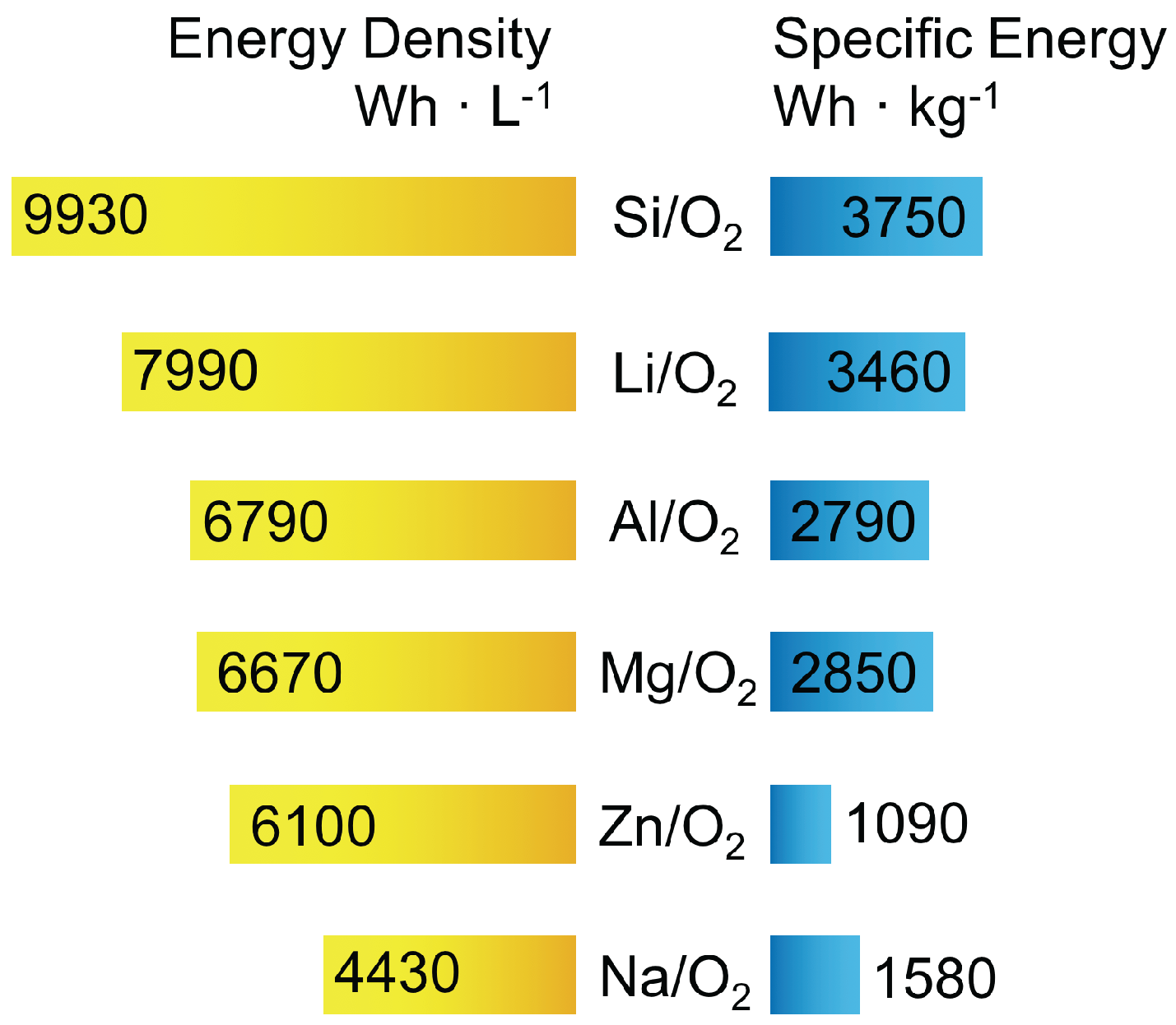
2. Zinc-Air Batteries
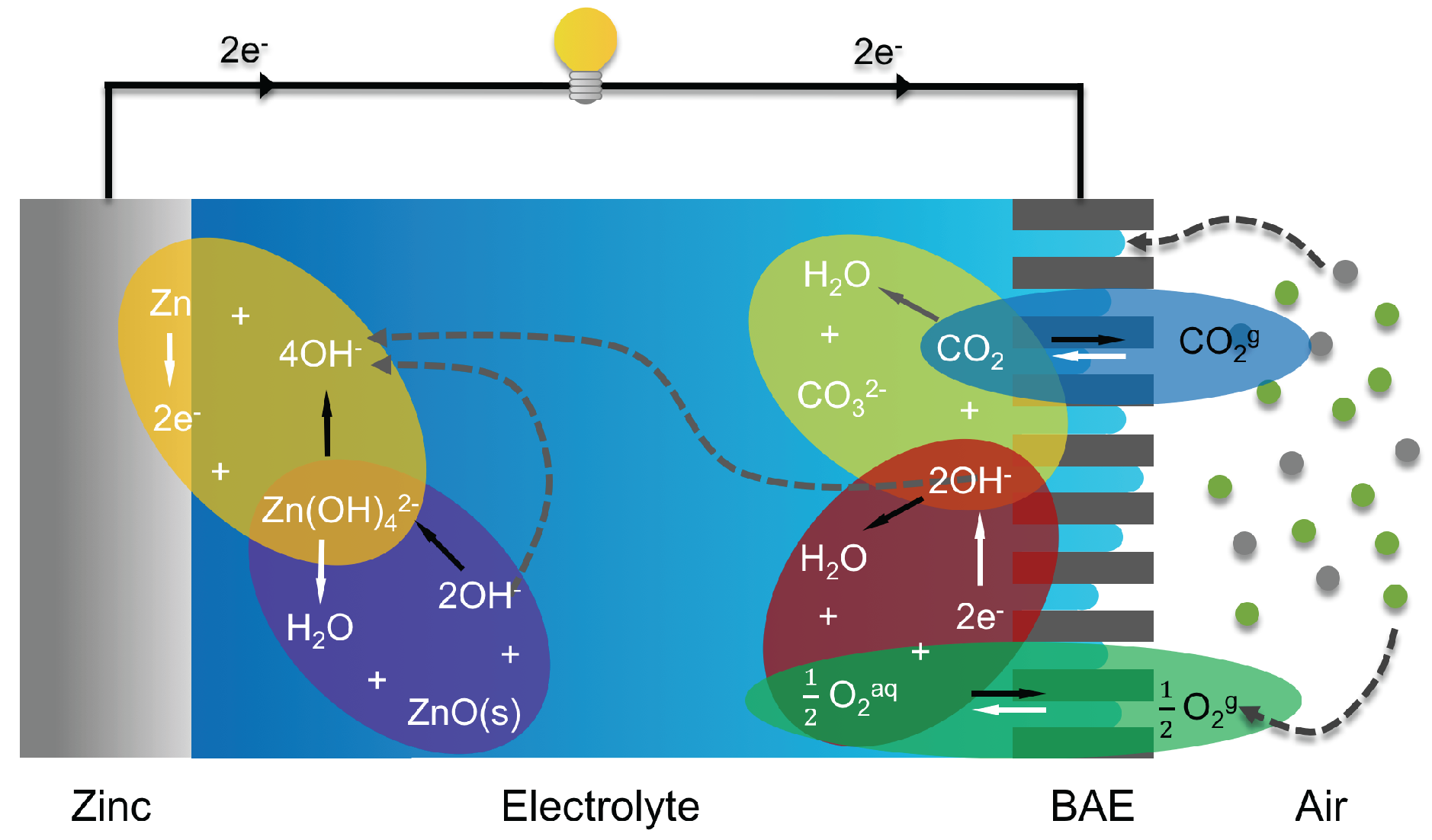
2.1. Working Principle
2.2. Challenges, Progress, and Opportunities
3. Numerical Modeling and Simulation
3.1. Material Development
3.1.1. Electrode Materials
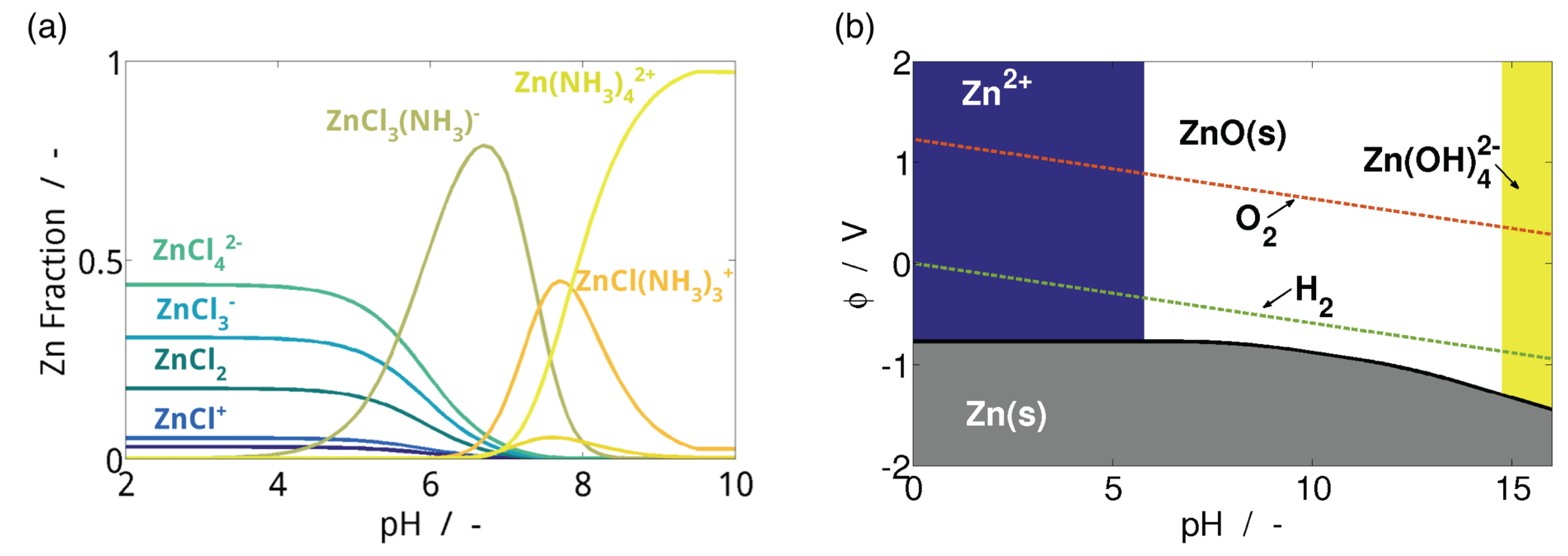
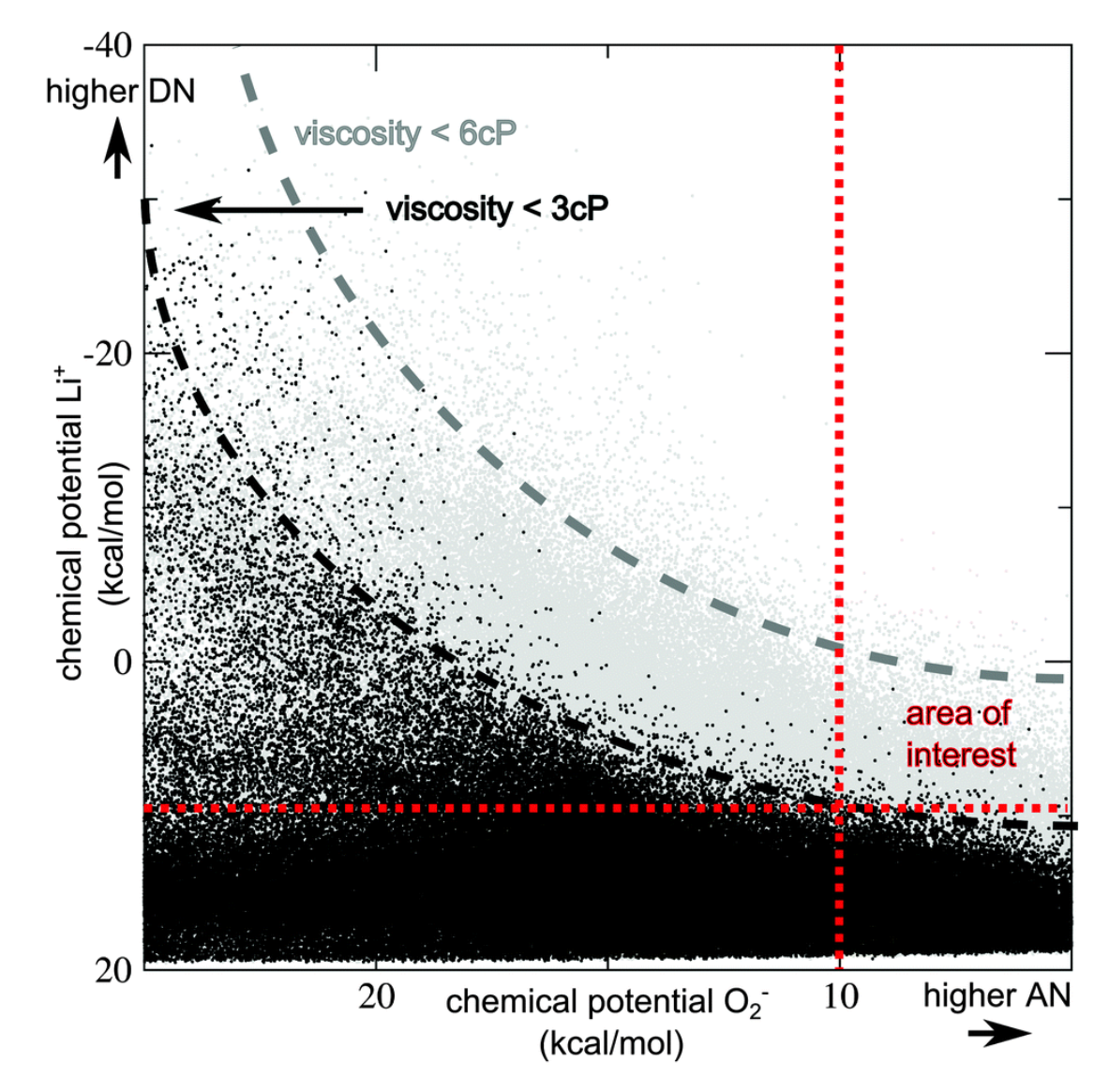
3.1.2. Electrolytes
3.2. Electrode Design
3.2.1. Bi-Functional Air Electrode (BAE)
3.2.2. Metal Electrode
3.3. Cell Modeling
4. Model-Based Battery Engineering
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Gröger, O.; Gasteiger, H.A.; Suchsland, J.P. Review—Electromobility: Batteries or Fuel Cells? J. Electrochem. Soc. 2015, 162, A2605–A2622. [Google Scholar]
- Rahman, M.A.; Wang, X.; Wen, C. High Energy Density Metal-Air Batteries: A Review. J. Electrochem. Soc. 2013, 160, A1759–A1771. [Google Scholar] [CrossRef]
- Clark, S.; Latz, A.; Horstmann, B. Rational Development of Neutral Aqueous Electrolytes for Zinc-Air Batteries. ChemSusChem 2017, 10, 4735–4747. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhang, X.; Li, H.B.; Yoo, H.D.; Chi, X.; An, Q.; Liu, J.; Yu, M.; Wang, W.; Yao, Y. Mixed-phase mullite electrocatalyst for pH-neutral oxygen reduction in magnesium-air batteries. Nano Energy 2016, 27, 8–16. [Google Scholar] [CrossRef]
- Li, C.S.; Sun, Y.; Gebert, F.; Chou, S.L. Current Progress on Rechargeable Magnesium-Air Battery. Adv. Energy Mater. 2017, 7. [Google Scholar] [CrossRef]
- Chen, L.D.; Norskov, J.K.; Luntz, A.C. Theoretical Limits to the Anode Potential in Aqueous Mg-Air Batteries. J. Phys. Chem. C 2015, 119, 19660–19667. [Google Scholar] [CrossRef]
- Vardar, G.; Sleightholme, A.E.S.; Naruse, J.; Hiramatsu, H.; Siegel, D.J.; Monroe, C.W. Electrochemistry of magnesium electrolytes in ionic liquids for secondary batteries. ACS Appl. Mater. Interfaces 2014, 6, 18033–18039. [Google Scholar] [CrossRef] [PubMed]
- Mokhtar, M.; Talib, M.Z.M.; Majlan, E.H.; Tasirin, S.M.; Ramli, W.M.F.W.; Daud, W.R.W.; Sahari, J. Recent developments in materials for aluminum-air batteries: A review. J. Ind. Eng. Chem. 2015, 32, 1–20. [Google Scholar] [CrossRef]
- Zhang, Z.; Zuo, C.; Liu, Z.; Yu, Y.; Zuo, Y.; Song, Y. All-solid-state Al-air batteries with polymer alkaline gel electrolyte. J. Power Sources 2014, 251, 470–475. [Google Scholar] [CrossRef]
- Fu, G.; Chen, Y.; Cui, Z.; Li, Y.; Zhou, W.; Xin, S.; Tang, Y.; Goodenough, J.B. Novel Hydrogel-Derived Bifunctional Oxygen Electrocatalyst for Rechargeable Air Cathodes. Nano Lett. 2016, 16, 6516–6522. [Google Scholar] [CrossRef] [PubMed]
- Adelhelm, P.; Hartmann, P.; Bender, C.L.; Busche, M.; Eufinger, C.; Janek, J. From lithium to sodium: Cell chemistry of room temperature sodium-air and sodium-sulfur batteries. Beilstein J. Nanotechnol. 2015, 6, 1016–1055. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, P.; Bender, C.L.; Vračar, M.; Dürr, A.K.; Garsuch, A.; Janek, J.; Adelhelm, P. A rechargeable room-temperature sodium superoxide (NaO2) battery. Nat. Mater. 2012, 12, 228–232. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Park, H.; Lee, B.; Seong, W.M.; Lim, H.D.; Bae, Y.; Kim, H.; Kim, W.K.; Ryu, K.H.; Kang, K. Dissolution and ionization of sodium superoxide in sodium–oxygen batteries. Nat. Commun. 2016, 7, 10670. [Google Scholar] [CrossRef] [PubMed]
- Durmus, Y.E. Modeling of Silicon Air-Batteries. Master’s Thesis, Ulm University, Ulm, Germany, 2013; p. 106. [Google Scholar]
- Cohn, G.; Ein-Eli, Y. Study and development of non-aqueous silicon-air battery. J. Power Sources 2010, 195, 4963–4970. [Google Scholar] [CrossRef]
- Durmus, Y.E.; Aslanbas, O.; Kayser, S.; Tempel, H.; Hausen, F.; de Haart, L.G.; Granwehr, J.; Ein-Eli, Y.; Eichel, R.A.; Kungl, H. Long run discharge, performance and efficiency of primary Silicon–air cells with alkaline electrolyte. Electrochim. Acta 2017, 225, 215–224. [Google Scholar] [CrossRef]
- Girishkumar, G.; McCloskey, B.; Luntz, A.C.; Swanson, S.; Wilcke, W. Lithium-air battery: Promise and challenges. J. Phys. Chem. Lett. 2010, 1, 2193–2203. [Google Scholar] [CrossRef]
- Lee, J.S.; Kim, S.T.; Cao, R.; Choi, N.S.; Liu, M.; Lee, K.T.; Cho, J. Metal-air batteries with high energy density: Li-air versus Zn-air. Adv. Energy Mater. 2011, 1, 34–50. [Google Scholar] [CrossRef]
- Li, Y.; Dai, H. Recent advances in zinc–air batteries. Chem. Soc. Rev. 2014, 43, 5257–5275. [Google Scholar] [CrossRef] [PubMed]
- Blurton, K.F.; Sammells, A.F. Metal/air batteries: Their status and potential—A review. J. Power Sources 1979, 4, 263–279. [Google Scholar] [CrossRef]
- Abraham, K.M.; Jiang, Z. A Polymer Electrolyte-Based Rechargeable Lithium/Oxygen Battery. J. Electrochem. Soc. 1996, 143, 1–5. [Google Scholar]
- Xu, W.; Xu, K.; Viswanathan, V.V.; Towne, S.A.; Hardy, J.S.; Xiao, J.; Nie, Z.; Hu, D.; Wang, D.; Zhang, J.G. Reaction mechanisms for the limited reversibility of Li-O2 chemistry in organic carbonate electrolytes. J. Power Sources 2011, 196, 9631–9639. [Google Scholar] [CrossRef]
- McCloskey, B.D.; Bethune, D.S.; Shelby, R.M.; Girishkumar, G.; Luntz, A.C. Solvents critical role in nonaqueous Lithium-Oxygen battery electrochemistry. J. Phys. Chem. Lett. 2011, 2, 1161–1166. [Google Scholar] [CrossRef] [PubMed]
- Freunberger, S.A.; Chen, Y.; Peng, Z.; Griffin, J.M.; Hardwick, L.J.; Bardé, F.; Novák, P.; Bruce, P.G. Reactions in the rechargeable lithium-O2 battery with alkyl carbonate electrolytes. J. Am. Chem. Soc. 2011, 133, 8040–8047. [Google Scholar] [CrossRef] [PubMed]
- McCloskey, B.D.; Speidel, A.; Scheffler, R.; Miller, D.C.; Viswanathan, V.; Hummelshøj, J.S.; Nørskov, J.K.; Luntz, A.C. Twin problems of interfacial carbonate formation in nonaqueous Li-O2 batteries. J. Phys. Chem. Lett. 2012, 3, 997–1001. [Google Scholar] [CrossRef] [PubMed]
- Albertus, P.; Girishkumar, G.; McCloskey, B.; Sanchez-Carrera, R.S.; Kozinsky, B.; Christensen, J.; Luntz, A.C. Identifying Capacity Limitations in the Li/Oxygen Battery Using Experiments and Modeling. J. Electrochem. Soc. 2011, 158, A343–A351. [Google Scholar] [CrossRef]
- Monroe, C.W. Does Oxygen Transport Affect the Cell Voltages of Metal/Air Batteries? J. Electrochem. Soc. 2017, 164, E3547–E3551. [Google Scholar] [CrossRef]
- Visco, S.J.; Katz, B.D.; Nimon, Y.S.; De Jonghe, L.C. Protected Active Metal Electrode and Battery Cell Structures with Non-Aqueous Interlayer Architecture. U.S. Patent 7282295 B2, 16 October 2007. [Google Scholar]
- Visco, S.J.; Nimon, Y.S. Active Metal/aqueous Electrochemical Cells and Systems. U.S. Patent 7645543 B2, 12 January 2010. [Google Scholar]
- Horstmann, B.; Danner, T.; Bessler, W.G. Precipitation in aqueous lithium–oxygen batteries: A model-based analysis. Energy Environ. Sci. 2013, 6, 1299–1314. [Google Scholar] [CrossRef]
- Hummelshøj, J.S.; Luntz, A.C.; Norskov, J.K. Theoretical evidence for low kinetic overpotentials in Li-O2 electrochemistry. J. Chem. Phys. 2013, 138, 034703. [Google Scholar] [CrossRef] [PubMed]
- Sandhu, S.S.; Brutchen, G.W.; Fellner, J.P. Lithium/air cell: Preliminary mathematical formulation and analysis. J. Power Sources 2007, 170, 196–209. [Google Scholar] [CrossRef]
- Zheng, J.P.; Liang, R.Y.; Hendrickson, M.; Plichta, E.J. Theoretical Energy Density of Li–Air Batteries. J. Electrochem. Soc. 2008, 155, A432–A437. [Google Scholar] [CrossRef]
- Sahapatsombut, U.; Cheng, H.; Scott, K. Modelling of operation of a lithium-air battery with ambient air and oxygen-selective membrane. J. Power Sources 2014, 249, 418–430. [Google Scholar] [CrossRef]
- Horstmann, B.; Gallant, B.; Mitchell, R.; Bessler, W.G.; Shao-Horn, Y.; Bazant, M.Z. Rate-dependent morphology of Li2O2 growth in Li-O2 batteries. J. Phys. Chem. Lett. 2013, 4, 4217–4222. [Google Scholar] [CrossRef] [PubMed]
- Danner, T.; Horstmann, B.; Wittmaier, D.; Wagner, N.; Bessler, W.G. Reaction and transport in Ag/Ag2O gas diffusion electrodes of aqueous Li-O2 batteries: Experiments and modeling. J. Power Sources 2014, 264, 320–332. [Google Scholar] [CrossRef]
- Lu, J.; Jung Lee, Y.; Luo, X.; Chun Lau, K.; Asadi, M.; Wang, H.H.; Brombosz, S.; Wen, J.; Zhai, D.; Chen, Z.; et al. A lithium–oxygen battery based on lithium superoxide. Nature 2016, 529, 377–382. [Google Scholar] [CrossRef] [PubMed]
- Johnson, L.; Li, C.; Liu, Z.; Chen, Y.; Freunberger, S.A.; Ashok, P.C.; Praveen, B.B.; Dholakia, K.; Tarascon, J.M.; Bruce, P.G. Erratum: The role of LiO2 solubility in O2 reduction in aprotic solvents and its consequences for Li-O2 batteries. Nat. Chem. 2014, 7, 87. [Google Scholar] [CrossRef]
- Gao, X.; Chen, Y.; Johnson, L.; Bruce, P.G. Erratum: Promoting solution phase discharge in Li-O2 batteries containing weakly solvating electrolyte solutions. Nat. Mater. 2016, 15, 918. [Google Scholar] [CrossRef] [PubMed]
- McCloskey, B.D.; Bethune, D.S.; Shelby, R.M.; Mori, T.; Scheffler, R.; Speidel, A.; Sherwood, M.; Luntz, A.C. Limitations in rechargeability of Li-O2 batteries and possible origins. J. Phys. Chem. Lett. 2012, 3, 3043–3047. [Google Scholar] [CrossRef] [PubMed]
- Vegge, T.; Garcia-Lastra, J.M.; Siegel, D.J. Lithium–oxygen batteries: At a crossroads? Curr. Opin. Electrochem. 2017, 6, 100–107. [Google Scholar] [CrossRef]
- Pei, P.; Wang, K.; Ma, Z. Technologies for extending zinc-air battery’s cyclelife: A review. Appl. Energy 2014, 128, 315–324. [Google Scholar] [CrossRef]
- Thomas Goh, F.W.; Liu, Z.; Hor, T.S.A.; Zhang, J.; Ge, X.; Zong, Y.; Yu, A.; Khoo, W. A Near-Neutral Chloride Electrolyte for Electrically Rechargeable Zinc-Air Batteries. J. Electrochem.Soc. 2014, 161, A2080–A2086. [Google Scholar] [CrossRef]
- Sumboja, A.; Ge, X.; Zheng, G.; Goh, F.T.; Hor, T.A.; Zong, Y.; Liu, Z. Durable rechargeable zinc-air batteries with neutral electrolyte and manganese oxide catalyst. J. Power Sources 2016, 332, 330–336. [Google Scholar] [CrossRef]
- MacFarlane, D.R.; Tachikawa, N.; Forsyth, M.; Pringle, J.M.; Howlett, P.C.; Elliott, G.D.; Davis, J.H.; Watanabe, M.; Simon, P.; Angell, C.A. Energy applications of ionic liquids. Energy Environ. Sci. 2014, 7, 232–250. [Google Scholar] [CrossRef]
- Liu, Z.; Abedin, S.Z.E.; Endres, F. Electrodeposition of zinc films from ionic liquids and ionic liquid/water mixtures. Electrochim. Acta 2013, 89, 635–643. [Google Scholar] [CrossRef]
- Liu, Z.; El Abedin, S.Z.; Endres, F. Dissolution of zinc oxide in a protic ionic liquid with the 1-methylimidazolium cation and electrodeposition of zinc from ZnO/ionic liquid and ZnO/ionic liquid-water mixtures. Electrochem. Commun. 2015, 58, 46–50. [Google Scholar] [CrossRef]
- Fu, J.; Cano, Z.P.; Park, M.G.; Yu, A.; Fowler, M.; Chen, Z. Electrically Rechargeable Zinc–Air Batteries: Progress, Challenges, and Perspectives. Adv. Mater. 2017, 29, 1604685. [Google Scholar] [CrossRef] [PubMed]
- Amendola, S.; Binder, M.; Black, P.J.; Sharp-Goldman, S.; Johnson, L.; Kunz, M.; Oster, M.; Chciuk, T.; Johnson, R. Electrically Rechargeable, Metal-Air Battery Systems and Methods. U.S. Patent 2012/0021303 A1, 26 January 2012. [Google Scholar]
- Friesen, C.; Krishnan, R.; Friesen, G. Rechargeable Electrochemical Cell System with a Charging Electrode Charge/discharge Mode Switching in the Cells. U.S. Patent US 2011/0070506 A1, 24 March 2011. [Google Scholar]
- Lee, D.U.; Xu, P.; Cano, Z.P.; Kashkooli, A.G.; Park, M.G.; Chen, Z. Recent progress and perspectives on bi-functional oxygen electrocatalysts for advanced rechargeable metal–air batteries. J. Mater. Chem. A 2016, 4, 7107–7134. [Google Scholar] [CrossRef]
- Neburchilov, V.; Wang, H.; Martin, J.J.; Qu, W. A review on air cathodes for zinc-air fuel cells. J. Power Sources 2010, 195, 1271–1291. [Google Scholar] [CrossRef]
- Stoerzinger, K.a.; Risch, M.; Han, B.; Shao-Horn, Y. Recent Insights into Manganese Oxides in Catalyzing Oxygen Reduction Kinetics. ACS Catal. 2015, 5, 6021–6031. [Google Scholar] [CrossRef]
- Horn, Q.C.; Shao-Horn, Y. Morphology and Spatial Distribution of ZnO Formed in Discharged Alkaline Zn/MnO2 AA Cells. J. Electrochem. Soc. 2003, 150, A652–A658. [Google Scholar] [CrossRef]
- Stamm, J.; Varzi, A.; Latz, A.; Horstmann, B. Modeling nucleation and growth of zinc oxide during discharge of primary zinc-air batteries. J. Power Sources 2017, 360, 136–149. [Google Scholar] [CrossRef]
- Jörissen, L. Bifunctional oxygen/air electrodes. J. Power Sources 2006, 155, 23–32. [Google Scholar] [CrossRef]
- Drillet, J.F.; Holzer, F.; Kallis, T.; Müller, S.; Schmidt, V. Influence of CO2 on the stability of bifunctional oxygen electrodes for rechargeable zinc/air batteries and study of different CO2 filter materials. Phys. Chem. Chem. Phys. 2001, 3, 368–371. [Google Scholar] [CrossRef]
- Hwang, B.; Oh, E.S.; Kim, K. Observation of electrochemical reactions at Zn electrodes in Zn-air secondary batteries. Electrochim. Acta 2016, 216, 484–489. [Google Scholar] [CrossRef]
- Suresh Kannan, A.R.; Muralidharan, S.; Sarangapani, K.B.; Balaramachandran, V.; Kapali, V. Corrosion and anodic behaviour of zinc and its ternary alloys in alkaline battery electrolytes. J. Power Sources 1995, 57, 93–98. [Google Scholar] [CrossRef]
- Vorkapicc, L.Z.; Drazzicc, D.M.; Despic, A.R. Corrosion of Pure and Amalgamated Zinc in Concentrated Alkali Hydroxide Solutions. J. Electrochem. Soc. 1974, 121, 1385–1392. [Google Scholar] [CrossRef]
- Baugh, L.M.; Tye, F.L.; White, N.C. Corrosion and polarization characteristics of zinc in battery electrolyte analogues and the effect of amalgamation. J. Appl. Electrochem. 1983, 13, 623–635. [Google Scholar] [CrossRef]
- Dirkse, T.; Hampson, N. The anodic behaviour of zinc in aqueous solution—-III. Passivation in mixed KF-KOH solutions. Electrochim. Acta 1972, 17, 813–818. [Google Scholar] [CrossRef]
- Schröder, D.; Sinai Borker, N.N.; König, M.; Krewer, U. Performance of zinc air batteries with added K2CO3 in the alkaline electrolyte. J. Appl. Electrochem. 2015, 45, 427–437. [Google Scholar] [CrossRef]
- Mainar, A.R.; Leonet, O.; Bengoechea, M.; Boyano, I.; de Meatza, I.; Kvasha, A.; Guerfi, A.; Blazquez, J.A. Alkaline aqueous electrolytes for secondary zinc-air batteries: An overview. Int. J. Energy Res. 2016, 40, 1032–1049. [Google Scholar] [CrossRef]
- Mainar, A.R.; Iruin, E.; Colmenares, L.C.; Kvasha, A.; de Meatza, I.; Bengoechea, M.; Leonet, O.; Boyano, I.; Zhang, Z.; Blazquez, J.A. An overview of progress in electrolytes for secondary zinc-air batteries and other storage systems based on zinc. J. Energy Storage 2018, 15, 304–328. [Google Scholar] [CrossRef]
- Kar, M.; Winther-Jensen, B.; Forsyth, M.; MacFarlane, D.R. Chelating ionic liquids for reversible zinc electrochemistry. Phys. Chem. Chem. Phys. 2013, 15, 7191–7197. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.S.; Lee, T.; Song, H.K.; Cho, J.; Kim, B.S. Ionic liquid modified graphene nanosheets anchoring manganese oxide nanoparticles as efficient electrocatalysts for Zn–air batteries. Energy Environ. Sci. 2011, 4, 4148–4154. [Google Scholar] [CrossRef]
- Endres, F.; Abbott, A.; MacFarlane, D.R. (Eds.) Electrodeposition from Ionic Liquids, 1st ed.; Wiley-VCH: Weinheim, Germany, 2008; p. 410. [Google Scholar]
- Xu, M.; Ivey, D.G.; Xie, Z.; Qu, W. Rechargeable Zn-air batteries: Progress in electrolyte development and cell configuration advancement. J. Power Sources 2015, 283, 358–371. [Google Scholar] [CrossRef]
- Mclarnon, F.R.; Cairns, E.J. The Secondary Alkaline Zinc Electrode. J. Electrochem. Soc. 1991, 138, 645–664. [Google Scholar] [CrossRef]
- Kim, H.; Jeong, G.; Kim, Y.U.; Kim, J.H.; Park, C.M.; Sohn, H.J. Metallic anodes for next generation secondary batteries. Chem. Soc. Rev. 2013, 42, 9011–9034. [Google Scholar] [CrossRef] [PubMed]
- Bockris, J.O.; Nagy, Z.; Damjanovic, A. On the Deposition and Dissolution of Zinc in Alkaline Solutions. J. Electrochem. Soc. 1972, 119, 285–295. [Google Scholar] [CrossRef]
- Sun, K.E.; Hoang, T.K.; Doan, T.N.L.; Yu, Y.; Zhu, X.; Tian, Y.; Chen, P. Suppression of Dendrite Formation and Corrosion on Zinc Anode of Secondary Aqueous Batteries. ACS Appl. Mater. Interfaces 2017, 9, 9681–9687. [Google Scholar] [CrossRef] [PubMed]
- Banik, S.J.; Akolkar, R. Suppressing Dendritic Growth during Alkaline Zinc Electrodeposition using Polyethylenimine Additive. Electrochim. Acta 2015, 179, 475–481. [Google Scholar] [CrossRef]
- Diggle, J.W.; Damjanovic, A. The inhibition of the dendritic electrocrystallization of zinc from doped alkaline zincate solutions. J. Electrochem. Soc. 1972, 119, 1649–1658. [Google Scholar] [CrossRef]
- Schmid, M.; Willert-Porada, M. Electrochemical behavior of zinc particles with silica based coatings as anode material for zinc air batteries with improved discharge capacity. J. Power Sources 2017, 351, 115–122. [Google Scholar] [CrossRef]
- Zelger, C.; Laumen, J.; Laskos, A.; Gollas, B. Rota-Hull Cell Study on Pulse Current Zinc Electrodeposition from Alkaline Electrolytes. Electrochim. Acta 2016, 213, 208–216. [Google Scholar] [CrossRef]
- Liu, M.B. Passivation of Zinc Anodes in KOH Electrolytes. J. Electrochem. Soc. 1981, 128, 1663–1668. [Google Scholar] [CrossRef]
- Dirkse, T.; Hampson, N. The anodic behaviour of zinc in aqueous KOH solution—II. passivation experiments using linear sweep voltammetry. Electrochim. Acta 1972, 17, 387–394. [Google Scholar] [CrossRef]
- Zhang, X.G. Corrosion and Electrochemistry of Zinc, 1st ed.; Plenum Press: New York, NY, USA, 1996. [Google Scholar]
- Prentice, G. A Model for the Passivation of the Zinc Electrode in Alkaline Electrolyte. J. Electrochem. Soc. 1991, 138, 890–894. [Google Scholar] [CrossRef]
- Jung, J.I.; Risch, M.; Park, S.; Kim, M.G.; Nam, G.; Jeong, H.Y.; Shao-Horn, Y.; Cho, J. Optimizing nanoparticle perovskite for bifunctional oxygen electrocatalysis. Energy Environ. Sci. 2016, 9, 176–183. [Google Scholar] [CrossRef]
- Mainar, A.R.; Colmenares, L.C.; Leonet, O.; Alcaide, F.; Iruin, J.J.; Weinberger, S.; Hacker, V.; Iruin, E.; Urdanpilleta, I.; Blazquez, J.A. Manganese oxide catalysts for secondary zinc air batteries: From electrocatalytic activity to bifunctional air electrode performance. Electrochim. Acta 2016, 217, 80–91. [Google Scholar] [CrossRef]
- Li, Y.; Gong, M.; Liang, Y.; Feng, J.; Kim, J.E.; Wang, H.; Hong, G.; Zhang, B.; Dai, H. Advanced zinc-air batteries based on high-performance hybrid electrocatalysts. Nat. Commun. 2013, 4, 1805. [Google Scholar] [CrossRef] [PubMed]
- Tan, P.; Kong, W.; Shao, Z.; Liu, M.; Ni, M. Advances in modeling and simulation of Li–air batteries. Prog. Energy Combust. Sci. 2017, 62, 155–189. [Google Scholar] [CrossRef]
- Grew, K.N.; Chiu, W.K. A review of modeling and simulation techniques across the length scales for the solid oxide fuel cell. J. Power Sources 2012, 199, 1–13. [Google Scholar] [CrossRef]
- Sholl, D. S.; Steckel, J.A. Density Functional Theory: A Practical Introduction, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Mattsson, A.E.; Schultz, P.A.; Desjarlais, M.P.; Mattsson, T.R.; Leung, K. Designing meaningful density functional theory calculations in materials science—A primer. Model. Simul. Mater. Sci. Eng. 2005, 13, 1–31. [Google Scholar]
- Hörmann, N.G.; Jäckle, M.; Gossenberger, F.; Roman, T.; Forster-Tonigold, K.; Naderian, M.; Sakong, S.; Groß, A. Some challenges in the first-principles modeling of structures and processes in electrochemical energy storage and transfer. J. Power Sources 2015, 275, 531–538. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Rossmeisl, J.; Logadottir, A.; Lindqvist, L.; Kitchin, J.R.; Bligaard, T.; Jónsson, H. Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B 2004, 108, 17886–17892. [Google Scholar] [CrossRef]
- Viswanathan, V.; Hansen, H.A.; Rossmeisl, J.; Nørskov, J.K. Universality in oxygen reduction electrocatalysis on metal surfaces. ACS Catal. 2012, 2, 1654–1660. [Google Scholar] [CrossRef]
- Hansen, H.A.; Viswanathan, V.; Nørskov, J.K. Unifying kinetic and thermodynamic analysis of 2 e- and 4 e-reduction of oxygen on metal surfaces. J. Phys. Chem. C 2014, 118, 6706–6718. [Google Scholar] [CrossRef]
- Viswanathan, V.; Nørskov, J.K.; Speidel, A.; Scheffler, R.; Gowda, S.; Luntz, A.C. Li-O2 kinetic overpotentials: Tafel plots from experiment and first-principles theory. J. Phys. Chem. Lett. 2013, 4, 556–560. [Google Scholar] [CrossRef] [PubMed]
- Aetukuri, N.B.; McCloskey, B.D.; Garcia, J.M.; Krupp, L.E.; Viswanathan, V.; Luntz, A.C. Solvating additives drive solution-mediated electrochemistry and enhance toroid growth in non-aqueous Li-O2 batteries. Nat. Chem. 2015, 7, 50–56. [Google Scholar] [CrossRef] [PubMed]
- Eberle, D.; Horstmann, B. Oxygen Reduction on Pt(111) in Aqueous Electrolyte: Elementary Kinetic Modeling. Electrochim. Acta 2014, 137, 714–720. [Google Scholar] [CrossRef]
- Tripkovic, V.; Vegge, T. Potential and Rate Determining Step for Oxygen Reduction on Pt(111). J. Phys. Chem. C 2017, 121, 26785–26793. [Google Scholar] [CrossRef]
- Vazquez-Arenas, J.; Ramos-Sanchez, G.; Franco, A.A. A multi-scale model of the oxygen reduction reaction on highly active graphene nanosheets in alkaline conditions. J. Power Sources 2016, 328, 492–502. [Google Scholar] [CrossRef]
- Siahrostami, S.; Tripković, V.; Lundgaard, K.T.; Jensen, K.E.; Hansen, H.A.; Hummelshøj, J.S.; Mýrdal, J.S.G.; Vegge, T.; Nørskov, J.K.; Rossmeisl, J. First principles investigation of zinc-anode dissolution in zinc–air batteries. Phys. Chem. Chem. Phys. 2013, 15, 6416–6421. [Google Scholar] [CrossRef] [PubMed]
- Jäckle, M.; Groß, A. Microscopic properties of lithium, sodium, and magnesium battery anode materials related to possible dendrite growth. J. Chem. Phys. 2016, 141. [Google Scholar] [CrossRef] [PubMed]
- Hummelshøj, J.S.; Blomqvist, J.; Datta, S.; Vegge, T.; Rossmeisl, J.; Thygesen, K.S.; Luntz, A.C.; Jacobsen, K.W.; Nørskov, J.K. Communications: Elementary oxygen electrode reactions in the aprotic Li-air battery. J. Chem. Phys. 2010, 132. [Google Scholar] [CrossRef] [PubMed]
- Radin, M.D.; Rodriguez, J.F.; Tian, F.; Siegel, D.J. Lithium peroxide surfaces are metallic, while lithium oxide surfaces are not. J. Am. Chem. Soc. 2012, 134, 1093–1103. [Google Scholar] [CrossRef] [PubMed]
- Radin, M.D.; Siegel, D.J. Charge transport in lithium peroxide: relevance for rechargeable metal–air batteries. Energy Environ. Sci. 2013, 6, 2370. [Google Scholar] [CrossRef]
- Radin, M.D.; Monroe, C.W.; Siegel, D.J. How dopants can enhance charge transport in Li2O2. Chem. Mater. 2015, 27, 839–847. [Google Scholar] [CrossRef]
- Dirkse, T.P. The Nature of the Zinc-Containing Ion in Strongly Alkaline Solutions. J. Electrochem. Soc. 1954, 101, 328. [Google Scholar] [CrossRef]
- Larcin, J.; Maskell, W.C.; Tye, F.L. Leclanche cell investigations I: Zn(NH3)2Cl2 solubility and the formation of ZnCl2·4Zn(OH)2·H2O. Electrochim. Acta 1997, 42, 2649–2658. [Google Scholar] [CrossRef]
- Zhang, Y.; Muhammed, M. Critical evaluation of thermodynamics of complex formation of metal ions in aqueous solutions—VI. Hydrolysis and hydroxo-complexes of Zn2+ at 298.15 K. Hydrometallurgy 2001, 60, 215–236. [Google Scholar] [CrossRef]
- Clark, S.; Latz, A.; Horstmann, B. Cover Feature: Rational Development of Neutral Aqueous Electrolytes for Zinc-Air Batteries. ChemSusChem 2017, 10, 4666. [Google Scholar] [CrossRef]
- Smith, R.; Martell, A. Critical Stability Constants; Springer: New York, NY, USA, 1976; Volume 4. [Google Scholar]
- Martell, A.E.; Smith, R.M. Critical Stability Constants; Springer: New York, NY, USA, 1977; Volume 5. [Google Scholar]
- Martell, A.; Smith, R. Other Organic Ligands, 1st ed.; Springer: New York, NY, USA, 1977. [Google Scholar]
- Dirkse, T. The Solubility Product Constant of ZnO. J. Electrochem. Soc. 1986, 133, 1656–1657. [Google Scholar] [CrossRef]
- Limpo, J.; Luis, A. Solubility of zinc chloride in ammoniacal ammonium chloride solutions. Hydrometallurgy 1993, 32, 247–260. [Google Scholar] [CrossRef]
- Limpo, J.; Luis, A.; Cristina, M. Hydrolysis of zinc chloride in aqueous ammoniacal ammonium chloride solutions. Hydrometallurgy 1995, 38, 235–243. [Google Scholar] [CrossRef]
- Vazquez-Arenas, J.; Sosa-Rodriguez, F.; Lazaro, I.; Cruz, R. Thermodynamic and electrochemistry analysis of the zinc electrodeposition in NH4Cl-NH3 electrolytes on Ti, Glassy Carbon and 316L Stainless Steel. Electrochim. Acta 2012, 79, 109–116. [Google Scholar] [CrossRef]
- Rojas-Hernández, A.; Ramírez, M.T.; Ibáñez, J.G.; González, I. Construction of multicomponent Pourbaix diagrams using generalized species. J. Electrochem. Soc. 1991, 138, 365–371. [Google Scholar] [CrossRef]
- Newman, J.; Thmoas-Alyea, K.E. Electrochemical Systems, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Husch, T.; Korth, M. Charting the known chemical space for non-aqueous lithium–air battery electrolyte solvents. Phys. Chem. Chem. Phys. 2015, 17, 22596–22603. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for Fluid Flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Trouette, B. Lattice Boltzmann simulations of a time-dependent natural convection problem. Comput. Math. Appl. 2013, 66, 1360–1371. [Google Scholar] [CrossRef]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann Method for Complex Flows. Annu. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Sukop, M.C.; Thorne, D.T. Lattice Boltzmann Modeling; Springer: Berlin, Germany, 2006; Volume 79, p. 016702. [Google Scholar]
- He, X.; Li, N. Lattice Boltzmann simulation of electrochemical systems. Comput. Phys. Commun. 2000, 129, 158–166. [Google Scholar] [CrossRef]
- Niu, X.D.; Munekata, T.; Hyodo, S.A.; Suga, K. An investigation of water-gas transport processes in the gas-diffusion-layer of a PEM fuel cell by a multiphase multiple-relaxation-time lattice Boltzmann model. J. Power Sources 2007, 172, 542–552. [Google Scholar] [CrossRef]
- Hao, L.; Cheng, P. Lattice Boltzmann simulations of water transport in gas diffusion layer of a polymer electrolyte membrane fuel cell. J. Power Sources 2010, 195, 3870–3881. [Google Scholar] [CrossRef]
- Molaeimanesh, G.R.; Akbari, M.H. A three-dimensional pore-scale model of the cathode electrode in polymer-electrolyte membrane fuel cell by lattice Boltzmann method. J. Power Sources 2014, 258, 89–97. [Google Scholar] [CrossRef]
- Kim, K.N.; Kang, J.H.; Lee, S.G.; Nam, J.H.; Kim, C.J. Lattice Boltzmann simulation of liquid water transport in microporous and gas diffusion layers of polymer electrolyte membrane fuel cells. J. Power Sources 2015, 278, 703–717. [Google Scholar] [CrossRef]
- Ostadi, H.; Rama, P.; Liu, Y.; Chen, R.; Zhang, X.X.; Jiang, K. 3D reconstruction of a gas diffusion layer and a microporous layer. J. Membr. Sci. 2010, 351, 69–74. [Google Scholar] [CrossRef]
- Danner, T.; Eswara, S.; Schulz, V.P.; Latz, A. Characterization of gas diffusion electrodes for metal-air batteries. J. Power Sources 2016, 324, 646–656. [Google Scholar] [CrossRef]
- Sunu, W.G.; Bennion, D.N. Transient and Failure Analyses of the Porous Zinc Electrode. J. Electrochem. Soc. 1980, 127, 2007–2016. [Google Scholar] [CrossRef]
- Bockelmann, M.; Reining, L.; Kunz, U.; Turek, T. Electrochemical characterization and mathematical modeling of zinc passivation in alkaline solutions: A review. Electrochim. Acta 2017, 237, 276–298. [Google Scholar] [CrossRef]
- Neidhardt, J.P.; Fronczek, D.N.; Jahnke, T.; Danner, T.; Horstmann, B.; Bessler, W.G. A Flexible Framework for Modeling Multiple Solid, Liquid and Gaseous Phases in Batteries and Fuel Cells. J. Electrochem. Soc. 2012, 159, A1528–A1542. [Google Scholar] [CrossRef]
- Hein, S.; Latz, A. Influence of local lithium metal deposition in 3D microstructures on local and global behavior of Lithium-ion batteries. Electrochim. Acta 2016, 201, 354–365. [Google Scholar] [CrossRef]
- Hein, S.; Feinauer, J.; Westhoff, D.; Manke, I.; Schmidt, V.; Latz, A. Stochastic microstructure modeling and electrochemical simulation of lithium-ion cell anodes in 3D. J. Power Sources 2016, 336, 161–171. [Google Scholar] [CrossRef]
- Latz, A.; Zausch, J. Thermodynamic consistent transport theory of Li-ion batteries. J. Power Sources 2011, 196, 3296–3302. [Google Scholar] [CrossRef]
- Mao, Z.; White, R.E. Mathematical modeling of a primary zinc/air battery. J. Electrochem. Soc. 1992, 139, 1105–1114. [Google Scholar] [CrossRef]
- Deiss, E.; Holzer, F.; Haas, O. Modeling of an electrically rechargeable alkaline Zn-air battery. Electrochim. Acta 2002, 47, 3995–4010. [Google Scholar] [CrossRef]
- Andrei, P.; Zheng, J.P.; Hendrickson, M.; Plichta, E.J. Some Possible Approaches for Improving the Energy Density of Li-Air Batteries. J. Electrochem. Soc. 2010, 157, A1287–A1295. [Google Scholar] [CrossRef]
- Schröder, D.; Krewer, U. Model based quantification of air-composition impact on secondary zinc air batteries. Electrochim. Acta 2014, 117, 541–553. [Google Scholar] [CrossRef]
- Arlt, T.; Schröder, D.; Krewer, U.; Manke, I. In operando monitoring of the state of charge and species distribution in zinc air batteries using X-ray tomography and model-based simulations. Phys. Chem. Chem. Phys. 2014, 16, 22273–22280. [Google Scholar] [CrossRef] [PubMed]
- Xue, K.H.; Nguyen, T.K.; Franco, A.A. Impact of the Cathode Microstructure on the Discharge Performance of Lithium Air Batteries: A Multiscale Model. J. Electrochem. Soc. 2014, 161, E3028–E3035. [Google Scholar] [CrossRef]
- Grübl, D.; Bessler, W.G. Cell design concepts for aqueous lithium-oxygen batteries: A model-based assessment. J. Power Sources 2015, 297, 481–491. [Google Scholar] [CrossRef]
- Yin, Y.; Gaya, C.; Torayev, A.; Thangavel, V.; Franco, A.A. Impact of Li2O2 Particle Size on Li-O2 Battery Charge Process: Insights from a Multiscale Modeling Perspective. J. Phys. Chem. Lett. 2016, 7, 3897–3902. [Google Scholar] [CrossRef] [PubMed]
- Bazant, M.Z. Theory of chemical kinetics and charge transfer based on nonequilibrium thermodynamics. Acc. Chem. Res. 2013, 46, 1144–1160. [Google Scholar] [CrossRef] [PubMed]
- Latz, A.; Zausch, J. Thermodynamic derivation of a Butler-Volmer model for intercalation in Li-ion batteries. Electrochim. Acta 2013, 110, 358–362. [Google Scholar] [CrossRef]
- Breiter, M. Dissolution and passivation of vertical porous zinc electrodes in alkaline solution. Electrochim. Acta 1970, 15, 1297–1304. [Google Scholar] [CrossRef]
- Bai, P.; Bazant, M.Z. Charge transfer kinetics at the solid-solid interface in porous electrodes. Nat. Commun. 2014, 5, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.; Smith, R.B.; Bai, P.; Bazant, M.Z. Simple formula for Marcus-Hush-Chidsey kinetics. J. Electroanal. Chem. 2014, 735, 77–83. [Google Scholar] [CrossRef]
- Zeng, Y.; Bai, P.; Smith, R.B.; Bazant, M.Z. Simple formula for asymmetric Marcus-Hush kinetics. J. Electroanal. Chem. 2015, 748, 52–57. [Google Scholar] [CrossRef]
- Melander, M.; Jónsson, E.O.; Mortensen, J.J.; Vegge, T.; García Lastra, J.M. Implementation of Constrained DFT for Computing Charge Transfer Rates within the Projector Augmented Wave Method. J. Chem. Theory Comput. 2016, 12, 5367–5378. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Yu, J.S.; Sunden, B. Review on mechanisms and continuum models of multi-phase transport phenomena in porous structures of non-aqueous Li-Air batteries. J. Power Sources 2015, 278, 352–369. [Google Scholar] [CrossRef]
- Andersen, C.P.; Hu, H.; Qiu, G.; Kalra, V.; Sun, Y. Pore-Scale Transport Resolved Model Incorporating Cathode Microstructure and Peroxide Growth in Lithium-Air Batteries. J. Electrochem. Soc. 2015, 162, A1135–A1145. [Google Scholar] [CrossRef]
- Monroe, C.W.; Delacourt, C. Continuum transport laws for locally non-neutral concentrated electrolytes. Electrochim. Acta 2013, 114, 649–657. [Google Scholar] [CrossRef]
- Latz, A.; Zausch, J. Multiscale modeling of lithium ion batteries: Thermal aspects. Beilstein J. Nanotechnol. 2015, 6, 987–1007. [Google Scholar] [CrossRef] [PubMed]
- Xue, K.H.; McTurk, E.; Johnson, L.; Bruce, P.G.; Franco, A.A. A Comprehensive Model for Non-Aqueous Lithium Air Batteries Involving Different Reaction Mechanisms. J. Electrochem. Soc. 2015, 162, A614–A621. [Google Scholar] [CrossRef]
- Grübl, D.; Bergner, B.; Schröder, D.; Janek, J.; Bessler, W.G. Multistep Reaction Mechanisms in Nonaqueous Lithium-Oxygen Batteries with Redox Mediator: A Model-Based Study. J. Phys. Chem. C 2016, 120, 24623–24636. [Google Scholar] [CrossRef]
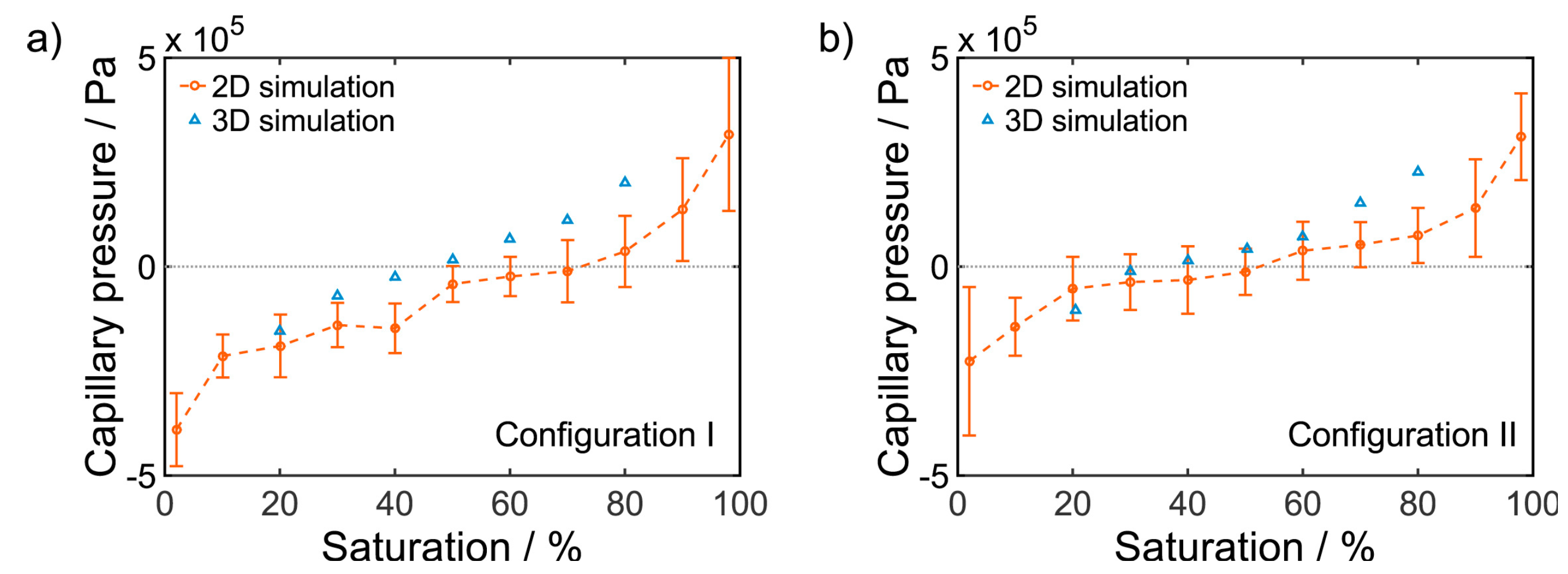
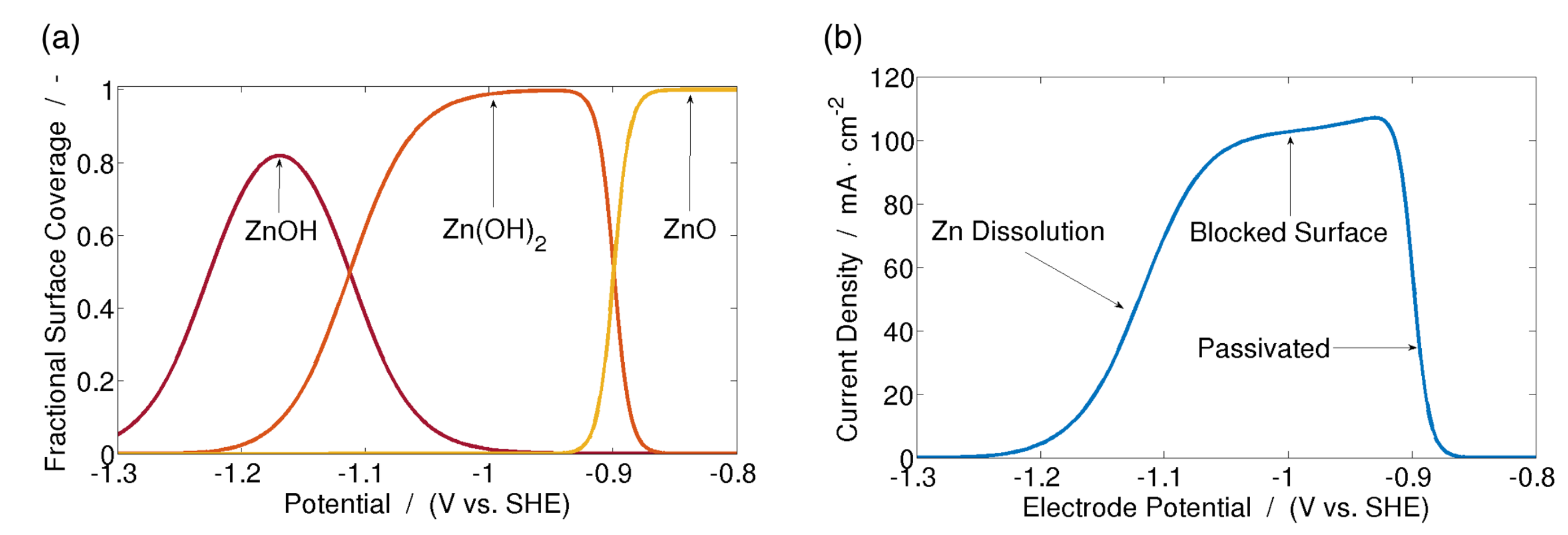
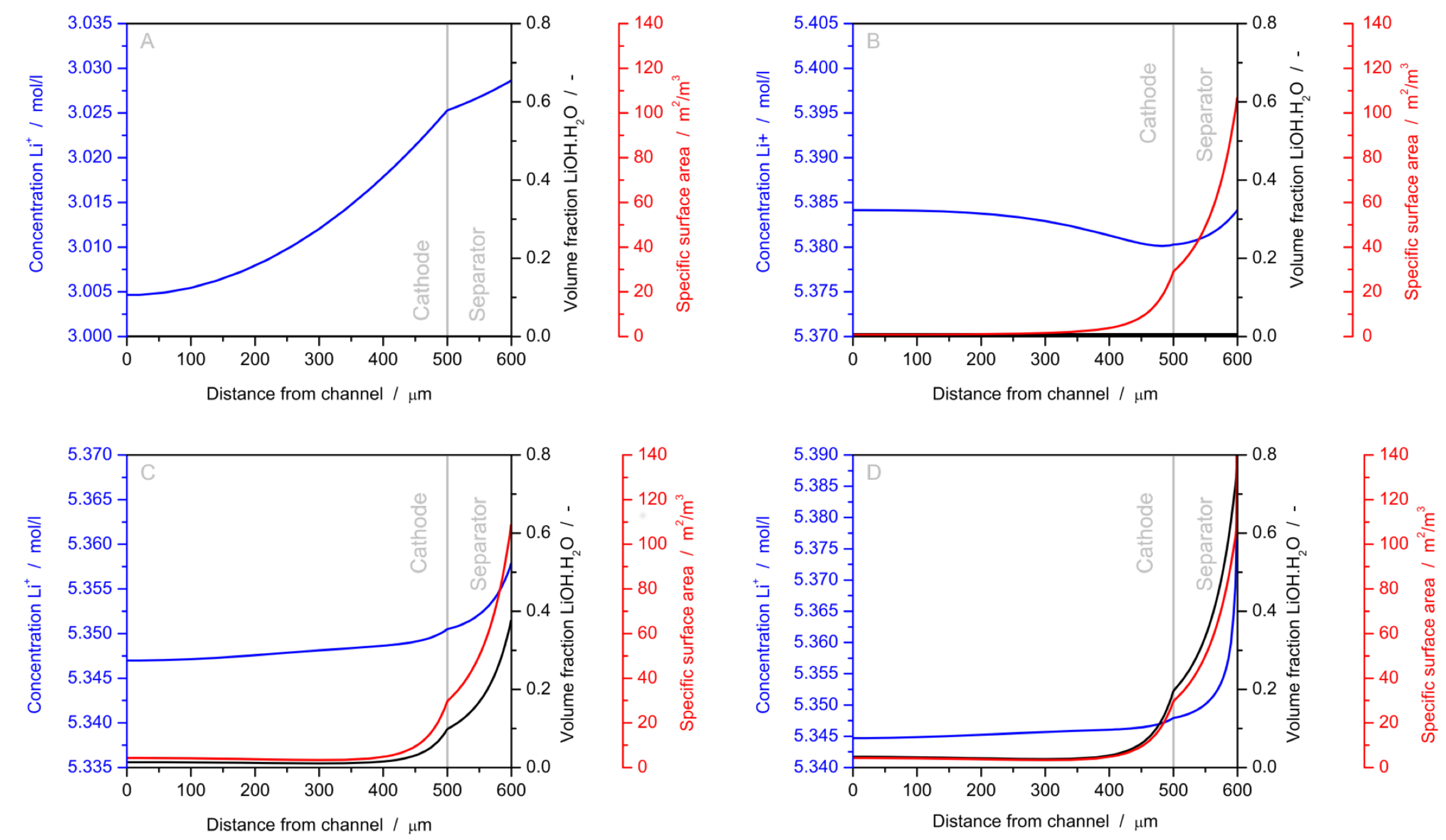
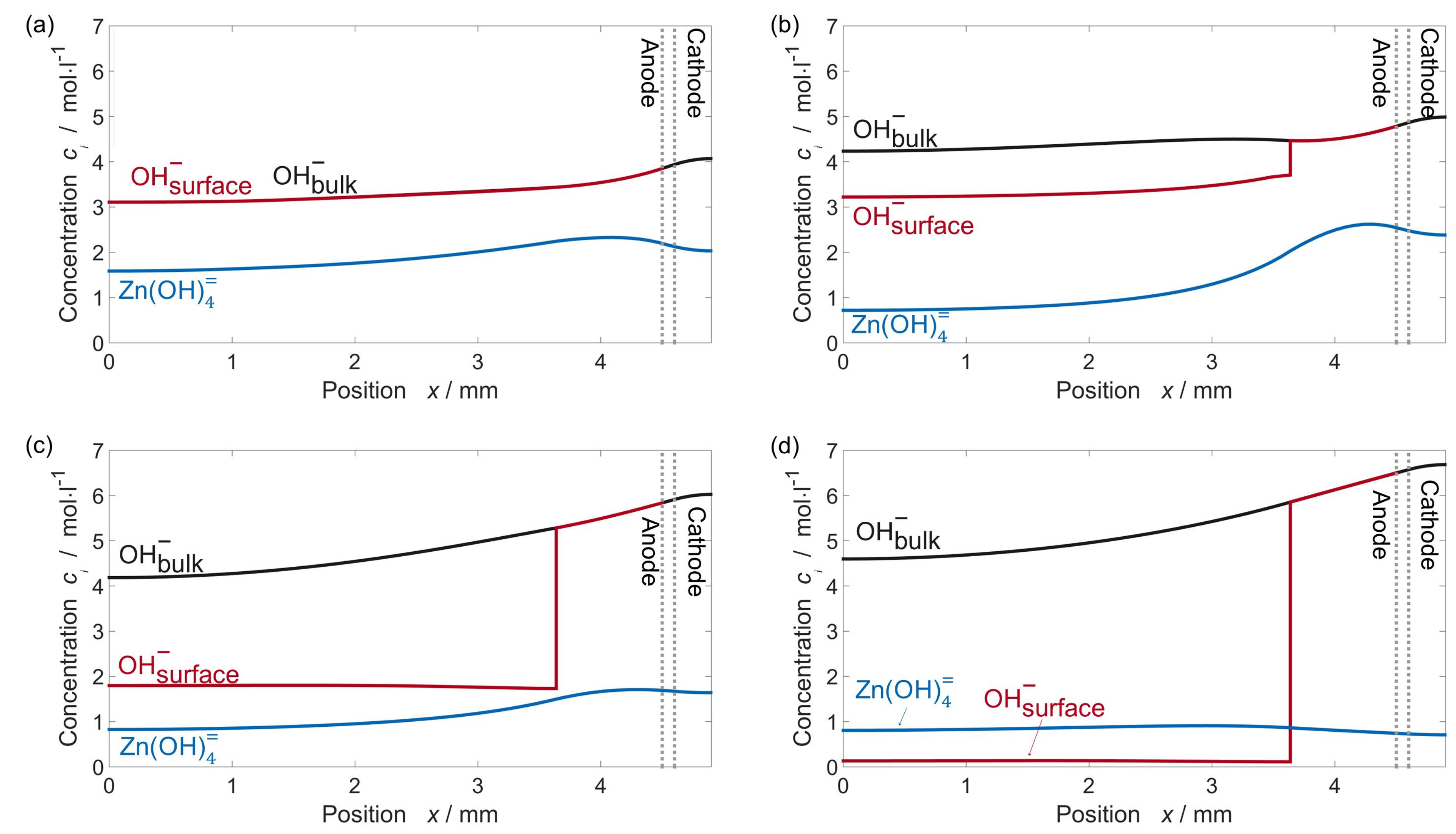
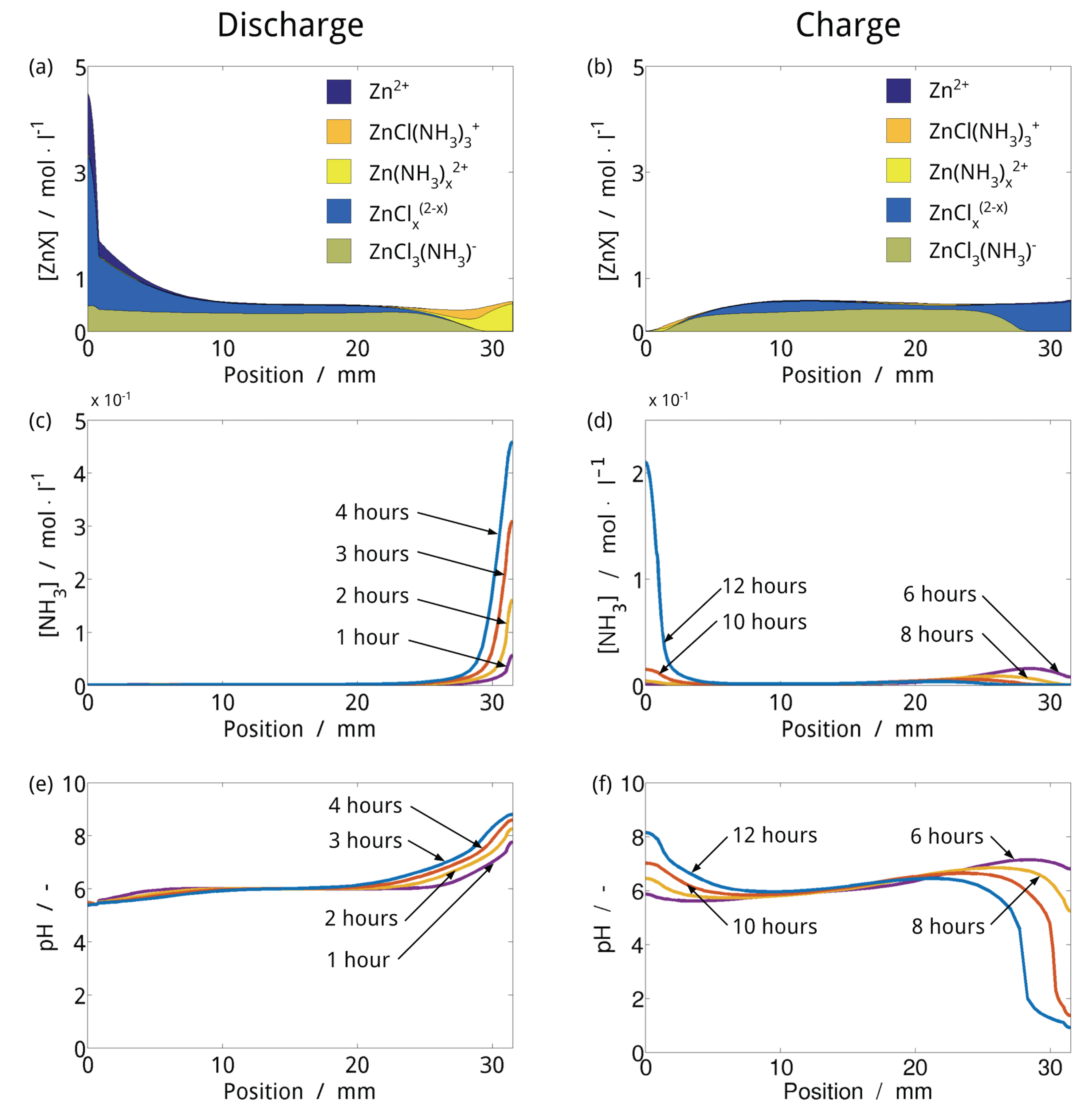
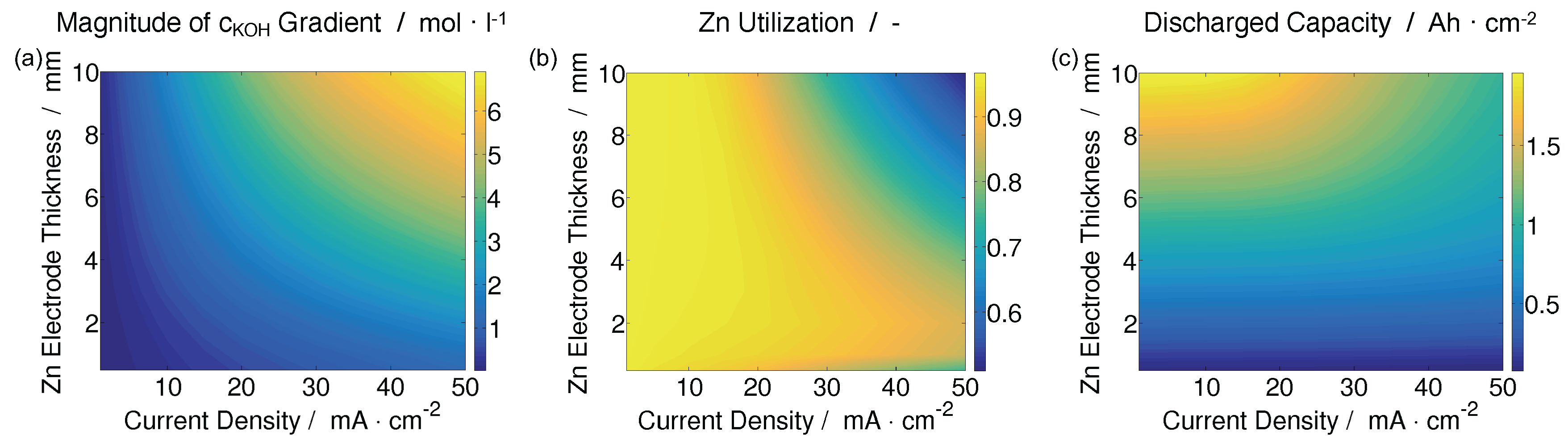
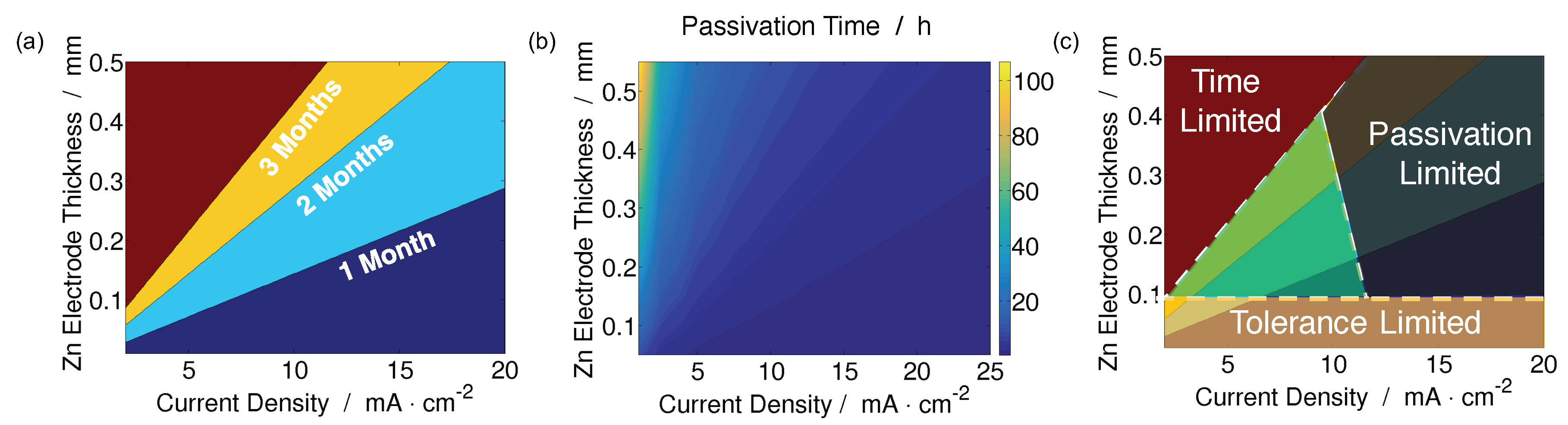
| Year | Authors | System | Dimension | Transport Model | Notes | Source |
|---|---|---|---|---|---|---|
| 1980 | Sunu, et al. | Zn-Air | 1D | CST | Zn & ZnO shape change | [129] |
| 1991 | Mao, et al. | Zn-Air | 1D | CST | Precipitation of K2Zn(OH)4 | [135] |
| 2002 | Deiss, et al. | Zn-Air | 1D | DST | Concentration profiles and cell voltage | [136] |
| 2010 | Andrei, et al. | Li-Air | 1D | CST | LAB modeling framework | [137] |
| 2011 | Albertus, et al. | Li-Air | 1D | CST | O2 transport and Li2O2 precipitation | [26] |
| 2012 | Neidhardt, et al. | Multiple | 1D | CST + Multi-Phase | Flexible framework, convective transport | [131] |
| 2013 | Horstmann, et al. | Li-Air | 1D | CST + Multi-Phase | Inhomogeneous Li2O2 precipitation, aqueous electrolyte | [35] |
| 2014 | Danner, et al. | Li-Air | 1D | CST + Multi-Phase | Air electrode model with pressure-saturation | [36] |
| 2014 | Schröder, et al. | Zn-Air | 0D | CST | Effect of air composition on cell performance | [138] |
| 2014 | Arlt, et al. | Zn-Air | 0D | CST | State-of-charge monitoring with x-ray CT | [139] |
| 2014 | Xue, et al. | Li-Air | 1D | CST | Li2O2 pore clogging with pore size distribution | [140] |
| 2015 | Grübl, et al. | Li-Air | 1D | CST + Multi-Phase | Engineering evaluation of system design | [141] |
| 2016 | Yin, et al. | Li-Air | 1D | DST | Affect of Li2O2 particle size on charging profile | [142] |
| 2017 | Stamm, et al. | Zn-Air | 1D | CST + Multi-Phase | Affect of ZnO nucleation and growth on cell discharge profile | [55] |
| 2017 | Clark, et al. | Zn-Air | 1D | CST + Multi-Phase | Framework for buffered near-neutral electrolytes | [3] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clark, S.; Latz, A.; Horstmann, B. A Review of Model-Based Design Tools for Metal-Air Batteries. Batteries 2018, 4, 5. https://doi.org/10.3390/batteries4010005
Clark S, Latz A, Horstmann B. A Review of Model-Based Design Tools for Metal-Air Batteries. Batteries. 2018; 4(1):5. https://doi.org/10.3390/batteries4010005
Chicago/Turabian StyleClark, Simon, Arnulf Latz, and Birger Horstmann. 2018. "A Review of Model-Based Design Tools for Metal-Air Batteries" Batteries 4, no. 1: 5. https://doi.org/10.3390/batteries4010005
APA StyleClark, S., Latz, A., & Horstmann, B. (2018). A Review of Model-Based Design Tools for Metal-Air Batteries. Batteries, 4(1), 5. https://doi.org/10.3390/batteries4010005





