Abstract
This paper presents a new control strategy for isolated micro-grids including wind turbines (WT), fuel cells (FC), photo-voltaic (PV) and battery energy storage systems (BESS). FC have been used in parallel with BESSs in order to increase their lifetime and efficiency. The changes in some parameters such as wind speed, sunlight, and consumption, lead to improper performance of droop. To overcome this challenge, a new intelligent method using a combination of fuzzy controller and cuckoo optimization algorithm (COA) techniques for active power controllers in isolated networks is proposed. In this paper, COA is compared with genetic algorithm (GA) and particles swarm optimization algorithm (PSO). In order to show efficiency of the proposed controller, this optimal controller has been compared with droop, optimized droop, and conventional fuzzy methods, the dynamic analysis of the island is implemented to assess the behavior of isolated generations accurately and simulation results are reported.
1. Introduction
In today’s world, the depletion of fossil–fuel resources and also growing concerns about Co2 emissions and global warming have led to an increasing utilization of renewable energy sources and distributed generation (DG) [1,2]. In this situation, photovoltaic energy conversion is expected to have large potential to become an alternative power source especially for small distributed areas [3]. Regarding the problems with complexity and financial inefficiency of transmission lines for supplying rural and remote areas with electrical power, DG is usually preferred for stand-alone operations [4]. Wind and solar energy systems are taking the biggest share from this trend [5], so photovoltaic (PV) and wind turbine (WT) power generations, as clean electric power supplies, play an important role among renewable power generators. To increase energy reliability, WT and PV systems are used together in isolated networks [6,7]. Storage energy system plays an important role in establishing a balance between production and consumption in isolated networks. Among storage systems, battery and fuel cells (FC) store energy during a long time, whereas super-conductor and ultra-capacitor (UC) do it in a short time [6]. The energy storage systems discussed in this paper are UCs which significantly offer better performance especially during acceleration and braking manner due to charge time and discharge time of UCs can change broadly [8,9,10]. The management and control of isolated networks deploying WT/PV/FC/UC is one of the most important issues in such networks. Heretofore, many methods have been utilized for the management of isolated and micro-grid networks. Optimal management of these networks maximizes the efficiency of these networks [11,12]. One of the fundamental approaches for controlling the output active power of the DGs in micro-grids and isolated networks is frequency droop characteristics [13]. Also, improved droop control method is one of the best methods for voltage and frequency control in micro-grids and isolated networks [14]. Employing fuzzy logic controllers (FLCs) for solving control problems has also increased in various power system control applications [15]. Some of the fuzzy controller applications include excitation control, voltage and frequency control, power system stabilizers, etc. Regarding its efficiency and flexibility, the fuzzy controller is utilized for power management and frequency control in isolated micro-grids. Because of the uncertainty in system structure and also changes between production and consumption, droop controllers and fuzzy controllers cannot fulfill expectations. Also, isolated micro-grid systems are independent from the main net; this issue makes the control of the produced and consumed power even more difficult. In order to make the maximum benefit from these controllers, coefficients of the controllers have been optimized using COA.
2. Modeling Isolated Micro-Grid
Figure 1 illustrates the system configuration for the recommended method (hybrid alternative energy system). In this scheme, it is clear that battery energy storage system (BESS) is used for storing energy; both WT and PV technologies are primary energy producers and finally FC is issued as the energy supporter (backup). A mathematical model is applied to the proposed hybrid power technology. In simulation of hybrid systems, the dynamic response of each DG is individually considered in the dynamic model [16].
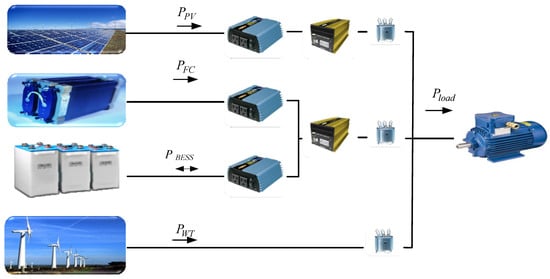
Figure 1.
The block diagram of the proposed hybrid isolated micro-grids.
2.1. Photovoltaic
Using PVs is a totally renewable and natural way for clean power generation. As presented in [17], the main factors affecting output power of PVs are namely sun irradiances, solar cell temperature, and PV array zone. The equivalent circuit of PV model mainly consists of a current source IL whose magnitude can be influenced by temperature and irradiance of sun, diode D, and internal shunt and series resistances RSh and RS. V-I characteristic can be given by (1):
Voltage of each cell is denoted by with IPV being the current. Moreover, Io, , , , and are the reverse saturation current of diode, electron load, desirable p-n conjunction coefficient, Boltzmann constant, and temperature of cells, respectively [18]. The factors on which the outputs of PV panels depend are sun radiations, cellular temperature, and the system ingredient performances. Therefore, it is expected that the acceptable output power should avail in various criteria. To achieve this task, multiple types of techniques are discussed in the literatures [19,20,21]. The model parameters used in this research are summarized in Table 1. These parameters are presented according to the data given in [22].

Table 1.
Photovoltaic parameters [22].
2.2. Wind Turbine
For blade pitch regulation variable-speed operation is necessary [23]. The extracted power that is produced by WT is as follows:
where , and Cp are wind velocity, swept area of rotor, and power factor respectively. Cp depends on wind velocity (), the rotatory velocity of the turbine, and blade parameters; it can be presented as:
where RBW is the radius of blades in meters (m), ωbw is the rotational speed of blades in radian per second , is the pitch angle of blades, and C1-C9 are the constants.
2.3. Fuel Cell
FCs have different structures such as FCs working with polymer electrolyte, solid oxide fuel cell (SOFC), and alkaline FC. SOFC has been used in this study, which enjoys high efficiency and thermal robustness for high power systems. A perfect model of solid oxide fuel cell described in [24] is utilized in this study. The relationships between these parameters are given in [25]. The power supplied by SOFC is obtained by:
where and are the output voltage and output current, respectively. Output voltage of Fuel cell is calculated using the following equation:
Fuel utilization is the ratio between the reacted and supplied hydrogen as follows:
Ratio between hydrogen and oxygen flow rate is defined as:
Boost DC/DC Converter
Due to its slow dynamics, FC is usually unable to satisfactorily supply the energy demand during the start-up period or abrupt load accelerations. In order to link an FC to an external system, FC voltage or the number of its cells should be increased. DC/DC boost converter in order to control the FC power, and to regulate the voltage increases the FC voltage. The boost converter is described by two non-linear state space averaged equations [25].
2.4. Battery Energy Storage System
Dynamic model of battery is illustrated in Figure 2. Batteries are among the most important energy storage devices in power systems. Although batteries have a slow dynamic response, their robustness and low price make them very practical. The BESS model consists of a controlled voltage source E and an internal resistor R. Moreover, the state of charge (SOC) depends on the capacity of battery and is calculated using (16) and (17) [18].
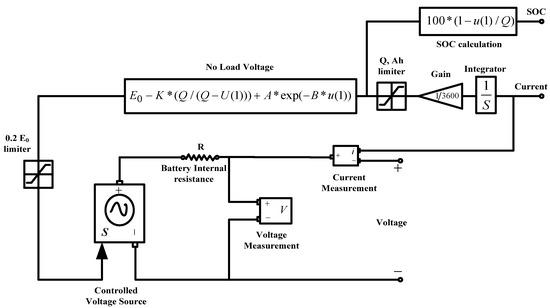
Figure 2.
Dynamic model of a battery.
3. Controller System
Controlling isolated networks and designing a controller for them are the most important issues about these networks. There are various applicable schemes for controlling isolated networks, including classic controllers, fuzzy controllers, adaptive and neural methods. Each one has its particular advantages and disadvantages like precision, speed, complexity, and resistivity in various dynamical conditions, implementation considerations, and so on. In this article, we use fuzzy and droop controllers because of their suitable features like simplicity, flexibility and high precision in a network consisting of WT/FC/BESS/PV. The duty of main controller is to determine the reference power of each unit by gathering the voltage and current data from network lines. This section describes the control system which is able to control the parallel operation of FC and BESS systems. Section 3.1 explains the basic concept of the frequency controller. Section 3.2 describes controller configuration of the droop control system and evaluates its performance and limitations of performance improvement. In the third subsection, the fuzzy controller design is discussed in order to determine the reference power produced by the FC and BESS. In the fourth section, the COA and its implementation for the optimization of droop and fuzzy controllers will be discussed.
3.1. Frequency Control Concept
When weather conditions change, power generations of WT and PV are affected. Also load variations during a day should not be neglected. So imbalances between production and consumption arise and therefore a suitable controller is needed for suitable power adjustment. In the studied parallel energy system, the electrical energy supplied by PV and WT are added through FC and BESS to assure the load demand. The total power of all generation units or Ptotal is given by:
The power balance equation can be written as:
The transfer function from power balance to frequency deviation can be written as:
where M and D are positive constant which indicate the equivalent inertia and damping of the hybrid isolated Micro-grids and K is the hybrid system frequency characteristic constant [26].
3.2. Design of the Droop Controller
Figure 3 shows the droop characteristic of each unit. Appropriate load sharing between each unit can be obtained by suitable droop coefficients mFC and mBESS.
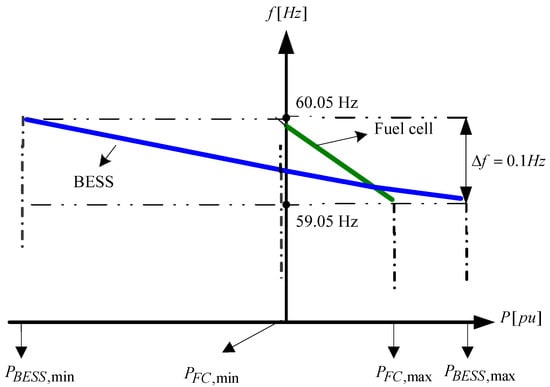
Figure 3.
The droop characteristics of each unit.
3.3. Fuzzy Logic Strategies
Owing to its low computational burden and stability, fuzzy controller is really appealing as an option. Some advantages of using FLC are sorted by numerous researchers who have placed their attention mainly on this issue [27,28]. Fuzzy logic displays distinctions conforming to various shapes of membership functions (MFs) in system experiences. Fuzzification, rule base, inference engine, and defuzzification are four main components of a Mamdani fuzzy logic controller. The Fuzzy controller duty is to satisfy the power demand by managing the power flow obtained by different power sources. Since frequency deviation is in the range of (+0.1, −0.1), the control input is also in this interval. The second input is the derivative of these deviations. The structure of frequency FLC of the proposed hybrid isolated Micro-grid is shown in Figure 4.
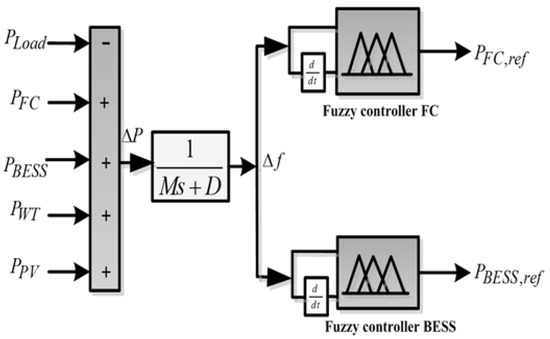
Figure 4.
Employing fuzzy logic controller (FLC) structure of the proposed isolated Micro-grids.
3.3.1. Design of a Controller for Fuel Cells System
Fuzzy Logic Cintroller is intended to determine the power set-point for frequency control. This part fully explains the fuzzy controller design. The input variables of fuzzy system are frequency changes and derivative of frequency changes. The complete, consistent and normal membership functions are chosen as NB, NS, Z, PS and PB in the normalized interval for each of the input variables. Figure 5 shows the membership functions related to fuzzy controller input variables. The fuzzy controller determines the reference power of FC. FC controller output also has five MFs. In Table 2 the rule bases are designed based on system condition and designer’s experience to control the FC. In this table, the error corresponds to frequency deviation and error change corresponds to derivative of frequency deviation.
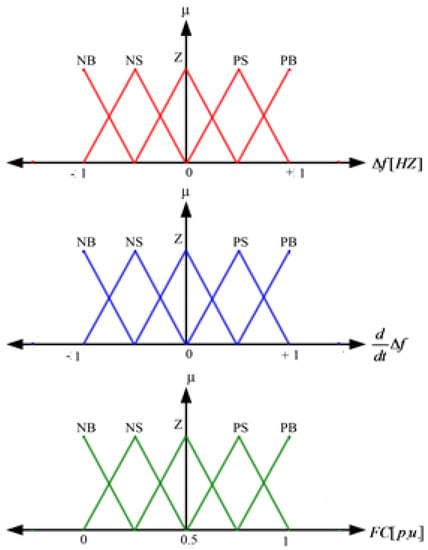
Figure 5.
Membership functions for the input and output signals of fuzzy controller.

Table 2.
Input and output rule bases of fuel cells (FC) fuzzy controller.
3.3.2. Design of a Controller for Battery Energy Storage Systems
The fuzzy controller for BESS is also includes MFs for its inputs and outputs similar to the previous section. Input variables include frequency changes and derivative of frequency changes of the hybrid isolated micro-grid and the output is set-point for the generated power. The fuzzy rules are summarized in Table 3. Fuzzy rules are designed based on frequency deviation compensation gained by BESS and the frequency regulations achieved by FC system.

Table 3.
Input and output rule bases of battery energy storage systems (BESS) fuzzy controller.
4. Cuckoo Optimization Algorithm (COA)-Fuzzy Frequency Controller
Recently, optimization methods have been applied to enhance capabilities of the controllers. There are a couple of methods to optimize fuzzy controllers:
- (1)
- Optimization of membership functions
- (2)
- Optimization of coefficients of the controller
Since membership functions are similar to each other, changing them does not have a substantial effect on reducing the system error, and because of the fact that deriving the precise interval of fuzzy controllers is difficult, the second method is chosen. Algorithms like genetic, ants’ colony, bees’ colony, and so on can be used to optimize controllers [29]. We have used COA because of its advantages [30]. The considered system has two fuzzy controllers; each controller has three coefficients that must be optimized in inputs and outputs. Figure 6 shows the optimized fuzzy controller. The optimized coefficients include:
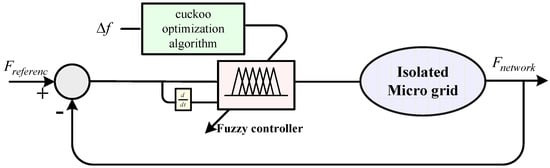
Figure 6.
The optimal fuzzy structure of the proposed isolated network.
- (1)
- Input gain of the controllers that includes error and change error. (Error corresponding to frequency deviation and change error corresponding to derivative of frequency deviation).
- (2)
- The output gain that is related to the optimization of controlling signal.
The COA is a direct search optimization method based on natural models which can find an optimal solution for the optimization problems [30]. The main advantage of the COA in comparison with other intelligent methods is the simplicity of implementation. Other outstanding features of the COA are pointed out in [31].
Structure of Cuckoo Optimization Algorithm
COA is a novel evolutionary optimization algorithm which is inspired by cuckoo’s unique lifestyle. A brief review of this bird’s survival and reproduction process can help us understand the main idea behind this algorithm. Known as “brood parasites”, cuckoos never parent their own eggs, they lay eggs in other birds’ nests and let other species take care of them and grow their young. Although cuckoos try to mimic hosts’ eggs and improve this mimicry for the next time, there are some species that can detect the parasitic eggs and destroy them. This challenge between the parasite and host goes on and they both try to out-survive.
Figure 7 shows the flowchart for COA. This algorithm has an initial population of cuckoos as its starting point. Then this population starts laying their eggs in the hosts’ nests. Some of these eggs that are similar to the hosts’ ones have the chance to survive and grow up. Others get detected by the host and will be killed. The number of the surviving cuckoos can be a measure of the suitability of that area as a habitat for cuckoos. In fact, COA is trying to optimize the position, in which more eggs will survive and find the best habitat for them.
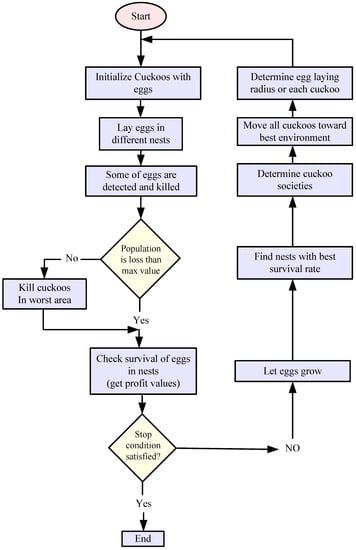
Figure 7.
Flowchart of cuckoo optimization algorithm (COA).
In order to use COA, first we have to define an initial habitat. Like “chromosome” in genetic algorithm (GA) and “particle position” in particles swarm optimization algorithm (PSO), a habitat is an array of in which variables are floating point numbers. This array represents cuckoo’s current living position:
Then a profit function should be determined to evaluate each habitat:
By determining the number of the eggs that each cuckoo can lay and variable limits ( and ) and also dedicating an “Egg Laying Radius” (ELR) to them, optimization algorithm sets out to maximize the profit:
By adjusting the coefficient α we can alter the maximum ELR as we desire. Note that cuckoo grouping is done by using K-means clustering method. The optimization process uses K-means clustering method for grouping the cuckoos. Then, by calculating the mean profit value and pointing out the best habitat with maximum profit, the cuckoos will move toward the best habitat as much as they can. Obviously, cuckoos cannot fly all the way to the best habitat; they fly a percentage of distance () and they have deviations from the point (). This reproduction and immigration cycle will continue till most cuckoos are gathered in a particular area (optimum point). Clearly, the two parameters λ and are defined as:
COA uses all the aforementioned parameters and finds new habitats for each generation of cuckoos. In several iterations, the optimum point with maximum profit is reached.
5. Cuckoo Optimization Algorithm Optimized Droop Controller
As we have discussed in the last section, coefficients related to the droop controllers are derived. However, the derived relations are not exact and we would not have a suitable controlling scheme. In order to optimize droop coefficients, initial values are obtained by equations of main drop controller. Then, by considering nominal value of each generator an interval is chosen for each coefficient. The goal is to minimize frequency changes by choosing the optimal coefficients using COA. The structure of optimal droop frequency controller of the proposed isolated Micro-grid is shown in Figure 8.
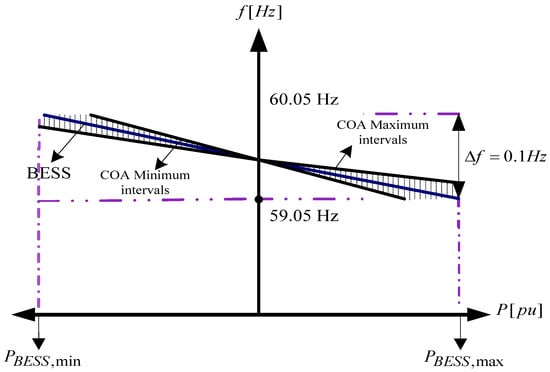
Figure 8.
Optimal droop characteristics of battery energy storage systems (BESS).
6. Simulation Results
Simulations are organized in two scenarios. In the simulation studies, the proposed setup system has been developed in MATLAB/SIMULINK environment. The system in this paper has been tested under the given data from each part of the system (load power demand data, PV data, and WT data). The results attained by applying the algorithms are presented in Table 4. In this paper, a comparison is made between COA and two other optimization algorithms, namely GA and PSO, and its higher efficiency is demonstrated. In this table, the error of frequency deviation has been used as an index for evaluating efficiency of these algorithms. The results shown in this table approve that COA is more efficient.

Table 4.
Compare between difference optimization algorithms.
6.1. Case Study 1
The hourly solar radiation data and wind speed during this scenario are presented in Figure 9 and Figure 10, respectively. It assumed that wind speed is changing between 10 and 13 m/s and irradiation energy of sun can be obtained from 6:30 to 18:00 in local time zone.
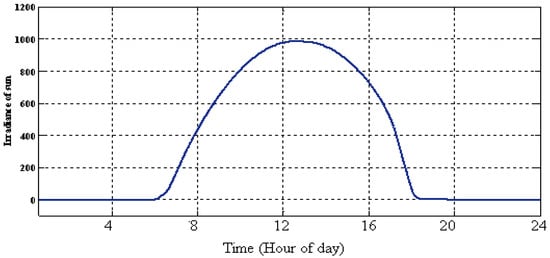
Figure 9.
Irradiance of sun.
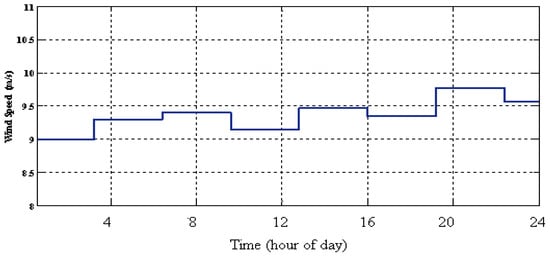
Figure 10.
Wind speed curve.
The load demand power curve during 24 h is shown in Figure 11. It can be seen that variations of the load demand is between 0.45(p.u.) and 0.95(p.u.) which this behavior is depended on the variety of loads and seasons changes during the years.
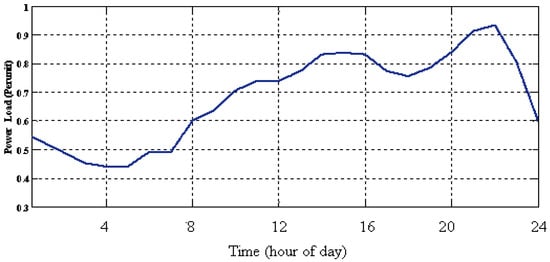
Figure 11.
The load power demand. (Non-Linear load).
In Figure 12 and Figure 13 the generated power of PV and WT are shown respectively. It has been expected that the output of PV power generation has the same behavior as irradiance of sun in Figure 9 and output power of wind turbine during the time be similar to wind profile. Priorities in this paper are benefiting from PV and WT generations in the first place.
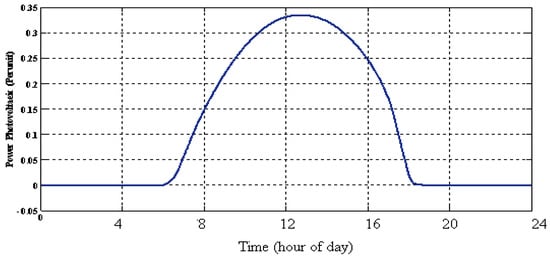
Figure 12.
Output power of photo-voltaic (PV).
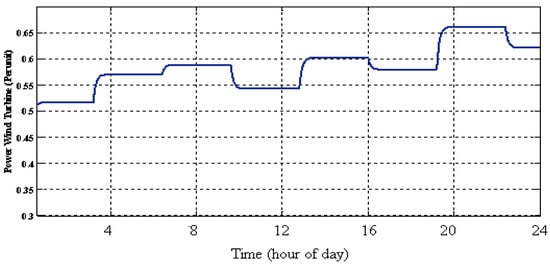
Figure 13.
Output power of wind turbines (WT).
The SOFC system power command is achieved according to the values of demanded power deviations, BESS power and WT. It can be seen that in the hours from 18:00 to 24:00 there is no solar radiation, and high demand is for consumption. It is expected to compensate this demand by SOFC and BESS generations. The power produced by SOFC system is shown in Figure 14. The power applied by BESS units in this hybrid isolated network for controlling the frequency deviation is illustrated in Figure 15. Deviation in the frequency is the result of difference between energy demand and the energy provided by WT/FC/PV/BESS systems which is illustrated in Figure 16. By coordination of FC and BESS, this deviation can be controlled. Figure 16 compares the proposed optimal fuzzy controller method with droop, fuzzy, and optimal droop controllers and the superiority of the proposed optimal fuzzy controller can be seen.
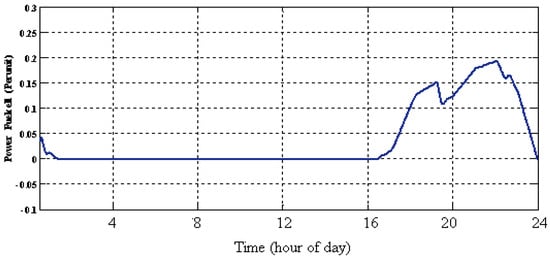
Figure 14.
Output power of solid oxide fuel cell (SOFC) using the proposed method.
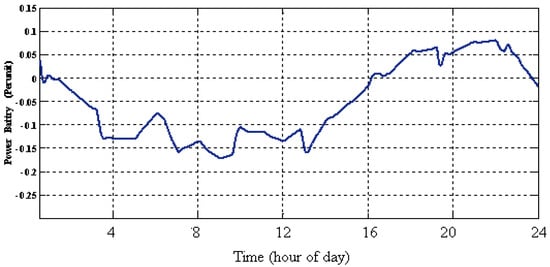
Figure 15.
Applied power of BESS unit.
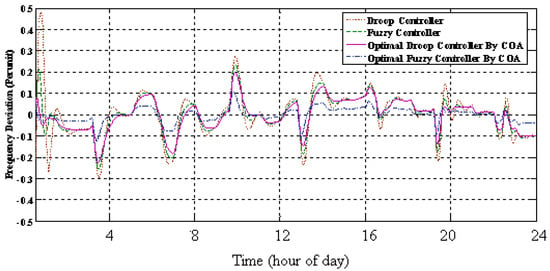
Figure 16.
The frequency deviation.
6.2. Case Study 2
In this scenario it is assumed that wind speed is changing between 7 m/s and 11 m/s. The hourly solar radiation data by considering the effects of clouds in the sky and wind speed during this simulation process are presented in Figure 17 and Figure 18, respectively. Priorities in this scenario are benefiting from PV and WT generations in the first place as like as previous scenario.
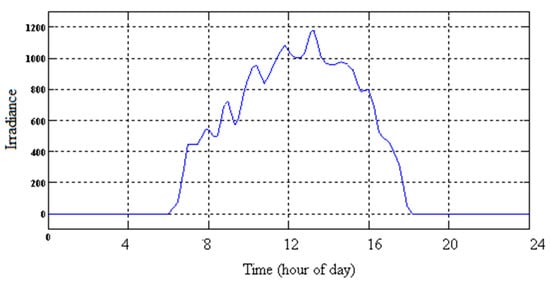
Figure 17.
Irradiance of sun.
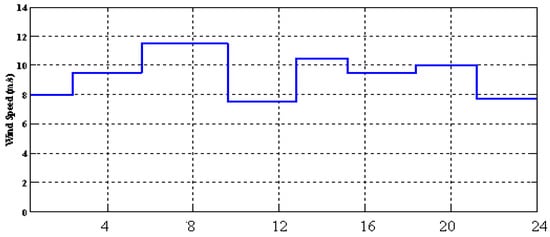
Figure 18.
Wind speed curve.
The load demand power in 24 h is shown in Figure 19. The peak hours are between 15:00 and 23:00 according to local time zone.
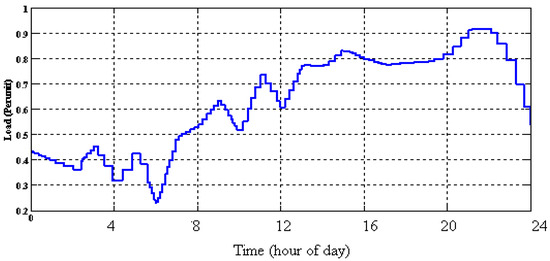
Figure 19.
The load power demand.
Figure 20 shows PV power generation in respect to irradiance of sun despite the clouds in the sky and Figure 21 shows wind speed during 24 h in respect to wind profile.
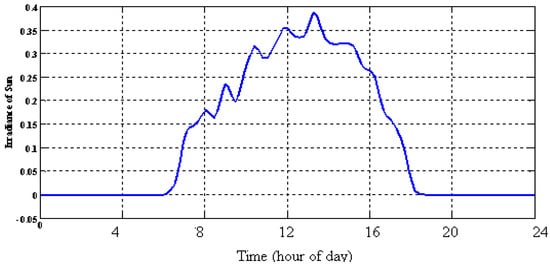
Figure 20.
Output power of PV.
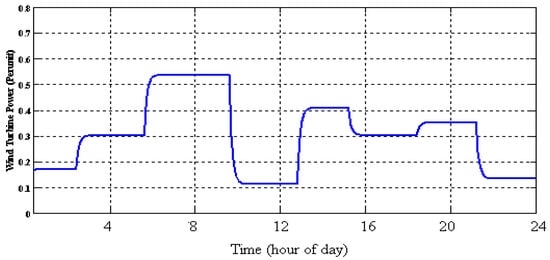
Figure 21.
Output power of WT.
The SOFC system generation is shown in Figure 22 and Figure 23 shows the BESS generation, which consists of the exceeded power of load demand. It can be seen whenever in spite of no SOFC generation, the total generation using WT and PV exceeds consumption, BESS can absorb the surplus generation, and thus battery power becomes negative. The controlled frequency deviation by coordination of FC and BESS is shown in Figure 24. The comparison between the optimal fuzzy controller method with droop, fuzzy, and optimal droop controllers is shown in Figure 24 and the simulation results show a good performance of the optimal fuzzy controller.
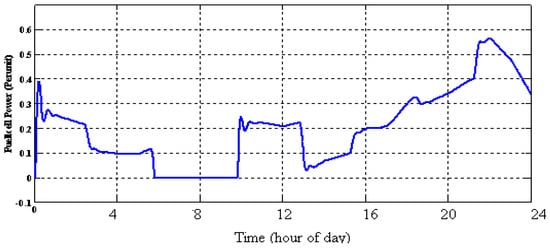
Figure 22.
Output power of SOFC using the proposed method.
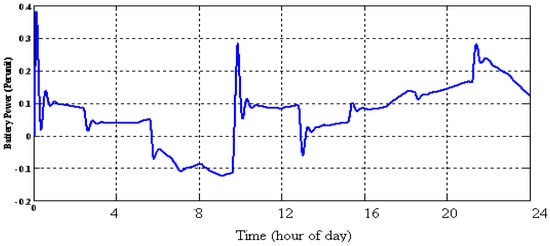
Figure 23.
Applied power of BESS unit.
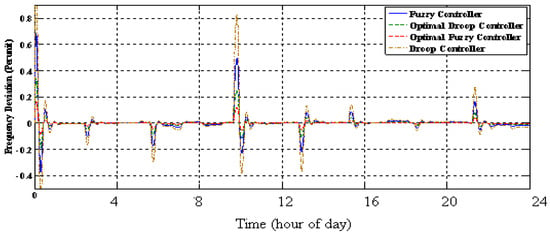
Figure 24.
The frequency deviation.
7. Conclusions
In this paper, a new control strategy in isolated micro-grids in the presence of BESS/FC/PV/WT was implemented and a dynamic response was simulated. The WT and PV system outputs change under different weather conditions. In the case of BESS failure, FC is connected to the network. In this paper, three optimization algorithms were utilized for optimizing fuzzy controllers. Among these three algorithms, it was shown that COA led to better results in setting the fuzzy controller coefficients with 59% and 68% fewer errors compared to GA and PSO. The proposed hybrid power system combined with the new optimal FLC algorithm reduced the FC system size while satisfying the peak power demand. In this study, a controller with droop method was suggested which did not show a high efficiency in reducing frequency changes. In order to enhance the efficiency of the controllers, each one was optimized by COA. Simulation results showed that the optimal fuzzy controller has superior efficiency over the other methods.
Author Contributions
The main idea of this article is designed and co-authored by all individuals. Mohsen Einan has been involved in computer simulations; Hossein Torkaman has collaborated on the guiding and writing the power system section of the paper; Mahdi Pourgholi has collaborated on the guiding and writing controller design section.
Conflicts of Interest
The authors declare no conflict of interest
Nomenclature
| Ideal standard potential | Response time for water flow | ||
| F | Faraday’s constant | Response time for oxygen flow | |
| Fuel cell current | Short circuit current | ||
| Kan | Anode valve constant | Open circuit voltage | |
| Valve molar constant for hydrogen | Conversion efficiency | ||
| Valve molar constant for water | Fill factor | ||
| Valve molar constant for oxygen | Power at MPP | ||
| Constant (=N0/4F) | Voltage at MPP | ||
| Molecular mass of hydrogen | Current at MPP | ||
| Number of hydrogen moles in the anode channel | Series resistance | ||
| Number of cells in series in the stack | Parallel resistance | ||
| Partial pressure | Tip speed ratio | ||
| Input fuel flow | Blade angular speed (mechanical rad/s) | ||
| Output fuel flow | Blade radius (m) | ||
| Fuel flow that reacts | Wind speed (m/s) | ||
| R | Ohmic loss | Mechanical power from the wind blade (kW) | |
| RH-O | Ratio of hydrogen to oxygen | Air density (kg/m3) | |
| R | Universal gas constant | Power coefficient | |
| T | Absolute temperature | Mechanical torque from wind blade (N/m) | |
| U | Fuel Utilization factor | Volume of anode | |
| Response time for hydrogen flow | Fuel cell voltage |
References
- Kobayakawa, T.; Kandpal, T.C. Analysis of electricity consumption under a photovoltaic micro-grid system in India. Sol. Energy 2015, 116, 177–183. [Google Scholar] [CrossRef]
- Mohammadi, M.; Hosseinian, S.H.; Gharehpetian, G.B. Optimization of hybrid solar energy sources/wind turbine systems integrated to utility grids as microgrid (MG) under pool/bilateral/hybrid electricity market using PSO. Sol. Energy 2012, 86, 112–125. [Google Scholar] [CrossRef]
- Kato, K.; Murata, A.; Sakuta, K. Energy payback time and life-cycle Co2 mission of residental PV power with silicon PV module. Prog. Photovolt. Res. Appl. 1998, 6, 105–115. [Google Scholar] [CrossRef]
- Wu, Z.; Xia, X. Optimal switching renewable energy system for demand side management. Sol. Energy 2015, 114, 278–288. [Google Scholar] [CrossRef]
- Ranaboldo, M.; Domenech, B.; Reyes, G.A.; Ferrer-Martí, L.; Moreno, R.P.; García-Villoria, A. Off-grid community electrification projects based on wind and solar energies: A case study in Nicaragua. Sol. Energy 2015, 117, 268–281. [Google Scholar] [CrossRef]
- Kayal, P.; Chanda, C.K. A multi-objective approach to integrate solar and wind energy sources with electrical distribution network. Sol. Energy 2015, 112, 397–410. [Google Scholar] [CrossRef]
- Veneri, O. Technologies and Applications for Smart Charging of Electric and Plug-In Hybrid Vehicles; Springer: Naples, Italy, 2017. [Google Scholar]
- Glavin, M.E.; Hurley, W.G. Optimisation of a photovoltaic battery ultracapacitor hybrid energy storage system. Sol. Energy 2012, 86, 3009–3020. [Google Scholar] [CrossRef]
- Trifkovic, M.; Sheikhzadeh, M.; Nigim, K.; Daoutidis, P. Modeling and Control of a Renewable Hybrid Energy System with Hydrogen Storage. IEEE Trans. Control Syst. Technol. 2014, 22, 169–179. [Google Scholar] [CrossRef]
- Onar, O.C.; Uzunoglu, M.; Alam, M.S. Modeling, control and simulation of an autonomous wind turbine/photovoltaic/fuel cell/ultra-capacitor hybrid power system. J. Power Sources 2008, 185, 1273–1283. [Google Scholar] [CrossRef]
- Onar, O.C.; Uzunoglu, M.; Alam, M.S. Dynamic modeling, design and simulation of a wind/fuel cell/ultra-capacitor-based hybrid power generation system. J. Power Sources 2006, 161, 707–722. [Google Scholar] [CrossRef]
- Ipsakis, D.; Voutetakis, S.; Seferlis, P.; Stergiopoulos, F.; Elmasides, C. Power management strategies for a stand-alone power system using renewable energy sources and hydrogen storage. Int. J. Hydrog. Energy 2009, 34, 7081–7095. [Google Scholar] [CrossRef]
- Arboleya, P.; Diaz, D.; Guerrero, J.M.; Garcia, P.; Briz, F.; Gonzalez-Moran, C.; Gomez Aleixandre, J. An improved control scheme based in droop characteristic for microgrid converters. Electric Power Syst. Res. 2010, 80, 1215–1221. [Google Scholar] [CrossRef]
- Goya, T.; Omine, E.; Kinjyo, Y.; Senjyu, T.; Yona, A.; Urasaki, N.; Funabashi, T. Frequency control in isolated island by using parallel operated battery systems applying H∞ control theory based on droop characteristics. IET Renew. Power Gener. 2011, 5, 160–166. [Google Scholar] [CrossRef]
- Bevrani, H.; Daneshmand, P.R. Fuzzy Logic-Based Load-Frequency Control Concerning High Penetration of Wind Turbines. IEEE Syst. J. 2012, 6, 173–180. [Google Scholar] [CrossRef]
- Nayeripour, M.; Hoseintabar, M.; Niknam, T. Frequency deviation control by coordination control of FC and double-layer capacitor in an autonomous hybrid renewable energy power generation system. Renew. Energy 2011, 36, 1741–1746. [Google Scholar] [CrossRef]
- Wang, L.; Lee, D.J.; Lee, W.J.; Chen, Z. Analysis of a novel autonomous marine hybrid power generation/energy storage system with a high-voltage direct current link. J. Power Sources 2008, 185, 1284–1292. [Google Scholar] [CrossRef]
- Koutroulis, E.; Kalaitzakis, K.; Voulgaris, N.C. Development of a microcontroller-based, photovoltaic maximum power point tracking control system. IEEE Trans. Power Electron. 2001, 16, 46–54. [Google Scholar] [CrossRef]
- Esram, T.; Chapman, P.L. Comparison of Photovoltaic Array Maximum Power Point Tracking Techniques. IEEE Trans. Energy Convers. 2007, 22, 439–449. [Google Scholar] [CrossRef]
- Zhang, F.; Maddy, J.; Premier, G.; Guwy, A. Novel current sensing photovoltaic maximum power point tracking based on sliding mode control strategy. Sol. Energy 2015, 118, 80–86. [Google Scholar] [CrossRef]
- Chen, P.-C.; Chen, P.-Y.; Liu, Y.-H.; Chen, J.-H.; Luo, Y.-F. A comparative study on maximum power point tracking techniques for photovoltaic generation systems operating under fast changing environments. Sol. Energy 2015, 119, 261–276. [Google Scholar] [CrossRef]
- Wang, C. Modeling and Control of Hybrid Wind/Photovoltaic/Fuel Cell Distributed Generation Systems. Ph.D. Thesis, Montana State University, Bozeman, MT, USA, 2006. [Google Scholar]
- Abdeddaim, S.; Betka, A.; Drid, S.; Becherif, M. Implementation of MRAC controller of a DFIG based variable speed grid connected wind turbine. Energy Convers. Manag. 2014, 79, 281–288. [Google Scholar] [CrossRef]
- Sendjaja, A.Y.; Kariwala, V. Decentralized Control of Solid Oxide Fuel Cells. IEEE Trans. Ind. Inform. 2011, 7, 163–170. [Google Scholar] [CrossRef]
- Hajizadeh, A.; Golkar, M.A. Intelligent power management strategy of hybrid distributed generation system. Int. J. Electr. Power Energy Syst. 2007, 29, 783–795. [Google Scholar] [CrossRef]
- Senjyu, T.; Nakaji, T.; Uezato, K.; Funabashi, T. A hybrid power system using alternative energy facilities in isolated island. IEEE Trans. Energy Convers. 2005, 20, 406–414. [Google Scholar] [CrossRef]
- Rajesh, R.; Mabel, M.C. Efficiency analysis of a multi-fuzzy logic controller for the determination of operating points in a PV system. Sol. Energy 2014, 99, 77–87. [Google Scholar] [CrossRef]
- Safari, S.; Ardehali, M.M.; Sirizi, M.J. Particle swarm optimization based fuzzy logic controller for autonomous green power energy system with hydrogen storage. Energy Convers. Manag. 2013, 65, 41–49. [Google Scholar] [CrossRef]
- Laghari, J.A.; Mokhlis, H.; Bakar, A.H.A.; Mohamad, H. Application of computational intelligence techniques for load shedding in power systems: A review. Energy Convers. Manag. 2013, 75, 130–140. [Google Scholar] [CrossRef]
- Berrazouane, S.; Mohammedi, K. Parameter optimization via cuckoo optimization algorithm of fuzzy controller for energy management of a hybrid power system. Energy Convers. Manag. 2014, 78, 652–660. [Google Scholar] [CrossRef]
- Gandomi, A.; Yang, X.-S.; Alavi, A. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).