Abstract
A density functional theory (DFT) study has been carried out on transition metal phosphates with olivine structure and formula LiMPO (M = Fe, Mn, Co, Ni) to assess their potential as cathode materials in rechargeable Li-ion batteries based on their chemical and structural stability and high theoretical capacity. The investigation focuses on LiMnPO, which could offer an improved cell potential (4.1 V) with respect to the reference LiFePO compound, but it is characterized by poor lithium intercalation/de-intercalation kinetics. Substitution of cations like Co and Ni in the olivine structure of LiMnPO was recently reported in an attempt to improve the electrochemical performances. Here the electronic structure and lithium intercalation potential of Ni- and Co-doped LiMnPO were calculated in the framework of the Hubbard U density functional theory (DFT+U) method for highly correlated materials. Moreover, the diffusion process of lithium in the host structures was simulated, and the activation barriers in the doped and pristine structures were compared. Our calculation predicted that doping increases Li insertion potential while activation barriers for Li diffusion remain similar to the pristine material. Moreover, Ni and Co doping induces the formation of impurity states near the Fermi level and significantly reduces the band gap of LiMnPO.
1. Introduction
Lithium-ion batteries are fundamental in powering portable electronics, and are the most credible candidate for enabling the future of electric mobility, as their energy density is superior to all other secondary batteries [1,2]. Two approaches for improving the energy and power densities of lithium-ion batteries are frequently proposed: either the discharge capacity of the cathode could be enhanced [3,4], or the working potential of the cathode materials could be increased [5,6,7]. In this scenario, LiFePO and related materials with olivine-like structures are widely applied to build cathodes for rechargeable lithium-ion batteries as a viable alternative to the commonly-used transition metal oxides (LiCo, LiNiO, LiMnO). Transition metal oxides suffer from deterioration with use at moderately high temperatures, have raised stability problems (reactivity with organic-based electrolytes), and have environmental concerns with their disposal [8]. In contrast, LiFePO is much more stable, while having similar theoretical capacity and voltage characteristics as well as potential cost and environmental advantages [9]. The main drawback of LiFePO relates to the low electrical and ionic conductivities that seriously limit the charge transport and Li insertion and extraction rates in these materials. In recent years, there have been extensive efforts to overcome these barriers by reducing the size of LiFePO particles to the nanoscale and applying conductive surface coatings such as carbon. On the other hand, the high insertion potential of Li from LiMnPO (about 4.1 V) and the high theoretical capacity of the material (140 mAh/g [10]) makes lithium–manganese–phosphate a promising alternative to LiFePO. However, severe kinetic problems during cycling and low electronic and ionic conductivity have prevented its application so far [11]. Moreover, the other possible candidate materials—namely, LiNiPO and LiCoPO—suffer, respectively, from the lack of suitable electrolytes (as the redox potential of the Ni/Ni couple is 5.1 V [12]) and from low energy density and high capacity fading with the current electrolytes and organic solvents [13]. The substitution of cations like Mn, Fe, Ni, and Co in a single olivine structure is one of the most popular approaches to improving the ionic and electronic conductivity of the materials. Minakshi and Kandhasamy reported the synthesis of LiMnPO doped with Ni and Co cations in substitutional positions, showing improved cell voltage and capacity [14]. The prediction of the physical and electrochemical properties of doped olivine materials is useful for the improvement of the performance of modern lithium-ion batteries. LiMPO compounds (M = Mn, Fe, Co, and Ni) have very complex magnetic behaviour with an anti-ferromagnetic ground state, and electrochemical properties are known to be affected by magnetic effects [15]. A number of theoretical studies have been devoted to the computation of the properties of LiMPO compounds on the basis of the Hubbard U density functional theory (DFT+U) approach [16,17,18,19]. The DFT+U method is a well-established model to deal with electron correlation in transition metal and rare earth compounds: it combines the relatively low computational cost of standard density functional theory (DFT) [20] and an explicit treatment of correlation with a Hubbard-type model for a subset of electronic states in the system. DFT+U is able to give reasonable predictions of the structural, magnetic, and electronic properties and the Li insertion potential of LiMPO structures. In this work, we report on the computation of structural and electronic properties of LiMnNiPO- and LiMnCoPO-doped olivines. Those specific stoichiometries were selected because they represent a realistic doping level [14], and at the same time require structural models simple enough to be treated with a reasonable computational effort. An analogous approach was successfully used by Lin et al. [21] to study Li diffusion in vanadium-doped LiFePO. Moreover, the activation barriers for the diffusion of Li ions in both the doped and pristine structures are compared. The doping of LiMnPO raised a great scientific interest in the last years and was reported in several studies [22,23,24,25]. To the best of our knowledge, this is the first theoretical study reporting the structural and electronic properties as well as the lithium diffusion activation barriers of LiMnPO doped with cobalt and nickel. Few experimental studies [14,26,27] have been devoted to Co- and Ni-doped LiMnPO, and our data can be useful to better understand and support the experimental findings.
2. Computational Details
All the calculations in this work were performed using the density functional theory [28,29] and a plane-waves pseudo-potentials basis set as implemented in the Quantum Espresso code [30]. The total energies and properties were calculated using the Perdew–Burke–Ernzerhof (PBE) version of the generalized gradient approximation (GGA) [31]. We adopted the ultrasoft pseudo-potentials [32] optimized for accuracy supplied by the Standard Solid State Pseudopotential library [33,34]. An energy cutoff of 70 Ry and a 64 k-point mesh were chosen to ensure that the total energies converged within 3 mRy per formula unit of LiMPO. To treat the electron correlation of the localized d electronic states, the simplified (rotationally invariant) approach to the DFT+U theory introduced by Dudarev et al. [35] was applied. The results of the GGA+U method are known to depend on the value of the U parameter, which depends on the valence state of the transition-metal ion and the crystal environment. The value of U can be obtained ab initio by linear response theory [19,36] or simply adjusted to reproduce specific properties of the material (e.g., electronic band gap, Li insertion potential) [37,38]. In this work, we used U = 4.5 eV for Mn, U = 5.7 eV for Ni, and U = 6.1 eV for Co, as calculated ab initio for olivine structures by Zhuo et al. [19]. We verified that the predicted lithium insertion potentials in the Mn, Ni, and Co olivines varied by only 0.1 V when changing the U values by ±0.5 V with respect to the selected values, clearly indicating that the results are not strongly dependent on the choice of the U parameter. Moreover, we assumed that the U values used for the simple compounds could be adopted for the doped systems. This approach is quite common in the literature [21,39], and it is justified by the fact that—as we verified—the results do not depend strongly on the selected values of U.
The bulk LiMPO and MPO (M = Fe, Mn, Ni, and Co) are paramagnetic at room temperature and anti-ferromagnetic below their Néel temperatures [40]. Because the energetic differences between the anti-ferromagnetic and ferromagnetic states are small (about 10 Ry per formula unit), we assumed ferromagnetic in order to account for the effect of spin polarization without facing the complexity of the anti-ferromagnetic behaviour. Moreover, the applications of these materials are at room temperature and above, and no spin-ordering effects are present in those conditions. This approach was already used by Holzwarth and Tang [41] to simulate LiFePO and related materials. The atomic positions and cell parameters were optimized using the Broyden-Fletcher-Goldfarb-Shanno structural optimization algorithm [42,43,44,45]. When Li is inserted (intercalated) into a host crystal structure like the transition metal olivines, its charge is compensated by an electron absorbed from the external circuit. This process can be described by Equation (1):
The intercalation voltage V of the cell can be obtained by calculating the electrical energy associated with the discharging between LiMPO and LiMPO (with x > x). Following Aydinol et al. [46], the energy is the integral of the voltage times the displaced charge , where e is the charge of the electron:
In Equation (2), is the chemical potential of Li per atom in the intercalation compound, is the constant chemical potential of metallic Li. The displaced charge can be written as , resulting in:
where G is the Gibbs free energy. Then, the average intercalation voltage between x and x results to be:
where F is the Faraday constant. Since the Li intercalation in olivine LiMnPO occurs via a two-phase reaction involving the phase separation of LiMnPO and MnPO [10], the potential for the complete discharging of the olivine structures can be calculated setting x = 1 and x = 0 in Equation (4). The calculation can be further simplified approximating the change of Gibbs free energy (), with the change of internal energy . This is indeed a very good approximation, since is on the order of some eV per moles, and the term—with the calculated volume variations (about 5%–6%, see the following Table 1)—is on the order of 10 eV. Moreover, being on the order of the thermal energy, the term is also much smaller than the internal energy change. Neglecting the entropic and contributions [46], the potential V can simply be determined by computing the internal energy of LiMPO, MPO, and Li:

Table 1.
Optimized lattice parameters for LiMnPO, MnPO, and for the doped materials. For the starting materials, experimental values (Exp.) [10] are reported for comparison. The introduction of Ni and Co in the structure results in a contraction of the cell.
The energy for lithium E can be obtained for the cubic body-centered (BCC) structure optimizing the cell parameter with the same energy cut-off adopted for the simulation of olivines.
The activation barriers for lithium diffusion were obtained through the nudged elastic band (NEB) method [47], calculating the minimum energy path between two local stable sites of the Li ion along the (0 1 0) direction (b axis). To avoid image interactions due to the periodic boundary conditions, a 1 × 2 × 1 supercell doubled along the b axis and containing eight unit formula was used for the NEB calculations. To maintain acceptable computational cost for supercell calculations, k-space sampling was limited to the point.
3. Crystal Structures
LiMPO and MPO compounds display the olivine structure with symmetry group Pnma (number 62) [48]; Figure 1 shows a typical crystal cell. The oxygen atoms form a nearly tetrahedral arrangement around each phosphorus site and an approximately octahedral arrangement around each transition metal site. The structure presents channels along the b axis, which are able to accommodate the mobile Li ions: Ceder et al. demonstrated that the Li diffusion is possible only along those preferential paths [49]. When Li ions and electrons are removed from LiMPO, the remaining MPO framework maintains the same structure, with a reduction in volume of about 5%. The unit cell contains four formula units.
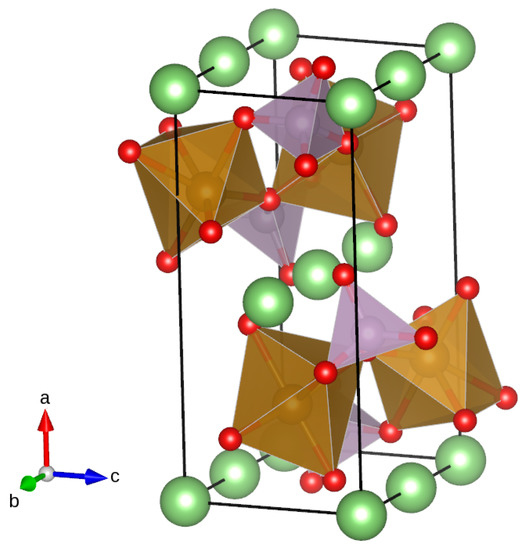
Figure 1.
Olivine structure of LiMPO: Li atoms are represented in green, O atoms in red, and P and Mn atoms, respectively, by distorted tetrahedra (violet) and octahedra (brown). The coordinate system is reported on the left of the structure. The picture shows that Li ions are aligned along the b-axis: the structure presents 1D channels along the b-axis that are responsible for lithium transport. Mn ions occupy 4c Wickoff positions at the center of octahedra: for the simulation of doping, one Mn ion was substituted with Ni or Co. The figure was produced using the Vesta visualization system [50].
We considered the solid solutions LiMnXPO (X = Co, Ni) formed by substituting one manganese atom in the special position 4c with one nickel or cobalt atom: the symmetry is then lowered to the Pm space group (number 6). This simplified model—even if not addressing the complexity of transition metal cation ordering—was effectively used by Lin et al. [21] to study Li diffusion in vanadium-doped LiFePO and by Wang et al. [51] to simulate the modification of the electronic structure induced by doping LiMnPO with iron and aluminium.
4. Structural and Electronic Properties
The cell geometries of all considered structures were optimized as a preliminary step. Table 1 reports the cell parameters and volumes for all the simulated compounds. The calculated cell parameters of LiMPO and MPO are overestimated with respect to the experimental data, but this is a well-known systematic behaviour of GGA functionals [52]: the deviations from experimental cell parameters can be considered acceptable and within the standard accuracy of the method. It is clear that the doping with Ni and Co—as expected on the basis of the smaller ionic radius in comparison to Mn—causes a contraction of the cell volume.
The lithium insertion potentials and band gaps are reported in Table 2: the DFT+U model predicts a band gap for LiMnPO and an insertion potential for the process MnPO + Li + e→ LiMnPO in accordance with the experimental data. Moreover, the doped structures—even if remaining wide band gap semiconductors—show a reduced band gap with respect to LiMnPO. In addition, for the doped systems, the calculations predict a larger lithium insertion potential with respect to LiMnPO. Since the predicted values are below 5 V and still compatible with existing electrolytes, this could enable the production of batteries with enhanced energy density. Kwon and Fromm [53] reported a capacity of 165 mAh/g (about 1.1 mAh/mol) for LiMnPO and an electrochemical window between 4.1 and 2.5 V: if we suppose that the doping does not change the molar capacity and the minimum operating voltage of the material too much, the increase in the maximum potential implies an improvement of the energy storage density (15% and 11% for Ni and Co doping, respectively).

Table 2.
Properties of LiMnPO and derived doped structures: band gap , lithium insertion potential, and cell magnetization per unit formula. Experimental band gap for LiMnPO was taken form García-Moreno et al. [54] and insertion potential form Li et al. [10]. The simulations agree very well with the experimental measurements. No experimental data are available for the doped structures. The delithiated structures show a metallic behaviour with zero band gap, and are not reported in the table.
The density of states for the six simulated structures are plotted in Figure 2 and Figure 3. Projected densities of states on atoms are also reported in the figures: it is clear that the valence states are formed mainly by the mixing of the 3d orbitals of Mn and the 2sp orbitals of oxygen (so the bonding of the crystal has a partial covalent nature). The situation is similar in the doped systems in which the 3d states of Ni or Co also contribute to the bonding. The electronic levels of Li are out of the energy range reported in the figure, and as expected, scarcely contribute to the bonding of the solids. Concerning the spin polarization, it can be observed that magnetization is associated mainly to the 3d states of the transition metal ions. In LiMnPO, the spin-up 3d states are completely filled, giving a magnetic moment of the cell of 5 per formula unit, while the conduction states above the Fermi level are composed of 3d spin-down orbitals. The dopants generate spin-down states in both the valence and conduction regions: those valence states lower the cell magnetization to 4.25 and 4.5 for Ni and Co, respectively, and conduction states are responsible for the reduced band gap. Similar considerations apply to delithiated structures, even if they show a metallic behaviour.
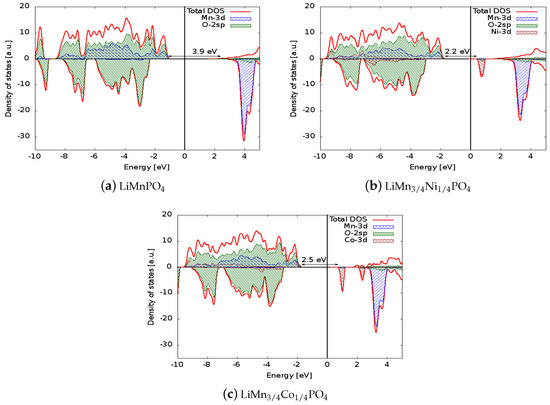
Figure 2.
Comparison between the densities of states (DOSs) of (a) LiMnPO, (b) LiMnNiPO, and (c) LiMnCoPO. The Fermi energy was set to zero to allow direct comparison of the electronic structures. The positive (negative) axis is the majority (minority) spin direction. All materials are wide band gap semiconductors. Projected densities of states on transition metal atoms and oxygen are also reported.
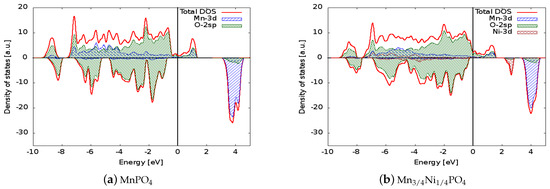
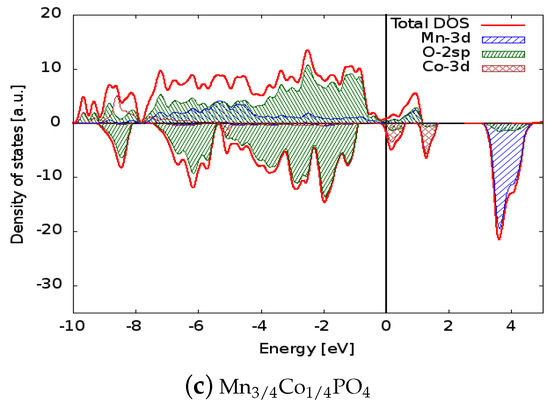
Figure 3.
Comparison between the densities of states of (a) MnPO, (b) MnNiPO, and (c) MnCoPO. The Fermi energy was set to zero to allow direct comparison of the electronic structures. The positive (negative) axis is the majority (minority) spin direction. All materials have metallic behaviour. Projected densities of states on transition metal atoms and oxygen are also reported.
5. Lithium Ion Diffusion
It is well known that the electrochemical performances of olivine phosphates are primarily limited by the electronic conductivity [55]. However, recent studies showed that Li ion diffusion can also play a major role [56]. It is well-known that Li transport in the olivine structures happens through 1D-like channels along the b axis (see Figure 1) [49]. For studying the Li diffusion in lithiated/delithiated systems and calculating the corresponding activation energies using the NEB method, a single Li ion vacancy was introduced in the pure (doped) LiMnPO supercell, while a single ion was added in pure (doped) MnPO. Nine intermediate images were constructed to interpolate the diffusion path between the initial and final states. The calculated activation barriers are reported in Table 3.

Table 3.
Barrier activation energies (E) in eV for the pristine and doped systems. In lithiated structures, the values refer to Li vacancy diffusion; in delithiated structures, the data refer to Li ion diffusion.
The calculated activation barriers are very similar to each other, as could be expected, since the substitution of a Mn atom in the cell does not substantially change the structure of the crystals. A larger variation of the activation energy was observed in LiMnNiPO, and this can be easily explained on the basis of the increased Pauli repulsion between Li ions and MO (M = Mn, Ni, Co) octahedra, since LiMnNiPO shows the strongest cell contraction when compared to the pristine structure (see Table 1). Based on our simulations, similar lithium diffusion coefficients are expected for LiMnPO and for the doped materials, so carbon coating—the common strategy used for improving the conductivity of LiFePO [57]—should be adopted. On the other hand the improved lithium insertion potentials of the doped systems could contribute to enhanced electrochemical performances. In particular, as nickel is less environmentally threatening than cobalt, LiMnNiPO appears to be a good candidate for producing cathodes for Li-ion batteries.
6. Conclusions
The GGA + U method predicts Li insertion potentials with remarkably good accuracy in phosphate olivines, in contrast to previously standard GGA approaches. We have used this method to obtain information about the doping of LiMnPO with Ni and Co, for which available experimental data about structural and electronic properties are scarce. Our calculations predict an improved Li insertion potential in the doped systems and activation barriers for Li diffusion similar to the starting pristine material. Furthermore, the density of states calculations suggest that Ni and Co doping induces the formation of impurity states near the Fermi level and significantly reduces the band gap of LiMnPO. Based on the calculated cell volumes, we estimate that the density and theoretical gravimetric capacity of the doped compounds will remain similar to those of the pristine material. For this reason, the greater lithium extraction voltage associated with the doping could allow an improvement of the gravimetric energy storage density of about 6% at full cell level. In summary, Ni- and Co-doped LiMnPO represent promising systems for further theoretical and experimental investigations as cathode materials for lithium-ion batteries.
Acknowledgments
We would like to acknowledge the European Commission Seventh Framework Programme for having funded this research within the ORION collaborative project (NMP-229036). Moreover we are grateful to Giuseppe Mattioli, Matteo Cococcioni and Paolo Giannozzi for the help and suggestions. Research in Mons was also supported by the Belgian Federal Science Policy Office (PAI 7/05) and FNRS-FRFC. David Beljonne is a FNRS research director.
Author Contributions
Mauro Francesco Sgroi and Roberto Lazzaroni conceived and designed the simulations; Mauro Francesco Sgroi performed the density functional calculations; Daniele Pullini and David Beljonne contributed to the analysis of the data and discussion of results; Mauro Francesco Sgroi wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| DFT | Density functional theory |
| DFT+U | Hubbard U density functional theory |
| GGA | Generalized gradient approximation |
References
- Van Schalkwijk, W.; Scrosati, B. Advances in Lithium-Ion Batteries; Springer: Boston, MA, USA, 2002. [Google Scholar]
- Nitta, N.; Wu, F.; Lee, J.T.; Yushin, G. Li-ion battery materials: Present and future. Mater. Today 2015, 18, 252–264. [Google Scholar] [CrossRef]
- Afyon, S.; Krumeich, F.; Mensing, C.; Borgschulte, A.; Nesper, R. New high capacity cathode materials for rechargeable Li-ion batteries: Vanadate-borate glasses. Sci. Rep. 2014, 4, 7113. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Meng, F.; Jin, S. High-capacity lithium-ion battery conversion cathodes cased on iron fluoride nanowires and insights into the conversion mechanism. Nano Lett. 2012, 12, 6030–6037. [Google Scholar] [CrossRef] [PubMed]
- Eglitis, R.; Borstel, G. Towards a practical rechargeable 5 v Li ion battery. Phys. Status Solidi (A) 2005, 202, R13–R15. [Google Scholar] [CrossRef]
- Eglitis, R.I. Theoretical prediction of the 5 V rechargeable Li ion battery using Li2CoMn3O8 as a cathode. Phys. Scr. 2015, 90, 094012. [Google Scholar] [CrossRef]
- Yi, T.F.; Zhu, Y.; Zhu, R. Density functional theory study of lithium intercalation for 5 V LiNi0.5Mn1.5O4 cathode materials. Solid State Ionics 2008, 179, 2132–2136. [Google Scholar] [CrossRef]
- Linden, D.; Reddy, T. Handbook of Batteries, 3rd ed.; McGraw-Hill: New York, NY, USA, 2002; Chapter 35. [Google Scholar]
- Padhi, A.; Nanjundaswamy, K.; Goodenough, J. Phospho-olivines as positive-electrode materials for rechargeable lithium batteries. J. Electrochem. Soc. 1997, 144, 1188–1194. [Google Scholar] [CrossRef]
- Li, G.; Azuma, H.; Tohda, M. LiMnPO4 as the cathode for lithium batteries. Electrochem. Solid-State Lett. 2002, 5, A135–A137. [Google Scholar] [CrossRef]
- Yamada, A.; Yonemura, M.; Takei, Y.; Sonoyama, N. Comparative kinetic study of olivine LixMPO4 (M = Fe, Mn). J. Electrochem. Soc. 2004, 151, A1352–A1356. [Google Scholar]
- Wolfenstine, J.; Allen, J. Ni3+/Ni2+ redox potential in LiNiPO4. J. Power Sources 2005, 142, 389–390. [Google Scholar] [CrossRef]
- Bramnik, N.N.; Bramnik, K.G.; Baehtz, C.; Ehrenberg, H. Study of the effect of different synthesis routes on Li extraction-insertion from LiCoPO4. J. Power Sources 2005, 145, 74–81. [Google Scholar] [CrossRef]
- Minakshi, M.; Kandhasamy, S. Utilizing active multiple dopants (Co and Ni) in olivine LiMnPO4. Curr. Opin. Solid State Mater. Sci. 2012, 16, 163–167. [Google Scholar] [CrossRef]
- Li, J.; Garlea, V.O.; Zarestky, J.L.; Vaknin, D. Spin-waves in antiferromagnetic single-crystal LiFePO4. Phys. Rev. B 2006, 73, 024410. [Google Scholar] [CrossRef]
- Zhou, F.; Kang, K.; Maxisch, T.; Ceder, G.; Morgan, D. The electronic structure and band gap of LiFePO4 and LiMnPO4. Solid State Commun. 2004, 132, 181–186. [Google Scholar] [CrossRef]
- Zhou, F.; Cococcioni, M.; Kang, K.; Ceder, G. The Li intercalation potential of LiMPO4 and LiMSiO4 olivines with M = Fe, Mn, Co, Ni. Electrochem. Commun. 2004, 6, 1144–1148. [Google Scholar] [CrossRef]
- Zhou, F.; Marinetti, C.; Cococcioni, M.; Morgan, D.; Ceder, G. Phase separation in LixFePO4 induced by correlation effects. Phys. Rev. B 2004, 69, 201101. [Google Scholar] [CrossRef]
- Zhou, F.; Marinetti, C.; Cococcioni, M.; Morgan, D.; Ceder, G. First-principles prediction of redox potentials in transition-metal compounds with LDA + U. Phys. Rev. B 2004, 70, 235121. [Google Scholar] [CrossRef]
- Anisimov, V.; Izyumov, Y. Electronic Structure of Strongly Correlated Materials; Springer-Verlag Berlin Heidelberg: Heidelberg, German, 2010. [Google Scholar]
- Lin, H.; Wen, Y.; Zhang, C.; Zhang, L.; Huang, Y.; Shan, B.; Chen, R. A GGA + U study of lithium diffusion in vanadium doped LiFePO4. Solid State Commun. 2012, 152, 999–1003. [Google Scholar] [CrossRef]
- Inseok, S.; Senthilkumar, B.; Kim, K.H.; Kim, J.K.; Kim, Y.; Ahn, J.H. Atomic structural and electrochemical impact of Fe substitution on nano porous LiMnPO4. J. Power Sources 2016, 320, 59–67. [Google Scholar]
- Ni, J.; Gao, L. Effect of copper doping on LiMnPO4 prepared via hydrothermal route. J. Power Sources 2011, 196, 6498–6501. [Google Scholar] [CrossRef]
- Oh, S.; Jung, H.G.; Yoon, C.S.; Myung, S.; Chen, Z.; Amine, K.; Sun, Y.K. Enhanced electrochemical performance of carbon-LiMn1-xFexPO4 nanocomposite cathode for lithium-ion batteries. J. Power Sources 2011, 196, 6924–6928. [Google Scholar] [CrossRef]
- Fang, H.; Dai, E.; Yang, B.; Yao, Y.; Ma, W. LiMn0.8Fe0.19Mg0.01PO4/C as a high performance cathode material for lithium ion batteries. J. Power Sources 2012, 204, 193–196. [Google Scholar] [CrossRef]
- Wang, K.; Maljuk, A.; Blum, C.; Kolb, T.; Jähne, C.; Neef, C.; Grafe, H.; Giebeler, L.; Wadepohl, H.; Meyer, H.; et al. Growth, characterization, and magnetic properties of a Li(Mn,Ni)PO4 single crystal. J. Cryst. Growth 2014, 386, 16–21. [Google Scholar] [CrossRef]
- Yang, G.; Ni, H.; Liu, H.; Gao, P.; Ji, H.; Roy, S.; Pinto, J.; Jiang, X. The doping effect on the crystal structure and electrochemical properties of LiMnxM1-xPO4 (M = Mg, V, Fe, Co, Gd). J. Power Sources 2011, 196, 4747–4755. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B Rapid Commun. 1990, 41, 7892. [Google Scholar] [CrossRef]
- Materialscloud. Available online: http://materialscloud.org (accessed on 15 March 2014).
- Lejaeghere, K.; Bihlmayer, G.; Björkman, T.; Blaha, P.; Blügel, S.; Blum, V.; Caliste, D.; Castelli, I.E.; Clark, S.J.; Dal Corso, A.; et al. Reproducibility in density functional theory calculations of solids. Science 2016, 351, aad3000. [Google Scholar] [CrossRef] [PubMed]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron energy loss spectra and the structural stability of nickel oxide: An LDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 2005, 71, 035105. [Google Scholar] [CrossRef]
- Park, S.G.; Magyari-Köpe, B.; Nishi, Y. Electronic correlation effects in reduced rutile TiO2 within the LDA+U method. Phys. Rev. B 2010, 82, 115109. [Google Scholar] [CrossRef]
- Dathar, G.K.P.; Sheppard, D.; Stevenson, K.J.; Henkelman, G. Calculations of Li-ion diffusion in olivine phosphates. Chem. Mater. 2011, 23, 4032–4037. [Google Scholar] [CrossRef]
- Xin, X.-G.; Shen, J.-Q.; Shi, S.-Q. Structural and magnetic properties of LiNi0.5Mn1.5O4 and LiNi0.5Mn1.5O4-δ spinels: A first-principles study. Chin. Phys. B 2012, 21, 128202. [Google Scholar] [CrossRef]
- Santoro, R.P.; Newnham, R.E. Antiferromagnetism in LiFePO4. Acta Crystallogr. 1967, 22, 344–347. [Google Scholar] [CrossRef]
- Tang, P.; Holzwarth, N.A.W. Electronic structure of FePO4 , LiFePO4, and related materials. Phys. Rev. B 2003, 68, 165107. [Google Scholar] [CrossRef]
- Broyden, C.G. The convergence of a class of double-rank minimization algorithms. J. Inst. Math. Appl. 1970, 6, 76–90. [Google Scholar] [CrossRef]
- Fletcher, R. A new approach to variable metric algorithms. Computer J. 1970, 13, 317–322. [Google Scholar] [CrossRef]
- Goldfarb, D. A family of variable metric updates derived by variational means. Math. Comput. 1970, 24, 23–26. [Google Scholar] [CrossRef]
- Shanno, D.F. Conditioning of quasi-Newton methods for function minimization. Math. Comput. 1970, 24, 647–656. [Google Scholar] [CrossRef]
- Aydinol, M.K.; Kohan, A.F.; Ceder, G.; Cho, K.; Joannopoulos, J. Ab initio study of lithium intercalation in metal oxides and metal dichalcogenides. Phys. Rev. B 1997, 56, 1354–1365. [Google Scholar] [CrossRef]
- Henkelman, G.; Uberuaga, B.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
- Hahn, T. International Tables for Crystallography, Volume A: Space Group, 5th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Morgan, D.; der Ven, A.V.; Ceder, G. Li Conductivity in LixMPO4 (M = Mn, Fe, Co, Ni Olivine Materials). Electrochem. Solid-State Lett. 2004, 7, A30–A32. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, L.; Li, J.; Gao, J.; Jiang, C.; He, X. First-principles study of doping in LiMnPO4. Int. J. Electrochem. Sci. 2012, 7, 3362–3370. [Google Scholar]
- Haas, P.; Tran, F.; Blaha, P. Calculation of the lattice constant of solids with semilocal functionals. Phys. Rev. B 2009, 79, 085104. [Google Scholar] [CrossRef]
- Kwon, N.H.; Fromm, K.M. Enhanced electrochemical performance of <30 nm thin LiMnPO4 nanorods with a reduced amount of carbon as a cathode for lithium ion batteries. Electrochim. Acta 2012, 69, 38–44. [Google Scholar]
- García-Moreno, O.; Alvarez-Vega, M.; García-Alvarado, F.; García-Jaca, J.; Gallardo-Amores, J.M.; Sanjuán, M.L.; Amador, U. Influence of the structure on the electrochemical performance of lithium transition metal phosphates as cathodic materials in rechargeable lithium batteries: A new high-pressure form of LiMPO4 (M = Fe and Ni). Chem. Mater. 2001, 13, 1570–1576. [Google Scholar] [CrossRef]
- Wang, C.; Hong, J. Ionic/electronic conducting characteristics of LiFePO4 cathode materials. Electrochem. Solid-State Lett. 2007, 10, A65–A69. [Google Scholar] [CrossRef]
- Sun, C.; Zhou, Z.; Xu, Z.; Wang, D.; Wei, J.; Bian, X.; Yan, J. Improved high-rate charge/discharge performances of LiFePO4/C via V-doping. J. Power Sources 2009, 193, 841–845. [Google Scholar] [CrossRef]
- Wang, K.; Cai, R.; Yuan, T.; Yu, X.; Ran, R.; Shao, Z. Process investigation, electrochemical characterization and optimization of LiFePO4/C composite from mechanical activation using sucrose as carbon source. Electrochim. Acta 2009, 54, 2861–2868. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).