Abstract
The cell case temperature versus time profiles of a multistage fast charging technique (4C-1C-constant voltage (CV))/fast discharge (4C) in a 2.3 Ah cylindrical lithium-ion cell are analyzed using a thermal model. Heat generation is dominated by the irreversible component associated with cell overpotential, although evidence of the reversible component is also observed, associated with the heat related to entropy from the electrode reactions. The final charging stages (i.e., 1C-CV) significantly reduce heat generation and cell temperature during charge, resulting in a thermally safe charging protocol. Cell heat capacity was determined from cell-specific heats and the cell materials’ thickness. The model adjustment of the experimental data during the 2 min resting period between discharge and charge allowed us to calculate both the time constant of the relaxation process and the cell thermal resistance. The obtained values of these thermal parameters used in the proposed model are almost equal to those found in the literature for the same cell model, which suggests that the proposed model is suitable for its implementation in thermal management systems.
1. Introduction
In recent years, fast battery charging has become a thriving area of research, as a result of the increasing demands in portable electronics [1], electric vehicles [2] and electrical energy storage systems [3]. Despite its convenience, fast battery charging can drastically reduce cell longevity if improperly addressed. This is primarily caused by the elevated cell temperatures and high currents used during fast charging, which are identified as the two main factors that accelerate battery degradation [4] and reduce battery state-of-safety [5].
Even so, fast battery charging capabilities can be enhanced by modifying cell active materials and cell design [6], and improving the charging algorithm [7,8]. In addition, the effect of battery heat generation also plays a major role in fast charging [9]. Hence, a detailed battery thermal analysis during fast charging could be used to design safer, quicker and more efficient charging protocols.
In this work, we propose a thermal model to decipher the heat generation contributions (both reversible and irreversible) during fast battery charging. The fast battery charging technique thermally studied here was previously reported in [10], and was validated to attain quick recharges while causing no accelerated cell degradation [11]. The proposed thermal model is similar to several thermal models found in the literatures [12,13,14,15], but it presents a low computational complexity, and utilizes the external cell surface temperature as the main variable to infer heat generation during operation. Despite using a similar approach as the one presented here, other models [16] present more complex, higher-order differential equations which could be more difficult to implement in commercial battery management systems (BMS).
The findings from this work improve the understanding of the thermal behavior of this particular fast charging technique, while using a simple, effective thermal model.
The paper is organized as follows: Section 2 presents the main features of the fast charging method as well as the measurements made to implement the thermal analysis; Section 3 explains the thermal model and Section 4 shows and discusses the obtained results, highlighting how the thermal capacity and the thermal resistance of the cell are obtained; finally, Section 5 presents the conclusions.
2. Experimental
The experiments were conducted on a commercial graphite/LiFePO4 (C/LFP) cylindrical cell, manufactured by A123 Systems (ANR26650M1, Livonia, MI, USA). These cells have a rated capacity of 2.3 Ah and a nominal cell voltage of 3.3 V when evaluated at nominal cell conditions, i.e., 1C rate. The cells have an average weight of 0.075 kg. The specific energy under nominal conditions is about 99.2 Wh∙kg−1 [17]. Cell characterization and cycle aging were conducted using a multi-channel Arbin BT-2000 battery tester (College Station, TX, USA). The cell-surface temperature was monitored using T-type thermocouples manufactured by Omega (Norwalk, CT, USA). The thermocouples were attached to the lateral cell surface using self-adhesive thermocouple pads. A climate chamber manufactured by Memmert (Schwabach, Germany) was used to maintain constant ambient temperature of 22 °C throughout testing.
The cells were started with the commissioning test, in which they were identified and weighted, and the open circuit voltage (OCV) was measured. Next, a conditioning series was performed following the United States Advanced Battery Consortium (USABC) test procedure #2 [18]: several cycles of standard 1C charges and C/3, C/2, 1C, C/3 discharges until to achieve stability of cell capacity. Thereafter, C/25 charge and discharge cycles were carried out to determine a practical maximum capacity with minimal kinetic effects [19,20]. Subsequently, the cells were subjected to cycling. The cycling scheme consisted in fast charging and fast discharging. Fast charging consisted of a multistage fast charging technique using three charging steps at 4C (9.2 A), 1C (2.3 A) under constant current, and a fixed 5 min length constant voltage (CV) stage at 3.6 V. Discharges were carried out at 4C (−9.2 A) to 2.0 V cut off voltage. After a resting time of 2 min the process starts again.
The used multistage fast charging technique profile is shown in Figure 1, showing the evolution of cell voltage, current and temperature (both cell temperature surface and ambient temperature), for three consecutive cycles. The fast charging protocol approximately completes the charge in 25 min, while a standard charging protocol at 1C needs 1 h. The 4C step lasts about 15 min, the 1C stage lasts about 4 min and the 5 last min of the CV step allows the charge to be completed. The goal of the 4C step is quickly provides the most of the capacity while the temperature increases. The 1C-CV steps complete at the charge at slow speed and reduce the temperature. More details of this method can be found in our previous work [10,11].
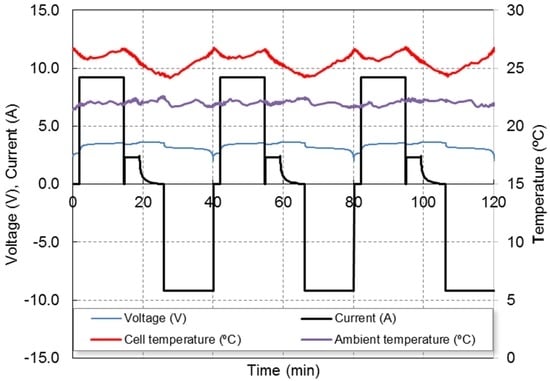
Figure 1.
Cell temperature, current and voltage evolution during 4C-1C-constant voltage (CV)/4C cycling.
This fast charging/fast discharging sequence was performed continuously for 300 cycles, after which the reference tests were performed. The test sequence includes a final constant current charge and discharge cycle at C/25 (0.092 A). The C/25 rate is considered slow enough to obtain a practical approach to the OCV of the cell [21]. If the OCV is represented as a function of the estate of charge, E(SOC), it provides a pseudo-thermodynamic description of the cell voltage with negligible kinetic effects, and it is used as a reference to obtain the resistance of the cell Rcell(SOC) during the charge and the discharge. Both resistances are necessary to measure the irreversible component of the heat generation.
Taking into account that charging current is considered positive and discharging current is considered negative, the cell resistance is defined as Equation (1):
where V(SOC) is the battery voltage for both charge (V(SOC) > E(SOC)) and discharge (V(SOC) < E(SOC)).
Figure 1 also shows the temperature profile at the battery casing measured by means of a thermocouple. The ambient temperature is 22 °C. A repetitive pattern can be observed: the casing temperature varies between 24 °C at the end of the charge and 27 °C at the end of both 4C charge and discharge stages.
To obtain the average thermal capacity of the cell from the specific density and specific heat of its components the cell has been open in glove box and the thickness of the collectors, separators and electrodes have been measured by means of a micrometer screw.
3. Model
The cell is assumed to be small enough so that it is considered a body with constant thermal capacity, Ccell (J/K), and uniform internal temperature Tint (K). This temperature will change (Equation (2)) as a result of the balance between the stored internal energy, the heat generated (W) by the cell operation and the heat exchanged (W) with the outside environment at constant temperature Text (K).
The exchanged heat (Equation (3)) is considered proportional to: (a) the total area (lateral and bases), Acell (m2), of the cell; and (b) the temperature difference between the ambient temperature, Text, and the battery casing temperature, T (K).
The proportionality constant is the heat transfer coefficient, hext (W·m−2·K−1), which only depends on convective cooling conditions.
Heat generated inside the cell, when a current flows through the cell, has two main components during normal operation. The first is the irreversible heat linked to full overpotential which includes the charge transfer processes of the reactions at the surface of the electrode particles, the mass transport by diffusion to/from the surface, and the voltage drop on the metal parts and the electrolyte. These processes are responsible for the overpotential, defined as the difference between the battery voltage (V) when current flows through the battery and the quasi-equilibrium voltage of the battery (E). This irreversible heat is defined by Equation (4) for both charge and discharge. It is an exothermic dissipative component () that heats the cell for both charge and discharge.
The heat generated reversibly is linked to the entropic change of electrode reactions. Applying basic thermodynamic relationships, the definition of the reversible component is given by Equation (5):
where the current is positive for charge and negative for discharge, and the thermal coefficient of the cell is dE/dT for both charge and discharge. If the discharge reaction of the cell is exothermic and warms the cell, the charge reaction of the cell is endothermic and cools the cell.
A part of the heat generated by the cell is transported first by conduction from inside the cell, where the temperature is Tint, to the outer surface of the cell casing, where the temperature is T, and then from the cell casing to outside the cell, where the temperature is Text. This heat flow is expressed by Equation (6):
where the internal heat transfer coefficient, hint, is considered an effective amount that absorbs any difference in the thermal conductivities that may exist in the radial direction and the axial direction of the cylindrical cell.
Inverse coefficients hint and hext are the corresponding thermal resistances Rth,int and Rth,ext, respectively. The sum of these two resistances, Rth (K/W), is defined by Equation (7):
Internal temperature (Tint), which is not measurable, is eliminated from Equation (2) using Equations (3), (6) and (7). The outer surface of the cell casing, T, and the environment temperature, Text, appear instead of Tint. Both T and Text are easily measurable. Equation (2) becomes Equation (8):
For small cells, this simplified model provides good results with little computational effort. As shown in the next section, the obtained values for thermal parameters Ccell and Rth are almost identical to those obtained with other methods in [15].
4. Results and Discussion
The time axis of Figure 1 is transformed into the SOC axis for discussing the temperature profiles. The used relationships were (Equation (9)):
where Idis = −9.2 A for the fast discharge at 4C. For the 4C-1C-CV multistage charging method Ich = 9.2 A for the CC stage at 4C, Ich = 2.3 A for the charge stage at CC stage at 1C and Ich = I(t) for the CV stage. The measured battery capacity at C/25 is taken as the maximum capacity for both charge and discharge: Qmax = 2.3 Ah. The discharge capacity at 4C is slightly lower than Qmax. The charge capacity using the 4C-1C-CV multistage charging method is almost equal to Qmax due to the final CV stage.
Figure 2a shows the measured voltage for the quasi-thermodynamic discharge at C/25, the measured voltage for a fast discharge at 4C, Idis = −9.2 A, and the internal resistance of the cell obtained by applying Equation (1). The value of the internal resistance is about 20 mΩ, except near the full discharge area (SOC = 0), where the E(SOC) − V(SOC) polarization is very high. The internal resistance presents intermediate peaks due to there being steps in the voltage curve E(SOC). These voltage steps are caused by the intercalation compounds of the cell graphite [22]. Figure 2b shows the value of the internal resistance for a 4C-1C-CV fast charge cycle. At C/25, charging curve E is slightly higher than discharging curve E due to structural hysteresis [23]. The resistance step near the full charge area (SOC = 90) shown in Figure 2b is generated by the corresponding step in the 4C-1C-CV multistage charging voltage. The resistance values are lower for charge than for discharge. For charge, the typical value for internal resistance is 15 mΩ, which is according with references [24,25]. Unlike at the end of discharge, polarization I·Rcell = V − E near full charge tends to be a very low value because the CV stage ends with a very low current value when E(SOC) ≈ V(SOC).
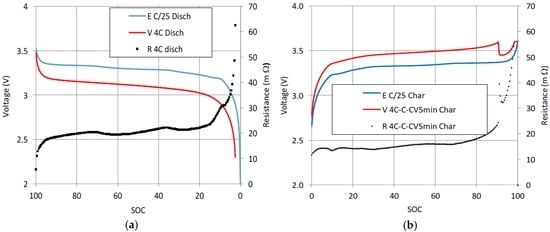
Figure 2.
(a) Internal resistance evolution profile versus state of charge of the cell, 4C discharge; and (b) 4C-1C-CV 5 min charge.
The heat generation power is shown in Figure 3a for a 4C discharge and it is shown in Figure 3b for a fast multistage charge. The reversible component of heat has been calculated by means of Equation (5). The thermal coefficient dE/dT was obtained from reference [15]. It can be observed that the reversible component of heat corresponds to an endothermic reaction (heat is absorbed) at the beginning of discharge at 4C, but it corresponds to an exothermic reaction (heat is released) when SOC is lower than 40%. When the charge begins at 4C, the reversible component of heat corresponds to an endothermic reaction. The reversible absorbed heat at the beginning of the charge at 4C is equal in magnitude to the reversible released heat at the end of discharge at 4C. Also for charge, when SOC is greater than 40%, reactions become exothermic and the reversible component of heat is released. The reversible released heat during the end charge is lower than the reversible absorbed heat during the initial discharge due to the 1C-CV charging stages. These reversible components of heat present variations related to the intercalation compounds of graphite [26]. Although at low C rates (<1C) the reversible components of heat have a considerable weight [27], it can be observed in Figure 3 that the type Joule (α·I2) irreversible components dominate the total heat generation due to the high rates (4C) used in this work. For this reason, the beginning of the 1C charge stage, see Figure 3b, is crucial to reduce the cell overheating. The heat generation of discharge at 4C interpolates well between the values of reference [16] for discharges at 3C and 6C for the same cell.
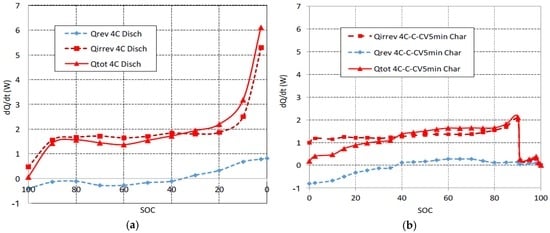
Figure 3.
(a) Reversible component of heat, irreversible component of heat and total heat evolution profile versus state of charge of the cell, 4C discharge; and (b) 4C-1C-CV 5 min charge.
The correlation between the total heat generation, the heat exchange with the environment and temperature variations can be seen in Figure 4a for the 4C discharge and in Figure 4b for the 4C-1C-CV fast charge. For discharge, there is an initial cooling followed by an approximately linear heating for both temperature and heat generation, more noticeable in the area where SOC ranges from 60% to 20%. Below 20% of SOC, the heat generation increases faster due to the high value of Rcell shown in Figure 2a, but the temperature continues to increase linearly. This fact implies an overestimation of the cell resistance or a very effective evacuation of heat to the outside. The decrease of the temperature at the start of the charge, as shown in Figure 4b, is induced by the resting period of 2 min between charge and discharge (not represented), a moderate heat generation due to the endothermic effect shown in Figure 3b and the progressive cooling to the outside.
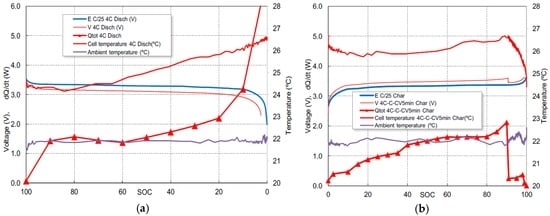
Figure 4.
(a) Voltages, case temperature and total heat evolution profile versus state of charge of the cell, 4C discharge; and (b) 4C-1C-CV 5 min charge.
For charge, the heat generation reaches the maximum when SOC is 90%, at the end of the 4C charge stage. It can be observed that the cell temperature and heat dissipation are drastically reduced when the 1C charge stage begins.
Reversible heat generation has not been directly measured in this work but has been estimated from values of dE/dT extracted from [15]. There is also uncertainty in the assessment of the SOC scale, related to the fact that discharge at 4C does not end with a CV stage and there is no guarantee that the cell charge begins at SOC = 0% for all the charging cycles. For these reasons, we made a partial adjustment of the experimental data to the thermal model. The current is zero and there is no heat generation during the resting period, 2 min, between the end of the discharge at 4C and the beginning of the charge at 4C, as shown in Figure 1. Equation (8) becomes Equation (10):
which is a first-order differential equation with a time constant τth.
The integration of Equation (10) and the adjustment of the experimental data corresponding to the resting period provides τth = 940 s.
The average thermal capacity (J/K) of the cell (C/LFP, 2.3 Ah) can be determined by means of Equation (11) [28]:
and data from Table 1. The thickness, Li, of cell materials has been obtained by dismantling the cell and measuring them. Densities (ρi) and specific heats (CP,i) have been taken from reference [16]. The cell mass was wcell = 0.075 kg. The result for the thermal capacity is Ccell = 75.6 J/K, which is in accordance with the value of 75.56 J/K of reference [15], which was measured by means of a direct adjustment of the temperature-time data in the transient area of a thermal cycle once the thermal resistances were measured in a stationary state.

Table 1.
Several properties of commercial graphite/LiFePO4 (C/LFP) 2.3Ah materials.
The total thermal resistance (internal and external) can be determined by means of the time constant of Equation (10). It has been obtained that Rth = τth/Ccell = (940 s)/(75.6 J/K) = 12.4 K/W. This value is also identical to that obtained by [15].
5. Conclusions
A study of the thermal behavior of a previous fast charge protocol developed by the authors has been made. The time patterns of the casing temperature during cycling have been qualitatively explained by means of a simple thermal model. This model assumes a uniform internal temperature in the cell. Data from the resting period of the protocol between charge and discharge has been used to adjust the model. The thickness of the cell materials measured by the authors and the thermal properties of the cell materials obtained from literature have been used to determine the thermal parameters of the model: thermal capacity and thermal resistance. For both parameters, the obtained values fully agree with published values that have been obtained with other methodologies. This fact supports the use of the simple thermal model. For future works, a non-linear adjustment of the whole temperature profile will be carried out. This adjustment will allow the two components of thermal resistance to disaggregate.
Acknowledgments
This study was funded in part by the Spanish Ministry of Science and Innovation under Grants DPI2013-46541-R and TIN2014-56967-R and by the Principality of Asturias Government under Project FC-15-GRUPIN14-073.
Author Contributions
Victor Manuel García Fernández developed the thermal model and wrote de paper with Cecilio Blanco Viejo; David Anseán González and Manuela González Vega conceived and designed the fast charging experiments; David Anseán González performed the experiments; David Anseán González and Victor Manuel García Fernández dismantled the cell; Yoana Fernández Pulido and Victor Manuel García Fernández evaluated the thermal data; Juan Carlos Alvarez Antón was consulted on the paper structure and overall idea, and discussed the results.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, J.; Yang, F.; Lai, C.; Hwang, Y.; Lee, R. A high-efficiency multimode Li-ion battery charger with variable current source and controlling previous-stage supply voltage. IEEE Trans. Ind. Electron. 2009, 56, 2469–2478. [Google Scholar] [CrossRef]
- Neubauer, J.S.; Wood, E. Will your battery survive a world with fast chargers? SAE Tech. Int. 2015. [Google Scholar] [CrossRef]
- Dunn, B.; Kamath, H.; Tarascon, J.-M. Electrical energy storage for the grid: A battery of choices. Science 2011, 334, 928–935. [Google Scholar] [CrossRef] [PubMed]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.-C.; Besenhard, J.O.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Zhang, J.; Su, L.; Li, Z.; Sun, Y.; Wu, N. The evolution of lithium-ion cell thermal safety with aging examined in a battery testing calorimeter. Batteries 2016, 2. [Google Scholar] [CrossRef]
- Braun, P.; Cho, J.; Pikul, J.; King, W.; Zhang, H. High power rechargeable batteries. Curr. Opin. Solid State Mater. Sci. 2012, 16, 186–198. [Google Scholar] [CrossRef]
- Guo, Z.; Liaw, B.Y.; Qiu, X.; Gao, L.; Zhang, C. Optimal charging method for lithium ion batteries using a universal voltage protocol accommodating aging. J. Power Sources 2015, 274, 957–964. [Google Scholar] [CrossRef]
- Notten, P.H.L.; Veld, J.H.G.O.H.; van Beek, J.R.G. Boostcharging Li-ion batteries: A challenging new charging concept. J. Power Sources 2015, 145, 89–94. [Google Scholar] [CrossRef]
- Khandelwal, A.; Hariharan, K.S.; Gambhire, P.; Kolake, S.M.; Yeo, T.; Doo, S. Thermally coupled moving boundary model for charge–discharge of LiFePO4/C cells. J. Power Sources 2015, 279, 180–196. [Google Scholar] [CrossRef]
- Anseán, D.; González, M.; Viera, J.C.; García, V.M.; Blanco, C.; Valledor, M. Fast charging technique for high power lithium iron phosphate batteries: A cycle life analysis. J. Power Sources 2013, 239, 9–15. [Google Scholar] [CrossRef]
- Anseán, D.; Dubarry, M.; Devie, A.; Liaw, B.Y.; García, V.M.; Viera, J.C.; Anse, D. Fast charging technique for high power LiFePO4 batteries: A mechanistic analysis of aging. J. Power Sources 2016, 321, 201–209. [Google Scholar] [CrossRef]
- Pals, C.R.; Newman, J. Thermal Modeling of the lithium/polymer battery. J. Electrochem. Soc. 1994, 142, 3282–3288. [Google Scholar] [CrossRef]
- Onda, K.; Ohshima, T.; Nakayama, M.; Fukuda, K.; Araki, T. Thermal behavior of small lithium-ion battery during rapid charge and discharge cycles. J. Power Sources 2006, 158, 535–542. [Google Scholar] [CrossRef]
- Inui, Y.; Kobayashi, Y.; Watanabe, Y.; Watase, Y.; Kitamura, Y. Simulation of temperature distribution in cylindrical and prismatic lithium ion secondary batteries. Energy Convers. Manag. 2007, 48, 2103–2109. [Google Scholar] [CrossRef]
- Forgez, C.; Vinh, D.; Friedrich, G.; Morcrette, M.; Delacourt, C. Thermal modeling of a cylindrical LiFePO4/graphite lithium-ion battery. J. Power Sources 2010, 195, 2961–2968. [Google Scholar] [CrossRef]
- Ye, Y.; Saw, L.H.; Shi, Y.; Somasundaram, K.; Tay, A.A.O. Effect of thermal contact resistances on fast charging of large format lithium ion batteries. Electrochim. Acta 2014, 134, 327–337. [Google Scholar] [CrossRef]
- Anseán, D.; García, V.M.; González, M.; Viera, J.C.; Antón, J.C.; Blanco, C. Evaluation of LiFePO4 batteries for electric vehicle applications. IEEE Trans. Ind. Appl. 2015, 51, 1855–1863. [Google Scholar] [CrossRef]
- Electric Vehicle Battery Test Procedures Manual, Revision 2; United States Advanced Battery Consortium (USABC) and US Department of Energy, Idaho National Laboratory: Idaho Falls, ID, USA, 1996.
- Dubarry, M.; Liaw, B.Y. Identify capacity fading mechanism in a commercial LiFePO4 cell. J. Power Sources 2009, 194, 541–549. [Google Scholar] [CrossRef]
- Bloom, I.; Jones, S.A.; Polzin, E.G.; Battaglia, V.S.; Henriksen, G.L.; Motloch, C.G.; Wright, R.B.; Jungst, R.G.; Case, H.L.; Doughty, D.H. Mechanisms of impedance rise in high-power, lithium-ion cells. J. Power Sources 2002, 111, 152–159. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Liaw, B.Y. Synthesize battery degradation modes via a diagnostic and prognostic model. J. Power Sources 2012, 219, 204–216. [Google Scholar] [CrossRef]
- Dahn, J. Phase diagram of LixC6. Phys. Rev. B 1991, 44, 9170–9177. [Google Scholar] [CrossRef]
- Dreyer, W.; Jamnik, J.; Guhlke, C.; Huth, R.; Moskon, J.; Gaberscek, M. The thermodynamic origin of hysteresis in insertion batteries. Nat. Mater. 2010, 9, 448–453. [Google Scholar] [CrossRef] [PubMed]
- Roscher, M.A.; Vetter, J.; Sauer, D.U. Characterisation of charge and discharge behaviour of lithium ion batteries with olivine based cathode active material. J. Power Sources 2009, 191, 582–590. [Google Scholar] [CrossRef]
- Anseán, D.; García, V.M.; González, M.; Viera, J.C.; Blanco, C.; Antuña, J.L. DC Internal Resistance during Charge: Analysis and Study on LiFePO4 Batteries. In Proceedings of the 2013 World Electric Vehicle Symposium and Exhibition (EVS27), Barcelona, Spain, 17–20 November 2013.
- Reynier, Y.; Yazami, R.; Fultz, B. The entropy and enthalpy of lithium intercalation into graphite. J. Power Sources 2003, 119–121, 850–855. [Google Scholar] [CrossRef]
- Khandelwal, A.; Hariharan, K.S.; Kumar, V.S.; Gambhire, P.; Kolake, S.M.; Oh, D.; Doo, S. Generalized moving boundary model for charge–discharge of LiFePO4/C cells. J. Power Sources 2014, 248, 101–114. [Google Scholar] [CrossRef]
- Chen, S.C.; Wan, C.C.; Wang, Y.Y. Thermal analysis of lithium-ion batteries. J. Power Sources 2005, 140, 111–124. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).