Experimental Testing and Modeling of Li-Ion Battery Performance Based on IEC 62660-1 Standard
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Experimental Equipment
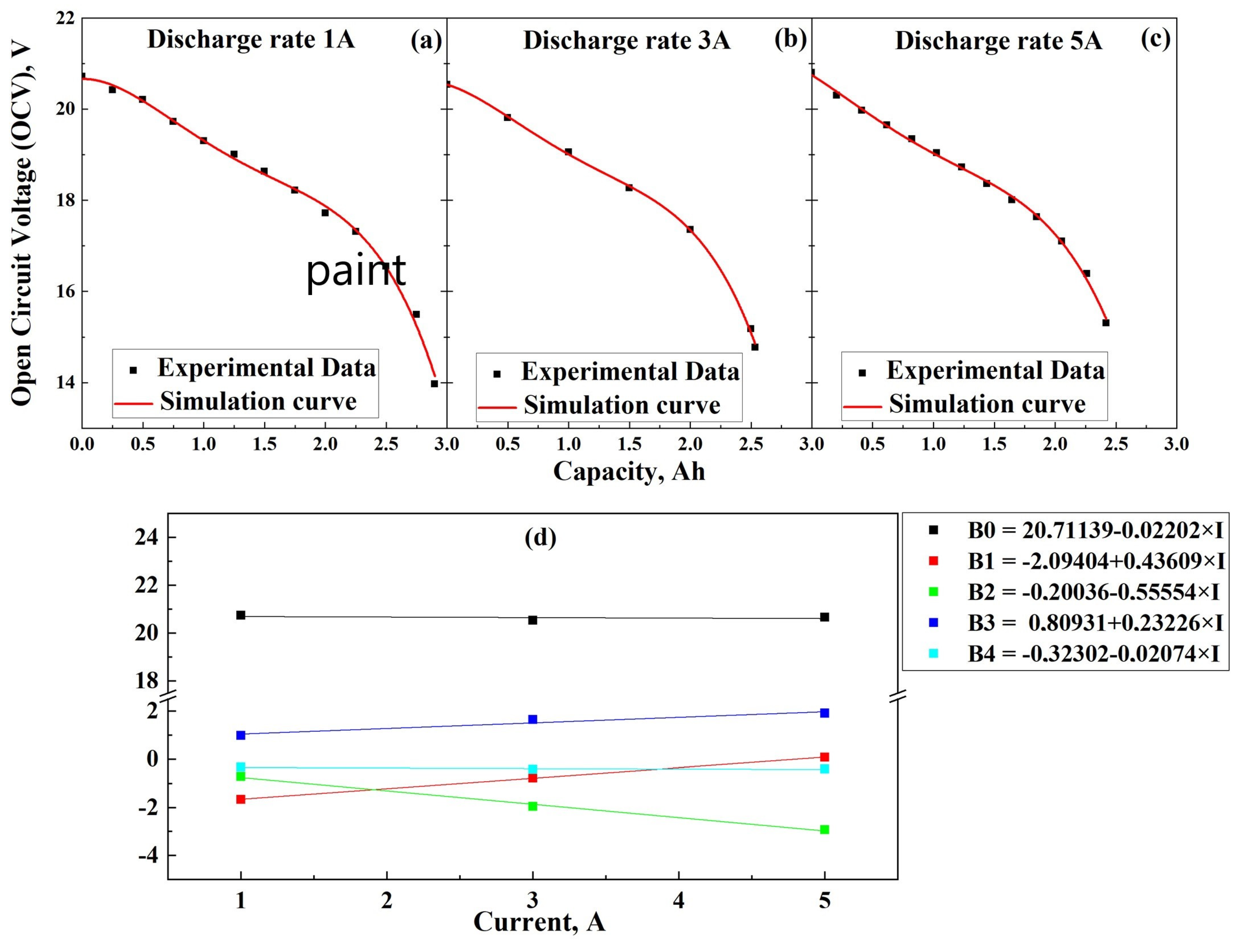
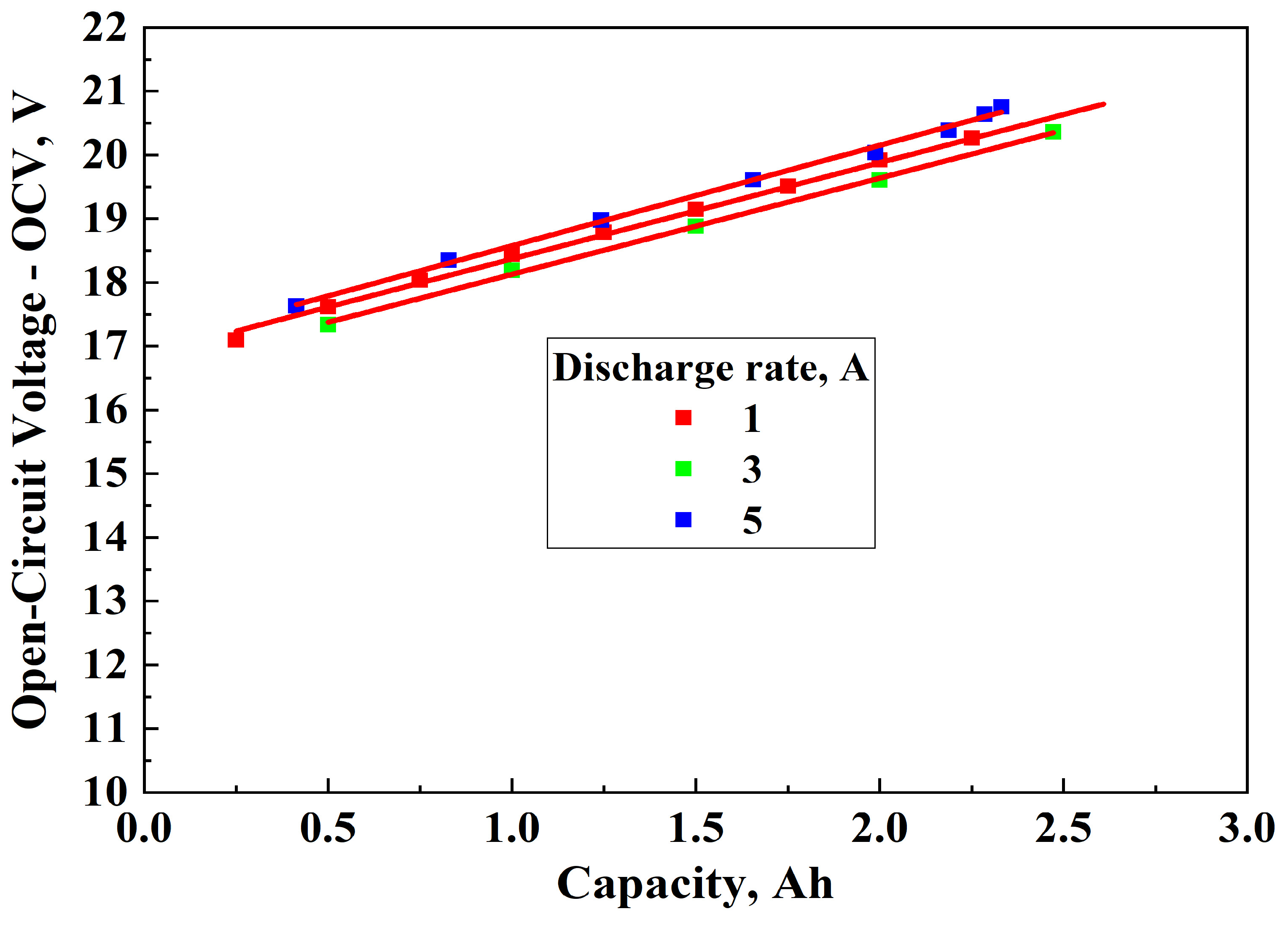
2.2. Determination of OCV
2.3. Experimental Model
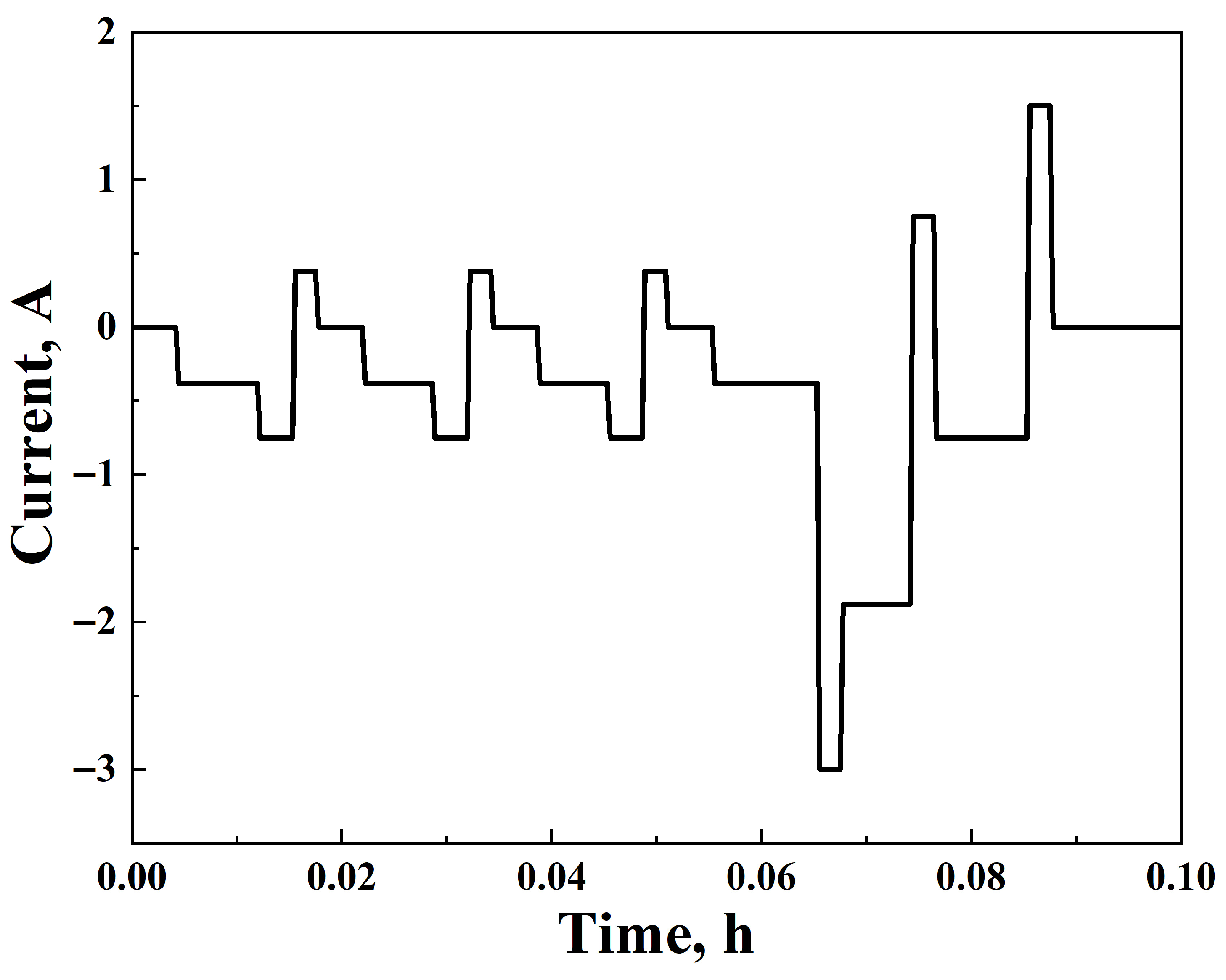
2.4. IEC 62660-1 Standard
- The ambient temperature shall be 25 °C or 45 °C.
- The cell should be fully discharged by the method specified by the manufacturer.
- The cells should be fully charged by the method specified by the manufacturer.
- Discharge the cells following the Dynamic Discharged Profile B, given in [17], one time.
- Discharge the cells following the Dynamic Discharge Profile A, given in [17], until the overall discharge capacity reaches the equivalent of 80% of the initial capacity.
- After the repetition of the steps above for 28 test days, the cells’ performance should be evaluated.
3. Results
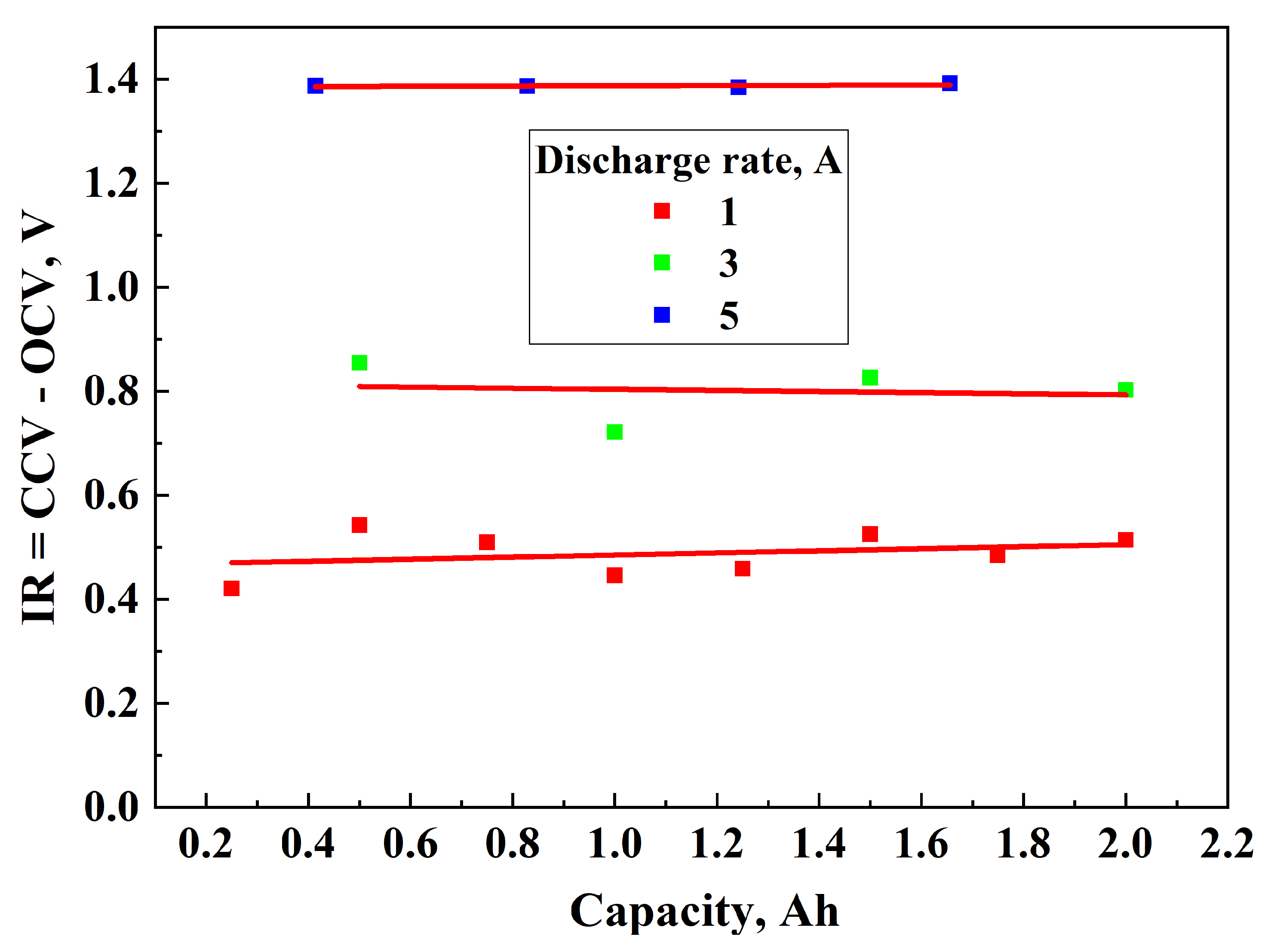
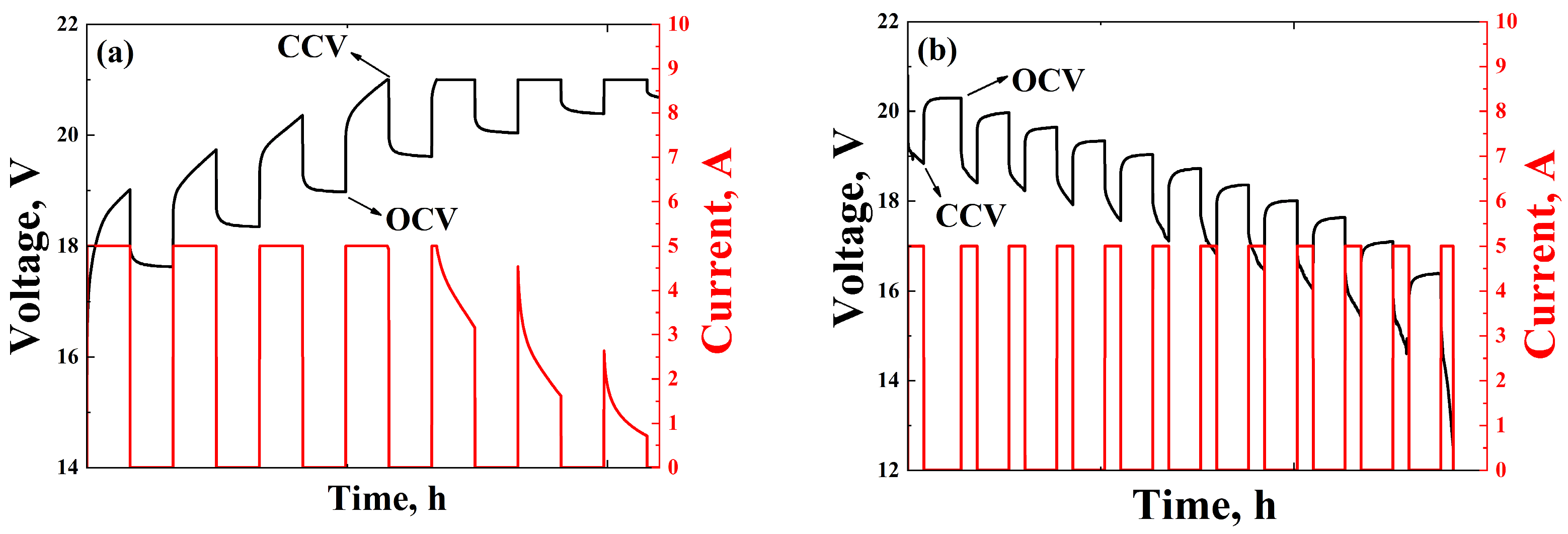
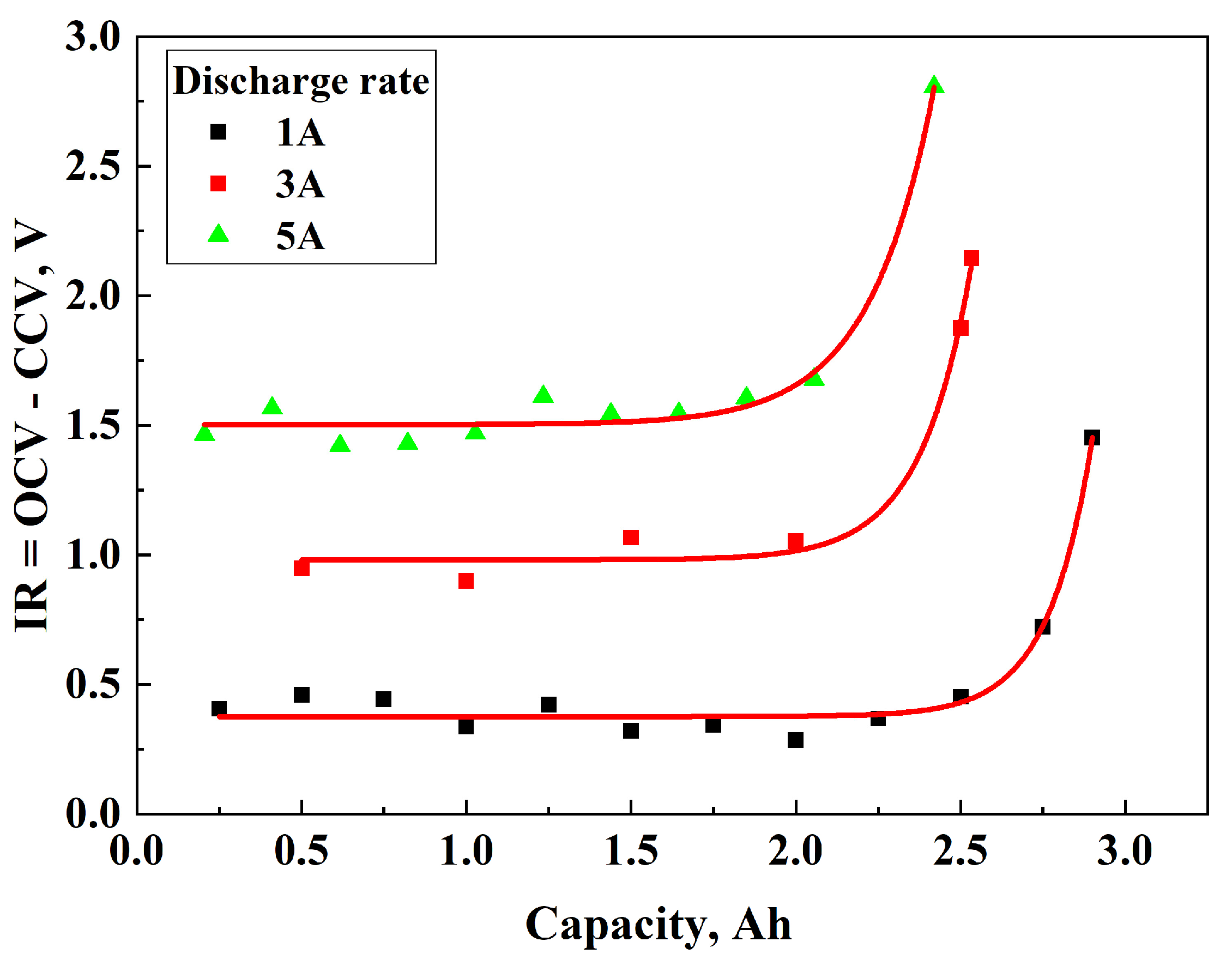
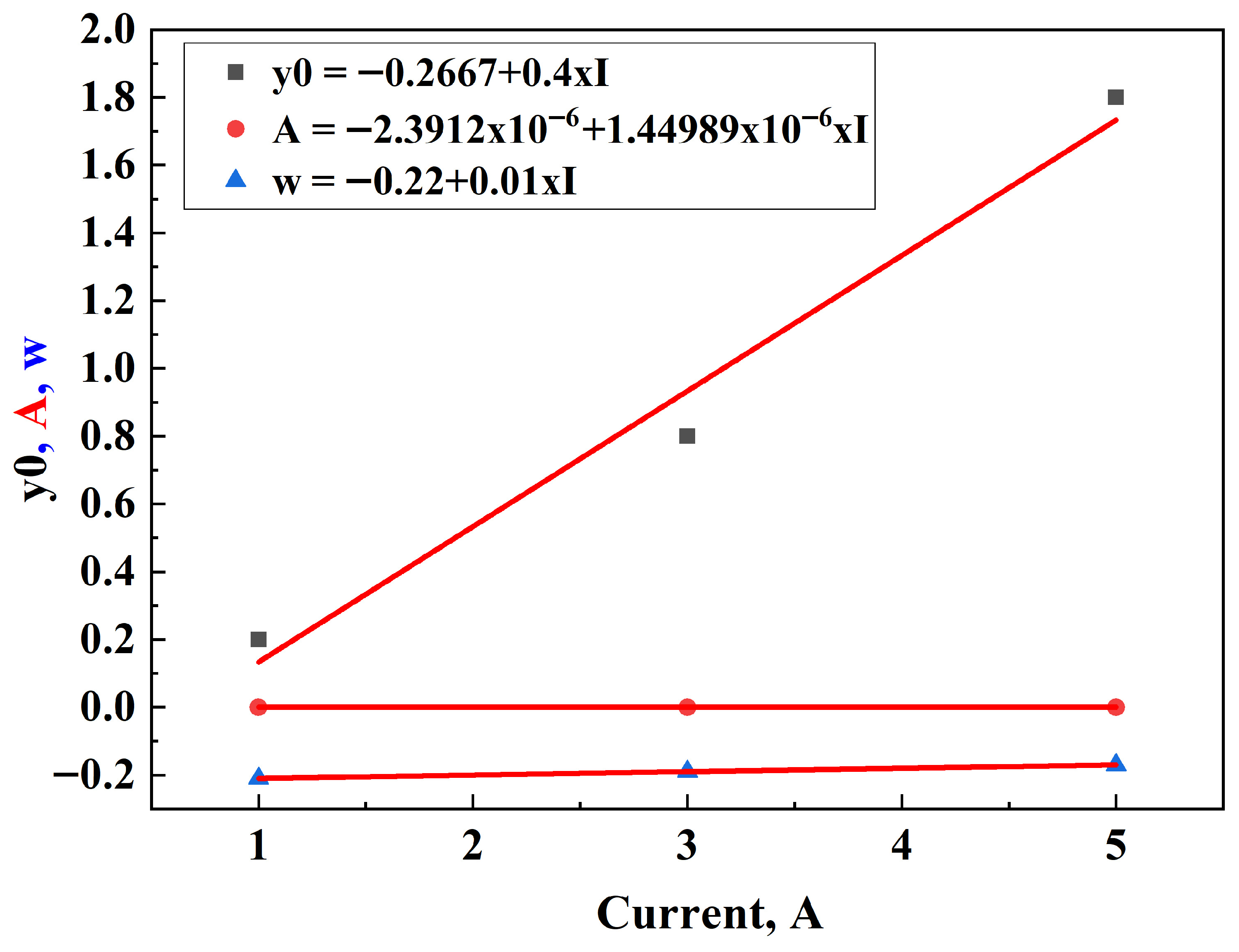
3.1. Determination of OCV and IR During Discharging
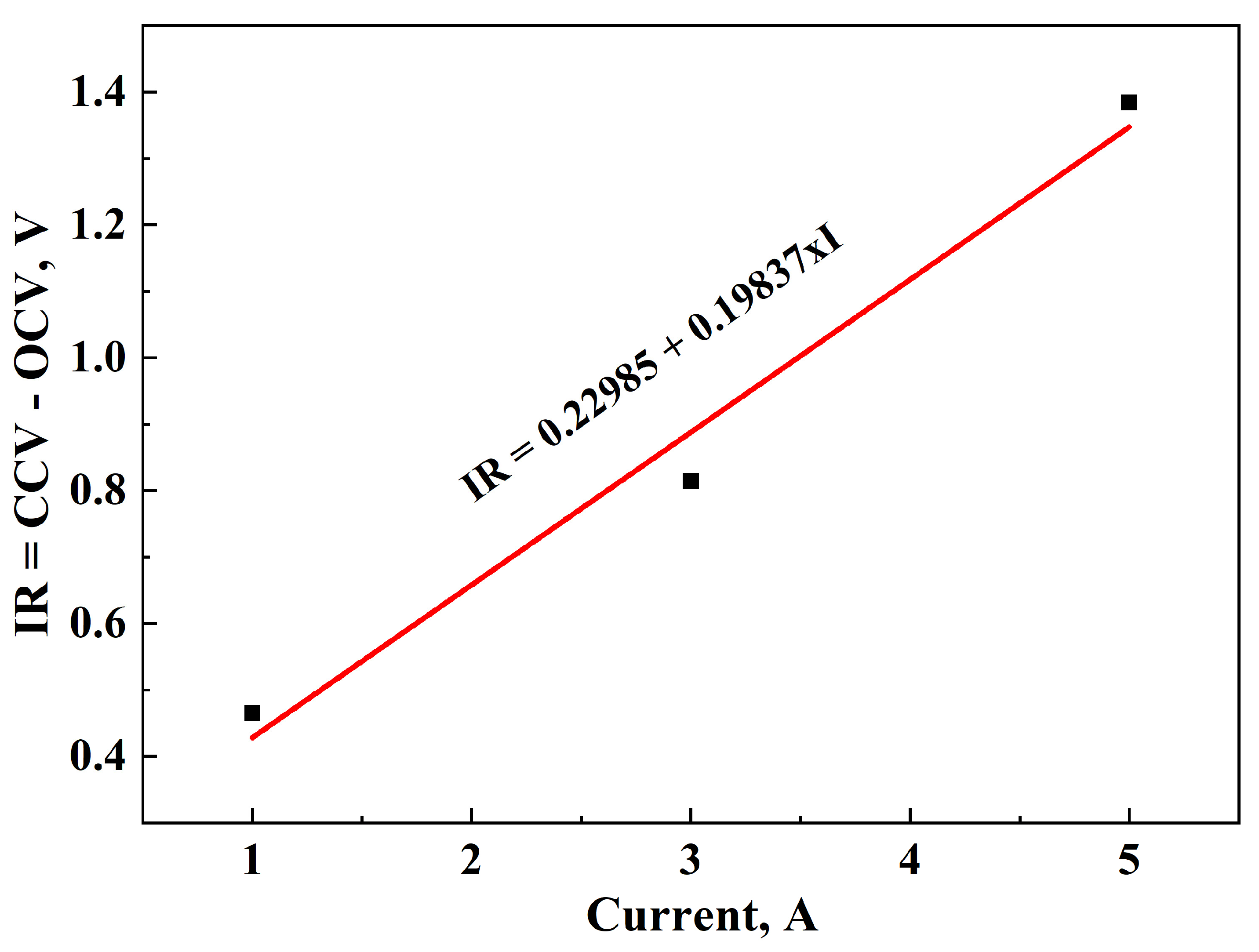
3.2. Determination of OCVch and IR During Charging
- 0.46504 V at 1A;
- 0.81425 V at 3A;
- 1.38445 V at 5A.
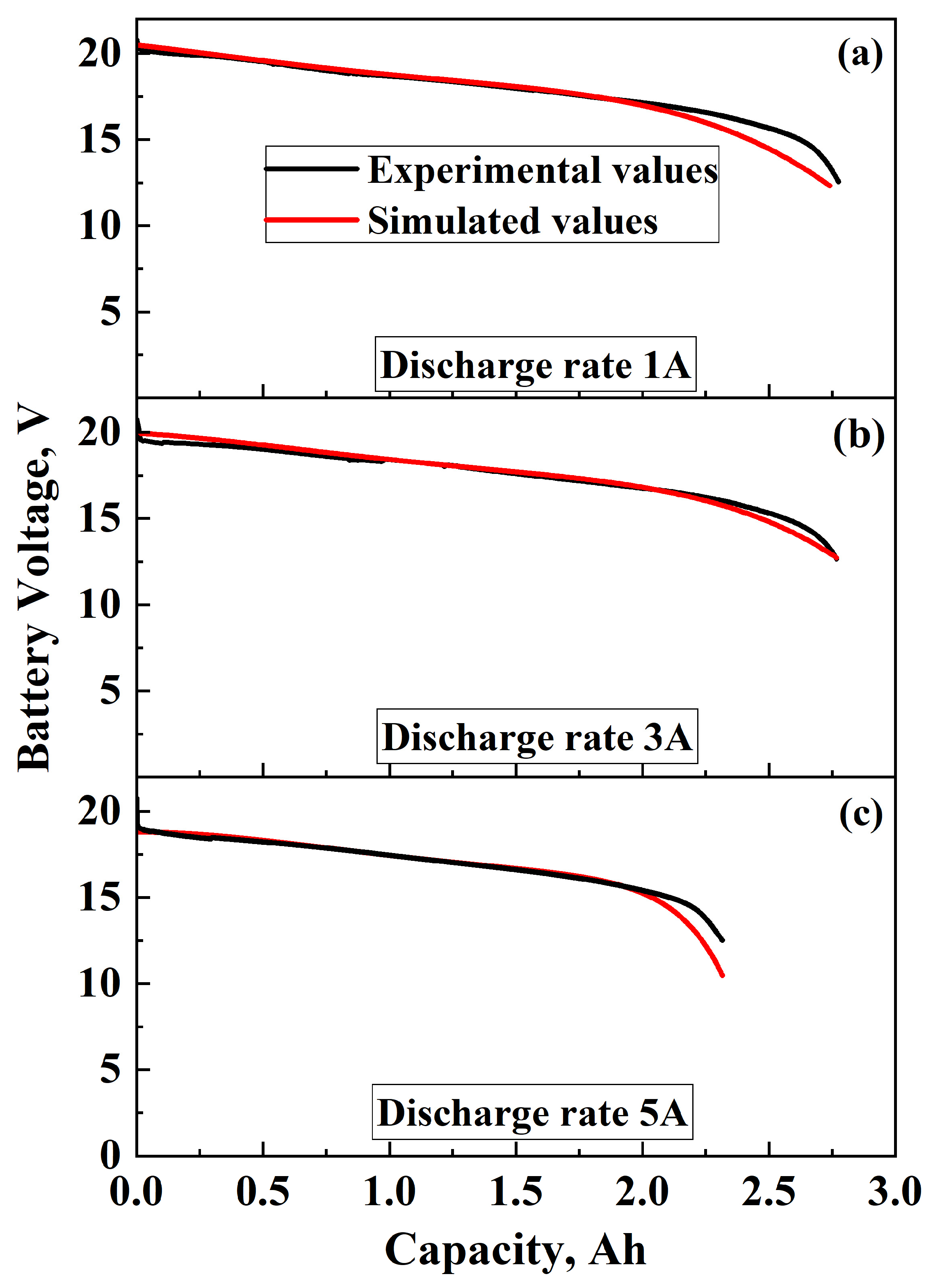
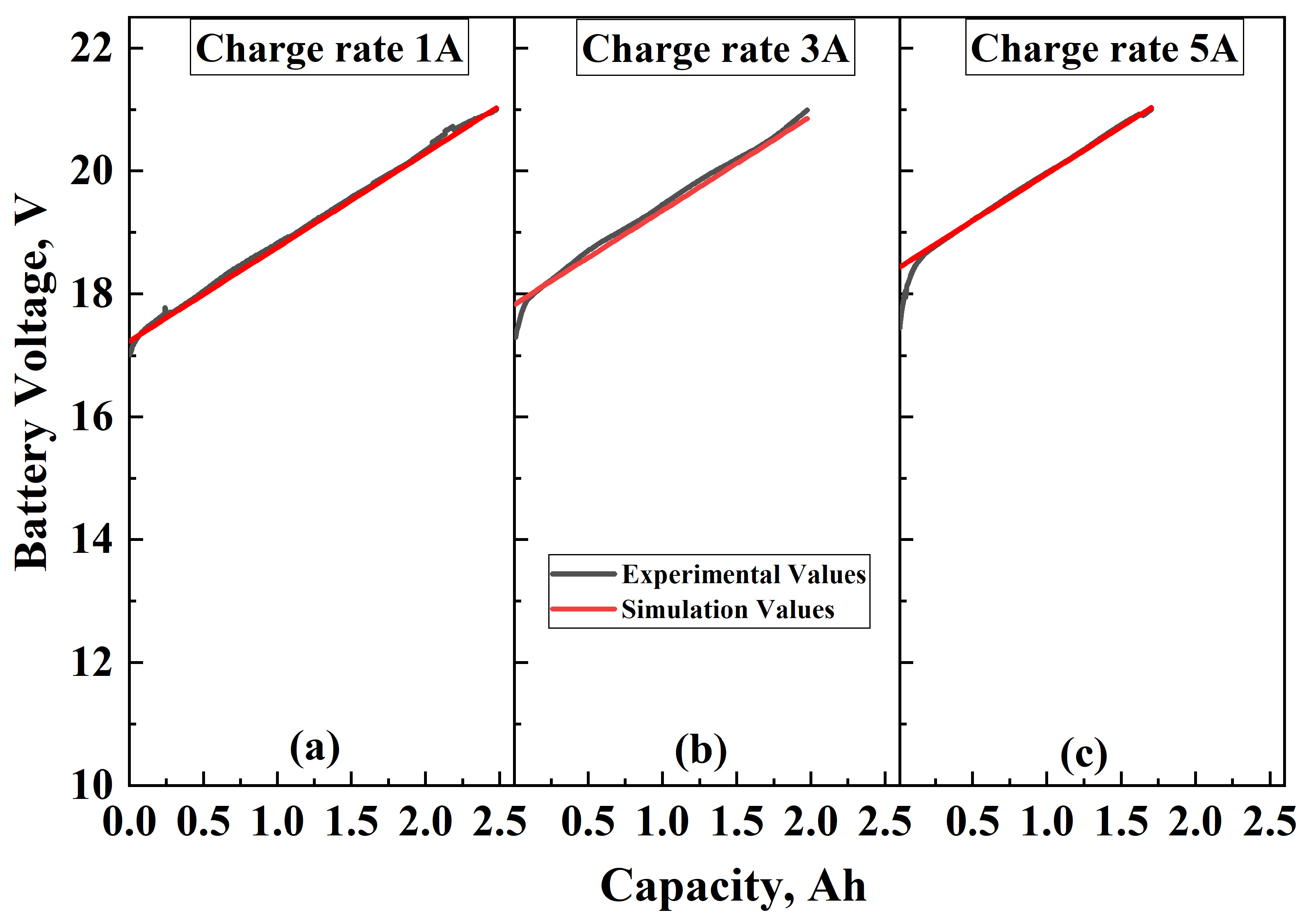
3.3. Model Validation
3.3.1. Discharging
3.3.2. Charging
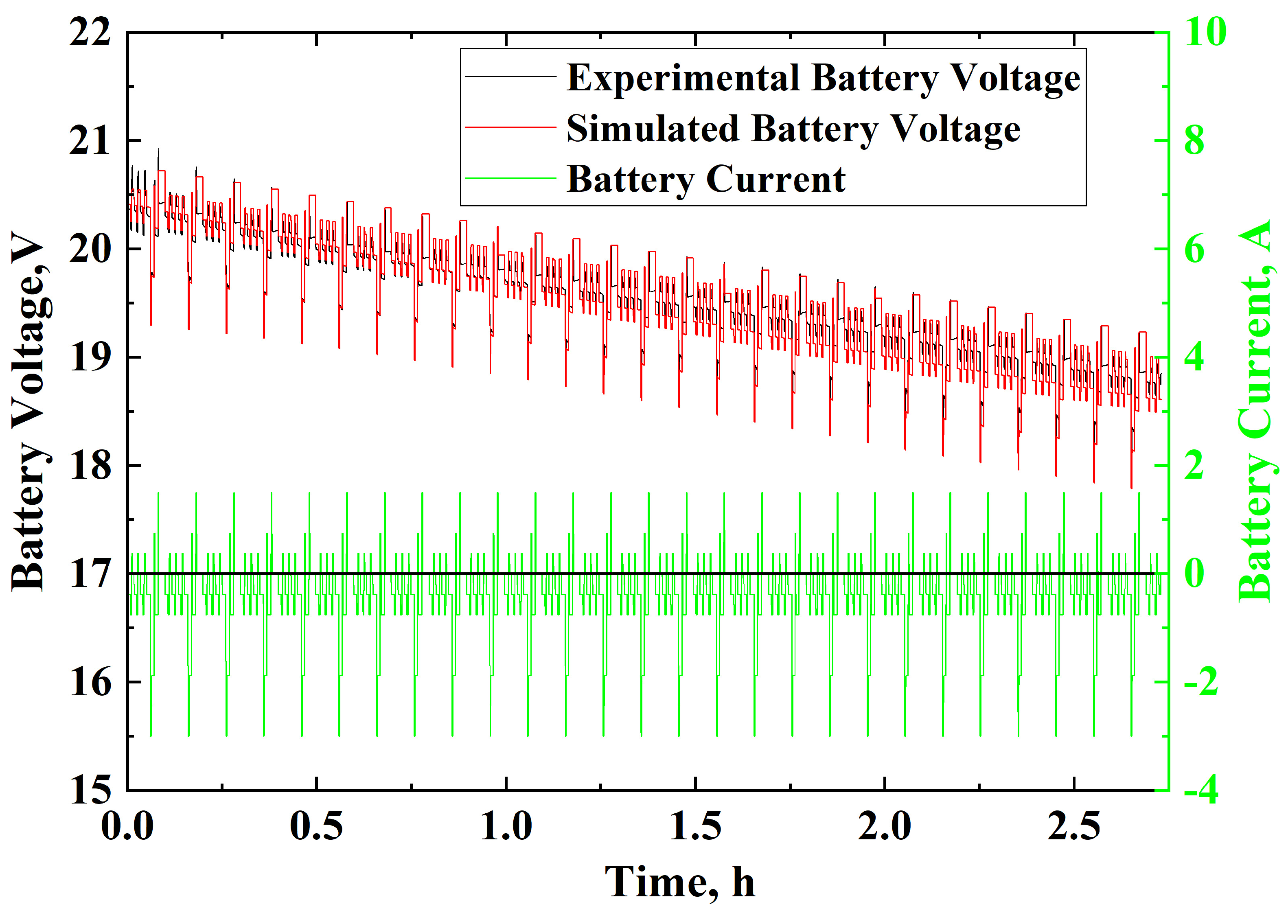
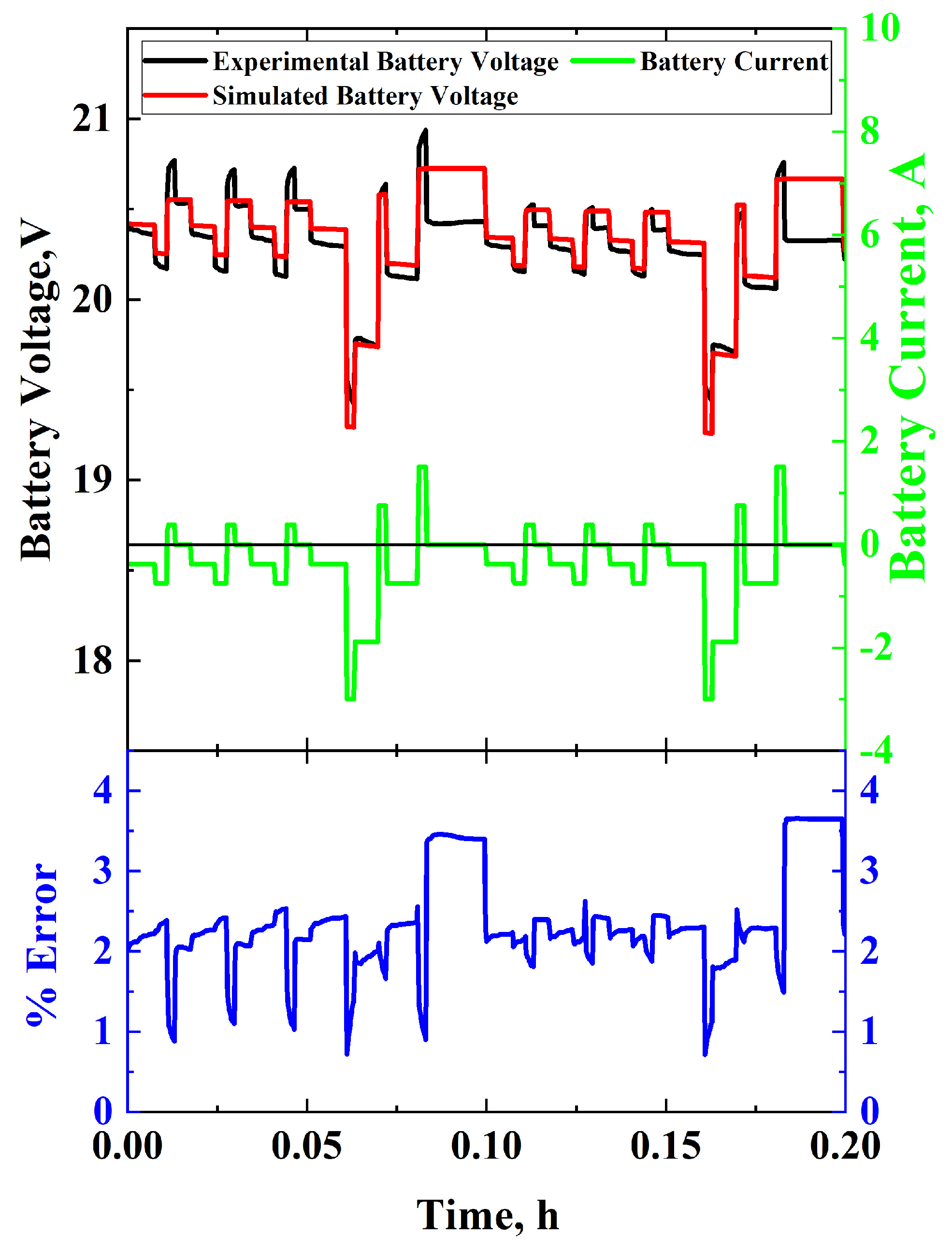
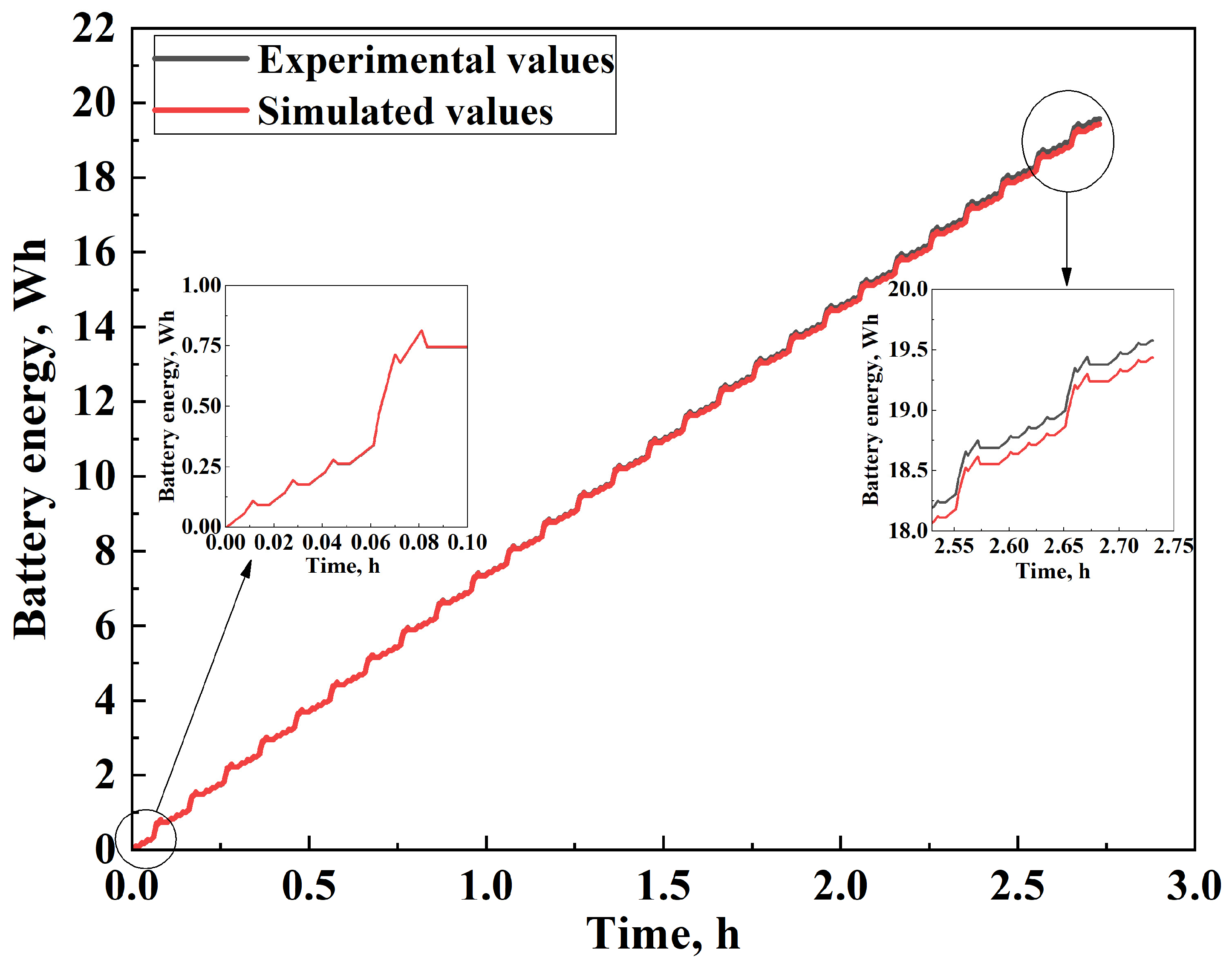
3.3.3. IEC 62660-1 Standard Simulation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BEV | Battery Electric Vehicle |
| BMS | Battery Management System |
| CCV | Closed-Circuit Voltage |
| EV | Electric Vehicle |
| OCV | Open-Circuit Voltage |
| P2D | Pseudo-Two-Dimensional |
| SoC | State of Charge |
References
- Diana Gragg Fast Facts About Energy for Transportation 2025. Available online: https://understand-energy.stanford.edu/energy-services/energy-transportation#fast-facts-header (accessed on 6 August 2025).
- Al-Refai, A.; Alkhateeb, A.; Dalala, Z.M. Enhancing the LCO 18,650 Battery Charging/Discharging Using Temperature and Electrical Based Model. Batteries 2022, 8, 199. [Google Scholar] [CrossRef]
- Tran, M.-K.; DaCosta, A.; Mevawalla, A.; Panchal, S.; Fowler, M. Comparative Study of Equivalent Circuit Models Performance in Four Common Lithium-Ion Batteries: LFP, NMC, LMO, NCA. Batteries 2021, 7, 51. [Google Scholar] [CrossRef]
- Rotas, R.; Iliadis, P.; Nikolopoulos, N.; Rakopoulos, D.; Tomboulides, A. Dynamic Battery Modeling for Electric Vehicle Applications. Batteries 2024, 10, 188. [Google Scholar] [CrossRef]
- Baccouche, I.; Jemmali, S.; Manai, B.; Omar, N.; Amara, N.E.B. Improved OCV Model of a Li-Ion NMC Battery for Online SOC Estimation Using the Extended Kalman Filter. Energies 2017, 10, 764. [Google Scholar] [CrossRef]
- Khan, M.I.; Gilani, R.; Hafeez, J.; Ayoub, R.; Zahoor, I.; Saira, G. Chapter 3—Advantages and Disadvantages of Lithium-Ion Batteries. In Nanostructured Lithium-Ion Battery Materials; Micro and Nano Technologies; Thomas, S., Gueye, A.B., Savadogo, O., Maria, H.J., Eds.; Elsevier: Amsterdam, The Netherlands, 2025; pp. 47–64. ISBN 978-0-443-13338-1. [Google Scholar]
- Tamilselvi, S.; Gunasundari, S.; Karuppiah, N.; Razak Rk, A.; Madhusudan, S.; Nagarajan, V.M.; Sathish, T.; Shamim, M.Z.M.; Saleel, C.A.; Afzal, A. A Review on Battery Modelling Techniques. Sustainability 2021, 13, 10042. [Google Scholar] [CrossRef]
- B S, S.; Hampannavar, S.; B, D.; Bairwa, B. Applications of Battery Management System (BMS) in Sustainable Transportation: A Comprehensive Approach from Battery Modeling to Battery Integration to the Power Grid. World Electr. Veh. J. 2022, 13, 80. [Google Scholar] [CrossRef]
- Tremblay, O.; Dessaint, L.-A.; Dekkiche, A.-I. A Generic Battery Model for the Dynamic Simulation of Hybrid Electric Vehicles. In Proceedings of the 2007 IEEE Vehicle Power and Propulsion Conference, Arlington, TX, USA, 9–12 September 2007; pp. 284–289. [Google Scholar]
- Campagna, N.; Castiglia, V.; Miceli, R.; Mastromauro, R.A.; Spataro, C.; Trapanese, M.; Viola, F. Battery Models for Battery Powered Applications: A Comparative Study. Energies 2020, 13, 4085. [Google Scholar] [CrossRef]
- Han, S.; Tang, Y.; Khaleghi Rahimian, S. A Numerically Efficient Method of Solving the Full-Order Pseudo-2-Dimensional (P2D) Li-Ion Cell Model. J. Power Sources 2021, 490, 229571. [Google Scholar] [CrossRef]
- Jokar, A.; Rajabloo, B.; Désilets, M.; Lacroix, M. Review of Simplified Pseudo-Two-Dimensional Models of Lithium-Ion Batteries. J. Power Sources 2016, 327, 44–55. [Google Scholar] [CrossRef]
- Wickramanayake, T.; Javadipour, M.; Mehran, K. A Novel Solver for an Electrochemical–Thermal Ageing Model of a Lithium-Ion Battery. Batteries 2024, 10, 126. [Google Scholar] [CrossRef]
- Li, S.; Ke, B. Study of Battery Modeling Using Mathematical and Circuit Oriented Approaches. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–8. [Google Scholar]
- Zhang, Z.; Chen, S.; Lu, L.; Han, X.; Li, Y.; Chen, S.; Wang, H.; Lian, Y.; Ouyang, M. High-Precision and Robust SOC Estimation of LiFePO4 Blade Batteries Based on the BPNN-EKF Algorithm. Batteries 2023, 9, 333. [Google Scholar] [CrossRef]
- Pepó, M.; Fullér, S.; Cseke, T.; Weltsch, Z. Advances in Standardised Battery Testing for Enhanced Safety and Innovation in Electric Vehicles: A Comprehensive Review. Batteries 2025, 11, 157. [Google Scholar] [CrossRef]
- IEC 62660-1:2018; Secondary Lithium-Ion Cells for the Propulsion of Electric Road Vehicles—Part 1: Performance Testing. The International Electrotechnical Commission (IEC): Geneva, Switzerland, 2018. Available online: https://webstore.iec.ch/en/publication/28965 (accessed on 6 May 2025).
- Estaller, J.; Kersten, A.; Kuder, M.; Thiringer, T.; Eckerle, R.; Weyh, T. Overview of Battery Impedance Modeling Including Detailed State-of-the-Art Cylindrical 18650 Lithium-Ion Battery Cell Comparisons. Energies 2022, 15, 3822. [Google Scholar] [CrossRef]
- Zatta, N.; De Cesaro, B.; Dal Cin, E.; Carraro, G.; Cristofoli, G.; Trovò, A.; Lazzaretto, A.; Guarnieri, M. Testing and Characterizing Commercial 18650 Lithium-Ion Batteries. Batteries 2024, 10, 248. [Google Scholar]
- Marzook, M.W.; Eaton, J.; Samieian, M.A.; Patel, Y.; Offer, G.; Marinescu, M. Performance Benchmarking of Lithium-Ion Batteries: The Effect of Test Conditions on the Down-Selection of Cylindrical Cells. SSRN 2023. [Google Scholar] [CrossRef]
- Motorcycle|Other Mobility. Available online: https://www.murata.com/en-eu/apps/mobility/other/motorcycle (accessed on 7 July 2025).
- Kawahara, Y.; Sakabe, K.; Nakao, R.; Tsuru, K.; Okawa, K.; Aoshima, Y.; Kudo, A.; Emori, A. Development of Status Detection Method of Lithium-Ion Rechargeable Battery for Hybrid Electric Vehicles. J. Power Sources 2021, 481, 228760. [Google Scholar] [CrossRef]
- Yu, Q.-Q.; Xiong, R.; Wang, L.-Y.; Lin, C. A Comparative Study on Open Circuit Voltage Models for Lithium-Ion Batteries. Chin. J. Mech. Eng. 2018, 31, 65. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Zhang, L.; Liu, S.; Wang, L.; Loh, P.C. A Generalized SOC-OCV Model for Lithium-Ion Batteries and the SOC Estimation for LNMCO Battery. Energies 2016, 9, 900. [Google Scholar] [CrossRef]
- Zhang, R.; Xia, B.; Li, B.; Cao, L.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W.; Wang, M. A Study on the Open Circuit Voltage and State of Charge Characterization of High Capacity Lithium-Ion Battery Under Different Temperature. Energies 2018, 11, 2408. [Google Scholar] [CrossRef]
- Somakettarin, N.; Funaki, T. Study on Factors for Accurate Open Circuit Voltage Characterizations in Mn-Type Li-Ion Batteries. Batteries 2017, 3, 8. [Google Scholar] [CrossRef]
- Liu, S.; Chen, J.; Zhang, C.; Jin, L.; Yang, Q. Experimental Study on Lithium-Ion Cell Characteristics at Different Discharge Rates. J. Energy Storage 2022, 45, 103418. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, J.; Liu, D.; Liu, Q.; Jiang, Y.; Wang, X.; Liu, H.; Tao, S.; Wei, X.; Schade, W.; et al. Internal Temperature Evolution of Lithium-Ion Battery over Long-Term Cycling via Advanced Fiber Sensing. J. Power Sources 2025, 652, 237604. [Google Scholar] [CrossRef]
- Jow, T.R.; Delp, S.A.; Allen, J.L.; Jones, J.-P.; Smart, M.C. Factors Limiting Li+ Charge Transfer Kinetics in Li-Ion Batteries. J. Electrochem. Soc. 2018, 165, A361. [Google Scholar] [CrossRef]


| Battery Voltage (V) | Battery Capacity | Fast Charge Current (A) | Discharge Current (A) | |||
|---|---|---|---|---|---|---|
| Min. | Typ. | Max. | Ah | Wh | Max. | Max. |
| 2.5 | 3.6 | 4.2 | 3 | 10.8 | 5 | 30 |
| 1A | 3A | 5A | |
|---|---|---|---|
| 20.74531 | 20.53343 | 20.65722 | |
| −1.66244 | −0.77681 | 0.08191 | |
| −0.71062 | −1.95754 | −2.93278 | |
| 0.97554 | 1.63815 | 1.90457 | |
| −0.3205 | −0.43178 | −0.40347 |
| 1A | 3A | 5A | |
|---|---|---|---|
| 0.37647 | 0.98062 | 1.50247 | |
| A | 4.20475 | 7.4997 | 5.76682 |
| w | −0.13387 | −0.15315 | −0.19628 |
| 1A | 3A | 5A | Average | |
|---|---|---|---|---|
| a | 16.85926 | 16.62012 | 17 | 16.82646 |
| b | 1.51014 | 1.50833 | 1.5753 | 1.5313 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Voltsi, Z.; Elmasides, C. Experimental Testing and Modeling of Li-Ion Battery Performance Based on IEC 62660-1 Standard. Batteries 2025, 11, 314. https://doi.org/10.3390/batteries11080314
Voltsi Z, Elmasides C. Experimental Testing and Modeling of Li-Ion Battery Performance Based on IEC 62660-1 Standard. Batteries. 2025; 11(8):314. https://doi.org/10.3390/batteries11080314
Chicago/Turabian StyleVoltsi, Zoi, and Costas Elmasides. 2025. "Experimental Testing and Modeling of Li-Ion Battery Performance Based on IEC 62660-1 Standard" Batteries 11, no. 8: 314. https://doi.org/10.3390/batteries11080314
APA StyleVoltsi, Z., & Elmasides, C. (2025). Experimental Testing and Modeling of Li-Ion Battery Performance Based on IEC 62660-1 Standard. Batteries, 11(8), 314. https://doi.org/10.3390/batteries11080314







