Accurate Prediction of Voltage and Temperature for a Sodium-Ion Pouch Cell Using an Electro-Thermal Coupling Model
Abstract
1. Introduction
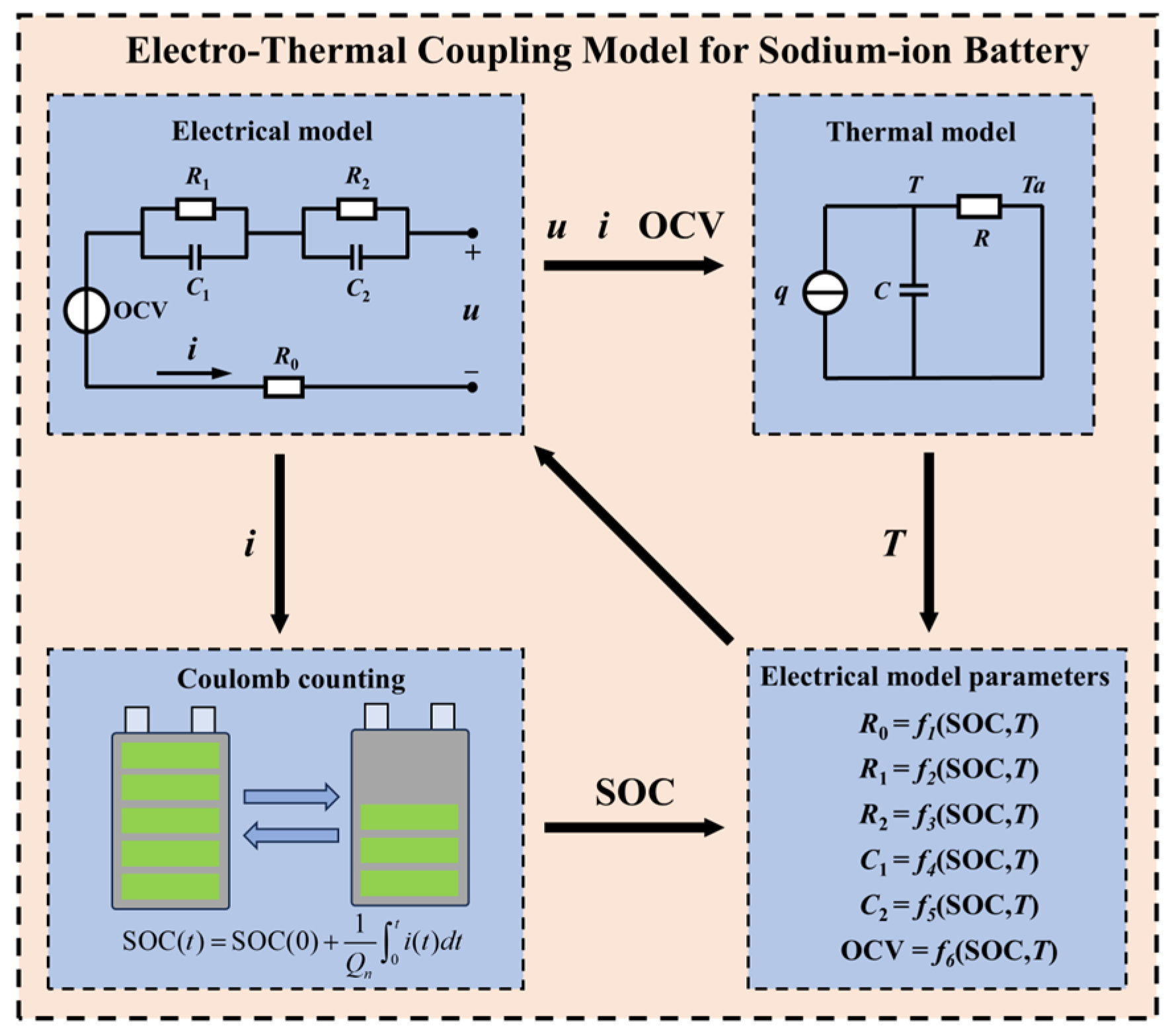
2. Electro–Thermal Modeling
2.1. Electrical Model
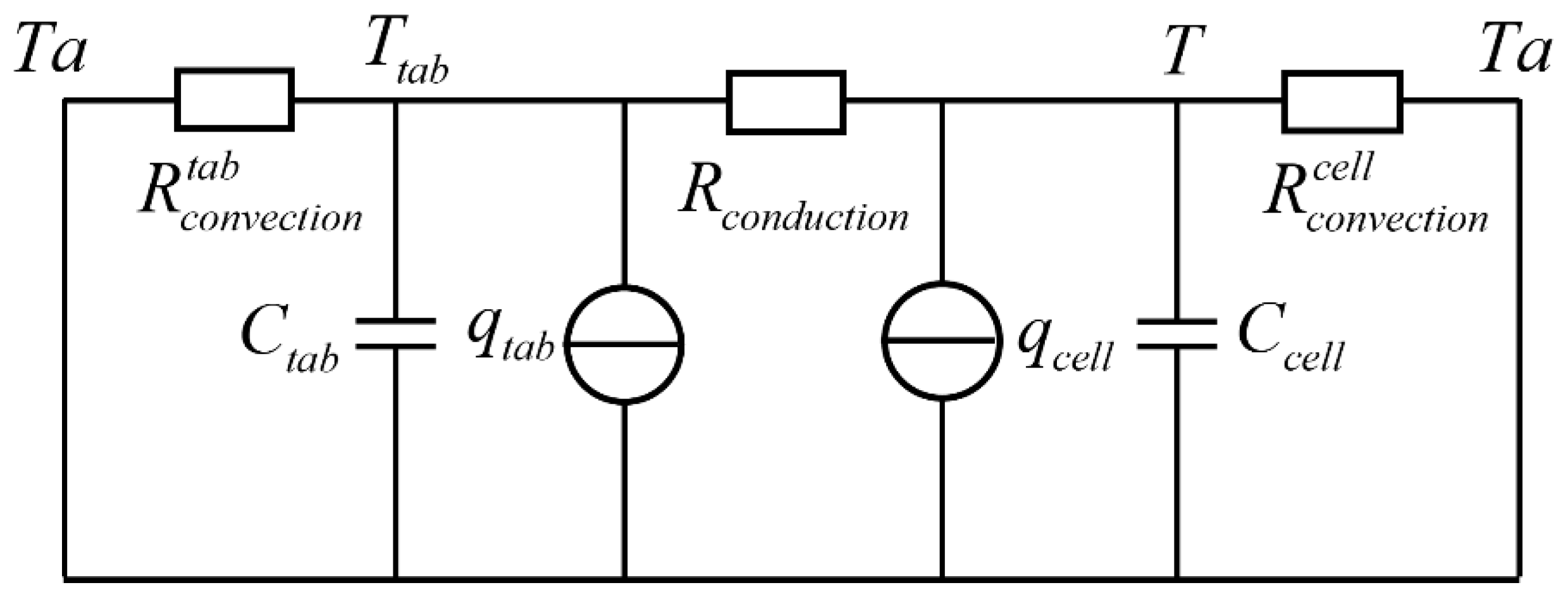
2.2. Thermal Model
3. Parameter Identification for the Equivalent Circuit Model
3.1. Experimental Setup and Test Procedure
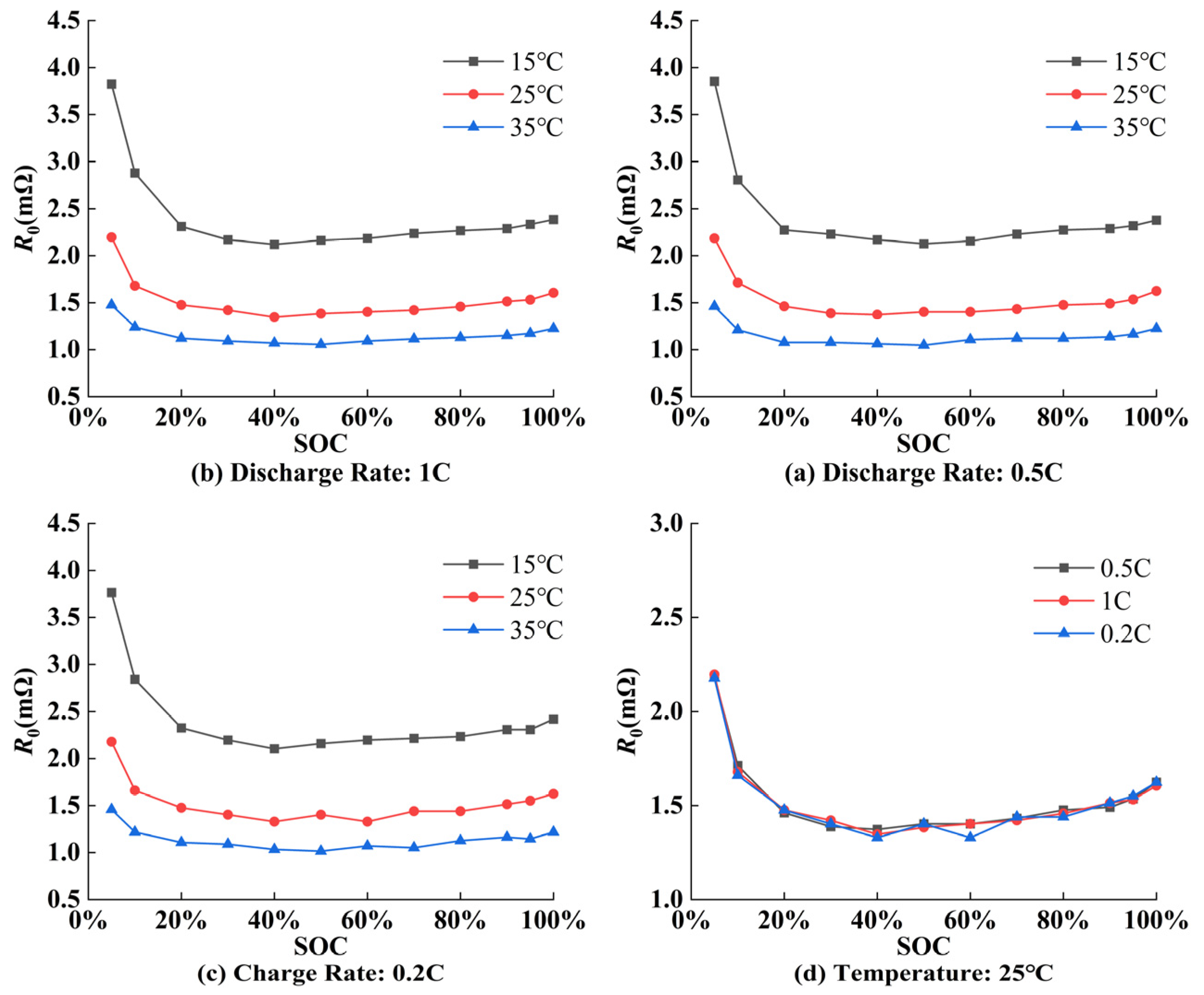
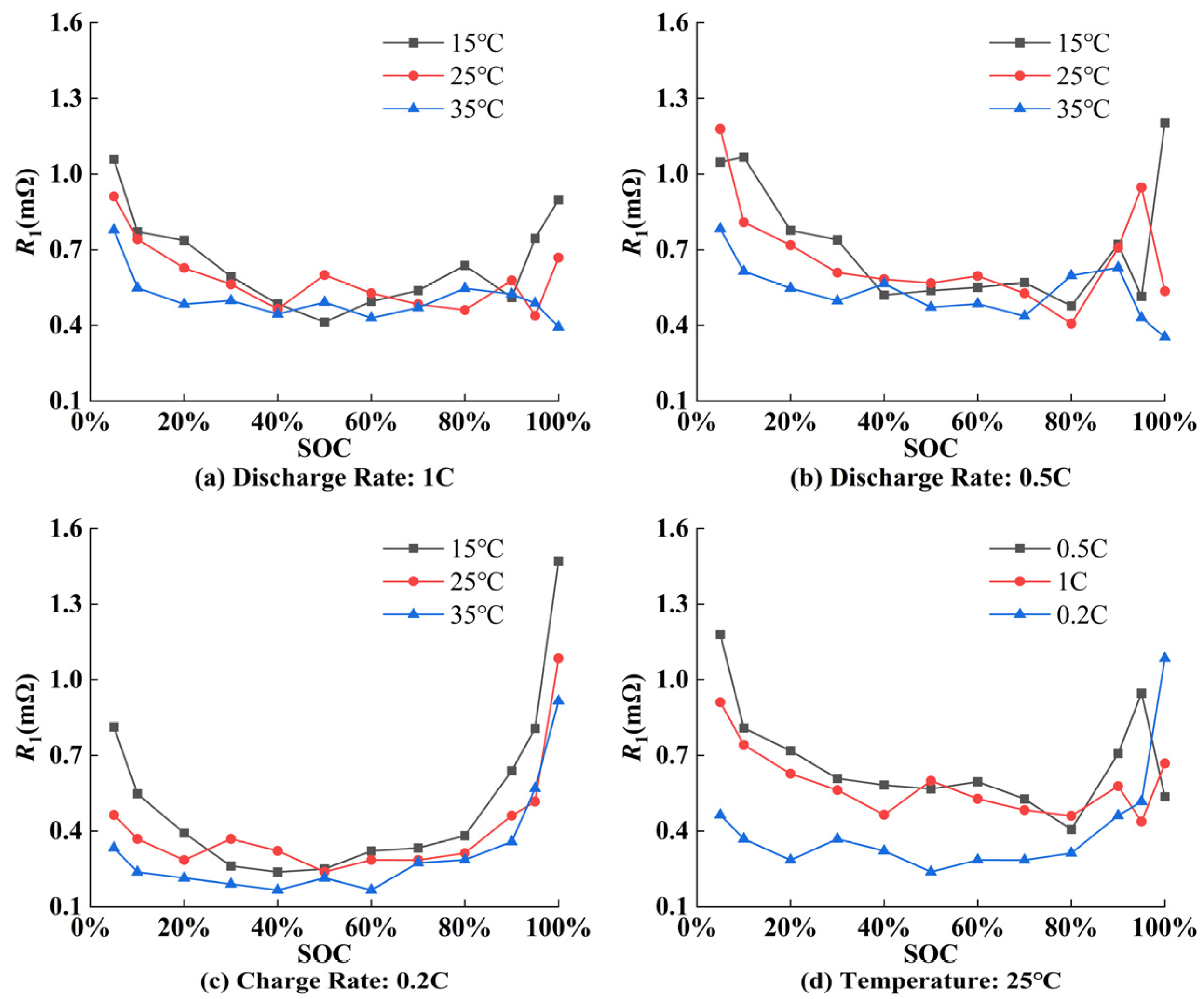
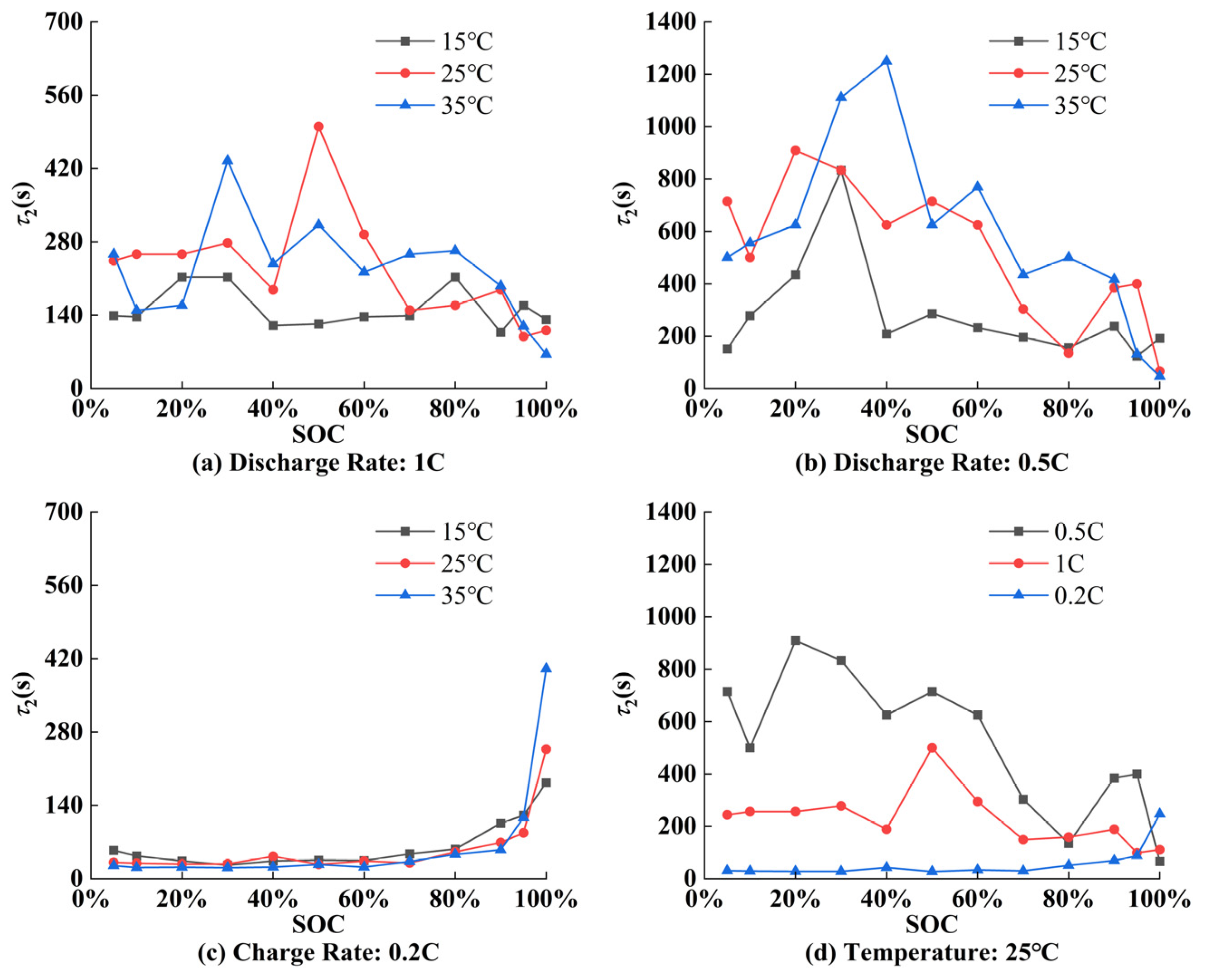
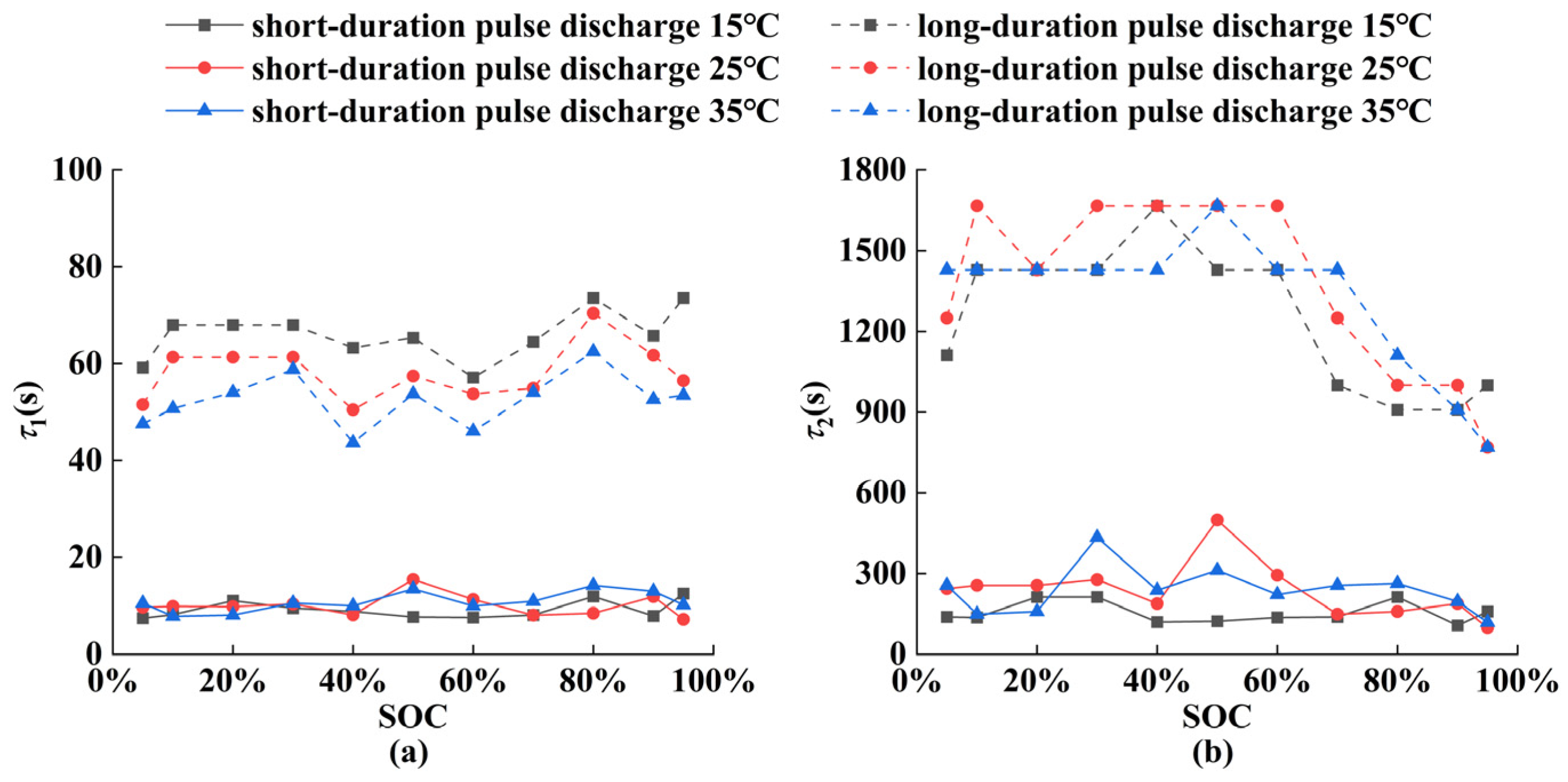
3.2. Calculation of ECM Parameters
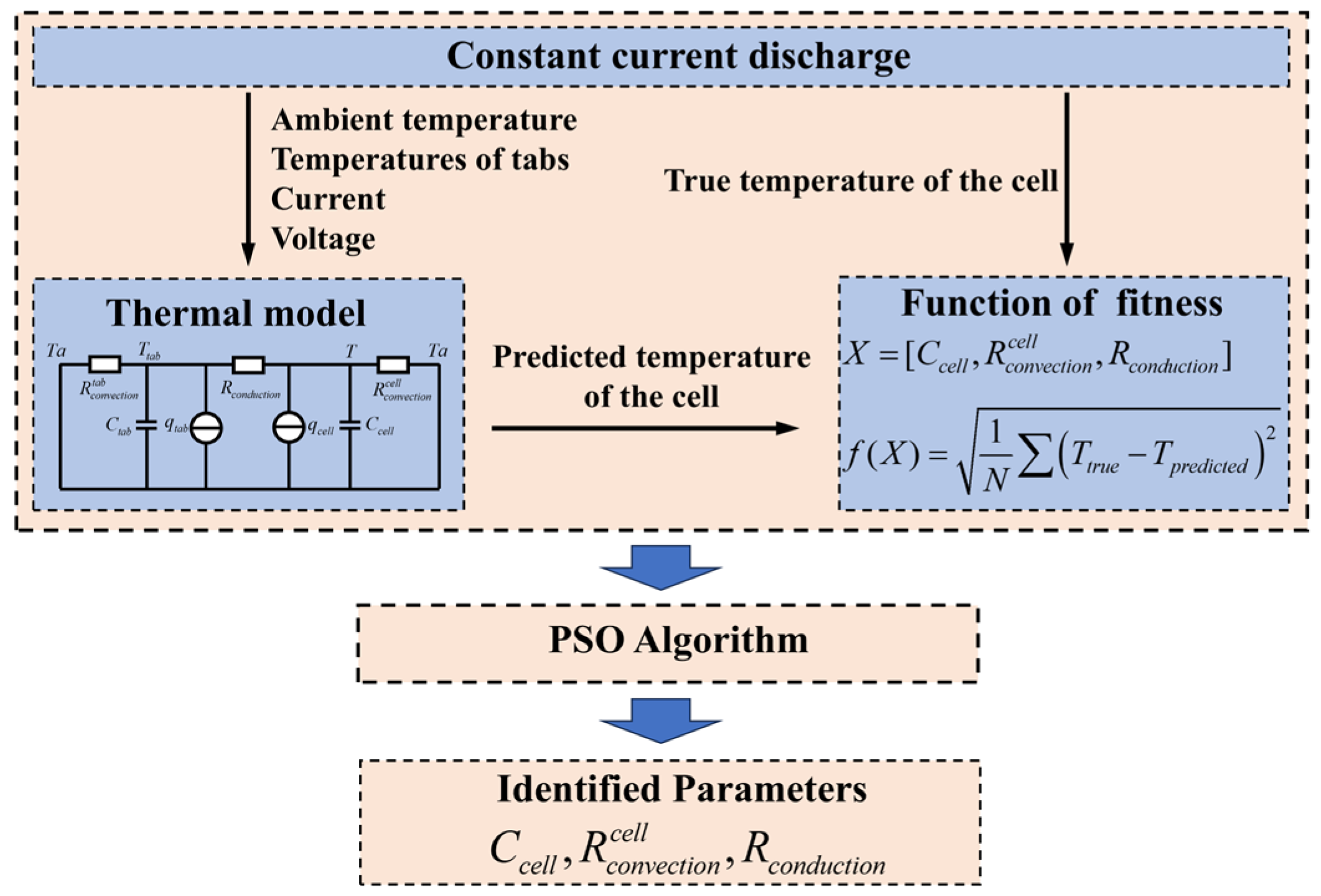
4. Parameter Identification for the Thermal Model
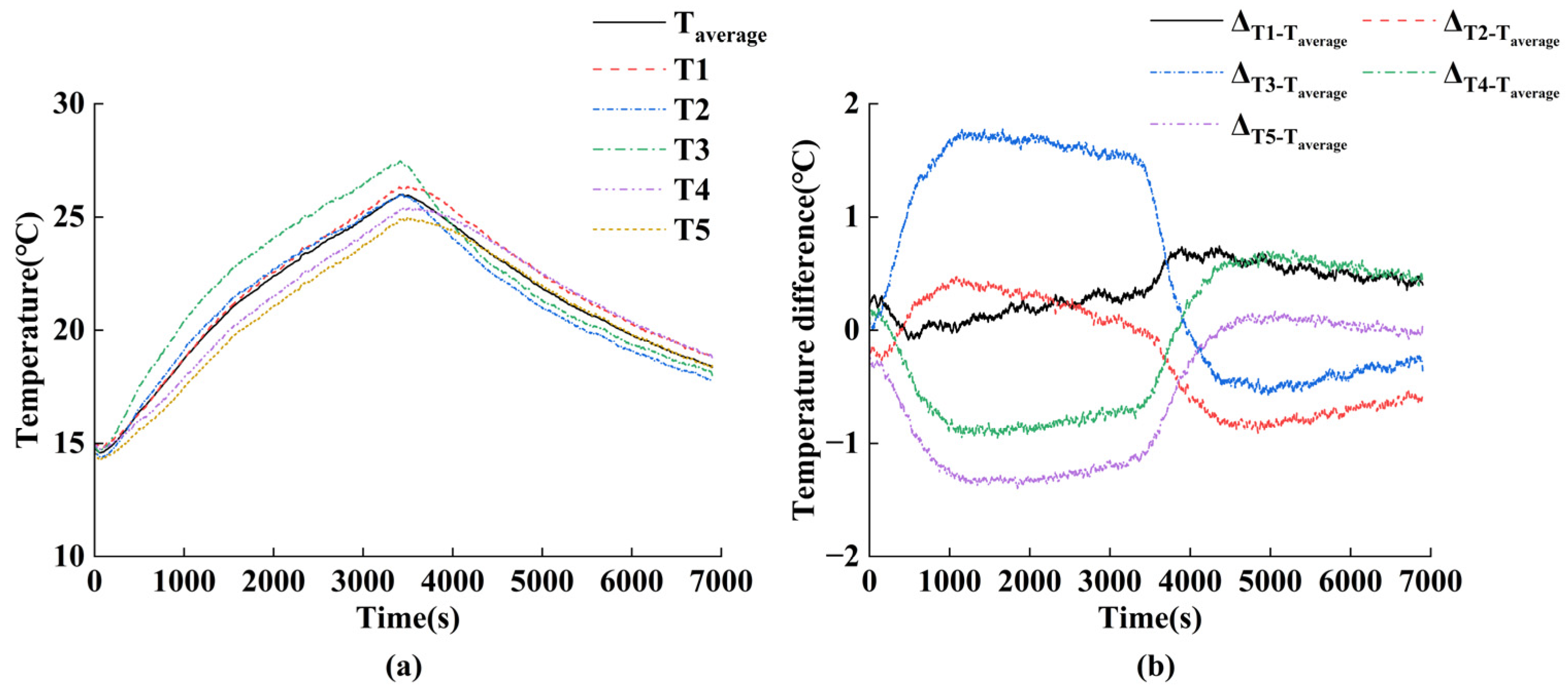
4.1. Experimental Setup and Test Procedure for Parameter Identification
4.2. Calculation of Thermal Model Parameters
4.3. Specific Heat Capacity Measurement Experiment for the Sodium-Ion Battery
5. Parameter Identification Results and Model Performance Validation
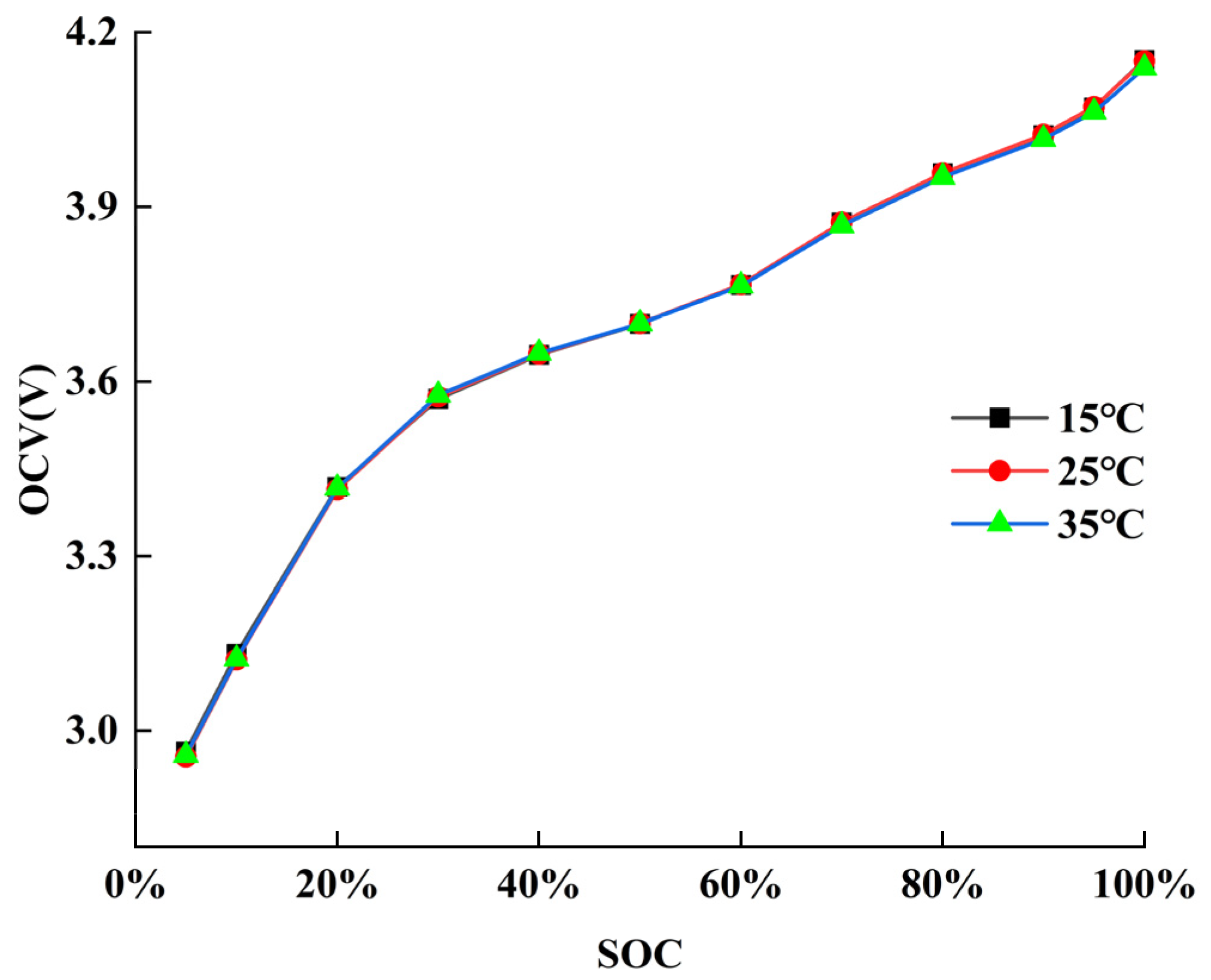
5.1. Parameter Identification Results of ECM
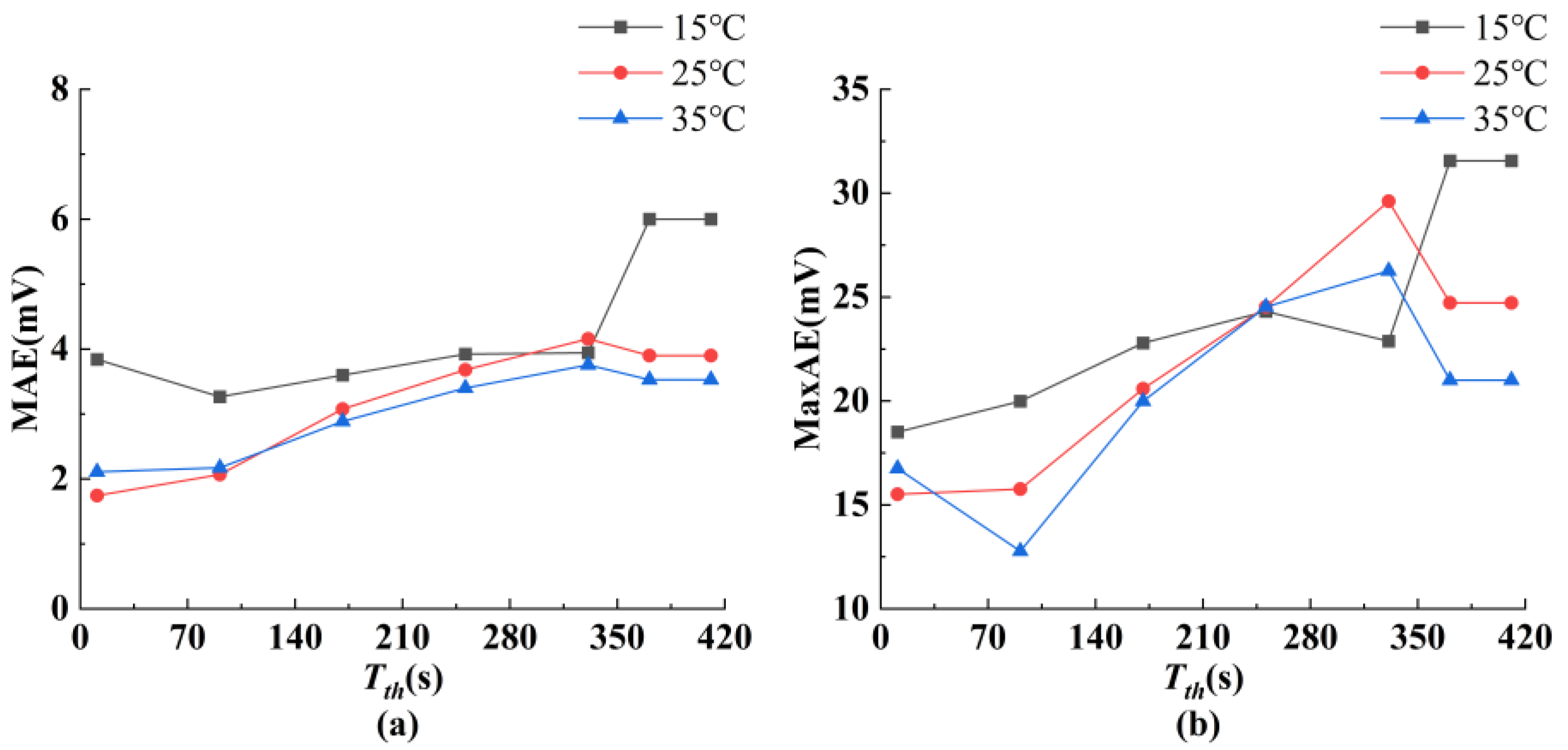
5.2. Voltage Prediction Results Under M-HPPC Conditions at Various Temperatures
5.3. The Specific Heat Capacity Measurement Experiment and Results of Thermal Model Parameter Identification
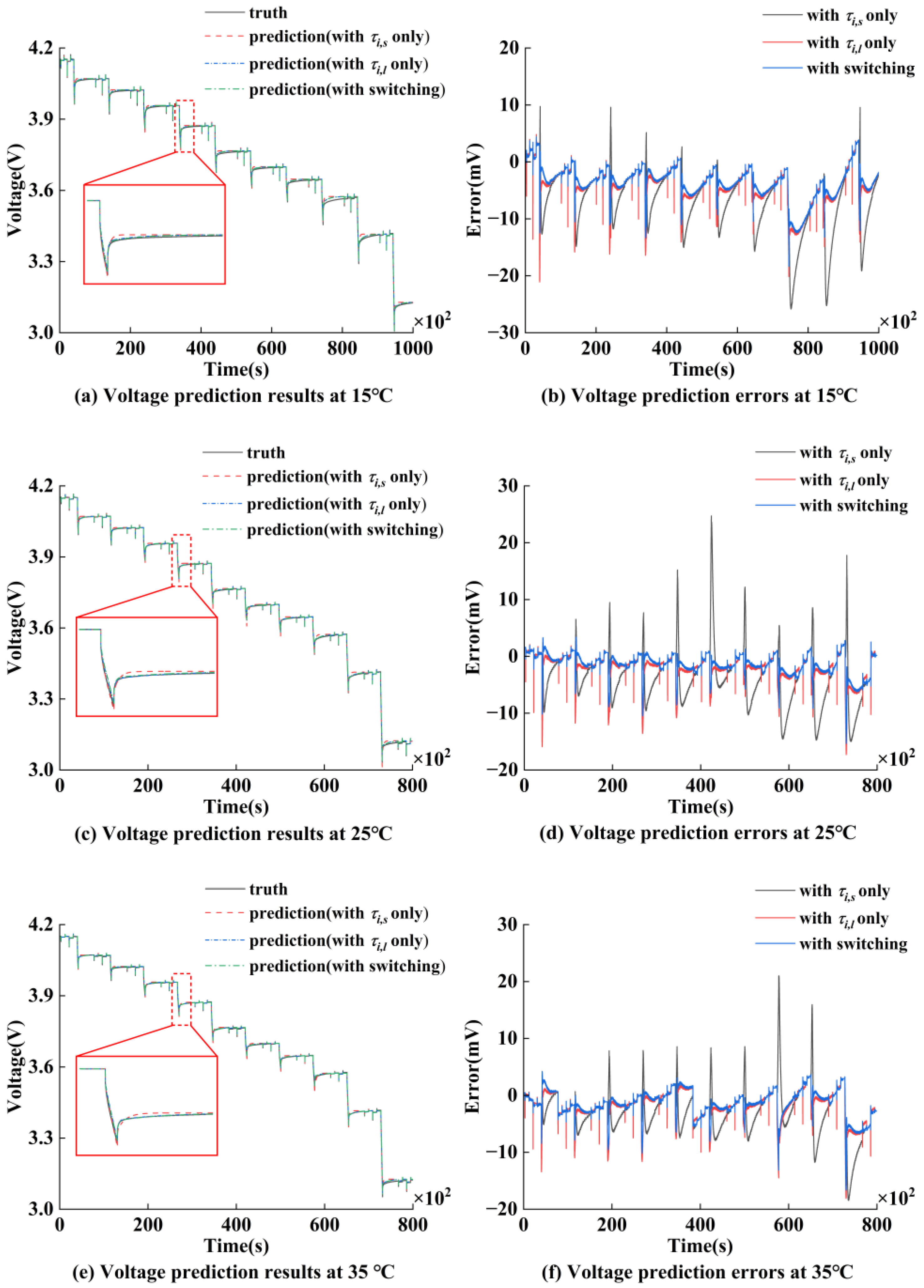
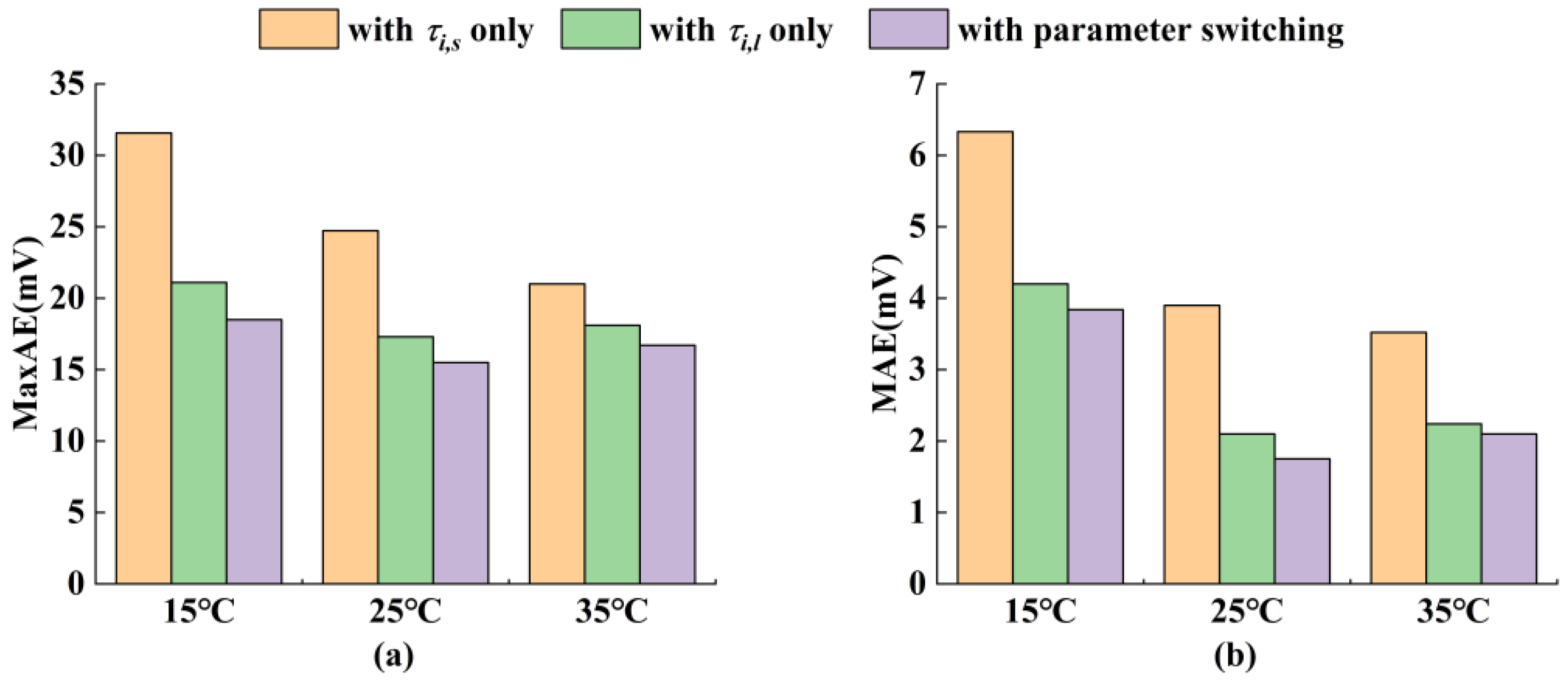
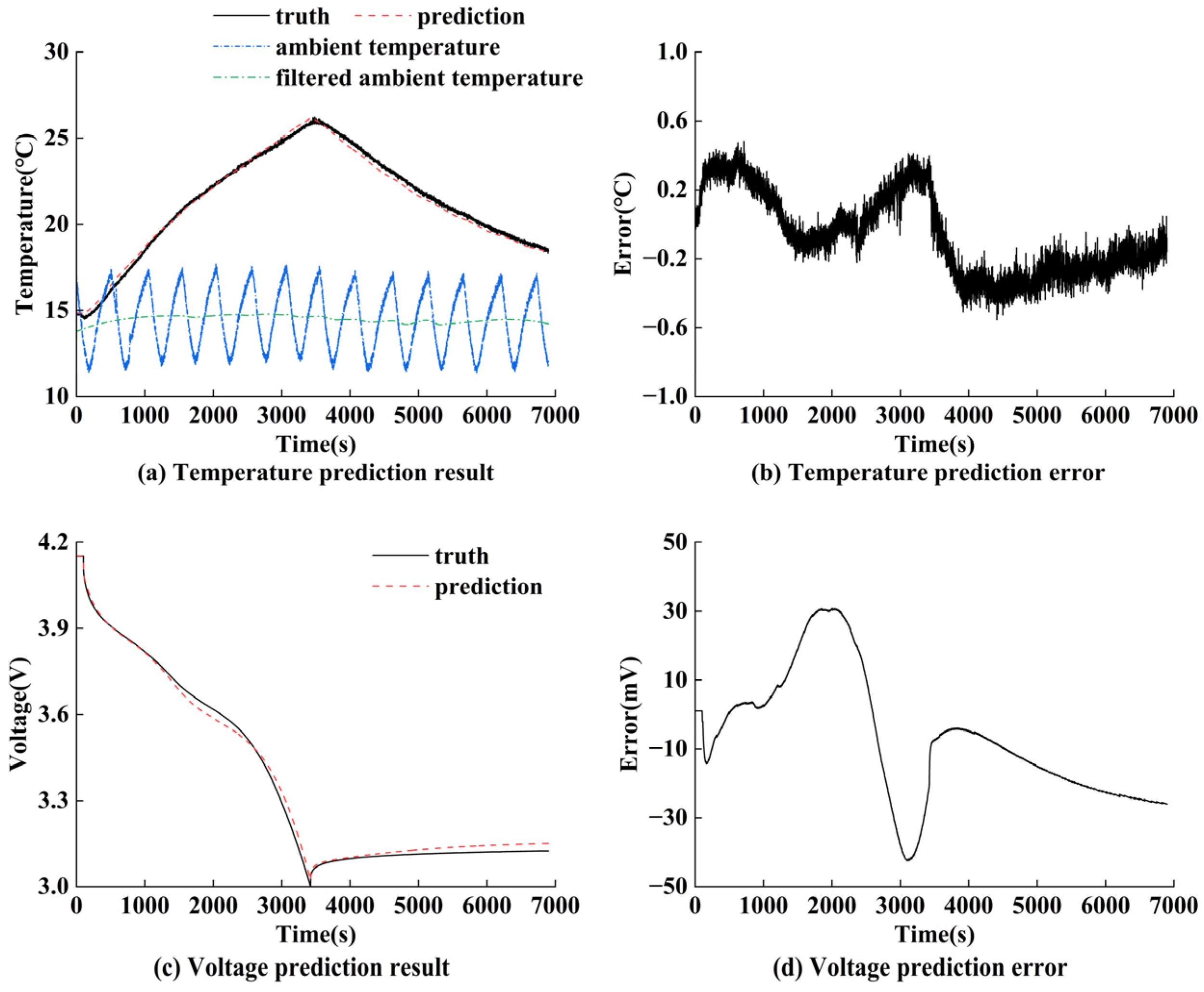
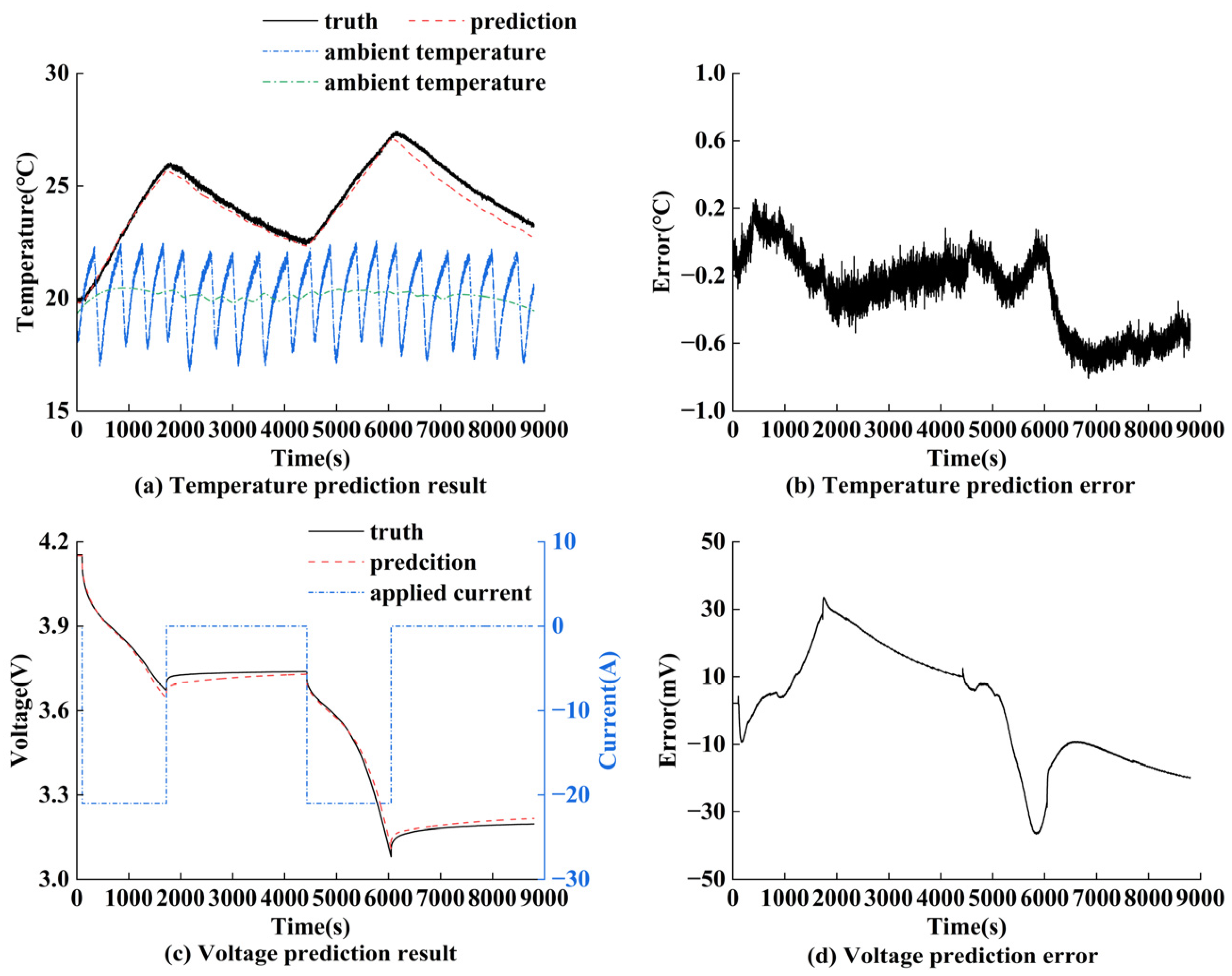
5.4. Validation of Electro–Thermal Coupling Model Prediction Performance
5.5. Comparative Analysis of Sodium-Ion Batteries and Lithium-Ion Batteries
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, R.; He, J.; Fan, X.; Qian, Y.; Deng, Y. The Distributed Temperature Abatement by the Phase Changing Materials for Battery in Electric Tools and Its Influence on Aging. Sustain. Energy Technol. Assess. 2022, 52, 102199. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, M.; Fan, H.; Chung, J.D. Multi-Objective Topology Optimization of Cold Plates for Enhanced Battery Thermal Management in Electric Vehicles. Case Stud. Therm. Eng. 2025, 66, 105794. [Google Scholar] [CrossRef]
- Lin, X.-W.; Shi, M.-Y.; Zhou, Z.-F.; Chen, B.; Lu, Y.-J.; Jing, D.-W. Multi-Objective Topology Optimization Design of Liquid-Based Cooling Plate for 280 Ah Prismatic Energy Storage Battery Thermal Management. Energy Convers. Manag. 2025, 325, 119440. [Google Scholar] [CrossRef]
- Hounjet, L.J. Comparing Lithium- and Sodium-ion Batteries for Their Applicability Within Energy Storage Systems. Energy Storage 2022, 4, e309. [Google Scholar] [CrossRef]
- Luo, H.; Wang, Y.; Feng, Y.-H.; Fan, X.-Y.; Han, X.; Wang, P.-F. Lithium-Ion Batteries under Low-Temperature Environment: Challenges and Prospects. Materials 2022, 15, 8166. [Google Scholar] [CrossRef]
- Quartarone, E.; Eisenmann, T.; Kuenzel, M.; Tealdi, C.; Marrani, A.G.; Brutti, S.; Callegari, D.; Passerini, S. Towards Advanced Sodium-Ion Batteries: Green, Low-Cost and High-Capacity Anode Compartment Encompassing Phosphorus/Carbon Nanocomposite as the Active Material and Aluminum as the Current Collector. J. Electrochem. Soc. 2020, 167, 080509. [Google Scholar] [CrossRef]
- Rudola, A.; Wright, C.J.; Barker, J. Reviewing the Safe Shipping of Lithium-Ion and Sodium-Ion Cells: A Materials Chemistry Perspective. Energy Mater. Adv. 2021, 2021, 9798460. [Google Scholar] [CrossRef]
- Abraham, K.M. How Comparable Are Sodium-Ion Batteries to Lithium-Ion Counterparts? ACS Energy Lett. 2020, 5, 3544–3547. [Google Scholar] [CrossRef]
- Zakharchenko, T.K.; Nikiforov, D.I.; Serdyukov, G.D.; Komissarov, P.V.; Shkuratov, M.O.; Dzuban, A.V.; Lakienko, G.P.; Gordienko, Y.A.; Yashina, L.V.; Itkis, D.M. Thermal Runaway of Na-Ion Batteries with Na3V2O2(PO4)2F Cathodes. Batter. Supercaps 2025, 8, e202400386. [Google Scholar] [CrossRef]
- Yu, T.; Li, G.; Duan, Y.; Wu, Y.; Zhang, T.; Zhao, X.; Luo, M.; Liu, Y. The Research and Industrialization Progress and Prospects of Sodium Ion Battery. J. Alloys Compd. 2023, 958, 170486. [Google Scholar] [CrossRef]
- Zhang, C.; Gao, R.; Zheng, L.; Hao, Y.; Liu, X. New Insights into the Roles of Mg in Improving the Rate Capability and Cycling Stability of O3-NaMn0.48Ni0.2Fe0.3Mg0.02O2 for Sodium-Ion Batteries. ACS Appl. Mater. Interfaces 2018, 10, 10819–10827. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Y.; Ben, L.; Lyu, Y.; Song, N.; Yang, Z.; Li, Y.; Mu, L.; Yang, H.; Gu, L.; et al. Fe-Based Tunnel-Type Na0.61[Mn0.27Fe0.34Ti0.39]O2 Designed by a New Strategy as a Cathode Material for Sodium-Ion Batteries. Adv. Energy Mater. 2015, 5, 1501156. [Google Scholar] [CrossRef]
- Qian, J.; Wu, C.; Cao, Y.; Ma, Z.; Huang, Y.; Ai, X.; Yang, H. Prussian Blue Cathode Materials for Sodium-Ion Batteries and Other Ion Batteries. Adv. Energy Mater. 2018, 8, 1702619. [Google Scholar] [CrossRef]
- He, M.; Liu, S.; Wu, J.; Zhu, J. Review of Cathode Materials for Sodium-Ion Batteries. Prog. Solid State Chem. 2024, 74, 100452. [Google Scholar] [CrossRef]
- Balogun, M.-S.; Luo, Y.; Qiu, W.; Liu, P.; Tong, Y. A Review of Carbon Materials and Their Composites with Alloy Metals for Sodium Ion Battery Anodes. Carbon 2016, 98, 162–178. [Google Scholar] [CrossRef]
- Rehm, M.; Fischer, M.; Gomez, M.R.; Schütte, M.; Sauer, D.U.; Jossen, A. Comparing the Electrical Performance of Commercial Sodium-Ion and Lithium-Iron-Phosphate Batteries. J. Power Sources 2025, 633, 236290. [Google Scholar] [CrossRef]
- He, M.; Davis, R.; Chartouni, D.; Johnson, M.; Abplanalp, M.; Troendle, P.; Suetterlin, R.-P. Assessment of the First Commercial Prussian Blue Based Sodium-Ion Battery. J. Power Sources 2022, 548, 232036. [Google Scholar] [CrossRef]
- Subasinghe, L.U.; Wang, C.; Gajjela, S.R.; Law, M.; Manikandan, B.; Balaya, P. A Study on Heat Generation Characteristics of Na3V2(PO4)3 Cathode and Hard Carbon Anode-Based Sodium-Ion Cells. J. Therm. Anal. Calorim. 2022, 147, 8631–8649. [Google Scholar] [CrossRef]
- Sophy-Mahfoudi, N.; Sekharam, S.-V.; Boutaous, M.; Xin, S. Model-Based Design of LFP Battery Thermal Management System for EV Application. Batteries 2024, 10, 329. [Google Scholar] [CrossRef]
- Ren, Z.; Ducq, C.; Wang, H.; Shao, J. Error Analysis of Model-Based State-of-Charge Estimation for Lithium-Ion Batteries at Different Temperatures. Int. J. Electrochem. Sci. 2020, 15, 9981–10006. [Google Scholar] [CrossRef]
- Hu, M.; Li, Y.; Li, S.; Fu, C.; Qin, D.; Li, Z. Lithium-Ion Battery Modeling and Parameter Identification Based on Fractional Theory. Energy 2018, 165, 153–163. [Google Scholar] [CrossRef]
- Panchal, S.; Mathew, M.; Fraser, R.; Fowler, M. Electrochemical Thermal Modeling and Experimental Measurements of 18650 Cylindrical Lithium-Ion Battery during Discharge Cycle for an EV. Appl. Therm. Eng. 2018, 135, 123–132. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Y.; Shao, J.; Li, J.; Yu, Q. An Electrochemical-Thermal Coupling Model for Prismatic Lithium-Ion Batteries over Wide Temperature Range. Appl. Therm. Eng. 2022, 217, 119282. [Google Scholar] [CrossRef]
- Alkhedher, M.; Al Tahhan, A.B.; Yousaf, J.; Ghazal, M.; Shahbazian-Yassar, R.; Ramadan, M. Electrochemical and Thermal Modeling of Lithium-Ion Batteries: A Review of Coupled Approaches for Improved Thermal Performance and Safety Lithium-Ion Batteries. J. Energy Storage 2024, 86, 111172. [Google Scholar] [CrossRef]
- Cai, Y.; Che, Y.; Li, H.; Jiang, M.; Qin, P. Electro-Thermal Model for Lithium-Ion Battery Simulations. J. Power Electron. 2021, 21, 1530–1541. [Google Scholar] [CrossRef]
- Dai, H.; Zhu, L.; Zhu, J.; Wei, X.; Sun, Z. Adaptive Kalman Filtering Based Internal Temperature Estimation with an Equivalent Electrical Network Thermal Model for Hard-Cased Batteries. J. Power Sources 2015, 293, 351–365. [Google Scholar] [CrossRef]
- Sun, Y.; Li, J.-C.; Zhou, H.; Guo, S. Wide-Temperature-Range Sodium-Metal Batteries: From Fundamentals and Obstacles to Optimization. Energy Environ. Sci. 2023, 16, 4759–4811. [Google Scholar] [CrossRef]
- Chayambuka, K.; Mulder, G.; Danilov, D.L.; Notten, P.H.L. Physics-Based Modeling of Sodium-Ion Batteries Part II. Model and Validation. Electrochim. Acta 2022, 404, 139764. [Google Scholar] [CrossRef]
- Garapati, V.K.; Huld, F.; Lee, H.; Lamb, J.J. Perspective and Comparative Analysis of Physics-Based Models for Sodium-Ion Batteries. Electrochim. Acta 2025, 514, 145573. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, J.; Liu, M.; Li, J.; Shao, J. A Simplified Electrochemical Modeling Method for Sodium-Ion Batteries. J. Energy Storage 2025, 112, 115495. [Google Scholar] [CrossRef]
- Jin, B.; Qiao, D.; Gao, W.; Yao, S.; Liu, J.; Zhu, Z.; Shao, Y.; Li, D.; Zheng, Y. Low-Temperature Sodium Dendrite-Induced Short Circuit Diagnosis for Sodium Battery. J. Energy Storage 2025, 111, 115359. [Google Scholar] [CrossRef]
- Feng, Y.-F.; Shen, J.-N.; Ma, Z.-F.; He, Y.-J. Equivalent Circuit Modeling of Sodium-Ion Batteries. J. Energy Storage 2021, 43, 103233. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, Y.; Sun, Z.; Li, M.; Chen, Z. Online Impedance-Based Temperature and States Co-Estimation for Sodium-Ion Batteries Using Fractional-Order Model. Energy 2025, 334, 137427. [Google Scholar] [CrossRef]
- Rabab, H.; Damay, N.; Forgez, C.; Mejdoubi, A.E.; Quelin, A. Equivalent Circuit Model For Sodium-Ion Batteries with Physical-Based Representations of Their Non-Linearities. In Proceedings of the 2023 IEEE Vehicle Power and Propulsion Conference (VPPC), Milan, Italy, 24–27 October 2023; IEEE: New York, NY, USA, 2023; pp. 1–6. [Google Scholar]
- Che, C.; Wu, F.; Li, Y.; Li, Y.; Li, S.; Wu, C.; Bai, Y. Challenges and Breakthroughs in Enhancing Temperature Tolerance of Sodium-Ion Batteries. Adv. Mater. 2024, 36, 2402291. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Zhuo, H.; Jing, Q.; Gu, Y.; Liao, Z.; Wang, K.; Hu, J.; Geng, D.; Sun, X.; Xiao, B. Low-temperature Performance of Na-ion Batteries. Carbon Energy 2024, 6, e546. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, L.; Liao, R.; Hu, C.; Xiao, Y.; Wu, J.; He, C.; Zhang, Y.; Li, S. Data-Driven Internal Temperature Estimation Methods for Sodium-Ion Battery Using Electrochemical Impedance Spectroscopy. J. Energy Storage 2024, 87, 111426. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, H.; Xu, C.; Zhang, R.; Wong, S.K.; Hong, Y.; Zhang, G.; Feng, X. Electro-Thermal Coupling Modeling and Thermal Characterization of Sodium-Ion Batteries. Appl. Therm. Eng. 2025, 272, 126439. [Google Scholar] [CrossRef]
- Sandri, C.; Di Rienzo, R.; Nicodemo, N.; Baronti, F.; Roncella, R.; Saletti, R. Electrical Circuit Model for Sodium-Ion Batteries. In Proceedings of the IECON 2024—50th Annual Conference of the IEEE Industrial Electronics Society, Chicago, IL, USA, 3–6 November 2024; IEEE: New York, NY, USA, 2024; pp. 1–6. [Google Scholar]
- Zuo, X.; Fu, X.; Han, X.; Sun, M.; Fan, Y. State of Charge Estimation for Sodium-Ion Batteries Based on LSTM Network and Unscented Kalman Filter. Batteries 2025, 11, 274. [Google Scholar] [CrossRef]
- Mesbahi, T.; Sugrañes, R.B.; Bakri, R.; Bartholomeüs, P. Coupled Electro-Thermal Modeling of Lithium-Ion Batteries for Electric Vehicle Application. J. Energy Storage 2021, 35, 102260. [Google Scholar] [CrossRef]
- Zhou, Y.; Deng, H.; Li, H.-X. Control-Oriented Galerkin-Spectral Model for 3-D Thermal Diffusion of Pouch-Type Batteries. IEEE Trans. Ind. Inform. 2023, 19, 7508–7516. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, H.; Xu, X. A Study on the Transient Heat Generation Rate of Lithium-Ion Battery Based on Full Matrix Orthogonal Experimental Design with Mixed Levels. J. Energy Storage 2021, 36, 102446. [Google Scholar] [CrossRef]
- Del Valle, Y.; Venayagamoorthy, G.K.; Mohagheghi, S.; Hernandez, J.-C.; Harley, R.G. Particle Swarm Optimization: Basic Concepts, Variants and Applications in Power Systems. IEEE Trans. Evol. Comput. 2008, 12, 171–195. [Google Scholar] [CrossRef]
- Damay, N.; Recoquillé, R.; Rabab, H.; Kozma, J.; Forgez, C.; El Mejdoubi, A.; El Kadri Benkara, K. Determination of a Sodium-Ion Cell Entropy-Variation. J. Power Sources 2023, 581, 233460. [Google Scholar] [CrossRef]
- Chen, L.; Hu, M.; Cao, K.; Li, S.; Su, Z.; Jin, G.; Fu, C. Core Temperature Estimation Based on Electro-thermal Model of Lithium-ion Batteries. Int. J. Energy Res. 2020, 44, 5320–5333. [Google Scholar] [CrossRef]
- Manikandan, B.; Yap, C.; Balaya, P. Towards Understanding Heat Generation Characteristics of Li-Ion Batteries by Calorimetry, Impedance, and Potentiometry Studies. J. Electrochem. Soc. 2017, 164, A2794–A2800. [Google Scholar] [CrossRef]
- Wei, F.; Li, P.; Zhang, Q.; Shao, G.; Mao, J. Entropy Change Characteristics for Sodium Ion Half/Full Cells Based on Na3V2(PO4)3 and Hard Carbon Materials. J. Electrochem. Soc. 2022, 169, 050503. [Google Scholar] [CrossRef]
- Damay, N.; Forgez, C.; Bichat, M.-P.; Friedrich, G. A Method for the Fast Estimation of a Battery Entropy-Variation High-Resolution Curve—Application on a Commercial LiFePO4/Graphite Cell. J. Power Sources 2016, 332, 149–153. [Google Scholar] [CrossRef]











| Parameters | Values |
|---|---|
| Rated capacity (25 °C) (Ah) | 21 |
| Voltage range (V) | 2.6–4.2 |
| Standard charge rate | 0.2C |
| Maximum allowable discharge rate | 0.5C |
| Weight (g) | 720 |
| Length/width/thickness (mm) | 220/140/11 |
| Parameters | Values |
|---|---|
| cp (J/(kg °C)) | 1194 |
| (°C/W) | 9.1 |
| Rconvection (°C/W) | 6.5 |
| SOC | Entropy Coefficient |
|---|---|
| Low SOC (15%) | 0 m V/K |
| Medium SOC (45%) | −0.13 m V/K |
| High SOC (80%) | −0.14 m V/K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zhang, Z.; Deng, Y.; Yu, J. Accurate Prediction of Voltage and Temperature for a Sodium-Ion Pouch Cell Using an Electro-Thermal Coupling Model. Batteries 2025, 11, 312. https://doi.org/10.3390/batteries11080312
Zhang H, Zhang Z, Deng Y, Yu J. Accurate Prediction of Voltage and Temperature for a Sodium-Ion Pouch Cell Using an Electro-Thermal Coupling Model. Batteries. 2025; 11(8):312. https://doi.org/10.3390/batteries11080312
Chicago/Turabian StyleZhang, Hekun, Zhendong Zhang, Yelin Deng, and Jianxu Yu. 2025. "Accurate Prediction of Voltage and Temperature for a Sodium-Ion Pouch Cell Using an Electro-Thermal Coupling Model" Batteries 11, no. 8: 312. https://doi.org/10.3390/batteries11080312
APA StyleZhang, H., Zhang, Z., Deng, Y., & Yu, J. (2025). Accurate Prediction of Voltage and Temperature for a Sodium-Ion Pouch Cell Using an Electro-Thermal Coupling Model. Batteries, 11(8), 312. https://doi.org/10.3390/batteries11080312






