State of Health Prediction of Lithium-Ion Batteries Based on Dual-Time-Scale Self-Supervised Learning

Abstract

Accurate estimation of the state of health (SOH) of lithium-ion batteries confronts two critical challenges: the extreme scarcity of labeled data in large-scale operational datasets and the mismatch between existing methods (relying on full charging–discharging conditions) and shallow charging–discharging conditions prevalent in real-world scenarios. To address these challenges, this study proposes a self-supervised learning framework for SOH estimation. The framework employs a dual-time-scale collaborative pre-training approach via masked voltage sequence reconstruction and interval capacity prediction tasks, enabling automatic extraction of cross-time-scale aging features from unlabeled data. Innovatively, it integrates domain knowledge into the attention mechanism and incorporates time-varying factors into positional encoding, significantly enhancing the capability to extract battery aging features. The proposed method is validated on two datasets. For the standard dataset, using only 10% labeled data, it achieves an average RMSE of 0.491% for NCA battery estimation and 0.804% for transfer estimation between NCA and NCM. For the shallow-cycle dataset, it achieves an average RMSE of 1.300% with only 2% labeled data. By synergistically leveraging massive unlabeled data and extremely sparse labeled samples (2–10% labeling rate), this framework reduces the labeling burden for battery health monitoring by 90–98%, offering an industrial-grade solution with near-zero labeling dependency.

1. Introduction

Amid the accelerated decarbonization of the global energy structure, lithium-ion batteries have gained widespread adoption in strategic fields such as transportation electrification and smart grid peak shaving, owing to their high energy conversion efficiency and cycling stability [1,2]. As the energy storage unit for electric vehicles, electric ships, electric aircraft, and other transportation systems, the performance and reliability of batteries directly determine critical metrics such as range endurance, charging speed, and operational efficiency [3]. However, during battery operation, aging-related side reactions (e.g., solid electrolyte interphase (SEI) layer growth, loss of active material (LAM), and lithium deposition) occur alongside primary charge/discharge reactions. These electrochemical mechanisms induce irreversible degradation, primarily manifested as capacity fade and increased internal resistance [4,5]. To assess the battery’s degradation degree, state of health (SOH) is typically evaluated using the capacity decay rate as the primary indicator, with the internal resistance change rate serving as a secondary aging parameter. Accurate SOH estimation forms the foundation for enhancing safety, optimizing performance, and managing battery lifetimes [6]. Currently, lithium-ion battery SOH estimation methods can be categorized into two types: model-based methods and data-driven methods [7].

Model-based methods establish mathematical mappings of battery states using electrochemical mechanisms (EMs) or equivalent circuit models (ECMs) [8]. Chen et al. [9] proposed a parameter identification method based on variational mode decomposition (VMD) to achieve joint estimation of SOC and SOH, but its limitation is that different battery types require reconfiguration of adaptive parameters. Zeng et al. [10] adopted the Metropolis–Hastings algorithm to eliminate the dependence of the Kalman filter model on initial states, but it entails substantial computational overhead. Compared to approximated simulations based on idealized circuit ECMs, EMs exhibit distinct advantages in mechanism-driven SOH prediction by rigorously modeling the kinetic equations of lithium-ion de-insertion, diffusion, and side reactions [11]. Chen et al. [12] developed a novel electrochemical–thermal–aging effect coupling model that updates model parameters based on aging effects and internal temperature, yet its computational complexity and parameter sensitivity have long hindered the embedded deployment of battery management systems (BMSs). Overall, while model-based methods provide physical interpretability, they exhibit limited adaptability to parameter drift under complex operating conditions.

Unlike explicit modeling approaches, data-driven methods provide an end-to-end alternative for SOH estimation by mining the implicit degradation patterns in battery operating data. Early prediction frameworks primarily employed feature engineering integrated with traditional regression models. Zhu et al. [13] input statistical features extracted from relaxation voltage into the XGBoost model to estimate the battery capacity. Weng et al. [14] derived the incremental capacity (IC) curve from constant current charging curves and found that the peak height of the IC curve is a monotonic function of the maximum battery capacity, enabling the determination of capacity loss. Unlike feature-dependent methods, sequence-based methods can automatically extract features from raw data. Tian et al. [15] used deep neural networks to predict capacity using partial voltage curves, achieving a prediction error as low as 16.9 mAh for a 0.74 Ah battery. Wang et al. [16] proposed a time-driven and difference-driven dual attention neural network (TDANet) that incorporates data characteristics into the model to achieve high-precision SOH prediction. Nevertheless, such methods exhibit limited cross-condition generalizability. To maintain high accuracy under varied operating scenarios, Tan et al. [17] introduced transfer learning, utilizing source domain data for pre-training and applying domain adaptation and model parameter fine-tuning during transfer. Ma et al. [18] applied transfer learning to SOH estimation, employing the maximum mean discrepancy (MMD) domain adaptation method to mitigate distributional shifts between training and testing battery data. Chen et al. [19] further integrated self-attention mechanisms with multi-kernel MMD to enable the model to transfer across different working conditions. Yang et al. [20] combined multi-task learning and physical neural networks with transfer learning to simultaneously achieve high-precision health status estimation, remaining life prediction, and short-term degradation path prediction, significantly improving generalization capabilities across materials and operating conditions.

In practical application scenarios involving new energy vehicles, energy storage stations, and the consumer electronics industry, accurate capacity estimation of power battery systems faces dual challenges. On the one hand, manufacturers strictly limit deep charge–discharge operations to extend battery lifespan, causing the system to operate in the shallow charge–discharge cycle zone for extended periods. This hinders the acquisition of complete charge–discharge curves. On the other hand, due to limitations in detection costs and operational conditions, capacity labels in practical engineering applications can only be obtained through sparse inspections (e.g., single capacity calibration during annual maintenance of electric vehicles, monthly inspections of energy storage stations, and factory inspections of consumer electronics), resulting in a typical scenario of “incomplete charge–discharge data without labels and sparse labeled data.” The aforementioned methods belong to supervised learning approaches. To achieve high-precision estimation, these methods generally require large amounts of labeled data, limiting their applicability in the described scenarios. In recent years, semi-supervised learning has emerged as an effective alternative that reduces reliance on labeled data. Guo et al. [21] proposed an interpretable semi-supervised learning technique, where a labeled training model is used to generate pseudo-labels for unlabeled data, which are then used for collaborative training with labeled and unlabeled data. Xiong et al. [22] implemented semi-supervised battery capacity estimation via electrochemical impedance spectroscopy. Li et al. [23] constructed an LSTM-based semi-supervised model by extracting statistical features from complete charge/discharge curves, while Yao et al. [24] enhanced semi-supervised performance through adversarial learning. These methods partially reduce label dependence but still require multiple batteries with complete charge–discharge cycles and sufficient labeled data during training. Since semi-supervised learning relies on generating pseudo-labels from unlabeled data, producing reliable pseudo-labels fundamentally requires adequate high-quality labeled data. Consequently, this approach fails to address practical deployment challenges.

To fundamentally address this challenge, developing novel learning paradigms capable of directly extracting degradation patterns from incomplete, unlabeled data is imperative. This work introduces a self-supervised learning (SSL) paradigm, whose core lies in designing pretext tasks to prompt the model to autonomously construct supervision signals from unlabeled data, thereby enabling representation learning [25]. Specifically, this paper presents an SOH estimation framework based on dual-time-scale task-driven self-supervised learning. The core premise of this framework is to leverage massive unlabeled battery data by designing multi-scale auxiliary tasks for collaborative pre-training. The former compels the model to learn local physical laws governing intra-cycle voltage dynamics via random masking reconstruction, while the latter constructs cross-cycle aging-aware signals by exploiting the strong correlation between capacity within specific easily accessible voltage intervals and the overall health state. The main contributions of this paper are as follows:

(1) A dual-time-scale self-supervised learning framework for battery SOH estimation is established. The self-supervised approach reduces label dependence, while the dual-time-scale design overcomes the limitation of single-scale methods by simultaneously capturing local variations and long-term trends.

(2) The conventional transformers’ limitations in battery data processing are overcome. Domain knowledge is injected into the attention mechanism, solving the problem of aging key feature dilution caused by uniform attention distribution, while a time-varying factor is introduced into positional encoding to overcome the limitations of traditional positional encoding that cannot represent the aging process.

(3) The superiority of the method is verified under low-labeling conditions. On the Tongji dataset, with only 10% labeled data, the model achieves an average RMSE of 0.491% for NCA battery estimation and 0.804% for transfer estimation between NCA and NCM. On Dataset 2 containing shallow-cycle data, with merely 2% labeled data, it attains an average RMSE of 1.300%.

The remainder of this paper is organized as follows: Section 2 introduces the aging characteristics and testing process of lithium-ion battery data; Section 3 details our proposed self-supervised learning-based SOH estimation method; Section 4 discusses the experimental results; and Section 5 presents conclusions and an outlook.

2. Materials and Methods

2.1. Tongji Dataset

Zhu et al. [13] established a comprehensive cycling dataset, referred to as the Tongji dataset, containing three commercial battery types: NCA, NCM, and NCA+ NCM. All cells were aged in environmental chambers under controlled temperatures (25 °C, 35 °C, and 45 °C) with charge/discharge rates ranging from 0.25C to 4C; cycling was terminated when capacity faded to 71% of the nominal capacity. The NCA and NCM cells (nominal capacity: 3.5 Ah) were charged using constant-current constant-voltage (CC-CV) protocols and discharged at 1C constant-current (CC) rate, with 30 min rest periods after each charge to monitor voltage recovery. From this comprehensive dataset, seven cells were selected to ensure coverage of critical experimental variables: two temperature conditions (25 °C and 45 °C) and two electrode chemistries (NCA and NCM). The complete specifications of these selected cells are provided in

Table 1. Batteries and cycling conditions for the Tongji dataset.

Battery	Battery Type	Temperature	Charge Current Rate/Discharge Rate	Number of Batteries
NCA_45_05_#1-#5	NCA battery Type: 18650 Cutoff voltage: 2.65–4.2 V Nominal capacity: 3.5 Ah	45 °C	0.5C/1C	5
NCM_35_05_#1-#2	NCM battery Type: 18650 Cutoff voltage: 2.5–4.2 V Nominal capacity: 3.5 Ah	35 °C	0.5C/1C	2

. The degradation behavior varied significantly across operating conditions, as shown by the capacity fade curves of the selected cells in Figure 1a.

2.2. CALCE Dataset

The CALCE dataset, developed by the CALCE Battery Research Group, provides aging data for graphite/LiCoO₂ pouch cells [26]. This dataset includes batteries with a nominal capacity of 1.5 Ah and a nominal voltage of 3.7 V, cycled under semi-controlled conditions at 25 ± 2 °C; detailed parameters are listed in

Table 2. Batteries and cycling conditions for the CALCE dataset.

Battery	Battery Type	Temperature	Charge Current Rate/Discharge Rate	Number of Batteries
PL21, PL23	LCO battery Cutoff voltage:2.75–4.2 V Nominal capacity:1.5 Ah	25 °C	0.5C/0.5C	2
PL19, PL24				2

. To simulate real-world applications where batteries typically operate within partial SOC ranges, a specialized testing protocol is implemented in this study. The experimental procedure involves charging via CC-CV protocol at a C/2 rate until reaching 100% SOC, followed by a C/2 constant-current discharge to predetermined SOC lower limits (e.g., 20% SOC for the 20–80% range) and subsequent charging to SOC upper limits (e.g., 80% SOC for the 20–80% range) according to specified protocols. Each charge–discharge cycle concludes with a 30 min rest period. During cycling tests, standard capacity calibration is performed every 50 or 100 cycles to determine the actual maximum discharge capacity, enabling dynamic adjustment of partial cycling SOC control ranges. Unlike conventional fixed-voltage-window protocols, this experiment employs a capacity-percentage-guided strategy. For the 20–80% SOC partial cycling range, operations consistently utilize 60% of the battery’s current available capacity (which degrades with aging). This dynamic adjustment mechanism maintains a consistent SOC span across degradation stages while avoiding polarization artifacts inherent in fixed-voltage approaches. The complete degradation trajectories are presented in Figure 1b.

3. Methodology

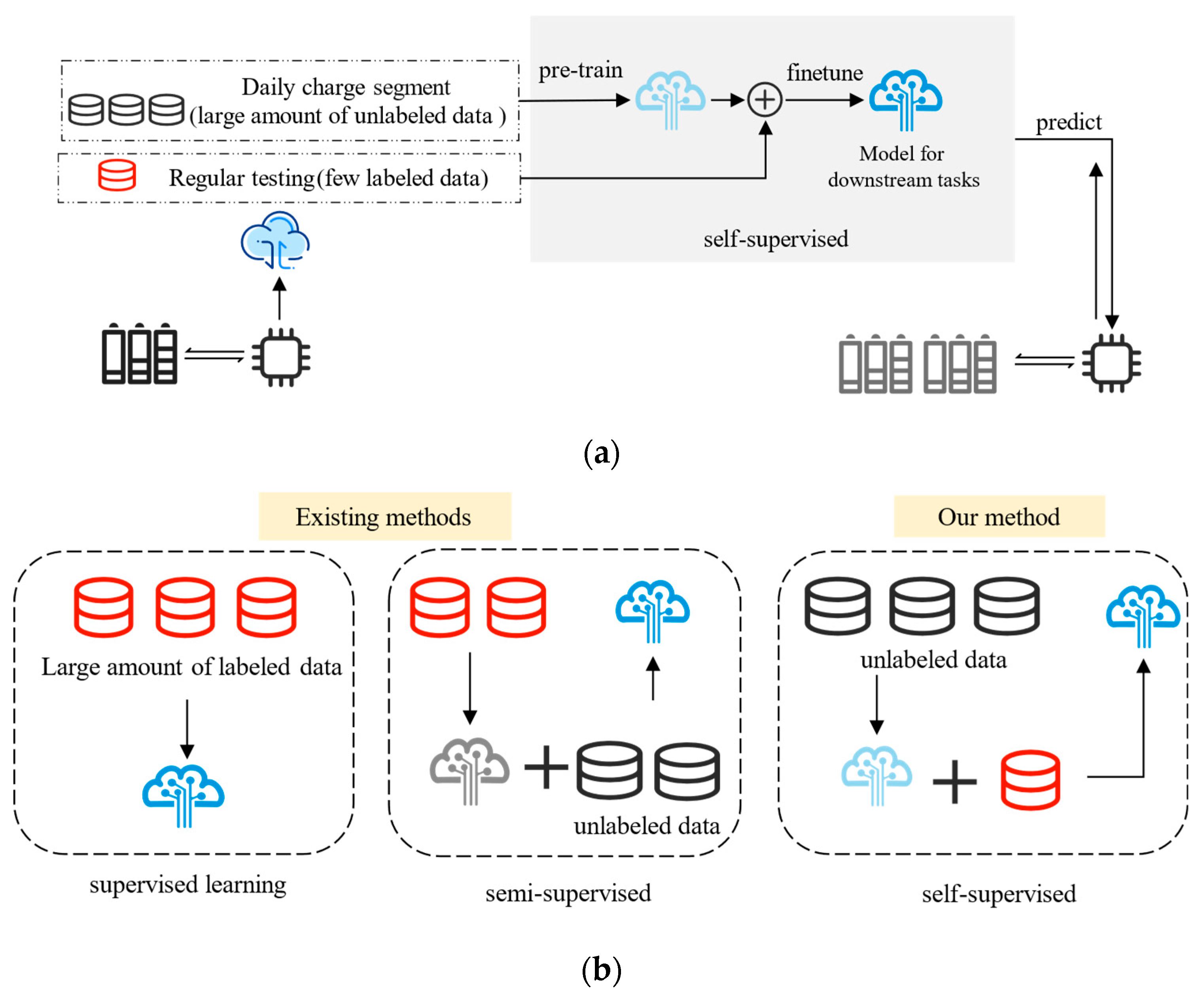
As established in prior discussions, the practical challenges in battery SOH prediction primarily stem from shallow charge–discharge cycles and the prohibitive costs of full-cycle capacity testing, which collectively limit the availability of complete capacity labels throughout a battery’s operational lifespan. To effectively address this challenge, this paper introduces a self-supervised learning method that leverages the potential of massive unlabeled data to achieve low-annotation-dependency SOH estimation. The application framework of the proposed method is shown in Figure 2a. First, data collected by the BMS is stored in the cloud for preprocessing and analysis. Next, unlabeled data is input into the model for representation learning; after fine-tuning with a small amount of labeled data, the model is applied to practical SOH estimation. Figure 2b shows the comparison of self-supervised learning methods with other commonly used SOH estimation methods, such as supervised learning and semi-supervised learning. Supervised learning, the most widely used approach, relies on large amounts of labeled data and cannot effectively utilize unlabeled data. Both semi-supervised and self-supervised learning utilize unlabeled data, but their methodologies differ. In semi-supervised learning, generating reliable pseudo-labels for unlabeled data requires sufficient labeled data. In contrast, self-supervised learning directly extracts aging features from unlabeled data, a process independent of labeled data. Thus, this paper adopts the self-supervised learning paradigm.

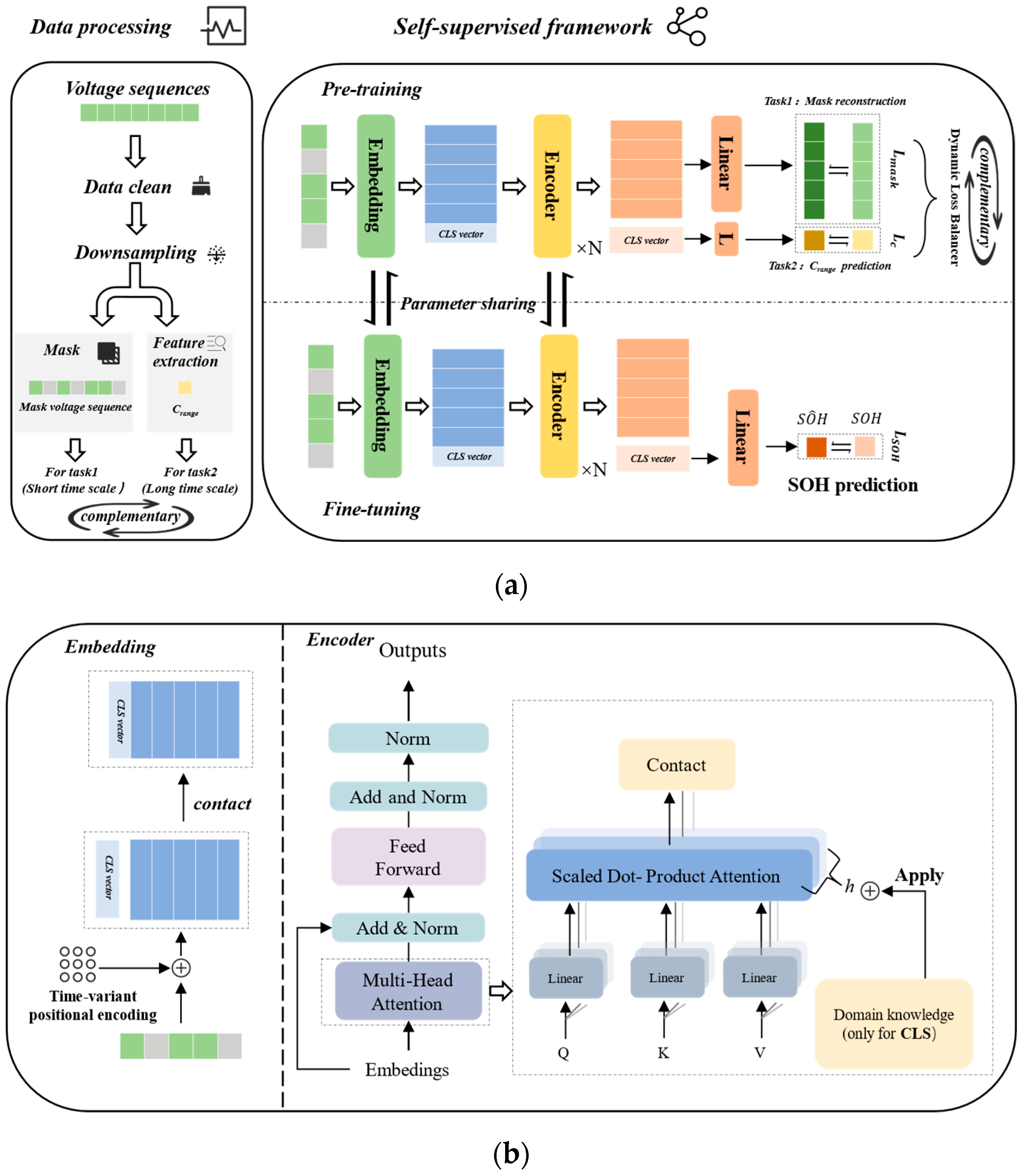
This section details the development process of dual-time-scale self-supervised learning for SOH estimation. On the short timescale, the model learns dynamic changes in local voltage via the masked voltage reconstruction task (Task 1); on the long timescale, it integrates global aging features by embedding a CLS vector at the start of the input sequence, enabling direct prediction of interval capacity (Task 2). This design allows the interval capacity to serve as a macro-level supervisory signal that guides the representations learned in the local voltage reconstruction task to correlate with battery capacity degradation. The framework of the specific development process is shown in Figure 3a, which is divided into two main parts. The first part is data preprocessing, which includes constructing masked voltage sequences as input for Task 1 and extracting interval capacity as the supervisory signal for Task 2. The second part is the self-supervised learning network architecture, which includes embedding, encoder, and pre-training and fine-tuning modules, as detailed in Figure 3b. The embedding module explains how to map voltage sequences and positional information to high-dimensional space. Time-varying factors are incorporated into positional encoding within this module to integrate recurrent temporal features. The encoder module describes the encoder structure, where domain knowledge is injected into the attention mechanism to enhance the model’s ability to capture key battery aging features. The pre-training and fine-tuning modules primarily introduce details regarding the selection of loss functions, optimizers, and hyperparameters.

3.1. Data Preprocessing

This part introduces the steps of data preprocessing, as shown in the “Data processing” step in Figure 3a, which is primarily divided into data cleaning and normalization, voltage mask sequence construction, and supervised signal extraction. The specific steps are as follows.

Data Cleaning and Normalization: In general, a battery’s discharge process is highly influenced by load, whereas the charging process is typically artificially designed and more stable. The proposed method utilizes the constant current (CC) charging segment for SOH estimation. To eliminate differences in sampling frequency in the raw data, linear interpolation is used to downsample the voltage and current of the time-series signal, resulting in a uniform sampling frequency of 0.05 Hz post-downsampling. Additionally, to address the issue of varying CC segment lengths across charging cycles, undersized segments are padded. One of the inputs for the proposed method is the CC charging voltage segment u = [u₁, u₂, …, u_n], and the normalization formula for each voltage sequence is as follows:

$$x_{\mathrm{norm}}={\displaystyle \frac{x-x_{\min }}{x_{\max }-x_{\min }}}$$

(1)

where x_min denotes the minimum value in the voltage sequence, and x_max is the maximum value in the voltage sequence. This normalizes the voltage sequence to the range [0, 1].

Voltage Mask Sequence Construction (For Task 1): For the proposed method’s masked voltage reconstruction task, the input involves constructing masks from voltage sequences. Based on the degradation characteristics of lithium-ion batteries, this study proposes a hybrid masking strategy, with the total number of masks accounting for 20% of the sequence length. Specifically, 50% of the masks are concentrated in the electrochemically critical regions determined by incremental capacity analysis (ICA) of the target battery. Each continuous masked segment has a length of at least five sampling points. When the available length in the critical region is insufficient, the algorithm automatically switches to the general degradation feature region to apply high-density masking. To enhance the model’s generalization capability for global degradation patterns, the remaining 50% of masks are randomly distributed across the remaining voltage intervals. The values in all masked regions are replaced by the median value of unmasked voltage segments in the current sequence, thereby constructing training samples with physical plausibility.

Supervised Signal Extraction (For Task 2): The proposed method extracts relevant features from the voltage curve as target variables for the interval capacity prediction task. For discharge curves in actual applications, we introduce the interval capacity feature, which is strongly related to battery aging. Since batteries do not always yield complete charge–discharge curves in practical applications, this study introduces the interval capacity feature, which is strongly correlated with battery aging. This feature is defined as the capacity value derived by integrating current over time within a specific voltage interval, as shown in the following formula:

$$C_{\mathrm{range}}={\displaystyle {\int }_{v_{\mathrm{lower}}}^{v_{\mathrm{upper}}}I\mathrm{dt}}$$

(2)

where v_upper denotes the upper voltage limit, and v_lower denotes the lower voltage limit. Through incremental capacity analysis, voltage intervals are selected for different battery chemistries: for NCA and NCM, the selected voltage interval is [3.6 V, 3.8 V]; for LCO, it is [3.8 V, 4.0 V]. This feature effectively addresses the issue of feature observability in partial charge–discharge scenarios, making it more suitable for practical applications. Compared to features derived from full-cycle curves, this feature effectively addresses the issue of feature observability in partial charge–discharge scenarios, rendering it more suitable for practical applications.

3.2. Self-Supervised Learning

As a learning paradigm that eliminates the need for manual annotation, self-supervised learning derives supervisory signals by exploiting the intrinsic structure of data. It primarily falls into two main categories: generative methods (such as reconstructing original data by predicting masked parts) and contrastive methods (requiring the model to distinguish different inputs in the feature space) [27]. Contrastive methods typically rely on the construction of high-quality positive/negative samples and complex stability strategies, whereas generative methods can circumvent these constraints. Their task of reconstructing the global distribution of raw data is more aligned with the characteristics of battery voltage sequences [28]. Based on this, and considering the superior performance of the transformer in processing time-series tasks [29], this study employs its architecture to reconstruct raw voltage data. However, the general representations learned solely from the sequence reconstruction may not directly relate to battery capacity. Inspired by the design philosophy of the Bert model [30], a learnable CLS vector is introduced at the front of the sequence as a global supervisory signal. This enables the model to predict interval capacity features strongly correlated with SOH, thereby guiding it to capture key representations of capacity degradation. The proposed self-supervised learning framework is illustrated in the “Self-supervised framework” in Figure 3a, where the embedding and encoder modules have been modified based on the original transformer structure. The position encoding in the embedding module introduces a time-varying factor, overcoming the limitation of traditional transformer position encoding that cannot represent the aging process. The attention mechanism in the encoder module integrates domain knowledge, focusing on critical aging regions, addressing the issue of dilution of critical aging features caused by uniform attention distribution in battery data.

Notably, the two tasks in the proposed method are complementary across time scales. The masked voltage reconstruction task enables the model to learn internal variation patterns of the voltage curve, capturing the dynamic processes within the cycle through short-time-scale learning. Combined with the interval capacity prediction task—which captures long-range temporal correlations—the two tasks collaborate in pre-training to overcome the limitations of single-time-scale tasks, which cannot simultaneously capture local variations and long-term trends.

3.2.1. Embedding Part with Time-Varying Factors

The embedding module maps the battery voltage sequence to a high-dimensional representation space and incorporates positional information. This study proposes an embedding architecture that integrates time-varying factors, incorporating the battery aging process into the position encoding. The specific structure is shown in the embedding section of Figure 3b. The input voltage sequence is $\mathbf{u}\in {\mathbb{R}}^{L\times 1}$, where L denotes the length of the voltage sequence. The dimension of the input vector is transformed from L × 1 to L × d via a nonlinear transformation for model embedding, with the embedded vector denoted as E_v. When incorporating positional information, given that traditional transformer positional encoding emphasizes only temporal order and remains identical across different cycles of time series, failing to characterize the aging process, the battery cycle count is integrated as a time-varying factor into positional encoding, as given in Equation (3):

$$\begin{array}{c}\mathrm{PEC}(pos,2i)=\sin \left({\displaystyle \frac{pos}{{10000}^{2i/d_{\mathrm{model}}}}}+{\displaystyle \frac{{cyc}_{\mathrm{num}}}{\epsilon }}\right)\\ \mathrm{PEC}(pos,2i+1)=\cos \left({\displaystyle \frac{pos}{{10000}^{2i/d_{\mathrm{model}}}}}+{\displaystyle \frac{{cyc}_{\mathrm{num}}}{\xi }}\right)\end{array}$$

(3)

where pos∈ [0, L] denotes the time-step position within the sequence, i∈ [0, d_model/2], cyc_num denotes the current cycle count, and ε, ξ are learnable scaling coefficients. After fusing the voltage embedding with the position embedding, the learnable vector $\mathbf{C}\mathbf{L}\mathbf{S}\in {\mathbb{R}}^{1\times d_{model}}$ is concatenated to obtain the final embedding vector ${\mathbf{E}}_F\in {\mathbb{R}}^{\left(L+1\right)\times d_{model}}$, which serves as the input to the encoder module.

3.2.2. Encoder Part with Domain Knowledge

This section employs the transformer’s encoder structure, which adopts a multi-layer stacked architecture. To address the issue of feature dilution caused by uniform attention distribution in the original structure, domain knowledge is incorporated into the attention mechanism to highlight critical aging regions. The encoder’s basic framework is illustrated in Figure 3b. Each layer comprises two core modules: multi-head self-attention and a feedforward neural network (FFN). Given an embedding layer output ${\mathbf{E}}_F\in {\mathbb{R}}^{\left(L+1\right)\times d_{model}}$, linear projections are used to generate query, key, and value matrices:

$$\left\{\begin{array}{l}{Q}_i=E\times W_Q^{(i)},\hspace{1em}{W}_Q^{(i)}\in {ℝ}^{d_h\times d_k}\\ K_i=E\times W_K^{(i)},\hspace{1em}{W}_K^{(i)}\in {ℝ}^{d_h\times d_k}\\ V_i=E\times W_V^{(i)},\hspace{1em}{W}_V^{(i)}\in {ℝ}^{d_h\times d_v}\end{array}\right.$$

(4)

where i ∈ {1, 2, …, h} denotes the index of the attention head, with h representing the number of attention heads. The matrices ${\mathit{W}}_{\mathit{Q}}^{\left(\mathit{i}\right)}$, ${\mathit{W}}_{\mathit{K}}^{\left(\mathit{i}\right)}$, and ${\mathit{W}}_{\mathit{V}}^{\left(\mathit{i}\right)}$ are learned during training, with dimensions satisfying $d_k=d_{\nu }=d_h/h$. The attention score for each attention head is calculated as follows:

$$\left\{\begin{array}{l}{A}_i={\displaystyle \frac{Q_i{K}_i^T}{\sqrt{d_k}}}\\ {\mathrm{head}}_i=\mathrm{softmax}\left(A_i+M\right)V_i\end{array}\right.$$

(5)

where ${\mathit{A}}_i\in {\mathbb{R}}^{L\times L}$ denotes the attention score matrix, and M marks the padding positions. As a fine-grained reconstruction task, the masking task requires the model to capture local temporal dynamic features, which aligns naturally with the attention mechanism. However, the interval capacity prediction task requires the CLS vector to aggregate global features and extract critical components. Traditional attention distributions uniformly focus on all time steps, struggling to capture aging-sensitive key segments and leading to poor CLS aggregation performance. To address this limitation, domain knowledge is integrated into the attention mechanism to direct its focus toward critical aging regions. Given that the voltage phase transition zone of lithium-ion batteries (i.e., the thermodynamic equilibrium plateau formed by lattice restructuring of electrode materials in charge–discharge curves) exhibits a strong correlation with aging mechanisms such as active lithium loss and internal resistance increase [31] and that voltage changes within this zone are typically flat, the reciprocal of the voltage difference is employed as domain knowledge embedded into the attention mechanism. This domain knowledge acts on the CLS vector to enhance its attention weight toward the plateau region. The specific calculation process is as follows:

$$\left\{\begin{array}{l}B=f(1/\mathsf{\Delta }u)\\ \tilde{A}i[:,0,:]=Ai[:,0,:]+\alpha \cdot Bi\\ \widetilde{{\mathrm{head}}_i}=\mathrm{softmax}\left(\tilde{A}i+M\right)V_i\end{array}\right.$$

(6)

where $\mathsf{\Delta }\mathbf{u}\in {\mathbb{R}}^{B\times (L-1)}$ represents the voltage difference, $\mathbf{B}\in {\mathbb{R}}^{B\times h\times \left(L+1\right)}$ represents the adjustment term for the attention scores applied to the CLS for each attention head, h represents the number of attention heads, f represents a linear transformation and padding operation, and α is a learnable weight coefficient. By converting voltage difference signals into attention biases, this approach achieves an upgrade from black-box fitting to physical law-guided learning. Meanwhile, dynamically adjusting aggregation weights based on input voltage enhances the capability of CLS vectors to extract critical aging information. Then, these results from different attention heads are concatenated and connected to the input via a residual connection, as shown in the following equation:

$$H_{\mathrm{atten}}=\mathrm{LayerNorm}(\mathrm{Concat}({\mathrm{head}}_1,\dots ,{\mathrm{head}}_h)W_O+E)$$

(7)

where ${\mathit{W}}^{\mathit{O}}\in {\mathbb{R}}^{h{d}_v\times d_{model}}$ is the output matrix. This output is then fed into the feedforward network, where residual connections are also applied. Each encoder layer includes a self-attention mechanism and a feedforward network, which are then stacked hierarchically. The final output obtained through stacking is ${\mathbf{H}}_{\mathrm{e}\mathrm{n}\mathrm{c}}^{{\mathrm{N}}_{\mathrm{l}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}}}\in {\mathbb{R}}^{B\times (L+1)\times d_{model}}$. The number of stacked layers is a hyperparameter optimized via the algorithm.

3.2.3. Pre-Training and Fine-Tuning

During pre-training, the ${\mathit{H}}_{\mathrm{enc}}^{N_{\mathrm{layer}}}$ output by the encoder is used to extract ${\mathit{H}}_{\mathrm{cls}}$ and ${\mathit{H}}_{\mathrm{vol}}$, which are employed to predict the interval capacity and voltage sequence through different linear layers. After obtaining the predicted values for these two tasks, the error is computed as follows:

$$\left\{\begin{array}{l}{\mathcal{L}}_{\mathrm{c}}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N}{({\widehat{C}}_{\mathrm{range},\mathrm{i}}-C_{\mathrm{range},\mathrm{i}})}^2\\ {\mathcal{L}}_{\mathrm{mask}}={\displaystyle \frac{1}{\left|\mathsf{\Omega }\right|}}\sum _{(i,j)\in \mathsf{\Omega }}{({\widehat{V}}_{i,j}-V_{i,j}^{\mathrm{true}})}^2\end{array}\right.$$

(8)

where N denotes the number of samples and Ω represents the set of mask positions. The losses of the two tasks are weighted via a dynamic loss balancer. Finally, the joint optimization objective for the pre-training stage is obtained:

$${\mathcal{L}}_{\mathrm{pre}-\mathrm{train}}=w_{\mathrm{mask}}\cdot {\mathcal{L}}_{\mathrm{mask}}+w_{\mathrm{C}}\cdot {\mathcal{L}}_{\mathrm{C}}$$

(9)

After completing the pre-training, the parameters of the embedding layer and encoder layer are frozen. A linear classifier is appended after CLS for fine-tuning to predict SOH. The loss function for the fine-tuning phase is as follows:

$${\mathcal{L}}_{\mathrm{fine}-\mathrm{tune}}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{(y_i-\widehat{y}i)}^2$$

(10)

where N denotes the total number of samples, $y_i$ represents the actual SOH value, and ${\widehat{y}}_i$ represents the predicted SOH value.

During the pre-training of the model, this study used a Bayesian optimization framework to systematically search for the optimal combination of hyperparameters. The search space included two categories of parameters: model structure and training control parameters. The specific parameter settings are detailed in

Table 3. Hyperparameters to be optimized.

Hyperparameter Type		Search Space
Network structure parameters	hidden size	{256, 512, 768}
	head of attention	{4, 8}
	encoder layers	{2, 3, 4}
Training control parameters	learning rate scheduler	cosine
		exponential
		step
	learn rate	[10−6, 10−3]
	batch size	{16, 32, 64}

. The optimization process was implemented using 5-fold cross-validation, with an early stopping mechanism integrated into each fold to mitigate the risk of overfitting. After 50 iterations of Bayesian optimization, the optimizer balances exploration and exploitation in the parameter space, determining the optimal configuration via Pareto front analysis.

In addition, the AdamW optimizer was used during the learning process, with RMSE, MAE, and MAPE serving as metrics to evaluate the method’s effectiveness, as shown in the equations below:

$$\begin{array}{c}\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle {\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}}\\ \mathrm{MAE}={\displaystyle \frac{1}{N}}\left|y_i-{\widehat{y}}_i\right|\\ \mathrm{MAPE}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N}{\displaystyle \frac{\left|y^i-{\widehat{y}}^i\right|}{y^i}}\times 100\%\end{array}$$

(11)

4. Results and Discussions

This study was comprehensively validated on the Tongji and CALCE public datasets, with the primary aim of assessing performance in situations characterized by limited labeled data. On the Tongji dataset, two experiments were designed: a baseline test (NCA battery) and a transfer test (transfer between NCA and NCM), which validated the feasibility and generalization ability of the proposed model. The CALCE dataset was used to validate the model’s adaptability in shallow cycle scenarios and its accuracy in situations where data is extremely scarce. All experiments were conducted under a unified hardware configuration (NVIDIA RTX 4060 GPU/Intel i9-12900 CPU/16 GB DDR5 memory) and software environment (Python 3.9 + PyTorch 2.4.0) to ensure the controllability of experimental conditions. This validation framework not only covers the basic accuracy assessment of the model but also examines its transfer robustness in real-world application scenarios.

4.1. Tongji Dataset

4.1.1. NCA Battery

Under the same operating conditions (45 °C, 0.5C charging, 1C discharging), experiments were conducted using five NCA batteries (designated as NCA_45_05_#1 to #5). The proposed method pre-trains the model using unlabeled data from batteries #1 and #2, followed by fine-tuning with 10% of the labeled data. As shown in

Table 4. Test results for NCA battery estimation.

Pre-Train	Fine-Tune	Test	RMSE (%)	MAE (%)	MAPE (%)
NCA_45_05_#1	NCA_45_05_#1	NCA_45_05_#3	0.349	0.274	0.334
NCA_45_05_#2	NCA_45_05_#2	NCA_45_05_#4	0.607	0.496	0.606
(unlabeled)	(10% labeled)	NCA_45_05_#5	0.518	0.425	0.518
Average			0.491	0.398	0.486

, this method demonstrates excellent predictive performance on test batteries #3–#5, with average RMSE, MAE, and MAPE values of 0.491%, 0.398%, and 0.486%, respectively.

To further validate the superiority of the proposed method, two comparative experiments were conducted using XGBoost [13] and CNN-BiLSTM based on the attention mechanism [32]. XGBoost utilized manually constructed statistical features as input, while CNN-BiLSTM employed raw voltage sequences; both were trained with 100% labeled data. Given that the existing semi-supervised learning methods mentioned earlier, while reducing reliance on labeled data, still require labeled data for the entire battery and cannot be compared with the proposed method using 10% labeled data, no semi-supervised comparison experiments were conducted. As shown in

Table 5. Test results of comparative experiments for NCA batteries.

Train	Test	XGBoost			CNN-BiLSTM
		RMSE (%)	MAE (%)	MAPE (%)	RMSE (%)	MAE (%)	MAPE (%)
NCA_45_05_#1	NCA_45_05_#3	0.887	0.749	0.953	0.613	0.541	0.677
NCA_45_05_#2	NCA_45_05_#4	0.991	0.778	0.928	0.700	0.468	0.548
(100% labeled)	NCA_45_05_#5	0.634	0.528	0.645	0.354	0.283	0.34
Average		0.837	0.685	0.842	0.556	0.431	0.522

, the prediction accuracy of XGBoost was RMSE = 0.837%, MAE = 0.685%, and MAPE = 0.842%; the prediction accuracy of CNN-BiLSTM was RMSE = 0.556%, MAE = 0.431%, and MAPE = 0.522%. Notably, the proposed method outperformed using only 10% labeled data (reducing labeling costs by 90% relative to comparative methods). This advantage originates from its dual-time-scale collaborative mechanism: the masked voltage reconstruction task precisely captures local variations in intra-cycle voltage curves, addressing the limitations of XGBoost’s reliance on single feature types; the interval capacity prediction establishes cross-cycle aging correlations, overcoming the constraints of CNN-BiLSTM’s single-sequence local modeling and enhancing the extraction of lifecycle-wide aging characteristics.

Figure 4 illustrates the SOH prediction trajectories and error distributions of the three methods. For prediction trajectories (Figure 4a–c), the SOH curves predicted by the proposed method were highly consistent with actual decay profiles, maintaining stable tracking even during the late-stage nonlinear decay. In contrast, XGBoost and CNN-BiLSTM exhibited marked increases in tracking error during this phase due to inherent limitations in feature extraction or modeling architectures, further validating the proposed method’s adaptability to full-lifecycle battery aging. Regarding error distributions (Figure 4d–f), the proposed method’s error boxplots were the most concentrated, indicating greater stability in predictions; XGBoost and CNN-BiLSTM displayed higher error dispersion, statistically confirming the proposed method’s accuracy superiority.

In addition, this study quantified the parameter counts and training times of various models, as presented in

Table 6. Comparison of parameter counts and training times for different models.

Model	Parameter Counts	Training Times
XGBoost	8276	29.76s
CNN-LSTM	643,938	221.77s
PL23	6,702,477	1171.34s

. The simplest model, XGBoost, had 8 K parameters; CNN-LSTM had 644 K; and the proposed method had 6.7 M parameters. As the model complexity increased, parameter counts exhibited exponential growth; however, comparative analysis (Table 6) revealed that despite an 809-fold increase in parameters, the training time of the proposed model increased by only 39 times, demonstrating significant computational efficiency advantages.

Through dual-time-scale collaborative self-supervised pre-training, the method efficiently harnesses large volumes of unlabeled data, achieving high accuracy with only 10% labeled samples and reducing battery health monitoring labeling costs by 90%. Experiments fully demonstrate that the model can capture common degradation features of batteries under the same operating conditions, providing a more economical and practical technical approach for lithium-ion battery SOH estimation. In industrial settings, this enables replacing full inspections with periodic sampling, significantly shortening the testing period, lowering health monitoring costs, and providing an efficient, near-zero labeling-dependent solution for battery production and maintenance.

4.1.2. Transfer Between NCA and NCM

To validate the model’s generalization capability across different chemical systems, two NCA batteries (NCA_45_05_#1–#2) and two NCM batteries (NCM_35_05_#1–#2) were selected for experimentation. The experimental design was a cross-system transfer validation: first, the model was pre-trained using the unlabeled data from NCA_45_05_#1, then fine-tuned using 10% labeled data from NCM batteries, and finally tested on the complete NCM battery dataset. Symmetrically, the model was pre-trained using the unlabeled data from NCM batteries and transferred to NCA batteries for validation. This bidirectional transfer experimental setup enhances the robustness of the conclusions.

The test results are presented in

Table 7. Test results for transfer estimation between NCA and NCM.

Pre-Train	Fine-Tune (10% Labeled)	Test	RMSE (%)	MAE (%)	MAPE (%)
NCA_45_05 1#	NCM_35_05#1	NCM_35_05#1	0.7	0.493	0.633
	NCM_35_05#2	NCM_35_05#2	0.91	0.624	0.805
NCM_35_05#1	NCA_45_05#1	NCA_45_05 #1	0.915	0.695	0.846
	NCA_45_05#2	NCA_45_05 #2	0.691	0.487	0.602
Average			0.804	0.575	0.976

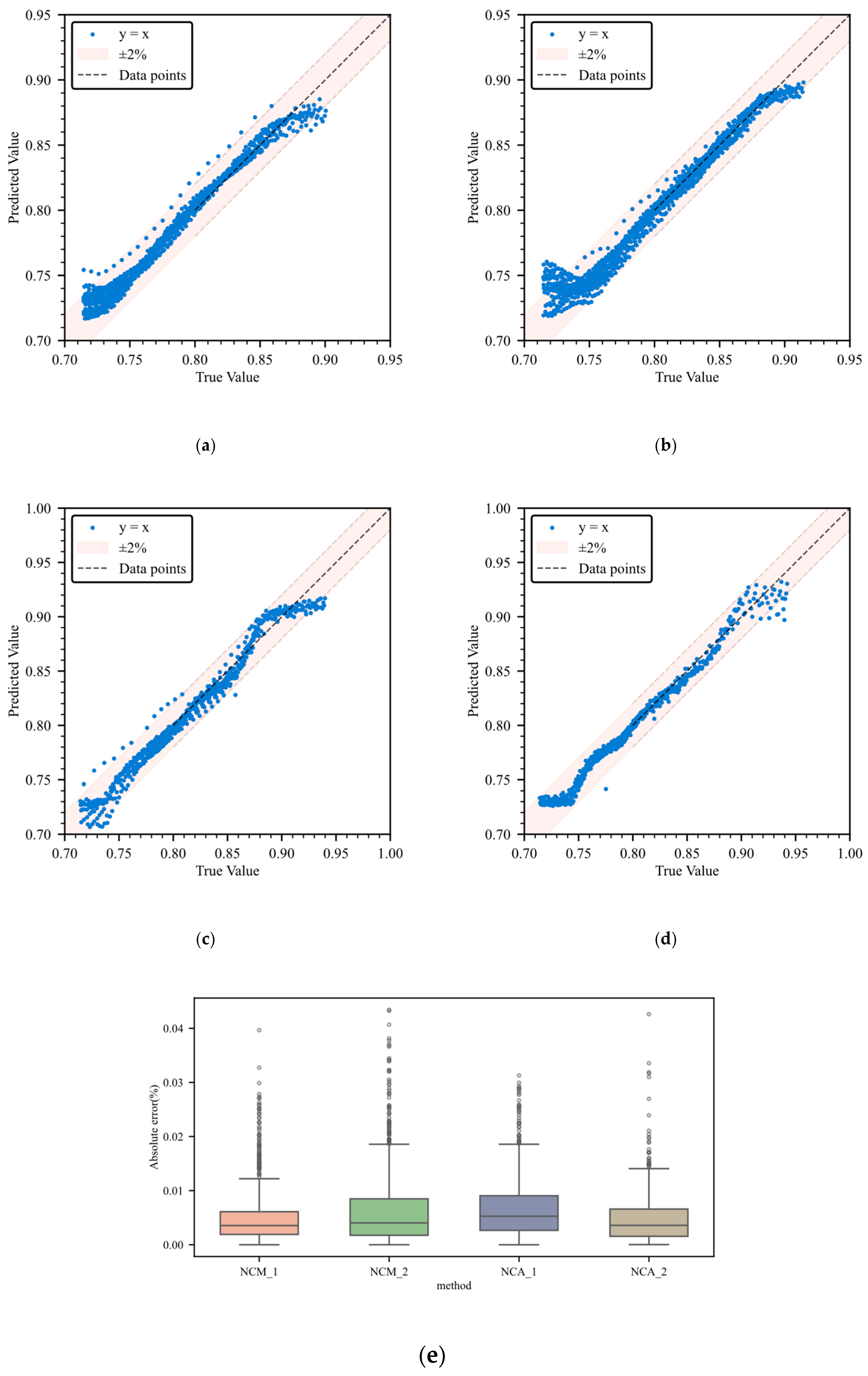
and Figure 5. As shown in Table 6, the model achieved an average prediction accuracy of RMSE = 0.804%, MAE = 0.575%, and MAPE = 0.976% across the four transfer tasks. As shown in the scatter plots in Figure 5a–d, the predicted values and actual values are closely clustered within the ±2% error band around the y = x baseline, intuitively demonstrating their strong correlation; Figure 5e shows the absolute error distribution, with error peaks ≤ 0.05%, and the box plot indicates a narrow interquartile range and few outliers (less than 5%), validating the model’s excellent stability in cross-system predictions.

Experiments demonstrate that this method exhibits exceptional adaptability in cross-chemical system testing. This is due to two factors: first, the dual-time-scale task enables the identification of common aging characteristics across different chemical material batteries; second, the injected domain knowledge and time-varying factors can adaptively adjust according to different batteries, further enhancing the extraction of aging features. Therefore, the model only requires fine-tuning with 10% labeled data from the target domain to adapt to the differences between chemical systems such as NCA and NCM.

4.2. CALCE Dataset

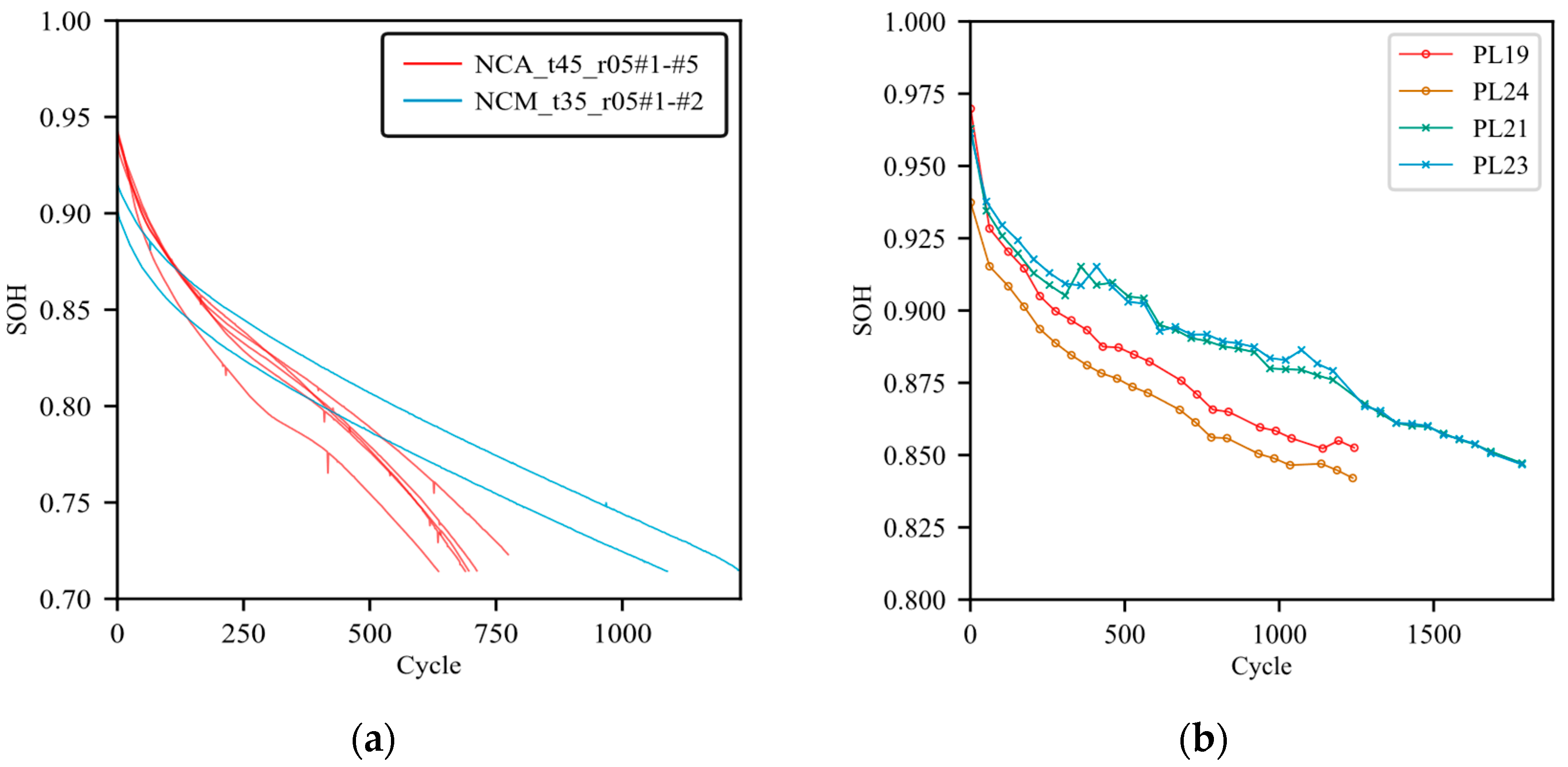
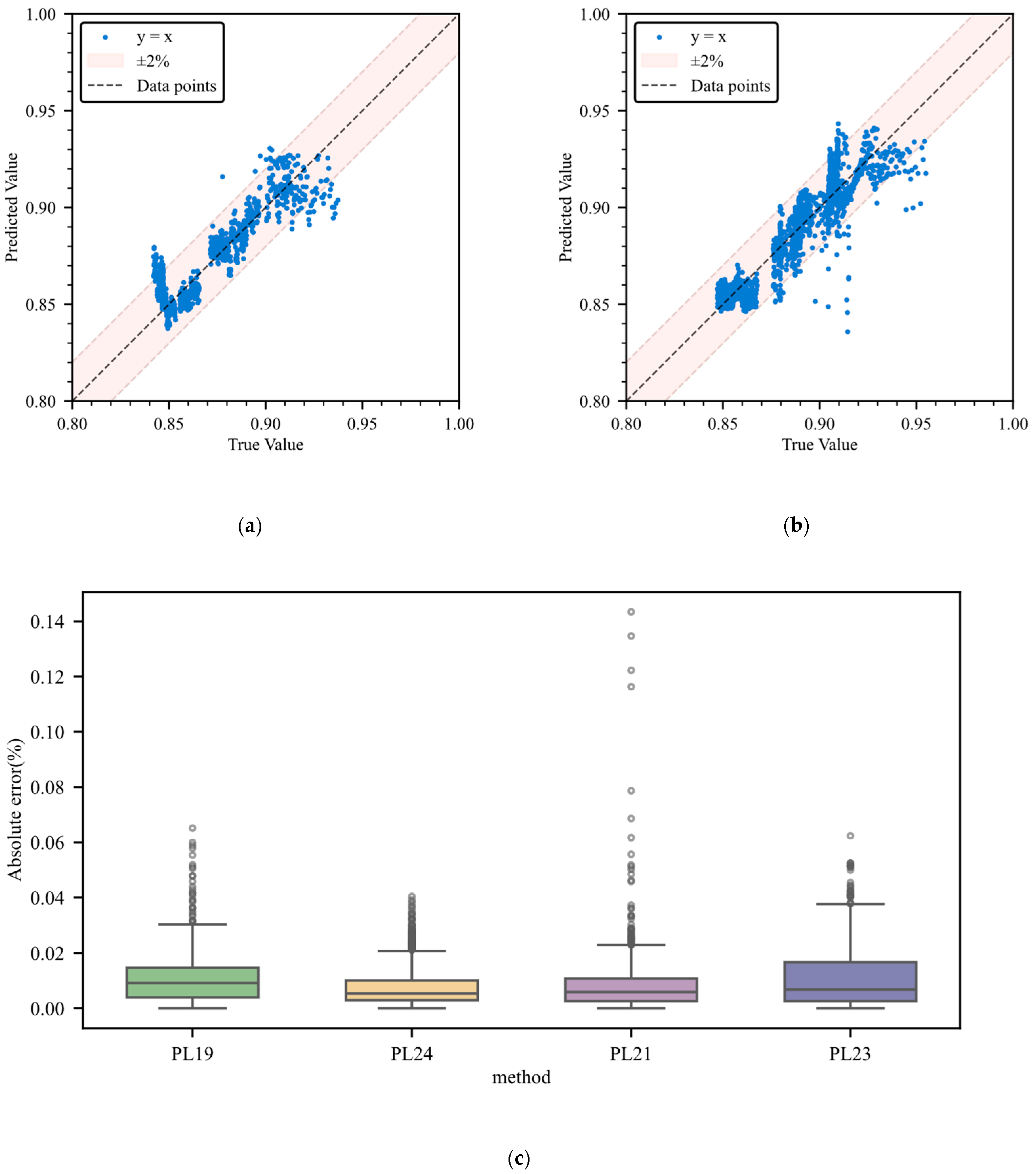
This study, utilizing the CALCE dataset (25 °C, 0.5C operating conditions), investigated the state of health (SOH) prediction performance of lithium batteries under shallow cycle fragment data and extremely sparse labeling scenarios. Two groups of four batteries with different discharge depth (DOD) characteristics were selected: PL19 (40–100%, 1068 cycles, 22 labeled), PL24 (40–100%, 1063 cycles, 22 labeled), PL21, and PL23 (20–80%, 1684 cycles, 34 labeled). The proportion of labeled data for each battery was less than 2%. A cross-validation strategy was employed: first, the model was pre-trained using the unlabeled shallow cycle data from PL19, then fine-tuned with a small amount of labeled data from the same battery, and finally tested on the PL24 battery (the PL24 battery’s full-lifecycle degradation curve was generated using cubic Hermite interpolation to ensure data continuity); symmetrically, the model was pre-trained and fine-tuned using PL24 and then tested on PL19. For PL21 and PL23 with DOD ranging from 20% to 80%, the cross-validation process was repeated to cover characteristics across different SOC intervals.

Test results are shown in Figure 6 and

Table 8. Test results on the CALCE dataset.

Pre-Train	Fine-Tune	Test	RMSE (%)	MAE (%)	MAPE (%)
PL19	PL19	PL24	1.396	1.068	1.202
PL24	PLl24	PL19	1.046	0.771	0.884
PL21	PL21	PL23	1.241	0.799	0.894
PL23	PL23	PL21	1.516	1.087	1.208
Average			1.300	0.931	1.047

, with the model achieving an average prediction accuracy of RMSE = 1.300%, MAE = 0.931%, and MAPE = 1.047% across the four battery groups. In Figure 6a,b, the predicted SOH values for PL24 and PL21 closely align with the y = x baseline, with over 95% of data points falling within the ±2% error band, indicating a strong correlation; the error boxplot in Figure 6c reveals highly concentrated absolute error distributions: PL24 exhibits the lowest median error with <5% outliers, while PL21 has a 3.54% outlier rate, containing minimal large deviants within acceptable statistical limits, validating the model’s stability in extremely sparse labeling conditions.

Notably, the error in the 40–100% SOC group (PL19/PL24) is smaller than that in the 20–80% SOC group (PL21/PL23), and the error distribution of PL19/PL24 is more compact. The reason stems from the high signal recognition of oxidation reactions in the high-voltage zone of the 40–100% SOC range, enabling the mask voltage reconstruction task to precisely capture the oxidation–depletion correlation within the voltage curve during cycles. In contrast, late-stage degradation in the 20–80% SOC interval involves coupled lithium plating and SEI film thickening mechanisms, whose complex electrochemical interactions exceed the feature decomposition capacity of the existing dual-time-scale framework, leading to slightly elevated errors. This finding informs industrial applications: deploying SOH monitoring in high-DOD intervals (e.g., 40–100%) for automotive battery management systems (BMS) can leverage the strong discriminability of oxidation signals to enhance prediction accuracy; full-SOC interval coverage necessitates future task design optimizations to model complex degradation couplings. This pattern has guiding value for industrial applications. Vehicle-grade BMS deploying SOH monitoring in high DOD intervals (e.g., 40–100%) can leverage the high distinguishability of oxidation signals to enhance prediction accuracy. If full SOC interval coverage is required, task design must be further optimized to adapt to complex decay mechanisms.

This work directly addresses limited labeling scenarios in industrial applications such as electric vehicle quarterly maintenance, energy storage station annual inspections, and consumer electronics refurbishment testing. By utilizing <2% labeled data alongside massive unlabeled operational data, it overcomes the data dependency limitations of traditional supervised models. Through dual-time-scale tasks, the model learns degradation response mechanisms under different DOD conditions. Domain knowledge injection enables the attention mechanism to automatically adapt to battery characteristic differences, quickly capturing aging features across different DOD intervals. Experimental validation confirms the effectiveness of the proposed method in extremely sparse-labeled LCO battery scenarios, enabling industrial-grade health status monitoring, thereby extending battery service life and reducing operational costs.

4.3. Ablation Experiment

To validate the contribution of introducing time-varying factors in position encoding and domain knowledge injection in the attention mechanism, ablation experiments were conducted on the Tongji dataset. Three comparative models were designed: Model1 eliminates both time-varying factors in position encoding and domain knowledge in the attention mechanism (dual-component removal); Model2 eliminates only domain knowledge in the attention mechanism (single-component removal); and Model3 eliminates only time-varying factors in position encoding (single-component removal). The complete model (ours) served as a benchmark for comparative analysis.

Experimental results are presented in Figure 7 and

Table 9. Results of ablation experiments on the Tongji dataset.

Test		Model 1	Model 2	Model 3	Ours
NCA_45_05_#3	RMSE (%)	2.918	1.267	1.538	0.349
	MAE (%)	2.648	1.036	1.317	0.274
	MAPE (%)	3.116	1.302	1.586	0.334
NCA_45_05_#4	RMSE (%)	3.171	1.302	1.246	0.607
	MAE (%)	2.898	1.053	1.018	0.496
	MAPE (%)	3.506	1.304	1.215	0.606
NCA_45_05_#5	RMSE (%)	3.073	1.324	1.499	0.518
	MAE (%)	2.635	1.002	1.286	0.425
	MAPE (%)	3.068	1.257	1.561	0.518

. The complete model (ours) significantly outperformed the control groups in terms of RMSE (0.491%), MAE (0.398%), and MAPE (0.486%) on the Tongji dataset: its RMSE was only 16.1% of Model1 (3.054%) and 37.8% of Model2 (1.298%); its MAE was 61.4% lower than that of the second-best model (Model2: 1.030%); and its MAPE was 15.1% of Model1 (3.230%). Table 8 further elaborates on the role of components across different battery samples. For battery #3, domain knowledge in the attention mechanism reduced MAE from 1.036% to 0.274% (73.6% decrease), with this improvement attributed to domain knowledge enhancing feature extraction in the voltage plateau phase transition region—where voltage changes are strongly correlated with aging depth. Domain knowledge guides attention to this region, thereby improving feature discriminability. For battery #4, time-varying factors in position encoding reduced RMSE by 51.3% because they incorporate dynamic characteristics of the aging process, enabling adaptation to the time-varying laws of battery aging. Model1, with both components removed, exhibited the highest MAPE (3.506%), confirming the necessity of these two innovations for maintaining baseline prediction capabilities.

Component contributions were quantified using the average MAE across multiple battery samples: domain knowledge in the attention mechanism contributed approximately 60% of the error reduction (based on the proportion of MAE difference between Model2 and ours); time-varying factors in position encoding contributed about 35% (based on the proportion of MAE difference between Model3 and ours); and their synergy generated approximately 5% interactive gain, collectively supporting the model’s robustness in sparse labeling scenarios.

5. Conclusions

This study proposes an innovative self-supervised learning framework to address the two core challenges of limited availability of labeled data and mismatched operating conditions in lithium-ion battery state of health (SOH) estimation. Through a dual-time-scale, dual-auxiliary task collaborative pre-training mechanism that combines voltage sequence reconstruction and interval capacity prediction, the model enables cross-time-scale feature mining from unlabeled data. By integrating domain knowledge into attention mechanisms and introducing time-varying factors in position encoding, the model embeds the physical principles of battery degradation into the self-supervised architecture, significantly enhancing its capability to capture aging-sensitive features. This method has good generalization capabilities for batteries of different chemical types and discharge depths. Experimental validation demonstrates that on the standard dataset (Tongji), only 10% labeled data is required to achieve an estimation accuracy of RMSE = 0.491% for the NCA battery and RMSE = 0.804% for transfer between NCA and NCM; on the shallow-cycle dataset (CALCE), an average RMSE of 1.300% is achieved with only 2% labeled data, reducing the labeling cost for battery health monitoring by 90–98%. This “self-supervised pre-training and extremely sparse fine-tuning” paradigm offers a low-labeling-requirement solution for battery health management that is feasible for engineering deployment. It is for scenarios such as quarterly inspections of electric vehicles and annual maintenance of energy storage stations, effectively overcoming the bottleneck of traditional supervised models’ reliance on large-scale labeled data.

The current training paradigm primarily targets specific charge–discharge ranges. When input data spans significantly disparate SOC intervals, the model encounters challenges in feature space decoupling. This challenge arises from the distinct electrochemical behaviors exhibited by lithium-ion batteries across disparate SOC ranges, with existing self-supervised tasks lacking the capability to distinguish cross-range feature clusters. To address this challenge, future research will introduce a distribution-aware contrastive learning strategy. By constructing cross-domain negative samples and designing a contrastive loss function to force the model to distinguish feature clusters across disparate SOC ranges, interference from cross-range electrochemical behaviors can be decoupled. This innovative method is expected to overcome existing limitations, offering more robust monitoring solutions for complex charging and discharging scenarios and further expanding the application scope of low-labeling health management technologies. At the same time, this study will also use neural architecture search (NAS) to compress the number of model parameters to meet BMS deployment requirements [33].