Incremental Capacity-Based Variable Capacitor Battery Model for Effective Description of Charge and Discharge Behavior †
Abstract
1. Introduction
- A voltage-dependent capacitor battery model is proposed, which is directly obtained from the IC curve.
- Equivalent capacitance is introduced to approximately calculate the balancing time process, together with the circuit equivalent resistance.
- A balancing time calculation process is formulated for active balancing topologies as well as a passive balancing circuit.
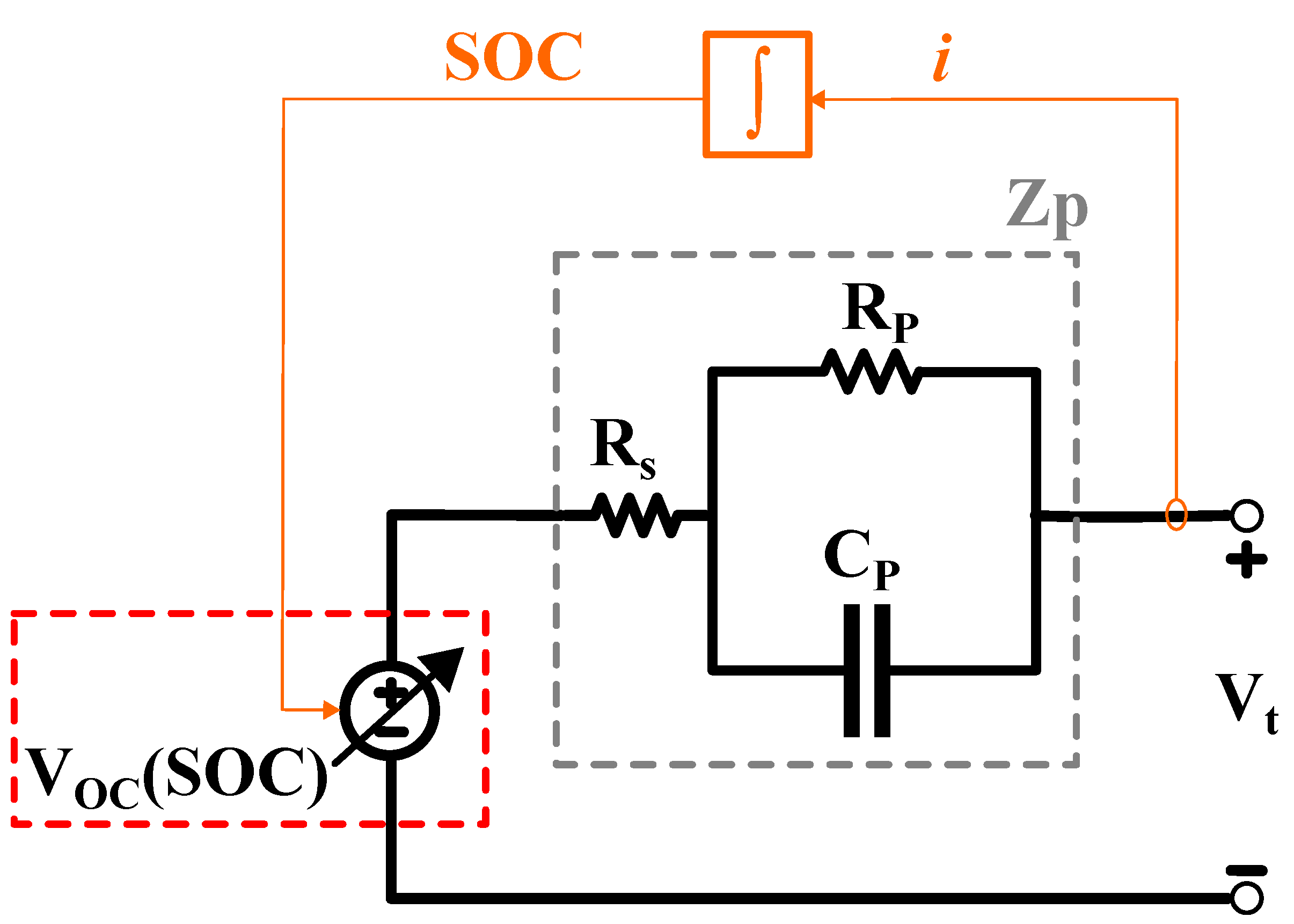
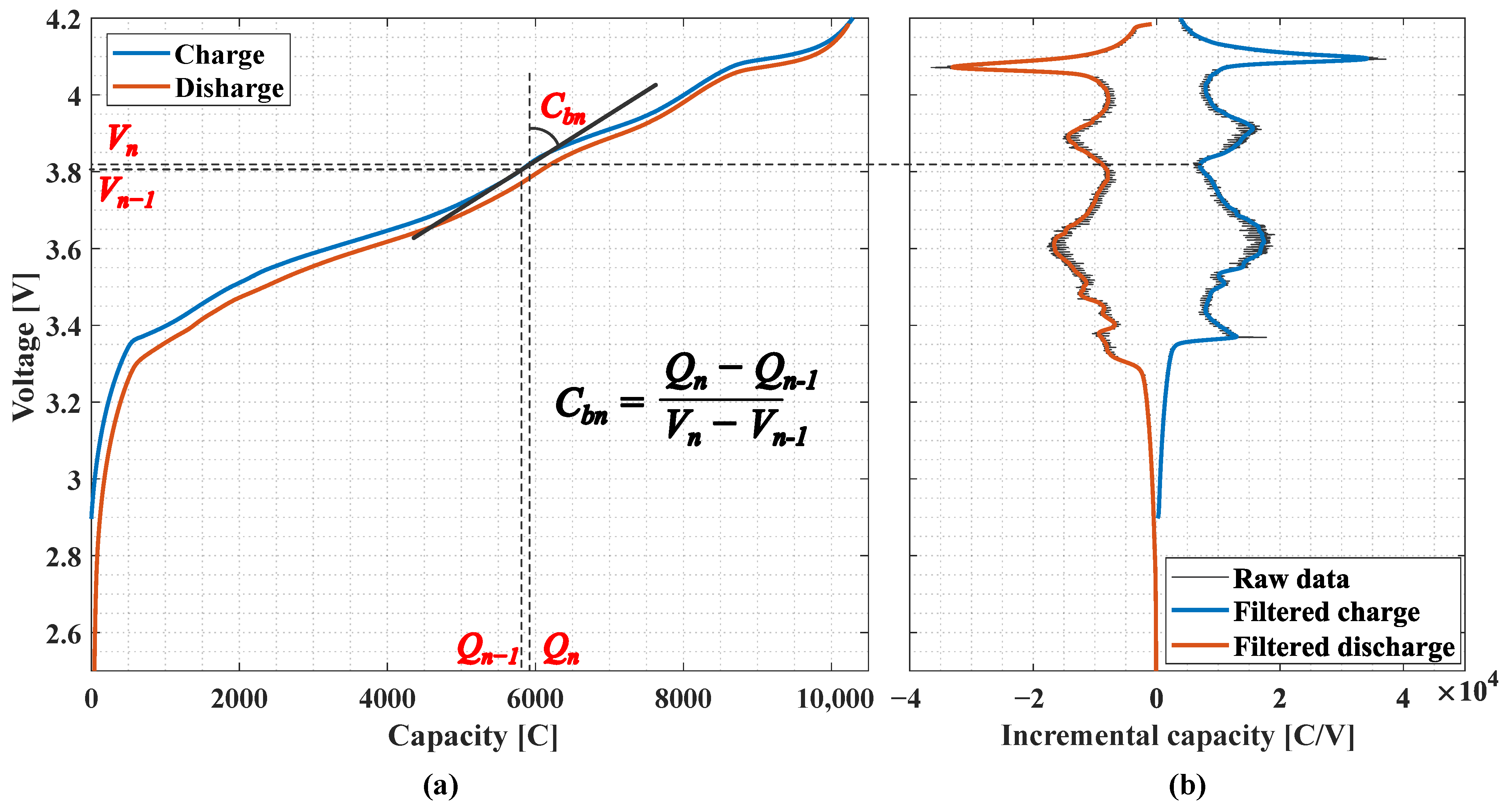
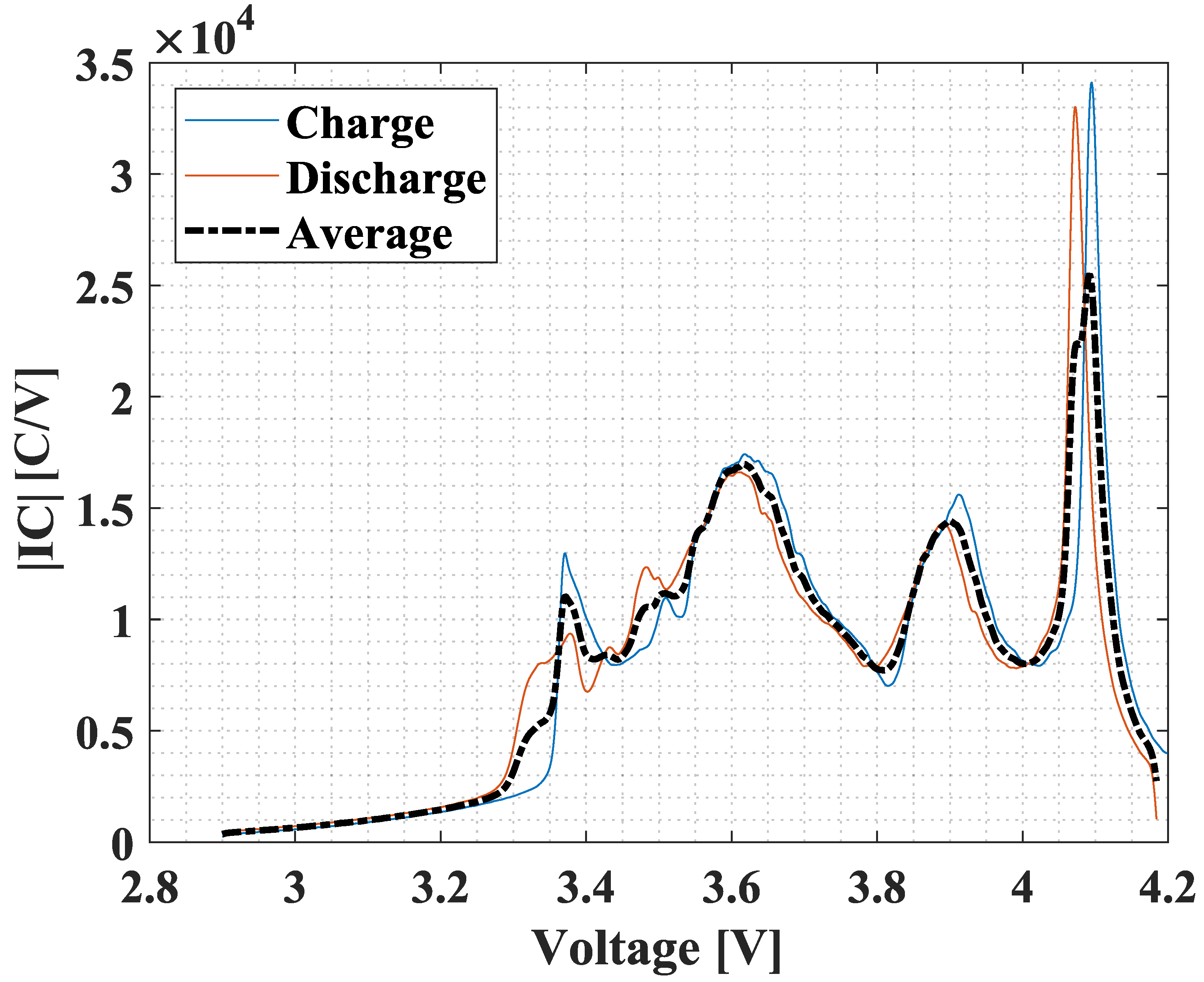
2. IC-Based Variable Capacitor Battery Model
2.1. Model Formulation
2.2. Model Validation
3. CDT Calculation for Cell Balancing
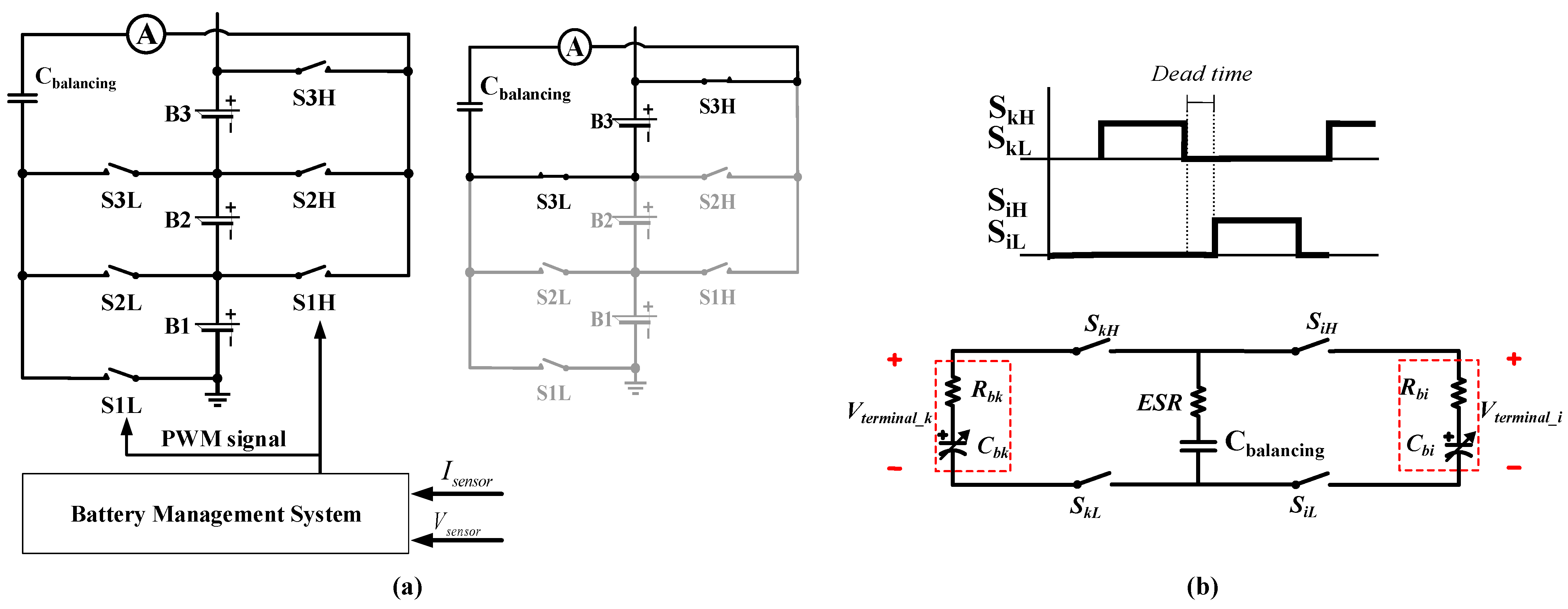
3.1. Active Cell Balancing
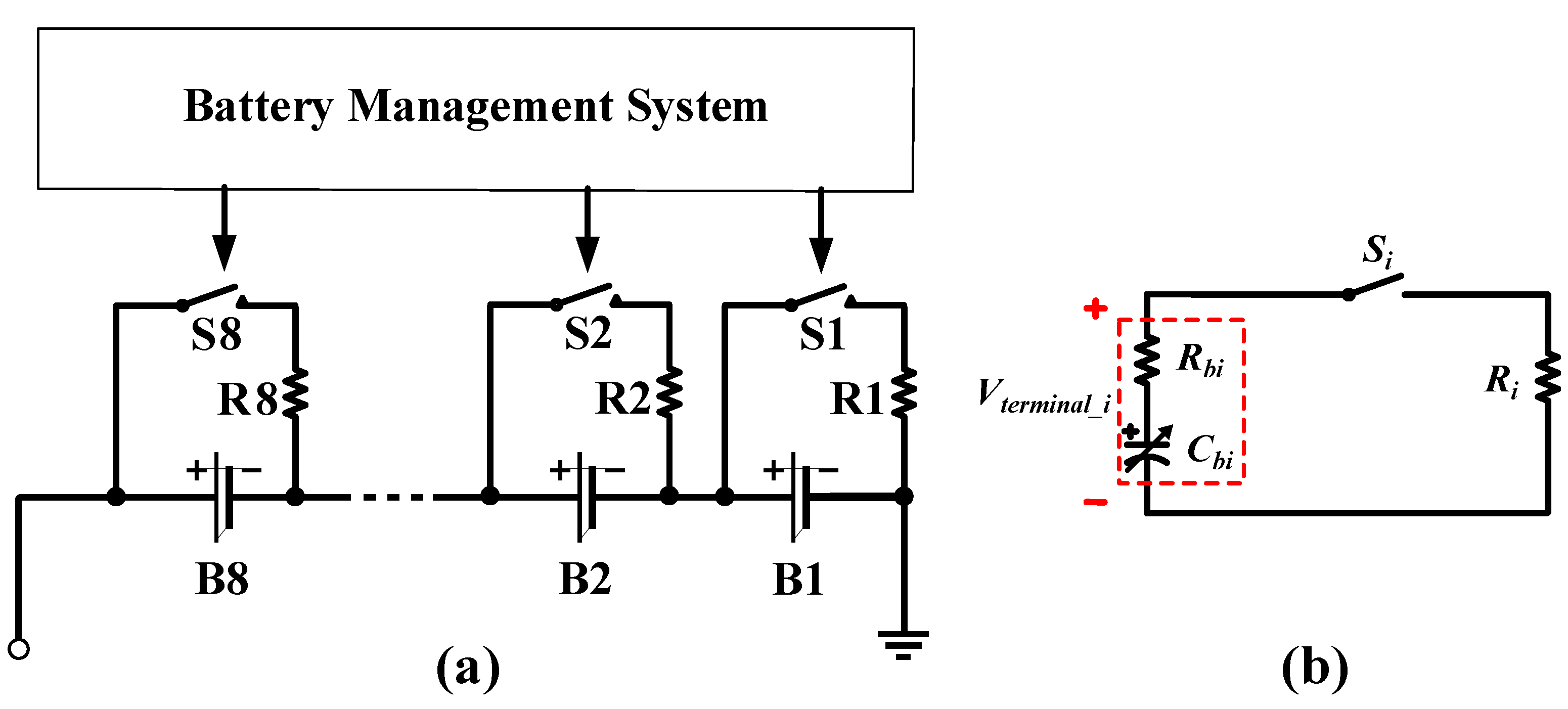
3.2. Passive Cell Balancing
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Einhorn, M.; Roessler, W.; Fleig, J. Improved performance of serially connected Li-ion batteries with active cell balancing in electric vehicles. IEEE Trans. Veh. Technol. 2011, 60, 2448–2457. [Google Scholar] [CrossRef]
- Dubarry, M.; Devie, A.; Liaw, B.Y. Cell-balancing currents in parallel strings of a battery system. J. Power Sources 2016, 321, 36–46. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, X.; Shang, B.; Li, G. Unbalanced discharging and aging due to temperature differences among the cells in a lithium-ion battery pack with parallel combination. J. Power Sources 2016, 306, 733–741. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, C.; Sang, S.; Yu, S. Estimation of remaining energy and available power for Li-Ion battery packs considering energy consumption by heat convection. J. Power Electron. 2023, 23, 139–148. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z. A framework for state-of-charge and remaining discharge time prediction using unscented particle filter. Appl. Energy 2020, 260, 114324. [Google Scholar] [CrossRef]
- Ren, D.; Lu, L.; Shen, P.; Feng, X.; Han, X.; Ouyang, M. Battery remaining discharge energy estimation based on prediction of future operating conditions. J. Energy Storage 2019, 25, 100836. [Google Scholar] [CrossRef]
- Bak, Y. Hardware-simulator development and implementation of battery charger for personal mobility devices. J. Power Electron. 2023, 23, 211–218. [Google Scholar] [CrossRef]
- Choi, J.; Bak, Y. Dynamic characteristic improvement of battery chargers for personal mobility devices using sliding mode control. J. Power Electron. 2024, 24, 140–146. [Google Scholar] [CrossRef]
- Choi, H. Overview of charging technology evolution in smartphones. J. Power Electron. 2023, 23, 1931–1941. [Google Scholar] [CrossRef]
- Pedram, M.; Wu, Q. Design considerations for battery-powered electronics. In Proceedings of the 36th Annual ACM/IEEE Design Automation Conference, New Orleans, LA, USA, 21–25 June 1999; pp. 861–866. [Google Scholar]
- Baronti, F.; Roncella, R.; Saletti, R. Performance comparison of active balancing techniques for lithium-ion batteries. J. Power Sources 2014, 267, 603–609. [Google Scholar] [CrossRef]
- Chen, M.; Rincon-Mora, G.A. Accurate electrical battery model capable of predicting runtime and IV performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- La, P.H.; Choi, S.J. Direct cell-to-cell equalizer for series battery string using switch-matrix single-capacitor equalizer and optimal pairing algorithm. IEEE Trans. Power Electron. 2022, 37, 8625–8639. [Google Scholar] [CrossRef]
- Bouchhima, N.; Schnierle, M.; Schulte, S.; Birke, K.P. Active model-based balancing strategy for self-reconfigurable batteries. J. Power Sources 2016, 322, 129–137. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, S. Energy balance control of multi group lithium ion batteries under internet of things technology. IEEE Access 2024, 12, 102784–102797. [Google Scholar] [CrossRef]
- Khan, A.B.; Choi, W. Optimal charge pattern for the high-performance multistage constant current charge method for the li-ion batteries. IEEE Trans. Energy Convers. 2018, 33, 1132–1140. [Google Scholar] [CrossRef]
- Jiang, L.; Li, Y.; Huang, Y.; Yu, J.; Qiao, X.; Wang, Y.; Huang, C.; Cao, Y. Optimization of multi-stage constant current charging pattern based on Taguchi method for Li-Ion battery. Appl. Energy 2020, 259, 114148. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Tamilselvi, S.; Gunasundari, S.; Karuppiah, N.; Razak RK, A.; Madhusudan, S.; Nagarajan, V.M.; Sathish, T.; Shamim, M.Z.M.; Saleel, C.A.; Afzal, A. A review on battery modelling techniques. Sustainability 2021, 13, 10042. [Google Scholar] [CrossRef]
- Bruch, M.; Millet, L.; Kowal, J.; Vetter, M. Novel method for the parameterization of a reliable equivalent circuit model for the precise simulation of a battery cell’s electric behavior. J. Power Sources 2021, 490, 229513. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Pham, N.T.; Kim, J.H.; Choi, S.J. Novel battery model employing variable capacitor for effective description of SOC behavior. In Proceedings of the 2024 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 25–29 February 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 3035–3040. [Google Scholar]
- Khan, A.B.; Pham, V.L.; Nguyen, T.T.; Choi, W. Multistage constant-current charging method for Li-Ion batteries. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Busan, Republic of Korea, 1–4 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 381–385. [Google Scholar]
- Johnson, V. Battery performance models in ADVISOR. J. Power Sources 2002, 110, 321–329. [Google Scholar] [CrossRef]
- Tian, N.; Fang, H.; Chen, J.; Wang, Y. Nonlinear double-capacitor model for rechargeable batteries: Modeling, identification, and validation. IEEE Trans. Control Syst. Technol. 2020, 29, 370–384. [Google Scholar] [CrossRef]
- Dubarry, M.; Liaw, B.Y. Identify capacity fading mechanism in a commercial LiFePO4 cell. J. Power Sources 2009, 194, 541–549. [Google Scholar] [CrossRef]
- Dubarry, M.; Svoboda, V.; Hwu, R.; Liaw, B.Y. Capacity and power fading mechanism identification from a commercial cell evaluation. J. Power Sources 2007, 165, 566–572. [Google Scholar] [CrossRef]
- Anseán, D.; García, V.M.; González, M.; Blanco-Viejo, C.; Viera, J.C.; Pulido, Y.F.; Sánchez, L. Lithium-ion battery degradation indicators via incremental capacity analysis. IEEE Trans. Ind. Appl. 2019, 55, 2992–3002. [Google Scholar] [CrossRef]
- Schaltz, E.; Stroe, D.I.; Nørregaard, K.; Ingvardsen, L.S.; Christensen, A. Incremental capacity analysis applied on electric vehicles for battery state-of-health estimation. IEEE Trans. Ind. Appl. 2021, 57, 1810–1817. [Google Scholar] [CrossRef]
- Plexim GmbH. PLECS User Manual; Plexim GmbH: Zurich, Switzerland, 2025; Available online: https://www.plexim.com (accessed on 1 August 2025).
- Daowd, M.; Omar, N.; Van Den Bossche, P.; Van Mierlo, J. Passive and active battery balancing comparison based on MATLAB simulation. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–7. [Google Scholar]
- Ye, Y.; Cheng, K.W.E.; Fong, Y.C.; Xue, X.; Lin, J. Topology, modeling, and design of switched-capacitor-based cell balancing systems and their balancing exploration. IEEE Trans. Power Electron. 2016, 32, 4444–4454. [Google Scholar] [CrossRef]
- Chapra, S.C.; Canale, R.P. Numerical Methods for Engineers; Mcgraw-Hill: New York, NY, USA, 2011; Volume 1221. [Google Scholar]
- Omariba, Z.B.; Zhang, L.; Sun, D. Review of battery cell balancing methodologies for optimizing battery pack performance in electric vehicles. IEEE Access 2019, 7, 129335–129352. [Google Scholar] [CrossRef]
- Ben-Yaakov, S.; Evzelman, M. Generic and unified model of switched capacitor converters. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 3501–3508. [Google Scholar]
- Ye, Y.; Cheng, K.W.E. Analysis and design of zero-current switching switched-capacitor cell balancing circuit for series-connected battery/supercapacitor. IEEE Trans. Veh. Technol. 2017, 67, 948–955. [Google Scholar] [CrossRef]
- Li, S.; Mi, C.C.; Zhang, M. A high-efficiency active battery-balancing circuit using multiwinding transformer. IEEE Trans. Ind. Appl. 2012, 49, 198–207. [Google Scholar] [CrossRef]
- Peng, J.; Zhao, X.; Ma, J.; Meng, D.; Jia, S.; Zhang, K.; Gu, C.; Ding, W. State of Health Estimation of Li-Ion Battery via Incremental Capacity Analysis and Internal Resistance Identification Based on Kolmogorov–Arnold Networks. Batteries 2024, 10, 315. [Google Scholar] [CrossRef]



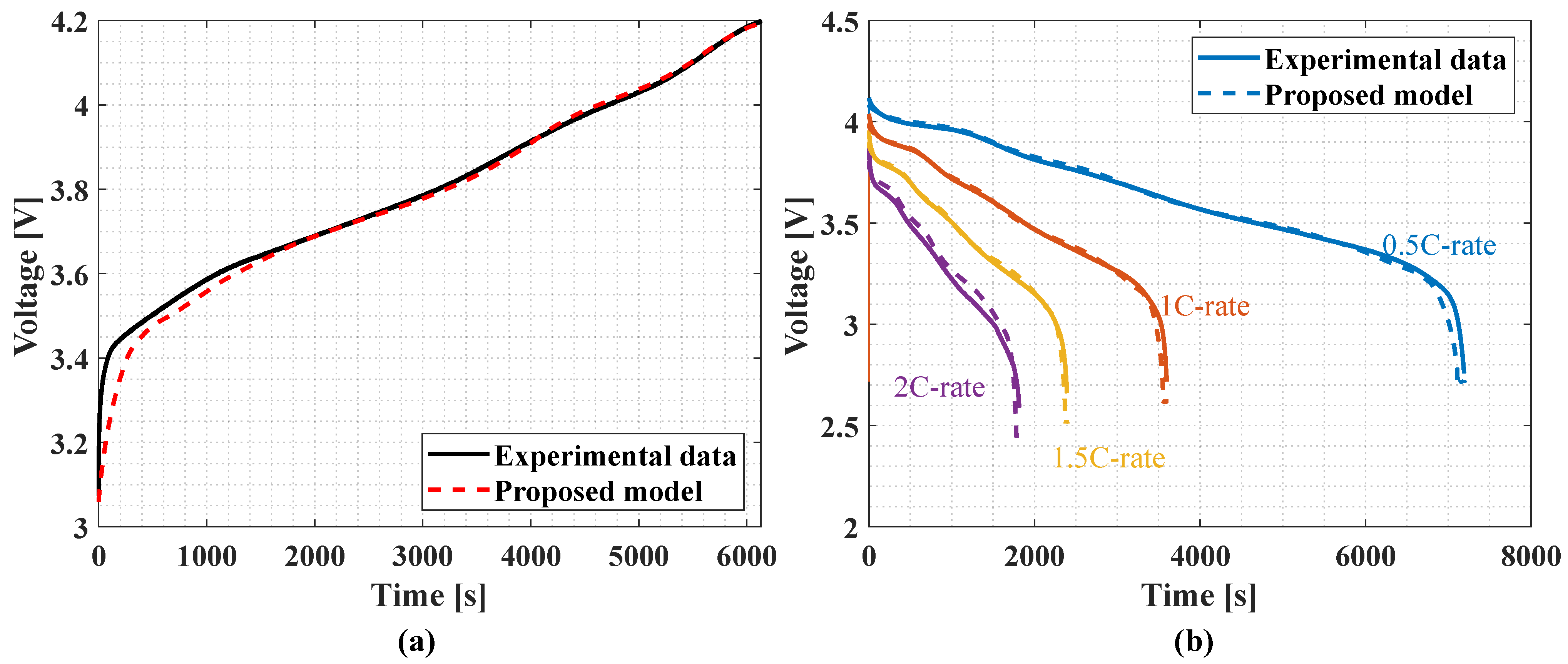



| Stage | Current | MAPE [%] |
|---|---|---|
| Charge | 0.5 C-rate | 0.031 |
| Discharge | 0.5 C-rate | 0.040 |
| 1 C-rate | 0.046 | |
| 1.5 C-rate | 0.033 | |
| 2 C-rate | 0.124 |
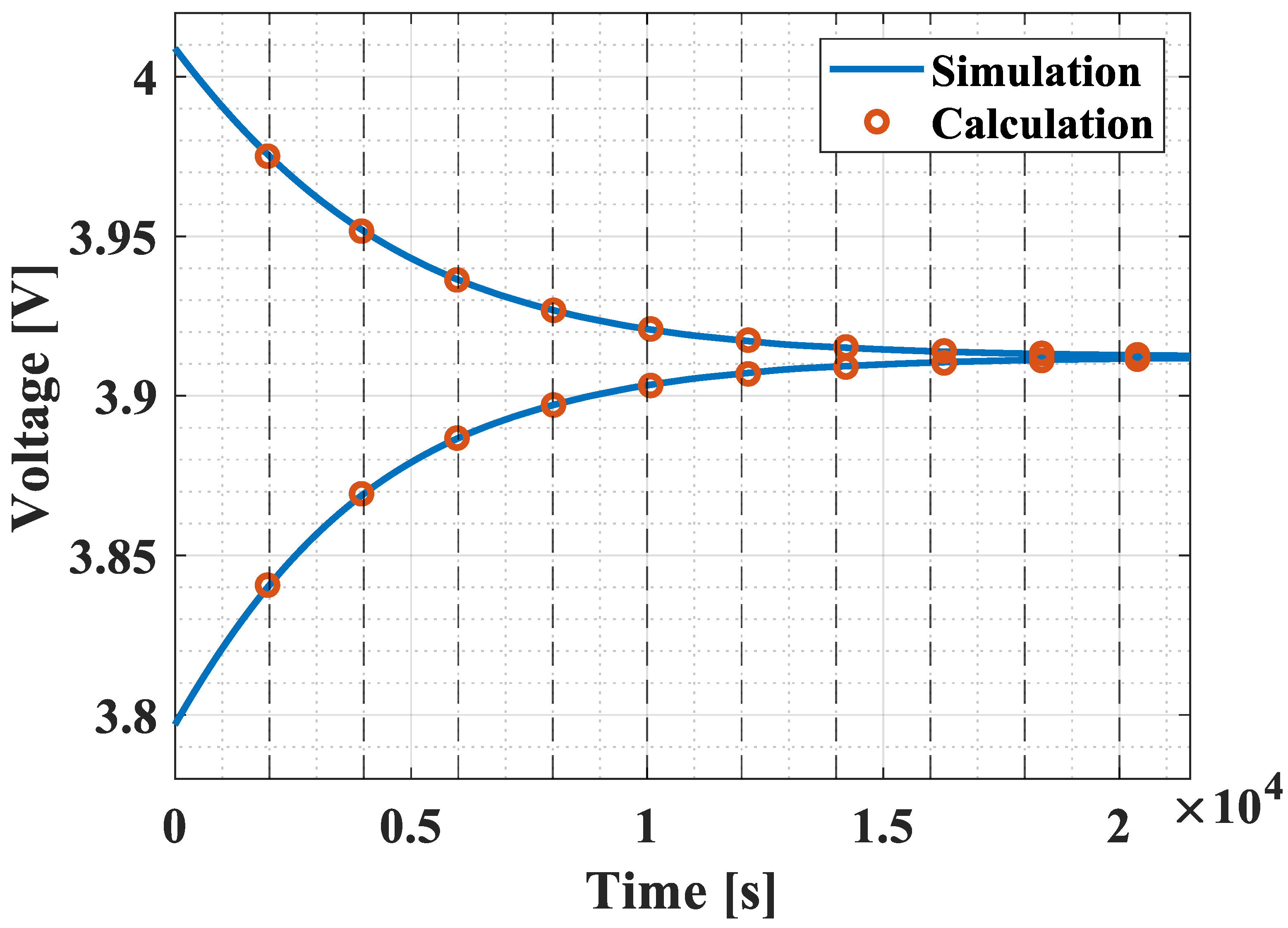
| Time [s] | [V] | [V] | [F] | [F] | [mV] | [s] | [s] | [%] |
|---|---|---|---|---|---|---|---|---|
| 2000 | 3.975 | 3.841 | 12,002.63 | 9283.09 | 134.43 | 2000 | 1959.11 | 2.04 |
| 4000 | 3.952 | 3.869 | 11,490.82 | 9100.40 | 82.32 | 4000 | 3949.03 | 1.27 |
| 6000 | 3.936 | 3.887 | 11,183.37 | 9039.34 | 49.58 | 6000 | 5971.65 | 0.47 |
| 8000 | 3.927 | 3.897 | 11,004.61 | 9022.76 | 29.67 | 8000 | 8016.20 | −0.20 |
| 10,000 | 3.921 | 3.903 | 10,900.80 | 9020.14 | 17.72 | 10,000 | 10,073.07 | −0.73 |
| 12,000 | 3.917 | 3.907 | 10,840.22 | 9021.14 | 10.57 | 12,000 | 12,140.47 | −1.17 |
| 14,000 | 3.915 | 3.909 | 10,804.68 | 9022.64 | 6.31 | 14,000 | 14,209.55 | −1.50 |
| 16,000 | 3.914 | 3.910 | 10,783.58 | 9023.85 | 3.76 | 16,000 | 16,289.74 | −1.81 |
| 18,000 | 3.913 | 3.911 | 10,771.21 | 9024.68 | 2.25 | 18,000 | 18,355.77 | −1.98 |
| 20,000 | 3.913 | 3.912 | 10,763.67 | 9025.19 | 1.36 | 20,000 | 20,383.05 | −1.92 |
| Experimental Item | Specification |
|---|---|
| Battery cell | SDI, INR18650-29E, 3.6 V/2.85 Ah |
| Temperature | Room temperature |
| Passive balancing chip | Analog device, LTC6804 |
| Data logger | HIOKI, LR8420 |
| Impedance analyzer | Zive SP10 |
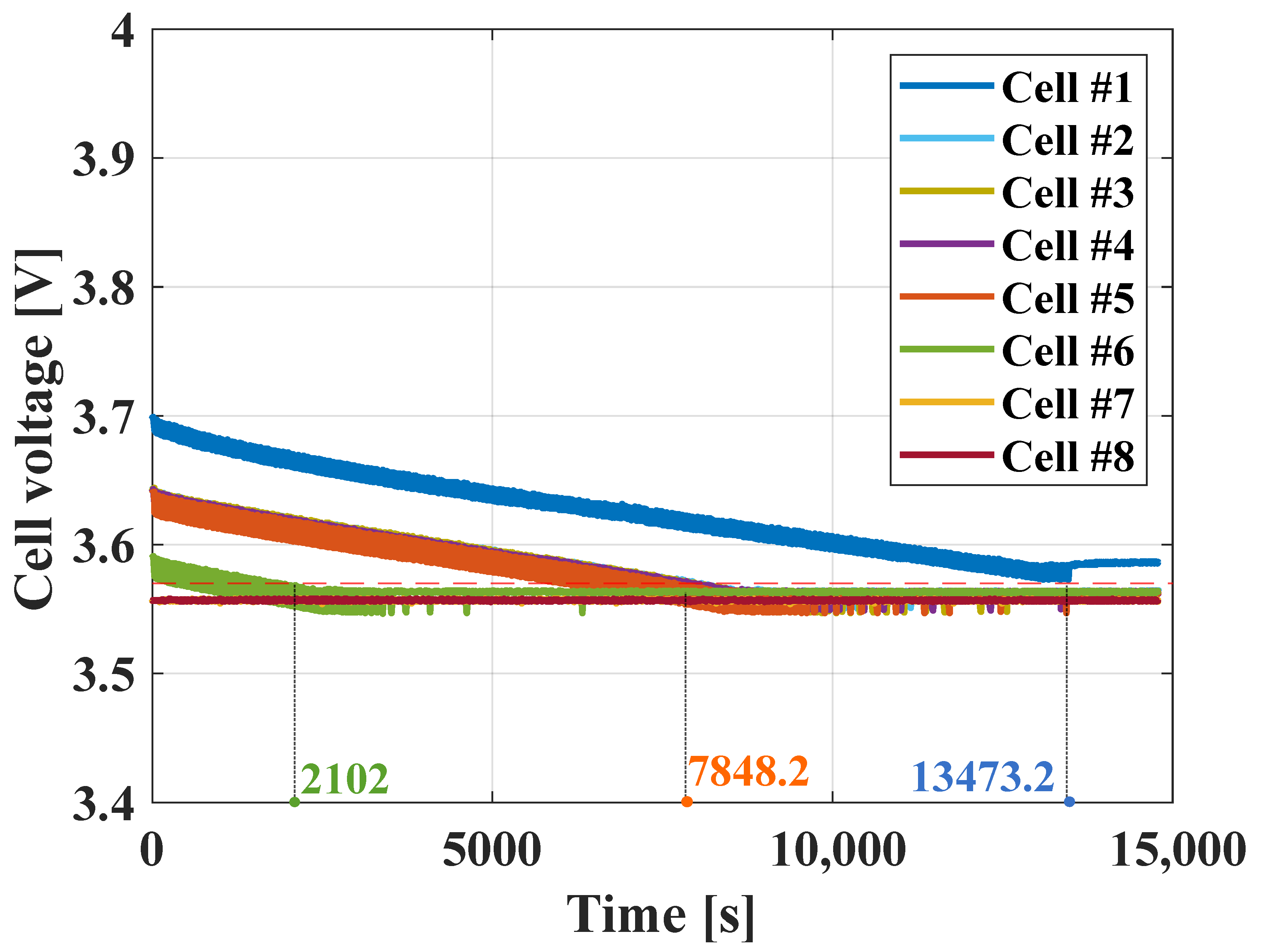
| Cell | [V] | [V] | [F] | [] | [s] | [s] | [%] | ||
|---|---|---|---|---|---|---|---|---|---|
| #1 | 0.49 | 0.32 | 3.698 | 3.57 | 13,731.574 | 27.355 | 13,232.046 | 13,473.2 | 1.790 |
| #2, #3, #4 | 0.42 | 0.32 | 3.643 | 3.57 | 14,029.867 | 27.355 | 7768.587 | 7848.2 | 1.014 |
| #5 | 0.34 | 0.32 | 3.59 | 3.57 | 14,031.207 | 27.355 | 2144.272 | 2102 | −2.011 |
| #6, #7 | 0.30 | - | 3.557 | - | - | - | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, N.-T.; Kwon, S.; Choi, S.-J. Incremental Capacity-Based Variable Capacitor Battery Model for Effective Description of Charge and Discharge Behavior. Batteries 2025, 11, 300. https://doi.org/10.3390/batteries11080300
Pham N-T, Kwon S, Choi S-J. Incremental Capacity-Based Variable Capacitor Battery Model for Effective Description of Charge and Discharge Behavior. Batteries. 2025; 11(8):300. https://doi.org/10.3390/batteries11080300
Chicago/Turabian StylePham, Ngoc-Thao, Sungoh Kwon, and Sung-Jin Choi. 2025. "Incremental Capacity-Based Variable Capacitor Battery Model for Effective Description of Charge and Discharge Behavior" Batteries 11, no. 8: 300. https://doi.org/10.3390/batteries11080300
APA StylePham, N.-T., Kwon, S., & Choi, S.-J. (2025). Incremental Capacity-Based Variable Capacitor Battery Model for Effective Description of Charge and Discharge Behavior. Batteries, 11(8), 300. https://doi.org/10.3390/batteries11080300







