SOC Estimation of Lithium-Ion Batteries Utilizing EIS Technology with SHAP–ASO–LightGBM
Abstract
1. Introduction
- SOC(t0+Δt): SOC value at time t0 + Δt;
- SOC(t0): SOC value at time t0;
- η: Efficiency of the battery’s charge and discharge process;
- I(t): Current during charging or discharging at time t;
- C(total): Total available capacity of the battery.
- Development of an EIS Data Test Bench: An EIS test bench was established to collect EIS data at different SOC points under specified temperature conditions. Using this setup, EIS datasets were successfully obtained for two lithium iron phosphate (LFP) battery cells with a capacity of 3.2 V and 104 Ah.
- Focus on Large-Capacity Lithium-Ion Batteries: Unlike most reported studies, which rarely examine EIS data for large-capacity lithium-ion batteries, particularly those exceeding 100 Ah, this research extracts EIS data from LFP batteries with a capacity of 3.2 V and 104 Ah. The feature data are derived using the SHAP method.
- ML-Based SOC Estimation: An ML approach utilizing the ASO–LightGBM model was developed for SOC estimation using EIS. The ASO algorithm optimizes the hyperparameters of the LightGBM model, while the extracted feature data are used for model training and SOC prediction.
- Validation of Accuracy and Robustness: The proposed SHAP–ASO–LightGBM algorithm for SOC estimation was rigorously validated against existing methods. Comparative results demonstrated that the SHAP–ASO–LightGBM approach significantly improves the accuracy and robustness of SOC estimation for lithium-ion batteries.
2. EIS-Based SOC Estimation: Current Status and Analysis
2.1. The Basic Principles of EIS Techniques
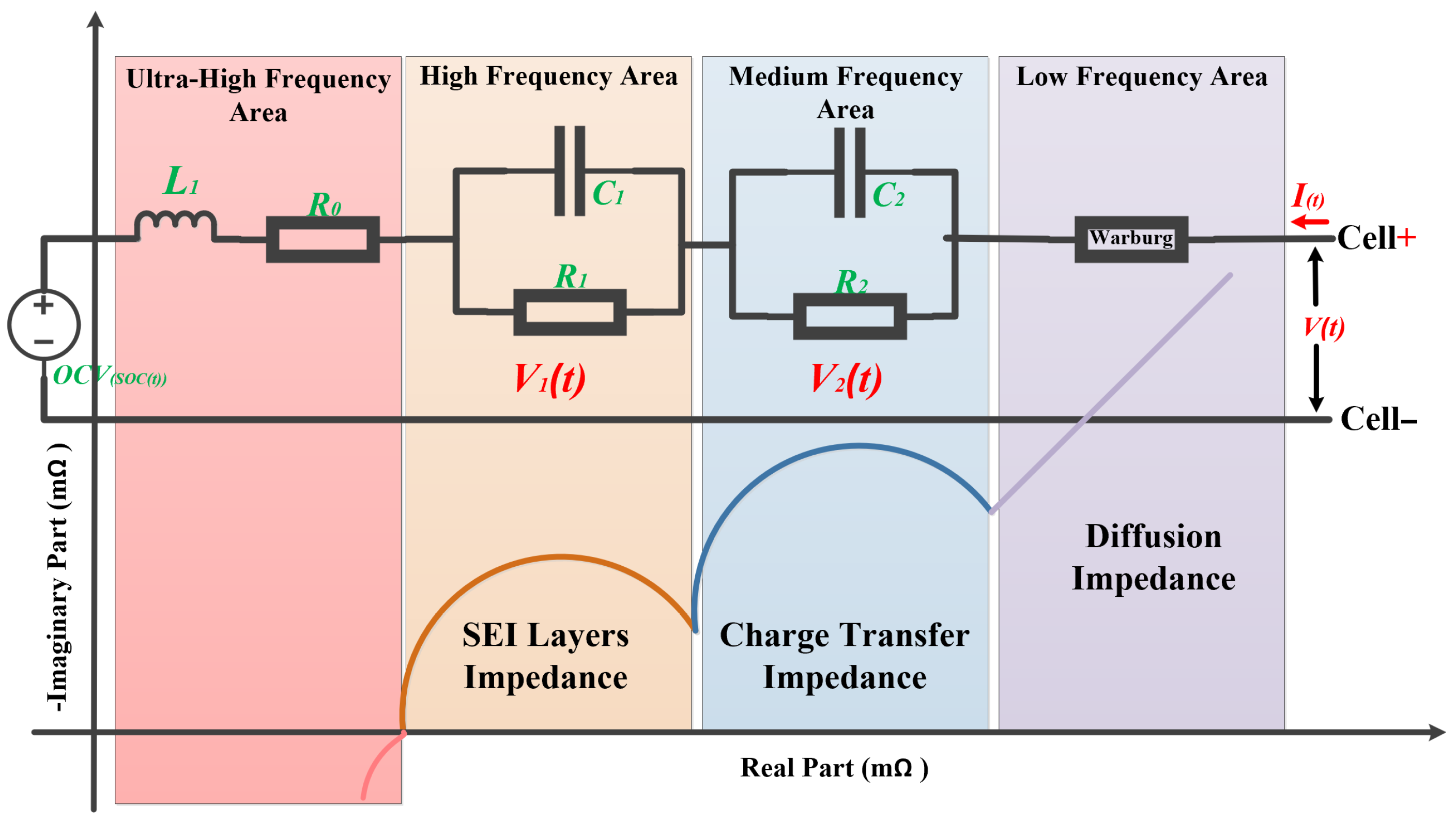
2.2. The Calculation of Impedance Spectrum
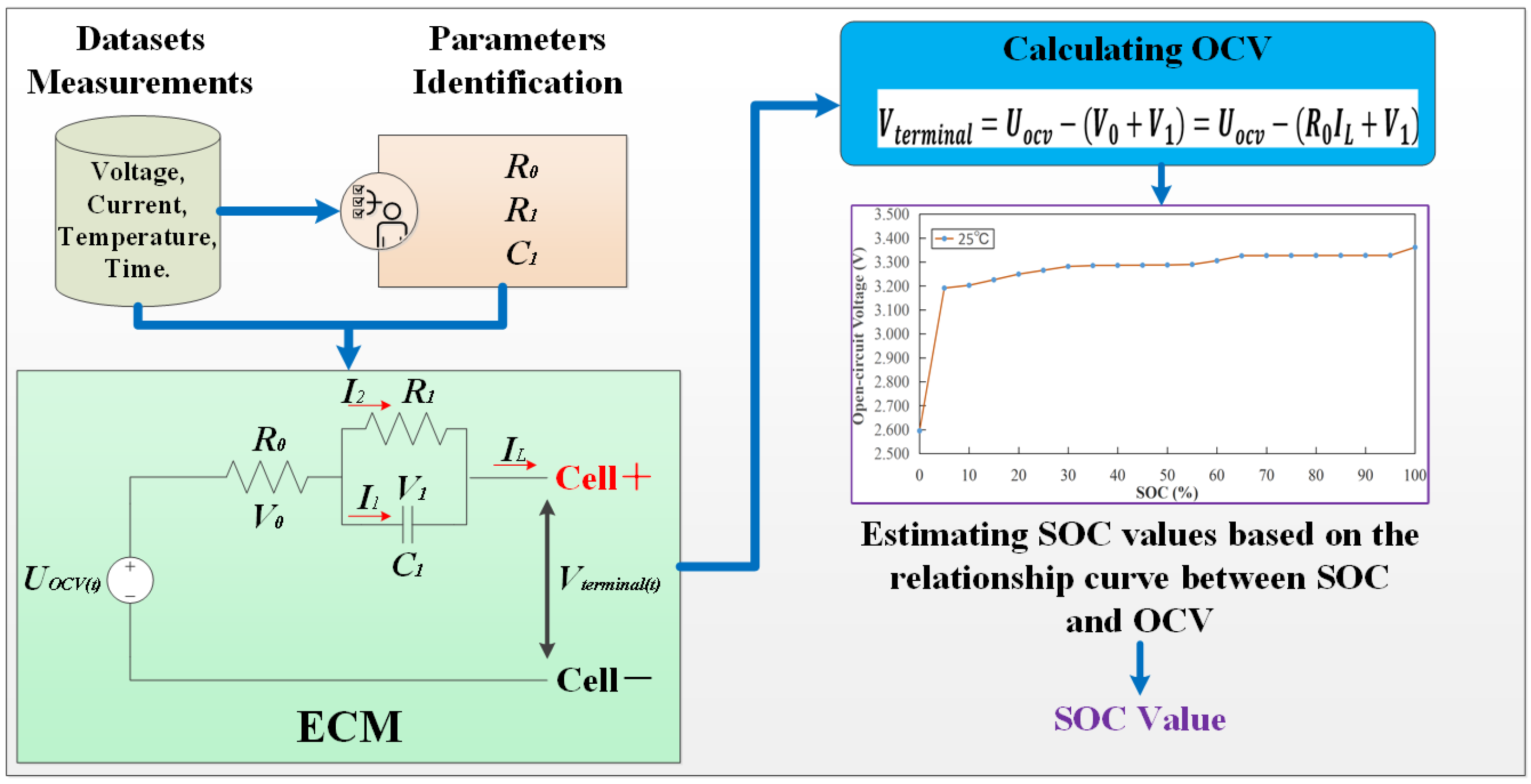
2.3. EIS-Based SOC Estimation
3. Experimental Testing and Feature Extraction Method (FEM)
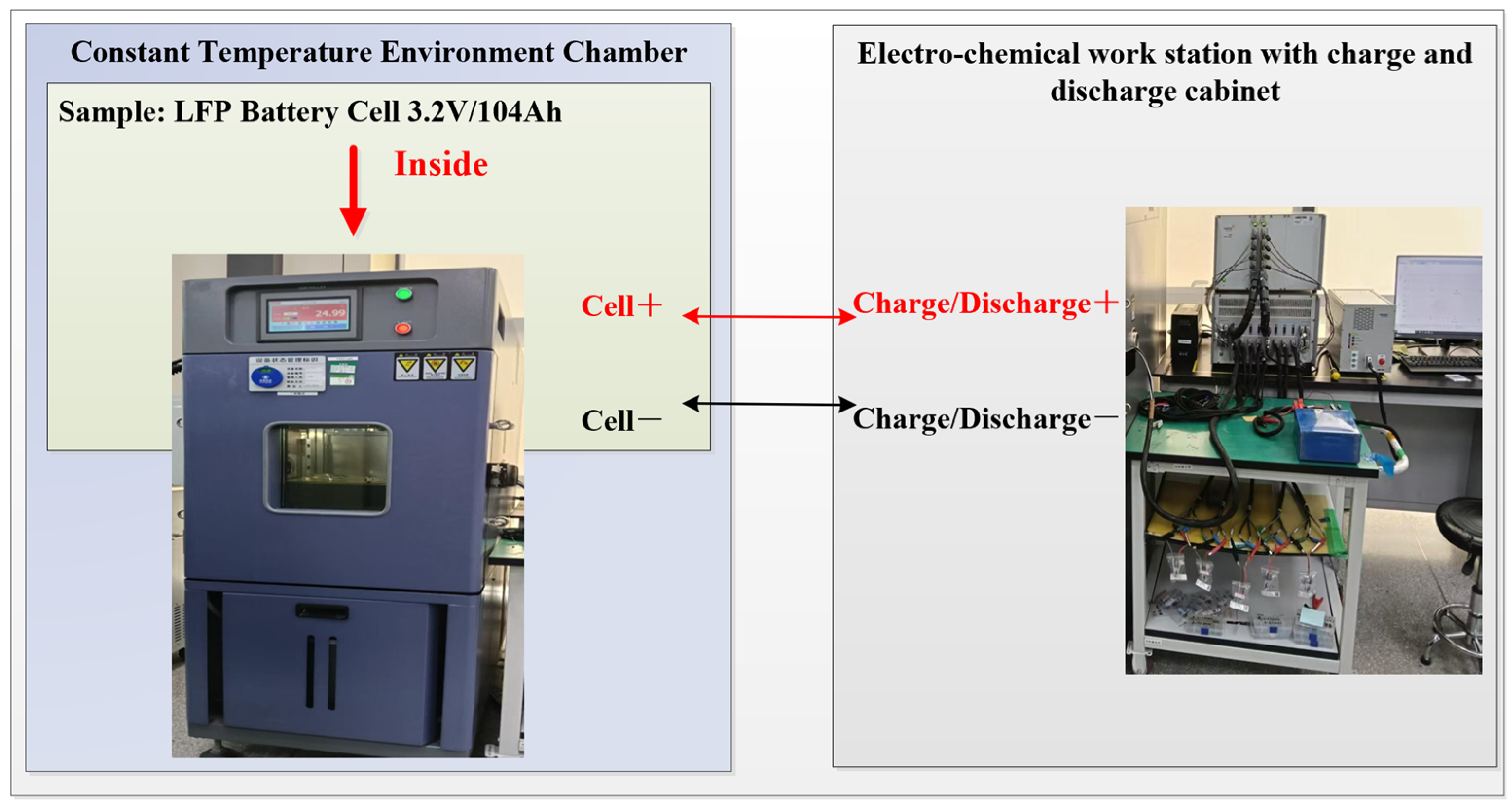
3.1. EIS Data Collection: Experimental Procedure
3.2. Feature Extraction Method (FEM)
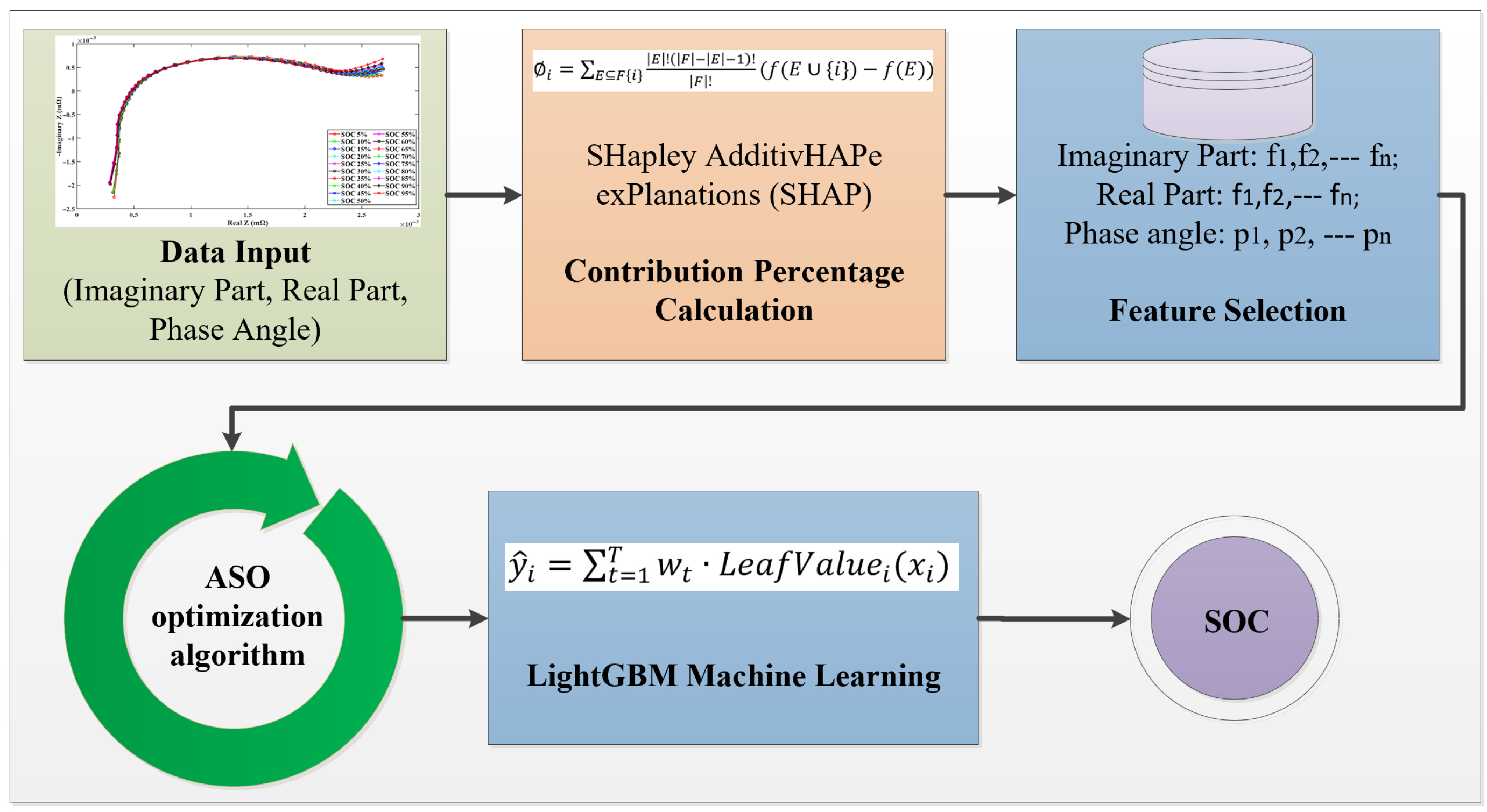
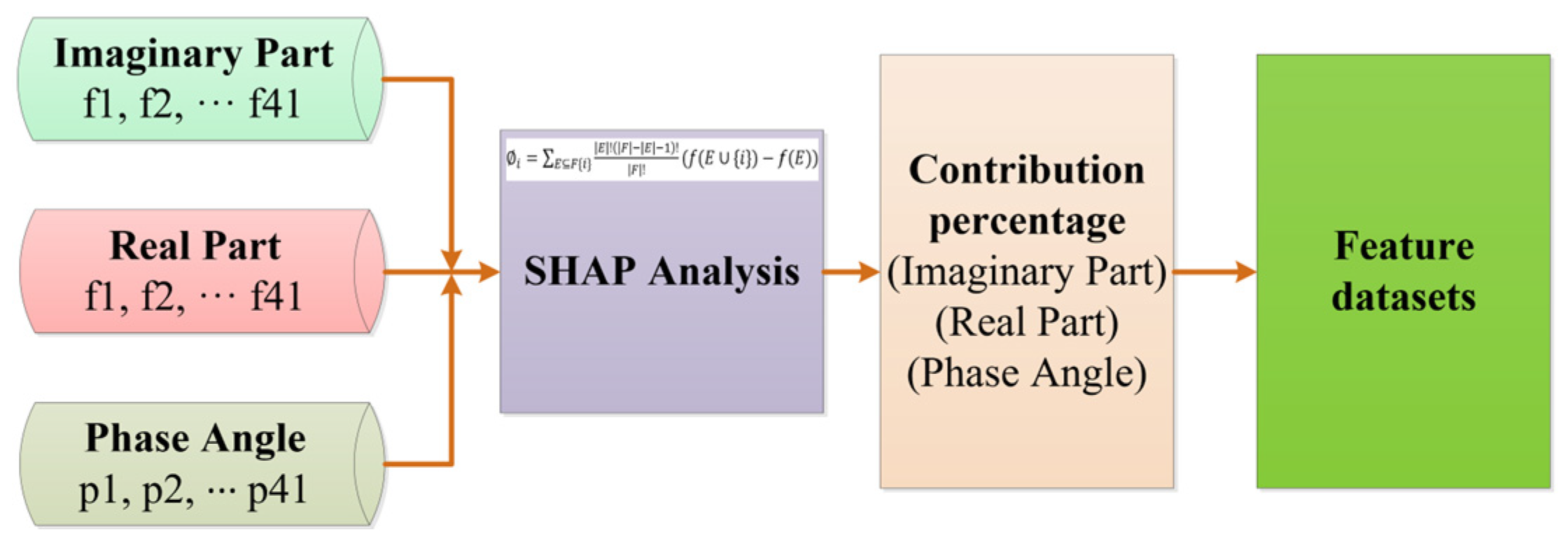
4. The Proposed SHAP–ASO–LightGBM ML Method
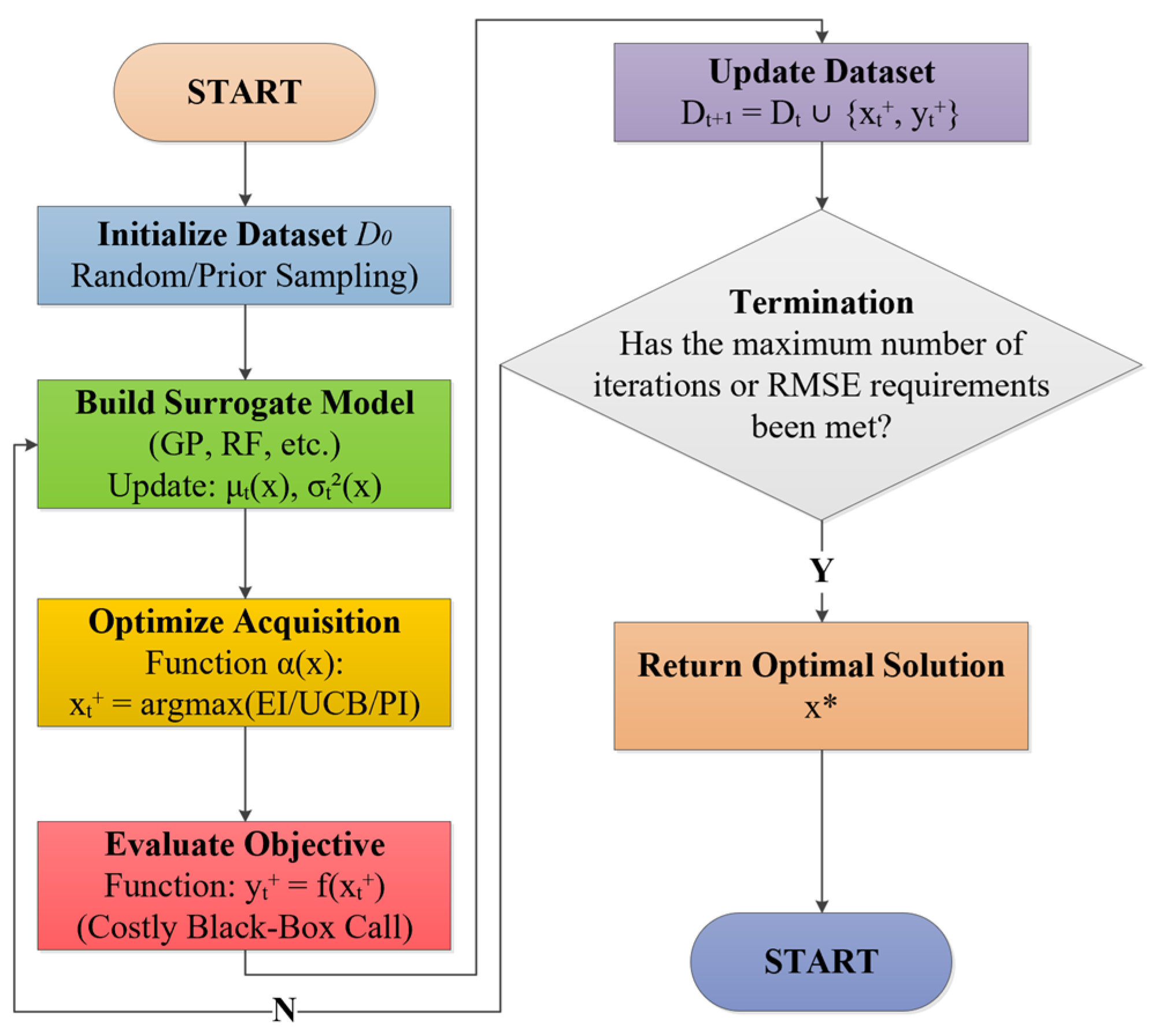
4.1. Atom Search Optimization (ASO) Algorithms
- The first step is the initialization of the population, which randomly generates the initial positions of N atoms (Xi) within the search space. The following formula is utilized, where Xmax and Xmin is the upper and lower bounds of the search space, and rand is a uniformly distributed random number [0, 1].
- The second step is to calculate the fitness value of each atom and record the current global optimal solution according to target function, which is expressed as follows.
- The third step is to calculate the interaction forces between atoms. Interaction forces include attractive and repulsive forces. Attraction can cause atoms to move towards a better solution (promoting local development applications). Repulsive force (Repulsion) can prevent the aggregation of atoms from converging prematurely (maintaining global exploration). The Coulomb force model is usually adopted in this step, which is shown as follows, where Fij and Fi express interaction forces and the resultant force, respectively. rij represents Euclidean distance between Xi and Xj, Ke manifests the Coulomb constant, and qi and qj represent the charge values, respectively.
- The fourth step is to update the motion state of the atom, which includes the acceleration, velocity, and position of the atom according to Newton’s laws of motion, which are expressed as follows. Where ai represents acceleration, and mi represents mass. w is the inertia weight (hyperparameter, usually set to linearly decrease from 0.9 to 0.4), and Δt denotes the time step.
- The fifth step is to update the global optimal solution. This process will compare the fitness values of all atoms and update the global optimal solution, which is represented as follows, where xbest represents the global optimal solution.
- The sixth step is to determine whether the maximum number of iterations or the global optimal solution has been reached. If it has been reached, the process ends; if not, it will continue to return to the third step for loop execution.
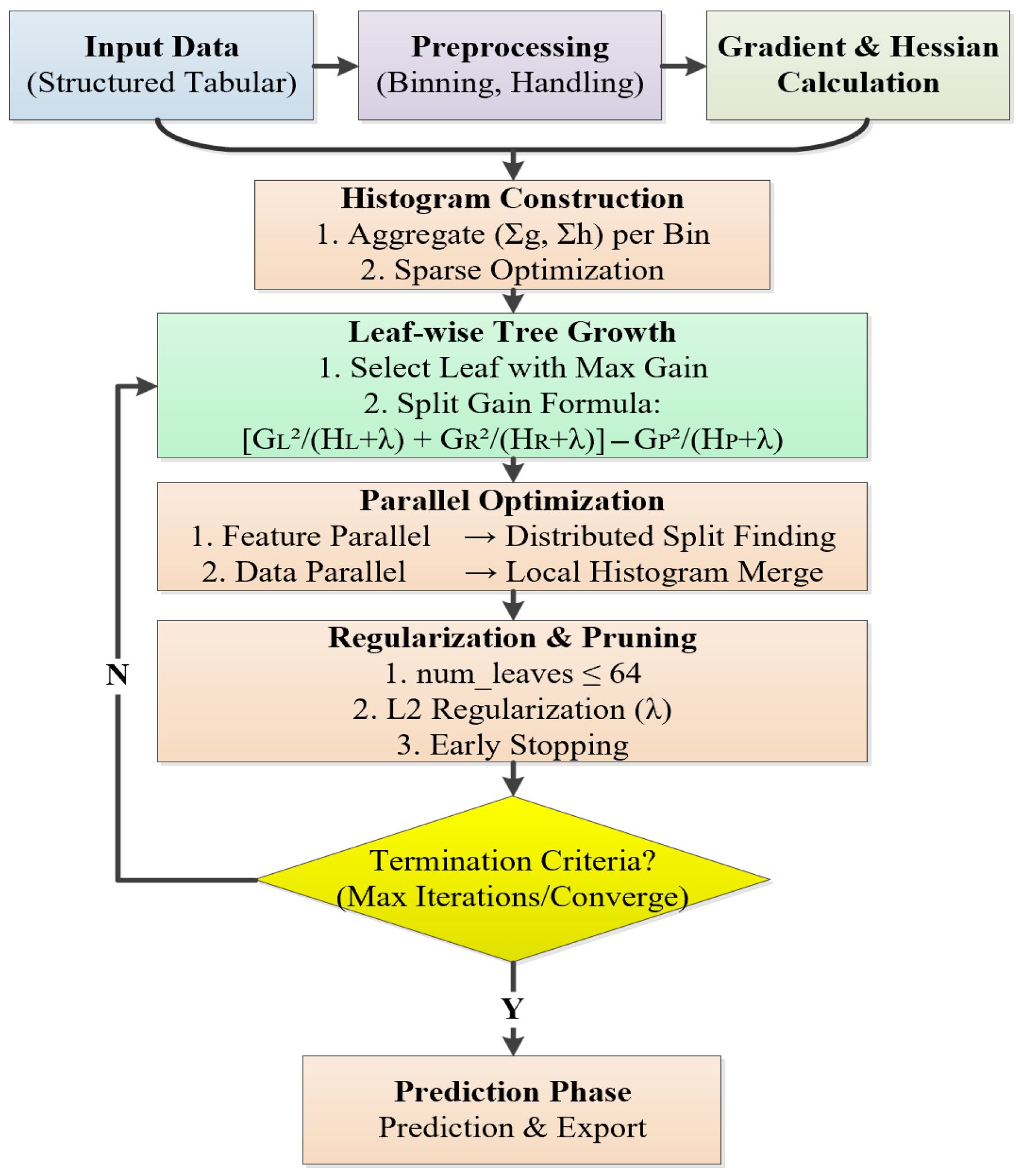
4.2. LightGBM Machine Learning Algorithms
- The first step is data input, which should be in a structured tabular format.
- The second step is Data Preprocessing, which mainly includes category feature processing: sorting by category occurrence frequency and binning to avoid dimension explosion. And continuous feature binning: discretizing into 256 intervals, which can be expressed by the following formula, where x is the original feature value, while xmin and xmax are the minimum and maximum values of this feature. Bin(x) is the discretized result of the feature value x after binning, with a value range from 0 to 255.
- The third step is the calculation of gradients, which can be expressed as follows. Where represents the first-order gradient, denotes second-order gradient.
- The fourth step is histogram construction, which mainly includes gradient aggregation and histogram storage. Gradient aggregation mainly accumulates the gradient g and the second derivative h for each bin of the feature. The histogram storage mainly stores the Gb and Hb of all bins, which can be formulated as follows.
- The fifth step is tree growth, which employs a leaf-wise strategy to split nodes with maximum gain.
- The sixth step is parallel optimization, mainly including feature parallelism and data parallelism. Feature parallelism mainly involves multiple machines/threads, respectively, handling the selection of split points for different features and merging the optimal results. Data parallelism mainly involves dividing the data into blocks, with each node independently constructing local histograms and merging them into a global histogram.
- The seventh step is regularization and pruning strategies.
- Finally, there is a model prediction and termination condition judgment. For each input sample, traverse the nodes of each tree and enter the left or right subtree based on the split condition. After reaching the leaf nodes, accumulate the predicted values of all trees and output the result. Then, the termination condition is judged. The process will be terminated when the maximum number of iterations is reached or the most appropriate convergence degree is achieved. The prediction values can be expressed as follows.
5. Results and Discussion
5.1. Simulation Settings and Performance Metrics
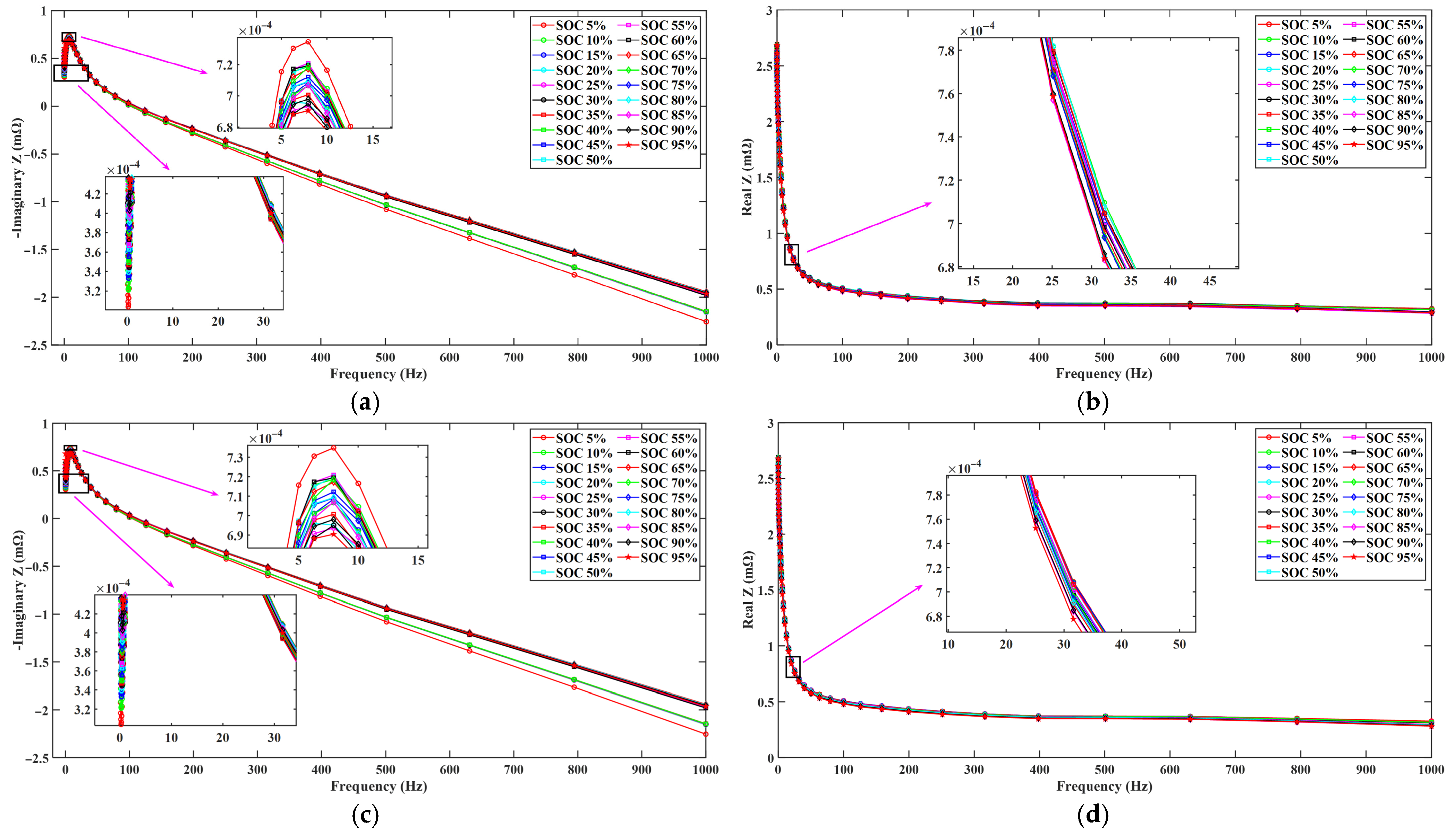
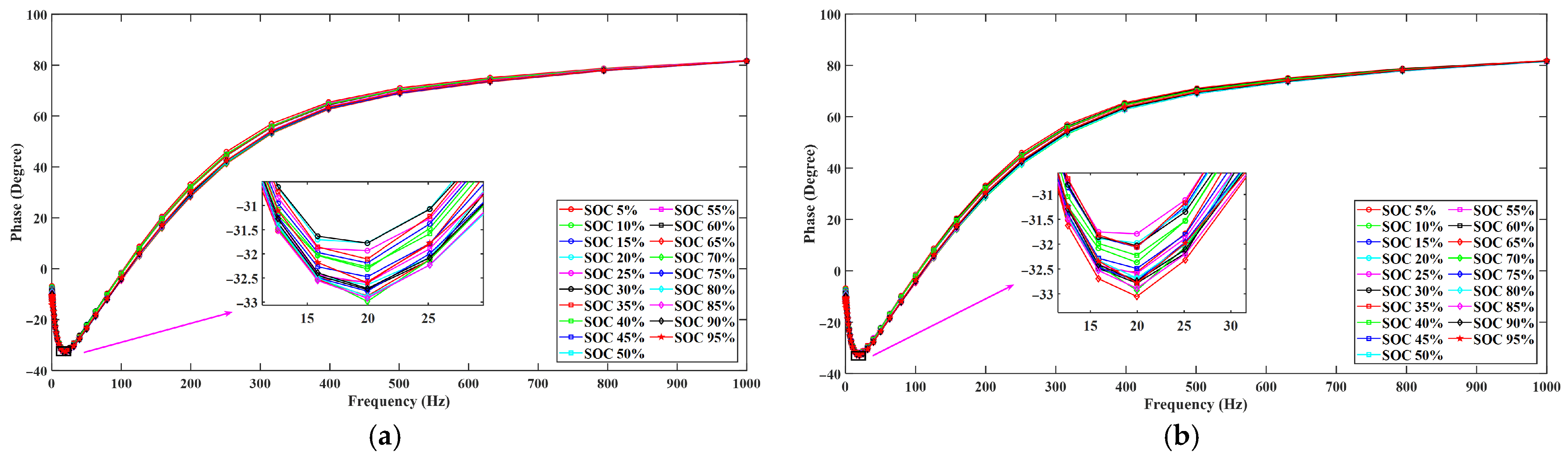
5.2. Feature Extraction of EIS Datasets
5.2.1. Feature Data Analysis
5.2.2. Contribution Percentage Analysis of Feature Data
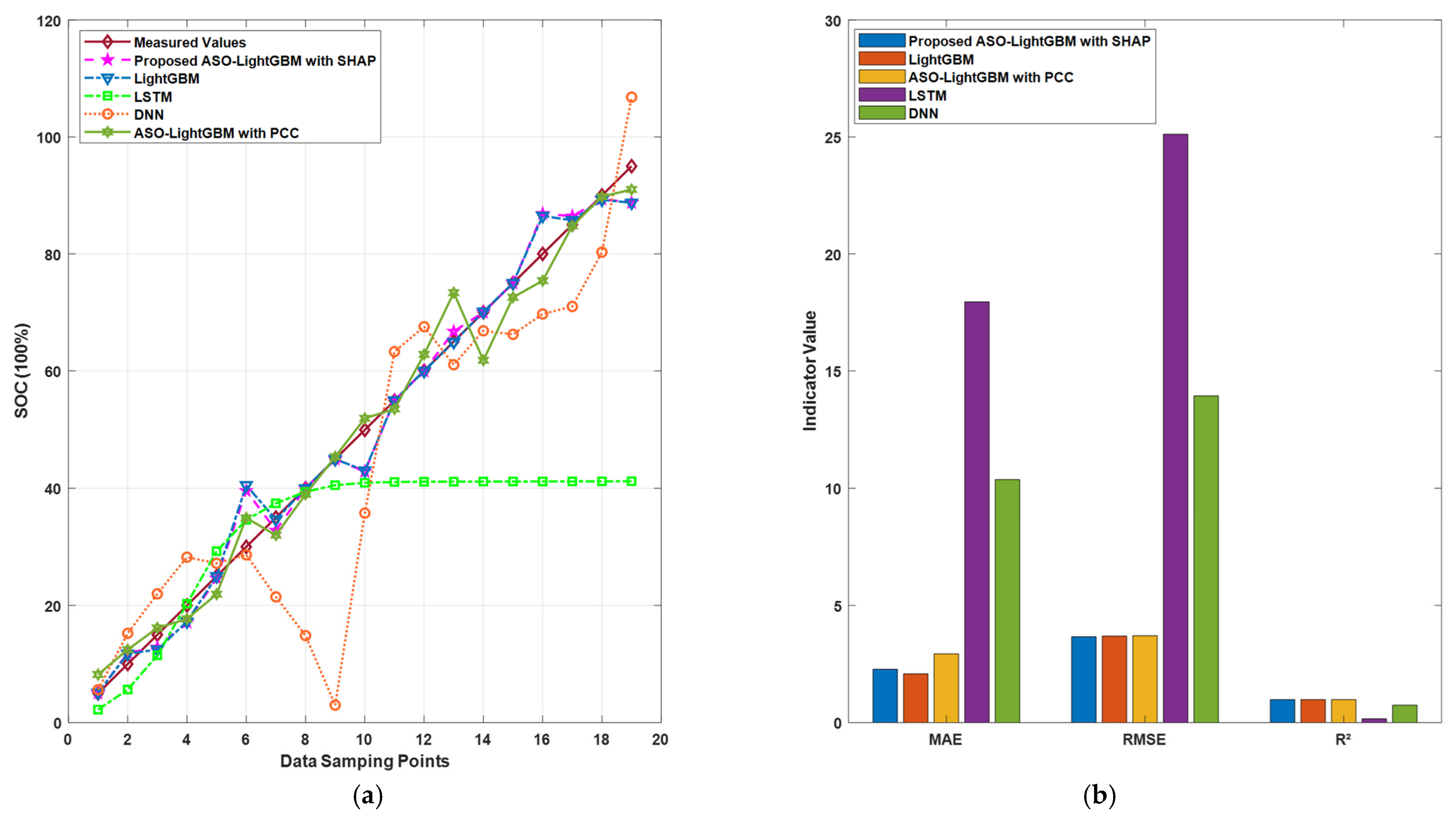
5.3. Comparative Evaluation and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASO | Atomic search optimization |
| A-LGBM-S | ASO–LightGBM with SHAP |
| A-LGBM-P | ASO–LightGBM with PCC |
| BMS | Battery management system |
| DNN | Deep neural network |
| EIS | Electrochemical impedance spectroscopy |
| EVs | Electric vehicles |
| ESS | Energy storage system |
| FEM | Feature extraction method |
| LSTM | Long short-term memory |
| LIBs | Lithium-ion batteries |
| LightGBM | Light Gradient Boosting Machine |
| LGBM-S | LightGBM method without ASO and with SHAP |
| ML | Machine learning |
| MAE | Mean Absolute Error |
| PCC | Pearson correlation coefficient |
| RMSE | Root Mean Squared Error |
| R2 | Coefficient of Determination |
| SOC | State of charge |
| SHAP | SHapley Additive exPlanations |
References
- Chai, H.; Gao, Z.; Jiao, Z.; Zhou, B. State of charge estimation of lithium-ion batteries with unknown parameters using an adaptive fractional-order center difference Kalman filter. Measurement 2025, 247, 116705. [Google Scholar] [CrossRef]
- Monsalve, G.; Acevedo-Bueno, D.; Cardenas, A.; Martinez, W. An Improved ECM-Based State-of-Charge Estimation for SLA and LFP Batteries Used in Low-Cost Agricultural Mobile Robots. IEEE Access 2024, 12, 146265–146276. [Google Scholar] [CrossRef]
- Hu, P.; Tang, W.F.; Li, C.H.; Mak, S.-L.; Li, C.Y.; Lee, C.C. Joint State of Charge (SOC) and State of Health (SOH) Estimation for Lithium-Ion Batteries Packs of Electric Vehicles Based on NSSR-LSTM Neural Network. Energies 2023, 16, 5313. [Google Scholar] [CrossRef]
- Shu, X.; Li, Y.; Wei, K.; Yang, W.; Yang, B.; Zhang, M. Research on the output characteristics and SOC estimation method of lithium-ion batteries over a wide range of operating temperature conditions. Energy 2025, 317, 134726. [Google Scholar] [CrossRef]
- Xiong, X.; Wang, S.L.; Fernandez, C.; Yu, C.M.; Zou, C.Y.; Jiang, C. A novel practical state of charge estimation method: An adaptive improved ampere-hour method based on composite correction factor. Int. J. Energy Res. 2020, 44, 11385–11404. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, X.; Li, G. State of charge estimation for pulse discharge of a LiFePO4 battery by a revised Ah counting. Electrochim. Acta 2015, 151, 63–71. [Google Scholar] [CrossRef]
- Meng, S.; Meng, F.; Chi, H.; Chen, H.; Pang, A. A robust observer based on the nonlinear descriptor systems application to estimate the state of charge of lithium-ion batteries. J. Frankl. Inst. 2023, 360, 11397–11413. [Google Scholar] [CrossRef]
- Chen, G.; Zhou, H.; Ba, T.; Xu, Y.; Yang, J.; Xiao, R.; Pan, N.; Gong, H. Online joint estimation of state of charge and state of health based on equivalent circuit model with limited test time for lithium-ion batteries. Sens. Actuators A Phys. 2025, 383, 116250. [Google Scholar] [CrossRef]
- Guo, W.; Wang, Q.; Li, G.; Xie, S. Dual-time scale collaborative estimation of SOC and SOH for lithium-ion batteries based on FOMIRUKF-EKF. Comput. Electr. Eng. 2025, 123, 110048. [Google Scholar] [CrossRef]
- Hu, P.; Tsang, C.-W.; Lu, X.-Y.; Li, C.Y.; Lee, C.C. Enhancing Electric Wheelchair Safety via Battery State of Charge Estimation With PCC–NSSR–LSTM Method. Electron. Lett. 2025, 61, e70228. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, K.; Zhu, C.; Zhang, X.; Zhang, D. Co-Estimation of State-of- Charge and State-of- Health for Lithium-Ion Batteries Using an Enhanced Electrochemical Model. IEEE Trans. Ind. Electron. 2022, 69, 2684–2696. [Google Scholar] [CrossRef]
- Yang, R.; Li, Z.; Chen, Z.; Ali, M.S.; Chen, G. Fast State-of-Charge Estimation for Lithium-Ion Batteries Using a Simplified Electrochemical Model Without Initial State Restrictions. IEEE Trans. Transp. Electrif. 2024, 10, 4159–4172. [Google Scholar] [CrossRef]
- Yang, K.; Tang, Y.; Zhang, S.; Zhang, Z. A deep learning approach to state of charge estimation of lithium-ion batteries based on dual-stage attention mechanism. Energy 2022, 244, 123233. [Google Scholar] [CrossRef]
- Cui, Z.; Kang, L.; Li, L.; Wang, L.; Wang, K. A hybrid neural network model with improved input for state of charge estimation of lithium-ion battery at low temperatures. Renew. Energy 2022, 198, 1328–1340. [Google Scholar] [CrossRef]
- Wang, Y.-X.; Chen, Z.; Zhang, W. Lithium-ion battery state-of-charge estimation for small target sample sets using the improved GRU-based transfer learning. Energy 2022, 244, 123178. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Wu, J.; Cheng, W.; Zhu, Q. SOC estimation for lithium-ion battery using the LSTM-RNN with extended input and constrained output. Energy 2023, 262, 125375. [Google Scholar] [CrossRef]
- Ji, C.; Jin, G.; Zhang, R. State of charge estimation for lithium-ion batteries based on a digital twin hybrid model. Energy Rep. 2025, 13, 2174–2185. [Google Scholar] [CrossRef]
- Messing, M.; Shoa, T.; Ahmed, R.; Habibi, S. Battery SoC Estimation from EIS using Neural Nets. In Proceedings of the 2020 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 23–26 June 2020; pp. 588–593. [Google Scholar] [CrossRef]
- Bourelly, C.; Vitelli, M.; Milano, F.; Molinara, M.; Fontanella, F.; Ferrigno, L. EIS-Based SoC Estimation: A Novel Measurement Method for Optimizing Accuracy and Measurement Time. IEEE Access 2023, 11, 91472–91484. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, H.; Wang, X.; Li, M. State-of-charge estimation for lithium primary batteries: Methods and verification. J. Energy Storage 2024, 86, 111189. [Google Scholar] [CrossRef]
- Kong, L.; Fang, S.; Niu, T.; Chen, G.; Yang, L.; Liao, R. Fast State of Charge Estimation for Lithium-ion Battery Based on Electrochemical Impedance Spectroscopy Frequency Feature Extraction. IEEE Trans. Ind. Appl. 2024, 60, 1369–1379. [Google Scholar] [CrossRef]
- Carthy, K.M.; Gullapalli, H.; Ryan, K.M.; Kennedy, T. Review—Use of impedance spectroscopy for the estimation of Li-ion battery state of charge, state of health and internal temperature. J. Electrochem. Soc. 2021, 168, 080517. [Google Scholar] [CrossRef]
- Meddings, N.; Heinrich, M.; Overney, F.; Lee, J.-S.; Ruiz, V.; Napolitano, E.; Seitz, S.; Hinds, G.; Raccichini, R.; Gaberšček, M.; et al. Application of electrochemical impedance spectroscopy to commercial Li-ion cells: A review. J. Power Sources 2020, 480, 228742. [Google Scholar] [CrossRef]
- Chang, C.; Pan, Y.; Wang, S.J.; Jiang, J.C.; Tian, A.; Gao, Y.; Jiang, Y.; Wu, T.Z. Fast EIS acquisition method based on SSA-DNN prediction model. Energy 2024, 288, 129768. [Google Scholar] [CrossRef]
- Babaeiyazdi, I.; Rezaei-Zare, A.; Shokrzadeh, S. State of charge prediction of EV Li-ion batteries using EIS: A machine learning approach. Energy 2021, 223, 120116. [Google Scholar] [CrossRef]
- Ojukwu, S.J.; Maheshwari, S.; Shafik, R.; Yakovlev, A.; Mamlouk, M. AI-Driven Battery State-of-Charge Estimation using Electrochemical Impedance Spectroscopy. In Proceedings of the 2023 International Symposium on the Tsetlin Machine (ISTM), Newcastle upon Tyne, UK, 29–30 August 2023. [Google Scholar] [CrossRef]
- Santoni, F.; De Angelis, A.; Moschitta, A.; Carbone, P. Training Gaussian process regression through data augmentation for battery SOC estimation. J. Energy Storage 2024, 98, 113073. [Google Scholar] [CrossRef]
- Hu, P.; Lam, S.S.K.; Li, C.Y.; Lee, C.C. Novel Passive Equalization Methods for Lithium-Ion Batteries Utilizing Real-Time Internal Resistance Measurements. IEEE Access 2024, 12, 186362–186379. [Google Scholar] [CrossRef]
- Ye, Z.W.; Xu, Y.; He, Q.Y.; Wang, M.W.; Bai, W.F.; Xiao, H.W. Feature Selection Based on Adaptive Particle Swarm Optimization with Leadership Learning. Comput. Intell. Neurosci. 2022, 2022, 1825341. [Google Scholar] [CrossRef] [PubMed]
- Gu, X.; See, K.W.; Wang, Y.; Zhao, L.; Pu, W. The Sliding Window and SHAP Theory—An Improved System with a Long Short-Term Memory Network Model for State of Charge Prediction in Electric Vehicle Application. Energies 2021, 14, 3692. [Google Scholar] [CrossRef]
- Ji, X.; Liao, Y.; Tu, J.; Liu, Q.; Qing, X. PSO-GPR model for state estimation of lithium-ion battery using ultrasonic guided waves with multi-feature fusion technique. J. Energy Storage 2025, 112, 115580. [Google Scholar] [CrossRef]
- Ly, A.; Marsman, M.; Wagenmakers, E.J. Analytic posteriors for Pearson’s correlation coefficient. Stat. Neerl. 2018, 72, 4–13. [Google Scholar] [CrossRef] [PubMed]
- Valencia, D.; Lillo, R.E.; Romo, J. A Kendall correlation coefficient between functional data. Adv. Data Anal. Classif. 2019, 13, 1083–1103. [Google Scholar] [CrossRef]
- Kumar, A.; Abirami, S. Aspect-based opinion ranking framework for product reviews using a Spearman’s rank correlation coefficient method. Inf. Sci. 2018, 460–461, 23–41. [Google Scholar] [CrossRef]
- Pandis, N. The chi-square test. Am. J. Orthod. Dentofac. Orthop. 2016, 150, 898–899. [Google Scholar] [CrossRef] [PubMed]
- Hua, L.; Zhang, C.; Peng, T.; Ji, C.; Shahzad Nazir, M. Integrated framework of extreme learning machine (ELM) based on improved atom search optimization for short-term wind speed prediction. Energy Convers. Manag. 2022, 252, 115102. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.H.; Wu, T.Z. Estimation of state of health based on charging characteristics and back-propagation neural networks with improved atom search optimization algorithm. Glob. Energy Interconnect. 2023, 6, 228–237. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowl.-Based Syst. 2019, 163, 283–304. [Google Scholar] [CrossRef]
- Zhou, Y.F.; Wang, S.L.; Li, Z.H.; Feng, R.J.; Fernandez, C. Battery pack capacity estimation based on improved cooperative co-evolutionary strategy and LightGBM hybrid models using indirect health features. J. Energy Storage 2025, 114, 115914. [Google Scholar] [CrossRef]
- Xu, Y.; Goodacre, R. On Splitting Training and Validation Set: A Comparative Study of Cross-Validation, Bootstrap and Systematic Sampling for Estimating the Generalization Performance of Supervised Learning. J. Anal. Test. 2018, 2, 249–262. [Google Scholar] [CrossRef] [PubMed]
- Sulaiman, M.H.; Mustaffa, Z. State of charge estimation for electric vehicles using random forest. Green Energy Intell. Transp. 2024, 3, 100177. [Google Scholar] [CrossRef]





| FEMs | Computational Efficiency | Numeric Data | Time-Sequence Data | Nonlinear Data | Tolerance for Missing Values |
|---|---|---|---|---|---|
| SHAP [29] | Medium | √ (Good) | √ (Good) | √٭ (Best) | Low |
| PCC [32] | High | √٭ (Best) | Δ (Limited) | × | Low |
| Kendall’s Tau [33] | Medium | √ (Good) | Δ (Limited) | Δ (Limited) | High |
| SRCC [34] | High | √ (Good) | Δ (Limited) | Δ (Limited) | Medium |
| CST [35] | High | × | × | × | Medium |
| Categories | Parameters |
|---|---|
| Shape of the cell | Rectangular aluminum shell |
| Anode | Graphite |
| Cathode | LiFePO4 (LFP) |
| Rated Capacity | 104 Ah |
| Charge Cut-off Voltage | 3.65 V |
| Discharge Cut-off voltage | 2.0 V |
| AC Impedance | ≤5 mΩ (25 °C ± 2 °C, SOC 17 ± 3%) |
| Weight | 1909 ± 57 g |
| Size | Thickness × Width × Height: 52.3 ± 0.3 mm × 148.6 ± 0.3 mm × 118.9 ± 0.3 mm |
| Imaginary Part | Frequency (Hz) | Real Part | Frequency (Hz) | Phase Angle | Angle (Degree) |
|---|---|---|---|---|---|
| f1 | 1000 | f1 | 1000 | p2 (794.33 Hz) | 78.76 |
| f3 | 630.96 | f2 | 794.33 | p3 (630.96 Hz) | 75.12 |
| f4 | 501.19 | f4 | 501.19 | p8 (199.53 Hz) | 33.19 |
| f6 | 316.23 | f6 | 316.23 | p12 (79.43 Hz) | −9.70 |
| f10 | 125.89 | f8 | 199.53 | p14 (50.12 Hz) | −22.25 |
| f11 | 100.00 | f9 | 158.49 | p15 (39.81 Hz) | −26.69 |
| f14 | 50.12 | f11 | 100 | p16 (31.62 Hz) | −29.76 |
| f30 | 1.2589 | f12 | 79.433 | p27 (2.5119 Hz) | −16.51 |
| f31 | 1 | f13 | 63.10 | p28 (1.9953 Hz) | −14.67 |
| f32 | 0.7943 | f16 | 31.62 | p29 (1.5849 Hz) | −13.12 |
| f34 | 0.5012 | f17 | 25.12 | p32 (0.7943 Hz) | −9.47 |
| f36 | 0.3162 | f41 | 0.1 Hz | p34 (0.5012 Hz) | −7.92 |
| f37 | 0.2512 | - | - | p37 (0.2512 Hz) | −6.90 |
| f38 | 0.1995 | - | - | p38 (0.1995 Hz) | −6.76 |
| f39 | 0.1585 | - | - | p39 (0.1585 Hz) | −6.78 |
| f40 | 0.1259 | - | - | p40 (0.1259 Hz) | −6.83 |
| f41 | 0.1 | - | - | - | - |
| Relevant Methods | LIBs’ Type | Cap (Ah) | FEM | ML Algorithms | RMSE | MAE | R2 | Scenarios |
|---|---|---|---|---|---|---|---|---|
| ASO–LightGBM with SHAP | LFP | 104 | SHAP | ASO–LightGBM | 3.67% | 2.28% | 0.982 | Online |
| ASO–LightGBM with PCC | LFP | 104 | PCC [25] | ASO–LightGBM | 3.71% | 2.93% | 0.981 | Online |
| LightGBM without ASO | LFP | 104 | SHAP | LightGBM | 3.69% | 2.08% | 0.981 | Online |
| LSTM [26] | NCM | 2.6 | Without | LSTM | 25.12% | 17.94% | 0.159 | Offline |
| DNN [18] | NCM | 4.8 | Without | DNN | 13.95% | 10.37% | 0.740 | Offline |
| Relevant Methods | LIBs’ Type | Cap (Ah) | FEM | ML Algorithms | RMSE | MAE | R2 | Scenarios |
|---|---|---|---|---|---|---|---|---|
| ASO–LightGBM with SHAP | LFP | 104 | SHAP | ASO–LightGBM | 3.30% | 1.86% | 0.99 | Online |
| ASO–LightGBM with PCC | LFP | 104 | PCC [25] | ASO–LightGBM | 3.59% | 2.53% | 0.98 | Online |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, P.; Li, C.Y.; Lee, C.C. SOC Estimation of Lithium-Ion Batteries Utilizing EIS Technology with SHAP–ASO–LightGBM. Batteries 2025, 11, 272. https://doi.org/10.3390/batteries11070272
Hu P, Li CY, Lee CC. SOC Estimation of Lithium-Ion Batteries Utilizing EIS Technology with SHAP–ASO–LightGBM. Batteries. 2025; 11(7):272. https://doi.org/10.3390/batteries11070272
Chicago/Turabian StyleHu, Panpan, Chun Yin Li, and Chi Chung Lee. 2025. "SOC Estimation of Lithium-Ion Batteries Utilizing EIS Technology with SHAP–ASO–LightGBM" Batteries 11, no. 7: 272. https://doi.org/10.3390/batteries11070272
APA StyleHu, P., Li, C. Y., & Lee, C. C. (2025). SOC Estimation of Lithium-Ion Batteries Utilizing EIS Technology with SHAP–ASO–LightGBM. Batteries, 11(7), 272. https://doi.org/10.3390/batteries11070272







