Interpretable Deep Learning Using Temporal Transformers for Battery Degradation Prediction

Abstract

Accurate modelling of lithium-ion battery degradation is a complex problem, dependent on multiple internal mechanisms that can be affected by a multitude of external conditions. In this study, a transformer-based approach, capable of leveraging historical conditions and known-future inputs is introduced. The model can make predictions from as few as 100 input cycles, and compared to other state-of-the-art techniques, our approach shows an increase in accuracy. The model utilises specialised components within its architecture to provide interpretable results, introducing the possibility of understanding path-dependency in Li-Ion battery degradation. The ability to incorporate static metadata opens the door for a foundational deep learning model for battery degradation forecasting.

1. Introduction

Lithium-ion batteries have emerged as a cornerstone technology across multiple industries worldwide. Notably, they play a crucial role in the rapid advancement of electric vehicles (EVs) and large-scale battery energy storage systems (BESSs), two sectors that are pivotal to the transition towards sustainable energy solutions. For both of these applications, the associated Battery Management System (BMS) is responsible for optimising battery performance by managing parameters such as voltage, current, and temperature [1]. There is considerable motivation from researchers globally to improve the performance of BMSs [2], as they can extend battery life, reduce failure risks, and mitigate thermal runaway.

EVs rely heavily on efficient battery management to operate safely. The BMS is responsible for several critical functions, including temperature control, cell equalisation, charging and discharging management, and fault analysis. Effective battery state estimation, encompassing the State of Charge (SoC), state of health (SoH), and Remaining Useful Life (RUL), is vital for ensuring EV safety and performance [3]. Traditional estimation methods, such as the Kalman filter, often lack the adaptability needed to account for battery ageing effects, potentially compromising BMS performance [4].

In addition, BESSs are increasingly crucial in efforts to decarbonise the power sector. By facilitating the integration of renewable energy sources into the power grid, BESSs also contribute to grid stability and reliability. The BMS is vital to the viability of BESS projects. It is responsible for safety, the efficient management of performance, and determining the SoH of batteries. SoH predictions provide crucial information for the maintenance and replacement of batteries. Furthermore, trading strategies for BESSs must consider and optimise the SoH to balance short-term gains and long-term battery life.

However, the gains generated by BESSs through providing flexibility services can be offset by the degradation cost of the lithium-ion batteries. In addition to lifetime and number of cycles, this degradation is sensitive to energy throughput, temperature, SoC, depth of discharge (DoD) and charge/discharge rate (C-rate) [5]. Furthermore, accurate state-of-health (SoH) estimation is crucial as it dictates the energy throughput, which determines the energy available for trading. This directly impacts the revenue generated from BESS projects and influences key financial metrics such as the Levelised Cost of Storage (LCOS) and Internal Rate of Return (IRR), ultimately governing the economic viability of these projects.

A major difficulty for SoH predictions in both EV and BESS applications is the inherent path dependency [6], i.e., the impact of the precise chronological usage of the battery on the SoH. Accounting for path dependency is not inherent to model-based methods—whether they are based on fundamental electrochemical equations [7,8,9] or circuit-based equivalent models combined with filtering techniques [10]—because path dependency is still not well understood. Moreover, capturing long-term SoH dependencies on the degradation stress factors mentioned previously within such frameworks require a large quantity of data to be collected over long periods of time, as demonstrated in Ref. [11].

A more efficient approach to SoH prediction is to employ data-driven methods [12] that can store and update key information from degradation data as they become available. Traditional data-driven methods for SoH prediction often involve handcrafted feature extraction followed by regression techniques. For instance, Feng et al. [13] used Gaussian process regression (GPR) and polynomial regression to predict SoH and RUL, extracting health indicators from charging current. These methods, while effective, can be time-consuming and labour-intensive, requiring expertise in feature design. Additionally, kernel methods, like support vector machines (SVMs), have been applied for SoH estimation [14]. However, selecting dominant data points can dilute path dependency and reduce prediction accuracy. Neural network (NN)-based techniques can be effective because they have an internal state that can represent path information.

The long short-term memory (LSTM) neural network architecture is a popular approach for time-series forecasting due to its ability to capture some long-term dependencies. Zhang et al. [15] studied LSTM-based neural networks for SoH predictions. Their results indicated that LSTM networks were generally more accurate and precise than SVM-based models. More recent studies have focused on end-to-end deep learning approaches using measurement data such as voltage, current, and temperature. Li et al. [16] combined LSTM and CNN networks to separately predict SoH and remaining useful life (RUL) in an end-to-end mode. LSTM models are well suited for time-series data and can capture some long-term dependencies, which are essential for battery SoH predictions. However, they have limitations such as long training times and a restricted ability to capture very long-term dependencies, which can affect their practical application. This is particularly relevant for SoH prediction as accurate modelling over a large number of cycles is desirable.

Recognising the limitations of LSTM models, researchers have explored more advanced architectures. Cai et al. [17] demonstrated that transformers, when combined with deep neural networks (DNNs), were more effective for battery SoH prediction. The attention mechanism in transformers allows them to assign importance to specific timesteps, thereby capturing long-term dependencies more efficiently than LSTM models. Song et al. [18] further enhanced prediction accuracy by incorporating positional and temporal encoding in transformers to predict battery RUL, addressing the challenge of capturing sequence information.

Zhang et al. [19] integrated an attention layer into a gated residual unit (GRU) architecture, combining it with particle filter information to make accurate RUL predictions. This approach leveraged the strengths of both attention mechanisms and traditional filtering techniques, enhancing the robustness of the predictions.

Fan et al. [20] designed a gated recurrent unit–convolutional neural network (GRU-CNN) for direct SoH prediction, which combined the temporal processing capabilities of GRUs with the spatial feature extraction power of CNNs. Gu et al. [21] created a model by combining a CNN and transformer for SoH prediction. The CNN was used to incorporate time-dependent features, whereas the transformer modelled time-independent features. This hybrid approach effectively utilised different neural network architectures to enhance prediction accuracy.

Despite these advancements, previous approaches often struggle with capturing complex dependencies and require extensive computational resources for training. This study presents a novel method for modelling battery degradation and thus sheds light on a critical component of understanding this capability—interpretability of underlying stress factors—using a Temporal Fusion Transformer (TFT) [22]. The TFT model has proven to be more accurate than standard deep learning approaches for various sequence lengths. It leverages historical conditions and known future inputs to make predictions from as few as 100 input cycles. The model integrates specialised components to provide interpretability, offering insights into path-dependent degradation processes. By incorporating static metadata, our approach provides a robust solution applicable to various battery chemistries and operating conditions. This work aims to enhance the reliability and safety of BMS SoH estimation for EV and BESS applications, providing valuable insights into battery degradation processes and informing optimal management strategies.

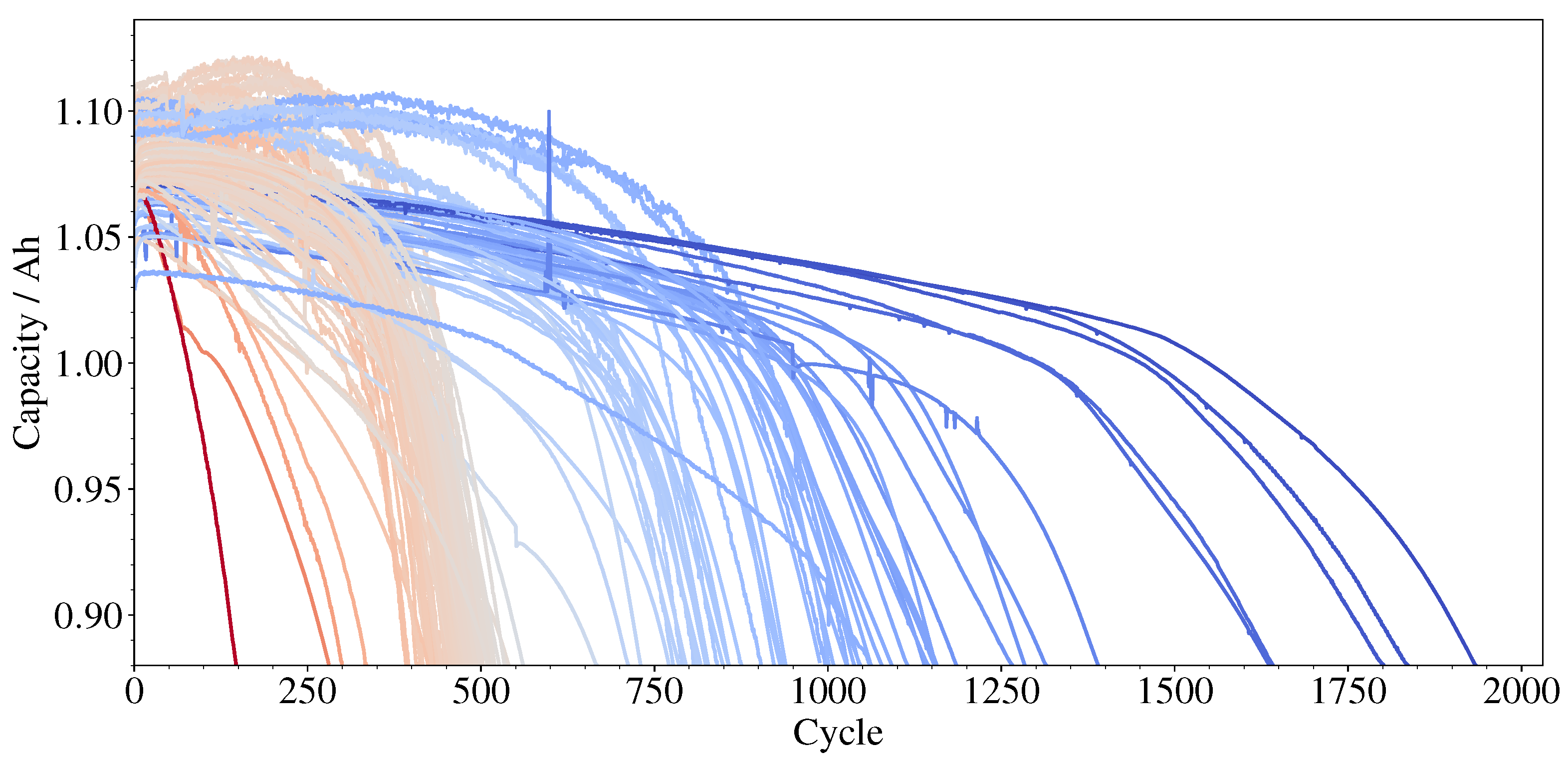
In this study, we outline our approach, apply it to a dataset comprising over 100 cells, evaluate its performance relative to other standard neural networks, and demonstrate its potential for interpretability.

2. Framework

2.1. Dataset Description

Severson et al. [23] generated a comprehensive dataset consisting of 124 LFP/graphite cells that were cycled under fast-charging conditions, as shown in Figure 1. The C-rates for the charging and discharging protocols varied from 1C to 8C. The experiments were stopped when the batteries reached end-of-life (EOL) criteria. EOL cycle number ranged from 150 to 2300. This is subsequently referred to as the “Severson dataset”. The dataset comprises three batches: batch “12-05-2017”, batch “30-06-2017”, and batch “12-04-2018”.

Table 1. List of variables used in the TFT training.

Variable Description	Name	Type
Cycle number	Cycle	Timestep
Current capacity	QD	Continuous, input
Future capacity	QD_target	Continuous, target
Battery	Battery	Categorical, input
Average charging voltage	v_c_mean	Continuous, input
Average discharging voltage	v_d_mean	Continuous, input
Standard deviation of charging voltage	v_c_std	Continuous, input
Standard deviation of discharging voltage	v_d_std	Continuous, input
Depth of discharge	dod	Continuous, input
Average charging current	cur_c_mean	Continuous, input
Average discharging current	cur_d_mean	Continuous, input
Standard deviation of charging current	cur_c_std	Continuous, input
Standard deviation of discharging current	cur_d_std	Continuous, input
Average charging temperature	T_c_mean	Continuous, input
Average discharging temperature	T_d_mean	Continuous, input
Standard deviation of charging temperature	T_c_std	Continuous, input
Standard deviation of discharging temperature	T_d_std	Continuous, input
Minimum charging temperature	T_c_min	Continuous, input
Minimum discharging temperature	T_d_min	Continuous, input
Maximum charging temperature	T_c_max	Continuous, input
Maximum discharging temperature	T_d_max	Continuous, input

summarises key operational battery variables, including cycle number, capacity metrics, voltage/current/temperature statistics (mean, std, min, max), and depth of discharge, serving as inputs to predict future capacity.

2.2. Evaluation Metrics

For predicting the battery capacity curve, the average mean squared error (MSE) and mean absolute percentage error (MAPE) were calculated across the output sequence. They are defined as:

$$\mathrm{MSE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-{\hat{y}}_i)}^2,$$

(1)

$$\mathrm{MAPE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|{\displaystyle \frac{y_i-{\hat{y}}_i}{y_i}}\right|,$$

(2)

where $y_i$ and ${\hat{y}}_i$ are the true and predicted capacities at the ith output point, respectively, and n is the number of timesteps in the prediction.

2.2.1. Attention

Transformer networks make use of attention, which maps a set of queries Q and corresponding key–value pairs ($K,V$) to an output. For each query and each key—both of dimension $d_k$—we compute their dot product, scale by ${\displaystyle \frac{1}{\sqrt{d_k}}}$, and then apply a softmax function to turn these scores into normalized weights. Those weights are used to take a weighted sum of the values (V). Formally:

$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}}\right)V.$$

(3)

To improve the learning capacity of the model, multi-head attention is employed to increase representational power:

$$\mathrm{MultiHead}(Q,K,V)=\mathrm{Concat}[{\mathrm{head}}_1;{\mathrm{head}}_2;\dots ;{\mathrm{head}}_h]W^O,$$

(4)

where

$${\mathrm{head}}_i=\mathrm{Attention}(Q{W}_i^Q,K{W}_i^K,V{W}_i^V).$$

(5)

2.2.2. LSTM Layers

In time-series problems, the location of the data points within the sequence is significant. The TFT leverages local context within sequences through the use of an LSTM model, leading to performance improvement in attention-based architectures. This also serves as a replacement for more traditional positional encoding—which makes use of sine and cosine functions to produce a higher dimensional vector that includes information on the location of data within the sequence—by providing an inductive bias for the time ordering of the inputs.

The LSTM encoder is made up of cells that contain the current hidden state. As the information moves through the chain of cells, the hidden state is updated. This is controlled by three internal gates, commonly denoted as input (i), output (o), and forget (f) gates. Each gate multiplies the inputs by a weight matrix, adds a bias term, and then applies a sigmoid activation function (${\sigma }_g$). The gates allow the LSTM to effectively either remember or forget different aspects of the input sequence. At time t, the equations describing the LSTM cell and gates are:

$$\begin{array}{cc}\hfill f_t& ={\sigma }_g(W_f{x}_t+U_f{h}_{t-1}+b_f)\hfill \\ \hfill i_t& ={\sigma }_g(W_i{x}_t+U_i{h}_{t-1}+b_i)\hfill \\ \hfill o_t& ={\sigma }_g(W_o{x}_t+U_o{h}_{t-1}+b_o)\hfill \\ \hfill {\tilde{c}}_t& =tanh(W_c{x}_t+U_c{h}_{t-1}+b_c)\hfill \\ \hfill c_t& =f_t\odot c_{t-1}+i_t\odot {\tilde{c}}_t\hfill \\ \hfill h_t& =o_t\odot tanh{c}_t,\hfill \end{array}$$

(6)

where c is the cell state, h is the hidden state, W and U are weight matrices, b is the bias term. The hidden state of the final encoder cell is passed to the next layer in the model.

2.2.3. Variable Selection

The model uses three types of input: past inputs, known future inputs, and static metadata. Each input is initially passed through a variable selection network. This involves transforming the inputs before passing them through a Gated Residual Network (GRN) [22]. Linear transformations are used for continuous variables and entity embeddings [24] are used for the categorical variables. The GRN allows some inputs to skip layers of the network. This enhances the model’s ability to deal with noisy inputs, and prevents the network from becoming too complex. Specifically, the GRN operation is given by:

$$GR{N}_{\omega }(\mathit{a},\mathit{c})=\mathrm{LayerNorm}(\mathit{a}+GL{U}_{\omega }\left({\mathit{\eta }}_1\right)),$$

(7)

with the intermediate dense layers ${\eta }_1$ and ${\eta }_2$ given by:

$$\begin{array}{cc}\hfill {\mathit{\eta }}_1& ={\mathit{W}}_{1,\omega }{\mathit{\eta }}_2+{\mathit{b}}_{1,\omega }\hfill \\ \hfill {\mathit{\eta }}_2& =ELU({\mathit{W}}_{2,\omega }\mathit{a}+{\mathit{W}}_{3,\omega }\mathit{c}+{\mathit{b}}_{2,\omega }),\hfill \end{array}$$

(8)

where $\mathit{a}$ is the primary input, $\mathit{c}$ is a context vector, $ELU$ is the the Exponential Linear Unit activation function [25].

The variable selection network takes the transformed inputs, represented by ${\Xi }_t={\left[{\xi }_t^{{\left(1\right)}^T},...,{\xi }_t^{{\left(m_{\chi }\right)}^T}\right]}^T$, where ${\xi }_t^{\left(j\right)}$ is the transformed input of the jth variable at time t. ${\Xi }_t$ is passed into the variable selection network along with an external context vector ${\mathit{c}}_s$, and the result is passed through a softmax function:

$${\nu }_{\chi t}=\mathrm{Softmax}\left(GRN{\nu }_{\chi }({\Xi }_t,{\mathit{c}}_s)\right);.$$

(9)

${\nu }_{\chi t}$ is the resulting vector of variable selection weights at time t, with each element indicating the model’s learned importance for a corresponding input variable at that time step. These weights are then used to compute a weighted combination of the inputs at each time step, enabling the model to dynamically adjust its focus to the most relevant features throughout the sequence.

To quantify overall variable importance, the weights ${\mathit{\nu }}_{\chi t}$ are extracted at inference time across all time steps and averaged temporally. These average weights are then further averaged across the five test cells to yield a single importance score for each variable.

In this way, the model’s learned attentional focus over time and across different test cases is summarised by interpretable importance scores. This is explored further in Section 2.3.

2.3. Interpretability

Temperature Effect

A study of the model’s interpretability is presented in Section 3.4. To do this, test cells which had irregular behaviour in a particular variable were used. Then, the variable importance scores were measured to assess whether the model accounted for that variable’s impact on the degradation. The most obvious choice for this variable was temperature.

The effect of temperature on battery degradation is well studied. The exact implications of operating temperature depend on the dominant ageing mechanism; however, temperatures over 25 °C generally leads to accelerated ageing, due to increased reaction rates within the cell [26]. The description of temperature dependency of chemical reactions is given by the Arrhenius equation:

$$r=Aexp\left(-{\displaystyle \frac{E_a}{k_{B}T}}\right),$$

(10)

where $E_a$ is the activation energy, $k_B$ is the Boltzmann constant, T is the absolute temperature, and A is a pre-exponential factor.

3. Results

To evaluate the model’s performance, a prediction of the cell’s capacity curve was performed. The results are shown in

Table 2. Performance comparison of different models for varying sequence lengths.

Model	100I, 400O		200I, 400O		200I, 600O
	MAPE	MSE	MAPE	MSE	MAPE	MSE
CNN	1.12	2.82	0.87	1.73	0.89	1.86
LSTM	1.38	3.84	0.87	2.07	1.02	2.07
Transformer	1.43	3.95	1.02	2.54	1.40	3.35
Our model	0.67	1.52	0.37	0.41	0.68	1.83

.

3.1. Variables

The training variables for the model were intentionally selected for ease of calculation, with all continuous variables determined on a per-cycle basis. This approach simplifies the model’s deployment in real-world scenarios. The variables are listed in Table 1.

3.2. Training Procedure

For the experiments, the dataset was partitioned into training, test, and validation splits, with five cells reserved for testing, five for validation, and the remaining cells used for training. This allocation balanced the need for sufficient training diversity with reliable model selection and evaluation. The validation and test cells were selected to reflect a representative range of initial capacities and cycling conditions. All experiments were run on a single Nvidia V100 GPU. Each epoch took approximately 50 s to train, and each model was trained for a maximum of 30 epochs. Hyperparameter optimisation was conducted via random search, scanning over a grid of predefined parameters as defined in

Table 3. Search values for each hyperparameter used in the optimisation.

Hyperparameter	Values
Dropout rate	[0.1, 0.2, 0.3, 0.4, 0.5, 0.7, 0.9]
Hidden layer Size	[10, 20, 40, 80]
Minibatch size	[64, 128, 256]
Learning rate	[0.0001, 0.001, 0.01]
Max. gradient norm	[0.01, 1.0, 100.0]
Num. heads	[1, 4]

:

One test condition is displayed in Section 3.3. Further testing conditions (different permutations of train/test/validation splits) are displayed in Appendix B.

3.3. Model Accuracy Results

The proposed method was compared to a range of conventional data-driven techniques to provide accuracy benchmarks. To do this, the data were split up into the standard train/test/validation groupings. Six cells were reserved for testing, six for validation, and the remainder were used for training. Early stopping was used to avoid overtraining. Three different permutations of train/test/validation were tested in total (results for the last two are presented in Appendix B). To assess the ability of the model to perform over a variety of context windows, three different combinations of varying input/output length were chosen. The details of each experiment are summarised in

Table 4. Input and output sequence length configurations for each permutation setting.

Permutation	Input Length	Output Length
1	100	400
2	100	400
3	100	400
1	200	400
2	200	400
3	200	400
1	200	600
2	200	600
3	200	600

.

When evaluated using the Severson dataset, the model demonstrated substantial performance improvements. Unlike purely physics-based methods, the model does not require any prior electrochemical knowledge of the battery cell. Additionally, by incorporating battery type and capacity as static inputs (metadata), the model enables the training of a generalized model on datasets that include degradation data from various cells. This allows the model to leverage shared knowledge from similar degradation patterns across different cells. An example of the model’s capacity prediction for two cells is shown in Figure 2, additional plots are shown in Appendix B.2.

Interestingly, as the input length increased from 100 cycles to 200 cycles (while keeping the output length fixed at 400), both the MAPE and MSE worsened, indicating a decrease in performance. Several factors may explain this. First, the LSTM input encoder and self-attention layers, which have a complexity of $O\left(n^2\right)$ with respect to input length [27], may cause bottlenecks during training. Second, this suggests that the most recent input timesteps are generally more influential. The model may become “distracted” by earlier timesteps, leading to overfitting and decreased accuracy as the input length grows.

However, as shown in Table 2, when the output length was increased to 600 cycles, the model outputs remained accurate compared to the benchmarks.

3.4. Interpretability

Having established the accuracy of the model, we now demonstrate how relationships between the data that lead to predictions can be interpreted. While some conventional data-driven techniques can produce accurate results, the relative contributions of each of the potentially many features to the overall degradation remain unknown. Variable selection considers both static and time-dependent covariates, quantifying the impact of each feature per instance and filtering out unnecessary, noisy inputs.

The Severson dataset was used to investigate the usefulness of the model’s variable importance scores. To do this, outlier cells in specific variables were used; these are referred to as “importance test cells”. For example, a cell with a relatively high charging temperature could be used, as it is expected that the degradation of this cell would be more strongly affected by the charging temperature compared with an average cell. By calculating the variable importance score for this cell and comparing it with the average scores across the dataset, we can assess the model’s ability to make realistic estimates. If the charging temperature’s importance score for the test cell exceeds the average, it suggests that the model accurately reflects the relative importance of that variable.

Figure 3 shows the variable importance weights for the whole Severson dataset. As expected, the cycle number, i.e., the age of the cell, was the most important factor affecting the degradation. The second and third most important variables were both temperature variables, which is also sensible.

Several test cases were identified for studying variable importance. Here, we present importance test cell 2 as an example, and others are shown in Appendix A. The charging temperature for that cell was much higher than average, as shown in Figure 4. The corresponding attention scores for that cell are shown in Figure 5. Comparing this with Figure 3 demonstrates that the test cell had a higher attention score for the mean charging temperature (labelled T_c_mean) than the average score for the whole dataset. The cell’s attention score for that variable was 5.48%, making it the fifth most important variable; whereas the average score was 4.79%, which ranked as the eighth most important variable. In this way, the model can correctly assign a higher importance where a particular feature plays a greater role in the cell’s degradation.

4. Conclusions

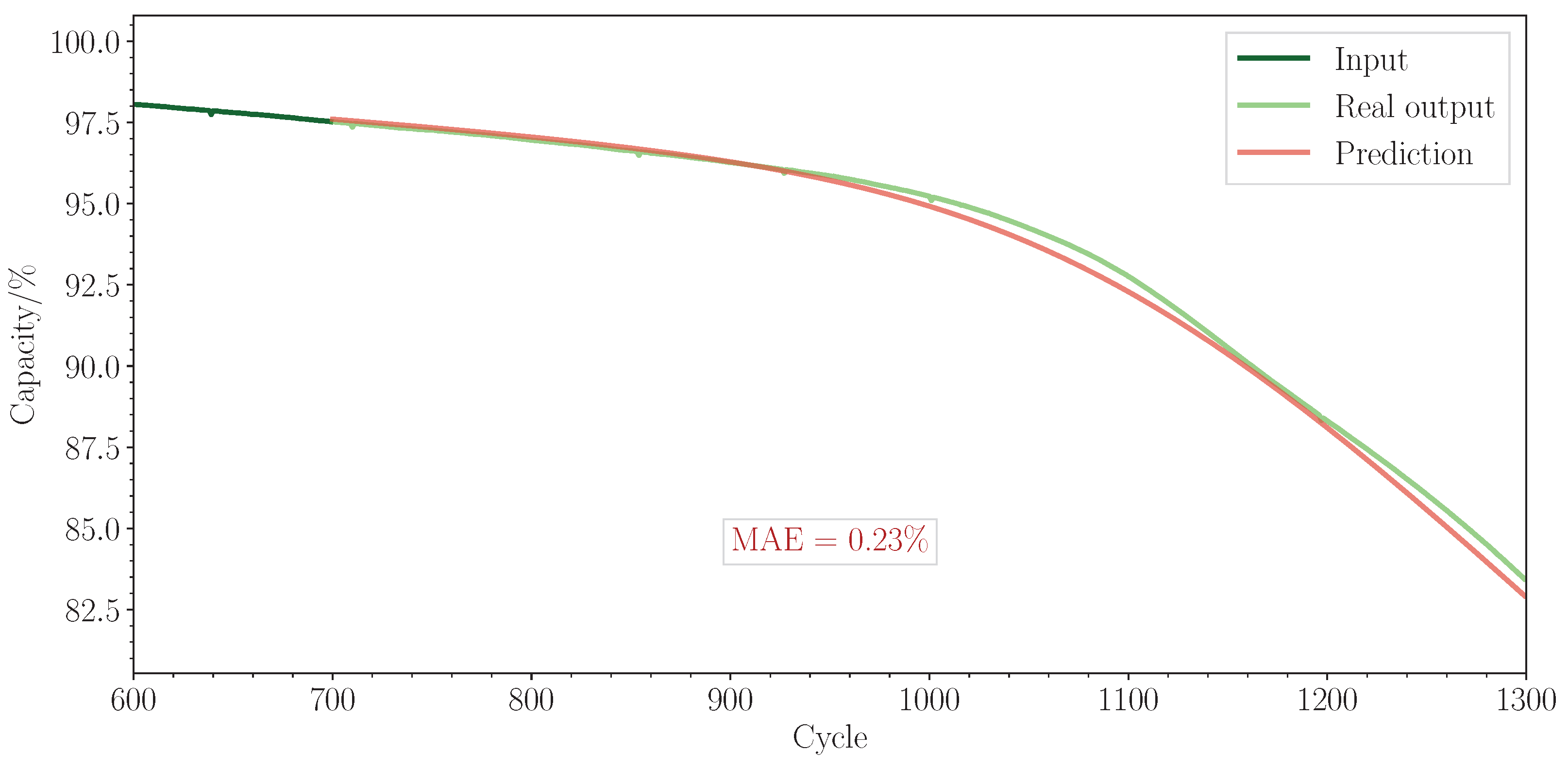
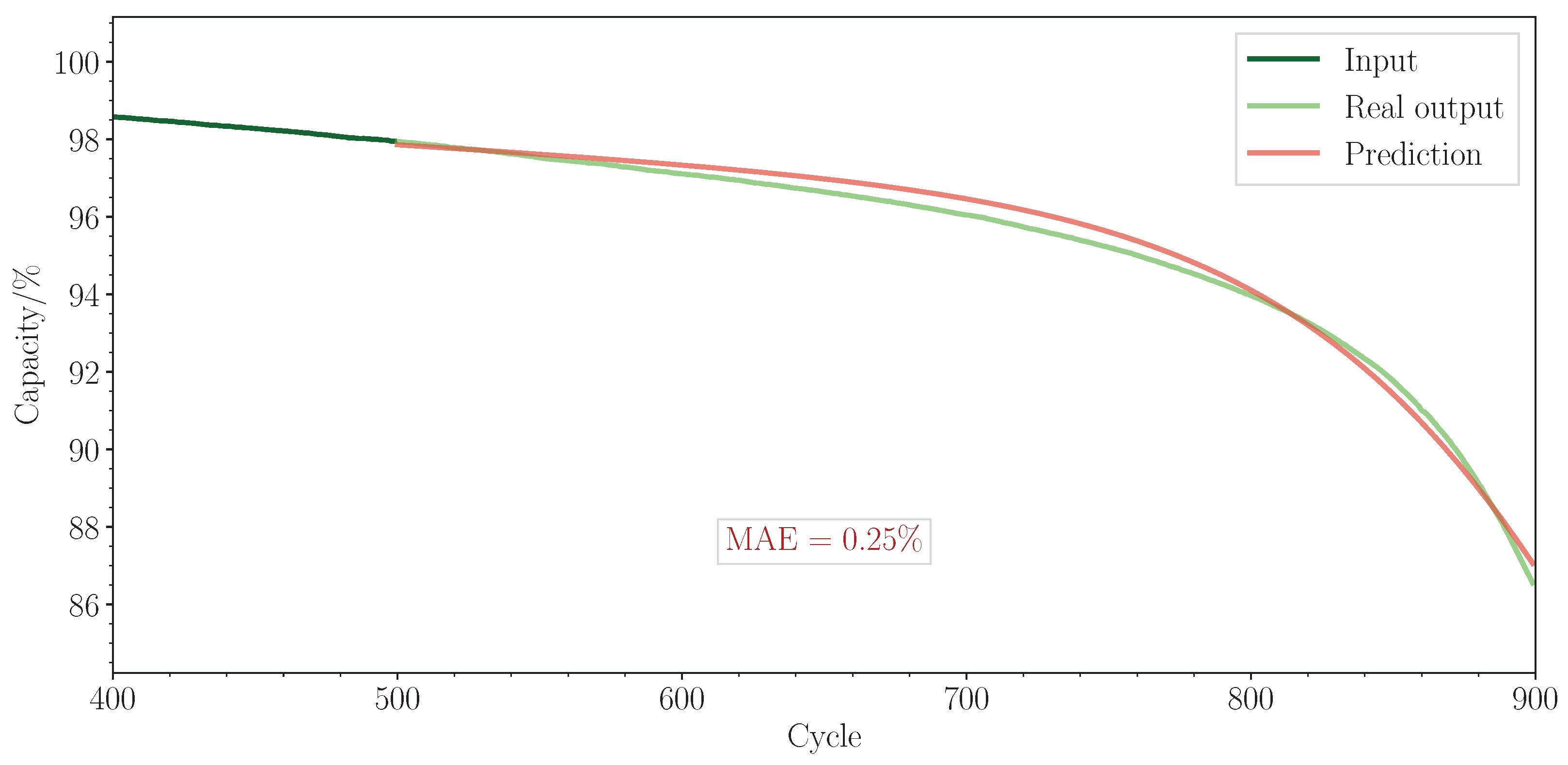
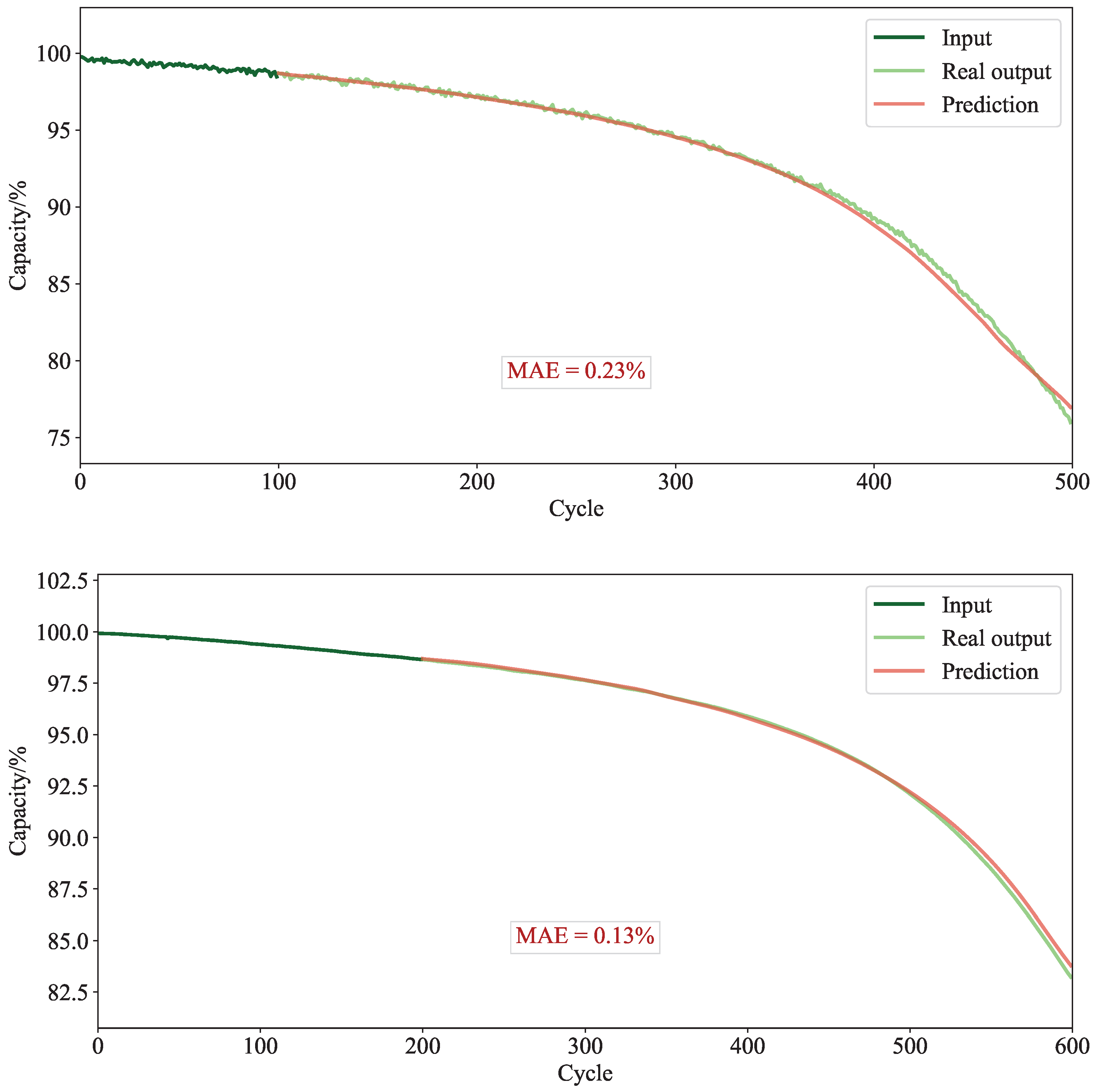
This study presented a novel approach for modelling battery degradation using a Temporal Fusion Transformer. The proposed model demonstrated superior accuracy compared to standard deep learning methods across various sequence lengths. The mean absolute error for the predicted capacity curve was found to be between 0.67% and 0.85%, compared with 0.87–1.40% for the benchmark models.

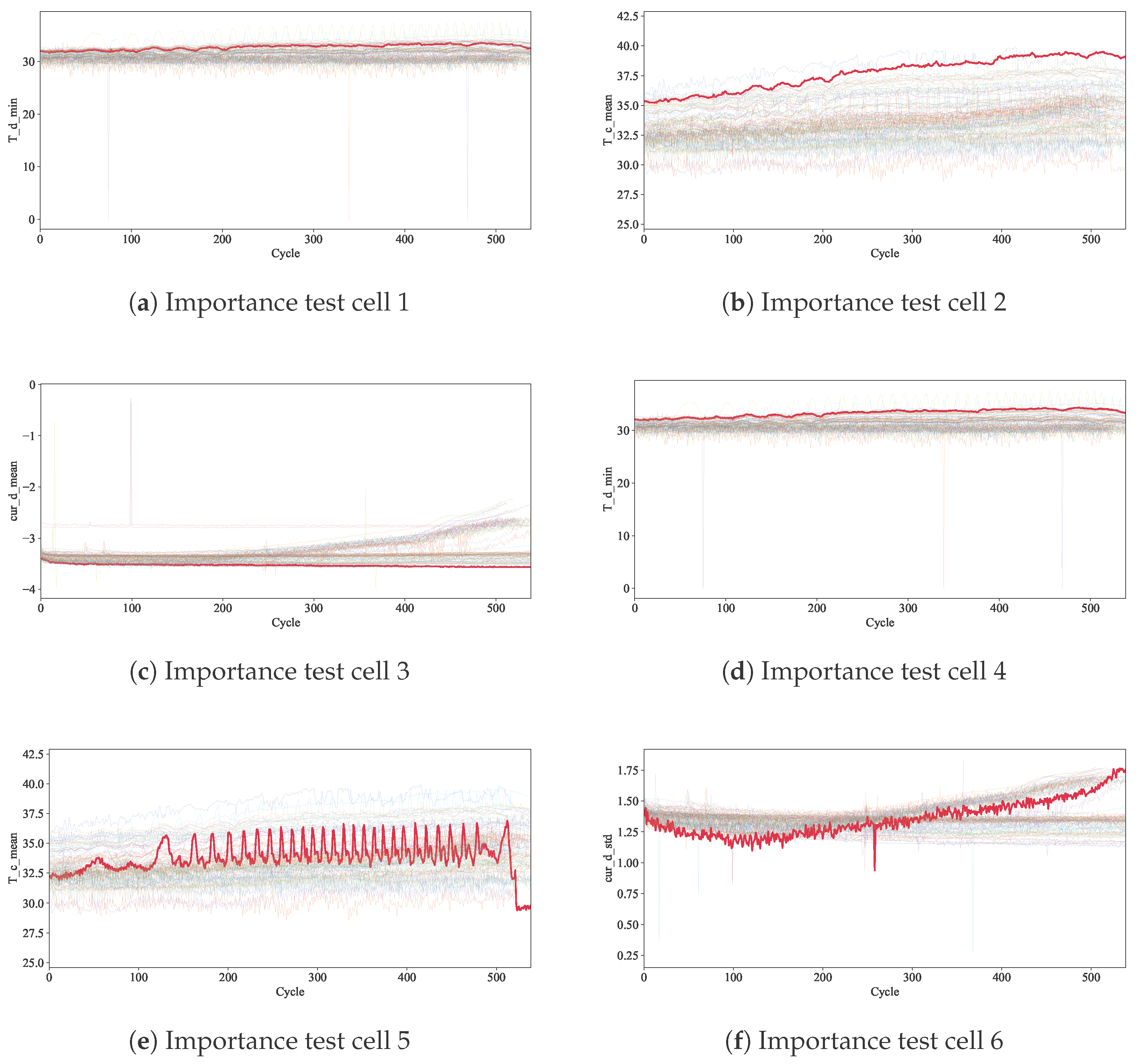
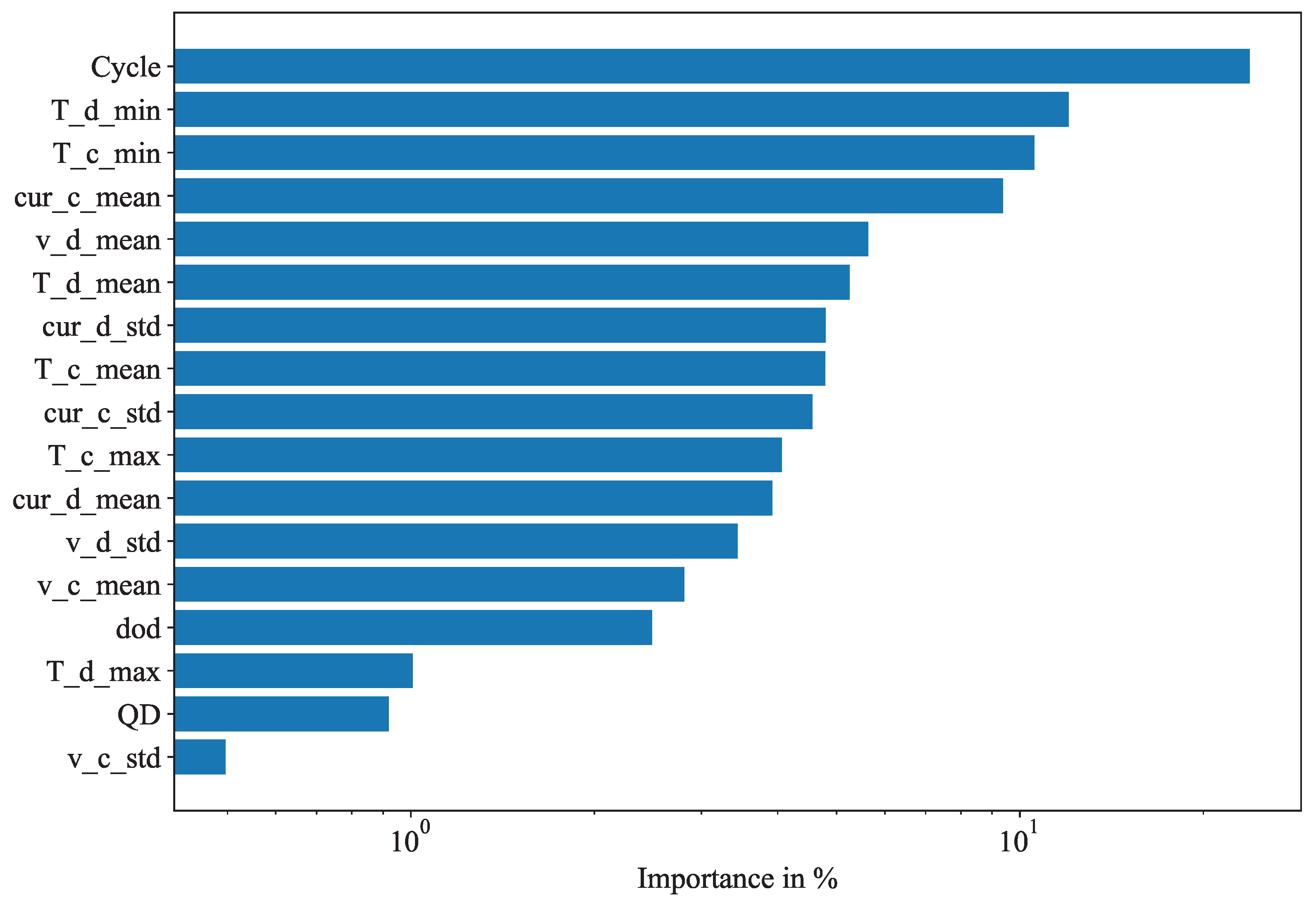
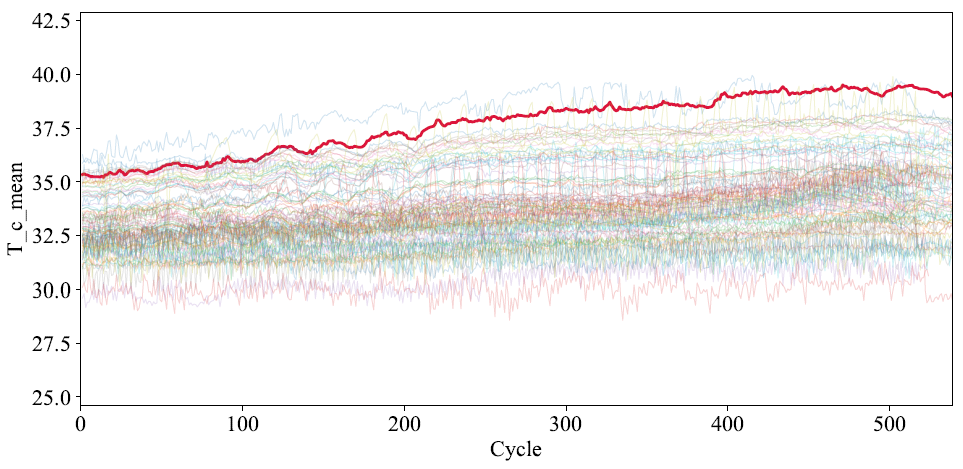
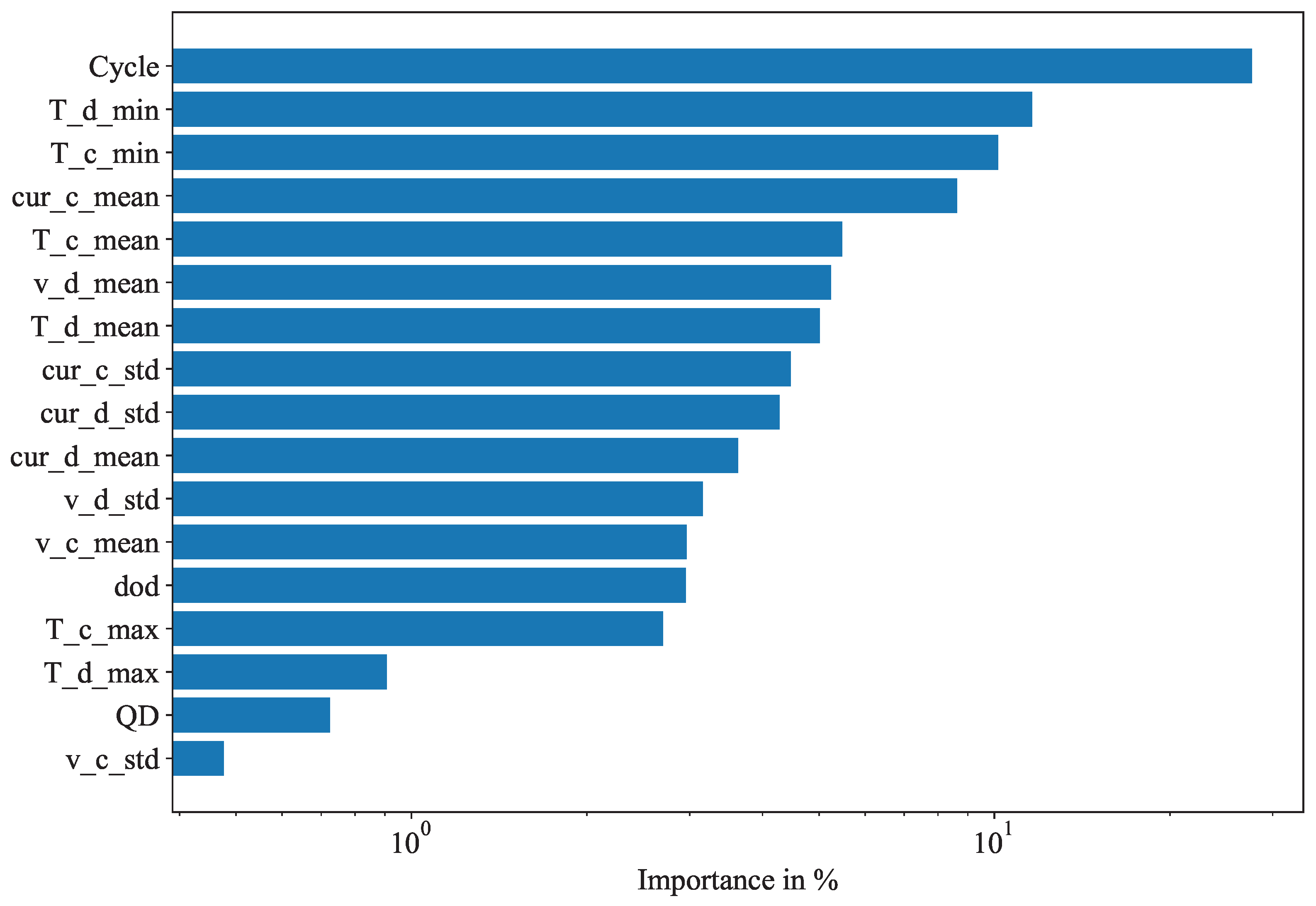
The model effectively integrates both continuous and categorical inputs, which can be either static or time-varying. In addition, it offers interpretable outputs, yielding valuable insights into specific factors that impact a given battery’s degradation. This could enable a user to extend the life of a battery during operation. Moreover, the model is capable of accurately forecasting degradation curves with as few as 100 input cycles.

The model presented in this study has great potential to enhance the reliability and safety of lithium-ion batteries in electric vehicles or energy storage systems. Moreover, the model is agnostic to cell chemistry and can be readily applied to other battery types, provided that suitable training data are available.