Abstract
The accurate estimation of the state of health (SOH) is crucial for effective battery management systems. This paper proposes a deep learning model dimension-wise convolutions-globalfilter networks (DimConv-GFNet) for lithium-ion battery SOH estimation. Particularly, the DimConv-GFNet comprises the dimension-wise convolutions (DimConv), which collect the multi-scale local features from different sensor signals, and lightweight global filter networks (GFNet) to capture long-range dependencies in the Fourier frequency domain. Unlike Transformer attention architectures, GFNet utilizes spectral properties to facilitate global information exchange with a lower computational complexity. Experiments on two datasets with a total of 167 commercial LFP/graphite cells validate the effectiveness of DimConv-GFNet. Although the model shows slightly lower accuracy compared to the DimConv-Transformer baseline, it delivers competitive performance with a root mean squared error (RMSE) of 0.335%, mean absolute error (MAE) of 0.233% and a mean absolute percentage error (MAPE) of 0.230%. Remarkably, the DimConv-GFNet substantially reduces computational demands, requiring fewer than one-third of the Floating Point Operations (FLOPs) and parameters of DimConv-Transformer. These results demonstrate DimConv-GFNet strikes a good balance between accuracy and efficiency, positioning it as a promising solution for efficient and accurate SOH estimation in battery management applications.
1. Introduction
Lithium-ion batteries have become a critical pillar in the global transition to clean energy, owing to their high energy density, long cycle life, and low self-discharge rate. They are widely deployed in portable electronics, electric vehicles, and renewable energy storage systems [1,2,3], significantly enhancing energy efficiency and reducing greenhouse gas emissions, providing strong support for sustainable development. Despite their widespread adoption, lithium-ion batteries are subject to gradual degradation over their lifespan, primarily driven by inherent electrochemical side reactions and material aging [4].
The state of health (SOH), defined as the ratio of the current maximum discharge capacity to the nominal capacity, is typically utilized to assess the battery degradation extent, primarily because SOH serves as a gauge of a battery’s general condition and ability to provide the intended performance compared to the ideal conditions [5]. As a result, precise estimation and efficient battery SOH monitoring are essential for maintaining safe, effective, and optimal energy system performance as well as for appropriate maintenance and retirement schemes [6]. Nevertheless, in practical applications, the capacity of a working battery cannot be directly measured by measuring instruments [7], indicating that estimation algorithms based on other measured signals (e.g., voltage, current, and temperature) become the only solution to acquire the value of SOH, which is a challenging task [8].
Various methods have been investigated for SOH estimation algorithms, which can be divided into three main classes as follows: experimental methods, model-based approaches, and data-driven techniques [9].
The experimental methods encompass the ampere-hour concept, the open circuit voltage approach, and impedance spectroscopy method [10]. All these approaches are capable of obtaining extensive degradation information and accurate SOH estimation outcomes straightforwardly. However, they require high-precision measurements, multiple operations, and may permanently degrade the lifespan of the battery. Hence, experimental methods are more suitable in specialized laboratories while practical applications are somewhat restricted [5].
Model-based methods generally estimate SOH by identifying the parameters of an electrochemical model or an equivalent circuit model [11]. Based on the chemical reactions and transport mechanisms occurring inside lithium-ion batteries, the electrochemical model establishes partial differential equations to describe the battery’s properties [12]. It has a distinct physical meaning and offers exceptional precision, yet it demands specialized knowledge of electrochemical theory and its partial differential equations are challenging to solve [13]. Magri et al. even couple the thermal behavior of the battery with the electrochemical model, which can indeed provide a more accurate simulation of battery behavior, but this makes practical application more challenging [14]. The equivalent circuit model represents the battery as a circuit composed of resistors and capacitors [15]. Resistors characterize internal resistance and polarization internal resistance of the battery, while capacitors simulate the dynamic process of polarization phenomena. SOH estimation can be achieved by identifying the circuit component parameters combined with various Kalman filtering algorithms [16,17]. However, the parameter identification error tends to increase as the battery ages, causing the inaccuracy in SOH estimation.
Unlike model-based methods that require specialized expertise, data-driven approaches tend to establish the connection between collected operating data and SOH straightforwardly, which encompass traditional machine learning and deep learning techniques. Over the last decade, numerous machine learning algorithms have been applied to estimate SOH, ranging from k-nearest neighbor regression [18], random forest regression [19], linear regression analysis [20], and support vector machines [21] to Gaussian process regression [22] and extreme learning machine [23]. All these traditional machine learning models are able to extract complex connections between features and SOH as well as battery degradation patterns, but their accuracy and effectiveness highly depend on meticulous feature engineering.
Conversely, deep learning markedly diminishes reliance on manually engineered features, instead autonomously deriving abstract representations from raw data through multi-layered networks. This inherent capability confers a considerable advantage in the processing of complex, high-dimensional, and nonlinear data; thus, increasing attention has been directed toward exploring the employment of deep learning approaches for SOH estimation and battery prognosis [24,25,26]. Through leveraging deep neural networks, researchers are able to automatically extract valuable features from battery historical data, leading to more accurate and reliable SOH estimation. Convolutional neural networks (CNNs) are proficient in gathering local variables hierarchically through their convolutional operations and preserve all local cues as feature maps [5]. For example, Yang et al. employed a CNN to extract indicators for estimating SOH [27]. Given that SOH estimation algorithms are handling sequential data to derive the final result, SOH estimation can be characterized as a time-series problem. Furthermore, recurrent neural networks like long short-term memory (LSTM) neural networks and gated recurrent unit (GRU) neural networks, are well-suited for modeling such sequences owing to their capability to capture temporal dependencies. For instance, Ma et al. applied LSTM with a differential evolution gray wolf optimizer to learn the temporal relationships for SOH estimation by using its internal memory [10]. Xu et al. leveraged the advantages of both CNN and LSTM to improve the SOH estimation accuracy [28], yielding remarkable outcomes. To further improve the monitoring of SOH, a study introduced a model that integrates CNN and bidirectional gated recurrent unit (BiGRU) networks for SOH estimation [29], which highlights that GRU offers a more streamlined architecture and better computational efficiency compared to the LSTM.
It is worth noting that whether using CNN, LSTM, or GRU, these models can only capture local or short-term features. For batteries, the entire charge-discharge process at various stages affects their health state and degradation. The Transformer model, with its multi-head self-attention mechanism, excels at global feature extraction [30]. However, it often overlooks local feature details, which can be crucial for accurate analysis. To address this constraint, the hybrid CNN-Transformer model proposed by Gu et al. combines the CNN’s hierarchical local feature extraction with Transformer’s global property aggregation [5], ensuring the precise estimations of battery SOH. In order to conserve the computational resources associated with attention mechanisms and optimize the efficiency of SOH estimation, Zhao et al. utilized a multi-head sparse self-attention mechanism, which proved impressive effectiveness in achieving accurate estimations and facilitating rapid training [31].
With the continuous exploration of deep learning in the field of battery SOH estimation, the CNN-Transformer hybrid model has shown excellent performance after being improved by researchers, achieving accurate SOH estimation. However, in practical applications, there are still several aspects that warrant further investigation. Firstly, the CNN used in the aforementioned models to extract local features are mostly based on the time-series property, which may not fully account for the internal connections among multiple physics measurement signals. Secondly, the Transformer attention architecture, while aggregating local features to capture global features, still faces issues like quadratic time complexity and heavy memory consumption [31]. This might impact its efficiency in certain cases. To conquer these problems, this study proposes the dimension-wise convolutions-global filter networks (DimConv-GFNet), a hybrid architecture that effectively captures both local and global dependencies across various physics measurement signals, while maintaining better computational efficiency than Transformer attention architecture.
The core innovations of DimConv-GFNet lie in two aspects as follows:
Firstly, by utilizing dimension-wise convolutions (DimConv) applied to different dimensions, the proposed model can capture inter-signal relationships at multiple scales. This allows DimConv-GFNet to handle various physical measurements (voltage, current, temperature, and time) across both temporal and spatial dimensions. By considering these signals at varying scales, the model can better represent the underlying physical behavior of the battery. This multi-scale approach improves our understanding of complex signal interactions, leading to better performance for SOH estimation in real-world applications.
Secondly, this paper employs global filter networks (GFNets) that can be regarded as a replacement for the conventional Transformer attention architectures. A GFNet operates in the Fourier frequency domain by applying the element-wise multiplication of the input spectrum with a learnable global filter. Such an operation significantly reduces computational complexity while effectively capturing global dependencies. Notably, it takes advantage of the conjugate symmetric property of the spectrum, allowing it to process only half of the spectral values. This approach not only simplifies computations but also substantially decreases overall computational costs. The lightweight global filter network enhances model efficiency, capturing long-range dependencies while remaining resource-efficient. This change is especially beneficial for real-world applications in the resource-constrained conditions, since it significantly lowers computational requirements with only a slight compromise in performance.
These advancements permit DimConv-GFNet to achieve accurate SOH estimation efficiently, making it highly suitable for battery management systems. The rest of this paper is organized as follows. Section 2 presents the architecture and design of the DimConv-GFNet model. Section 3 introduces datasets and data processing and then outlines the experimental setup. Section 4 show the experimental results and provides a discussion. Section 5 concludes the paper and discusses potential future directions.
2. Methodology
2.1. DimConv
Two-dimensional convolution can efficiently capture the local potential relationships within the input data. The two-dimensional data are processed by moving a convolutional kernel to extract the spatial latent features. Essentially, this process is a weighted summation of the data within the input region, followed by the addition of a bias term, which can be defined as follows:
where the kernel size is 3 × 3. Therefore, in this paper, two-dimensional convolution is used to handle the mapping association between the voltage, current, temperature, time, and SOH.
DimConv (Figure 1) initially executes two-dimensional convolutions across various dimensions. Subsequently, the respective features are uniformly shuffled and fused through a further layer that computes a linear combination of the output via 1 × 1 convolution [32]. Specifically, there are different convolutional kernels sliding along the planes perpendicular to the depth, height, and width dimensions. Specifically, as the convolution kernel moves along the plane perpendicular to the depth (depth-wise convolution), it captures the features among voltage, current, temperature, and time at a smaller temporal scale, while the convolution kernel moving along the plane perpendicular to the height (height-wise convolution) learns features over a larger temporal scale. Furthermore, the convolution kernel moving along the plane perpendicular to the width dimension (width-wise convolution)extracts features representing the individual spatial characteristics of voltage, current, temperature, and time at another time scale. Then, the output of various dimensions are uniformly shuffled. A 1 × 1 convolution, with input channels that are three times that of the output channels, is ultimately used to fuse the features derived from the three dimensions with the PReLU activation function, achieving the integration of two temporal scales and the enhancement of an individual feature in this process. This results in the retrieval of multi-scale local fusion features (N, H, W), where (H, W) is the size of each patch and N is the number of patches, which also serves as the effective input sequence length for global filter network.
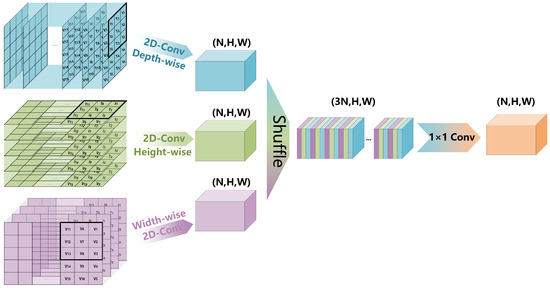
Figure 1.
Dimension-wise convolutions.
2.2. GFNet
Since the input data for the global filter must be two-dimensional, a patch embedding layer is introduced to bridge the DimConv and the global filter layer. This layer flattens the local features of each patch from (H, W) to (H × W) and maps them to D dimensions using a trainable linear projection [33], finally reshaping them into (D, N).
As a fundamental technique in digital signal processing, the Fourier transform shifts signals from the time domain to the frequency domain [34]. Consequently, the global filter network is designed to facilitate global information exchange among patches in the Fourier frequency domain. This network comprises a stack of identical layers, each containing two sublayers. The first sublayer is a global filter layer, while the second is a feed-forward layer. Each sublayer is preceded by layer normalization to enhance model stability and mitigate issues such as gradient vanishing and explosion. Additionally, we employ a residual connection around each layer to improve gradient flow within the network [35].
2.2.1. Discrete Fourier Transform
In fact, actual data are typically discrete, thus we employ the two-dimensional discrete Fourier transform (2D DFT) to convert the local features from the temporal and spatial domain to the Fourier frequency domain. Given the 2D matrix , , , the frequency domain representation of is given by the following:
where represent the frequency domain coordinates, , . It is worth noting that are conjugate symmetric, which can be proved as follows:
where is the complex conjugate of .
Leveraging the conjugate symmetric property, only half of the values in X need to be fed into the global filter encoder, while the full information is preserved at the same time [36]. Finally, given the 2D DFT , we can recover the original matrix by the inverse DFT (IDFT) as follows:
2.2.2. Global Filter Design
As the core component of the global filter networks, the global filter needs to capture the global features among patches, whose input data must be two-dimensional. Following the flattening, mapping, and reshaping processes of the patch embedding layer, all the features are converted to the Fourier frequency domain, which can be represented by the following equation:
where denotes the 2D DFT. Note that is a complex tensor and represents the spectrum of x. Since x is a real tensor and the corresponding spectrum is conjugate symmetric, only half of the is needed for further processing as follows [37]:
where is the least integer that is at least . According to the spectral convolution theorem in Fourier theory, a single value modification in the spectral domain produces a global effect on the entire original data [38], providing insights into design operations with the non-local receptive field. In other words, the Fourier transform amalgamates the entire information into distinct elements of the spectrum. Consequently, we can represent the global context through a rudimentary element-wise multiplication between the spectrum and a learnable global filter K as follows:
where ⊙ is the Hadamard product, , weighting the features of each patch in the Fourier frequency domain. Ultimately, the inverse DFT (IDFT) is adopted to transform the modulated spectrum back, as follows:
Subsequent to the global filter layer, a Feed Forward Network (FFN) is utilized. The FFN, via linear transformations and nonlinear activation of neural units, substantially bolsters the feature extraction proficiency of the global filter network. FFN operations are as follows.
2.3. Overview of DimConv-GFNet
Figure 2 shows the complete DimConv-GFNet-based SOH estimation framework. The model primarily consists of four parts, dimension-wise fusion convolutions, the global filter layer, the average pooling layer, and the multi-layer perceptron. The sensor signals of the battery (voltage, current, temperature, and time of a single cycle) are first uniformly interpolated and resampled to the required number of sample points for the model. Then, the data are divided into different patches and reshaped into a three-dimensional tensor. DimConv is applied to extract multi-scale fused local features, followed by the use of GFNet to exchange and mix information between patches to capture global features. The global features are then subjected to an average pooling layer and passed through a multi-layer perceptron to output the estimated SOH. The model workflow is summarized in Table 1.
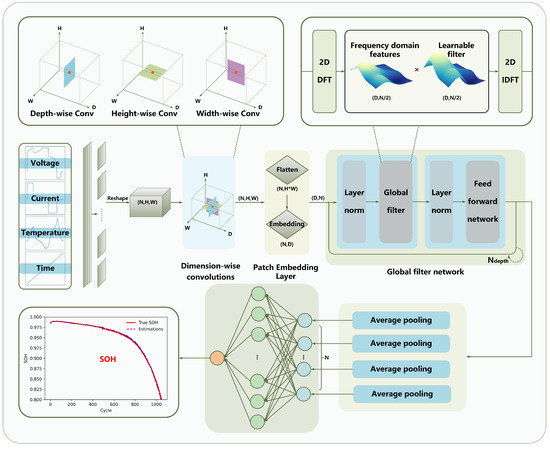
Figure 2.
Framework of the proposed DimConv-GFNet for SOH estimation.

Table 1.
Model workflow.
3. Experiment
3.1. Datasets Description
Datasets containing fast charging cycling data are originally provided by Severson et al. [39] and Attia et al. [40]. They involve a total of 169 commercial lithium ion phosphate (LFP)/graphite cells manufactured by A123 System (APR18650M1A), each with a nominal capacity of 1.1 Ah. All cells were cycled until they reached end-of-life (defined as 80% of their nominal capacity). The cell charging conditions consist of different types of multi-stage constant current (CC) charging, employing one-step, two-step, or four-step fast-charging strategies up to 80% state-of-charge (SOC) (Figure 3), mostly ranging from 3C to 8C [41]. Subsequently, the batteries were charged at 1C using a uniform constant current-constant voltage (CC-CV) protocol to a cutoff voltage of 3.6 V and a cutoff current of 0.02C. Finally, all batteries were discharged at a rate of 4C to a cutoff voltage of 2.0 V [39,40]. Voltage, current, and temperature directly from sensors were recorded during aging cycles. The discharge profiles exhibited differences across individual batteries, with most having a cycle life ranging from 500 to 1100 cycles. From Figure 3, it can be seen that the datasets provide rich voltage, current, and temperature information, which can be used by our model to further capture the underlying physical behaviors of the battery. Note that two of the 169 cells are excluded due to abnormal recorded data.
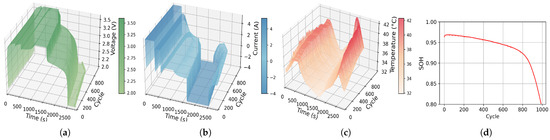
Figure 3.
Two-step fast-charging battery example b3c25. (a) Voltage, (b) current, (c) temperature, and (d) SOH.
The SOH of battery is defined as the ratio of the current capacity to its nominal capacity as follows:
3.2. Data Processing
Different batteries have different sampling point counts for each cycle due to their different charging policies and varying aging degrees. As shown in Figure 3, different SOH values are associated with distinct sets of voltage, current, and temperature profiles. In other words, the voltage, current, and temperature are all time-varying series that correspond to a specific SOH [42]. Nevertheless, to meet the requirement of the model, the number of sampling points must be consistent and fixed. Therefore, using time as the reference, the voltage, current and temperature data are uniformly interpolated to a fixed length of 480. To accelerate the algorithm’s convergence and improve the estimation accuracy of the model, the resampled data are min–max-normalized to standardize the data scale within the range of [−1, 1] [31], which is expressed as follows:
3.3. Experimental Settings
Previous studies have demonstrated that generic CNNs and GRU/LSTM models underperform individually compared to their hybrid models [5,29]. Consequently, we did not include them in the comparison with our proposed model. Instead, we compared our SOH estimation framework DimConv-GFNet with four additional models. These models included the CNN-LSTM, CNN-GRU, CNN-Transformer, and DimConv-Transformer. All the CNN components in these models consist of two layers of stacked convolutional, activation and pooling operations, while both LSTM and GRU are implemented with two layers as well. Note that the Transformer attention architecture also has a depth of two layers. Furthermore, Table 2 shows the main hyperparameters of our proposed model.

Table 2.
Model hyperparameters.
Model validation was performed on a server equipped with an AMD EPYC 7542 CPU operating at 2.9 GHz, along with an NVIDIA GeForce GTX 4090 graphics card. The proposed SOH estimation framework and the comparison methods were implemented using Python 3.8, utilizing the ‘Torch’ package.
4. Result and Discussion
4.1. Evaluation Criteria
In order to assess the performance of the SOH estimation methods, several evaluation metrics are utilized. These metrics include mean absolute error (MAE), mean absolute percentage error (MAPE), and root mean squared error (RMSE). RMSE quantifies the deviation between the estimated and reference values, providing an indication of the estimation accuracy. MAE reflects the average magnitude of the errors generated by the proposed method. MAPE measures the relative percentage error between the predicted and true values [43]. Formulas for the , , and are provided below.
4.2. Experimental Results and Discussion
Since the batteries in the two datasets are identical, except for the charging and discharging conditions, we randomly shuffled the 167 batteries from both datasets. Then, we chose 117 batteries (70%) for training the model, and the remaining 50 batteries (30%) were used to evaluate the performance of the proposed method.
Figure 4 and Table 3 illustrate the overall test results. The CNN-Transformer, DimConv-Transformer, and DimConv-GFNet models demonstrate superior SOH estimation accuracy compared to the CNN-GRU and CNN-LSTM frameworks, which focus solely on time-series characteristics. The RMSE, MAE, and MAPE for the former models are all lower than those of the latter. According to Table 3, DimConv-Transformer achieved a RMSE of 0.227%, MAE of 0.146%, and MAPE of 0.144%, compared to CNN-Transformer’s 0.365% RMSE, 0.242% MAE, and 0.240% MAPE. This demonstrates that dimension-wise convolutions contribute to improved SOH estimation accuracy. In Figure 4, the box plot for DimConv-Transformer shows a significantly reduced height, narrower spread, and a more concentrated error range, further indicating that by adequately learning the underlying relationships among battery operating signals, we can ensure the stability of SOH estimation accuracy to a certain extent.
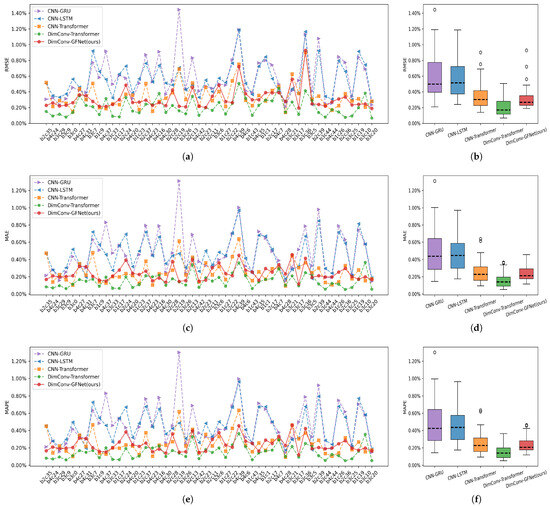
Figure 4.
Comparison of different models for all test batteries. (a,b) RMSE, (c,d) MAE, and (e,f) MAPE.

Table 3.
Comparison of estimation results.
To evaluate the complexity and efficiency of our deep learning model for SOH estimation, we consider the following two key metrics: Floating Point Operations (FLOPs) and Parameters (Params). FLOPs quantify the sum number of floating-point operations required for a single forward pass of the model. Generally speaking, a higher FLOP counts typically suggests a more complicated model that takes more processing resources [44]. Furthermore, Params represent the number of trainable parameters within the model, directly impacting the model’s storage needs and training complexity. Although DimConv-GFNet exhibits a RMSE of 0.335%, MAE of 0.233%, and MAPE of 0.230%, which are slightly inferior in accuracy compared to DimConv-Transformer, Table 4 indicates that the FLOPs and parameters of DimConv-GFNet are less than one-third of those of DimConv-Transformer, with both models having the same depth of two layers. The FLOPs and Params of DimConv-GFNet are less than one-third of those of DimConv-Transformer, demonstrating that the GFNet in this paper maintains the ability to learn global information while also being efficient and having lower computational complexity than the Transformer.

Table 4.
Comparison of model complexity.
Figure 5 shows some SOH estimation results for batteries from four batches. It can be observed that the estimation results of DimConv-GFNet are not only closer to the true values in terms of overall trends but also more accurate at points of capacity fluctuation. The absolute error plots on the right side of Figure 5 clearly demonstrate that the DimConv-GFNet model (red line) consistently exhibits the lower estimation errors across all battery cycles. In contrast, other models experience significant error increases, particularly in the later stages. This indicates that the DimConv-GFNet model offers considerable efficiency and accuracy in SOH estimation tasks.
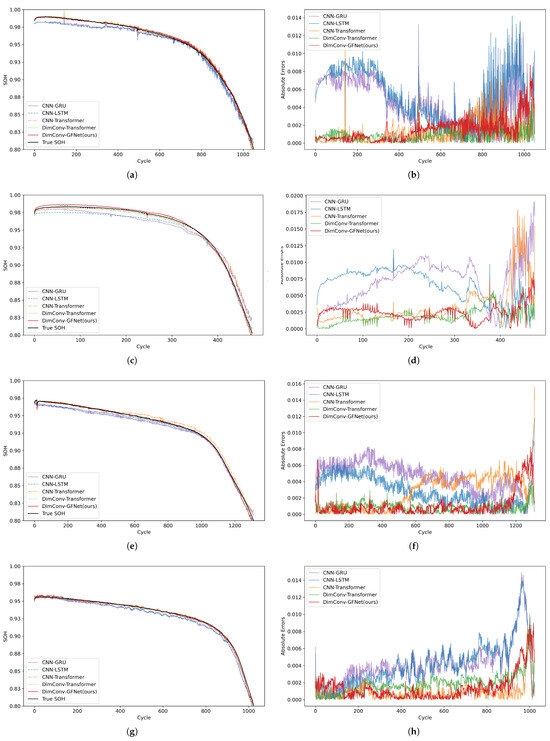
Figure 5.
(a,b) b1c9 results (c,d) b2c37 results (e,f) b3c17 results (g,h) b4c23 results.
5. Conclusions
An innovative hybrid DimConv-GFNet model for SOH estimation is proposed in this paper, which is formed using a combination of dimension-wise convolutions and a global filter net. By exploring the relationships among voltage, current, temperature, and time, DimConv successfully extracts multi-scale local features. The following GFNet further captures global long-range dependencies in the Fourier frequency domain efficiently. Compared to traditional Transformer attention architectures, the GFNet shows improved performance regarding complexity and computational efficiency, achieving precise and efficient SOH estimation.
Although this study demonstrates superior accuracy and computational efficiency with DimConv-GFNet, there still remain some limitations. For example, the model requires fixed-length data for the entire cycle, which is a problem to be improved for some special battery operational conditions in the real word. Compared to traditional machine learning methods, DimConv-GFNet still needs to be further simplified. In addition, the selection of sampling points and the division of patches require further exploration. Future research will aim to improve the aforementioned limitations, thereby strengthening its applicability to real-world operating batteries.
To conclude, the introduced DimConv-GFNet model represents an important step forward in the field of battery SOH estimation, offering a novel perspective for deep learning-based battery state estimation algorithms. Ongoing refinements and optimizations in the future may facilitate its application in engineering practice.
Author Contributions
Conceptualization, K.H.; methodology, K.H.; validation, K.H., J.K., and O.W.; formal analysis, K.H., J.K., and O.W.; investigation, K.H.; resources, K.H.; data curation, K.H.; writing—original draft preparation, K.H.; writing—review and editing, K.H. and O.W.; visualization, K.H. and O.W.; supervision, J.K., J.V.W., Q.W., and O.W.; funding acquisition, J.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China grant number 52277224 and National Key Laboratory of Electromagnetic Energy under grant number 61422172320104.
Data Availability Statement
The data that support the findings of this study are openly available at URL/DOI: https://data.matr.io/1, accessed on 21 August 2024.
Acknowledgments
The authors would like to thank Severson and Attia for providing the original battery cycling data.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SOH | State of health |
| DimConv | Dimension-wise convolutions |
| GFNet | Global filter network |
| FLOPs | Floating point operations |
| Params | Parameters |
References
- Vignesh, S.; Che, H.S.; Selvaraj, J.; Tey, K.S.; Lee, J.W.; Shareef, H.; Errouissi, R. State of Health (SoH) estimation methods for second life lithium-ion battery—Review and challenges. Appl. Energy 2024, 369, 123542. [Google Scholar]
- Masias, A.; Marcicki, J.; Paxton, W.A. Opportunities and challenges of lithium ion batteries in automotive applications. ACS Energy Lett. 2021, 6, 621–630. [Google Scholar] [CrossRef]
- Costa, C.M.; Barbosa, J.C.; Gonçalves, R.; Castro, H.; Del Campo, F.; Lanceros-Méndez, S. Recycling and environmental issues of lithium-ion batteries: Advances, challenges and opportunities. Energy Storage Mater. 2021, 37, 433–465. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, C.; Jiang, J.; Zhang, W.; Zhang, L.; Wang, Y. Review on state-of-health of lithium-ion batteries: Characterizations, estimations and applications. J. Clean. Prod. 2021, 314, 128015. [Google Scholar] [CrossRef]
- Gu, X.; See, K.W.; Li, P.; Shan, K.; Wang, Y.; Zhao, L.; Lim, K.C.; Zhang, N. A novel state-of-health estimation for the lithium-ion battery using a convolutional neural network and transformer model. Energy 2023, 262, 125501. [Google Scholar] [CrossRef]
- Cao, Z.; Gao, W.; Fu, Y.; Kurdkandi, N.V.; Mi, C. A general framework for lithium-ion battery state of health estimation: From laboratory tests to machine learning with transferability across domains. Appl. Energy 2025, 262, 125086. [Google Scholar] [CrossRef]
- Chen, L.; Xie, S.; Lopes, A.M.; Li, H.; Bao, X.; Zhang, C.; Li, P. A new SOH estimation method for Lithium-ion batteries based on model-data-fusion. Energy 2024, 286, 129597. [Google Scholar] [CrossRef]
- Ding, P.; Liu, X.; Li, H.; Huang, Z.; Zhang, K.; Shao, L.; Abedinia, O. Useful life prediction based on wavelet packet decomposition and two-dimensional convolutional neural network for lithium-ion batteries. Renew. Sustain. Energy Rev. 2021, 148, 111287. [Google Scholar] [CrossRef]
- Demirci, O.; Taskin, S.; Schaltz, E.; Demirci, B.A. Review of battery state estimation methods for electric vehicles-Part II: SOH estimation. J. Energy Storage 2024, 96, 112703. [Google Scholar] [CrossRef]
- Ma, Y.; Shan, C.; Gao, J.; Chen, H. A novel method for state of health estimation of lithium-ion batteries based on improved LSTM and health indicators extraction. Energy 2022, 251, 123973. [Google Scholar] [CrossRef]
- Fu, S.; Tao, S.; Fan, H.; He, K.; Liu, X.; Tao, Y.; Zuo, J.; Zhang, X.; Wang, Y.; Sun, Y. Data-driven capacity estimation for lithium-ion batteries with feature matching based transfer learning method. Appl. Energy 2024, 353, 121991. [Google Scholar] [CrossRef]
- Che, Y.; Hu, X.; Lin, X.; Guo, J.; Teodorescu, R. Health prognostics for lithium-ion batteries: Mechanisms, methods, and prospects. Energy Environ. Sci. 2023, 16, 338–371. [Google Scholar] [CrossRef]
- Chen, S.-Z.; Liu, J.; Yuan, H.; Tao, Y.; Xu, F.; Yang, L. AM-MFF: A multi-feature fusion framework based on attention mechanism for robust and interpretable lithium-ion battery state of health estimation. Appl. Energy 2025, 381, 125116. [Google Scholar] [CrossRef]
- Magri, L.; Sequino, L.; Ferrari, C. Simulating the Electrochemical-Thermal Behavior of a Prismatic Lithium-Ion Battery on the Market under Various Discharge Cycles. Batteries 2023, 9, 397. [Google Scholar] [CrossRef]
- Tran, M.-K.; Mathew, M.; Janhunen, S.; Panchal, S.; Raahemifar, K.; Fraser, R.; Fowler, M. A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 2021, 16, 103252. [Google Scholar] [CrossRef]
- Yi, B.; Du, X.; Zhang, J.; Wu, X.; Hu, Q.; Jiang, W.; Hu, X.; Song, Z. Bias-compensated state of charge and state of health joint estimation for lithium iron phosphate batteries. IEEE Trans. Power Electron. 2024, 40, 3033–3042. [Google Scholar] [CrossRef]
- Mu, A.X.; Zhang, B.J.; Li, C.G.; Xiao, D.Z.; Zeng, E.F.; Liu, F.J. Estimating SOC and SOH of energy storage battery pack based on voltage inconsistency using reference-difference model and dual extended Kalman filter. J. Energy Storage 2024, 81, 110221. [Google Scholar] [CrossRef]
- Hu, C.; Jain, G.; Zhang, P.; Schmidt, C.; Gomadam, P.; Gorka, T. Data-driven method based on particle swarm optimization and k-nearest neighbor regression for estimating capacity of lithium-ion battery. Appl. Energy 2014, 129, 49–55. [Google Scholar] [CrossRef]
- Li, Y.; Zou, C.; Berecibar, M.; Nanini-Maury, E.; Chan, J.C.-W.; Van den Bossche, P.; Van Mierlo, J.; Omar, N. Random forest regression for online capacity estimation of lithium-ion batteries. Appl. Energy 2018, 232, 197–210. [Google Scholar] [CrossRef]
- Kang, S.-H.; Noh, T.-W.; Lee, B.-K. Machine learning-based SOH estimation algorithm using a linear regression analysis. Trans. Korean Inst. Power Electron. 2021, 26, 241–248. [Google Scholar]
- Zhang, Y.; Liu, Y.; Wang, J.; Zhang, T. State-of-health estimation for lithium-ion batteries by combining model-based incremental capacity analysis with support vector regression. Energy 2022, 239, 121986. [Google Scholar] [CrossRef]
- Cai, L.; Lin, J. A charging-feature-based estimation model for state of health of lithium-ion batteries. Expert Syst. Appl. 2024, 238, 122034. [Google Scholar] [CrossRef]
- Sui, X.; He, S.; Teodorescu, R. Small-sample-learning-based lithium-ion batteries health assessment: An optimized ensemble framework. IEEE Trans. Ind. Appl. 2024, 60, 4366–4380. [Google Scholar] [CrossRef]
- Zhao, J.; Han, X.; Ouyang, M.; Burke, A.F. Specialized deep neural networks for battery health prognostics: Opportunities and challenges. J. Energy Chem. 2023, 87, 416–438. [Google Scholar] [CrossRef]
- Yuan, Z.; Tian, T.; Hao, F.; Li, G.; Tang, R.; Liu, X. A hybrid neural network based on variational mode decomposition denoising for predicting state-of-health of lithium-ion batteries. J. Power Sources 2024, 609, 234697. [Google Scholar] [CrossRef]
- Guo, R.; Zhang, K.; He, S.; Tao, S.; Zhang, X.; Liu, K.; Li, X.; Tian, J.; Shen, W.; Chung, C.Y. Robust Health Monitoring for Lithium-Ion Batteries under Guidance of Proxy Labels: A Deep Multi-Task Learning Approach. IEEE Trans. Power Electron. 2025. [Google Scholar] [CrossRef]
- Yang, N.; Song, Z.; Hofmann, H.; Sun, J. Robust State of Health estimation of lithium-ion batteries using convolutional neural network and random forest. J. Energy Storage 2022, 48, 103857. [Google Scholar] [CrossRef]
- Xu, H.; Wu, L.; Xiong, S.; Li, W.; Garg, A.; Gao, L. An improved CNN-LSTM model-based state-of-health estimation approach for lithium-ion batteries. Energy 2023, 276, 127585. [Google Scholar] [CrossRef]
- Mazzi, Y.; Sassi, H.B.; Errahimi, F. Lithium-ion battery state of health estimation using a hybrid model based on a convolutional neural network and bidirectional gated recurrent unit. Eng. Appl. Artif. Intell. 2024, 127, 107199. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, Y.; Yang, L.; Liu, Q.; Yan, K.; Du, Y. Short-term photovoltaic power forecasting based on long short term memory neural network and attention mechanism. IEEE Access 2019, 7, 78063–78074. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Z. Specialized convolutional transformer networks for estimating battery health via transfer learning. Energy Storage Mater. 2024, 71, 103668. [Google Scholar] [CrossRef]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Kollar, Z.; Plesznik, F.; Trumpf, S. Observer-based recursive sliding discrete Fourier transform [tips & tricks]. IEEE Signal Process. Mag. 2018, 35, 100–106. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Liu, Y.; Yu, R.; Wang, J.; Zhao, X.; Wang, Y.; Tang, Y.; Yang, Y. Global spectral filter memory network for video object segmentation. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 648–665. [Google Scholar]
- Rao, Y.; Zhao, W.; Zhu, Z.; Lu, J.; Zhou, J. Global filter networks for image classification. Adv. Neural Inf. Process. Syst. 2021, 34, 980–993. [Google Scholar]
- Li, Y.; Gan, J.; Lin, X.; Qiu, Y.; Zhan, H.; Tian, H. DS-TDNN: Dual-stream time-delay neural network with global-aware filter for speaker verification. IEEE/ACM Trans. Audio, Speech, Lang. Process. 2024, 32, 2814–2827. [Google Scholar] [CrossRef]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D. Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef]
- Attia, P.M.; Grover, A.; Jin, N.; Severson, K.A.; Markov, T.M.; Liao, Y.-H.; Chen, M.H.; Cheong, B.; Perkins, N.; Yang, Z. Closed-loop optimization of fast-charging protocols for batteries with machine learning. Nature 2020, 578, 397–402. [Google Scholar] [CrossRef]
- Kim, S.; Jung, H.; Lee, M.; Choi, Y.Y.; Choi, J.-I. Model-free reconstruction of capacity degradation trajectory of lithium-ion batteries using early cycle data. eTransportation 2023, 17, 100243. [Google Scholar] [CrossRef]
- Zhu, C.; Gao, M.; He, Z.; Wu, H.; Sun, C.; Zhang, Z.; Bao, Z. State of health prediction for li-ion batteries with end-to-end deep learning. J. Energy Storage 2023, 65, 107218. [Google Scholar] [CrossRef]
- Wang, S.; Takyi-Aninakwa, P.; Jin, S.; Yu, C.; Fernandez, C.; Stroe, D.-I. An improved feedforward-long short-term memory modeling method for the whole-life-cycle state of charge prediction of lithium-ion batteries considering current-voltage-temperature variation. Energy 2022, 254, 124224. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, X.; He, Y.; Zhang, S.; Cai, Y. Edge–cloud collaborative estimation lithium-ion battery SOH based on MEWOA-VMD and Transformer. J. Energy Storage 2024, 99, 113388. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).