Exploiting Artificial Neural Networks for the State of Charge Estimation in EV/HV Battery Systems: A Review
Abstract
1. Introduction
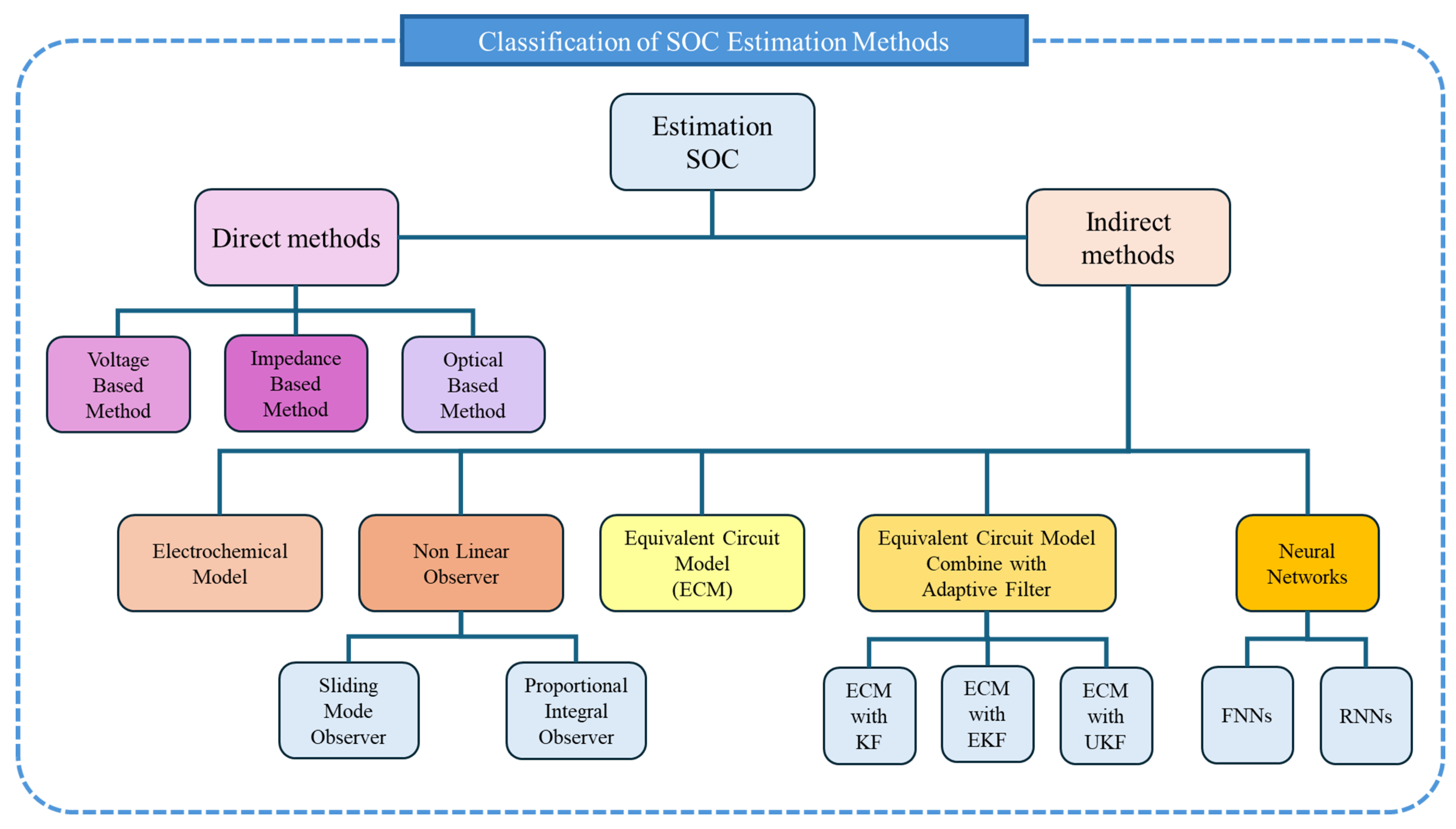
2. Methods Analyzed
- Feedforward Neural Networks (FNNs);
- Recurrent Neural Networks (RNNs).
- Consistent Quality Metrics: Utilize identical or comparable quality indices across studies to ensure that the evaluation criteria are uniform and allow for objective comparisons. These metrics could include Mean Absolute Error (MAE), root mean squared error (RMSE), or accuracy percentages, as referenced in the literature;
- Dataset Transparency: Clearly state the dataset used for training and testing, specifying whether it is a standard publicly available dataset or a custom dataset obtained from specific battery configurations. This helps in understanding the results;
- Algorithm Complexity: Analyze the computational complexity of the proposed methods, highlighting their advantages and drawbacks. This includes evaluating processing time, memory requirements, and the feasibility of real-time implementation on embedded systems;
- Different Approach: we chose articles that presented a particular method that differed in the interesting way in which they addressed the problem of SOC estimation.
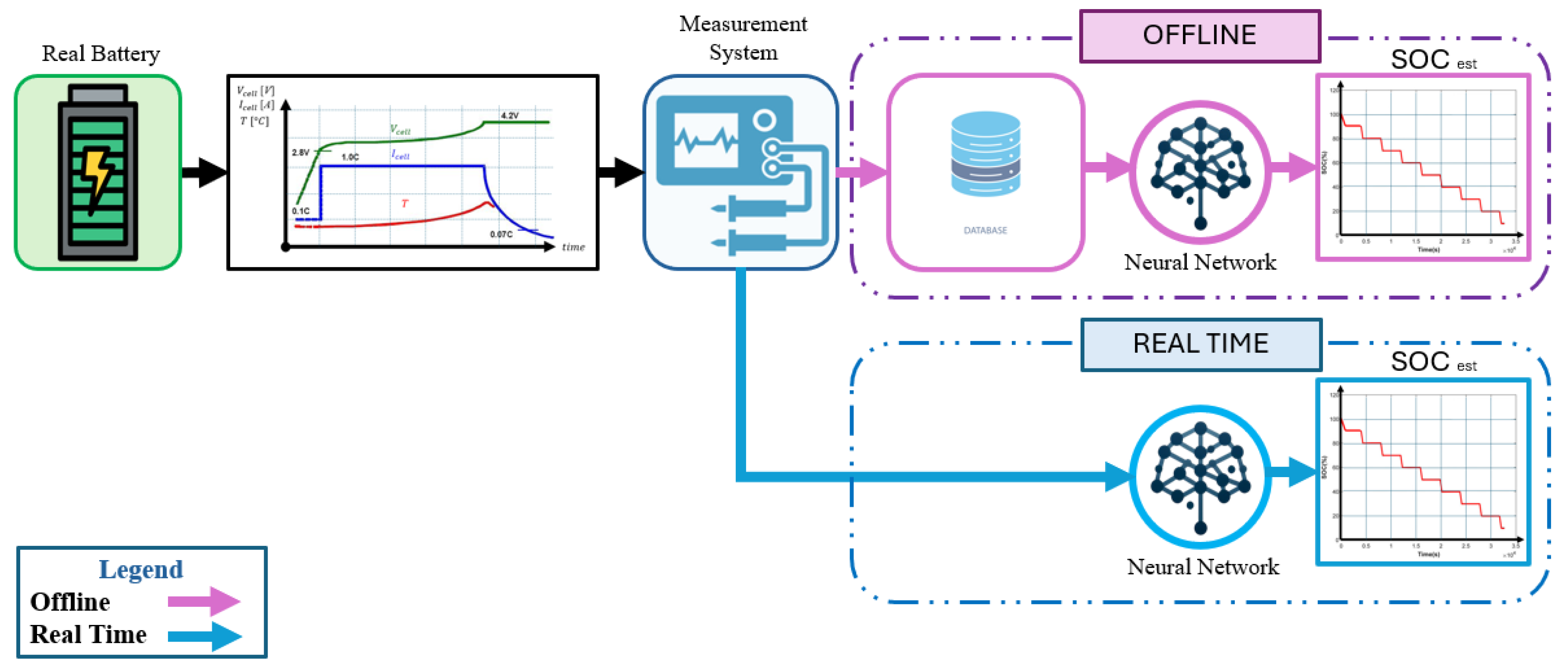
3. Feedforward Neural Networks (FNNs) for Battery SOC Estimation
4. Recurrent Neural Networks (RNNs) for Battery SOC Estimation
4.1. LSTM Neural Network
- Forget Gate : Controls how much information from the previous memory cell should be retained.
- Input Gate : Regulates how much of the new information will be added to the memory cell.
- Output Gate : Determines how much of the information from the memory cell should be used in the output .
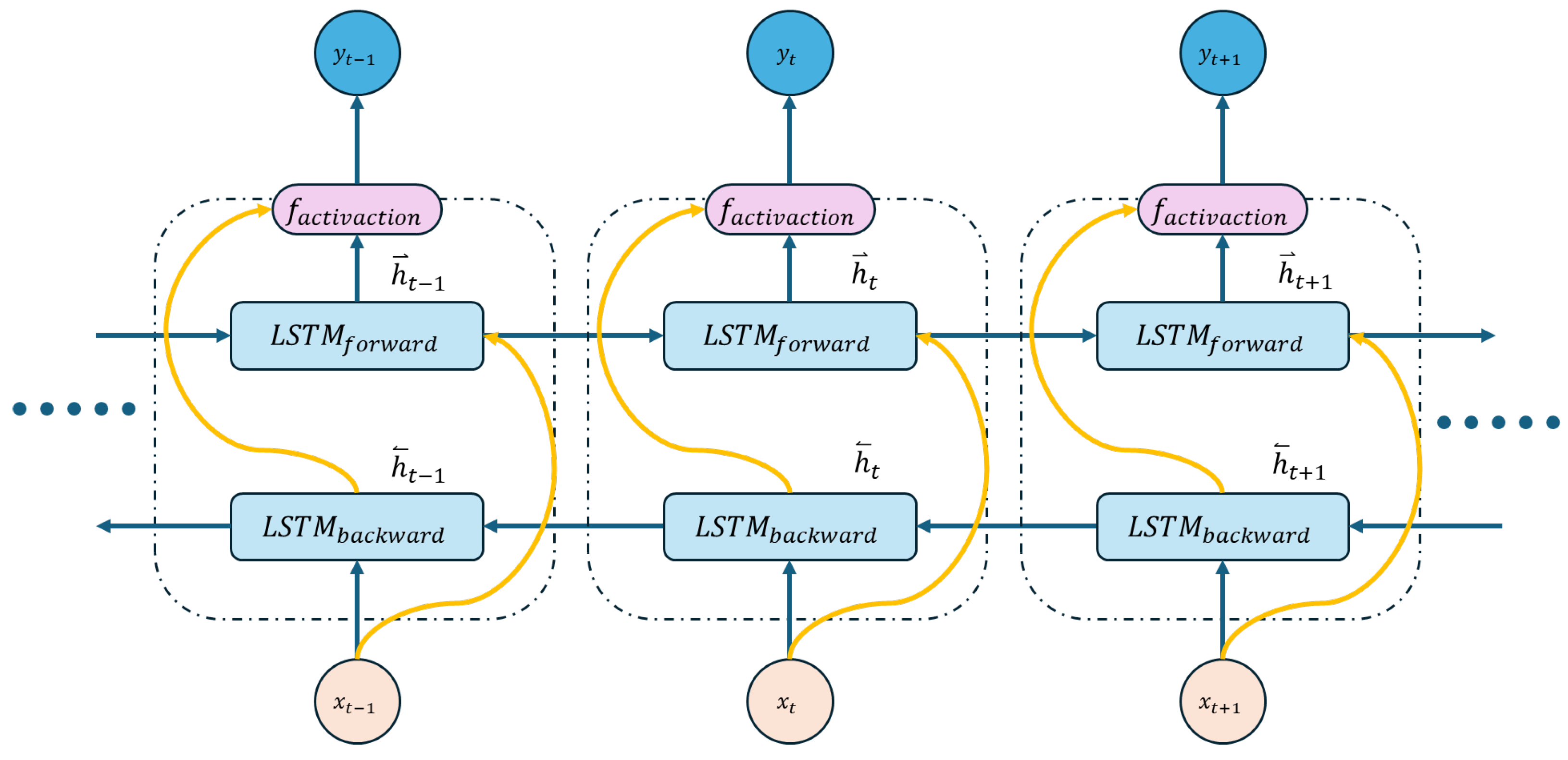
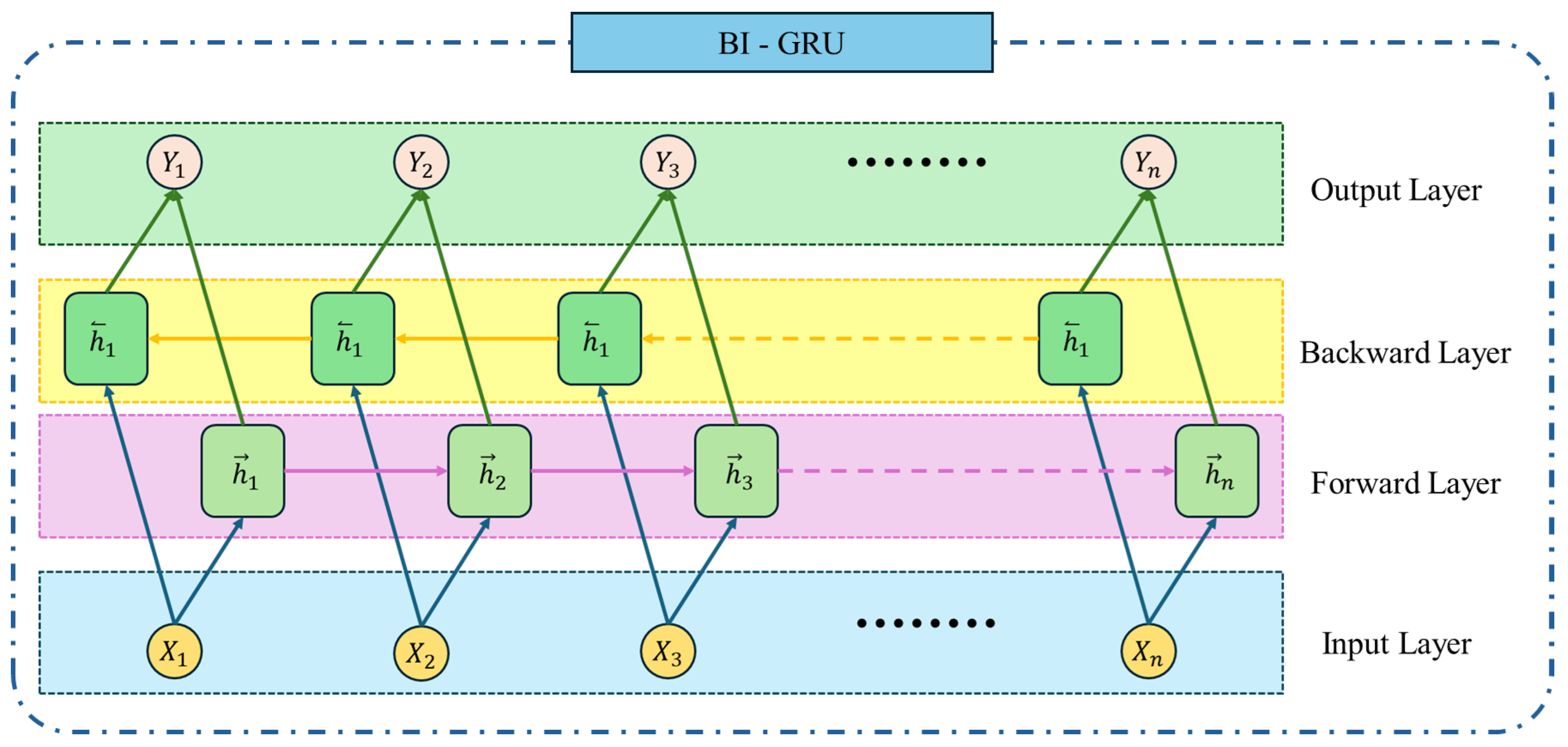
4.2. Bidirectional LSTM Neural Networks
- Forward LSTM: Processes the input sequence from the first time step to the last , generating a sequence of hidden states.Here, represents the hidden state at time t for the forward LSTM;
- Backward LSTM: Processes the same input sequence in reverse, from back to , generating another sequence of hidden states.is the hidden state at time t for the backward LSTM;
- Combined Output: The output of the BiLSTM at each time step t is a combination of the hidden states from the forward and backward LSTMs. The combination is typically achieved using concatenation, summation, or averaging:where is a function that combines the two hidden states, such as
- -
- Concatenation:
- -
- Summation:
- Forward LSTM Hidden State:where , , and are the weights and biases for the forward LSTM;
- Backward LSTM Hidden State:where , , and are the weights and biases for the backward LSTM;
- Output Combination:Depending on the task, the choice of f (concatenation, summation, or averaging) can vary.
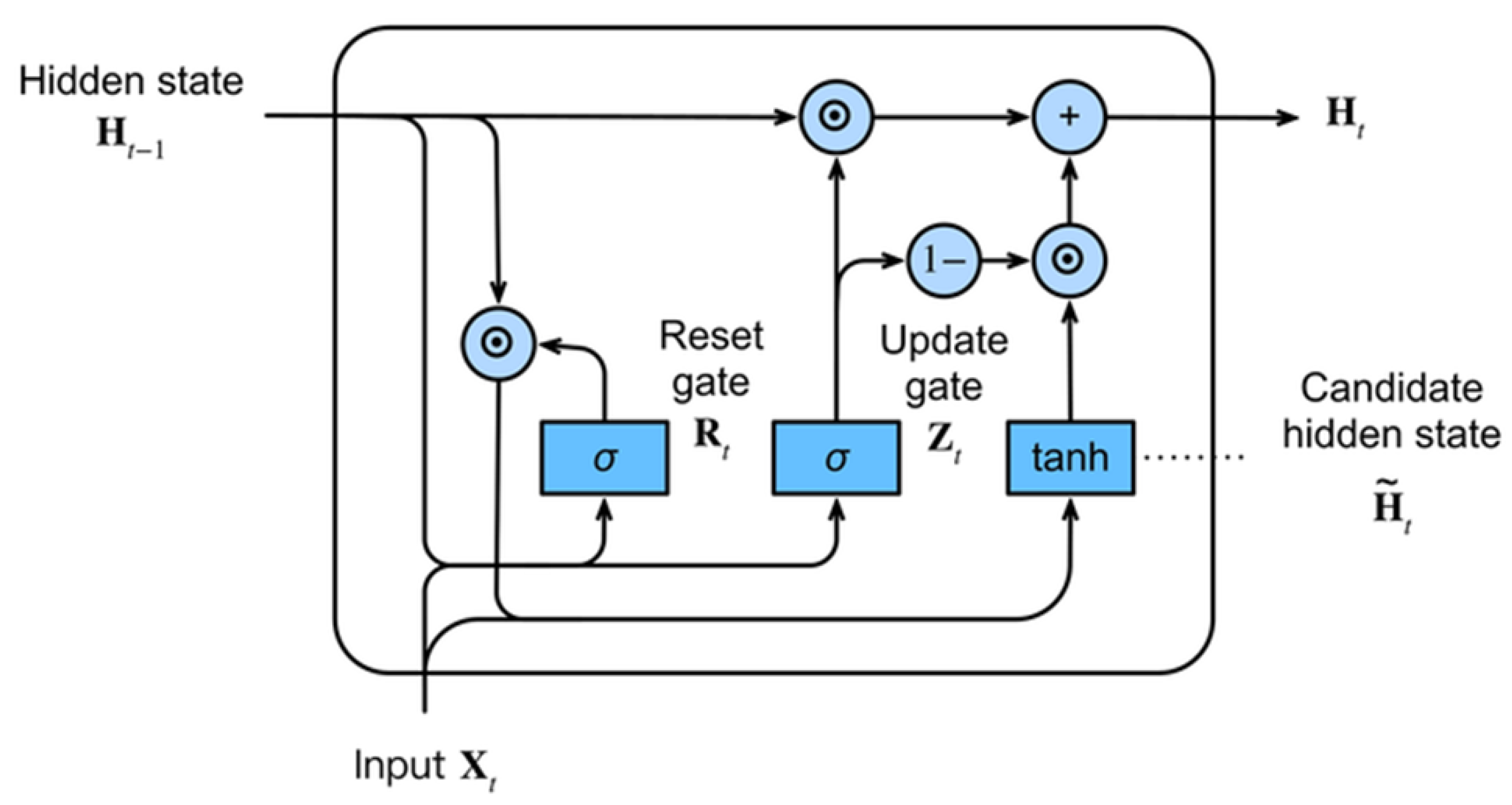
4.3. Gated Recurrent Unit Neural Networks
- Reset Gate (): Controls how much of the past information to forget;
- Update Gate (): Determines how much of the previous state to retain and how much to update with new information.
- Update Gate:where is the input vector at time step k, is the hidden state from the previous time step, and are weight matrices, is the bias term, and is the sigmoid activation function;
- Reset Gate:Here, , , and are the corresponding weight matrices and bias for the reset gate;
- Candidate Hidden State: The reset gate determines how much of the past hidden state contributes to the candidate hidden state.where ⊙ denotes the element-wise multiplication, and tanh is the hyperbolic tangent activation function;
- Current Hidden State: The update gate determines the final hidden state as a combination of the previous hidden state and the candidate hidden state.
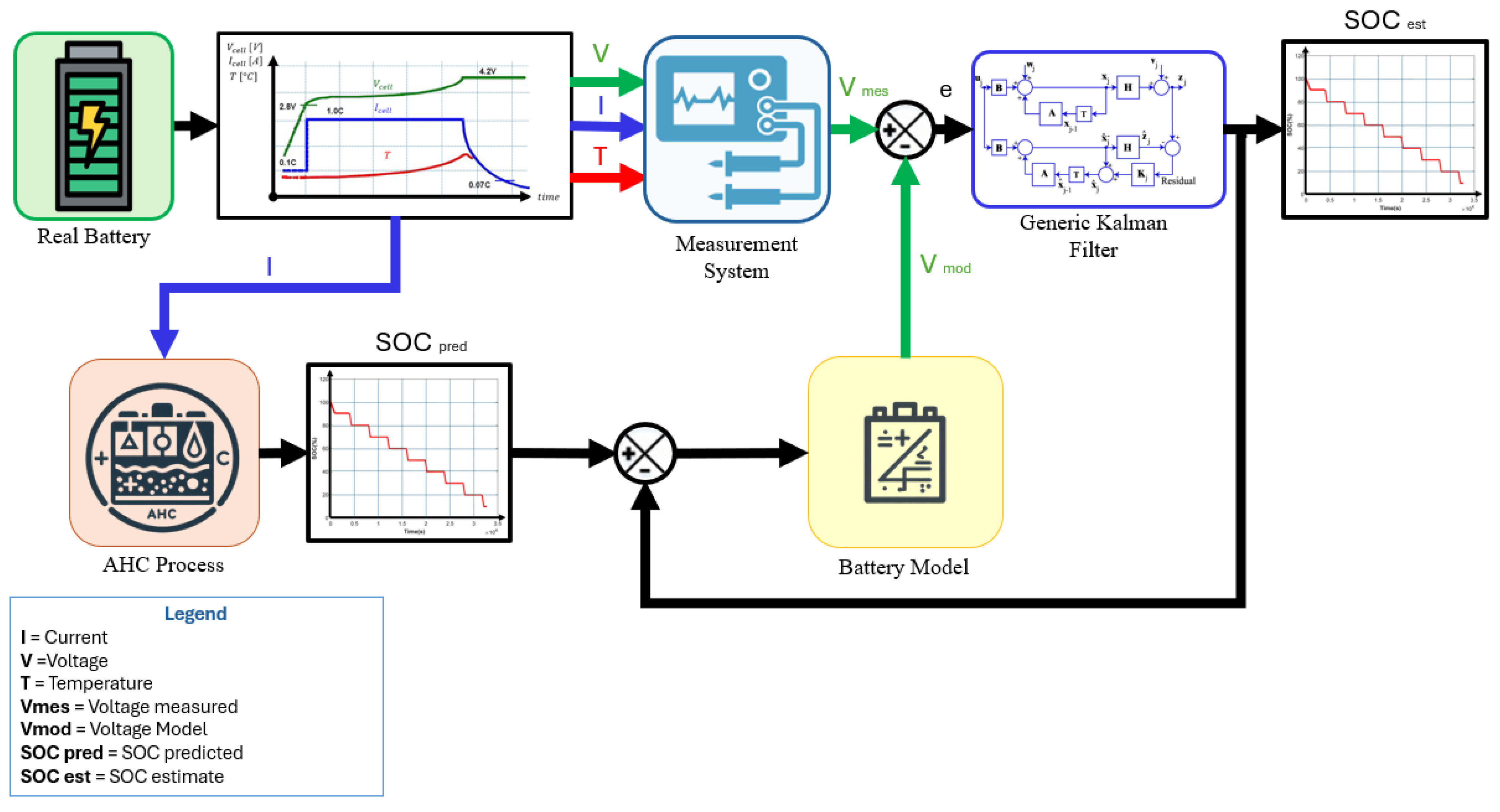
5. Discussion
5.1. Challenges in Machine Learning-Based SOC Estimation
- Inconsistencies in Model Evaluation: Comparing different models remains challenging due to variability in datasets, hyperparameter settings, optimization algorithms, and computational resources used across studies [107]. These inconsistencies complicate cross-study benchmarking and make it difficult to assess the relative effectiveness of different approaches. Furthermore, the use of complex composite algorithms, which often combine serial or parallel structures, increases model complexity [108]. As the number of modules grows, the model’s overall controllability diminishes, making it more vulnerable to disturbances and raising concerns about its robustness in practical applications [109];
- Dataset Limitations: Large variations in datasets are caused by differences in experimental conditions and the mismatch between training data and real-world electric vehicle operation [110]. This discrepancy impacts even the most sophisticated models, reducing their accuracy and applicability in real-world scenarios [111]. The lack of standardized, comprehensive datasets exacerbates this issue;
- Computational Complexity: Many advanced SOC estimation algorithms require significant computational power due to their intricate structures and optimization techniques. This increases the demands on hardware resources, potentially hindering the real-time performance of SOC estimation systems [112]. Balancing computational efficiency with accuracy is critical for enabling online SOC estimation;
- Lack of Open-Source Tools: Few researchers publish their code, and there is often little transparency regarding preprocessing techniques, input parameter choices, and hyperparameter tuning. These gaps hinder reproducibility and prevent effective collaboration within the research community. Without standardized benchmarks, it is difficult to attribute performance improvements to either the model or preprocessing techniques [113];
- Generalization to Diverse Conditions: We must adapt SOC estimation models to perform reliably across a wide range of driving conditions and environmental factors [116].
5.2. Areas for Improvement and Key Observations
- Standardization of Datasets and Data Quality: Machine learning models often depend on specific datasets that limit generalization. We must develop high-quality, standardized datasets with precise measurements and diverse data types. Researchers should also improve data quality by applying advanced data preprocessing techniques [117], sensor fusion methods, and machine learning-based denoising algorithms to ensure accurate and reliable input data [118];
- Open-Source Benchmarks: Creating open-source initiatives and establishing standardized benchmarks for data preprocessing, model architectures, and hyperparameter tuning may lead to significant improvements [119]. Adopting uniform techniques to clean, normalize, and prepare data establishes a consistent foundation for experiments. Designing model architectures with comparable features and systematically tuning hyperparameters—by adjusting factors like learning rates and network layers—minimizes biases from arbitrary decisions. This approach promises enhanced reproducibility, fair comparisons among methods, and increased collaboration, ultimately accelerating progress in ANN-based SOC estimation for electric vehicle batteries [120];
- Balanced Algorithm Complexity: In pursuit of increased accuracy, SOC estimation models must deliver computational efficiency and meet real-world constraints [121]. Evaluating these models from diverse perspectives—including robustness, adaptability, and efficiency—ensures practicality for deployment;
- Generalization and Transfer Learning: One of the challenges in achieving accurate State of Charge estimation is that vehicles are subjected to a wide range of driving conditions, many of which are not fully represented during the training phase. Ensuring that these models generalize well across such diverse conditions remains a significant concern [122]. Transfer learning is emerging as a promising approach to adapt these models to varying scenarios, with researchers actively exploring how to leverage knowledge from one domain to enhance performance in another;
- AI Hardware Acceleration: The advent of specialized hardware for AI and machine learning is expected to accelerate the deployment of complex models in real-time applications [123]. In particular, hardware accelerators such as GPUs and TPUs drastically reduce training and inference times, paving the way for the development and integration of increasingly sophisticated state-of-charge estimation models in electric vehicles;
- Big Data and Cloud Computing: Integrating big data analytics with cloud computing platforms can optimization SOC management. Cloud-based solutions provide scalability and allow remote monitoring and optimization by analyzing data from large fleets, leading to more robust and adaptive management strategies [124];
- Advanced Machine Learning Techniques: Advanced models—including Convolutional Neural Networks (CNNs) and Transformer-based architectures—promise significant improvements [125]. These techniques excel at feature extraction and capture complex, non-linear relationships in battery data. For example, models using attention mechanisms (such as AMBiLSTM) and multi-head self-attention in Transformers effectively identify intricate patterns and dynamic operating conditions [126];
- Hybrid Models and Optimization Strategies: Combining multiple architectures (e.g., GRU–ASG, GLA–CNN–BiLSTM) in hybrid models can improve accuracy and robustness [127]. Researchers must optimize these models to manage increased computational complexity. Likewise, advanced optimization strategies (as seen in RS-LSTM) can boost performance while requiring more computational resources [128].
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hindawi, M.; Basheer, Y.; Qaisar, S.M.; Waqar, A. An Overview of Artificial Intelligence Driven Li-Ion Battery State Estimation. In IoT Enabled-DC Microgrids; CRC Press: Boca Raton, FL, USA, 2024; pp. 121–157. [Google Scholar]
- Dini, P.; Paolini, D.; Saponara, S.; Minossi, M. Leaveraging Digital Twin & Artificial Intelligence in Consumption Forecasting System for Sustainable Luxury Yacht. IEEE Access 2024, 12, 160700–160714. [Google Scholar]
- Lu, C.; Li, S.; Lu, Z. Building energy prediction using artificial neural networks: A literature survey. Energy Build. 2022, 262, 111718. [Google Scholar] [CrossRef]
- Moayedi, H.; Mosavi, A. Double-target based neural networks in predicting energy consumption in residential buildings. Energies 2021, 14, 1331. [Google Scholar] [CrossRef]
- Dzedzickis, A.; Subačiūtė-Žemaitienė, J.; Šutinys, E.; Samukaitė-Bubnienė, U.; Bučinskas, V. Advanced applications of industrial robotics: New trends and possibilities. Appl. Sci. 2021, 12, 135. [Google Scholar] [CrossRef]
- Tsapin, D.; Pitelinskiy, K.; Suvorov, S.; Osipov, A.; Pleshakova, E.; Gataullin, S. Machine learning methods for the industrial robotic systems security. J. Comput. Virol. Hacking Tech. 2024, 20, 397–414. [Google Scholar] [CrossRef]
- Manoharan, A.; Begam, K.; Aparow, V.R.; Sooriamoorthy, D. Artificial Neural Networks, Gradient Boosting and Support Vector Machines for electric vehicle battery state estimation: A review. J. Energy Storage 2022, 55, 105384. [Google Scholar] [CrossRef]
- Djaballah, Y.; Negadi, K.; Boudiaf, M. Enhanced lithium–ion battery state of charge estimation in electric vehicles using extended Kalman filter and deep neural network. Int. J. Dyn. Control 2024, 12, 2864–2871. [Google Scholar] [CrossRef]
- Allal, Z.; Noura, H.N.; Salman, O.; Chahine, K. Machine learning solutions for renewable energy systems: Applications, challenges, limitations, and future directions. J. Environ. Manag. 2024, 354, 120392. [Google Scholar] [CrossRef]
- Rinchi, O.; Alsharoa, A.; Shatnawi, I.; Arora, A. The Role of Intelligent Transportation Systems and Artificial Intelligence in Energy Efficiency and Emission Reduction. arXiv 2024, arXiv:2401.14560. [Google Scholar]
- Chen, W.; Men, Y.; Fuster, N.; Osorio, C.; Juan, A.A. Artificial intelligence in logistics optimization with sustainable criteria: A review. Sustainability 2024, 16, 9145. [Google Scholar] [CrossRef]
- Qadir, S.A.; Ahmad, F.; Al-Wahedi, A.M.A.; Iqbal, A.; Ali, A. Navigating the complex realities of electric vehicle adoption: A comprehensive study of government strategies, policies, and incentives. Energy Strategy Rev. 2024, 53, 101379. [Google Scholar] [CrossRef]
- Möring-Martínez, G.; Senzeybek, M.; Jochem, P. Clustering the European Union electric vehicle markets: A scenario analysis until 2035. Transp. Res. Part D Transp. Environ. 2024, 135, 104372. [Google Scholar] [CrossRef]
- Raganati, F.; Ammendola, P. CO2 post-combustion capture: A critical review of current technologies and future directions. Energy Fuels 2024, 38, 13858–13905. [Google Scholar] [CrossRef]
- al Irsyad, M.I.; Firmansyah, A.I.; Harisetyawan, V.T.F.; Supriatna, N.K.; Gunawan, Y.; Jupesta, J.; Yaumidin, U.K.; Purwanto, J.; Inayah, I. Comparative total cost assessments of electric and conventional vehicles in ASEAN: Commercial vehicles and motorcycle conversion. Energy Sustain. Dev. 2025, 101599. [Google Scholar] [CrossRef]
- Hussein, H.M.; Aghmadi, A.; Abdelrahman, M.S.; Rafin, S.S.H.; Mohammed, O. A review of battery state of charge estimation and management systems: Models and future prospective. Wiley Interdiscip. Rev. Energy Environ. 2024, 13, e507. [Google Scholar]
- Nekahi, A.; Madikere Raghunatha Reddy, A.K.; Li, X.; Deng, S.; Zaghib, K. Rechargeable Batteries for the Electrification of Society: Past, Present, and Future. Electrochem. Energy Rev. 2025, 8, 1–30. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S.; Colicelli, A. Overview on battery charging systems for electric vehicles. Electronics 2023, 12, 4295. [Google Scholar] [CrossRef]
- Ria, A.; Dini, P. A Compact Overview on Li-Ion Batteries Characteristics and Battery Management Systems Integration for Automotive Applications. Energies 2024, 17, 5992. [Google Scholar] [CrossRef]
- Demirci, O.; Taskin, S.; Schaltz, E.; Demirci, B.A. Review of battery state estimation methods for electric vehicles-Part I: SOC estimation. J. Energy Storage 2024, 87, 111435. [Google Scholar] [CrossRef]
- Pillai, P.; Sundaresan, S.; Kumar, P.; Pattipati, K.R.; Balasingam, B. Open-circuit voltage models for battery management systems: A review. Energies 2022, 15, 6803. [Google Scholar] [CrossRef]
- Movassagh, K.; Raihan, A.; Balasingam, B.; Pattipati, K. A critical look at coulomb counting approach for state of charge estimation in batteries. Energies 2021, 14, 4074. [Google Scholar] [CrossRef]
- Lipu, M.H.; Hannan, M.; Hussain, A.; Ayob, A.; Saad, M.H.; Karim, T.F.; How, D.N. Data-driven state of charge estimation of lithium-ion batteries: Algorithms, implementation factors, limitations and future trends. J. Clean. Prod. 2020, 277, 124110. [Google Scholar] [CrossRef]
- Tao, Z.; Zhao, Z.; Wang, C.; Huang, L.; Jie, H.; Li, H.; Hao, Q.; Zhou, Y.; See, K.Y. State of charge estimation of lithium Batteries: Review for equivalent circuit model methods. Measurement 2024, 236, 115148. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S. Overview of model-based online state-of-charge estimation using Kalman filter family for lithium-ion batteries. Renew. Sustain. Energy Rev. 2019, 113, 109233. [Google Scholar] [CrossRef]
- Farea, A.; Yli-Harja, O.; Emmert-Streib, F. Understanding physics-informed neural networks: Techniques, applications, trends, and challenges. AI 2024, 5, 1534–1557. [Google Scholar] [CrossRef]
- Reza, M.; Mannan, M.; Mansor, M.; Ker, P.J.; Mahlia, T.I.; Hannan, M. Recent advancement of remaining useful life prediction of lithium-ion battery in electric vehicle applications: A review of modelling mechanisms, network configurations, factors, and outstanding issues. Energy Rep. 2024, 11, 4824–4848. [Google Scholar] [CrossRef]
- Rahman, T.; Alharbi, T. Exploring lithium-Ion battery degradation: A concise review of critical factors, impacts, data-driven degradation estimation techniques, and sustainable directions for energy storage systems. Batteries 2024, 10, 220. [Google Scholar] [CrossRef]
- Marzbani, F.; Osman, A.H.; Hassan, M.S. Electric vehicle energy demand prediction techniques: An in-depth and critical systematic review. IEEE Access 2023, 11, 96242–96255. [Google Scholar] [CrossRef]
- Memon, S.A.; Hamza, A.; Zaidi, S.S.H.; Khan, B.M. Estimating state of charge and state of health of electrified vehicle battery by data driven approach: Machine learning. In Proceedings of the 2022 International Conference on Emerging Technologies in Electronics, Computing and Communication (ICETECC), Jamshoro, Pakistan, 7–9 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–9. [Google Scholar]
- Dini, P.; Colicelli, A.; Saponara, S. Review on modeling and soc/soh estimation of batteries for automotive applications. Batteries 2024, 10, 34. [Google Scholar] [CrossRef]
- Ferriol-Galmés, M.; Suárez-Varela, J.; Paillissé, J.; Shi, X.; Xiao, S.; Cheng, X.; Barlet-Ros, P.; Cabellos-Aparicio, A. Building a digital twin for network optimization using graph neural networks. Comput. Netw. 2022, 217, 109329. [Google Scholar] [CrossRef]
- Di Fonso, R.; Teodorescu, R.; Cecati, C.; Bharadwaj, P. A Battery Digital Twin From Laboratory Data Using Wavelet Analysis and Neural Networks. IEEE Trans. Ind. Inform. 2024, 20, 6889–6899. [Google Scholar] [CrossRef]
- Li, W.; Li, Y.; Garg, A.; Gao, L. Enhancing real-time degradation prediction of lithium-ion battery: A digital twin framework with CNN-LSTM-attention model. Energy 2024, 286, 129681. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, J.; Wang, P.; Law, J.; Calinescu, R.; Mihaylova, L. A deep learning-enhanced Digital Twin framework for improving safety and reliability in human–robot collaborative manufacturing. Robot. Comput.-Integr. Manuf. 2024, 85, 102608. [Google Scholar] [CrossRef]
- Iliuţă, M.E.; Moisescu, M.A.; Pop, E.; Ionita, A.D.; Caramihai, S.I.; Mitulescu, T.C. Digital Twin—A Review of the Evolution from Concept to Technology and Its Analytical Perspectives on Applications in Various Fields. Appl. Sci. 2024, 14, 5454. [Google Scholar] [CrossRef]
- Chen, S.; Billings, S.A. Neural networks for nonlinear dynamic system modelling and identification. Int. J. Control 1992, 56, 319–346. [Google Scholar] [CrossRef]
- Arulampalam, G.; Bouzerdoum, A. A generalized feedforward neural network architecture for classification and regression. Neural Netw. 2003, 16, 561–568. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Rane, C.; Tyagi, K.; Kline, A.; Chugh, T.; Manry, M. Optimizing performance of feedforward and convolutional neural networks through dynamic activation functions. Evol. Intell. 2024, 17, 4083–4093. [Google Scholar] [CrossRef]
- Szandała, T. Review and comparison of commonly used activation functions for deep neural networks. In Bio-Inspired Neurocomputing; Springer: Singapore, 2021; pp. 203–224. [Google Scholar]
- Hammad, M. Deep Learning Activation Functions: Fixed-Shape, Parametric, Adaptive, Stochastic, Miscellaneous, Non-Standard, Ensemble. arXiv 2024, arXiv:2407.11090. [Google Scholar]
- Narkhede, M.V.; Bartakke, P.P.; Sutaone, M.S. A review on weight initialization strategies for neural networks. Artif. Intell. Rev. 2022, 55, 291–322. [Google Scholar] [CrossRef]
- Dang, X.; Yan, L.; Jiang, H.; Wu, X.; Sun, H. Open-circuit voltage-based state of charge estimation of lithium-ion power battery by combining controlled auto-regressive and moving average modeling with feedforward-feedback compensation method. Int. J. Electr. Power Energy Syst. 2017, 90, 27–36. [Google Scholar] [CrossRef]
- Feng, S.; Li, X.; Zhang, S.; Jian, Z.; Duan, H.; Wang, Z. A review: State estimation based on hybrid models of Kalman filter and neural network. Syst. Sci. Control Eng. 2023, 11, 2173682. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Chen, C.; Pecht, M. State of charge estimation for Li-ion batteries using neural network modeling and unscented Kalman filter-based error cancellation. Int. J. Electr. Power Energy Syst. 2014, 62, 783–791. [Google Scholar] [CrossRef]
- Murawwat, S.; Gulzar, M.M.; Alzahrani, A.; Hafeez, G.; Khan, F.A.; Abed, A.M. State of charge estimation and error analysis of lithium-ion batteries for electric vehicles using Kalman filter and deep neural network. J. Energy Storage 2023, 72, 108039. [Google Scholar]
- Chen, C.; Xiong, R.; Yang, R.; Shen, W.; Sun, F. State-of-charge estimation of lithium-ion battery using an improved neural network model and extended Kalman filter. J. Clean. Prod. 2019, 234, 1153–1164. [Google Scholar] [CrossRef]
- Srihari, S.; Vasanthi, V. SOC Estimation Using Extended Kalman Filter in Electric Vehicle Batteries. In Proceedings of the 2024 International Conference on Advancements in Power, Communication and Intelligent Systems (APCI), Kannur, India, 21–22 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–5. [Google Scholar]
- Khan, U.; Kirmani, S.; Rafat, Y.; Rehman, M.U.; Alam, M.S. Improved deep learning based state of charge estimation of lithium ion battery for electrified transportation. J. Energy Storage 2024, 91, 111877. [Google Scholar] [CrossRef]
- Vidal, C.; Haußmann, M.; Barroso, D.; Shamsabadi, P.M.; Biswas, A.; Chemali, E.; Ahmed, R.; Emadi, A. Hybrid energy storage system state-of-charge estimation using artificial neural network for micro-hybrid applications. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo (ITEC), Long Beach, CA, USA, 13–15 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1075–1081. [Google Scholar]
- Cui, X.; Liu, S.; Ruan, G.; Wang, Y. Data-driven aggregation of thermal dynamics within building virtual power plants. Appl. Energy 2024, 353, 122126. [Google Scholar] [CrossRef]
- Barik, S.; Saravanan, B. Recent developments and challenges in state-of-charge estimation techniques for electric vehicle batteries: A review. J. Energy Storage 2024, 100, 113623. [Google Scholar] [CrossRef]
- Vidal, C.; Gross, O.; Gu, R.; Kollmeyer, P.; Emadi, A. xEV Li-ion battery low-temperature effects. IEEE Trans. Veh. Technol. 2019, 68, 4560–4572. [Google Scholar] [CrossRef]
- Bian, C.; Duan, Z.; Hao, Y.; Yang, S.; Feng, J. Exploring large language model for generic and robust state-of-charge estimation of Li-ion batteries: A mixed prompt learning method. Energy 2024, 12, 131856. [Google Scholar] [CrossRef]
- Rastegarpanah, A.; Asif, M.E.; Stolkin, R. Hybrid Neural Networks for Enhanced Predictions of Remaining Useful Life in Lithium-Ion Batteries. Batteries 2024, 10, 106. [Google Scholar] [CrossRef]
- Badfar, M.; Yildirim, M.; Chinnam, R. State-of-charge estimation across battery chemistries: A novel regression-based method and insights from unsupervised domain adaptation. J. Power Sources 2025, 628, 235760. [Google Scholar] [CrossRef]
- Han, J.; Moraga, C.; Sinne, S. Optimization of feedforward neural networks. Eng. Appl. Artif. Intell. 1996, 9, 109–119. [Google Scholar] [CrossRef]
- Ojha, V.K.; Abraham, A.; Snášel, V. Metaheuristic design of feedforward neural networks: A review of two decades of research. Eng. Appl. Artif. Intell. 2017, 60, 97–116. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.; Hussain, S.S.; Ustun, T.S.; Sarker, M.R.; Hannan, M.A.; Mohamed, R.; Ali, J.A.; Mekhilef, S.; Milad, A. Artificial neural networks based optimization techniques: A review. Electronics 2021, 10, 2689. [Google Scholar] [CrossRef]
- Tong, S.; Lacap, J.H.; Park, J.W. Battery state of charge estimation using a load-classifying neural network. J. Energy Storage 2016, 7, 236–243. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Saad, M.H.; Ayob, A. Neural network approach for estimating state of charge of lithium-ion battery using backtracking search algorithm. IEEE Access 2018, 6, 10069–10079. [Google Scholar] [CrossRef]
- Vidal, C.; Kollmeyer, P.; Naguib, M.; Malysz, P.; Gross, O.; Emadi, A. Robust xev battery state-of-charge estimator design using a feedforward deep neural network. SAE Int. J. Adv. Curr. Pract. Mobil. 2020, 2, 2872–2880. [Google Scholar] [CrossRef]
- Naguib, M.; Kollmeyer, P.; Vidal, C.; Emadi, A. Accurate surface temperature estimation of lithium-ion batteries using feedforward and recurrent artificial neural networks. In Proceedings of the 2021 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 21–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 52–57. [Google Scholar]
- Baraean, A.; Kassas, M.; Abido, M. Physics-Informed NN for Improving Electric Vehicles Lithium-Ion Battery State-of-Charge Estimation Robustness. In Proceedings of the 2024 IEEE 12th International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 18–20 August 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 245–250. [Google Scholar]
- Guo, Z.; Li, Y.; Yan, Z.; Chow, M.Y. A Neural-Network-Embedded Equivalent Circuit Model for Lithium-ion Battery State Estimation. arXiv 2024, arXiv:2407.20262. [Google Scholar]
- Michailidis, P.; Michailidis, I.; Gkelios, S.; Kosmatopoulos, E. Artificial Neural Network Applications for Energy Management in Buildings: Current Trends and Future Directions. Energies 2024, 17, 570. [Google Scholar] [CrossRef]
- Hu, Y.; Huber, A.; Anumula, J.; Liu, S.C. Overcoming the vanishing gradient problem in plain recurrent networks. arXiv 2018, arXiv:1801.06105. [Google Scholar]
- Mienye, I.D.; Swart, T.G.; Obaido, G. Recurrent neural networks: A comprehensive review of architectures, variants, and applications. Information 2024, 15, 517. [Google Scholar] [CrossRef]
- Mousaei, A.; Naderi, Y.; Bayram, I.S. Advancing state of charge management in electric vehicles with machine learning: A technological review. IEEE Access 2024, 12, 43255–43283. [Google Scholar] [CrossRef]
- Graves, A.; Mohamed, A.r.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 6645–6649. [Google Scholar]
- Pascanu, R. On the difficulty of training recurrent neural networks. arXiv 2013, arXiv:1211.5063. [Google Scholar]
- Graves, A.; Graves, A. Long short-term memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar]
- Yao, Q.; Kollmeyer, P.J.; Lu, D.D.C.; Emadi, A. A Comparison Study of Unidirectional and Bidirectional Recurrent Neural Network for Battery State of Charge Estimation. In Proceedings of the 2024 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, USA, 19–21 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–6. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Zhang, S.; Wu, Y.; Che, T.; Lin, Z.; Memisevic, R.; Salakhutdinov, R.R.; Bengio, Y. Architectural complexity measures of recurrent neural networks. arXiv 2016, arXiv:1602.08210. [Google Scholar] [CrossRef]
- El Fallah, S.; Kharbach, J.; Vanagas, J.; Vilkelytė, Ž.; Tolvaišienė, S.; Gudžius, S.; Kalvaitis, A.; Lehmam, O.; Masrour, R.; Hammouch, Z.; et al. Advanced state of charge estimation using deep neural network, gated recurrent unit, and long short-term memory models for lithium-Ion batteries under aging and temperature conditions. Appl. Sci. 2024, 14, 6648. [Google Scholar] [CrossRef]
- Duan, J.; Zhang, P.F.; Qiu, R.; Huang, Z. Long short-term enhanced memory for sequential recommendation. World Wide Web 2023, 26, 561–583. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A. Long short-term memory networks for accurate state-of-charge estimation of Li-ion batteries. IEEE Trans. Ind. Electron. 2017, 65, 6730–6739. [Google Scholar] [CrossRef]
- Charkhgard, M.; Farrokhi, M. State-of-charge estimation for lithium-ion batteries using neural networks and EKF. IEEE Trans. Ind. Electron. 2010, 57, 4178–4187. [Google Scholar] [CrossRef]
- Data, M. Panasonic 18650PF Li-ion Battery Data. 2018. Available online: https://data.mendeley.com/datasets/wykht8y7tg/1 (accessed on 1 January 2025).
- Song, X.; Yang, F.; Wang, D.; Tsui, K.L. Combined CNN-LSTM network for state-of-charge estimation of lithium-ion batteries. IEEE Access 2019, 7, 88894–88902. [Google Scholar] [CrossRef]
- Tian, Y.; Lai, R.; Li, X.; Xiang, L.; Tian, J. A combined method for state-of-charge estimation for lithium-ion batteries using a long short-term memory network and an adaptive cubature Kalman filter. Appl. Energy 2020, 265, 114789. [Google Scholar] [CrossRef]
- Wei, M.; Ye, M.; Li, J.B.; Wang, Q.; Xu, X. State of charge estimation of lithium-ion batteries using LSTM and NARX neural networks. IEEE Access 2020, 8, 189236–189245. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Wu, J.; Cheng, W.; Zhu, Q. SOC estimation for lithium-ion battery using the LSTM-RNN with extended input and constrained output. Energy 2023, 262, 125375. [Google Scholar] [CrossRef]
- Chai, X.; Li, S.; Liang, F. A novel battery SOC estimation method based on random search optimized LSTM neural network. Energy 2024, 306, 132583. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The performance of LSTM and BiLSTM in forecasting time series. In Proceedings of the 2019 IEEE International conference on big data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 3285–3292. [Google Scholar]
- Liu, K.; Peng, Q.; Che, Y.; Zheng, Y.; Li, K.; Teodorescu, R.; Widanage, D.; Barai, A. Transfer learning for battery smarter state estimation and ageing prognostics: Recent progress, challenges, and prospects. Adv. Appl. Energy 2023, 9, 100117. [Google Scholar] [CrossRef]
- Alizadegan, H.; Rashidi Malki, B.; Radmehr, A.; Karimi, H.; Ilani, M.A. Comparative study of long short-term memory (LSTM), bidirectional LSTM, and traditional machine learning approaches for energy consumption prediction. Energy Explor. Exploit. 2024, 43, 01445987241269496. [Google Scholar] [CrossRef]
- Zhao, D.; Li, H.; Zhou, F.; Zhong, Y.; Zhang, G.; Liu, Z.; Hou, J. Research progress on data-driven methods for battery states estimation of electric buses. World Electr. Veh. J. 2023, 14, 145. [Google Scholar] [CrossRef]
- Begni, A.; Dini, P.; Saponara, S. Design and test of an lstm-based algorithm for li-ion batteries remaining useful life estimation. In Proceedings of the International Conference on Applications in Electronics Pervading Industry, Environment and Society, Genoa, Italy, 26–27 September 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 373–379. [Google Scholar]
- Khan, M.K.; Abou Houran, M.; Kauhaniemi, K.; Zafar, M.H.; Mansoor, M.; Rashid, S. Efficient state of charge estimation of lithium-ion batteries in electric vehicles using evolutionary intelligence-assisted GLA–CNN–Bi-LSTM deep learning model. Heliyon 2024, 10, e35183. [Google Scholar] [CrossRef]
- Sherkatghanad, Z.; Ghazanfari, A.; Makarenkov, V. A self-attention-based CNN-Bi-LSTM model for accurate state-of-charge estimation of lithium-ion batteries. J. Energy Storage 2024, 88, 111524. [Google Scholar] [CrossRef]
- Xu, P.; Wang, C.; Ye, J.; Ouyang, T. State-of-charge estimation and health prognosis for lithium-ion batteries based on temperature-compensated Bi-LSTM network and integrated attention mechanism. IEEE Trans. Ind. Electron. 2023, 71, 5586–5596. [Google Scholar] [CrossRef]
- Shiri, F.M.; Perumal, T.; Mustapha, N.; Mohamed, R. A comprehensive overview and comparative analysis on deep learning models: CNN, RNN, LSTM, GRU. arXiv 2023, arXiv:2305.17473. [Google Scholar]
- Su, Y.; Kuo, C.C.J. Recurrent neural networks and their memory behavior: A survey. APSIPA Trans. Signal Inf. Process. 2022, 11, e26. [Google Scholar] [CrossRef]
- Zhou, R.; Dai, X.; Lin, F.; Zhang, J.; Ma, H. TGT: Battery State of Charge Estimation with Robustness to Missing Data. In Proceedings of the 2024 CPSS & IEEE International Symposium on Energy Storage and Conversion (ISESC), Xi’an, China, 8–11 November 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 431–436. [Google Scholar]
- Kanai, S.; Fujiwara, Y.; Iwamura, S. Preventing gradient explosions in gated recurrent units. In Proceedings of the NIPS’17: Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Salem, F.M.; Salem, F.M. Gated RNN: The Gated Recurrent Unit (GRU) RNN. In Recurrent Neural Networks: From Simple to Gated Architectures; Springer: Cham, Switzerland, 2022; pp. 85–100. [Google Scholar]
- Rodriguez, S. Gated Recurrent Units-Enhancements and Applications: Studying Enhancements to Gated Recurrent Unit (GRU) Architectures and Their Applications in Sequential Modeling Tasks. Adv. Deep Learn. Tech. 2023, 3, 16–30. [Google Scholar]
- Yang, F.; Li, W.; Li, C.; Miao, Q. State-of-charge estimation of lithium-ion batteries based on gated recurrent neural network. Energy 2019, 175, 66–75. [Google Scholar] [CrossRef]
- Cahuantzi, R.; Chen, X.; Güttel, S. A comparison of LSTM and GRU networks for learning symbolic sequences. In Proceedings of the Science and Information Conference, London, UK, 22–23 June 2023; Springer: Cham, Switzerland, 2023; pp. 771–785. [Google Scholar]
- Li, X.; Ma, X.; Xiao, F.; Wang, F.; Zhang, S. Application of gated recurrent unit (GRU) neural network for smart batch production prediction. Energies 2020, 13, 6121. [Google Scholar] [CrossRef]
- Zhang, Z.; Dong, Z.; Gao, M.; Han, Y.; Ji, X.; Wang, M.; He, Y. State-of-Charge Estimation of Lithium-ion Batteries Using the Nesterov Accelerated Gradient Algorithm Based Bi-GRU. In Proceedings of the 2020 8th International Conference on Power Electronics Systems and Applications (PESA), Hong Kong, China, 7–10 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–4. [Google Scholar]
- Jiao, M.; Wang, D.; Qiu, J. A GRU-RNN based momentum optimized algorithm for SOC estimation. J. Power Sources 2020, 459, 228051. [Google Scholar] [CrossRef]
- Lu, J.; He, Y.; Liang, H.; Li, M.; Shi, Z.; Zhou, K.; Li, Z.; Gong, X.; Yuan, G. State of charge estimation for energy storage lithium-ion batteries based on gated recurrent unit neural network and adaptive Savitzky-Golay filter. Ionics 2024, 30, 297–310. [Google Scholar] [CrossRef]
- Liao, L.; Li, H.; Shang, W.; Ma, L. An empirical study of the impact of hyperparameter tuning and model optimization on the performance properties of deep neural networks. ACM Trans. Softw. Eng. Methodol. (TOSEM) 2022, 31, 1–40. [Google Scholar] [CrossRef]
- Zhan, Z.H.; Shi, L.; Tan, K.C.; Zhang, J. A survey on evolutionary computation for complex continuous optimization. Artif. Intell. Rev. 2022, 55, 59–110. [Google Scholar] [CrossRef]
- Raiaan, M.A.K.; Mukta, M.S.H.; Fatema, K.; Fahad, N.M.; Sakib, S.; Mim, M.M.J.; Ahmad, J.; Ali, M.E.; Azam, S. A review on large language models: Architectures, applications, taxonomies, open issues and challenges. IEEE Access 2024, 12, 26839–26874. [Google Scholar] [CrossRef]
- Pozzato, G.; Allam, A.; Pulvirenti, L.; Negoita, G.A.; Paxton, W.A.; Onori, S. Analysis and key findings from real-world electric vehicle field data. Joule 2023, 7, 2035–2053. [Google Scholar] [CrossRef]
- Fang, W.; Chen, H.; Zhou, F. Fault diagnosis for cell voltage inconsistency of a battery pack in electric vehicles based on real-world driving data. Comput. Electr. Eng. 2022, 102, 108095. [Google Scholar] [CrossRef]
- Wong, R.H.; Sooriamoorthy, D.; Manoharan, A.; Binti Sariff, N.; Hilmi Ismail, Z. Balancing accuracy and efficiency: A homogeneous ensemble approach for lithium-ion battery state of charge estimation in electric vehicles. Neural Comput. Appl. 2024, 36, 19157–19171. [Google Scholar] [CrossRef]
- Sesidhar, D.; Badachi, C.; Green, R.C., II. A review on data-driven SOC estimation with Li-Ion batteries: Implementation methods & future aspirations. J. Energy Storage 2023, 72, 108420. [Google Scholar]
- Nagarale, S.D.; Patil, B. Accelerating AI-Based Battery Management System’s SOC and SOH on FPGA. Appl. Comput. Intell. Soft Comput. 2023, 2023, 2060808. [Google Scholar] [CrossRef]
- He, Z.; Shen, X.; Sun, Y.; Zhao, S.; Fan, B.; Pan, C. State-of-health estimation based on real data of electric vehicles concerning user behavior. J. Energy Storage 2021, 41, 102867. [Google Scholar] [CrossRef]
- Hashemi, S.R.; Bahadoran Baghbadorani, A.; Esmaeeli, R.; Mahajan, A.; Farhad, S. Machine learning-based model for lithium-ion batteries in BMS of electric/hybrid electric aircraft. Int. J. Energy Res. 2021, 45, 5747–5765. [Google Scholar] [CrossRef]
- Li, S.; He, H.; Zhao, P.; Cheng, S. Data cleaning and restoring method for vehicle battery big data platform. Appl. Energy 2022, 320, 119292. [Google Scholar] [CrossRef]
- Akbar, K.; Zou, Y.; Awais, Q.; Baig, M.J.A.; Jamil, M. A machine learning-based robust state of health (SOH) prediction model for electric vehicle batteries. Electronics 2022, 11, 1216. [Google Scholar] [CrossRef]
- Zhang, H.; Gui, X.; Zheng, S.; Lu, Z.; Li, Y.; Bian, J. BatteryML: An open-source platform for machine learning on battery degradation. arXiv 2023, arXiv:2310.14714. [Google Scholar]
- Zhang, D.; Zhong, C.; Xu, P.; Tian, Y. Deep learning in the state of charge estimation for li-ion batteries of electric vehicles: A review. Machines 2022, 10, 912. [Google Scholar] [CrossRef]
- Rivera-Barrera, J.P.; Muñoz-Galeano, N.; Sarmiento-Maldonado, H.O. SoC estimation for lithium-ion batteries: Review and future challenges. Electronics 2017, 6, 102. [Google Scholar] [CrossRef]
- Liu, F.; Yu, D.; Su, W.; Ma, S.; Bu, F. Adaptive Multitimescale Joint Estimation Method for SOC and Capacity of Series Battery Pack. IEEE Trans. Transp. Electrif. 2023, 10, 4484–4502. [Google Scholar] [CrossRef]
- Timilsina, L.; Hoang, P.H.; Moghassemi, A.; Buraimoh, E.; Chamarthi, P.K.; Ozkan, G.; Papari, B.; Edrington, C.S. A real-time prognostic-based control framework for hybrid electric vehicles. IEEE Access 2023, 11, 127589–127607. [Google Scholar] [CrossRef]
- He, H.; Meng, X.; Wang, Y.; Khajepour, A.; An, X.; Wang, R.; Sun, F. Deep reinforcement learning based energy management strategies for electrified vehicles: Recent advances and perspectives. Renew. Sustain. Energy Rev. 2024, 192, 114248. [Google Scholar] [CrossRef]
- Guirguis, J.; Ahmed, R. Transformer-based deep learning models for state of charge and state of health estimation of li-ion batteries: A survey study. Energies 2024, 17, 3502. [Google Scholar] [CrossRef]
- Salucci, C.B.; Bakdi, A.; Glad, I.K.; Vanem, E.; De Bin, R. A novel semi-supervised learning approach for State of Health monitoring of maritime lithium-ion batteries. J. Power Sources 2023, 556, 232429. [Google Scholar] [CrossRef]
- Zafar, M.H.; Mansoor, M.; Abou Houran, M.; Khan, N.M.; Khan, K.; Moosavi, S.K.R.; Sanfilippo, F. Hybrid deep learning model for efficient state of charge estimation of Li-ion batteries in electric vehicles. Energy 2023, 282, 128317. [Google Scholar] [CrossRef]
- Krzywanski, J.; Sosnowski, M.; Grabowska, K.; Zylka, A.; Lasek, L.; Kijo-Kleczkowska, A. Advanced computational methods for modeling, prediction and optimization—A review. Materials 2024, 17, 3521. [Google Scholar] [CrossRef]
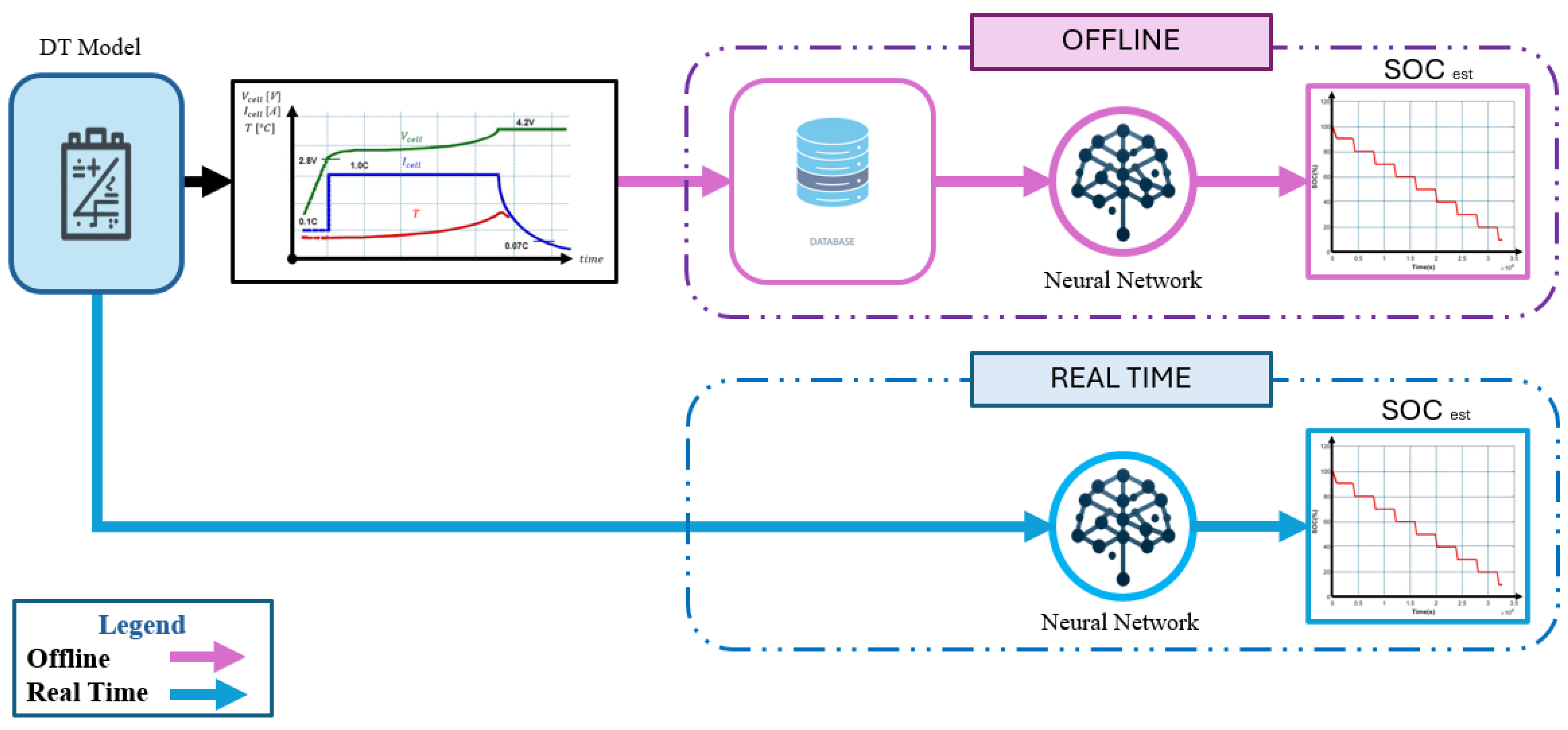
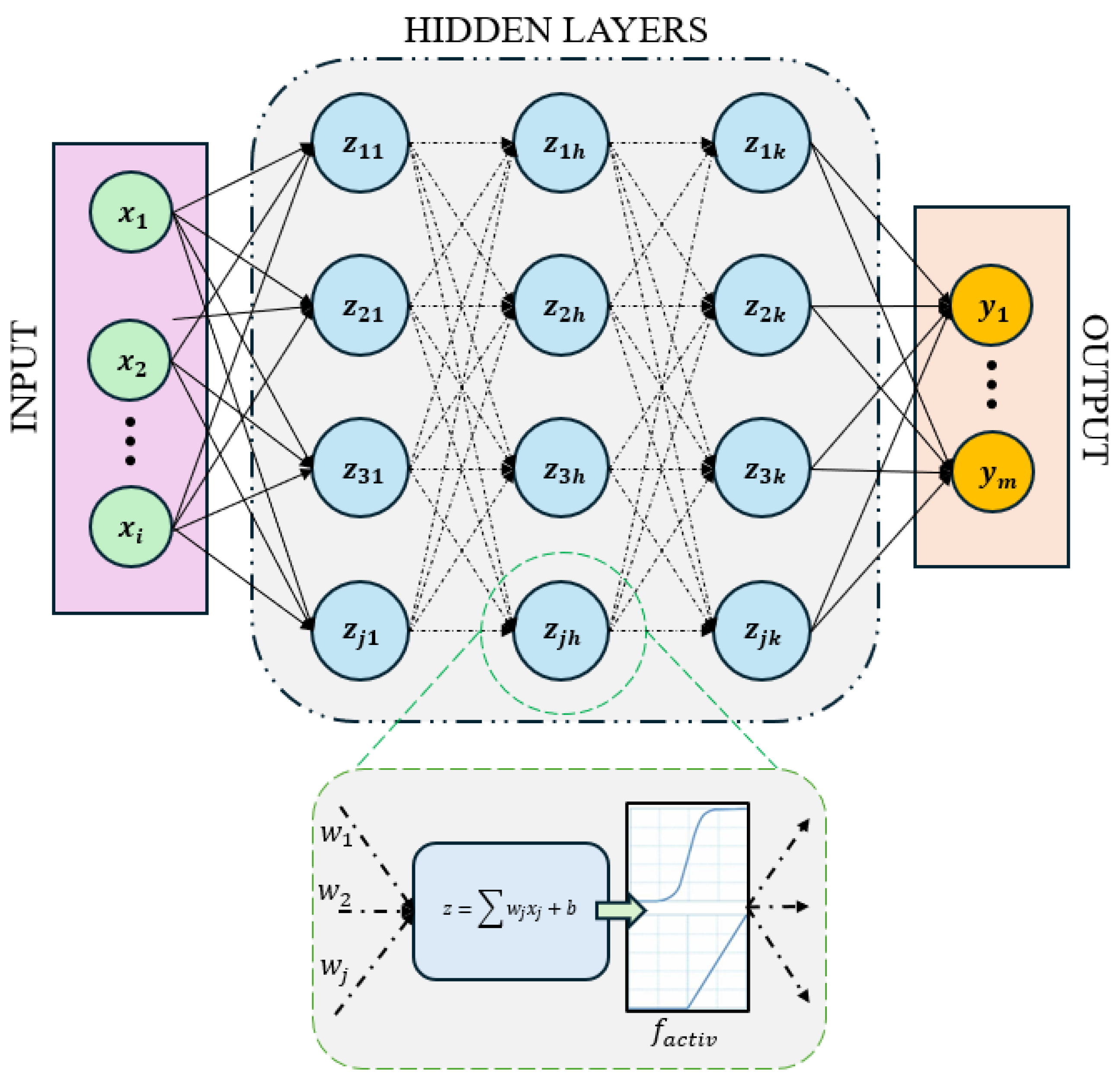
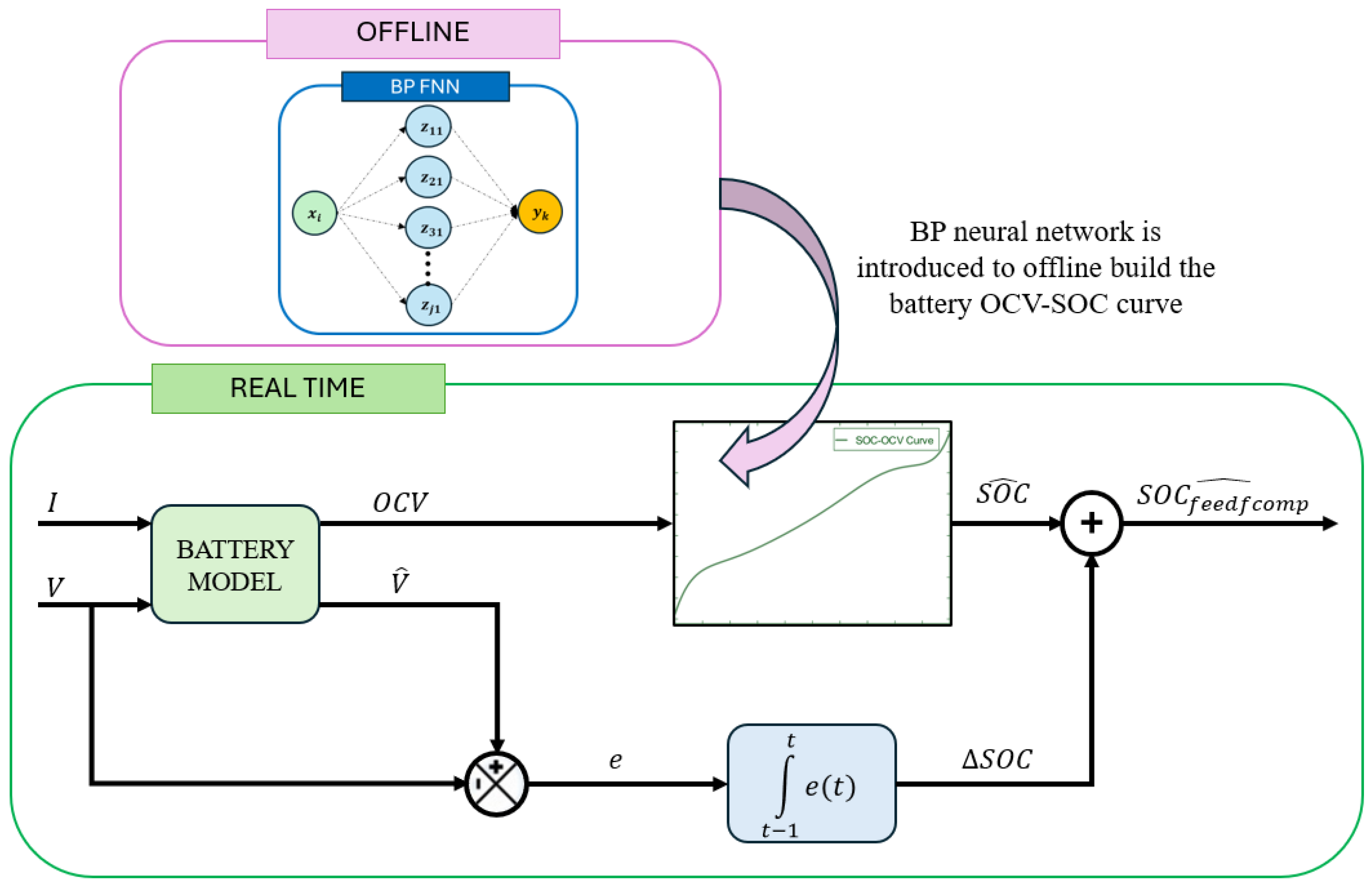
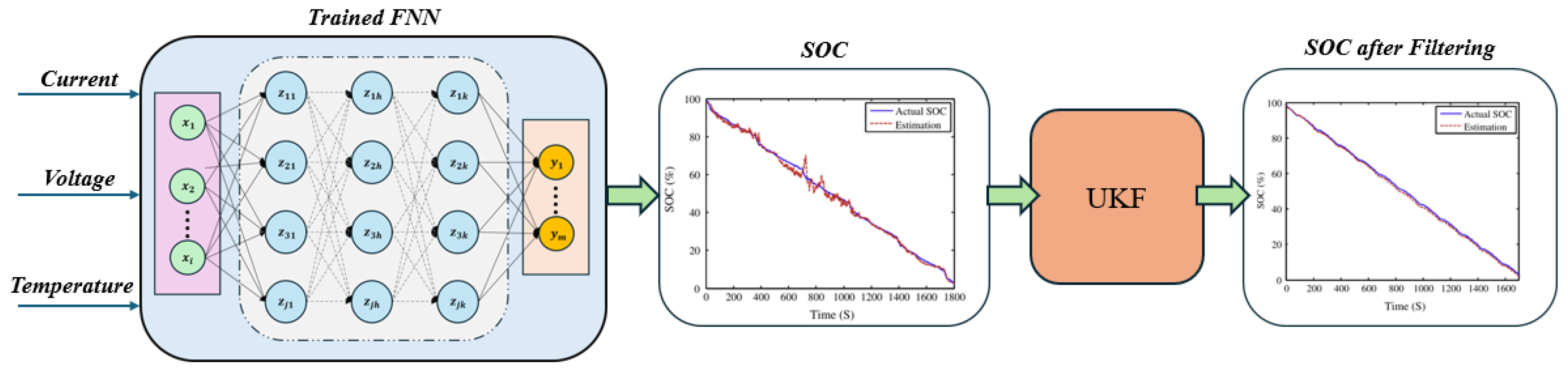
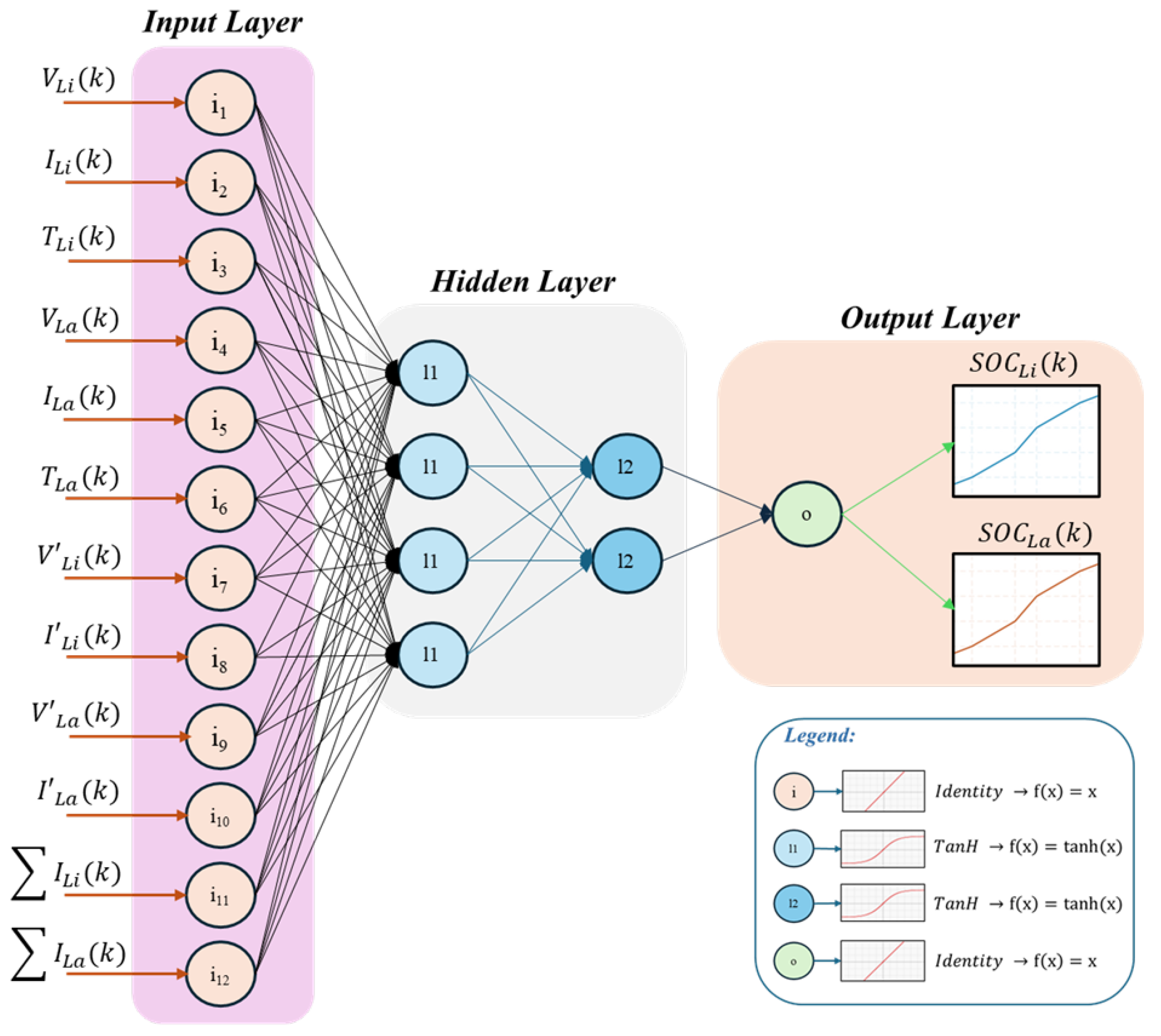
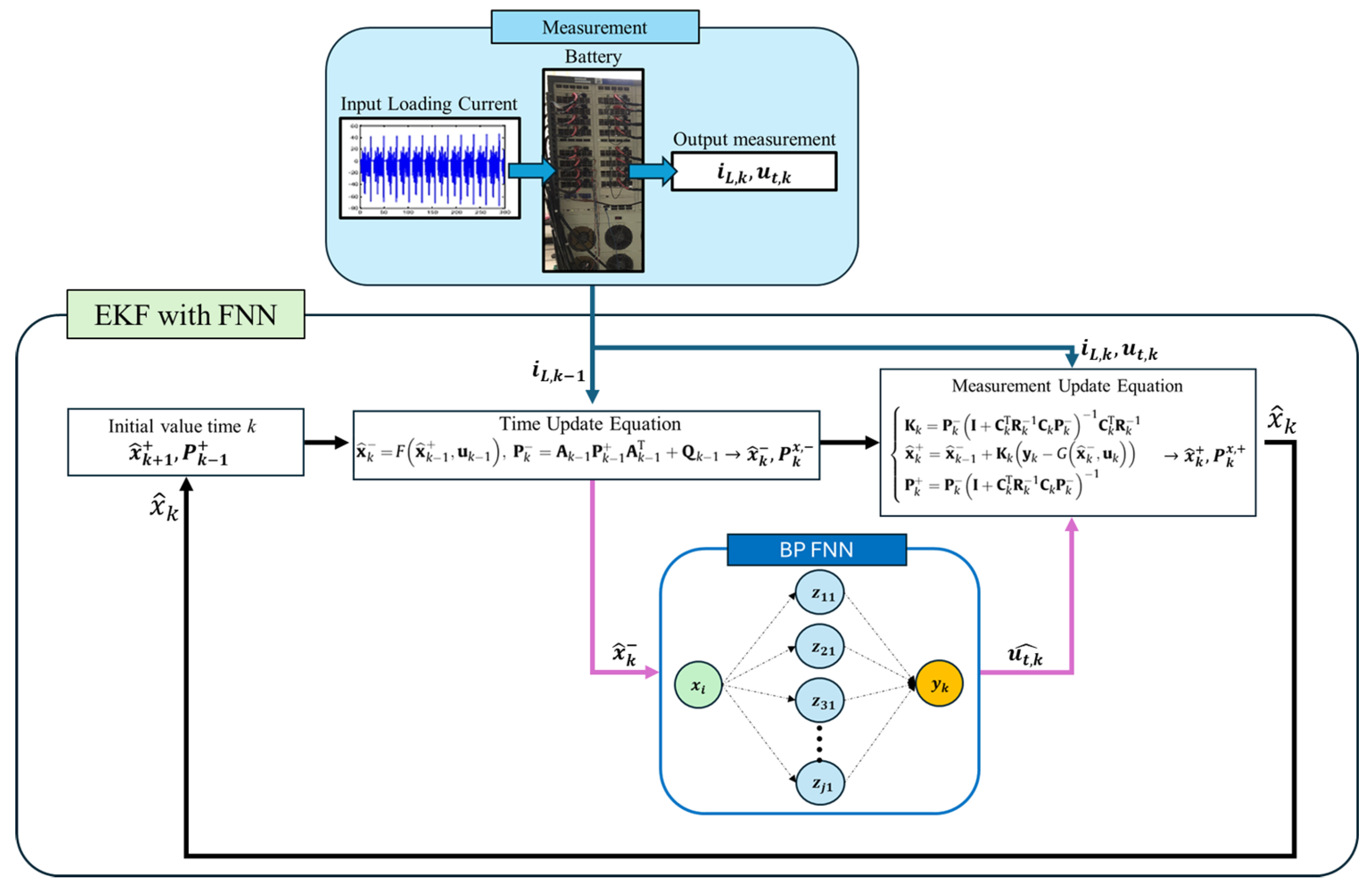
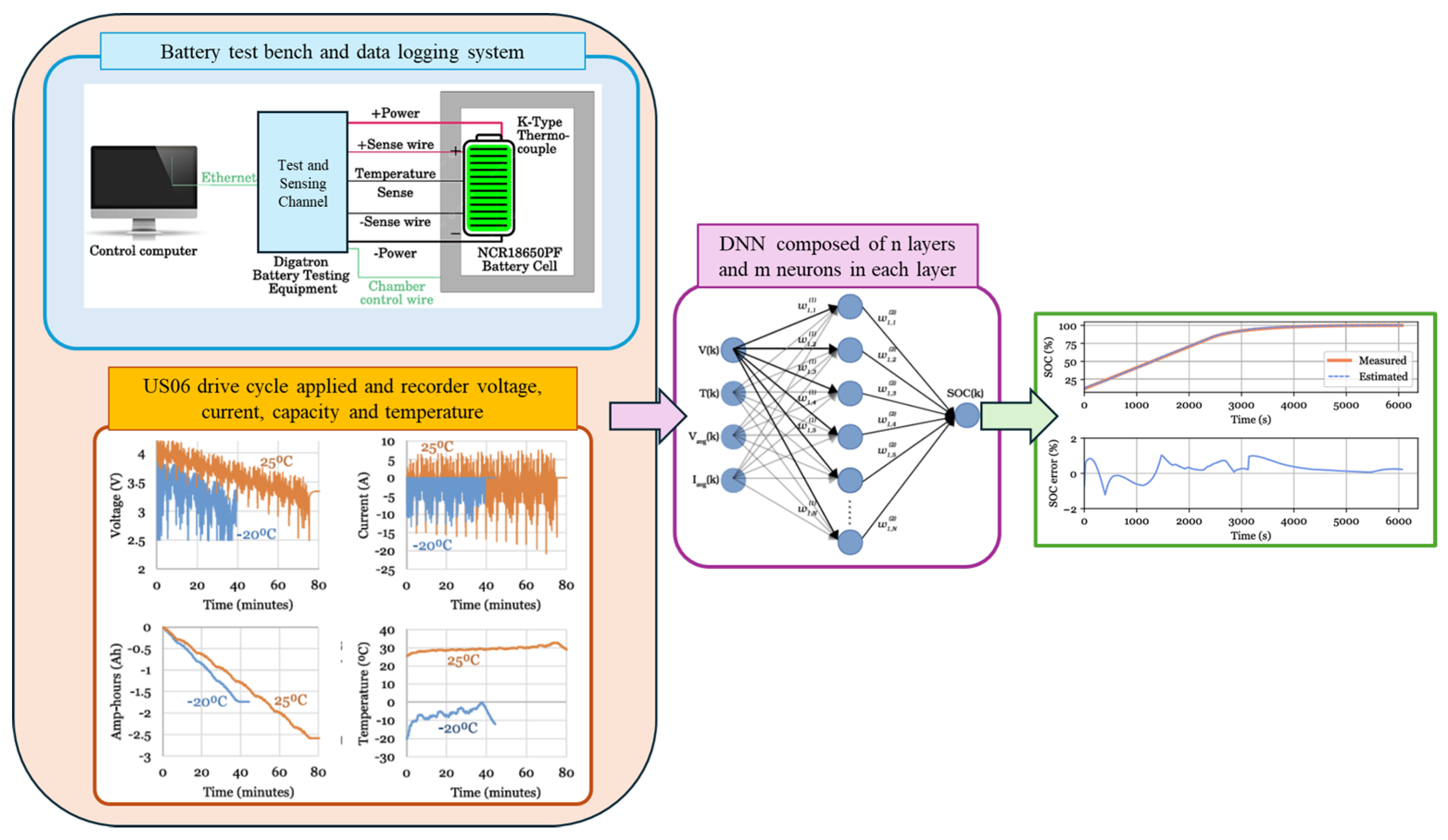
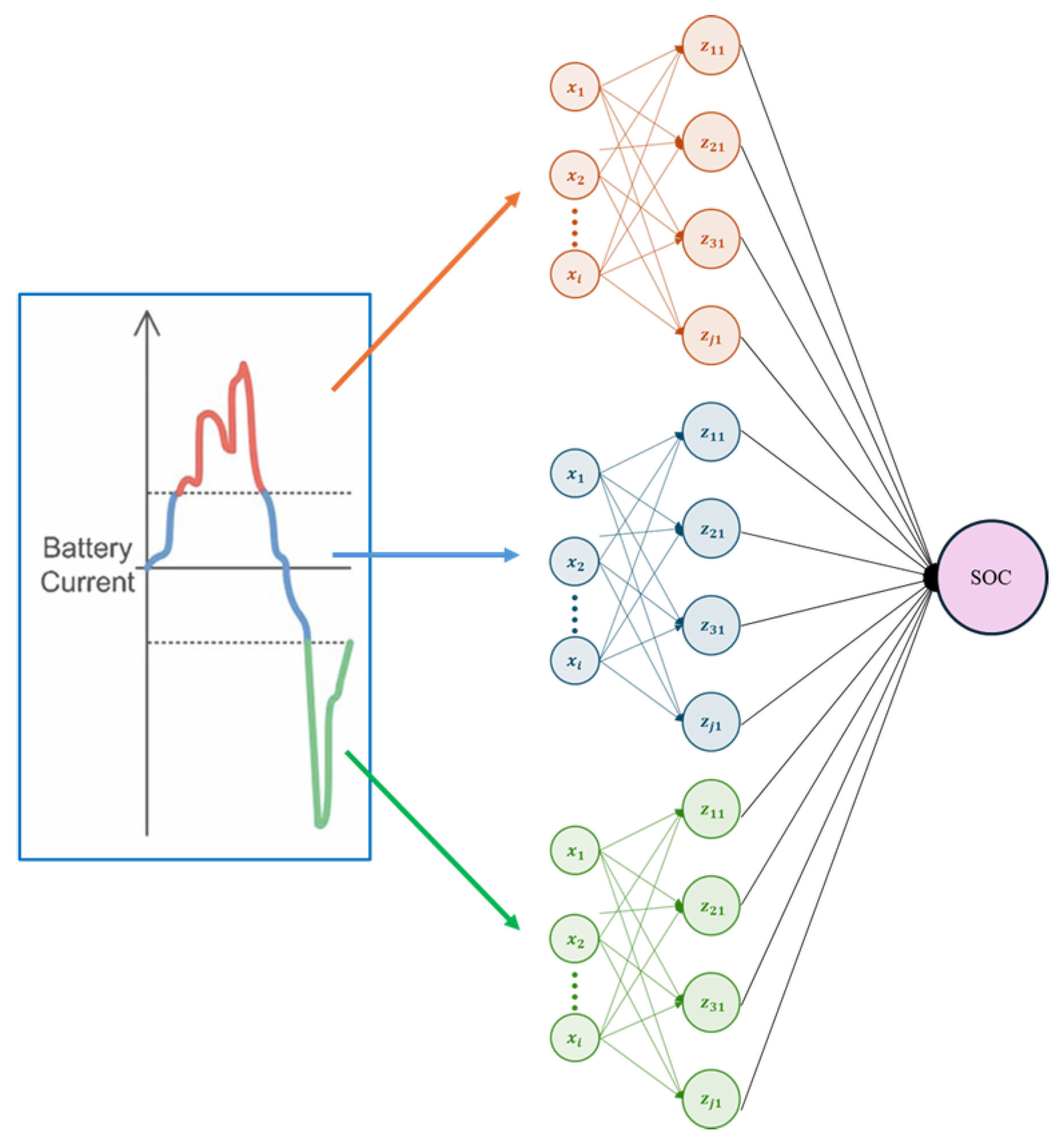

| Article | Innovations | Dataset & EV Tests | Performance | Advantages | Disadvantages | Computational Cost |
|---|---|---|---|---|---|---|
| UKF for SOC Estimation | OCV–SOC-T table with temperature (0–50 °C); UKF for nonlinearity handling; Simplified Rint model. | Lab tests on LiFePO4 (18650) with DST, OCV–SOC-T, FUDS; No direct EV tests. | RMS error < 5% (40 °C), up to 16.4% (0 °C). | Accurate SOC estimation with temperature integration; Real-time capable. | Poor performance at low temperatures; Sensitive to flat OCV–SOC regions. | Low; optimized for BMS real-time use. |
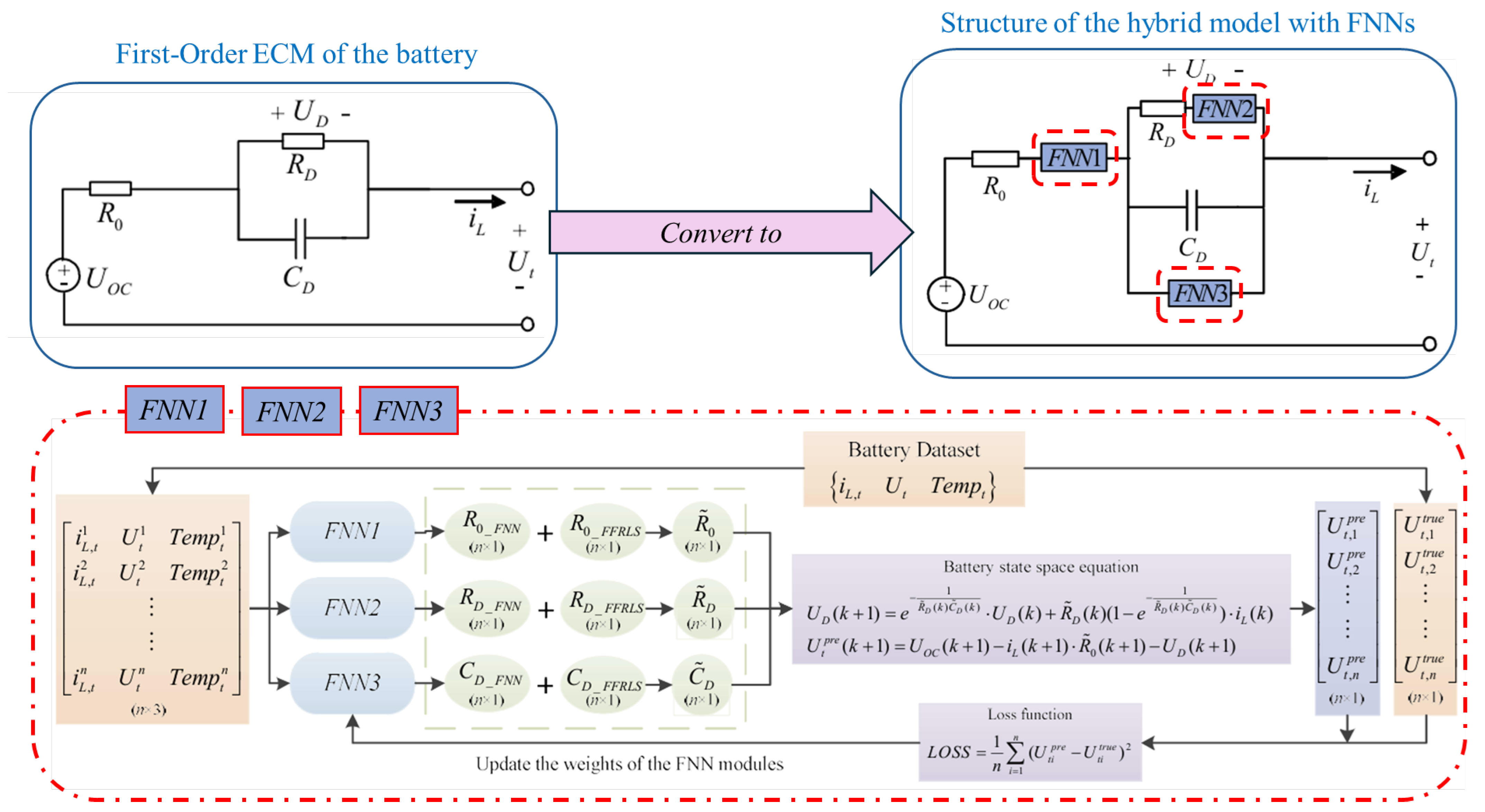
| Neural-Network-Embedded ECM [66] | ECM with 3 feedforward NNs for residual error correction; Physics-informed loss in training. | Panasonic 18650PF; HPPC, US06, HWFET at 10 °C to −20 °C; Lab-tested under EV conditions. | MSE reduced by 82.5% (US06); RMSE improved 33–64% (US06), 5–29% (HWFET). | High accuracy, especially in extreme conditions; Adaptive to uncertainties. | Initial/final phase errors; Complex offline training, requires retraining. | Offline: 264–450 s; Online: 1.3–2.2 s (real-time suitable). |
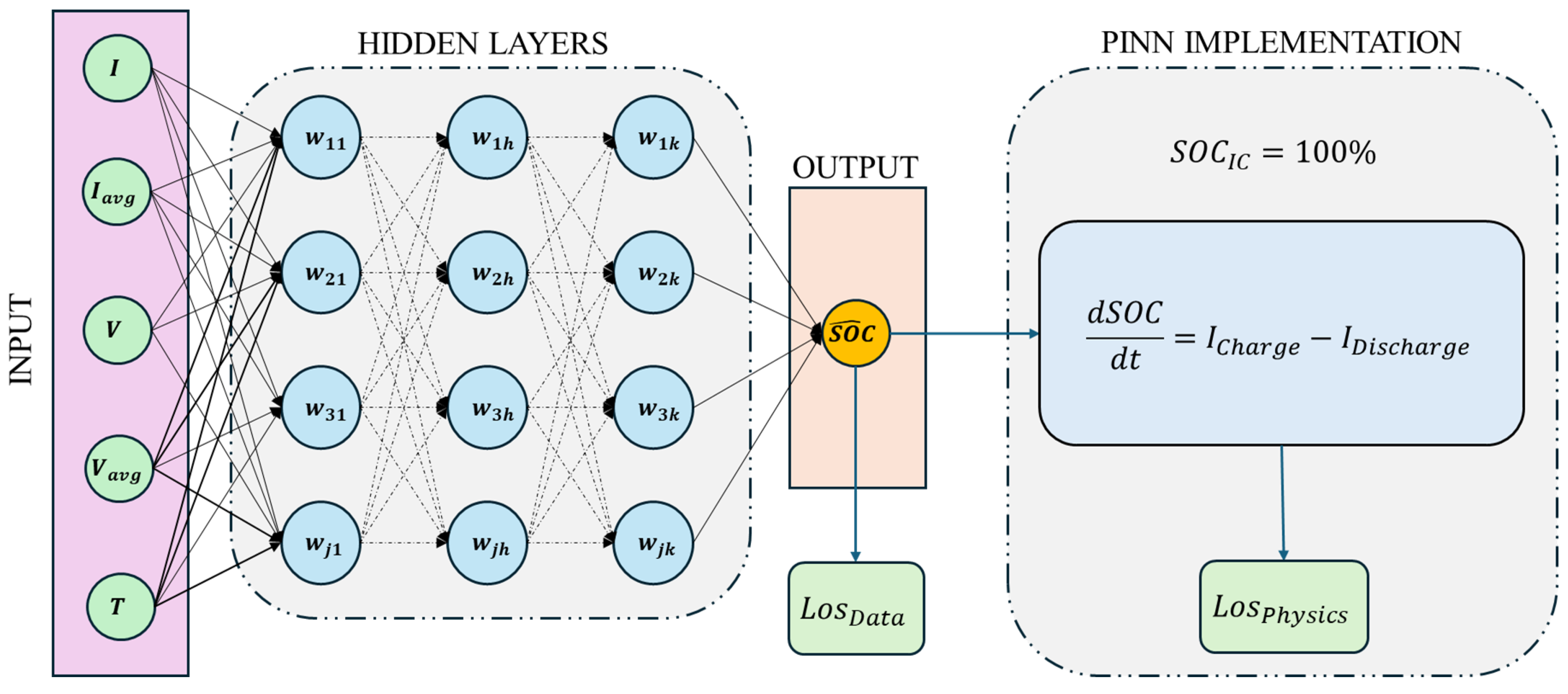
| Physics-Informed NN (PINN) [63] | Deep FNN with physics-constrained loss (data + charge conservation). | McMaster Univ. (LG HG2, 3Ah); UDDS, US06, LA92, HWFET, Mix; −10 °C to 25 °C; Climatic chamber tests. | RMSE < 2.85%; Outperforms NN-only and AKF methods. | High accuracy and robustness with noisy/sparse data; Physically consistent solutions. | Demanding offline training; Complex design. | Offline: demanding; Online: efficient, real-time capable. |
| NN + UKF for Error Cancellation [45] | Hybrid NN for SOC estimation + UKF for noise/error reduction; No OCV–SOC table needed. | Dynamic tests; NN trained on DST, validated on US06/FUDS; Li-ion (mostly LiFePO4) under EV conditions. | RMS error (US06, 0 °C) reduced from 4.1% (NN only) to 2.4% (NN + UKF). | Higher robustness via UKF filtering; No need for OCV–SOC table. | Risk of NN overfitting; Complex NN–UKF integration. | Offline: structural optimization; Online: real-time with filtered errors. |
| Article | Innovations | Dataset & EV Tests | Performance | Advantages | Disadvantages | Computational Cost |
|---|---|---|---|---|---|---|
| Hybrid FNNs for SOC [51] | Hybrid FNN model for SOC estimation; NN optimization to improve generalization and reduce errors. | Lab data on Li-ion (LiFePO4) batteries; DST, US06, FUDS at variable temperatures. | RMS error < 3–4% under optimal conditions. | Robust to nonlinearities; No need for OCV–SOC tables. | Complex offline training; Requires careful optimization. | Offline: demanding; Online: real-time capable. |
| FNN + EKF [48] | Hybrid approach: FNN + EKF with parameter for filter update; Direct SOC estimation without OCV–SOC table. | Lab data on Li-ion (LiFePO4); DST, US06, FUDS under various temperatures. | Reduced RMS and max errors; Stable SOC estimation. | Accurate and robust; EKF ensures real-time applicability. | EKF less accurate in strong nonlinearities; Requires tuning and sensor calibration. | Offline: demanding; Online: real-time suitable. |
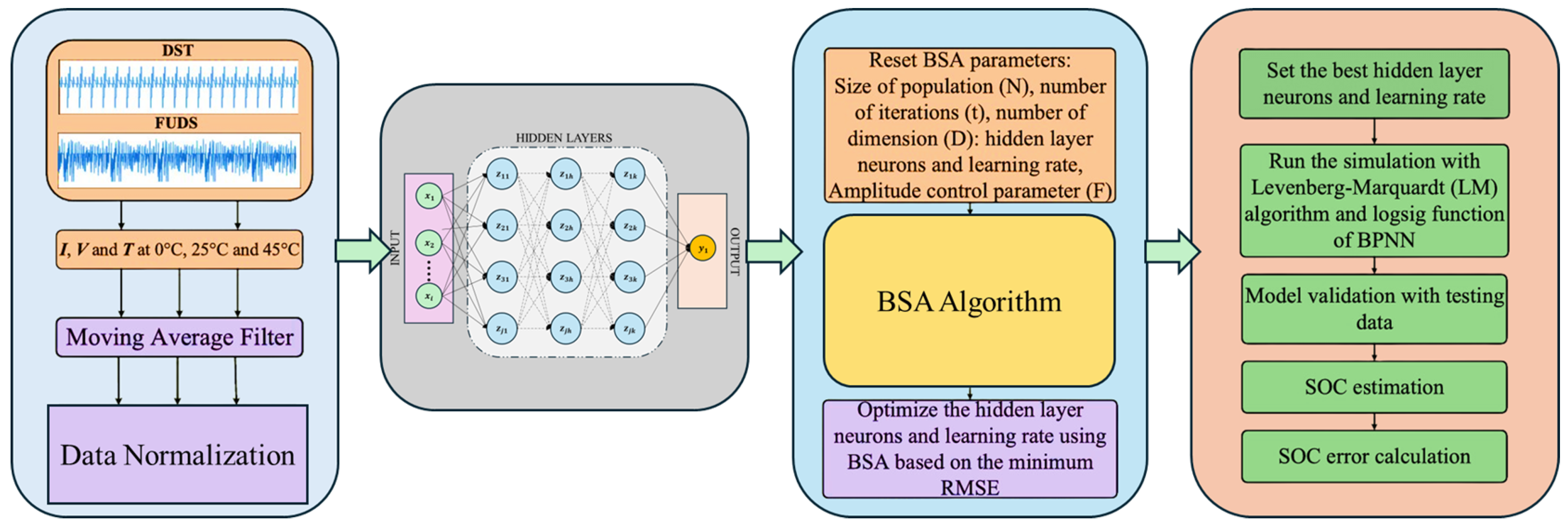
| BPNN + BSA Model [62] | BPNN with BSA model for direct SOC estimation; Improved data fusion (voltage, current, temperature). | Lab data on Li-ion (LiFePO4); DST, US06, FUDS at various temperatures. | RMS and MAE errors typically < 5%. | Strong nonlinear learning; No OCV–SOC table needed. | Complex training; Requires high-quality data. | Offline: computationally heavy; Online: real-time feasible. |
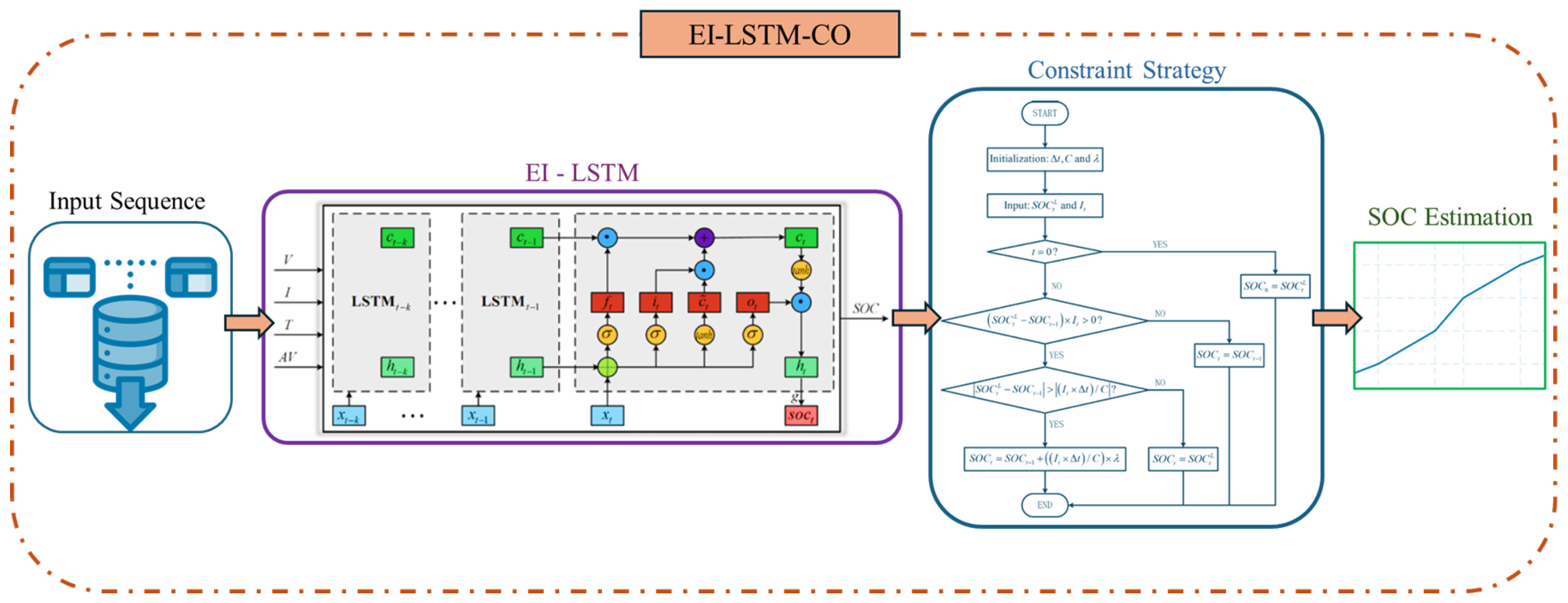
| LSTM–RNN for SOC [85] | EI-LSTM-CO model: extended input (avg. voltage via sliding window), output constrained by AhI strategy for stability. | Public dataset (CALCE, LiFePO4); DST for training, US06 and FUDS for validation (7 temperatures, 1s sampling). | RMSE < 1.3%, MAXE < 3.2%; Improved stability vs. standard LSTM–RNN. | Smooth SOC estimation; No need for accurate initial SOC; High accuracy for BMS. | Requires careful tuning (epochs, window size, constraints); More complex than conventional NNs. | Offline: 150 epochs, window size 50; Online: fast, real-time capable. |
| Article | Innovations | Dataset & EV Tests | Performance | Advantages | Disadvantages | Computational Cost |
|---|---|---|---|---|---|---|
| CNN–LSTM for SOC [82] | Hybrid CNN–LSTM for feature extraction and temporal modeling; Robust to unknown initial SOC and temperature variations. | A123 18650 LiFePO4; DST, FUDS, US06; Climatic chamber tests. | MAE < 1%, RMSE < 2% (unknown initial SOC); RMSE < 2%, MAE < 1.5% (temperature variations). | Stable and accurate SOC estimation; Rapid convergence; Good adaptation to environmental variations. | Complex architecture; Long offline training and parameter tuning. | Offline: 10,000 epochs (161 min on GPU); Online: 0.098 ms per time step (real-time suitable). |
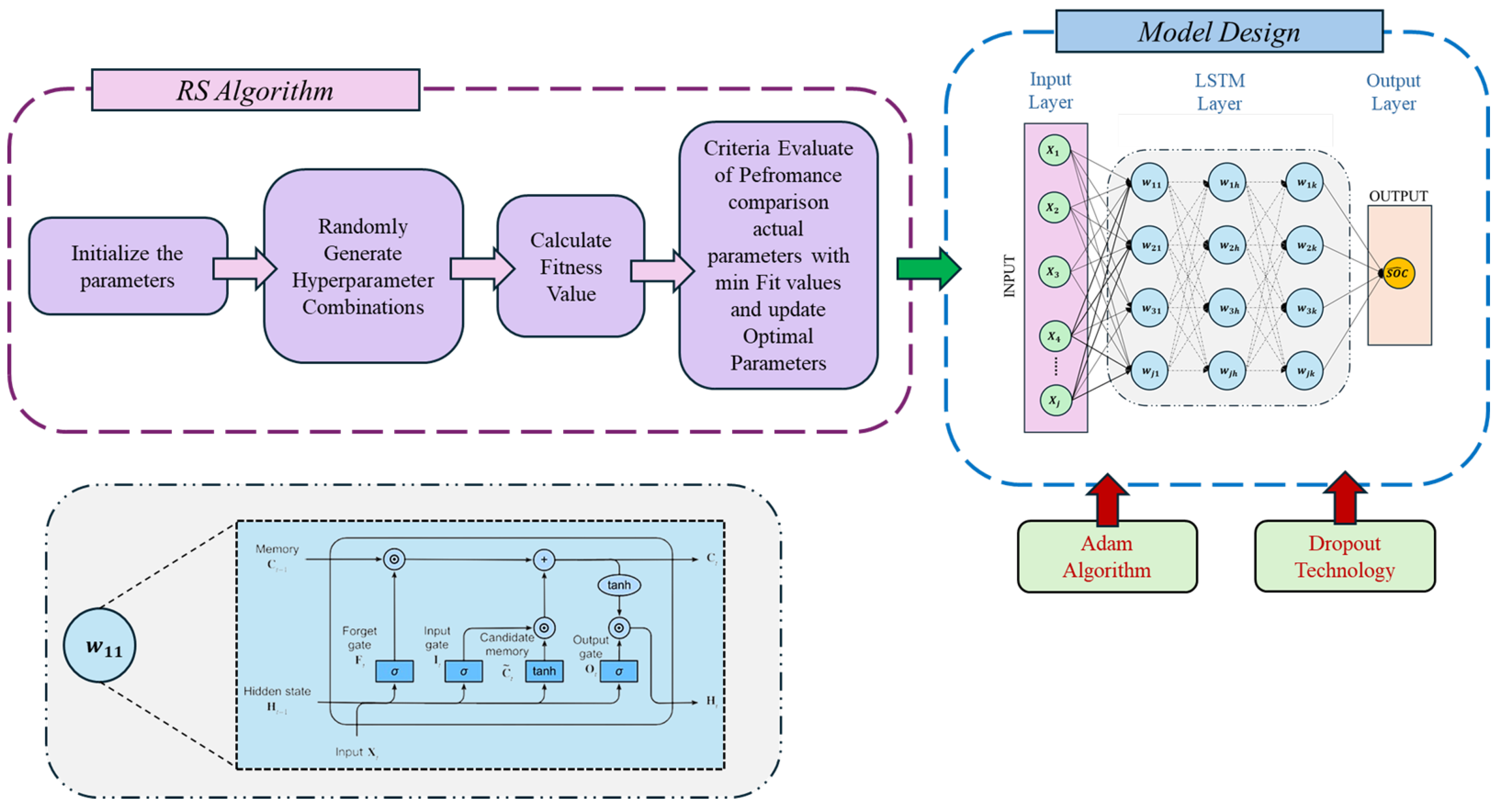
| RS-LSTM (Random Search LSTM) [86] | LSTM with Random Search optimization; Random Forest for feature selection; Auto-tuned hyperparameters. | CALCE dataset (INR 18650-20R); DST, FUDS, US06; Lab and real vehicle data at different temperatures. | Optimal settings: Look back = 45, Epochs = 177, Batch = 64, LR = 0.0026; MAE = 0.221%, RMSE = 0.262%. | Reduces noise via Random Forest; Auto-optimized hyperparameters; High accuracy and stability. | High offline computation due to hyperparameter search; Complex model tuning. | Offline: intensive training; Online: fast, real-time capable. |
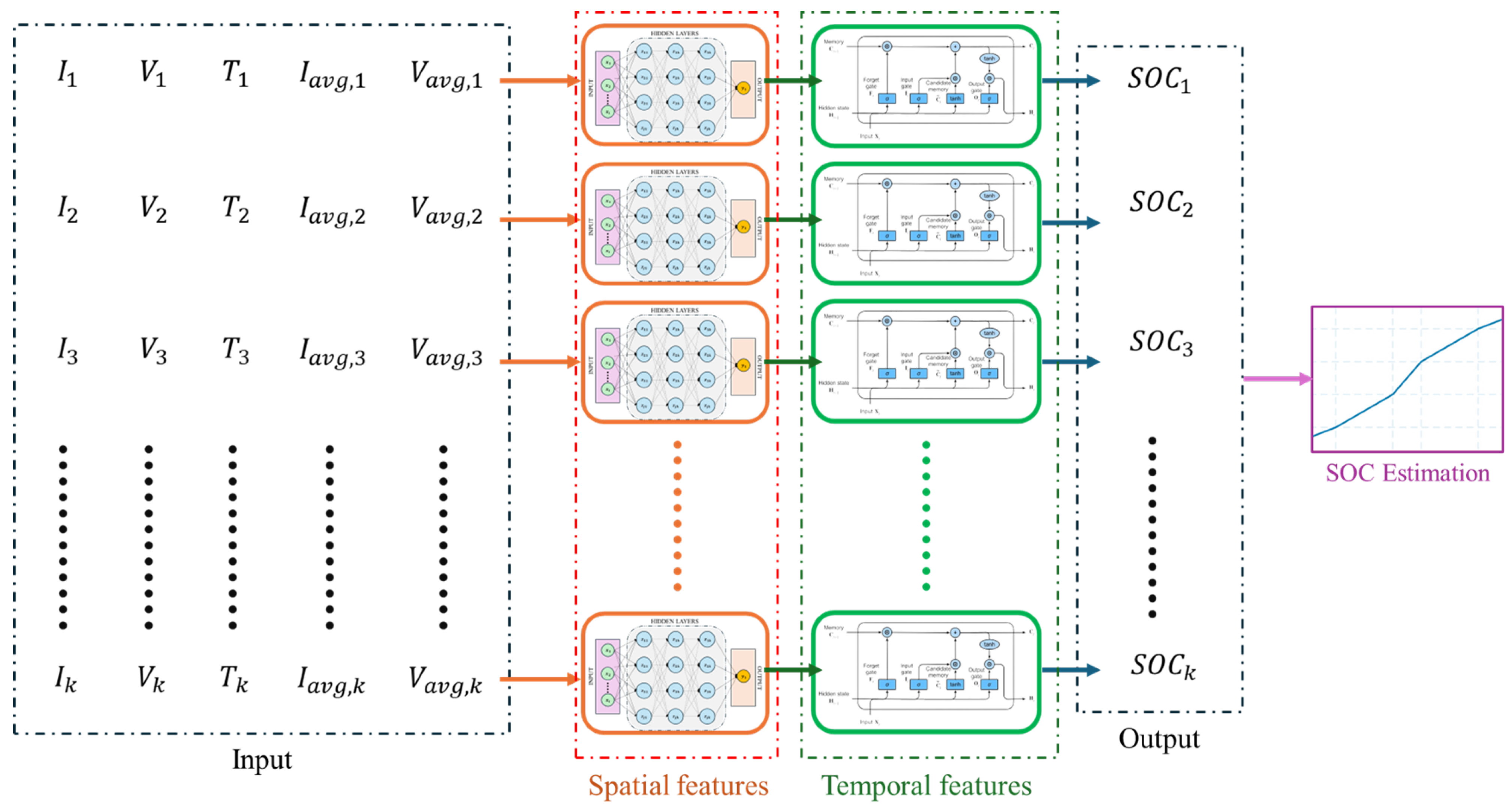
| GLA–CNN–BiLSTM for SOC [92] | CNN for spatial and BiLSTM for temporal features; GLA for automatic hyperparameter tuning. | Six EV discharge datasets (HWFET, US06, BJDST, DST, FUDS, UDDS); Lab tests on Li-ion. | MAE < 1%, RMSE < 1%, Max error < 2%. | Combines CNN (features) + BiLSTM (time); GLA ensures fast convergence and adaptability. | Intensive offline training; Complex hyperparameter tuning. | Offline: high due to GLA; Online: fast, real-time suitable. |
| Article | Innovations | Dataset & EV Tests | Performance | Advantages | Disadvantages | Computational Cost |
|---|---|---|---|---|---|---|
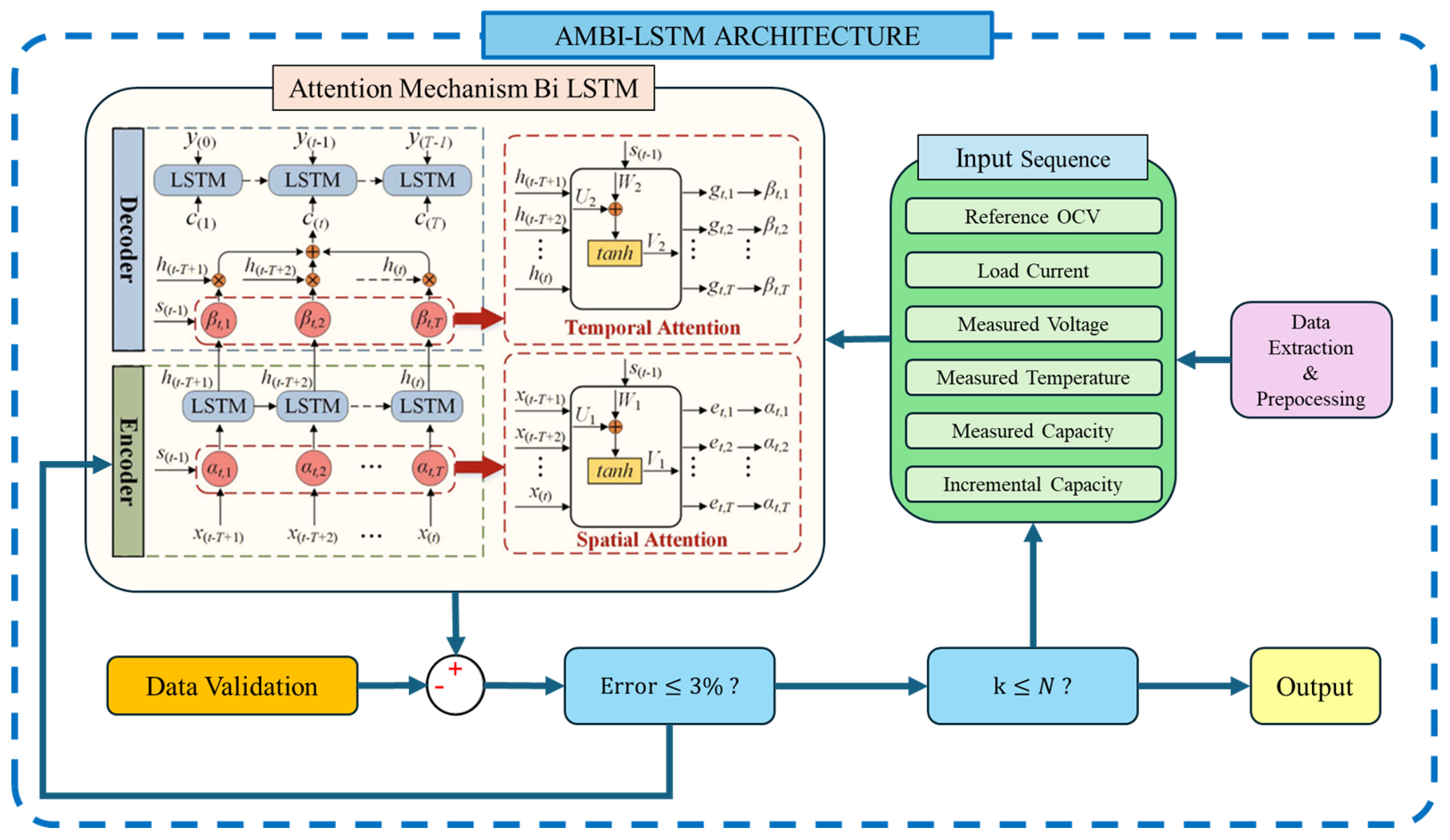
| AMBiLSTM with Attention [94] | BiLSTM with spatial/temporal attention; Temperature compensation in OCV and capacity; SOC and SOH co-estimation. | Lab tests on LiNiCoAlO2 (2.6 Ah); 0–40 °C; DST, UDDS; 1 s/10 s sampling. | DST (25 °C): RMSE ↓9.39%; UDDS (25 °C): RMSE ↓22.36%; SOH ↑21.45%. | Improved feature extraction; Robust to temperature variations; Simultaneous SOC/SOH estimation. | Complex model; Requires large dataset and intensive training; Potential short-sequence errors. | Offline: GPU-intensive (RTX 3090); Online: fast, real-time feasible. |
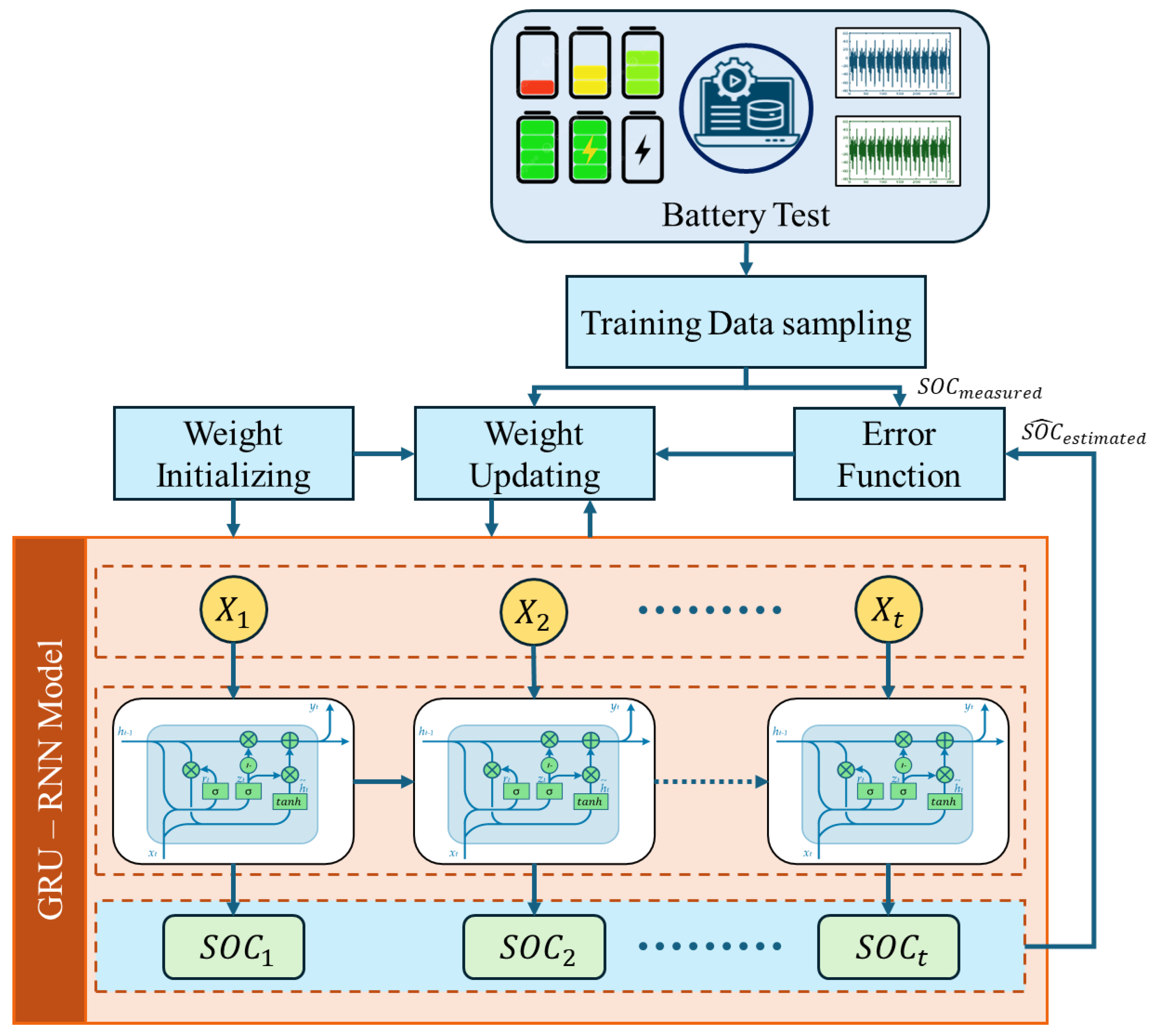
| GRU–RNN with Momentum [105] | GRU–RNN with momentum gradient algorithm; Noise injection to prevent overfitting. | Lab tests on BTcap 21700 (2.2 Ah); Charge-discharge cycles; Voltage-current measurements. | Sigma = 0.03: RMSE = 0.0092, MAE = 0.0041, R2 = 0.9990. | Fast convergence; Reduced weight oscillations; High accuracy and generalization. | Requires precise tuning of momentum (beta) and hyperparameters. | Offline: intensive; Online: extremely fast, real-time capable. |
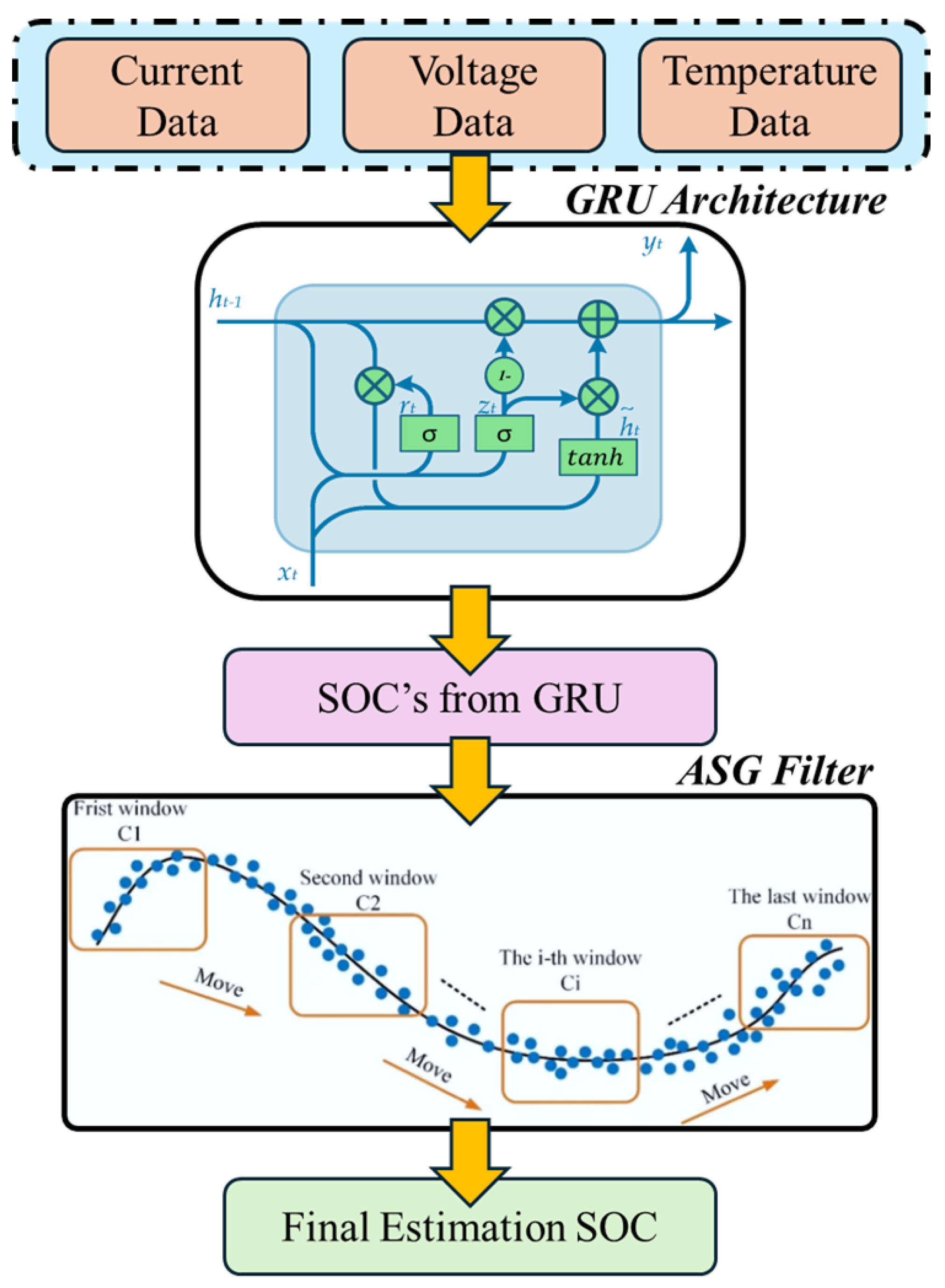
| GRU–ASG for SOC [106] | GRU with adaptive Savitzky–Golay (ASG) filter; Spearman coefficient for dynamic window selection. | Real data from LiFePO4 (280 Ah, 3.2 V); Energy storage plant; Six discharge datasets. | MSE < 0.15%, MAE < 3%; Outperforms standard GRU and filters. | Robust in varying conditions; Adaptive filter eliminates manual tuning; Effective memory structure. | Complex integration of NN with adaptive filtering; Additional online computation. | Offline: GPU training (GTX 1060, TensorFlow); Online: fast, real-time suitable. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dini, P.; Paolini, D. Exploiting Artificial Neural Networks for the State of Charge Estimation in EV/HV Battery Systems: A Review. Batteries 2025, 11, 107. https://doi.org/10.3390/batteries11030107
Dini P, Paolini D. Exploiting Artificial Neural Networks for the State of Charge Estimation in EV/HV Battery Systems: A Review. Batteries. 2025; 11(3):107. https://doi.org/10.3390/batteries11030107
Chicago/Turabian StyleDini, Pierpaolo, and Davide Paolini. 2025. "Exploiting Artificial Neural Networks for the State of Charge Estimation in EV/HV Battery Systems: A Review" Batteries 11, no. 3: 107. https://doi.org/10.3390/batteries11030107
APA StyleDini, P., & Paolini, D. (2025). Exploiting Artificial Neural Networks for the State of Charge Estimation in EV/HV Battery Systems: A Review. Batteries, 11(3), 107. https://doi.org/10.3390/batteries11030107







