A Hybrid CNN–LSTM–Attention Mechanism Model for Anomaly Detection in Lithium-Ion Batteries of Electric Bicycles
Abstract
1. Introduction
2. Materials and Methods
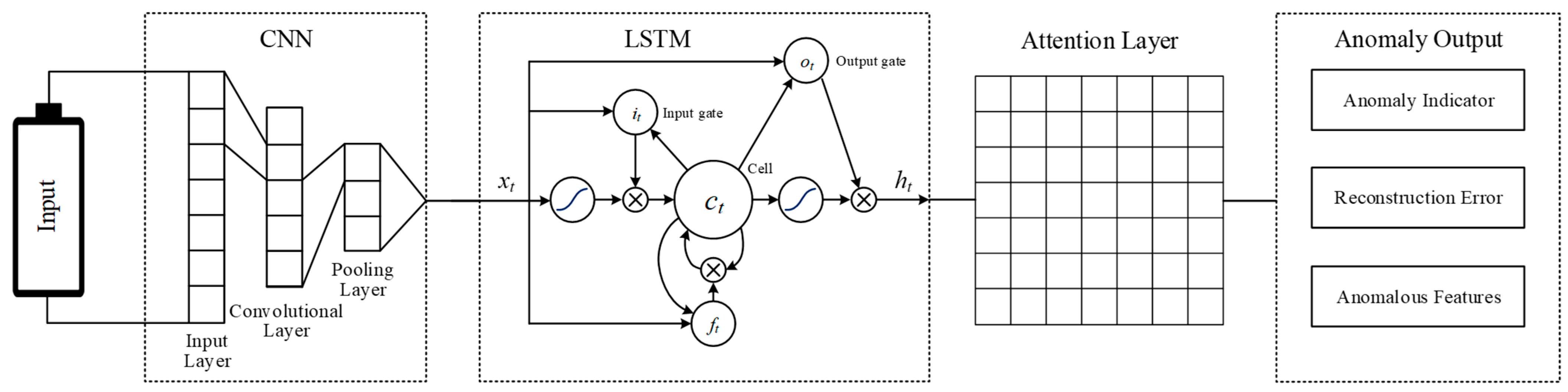
2.1. CNN–LSTM–Attention Model
- Feature Extraction and Temporal Modeling
- 2.
- Attention Weighting
- 3.
- Reconstruction and Error Calculation
2.2. Research Dataset
2.3. Environment Setup
2.4. Model Training and Data Detection
3. Results
- Isolation Forest (IF): A tree-based ensemble method that recursively partitions the feature space to isolate anomalous points.
- One-Class Support Vector Machine (OCSVM): A kernel-based model that learns the boundary of normal samples and identifies points outside the boundary as anomalies.
- Autoencoder (AE): A typical deep learning tool based on reconstruction error, employing a symmetric encoder–decoder architecture with the objective of minimizing reconstruction loss.
- Anomaly Detection Transformer with Convolution (ADTC-Transformer): A recently proposed anomaly detection framework based on Transformer structures, which leverages temporal self-attention to enhance feature interactions and improve detection stability.
- Attention Mechanism–Multi-scale Feature Fusion (AM-MFF): An attention-based multi-scale feature fusion model that combines convolutional and recurrent components with feature fusion mechanisms to capture complex temporal dependencies in battery data.
3.1. Training Phase
3.1.1. Convergence Analysis
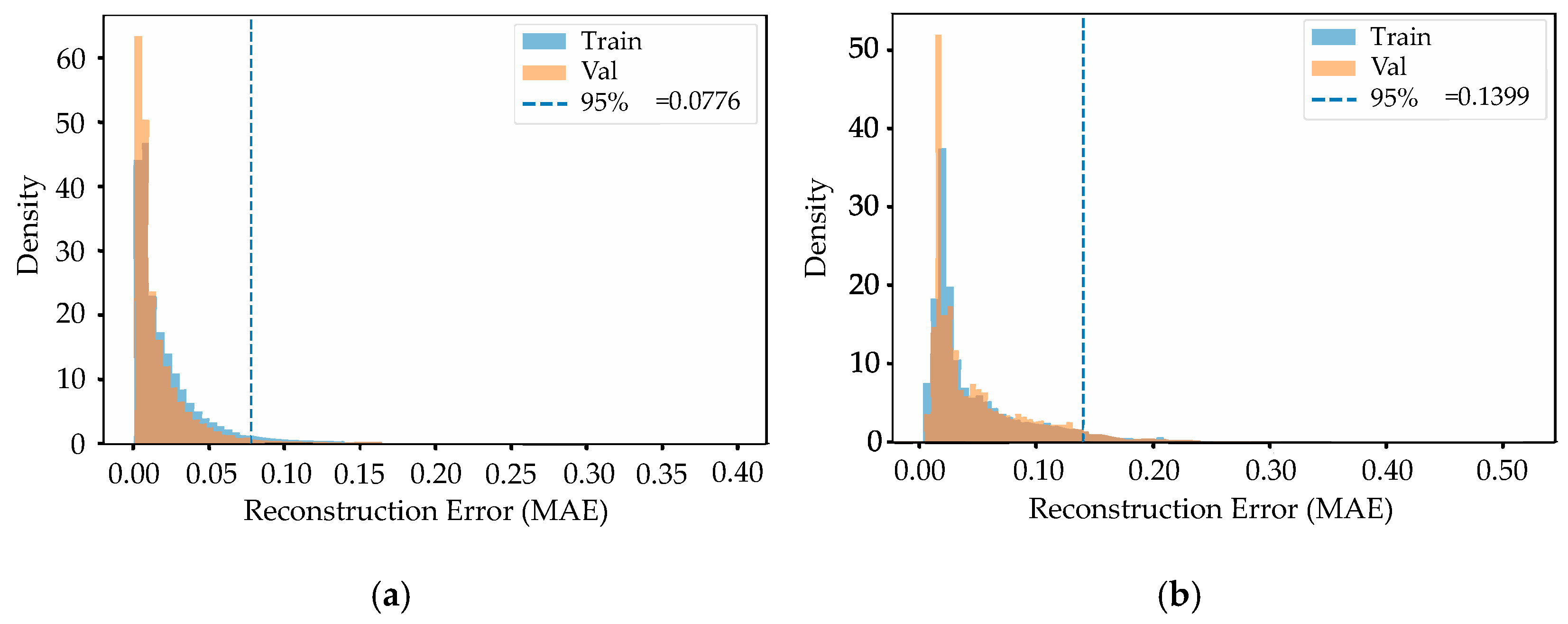
3.1.2. Generalization Verification
3.2. Detection Phase
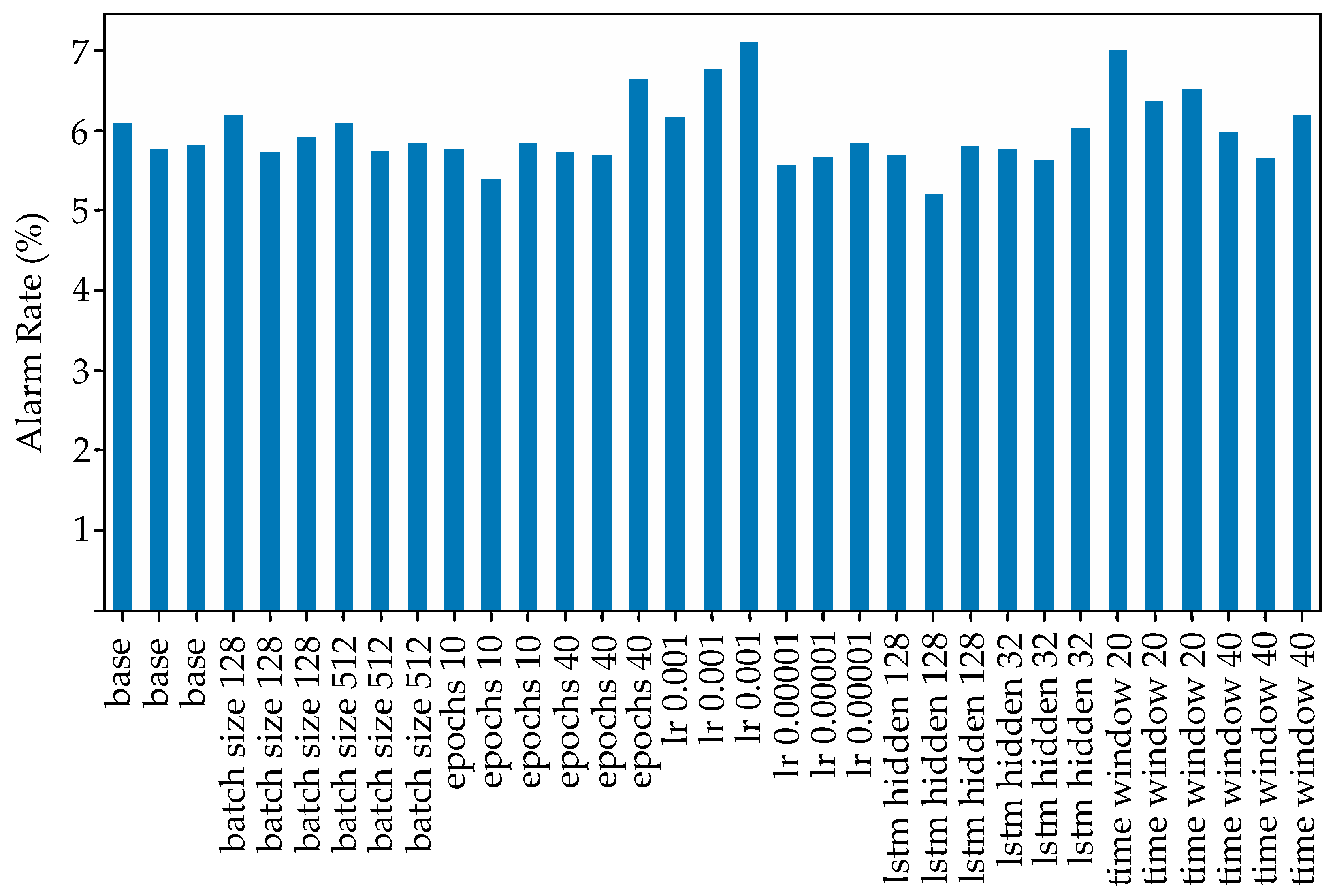
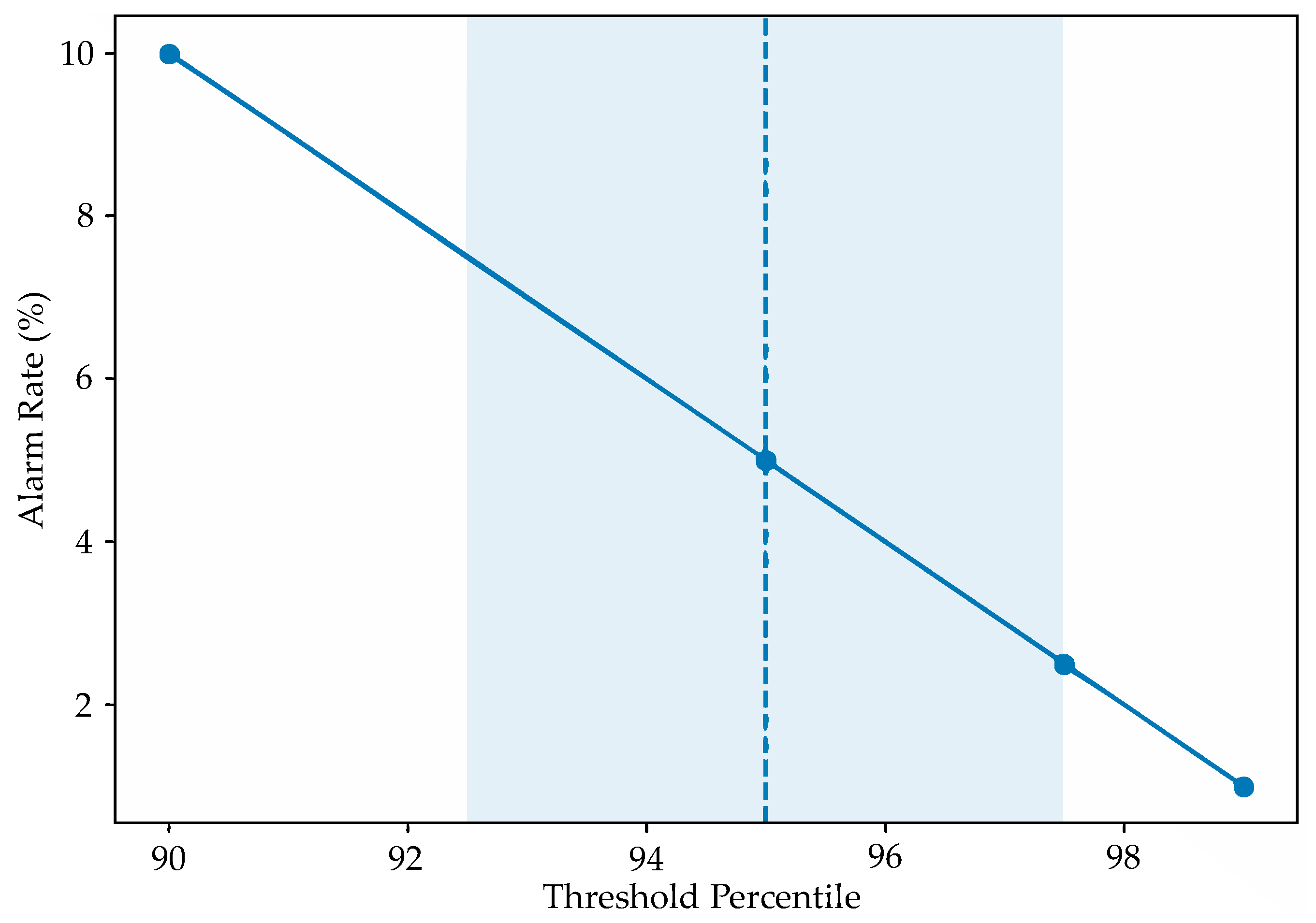
3.2.1. Threshold and Alarm Rate Stability
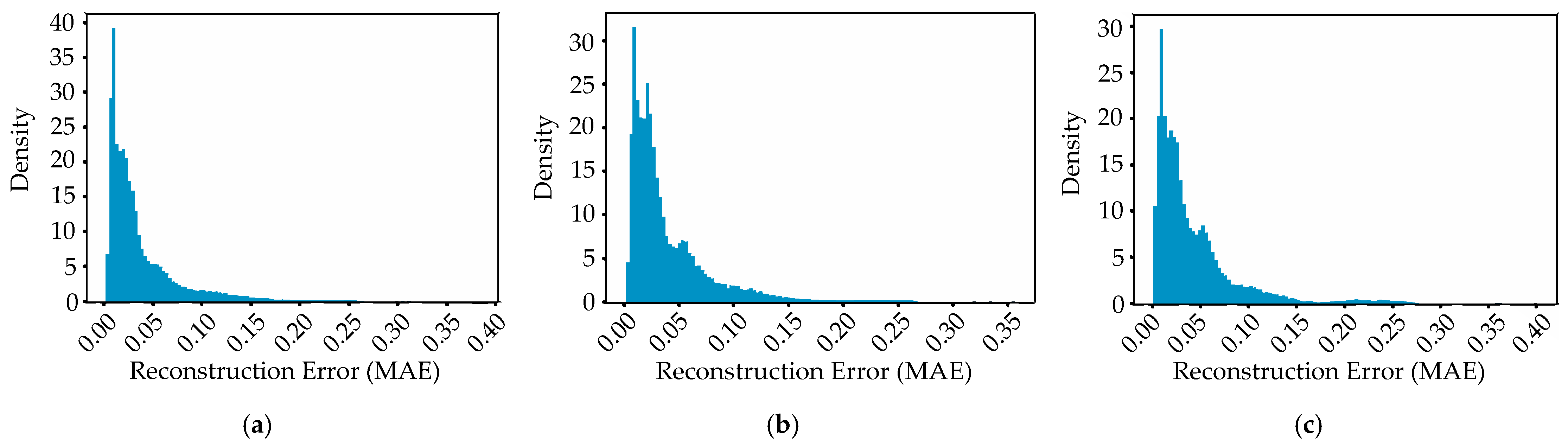
3.2.2. Distribution of Anomaly Scores
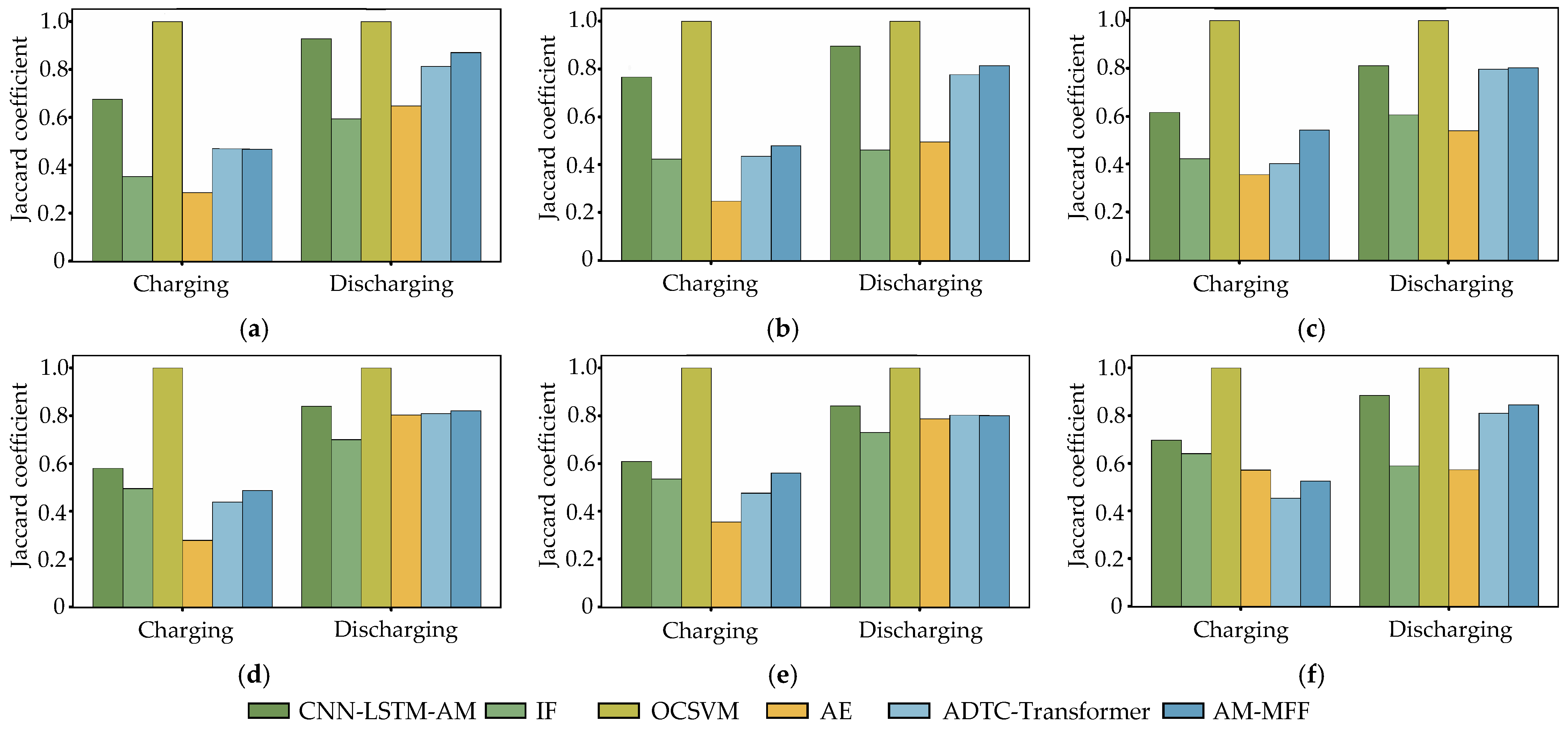
3.2.3. Top-K Anomaly Stability
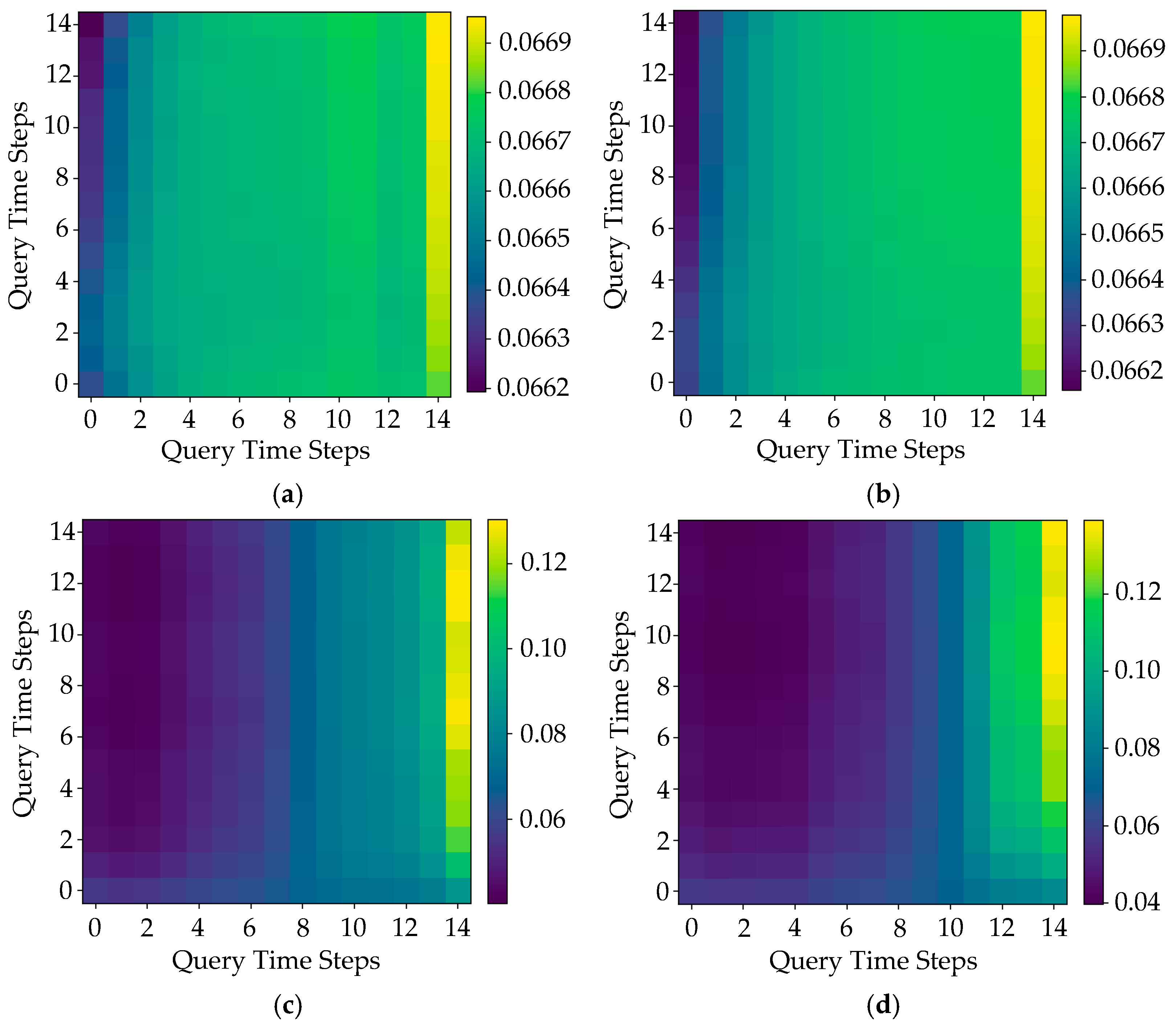
3.2.4. Attention Visualization and Interpretability
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Kang, Y.; Zhao, Y.; Wang, L.; Liu, J.; Li, Y.; Liang, Z.; He, X.; Li, X.; Tavajohi, N.; et al. A review of lithium-ion battery safety concerns: The issues, strategies, and testing standards. J. Energy Chem. 2021, 59, 83–99. [Google Scholar] [CrossRef]
- Guo, R.; Lu, L.; Ouyang, M.; Feng, X. Mechanism of the entire overdischarge process and overdischarge-induced internal short circuit in lithium-ion batteries. Sci. Rep. 2016, 6, 30248. [Google Scholar] [CrossRef]
- Qian, L.; Yi, Y.; Zhang, W.; Fu, C.; Xia, C.; Ma, T. Revealing the Impact of High Current Overcharge/Overdischarge on the Thermal Safety of Degraded Li-Ion Batteries. Int. J. Energy Res. 2023, 2023, 8571535. [Google Scholar] [CrossRef]
- Xie, S.; Gong, Y.; Ping, X.; Sun, J.; Chen, X.; He, Y. Effect of overcharge on the electrochemical and thermal safety behaviors of LiNi0.5Mn0.3Co0.2O2/graphite lithium-ion batteries. J. Energy Storage 2022, 46, 103829. [Google Scholar] [CrossRef]
- Yin, T.; Jia, L.; Li, X.; Zheng, L.; Dai, Z. Effect of High-Rate Cycle Aging and Over-Discharge on NCM811 (LiNi0.8Co0.1Mn0.1O2) Batteries. Energies 2022, 15, 2862. [Google Scholar] [CrossRef]
- Tran, M.-K.; Fowler, M. A Review of Lithium-Ion Battery Fault Diagnostic Algorithms: Current Progress and Future Challenges. Algorithms 2020, 13, 62. [Google Scholar] [CrossRef]
- Samanta, A.; Chowdhuri, S.; Williamson, S.S. Machine Learning-Based Data-Driven Fault Detection/Diagnosis of Lithium-Ion Battery: A Critical Review. Electronics 2021, 10, 1309. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Jiang, B.; He, H.; Huang, S.; Wang, C.; Zhang, Y.; Han, X.; Guo, D.; He, G.; et al. Realistic fault detection of li-ion battery via dynamical deep learning. Nat Commun 2023, 14, 5940. [Google Scholar] [CrossRef]
- Fan, Y.; Huang, Z.; Li, H.; Yuan, W.; Yan, L.; Liu, Y.; Chen, Z. Fault detection for Li-ion batteries of electric vehicles with feature-augmented attentional autoencoder. Sci. Rep. 2025, 15, 18534. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Ma, J.; Ma, Y.; Gong, X.; Xiangli, K.; Zhao, X. Identification of voltage abnormality in the battery system based on fusion of multiple sparse data observers for real-world electric vehicles. J. Energy Storage 2025, 114, 115727. [Google Scholar] [CrossRef]
- Nazim, M.S.; Jang, Y.M.; Chung, B. Machine Learning Based Battery Anomaly Detection Using Empirical Data. In Proceedings of the 2024 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Osaka, Japan, 19–22 February 2024; pp. 847–850. [Google Scholar]
- Sharapatov, A.; Saduov, A.; Assirbek, N.; Abdyrov, M.; Zhumabayev, B. Prediction of rare and anomalous minerals using anomaly detection and machine learning techniques. Appl. Comput. Geosci. 2025, 26, 100250. [Google Scholar] [CrossRef]
- Lu, X.-Q.; Tian, J.; Liao, Q.; Xu, Z.-W.; Gan, L. CNN-LSTM based incremental attention mechanism enabled phase-space reconstruction for chaotic time series prediction. J. Electron. Sci. Technol. 2024, 22, 100256. [Google Scholar] [CrossRef]
- Chen, H.; Wang, K.; Zhao, M.; Chen, Y.; He, Y. A CNN-LSTM-attention based seepage pressure prediction method for Earth and rock dams. Sci. Rep. 2025, 15, 12960. [Google Scholar] [CrossRef]
- Tayeh, T.; Aburakhia, S.; Myers, R.; Shami, A. An Attention-Based ConvLSTM Autoencoder with Dynamic Thresholding for Unsupervised Anomaly Detection in Multivariate Time Series. Mach. Learn. Knowl. Extr. 2022, 4, 350–370. [Google Scholar] [CrossRef]
- Qazi, H.; Kaushik, B.N. A Hybrid Technique using CNN LSTM for Speech Emotion Recognition. Int. J. Eng. Adv. Technol. 2020, 9, 1126–1130. [Google Scholar] [CrossRef]
- Borre, A.; Seman, L.O.; Camponogara, E.; Stefenon, S.F.; Mariani, V.C.; Coelho, L.d.S. Machine Fault Detection Using a Hybrid CNN-LSTM Attention-Based Model. Sensors 2023, 23, 4512. [Google Scholar] [CrossRef] [PubMed]
- Wahid, A.; Breslin, J.G.; Intizar, M.A. Prediction of Machine Failure in Industry 4.0: A Hybrid CNN-LSTM Framework. Appl. Sci. 2022, 12, 4221. [Google Scholar]
- Gamaleldin, W.; Attayyib, O.; Alnfiai, M.M.; Alotaibi, F.A.; Ming, R. A hybrid model based on CNN-LSTM for assessing the risk of increasing claims in insurance companies. PeerJ Comput. Sci. 2025, 11, e2830. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, Y.; Yang, F.; Peng, W. State of health estimation of lithium-ion battery with automatic feature extraction and self-attention learning mechanism. J. Power Sources 2023, 556, 232466. [Google Scholar] [CrossRef]
- Ouyang, J.; Lin, Z.; Hu, L.; Fang, X. Voltage faults diagnosis for lithium-ion batteries in electric vehicles using optimized graphical neural network. Sci. Rep. 2025, 15, 27328. [Google Scholar] [CrossRef]
- Shi, D.; Zhao, J.; Wang, Z.; Zhao, H.; Wang, J.; Lian, Y.; Burke, A.F. Spatial-Temporal Self-Attention Transformer Networks for Battery State of Charge Estimation. Electronics 2023, 12, 2598. [Google Scholar] [CrossRef]
- Hussein, H.M.; Esoofally, M.; Donekal, A.; Rafin, S.M.S.H.; Mohammed, O. Comparative Study-Based Data-Driven Models for Lithium-Ion Battery State-of-Charge Estimation. Batteries 2024, 10, 89. [Google Scholar] [CrossRef]
- Yamashita, R.; Nishio, M.; Do, R.K.G.; Togashi, K. Convolutional neural networks: An overview and application in radiology. Insights Imaging 2018, 9, 611–629. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A search space odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2222–2232. [Google Scholar] [CrossRef] [PubMed]
- Madani, S.S.; Ziebert, C.; Vahdatkhah, P.; Sadrnezhaad, S.K. Recent Progress of Deep Learning Methods for Health Monitoring of Lithium-Ion Batteries. Batteries 2024, 10, 204. [Google Scholar] [CrossRef]
- IEC 62660-1; Secondary Lithium-Ion Cells for the Propulsion of Electric Road Vehicles—Part 1: Performance Testing. International Electrotechnical Commission: Geneva, Switzerland, 2018.
- IEC 62660-2; Secondary Lithium-Ion Cells for the Propulsion of Electric Road Vehicles—Part 2: RELIABILITY and Abuse Testing. International Electrotechnical Commission: Geneva, Switzerland, 2018.
- GB/T 36972-2018; Lithium-Ion Battery for Electric Bicycle. Administration for Market Regulation of the People’s Republic of China. Standardization Administration of the People’s Republic of China: Beijing, China, 2018.
- Lee, J.; Wang, L.; Jung, H.; Lim, B.; Kim, D.; Liu, J.; Lim, J. Deep Neural Network with Anomaly Detection for Single-Cycle Battery Lifetime Prediction. Batteries 2025, 11, 288. [Google Scholar] [CrossRef]
- Goldstein, M.; Uchida, S. A Comparative Evaluation of Unsupervised Anomaly Detection Algorithms for Multivariate Data. PLoS ONE 2016, 11, e0152173. [Google Scholar] [CrossRef]
- Mejri, N.; Lopez-Fuentes, L.; Roy, K.; Chernakov, P.; Ghorbel, E.; Aouada, D. Unsupervised anomaly detection in time-series: An extensive evaluation and analysis of state-of-the-art methods. Expert Syst. Appl. 2024, 256, 124922. [Google Scholar] [CrossRef]
- González-Muñiz, A.; Díaz, I.; Cuadrado, A.A.; García-Pérez, D.; Pérez, D. Two-step residual-error based approach for anomaly detection in engineering systems using variational autoencoders. Comput. Electr. Eng. 2022, 101, 108065. [Google Scholar] [CrossRef]
- Lachekhab, F.; Benzaoui, M.; Tadjer, S.A.; Bensmaine, A.; Hamma, H. LSTM-Autoencoder Deep Learning Model for Anomaly Detection in Electric Motor. Energies 2024, 17, 2340. [Google Scholar] [CrossRef]
- Massey, F.J., Jr. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Peyré, G.; Cuturi, M. Computational optimal transport: With applications to data science. Found. Trends® Mach. Learn. 2019, 11, 355–607. [Google Scholar] [CrossRef]
- Jaccard, P. Étude comparative de la distribution florale dans une portion des Alpes et des Jura. Bull. Soc. Vaudoise Sci. Nat. 1901, 37, 547–579. [Google Scholar]
- Real, R.; Vargas, J.M. The probabilistic basis of Jaccard’s index of similarity. Syst. Biol. 1996, 45, 380–385. [Google Scholar] [CrossRef]

| Type | Parameter | Description |
|---|---|---|
| Discharging Features | batV | Discharge voltage |
| batI | Discharge current | |
| temp1 | Temperature sensor 1 | |
| temp2 | Temperature sensor 2 | |
| useUpWh | Accumulated discharge energy | |
| dischargeHTemp | Maximum discharge temperature | |
| dischargeLTemp | Minimum discharge temperature | |
| shortCircuitCount | Number of short circuits | |
| Charging Features | batteryU | Charging voltage |
| batteryI | Charging current | |
| batterySoc | State of charge | |
| batteryUseUpWh | Accumulated charging energy | |
| temp | Temperature sensor | |
| chargeState | Charging state | |
| chargeStatus | Charging mode | |
| safePower | Safe power |
| Feature Type | KS Statistic | Wasserstein Distance | 95% Threshold |
|---|---|---|---|
| Discharging | 0.1027 | 0.004900 | 0.0776 |
| Charging | 0.1104 | 0.002440 | 0.1399 |
| Feature Type | Method | KS Statistic | Wasserstein Distance |
|---|---|---|---|
| Discharging | AE | 0.0030 | 0.0000 |
| IF | 0.0035 | 0.0002 | |
| OCSVM | 0.0032 | 2.0140 | |
| ADTC-Transformer | 0.1426 | 0.0132 | |
| AM-MFF | 0.1752 | 0.0107 | |
| Charging | AE | 0.0046 | 0.0001 |
| IF | 0.0036 | 0.0003 | |
| OCSVM | 0.0056 | 2.0703 | |
| ADTC-Transformer | 0.1203 | 0.0095 | |
| AM-MFF | 0.1801 | 0.0088 |
| Battery ID | Charging Features | Discharging Features | Overall Alarm Rate | ||
|---|---|---|---|---|---|
| Threshold | Alarm Rate | Threshold | Alarm Rate | ||
| 342421544 | 0.0776 | 4.88% | 0.1399 | 5.04% | 4.96% |
| 342425605 | 0.0776 | 5.16% | 0.1399 | 5.27% | 5.21% |
| 342429831 | 0.0776 | 5.00% | 0.1399 | 5.17% | 5.09% |
| Battery ID | Type | AE | IF | OCSVM | ADTC | AM-MFF |
|---|---|---|---|---|---|---|
| 342421544 | Discharging | 2.34% | 3.96% | 2.54% | 5.86% | 6.03% |
| Charging | 1.47% | 4.23% | 1.70% | 6.74% | 8.61% | |
| 342425605 | Discharging | 5.70% | 6.47% | 4.97% | 6.55% | 7.10% |
| Charging | 0.41% | 2.31% | 1.00% | 6.59% | 6.61% | |
| 342429831 | Discharging | 10.89% | 2.65% | 7.34% | 7.76% | 7.06% |
| Charging | 1.97% | 6.38% | 2.13% | 7.68% | 6.82% | |
| Overall Alarm Rate | 3.80% | 4.33% | 3.28% | 6.87% | 7.04% | |
| Battery ID | Type | P50 | P90 | P95 | P99 | Max | Remarks |
|---|---|---|---|---|---|---|---|
| 342421544 | Overall | 0.0371 | 0.0612 | 0.0745 | 0.1013 | 0.2824 | Right-skewed distribution with moderate tail |
| Discharging | 0.0743 | Close to threshold | |||||
| Charging | 0.1400 | Slightly above threshold | |||||
| 342425605 | Overall | 0.0380 | 0.0631 | 0.0766 | 0.1048 | 0.2975 | Right-skewed distribution with short tail |
| Discharging | 0.0764 | Close to threshold | |||||
| Charging | 0.1406 | Slightly above threshold | |||||
| 342429831 | Overall | 0.0375 | 0.0618 | 0.0749 | 0.1025 | 0.2896 | Right-skewed distribution with high concentration |
| Discharging | 0.0748 | Below threshold | |||||
| Charging | 0.1398 | Close to threshold |
| Battery ID | Type | Top 1% | Top 5% |
|---|---|---|---|
| 342421544 | Discharging | 0.928591 | 0.840445 |
| Charging | 0.676273 | 0.580456 | |
| 342425605 | Discharging | 0.896721 | 0.841555 |
| Charging | 0.766108 | 0.609360 | |
| 342429831 | Discharging | 0.810942 | 0.885450 |
| Charging | 0.616240 | 0.697611 |
| Battery ID | Type | Method | Top 1% | Top 5% |
|---|---|---|---|---|
| 342421544 | Discharging | IF | 0.5941 | 0.7005 |
| OCSVM | 1.0000 | 1.0000 | ||
| AE | 0.6484 | 0.8050 | ||
| ADTC-Transformer | 0.8131 | 0.8097 | ||
| AM-MFF | 0.8706 | 0.8213 | ||
| Charging | IF | 0.3531 | 0.4963 | |
| OCSVM | 1.0000 | 1.0000 | ||
| AE | 0.2850 | 0.2791 | ||
| ADTC-Transformer | 0.4693 | 0.4386 | ||
| AM-MFF | 0.4661 | 0.4868 | ||
| 342425605 | Discharging | IF | 0.4627 | 0.7303 |
| OCSVM | 1.0000 | 1.0000 | ||
| AE | 0.4960 | 0.7884 | ||
| ADTC-Transformer | 0.7766 | 0.8027 | ||
| AM-MFF | 0.8148 | 0.8014 | ||
| Charging | IF | 0.4229 | 0.5367 | |
| OCSVM | 1.0000 | 1.0000 | ||
| AE | 0.2468 | 0.3561 | ||
| AM-MFF | 0.4801 | 0.5606 | ||
| CNN-LSTM-AM | 0.8109 | 0.8854 | ||
| 342429831 | Discharging | IF | 0.6066 | 0.5896 |
| OCSVM | 1.0000 | 1.0000 | ||
| AE | 0.5401 | 0.5736 | ||
| ADTC-Transformer | 0.7977 | 0.8098 | ||
| AM-MFF | 0.8030 | 0.8456 | ||
| Charging | IF | 0.4231 | 0.6407 | |
| OCSVM | 1.0000 | 1.0000 | ||
| AE | 0.3565 | 0.5719 | ||
| ADTC-Transformer | 0.4029 | 0.4537 | ||
| AM-MFF | 0.5432 | 0.5252 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Ye, W.; Mao, Y.; Sui, Y. A Hybrid CNN–LSTM–Attention Mechanism Model for Anomaly Detection in Lithium-Ion Batteries of Electric Bicycles. Batteries 2025, 11, 384. https://doi.org/10.3390/batteries11100384
Sun Z, Ye W, Mao Y, Sui Y. A Hybrid CNN–LSTM–Attention Mechanism Model for Anomaly Detection in Lithium-Ion Batteries of Electric Bicycles. Batteries. 2025; 11(10):384. https://doi.org/10.3390/batteries11100384
Chicago/Turabian StyleSun, Zhaoyang, Weiming Ye, Yuxin Mao, and Yuan Sui. 2025. "A Hybrid CNN–LSTM–Attention Mechanism Model for Anomaly Detection in Lithium-Ion Batteries of Electric Bicycles" Batteries 11, no. 10: 384. https://doi.org/10.3390/batteries11100384
APA StyleSun, Z., Ye, W., Mao, Y., & Sui, Y. (2025). A Hybrid CNN–LSTM–Attention Mechanism Model for Anomaly Detection in Lithium-Ion Batteries of Electric Bicycles. Batteries, 11(10), 384. https://doi.org/10.3390/batteries11100384







