Online Parameter Identification of a Fractional-Order Chaotic System for Lithium-Ion Battery RC Equivalent Circuit Using a State Observer

Abstract

Due to the highly nonlinear, dynamic, and slowly time-varying nature of lithium-ion batteries (LIBs) during operation, achieving accurate and real-time parameters online identification in first-order RC equivalent circuit models (ECMs) remains a significant challenge, including low accuracy and poor real-time performance. This paper establishes a fractional-order chaotic system for first-order RC-ECM based on a charge-controlled memristor. The system exhibits chaotic behavior when parameters are tuned. Then, based on the principle of the state observer, an identification observer is designed for each unknown parameter of the first-order RC-ECM, achieving online identification of these unknown parameters of the first-order RC-ECM of LIB. The proposed method addresses key limitations of traditional parameter identification techniques, which often rely on large sample datasets and are sensitive to variations in ambient temperature, road conditions, load states, and battery chemistry. Experimental validation was conducted under the HPPC, DST, and UDDS conditions. Using the actual terminal voltage of a single cell as a reference, the identified first-order RC-ECM parameters enabled accurate prediction of the online terminal voltage. Comparative results demonstrate that the proposed state observer achieves significantly higher accuracy than the forgetting factor recursive least squares (FFRLS) algorithm and Kalman filter (KF) algorithm, while offering superior real-time performance, robustness, and faster convergence.

1. Introduction

With the rapid development of society, the imbalance between petroleum resource supply and demand has reached increasingly prominent, unprecedented levels. Concurrently, the combustion of fossil fuels releases significant quantities of harmful gases, contributing to global warming and frequent smog events, which in turn exert a profound negative impact on the global environment and human health. In alignment with the strategy for the sustainable and green development strategy, countries worldwide are actively advancing the adoption and development of renewable energy sources. Consequently, large-scale energy storage technologies have recently become an effective solution to mitigate the intermittency and instability of renewable energy [1,2]. With advantages such as a simple design, high cycle life, cost-effectiveness, and high stability, LIBs have gained significant research interest in energy storage. Their extensive adoption in China’s automotive, medical, and aerospace sectors is driving a substantial reduction in oil dependence and fostering a greener energy structure [3]. Nevertheless, LIBs are highly susceptible to safety issues such as overheating, overcharging, and over-discharging during operation, which not only seriously compromise battery performance but also present serious risks to human life and safety. To mitigate these risks, a corresponding battery management system (BMS) is essential for the secure implementation of power batteries. As a consequence, real-time monitoring of battery voltage, current, and temperature during operation and charging is essential, along with accurate estimation of key state variables such as state of charge (SOC), state of power (SOP), state of energy (SOE), and state of health (SOH), and effective management of the charging and discharging processes. Accurate online identification of battery model parameters can significantly enhance the precision of state estimation and ensure the safety of battery charging and discharging, thereby emerging as one of the core technologies in BMS research [4,5,6].

Currently, commonly used battery models include electrochemical models, black box models, and ECMs. The electrochemical model is developed based on the fundamental electrochemical principles governing battery behavior. However, this model mainly relies on experimentally determined parameters, which may exhibit significant uncertainties and variability [7]. Moreover, parameter values reported by different researchers under varying conditions may differ substantially, thereby further increasing the model’s uncertainty [8,9]. The black-box model is constructed from test data reflecting the external characteristics of the battery, which is generally regarded as a data-driven approach since it does not account for internal electrochemical reactions.

Representative techniques include fuzzy logic models, artificial neural network models, and support vector machine models [10,11]. However, black-box models are highly sensitive to noise and outliers in the input data, which may result in unreliable predictions. Owing to the lack of transparency, black-box models are difficult to apply in practical applications [12,13]. ECM employs electrical components such as resistors, capacitors, and inductors to simulate the battery’s dynamic characteristics. This approach provides an intuitive model structure, simplicity in design, low computational load, and ease of interpretation. Moreover, it can be calculated using electrical element operation formulas [14,15,16]. In current research on ECMs, many scholars usually adopt integer-order characteristics in the process of studying ECMs, while they seldom use a fractional-order approach to describe the nonlinear characteristics of RC-ECM. Additionally, the integer-order ECM is merely a special case among mathematical models and is difficult to fully describe the nonlinear dynamic characteristics inside LIBs, which inevitably limits the accuracy of the ECM. In contrast, the fractional-order ECM can effectively reflect the internal reaction mechanism of LIBs [17]. Therefore, to enhance the accuracy of battery modeling, this paper employs a fractional-order approach to establish a first-order RC-ECM and applies it to parameter identification.

Accurately obtaining the parameters of the battery ECM is crucial for improving the accuracy of battery state estimation and enhancing operational safety [18]. With precise ECM parameters, the internal voltage drop of the battery can be accurately calculated with high accuracy. Subsequently, the voltage method enables the real-time and accurate estimation of SOC and other key variables, such as SOH and SOP. Furthermore, the remaining driving range of an electric vehicle can be estimated, thereby enhancing vehicle stability and driving safety. In battery thermal management, identified ECM parameters enable the calculation of heat generation and accurate prediction of the surface temperature, ensuring operation within a safe temperature range. Therefore, accurate identification of ECM parameters has become a major research focus [19,20]. Parameter identification methods for ECM of LIB are generally classified into time-domain and frequency-domain methods. The most representative frequency-domain method is the electrochemical impedance spectroscopy (EIS) [21]. Additionally, the distribution of relaxation times (DRT) method can more precisely distinguish the voltage drop caused by each polarization in the frequency domain, and then allocate a reasonable time constant for each polarization loss. Accordingly, Zhou et al. [22] combined the DRT method with a physical-based impedance model to separate solid-phase and liquid-phase diffusion polarization drop. However, the frequency-domain analysis method requires excitation signals ranging from fractions of a hertz to the megahertz range. Currently, on-board BMS cannot meet this requirement, making continuous identification during battery operation infeasible. Furthermore, while this method has been mainly applied to SOH estimation in laboratory settings, it has not yet been adopted for practical ECM parameter estimation [23]. In contrast, time-domain methods identify ECM parameters by relying solely on instantaneous voltage and current measurements, without specialized excitation signals. As a result, they are more practical and easier to implement than frequency-domain methods, leading to broader real-world applications [23]. Time-domain methods are generally classified into model-based and data-driven methods. Under the given expected indicators, the model-based methods usually select the best parameter values in the specified dataset according to certain principles, so that the performance indicators of the system output reach the optimal level. Typical examples include the extended Kalman filter (EKF) [24], particle swarm optimization (PSO) [25], and recursive least squares (RLS) [26]. For instance, reference [27] proposed a least squares method using eigenvalue addition/deletion with a forgetting factor and applied it to the online identification of ECM parameters of LIBs. Reference [28] estimated the parameters of lithium-ion battery packs in real time online using an adaptive stabilizer. Compared with the earlier adaptive stabilizers, no offline experiments in the early stage or subsequent data processing of the experiments were required. However, the aforementioned model-based approaches are prone to local optima and often fail to achieve real-time online parameter identification. The identification accuracy is constrained by the model accuracy, and it suffers drawbacks such as slow convergence speed, poor robustness, and limited estimation accuracy [29]. Data-driven methods mine the mapping between intrinsic battery measurement features (e.g., current, voltage, temperature, and internal resistance) and model parameters. They directly estimate battery model parameters from the dataset. Typical techniques include long short-term memory (LSTM) networks [30], support vector machines (SVMs) [31], gated recurrent unit (GRU) networks [32], and improved crow-top bird optimization algorithms [33]. For example, Chun et al. [34] designed a deep neural network (DNN) for real-time parameter identification of LIBs, comprising an LSTM network and two fully connected layers. The inputs consist of voltage, current, temperature, and state of charge, while the outputs correspond to the identified parameters. As demonstrated, data-driven approaches offer the advantage of operating without requiring an explicit battery model and are often more effective than electrochemical models. However, accurate estimation relies on high-quality measurement data, and model training remains highly time-consuming. Moreover, the effective integration of data-driven models with optimization strategies continues to pose a significant challenge [35].

A review of the literature reveals a lack of research on the online parameter identification of first-order RC-ECMs for LIBS; the on-board BMS cannot meet this requirement of the frequency-domain analysis method, which requires input of excitation signals ranging from fractions of a hertz to the megahertz range. The frequency-domain analysis method is usually conducted in a laboratory environment, but it cannot be used for actual systems for estimating ECM parameters. While data-driven models are heavily reliant on high-quality measurement data for accurate estimation, and their training is additionally characterized by significant time consumption, the model-based approaches are prone to local optima and lack real-time and online parameter identification capability. Furthermore, the accuracy of model-based identification is inherently limited by the model’s accuracy. In order to solve the above problems and achieve the real-time accurate parameters of the battery, in this paper, electronic components such as memristors are used as the external load of the first-order RC-ECM to construct a fourth-order hyperchaotic system. Then, the unknown parameter identification state observer of the first-order RC-ECM is designed by using the unknown parameter identification theory of chaotic systems. The online, real-time, and accurate identification of unknown parameters of the first-order RC-ECM is realized. Finally, the validity and accuracy of the state observer designed in this paper are verified by using MATLAB R2016b software. The key contributions of this paper are as follows.

(1)

A fractional-order chaotic system of first-order RC-ECM for LIBs was established by combining charge-controlled memristors and electronic components, such as inductors and capacitors. The nonlinear characteristics of this fractional-order chaotic system were analyzed.

(2)

A state observer is constructed and applied to identify these unknown parameters of the fractional-order chaotic system of first-order RC-ECM for LIB, enabling real-time online parameter estimation of the first-order RC-ECM for LIB.

(3)

The real-time performance, accuracy, and robustness of the state observer proposed in this paper were verified under different environmental temperatures through HPPC, DST, and UDDS operating conditions.

This research investigates whether the proposed memristor-based battery model can more accurately capture the nonlinear voltage hysteresis and state-dependent dynamics than traditional ECMs. The validity of this hypothesis was verified by comparing the model’s voltage prediction accuracy and parameter identification robustness with those of the FFRLS and KF algorithms under dynamic stress test conditions. Section 2 of this paper establishes the first-order RC-ECM chaotic system and discusses its dynamic characteristics. Section 3 of this paper covers the theoretical framework for identifying unknown parameters within the first-order RC-ECM chaotic system. Section 4 of this paper applies this identification framework to estimate the parameters of the first-order RC-ECM. Section 5 of this paper provides the experimental results and a detailed performance analysis. Finally, Section 6 concludes the paper.

2. Establishment of First-Order RC-ECM Fractional-Order Chaotic System

2.1. Fractional Calculus

Fractional calculus provides a generalized mathematical framework that unifies differentiation and integration operations, extending the concept of calculus from integer orders to fractional orders. This concept of fractional calculus was first proposed in the 17th century in correspondence between L. Hopital and Leibniz. Initially, its practical adoption was long hindered by the lack of physical interpretation and computational tools. Over the past two decades, with advancements in computational capabilities, fractional calculus has been increasingly applied in practical engineering.

The most commonly used definitions of fractional calculus primarily fall into three categories [36]: Riemann–Liouville (R-L) fractional integral and derivative definition, Caputo fractional derivative definition, and G-L fractional calculus definition. In this paper, the first-order RC-ECM fractional mathematical model of the LIB is established by using Caputo’s fractional differentiation.

Caputo’s fractional-order differential is defined as follows [37]:

$${}_r{}^{}D_t^{\alpha }f(t)={\displaystyle \frac{1}{\Gamma (\alpha -n)}}{\displaystyle {\int }_r^t\frac{f^n(\tau )}{{(t-\tau )}^{\alpha -n+1}}d\tau }(n-1\le \alpha \le n)$$

(1)

where the operator ${}_r{}^{}D_t^{\alpha }$ denotes the fractional-order calculus operation, r, t are the upper and lower limits of the integral; $\alpha$ is the fractional-order, and $\Gamma (•)$ is the Gamma function.

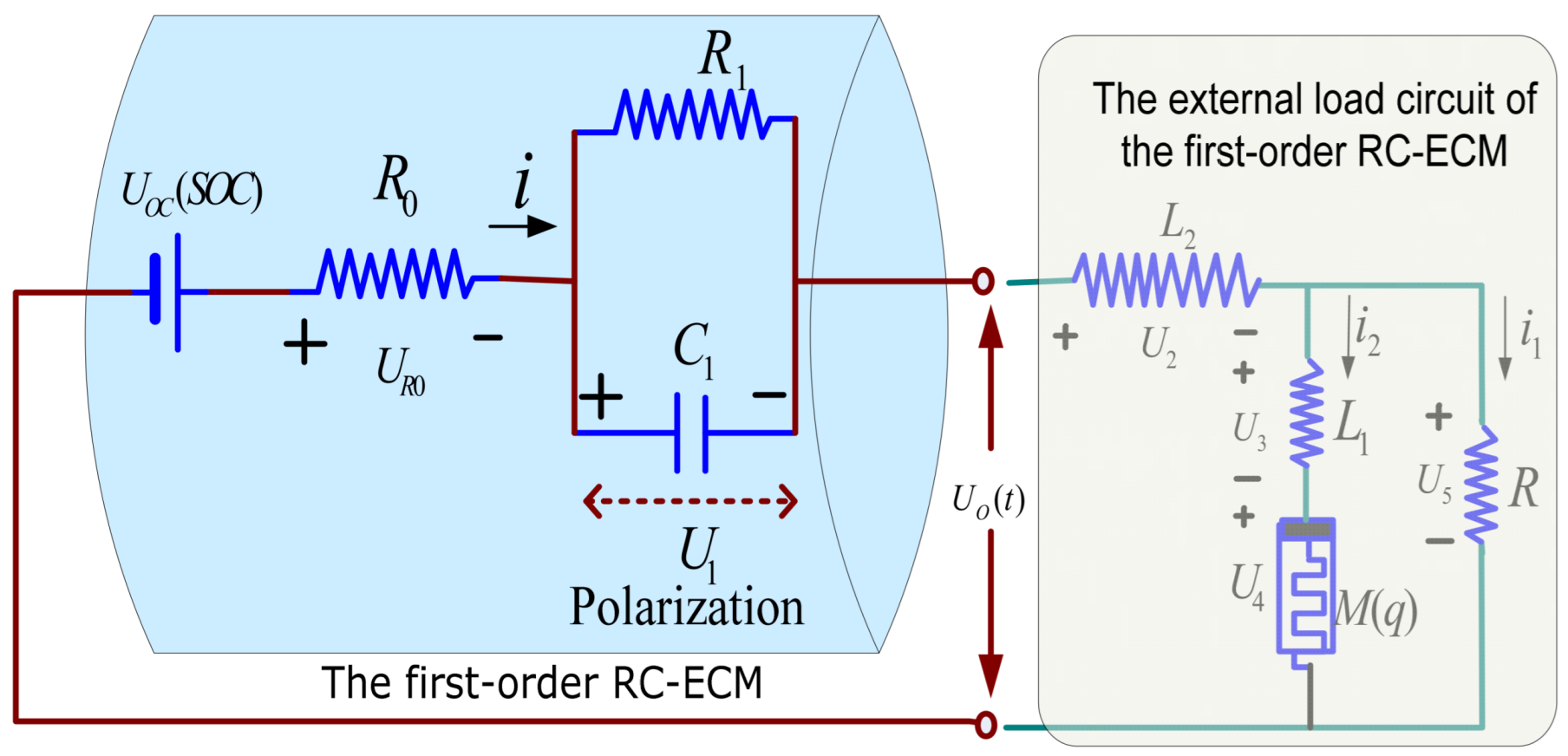
2.2. First-Order RC-ECM Fractional-Order Model

With its simple structure and capability for real-time online parameter identification and online identification of model parameters, ECM is widely adopted to describe the internal dynamics characteristics of LIBs. Given its simple mathematical formulation, high accuracy, and suitability for online parameter identification, the first-order RC-ECM is selected in this study to represent LIB’s dynamic characteristics; this choice effectively balances the trade-offs between model complexity, accuracy, and robustness. The fractional-order mathematical model of the first-order RC-ECM is formulated using Caputo’s fractional differential [38], as shown in Equation (2), and its schematic representation is shown in Figure 1. In the subsequent research, we applied the fractional-order chaotic system proposed in this research to the online parameter identification of second-order RC-ECM or third-order RC-ECM to further verify the robustness of the state observer.

$$\left\{\begin{array}{l}{}_0{}^{}D_t^{\alpha }{U}_1(t)={\displaystyle \frac{1}{C_1}}i(t)-{\displaystyle \frac{U_1(t)}{C_1{R}_1}}\hfill \\ U_0(t)=U_{oc}(SOC)-i(t)R_0-U_1(t)\hfill \end{array}\right.$$

(2)

where U_oc is the open-circuit voltage of the first-order RC-ECM; U₀(t) is the terminal voltage; R₁ is the polarization resistance of LIB; R₀ is the ohmic internal resistance of LIB; and C₁ is the polarization capacitor. $\alpha$ is the fractional-order number of C₁, $\alpha \in (0,1)$.

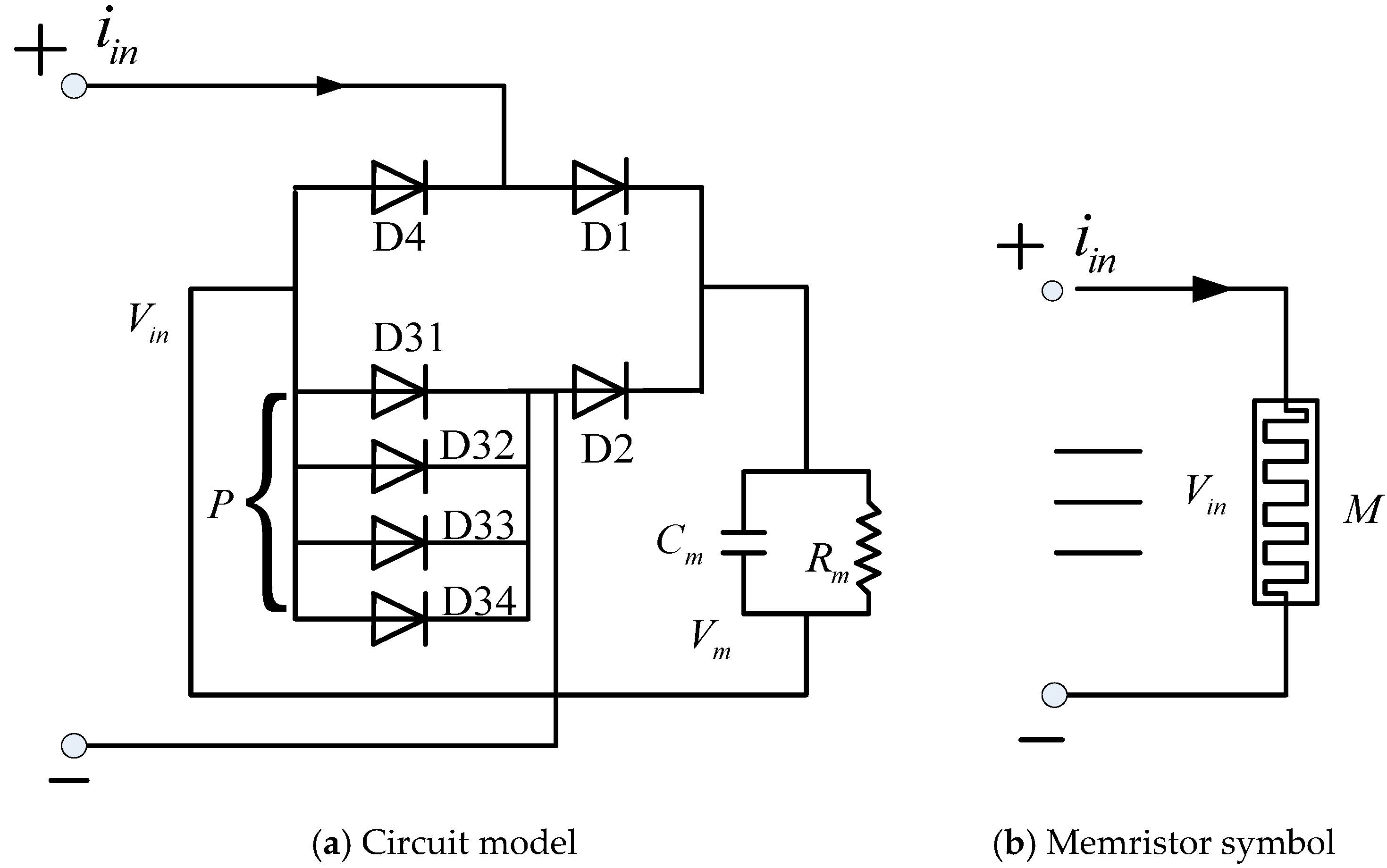
2.3. First-Order RC-ECM Fractional-Order Chaotic System Based on Memristors

The postulation of the memristor as the fourth fundamental two-terminal circuit element was first made by Professor Leon Chua in 1971, derived from the symmetry relationship between magnetic flux and charge [39]. From its theoretical inception, it was not until 2008 that a practical nanoscale device was fabricated and announced by researchers at HP Laboratories [40]. Memristors [41,42], characterized by non-volatility, memory, and low power consumption, are passive nonlinear devices with considerable application potential in computer storage, intelligent computing, and nonlinear simulation. Furthermore, this inherent nonlinearity also allows them to serve as the core component in chaotic circuits (e.g., charge- or magnetic-controlled [43]), generating a wide range of complex dynamic behaviors. The high cost and technical challenges of producing nanoscale memristors impede their commercialization, keeping much of the research confined to laboratories. However, to overcome these barriers, circuit-based memristor emulation has emerged as a key strategy to unlock their practical value. Following the design in Ref. [44], an asymmetric diode bridge memristor emulator is implemented and applied to the parameter identification of a fractional-order chaotic system in a first-order RC-ECM. The asymmetrical diode bridge memristor model is shown in Figure 2, where D1, D2, D4, D31, D32, D33, and D34 are diodes, respectively, i_in is the input current, V_in is the input voltage, and P is the number of series diodes.

Since this research mainly focuses on realizing the nonlinear variation characteristics of the memristor through charge variation rather than magnetic flux change, the memristor is connected as a load to the first-order RC-ECM of the battery for experimental convenience, as shown in Figure 3. L₁ and L₂ are two inductor coils of different sizes; R is the resistance; M_(q) is a load-controlled memristor; U₁ is the voltage across the terminals of C₁; U₂ is the voltage across the terminals of L₂; U₃ is the voltage across the terminals of L₁; U₄ is the voltage across the terminals of M_(q); U₅ is the voltage across the terminals of R; i is the current flowing through R; i₁ is the current flowing through R; and i₂ is the current flowing through M_(q). The mathematical model of the gain memristance M(q) of the hysteresis-controlled memristor is given as follows:

$$M(q)={\displaystyle \frac{d\phi (q)}{dt}}=a+3d{q}^2$$

(3)

where a and d are constants, and a < 0, d > 0.

Assuming the specified direction as the reference current direction of the current in the circuit, and in accordance with Kirchhoff’s law [45], the system satisfies Equation (4):

$$\left\{\begin{array}{l}i=i_1+i_2\hfill \\ u_{oc}=u_{R0}+u_1+u_2+u_5\hfill \\ u_5=u_3+u_4\hfill \end{array}\right.$$

(4)

Based on the voltage–current relationships of various electronic components (e.g., resistors and memristors), the system of differential equations corresponding to the model in Figure 2 can be derived:

$$\left\{\begin{array}{l}{L}_1{\displaystyle \frac{d{i}_2}{dt}}=R{i}_1-M(q)i_2\hfill \\ L_2{\displaystyle \frac{di}{dt}}=u_{oc}-R_{0}i-u_1-R{i}_1\hfill \\ C_1{\displaystyle \frac{d{u}_1}{dt}}=i-{\displaystyle \frac{u_1}{R_1}}\hfill \\ {\displaystyle \frac{dq}{dt}}=i_2\hfill \end{array}\right.$$

(5)

where the value of the memresistor $M(q)$ is $M(q)=a+3d{q}^2$, and $q={\displaystyle \int i_{2}dt}$. Substituting $i_1=i-i_2$ into Equation (5) and considering $\dot{x}={\dot{i}}_2,\dot{y}=\dot{i},\dot{z}={\dot{u}}_1,\dot{w}=\dot{q},u_{oc}=0$ (take $x,y,z,w$ as four state variables), this yields the following:

$$\left\{\begin{array}{l}\dot{x}={\displaystyle \frac{1}{L_1}}(Ry-(R+M(w))x)\hfill \\ \dot{y}={\displaystyle \frac{1}{L_2}}(Rx-(R_0+\mathrm{R})\mathrm{y}-z)\hfill \\ \dot{z}={\displaystyle \frac{1}{C_1}}(y-{\displaystyle \frac{z}{R_1}})\hfill \\ \dot{w}=x\hfill \end{array}\right.$$

(6)

Let $\rho ={\displaystyle \frac{1}{L_1}},\beta ={\displaystyle \frac{1}{L_2}},\gamma ={\displaystyle \frac{1}{C_1}}$, then the system can be represented as follows:

$$\left\{\begin{array}{l}\dot{x}=\rho (Ry-(R+M(w))x)\hfill \\ \dot{y}=\beta (Rx-(R_0+\mathrm{R})\mathrm{y}-z)\hfill \\ \dot{z}=\gamma (y-{\displaystyle \frac{z}{R_1}})\hfill \\ \dot{w}=x\hfill \end{array}\right.$$

(7)

With the parameters in the mathematical model of the fourth-order chaotic system dynamics, Equation (7), specified as $\rho =8.6,\beta =1.1,\mathrm{R}=1.12$, where $M(q)$: $a=-1.34,d=0.46$, and defining $A=1.1\times R_0,B=\gamma ,E={\displaystyle \frac{\gamma }{R_1}}$, the system equations derived from Equation (7) can be expressed as follows:

$$\left\{\begin{array}{l}\dot{x}=9.804(y-x)-8.6(-1.34+1.2w^2)x\hfill \\ \dot{y}=1.254(x-y)-Ay-1.1z\hfill \\ \dot{z}=By-Dz\hfill \\ \dot{w}=x\hfill \end{array}\right.$$

(8)

where A = 1.1 × R₀, and $B=\gamma ={\displaystyle \frac{1}{C_1}}$, $D={\displaystyle \frac{\gamma }{R_1}}={\displaystyle \frac{1}{R_1{C}_1}}$.

According to Caputo’s definition of fractional derivatives, the fractional-order counterpart of the above fourth-order hyperchaotic system can be formulated as follows:

$$\left\{\begin{array}{l}{\displaystyle \frac{d^{\theta }x}{d{t}^{\theta }}}=9.804(y-x)-8.6(-1.34+1.2w^2)x\hfill \\ {\displaystyle \frac{d^{\theta }y}{d{t}^{\theta }}}=1.254(x-y)-Ay-1.1z\hfill \\ {\displaystyle \frac{d^{\theta }z}{d{t}^{\theta }}}=By-Dz\hfill \\ {\displaystyle \frac{d^{\theta }w}{d{t}^{\theta }}}=x\hfill \end{array}\right.$$

(9)

From Equation (9), the unknown parameters of the constructed first-order RC-ECM chaotic system based on the memristor are A, B, and D, where A is linearly related to the ohmic resistance R₀, B is the reciprocal of the polarization capacitance, D is the reciprocal of the product of the polarization resistance and the polarization capacitance, and the corresponding state variables are x, y, z and w.

When A = 0.25, B = 14.26, D = 0.09, θ = 0.98, and the initial state vector is set to (0.0, 0.01, 0.0, 0.0), the experiment is performed using MATLAB with the fourth-order Longacurta method and a step size of 0.01. The phase trajectory plots and time-domain waveforms of the system are presented in Figure 4. The experimental results indicate that the system modeled by Equation (9) produces a double vortex chaotic attractor, characteristic of a fourth-order hyperchaotic system [46,47].

3. Dynamic Characteristics Analysis of First-Order RC-ECM Fractional-Order Chaotic Systems

3.1. System Equilibrium Point Analysis

The equilibrium point of the system [48], defined by ${\displaystyle \frac{d^{\theta }x}{d{t}^{\theta }}}={\displaystyle \frac{d^{\theta }y}{d{t}^{\theta }}}={\displaystyle \frac{d^{\theta }z}{d{t}^{\theta }}}={\displaystyle \frac{d^{\theta }w}{d{t}^{\theta }}}=0$, is obtained from Equation (9) as (0, 0, 0, 0). By substituting these equilibrium points, the Jacobian matrix J_A of the system at the equilibrium points can be derived as follows:

$$J_A=\left[\begin{array}{cccc}1.72& 9.804& 0& 0\\ 1.254& -(1.254+A)& -1.1& 0\\ 0& B& D& 0\\ 1& 0& 0& 0\end{array}\right]$$

(10)

Then $A=0.36,B=14.26,D=0.16$, according to $\det \left|\lambda I-J_A\right|=0$; the characteristic equation of the system at the equilibrium point can be expressed as

$${\lambda }^3-0.266{\lambda }^2+0.6327\lambda -24.57=0$$

(11)

The eigenvalues of J_A at the equilibrium point (0, 0, 0, 0) can be given by:

$$\left\{\begin{array}{l}{\lambda }_1=2.92\hfill \\ {\lambda }_2=-1.33+2.58i\hfill \\ {\lambda }_3=-1.33-2.58i\hfill \\ {\lambda }_4=0\hfill \end{array}\right.$$

(12)

Based on the linear stability theorem, the equilibrium point is identified as an unstable saddle-focus. As a result, the system trajectories tend to either approach a limit cycle, evolve into a chaotic attractor, or diverge to infinity.

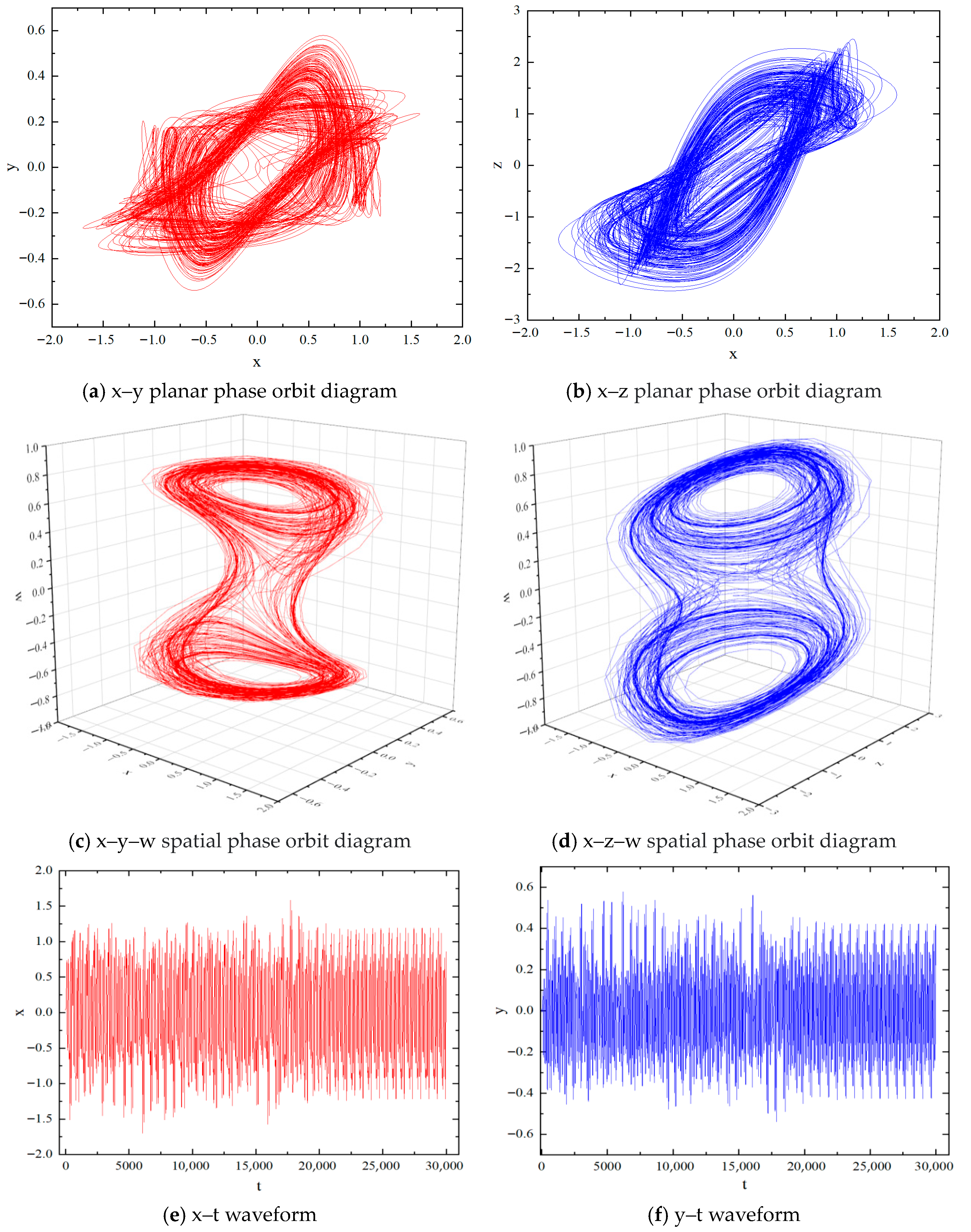
3.2. System Dissipation and Attractor Existence Analysis

To assess whether a chaotic system exhibits dissipation, the divergence of its vector field is commonly used as the criterion [49,50]. The divergence is expressed as

$$\Delta V={\displaystyle \frac{\partial \dot{x}}{\partial x}}+{\displaystyle \frac{\partial \dot{y}}{\partial y}}+{\displaystyle \frac{\partial \dot{z}}{\partial z}}+{\displaystyle \frac{\partial \dot{\omega }}{\partial \omega }}=-9.804+8.6\times 1.34-(1.254+A)-D$$

(13)

When A = 0.36 and D = 0.16, the parameters of the fractional-order chaotic dynamics mathematical model in Equation (13) yield $\Delta V=-0.054$, indicating that the system converges according to $V(t)=V(0)e^{-0.054t}$. As $t\to \infty$, each volume element of the trajectory in the fourth-order fractional-order chaotic dynamical system decays to zero at an exponential rate of −0.054, and the trajectory ultimately becomes confined to a specific limit set of zero volume. Therefore, it can be concluded that the attractor of the proposed first-order RC-ECM fractional-order chaotic dynamical mathematical model indeed exists.

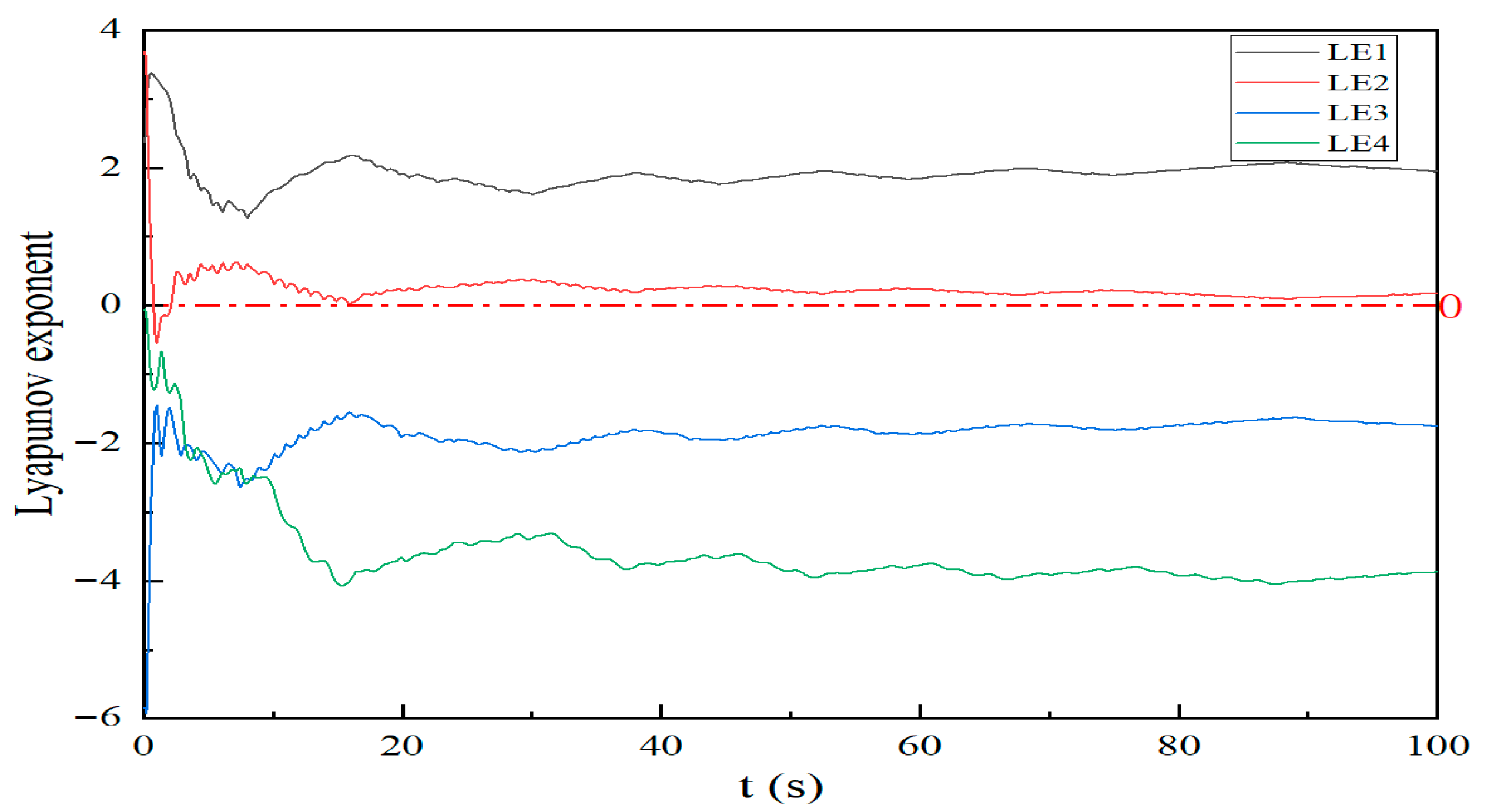
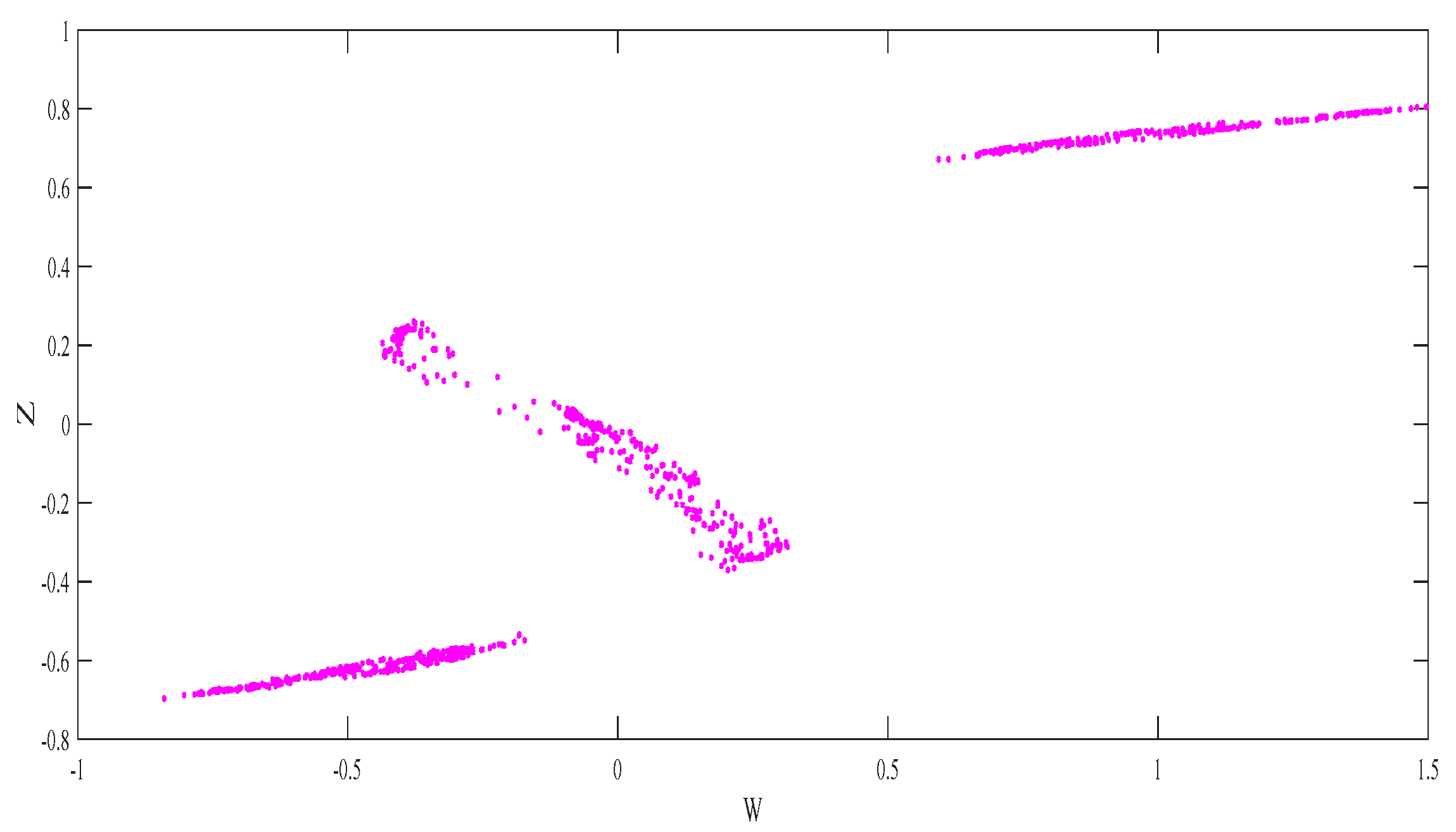
3.3. System Lyapunov Exponent Spectrum Analysis and Poincaré Section

The Lyapunov exponents were computed in MATLAB from the Jacobian matrix of the four-dimensional hyperchaotic system given by Equation (10), As shown in Figure 5, the Lyapunov exponent [51,52] spectrum of the four-dimensional hyperchaotic system proposed is (+, +, −, −), with LE₁ > 0, LE2 > 0, LE3 < 0, LE4 < 0. Based on Equation (9), by using the fifth-order Runge–Kuta method in the MATLAB R2016b software, the Poincaré sections of the four-dimensional chaotic system established at x = 0 and y = 0 in this paper can be obtained. As shown in Figure 5 and Figure 6, the proposed memristor-based first-order RC-ECM chaotic system generates double-vortex attractors, exhibiting rich nonlinear dynamic behaviors, thereby collectively confirming that the system belongs to the category of four-dimensional hyperchaotic systems, which is suitable for using the state observer to conduct online identification of the unknown parameters of the first-order RC-ECM fractional-order chaotic dynamic system.

4. Construction of State Observers for Unknown Parameters of Fractional-Order Chaotic Systems

4.1. Theory of Unknown Parameter Identification Based on Observer

For a class of n dimensional nonlinear chaotic systems [53,54,55,56],

$$\left\{\begin{array}{l}{\dot{x}}_1=F_1(X_1)\hfill \\ {\dot{x}}_2=F_2(X_2)\hfill \\ ⋮\hfill \\ {\dot{x}}_i=F_i(X_i)+{\alpha }_j{G}_i(Y_i)\hfill \\ ⋮\hfill \\ {\dot{x}}_n=F_n(X_n)\hfill \end{array}\right.$$

(14)

where $X={(x_1,x_2,\cdots ,x_n)}^T\in R^n$ is the state variable; $F_i,G_j(\forall i=1,2,\cdots ,n,\forall j\in N)$ is a linear or nonlinear function; $X_i=(x_{i1},x_{i2},\cdots ,x_{i{m}_i}),\forall x_{ij}\in X,i,j\in N,i\le n,$$j\le m_i\le n$, $Y_i=(y_{i1},y_{i2},\cdots ,y_{i{n}_i}),\forall y_{ij}\in X,i,j\in N,i\le n,j\le n_i\le n$ is a set of partial state variables; and $\alpha ={({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_j,\cdots )}^T$ are parameter variables.

Let ${\widehat{\alpha }}_j$ be the identification value of the unknown parameter ${\alpha }_j$, where clearly, ${\dot{\alpha }}_j=0$. From the system (14), there is $-{\alpha }_j{G}_i(Y_i)+x_i-F_i(X_i)=0$. Assume the following:

$${\dot{\widehat{\alpha }}}_j=-l_j(Y_i)G_i(Y_i){\widehat{\alpha }}_j+l_i(Y_i)\left|{\dot{x}}_i-F_i(X_i)\right|$$

(15)

Define the parameter error as ${\dot{e}}_j={\widehat{\alpha }}_j-{\alpha }_j$, so there is

$${\dot{e}}_j=-l_i(Y_i)G_i(Y_i)e_j$$

(16)

where l_i(Y_i) is a gain function that is designed; however, usually, it is very difficult to predict x_i. Therefore, it is impossible to be exploited. To overcome the aforementioned shortcomings, auxiliary variables are defined as follows:

$$\left\{\begin{array}{ll}{p}_i={\widehat{\alpha }}_j+{\varphi }_j(Y_i),\hfill & x_i\in Y_i\hfill \\ p_j={\widehat{\alpha }}_j+{\varphi }_j(Y_i,x_i),\hfill & x_i\notin Y_i\hfill \end{array}\right.$$

(17)

where ${\varphi }_j(Y_i)$ is an auxiliary function designed at $x_i\in Y_i$ and ${\varphi }_j(Y_i,x_i)$ is an auxiliary function designed at $x_i\notin Y_i$. They all satisfy ${\displaystyle \frac{\partial {\varphi }_j}{\partial x_i}}=-l_j(Y_i)$, as discussed above. When $x_i\in Y_i$ and $x_i=y_{ik}$, and when $x_i\notin Y_i$, respectively,

$$\begin{array}{l}{\dot{p}}_i=l_i(Y_i)\{[{\varphi }_j(Y_i)-p_j]G_i(Y_i)-F_i(X_i)\}+\\ {\displaystyle \frac{\partial {\varphi }_j}{\partial y_{i1}}}{\dot{y}}_{i1}+\cdots +{\displaystyle \frac{\partial {\varphi }_j}{\partial y_{i(k-1)}}}{\dot{y}}_{i(k-1)}+{\displaystyle \frac{\partial {\varphi }_j}{\partial y_{i(k+1)}}}{\dot{y}}_{i(k+1)}+\cdots +{\displaystyle \frac{\partial {\varphi }_j}{\partial y_{i{n}_i}}}{\dot{y}}_{i{n}_i}\end{array}$$

(18)

$$\begin{array}{l}{\dot{p}}_j=l_j(Y_i)\{[{\varphi }_j(Y_i,x_i)-p_j]G_i(Y_i)-F_i(X_i)\}+\\ {\displaystyle \frac{\partial {\varphi }_j}{\partial y_{i1}}}{\dot{y}}_{i1}+{\displaystyle \frac{\partial {\varphi }_j}{\partial y_{i2}}}{\dot{y}}_{i2}+\cdots +{\displaystyle \frac{\partial {\varphi }_j}{\partial y_{i{n}_i}}}{\dot{y}}_{i{n}_i}\end{array}$$

(19)

Equations (17)–(19) can quickly identify unknown parameters. The gain function $l_j(Y_i)$ can be selected as $l_j(Y_i)=k_j{(G_i(Y_i))}^{2n_j-1}$, where $k_j>0,n_j\in N$. Therefore, the error system can be written as

$${\dot{e}}_j(t)=-k_j{(G_i(Y_i))}^{2n_j}{e}_j(t)$$

(20)

although $G_i(Y_i)$ cannot approach zero. However, there is ${\displaystyle {\int }_0^{+\infty }{k}_j}{(G_i(Y_i))}^{2n_j}dt\to +\infty$; hence,$\underset{t\to +\infty }{\lim }‖e_j(t)‖=\underset{t\to +\infty }{\lim }‖{\widehat{\alpha }}_j(t)-{\alpha }_j(t)‖=0,\forall j\in N$. Therefore, $l_j(Y_i)$ option $l_j(Y_i)=k_j{G}_i(Y_i)$. The corresponding auxiliary function is

$$\left\{\begin{array}{ll}{\varphi }_j(Y_i)=-k_j{\displaystyle \int G_i}(Y_i)dx,\hfill & x_i\in Y_i\hfill \\ {\varphi }_j(Y_i,x_i)=-k_j{G}_i(Y_i),\hfill & x_i\notin Y_i\hfill \end{array}\right.$$

(21)

It can be obtained again from Equation (17):

$$\left\{\begin{array}{ll}{\widehat{\alpha }}_j=p_i-{\varphi }_j(Y_i),\hfill & x_i\in Y_i\hfill \\ {\widehat{\alpha }}_j=p_j-{\varphi }_j(Y_i,x_i),\hfill & x_i\notin Y_i\hfill \end{array}\right.$$

(22)

The above analysis shows that the nonlinear unknown parameters a_j in the n-dimensional chaotic system defined by Equations (17) and (22) can be identified rapidly and accurately with the proposed approach. However, experimental simulation verifies that when the designed unknown parameter state observer is applied to a non-chaotic system, the parameter error $\underset{t\to +\infty }{\lim }‖e_j(t)‖=\underset{t\to +\infty }{\lim }‖{\widehat{\alpha }}_j(t)-{\alpha }_j(t)‖\ne 0,\forall j\in N$ cannot effectively converge to zero, thus preventing accurate identification.

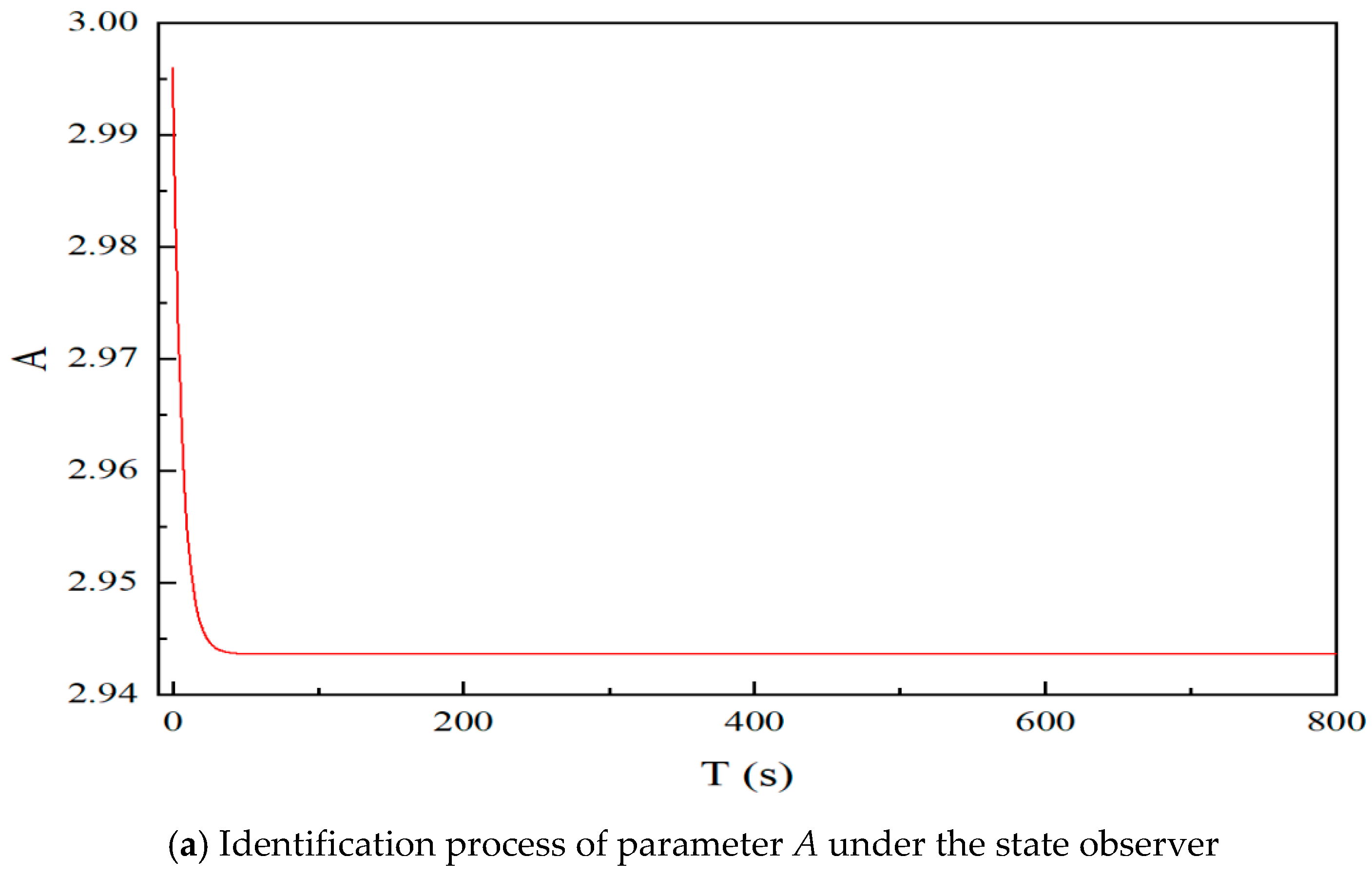
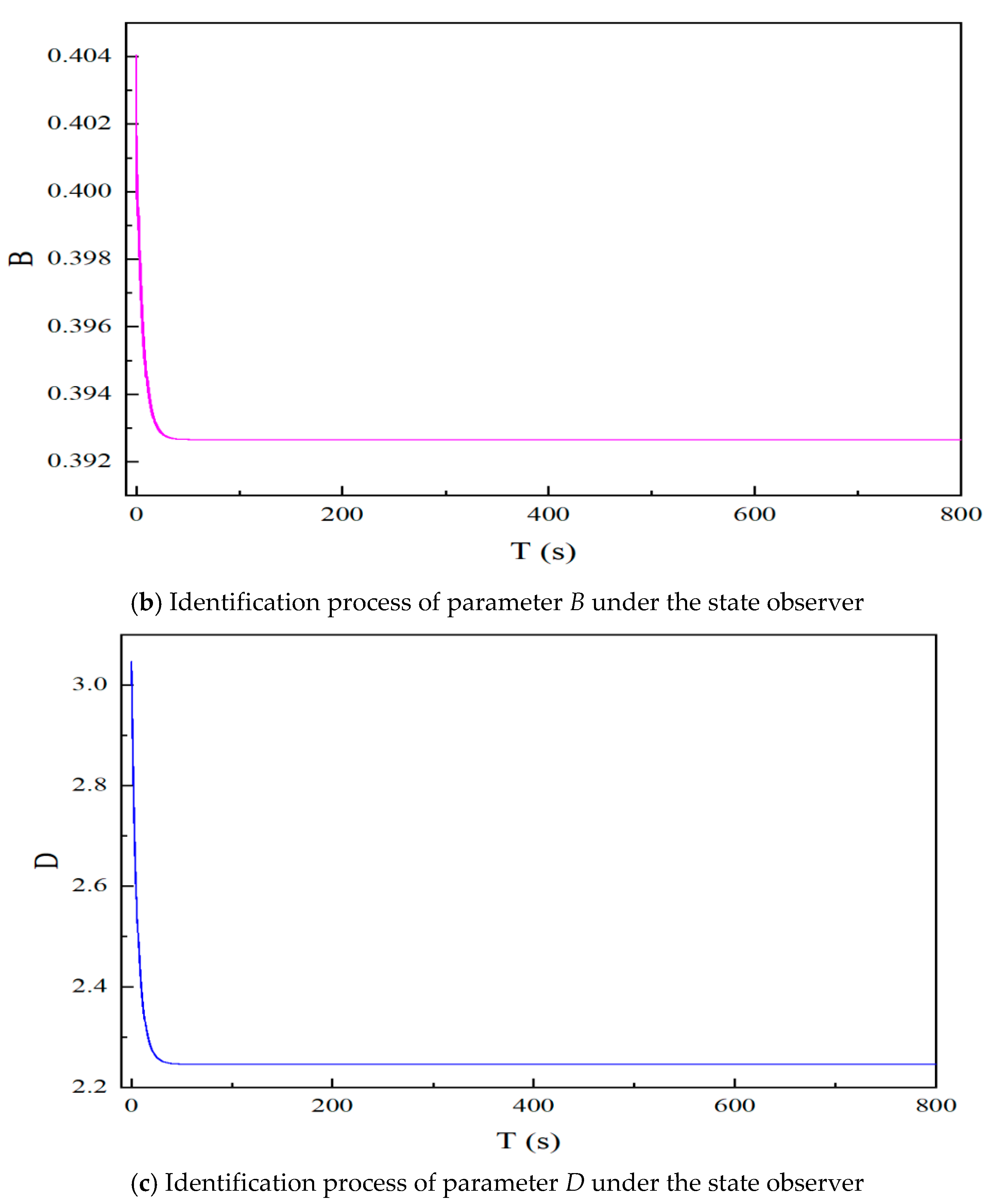
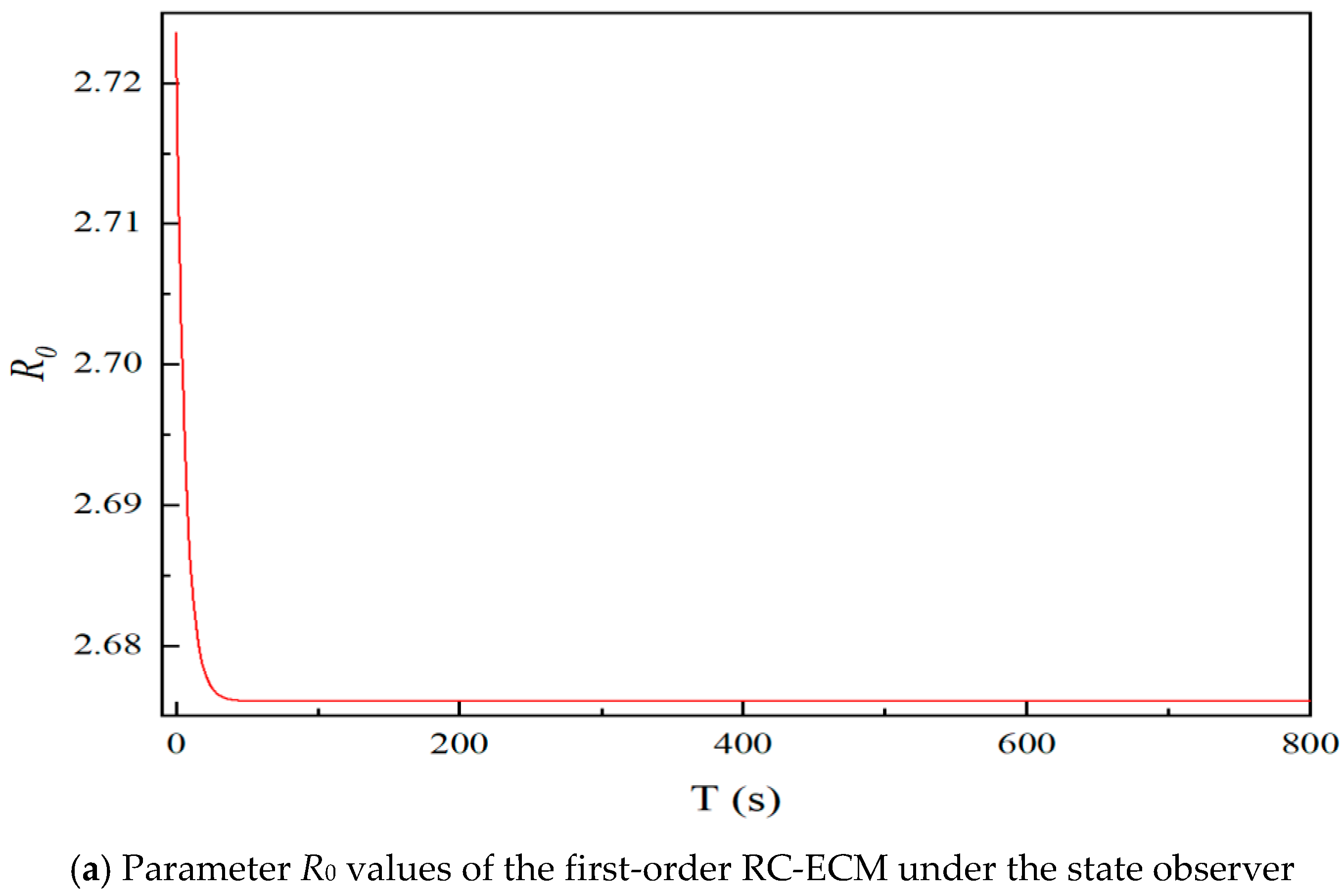
4.2. Construction of State Observer

Given its ability to identify unknown parameters in fractional-order chaotic systems in real time, the state observer [57] offers high timeliness, computational efficiency, and improved real-time performance. The state observer also exhibits fast convergence and good accuracy. For this reason, this research employs a state observer to identify the unknown parameters (R₀, R₁, and C₁) of the first-order RC-ECM within the fourth-order fractional-order chaotic system.

Since the unknown parameters (A, B, and D) in the proposed fractional-order chaotic system demonstrate nonlinear and slow time-varying characteristics, their gain functions can be designed using the state observer theory as follows:

$$l_A\left(y\right)=k_{A}y,l_B(x_2)=k_{B}y,l_D(z)=k_{D}z$$

(23)

Here, $k_A,k_B,k_D$ is the control gain. The corresponding auxiliary function is then designed as

$$\left(\begin{array}{l}{\phi }_1(y)={\displaystyle \frac{1}{2}}{k}_A{y}^2\hfill \\ {\phi }_2(z)=-{\displaystyle \frac{1}{2}}{k}_B{y}^2\hfill \\ {\phi }_3(z)={\displaystyle \frac{1}{2}}{k}_D{z}^2\hfill \end{array}\right.$$

(24)

Based on Equations (23) and (24), a state observer for the unknown parameters of a fractional-order chaotic system can be constructed [58,59,60].

$$\left\{\begin{array}{l}{\dot{p}}_1=-l_A(y)(p_1-{\phi }_1(y))y+l_A(y)(1.254(x-y)-1.1z)\hfill \\ \widehat{A}=p_1-{\phi }_1(y)\hfill \end{array}\right.$$

(25)

$$\left\{\begin{array}{l}{\dot{p}}_2=-l_B(y)(p_2-{\phi }_2(y))y-l_B(y)Dz\hfill \\ \widehat{B}=p_2-{\phi }_2(y)\hfill \end{array}\right.$$

(26)

$$\left\{\begin{array}{l}{\dot{p}}_3=l_D(z)(p_3-{\phi }_3(z))z+l_D(z)By\hfill \\ \widehat{D}=p_3-{\phi }_3(z)\hfill \end{array}\right.$$

(27)

In this study, numerical simulations are conducted to verify the effectiveness of the proposed state observer in identifying the unknown parameters of the fractional-order chaotic system. The state variables are initialized as (0.03, 0.01, 0.09, and 0.10), and the initial estimates for parameters (A, B, and D) are set to (2.995, 0.404, and 3.080). The actual values of the unknown parameters (A, B, and D) in the first-order RC-ECM fractional-order chaotic system of Equation (9) are assumed to be (3.000, 0.400, and 2.300), and all control gains are set to 1. The identified values of unknown parameters (A, B, and D) are obtained as (2.9436, 0.3927, and 2.2465), with corresponding errors from the actual values (3.000, 0.400, and 2.300) being (0.0564, 0.0073, and 0.0535), respectively. The identification curves of the unknown parameters (A, B, and D) are shown in Figure 7. According to Equation (28), the identified values of the first-order RC-ECM parameters R0, R1, and C1 are calculated to be 2.676, 2.5468, and 0.1748, respectively. The errors compared with the actual values of R0, R1, and C1 (2.727, 2.5, and 0.1739) are, respectively, (0.051, −0.0468, and −0.0009), and the identification curve of the first-order RC-ECM parameters R0, R1, and C1 is shown in Figure 8.

$$\left\{\begin{array}{l}{R}_0={\displaystyle \frac{A}{1.1}}\hfill \\ C_1={\displaystyle \frac{1}{\gamma }}={\displaystyle \frac{1}{B}}\hfill \\ R_1={\displaystyle \frac{\gamma }{D}}={\displaystyle \frac{B}{D}}\hfill \end{array}\right.$$

(28)

To further validate the accuracy of the state observer proposed in this paper in identifying unknown parameters of hyperchaotic systems, the memristor parameters (a and d) in Equation (3) are adjusted to a = −1.8 and d = 1, respectively, driving the system into a non-chaotic state. The state variables are initialized as (0.03, 0.01, 0.09, and 0.10), and the initial estimates for parameters (A, B, and D) are set to (2.995, 0.404, and 3.080). Subsequently, the state observer is applied to identify the unknown parameters (R₀, R₁, and C₁) of the first-order RC-ECM, and the identification results are shown in Figure 9. The identified parameters (R₀, R₁, and C₁) of the first-order RC-ECM are calculated as 0.5128, 2.118, and 5.243, respectively. These identified values deviate significantly from the actual values (2.727, 2.5, and 0.1739) when the system is in a non-chaotic state. The result demonstrates that the designed state observer achieves high accuracy in parameter identification for chaotic systems.

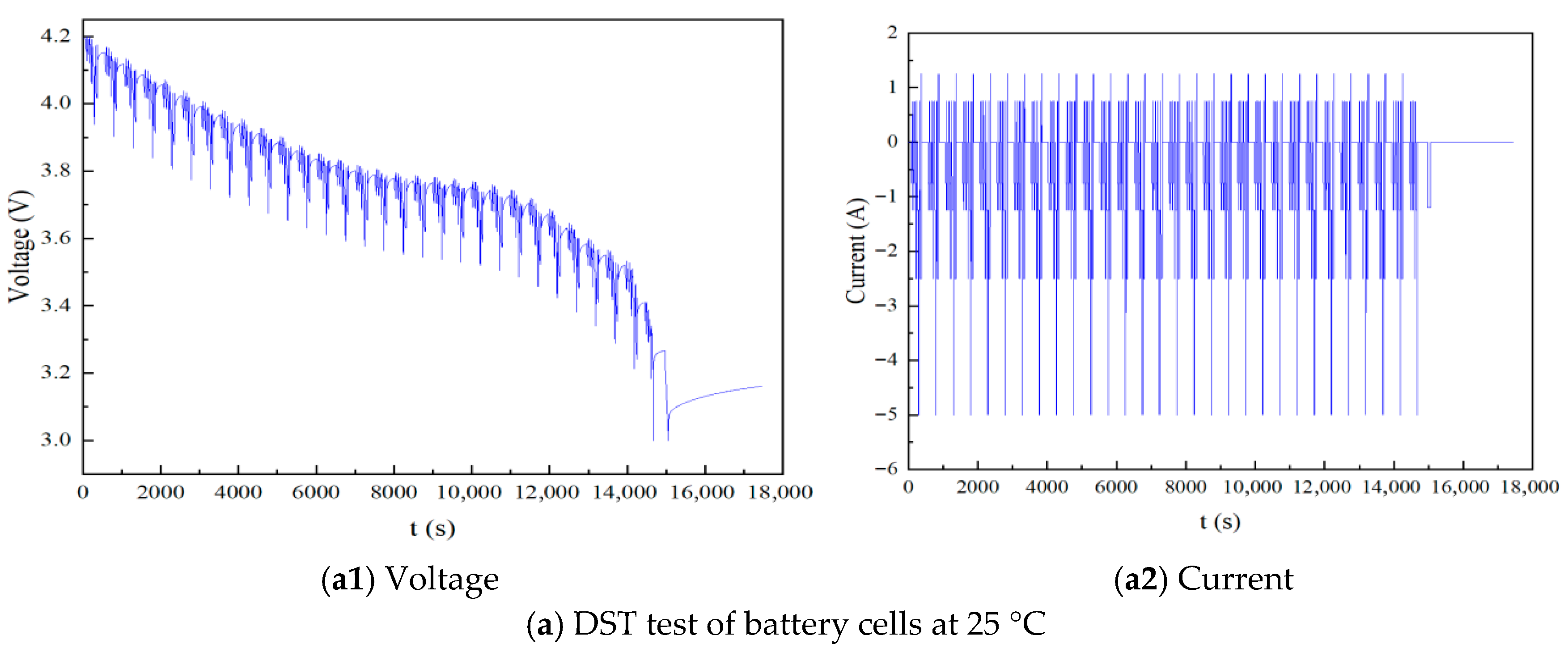
5. Experimental Results

This study applies the state observer, FFRLS, and KF algorithms concurrently for real-time online identification of the unknown parameters in the first-order RC-ECM under HPPC conditions at 25 °C ambient temperature. To rigorously evaluate their accuracy, a comparative analysis of parameter identification performance was conducted under DST conditions under the DST condition at an ambient temperature of 25 °C and the UDDS condition at an ambient temperature of 40 °C.

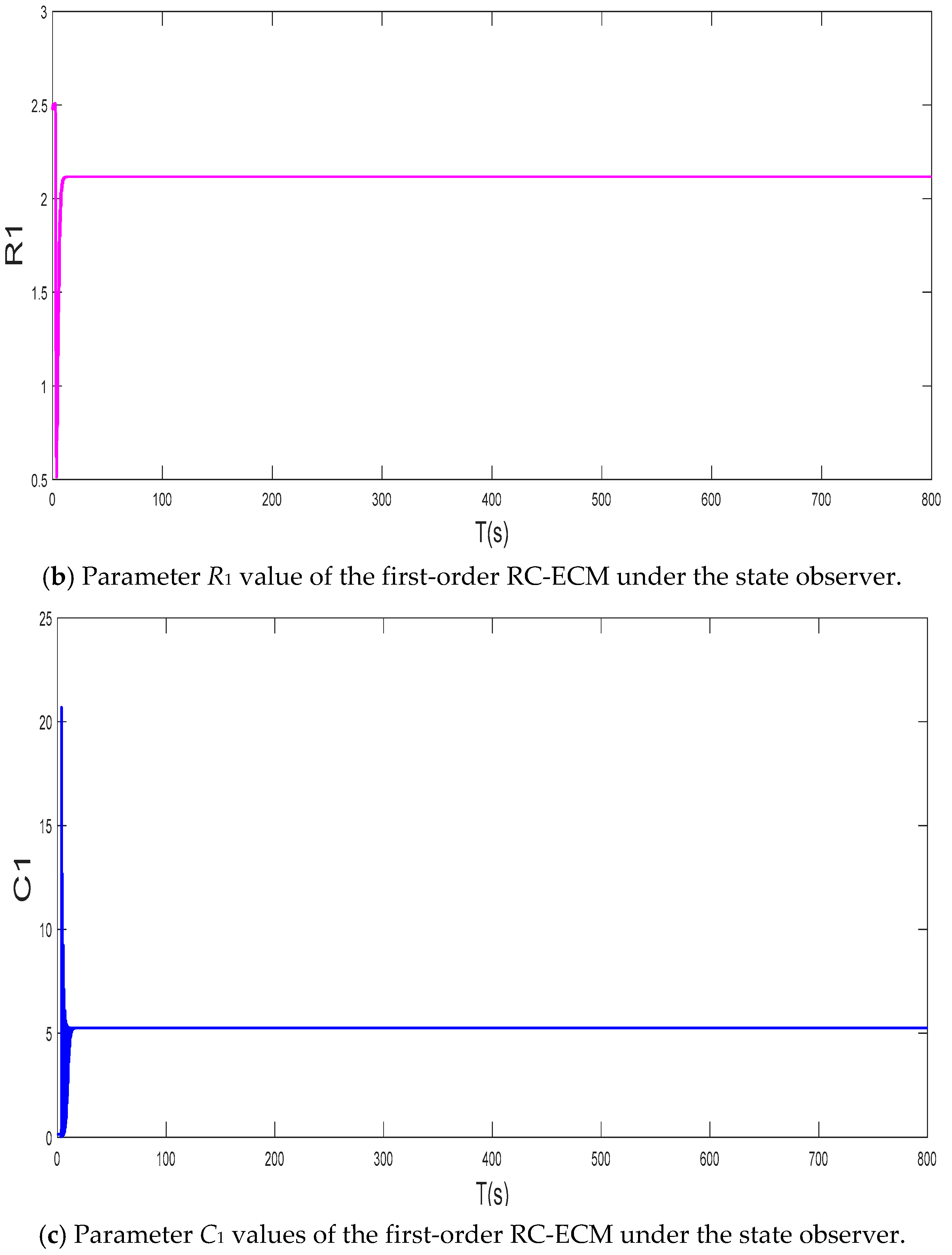
5.1. Experimental Investigation

In this study, under the HPPC condition, the experimental ambient temperature was set to 25 °C. The test object was a Samsung INR18650-20R LIB (Jizhou Technology Co., Ltd., Shenzhen City, China) with a rated capacity of 2000 mAh and a nominal voltage of 3.6 V. The cut-off voltages were set to 4.2 V for charging and 2.5 V for discharging. Real-time tests were carried out using the Arbin BT200 system (ARBIN Instrument Company, College Station, TX, USA). The HPPC operating profile is illustrated in Figure 10, and the detailed procedure is as follows:

First, charge the battery at a constant current of 0.2 C until the voltage reaches 4.2 V, then switch to constant-voltage charging at 4.2 V. The charging process is to be terminated when the current decreases to a cut-off threshold of 0.02 C. Allow the battery to rest for 2 h to migrate polarization effect. Subsequently, discharge the battery at a constant current of 1 C. When the discharged capacity reaches 10% of the nominal capacity, terminate the discharge. At this point, the battery SOC is to be recorded as 0.9.

Perform a sequence of pulse discharges and charges as follows:

(1)

Fully charge the battery, discharge at 1 C to 10% DOD, rest for 40 min, then discharge at 5 C for 10 s, rest for 30 s, and charge for 10 s.

(2)

Fully charge the battery, discharge at 1 C to 20% DOD, rest for 40 min, then discharge at 2 C for 10 s, rest for 30 s, and charge for 10 s.

(3)

Fully charge the battery, discharge at 1 C to 30% DOD, rest for 40 min, then discharge at 2 C for 10 s, rest for 30 s, and charge for 10 s.

(4)

Fully charge the battery, discharge at 1 C to 40% DOD, rest for 40 min, then discharge at 2 C for 10 s, rest for 30 s, and charge for 10 s.

(5)

Fully charge the battery, discharge at 1 C to 50% DOD, rest for 40 min, then discharge at 2 C for 10 s, rest for 30 s, and charge for 10 s.

(6)

Fully charge the battery, discharge at 1 C to 60% DOD, rest for 40 min, then discharge at 2 C for 10 s, rest for 30 s, and charge for 10 s.

(7)

Fully charge the battery, discharge at 1 C to 70% DOD, rest for 40 min, then discharge at 2 C for 10 s, rest for 30 s, and charge for 10 s.

(8)

Fully charge the battery, discharge at 1 C to 80% DOD, rest for 40 min, then discharge at 2 C for 10 s, rest for 30 s, and charge for 10 s.

(9)

Fully charge the battery, discharge at 1 C to 90% DOD, rest for 40 min, then discharge at 2 C for 10 s, rest for 30 s, and charge for 10 s.

During the tests conducted from SOC = 0.9 to SOC = 0.1, data, including voltage, current, charge, and sampling time, were synchronously recorded. The unknown parameters (A, B, and D) for the first-order RC-ECM fractional-order chaotic system were identified by substituting measured data (voltage, current, and charge) into Equation (9), followed by the application of the designed state observers in Equations (25)–(27). Finally, the identification values R₀, R₁, and C₁ of the first-order RC-ECM parameters are calculated and obtained by using Equation (21). The battery terminal voltage was predicted in real-time online by substituting the identified parameters (R₀, R₁, and C₁) into the first-order RC-ECM, and this prediction was subsequently compared with the actual measured voltage. Similarly, the predicted values of the battery terminal voltage of the FFRLS algorithm and the KF algorithm were obtained. Finally, we verified the accuracy of the state observer using the RMSE, MAE, and MAPE between the predicted battery terminal voltage and the actual measured terminal voltage using MATLAB-based graphical simulation. To further validate the robustness of the proposed state observer under different operational and thermal conditions, tests were conducted across multiple drive cycles (HPPC, DST, and UDDS) at two ambient temperatures: 25 °C and 40 °C. This design allows for a comprehensive evaluation of observer performance. The DST operating condition is shown in Figure 11, and the UDDS operating condition is shown in Figure 12.

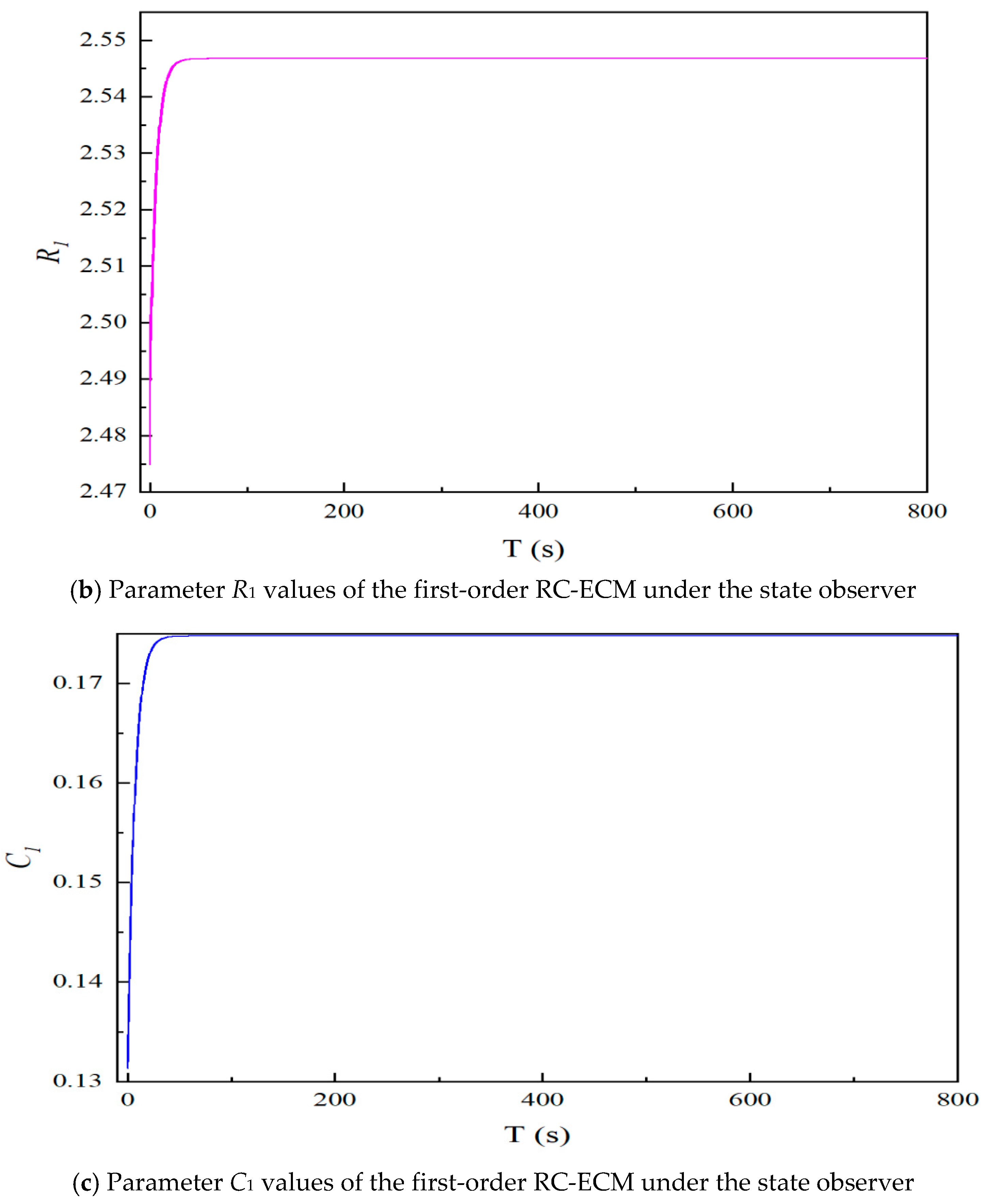
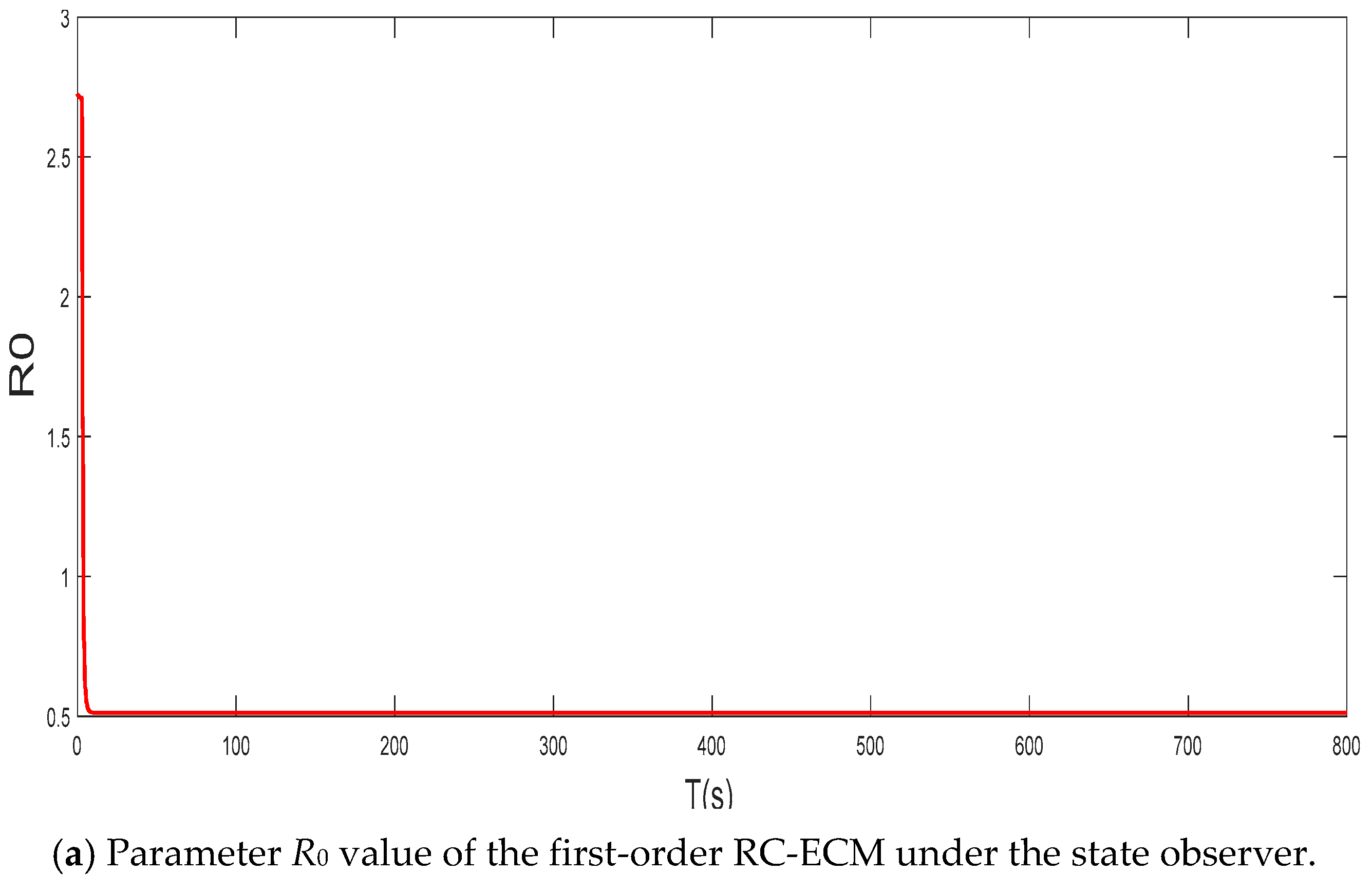
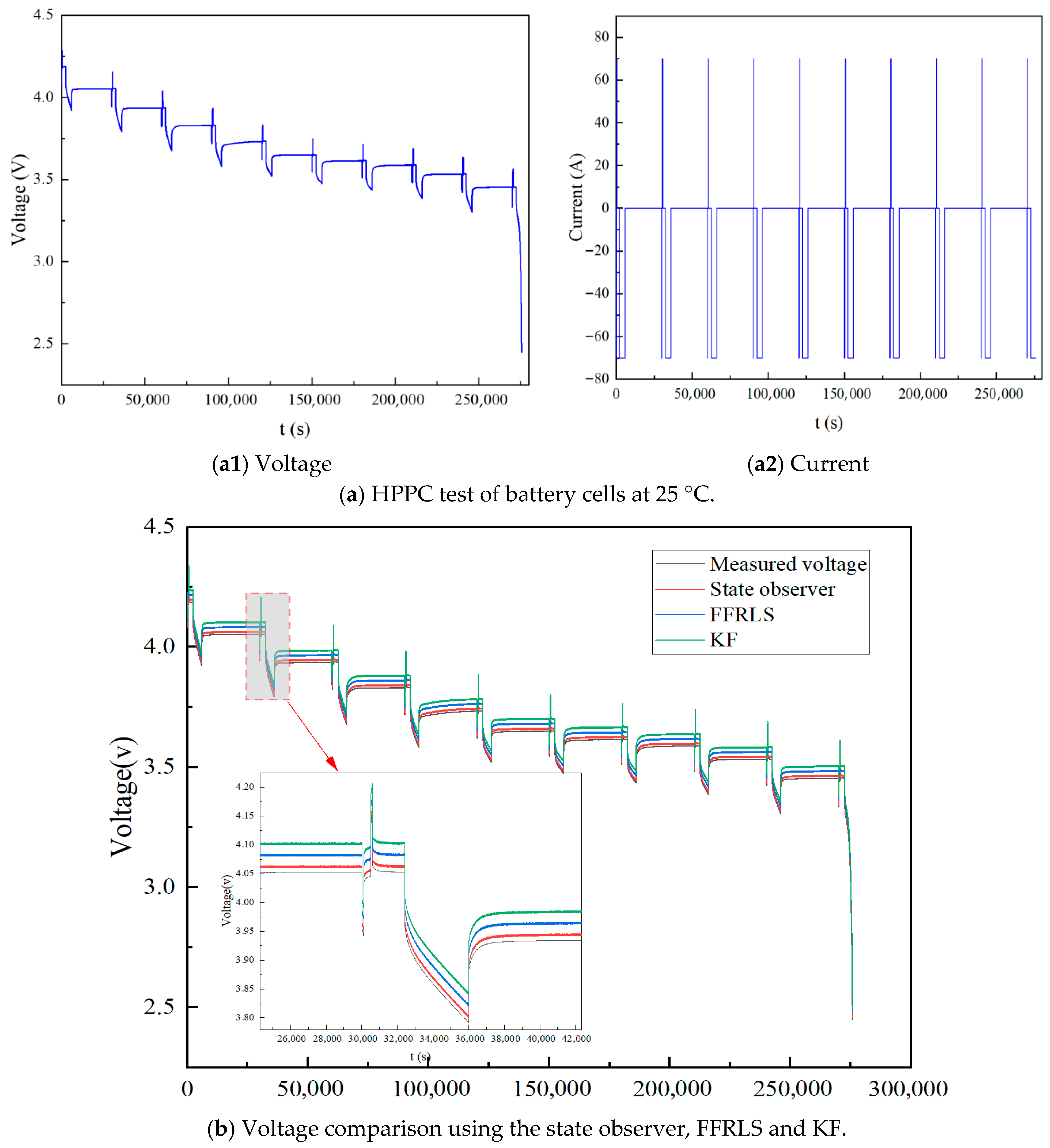
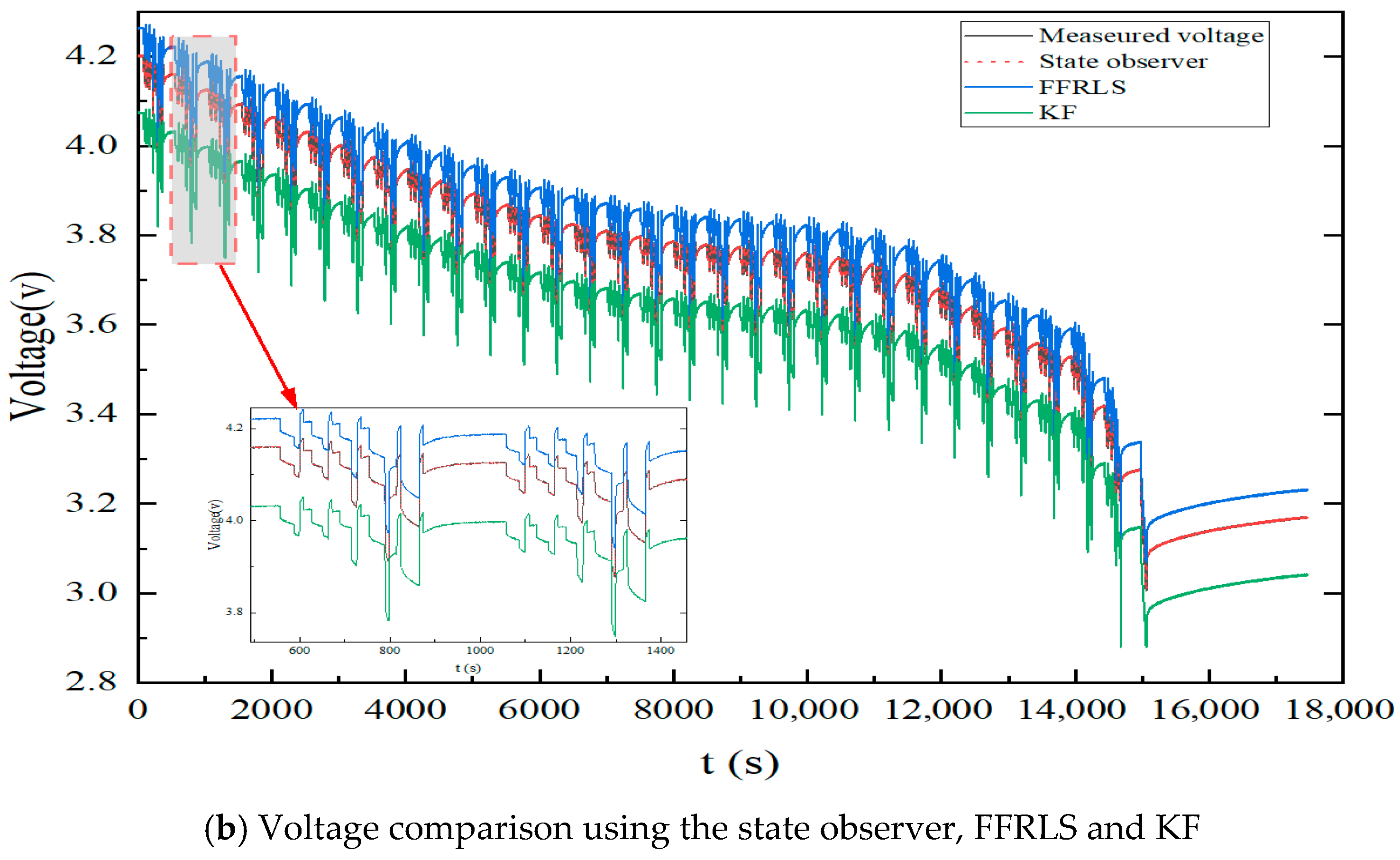
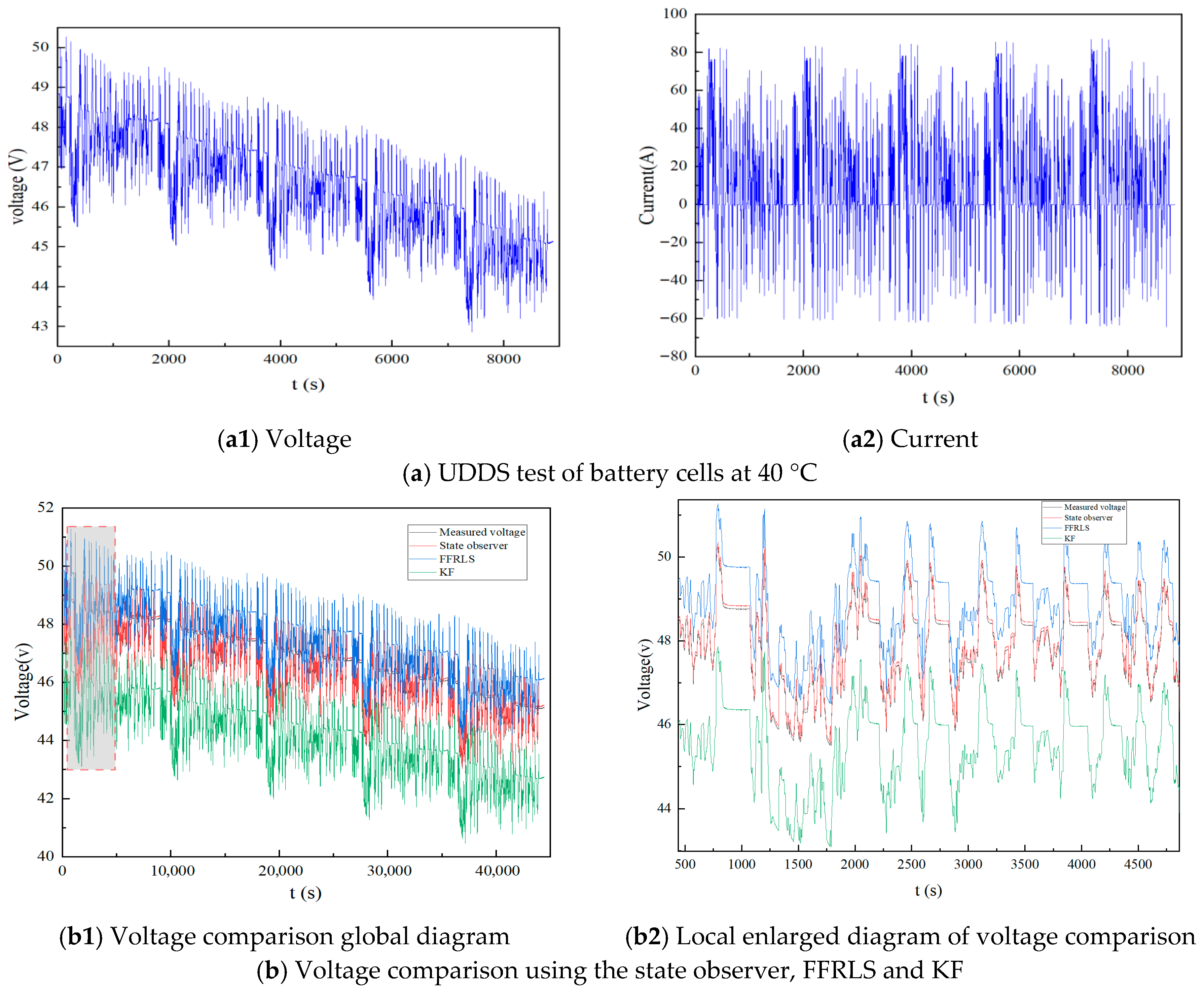
5.2. Analysis of Experimental Results

To quantitatively evaluate the fitting and parameter-identification performance of the proposed state observer for the first-order RC-ECM fractional-order chaotic system, three common metrics RMSE, MAE, and MAPE [61,62] are employed. The definitions of these metrics are given as follows:

$$MAE={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N\left|{\widehat{S}}_i-S_i\right|}$$

(29)

$$RMSE=\sqrt{{\displaystyle \frac{{\displaystyle \sum _{i=1}^N{({\widehat{S}}_i-S_i)}^2}}{N}}}$$

(30)

$$MAPE={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N\left|\frac{{\widehat{S}}_i-S_i}{S_i}\right|}$$

(31)

In the above Equations (29)–(31), $S_i$ denotes the measured value; ${\widehat{S}}_i$ denotes the estimated value; and N denotes the total amount of data.

According to

Table 1. Comparison of identification performance of State observer, FFRLS, and KF algorithm under HPPC, DST, and UDDS conditions of 25 °C and 40 °C.

Identification Model	Temperature in Working Conditions	Mean Relative Error (%)	Mean Absolute Error (mV)	Root Mean Square Error (%)
State observer	HPPC conditions at 25 °C	0.27	1.36	0.34
FFRLS		1.68	27.6	2.78
KF		3.37	67.6	5.49
State observer	DST conditions at 25 °C	0.21	2.36	0.22
FFRLS		1.91	31.2	2.36
KF		3.28	74.9	4.46
State observer	UDDS conditions at 40 °C	0.17	1.62	0.19
FFRLS		2.15	35.9	2.92
KF		3.87	52.8	8.59

, Figure 10, Figure 11 and Figure 12, Under HPPC conditions and 25 °C, Under HPPC conditions at 25 °C, the proposed state observer algorithm yields a mean relative error of 0.27%, which represents a reduction of 1.41 percentage points compared to the FFRLS (1.68%) and 3.1 percentage points compared to the KF (3.37%). Under DST conditions and 25 °C, the proposed state observer exhibits a mean absolute error of 2.36 mV. This represents a substantial improvement, being 28.84 mV lower than the FFRLS (31.2 mV) and 71.54 mV lower than the KF (74.9 mV). Under the UDDS condition and at 40 °C, the proposed state observer yields a root mean square error of 0.19%. This corresponds to a 1.02% reduction compared to the FFRLS (1.21%) and an 8.4% reduction compared to the KF (8.59%). Therefore, these error comparisons demonstrate that the proposed state observer outperforms the FFRLS algorithm and the KF algorithm in identification accuracy. Simultaneously, these results indicate the state observer’s superior nonlinear-fitting capability and robustness, achieving high estimation accuracy when identifying the unknown parameters of the first-order RC-ECM fractional-order chaotic model.

6. Discussion

While the high cost and complexity of manufacturing nanoscale memristors have largely confined their study to the experimental phase, there is a growing need for circuit-based emulators to unlock their commercial potential. In response, this paper presents a memristor-equivalent model built with an asymmetric diode bridge, providing a practical platform for exploring their value. Experimental results demonstrate that the implemented asymmetric diode bridge memristor model is capable of inducing pronounced nonlinear dynamic characteristics in a first-order RC-ECM-based fractional-order chaotic system. Currently, achieving a chaotic state relies on the manual tuning of memristor parameters. Consequently, developing principled parameter adjustment criteria is a key objective for our subsequent work. Meanwhile, the presence of chaotic and hyper-chaotic states is bound to affect key performance aspects of the state observer, such as estimation accuracy, convergence speed, and operational stability. Refining the influence of chaotic and hyper-chaotic states on the performance of the state observer will provide a basis for the improved design of the state observer.

This study implements a charge-controlled memristor, where its nonlinear characteristics are governed by charge rather than flux. In the experimental setup, this memristor is connected as a load to a first-order RC-ECM of LIB. During performance tests under DST, UDDS, and HPPC conditions, no safety issues or incompatibility problems related to the BMS were observed. It was observed through experimentation that the type of ECM selected is of considerable importance. In general, increased ECM complexity, such as in a second-order versus a first-order RC-ECM, yields richer nonlinear dynamic characteristics. However, taking the second-order RC-ECM as an example, compared with the first-order RC-ECM, the addition of an RC branch structure necessarily increases the difficulty of designing a state observer, while consequently imposing greater challenges in achieving fast convergence and high estimation accuracy. Therefore, finding the optimal balance between identification accuracy, robustness, and practical constraints is crucial.

7. Conclusions

In this paper, a fractional-order chaotic system of first-order RC-ECM is proposed. In addition, the parameter identification method of first-order RC-ECM is presented. The following conclusions were drawn:

(1)

A fractional-order hyperchaotic system was developed by integrating a charge-controlled memristor with electronic components (e.g., inductors and capacitors), based on the first-order RC-ECM.

(2)

The parameters of the charge-controlled memristor were tuned to induce chaotic behavior in the system, and the nonlinear dynamic characteristics of the fractional-order hyperchaotic system were thoroughly analyzed. A state observer for unknown parameter estimation in fractional-order chaotic systems was designed and applied for online identification of unknown parameters in the first-order RC-ECM. The validity of the designed state observer was verified through experiments conducted under various driving conditions, including DST, UDDS, and HPPC profiles.

(3)

The experimental validation confirms the superiority of the proposed state observer compared to FFRLS and KF algorithms. It exhibits enhanced superior real-time performance, identification accuracy, and robustness, effectively addressing critical limitations related to sample data size and demonstrating strong resilience against environmental variabilities, including temperature, road conditions, load variations, and battery material properties. To further verify the robustness of the proposed state observer, future work will focus on applying it to parameter identification in second-order or third-order RC-ECMs.