Multi-Timescale Estimation of SOE and SOH for Lithium-Ion Batteries with a Fractional-Order Model and Multi-Innovation Filter Framework

Abstract

Based on a fractional-order equivalent circuit model, this paper proposes a multi-timescale collaborative State of Energy (SOE) and State of Health (SOH) estimation method (FOASTFREKF-EKF) for lithium batteries to mitigate the influence of model inaccuracies and battery aging on SOE estimation. Initially, a fractional-order equivalent circuit model is built, and its parameters are identified offline using the Starfish Optimization Algorithm (SFOA) to establish a high-fidelity battery model. An H∞ filter is then integrated to improve the algorithm’s resilience to external disturbances. Furthermore, an adaptive noise covariance adjustment mechanism is employed to reduce the effect of operational noise, and a time-varying attenuation factor is introduced to improve the algorithm’s tracking and convergence capabilities during abrupt system-state changes. A joint estimator is subsequently constructed, which uses an Extended Kalman Filter (EKF) for the online determination of battery parameters and SOH assessment. This approach minimizes the effect of varying model parameters on SOE accuracy while reducing computational load through multi-timescale methods. Experimental validation under diverse operating conditions shows that the proposed algorithm achieves root mean square errors (RMSE) of less than 0.21% for SOE and 0.31% for SOH. These findings demonstrate that the method provides high accuracy and reliability under complex operating conditions.

1. Introduction

Driven by the global energy system’s transformation towards clean and low-carbon, the popularity of electric vehicles (EVs) is increasing [1,2]. Lithium-ion batteries have become the primary power source for EVs due to their characteristics, including long cycle life, high energy density, and no memory effect [3,4]. However, the complex internal degradation mechanisms of these batteries are highly coupled, nonlinear, and time-varying, which complicates accurate state estimation. Accurately estimating the State of Energy (SOE) and State of Health (SOH) of batteries is crucial for a battery management system (BMS), as it directly influences operational safety, energy management efficiency, and lifetime prediction accuracy [5]. Consequently, high-precision, real-time joint estimation of SOE and SOH is critical for advancing battery management technology.

State of Energy (SOE) is a vital parameter that describes the dynamic charging and discharge process of lithium-ion batteries. It is defined as the ratio of a battery’s remaining energy to its rated energy. According to current research, battery SOE estimate techniques may be broadly divided into three categories: power integration methods, data-driven methods, and model-based methods [6,7,8]. The power integration method determines SOE by cumulatively integrating current over time, benefiting from computational simplicity. However, its reliance on an accurate initial SOE value and sensitivity to cumulative errors restrict its widespread application [9]. In contrast, data-driven methods utilize operational data (e.g., current, voltage) with machine learning algorithms to estimate SOE without an explicit battery model, thereby capturing complex nonlinear relationships. A key drawback, however, is their dependence on large training datasets and potentially limited robustness in unseen scenarios [10,11]. Consequently, model-based methods have garnered a lot of attention due to their simplicity, reliability, and stability. The model-based method achieves precise SOE estimation by fusing high-fidelity battery models with advanced filters, which dynamically correct the system state based on the difference between measured values and model predictions [12].

Based on battery models, the Kalman filter (KF) algorithm has become the mainstream technique for SOE estimation [13,14]. By minimizing the mean square error covariance of the state estimate, the Kalman filter (KF) provides the best unbiased estimation for linear Gaussian systems. It iteratively corrects predictions during operation and exhibits robust convergence even with initial state errors. However, the KF algorithm assumes that system noise statistics are stationary and follow a Gaussian distribution. In real-world battery systems, this assumption is often violated, which can lead to divergence or growing estimation errors due to noise mismatches. Consequently, researchers have developed several improved algorithms [15,16,17,18]. Due to its manageable computational complexity, the EKF has emerged as a common choice for nonlinear SOE estimation. Nevertheless, its performance is highly dependent on model accuracy and the empirical tuning of noise covariance matrices. This limitation necessitates the integration of adaptive mechanisms to ensure robustness across all operating conditions [19].

The accuracy of model-based methods is heavily reliant on how well the model represents the intricate electrochemical behavior of the battery. Therefore, establishing a precise battery model is essential [20]. Battery models are primarily categorized as electrochemical models and equivalent circuit models (ECMs). ECMs represent complex electrochemical systems using circuit-based networks. Despite utilizing only a limited number of electrical components, ECMs can achieve high accuracy and are divided into integer-order models (IOMs) or fractional-order models (FOMs) [21]. FOMs characterize battery dynamics more accurately than IOM, particularly for voltage transients under dynamic and non-equilibrium conditions. For instance, Reference [22] demonstrated that under diverse operating conditions, FOMs capture battery characteristics more accurately, significantly enhancing the precision of terminal voltage estimation. Given these advantages, FOMs are widely utilized for battery state estimation and performance optimization [23].

The accurate estimation of the State of Energy (SOE) is challenged by factors such as noise interference, state limitations, and parameter uncertainty during lithium-ion battery operation [24,25,26]. To address these challenges, several joint estimation methods have been proposed. For instance, Reference [27] presents a method that first updates battery model parameters and capacity in real-time before using UKF for joint SOE-SOH estimation. To mitigate SOE estimation errors caused by declining SOH, Reference [28] utilizes an enhanced dual extended Kalman filter (DEKF) algorithm to estimate SOE and SOH. However, many existing methods struggle with the highly complex nature of battery operation. Focusing on SOE estimation errors induced by environmental temperature and parameter coupling, Reference [25] proposes a collaborative estimation method of SOE and maximum available energy based on an adaptive dual-fractional-order Kalman filter, which improves SOE accuracy by updating the maximum available energy in real time. However, existing methods often lack the responsiveness and adaptability to accommodate shifting operational conditions. Moreover, they frequently fail to systematically address the impact of time-varying noise on the stability and accuracy of filter estimates, which constrains their reliability in real-world applications. This challenge of achieving robust and accurate state estimation under uncertainty is a significant frontier in battery research. As a recent review of energy storage technologies has highlighted, there is growing recognition of the need to augment model-based estimators with adaptive mechanisms. Looking ahead, the integration of multi-physics sensor data will be essential for overcoming inherent limitations and enhancing reliability [29].

To address these gaps and meet the practical requirements of BMS, this study proposes a novel joint estimation approach for SOE and SOH based on a fractional-order adaptive strong-tracking robust EKF framework (FOASTFREKF-EKF).

The main contributions of this paper are as follows:

• The algorithm incorporates adaptive theory and H∞ filtering to update noise statistics in real time, significantly enhancing the stability and accuracy of SOE estimation.
• A time-varying attenuation factor is integrated into the filtering process to minimize dependence on historical data and improve sensitivity to sudden changes in operating conditions.
• The framework explicitly accounts for the impact of battery aging on SOE. An EKF is employed for online battery parameter identification and SOH estimation, thereby improving the overall precision.
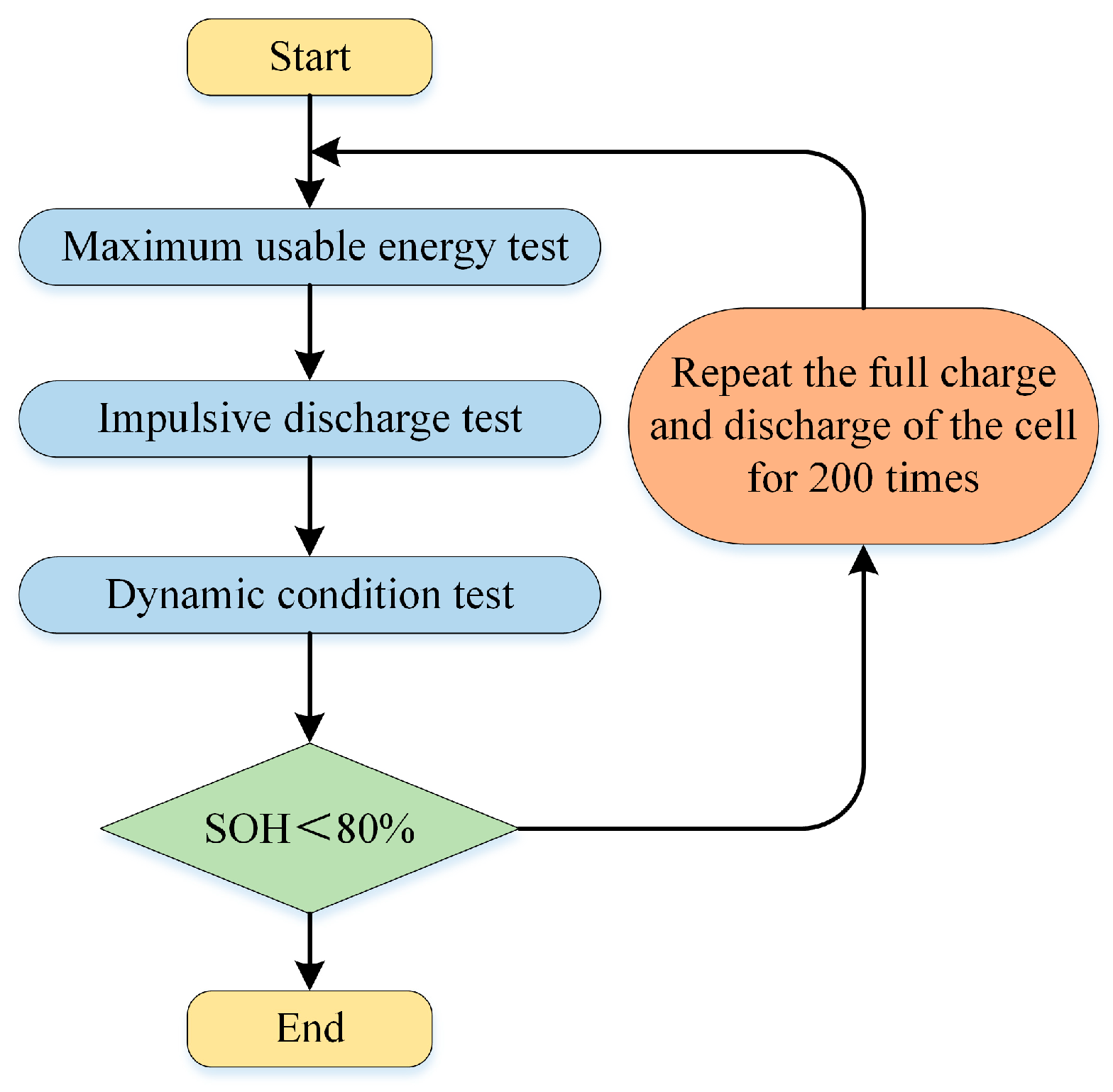
• A multi-timescale strategy is adopted for the joint estimation of SOE and SOH to reduce computational complexity. The proposed method is validated using experimental data from a custom-built test platform. The results confirm its effectiveness and demonstrate its capabilities.

2. State Estimation of Lithium Batteries

The EKF is a prevalent technique for SOE estimation due to its effectiveness in dynamic state estimation. Although well-suited for high-dimensional nonlinear systems, the EKF algorithm suffers from reduced accuracy and robustness when applied to complex battery models. Furthermore, battery aging induces time-varying characteristics in the model parameters, causing batteries with identical SOE levels to exhibit markedly different behaviors depending on their varying degrees of degradation. Consequently, high-precision SOE estimation must account for the battery aging state as a critical influencing factor. To address these limitations, this section presents a novel FOASTFREKF-EKF algorithm. This method enhances the traditional EKF by integrating H∞ filtering and adaptive theory, and introduces a time-varying attenuation factor to lessen the model’s reliance on historical data. The proposed framework explicitly incorporates the impact of battery aging and performs simultaneous online estimation of battery parameters, SOH, and SOE, thereby achieving significant improvements in both stability and accuracy.

2.1. Fractional-Order Model

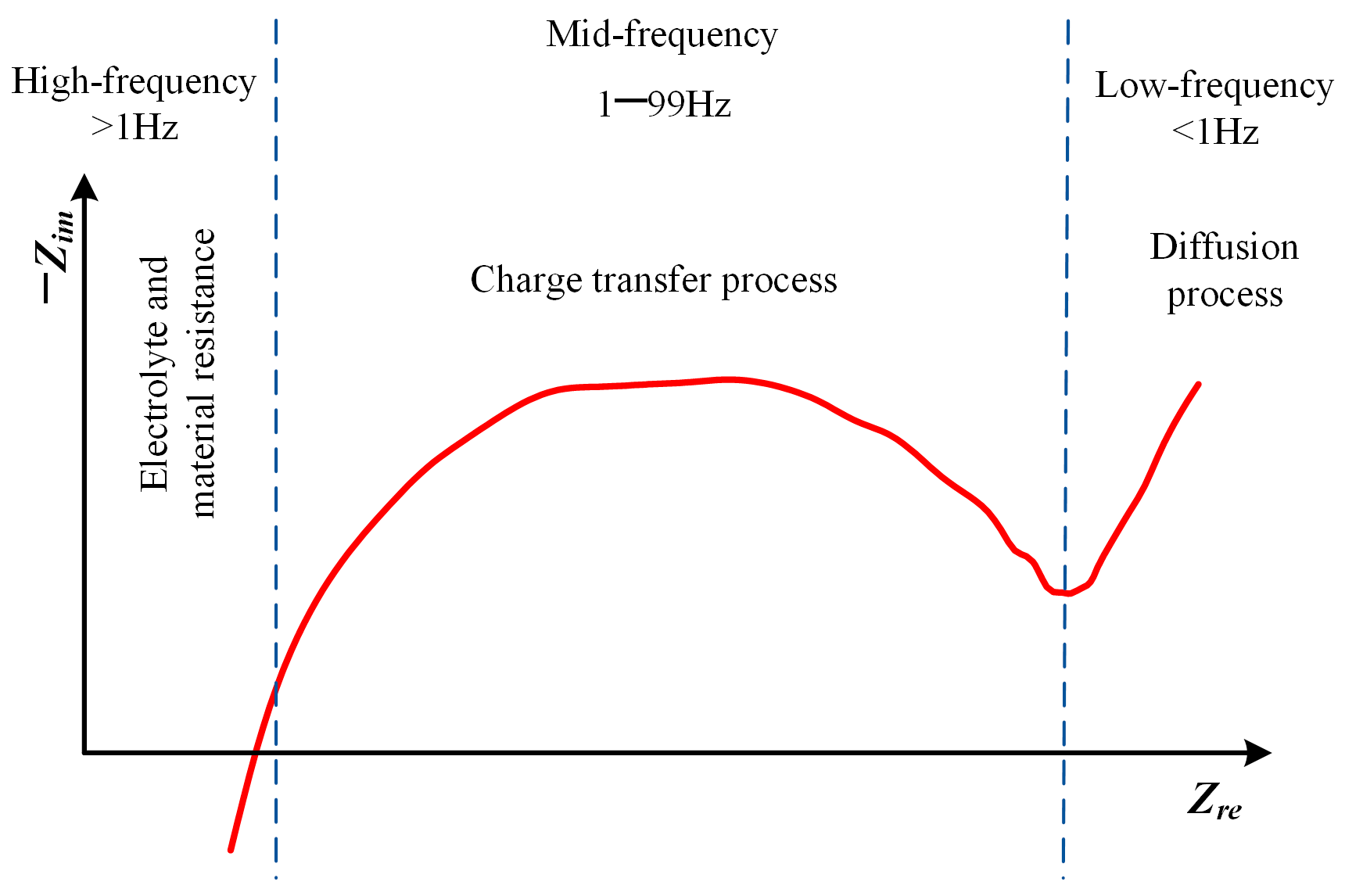
Electrochemical impedance spectroscopy (EIS) characterizes the impedance changes of lithium-ion batteries at different frequencies [30]. The resulting data is commonly represented as a Nyquist plot, where the shape of specific regions corresponds to the changes in the internal state of the battery, as illustrated in Figure 1.

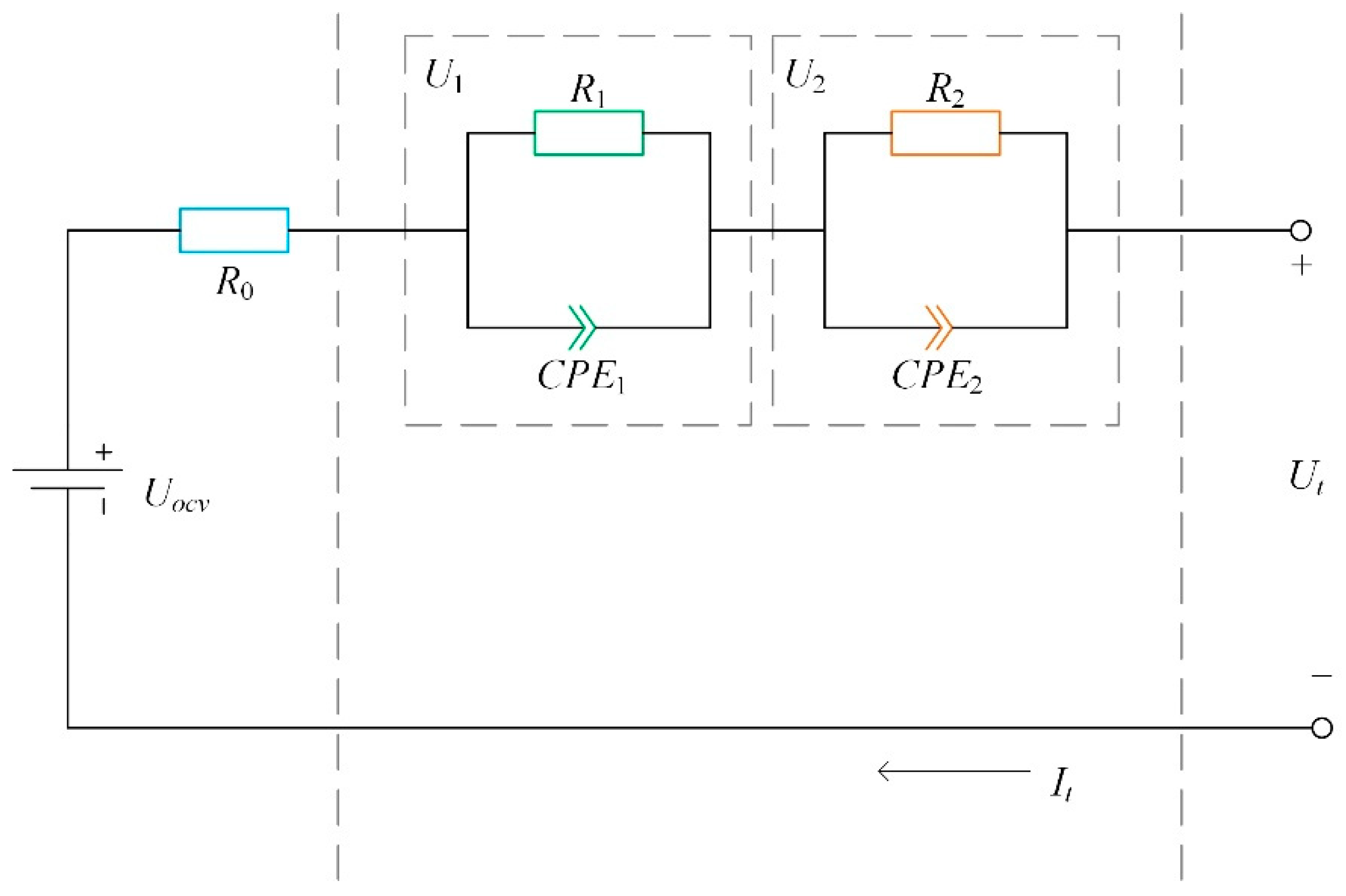
Traditional integer-order equivalent circuit models use ordinary differential equations to describe battery dynamics. These models’ ideal capacitive elements neglect microscopic inhomogeneities at the electrode interface and thus fail to accurately fit the flattened semicircle observed in the mid-frequency region of EIS, i.e., the “dispersion effect”. This results in significant discrepancies between the models and the experimental data. To better represent the nonlinear and dynamic electrochemical processes in lithium-ion batteries, this paper replaces the ideal capacitive components with a constant phase element (CPE). This modification enables the establishment of a fractional-order equivalent circuit model, as shown in Figure 2.

In this model, Uocv is the open circuit voltage, R₀ is the ohmic internal resistance, R₁ and CPE₁ are the polarization resistance and capacitance, respectively; R₂ and CPE₂ are the diffusion resistance and capacitance, respectively; and Ut is the terminal voltage. Based on Kirchhoff’s laws of current and voltage, the state equations and observation equation for the fractional-order model are derived:

$$\left\{\begin{array}{c}{\displaystyle \frac{d^m{U}_1}{d{t}^m}}=-{\displaystyle \frac{1}{R_1{C}_1}}{U}_1+{\displaystyle \frac{1}{C_1}}{I}_t\\ {\displaystyle \frac{d^n{U}_2}{d{t}^n}}=-{\displaystyle \frac{1}{R_2{C}_2}}{U}_2+{\displaystyle \frac{1}{C_2}}{I}_t\\ SOE(k+1)=SOE(k)-{\displaystyle \frac{U_t(k)I_t(k)T_s}{E_n}}\end{array}\right.$$

(1)

$$U_t=U_{OCV}-U_1-U_2-I_t{R}_0$$

(2)

where U₁ and U₂ are the voltages across the resistance and capacitance, I_t is the operating current, m and n are respectively the orders of the CPE₁ and CPE₂, T_S is the time step, and En is the maximum available energy of the battery.

Equation (1) must be discretized for battery state estimation. The Grünwald-Letnikov (G-L) fractional calculus introduces the concept of discrete differences, which makes it suitable for handling non-integer order calculus operations. Consequently, this paper processes fractional-order differential terms using the G-L fractional calculus. The definition of G-L fractional calculus is as follows:

$$D_t^{a}f(t)=\underset{T_s\to 0}{\lim }{T}_s^{-a}\sum _{j=0}^{[t/T_s]}{(-1)}^j\left(\begin{array}{c}a\\ j\end{array}\right)f(t-j{T}_s)$$

(3)

where $D_t^a$ is the fractional order differential operator, a and t are the lower and upper limits of integration, respectively, and $\left(\begin{array}{c}a\\ j\end{array}\right)$ is the binomial coefficient.

Equation (1) can be discretized as follows:

$$x_k=A{x}_{k-1}+B{u}_{k-1}-\sum _{j=1}^k{K}_j{x}_{k-j}$$

(4)

where $x_k=\left[\begin{array}{c}{U}_{1,k}\\ U_{2,k}\\ SO{E}_k\end{array}\right]$, $A=\left[\begin{array}{ccc}-{\displaystyle \frac{T_s^m}{R_1{C}_1}}& 0& 0\\ 0& -{\displaystyle \frac{T_s^n}{R_2{C}_2}}& 0\\ 0& 0& 1\end{array}\right]$, $B=\left[\begin{array}{c}{\displaystyle \frac{T_s^m}{C_1}}\\ {\displaystyle \frac{T_s^n}{C_2}}\\ -{\displaystyle \frac{U_{t,k}{T}_s}{E_n}}\end{array}\right]$, $u_{k-1}=I_t(k-1)$, $K_j=\left[\begin{array}{ccc}{(-1)}^j\left(\begin{array}{c}m\\ j\end{array}\right)& 0& 0\\ 0& {(-1)}^j\left(\begin{array}{c}n\\ j\end{array}\right)& 0\\ 0& 0& 0\end{array}\right]$.

Equation (2) simplifies to the following at time k after discretization:

$$y_k=C{x}_k-R_0{u}_k+U_{OCV}$$

(5)

where $C_k=\left[\begin{array}{ccc}-1& -1& 0\end{array}\right]$, $y_k=U_t(k)$.

2.2. Parameter Identification

Based on the fractional-order equivalent circuit model established here, the following parameters now require identification: R₀, R₁, R₂, CPE₁, CPE₂, m, and n. Fractional-order models usually use offline identification to guarantee identification accuracy and minimize computing complexity. To achieve optimal identification performance, this paper utilizes the Starfish Optimization Algorithm (SFOA), which has greater effectiveness than the mainstream Adaptive Genetic Algorithm (AGA) [31,32,33] for multi-parameter optimization. The SFOA effectively addresses AGA’s limitations toward premature convergence and parameter sensitivity through its unique balanced search mechanism, which strategically integrates global exploration with local exploitation.

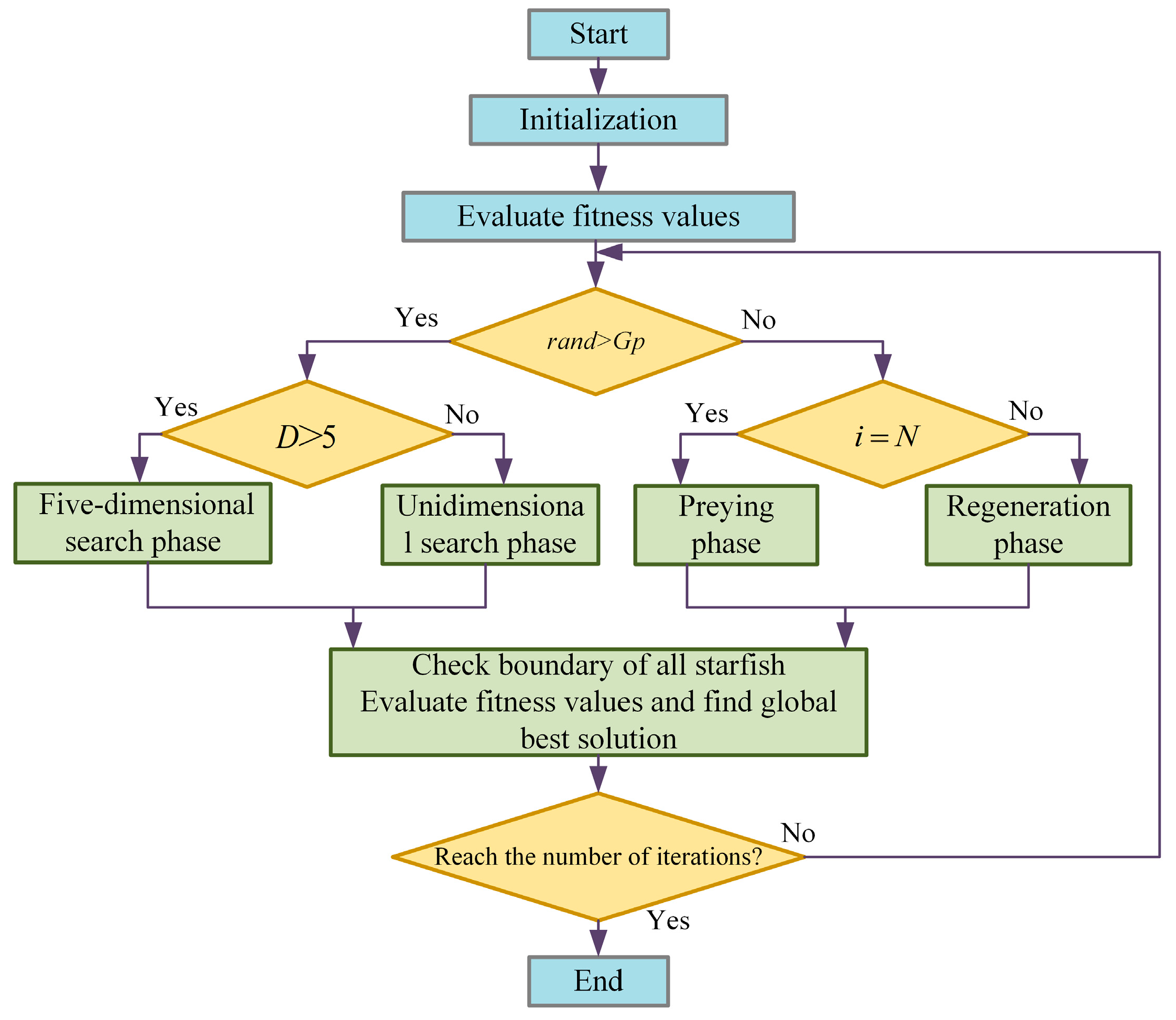
A recent heuristic algorithm called the Starfish Optimization Algorithm (SFOA) addresses optimization problems by emulating the collective behaviors of starfish, such as collaborative exploration, predation, and regeneration [34]. Exploration and exploitation are the two main phases of the SFOA. The exploration resembles the exploratory behavior of starfish. Depending on the dimensionality (D) of the optimization problem, the algorithm uses either a five-dimensional or one-dimensional search model for different optimization tasks. The exploitation phase simulates starfish predation and regeneration behaviors to update the population and converge toward the global optimum. Since starfish move slowly during regeneration, the regeneration phase of the SFOA is applied only to the last individual in the population (i = N).

The key advantage of the SFOA is its effective balance between global exploration and local exploitation, enabled by a unique collaborative branch exploration mechanism and an adaptive regenerative process. These features collectively ensure the algorithm’s efficient convergence and overall robustness.

The SFOA consists of the following steps:

(1)

Initialization: An initial population of starfish individuals is generated randomly, each representing a potential solution.

(2)

Calculate individual fitness: A fitness function is defined, and the fitness values for each starfish are computed at the current iteration.

(3)

Update starfish positions: In the exploration phase, the positions are updated according to the problem’s dimensionality (D). In the exploitation phase, positions are updated by simulating predation and regeneration.

(4)

Archive updates: The optimal positions of each starfish are updated by comparing its current fitness value with those of all other starfish.

(5)

Output results: When the iteration termination criteria are met, the SFOA ends, achieving identification of circuit model parameters.

Figure 3 illustrates the algorithm’s flowchart, where rand denotes a random number within [0, 1], and Gp is set to 0.5 in this study.

By searching for the optimal parameter set, the SFOA minimizes the error between the terminal voltage that the model predicts and the actual terminal voltage.

2.3. REKF Based on a Fractional-Order Model

A state-space representation of the fractional-order equivalent circuit model must be established before applying the EKF for dynamic system estimation:

$$x_k=f\left({\mathit{x}}_{k-1},u_{k-1}\right)+{\omega }_{k-1}=A{x}_{k-1}+B{u}_{k-1}-\sum _{j=1}^k{K}_j{x}_{k-j}+{\omega }_{k-1}$$

(6)

$$y_k=h\left(x_k,u_k\right)+{\nu }_k=C{x}_k-R_0{u}_k+U_{OCV}+{\nu }_k$$

(7)

where x_k is the state vector, y_k is the observation value, ω_k is the process noise whose covariance matrix is Q_k, and v_k is the observation noise whose covariance matrix is R_k.

The EKF provides an optimal estimate in the minimum error sense only if both the process and measurement noise are Gaussian white noise with known statistical properties. If this condition is not satisfied, the EKF performance degrades. In contrast, the H∞ filter employs a minimax criterion, designed to minimize the worst-case estimation error caused by disturbances, thereby significantly improving robustness [35,36].

The robust Extended Kalman Filter based on the fractional-order (FOREKF) is formulated by integrating the robustness of the H∞ filter into the traditional EKF framework. Based on the fractional-order battery model from Equations (5) and (6), the cost function J is defined as follows:

$$J={\displaystyle \frac{\sum _{k=0}^N{‖x_k-{\widehat{x}}_k‖}_{S_k}^2}{{‖x_0-{\widehat{x}}_0‖}_{P_0^{-1}}^2+\sum _{k=0}^N{‖w_k‖}_{Q_k^{-1}}^2+\sum _{k=0}^N{‖v_k‖}_{R_k^{-1}}^2}}$$

(8)

where P₀ is the covariance matrix of the initial error, and Sj is a positive definite matrix.

The H∞ filter is designed to minimize the upper bound of the cost function J:

$$\underset{{\widehat{x}}_k}{\min }\underset{w_k,v_k,x_0}{\max }J<\gamma$$

(9)

As a key design parameter, the value of γ must be balanced against the need for minimum variance and optimal filtering performance.

The specific FOREKF procedure is as follows:

(1)

Initialize the parameters x₀, P₀, Q₀, R₀.

(2)

Calculate the predicted values of the state variable and prior estimation error covariance matrix:

$$\left\{\begin{array}{l}{\widehat{x}}_k^{-}=A_{k-1}{\widehat{x}}_{k-1}^{+}+B_{k-1}{u}_{k-1}-{\displaystyle \sum _{j=1}^L}{K}_j{\widehat{x}}_{k-j}^{+}+{\omega }_{k-1}\\ P_k^{-}=\left(A_{k-1}-K_1\right)P_{k-1}^{+}{\left(\begin{array}{c}{A}_{k-1}-K_1\end{array}\right)}^T+{\displaystyle \sum _{j=2}^L}{K}_j{P}_{k-j}^{+}{K}_j^T+Q_{k-1}\end{array}\right.$$

(10)

(3)

Calculate the Kalman gain matrix and extended residual covariance matrix:

$$\left\{\begin{array}{l}{K}_k=P_k^{-}{H}_k^T{(H_k{P}_k^{-}{H}_k^T+R_k)}^{-1}\\ R_{e,k}=\left[\begin{array}{cc}{R}_k& 0\\ 0& -\gamma I\end{array}\right]+\left[\begin{array}{c}{H}_k\\ I\end{array}\right]P_k^{-}\left[\begin{array}{cc}{H}_k^T& I\end{array}\right]\end{array}\right.$$

(11)

(4)

Update of state variables, observations, and estimation error covariance matrix:

$$\left\{\begin{array}{l}{\widehat{x}}_k^{+}={\widehat{x}}_k^{-}+K_k\left(y_k-{\widehat{y}}_k\right)\\ {\widehat{y}}_k=H_k{\widehat{x}}_k-R_k{u}_k\\ P_k^{+}=P_k^{-}-P_k^{-}\left[\begin{array}{cc}{H}_k^T& I\end{array}\right]R_{e,k}^{-1}\left[\begin{array}{c}{H}_k\\ I\end{array}\right]\end{array}\right.$$

(12)

where I is the identity matrix. Steps (2) and (4) are repeated iteratively for each time step k = 1, 2, … until the sampling period concludes.

2.4. SOE Estimation Based on FOASTFREKF

The FOREKF, while based on the EKF framework, is optimal only under the assumption of fixed noise statistics. However, this assumption is often invalid for real-world battery systems, which exhibit time-varying noise properties, leading to reduced estimation accuracy. The REKF uses a first-order Taylor expansion to achieve local linearization in nonlinear systems. It retains only the Jacobian matrix but discards all higher-order terms. The iterative mechanism of the REKF means the current estimate depends heavily on the previous state estimate. When battery operating conditions change abruptly, this reliance can cause large estimation errors, which may accumulate over time and compromise performance or cause filter divergence.

To address these limitations and improve stability and accuracy, an adaptive mechanism is integrated into the FOREKF to enable real-time adjustment of noise statistics under dynamic operational conditions. Additionally, a time-varying attenuation factor λ_k is introduced to lessen the algorithm’s dependence on historical data.

(1)

Adaptive updating of Q_k and R_k:

The adaptive noise estimation mechanism uses a sliding window approach to dynamically adjust the Q_k and R_k noise covariance matrices by monitoring the statistical characteristics of the new information sequence in real-time.

The new information d_k and the filtered residual information r_k are defined as follows:

$$\left\{\begin{array}{l}{d}_k=H_k\left(x_k-{\widehat{x}}_k^{-}\right)+{\nu }_k\\ r_k=y_k-{\widehat{y}}_k=R_k{C}_{d_k}^{-1}{d}_k\end{array}\right.$$

(13)

$$C_{d_k}=\left\{\begin{array}{l}{\displaystyle \frac{k-1}{k}}{C}_{d_{k-1}}+{\displaystyle \frac{1}{k}}{d}_k{d}_k^T k\le \omega \\ {\displaystyle \frac{1}{\omega }}{\displaystyle \sum _{i=k-\omega +1}^k}{d}_i{d}_i^T k>\omega \end{array}\right.$$

(14)

where $C_{d_k}$ is the covariance of the new interest rate estimate, and ω is the length of the sliding data window. This paper uses a window length of 70.

Adaptive update noise is as follows:

$$\left\{\begin{array}{l}{Q}_{k-1}=K_k{C}_{d_k}{K}_k^T\\ R_k=C_{d_k}+H_k{P}_k{H}_k^T\end{array}\right.$$

(15)

(2)

Strong tracking state update:

A time-varying attenuation factor, λ_k, is introduced from the Strong Tracking Filter (STF) to modify the estimated error covariance matrix to enforce the orthogonality of the new state sequence. This technique strengthens the algorithm’s tracking capability during abrupt state changes by assigning less weight to historical data. The modified prior estimation error covariance matrix update formula is as follows:

$$P_{k,\lambda }^{-}={\lambda }_k\left[\left(\begin{array}{c}{A}_{k-1}-K_1\end{array}\right)P_{k-1}^{+}{\left(\begin{array}{c}{A}_{k-1}-K_1\end{array}\right)}^T+\sum _{j=2}^L{K}_j{P}_{k-j}^{+}{K}_j^T\right]+Q_{k-1}$$

(16)

where the calculation formula of λ_k is as follows:

$${\lambda }_k=\left\{\begin{array}{ll}{\lambda }_0& {\lambda }_0\ge 1\\ 1& {\lambda }_0<1\end{array}\right.$$

(17)

$${\lambda }_0={\displaystyle \frac{tr\left(V_k-H_k{Q}_{k-1}{H}_{k+1}^T-R_k\right)}{tr\left(A_k{P}_{k-1}{A}_k^T{H}_k^T{H}_k\right)}}$$

(18)

$$V_k=\left\{\begin{array}{ll}{r}_1{r}_1^T& k=1\\ {\displaystyle \frac{\rho V_{k-1}+r_k{r}_k^T}{1+\rho }}& k>1\end{array}\right.$$

(19)

where ρ is a forgetting factor, determined according to the specific model and application requirements.

2.5. Joint Estimation Method for SOE and SOH Across Multiple Time Scales

The SOE exhibits rapid changes during battery charging and discharging phases, whereas the SOH and related parameters are markedly more stable, often remaining consistent over one or more full charge–discharge cycles. Conventional single-timescale estimation methods struggle to accommodate these divergent dynamic characteristics, resulting in substantially increased computational complexity. To overcome this challenge, this paper proposes a multi-timescale joint estimation framework.

The discrete system equations for the multi-timescale joint estimation algorithm are as follows:

$$\left\{\begin{array}{l}{x}_k=f_x\left(x_{k-1},{\theta }_{i-1},u_{k-1}\right)+{\omega }_{k-1}\\ {\theta }_l=f_{\theta }\left({\theta }_{l-1}\right)+{\omega }_{l-1}\\ z_k=g\left(x_k,{\theta }_l,u_k\right)+v_k\end{array}\right.$$

(20)

where $x_k={\left[\begin{array}{ccc}{U}_{1,k}& U_{2,k}& {\mathrm{SOE}}_k\end{array}\right]}^T$, ${\mathit{\theta }}_l={\left[\begin{array}{cccccc}{R}_0& R_1& R_2& CP{E}_1& CP{E}_2& mn{Q}_n\end{array}\right]}^T$.

In the joint estimation framework, x_k is the state observer, θ_l is the parameter observer, and Q_n is the maximum available capacity. ω_k−1, ω_l−1, and v_k is the process noise. k is the time scale of the state observer, and l is the time scale of the parameter observer. To ensure the validity of the estimation results, this paper sets k to 1 s and l to 60 s.

The system state observer utilizes the FOASTFREKF algorithm to estimate the SOE. It operates on a fast timescale of seconds, enabling real-time tracking of current and voltage dynamics. The system parameter observer employs FOEKF to estimate SOH and update battery model parameters online. It operates on a slow timescale of minutes, tracking parameters that change slowly, such as capacity decay and internal resistance drift.

The specific process for estimating system parameters using FOEKF is as follows:

(1)

Initialize the parameters θ₀, P₀, Q₀.

(2)

Calculation of the predicted values of the state variable and prior estimation error covariance matrix:

$$\left\{\begin{array}{l}{\widehat{\theta }}_l^{-}={\widehat{\theta }}_{l-1}^{+}\\ P_l^{-}=P_{l-1}^{+}+Q_{l-1}\end{array}\right.$$

(21)

(3)

Calculation of the Kalman gain matrix:

$$K_l=P_l^{-}{H}_l^T{(H_l{P}_l^{-}{H}_l^T+R_l)}^{-1}$$

(22)

(4)

Update of state variables and estimation error covariance matrix:

$$\left\{\begin{array}{l}{\widehat{\theta }}_l^{+}={\widehat{\theta }}_l^{-}+K_l\left(z_k-{\widehat{z}}_k\right)\\ P_l^{+}=(I-K_l{H}_{l+1})P_l^{-}\end{array}\right.$$

(23)

Once the first state observer has completed its estimation, its state variables will serve as input for the second parameter observer. At the same time, the parameter variable estimates from the second observer will be fed into the first observer. This bidirectional data exchange, combined with the multi-timescale framework, enables the joint estimation of SOE and SOH. The complete workflow is depicted in Figure 4.

3. Results

3.1. Battery Experiment

Figure 5 illustrates the configuration of the experimental testing platform for lithium-ion batteries. This platform consists of a constant temperature and humidity chamber, a BTS CT-4008T battery testing system (5 V/12 A) manufactured by Xinwei in Shenzhen, China, and a host computer. The 18650 NCM batteries used for testing are produced by Tianjin Lishen in Tianjin, China.

Table 1. Parameters of the batteries.

Parameter	Values
Rated capacity	2 Ah
rated voltage	3.6 V
Charge cutoff voltage	4.2 ± 0.05 V
Discharge cutoff voltage	2.5 V

displays the battery’s specification parameters.

To confirm the proposed estimation method’s efficacy in complex situations, this study designed and conducted battery aging experiments at typical ambient temperatures (25 °C).

Figure 6 illustrates the following experimental procedures:

(1)

To ascertain the battery’s original capacity, the maximum useable energy test is performed.

(2)

The battery is subjected to charge–discharge cycling with a 1 C current. Each 200 cycles constitute one aging cycle.

(3)

Following each aging cycle, conduct the maximum usable capacity test, impulsive discharge test, and dynamic condition test (FUDS and US06).

(4)

Repeat steps 2 and 3 until the SOH status drops below 80%; at that point, the experiment is over.

3.2. Parameter Identification Results

This paper utilized three batteries at different aging conditions, corresponding to SOH values of 100%, 90.2%, and 83.03%. Using the impulsive discharge test data obtained in Section 3.1, the parameters R₀, R₁, R₂, CPE₁, CPE₂, m, and n were identified using SFOA, with the results presented in

Table 2. Model parameters identified by the SFOA.

SOH	R0 (Ω)	R1 (Ω)	R2 (Ω)	CPE1 (F)	CPE2 (F)	m	n
100%	0.0265	0.0228	0.0344	1143.59	42,142.86	0.9232	0.9864
90.20%	0.0334	0.0306	0.0399	1454.70	21,285.71	0.9727	0.9895
83.03%	0.0317	0.0344	0.0725	600	16,970.70	0.9690	0.9643

. The identified parameters from both the SFOA and AGA methods were validated by comparing the simulated circuit model output to the measured voltage. The verification results are shown in Figure 7. Model accuracy and estimation performance were quantified using mean error (ME), maximum error (Max Error), and root mean square error (RMSE). The terminal voltage estimation errors for battery models parameterized with SFOA and AGA are summarized in

Table 3. Terminal voltage estimation error.

SOH	Algorithms	ME (%)	Max Error (%)	RMSE
100%	SFOA	0.46	2.4	0.56
	AGA	0.48	3.75	0.63
90.20%	SFOA	0.42	2.92	0.55
	AGA	0.46	4.24	0.65
83.03%	SFOA	0.32	3.17	0.42
	AGA	0.37	4.58	0.59

.

The battery models parameterized with the SFOA demonstrated smaller voltage errors across all aging conditions than those identified with the AGA. This result confirms the SFOA’s superior precision and robustness for parameter identification. Specifically, the SFOA-identified models achieved lower errors than the traditional AGA and maintained a consistent overall error below 0.032 V. This further confirms that SFOA enhances the accuracy of modeled systems.

3.3. Validation of the SOE Estimation Methods

3.3.1. Analysis of SOE Estimation Results

This paper conducted tests under various driving conditions (FUDS and US06) and aging conditions (100%, 90.20%, and 83.03%). To test the algorithm’s ability to adjust when faced with larger initial error values, the SOE initial value was set to 0.8, with the true value being 1. For comparative analysis, the EKF, FOEKF, FOREKF, FOSTFREKF, and FOASTFREKF were selected as comparison algorithms. Figure 8 and Figure 9 present the SOE estimation results and error curves under various driving and aging situations, while

Table 4. SOE estimation error under FUDS condition.

SOH	Algorithms	ME (%)	Max Error (%)	RMSE
100%	EKF	1.5	4.29	1.94
	FOEKF	0.71	3.71	0.96
	FOREKF	0.60	2.99	0.81
	FOSTFREKF	0.55	2.16	0.69
	FOASTFREKF	0.44	1.33	0.53
	FOASTFREKF + EKF	0.15	0.29	0.18
90.20%	EKF	0.93	3.31	1.21
	FOEKF	0.58	2.53	0.82
	FOREKF	0.55	2.06	0.78
	FOSTFREKF	0.49	1.77	0.71
	FOASTFREKF	0.39	1.43	0.56
	FOASTFREKF + EKF	0.17	0.52	0.21
83.03%	EKF	0.68	2.8	0.88
	FOEKF	0.48	1.94	0.65
	FOREKF	0.45	1.55	0.62
	FOSTFREKF	0.42	1.22	0.55
	FOASTFREKF	0.35	0.93	0.45
	FOASTFREKF + EKF	0.18	0.50	0.21

and

Table 5. SOE estimation error under US06 condition.

SOH	Algorithms	ME (%)	Max Error (%)	RMSE
100%	EKF	1.48	3.36	1.69
	FOEKF	0.71	2.36	0.91
	FOREKF	0.65	2.04	0.85
	FOSTFREKF	0.56	1.63	0.71
	FOASTFREKF	0.44	1.02	0.51
	FOASTFREKF + EKF	0.15	0.48	0.21
90.20%	EKF	1.15	3.63	1.3
	FOEKF	0.58	3.24	0.79
	FOREKF	0.53	2.23	0.7
	FOSTFREKF	0.41	1.47	0.54
	FOASTFREKF	0.30	0.97	0.37
	FOASTFREKF + EKF	0.16	0.43	0.17
83.03%	EKF	1.14	3.06	1.37
	FOEKF	0.53	2.90	0.67
	FOREKF	0.50	1.87	0.60
	FOSTFREKF	0.38	0.90	0.45
	FOASTFREKF	0.29	0.61	0.34
	FOASTFREKF + EKF	0.14	0.29	0.16

summarize the quantitative error statistics.

The results demonstrate that SOE estimates converge rapidly to the true value under all tested operating conditions. Figure 8 and Figure 9 indicate that the FOASTFREKF-EKF algorithm achieves the closest alignment with the reference curve. Furthermore, the FOEKF shows superior accuracy and stability over the EKF across different driving and aging conditions, confirming that the fractional-order model better captures the battery’s nonlinear dynamics. In Figure 8 and Figure 9b, the FOREKF displays significantly less volatility than the FOEKF, demonstrating that the integration of H∞ filtering improves the algorithm’s robustness. Figure 8 and Figure 9b,d,f reveal that the FOASTFREKF and FOASTFREKF-EKF algorithms feature faster convergence and higher accuracy than the other three algorithms, a capability attributed to the inclusion of a time-varying attenuation factor and an adaptive strategy, which collectively enhance estimation performance.

As summarized in Table 4 and Table 5, the FOASTFREKF-EKF algorithm achieves significantly higher SOE estimation accuracy than the other five benchmark algorithms across all tested driving and aging conditions. The joint estimation framework yields a substantial reduction in RMSE, ME, and maximum error for SOE compared to the standalone FOASTFREKF, with an overall error reduction exceeding 50%. This demonstrates that the proposed method preserves high accuracy under diverse operating scenarios. Specifically, the maximum error remains below 0.52%, the ME below 0.18%, and the RMSE below 0.21% in all cases. These results confirm that the proposed joint estimation algorithm enables precise SOE estimation under challenging operating and aging conditions.

To provide a comprehensive statistical comparison of the estimation performance across different algorithms, the box plots of the SOE estimation errors are presented in Figure 10. The analysis shows that the FOASTFREKF-EKF algorithm proposed in this paper has a significantly lower median error than the other five algorithms across all operating conditions, reflecting its superior estimation accuracy. Moreover, its corresponding box is shorter, indicating a smaller interquartile range (IQR), and its whiskers are considerably shorter. This demonstrates the method’s highly stable estimation results, exhibiting minimal sensitivity to variations in battery operating conditions. The traditional EKF algorithm shows multiple outliers at the top of its box plot, suggesting a propensity for estimation divergence. In contrast, the proposed algorithm has few or no outliers, confirming its exceptional robustness.

3.3.2. Performance Evaluation and Comparative Study

To evaluate the performance of the proposed algorithm, we compare it with other estimation methods from the literature. Based on a fractional-order model, Reference [37] utilizes a dual adaptive Unscented Kalman filter for the cooperative estimation of SOC and SOH, reporting excellent accuracy and robustness under various complex operating conditions. Similarly, Reference [38] employs a first-order FOM with a square root cubature Kalman filter to estimate SOC and capacity, demonstrating its accuracy under varying battery states and temperatures.

Table 6. SOE estimation error with other methods under FUDS condition.

SOH	Algorithms	ME (%)	Max Error (%)	RMSE
100%	FOASTFREKF + EKF	0.15	0.29	0.18
	FOAUKF + AUKF	0.66	1.68	0.80
	FOSRCKF	0.72	3.72	0.82
90.20%	FOASTFREKF + EKF	0.17	0.52	0.21
	FOAUKF + AUKF	0.88	1.89	0.99
	FOSRCKF	0.46	1.81	0.64
83.03%	FOASTFREKF + EKF	0.18	0.50	0.21
	FOAUKF + AUKF	0.59	1.32	0.65
	FOSRCKF	1.31	2.99	1.52

and

Table 7. SOE estimation error with other methods under US06 condition.

SOH	Algorithms	ME (%)	Max Error (%)	RMSE
100%	FOASTFREKF + EKF	0.15	0.48	0.21
	FOAUKF + AUKF	0.99	1.49	1.04
	FOSRCKF	1.05	1.90	1.16
90.20%	FOASTFREKF + EKF	0.16	0.43	0.17
	FOAUKF + AUKF	1.00	1.75	1.12
	FOSRCKF	0.49	1.26	0.57
83.03%	FOASTFREKF + EKF	0.14	0.29	0.15
	FOAUKF + AUKF	0.45	0.82	0.50
	FOSRCKF	1.38	2.27	1.56

provide a detailed comparison, while error curves are illustrated in Figure 11 and Figure 12.

The results demonstrate that, under all test conditions, the FOASTFREKF-EKF algorithm rapidly converges to the reference value with minimal error. As illustrated in Figure 8 and Figure 9, the proposed FOASTFREKF-EKF algorithm closely tracks the reference curve. Furthermore, data in Table 4 and Table 5 confirm that the proposed algorithm achieved the smallest values for all three estimation error metrics across all tested driving and aging conditions. These findings collectively indicate a superior performance relative to other methods documented in the literature. This performance advantage arises from the comprehensive consideration of factors influencing estimation accuracy and the implementation of corresponding optimizations. Moreover, the refined identification method incorporates a more accurate battery model, which mitigates uncertainties introduced by experimental data errors.

3.4. Validation of the SOH Estimation Method

Figure 13 and Figure 14 present a comparison between the estimated and measured SOH values.

Table 8. Estimation error of SOH.

Conditions	SOH	ME (%)	Max Error (%)	RMSE
FUDS	100%	0.23	0.43	0.27
	90.20%	0.10	0.37	0.14
	83.03%	0.23	0.57	0.31
US06	100%	0.08	0.25	0.11
	90.20%	0.05	0.17	0.07
	83.03%	0.06	0.20	0.08

summarizes the ME, max error, and RMSE after SOH estimation stabilization for each driving condition and aging condition. As shown in the figures, the algorithm exhibits minor fluctuations, but these are confined to a narrow range. Specifically, the maximum error remains below 0.57%, the ME below 0.23%, and the RMSE below 0.31% across both driving cycles. These results demonstrate that the multi-timescale joint estimation algorithm delivers accurate SOH estimates while simultaneously providing precise SOE determination under different aging conditions.

To quantitatively assess the overall accuracy, stability, and robustness of the SOH estimation method, we conducted a box plot analysis of the SOH estimation error across all tested driving and aging conditions, depicted in Figure 15.

The results show that the median maximum SOH error remained below 0.25% across all six test conditions, confirming that the proposed method provides estimates close to the reference values under most operating conditions. Furthermore, the narrow interquartile range (IQR) indicates that the vast majority of estimation errors are contained within a limited band, demonstrating low variability and high consistency. Moreover, the SOH error distribution contains few outliers, all of which lie close to the main data cluster. This finding suggests that the method effectively suppresses aberrant estimation errors, even under complex conditions such as rapid changes in dynamic characteristics or noise interference during aging.

4. Conclusions

To improve the accuracy and robustness of State of Energy (SOE) and State of Health (SOH) estimation while reducing computational complexity, this study proposes a joint estimation approach for lithium-ion batteries based on a fractional-order model. The proposed framework begins by establishing a fractional-order equivalent circuit model, whose parameters are identified offline using the Starfish Optimization Algorithm (SFOA) for enhanced model fidelity. Subsequently, an H∞ filter is integrated into the structure to improve robustness against model uncertainties and external disturbances, forming the Fractional-Order Robust Extended Kalman Filter (FOREKF) framework. Furthermore, an adaptive noise covariance adjustment mechanism is incorporated to minimize the influence of operational noise. A time-varying attenuation factor is also included to enhance state tracking and response capabilities during sudden system changes, enabling accurate online SOE estimation.

This paper employs an Extended Kalman Filtering (EKF) for online battery parameter identification and SOH estimation, thereby accounting for the influence of parameter aging on SOE accuracy. Furthermore, a multi-timescale joint estimation algorithm for SOE and SOH is introduced, which effectively decouples the state coupling between the fast-varying SOE and the slow-varying SOH. This approach mitigates the impact of model errors on SOE estimation.

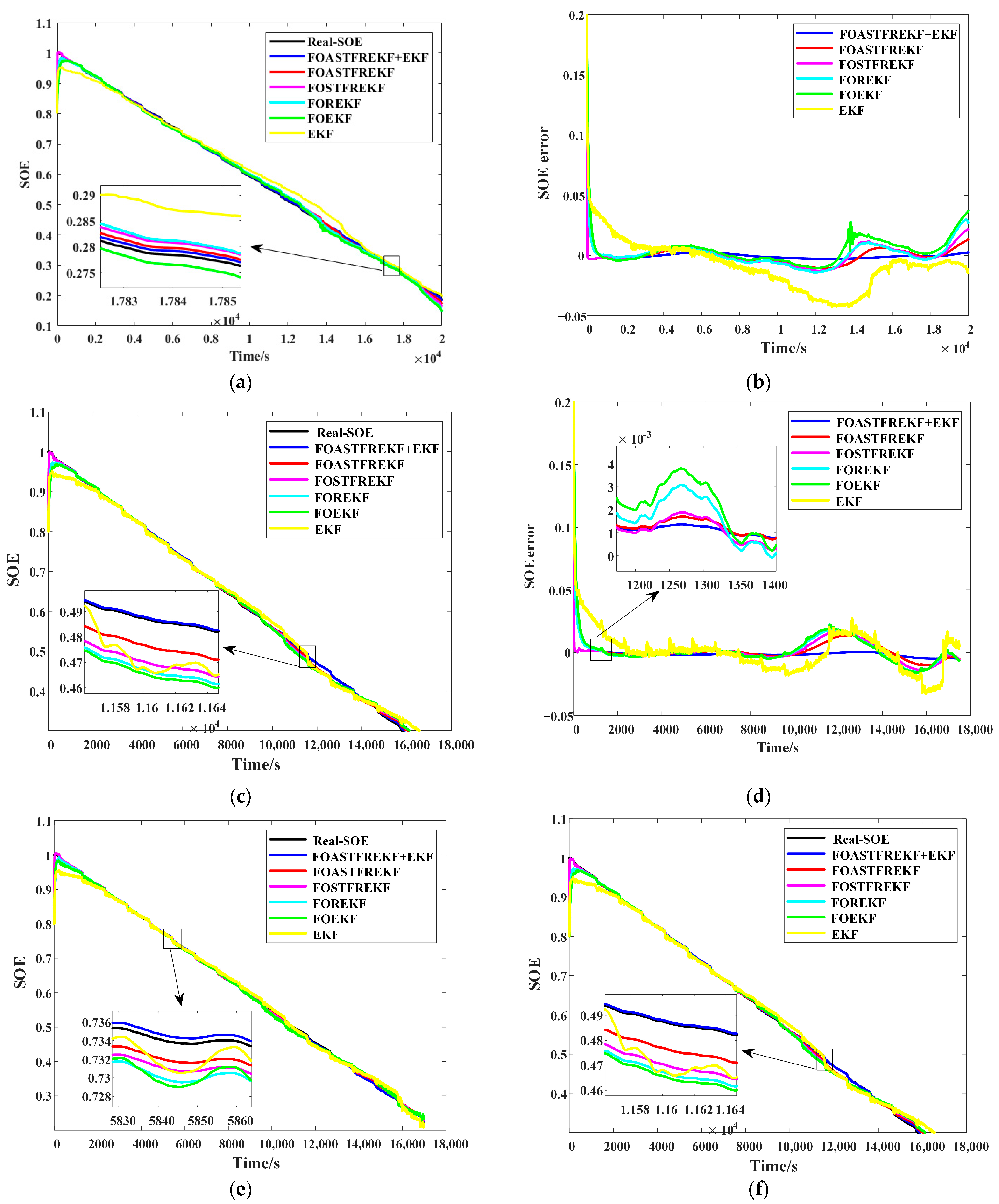
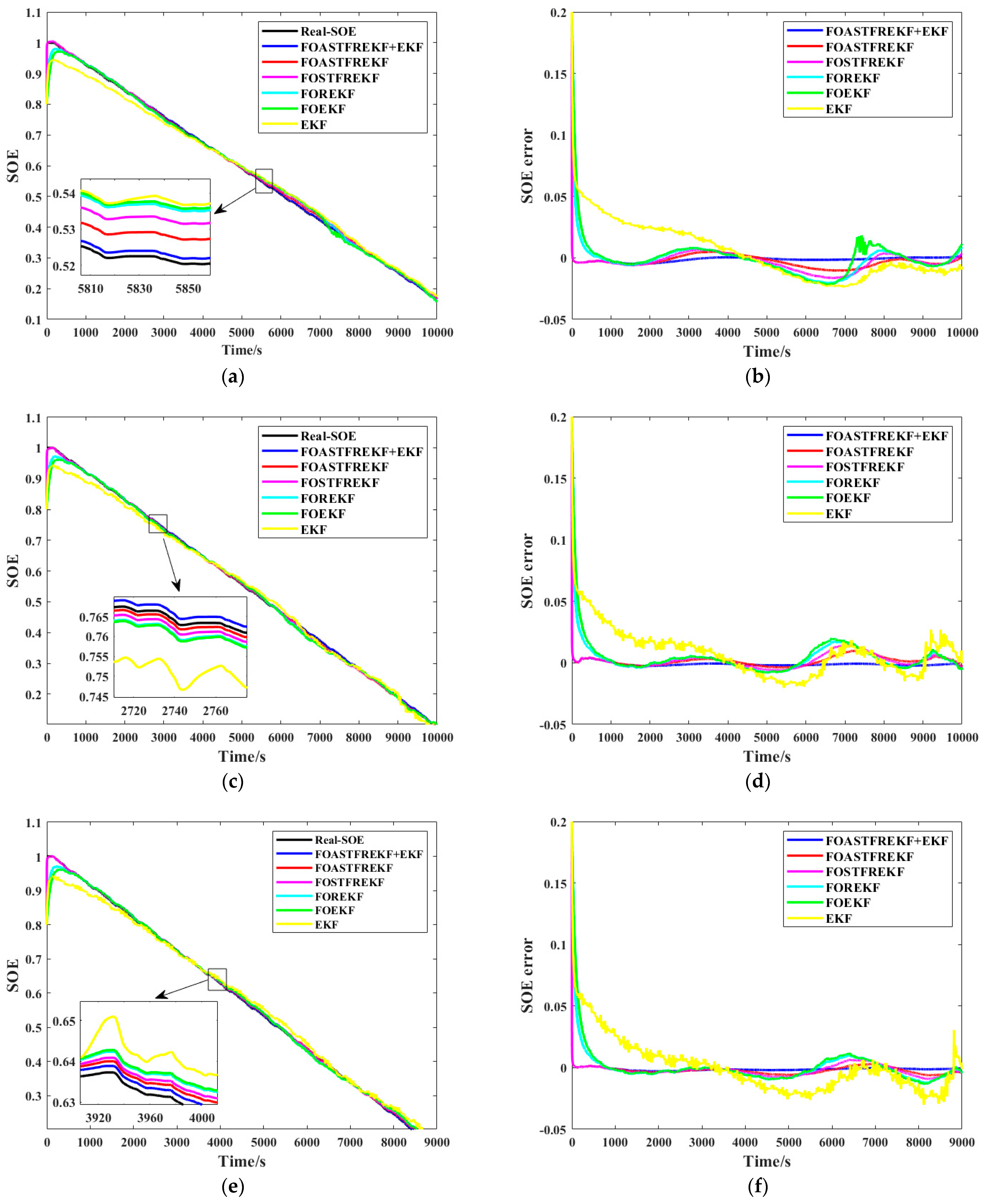
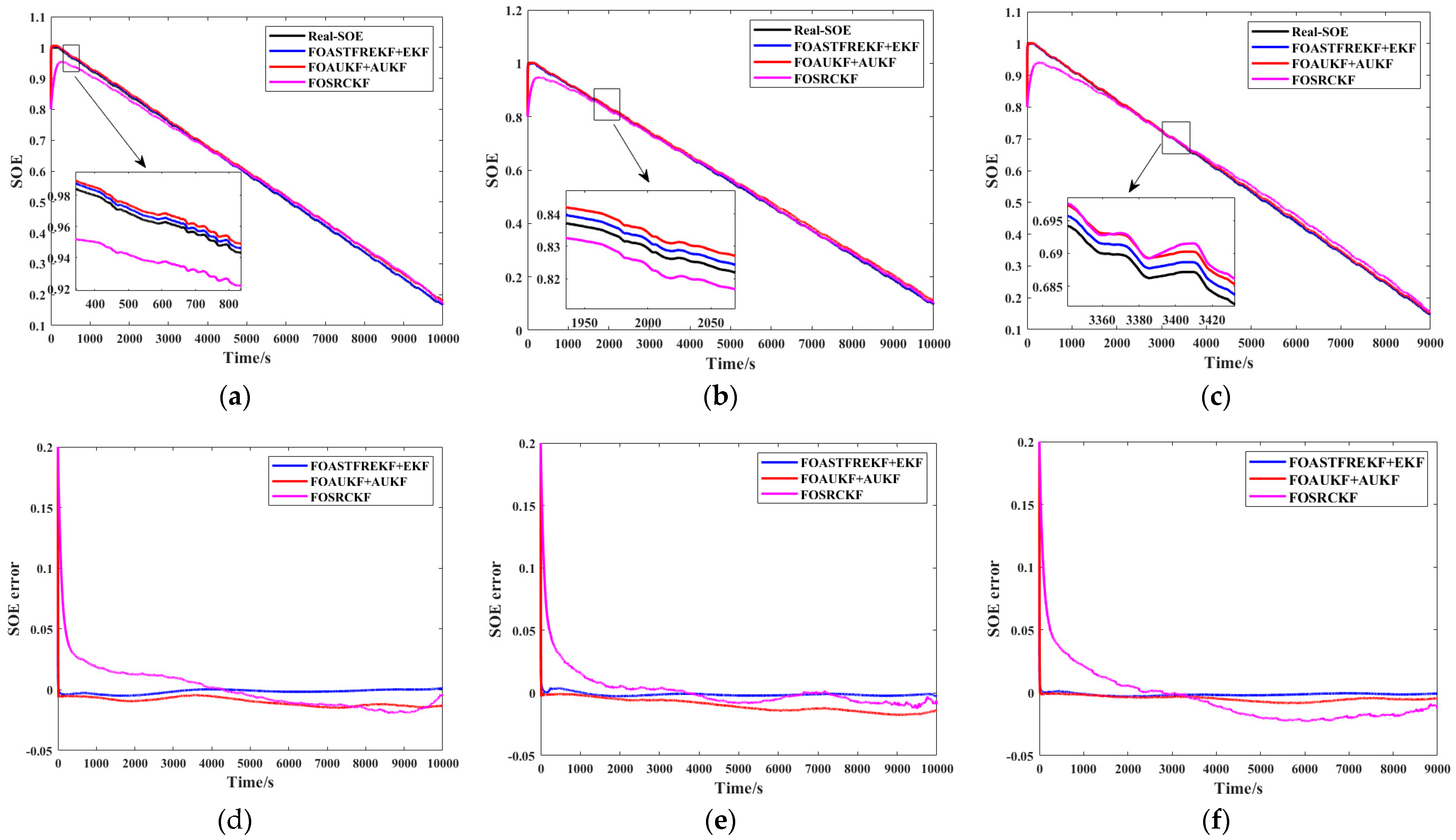
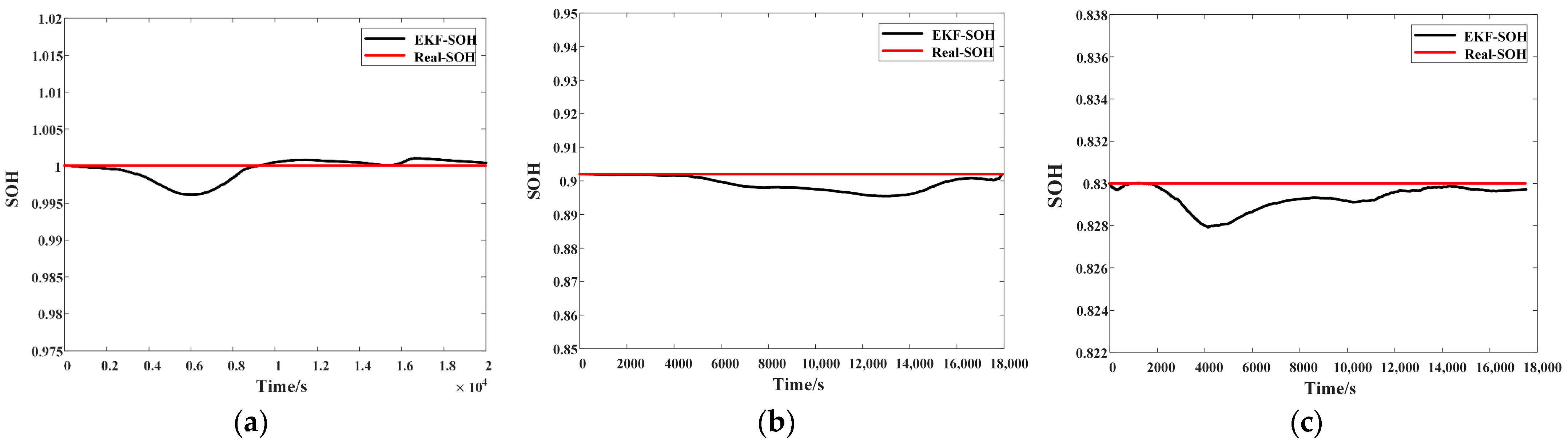
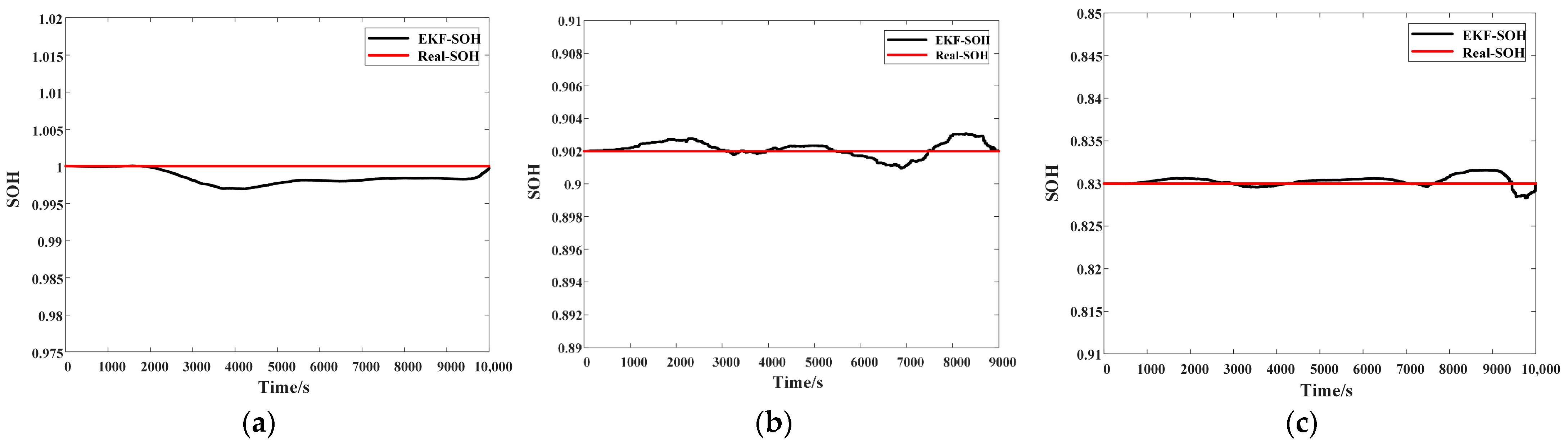
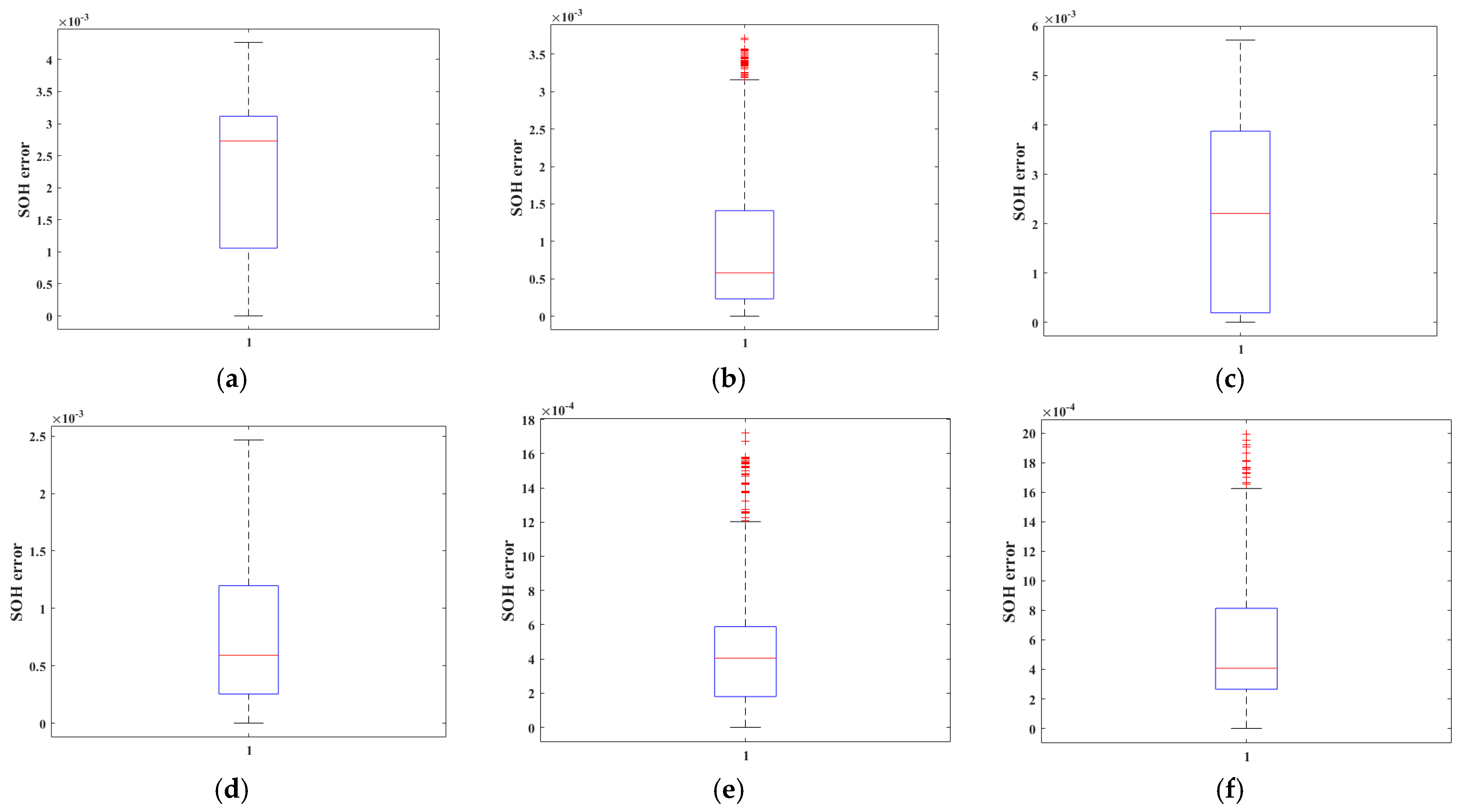
Experimental validation under diverse operating conditions demonstrates that the proposed algorithm achieves SOE estimation ME, Max error, and RMSE values consistently fall below 0.005. Similarly, for SOH estimation, the ME, Max error, and RMSE values remain below 0.0057. In comparison to other mainstream methods, the proposed algorithm provides superior accuracy and adaptability, offering a reliable solution for the joint battery state estimation under complex operating conditions.