An Empirical Multi-Stage One-Step Battery Thermal Runaway Model Based on Arrhenius Reaction Rate Formalism
Abstract
1. Introduction
2. Thermal Runaway Model
2.1. Gaussian Thermal Runaway Model
Polygon Resampling
2.2. Reaction Rate Thermal Runaway Model
2.2.1. One-Step Reaction Rate TR Models
2.2.2. Current One-Step Reaction Rate TR Model
2.2.3. Generalization Across Cell Chemistries
2.3. Identification of Reaction Parameters
2.3.1. Expected Impact of SoH and SoC on the Reaction Parameters
2.3.2. Expected Impact of the Cell Format on the Reaction Parameters
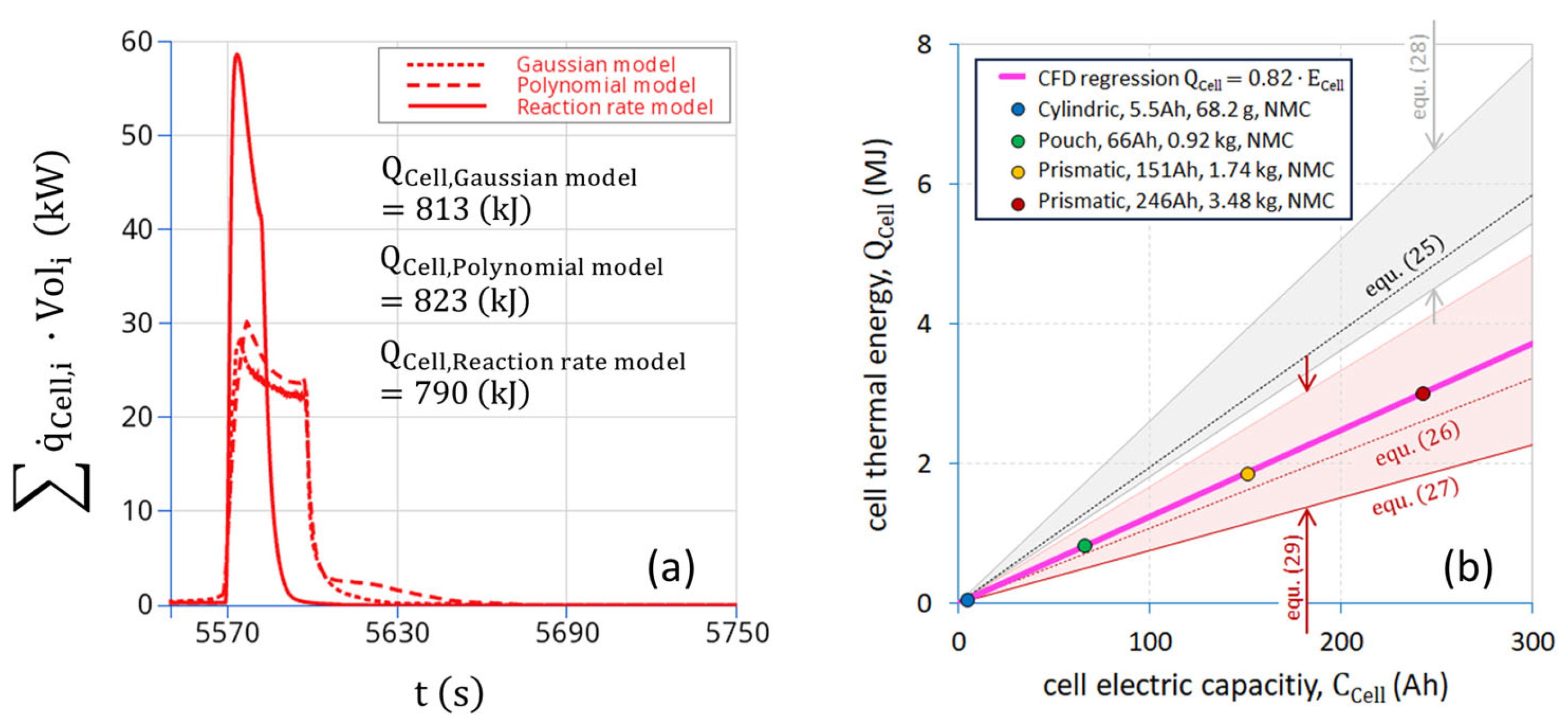
2.4. Estimation of Battery Thermal Energy
3. Battery Overheat Test
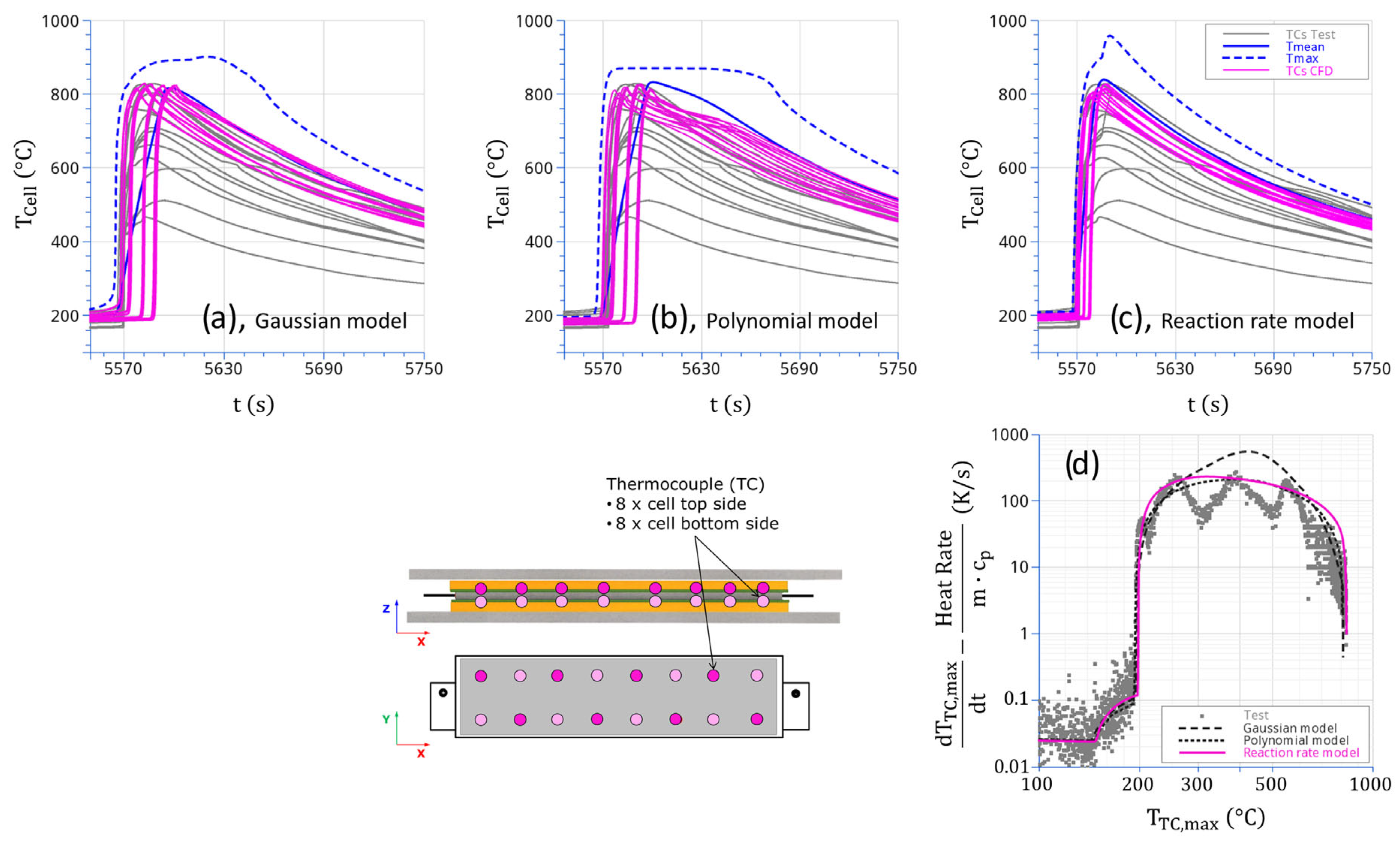
Test Results
4. CFD Results and Discussion
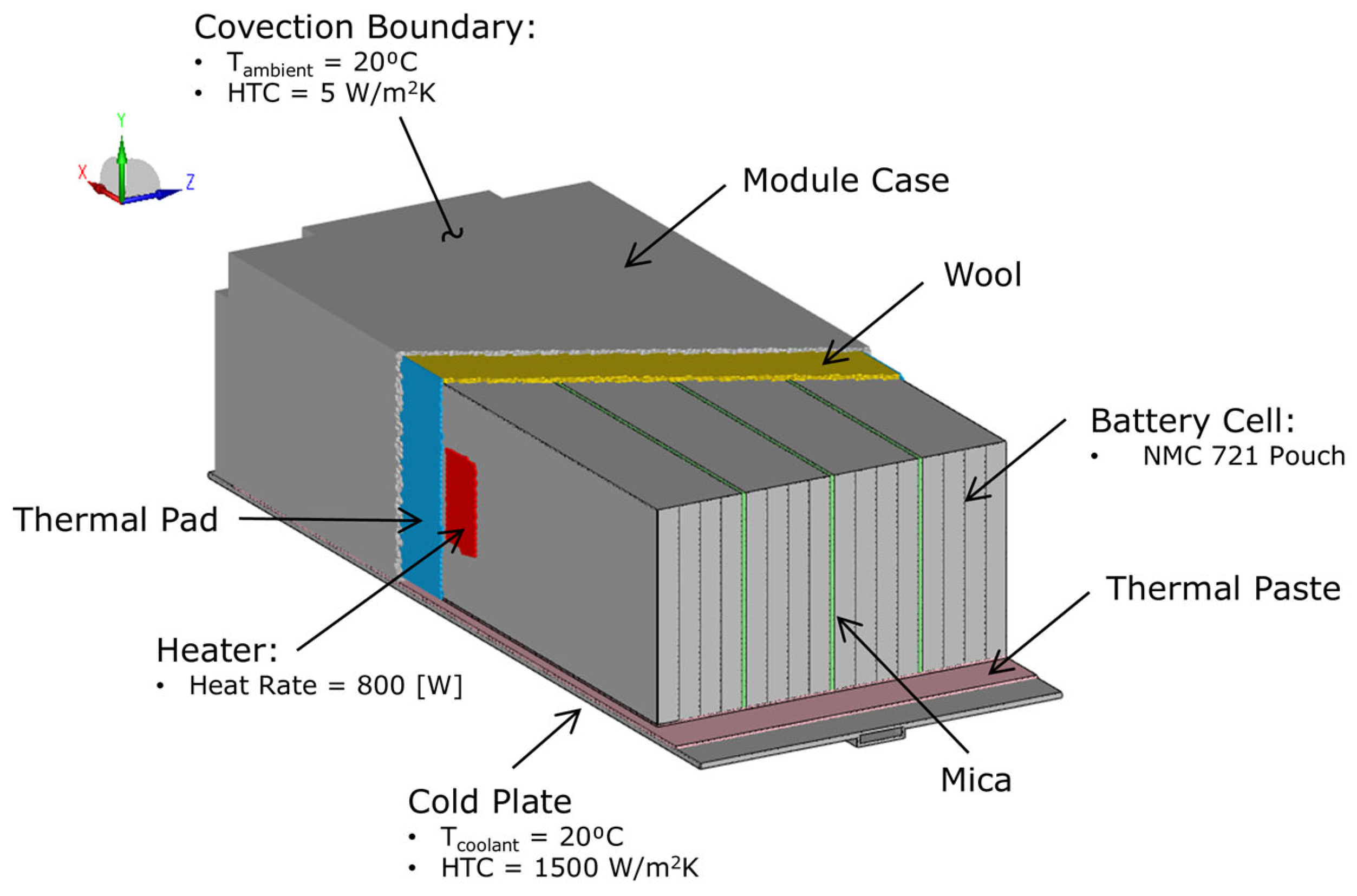
4.1. Solver and CFD Model
Limitations of the CFD Model
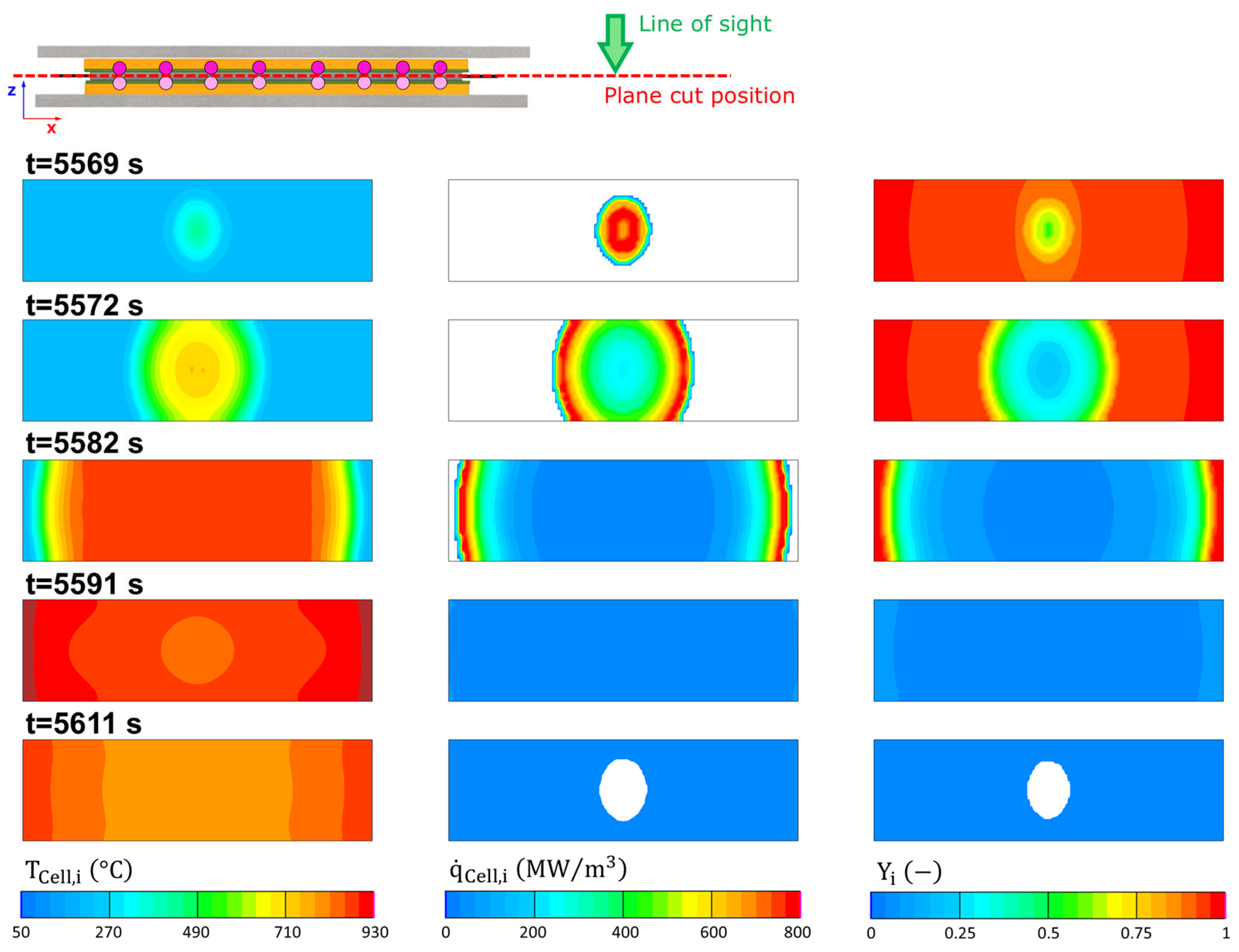
4.2. Single-Cell Thermal Runaway
4.3. Module Thermal Propagation
4.4. Model Sensitivity on the Convective Heat Transfer Coefficient
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TR | Thermal Runaway | [–] |
| TP | Thermal Propagation | [–] |
| Li-ion | Lithium-Ion Battery | [–] |
| ARC | Accelerating Rate Calorimetry | [–] |
| DSC | Differential Scanning Calorimeter | [–] |
| SEI | Solid Electrolyte Interphase | [–] |
| ISC | Internal Short Circuit | [–] |
| 3D | Three Dimensional | [–] |
| CFD | Computational Fluid Dynamics | [–] |
| CHT | Conjugate Heat Transfer | [–] |
| FV | Finite Volume | [–] |
| C | Battery Cell Electric Capacity | [Ah] |
| U | Battery Cell Open Circuit Voltage | [V] |
| Reaction Rate | [1/s] | |
| cp | Specific Heat | [J/kgK] |
| Density | [kg/m3] | |
| λ | Thermal Conductivity | [W/mK] |
| t | Time | [s] |
| x | x-Coordinate of Space | [m] |
| y | y-Coordinate of Space | [m] |
| z | z-Coordinate of Space | [m] |
| T | Temperature | [m] |
| A | Pre-Exponential Factor of Reaction Rate | [1/s] |
| Ea | Activation Energy of Reaction | [J/kg] |
| Heat of Reaction | [J/g] | |
| w | Specific Material Concentration | [g/m3] |
| Y | Specific Amount of Reactant | [–] |
| Current Heat Release | [W/m3] | |
| Q | Battery Total Thermal Energy | |
| E | Battery Electric Energy | |
| Proportionality of E and Q | [–] | |
| m | Mass | [kg] |
| slope | Slope of Temperature Rate | [K2/s] |
| b | Intercept | [–] |
| Vol | Total Volume of Battery Active Material | [m3] |
| BC | Boundary Condition | [–] |
| Ru | Universal Gas Constant | [J/molK] |
| R2 | Pearson Correlation Coefficient | [–] |
| Indexing of finite volumes | |
| Total number of finite volumes | |
| Indexing of chemical reactions | |
| j | Indexing for running averaging |
| Total number of chemical reactions | |
| k | Index for thermocouple |
| k | Running average trailing window size |
| m | Index for thermal runaway model stage |
| n | Time index |
| Cell | Battery cell active material |
| before | Cell state before ARC test |
| after | Cell state after ARC test |
| onset | Time when thermal runaway is triggered |
| End | End of ARC test |
| TC | Thermocouple temperature |
| mean | Arithmetic mean value |
| max | Absolute maximum of evaluated data |
| min | Absolute minimum of evaluated data |
| ad | Adiabatic condition |
| Vent | Heat coming from vent gas |
| Particle | Heat coming from emitted particles |
| total | Total heat released from battery |
References
- Warner, J.T. Chapter 3—Lithium-ion battery operation. In Lithium-Ion Battery Chemistries; Elsevier Inc.: Amsterdam, The Netherlands, 2019; pp. 43–77. [Google Scholar]
- Pfrang, A.; Kriston, A.; Ruiz, V.; Lebedeva, N.; di Persio, F. Chapter Eight—Safety of Rechargeable Energy Storage Systems with a focus on Li-ion Technology. In Emerging Nanotechnologies in Rechargeable Energy Storage Systems; Elsevier Inc.: Amsterdam, The Netherlands, 2017; pp. 253–290. [Google Scholar]
- Liu, K.; Liu, Y.; Lin, D.; Pei, A.; Cui, Y. Materials for lithium-ion battery safety. Sci. Adv. 2018, 4, eaas9820. [Google Scholar] [CrossRef]
- Citarella, M.; Suzzi, D.; Brunnsteiner, B.; Schiffbänker, P.; Maier, G.; Schneider, J. Computational Modelling of Thermal Runaway Propagation in Lithium-Ion Battery Systems. In Proceedings of the 2019 IEEE Transportation Electrification Conference (ITEC-India), Bengaluru, India, 17–19 December 2019. [Google Scholar]
- Ostanek, J.K.; Li, W.; Mukherjee, P.P.; Crompton, K.R.; Hacker, C. Simulating onset and evolution of thermal runaway in Li-ion cells using a coupled thermal and venting model. Appl. Energy 2020, 268, 114972. [Google Scholar] [CrossRef]
- Menz, F.; Bauer, M.; Böse, O.; Pausch, M.; Danzer, M.A. Investigating the Thermal Runaway Behaviour of Fresh and Aged Large Prismatic Lithium-Ion Cells in Overtemperature Experiments. Batteries 2023, 9, 159. [Google Scholar] [CrossRef]
- Golubkov, A.W.; Fuchs, D.; Wagner, J.; Wiltsche, H.; Stangl, C.; Fauler, G.; Voitic, G.; Thaler, A.; Hacker, V. Thermal-runaway experiments on consumer Li-ion batteries with metal-oxide and olivin-type cathodes. RSC Adv. 2013, 4, 3633–3642. [Google Scholar] [CrossRef]
- Li, Y.; Lu, Y.; Chen, L.; Hu, Y.-S. Failure analysis with a focus on thermal aspect towards developing safer Na-ion batteries. Chin. Phys. B 2020, 29, 048201. [Google Scholar] [CrossRef]
- Han, Z.; Zhao, L.; Zhao, J.; Xu, G.; Liu, H.; Chen, M. An Experimental Study on the Thermal Runaway Propagation of Cycling Aged Lithium-Ion Battery Modules. Fire 2024, 7, 119. [Google Scholar] [CrossRef]
- García, A.; Pastor, J.V.; Monsalve-Serrano, J.; Golke, D. Cell-to-cell dispersion impact on zero-dimensional models for predicting thermal runaway parameters of NCA and NMC811. Appl. Energy 2024, 369, 123571. [Google Scholar] [CrossRef]
- Willstrand, O.; Pushp, M.; Andersson, P.; Brandell, D. Impact of different Li-ion cell test conditions on thermal runaway characteristics and gas release measurements. J. Energy Storage 2023, 68, 107785. [Google Scholar] [CrossRef]
- Essl, C.; Golubkov, A.W.; Gasser, E.; Nachtnebel, M.; Zankel, A.; Ewert, E.; Fuchs, A. Comprehensive Hazard Analysis of Failing Automotive Lithium-Ion Batteries in Overtemperature Experiments. Batteries 2020, 6, 30. [Google Scholar] [CrossRef]
- Bugryniec, P.J.; Davidson, J.N.; Cumming, D.J.; Brown, S.F. Pursuing safer batteries: Thermal abuse of LiFePO4 cells. J. Power Sources 2019, 414, 557–568. [Google Scholar] [CrossRef]
- Golubkov, A.W.; Scheikl, S.; Planteu, R.; Voitic, G.; Wiltsche, H.; Stangl, C.; Fauler, G.; Thaler, A.; Hacker, V. Thermal runaway of commercial 18650 Li-ion batteries with LFP and NCA cathodes—Impact of state of charge and overcharge. RSC Adv. 2015, 5, 57171–57186. [Google Scholar] [CrossRef]
- Essl, C.; Golubkov, A.W.; Fuchs, A. Comparing Different Thermal Runaway Triggers for Two Automotive Lithium-Ion Battery Cell Types. J. Electrochem. Soc. 2020, 167, 130542. [Google Scholar] [CrossRef]
- Yeow, K.F.; Teng, H. Characterizing Thermal runaway of lithium-ion cells in a battery system using finite element analysis approach. SAE Int. J. Altern. Powertrains 2013, 2, 179–186. [Google Scholar] [CrossRef]
- Hatchard, T.D.; MacNeil, D.D.; Basu, A.; Dahn, J.R. Thermal Model of Cylindrical and Prismatic Lithium-Ion Cells. J. Electrochem. Soc. 2001, 7, 148. [Google Scholar] [CrossRef]
- Kim, G.-H.; Pesaran, A.; Spotnitz, R. A three-dimensional thermal abuse model for lithium-ion cells. J. Power Sources 2007, 170, 476–489. [Google Scholar] [CrossRef]
- Coman, P.T.; Darcy, E.C.; Veje, C.T.; White, R.E. Modelling Li-Ion Cell Thermal Runaway Triggered by an Internal Short Circuit Device Using an Efficiency Factor and Arrhenius Formulations. J. Electrochem. Soc. 2017, 164, A587–A593. [Google Scholar] [CrossRef]
- Ostanek, J.; Parhizi, M.; Jeevarajan, J. A novel method for alleviating numerical stiffness in Li-ion thermal abuse models. J. Power Sources Adv. 2023, 23, 100123. [Google Scholar] [CrossRef]
- Ostanek, J.K.; Parhizi, M.; Li, W.; Kilaz, G.; Crompton, K.R. CFD-Based Thermal Abuse Simulation including Gas Generation and Venting of an 18650 Li-Ion Battery Cell. J. Electrochem. Scociety 2023, 170, 090512. [Google Scholar] [CrossRef]
- Parhizi, M.; Jain, A.; Kilaz, G.; Ostanek, J.K. Accelerating the numerical solution of thermal runaway in Li-ion batteries. J. Power Sources 2022, 538, 231531. [Google Scholar] [CrossRef]
- Sorensen, A.; Utgikar, V.; Belt, J. A Study of Thermal Runaway Mechanisms in Lithium-Ion Batteries and Predictive Numerical Modeling Techniques. Batteries 2024, 10, 116. [Google Scholar] [CrossRef]
- Sun, T.; Wang, L.; Ren, D.; Shi, Z.; Chen, J.; Zheng, Y.; Feng, X.; Han, X.; Lu, L.; Wang, L.; et al. Thermal Runaway Characteristics and Modeling of LiFePO4 Power Battery for Electric Vehicles. Automot. Innov. 2023, 6, 414–424. [Google Scholar] [CrossRef]
- MacNeil, D.D.; Dahn, J.R. Test of Reaction Kinetics Using Both Differential Scanning and Accelerating Rate Calorimetries as Applied to the Reaction of LixCoO2 in Non-aqueous Electrolyte. J. Phys. Chem. A 2001, 105, 4430–4439. [Google Scholar] [CrossRef]
- Peng, P.; Jiang, F. Thermal safety of lithium-ion batteries with various cathode materials: A numerical study. Int. J. Heat Mass Transf. 2016, 103, 1008–1016. [Google Scholar] [CrossRef]
- Abada, S.; Petit, M.; Lecocq, A.; Marlair, G.; Sauvant-Moynot, V.; Huet, F. Combined experimental and modeling approaches of the thermal runaway of fresh and aged lithium-ion batteries. J. Power Sources 2018, 399, 264–273. [Google Scholar] [CrossRef]
- Kim, J.; Mallarapu, A.; Finegan, D.P.; Santhanagopalan, S. Modelling Cell Venting and Gas-Phase Reactions In 18650 Lithium Ion Batteries During Thermal Runaway. J. Power Sources 2020, 489, 229496. [Google Scholar] [CrossRef]
- Shelkea, A.V.; Buston, J.E.; Gill, J.; Howard, D.; Williams, R.C.; Read, E.; Abaza, A.; Cooper, B.; Richards, P.; Wen, J.X. Combined numerical and experimental studies of 21700 lithium-ion battery thermal runaway induced by different thermal abuse. Int. J. Heat Mass Transf. 2022, 194, 123099. [Google Scholar] [CrossRef]
- Hoelle, S.; Scharner, S.; Asanin, S.; Hinrichsen, O. Analysis on Thermal Runaway Behavior of Prismatic Lithium-Ion Batteries with Autoclave Calorimetry. J. Electrochem. Soc. 2021, 168, 120515. [Google Scholar] [CrossRef]
- Hoelle, S.; Zimmermann, S.; Hinrichsen, O. 3D Thermal Simulation of Thermal Runaway Propagation in Lithium-Ion Battery Cell Stack: Review and Comparison of Modeling Approaches. J. Electrochem. Soc. 2023, 170, 060516. [Google Scholar] [CrossRef]
- Verein Deutscher Ingenieure [Hrsg.]. VDI-Wärmeatlas; Springer Vieweg: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Koller, M.; Unterkofler, J.; Glanz, G.; Lager, D.; Bergmann, A.; Popp, H. Radial Thermal Conductivity Measurements of Cylindrical Lithium-Ion Batteries—An Uncertainty Study of the Pipe Method. Batteries 2022, 8, 16. [Google Scholar] [CrossRef]
- Feng, X.; He, X.; Ouyang, M.; Lu, L.; Wu, P.; Kulp, C.; Prasser, S. Thermal runaway propagation model for designing a safer battery pack with 25 Ah LiNi Co Mn O2 large format lithium ion battery. Appl. Energy 2015, 154, 74–91. [Google Scholar] [CrossRef]
- Feng, X.; Lu, L.; Ouyang, M.; Li, J.; He, X. A 3D thermal runaway propagation model for a large format lithium ion battery module. Energy 2016, 115, 194–208. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, Z.; Wu, W.; Gao, L.; Li, Y.; Huang, H.; Huang, Z.; Li, Y.; Song, Y. Three-Dimensional Modeling for the Internal Shorting Caused Thermal Runaway Process in 20Ah Lithium-Ion Battery. Energies 2022, 15, 6868. [Google Scholar] [CrossRef]
- Shi, C.; Zhu, D.; Zhang, L.; Song, S.; Sheldon, B.W. Transfer learning prediction on lithium-ion battery heat release under thermal runaway condition. Nano Res. Energy 2024, 3, e9120147. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Zheng, S.; Lu, Z.; Gui, X.; Xu, W.; Bian, J. Battery lifetime prediction across diverse ageing conditions with inter-cell deep learning. Nat. Mach. Intell. 2023, 7, 270–277. [Google Scholar] [CrossRef]






| Stage | ε | k | Tonset | ΔT | Slope | b | A | Ea | ΔH | R2 | RMSE | σ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [K/s] | [–] | [°C] | [K] | [K2/s] | [K/s] | [1/s] | [J/mol] | [J/m3] | [–] | [–] | [–] | |
| 2 | 0.033 | 100 | 146 | 50 | −1.418 · 104 | 29.27 | 1.027 · 1011 | 1.179 · 105 | 1.575 · 108 | 0.35 | 1.00 | 1.00 |
| 3a | 0.15 | 100 | 196 | 120 | −5.756 · 103 | 15.37 | 3.950 · 104 | 4.786 · 104 | 3.780 · 108 | 0.77 | 0.40 | 0.40 |
| 3b | 245 | 20 | 315 | 511 | 0 | 5.63 | 5.479 · 10−1 | 0 | 1.610 · 109 | −4.17 | 2.50 | 1.10 |
| Part | Base Material | Thermal Conductivity (λ) | Heat Capacity (cp) | Density () |
|---|---|---|---|---|
| [W/mK] | [J/kgK] | [kg/m3] | ||
| Jig, Module Case, Cold Plate | Stainless steel | 21 | 430 | 7770 |
| Copper Plate | Copper | 400 | 384 | 8960 |
| Mica Sheet | Mica | 0.15 | 866 | 2150 |
| DUT | NMC721 | x = 24 y = 24 z = 1 | 1050 | 3200 |
| Wool | Ceramic fiber | 0.2 | 1030 | 96 |
| Thermal Paste | Silicone | 2 | 770 | 2550 |
| Thermal Pad | Aerogel | 0.1 | 1100 | 160 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruth, A.; Hantinger, M.; Machold, A.; Ennemoser, A. An Empirical Multi-Stage One-Step Battery Thermal Runaway Model Based on Arrhenius Reaction Rate Formalism. Batteries 2025, 11, 371. https://doi.org/10.3390/batteries11100371
Ruth A, Hantinger M, Machold A, Ennemoser A. An Empirical Multi-Stage One-Step Battery Thermal Runaway Model Based on Arrhenius Reaction Rate Formalism. Batteries. 2025; 11(10):371. https://doi.org/10.3390/batteries11100371
Chicago/Turabian StyleRuth, Alexander, Martin Hantinger, Alexander Machold, and Andreas Ennemoser. 2025. "An Empirical Multi-Stage One-Step Battery Thermal Runaway Model Based on Arrhenius Reaction Rate Formalism" Batteries 11, no. 10: 371. https://doi.org/10.3390/batteries11100371
APA StyleRuth, A., Hantinger, M., Machold, A., & Ennemoser, A. (2025). An Empirical Multi-Stage One-Step Battery Thermal Runaway Model Based on Arrhenius Reaction Rate Formalism. Batteries, 11(10), 371. https://doi.org/10.3390/batteries11100371







