Passivity-Based Control for Transient Power Sharing and State of Charge Restoration in a Semi-Active Supercapacitor-Battery System
Abstract
1. Introduction
2. Background
2.1. Filter-Based Technique
2.2. SoC Recovery for SC
2.3. Passivity-Based Control Design
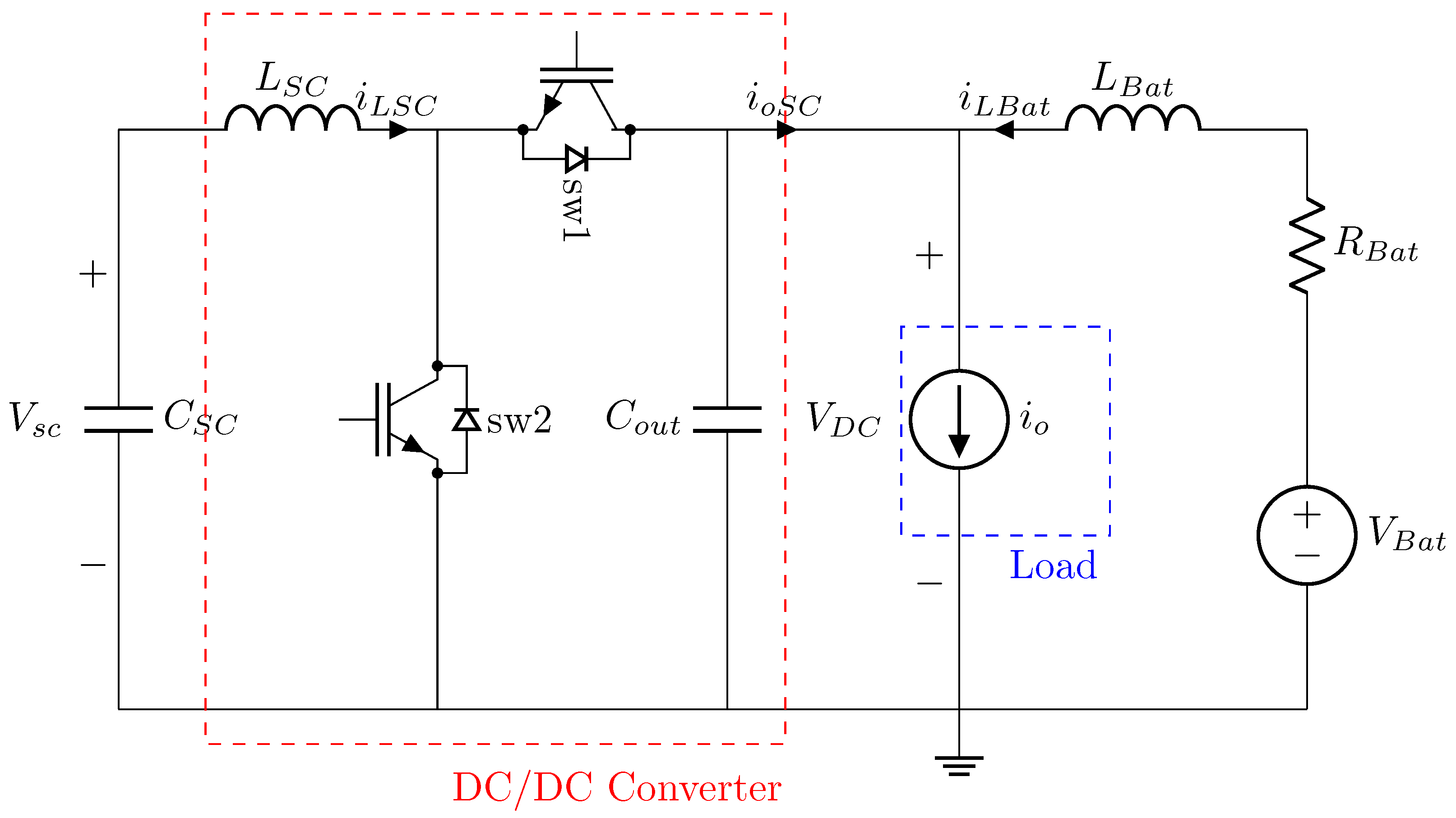
3. Proposed Control Strategy
3.1. Used Filter-Based Technique
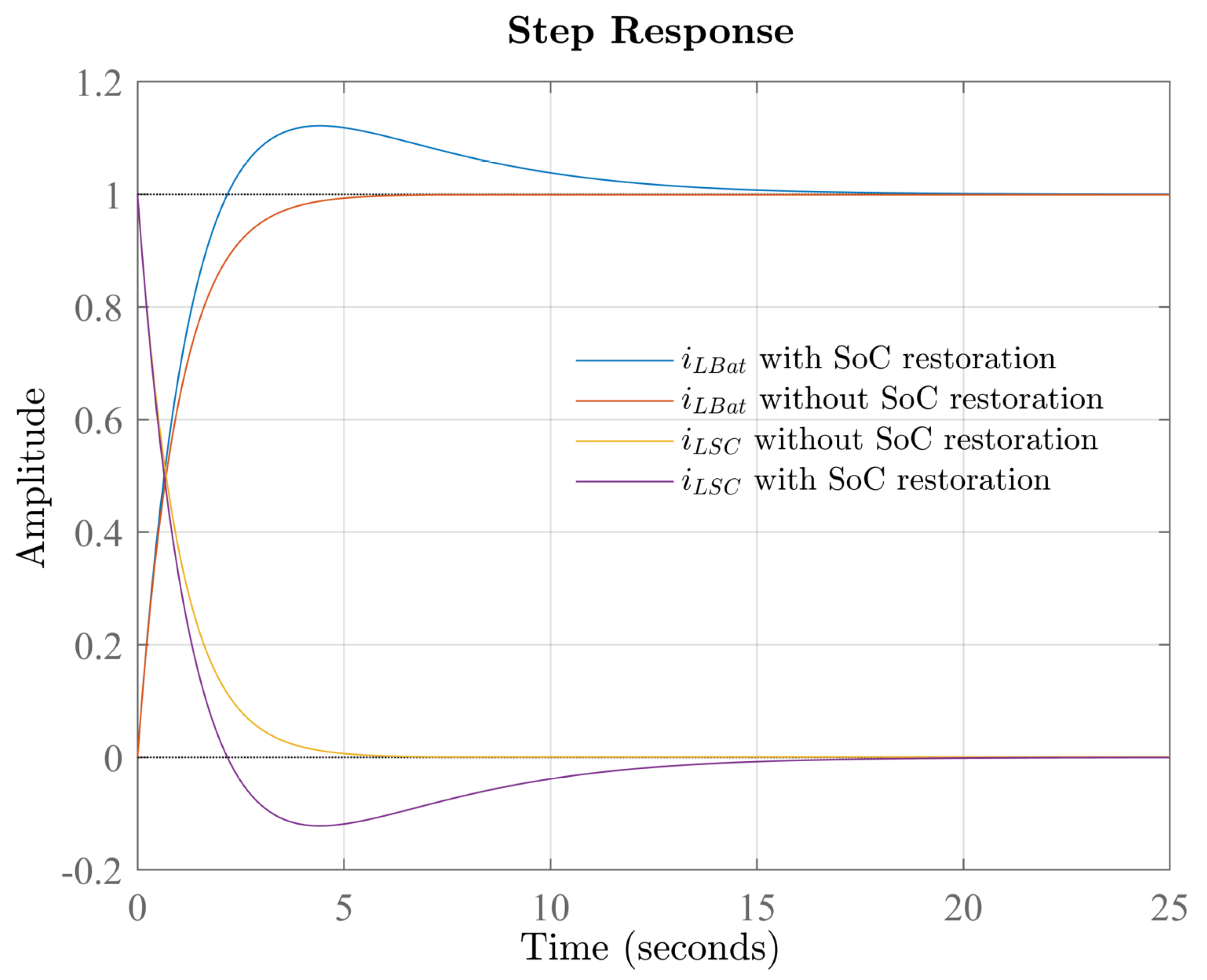
3.2. Proposed SoC Restoration Strategy
3.3. Current Passivity-Based Control Design
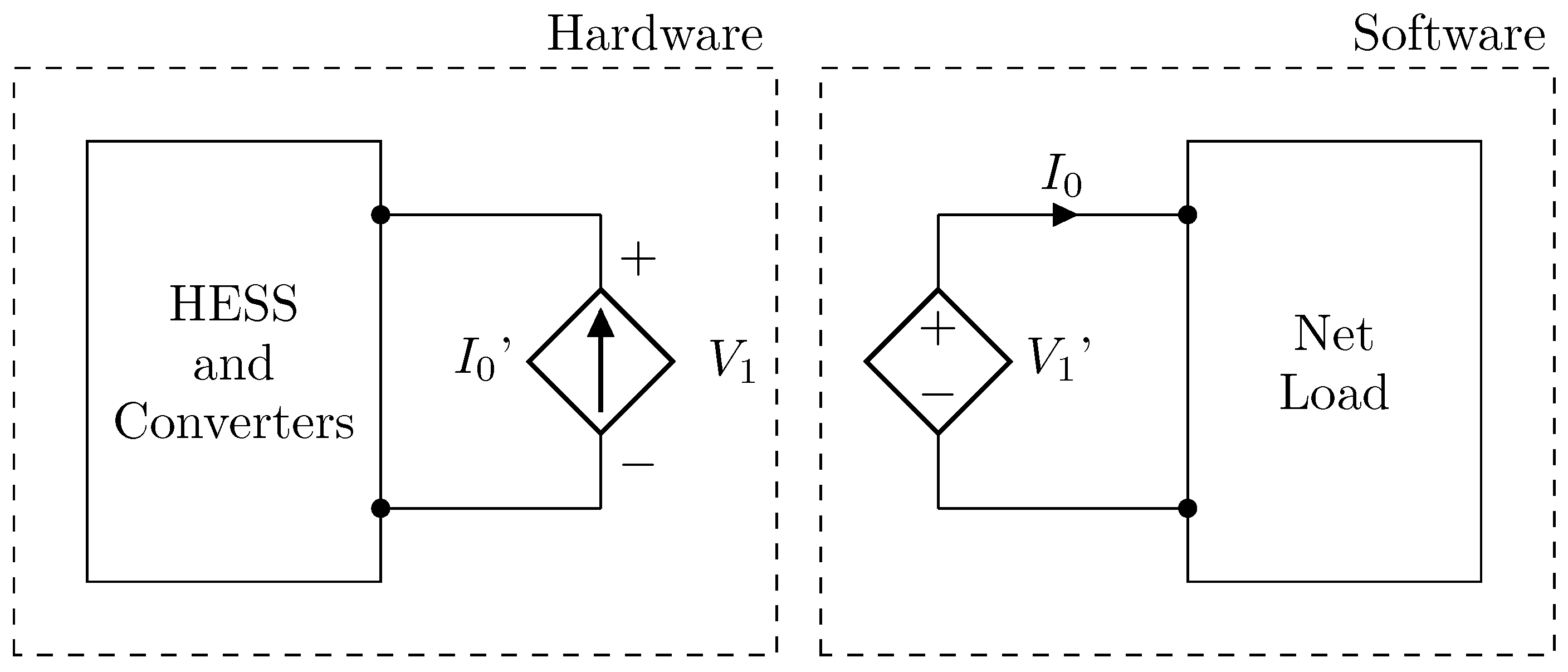
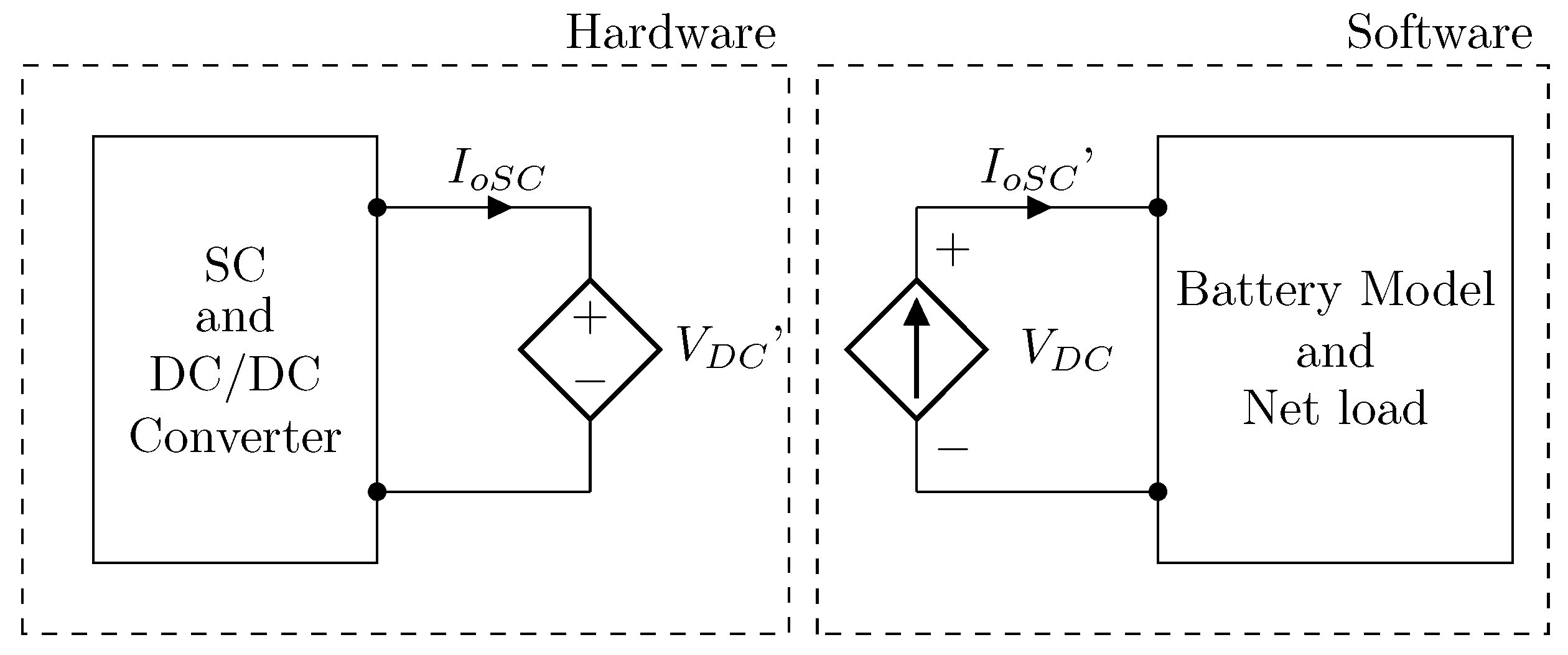
4. PHIL Simulation Setup
5. PHIL and Simulation Results
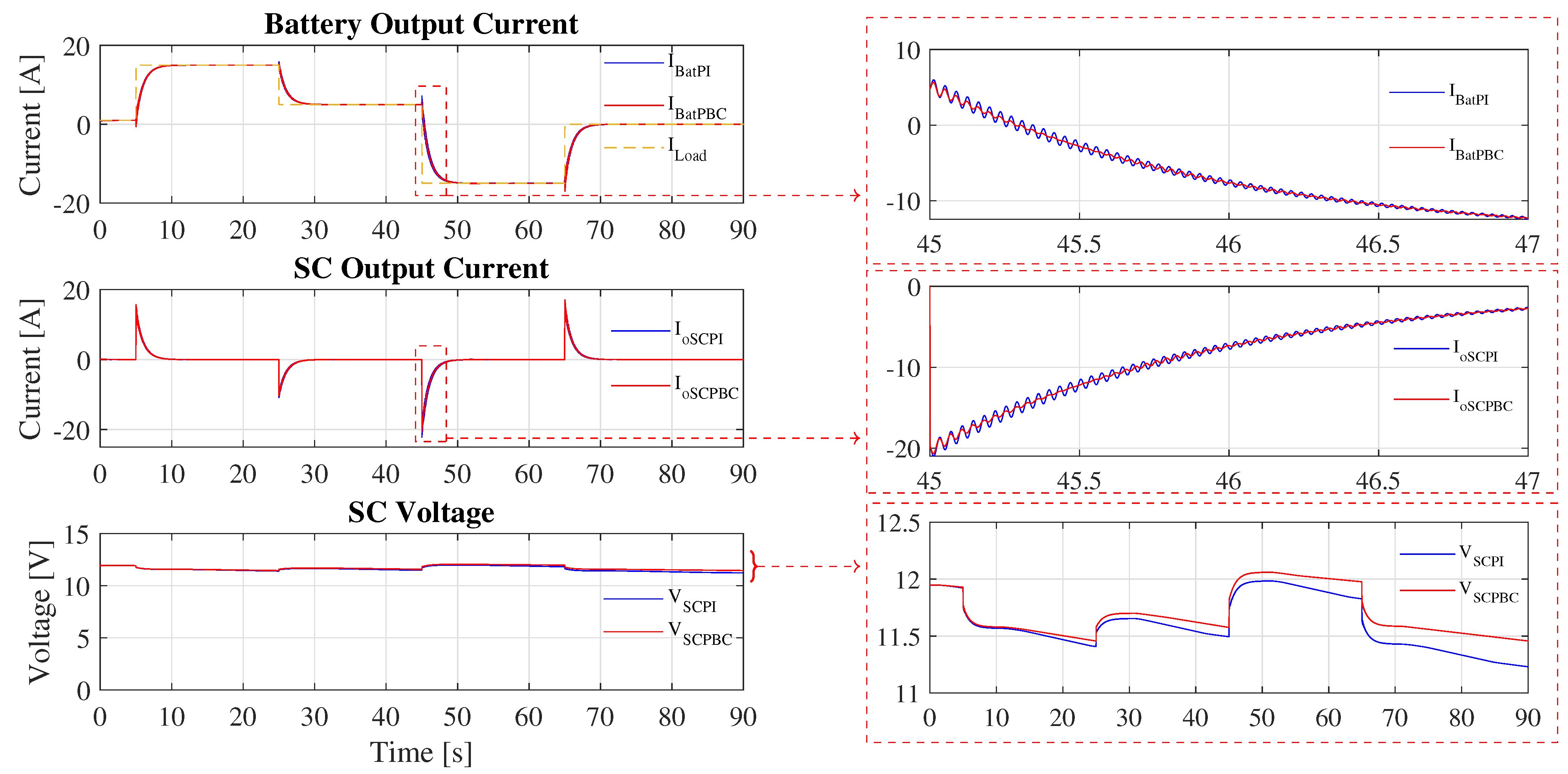
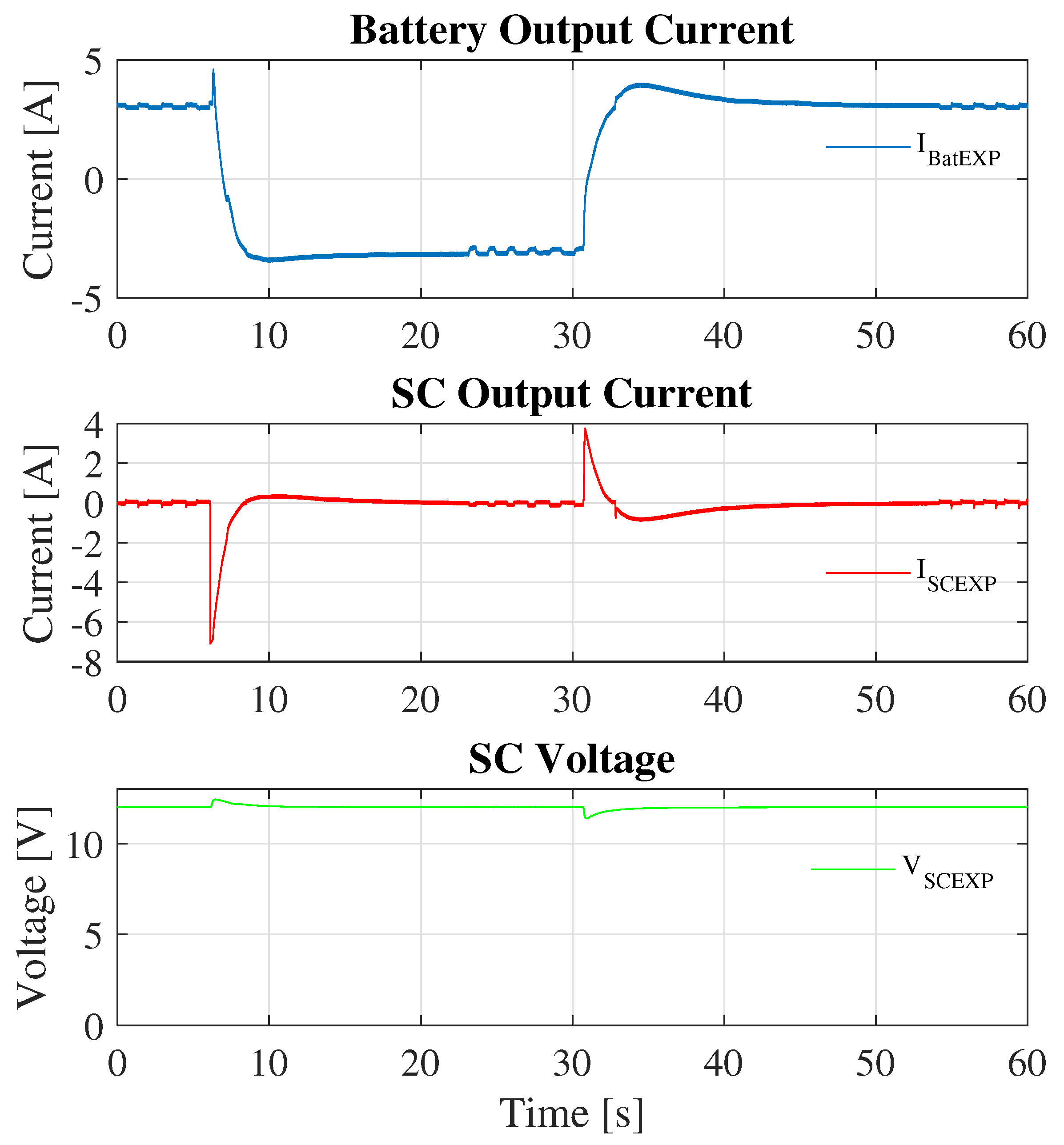
5.1. Simulation Results
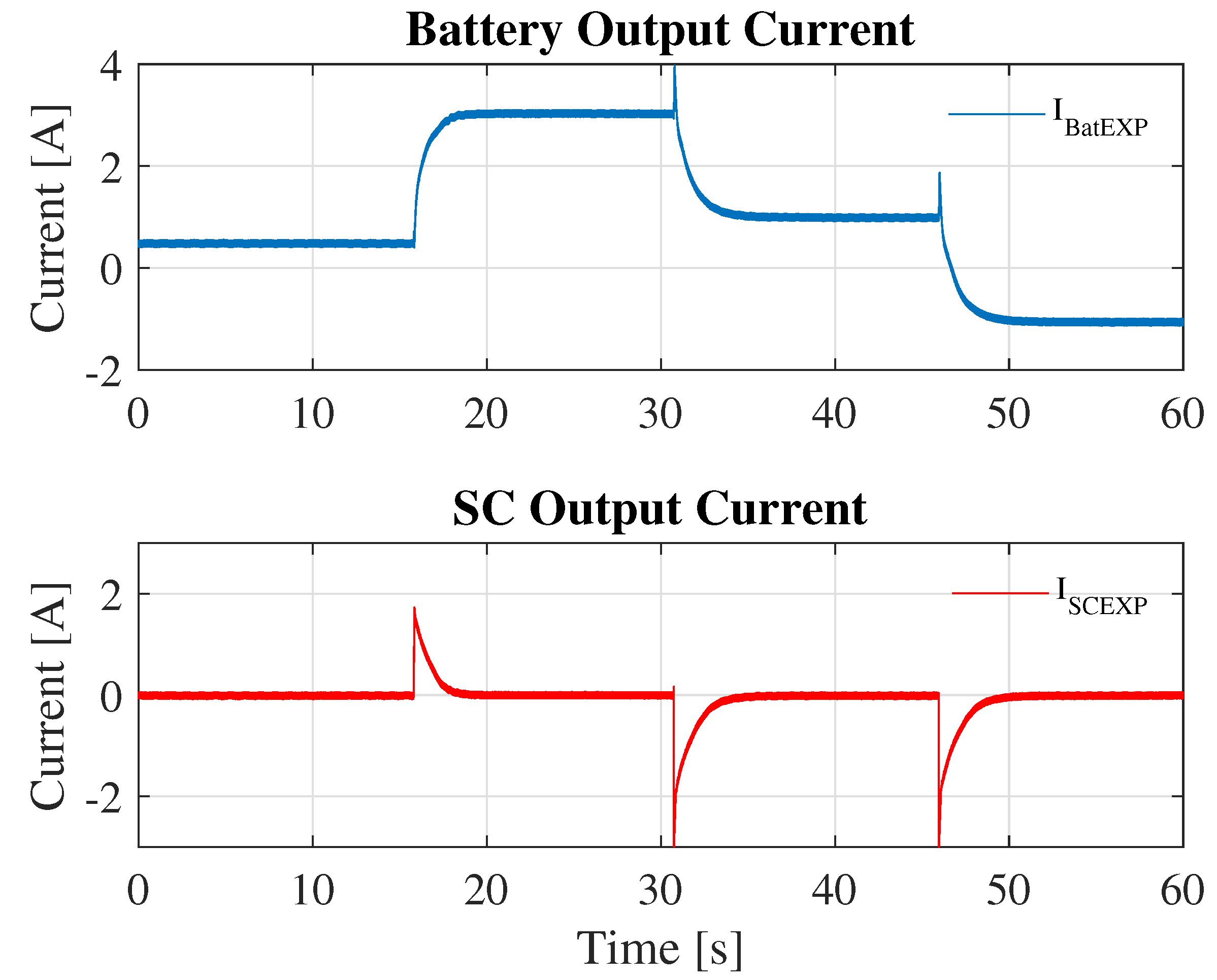
5.2. PHIL Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peñaranda, A.F.; Romero-Quete, D.; Cortés, C.A. Grid-scale battery energy storage for arbitrage purposes: A Colombian case. Batteries 2021, 7, 59. [Google Scholar] [CrossRef]
- Hajiaghasi, S.; Salemnia, A.; Hamzeh, M. Hybrid energy storage system for microgrids applications: A review. J. Energy Storage 2019, 21, 543–570. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, X.; Wang, Z.; Sun, F.; Dorrell, D.G. A review of supercapacitor modeling, estimation, and applications: A control/management perspective. Renew. Sustain. Energy Rev. 2018, 81, 1868–1878. [Google Scholar] [CrossRef]
- Babu, T.S.; Vasudevan, K.R.; Ramachandaramurthy, V.K.; Sani, S.B.; Chemud, S.; Lajim, R.M. A Comprehensive Review of Hybrid Energy Storage Systems: Converter Topologies, Control Strategies and Future Prospects. IEEE Access 2020, 8, 148702–148721. [Google Scholar] [CrossRef]
- Lin, X.; Zamora, R. Controls of hybrid energy storage systems in microgrids: Critical review, case study and future trends. J. Energy Storage 2022, 47, 103884. [Google Scholar] [CrossRef]
- Narvaez, A.; Cortes, C.; Trujillo, C.L. Topologies for Battery and Supercapacitor Interconnection in Residential Microgrids with Intermittent Generation. Ingeniería 2020, 25, 6–19. [Google Scholar] [CrossRef]
- Mali, V.; Tripathi, B.; Kumar, K.; Dwivedi, S.; Behera, R. Exploring various Topology using DC-DC Converter in Hybrid Energy Storage System for Electric Vehicles. In Proceedings of the IECON 2022—48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Takrouri, M.A.; Ayob, S.M.; Idris, N.R.N.; Aziz, M.J.A.; Ayop, R.; Said, M.F.B.M. Comparative Analysis of Passive and Semi-active Hybrid Energy Storage System Topologies for Electric Vehicle. In Proceedings of the 2023 IEEE Conference on Energy Conversion (CENCON), Kuching, Malaysia, 23–24 October 2023; pp. 75–80. [Google Scholar] [CrossRef]
- Rout, T.; Maharana, M.K.; Chowdhury, A.; Samal, S. A Comparative study of Stand-alone Photo-Voltaic System with Battery storage system and Battery Supercapacitor storage system. In Proceedings of the 2018 4th International Conference on Electrical Energy Systems (ICEES), Chennai, India, 7–9 February 2018; pp. 77–81. [Google Scholar] [CrossRef]
- Shchur, I.; Biletskyi, Y. Interconnection and damping assignment passivity-based control of semi-active and active battery/supercapacitor hybrid energy storage systems for stand-alone photovoltaic installations. In Proceedings of the 2018 14th International Conference on Advanced Trends in Radioelecrtronics, Telecommunications and Computer Engineering (TCSET), Lviv-Slavske, Ukraine, 20–24 February 2018; pp. 324–329. [Google Scholar] [CrossRef]
- Aharon, I.; Kuperman, A. Design of semi-active battery-ultracapacitor hybrids. In Proceedings of the 2010 IEEE 26th Convention of Electrical and Electronics Engineers in Israel, Eilat, Israel, 17–20 November 2010; pp. 000593–000597. [Google Scholar] [CrossRef]
- Lerman, C.; Horosov, A.; Kuperman, A. Capacitor semi-active battery-ultracapacitor hybrid energy source. In Proceedings of the 2012 IEEE 27th Convention of Electrical and Electronics Engineers in Israel, Eilat, Israel, 14–17 November 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Yuhimenko, V.; Lerman, C.; Kuperman, A. DC Active Power Filter-Based Hybrid Energy Source for Pulsed Power Loads. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 1001–1010. [Google Scholar] [CrossRef]
- Asensio, M.E.M.; Magallán, G.A.; Angelo, C.H.D. Control de un Sistema Híbrido de Almacenamiento de Energía para vehículos eléctricos. In Proceedings of the 2014 IEEE Biennial Congress of Argentina (ARGENCON), Bariloche, Argentina, 11–13 June 2014; pp. 570–575. [Google Scholar] [CrossRef]
- Kozhushko, Y.; Karbivska, T.; Pavković, D.; Bondarenko, O. Peak Current Control of Battery-Supercapacitor Hybrid Energy Storage. In Proceedings of the 2020 IEEE KhPI Week on Advanced Technology (KhPIWeek), Kharkiv, Ukraine, 5–10 October 2020; pp. 396–401. [Google Scholar] [CrossRef]
- Bhattacharyya, P.; Banerjee, A.; Sen, S.; Giri, S.K.; Sadhukhan, S. A Modified Semi-Active Topology for Battery-Ultracapacitor Hybrid Energy Storage System for EV Applications. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020), Cochin, India, 2–4 January 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, G. Experimental Study on a Semi-Active Battery-Supercapacitor Hybrid Energy Storage System for Electric Vehicle Application. IEEE Trans. Power Electron. 2020, 35, 1014–1021. [Google Scholar] [CrossRef]
- Asensio, M.; Magallán, G.; Angelo, C.D. Control por modos deslizantes de un Sistema Híbrido de Almacenamiento de Energía para vehículos eléctricos. In Proceedings of the 2016 IEEE Biennial Congress of Argentina (ARGENCON), Buenos Aires, Argentina, 15–17 June 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Russo, A.; Cavallo, A. Supercapacitor stability and control for More Electric Aircraft application. In Proceedings of the 2020 European Control Conference (ECC), St. Petersburg, Russia, 12–15 May 2020; pp. 1909–1914. [Google Scholar]
- Trovao, J.P.; Dubois, M.R.; Gomozov, O.; Kestelyn, X.; Bouscayrol, A. A Model Predictive Control with Non-Uniform Sampling Times for a Hybrid Energy Storage System in Electric Vehicle Application. In Proceedings of the 2015 IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Yi, F.; Lu, D.; Wang, X.; Pan, C.; Tao, Y.; Zhou, J.; Zhao, C. Energy Management Strategy for Hybrid Energy Storage Electric Vehicles Based on Pontryagin’s Minimum Principle Considering Battery Degradation. Sustainability 2022, 14, 1214. [Google Scholar] [CrossRef]
- Xu, Q.; Xiao, J.; Wang, P.; Pan, X.; Wen, C. A Decentralized Control Strategy for Autonomous Transient Power Sharing and State-of-Charge Recovery in Hybrid Energy Storage Systems. IEEE Trans. Sustain. Energy 2017, 8, 1443–1452. [Google Scholar] [CrossRef]
- Ortega, R.; García-Canseco, E. Interconnection and Damping Assignment Passivity-Based Control: A Survey. Eur. J. Control 2004, 10, 432–450. [Google Scholar] [CrossRef]
- Ortega, R.; Loria, A.; Nicklasson, P.J.; Sira-Ramirez, H. Passivity-Based Control of Euler-Lagrange Systems; Springer: London, UK, 1998. [Google Scholar] [CrossRef]
- Beltrán, C.A.; Diaz-Saldierna, L.H.; Langarica-Cordoba, D.; Martinez-Rodriguez, P.R. Passivity-Based Control for Output Voltage Regulation in a Fuel Cell/Boost Converter System. Micromachines 2023, 14, 187. [Google Scholar] [CrossRef] [PubMed]
- Bacha, S.; Munteanu, I.; Bratcu, A.I. Power Electronic Converters Modeling and Control; Springer: London, UK, 2014. [Google Scholar] [CrossRef]
- Asensio, M.; Magallán, G.; Amaya, G.; Angelo, C.D. Efficiency and Performance Analysis of Battery-Ultracapacitor based Semi-active Hybrid Energy Systems for Electric Vehicles. IEEE Lat. Am. Trans. 2018, 16, 2581–2590. [Google Scholar] [CrossRef]
- Cabrane, Z.; Lee, S.H. Electrical and Mathematical Modeling of Supercapacitors: Comparison. Energies 2022, 15, 693. [Google Scholar] [CrossRef]
- Sparn, B.; Krishnamurthy, D.; Pratt, A.; Ruth, M.; Wu, H. Hardware-in-the-Loop (HIL) Simulations for Smart Grid Impact Studies. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Viehweider, A.; Lauss, G.; Felix, L. Stabilization of Power Hardware-in-the-Loop simulations of electric energy systems. Simul. Model. Pract. Theory 2011, 19, 1699–1708. [Google Scholar] [CrossRef]
- Lauss, G.F.; Faruque, M.O.; Schoder, K.; Dufour, C.; Viehweider, A.; Langston, J. Characteristics and Design of Power Hardware-in-the-Loop Simulations for Electrical Power Systems. IEEE Trans. Ind. Electron. 2016, 63, 406–417. [Google Scholar] [CrossRef]
- Ren, W.; Steurer, M.; Baldwin, T.L. Improve the Stability and the Accuracy of Power Hardware-in-the-Loop Simulation by Selecting Appropriate Interface Algorithms. In Proceedings of the 2007 IEEE/IAS Industrial & Commercial Power Systems Technical Conference, Edmonton, AB, Canada, 6–11 May 2007; pp. 1–7. [Google Scholar] [CrossRef]
- Marks, N.D.; Kong, W.Y.; Birt, D.S. Stability of a Switched Mode Power Amplifier Interface for Power Hardware-in-the-Loop. IEEE Trans. Ind. Electron. 2018, 65, 8445–8454. [Google Scholar] [CrossRef]
- Fracica-Rodriguez, F.; Acevedo-Iles, M.; Romero-Quete, D.; Martinez, W.; Cortes, C.A. Simulink Model for a Hybrid Energy Storage System in Semi-Active Topology. 2024. Available online: https://github.com/ffracica/PBC-semiactive-HESS.git (accessed on 1 July 2024).





| Variable | Description | Value |
|---|---|---|
| Battery nominal voltage | 24 V | |
| SC nominal voltage | 16 V | |
| SC capacitance | 83 F | |
| Reference value | 12 V | |
| Switching frequency | 35 kHz | |
| Battery inductor | 4 mH | |
| SC converter inductor | 0.5 mH | |
| Converter output capacitor | 4700 μF | |
| k | PBC gain | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fracica-Rodriguez, F.; Acevedo-Iles, M.; Romero-Quete, D.; Martinez, W.; Cortes, C.A. Passivity-Based Control for Transient Power Sharing and State of Charge Restoration in a Semi-Active Supercapacitor-Battery System. Batteries 2024, 10, 322. https://doi.org/10.3390/batteries10090322
Fracica-Rodriguez F, Acevedo-Iles M, Romero-Quete D, Martinez W, Cortes CA. Passivity-Based Control for Transient Power Sharing and State of Charge Restoration in a Semi-Active Supercapacitor-Battery System. Batteries. 2024; 10(9):322. https://doi.org/10.3390/batteries10090322
Chicago/Turabian StyleFracica-Rodriguez, Fabian, Manuel Acevedo-Iles, David Romero-Quete, Wilmar Martinez, and Camilo A. Cortes. 2024. "Passivity-Based Control for Transient Power Sharing and State of Charge Restoration in a Semi-Active Supercapacitor-Battery System" Batteries 10, no. 9: 322. https://doi.org/10.3390/batteries10090322
APA StyleFracica-Rodriguez, F., Acevedo-Iles, M., Romero-Quete, D., Martinez, W., & Cortes, C. A. (2024). Passivity-Based Control for Transient Power Sharing and State of Charge Restoration in a Semi-Active Supercapacitor-Battery System. Batteries, 10(9), 322. https://doi.org/10.3390/batteries10090322







