1. Introduction
To respond positively to the national vision of ‘peak carbon’ and ‘carbon neutrality’, the development of power energy storage systems is crucial. Power lithium-ion batteries (LiBs) have been the focus of close attention in electric power storage systems and electric vehicles (EVs) due to their high output power, high contained energy density, and long service life. However, due to the different fabrication processes of LiBs, noisy, inaccurate, or missing data are present in the data collection process, making it difficult to extract favorable features in each battery charge/discharge profile, and the steps such as feature selection and dimensionality reduction also require complex computational resources. Moreover, currently known methods are difficult to capture short-term patterns and long-term dependency issues in time-series data as well as different layers of parallel processing power and computational speed to such an extent that higher accuracy and robustness in estimating battery state of health (SOH) cannot be achieved [
1,
2]. Therefore, it is important to accurately and promptly detect and assess the SOH of LiBs. Traditional physical model-based methods are usually based on the equivalent circuit model of the battery, and state estimation is performed by measuring parameters such as voltage, current, and temperature of the battery, combined with electrochemical characteristics [
3,
4]. These methods have achieved some results in the field of LiB SOH estimation, but there are some problems and limitations. Firstly, complex battery systems and variable operating conditions lead to challenging physical model building and parameter estimation. Secondly, physical models often require more a priori knowledge and experimental data support and are less adaptable to new battery materials and structures. In addition, physical models cannot fully exploit the potential patterns and features in battery data. Furthermore, understanding the impacts of abuse testing on battery performance, as highlighted by Gotz et al. [
5], underscores the necessity of developing robust and reliable SOH estimation methods.
To assess the aging levels of LiBs, SOH is suggested as a critical metric for evaluating battery capacity [
6,
7]. In this study, SOH is interpreted through capacity metrics, where a fall in SOH below 80% indicates that the lithium battery is beyond its safe operational life and should be replaced [
8,
9]. Lately, the advancement of deep learning has opened up fresh avenues for SOH assessments of LiBs. Utilizing neural networks, deep learning is an approach in machine learning [
10] capable of independently recognizing features and patterns by creating layered neural network models. This method exceeds conventional approaches by offering superior representation and broadening capabilities, enabling the identification of nonlinear relationships and intricate structures within data. Consequently, leveraging deep learning for SOH assessments in LiBs might enhance the precision and durability of these evaluations. SOH evaluation techniques have been outlined and reviewed by Xiong et al. [
11] in 2023 and previously in 2015 by Lin et al. [
12], who sorted these techniques into three types: (1) direct measurement methods; (2) model-based methods; (3) data-driven methods.
Methods for direct SOH measurement mainly involve measuring terminal voltages, currents, and impedances. For example, a common approach is to use the Coulomb counting method [
13] or the electrochemical impedance spectroscopy (EIS) method [
14]. Although the direct measurement method is simple in principle and can directly characterize the capacity and internal resistance of LiBs, this method requires expensive and complex equipment and experimental environments, which are less accessible for practical applications [
15]. In contrast, model-based approaches focus on SOH estimation by establishing a mapping between measured variables and health states [
16]. For example, equivalent circuit models [
17] or electrochemical models [
18] can be used. However, the accuracy of model-based approaches depends on the model chosen, and different models are selected for different battery types and must be iteratively corrected. Moreover, it is difficult to obtain accurate model parameters in reality [
19].
With the advancement of the information era, data-driven methods are increasingly prevalent in both industry and academia. These data-driven methods generally depend on operational variables such as current, voltage, and temperature from LiBs, while often neglecting the aging mechanisms and chemical transformations within the batteries. Li et al. [
20] implemented a two-layer integrated limit learning machine algorithm for the joint estimation of SOH and SOC in LiBs, which improved the estimation’s accuracy and robustness. Wu et al. [
21] refined a particle filtering algorithm for the joint estimation of SOH and SOC, achieving high accuracy through the use of internal resistance for feature extraction. Hsing et al. [
22] introduced a Bayesian tracking method for SOH estimation using historical data, coupled with an enhanced optimized decision tree (DT), which ensures highly robust and accurate estimation results. Kong et al. [
23] developed a hybrid model that merges long short-term memory with a deep convolutional neural network, integrating a unique health feature that connects the internal dynamics of LiBs with external aging features and has a strong correlation with capacity. The application of various models in machine learning and neural networks for the estimation of SOH in LiBs is on the rise [
24,
25,
26,
27]. Neural networks have become indispensable tools in machine learning, especially deep learning, where they solve complex nonlinear issues by interpreting patterns and features in data [
27,
28]. Prominent examples include recurrent neural networks (RNNs) [
29], long short-term memory (LSTM) networks [
30], and Transformers [
31]. These models excel at utilizing historical data to uncover hidden patterns and significantly enhance the estimation accuracy of the SOH of LiBs.
Despite some advances in battery SOH estimation through 1D CNN, GRU, LSTM, and various models, opportunities still exist to enhance precision and robustness. To advance SOH estimation further, a novel strategy involving the introduction of a Temporal Fusion Memory Network (TFMN) is proposed. Initially, the framework incorporates a 1D CNN as an initial layer to derive deeper local insights from the input data. This 1D CNN is adept at identifying immediate patterns in time-series data, thereby enriching the data context for subsequent, more complex model layers. Next, data progress to a channel self-attention module (CSAM), which avoids the zero-denominator instability issue and enhances focus on pertinent attributes. Subsequently, the model maximizes LSTM capabilities for time-series management, simultaneously integrating the Transformer’s self-attention features to elucidate series connections more effectively. This integration allows the LSTM to manage extended temporal dependencies, while the attention mechanism’s parallel processing faculties expedite both the training and analysis phases. Ultimately, a comprehensive prediction is executed through two interconnected layers.
In summary, the contributions of this paper are fourfold:
In this paper, a multi-feature hybrid feature extraction is proposed, i.e., time difference at equal voltage intervals, voltage difference at equal time intervals, cumulative integral of voltage change, and peak IC curve slope. These feature extraction methods effectively focus on factors affecting various aspects of battery aging. By simplifying the data processing process, the trend of battery health state over time can be effectively captured, providing a solid foundation for subsequent model construction.
In this paper, a new type of attention module, i.e., channel self-attention module (CSAM, channel self-attention module), is proposed. Tanh is chosen as the activation function. Compared with the self-attention module, this module does not have the instability problem of a zero denominator, allowing the model to pay more attention to the correct features while inhibiting the extraction of irrelevant features. Additionally, it does not have the problem of gradient disappearance or gradient explosion, thus improving the performance of the network.
In this paper, a novel framework for SOH estimation leveraging diverse features is introduced. Components such as 1D CNN, CSAM, LSTM, and multi-head self-attention are integrated to create a cohesive and efficient model architecture. The 1D CNN serves as the foundational layer, adeptly discerning the local characteristics of the battery data and converting these into more complex inputs, thereby establishing a robust groundwork for the model’s efficacy. Additionally, the integration of CSAM with LSTM and the incorporation of the Transformer’s self-attention feature into the framework facilitate a deeper understanding of the temporal connections within battery data, effectively addressing challenges of long-term dependencies. Furthermore, the LSTM’s synergy with the attention mechanism permits an exhaustive analysis of varied information layers within sequential data, thereby enhancing the model’s overall estimation capabilities. This multi-faceted and collaborative approach not only elevates the precision of estimations but also enhances the model’s adaptability to diverse data variations.
The robustness of the proposed model was experimentally confirmed even with noise present. Noise was incorporated into the model inputs to mimic potential data fluctuations in an actual setting. Impressively, the model still excelled under noisy conditions, further substantiating its sturdiness and dependability. This indicates that the model not only elevates precision but also sustains top-notch performance in volatile settings, offering a steadfast approach for the battery SOH estimation challenge.
The remainder of this paper is organized as follows: In
Section 2, the LiB experimental dataset and the four feature extraction methods employed are detailed. In
Section 3, the proposed innovative model TFMN, which fuses LSTM and attention modules and combines the properties of 1D CNN to better solve the battery SOH estimation problem, is illustrated. Then, in
Section 4, the experimental results are presented, along with an in-depth discussion and analysis of the effectiveness of the proposed TFMN. Finally, conclusions that summarize the main contributions and findings of this paper are provided in
Section 5.
2. Dataset and Feature Extraction
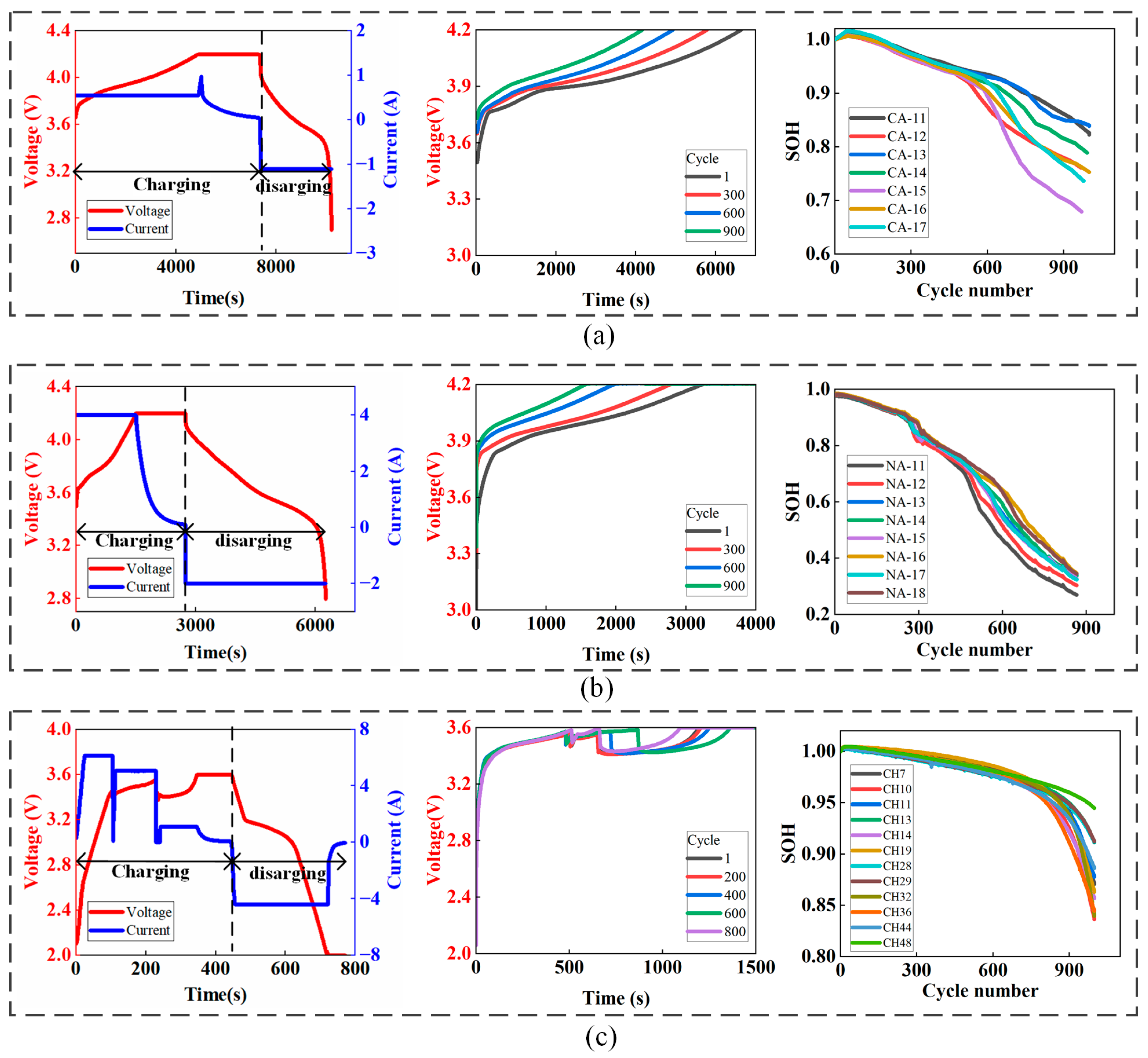
Datasets play a crucial role in machine learning, and having a sufficient dataset of LiBs helps to build robust general evaluation models. We established an experimental platform for battery cycle life testing with the Neware CT-4000 test equipment (Neware, Shenzhen, China), with a voltage and current error of 0.05%; two different charging and discharging conditions were designed using the platform, and the experiments were uniformly conducted in a temperature chamber (MGDW-408-20H, with a deviation of ≤±1 °C) at a constant temperature of 25 °C, as shown in
Figure 1, and were performed on dataset A and dataset B. To verify the generality of the model, the open-source dataset C, the open-source LiB dataset of Severson et al. from the Toyota Research Institute (in collaboration with Stanford University and the University of Maryland), was used again [
32,
33]. Due to the limitations of capacity measurements in practical applications, in this section, four features are extracted for SOH estimation based on battery cycling curves reflecting the aging mechanism of the battery. The focus of this paper will concentrate on the dataset used and the extraction method of the health features. The specifications of the three datasets are shown in
Table 1.
2.1. Dataset
Dataset A: The first dataset used in this study was measured on an experimental platform. Seven CS2 batteries from the same batch, labeled CA-11, CA-12, CA-13, CA-14, CA-15, CA-16, and CA-17, with a nominal capacity and nominal voltage of 2 Ah and 3.6 V, respectively, were selected. The experiments were carried out uniformly in a thermostat box (MGDW-408-20H, with a deviation of ≤±1 °C) at a constant temperature of 25 °C. The experimental setup included five battery pretreatments. The experimental setup consisted of 5 cycles of battery pretreatment, 50 cycles of battery aging, and 20 cycles of battery capacity calibration. As can be seen from each battery aging cycle curve, the battery was charged to 4.2 V at a constant current of 0.25 C and then continued to be charged at a constant voltage of 4.2 V until the current dropped to 0.05 A. After complete charging, the battery was depleted at a rate of 1 C until the terminal voltage dropped below the cut-off value of 2.7 V. The battery was fully charged and then depleted at a rate of 1 C until the terminal voltage dropped below the cut-off value of 2.7 V.
Dataset B: The experimental platform for the second dataset used in this study is the same as that of dataset A. The second dataset used in this study is the same as dataset A. Eight ICR18650P batteries from the same batch, labeled NA-11, NA-12, NA-13, NA-14, NA-15, NA-16, NA-17, and NA-18, with a nominal capacity and voltage of 2 Ah and 3.6 V, respectively, were selected and operated in the same steps. The batteries were first charged at a constant current of 2 C until the battery voltage reached 4.2 V. After a short rest, the batteries were fully charged using a constant voltage (CV) of 4.2 V with a cut-off current of 0.05 C and a cut-off voltage of 4.2 V. After resting for one hour, the batteries were discharged using 1 C until the voltage dropped to 2.7 V. The battery voltage was then reduced to 2.7 V.
Dataset C: The third dataset used in this paper uses the open-source lithium-ion battery dataset from the Toyota Research Institute (in collaboration with Stanford and Maryland) and Severson et al. [
32]. The dataset obtained from the Toyota Research Institute contains information on various aspects of the aging process, such as voltage, current, temperature, and charging time, to give a side-by-side view of the battery aging process.
Figure 2c shows the current and voltage variation curves, voltage curves, and capacity decay curves during a complete charge/discharge process. The work step setup firstly charges the battery with 5.5–6.1 C constant current charging until the voltage reaches 3.6 V. In the second step, the battery is charged with 2–4 C constant current until the voltage reaches 3.6 V. After that, the battery is charged with 1 C constant current and constant voltage. The upper and lower potentials are 3.6 volts and 2.0 volts, respectively, consistent with the manufacturer’s specifications. After some cycles, the batteries are charged at a constant voltage. The upper limit potential may be reached during rapid charging. All batteries are discharged at 4 C.
2.2. Feature Extraction
Battery cycle life can be expressed based on external characteristics such as voltage, internal resistance, and capacity, which can reflect the deterioration and health of a battery. To accurately estimate the SOH of a battery, it is crucial to extract characteristic variables that reliably reveal the aging trend of the battery.
Temporal features are the most direct indicators of changes in battery health status. The deep learning model learns complex nonlinear relationships from a large amount of data by learning time features associated with battery life trends. However, due to the short decay cycle of fast-charging batteries, the limited number of cycles and the amount of data limit the learning depth of the model and are among the main reasons for the gradient disappearance. In our battery dataset A, the SOH decayed to 80% in 6 months, and the fast-charging dataset B and dataset C took 1 month and 3 months, respectively. Temporal features are important in battery SOH estimation. They can provide information about battery degradation, historical behavior, dynamic changes, and failure warnings, helping the model to estimate battery health more accurately. Therefore, battery features such as the time difference of equal voltage intervals, the voltage difference of equal time intervals, the cumulative integral of the voltage change, and the peak slope of the IC curve were further extracted based on the time dimension through feature data analysis.
Fast-charging systems may use different charging strategies, including different combinations of voltage and current, depending on the chemistry of the battery, to optimize charging rate and battery life. However, fast charging may cause the battery to overheat, and to avoid safety issues and reduced life, the system monitors the battery temperature and adjusts the charging rate. This may lead to different stages in the charging process, and the fast-charging battery data are divided into multiple segments. Extracting features by time dimension leads to risks such as difficulty in model convergence, reduced generalization ability, and overfitting due to easy cross-confusion in extracting data from multiple segments together within the same cycle. Therefore, we utilized multi-segment data for feature extraction by automatically calculating the initial and end values of each segment of the cycle for battery data.
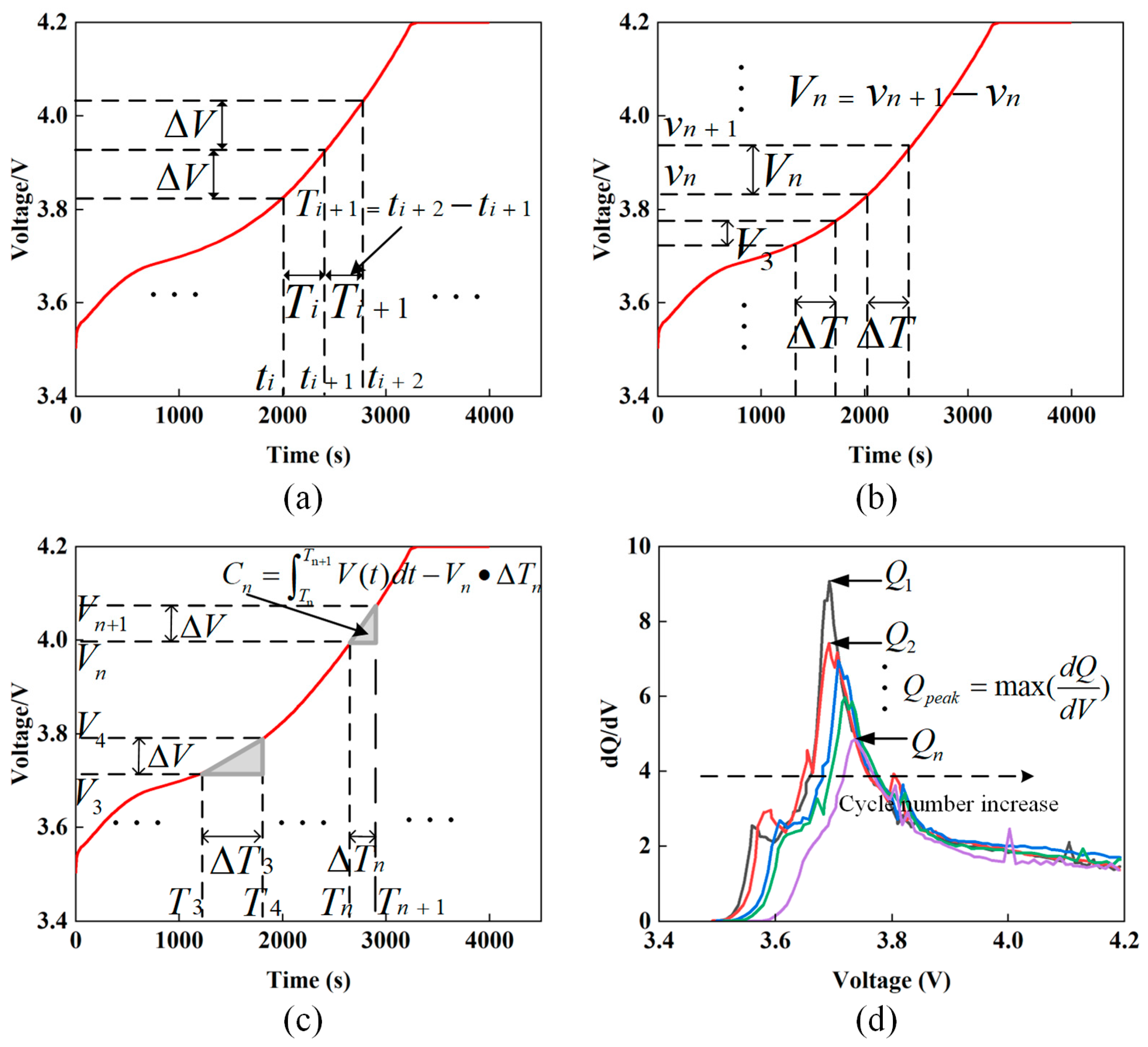
Figure 3 shows the extraction process of four features, where
Figure 3a,b are direct measurement features, which represent the time difference of equal voltage intervals and the voltage difference of equal time intervals, respectively.
Figure 3c,d shows the secondary measurement features, which represent the cumulative integral and differential capacity curve slope peaks of the voltage change, respectively.
2.2.1. Time Difference between Equal Voltage Intervals
Each battery underwent charge/discharge cycles during an aging process experiment, and the related experimental data for these cycles were collected. A specific charging voltage profile from these data was selected, and the voltage spectrum during charging was segmented into equal parts. The duration allocated to each segment was then identified as a feature. As depicted in
Figure 3a, a voltage spectrum from 3.6 to 4.2 V is established as the comprehensive interval of charging for both dataset A and dataset B, indicated by
.
represents the voltage span for each attribute, termed as the voltage sampling period or voltage resolution. The duration necessary for a consistent voltage sampling interval is selected as the attribute. Therefore, the total count of voltage sampling intervals, denoted as
n, is referred to as the count of attributes, and its mathematical formulation is presented in Equation (1):
The
operation truncates the value to an integer. The entire voltage interval
is segmented into equal
subintervals, some of which may be unoccupied. Consequently, the characteristic
is illustrated in Equation (2):
where
and
represent the beginning and conclusion of the
characterization subinterval, respectively. Consequently, each charging cycle of the battery is defined by
characteristic variables.
The same method is used for dataset C. The difference is that the voltage range of dataset C is 2.0–3.6 V.
2.2.2. Voltage Difference at Equal Time Intervals
Battery data, as time-series data, especially in the estimation of SOH decay, rely heavily on voltage features. The voltage difference in equal time intervals was calculated. From
Figure 3a, with an increase in the number of cycles, the duration of charging for each cycle shortens, and the variation in voltage across different cycles within the identical charging time interval progressively grows. Therefore, it can be deduced that the voltage difference within equal time intervals contains features of battery degradation. As shown in
Figure 3b, calculating the voltage difference allows these non-uniform changes to be captured more precisely.
The maximum and minimum values of time and the number of samples
are calculated for each cycle to determine the start and end voltages. The next feature extraction operation will be carried out within the voltage blocks divided based on the time intervals, and it should be noted that the calculation of the number of samples
has a direct impact on the next feature extraction. The number of time sampling intervals
and the equation of the voltage change in equal time intervals are as follows:
where
and
are the start and end voltages of the
feature subinterval, respectively, and
is the voltage difference, a feature related to the voltage dynamics during charging.
2.2.3. Cumulative Integral of Voltage Change
It is easy to see in
Figure 3a that the voltage curve is shifted to the upper left in the decay cycle of the fast-charging battery, and the slope of the voltage curve changes with it, with a slower voltage rise at the beginning of the charging period and a slower voltage rise when the charging is near completion. However, the simple instantaneous voltage value may not be able to fully reflect the state of the battery, while the cumulative integration can accumulate the voltage changes over a period, and the voltage changes are observed by means of cumulative integration, and the small voltage changes will be gradually amplified in the process of accumulation, thus more accurately characterizing the battery. In
Figure 3c, it can be seen that the cumulative integral
of the voltage profile in the nth second time interval is to the upper right of the cumulative integral
at the initial stage, and there is a significant difference in size.
The
in
Figure 3c represents the cumulative integral of the change in battery voltage during the charging cycle, i.e., the energy input of the battery during the charging process, calculated as follows:
where
denotes the nth time block of division, where
and
are determined by the time block of division.
2.2.4. IC Curve Peaks
The IC curve, which is the curve of current versus voltage during battery charging and discharging, contains many intuitive aging features. These features are highly correlated with the SOH of the battery [
34] and thus can be used to estimate the SOH of the battery. The area of the IC curve is used as a feature that is easy to obtain directly, but due to the small amount of data for a single cycle of a fast-charging battery, calculating the area of the integral may become difficult because the integral usually requires many data points to accurately approximate the curve of the function. the IC curve is relatively stable in the pre-cycling period However, it appears to be extremely unstable in the later data, and it is difficult to obtain effective confirmation of both the area and the peak value. Moreover, the integration operation generates the problem of error accumulation and noise amplification, and this instability may lead to the problem of gradient explosion, which reduces the SOH prediction accuracy. Gradient explosion refers to the fact that during the training process of a deep neural network, the gradients of the network parameters become very large, leading to excessive weight updates, which results in a rapid expansion of the network’s weight values and the loss of an effective representation of the data.
Thankfully, it was found that the position of the peaks during the charging process gradually shifted to the right compared to the first cycle, with the difference being obvious. Therefore, the calculation of area and peak height data, which are prone to anomalies, was avoided, and the most intuitive data, the peak horizontal position, was chosen. As shown in
Figure 3d, there is a clear horizontal displacement from
to
. The formula for calculating the horizontal value of the peak voltage slope is as follows:
where
is used to measure the horizontal value of the maximum slope of the change in battery voltage, the horizontal value of the maximum value of the rate of voltage rise of the battery during charging.
2.3. Correlation Analysis
To establish the relationship between the extracted health features and the state of health (SOH) of lithium-ion batteries, we conducted a comprehensive correlation analysis using all battery data features described in
Section 2.2. This analysis employed the Pearson correlation coefficient to quantify the linear relationships between these features and the SOH, aiming to enhance the accuracy and predictive power of our SOH estimation models.
Utilizing the Pearson correlation coefficient,
, we calculated this statistic according to the following formula:
Here, and represent the feature values and SOH measurements, respectively, with and being their mean values over the dataset.
Given the consistent operational conditions for individual batteries within each dataset, a representative subset comprising two batteries from each dataset was selected for the correlation analysis.
Table 2 displays the Pearson correlation coefficients for selected battery units CA-13, CA-16, NA-12, NA-18, CH-14, and CH-44. Evaluations were conducted on metrics including time differences, voltage differences, cumulative voltage, and IC curve peaks. The correlation coefficients, with absolute values ranging from 0.86 to 0.94, substantiate a significant linear relationship between the health features and the state of health (SOH), as presented in
Table 2.
This feature exhibits high positive correlations across all datasets (ranging from 0.87 to 0.94), indicating that the time batteries spend at specific voltage intervals is closely linked to their health status. A greater time difference typically suggests a faster discharge rate at reaching the same voltage, which may be an early indicator of declining battery health.
- 2.
Voltage Difference at Equal Time Intervals
This feature shows high negative correlations (−0.86 to −0.93), meaning that the change in voltage over equal time intervals is inversely related to battery health deterioration. An increase in voltage difference may indicate an increase in internal impedance, reflecting accelerated aging of the battery.
- 3.
Cumulative Integral of Voltage Change
This feature also demonstrates very high positive correlations (0.89 to 0.94) across all datasets, indicating a direct positive correlation with battery SOH. A higher cumulative integral of voltage change typically suggests that the battery releases energy more quickly during discharge, which may be related to a reduction in battery capacity.
- 4.
IC Curve Peaks
This feature exhibits high negative correlations with battery SOH (−0.87 to −0.92), indicating that variations in IC curve peaks are inversely related to battery health. A decline in IC curve peaks usually reflects a decrease in chemical reactivity during the charging and discharging processes, which is a significant indicator of battery aging.
The analysis above reveals clear linear relationships between the extracted health features and the battery’s state of health (SOH). The trends in these features not only provide a quantitative basis for assessing the health status of batteries but also help in predicting future battery performance. Therefore, integrating these features is crucial for enhancing the accuracy and predictive power of battery SOH estimation models.
2.4. Sliding Window Module
In battery SOH (state of health) estimation, the sliding window method for time series is frequently employed to manage the sequential data and glean insights into battery behavior and performance [
35]. The function of the sliding window is outlined as follows:
Data sampling and processing: The sliding window module is used to sample and process the historical data of the battery. It selects data over a period by sliding a fixed-size window, which will be used for subsequent feature extraction.
Feature extraction: The health state of the battery is influenced not only by present conditions but also by past actions. The sliding window technique in time series allows for the utilization of historical data as a framework to extract relevant features. These characteristics can offer valuable insights into the battery’s condition and activities, facilitating a finer assessment of the SoH (state of health) of the battery. By modifying the dimensions of the sliding window, it becomes feasible to manage the equilibrium between leveraging historical data and sustaining immediate performance.
Data Alignment: The sliding window module can help align temporal data. In the battery SOH estimation task, batteries with different operating conditions have different charge/discharge cycles and sampling rates. Through the sliding window module, the data from different batteries can be aligned to the same time window to ensure the consistency of the subsequent SOH estimation.
Sequence modeling: A sliding window for time series can be employed to build sequence models, including recurrent neural networks (RNNs) and long short-term memory (LSTM) networks, among others. These models are capable of accounting for the temporal aspects of the data, thereby more effectively capturing the dynamics of battery actions. Utilizing data within a sliding window as input, the model is able to discern the evolving patterns of battery state changes over time, enabling it to forecast future battery health states.
Therefore, the use of time-series sliding windows in battery SoH prediction facilitates the extraction of useful features from time-series data and the building of appropriate sequential models to improve the accuracy and robustness of predictions.
In the experiments of this paper, our data consist of a
loop of feature vector
and SoH labels
, which can be represented by Equations (8) and (9):
denotes one of the cycles, and
. The size of the time-series sliding window is then set to
w, and the time step of the estimation is set to
. The sliding window was utilized to construct the inputs for model training as in Equations (10) and (11):
where
and
denote the feature matrices and label vectors used to make predictions for cycle
, respectively, and
denotes the
-steps of advance prediction. Thereby, a set of sequence pairs comprising multivariate feature matrices and corresponding SOH label vectors is obtained. A set of training batches is created by combining the sequence pairs based on sequence lengths. In general, if the batch size is large, it may return a local optimum; if the batch size is too small, it may be difficult to achieve convergence. Therefore, it is important to set the appropriate batch size. In this paper, the batch size is set to 16.
3. Methodology
In this part, an in-depth explanation of the suggested model, Temporal Fusion Memory Network (TFMN), for estimating the SOH of LiBs is provided. Traditional models might struggle in certain scenarios, especially when managing long-term dependencies, and are often used to solve SOH estimation for datasets under standard charging conditions. There are very few models addressing SOH estimation for fast-charging datasets. To address this problem, an innovative SOH estimation model is proposed. TFMN effectively captures short-term patterns and long-term dependencies in battery data by fusing the powerful capabilities of a one-dimensional convolutional neural module, a channel self-attention mechanism, a long short-term memory module, and a multi-head self-attention module. With four feature extraction and sliding window techniques, a new efficient method for battery SOH estimation is provided.
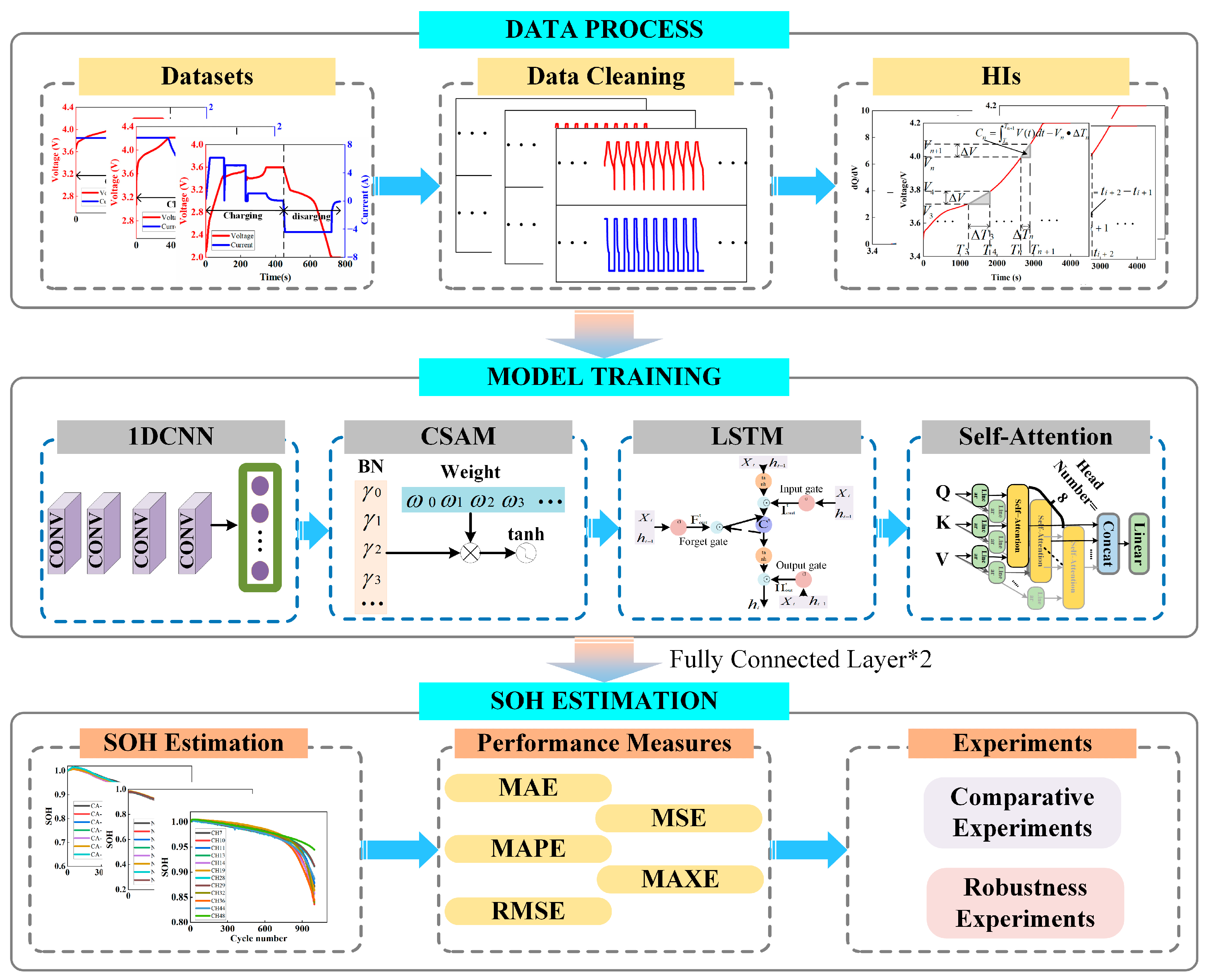
The process of the TFMN in assessing the SOH of LiBs is depicted in
Figure 4 and can be succinctly described as follows: Initially, data cleaning is applied to the raw data, followed by the retrieval of the four types of feature data. The one-dimensional convolutional neural module is utilized to thoroughly convolve the time-series data to extract the features, which are then handled using the time-series sliding window to derive the feature vectors. These vectors are subsequently inputted into the TFMN, where the model assimilates the correlation of the features with the battery SOH. Specifically, within the TFMN: (1) the feature vectors are standardized by splicing and acquiring temporal input data after filtering through the channel self-attention module (CSAM); (2) the temporal input data are refined through the long short-term memory module to generate the model data; (3) these model data are then advanced through the multi-head self-attention module to produce the resultant data; (4) ultimately, these resultant data are routed and transformed via the two-layer fully connected layer into the feature data, correlating it to the ultimate SOH prediction.
To address the problems in the prior art, a TFMN-based method for estimating the health state of LiBs is provided, which largely solves the problems of short-term patterns and long-term dependencies in the time-series data, improving the accuracy and robustness of SOH estimation.
3.1. 1DCNN Layer
In this study, the 1D convolutional neural network (1DCNN) not only proves essential for feature extraction but also significantly contributes to feature transformation. Our 1DCNN framework manipulates the input sequences through convolutional operations, converting the raw battery data into more complex feature representations. Specifically, we configure the output dimension of the 1DCNN to be four times the size of the input dimension. This amplification in dimension showcases the 1DCNN’s exceptional capacity to identify intricate patterns and temporal variations. Via convolutional operations, the 1DCNN identifies and amplifies subtle features within the input sequence, enhancing its discriminatory and expressive power. Therefore, the augmentation of the output dimension of the 1DCNN transcends mere size enhancement; it embodies a comprehensive depiction of the data’s inherent structure.
This enriched feature representation delivers extensive data in subsequent model layers, offering more detailed inputs to the neural network and boosting the model’s expressive power. By enlarging the output dimension of the 1DCNN to four times the input, we capture more critical features within the battery data, thus furnishing more substantial inputs to the following Transformer encoder and LSTM networks, thereby enhancing the overall predictive accuracy.
3.2. Channel Self-Attention Module
Attention mechanisms’ different features or feature channels are weighted to make the model pay more attention to features that are more meaningful or relevant to the task at hand, and to dependencies between different locations or time steps in the data. It can also help the model to focus on important information, thus improving the performance and accuracy of the model. It reduces the model’s dependence on the overall input, focuses computational resources and attention on the most relevant parts, and reduces the impact on invalid or noisy information, which helps to reduce overfitting and improve model robustness.
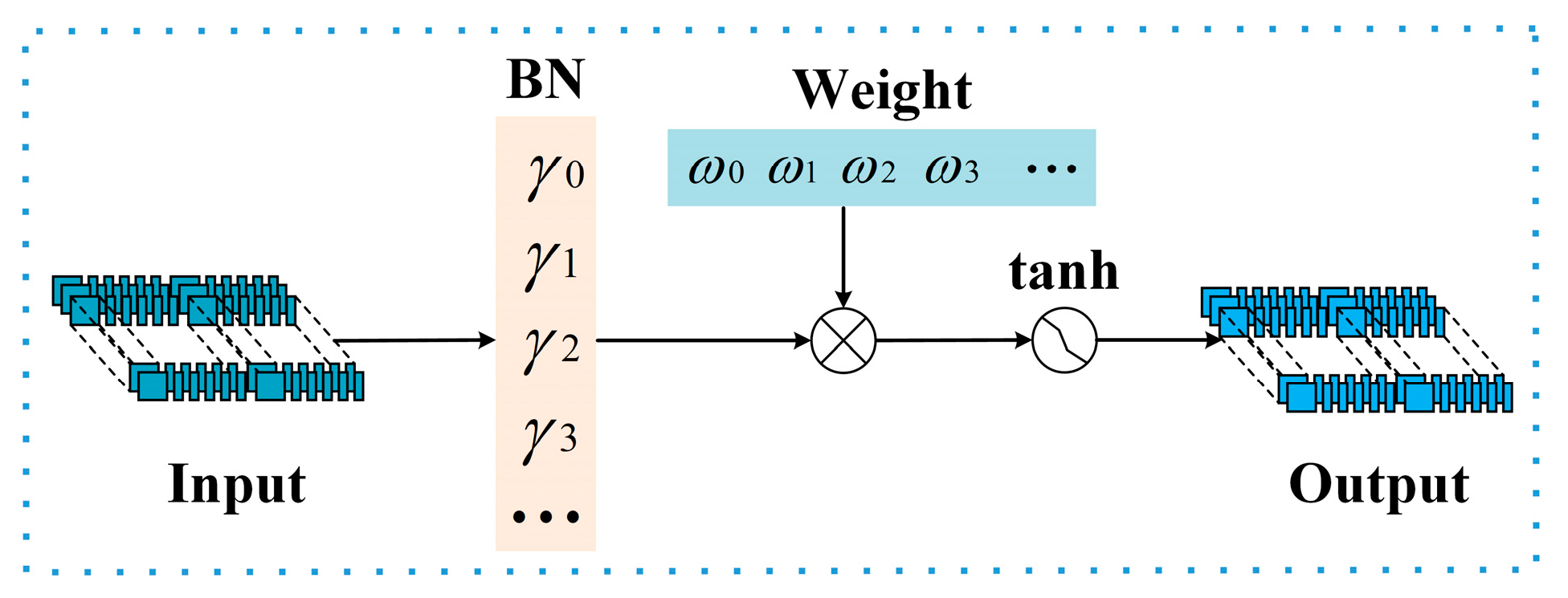
A channel self-attention module, as shown in
Figure 5, is proposed. Tanh is chosen as the activation function because it does not suffer from the instability problem of a zero denominator compared to the self-attention module. This allows the model to pay more attention to the correct features while suppressing the extraction of irrelevant features, without encountering the problem of vanishing or exploding gradients, thus improving network performance. The scale parameter in batch normalization signifies the significance of the weights. This factor represents the extent of variation for each channel and highlights the importance of the channel. The scaling factor, which is the variance in batch normalization, can react to the degree of change in the channel. If the variance is higher, the channel contains more information and is considered more significant. The result of the batch normalization operation
is as follows:
where
and
are the mean and standard deviation of the small batch, respectively;
is the affine transform displacement parameter for training;
is the batch normalization operation;
is the input to the channel self-attention module; and
is the hyperparameter that prevents the denominator of the formula from being zero.
The weights and output operations of this module are shown in Equations (13) and (14):
where
is the weight,
is the scaling factor of the channel, and
is the activation function.
CSAM has the following advantages over self-attention modules:
CSAM can improve the stability and robustness of the model by normalizing the attention scores before calculating the attention weights; the self-attention module may face numerical instability when calculating the attention weights; for example, for the division problem when the denominator is close to zero, through the normalization operation, the attention scores can be kept in a more reasonable range and the numerical instability can be reduced.
CSAM can better control the flow of information in the sequence through the normalization operation, the tanh function in CSAM will asymptote to 1 and −1 when the input tends to positive infinity or negative infinity, which ensures that the output value of the temporal transformation memory network is within a certain range, and will not suffer from the problem of vanishing or exploding gradient; when the input is in the range between [−1, 1], the tanh function’s function value changes are more sensitive than the Sigmoid function, making the model’s performance more stable in this interval, enabling the information to be transmitted and concentrated effectively in the sequence.
CSAM has less influence on outliers; if there are outliers or noisy data, the self-attention module may pay too much attention to these outliers, resulting in a decrease in the model performance; the channel self-attention module can mitigate the influence of outliers by limiting the attention weights to a certain range, improving the robustness of the model.
3.3. Long Short-Term Memory
Long short-term memory (LSTM) [
30] is a recurrent neural network framework specifically crafted for handling sequential data. It is depicted in
Figure 6. Its fundamental architecture is composed of three elements: a forgetting gate, an input gate, and an output gate. A neural network layer possesses two properties, namely a weight vector
and bias vector
, and for each element
of the input vector
, the neural network layer conducts operations on it as detailed in Equation (15):
where
represents the activation function; this study employs sigmoid and tanh functions as activation mechanisms.
The key for LSTM to stand out from RNN lies in the hidden state (unit state) of the neuron in the blue circle in
Figure 6; we can understand the hidden state of the neuron as the recurrent neural network’s “memory” of the input data, and use
to indicate the neuron’s “memory” after the
moment. This vector covers the recursive neural network’s “summary” of all input information until moment
.
These gates within the LSTM proficiently regulate the flow of feature information throughout the sequence, enabling the network to selectively retain and discard feature information across time steps, thus enhancing the capture of long-term dependencies. We detail the function of each gate individually below.
Within the LSTM, these gates efficiently manage the distribution of feature information throughout the sequence, thereby allowing the network to selectively preserve and omit feature information at different intervals, facilitating improved long-term dependency tracking. The functionality of each gate is explained separately below.
The primary function of the forget gate is to determine whether the network should erase prior memories at the current time step. This gate computes its value by utilizing the current input
and the previous time step’s hidden state
. The sigmoid function yields an output for the forgetting gate ranging from 0 to 1, which governs the level of information retention within the memory cells, with 0 indicating total erasure and 1 ensuring full preservation. The output vector
is defined in Equation (16):
where
and
are the weights and bias of the forgetting gate, respectively.
denotes the sigmoid function.
- 2.
Input Gate:
The input gate determines which new feature information is to be incorporated into the memory cell at the current time step. Analogous to the forgetting gate, the input gate calculates its values based on the current input
and the hidden state
from the previous time step. This gate generates a candidate memory cell (
) designed to hold potential new feature information. The output from the input gate, which ranges from 0 to 1, specifies how much information from the candidate memory cell is integrated into the memory cell, with 0 representing total omission and 1 indicating complete retention. These dynamics are detailed in Equations (17) and (18):
where
and
represent the weights and biases of the input gates, respectively.
and
constitute the weights and biases of the candidate memory cells, respectively. The function
denotes the tanh function.
- 3.
Cell State Update:
Memory cells update their contents under the guidance of forgetting gates and input gates. The forgetting gate determines what information is to be discarded from the previous memory cell, and the input gate determines what new information is to be added to the memory cell. Memory cell
can be represented by Equation (19):
where
denotes the candidate memory unit of the previous moment.
- 4.
Output Gate:
The output gate determines how, at a given time step, information from the memory cell influences the next hidden state. This gate uses the current input
and the previous hidden state
to perform its calculation. It modulates the hidden state values using a tanh function. The result,
, is formulated as follows in Equation (20):
where
symbolizes the hidden state at this moment;
and
stand for the weight and bias of the output gate.
LSTM architecture includes forgetting gates, input gates, and output gates, which enable the network to selectively forget, retain, and communicate data. This structure is particularly effective for managing sequences that extend over long periods, making it adept at processing data with long-term implications, such as battery performance data.
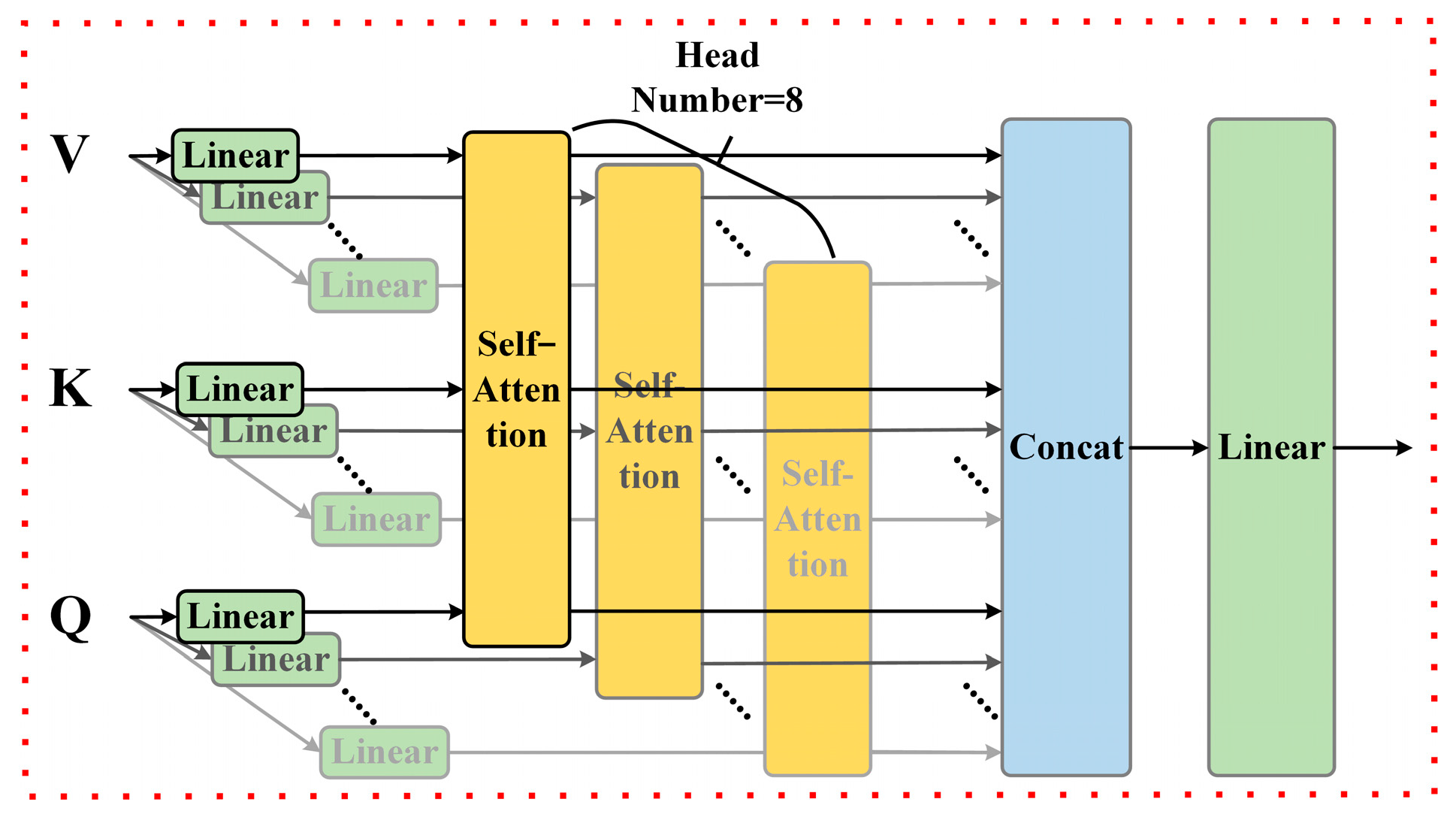
3.4. Multi-Head Self-Attention
The model incorporates a multi-head self-attention (MHSA) mechanism [
36], depicted in
Figure 7. The fundamental concept of the multi-head self-attention mechanism involves mapping the input features to various distinct attention subspaces, followed by the independent calculation of attention weights within each subspace. This approach enables the model to simultaneously focus on varied sequence positions and feature dimensions, thus enhancing its ability to fully grasp the sequence’s structure and significance. In detail, for every head, the multi-head self-attention mechanism generates a collection of attention weights, which are amalgamated to produce the conclusive attention output.
The formula used for the attention mechanism of each head is presented in Equation (21), while the multi-head attention mechanism itself is detailed in Equation (22):
where
,
, and
represent the linear transformations of the query, key, and value, respectively, and
represents the transposition of the key
.
represents the scaling factor, which controls the attention scores to remain at a stable gradient. The
function is used to compute the attention weights.
represents the attention weights in each of the subspaces.
In summary, the multi-head self-attention mechanism learns different feature representations from different subspaces by learning multiple attention heads in parallel, each of which can focus on different aspects or features in the sequence, thus providing richer expressive power; the multi-head self-attention mechanism simultaneously focuses on information at different locations in the sequence, and each of which learns dependencies at different granularities, which allows capturing the local and global dependencies in the input sequence, thus providing a more comprehensive understanding of the semantic structure of the sequence, speeding up model training and inference and improving model efficiency.
4. Result and Discussion
4.1. The Evaluation Criteria
In this study, several evaluation metrics are employed to provide a comprehensive assessment of the performance of the proposed TFMN estimation model. These metrics help to objectively measure the predictive ability of the model and reveal its accuracy and robustness from different perspectives. The following are the five evaluation metrics used:
- 2.
Root mean square error (RMSE): The RMSE is the square root of the mean square error, which represents the average difference between the predicted value and the true value. The RMSE is more sensitive to outliers and can be used to measure the accuracy of the model.
- 3.
Mean absolute error (MAE): The mean absolute error (MAE) is the average of the absolute differences between the forecast and the true value and measures the average error in the forecast. Unlike MSE, MAE does not amplify the effect of large errors and therefore better reflects the overall accuracy of the forecast.
- 4.
Mean percentage absolute error (MAPE): The mean percentage absolute error (MAPE) is the average of the relative differences between the predicted and true values, expressed as a percentage. It measures the relative error of the model over different data ranges and can reflect the relative accuracy of the predictions.
- 5.
Maximum Absolute Error (MAXE): The maximum absolute error (MAXE) is the maximum value of the absolute difference between the predicted value and the true value, which identifies the model’s worst-case prediction error. MAXE is particularly sensitive to outliers and is useful in understanding the model’s maximum risk in making predictions.
where
is the actual value of time,
is the
predicted value of time, and
is the number of predictions.
By using these evaluation metrics, we can comprehensively assess the performance of the TFMN estimation model to better understand its performance in battery health state assessment. A comprehensive analysis of these metrics will help us gain insight into the strengths and limitations of the model and provide valuable references for further research.
4.2. Experimental Settings
In this paper, three datasets are used. In dataset A, CA-11, CA-12, CA-14, CA-16, and CA-17 are used as the training validation set, while CA-13 and CA-15 are used as the test set. In dataset B, NA-11, NA-12, NA-14, NA-16, NA-17, and NA-17 are used as the training validation set, while NA-03 and NA-15 are used as the test sets. For dataset C, CH7, CH10, CH11, CH14, CH19, CH28, CH29, CH32, CH36, and CH44 are used as the training validation set, while CH13 and CH48 are used as the test set. The training–validation set is randomly divided into a training set and a validation set in the ratio of 8:2.
For network training, the mean square error (MSE) was selected as the model’s loss function. Subsequently, the gradient-driven AdamW optimization algorithm [
37] was employed to adjust the weights and biases in the network model, aiming to reduce the loss function. An initial learning rate of 0.0035 was chosen. Finally, an early stopping mechanism was used to prevent model overfitting. Specifically, model training was terminated if the validation loss did not decrease within the next 130 epochs. Notably, min–max normalization was performed on the data prior to feature extraction, as shown in the algorithm in Equation (28):
where is
the original data and
is the total amount of data.
signifies that the data undergoes normalization prior to being input into the model, which facilitates quicker convergence of the model during training. Additionally, the equipment setup and model parameters utilized in the experiment are detailed in
Table 3.
4.3. Robust Experiments
In robustness experiments, the effect of noise was assessed to determine the performance of the TFMN across varying noise intensities. Noise levels of 50 mV, 100 mV, and 150 mV were introduced to mimic the uncertainty typical of battery data. Analysis of the experimental outcomes provided insights into the stability and resilience of the TFMN when subjected to noise.
The results indicated that the efficacy of each model diminishes as the noise intensity escalates across all evaluation metrics. Despite this, the TFMN continues to exhibit high accuracy levels under various noise conditions. For instance, with the CA-15 dataset, as noise intensity increased from 50 mV to 150 mV, the MSE for TFMN rose only from 0.53 to 0.67, demonstrating TFMN’s greater noise resistance and its ability to mitigate data uncertainty effects. To confirm the experiment’s reliability, the parameter settings from
Section 4.2 were applied, and the tests were performed under consistent conditions. The outcomes are documented in
Table 4 and
Figure 8. Additionally, TFMN demonstrated consistent performance on the CA-13, NA-13, and CH48 datasets. Although all models show decreased performance at higher noise levels, TFMN consistently recorded low scores on various evaluation metrics, affirming its ability to handle diverse data qualities effectively.
Taken together, the outcomes of these robustness trials underscore TFMN’s superiority in managing noise interference. Compared with other models, TFMN shows stronger stability and robustness, which provides strong support for its reliability in practical applications, especially in battery data scenarios with uncertainty.
4.4. Comparative Experiments
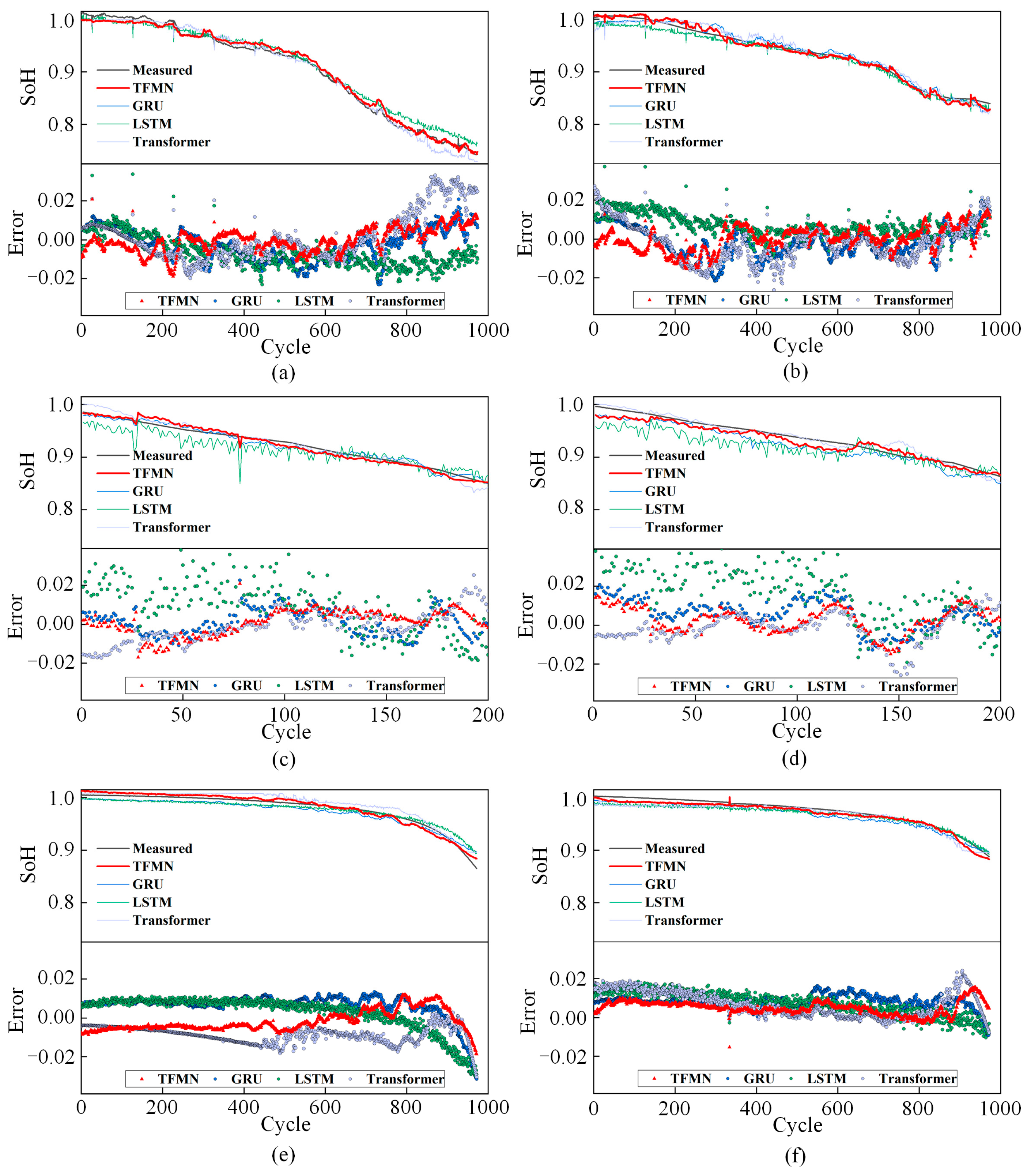
In the comparative tests, the precision of the proposed TFMN was further confirmed through trials with several open-source models (GRU, LSTM, and Transformer), utilizing dataset A, dataset B, and a public dataset for individual assessments. Consistent experimental parameters and identical environmental conditions were upheld to ensure uniformity in experimental outcomes. The findings are displayed in
Table 5 and
Figure 9.
From the experimental results, it can be clearly observed that TFMN demonstrates significant advantages under all evaluation metrics. Taking the CA-15 dataset as an example, TFMN exhibits reductions of about 53.4%, 45.8%, 44.9%, 38.2%, and 52.7% in five evaluation metrics, namely MSE, RMSE, MAE, MAPE, and MAXE, respectively, with respect to GRU, LSTM, and Transformer models. Similarly, on the XQ-18 dataset, TFMN achieves about 47.8%, 36.8%, 34.5%, 32.9%, and 52.7% performance improvement with respect to GRU, LSTM, and Transformer models, respectively.
These findings reinforce the TFMN’s advantage in terms of estimation precision. By delivering more precise estimation outcomes, TFMN offers a solid foundation for evaluating and managing battery health. An exhaustive review of the comparative testing results shows that TFMN yields more consistent and precise estimations across both our own dataset and the publicly accessible dataset. It exhibits a distinct edge over the open-source models GRU, LSTM, and Transformer across multiple evaluation metrics. This emphasizes TFMN’s exceptional capability in assessing the health state of lithium-ion batteries, offering a robust resource and insights for enhancing battery management and maintenance tactics.
5. Conclusions
This study aims to overcome two major challenges in the health state assessment of lithium-ion batteries, namely insufficient accuracy and poor robustness under fast-charging conditions. With the introduction of an innovative TFMN estimation model, significant breakthroughs have been made in these aspects. This conclusion section will briefly summarize the research results and analyze the experimental findings.
The TFMN model effectively tackles the problems of limited precision and inadequate robustness in estimating battery health state by integrating various modules such as 1DCNN, CSAM, LSTM, and multi-head self-attention. Initially, the 1DCNN module adeptly captures both local and global features from the raw battery data, furnishing enriched inputs for the subsequent modeling stages. Moreover, the combination of LSTM and the attention mechanism allows the model to more accurately discern long-term dependencies within the sequential data, thereby enhancing the precision of battery health state estimations.
In robustness experiments, the performance of TFMN was evaluated in different noise environments. Although the predictive performance of the model decreases in high-noise situations, TFMN still maintains higher estimation accuracy relative to other models. This demonstrates the robustness of the model in coping with noise disturbances in real-world environments.
In comparison experiments, TFMN was evaluated against widely adopted models like GRU, LSTM, and Transformer. The test outcomes demonstrate that TFMN markedly surpasses other models across all evaluation metrics, achieving a reduction in MSE by approximately 31.1%, RMSE by 24.5%, MAE by 26.7%, MAPE by 18.9%, and MAXE by 34.5%. These findings robustly confirm the superior performance of the model in estimating battery health state.
In summary, TFMN has achieved remarkable results in Li-ion battery health state assessment. It effectively overcomes the challenges of insufficient accuracy and poor robustness of SOH estimation under fast-charging conditions, solves the problem of short-term patterns and long-term dependencies in sequential data, accelerates the parallel processing of different levels of information, significantly improves the estimation performance and generalization ability of deep learning-based estimation methods, and overcomes the issues of insufficient accuracy, robustness, and real-time applicability faced by traditional methods. The model shows superior performance in different experiments. In the future, research will continue to deepen, further optimize the model, and apply it to practical scenarios of smart battery management and maintenance strategies to provide strong support and impetus for the development of the battery field.
6. Future Work
Our model has made great progress in SOH estimation under fast-charging conditions, and we decided to conduct the following studies in our future work:
(1) To satisfy SOH estimation under real working conditions, a battery test temperature sensor will be built to collect battery datasets under different working conditions at various temperatures. This will help understand the performance of the battery under different temperatures.
(2) Feature extraction is crucial for SOH estimation. Various features will be extracted, and an automated feature selection method will be used for correlation analysis to identify the features with the highest possible correlation.
(3) The processing performance of the model is a priority. Continuous optimization of the model will be conducted using a parameter optimization algorithm to find the optimal parameters for the model.
(4) Practical application: This result will be used as a standard to develop a complete practical application plan. The model will be integrated into the battery management system to verify its practicality in real-world battery management and maintenance, offering a more dependable tool for the battery industry.