Abstract
State of health (SOH) estimation plays a vital role in ensuring the safe and stable operation of lithium-ion battery management systems (BMSs). Data-driven methods are widely used to estimate SOH; however, existing methods often suffer from fixed or excessively high feature dimensions, impacting the model’s adjustability and applicability. This study first proposed a layered knee point strategy based on the charging voltage curve, which reduced the complexity of feature extraction. Then, a new hybrid framework called the adaptive gated sequence network (AGSN) model was proposed. This model integrated independently recurrent neural network (IndRNN) layers, active state tracking long short-term memory (AST-LSTM) layers, and adaptive gating mechanism (AGM) layers. By integrating a multi-layered structure and an adaptive gating mechanism, the SOH prediction performance was significantly improved. Finally, batteries under different operating conditions were tested using the NASA battery dataset. The results show that the AGSN model demonstrated higher accuracy and robustness in battery SOH estimation, with estimation errors consistently within 1%.
1. Introduction
1.1. Literature Review
Lithium-ion batteries have become the main power source for new energy vehicles due to their high energy density, long cycle life, and low self-discharge characteristics [1]. As the number of electric vehicles continues to grow, it is crucial to accurately predict the health of these batteries. Not only would this improve the battery’s performance and prolong its service life, but it would also improve its reliability and safety.
Estimation methods for the state of health (SOH) of lithium-ion batteries can be divided into a direct measurement method, a model method [2], and a data-driven method [3]. The direct measurement method estimates the SOH using critical parameters such as the open-circuit voltage (OCV), internal resistance, and impedance [4]. Although the computational complexity of the direct measurement method is not high, accurately measuring parameters such as the OCV, internal resistance, and impedance requires specific hardware equipment and particular conditions (such as a stationary state or specific charging and discharging conditions). This makes it difficult to apply this method under online working conditions. The methods of the model include the electrochemical model [5] and the equivalent circuit model [6]. The electrochemical model uses partial.
Differential equations are used to describe the internal battery degradation, which can accurately reflect the microscopic reaction but usually requires complex equation processing [7]. The equivalent circuit model considers the load, material, and degradation mechanisms but may be limited by the challenge of parameter identification and the computational complexity, which limits its practical application [8]. In contrast, data-driven models are more suitable for real-world applications because they can predict battery life with a large amount of operational data without requiring an in-depth understanding of internal battery physics.
Data-driven methods for predicting the lifespan of lithium-ion batteries typically involve two stages: feature extraction and the establishment of mapping models. In the feature extraction stage, the primary task is to identify indicators that accurately represent battery degradation. Battery health indicators are typically divided into two categories: direct features and indirect features. Direct features involve sampling key values directly from the charging voltage or current, response parameters, and model parameters [9]. Indirect features are derived from transforming voltage or temperature measurements; selecting the appropriate health indicators (HIs) as inputs is crucial. Yang et al. [10] proposed a new Gaussian process regression (GPR) model to estimate the health state of lithium-ion batteries and extracted four specific parameters from the charging curve as inputs to the model. These parameters can reflect battery aging from different perspectives, thereby improving the accuracy of battery health assessments. Another approach is through the use of indirect methods, such as an incremental capacity analysis (ICA) [11] or a differential voltage analysis (DVA) [12], which extract relevant SOH features by processing raw measurements. The authors of [13] used interpolation to obtain incremental capacity (IC) curves, extracted health indices from partial IC curves for a gray relational analysis, and used entropy weights to assess the importance of each health index.
In the second stage of predicting the lifespan of lithium-ion batteries, the correlation between health indicators and the SOH is established. Supervised machine learning techniques are employed, including a support vector machine (SVM) [14], long short-term memory (LSTM) networks [15], a Gaussian process regression (GPR) [16], and ensemble frameworks [17]. The authors of [18] proposed an LSTM network and a fine-tuning strategy with transfer learning (TL), constructing a unit mean SOH prediction model based on partial training data. To address the low-accuracy problem in traditional estimation methods, the authors of [19] proposed a new SOH estimation method that integrates an improved ant lion optimization (IALO) algorithm with support vector regression (SVR). This approach leverages the IALO algorithm to fine-tune the kernel parameters of SVR. By training the SOH estimation model with a battery dataset, they significantly enhanced the prediction accuracy. Hu et al. [20] introduced discharge cycle data as the primary predictive factor and used an RNN model to construct a battery SOH prediction model. The authors of [21] proposed a CNN-Bi-LSTM-AM model by integrating bidirectional long short-term memory (bi-LSTM) and a self-attention mechanism to achieve accurate state-of-charge estimations for lithium batteries over a wide temperature range.
1.2. Motivation and Contributions
Although data-driven methods are becoming increasingly popular in predicting the SOH of lithium-ion batteries, there are still challenges in the feature construction and model training stages. In terms of feature construction, the intricacy of training a model hinges on both the chosen machine learning algorithm and the selected feature dimensions. The invariance of existing feature dimensions often makes training SOH prediction models difficult. The dynamic control of feature complexity can enhance adaptability to different scenarios and improve prediction performance. In addition, when the traditional multi-layer stacked neural network processes the long-term sequence data of the battery, as the number of layers increases, degradation problems may occur. This can lead to difficulties for the model in effectively remembering and utilizing early input information, thereby affecting the prediction accuracy. Gradient attenuation leads to the slow update of deep network parameters, which affects the learning and convergence of the model. These problems may make it difficult for the network to learn and maintain long-term dependencies [22]. Finally, the performance data of lithium-ion batteries have significant temporal and spatial variation characteristics and short-term fluctuations, such as the battery’s regenerative capacity during charge–discharge cycles [23]. Regenerative capacity refers to the battery’s ability to restore its capacity after multiple cycles, which is a critical issue. These variations and fluctuations place higher demands on the model, making accurate predictions more difficult.
Inspired by the above literature, this study proposes a new adaptive gated sequence network (AGSN) model and fully verified the proposed method. This study makes the following main contributions:
- (1)
- A new hierarchical feature extraction method was proposed, which is based on the extraction of knee point features of the voltage curve. Its complexity can be dynamically controlled by the hierarchical level so that the model can better understand the complexity of the data.
- (2)
- By integrating independently recurrent neural network (IndRNN) layers and active state tracking long short-term memory (AST-LSTM) network layers, the AGSN model enhances our ability to capture long-term dependencies and short-term dynamic changes in sequence data. This characteristic makes an AGSN particularly suitable for handling long time span data in battery charge and discharge cycles, thereby improving the accuracy of battery health state predictions.
- (3)
- The adaptive gating mechanism (AGM) in the AGSN model allows the network to dynamically adjust the information flow according to the importance of the current input and historical information to ensure that key information is fully utilized in the prediction. This mechanism ensures that the model can still maintain a high prediction accuracy under changing operating conditions.
2. Estimation Method
2.1. Battery Prediction Framework
This research designed a prediction framework consisting of four steps for estimating the SOH of lithium-ion batteries, as shown in Figure 1.
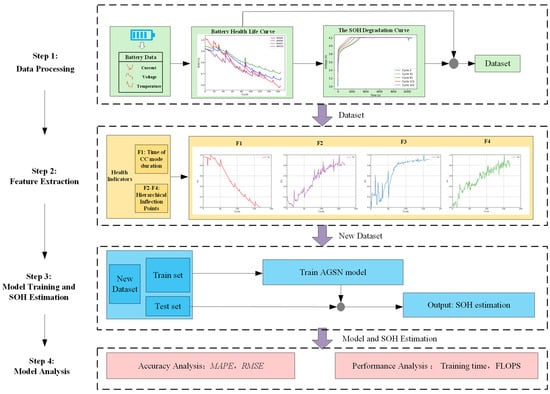
Figure 1.
Battery prediction framework based on AGSN model.
- Step 1: Data Processing
Raw lithium-ion battery data were collected from the NASA database, including charging voltage curves and battery capacity degradation curves, which were used as inputs for the model.
- Step 2: Feature Extraction
An innovative hierarchical knee point feature extraction method was proposed, dynamically controlled through hierarchical levels to extract key features based on the voltage curves’ hierarchical structure. The major features included the duration of the constant current mode and hierarchical knee point features.
- Step 3: Model Training and SOH Estimation
A complementary ensemble learning strategy was proposed, combining an IndRNN layer and an AST-LSTM layer to enhance the model’s ability to capture short-term fluctuations and long-term trends in battery performance data. The AGM layer dynamically adjusted the feature weights at each time step, ensuring that critical information was fully utilized in the predictions. The model was trained using the training dataset and optimized through multiple iterations and cross-validation.
- Step 4: Model Analysis
The trained AGSN model was evaluated using a test dataset. Prediction error metrics, including the RMSE and MAE, were calculated to validate the model’s predictive capability and stability.
2.2. Dataset Description
The lithium-ion battery degeneration data used in this experiment came from the NASA PCOE Research Center [24]. The battery underwent three different operations during each cycle of the experiment, including charging, discharging, and electrochemical impedance spectroscopy (EIS). The aging process of lithium-ion batteries (LIB) is accelerated by cyclic charging and discharging. According to the summary from the NASA database, during the charging test, the batteries were initially charged in CC mode at 1.5 A until they reached 4.2 V, and then they were switched to CV mode until the current decreased to 20 mA. In the discharge test, the batteries were discharged at a constant current until the voltage dropped to four preset stages (2 V, 2.2 V, 2.5 V, and 2.7 V). The termination condition for the tests was when the batteries reached 20% or 30% of their initial capacity. The data required for the simulations in this study included the initial capacity, charging current, charging voltage, end of charging current, and end of discharging voltage. Table 1 provides an overview of the lithium-ion batteries used in this study.

Table 1.
An overview of lithium-ion batteries information.
2.3. Definition of SOH
The SOH of a battery is a percentage measure of its current charge capacity relative to that of a new battery. It quantifies the aging and health status of the battery from the beginning to the end of its lifespan and is typically represented by the battery’s capacity [25], as shown in Equation (1):
where and denote the current capacity and rated capacity of the LIB, respectively.
Figure 2 shows the SOH curves from the NASA battery dataset. It was observed that, as the battery cycle proceeded, the SOH gradually decayed. However, a localized upward trend occasionally occurred. This phenomenon is known as regenerative charging (or self-charging), and it occurs due to the complex coupling effects of various physical and chemical reactions involving the electrolyte and electrodes. During the degradation process, these reactions can sometimes result in the battery capacity of cycle i + 1 being higher than that of cycle i, displaying a periodic characteristic. Therefore, it is difficult to apply a linear model directly to describe the overall degradation of the battery; instead, indirect information must be extracted from the available data to estimate the SOH.
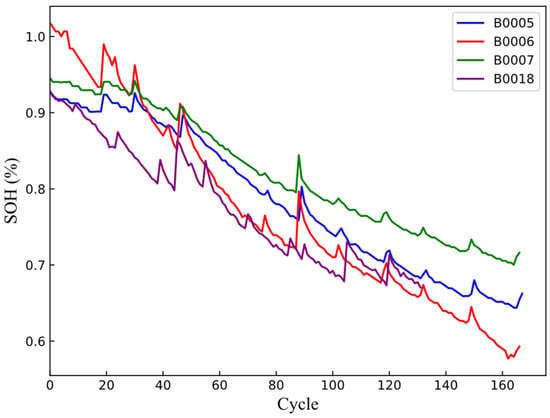
Figure 2.
SOH curve of the battery dataset.
2.4. Feature Extraction
- (1)
- Feature selection
Health indicators (HIs) play a crucial role in the estimation accuracy of data-driven methods. Selecting appropriate health factors can significantly enhance the model’s estimation effectiveness. In most cases, the charging process is more stable compared to the discharging process, with fewer external influencing factors. The charging curve is also more predictable and repeatable [26]. Therefore, a method of constructing features from the charging voltage curve was proposed.
In Figure 3a, the charging voltage curves for battery number B0005 are presented for different cycle numbers. It was observed that, at cycle 40, the constant current charging time was approximately 3000 s, whereas at cycle 160, it reduced to 1500 s. As the number of charge cycles increased, the constant current charging time decreased. This phenomenon was due to the degradation of lithium-ion battery materials over time. The constant-current charging time showed a certain pattern with increasing cycles.
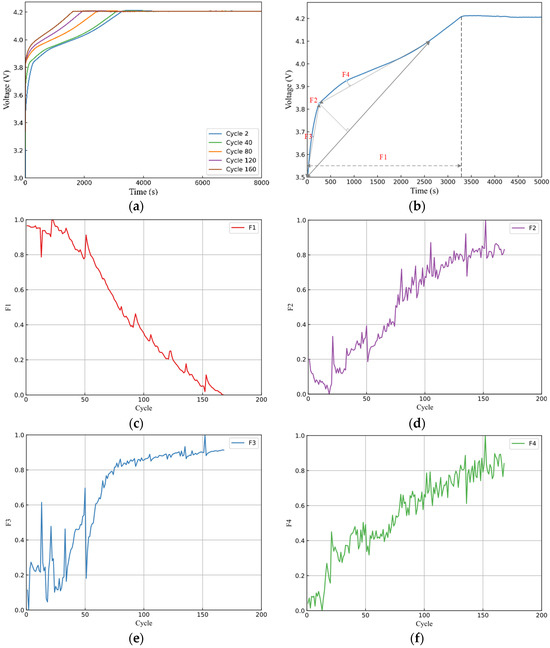
Figure 3.
The extracted features. (a) Voltage charging curve. (b) Feature selection method. (c) Constant current charging time. (d) Layered knee point F2. (e) Layered knee point F3. (f) Layered knee point F4.
Additionally, the voltage rapidly rose from 3.37 V to 3.85 V within the first 100 s. After reaching 3.85 V, the rate of voltage increase slowed down, forming a significant change point on the voltage curve known as the knee point. The knee point marks the transition of the voltage from a rapid rise to a relatively stable phase, representing a significant change in the battery parameters and being a key feature point during charging.
Therefore, a method for constructing features based on the charging voltage curve was proposed. The input features were extracted from the battery-charging voltage curves. These features included sequences with a time dimension, reflecting changes in the battery over different charging cycles. Specifically, they comprised two main types of features: the constant current mode duration (F1) and layered knee point features (F2, F3, and F4).
F1: constant current mode duration. Figure 3c shows the variation in the normalized F1 over the entire battery life cycle. With an increase in battery cycle times, chemical and physical changes will occur inside the battery, which will aggravate the polarization phenomenon and reduce the actual capacity of the battery [27]. Therefore, the charging duration of the battery in the constant current (CC) mode is correspondingly reduced, which clearly reflects the trend in battery degradation with aging.
F2–F4: layered knee point. Figure 3d–f show the variation in the normalized F2–F4 over the entire battery life cycle. The second aging feature adopted a hierarchical knee point strategy, and the feature selection strategy is shown in Figure 3b. This method included identifying the knee points on the voltage curve, using these knee points to decompose the complex voltage curve into multiple levels, and extracting the knee points of each layer. Different levels of knee points provide a comprehensive understanding of the battery life cycle and degradation trends.
- (2)
- Knee point recognition method
A geometric distance-based turning point identification method was used to determine significant knee points. As shown in Figure 3b for the feature selection method, the initial and terminal voltage points on the voltage segment were first identified, and an extreme line, , was established from the initial voltage point to the terminal voltage point. The vertical distance from each point on the voltage curve to the extreme line was then calculated.
Among all the data points, the point with the maximum vertical distance was identified as the voltage knee point of the first layer, defined as . This point was the most prominent on the curve, representing a key change in the aging process, and it was sampled as the first feature point. Based on the position of this knee point, the voltage curve was accordingly divided into two segments. This analysis was continued on the two segments to identify knee points in subsequent layers. Through this iterative segmentation method, the voltage curve was gradually subdivided into smaller segments, thereby revealing multi-layer key features.
The feature extraction Algorithm 1 was as follows:
| Algorithm 1: Hierarchical Voltage Feature Extraction |
| Input: The entire charging voltage curve V. The hierarchical level . Output: Voltage features 1: 2: 3: 4: for i = 1, 2…, do 5: 6: for j = 1, 2…, do 7: 8: 9: = Extreme Line () 10: 11: for k = 1, 2…, do 12: = projection Distance according to Equation (3) 13: 14: end for 15: 16: 17: end for 18: 19: end for 20: Return |
- (3)
- Feature correlation analysis
To quantitatively analyze the correlation between the HIs and the SOH of the battery, the Pearson correlation coefficient was used as the evaluation method. The Pearson correlation coefficient is a statistical tool used to evaluate the strength of the linear correlation between two variables and has been widely applied in various fields [28]. The proposed features, as shown in Figure 3c–f, exhibited corresponding trends with an increase in the charge cycles, empirically demonstrating that the proposed features can be used to estimate the SOH. This study utilized the Pearson coefficient to conduct a detailed analysis of the correlation between these features and the SOH. The calculation formula is as follows:
where and are the feature value and SOH of the battery, respectively, and and are their average values.
The correlation strength was determined by the absolute value of the correlation coefficient. The closer it was to 1, the stronger the correlation between the feature and the SOH. Figure 4 shows the Pearson correlation results of the features extracted from different batteries in the NASA dataset. These batteries are briefly described in Section 4. According to the principle of the Pearson correlation, when the magnitude of the correlation coefficient exceeded 0.90, it indicated that the characteristic factor was highly correlated with the SOH. The results clearly indicated a significant correlation between the derived aging features and the SOH. This relationship showed that the extracted hierarchical features were not only closely related to the instant health status of the battery, but also extremely important for an evaluation of the long-term battery performance.
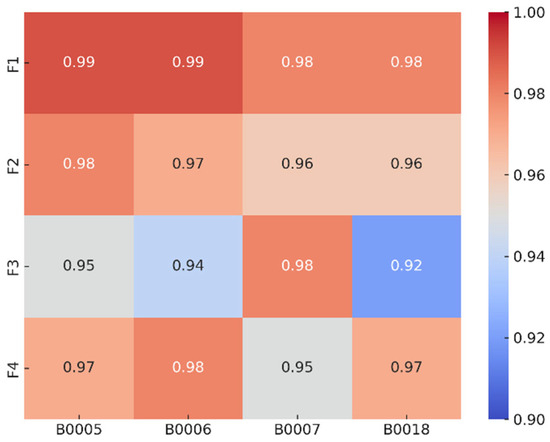
Figure 4.
Correlation analysis results of extracted features.
2.5. AGSN Model
This study proposes a novel AGSN-integrated model for accurately predicting the SOH of lithium-ion batteries. This model processes and optimizes information through a hierarchical structure, integrating the input layer, the IndRNN layer, the AST-LSTM layer, the AGM layer, and the output layer. The layers are connected in series and stacked in multiple layers. Different types of neural network layers are connected in sequence, while the IndRNN and AST-LSTM layers are stacked in multiple layers internally. By combining their respective advantages through a hierarchical model architecture, the model can accurately map complex features to the SOH prediction, enhancing the reliability of the final prediction results. The model structure is shown in Figure 5.
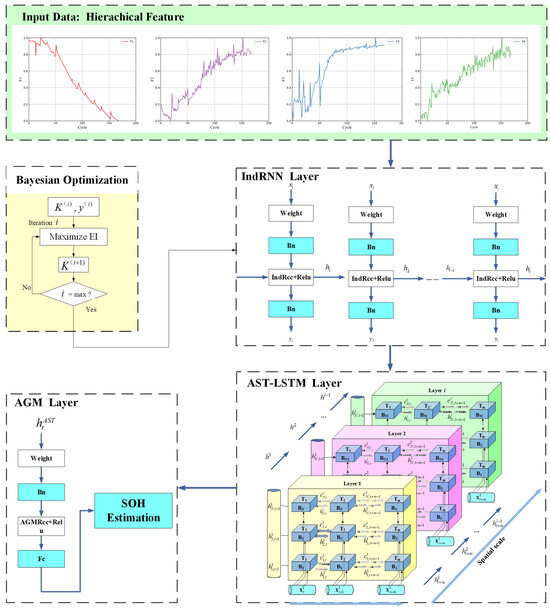
Figure 5.
AGSN model structure diagram.
- (1)
- Input layer: First, health indicators (HIs) reflecting the SOH of the battery are extracted from the charging voltage curves in the lithium-ion battery dataset. These features include the duration of the constant current (CC) mode and the aging characteristics of the voltage curve obtained through hierarchical direct sampling methods. The dataset is divided, with the training set’s HIs used as input to the IndRNN layer.
- (2)
- IndRNN layer: Traditional RNNs face issues of vanishing or exploding gradients when dealing with long time series data from battery-charging voltage curves, making it difficult for the model to remember and utilize early input information. The IndRNN layer addresses this problem by introducing independent recurrent weights, enabling the model to effectively capture and utilize information in long time series, thereby more accurately predicting the long-term health state of the battery.
- (3)
- AST-LSTM layer: Building on the IndRNN layer, the AST-LSTM layer uses an active state tracking mechanism to enhance the capture of complex spatiotemporal dynamics and short-term fluctuations in the battery under different charge–discharge states, thereby improving the prediction accuracy of the battery’s regenerative capacity.
- (4)
- AGM layer: The AGM layer combines the outputs of the IndRNN and AST-LSTM layers and dynamically adjusts the feature weights at each time step through an adaptive gating mechanism, ensuring that critical information is fully utilized in predictions while reducing the impact of less important information. This mechanism optimizes the model’s response and adaptability to different data features, allowing the model to handle various data changes more flexibly.
- (5)
- Output layer: The output of the AGM is transformed through a fully connected layer (FC), mapping the complex features processed through multiple layers to the SOH prediction.
Through the collaboration of these five core parts, the entire model combines the predictive information of the IndRNN and AST-LSTM models, forming an integrated model structure. This structure not only improves the performance of a single model but also enhances the model’s generalization ability and robustness.
In summary, the AGSN model, with its innovative hierarchical architecture and unique layer design, effectively addresses key issues in predicting the health state of lithium-ion batteries, including gradient problems with long time series data, dynamic predictions of the regenerative capacity, and dynamic adjustments of feature importance. This significantly enhances the model’s predictive performance and robustness.
2.5.1. Independently Recurrent Neural Network Layer (IndRNN)
When dealing with long-term time series data, the gradient of a traditional RNN may decrease or increase rapidly with the transmission of each layer, which makes it difficult for the network to learn information related to the early stage of the sequence. An IndRNN, as an improved RNN variant, overcomes this challenge by introducing independent recursive weights [29]. In the IndRNN, the update of each hidden unit only receives its past as context information rather than the state of all hidden units in the previous time step. In this way, the IndRNN can learn and represent complex dependencies in time series data more effectively, thereby improving the network’s ability to process long-term dependencies. The IndRNN uses unsaturated activation functions, such as ReLU, to improve its robustness, making it easier to train.
The traditional RNN processes sequence data through cyclic connections. In this network, the hidden state of each time step depends not only on the current input but also on the hidden state of the previous time step. The updated formula of the RNN can be expressed as follows:
where is the hidden state of the time step , is the input of the time step , is the weight matrix from the input layer to the hidden layer, is the cyclic weight matrix of the hidden layer, is the bias vector, and is the activation function. When processing long sequence data, the RNN may encounter the problem of a gradient explosion or gradient disappearance, which is caused by the exponential growth or decrease of a gradient in the process of back propagation.
The IndRNN solves these problems in the traditional RNN by using independent recursive weights in each hidden unit. This design avoids the use of a fully connected recursive weight matrix. Different from the traditional RNN, the hidden state update formula of the IndRNN is as follows:
where represents the Hadamard product (i.e., element-wise multiplication) and is the recurrent weight vector. This method allows each hidden unit to have its own independent recurrent weight, thereby simplifying the network structure and improving the stability of the training process.
Additionally, the IndRNN employs the non-saturating activation function ReLU to further enhance the model’s robustness, making the network easier to train while more effectively capturing dependencies in long-term time series. The ReLU activation function is defined as follows:
This activation function has a constant gradient in the positive region, effectively avoiding the vanishing gradient problem. Additionally, due to its non-linear properties, it enhances the model’s expressive power.
2.5.2. Active State Tracking Long Short-Term Memory Network Layer (AST-LSTM)
The long short-term memory (LSTM) network maintains long-term information through its unit state and controls the flow of information through three interactive gates (an input gate, a forgetting gate, and an output gate). However, this indirect control may affect the predictive performance of the model in some cases. To improve this, an AST-LSTM network was proposed as an improved version of LSTM [30]. AST-LSTM adopts a coupled input gate and forgetting gate mechanism to ensure that the network only chooses to forget some of the old information when receiving new input information. This coupling mechanism enhances the network’s ability to control information flow, making the model show higher adaptability and prediction accuracy in a dynamic environment.
In addition, AST-LSTM introduces a new mechanism that performs an element-level product operation between the new input and the historical cell state to filter and emphasize the most useful information for the current prediction. This strategy enables the network to dynamically adjust its internal state at each time step, effectively capturing and retaining the information features that contribute to short-term fluctuations and long-term predictions.
Finally, unlike traditional LSTM, which uses window connections on all doors, AST-LSTM only retains a weighted window connection from the cell state to the door on the output door. This simplified window connection strategy not only reduces the complexity of the model but also retains important state information to guide the activation of the output gate, thereby improving the efficiency and overall performance of the model. Figure 6 shows the unit structure of AST-LSTM, and Figure 7 shows the structure of deep AST-LSTM.
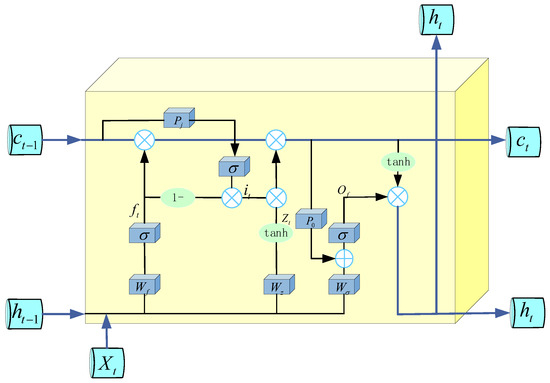
Figure 6.
Unit structure of AST-LSTM.
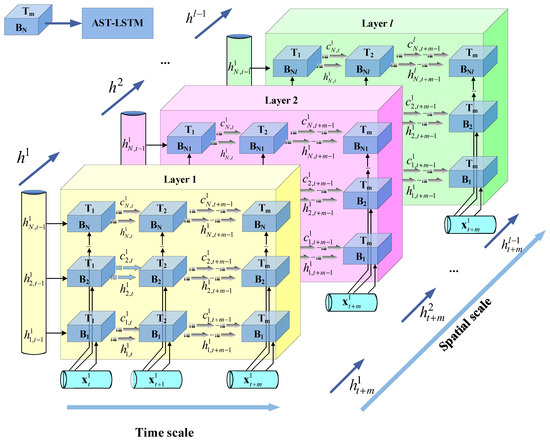
Figure 7.
Structure of deep AST-LSTM.
The forgetting gate and the input gate are coupled through a fixed connection, from the forgetting gate output to the candidate unit state. The mathematical expression of the forgetting gate is as follows:
where , , and are the input, recurrent, and bias weights of the forget gate, respectively, and is the sigmoid activation function.
The fusion state input vector in AST-LSTM is as follows:
where is the output vector of the forgetting gate, is the output vector of the input gate, is the cell state of the previous time step, and is the product of elements. The denotes the operation opposite to the forgetting gate, which determines how much new information will be saved. Among them is the weight of the window connection, which is used to adjust the amount of information transmitted by the previous state .
The unit state of AST-LSTM updates the unit state by using the output of the forgetting gate and the input gate, as follows:
The formula combines the results of the old cell state filtered by the forgotten gate and the new candidate cell state multiplied by the input gate to update the cell state.
The candidate state is calculated using the following expression:
where and are the input and recurrent weights of the block gate, is the activation vector of the block input, and is the activation function.
Finally, the output gate of AST-LSTM is as follows:
where , , and are the input weight matrix, recursive weight matrix, and window connection weight matrix of the output gate, respectively; is the bias matrix; and is the weighted information of the current state through the window connection , which helps the output gate to adjust its output according to the latest cell state.
Through the window connection, AST-LSTM can process time series data more efficiently and improve the adaptability and prediction accuracy of the model in a dynamic environment.
2.5.3. Adaptive Gating Mechanism (AGM) Layer
The AGM layer dynamically adjusts the information flow through the gating function, and its calculation can be expressed as follows:
where is the output of the gating function, is the gating weight matrix, represents the sigmoid activation function, is the gating bias term, and is the output of the AST-LSTM layer. The gating function determines which information in the output of the AST-LSTM layer should be retained and which information can reduce its impact by adjusting the weight of each element. Such a mechanism allows the network to optimize its information processing according to the dynamic needs of the current task.
The output of the AGM layer is obtained using the element-level product, calculated as follows:
This operation ensures that only important information will affect the final output of the network.
Finally, the output of the AGM is transformed into the final prediction result through the full connection layer, calculated as follows:
where is the final output of the time step t, is the weight matrix of the fully connected layer, and is the bias term.
2.5.4. Bayesian Optimization Algorithm
Bayesian optimization is a global optimization method based on the probability model, which is widely used in the hyperparameter optimization of high-cost evaluation functions [31]. This method combines the prior probability distribution and observation data to update the posterior probability distribution of the objective function and guide the search process toward better performance parameter regions.
In the adaptive gating sequence network, the performance of the model is deeply affected by its hyperparameter configuration, including (hidden layers), (the hidden layer size), (the batch size), (the learning rate), (the recursive weight initialization), and (the gating weight sensitivity). These parameters are directly related to the capacity, learning speed, and complexity control of the model and have a decisive influence on the generalization ability and prediction accuracy of the model. The traditional method finds the optimal value by traversing the parameter combination, but this method is time-consuming and inefficient for an integrated model with many parameters. Therefore, the introduction of Bayesian optimization can more efficiently determine the optimal model hyperparameters.
Bayesian optimization uses the Gaussian process as a prior model, and the optimization process is carried out within a predetermined number of iterations. In each iteration, based on the current Gaussian process model and the acquisition function, a parameter combination with the maximum expected improvement is selected to evaluate the objective function; that is, the AGSN model is trained, and the loss on the validation set is calculated. Then, the newly obtained observation data (the new parameter combination and its corresponding loss) are used to update the Gaussian process model to gradually find the optimal hyperparameters. The hyperparameters of the model trained on the dataset are shown in Table 2.

Table 2.
Hyperparameters of the model.
3. Simulation Analysis
3.1. Hardware and Software Environment
All the experiments were conducted on a computer featuring an Intel i5-11700K processor, 16 GB of RAM, and the Microsoft Windows 11 operating system. This study used Jupyter Notebook 5.6.0 as the software development platform and the PyTorch 2.4 deep learning framework to develop and test the data model in a Python 3.8 environment.
3.2. Evaluation Indicators
Various metrics, such as the root mean square error (RMSE), the mean absolute error (MAE), and the coefficient of determination (), were used to evaluate the performance of the integrated model and the control model. These indicators reliably assessed the difference between the model’s predicted and actual values, calculated as follows:
where is the actual SOH value, is the estimated SOH value, is the average of the actual value, and is the length of the capacity sequence.
3.3. Prediction Results
After data preprocessing, the raw data were divided into training and test sets, with the first 60% of the effective cycle data of lithium-ion batteries used as the training set and the remaining 40% as the test set. Features from the constant current voltage charging curve were selected as inputs, while the SOH of the battery was used as the output. This study systematically compared the AGSN model with several existing neural network models, including the RNN, LSTM, Bi-LSTM [32], and AST-LSTM. Cyclic aging tests were conducted on four different models of batteries (B0005, B0006, B0007, and B0018), with each battery undergoing cyclic aging experiments under different operating conditions. Therefore, the aging rates of the batteries differed under the same number of cycles; for example, at 100 cycles, the SOH of battery B0018 was 12.03% lower than that of battery B0005. These tests covered the performance of batteries under different operating conditions, with the evaluation metrics including RMSE, MAE, and R2.
Figure 8 shows the fitted curves and absolute error plots of the proposed AGSN model compared to existing models (RNN, LSTM, Bi-LSTM, and AST-LSTM) in predicting the SOH of the battery. The experiments were conducted at a temperature of 24 °C and a discharge current of 2 A, with the data being derived from the multi-cycle test results of four different battery models (B0005, B0006, B0007, and B0018).
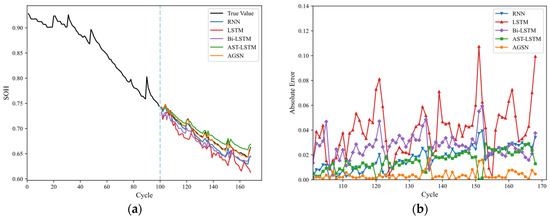
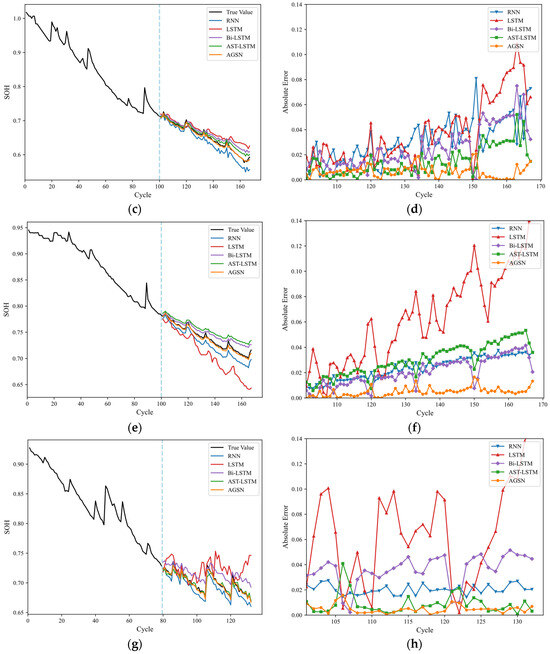
Figure 8.
SOH prediction results for batteries B0005, B0006, B0007, and B0018. (a) B0005 prediction results. (b) B0005 absolute error. (c) B0006 prediction results. (d) B0006 absolute error. (e) B0007 prediction results. (f) B0007 absolute error. (g) B0018 prediction results. (h) B0018 absolute error.
As seen in Figure 8, in the early and mid-stages of prediction, all the models performed well. However, as the number of prediction steps increased, the prediction errors of the RNN and LSTM models increased significantly. This was due to the fact that, during the aging process of lithium-ion batteries, internal structural alterations and intricate electrochemical reactions typically do not manifest in the initial stages of capacity degradation but rather accumulate over extended cycles [33]. Therefore, an SOH prediction in the later stages became more challenging for the sub-models, and the estimation error between the single LSTM and RNN models and the actual SOH was larger. The AST-LSTM model effectively improved the estimation accuracy but still fell short. The experimental results showed that, compared to other models, the AGSN prediction model provided the most accurate SOH estimates with the least error. This was mainly due to the AGSN model’s unique advantages in solving gradient issues by introducing independent recurrent weights and gating mechanisms, enabling the network to learn long-term trends.
Furthermore, during peak regeneration, the other four methods failed to capture the SOH change points and showed larger errors if local regeneration occurred. In contrast, the AGSN model quickly identified the battery’s peaks. This trend was particularly significant in the B0018 battery model compared to the other battery models. Nonetheless, the proposed AGSN method more effectively tracked the aging trajectory of battery B0018 and offered a higher prediction accuracy. The error of this method remained within 1% throughout the capacity decline period, demonstrating that the AGSN improved the prediction accuracy.
The performance metric bar chart in Figure 9 reveals substantial differences in the performance of individual models, whereas the integrated model exhibited consistent outcomes across various batteries. The AGSN model exhibited superior performance compared to traditional models across all the metrics. As shown in the figure, the mean absolute error (MAE) and the RMSE for all the batteries were the lowest among the four models.
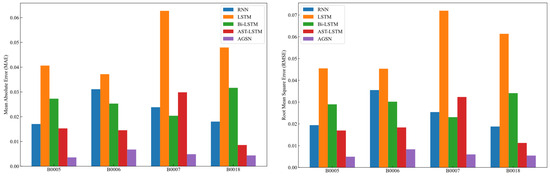
Figure 9.
Error histogram on NASA dataset.
Table 3 presents a comparison of the SOH estimation results for the four battery models (B0005, B0006, B0007, and B0018) under the conditions of a 24 °C temperature and a 2 A discharge current. This study used three main error metrics for the five prediction methods: the RMSE, the MAE, and R2. The results showed that the proposed method outperformed the other four prediction methods across all the metrics.

Table 3.
Comparison of battery error indicators (24 °C, 2 A).
When evaluating the performance of individual models such as the RNN and AST-LSTM, although they performed well in certain cases, such as the RMSE value for model B0006 being below 0.03, these models may lead to unreliable SOH estimates in some situations. For instance, for battery B0018, the RMSE of the RNN and AST-LSTM models was as high as 6%. To address this, this study proposes a new framework designed to integrate the advantages of the RNN and AST-LSTM layers. By using ensemble learning techniques, the proposed framework reduced the prediction errors associated with the individual models, thereby enhancing the overall reliability and accuracy of SOH estimation.
Using the B0005 battery model as an example, the proposed AGSN model achieved an RMSE of 0.0049, an MAE of 0.0036, and an R2 value of 0.9927. This indicates that the AGSN model can predict the battery’s state of health with high precision, significantly outperforming other models. Similar trends were observed for other battery models, with the new model demonstrating significantly higher prediction accuracy and precision than the benchmark models.
Based on the above discussion, the AGSN model demonstrated high accuracy and generalization in predicting the SOH of batteries.
4. Conclusions
In this study, a new battery SOH estimation method based on an AGSN ensemble learning model was proposed. This model was constructed based on an IndRNN layer, an AST-LSTM layer, and an AGM layer, and it was verified under different working conditions using a NASA battery dataset. In order to study the estimation performance of the model, we constructed four basic models—RNN, LSTM, Bi-LSTM, and AST-LSTM—as control models.
- (1)
- A feature extraction method based on the charging voltage curve was proposed. Four features were extracted using a hierarchical inflection point strategy as the sample input, and the correlation between these features and the SOH was verified using the battery dataset, which proved the effectiveness of the extracted features in SOH predictions.
- (2)
- In the SOH estimation results, the proposed AGSN model was superior to other neural network models, such as RNN, LSTM, Bi-LSTM, and AST-LSTM. The RMSE, MAE, and R2 results were the lowest, indicating that the integrated model proposed in this study has a better SOH estimation ability than the other models.
- (3)
- Using the AGSN model, the network can dynamically adjust the information flow according to the importance of the current input and historical information, ensure that key information is fully utilized in the prediction, and demonstrate better performance than a single model. The AGSN-integrated model is more accurate than a single model.
In future work, we plan to collect more battery data on different charging strategies and systematically analyze the extraction of battery features from partial charging states to further improve the applicability and accuracy of our method. Additionally, we will apply machine learning and data fusion techniques to optimize the feature set and enhance the model’s adaptability.
Author Contributions
Conceptualization, K.W. and X.P.; methodology, K.W. and X.P.; software, K.W.; validation, K.W.; formal analysis, K.W.; investigation, K.W. and X.P.; resources, X.P.; data curation, K.W.; writing—original draft preparation, K.W. and X.P.; writing—review and editing, X.P. and H.L.; visualization, K.W. and W.L.; supervision, Q.G.; project administration, Q.G.; funding acquisition, Q.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Shenyang Science and Technology Plan Project (Grant number 22-322-3-29), the Natural Science Foundation of Liaoning Province of China (Grant number 2022JH1/10400033 and 2023JH2/101700261).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Abbreviations
| Abbreviations | |
| SOH | state of health |
| OCV | opencircuit voltage |
| HIs | health indicators |
| IC | incremental capacity |
| CC | constant current |
| CV | constant voltage |
| SVM | support vector machine |
| LSTM | long short-term memory networks |
| RNN | recurrent neural networks |
| GPR | Gaussian process regression |
| Bi-LSTM | bidirectional long short-term memory networks |
| AGSN | adaptive gated sequence network |
| IndRNN | independently recurrent neural network |
| AST-LSTM | active state tracking long short-term memory network |
| AGM | adaptive gating mechanism |
| RMSE | root mean square error |
| MAE | mean absolute error |
| coefficient of determination | |
| Symbols | |
| the whole charging voltage curve | |
| the hierarchical level | |
| voltage features | |
| extreme line | |
| the vertical distance |
References
- Ruan, J.; Song, Q.; Yang, W. Applying a hybrid energy storage system with electrified continuously variable transmission in battery electric vehicles. Energy 2019, 183, 315–330. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, J.; Lund, P.D.; Zhang, Y. Co-estimating the state of charge and health of lithium batteries through combining a minimalist electrochemical model and an equivalent circuit model. Energy 2022, 240, 122815. [Google Scholar] [CrossRef]
- Gou, B.; Xu, Y.; Feng, X. An ensemble learning-based data-driven method for online state-of-health estimation of lithium-ion batteries. IEEE Trans. Transp. Electrif. 2020, 7, 422–436. [Google Scholar] [CrossRef]
- Galeotti, M.; Cinà, L.; Giammanco, C.; Cordiner, S.; Di Carlo, A. Performance analysis and SOH (state of health) evaluation of lithium polymer batteries through electrochemical impedance spectroscopy. Energy 2015, 89, 678–686. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Zhang, L.; Zou, C.; Dorrell, D.D. State-of-health estimation for Li-ion batteries by combing the incremental capacity analysis method with grey relational analysis. J. Power Sources 2019, 410, 106–114. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.; Cho, B.H. Complementary cooperation algorithm based on DEKF combined with pattern recognition for SOC/capacity estimation and SOH prediction. IEEE Trans. Power Electron. 2011, 27, 436–451. [Google Scholar] [CrossRef]
- Dong, H.; Mao, L.; Qu, K.; Zhao, J.; Li, F.; Jiang, L. State of Health Estimation for Li-ion Batteries using Improved Gaussian Process Regression and Multiple Health Indicators. Int. J. Electrochem. Sci. 2022, 17, 220832. [Google Scholar] [CrossRef]
- Tian, H.; Qin, P.; Li, K.; Zhao, Z. A review of the state of health for lithium-ion batteries: Research status and suggestions. J. Clean. Prod. 2020, 261, 120813. [Google Scholar] [CrossRef]
- Meng, J.; Cai, L.; Stroe, D.I.; Luo, G.; Sui, X.; Teodorescu, R. Lithium-ion battery state-of-health estimation in electric vehicle using optimized partial charging voltage profiles. Energy 2019, 185, 1054–1062. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X.; Pan, R.; Wang, Y.; Chen, Z. A novel Gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve. J. Power Sources 2018, 384, 387–395. [Google Scholar] [CrossRef]
- Cai, L.; Lin, J.; Liao, X. An estimation model for the state of health of lithium-ion batteries using energy-based features. J. Energy Storage 2022, 46, 103846. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, R.; Zheng, Y.; Zhang, L.; Guang, H.; Liu, X.; Yang, S. Online state of health estimation for lithium-ion batteries based on gene expression programming. Energy 2024, 294, 130790. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Wang, Z. State of health estimation for Li-ion battery via partial incremental capacity analysis based on support vector regression. Energy 2020, 203, 117852. [Google Scholar] [CrossRef]
- Feng, X.; Weng, C.; He, X.; Han, X.; Lu, L.; Ren, D.; Ouyang, M. Online state-of-health estimation for Li-ion battery using partial charging segment based on support vector machine. IEEE Trans. Veh. Technol. 2019, 68, 8583–8592. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Z.; Xiong, Q.; Ding, B.; Hou, J.; Luo, D.; Li, S. State-of-health estimation and remaining useful life prediction for the lithium-ion battery based on a variant long short-term memory neural network. J. Power Sources 2020, 459, 228069. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Li, X.; Wang, Z. State of health estimation for Li-Ion battery using incremental capacity analysis and Gaussian process regression. Energy 2020, 190, 116467. [Google Scholar] [CrossRef]
- He, T.; Gong, Z. State of health estimation for lithium-ion batteries using a hybrid neural network model with Multi-scale Convolutional Attention Mechanism. J. Power Sources 2024, 609, 234680. [Google Scholar] [CrossRef]
- Tan, Y.; Zhao, G. Transfer learning with long short-term memory network for state-of-health prediction of lithium-ion batteries. IEEE Trans. Ind. Electron. 2020, 67, 8723–8731. [Google Scholar] [CrossRef]
- Li, Q.; Li, D.; Zhao, K.; Wang, L.; Wang, K. State of health estimation of lithium-ion battery based on improved ant lion optimization and support vector regression. J. Energy Storage 2022, 50, 104215. [Google Scholar] [CrossRef]
- Chaoui, H.; Ibe-Ekeocha, C.C. State of charge and state of health estimation for lithium batteries using recurrent neural networks. IEEE Trans. Veh. Technol. 2017, 66, 8773–8783. [Google Scholar] [CrossRef]
- Sherkatghanad, Z.; Ghazanfari, A.; Makarenkov, V. A self-attention-based CNN-Bi-LSTM model for accurate state-of-charge estimation of lithium-ion batteries. J. Energy Storage 2024, 88, 111524. [Google Scholar] [CrossRef]
- Abuqaddom, I.; Mahafzah, B.A.; Faris, H. Oriented stochastic loss descent algorithm to train very deep multi-layer neural networks without vanishing gradients. Knowl.-Based Syst. 2021, 230, 107391. [Google Scholar] [CrossRef]
- Cui, Y.; Chen, Y. Prognostics of lithium-ion batteries based on capacity regeneration analysis and long short-term memory network. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K. Battery data set. In NASA AMES Prognostics Data Repository; NASA Ames Research Center: Moffett Field, CA, USA, 2007. [Google Scholar]
- Lee, J.H.; Lee, I.S. Lithium battery SOH monitoring and an SOC estimation algorithm based on the SOH result. Energies 2021, 14, 4506. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, J.; Zhang, L. State-of-health estimation for lithium-ion batteries based on the multi-island genetic algorithm and the Gaussian process regression. IEEE Access 2017, 5, 21286–21295. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.; Li, X.; Gu, F.; Zhang, L.; Liu, H.; Li, Q. Reacquainting the electrochemical conversion mechanism of FeS2 sodium-ion batteries by operando magnetometry. J. Am. Chem. Soc. 2021, 143, 12800–12808. [Google Scholar] [CrossRef] [PubMed]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J.; Chen, J.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Deng, Y.; Liu, X.; Jia, R.; Huang, Q.; Xiao, G.; Wang, P. Sag source location and type recognition via attention-based independently recurrent neural network. J. Mod. Power Syst. Clean Energy 2021, 9, 1018–1031. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Z.; Grosu, R.; Deng, Z.; Hou, J.; Rong, Y.; Wu, R. An end-to-end neural network framework for state-of-health estimation and remaining useful life prediction of electric vehicle lithium batteries. Renew. Sustain. Energy Rev. 2022, 156, 111843. [Google Scholar] [CrossRef]
- Kong, D.; Wang, S.; Ping, P. State-of-health estimation and remaining useful life for lithium-ion battery based on deep learning with Bayesian hyperparameter optimization. Int. J. Energy Res. 2022, 46, 6081–6098. [Google Scholar] [CrossRef]
- Xu, P.; Wang, C.; Ye, J.; Ouyang, T. State-of-charge estimation and health prognosis for lithium-ion batteries based on temperature-compensated Bi-LSTM network and integrated attention mechanism. IEEE Trans. Ind. Electron. 2023, 7, 5586–5596. [Google Scholar] [CrossRef]
- Teliz, E.; Zinola, C.F.; Díaz, V. Identification and quantification of ageing mechanisms in Li-ion batteries by Electrochemical impedance spectroscopy. Electrochim. Acta 2022, 426, 140801. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).