Abstract
Battery packs found in electric vehicles (EVs) require thermal management systems to maintain safe operating temperatures in order to improve device performance and alleviate irregular temperatures that can cause irreversible damage to the cells. Cylindrical lithium-ion batteries are widely used in the electric vehicle industry due to their high energy density and extended life cycle. This report investigates the thermal performance of three liquid cooling designs for a six-cell battery pack using computational fluid dynamics (CFD). The first two designs, vertical flow design (VFD) and horizontal flow design (HFD), are influenced by existing linear and wavy channel structures. They went through multiple geometry optimisations, where parameters such as inlet velocity, the number of channels, and channel diameter were tested before being combined into the third and final optimal design (OD). All designs successfully maintained the maximum temperature of the cells below 306.5 K at an inlet velocity of 0.5 ms−1, meeting the predefined performance thresholds derived from the literature. The HFD design was the only one that failed to meet the temperature uniformity goal of 5 K. The optimal design achieved a maximum temperature of 301.311 K, which was 2.223 K lower than the VFD, and 4.707 K lower than the HFD. Furthermore, it produced a cell temperature difference of 1.144 K, outperforming the next-best design by 1.647 K, thus demonstrating superior temperature regulation. The OD design can manage temperatures by using lower inlet velocities and reducing power consumption. However, the increased cooling efficiency comes at the cost of an increase in weight for the system. This prompts the decision on whether to accommodate the added weight for improved safety or to allocate it to the addition of more batteries to enhance the vehicle’s power output.
1. Introduction
1.1. Background
With increasing concerns about global warming, the need to transition to renewable energy sources and reduce greenhouse gas emissions is paramount for preserving the future of the planet. The transportation sector alone contributes to 24% of the UK’s total emissions, with cars accounting for 52% of the sector’s emissions [1]. The demand for electric vehicles (EVs) is expected to surge in the coming years due to the sustainability goals pursued by both the public and the government. Batteries are the primary power source for EVs, and continuous developments in battery technology have significantly improved EV performance, including charging speed, life cycle, and range. However, the absence of effective battery thermal management systems (BTMSs) can severely impact vehicle performance. For instance, abnormal temperatures can degrade the battery capacity, shorten the EV’s lifespan, and, in extreme cases, lead to thermal runaway, resulting in combustion and explosion [2]. Due to the critical role of battery thermal systems in EVs, this report will examine and present the development of three cooling structures, the vertical flow design (VFD), horizontal flow design (HFD), and optimal design (OD), and assess their effectiveness in regulating temperature within the battery pack.
1.2. Literature Review
The following literature review aims to provide a comprehensive summary of the key areas influencing EV BTMSs, focusing on battery types and different cooling methods.
1.2.1. Batteries
As of 2015, lithium-ion batteries accounted for 85.6% of deployed energy storage systems [3]. Their widespread use in EVs is attributed to several advantages over alternative rechargeable batteries, such as nickel-, sodium-, and lead-based batteries. These advantages include a higher operating voltage of up to 3.7 V, making them ideal for high-power applications, and exhibit a low self-discharge rate, enabling them to store charge for longer periods and therefore extending their lifespan [4]. EV manufacturers primarily utilise three cell shapes: cylindrical, prismatic, and pouch cells. Cylindrical cells are available in standardised dimensions of 18,650, 21,700, and 46,800; for example, all units are in millimetres, with 18 and 65 representing the cell diameter and height, respectively [5]. Prismatic cells do not have a universal size but are rectangular in shape, and compared to cylindrical cells, they feature lower voltage and fewer connections, resulting in slower discharge rates. However, their fewer connections allow for larger energy capacities [6]. Cylindrical and prismatic cells are the preferred choice for EV manufacturers; conversely, pouch batteries are an emerging technology, inducing high production costs, but most importantly, their low mechanical resistance makes them a risk for installation in vehicles [5]. The significant hazards associated with pouch cells make them an unpopular choice for designing battery packs.
Excessive heat generation within batteries occurs during the charging and discharging process because of changes in enthalpy, electrochemical polarisation, and resistive heating [7]. Additional thermal issues, such as uneven temperature distribution, can arise from capacity fading, self-discharge, and electrical imbalance. Liu et al. [8] found that when the temperature of the battery exceeds 353.15 K, the chemical reaction rate inside the cells increases, causing excessive internal heating and initiating the thermal runaway process. According to Ji et al. [9], the maximum temperature range before performance degradation for a lithium-ion battery is 253.15 K to 333.15 K, while the optimal operating range is between 298 K and 313 K. Uneven temperature distribution can also affect the battery lifespan, so the difference in maximum and minimum temperatures in a battery pack should be less than 5 K to achieve the best performance [10]. Thermal problems can affect the lifespan of the battery pack, which is why cooling methods are implemented to dissipate heat, manage heat flow, and ensure the battery packs are operating within the optimal temperature range with minimal temperature variation. The literature has presented the three main types of cell types, and the focus of this study will be on cylindrical cells, given their widespread use.
1.2.2. Cooling Methods
This section explores the different cooling methods that can be employed in BTMSs in order to alleviate abnormal temperatures. Air cooling and liquid cooling are universally the most used methods of cooling and will therefore be discussed to guide the development of the cooling structures showcased in this report.
Air Cooling
Despite its poor thermal conductivity, air cooling is a preferred choice for certain Chinese and Japanese EV manufacturers, such as BYD, Toyota, and Nissan [11], due to its simplicity and low costs. Air cooling can be classified into forced and passive air cooling. Passive cooling relies on the movement of the vehicle to naturally send air through the system but does not provide a sufficient cooling capacity compared to forced air cooling, which makes use of fans to blow air across the surface of the cells. Although liquid cooling contains a more complex geometry and heavier design, it can be 2–3 times more efficient than air cooling. The average liquid-cooled structure lowers the cell temperature by 3 K, resulting in energy savings of up to 40% while also making the battery pack more compact [11].
Liquid Cooling
Liquid cooling is held at a higher degree of importance to researchers as it is the most efficient cooling method, being employed by many EV manufacturers such as Tesla, BMW, and Chevrolet [12]. Liquid cooling can be classified into direct and indirect cooling, where direct cooling involves immersing the cells directly into a fluid, offering advantages like maximum contact area and enhanced thermal uniformity [13]. Despite these advantages, direct cooling is rarely employed in BTMSs because of the potential short circuits and electrochemical reactions that can arise from the difficulty of producing completely water-resistant battery packs [13]. Indirect cooling utilises metal cooling plates, tubes, or jackets containing embedded miniature coolant channels [12]. These metal structures contact the surface of the cell, allowing heat generated from the cells to be transferred through the plates to the flowing coolant, which carries the heat out of the system. This approach eliminates the direct contact between the battery and coolant, minimising the risk of electrical short-circuiting. Tang et al. [14] investigated the effect of the coolant velocity at the inlet for a cold plate prismatic cell pack. A discharge of 2C was applied to the cells, and velocities ranging from 0.1 ms−1 to 1 ms−1 were evaluated. Greater temperature reductions and thermal uniformity were observed at velocities above 0.5 ms−1. This was only tested with one coolant channel applied along the edge of the cell, opening the potential for investigation into more channels and their placements. Zhao et al. [15] investigated the common wavy/serpentine channel design, referencing a Tesla Model S battery pack consisting of 71, 18,650 Li-ion cells. The structure was made of an aluminium alloy with a width of 2 mm and a height of 65 mm. It consisted of a singular coolant channel spanning the length of the structure. Channel angles of 10°, 20°, 30°, and 40° were used, and the thermal performance improved as the angles increased. This improvement was attributed to the larger surface contact area achieved with larger channel angles, resulting in greater thermal transfer and a lower cell temperature. The study by Xu et al. [16] confirmed this effect and tested their own linear U-shaped structure with grooves to slot the cells into place. It was found to be inferior to the wavy channel design, achieving a lower maximum temperature of 0.37 K. A linear flowing channel design (LCD) constructed by Lloyd et al. [17] features a uniform arrangement with four channels and contact points per cell, providing 75% contact with the surface of each battery. This structure was able to maintain the cell temperature within the optimal operating range and achieve the recommended thermal uniformity proposed by Ji et al. [9]. A low mass flow rate of 7.5 × 105 kgs−1 was used to save energy consumption, and channels with diameters of 3 mm, 6 mm, and 9 mm were assessed. The results revealed that larger diameters only marginally reduced maximum temperatures. A mini channel-cooled cylinder (MCC) design by Yates et al. [18] consists of a 3 mm thick cylinder structure with multiple microchannels. This design fully encapsulates the cells and is therefore expected to provide the greatest heat transfer. Comparing the MCC design to the LCD at a cell operating at a 5C discharge rate, the maximum temperature of the MCC reached 309.308 K, while the LCD reached 310.26 K. This confirms that surface area contact plays an important role in determining the cooling effectiveness of designs.
The literature review has highlighted the importance of liquid cooling and the many types of cooling structures. The wavy channel design is prevalent, and this report will explore further angle variations, whilst examining various numbers of coolant channels to further optimise the design. Refining the linear channel design can potentially improve thermal capabilities, as it utilises less material while still providing commendable thermal regulation. Therefore, my iteration of the LCD will incorporate a slightly modified shape, and the coolant channel diameter will be adjusted accordingly. To further enhance the scientific relevance of the study, a third and unique design will also be included.
2. Materials and Methods
The objective of the project was to develop and evaluate the effectiveness of liquid cooling structures for thermal management within a battery pack. As identified in the literature, liquid cooling surpassed air cooling in terms of heat capacity and heat transfer efficiency, making it the chosen method for the investigation. Cylindrical cells are the most common cell geometries for battery packs; hence, the cooling system will be tailored to these specifications, as it offers more value and practicality.
2.1. Battery Chemistry
Lithium-ion batteries are the most popular type of battery, specifically those consisting of a LiFePO4 chemistry. In cylindrical cells, the internal components include the cathode, anode, separator, and current collectors, which are spirally wound [19]. The electrochemical reactions that occur during charging (←) and discharging (→) at the electrode/electrolyte interfaces are presented by Equations (1) and (2) [19]:
2.2. Battery Material and Properties
Modelling the physical and chemical reactions occurring within the cell can be challenging. Therefore, to reduce computational complexity, the internal battery components were simplified to a solid cylinder with uniform heat generation and homogeneous material properties. This simplification ensured a steady transfer of heat to the surroundings and reduced the computational requirements. The properties of the simplified cell model, sourced from Zhao et al. [20], are presented in Table 1, alongside other experimental materials, utilising the Ansys material database.

Table 1.
Material properties.
A battery undergoing a 5C discharge rate experiences significant strain and shock, which can increase the chance of chain reactions. Wang et al. [21] studied the effects of a single cell operating at this discharge rate and found that the heat generation increased linearly, reaching a maximum temperature of 351 K after running transiently for 720 s. These results were validated by Lloyd et al. [17], who calculated the equivalent heat generation rate of the cell to be 138,000 Wm−3. These findings served as the basis for establishing the heat generation of the battery pack in my own investigation.
Three models were created for the study. The first model featured a new partial jacket structure, resembling a four-point star configuration, which provides more contact with the cell. The second model focused on adapting the traditional wavy channel, where modifications were made to explore different channel angles and the number of coolant channels to assess variables not explored in the literature. Finally, the third and novel model integrated both the wavy channel design and the partial jacket design with the optimised parameters from the first two designs. One unique aspect of this model is the bidirectional flow of coolant, which has not been explored in the literature. Many parameters will need to be modified for each design, so utilising CAD and CFD software (Ansys 2024 R1) for modelling and experimentation will allow for an easy adjustment of the geometry and parameters. This approach will require significantly less time and resources as opposed to physical setup and model manufacture. SolidWorks 2022 will be used for model creation, and once these models are created, they will be downloaded as a STEP file and imported into Ansys 2024 R1, along with its fluent module, where meshing and simulations will take place to analyse the heat generation of the cell and the extent to which the cooling structures can manage the cell temperatures.
2.3. Numerical Model
The governing equations presented below explain the thermodynamics and coolant dynamic principles that are fundamental to the numerical investigation. The temperature (Tb) of a single lithium-ion cell can be modelled by the general conservation energy Equation (3) [19]:
where ρb denotes the generalised density of the battery, cp,b is the specific heat capacity of the battery, and kb signifies the generalised thermal conductivity of the battery. qgen is the total heat generation of the battery and can be determined by the simplified Bernardi Equation (4) [22]:
where Vb is the volume of the battery, Ib is the internal current of the battery, and Rb is the internal resistance of the battery. The term represents the temperature coefficient, a variable related to the electrochemical reaction of a cell and derived from the open-circuit voltage of the battery, Ub. Liquid water was the coolant used in the research, maintaining a constant mass throughout the system. According to Zhou et al. [23], the coolant flow and heat transfer can be expressed by continuity Equation (5) [23], momentum conservation Equation (6) [23], and energy conservation Equation (7) [23]:
where t represents time, w is the velocity of water, µw indicates the dynamic viscosity of water, and P represents pressure. The subscript ‘w’ is used to denote variables associated with water that have been previously identified. The heat transfer between the coolant, cooling channels, and the battery can be modelled by the heat flow Equations (8) and (9) [17]:
where Q is the thermal energy, is the mass flow rate, h is the heat transfer coefficient, and A is the surface area for heat transfer. The Reynold number (Re) (8) [16] can be used to calculate the coolant flow characteristics:
where d represents the characteristic length. The Reynolds number is used to determine the coolant flow characteristics, which can be laminar, transitional, or turbulent.
2.4. Battery Pack Development
The first model, the vertical flow design (VFD), draws inspiration from the structure created by Lloyd et al. [17]. The second model, the horizontal flow design (HFD), is based on the serpentine design by Tang et al. [24]. The third and final model combines the features of the VFD and HFD. The cooling systems were developed in SolidWorks and configured to regulate the temperature of six 18,650 cylindrical cells. These cells were uniformly arranged, with each cell positioned 20 mm apart from the adjacent cell.
2.4.1. Vertical Flow Design (VFD)
Typical linear liquid cooling structures contain a coolant domain located above and below the cells with one inlet and one outlet, as shown in Figure 1a. Both this model and a simplified version, as shown in Figure 1b, were tested with a set inlet velocity and cell heat generation. The results revealed only a minimal temperature difference of 0.02 K between the two designs. Therefore, the simplified version was adopted as it significantly reduced model complexity and simulation time. The four-point star-shaped structure, which is 65 mm in height, interlocks the cylindrical cell surfaces, as illustrated in the top view drawing in Figure 1c. This figure also depicts the variation in channel diameters, which will be evaluated in the simulations. Additionally, the inlet flow velocity will be tested at 0.01 ms−1, 0.05 ms−1, 0.1 ms−1, 0.5 ms−1, and 1 ms−1. These parameters were selected to explore untested variations in the cooling design and to validate against the existing literature.
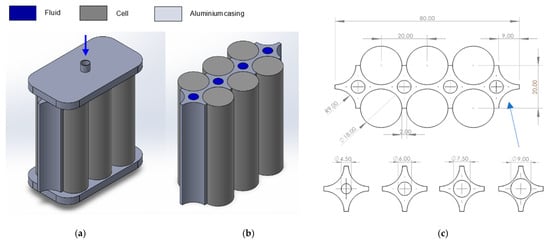
Figure 1.
VFD views and dimensions (mm): (a) isometric view of VFD with fluid domain and inlet; (b) isometric view of simplified VFD; (c) battery pack top view and arrow indicating the section of the design that will have channels of varying diameters.
2.4.2. Horizontal Flow Design (HFD)
The second model created is illustrated in Figure 2a. Figure 2b shows the top view of the pack, depicting the cooling plate thickness and channel angles of 45 °, 55 °, 65 °, and 75° selected for the investigation. Then, 1, 2, 3, and 5 coolant channels will be examined, with the width of these channels remaining constant. The varying height dimensions of the coolant domain are illustrated in a front view in Figure 2c.
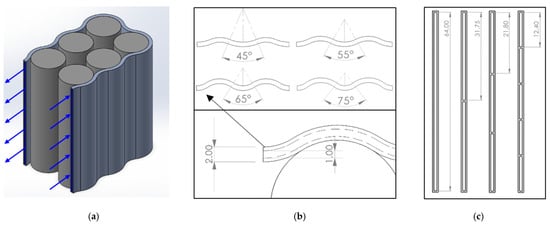
Figure 2.
HFD views and dimensions (mm): (a) HFD isometric view; (b) top view and dimensions, with an arrow showing the detailed view; (c) front view dimensions of the inlet/outlet fluid domains.
2.4.3. Optimal Design (OD)
Illustrated in Figure 3 is the OD, the third and final cooling structure. This figure also depicts the design methodology of the OD which combines components from both the HFD and VFD. The OD incorporates an outer wavy channel and a star-shaped configuration into a single design. Two horizontal channels with an angle of 65° were used, determined through testing of the thermal efficiency based on simulations of the VFD and HFD.

Figure 3.
Construction of OD model with coolant inlet and outlet directions.
2.5. CFD Configuration and Boundary Conditions
Once the CAD model’s geometries were created, they were imported into Ansys 2024 R1, and a tetrahedral-shaped mesh was selected due to its ease of generation in complex geometry cases. A mesh refinement study was conducted on the VFD to determine the optimal mesh density, using the maximum temperature as a basis to ensure accurate solutions. The results are presented in Figure 4 and show that the maximum temperature converges when more than 400,000 elements are produced. The final mesh utilises a 1 mm element size, producing 781,479 elements. As this mesh size produced satisfactory convergence, it was applied to the other designs as they share similar geometry. This mesh was further refined using inflation layers over walls, flow channels, and cells where heat transfer and thermal gradients are expected. The total number of mesh elements for each design and parameter change was maintained at a similar range where possible. Specifically, 781,479 elements were produced for the VFD, and 712,904 elements were produced for the HFD, as shown in Figure 5a,b, respectively.
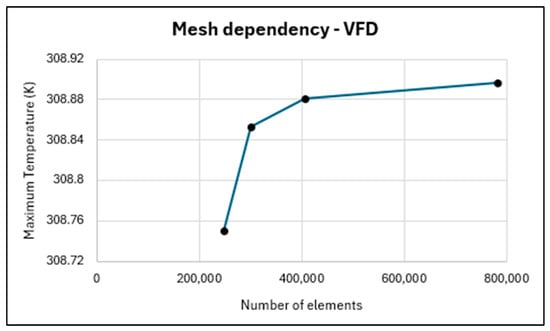
Figure 4.
Mesh dependency study on VFD.

Figure 5.
Mesh generation for (a) VFD and (b) HFD.
In the fluent module, the double precision solver option was selected along with four solver processors. A pressure-based solver and absolute velocity formulations with a transient time step were chosen. The fluent energy model was activated to enable heat transfer, utilising energy conservation Equation (7). The viscous standard k-ε model with enhanced wall treatment was selected, as the flow characteristics were expected to range from laminar to turbulent flow, depending on variations in channel diameter and inlet velocities as per Equation (8). As recommended by Yates et al. [18], the ambient temperature of the environment is set to 300 K, assuming an adiabatic environment for the battery packs. Therefore, the outer surfaces of the battery packs were designated as thermally insulating boundaries, considering their confined environments with restricted airflow and minimal thermal influence. Material properties used in this investigation are shown in Table 1, with aluminium being assigned as the cooling structure material, custom battery material for the cells, and liquid water for the coolant. Wall surfaces within the channel were set as stationary with a no-slip condition. The solid and coolant cell zones were set as coupled to allow for natural convection in the system.
A heat generation rate of 138,000 Wm−3 was applied to each cell, highlighted in green in Figure 6, to replicate heat generation in a cell undergoing a 5C charge/discharge rate. The temperature of the coolant at the inlet was set to 300 K, and the velocities were adjusted accordingly to the project aims. The inlet location and coolant path of both designs are depicted in Figure 6 by the blue arrows and blue lines.
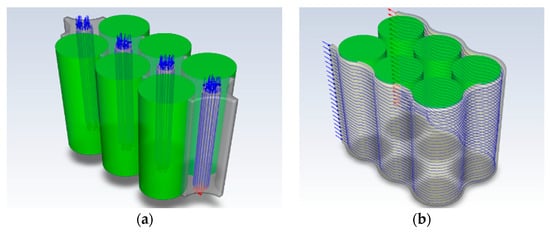
Figure 6.
Boundary condition selection for (a) VFD and (b) HFD.The calculation initialisation was computed from all zones, and the calculation was set to run for 720 s to replicate the time it takes a cell to reach maximum temperature at 5C.
The timestep was set to 1 s for boosted accuracy, with a maximum number of iterations per time step set to 400 to increase the chances of convergence. Although, the maximum number of iterations it took for the time step to converge was 20. Following the completion of each design and variable change in the investigation, the boundary conditions, solution activities, and monitors to record and plot the maximum and minimum temperatures for the cell volume were all transferred to the subsequent stages. The simplified CFD configuration process can be summarised by the flow chart from Figure 7.
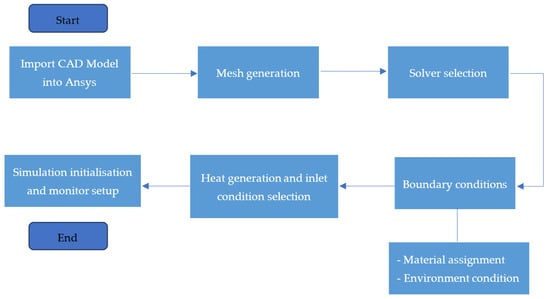
Figure 7.
Flow diagram outlining CFD configuration of each design.
3. Results
3.1. Vertical Flow Design Results and Analysis
3.1.1. Influence of Inlet Velocity on VFD
The first parameter optimisation study explored the impact of inlet velocity on the maximum temperature (Tmax) and temperature difference between the maximum and minimum (∆T) of the battery pack. For this study, 6 mm channels were used. Figure 8a presents the results for the effect of the five different velocity values on the Tmax of the cell. A clear trend is illustrated where increasing the velocity reduces the Tmax of the cells. This trend aligns with heat flow Equations (8) and (9), where the rate of heat flow is directly proportional to the mass flow rate and hence the velocity. Initially, the temperature rises rapidly for all velocities within the first 60 s of cell discharge, after which the temperatures begin to diverge. Beyond 320 s, the Tmax of the cell is reached and levels out for all velocities except for 0.01 ms−1. Table 2 provides the maximum temperature and uniformity achieved by the cell after 720 s for different velocities. Comparing the results reveals that the difference in final maximum temperatures between 0.5 ms−1 and 1 ms−1 is only 0.327 K, while the difference between 0.1 ms−1 and 0.5 ms−1 is 1.308 K, indicating the diminishing effectiveness of higher flow rates beyond 0.5 ms−1. This study can be validated against the work of Lloyd et al. [17], where their LCD of a six-cell lithium-ion battery pack with dimensions, material, and shape produced a Tmax of 309.308 K, which is 0.029% different to the Tmax from the work of this cooling structure.
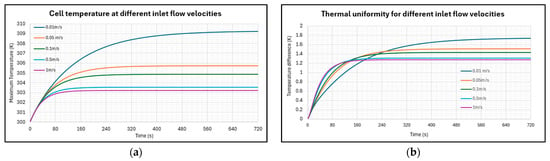
Figure 8.
Effects of flow velocity on (a) maximum cell temperature and (b) cell temperature difference.

Table 2.
Maximum temperature and uniformity achieved by the cells at different inlet velocities.
Figure 8b shows the relationship between increasing inlet velocity and thermal uniformity. The first 80 s of the simulation feature a steep rise in ∆T before it stabilises as the lithium-ion core cools at the same rate as the surface. A temperature differential is present because the VFD comes into contact with half of each cell, leaving the outer part exposed to the air. This makes it difficult for the heat generated to dissipate, resulting in higher temperatures than the rest of the pack. Table 2 reveals that the ∆T is only 0.462 K between the largest and smallest velocities tested. Despite the lowest velocity producing a ∆T of 1.733 K, it is still within the maximum ∆T goal of 5 K. These results demonstrate that the inlet velocities have a greater effect on the maximum temperature of the cell than on temperature uniformity. All examined velocities satisfy the desired operating temperatures of 298 K < Tmax < 313 K and ∆T < 5 K. As the results of the 0.5 ms−1 were very similar to and within 0.12% of the Tmax observed at a velocity of 1 ms−1, it will be used as the velocity for all remaining experiments as it balances effective thermal regulation and power consumption.
3.1.2. Influence of Channel Diameter on VFD
Next, the channel diameter for the VFD was varied while using a constant inlet velocity of 0.5 ms−1. Figure 9a shows the relationship between Tmax and channel diameter, indicating a reduction in Tmax as the channel diameter increases. This is explained by the heat flow Equations (8) and (9), which suggest that increasing the channel diameter increases the heat transfer area between the coolant and channel interior. Table 3 provides the Tmax and ∆T values recorded at the end of the battery discharge for the tested channel diameters. Notably, the Tmax of the 4.5 mm and 9 mm diameter channels measured 303.750 K and 303.297 K, respectively, only showing a marginal difference of 0.453 K. This can be attributed to the velocity in the channel decreasing as channel diameter increases, reducing the heat transfer coefficient, and counteracting the cooling capability.
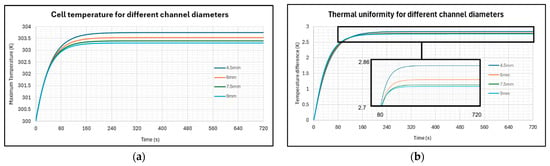
Figure 9.
Effects of channel diameter on (a) maximum cell temperature and (b) cell temperature difference with enlarged graph plot between ∆T of 2.7 K and 2.86 K and time step of 80 to 720.

Table 3.
Maximum temperature and uniformity achieved by the cells at different channel diameters.
The thermal uniformity for different diameters is shown in Figure 9b. While initial observations suggest a negligible difference between the variables, a closer examination within a time of 80–720 s and a ∆T of 2.7–2.86 reveals some variation. The 9 mm diameter exhibited a lower ∆T compared to the 4.5 mm at 720 s, but this was marginal; for the 4.5 mm channel, it was 2.840 K, and the 9 mm channel was 2.767 K, showing a difference of 0.0073 K. Although the channel diameter shows improvement in thermal uniformity, the impacts are minimal when compared to changing the velocity.
3.2. Horizontal Flow Design Results and Analysis
3.2.1. Influence of Channel Angle on HFD
For the HFD, channel angles of 45°, 55°, 65°, and 75° were tested with one flow channel. The relationship between Tmax and ∆T is presented in Figure 10a,b, and the final values achieved at the end of the battery discharge are presented in Table 4. These results indicate that using a lower channel angle worsens the thermal performance, with a difference of 0.802 K and 0.858 K between the largest and smallest angles for the Tmax and ∆T, respectively. The effect of channel angle has more influence on the thermal uniformity, with a 16.5% change in ∆T between the angles of 45° and 55°, compared to a 0.26% change in Tmax. The improved performance of higher contact angles results from geometry changes during each design test, as the curves of the aluminium structure wedge themselves into the gaps between the cells, creating more surface contact area. According to Equation (9), this allows for more heat transfer from the lithium-ion cell to the aluminium structure, thereby lowering the temperature of the cell and being the cause of the significant difference in thermal uniformity. The Tmax recorded was 306.250 K, meeting the condition of 298 K < Tmax < 313 K. However, none of the angles in the simulation satisfied the ∆T < 5 K thermal uniformity goal, with the best-performing angle (75°) only producing a temperature difference of 5.197 K at the end of the 720 s. While the contact angle of 75° showed better performance than smaller angles, this design uses more material and hence weight. The sharper angles may introduce slight pressure drops in the system.
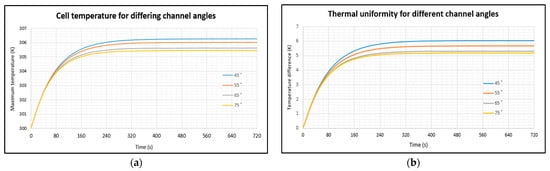
Figure 10.
Effects of channel angle on (a) maximum cell temperature and (b) cell temperature difference.

Table 4.
Maximum temperature and uniformity achieved by the cells at different channel angles.
3.2.2. Influence of Number of Coolant Channels on HFD
The graphs in Figure 11 present the results on how Tmax and ∆T of the cell vary when one, two, three, and five coolant plate channels are present in the HFD. As seen in the first 80 s, both Tmax and ∆T increase sharply, before diverging. Increasing the number of cooling channels leads to a decrease in the final Tmax and ∆T within the battery pack. However, beyond one channel, the influence becomes minimal, as indicated by Table 5, which shows a Tmax difference of 0.544 K between one and two channels, while the difference between Tmax of channels two and five is only 0.121 K. In addition, the temperature uniformity showed a similar relationship as the number of channels increased.
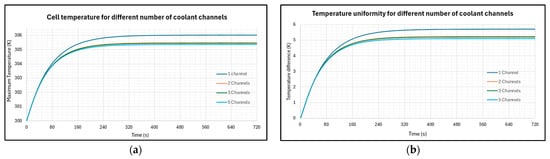
Figure 11.
Effects of number of coolant channels on (a) maximum cell temperature and (b) cell temperature difference.

Table 5.
Maximum temperature and uniformity achieved by the cells at different numbers of flow channels.
For both the channel angle and number of channel optimisations for the HFD, the temperature difference ∆T exceeds 5 K, which is greater than the desired condition of ∆T < 5 K. This phenomenon is caused by the design itself, where the aluminium structures only wrap around the outside of the cell arrangement, leaving the inner cells unattended. Additionally, as the channels loop around, they provide more cover for the two outer cells compared to the cells located closest to the inlet and outlet, causing excessive thermal gradients which are evident in the final temperature contour of the HFD, as shown in Figure 12a. The results for the HFD can be validated against the work of Tang et al. [24] who found the ∆T to be approximately 5.29 K, which is close to the values I obtained.

Figure 12.
Battery pack temperature contour after 720 s at 0.5 ms−1 inlet velocity: (a) HFD; (b) VFD.
3.3. Optimal Design Results and Analysis
The final optimal design (OD) for the six-cell 18,650 battery pack combines the VFD and HFD, featuring three vertical 6 mm diameter channels and two 31.75 mm × 1 mm horizontal channels for coolant flow, as shown in Figure 3. The thermal performances of the VFD, HFD, and OD are plotted in Figure 13, with the final Tmax and ∆T values presented in Table 6. The OD design excelled in the thermal management of the pack compared to the other designs, efficiently dissipating the heat generated by the cells after 50 s and maintaining Tmax at an extremely low temperature of 301.311 K for the remaining time steps. In contrast, the VFD took 160 s to reach a Tmax of 303.534 K, while the HFD showed the poorest cooling performance, reaching a Tmax of 306.018 K after 320 s. The superior performance of the OD is attributed to its greater contact surface area with the cells compared to the other designs; the cells are almost entirely encapsulated, whereas the HFD and VFD leave 50% of the cells without contact. The temperature contour of the OD is illustrated in Figure 14a. Furthermore, as explained by Equation (9), more heat generated by the battery can be transferred to the cooling structure and expelled from the system. All three designs comfortably met the 298 K < Tmax < 313 K requirement, with only the OD and VFD satisfying the ∆T < 5 K requirement.
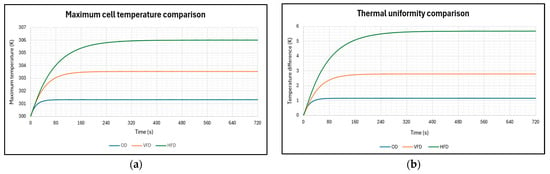
Figure 13.
VFD, HFD, and OD thermal comparison: (a) maximum cell temperature; (b) cell temperature difference.

Table 6.
Maximum temperature and uniformity of the OD, VFD and HFD.
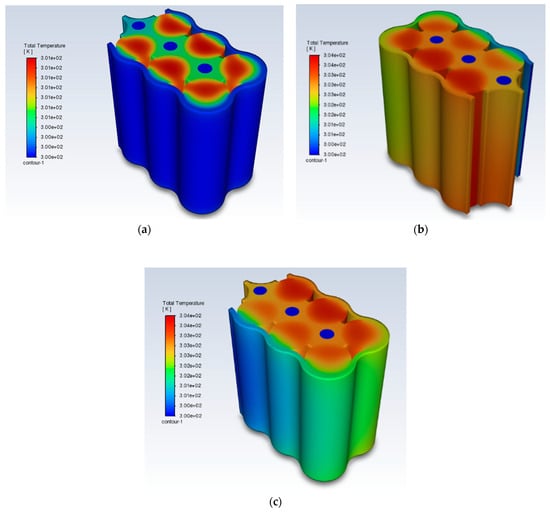
Figure 14.
OD thermal contours (a) at 0.5 ms−1; (b) at 0.01 ms−1, view 1; and (c) at 0.01 ms−1, view 2.
The OD exceeded thermal management expectations and was subsequently assessed with a smaller inlet velocity of 0.01 ms−1. The temperature contour for both the front and back view of the structure at this lower velocity are shown in Figure 14b,c, respectively. The results indicate that the Tmax at the end of the battery discharge cycle reached 304 K, well within the desired range of 298 K < Tmax < 313 K, suggesting that the structure can effectively conserve energy, by using lower flow rates while maintaining efficient thermal management. However, the thermal gradients become more pronounced, with a ∆T of 4.05 K, approaching the 5 K thermal uniformity limit. The observed temperature variation within the cells reveals that those situated closest to the inlet are cooler, while those closer to the outlet exhibit higher temperatures. This phenomenon arises from the slower velocity, which limits the heat transfer rate between the coolant and cold plates. By the time the coolant circulates through the structures, it heats up, resulting in a slower heat dissipation process, as explained by heat flow Equation (9). This effect is also evident in the wavy aluminium structure, which experiences significant heating due to the coolant’s reduced capacity to extract heat from the system at lower velocities. In contrast, the wavy structure from Figure 14a, remains closer to ambient temperature, due to the higher velocity of the coolant moving through the system, and providing a more even temperature distribution.
3.4. Summary of Key Findings
3.4.1. VFD—Influence of Inlet Velocity
- Increasing the inlet velocity reduces the Tmax of the cells.
- The effectiveness of higher flow rates diminishes beyond 0.5 ms−1.
- All tested velocities met the desired operating temperatures (298 K < Tmax < 313 K) and thermal uniformity (ΔT < 5 K).
- A value of 0.5 ms−1 was chosen for further experiments as it balanced thermal regulation and power consumption.
3.4.2. VFD—Influence of Channel Diameter
- Increasing the channel diameter reduces Tmax, but this effect is only minimal. The smallest diameter (4.5 mm) produced a Tmax of 0.453 K higher than the largest diameter (9 mm).
- Thermal uniformity improved slightly with larger diameters.
3.4.3. HFD—Influence of Channel Angle
- Larger channel angles displayed better thermal performance and uniformity than lower angles.
- All angles met the thermal range; however, none of the angles tested met the thermal uniformity requirement.
3.4.4. HFD—Influence of Number of Coolant Channels
- Increasing the number of coolant channels reduced Tmax, but this effect is minimal beyond one channel.
- The thermal uniformity improved when more than one channel is used but the effect is minimal when additional channels are used.
3.4.5. OD
- Superior thermal management was shown, maintaining a very low Tmax (301.311 K) and excellent thermal uniformity (1.144 K).
- OD met all thermal requirements and outperformed both the VFD and HFD.
- Lowering the inlet velocity to 0.01 ms−1 for OD still kept Tmax within the desired range, but thermal uniformity approached the 5 K limit (4.05 K).
4. Discussion and Conclusions
This investigative project evaluated two liquid cooling designs: one with water flowing in channels parallel to the cells (VFD), and the other with coolant channels placed perpendicular to the cells (HFD). These designs were investigated using CFD to assess their effectiveness in battery thermal management. Following the evaluation of the VFD and HFD, they were combined to create a novel cooling design, incorporating the most effective variables from each initial design. The simulations used a cylindrical 18,650 LiFePO4 battery model. The thermal generation within the cell was set to replicate a battery undergoing a 5C charge/discharge rate. The coolant and ambient temperatures were assumed to be 300 K. The influence of inlet velocity and channel diameter was investigated for the VFD model, while the influence of the wavy channel angle and number of channels was investigated for the HFD model. The performance of the liquid cooling structures was evaluated based on the maximum temperature reached and the temperature difference between the maximum and minimum temperatures within the cell. The main conclusions are as follows:
- Increasing the channel diameter in the VFD reduced the maximum temperature, and the thermal uniformity also improved due to the relationship between the surface contact area and heat transfer rate. These thermal effects were minimal in comparison to the effects of inlet velocity.
- As the inlet flow velocity increases, the maximum temperature and temperature difference decrease due to the relationship between flow velocity and heat transfer. The flow velocity was found to have a greater influence on temperature reduction compared to the other variables evaluated in the report. A value of 0.5 ms−1 was the most efficient choice.
- Increasing the number of channels in the HFD decreases the maximum temperature of the cells and improves thermal uniformity, but the effects are almost negligible as the number of channels increases. Two channels provide sufficient cooling and ease of manufacture.
- The maximum cell temperature increased as greater channel angles were used for the HFD. The angle increase also resulted in more of the casing coming into contact with the cell, providing greater temperature reduction and uniformity.
- The VFD produced a Tmax of 303.534 K and a ∆T of 2.791 K, meeting the thermal objectives of 298 K < Tmax < 313 K and ∆T < 5 K, using an inlet velocity of 0.5 ms−1 and 6 mm diameter channels.
- The HFD produced a Tmax of 306.018 K and a ∆T of 5.690 K, meeting the thermal objective of 298 K < Tmax < 313 K but failing to meet ∆T < 5 K, using two channels and an inlet velocity of 0.5 ms−1.
- The OD combines the HFD and VFD and produces a Tmax of 301.311 K and a ∆T of 1.144 K, comfortably within the thermal objective of 298 K < Tmax < 313 K and ∆T < 5 K. It should be noted, in theory, that increasing the velocity in the HFD and VFD designs would help meet the thermal targets, but at the cost of extra energy consumption.
The OD demonstrated exceptional thermal management for the battery pack; however, this is outweighed by the larger structure, more components, and a greater volume of coolant flowing through the system, resulting in increased overall weight. Consequently, the additional weight may require the vehicle to expend more energy for transportation, and the study by Carlson et al. [25] investigated the impact of additional weight and found that a 10% mass increase can result in a 3–4% energy consumption increase for electric vehicles. Taking only the mass of the aluminium structure for a six-cell pack, we find that the OD has a mass of 89.93 g while the HFD, a design that is commonly found in modern EVs, has a mass of 28.73 g. The added weight may impact vehicle driving range, and the additional components, such as cooling channels and flow directions, increase the complexity of the battery pack, and its compatibility in existing EVs. Furthermore, there is a greater risk of leakage due to the greater potential for seal failures. The other designs, despite utilising half the structure volume of the OD, managed to produce satisfactory thermal management and would be seen as the most preferable options for implementation in EVs, but the OD would be best suited for high-temperature and safety-critical applications. The excellent thermal management of the OD allows for the vehicle to produce higher discharge rates which in turn produces a greater power output, without the risk of exceeding the thermal limit. Therefore, the OD would be best suited for high-temperature, power-intensive and safety-critical applications.
The findings provide valuable insights into the influential parameters and effectiveness of novel liquid cooling designs, but there are certain limitations to the report such as the simplification of the battery pack, using only six cells to mitigate computational requirements, and ignoring components like busbars and casing, which can further influence the temperature of the entire system. Additionally, the cell arrangement used in the simulations is less compact than other battery pack configurations which poses a slight constraint on its suitability for EVs. The material properties were assumed to be homogenous throughout, and the heat generation model of the cell was assumed to be uniform across the entire volume.
Future work could analyse these models using a larger battery pack and include additional components to more accurately simulate a real EV battery pack.
Furthermore, exploring a wider range of innovative and lightweight materials for the structure, such as phase change materials, could be beneficial. Investigating emerging coolant options such as coolants with nanometal additives or liquid metals may also further refine these designs and enhance their performance.
Author Contributions
Conceptualisation, M.M. and M.A.; methodology, M.M. and M.A.; software, M.M. and M.A.; validation, M.M. and M.A.; formal analysis, M.M. and M.A.; investigation, M.A.; resources, M.A.; data curation, M.M. and M.A.; writing—original draft preparation, M.M.; writing—review and editing, M.M. and M.A.; visualisation, M.M.; supervision, M.A.; project administration, M.A.; funding acquisition, M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is available upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Variables | EV | electrical vehicle | |
| A | contact area (m2) | HFD | horizontal flow design |
| c | specific heat capacity (Jkg−1 K−1) | VFD | vertical flow design |
| d | channel diameter (mm) | PCM | phase change material |
| h | heat transfer coefficient (Wm−2 K−1) | ||
| I | current (A) | Greek letters | |
| k | thermal conductivity (Wm−1 K−1) | ∆ | difference |
| L | characteristic length (m) | µ | dynamic viscosity (kgm−1 s−1) |
| m | mass (kg) | ρ | mass density (kgm−3) |
| mass flow rate (kgs−1) | |||
| P | pressure (Pa) | Subscripts | |
| q | heat generation (Wm−3) | b | battery |
| Q | rate of heat flow (W) | gen | generation |
| R | resistance (Ω) | max | maximum |
| Re | Reynolds number | p | constant pressure process |
| T | temperature (K) | w | water |
| t | time (s) | ||
| U | open-circuit voltage (V) | ||
| V | volume (m3) | ||
| v | velocity (ms−1) | ||
| Acronyms | |||
| CAD | computer-aided design | ||
| CFD | computational fluid dynamics |
References
- Transport and Environment Statistics 2022. Available online: https://www.gov.uk/government/statistics/transport-and-environment-statistics-2022/transport-and-environment-statistics-2022 (accessed on 10 November 2023).
- Liu, W.; Placke, T.; Chau, K.T. Overview of Batteries and Battery Management for Electric Vehicles. Energy Rep. 2022, 8, 4058–4084. [Google Scholar] [CrossRef]
- Assad, M.; Rosen, M.A. Design and Performance Optimization of Renewable Energy Systems; Academic Press: Cambridge, MA, USA, 2021; pp. 205–219. [Google Scholar]
- Plett, G.L. Battery Management Systems. Volume I, Battery Modeling, 1st ed.; Artech House: Norwood, MA, USA, 2015. [Google Scholar]
- Comparison of Different Types of Electric Vehicle Battery Cells. Available online: https://www.keyence.co.uk/products/marker/laser-marker/resources/laser-marking-resources/comparison-of-different-types-of-electric-vehicle-battery-cells.jsp (accessed on 11 November 2023).
- Pros and Cons of Lithium Prismatic Cells vs. Cylindrical Cells. Available online: https://blog.epectec.com/pros-and-cons-of-lithium-prismatic-cells-vs-cylindrical-cells (accessed on 15 November 2023).
- Zhai, N.; Li, M.; Wang, L.; Majid, N.; Hafiz, S.; Arianto, S.; Kawano, S.; Nishimura, F.; Hazima, N.; Ismail, F.; et al. Simplified Heat Generation Model for Lithium Ion Battery Used in Electric Vehicle. IOP Conf. Ser. Mater. Sci. Eng. 2013, 53, 012014. [Google Scholar]
- Liu, K.; Liu, Y.; Lin, D.; Pei, A.; Cui, Y. Materials for Lithium-Ion Battery Safety. Sci. Adv. 2018, 4, eaas9820. [Google Scholar] [CrossRef] [PubMed]
- Ji, Y.; Zhang, Y.; Wang, C.-Y. Li-Ion Cell Operation at Low Temperatures. J. Electrochem. Soc. 2013, 160, A636–A649. [Google Scholar] [CrossRef]
- Akbarzadeh, M.; Kalogiannis, T.; Jaguemont, J.; Jin, L.; Behi, H.; Karimi, D.; Beheshti, H.; Van Mierlo, J.; Berecibar, M. A Comparative Study between Air Cooling and Liquid Cooling Thermal Management Systems for a High-Energy Lithium-Ion Battery Module. Appl. Therm. Eng. 2021, 198, 117503. [Google Scholar] [CrossRef]
- Xia, G.; Cao, L.; Bi, G. A Review on Battery Thermal Management in Electric Vehicle Application. J. Power Sources 2017, 367, 90–105. [Google Scholar] [CrossRef]
- Liu, J.; Chen, H.; Huang, S.; Jiao, Y.; Chen, M. Recent Progress and Prospects in Liquid Cooling Thermal Management System for Lithium-Ion Batteries. Batteries 2023, 9, 400. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Luo, L.; Fan, Y.; Du, Z. A Review on Thermal Management of Lithium-Ion Batteries for Electric Vehicles. Energy 2022, 238, 121652. [Google Scholar] [CrossRef]
- Tang, Z.; Liu, Z.; Li, J.; Cheng, J. A Lightweight Liquid Cooling Thermal Management Structure for Prismatic Batteries. J. Energy Storage 2021, 42, 103078. [Google Scholar] [CrossRef]
- Zhao, C. Thermal Behaviour Study of Discharging/Charging Cylindrical Lithium-Ion Battery Module Cooled by Channelled Liquid Flow. Int. J. Heat Mass Transf. 2018, 120, 751–762. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, X.; Xiang, G.; Li, H. Optimization of Liquid Cooling and Heat Dissipation System of Lithium-Ion Battery Packs of Automobile. Case Stud. Therm. Eng. 2021, 26, 101012. [Google Scholar] [CrossRef]
- Lloyd, R.; Akrami, M. A Critical Analysis of Helical and Linear Channel Liquid Cooling Designs for Lithium-Ion Battery Packs. Batteries 2022, 8, 236. [Google Scholar] [CrossRef]
- Yates, M.; Akrami, M.; Javadi, A.A. Analysing the Performance of Liquid Cooling Designs in Cylindrical Lithium-Ion Batteries. J. Energy Storage 2021, 33, 100913. [Google Scholar] [CrossRef]
- Amiribavandpour, P.; Shen, W.; Mu, D.; Kapoor, A. An Improved Theoretical Electrochemical-Thermal Modelling of Lithium-Ion Battery Packs in Electric Vehicles. J. Power Sources 2015, 284, 328–338. [Google Scholar] [CrossRef]
- Zhao, J.; Rao, Z.; Huo, Y.; Liu, X.; Li, Y. Thermal Management of Cylindrical Power Battery Module for Extending the Life of New Energy Electric Vehicles. Appl. Therm. Eng. 2015, 85, 33–43. [Google Scholar] [CrossRef]
- Wang, Z.; Li, X.; Zhang, G.; Lv, Y.; Wang, C.; He, F.; Yang, C.; Yang, C. Thermal Management Investigation for Lithium-Ion Battery Module with Different Phase Change Materials. RSC Adv. 2017, 7, 42909–42918. [Google Scholar] [CrossRef]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A General Energy Balance for Battery Systems. J. Electrochem. Soc. 1985, 132, 5–12. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, F.; Zhang, Q.; Wang, Q.; Song, Z. Thermal Management of Cylindrical Lithium-Ion Battery Based on a Liquid Cooling Method with Half-Helical Duct. Appl. Therm. Eng. 2019, 162, 114257. [Google Scholar] [CrossRef]
- Tang, Z.; Min, X.; Song, A.; Cheng, J. Thermal Management of a Cylindrical Lithium-Ion Battery Module Using a Multichannel Wavy Tube. J. Energy Eng. 2019, 145, 04018072. [Google Scholar] [CrossRef]
- Carlson, R.B.; Lohse-Busch, H.; Diez, J.; Gibbs, J. The Measured Impact of Vehicle Mass on Road Load Forces and Energy Consumption for a BEV, HEV, and ICE Vehicle. SAE Int. J. Altern. Powertrains 2013, 2, 105–114. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).