Abstract
Mechanical degradation in electrode materials during successive electrochemical cycling is critical for battery lifetime and aging properties. A common strategy to mitigate electrode mechanical degradation is to suppress the volume variation induced by Li/Na intercalation/deintercalation, thereby designing strain-less electrodes. In this study, we investigate the electrochemically-induced volume variation in layered and spinel compounds used in Li-ion and Na-ion battery electrode materials through density functional theory computations. Specifically, we propose to decompose the volume variation into electronic, ionic, and structural contributions. Based on this analysis, we suggest methods to separately influence each contribution through strategies such as chemical substitution, doping, and polymorphism. Altogether, we conclude that volume variations can be controlled by designing either mechanically hard or compact electrode materials.
1. Introduction
Continued advancements in lithium-ion batteries have positioned them as the predominant technology for electrical energy storage. However, current commercial positive electrode materials undergo significant volume changes during cycling, posing challenges to their long-term performance and stability. For instance, positive electrode materials like layered oxides based on Nickel, Manganese, and Cobalt (NMC’s) and the spinel LiMnO experience notable volume alterations, in particular, when charged to high voltages [1,2,3,4,5]. The mismatch between the lithiated and delithiated structures, differing in volume and shape, induces an important source of strain leading to mechanical stresses, which are at the origin of electrode material degradation and battery performance deterioration after repeated cycles [6,7,8,9,10,11]. More precisely, these changes affect the general morphology of electrode materials, a well-known cause of capacity loss [7]. The primary particles of the cathode, forming secondary particles, undergo repeated attachment and detachment during charging and discharging due to these volume changes [9,12]. This stress creates cracks inside the particles, leading to a loss of connectivity within the active material. As a consequence, the liquid electrolyte penetrates through these cracks, increasing the cathode electrolyte interface layer. Ultimately, these crystals break down, resulting in significant capacity loss and deterioration of battery performance [13,14]. These electrochemically-induced strains also pose threats to the separator and overall battery safety. In solid-state batteries, issues related to volume changes in positive electrode materials are even more problematic [15,16,17,18,19,20]. Apart from the formation of cracks and fractures in positive electrode materials, “breathing” electrodes lead to the diminution of the interface between the solid electrolyte and the electrode material, posing risks to the system’s integrity. Consequently, the volume changes in the cathode significantly impact battery performances, affecting long-term stability and discharge capacity, presenting a significant challenge to improving high-energy-density batteries. Hence, the ideal scenario involves employing cathode materials that undergo minimal volume changes and electrochemically-induced strain during lithium intercalation/deintercalation.
Over the leading factor that controls the electrochemically-induced strain, the nature of the Transition Metal (TM) is shown to play a critical role. More precisely, volume variations and capacity fading have been related, and are drastically modified when changing the Co, Mn and Ni ratios in NMC materials. In particular, high Ni content leads to significant volume changes and mechanical degradation at high voltage [13,21,22,23,24,25,26,27,28,29]. The crystal structure type is also expected to have a significant impact. For instance, in contrast to layered materials, it has been shown that disordered rocksalts, due to cation mixing which leads to a cubic structure, demonstrate minimal and isotropic volume changes during lithiation and delithiation processes [30,31,32,33]. Besides tuning the TM and the structure, various strategies have been proposed to achieve suppressed volume expansion and contraction towards zero-strain positive electrodes. In particular, electrode surface engineering or concentration gradient [27,34,35,36] and electrode material doping [28,37,38,39,40,41] have become popular.
In order to accelerate the design of strainless electrodes a quantitative or even qualitative evaluation of the different contributions to the electrochemically-induced strain is needed. To that aim, Zhao et al. have linked qualitatively the volumic variation with the t versus e character of the redox orbital and confirm that isotropic structures are more prone to reduce the volumic variations [33]. In this work, we investigate various factors controlling volume changes upon lithium removal in a family of AMO compounds, where A represents an alkali metal (Li or Na) and M represents a 3d TM. Two structural frameworks have been considered, namely the 2D layered and the 3D spinel structures. Firstly, our density functional theory computation shows that high spin (HS) and low spin (LS) TM configurations in the intercalated material drastically affect its cell volume in agreement with the corresponding tabulated ionic radius values. Additionally, van der Walls interactions play a significant role in decreasing the inter-layer spacing and thus the volume of deintercalated layered compounds. In a second step, we propose to decompose the volume variation in terms of ionic, electronic, and structural contributions. Considering the ionic contribution, we show that for Li-based compounds the deinsertion process is fairly compensated by the reminiscent electrostatic repulsion of the surrounding anions in the deintercalated phase. The substitution of Li by Na in a layered electrode leads to an increase of about ∼3.5Å of the cell volume variation per exchanged alkali, which corresponds to the sphere volume difference computed using Li and Na tabulated ionic radii. The electronic contribution is shown to be governed by the nature of the TM and can be estimated using also tabulated ionic radii of both the TM’s oxidized and reduced forms. The structural contribution is shown to be important and related to the elasticity of the material. For isotropic compounds, the structural contribution of the volume variation follows the electronic contribution and can be correlated to the isotropic elastic Bulk modulus . For layered materials the structural contribution follows the ionic contribution and is isotropic, i.e., the cell is stretched/contracted along the c parameter in order to minimize elastic energy since the elasticity perpendicular to the TM layer is lower than the elasticity in the plane parallel to the TM layer. Finally, based on our analysis we propose at the end of the manuscript hints to reduce volume variations by designing harder or more compact electrode materials.
2. Computational Details
We have studied layered AMO compounds, where A represents an alkali metal, Li or Na at stochiometry or 1 and M represents a 3d TM, ranging from Ti to Ni within the R-3m layered crystal structure. Spinel compounds LiMO within the Fd-3m symmetry group have also been studied for comparison, using the same 3d TM’s and for and 1. Density functional theory calculations were performed using the Vienna Ab initio Simulation Package (VASP) [42,43,44]. It uses a plane wave basis set and pseudopotentials using the projector augmented wave (PAW) potentials [45]. Both the kinetic energy cut-off and k-point grid were tested, with the criterion for convergence being an energy variation of less than 1 meV/atom. A plane wave energy cutoff of minimum 520 eV and a well converged -centered Monkhorst–Pack k-point grid were used in these calculations [46]. The energy difference convergence criteria of the global break condition for the electronic self-consistent loop was set to 10 eV, whereas the energy difference convergence criteria of the break condition for the ionic relaxation loop was set to 10 eV. Structural relaxations and energy calculations were performed using the Strongly Constrained and Appropriately Normed (SCAN) functional [47,48,49,50] with the inclusion of van der Waals (vdW) interactions by the means of the revised Vydrov–van Voorhis nonlocal correlation functional (rVV10) [51] called hereafter SCAN-rVV10 functional. These relaxations were also performed with the (rotationally invariant) DFT + U approach [52] on top of the Perdew–Burke–Ernzerhof (PBE) functional [53]. On-site Coulomb interaction strength (U) has been specified for each TM following the literature, i.e., U = 3.3 eV, U = 2.5 eV, U = 3.9 eV, U = 3.9 eV, U = 4.2 eV, U = 3.2 eV, U = 6.0 eV. Finally, PBE+U calculations have been performed with and without the inclusion of van der Waals interactions by means of the DFT-D3 method of Grimme et al. [54]. All of these materials were assumed to be ferromagnetic and both the HS and LS configurations were calculated. To access these configurations the difference between the total number of up and down spin electrons was fixed. The atomic charge distribution was computed using the Voronoi deformation density [55].
3. Results
3.1. Volumes and Relation with Ionic Radii
We initially focus on the volume of intercalated compounds shown in Figure 1 and deintercalated compounds in Figure 2, for the considered materials, using different functionals in order to evaluate our theoretical setup. As shown in Figure 1, the relaxed volumes of LiMO and NaMO per formula unit exhibit non-monotonous behavior as a function of the TM for all considered functionals. Considering different functionals, the SCAN-rVV10 compared to the PBE + U + D3 functional leads to a volume compression, while comparing the PBE + U and the PBE + U + D3 functionals leads to a volume dilatation, respectively. When compared with experimental data (see Supplementary Information SI1), a fair agreement is obtained for all functionals, with the PBE + U + D3 functional yielding the best mean errors and deviations. The behavior of the cell volume as a function of the TM is influenced by both the nature of the TM and its spin state. Indeed, as shown in Figure 1c the cell volume is linearly correlated to the ionic volume in an octahedral environment, where is the tabulated ionic radius of the metal M in an oxidation state , regardless of the functional considered. See Supplementary Information SI2 for the considered values of ionic radii. Importantly, the LS versus HS configurations lead to drastically different results for M = Mn, Fe, Co, and Ni (see Supplementary Information SI3a). Concerning the relative stability of the HS vs. LS configurations, our calculations indicate that for AMnO the HS configuration is energetically favored, while ACoO and ANiO adopt the LS configuration. LS states are associated with smaller ionic radii compared to HS configurations since for the latter more anti-bonding e states are filled and are associated with larger TM-O bonds due to the presence of anti-bonding type TM-O bonds. AFeO is predicted to be in the HS configuration with PBE + U and with PBE + U + D3, a result supported by experimental data showing that AFeO compounds are HS in different polymorphs [56]. The SCAN-rVV10 functional also predicts NaFeO to be HS but LiFeO to be LS. Given that the energy difference between the LS and HS configurations is rather low (∼10 meV/Formula unit), we have considered for LiFeO the results of the HS configuration in the manuscript for the sake of coherence. We observe an important local octahedral Jahn–Teller (JT) distortion which originates from electronic degeneracy in the e shell of the AMnO HS () and ANiO LS () configurations. As expected, it lowers the R-3m symmetry to Cm in the relaxed structure. A less important JT distortion is observed in AVO and ATiO which originates from the t degeneracy. Note, that the JT effect is not supposed to have a huge effect on the cell volume which is supported by the linear relation between the cell volume and the ionic radius. A similar linear relation between the cell volume and ionic volume is obtained considering the spinel structure, using the mean values between the corresponding ionic radius of M in the 3+ and 4+ oxidation states, see Supplementary Information SI4.
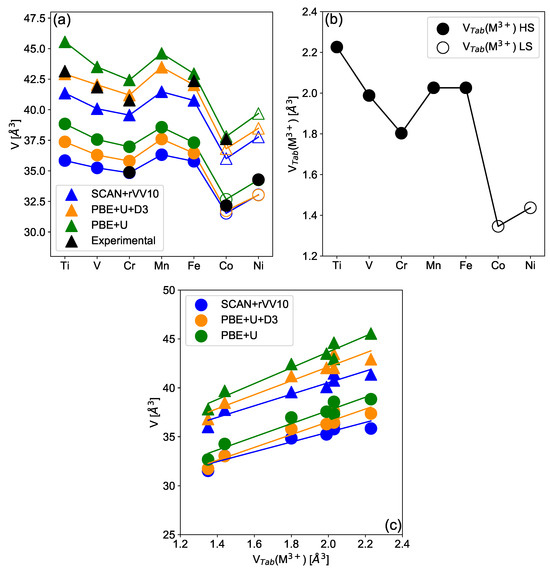
Figure 1.
Relaxed volume per MO stoichiometry of layered LiMO and NaMO (a) materials for different 3d transition metals ranging from Ti to Ni. Results are given for the lowest energy spin configuration obtained using different functionals, namey PBE + U (green symbols), PBE + U + D3 (orange symbols) and SCAN-rVV10 (blue symbols) compared with experimental data obtained from the literature (black symbols). Filled and open symbols correspond to the HS and LS states respectively. Tabulated ionic volume (b) for the LS and HS configurations of the different 3d transition metals in their +III state and in an octahedral environment. In (c) is shown the correlation between the relaxed volume of LiMO (circles) and NaMO (triangles) with the ionic volume computed using tabulated ionic radii (see text for details). Lines are guides for the eyes.
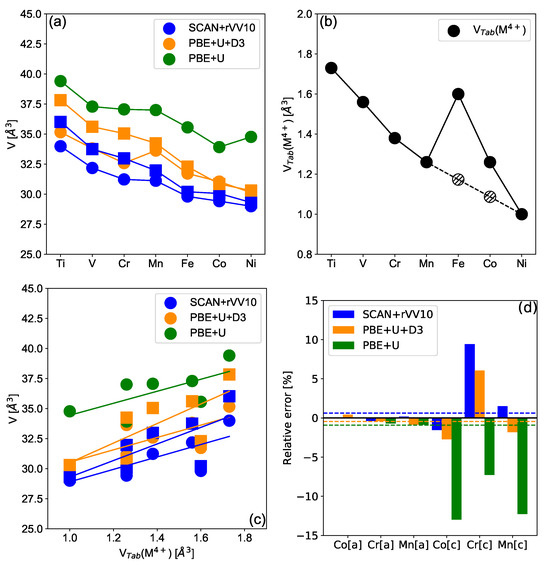
Figure 2.
(a) Relaxed volume per MO unit of deintercalated MO for the layered (circle) and spinel (square) polymorphs for different 3d transition metals ranging from Ti to Ni. Results are given for the lower energy spin configuration obtained using different functionals, namely PBE + U (green symbol), PBE + U + D3 (orange symbols) and SCAN-rVV10 (blue symbols) also compared with experimental volumes obtained from the literature. Color and symbol codes are consistent in all subfigures. (b) Tabulated ionic values of the TM’s in their +IV state in an octahedral environment. Hatched values for Fe and Co are calculated from the interpolation between Mn and Ni. (c) The correlation between the relaxed volume of MO and the ionic volume was computed using tabulated ionic radii. In (a–c) lines are guides for the eyes, and results are given for the LS/HS configuration leading to the minimum energy. (d) Relative difference (in %) between relaxed and experimental cell parameters [57,58,59,60] a and c for layered materials. The dashed lines represent the mean relative error for each functional.
In Figure 2, volumes of deintercalated MO layered and spinel compounds are shown, with M ranging from Ti to Ni, and as a function of the tabulated ionic volume of M for different functionals. In contrast with intercalated compounds, no ambiguities regarding the spin state emerge from our calculations, FeO, CoO, and NiO being in the LS configuration. Concerning layered compounds, the volume decays quasi-linearly with the electronic filling which is consistent with a consecutive filling of the t orbitals from zero to six electrons. Moreover, Figure 2b shows that similarly for sodiated and lithiated compounds, the volume of the MO structure follows the trend of M ionic volumes obtained through tabulated ionic radii, with an exception for the Iron and to a lesser extent for Cobalt compounds. However, the ionic radii provided in the table for Fe and Co must be approached with caution since the oxidation state for Fe and Co are quite exotic, as only a few compounds have been isolated; most of them are short-lived intermediaries in reactions, in particular, for Fe. The computed Voronoi volumes in MO compounds show as expected a quasi-linear decay as a function of the electronic filling, see Supplementary Information SI5. A similar trend for the cell volume as a function of the transition metals’ ionic radius is observed for spinel compounds. Note, that 3D spinel structures are shown to be more compact than the 2D layered structures. Concerning the functionals’ accuracies, the trend of the volume as a function of the considered transition metal appears to be independent of the considered functional. However, the PBE + U functional predicts a volume that is about ∼10% above the result obtained using the PBE + U + D3 and SCAN-rVV10 functionals. This overestimation obtained with the PBE+U functional can be attributed to an overestimation of the cell parameter c. Indeed, Figure 2c shows the relative error between experimental and computed a and c lattice parameters for synthesized compounds. While one observes a relatively weak mismatch between experimental and computed values for the a parameter, regardless of the functional, the c parameter is shown to be largely overestimated by the PBE + U functional compared to experimental values. The PBE + U + D3 and SCAN-rVV10 functionals are shown to provide much more reliable results, particularly for layered CoO and NiO. Yet, the large overestimation of the c parameter can be attributed to a poor estimation of the van der Waals interactions, which are better taken into account within the PBE + U + D3 and SCAN + rVV10 functionals. These results highlight the importance of the van der Waals interactions on the structural properties of layered oxides, particularly at low alkali content. For spinel materials, the PBE + U + D3 functional is shown to be sensitively more accurate than the SCAN-rVV10 functional. Altogether, in terms of functional reliability, PBE + U + D3 and SCAN-rVV10 are shown to provide structural parameters consistent with each other and consistent with experimental data when available. A typical margin of error for these functionals on the cell parameters would be around 3%, so the error on the volume should be of a similar magnitude. On the contrary, the PBE + U functional fails to take into account van der Walls interactions, which leads to a poor description of inter-layer spacing in layered compounds. For this reason, the PBE + U functional is discarded for the rest of the study. In terms of energy, the PBE + U + D3 appears to be more relevant to predict the right LS vs. HS configurations but also the electrochemical potentials, see Supplementary Information SI6.
3.2. Electrochemically-Induced Volume Variation
Given the relaxed intercalated and deintercalated volumes, we can define the electrochemically-induced volume variation per alkali A = Li or Na, following Zhao et al. [33].
where and are the volumes per formula unit () of the intercalated and deintercalated structures, is the number of exchanged alkali per formula unit, and finally is a volume per exchanded alkali (). In Figure 3 we show for the layered LiMO, NaMO and the spinel LiMnO materials using the PBE + U + D3 and the SCAN functionals. Interestingly, the profile of as a function of the considered TM differs in spinel and layered structures, while it follows the same trend when switching from Li to Na. For layered structures increases quasi-linearly with the electron filling from 2Å for M = Ti to 6Å for M = Fe. Then it is drastically reduced to 2Å for M = Co before slightly increasing to 2.5Å for M = Ni. The evolution is similar for both functionals and for the sodiated compounds but is shifted to higher values following the different ionic radii of Li and Na. For spinel compounds, shows an overall reduced amplitude compared with layered materials, in particular, for M = Ti, V, Cr, Fe and Co. The trend appears different between spinel and layered materials suggesting that the crystallographic structure plays an important role in governing . More precisely, while the cell volume of intercalated and deintercalated phases are shown to be qualitatively related to the ionic volume of the TM, does not follow for layered electrode materials. Consequently, is controlled by the choice of the TM in spinel compounds, (remember that the value of for iron is questionable) but also note that it is strongly influenced by other factors in layered electrodes. In a previous study, Zhao et al. proposed a qualitative argument to rationalize the amplitude of which is governed by the t versus e character of electronic states implied in the redox process [33]. Indeed, the redox associated with e states is expected to lead to larger volume variations than for t states since the e (t) states imply () type of TM-O bounds, and thus larger (smaller) TM-O distance variation along the redox reaction, respectively. To give rationality to this hypothesis, in Table 1 (d) we show the electronic filling of the e/t orbitals for the redox active TM’s. Following the t/e rule would imply that the largest value of is obtained for Mn (HS), Fe(HS) and Ni (LS) based compounds. For spinel structures, the t/e rule appears relevant. However, our results suggest that the relation between and the redox orbital t/e character is not straightforward in layered compounds. For instance, for the e active layered ANiO is lower (or equivalent) than for the t active AMO, where M = Ti, Cr and V using the PBE + U + D3 functional. Moreover, the volume variation associated with the deintercalation of an alkali in the HS AFeO compounds is associated with a filling change of two e electrons, which is not reflected by the volume variation. Finally, for the HS LiCoO and HS LiNiO compounds, imply a single or double change in the e orbital filling, and shows a comparable amplitude for LiCrO, which is associated with a t redox.
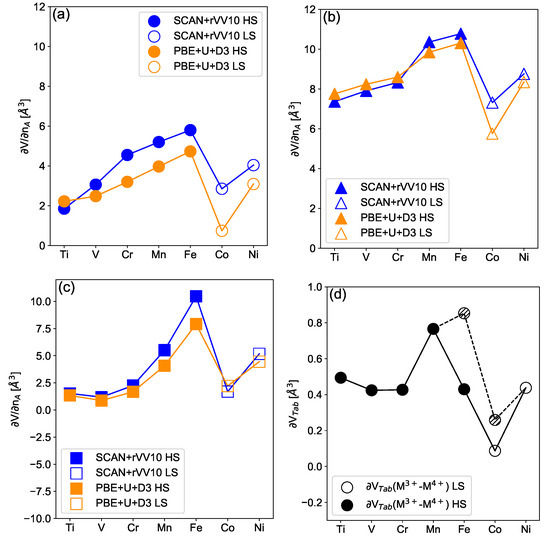
Figure 3.
Electrochemically-induced volume variation in the lithiated (a), sodiated (b) layered structures and for lithiated spinel (c) structure as a function of the transition metal ranging from Ti to Ni. Results are given for the PBE + U + D3 (orange symbols) and SCAN-rVV10 functionals (blue symbols). Tabulated ionic volume difference (d) between the +IV and +III (HS/LS) states. For all subfigures, filled (open) symbols highlight cases for which the intercalated compound is the most stable within the HS (LS) configuration, respectively. Lines are guides for the eyes.

Table 1.
Schematic representation of the electronic configurations of each TM with an oxidation degree of 3+ and 4+, also considering the high spin (HS) or low spin (LS) configurations. Cells in green highlight the lowest energy configuration for unambiguous cases (equivalent lowest energy configurations whatever the considered structure (layered vs. spinel), alkali (Li vs. Na) or functional (PBE + U + D3 vs. SCAN-rVV10). Orange cells represent the case of Fe-based compounds which is more controversial and is considered in the HS configuration for layered and spinel compounds (see text for details).
In order to understand the trend of the electrochemically-induced volume variation per alkali, we aim to decompose it into different contributions. One possible contribution is the term , which represents the effect of removing an alkali ion from the structure. This term is proportional to the ionic volume of the ion in its specific environment, whether it is in an octahedral (Oh) or tetrahedral (Td) coordination. This contribution is expected to weakly depend on the nature of the TM and on the long-range feature of the crystal structure beyond the first coordination sphere. In parallel, we consider an electronic contribution driven by the removal (addition) of electrons in the redox anti-bonding TM-O orbitals. This contribution takes into account the contraction (dilatation) of TM-O bonds upon deintercalation (intercalation), respectively, and is expected to solely depend on the TM’s nature and spin configuration. This contribution should be affected by the t/e nature of the redox center. The decomposition between the different contributions of the electrochemically-induced volume variation can be summarized in the following equation
where the last term corresponds to a contribution that depends on the Host crystal structure and might modulate ionic and electronic contributions.
The amplitude of the contribution associated with the addition/removal of an alkali ion is expected to be proportional to the alkali ionic radius. This assumption is confirmed by our calculations, as shown in Figure 4a. Indeed, it shows that is quasi-constant, i.e., independent of the TM. More precisely, assuming the electronic and structural contributions to be equivalent in iso-structural sodiated and lithiated compounds leads to . Note, that the value of Å is larger than the difference in atomic volume obtained using tabulated ionic radii Å, which appears coherent since small cations compress all other bonds in the structure, an effect that is known as chemical pressure. To go further into detail, we compute using the relaxed structure as
where and represent the mean volume of the AO octahedra computed in the intercalated (AHost) compound and the A-vacancy □O octahedra measured in the deintercalated (Host) structure. The volumes of the octahedra were calculated using the O-O distances in the relaxed structure. Since the octahedra are not regular, we decomposed them into four tetrahedrons and used the Cayley–Menger determinant to calculate their volumes [61]. Results are presented in Figure 4b for lithiated, sodiated layered materials and lithiated spinel materials. is shown to be quasi-constant for the spinel structure. It follows a trend similar to with an amplitude of ∼1 (2) Å between the minima for ACoO and maxima for AFeO for lithiated (sodiated) materials, respectively. Interestingly, a mean difference between trend lines for sodiated and lithiated compounds, Å is observed in Figure 4b. This value approximately corresponds to the difference between the volumes of Na and Li calculated using the tabulated ionic radii. The difference between and allows us to evaluate the effect of chemical pressure to be of about Å by substituting Na for Li. Another important piece of information from Figure 4b concerns the amplitude of . In particular, for lithiated compounds, shows an amplitude close to zero reflecting the fact that the volume of removed Li ions is compensated in the delithiated structure by the electrostatic repulsion between oxygen in the vacancy octahedra. Similar results are obtained using the SCAN-rVV10 functional, see Supplementary Information SI7.
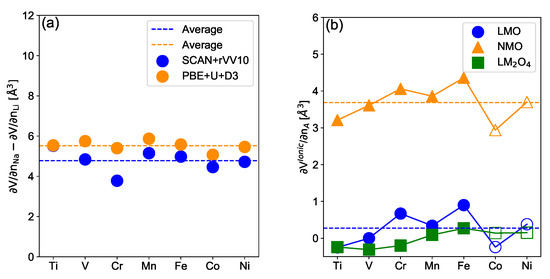
Figure 4.
Difference of electrochemically-induced volume variation (a) between the sodiated and lithiated layered materials as a function of the TM for the SCAN-rVV10 (blue circles) and PBE + U + D3 (orange circles) functionals. Ionic contribution (b) of the electrochemically-induced volume variation as defined in Equation (4) as a function of the TM for layered lithiated (blue circles), sodiated (orange triangles) and lithiated spinel (green squares) materials using the PBE + U + D3 functional. Filled and open symbols correspond to the HS and LS states respectively.
We focus now on the induced volume variation associated with the addition/removal of electrons. In order to evaluate quantitatively, we define the following equation
where () represents the mean volume of the AO octahedra computed in the intercalated (deintercalated) structure, respectively. In Figure 5a we show as a function of the transition metal M for the layered and spinel materials obtained with the PBE + U + D3 functional. Results for appear to be quasi-independent of the considered alkali and the structure type. More precisely, chemical pressure induced by switching from Na to Li does not affect drastically the TM-O bond lengths suggesting that the TMO octahedra are the most rigid entities in the structure. This is also supported by the relatively weak influence of the structure on . As expected, is influenced by the t/e character of the redox orbital showing higher amplitudes for Mn, Fe and Ni-based materials when Mn and Fe are in the HS configuration. represents the specific effects of different transition metals. More precisely, follows the same trend as the variation of the ionic volume computed with the tabulated ionic radii for the transition metal M, . Importantly, is tabulated with respect to the crystal field environment and spin configuration, thus taking into account the change in the t/e character of the redox orbital. Attention has to be paid to spinel systems. Indeed, some compounds show M/M disproportionation or charge density wave (CDW) in the intercalated phases while in other materials all of the TM’s are equivalent, which probably influences the results shown in Figure 5a. More precisely, as illustrated in Supplementary Information SI8, the PBE + U + D3 functional predicts a CDW for all compounds while SCAN-rVV10 predicts CDW only for M = Mn, Co and Ni-based LiMO spinel materials. Note, that the value of is not affected by the occurrence of CDW as the volume of MO octahedra in the intercalated structure remains constant upon deintercalation.
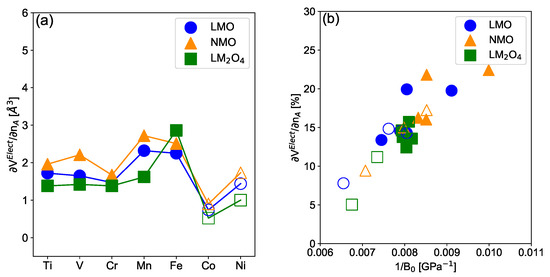
Figure 5.
Electronic contribution (a) of the electrochemically-induced volume variation as defined in Equation (4) as a function of the TM for layered lithiated (blue circle), sodiated (orange triangle) and lithiated spinel (green square) materials using the PBE + U + D3 functional. Lines are guides for the eyes. (b) Relation between the electronic part of the total electrochemically-induced strain as a function of the inverse of the Bulk modulus. In all subfigures, filled (Open) symbols correspond to cases where the intercalated compound is in the HS (LS) configuration, respectively.
The of the isotropic spinel material appears to be controlled by its electronic part. This is consistent with the fact that the TMO octahedra, being the most rigid part of the structure, should be the limiting factor for the elasticity of the material. Indeed, following Hooke’s law, one would expect that the volume change in the host matrix induced by the intercalation is proportional to the elastic modulus of the host matrix which is the case for spinel materials. More precisely, larger (smaller) volume variations are associated with lower (higher) bulk modulus, or equivalently, with softer (harder) compounds, respectively. On the contrary, for layered materials, the inverse of the Bulk modulus appears to be linearly correlated to rather than as we show in Figure 5. This is consistent with the fact that the bulk modulus or the mechanical hardness of the material is limited by the ionicity of the TM-O bonds, which is governed by the chemical nature of the TM and the electronic filling. Finally, in an anisotropic structure such as layered materials, the volume variation is also anisotropic and consequently it does not appear as directly related to isotropic elastic moduli such as the bulk modulus.
Finally, we show in Figure 6 the contribution to the electrochemically induced volume variation. follows for anisotropic layered electrodes but for the isotropic spinels. We found a quasi-perfect linear relation between and suggesting that results from a compromise between the elasticity along the different TM-O and A-O or □-O bonds. Moreover, layered material (and consequently ) is linearly related to the inverse of the elastic coefficient C measuring the materials’ elasticity in the direction perpendicular to the metallic sheets, see Figure 6c. As evidenced in other layered materials, this direction is supposed to be soft, in particular, in deintercalated material as vacancy-O bonds are expected to be soft [62]. Note, however, that the Jahn–Teller distortion might also influence the elastic coefficient in different directions, in particular, for based Fe and Mn materials, which might explain the non-perfect linear trend observed in Figure 6c. It contrasts with isotropic electrode materials such as spinels for which the elastic coefficient remains equivalent in all the directions such that is correlated with the isotropic bulk moduli, as already discussed, dictated by the limiting TM-O bond hardness. Overall, it suggests that the volume variations are dictated by the elasticity of the material and are consequently strongly influenced by the crystal’s structure. Yet, the anisotropy of the structure might induce softer (more elastic) directions along which the volume variations are expected to be increased such as for layered materials.
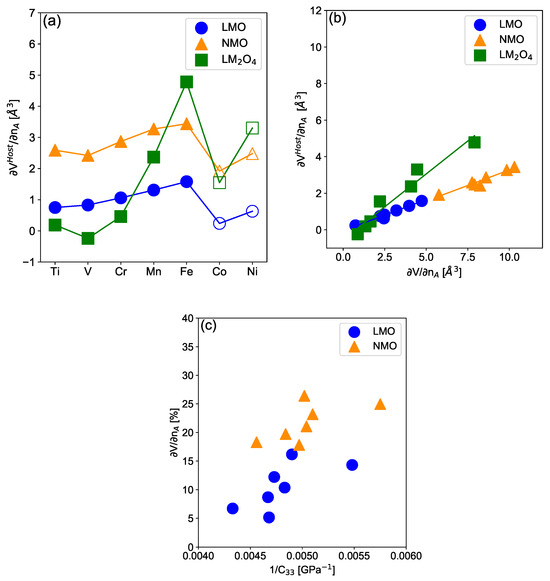
Figure 6.
Structural (Host) contribution (a) to the electrochemically-induced volume variation as defined in Equation (4) as a function of the TM for layered lithiated (blue circle), sodiated (orange triangle) and lithiated spinel (green square) materials using the PBE + U + D3 functional. Filled and open symbols correspond to the HS and LS states respectively. (b) Structural (Host) contribution to the electrochemically-induced volume variation as a function of the total electrochemically-induced volume variation. (c) Electrochemically-induced volume variation as a function of the inverse of the elastic contant C. In all subfigures, filled (Open) symbols correspond to cases where the intercalated compound is in the HS (LS) configuration, respectively. Lines are guides for the eyes.
4. Discussion and Conclusions
By decomposing the electrochemically-induced volume variation () between ionic, electronic and structural contributions we have shown that the ionic part depends mainly on the exchanged alkali type, Li vs. Na. Moreover, in the case of lithium, the volume loss associated with Li removal is nearly compensated by electrostatic interactions, resulting in an almost negligible effect.
The electronic contribution takes into account the t/e character of the redox orbital which plays an important role but does not constitute sufficient criteria to be predictive. However, the electronic contribution is shown to govern in isotropic materials such as spinels. Fortunately, it can be quantitatively estimated by using tabulated ionic radii associated with the concerned TM in the relevant environment and oxidation state. This appears to be a reliable descriptor to estimate this contribution except for Fe for which the Fe tabulated ionic radius has to be questioned.
Finally, the volume variation associated with the Host reaction to the addition of electrons and alkali ions is shown to result from a compromise between the elasticity associated with the different components. De facto, it depends strongly on the anisotropic character of the crystal structure.
Altogether, our results show that the overall volume variations are controlled by the elasticity of the material suggesting that the intercalation is an elastic, thus reversible process. For isotropic structures, the electrochemically induced strain is linearly correlated with the inverse of the Bulk modulus. The case of anisotropic materials is more complex as the elasticity is also anisotropic and the volume variations are consequently expected to be increased in the easiest (softer) direction. Consequently, cannot be directly predicted from tabulated ionic volumes or using the isotropic elastic moduli. In the case of layered material, we show that the volume variations are related to the elastic coefficient in the direction perpendicular to the layer that is believed to be lower than in a direction parallel to the layer.
In terms of material design, our results suggest that the most efficient way to reduce electrochemically-induced volume variations, besides manipulating the chemical nature of the alkali or transition metal, is to take advantage of the elastic character of intercalation. As evidence, harder materials, i.e., with higher elastic modulus, will experience fewer volume variations, but they might also be restrained in terms of capacity as the intercalation process might also be limited. The material’s hardness can be modulated using, for instance, chemical substitutions. Note, however, that to be efficient, the tuning of the hardness has to be performed isotropically such that no softer direction emerges and cancels the desired effect. Another strategy involves designing compact electrodes, as the volume variation is expected to be proportional to the material’s volume in an elastic system. This can be achieved in several ways: by focusing on compact polymorphs (generally 3D rather than 2D), by controlling the spin configurations to be LS, or by chemically doping with “small” ions, such as Al. In particular, the doping strategy can be especially efficient if, in addition to reducing the volume, it forces the LS configuration and increases the mechanical hardness of the material.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/batteries10080262/s1, SI0: Crystalloraphic structures; SI1: Benchmark of cell parameters of LiMO AND NaMO; SI2: Tabulated ionic radii; SI3: Influence of the spin configuration on the cell volume of LiMO and NaMO; SI4: Relation between cell volume and ionic radii in the spinel LiMO compounds; SI5: Voronoi volumes and charges for the LIMO and MO2 compounds; SI6: Electrochemical potentials; SI7: Decomposition of the volume variation into ionic, electronic and structural contributions; SI8: M/M disproportion (cdw) in LIMO compounds.
Author Contributions
Conceptualization, M.S.; Methodology, P.R. and M.S.; Formal analysis, M.M., R.B., P.R. and M.S.; Investigation, M.M.; Writing—original draft, M.M. and M.S.; Writing—review & editing, M.M., R.B., P.R. and M.S.; Visualization, M.M.; Supervision, R.B., P.R. and M.S.; Project administration, M.S.; Funding acquisition, P.R. and M.S. All authors have read and agreed to the published version of the manuscript.
Funding
The authors thank the French National Research Agency (STORE-EX Labex Project ANR-10-LABX-76-01) for financial support.
Data Availability Statement
The originale contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Berg, H. Neutron Diffraction Study of Electrochemically Delithiated LiMn2O4 Spinel. Solid State Ionics 1999, 126, 227–234. [Google Scholar] [CrossRef]
- Çapraz, Ö.Ö.; Bassett, K.L.; Gewirth, A.A.; Sottos, N.R. Electrochemical Stiffness Changes in Lithium Manganese Oxide Electrodes. Adv. Energy Mater. 2016, 7, 1601778. [Google Scholar] [CrossRef]
- Kondrakov, A.O.; Schmidt, A.; Xu, J.; Geßwein, H.; Mönig, R.; Hartmann, P.; Sommer, H.; Brezesinski, T.; Janek, J. Anisotropic Lattice Strain and Mechanical Degradation of High- and Low-Nickel NCM Cathode Materials for Li-Ion Batteries. J. Phys. Chem. C 2017, 121, 3286–3294. [Google Scholar] [CrossRef]
- Jangid, M.K.; Mukhopadhyay, A. Real-Time Monitoring of Stress Development during Electrochemical Cycling of Electrode Materials for Li-ion Batteries: Overview and Perspectives. J. Mater. Chem. A 2019, 7, 23679–23726. [Google Scholar] [CrossRef]
- Ruess, R.; Schweidler, S.; Hemmelmann, H.; Conforto, G.; Bielefeld, A.; Weber, D.A.; Sann, J.; Elm, M.T.; Janek, J. Influence of NCM Particle Cracking on Kinetics of Lithium-Ion Batteries with Liquid or Solid Electrolyte. J. Electrochem. Soc. 2020, 167, 100532. [Google Scholar] [CrossRef]
- De Biasi, L.; Schwarz, B.; Brezesinski, T.; Hartmann, P.; Janek, J.; Ehrenberg, H. Chemical, Structural, and Electronic Aspects of Formation and Degradation Behavior on Different Length Scales of Ni-Rich NCM and Li-Rich HE-NCM Cathode Materials in Li-Ion Batteries. Adv. Mater. 2019, 31, 1900985. [Google Scholar] [CrossRef] [PubMed]
- Edge, J.S.; O’Kane, S.; Prosser, R.; Kirkaldy, N.D.; Patel, A.N.; Hales, A.; Ghosh, A.; Ai, W.; Chen, J.; Yang, J.; et al. Lithium Ion Battery Degradation: What You Need to Know. Phys. Chem. Chem. Phys. 2021, 23, 8200–8221. [Google Scholar] [CrossRef]
- Stallard, J.C.; Vema, S.; Hall, D.S.; Dennis, A.R.; Penrod, M.E.; Grey, C.P.; Deshpande, V.S.; Fleck, N.A. Effect of Lithiation upon the Shear Strength of NMC811 Single Crystals. J. Electrochem. Soc. 2022, 169, 040511. [Google Scholar] [CrossRef]
- Stallard, J.C.; Wheatcroft, L.; Booth, S.G.; Boston, R.; Corr, S.A.; De Volder, M.F.; Inkson, B.J.; Fleck, N.A. Mechanical Properties of Cathode Materials for Lithium-Ion Batteries. Joule 2022, 6, 984–1007. [Google Scholar] [CrossRef]
- De Vasconcelos, L.S.; Xu, R.; Xu, Z.; Zhang, J.; Sharma, N.; Shah, S.R.; Han, J.; He, X.; Wu, X.; Sun, H.; et al. Chemomechanics of Rechargeable Batteries: Status, Theories, and Perspectives. Chem. Rev. 2022, 122, 13043–13107. [Google Scholar] [CrossRef]
- Park, S.H.; Lee, N.K.; Lee, S.G.; Han, J.H.; Lee, Y.J. Zero-Strain Cathodes for Lithium-Based Rechargeable Batteries: A Comprehensive Review. ACS Appl. Energy Mater. 2023, 6, 12–30. [Google Scholar] [CrossRef]
- Xu, Z.; Rahman, M.M.; Mu, L.; Liu, Y.; Lin, F. Chemomechanical Behaviors of Layered Cathode Materials in Alkali Metal Ion Batteries. J. Mater. Chem. A 2018, 6, 21859–21884. [Google Scholar] [CrossRef]
- Ryu, H.H.; Park, K.J.; Yoon, C.S.; Sun, Y.K. Capacity Fading of Ni-Rich Li[NixCoyMn1−x−y]O2 (0.6 ≤ x ≤ 0.95) Cathodes for High-Energy-Density Lithium-Ion Batteries: Bulk or Surface Degradation? Chem. Mater. 2018, 30, 1155–1163. [Google Scholar] [CrossRef]
- Ryu, H.H.; Namkoong, B.; Kim, J.H.; Belharouak, I.; Yoon, C.S.; Sun, Y.K. Capacity Fading Mechanisms in Ni-Rich Single-Crystal NCM Cathodes. ACS Energy Lett. 2021, 6, 2726–2734. [Google Scholar] [CrossRef]
- Koerver, R.; Aygün, I.; Leichtweiß, T.; Dietrich, C.; Zhang, W.; Binder, J.O.; Hartmann, P.; Zeier, W.G.; Janek, J. Capacity Fade in Solid-State Batteries: Interphase Formation and Chemomechanical Processes in Nickel-Rich Layered Oxide Cathodes and Lithium Thiophosphate Solid Electrolytes. Chem. Mater. 2017, 29, 5574–5582. [Google Scholar] [CrossRef]
- Koerver, R.; Zhang, W.; De Biasi, L.; Schweidler, S.; Kondrakov, A.O.; Kolling, S.; Brezesinski, T.; Hartmann, P.; Zeier, W.G.; Janek, J. Chemo-Mechanical Expansion of Lithium Electrode Materials—On the Route to Mechanically Optimized All-Solid-State Batteries. Energy Environ. Sci. 2018, 11, 2142–2158. [Google Scholar] [CrossRef]
- Shi, T.; Zhang, Y.Q.; Tu, Q.; Wang, Y.; Scott, M.C.; Ceder, G. Characterization of Mechanical Degradation in an All-Solid-State Battery Cathode. J. Mater. Chem. A 2020, 8, 17399–17404. [Google Scholar] [CrossRef]
- Doerrer, C.; Capone, I.; Narayanan, S.; Liu, J.; Grovenor, C.R.M.; Pasta, M.; Grant, P.S. High Energy Density Single-Crystal NMC/Li6PS5Cl Cathodes for All-Solid-State Lithium-Metal Batteries. ACS Appl. Mater. Interfaces 2021, 13, 37809–37815. [Google Scholar] [CrossRef] [PubMed]
- Yoon, K.; Kim, H.; Han, S.; Chan, T.S.; Ko, K.H.; Jo, S.; Park, J.; Kim, S.; Lee, S.; Noh, J.; et al. Detrimental Effect of High-Temperature Storage on Sulfide-Based All-Solid-State Batteries. Appl. Phys. Rev. 2022, 9, 031403. [Google Scholar] [CrossRef]
- Kalnaus, S.; Dudney, N.J.; Westover, A.S.; Herbert, E.; Hackney, S. Solid-State Batteries: The Critical Role of Mechanics. Science 2023, 381, eabg5998. [Google Scholar] [CrossRef]
- Noh, H.J.; Youn, S.; Yoon, C.S.; Sun, Y.K. Comparison of the Structural and Electrochemical Properties of Layered Li[NixCoyMnz]O2 (x = 1/3, 0.5, 0.6, 0.7, 0.8 and 0.85) Cathode Material for Lithium-Ion Batteries. J. Power Sources 2013, 233, 121–130. [Google Scholar] [CrossRef]
- Sun, H.H.; Choi, W.; Lee, J.K.; Oh, I.H.; Jung, H.G. Control of Electrochemical Properties of Nickel-Rich Layered Cathode Materials for Lithium Ion Batteries by Variation of the Manganese to Cobalt Ratio. J. Power Sources 2015, 275, 877–883. [Google Scholar] [CrossRef]
- Yoon, C.S.; Choi, M.H.; Lim, B.B.; Lee, E.J.; Sun, Y.K. Review—High-Capacity Li[Ni1−xCox/2Mnx/2]O2 (x = 0.1, 0.05, 0) Cathodes for Next-Generation Li-Ion Battery. J. Electrochem. Soc. 2015, 162, A2483–A2489. [Google Scholar] [CrossRef]
- Ishidzu, K.; Oka, Y.; Nakamura, T. Lattice Volume Change during Charge/Discharge Reaction and Cycle Performance of Li[NixCoyMnz]O2. Solid State Ionics 2016, 288, 176–179. [Google Scholar] [CrossRef]
- Friedrich, F.; Strehle, B.; Freiberg, A.T.S.; Kleiner, K.; Day, S.J.; Erk, C.; Piana, M.; Gasteiger, H.A. Editors’ Choice—Capacity Fading Mechanisms of NCM-811 Cathodes in Lithium-Ion Batteries Studied by X-ray Diffraction and Other Diagnostics. J. Electrochem. Soc. 2019, 166, A3760–A3774. [Google Scholar] [CrossRef]
- Yuan, K.; Li, N.; Ning, R.; Shen, C.; Hu, N.; Bai, M.; Zhang, K.; Tian, Z.; Shao, L.; Hu, Z.; et al. Stabilizing Surface Chemical and Structural Ni-rich Cathode via a Non-Destructive Surface Reinforcement Strategy. Nano Energy 2020, 78, 105239. [Google Scholar] [CrossRef]
- Liu, T.; Yu, L.; Lu, J.; Zhou, T.; Huang, X.; Cai, Z.; Dai, A.; Gim, J.; Ren, Y.; Xiao, X.; et al. Rational Design of Mechanically Robust Ni-rich Cathode Materials via Concentration Gradient Strategy. Nat. Commun. 2021, 12, 6024. [Google Scholar] [CrossRef] [PubMed]
- Park, N.Y.; Ryu, H.H.; Kuo, L.Y.; Kaghazchi, P.; Yoon, C.S.; Sun, Y.K. High-Energy Cathodes via Precision Microstructure Tailoring for Next-Generation Electric Vehicles. ACS Energy Lett. 2021, 6, 4195–4202. [Google Scholar] [CrossRef]
- Lv, H.; Li, C.; Zhao, Z.; Wu, B.; Mu, D. A Review: Modification Strategies of Nickel-Rich Layer Structure Cathode (Ni ≥ 0.8) Materials for Lithium Ion Power Batteries. J. Energy Chem. 2021, 60, 435–450. [Google Scholar] [CrossRef]
- Lee, J.; Urban, A.; Li, X.; Su, D.; Hautier, G.; Ceder, G. Unlocking the Potential of Cation-Disordered Oxides for Rechargeable Lithium Batteries. Science 2014, 343, 519–522. [Google Scholar] [CrossRef]
- Yabuuchi, N.; Nakayama, M.; Takeuchi, M.; Komaba, S.; Hashimoto, Y.; Mukai, T.; Shiiba, H.; Sato, K.; Kobayashi, Y.; Nakao, A.; et al. Origin of Stabilization and Destabilization in Solid-State Redox Reaction of Oxide Ions for Lithium-Ion Batteries. Nat. Commun. 2016, 7, 13814. [Google Scholar] [CrossRef] [PubMed]
- Nakajima, M.; Yabuuchi, N. Lithium-Excess Cation-Disordered Rocksalt-Type Oxide with Nanoscale Phase Segregation: Li1.25Nb0.25V0.5O2. Chem. Mater. 2017, 29, 6927–6935. [Google Scholar] [CrossRef]
- Zhao, X.; Tian, Y.; Lun, Z.; Cai, Z.; Chen, T.; Ouyang, B.; Ceder, G. Design Principles for Zero-Strain Li-ion Cathodes. Joule 2022, 6, 1654–1671. [Google Scholar] [CrossRef]
- Cho, J.; Kim, Y.J.; Kim, T.J.; Park, B. Zero-Strain Intercalation Cathode for Rechargeable Li-Ion Cell. Angew. Chem. 2001, 113, 3471–3473. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, H.; Choi, W.; Park, M.S. Bifunctional Surface Coating of LiNbO3 on High-Ni Layered Cathode Materials for Lithium-Ion Batteries. ACS Appl. Mater. Interfaces 2020, 12, 35098–35104. [Google Scholar] [CrossRef]
- Nguyen, A.; Zuo, P.; Jiang, H.; Wang, C.; Wang, D. Dual Protective Mechanism of AlPO4 Coating on High-Nickel Cathode Material for High Energy Density and Long Cycle Life Lithium-Ion Batteries. J. Electrochem. Soc. 2022, 169, 050523. [Google Scholar] [CrossRef]
- Mariyappan, S.; Marchandier, T.; Rabuel, F.; Iadecola, A.; Rousse, G.; Morozov, A.V.; Abakumov, A.M.; Tarascon, J.M. The Role of Divalent (Zn2+/Mg2+/Cu2+) Substituents in Achieving Full Capacity of Sodium Layered Oxides for Na-Ion Battery Applications. Chem. Mater. 2020, 32, 1657–1666. [Google Scholar] [CrossRef]
- Zhang, X.; Qiu, F.; Jiang, K.; He, P.; Han, M.; Guo, S.; Zhou, H. Improving the Structural and Cyclic Stabilities of P2-type Na 0.67 MnO 2 Cathode Material via Cu and Ti Co-Substitution for Sodium Ion Batteries. Chem. Commun. 2020, 56, 6293–6296. [Google Scholar] [CrossRef]
- Xin, F.; Zhou, H.; Zong, Y.; Zuba, M.; Chen, Y.; Chernova, N.A.; Bai, J.; Pei, B.; Goel, A.; Rana, J.; et al. What Is the Role of Nb in Nickel-Rich Layered Oxide Cathodes for Lithium-Ion Batteries? ACS Energy Lett. 2021, 6, 1377–1382. [Google Scholar] [CrossRef]
- Kong, W.; Zhang, J.; Wong, D.; Yang, W.; Yang, J.; Schulz, C.; Liu, X. Tailoring Co3d and O2p Band Centers to Inhibit Oxygen Escape for Stable 4.6 V LiCoO2 Cathodes. Angew. Chem. Int. Ed. 2021, 60, 27102–27112. [Google Scholar] [CrossRef]
- Ou, X.; Liu, T.; Zhong, W.; Fan, X.; Guo, X.; Huang, X.; Cao, L.; Hu, J.; Zhang, B.; Chu, Y.S.; et al. Enabling High Energy Lithium Metal Batteries via Single-Crystal Ni-rich Cathode Material Co-Doping Strategy. Nat. Commun. 2022, 13, 2319. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef]
- Sun, J.; Remsing, R.C.; Zhang, Y.; Sun, Z.; Ruzsinszky, A.; Peng, H.; Yang, Z.; Paul, A.; Waghmare, U.; Wu, X.; et al. Accurate First-Principles Structures and Energies of Diversely Bonded Systems from an Efficient Density Functional. Nat. Chem. 2016, 8, 831–836. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Sun, J.; Martin, R.M.; Delley, B. Semilocal Density Functionals and Constraint Satisfaction. Int. J .Quantum. Chem. 2016, 116, 847–851. [Google Scholar] [CrossRef]
- Zhang, Y.; Kitchaev, D.A.; Yang, J.; Chen, T.; Dacek, S.T.; Sarmiento-Pérez, R.A.; Marques, M.A.L.; Peng, H.; Ceder, G.; Perdew, J.P.; et al. Efficient First-Principles Prediction of Solid Stability: Towards Chemical Accuracy. NPJ Comput. Mater 2018, 4, 9. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Van Voorhis, T. Nonlocal van Der Waals Density Functional: The Simpler the Better. J. Chem. Phys. 2010, 133, 244103. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-Energy-Loss Spectra and the Structural Stability of Nickel Oxide: An LSDA+U Study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Fonseca Guerra, C.; Handgraaf, J.W.; Baerends, E.J.; Bickelhaupt, F.M. Voronoi Deformation Density (VDD) Charges: Assessment of the Mulliken, Bader, Hirshfeld, Weinhold, and VDD Methods for Charge Analysis. J. Comput. Chem. 2004, 25, 189–210. [Google Scholar] [CrossRef]
- Tabuchi, M.; Tsutsui, S.; Masquelier, C.; Kanno, R.; Ado, K.; Matsubara, I.; Nasu, S.; Kageyama, H. Effect of Cation Arrangement on the Magnetic Properties of Lithium Ferrites (LiFeO2) Prepared by Hydrothermal Reaction and Post-annealing Method. J. Solid State Chem. 1998, 140, 159–167. [Google Scholar] [CrossRef]
- Amatucci, G.G.; Tarascon, J.M.; Klein, L.C. CoO2, the End Member of the Lix CoO2 Solid Solution. J. Electrochem. Soc. 1996, 143, 1114. [Google Scholar] [CrossRef]
- Bo, S.H.; Li, X.; Toumar, A.J.; Ceder, G. Layered-to-Rock-Salt Transformation in Desodiated NaxCrO2 (x 0.4). Chem. Mater. 2016, 28, 1419–1429. [Google Scholar] [CrossRef]
- Bruce, P.G.; Armstrong, A.R.; Gitzendanner, R.L. New Intercalation Compounds for Lithium Batteries: Layered LiMnO2. J. Mater. Chem. 1999, 9, 193–198. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y. Synthesis and Formation Mechanism of Manganese Dioxide Nanowires/Nanorods. Chem. Eur. J. 2003, 9, 300–306. [Google Scholar] [CrossRef] [PubMed]
- Sabitov, I.K. Algebraic Methods for Solution of Polyhedra. Russ. Math. Surv. 2011, 66, 445–505. [Google Scholar] [CrossRef]
- Pearce, P.E.; Perez, A.J.; Rousse, G.; Saubanère, M.; Batuk, D.; Foix, D.; McCalla, E.; Abakumov, A.M.; Van Tendeloo, G.; Doublet, M.L.; et al. Evidence for Anionic Redox Activity in a Tridimensional-Ordered Li-rich Positive Electrode β-Li2IrO3. Nat. Mater 2017, 16, 580–586. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).