Holistic Testing and Characterization of Commercial 18650 Lithium-Ion Cells

Abstract

Reduced-order electrothermal models play a key role in the design and control of lithium-ion cell stacks, calling for accurate model parameter calibration. This paper presents a complete electrical and thermal experimental characterization procedure for the coupled modeling of cylindrical lithium-ion cells in order to implement them in a prototype Formula SAE hybrid racing car. The main goal of the tests is to determine how the cell capacity varies with the temperature and the discharge current to predict the open-circuit voltage of the cell and its entropic component. A simple approach for the characterization of the battery equivalent electrical circuit and a two-step thermal characterization method are also shown. The investigations are carried out on four commercial 18650 NMC lithium cells. The model was shown to predict the battery voltage with an RMS error lower than 20 mV and the temperature with an RMS error equal to 0.5 °C. The authors hope that this manuscript can contribute to the development of standardized characterization techniques for such cells while offering experimental data and validated models that can be used by researchers and BMS designers in different applications.

1. Introduction

Thanks to their high energy density and specific energy [1], lithium-ion batteries have gone through a dizzying diffusion in recent years, both in the automotive sector (passing from a market share of 0.2 % in 2013 to 13 % in 2022 [2]) and for portable electronic devices (15 billion mobile phones in the world in 2021 [3]). Among the different lithium-ion chemistries available [4], with some still at the prototype stage [5,6], lithium nickel manganese cobalt oxides (NMCs), lithium iron phosphate (LFP), and lithium titanium oxides (LTOs) emerge as the most competitive on the market. Cells are typically assembled in modules, or packs, where they are connected in series and/or parallel to provide the desired voltage and energy capacity. For instance, many electric cars operate in the range 400–800 volts, while individual cells generally have voltages ranging from 3 to 4 volts. Proper and safe module operation is ensured by the battery management system (BMS), whose effective design calls for an accurate and physically consistent electrical and thermal model of the Li-ion pack [7]. This applies to several BMS features, such as state-of-charge (SoC) measurements, state-of-health (SoH) estimation (also under extreme conditions), circuit balancing, and thermal runaway suppression to preclude fire hazards. This last aspect is more critical for lithium-ion batteries than for many other electrochemical energy storage technologies, such as supercapacitors [8], flow batteries [9], etc. Regarding this issue, the acceptable operational temperature for Li-ion cells spans from −20 °C to 60 °C, with optimal performance occurring between 15 °C and 35 °C. Nevertheless, heat generation within a Li-ion battery pack is inevitable due to various losses and entropic effects, resulting in an uneven temperature distribution with gradients among module cells. Uncontrolled heat generation can lead not only to thermal runaway but also to capacity loss and cell instability, so that the temperature differences among cells should be limited to 6 °C to ensure optimal operation and preserve the battery SoH.

Developing a BMS is a complex task that entails creating reduced battery models, estimators, and functionalities to guarantee the optimal performance of the battery under all operating conditions and throughout its entire lifespan. All of them must operate with limited computational resources on a cost-effective microcontroller. This calls for significant expertise and technical know-how, which may be lacking in the framework of a rapidly developing technology, a condition particularly evident in the battery industry with emerging chemistries, each presenting its own challenges, requirements, and features. To address this, an accurate characterization of the cells is vital.

This paper presents some experimental procedures for the precise characterization of the electrical and thermal properties of lithium-ion cells, aimed at accurately determining all physical parameters needed in reliable electrical and thermal lumped models. The study focuses on four commercial 18650 Li-ion cell models made by different manufacturers: the Molicel^® P28A, P28B, and P30B, as well as the Sony Murata VTC5D. The parameters evaluated include the cell capacity at varying temperatures and discharge currents (C-rates), the open-circuit voltage (OCV) at different SoCs, the entropic coefficient, and some electrical and thermal lumped parameters.

Building on a cooperation on the engineering of Li-ion batteries started between University of Padua and FIAMM Energy Technology some time ago [10], this research was carried out by the Electrochemical Energy Storage and Conversion Lab (EESCOLab), the Modelling, Analysis and Research in Turbomachinery and Energy Systems Laboratory (MARTES), and the RaceUp Formula SAE Students Team, in collaboration with FIAMM Energy Technology S.p.A. The goal was to analyze different lithium-ion cells for their use in a prototype Formula SAE hybrid racing car. Formula SAE is a student design competition organized by SAE International (formerly the Society of Automotive Engineers).

Few studies in the literature offer detailed descriptions of measurement techniques, experimental results, and their application in validated models. For the sake of comparison, some techniques documented in the literature were examined. This model provides the following:

• Simple and straightforward experimental protocols for the identification of the OCV, capacity, and electrical and thermal parameters of commercial 18650 cells;
• A fast approach for the measurement of the entropic contribution based on a positive adjustment method [11];
• A set of equivalent electrical circuit parameters for all four cell models tested at different temperatures.

The developed models successfully predicted the battery voltage with a root mean square error (RMSE) of less than 20 mV and the temperature with an RMSE of 0.5 °C. Section 2 describes the reduced-order electrical and thermal modeling of 18650 cells. Section 3 details the methods for the electrical and thermal characterization of the four cell models. The electrical characterization includes determining the cell capacity at different C-rate currents and temperatures, determining the relationship between the OCV and SoC, and performing impulsive current charge/discharge tests to identify equivalent circuit model (ECM) parameters, and determining the entropic contribution. The thermal characterization involves methods for determining key thermal parameters such as the cell thermal capacity, the thermal resistance between the cell bulk and surface, and the convection thermal resistance between the cell surface and the environment. Section 4 presents the validation of the battery models in the case of four different load profiles, demonstrating their accuracy. The significance of this work is discussed in the conclusion in Section 5.

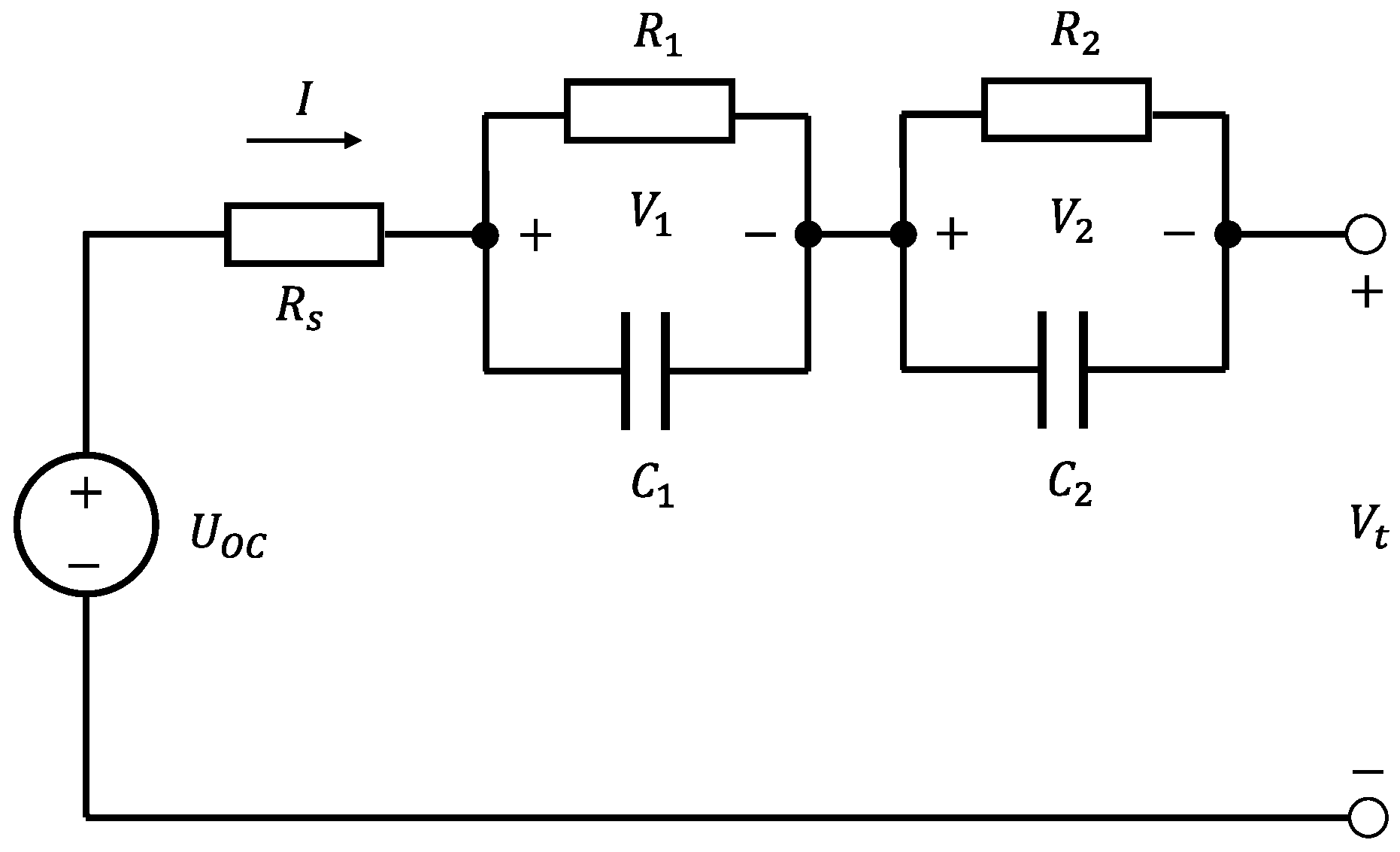
2. Reduced-Order Coupled Modeling of 18650 Cells

Several approaches are presented in the literature to develop reduced-order models capable of predicting the battery voltage and temperature for a short dynamic current cycle [12,13], spanning from electrochemical-based (such as the Pseudo-2D model) to circuit-based types [14], as well as empirical [15] and data-driven models for voltage prediction coupled with thermal models. Due to its ease of characterization and implementation in Simulink [16], an ECM approach was chosen to model the cell electrical behavior, coupled with an array-based thermal circuit model simulating the battery temperatures.

The ECM, represented in Figure 1, consists of a voltage source $U_{OC}$ giving the cell OCV, a resistor $R_s$, and the series of two $RC$ loops, each consisting of a resistor $R_i$ and a capacitor $C_i$. Similar models using only resistors and capacitors as passive elements are presented in the literature [17,18,19]. To account for the effects of the physical conditions on the cell performance, the ECM elements were assumed to be driven as follows: $U_{oc}$ is driven by the SoC, while $R_s$, $R_i$, and $C_i$ are driven by the SoC, operating temperature, and current sign. Consistent with the targeted model accuracy, minor dependencies such as the current magnitude and aging were neglected [19,20].

The electrical model is coupled with the thermal model through the heat generation equation [21]:

$$Q=I(V_t-U_{OC})+I{T}_{avg}\frac{dU}{dT},$$

(1)

where $T_{avg}$ [K] is the battery average temperature and $dU$/$dT$ [VK⁻¹] is the entropic coefficient, i.e., the temperature derivative of the OCV, which depends on the SoC [22].

The lumped thermal model is shown in Figure 2. As is commonly performed in the literature [21,23], the battery surface temperature was assumed to be homogeneous, and the battery thermal behavior was assumed to be perfectly axis-symmetric, so that heat exchanges at the top and bottom cell caps were neglected. The room temperature was assumed to be homogeneous and constant. The battery casing thermal capacity was neglected, because it was considered to be orders of magnitude smaller than that of the cell [24].

The equations of the thermal model are reported in Equation (2):

$$\begin{array}{c}\hfill \{\begin{array}{c}\hfill C_c\frac{d{T}_c}{dt}=\frac{T_s-T_c}{R_c}+Q,\\ \hfill 0=\frac{T_{air}-T_s}{R_u}+\frac{T_c-T_s}{R_c},\end{array}\end{array}$$

(2)

where $T_c$ is the cell bulk temperature, $T_s$ is the cell surface temperature, $C_c$ is the cell thermal capacity, $R_c$ is the conduction thermal resistance between the cell bulk and surface, and $R_u$ is the convection thermal resistance between the cell surface and the room, while Q is the heat rate generated by the cell losses.

3. Testing and Characterization

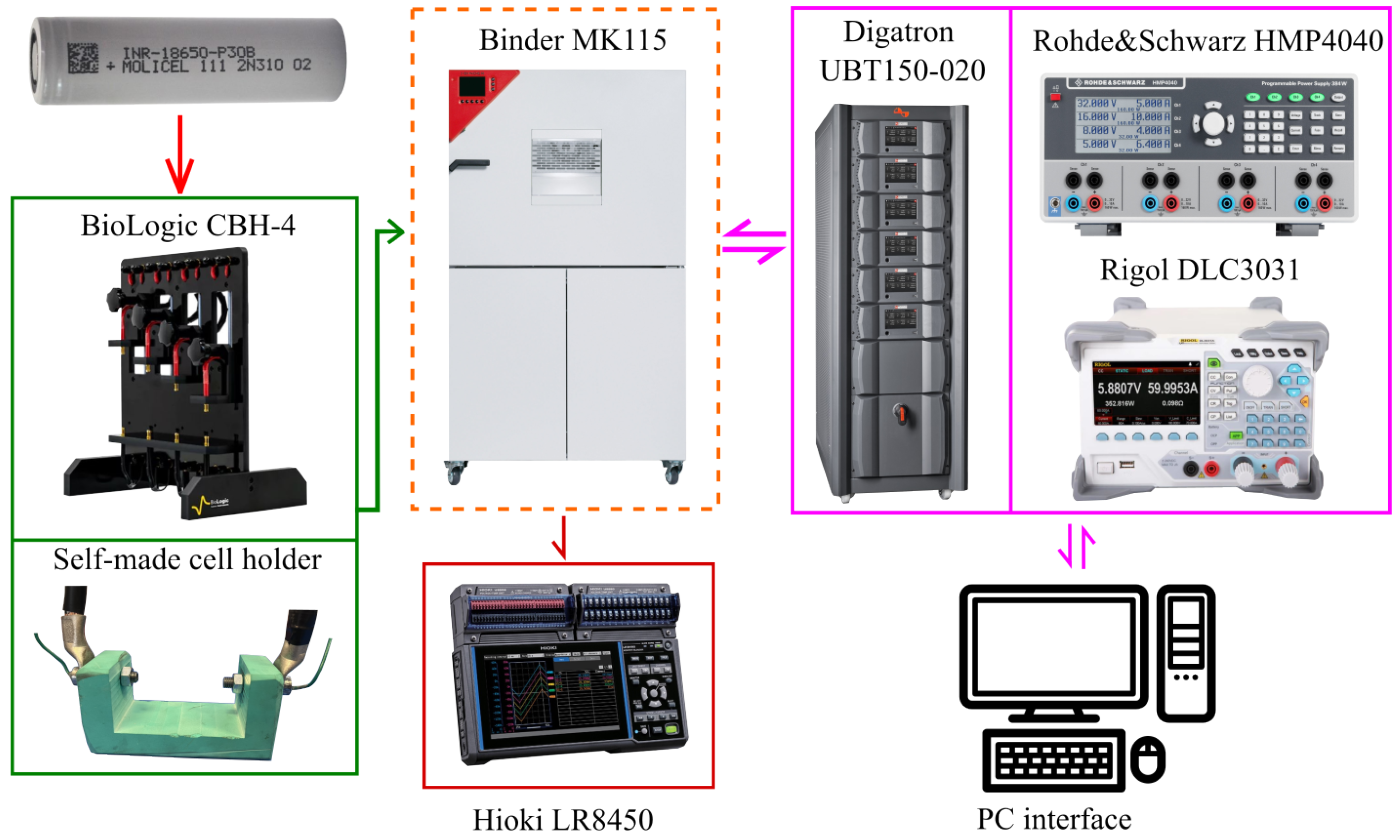
3.1. Materials and Experimental Set-Up

Four commercial 18650 Li-ion cells of different manufacturers underwent the testing procedure: the Molicel^® P28A, P28B, and P30B and the Sony Murata VTC5D (Figure 3). In

Table 1. Parameters of the tested cells (from manufacturers’ data sheets).

	P28A	P28B	P30B	VTC5D
Nominal capacity [mAh]	2800	2800	3000	2800
Minimum capacity [mAh]	2600	2650	2900	2500
Upper cut-off voltage [V]	4.2
Lower cut-off voltage [V]	2.5
Max. continuous discharge current [A]	35	40	30	30
Discharge temperature range [°C]	−40/+60	−40/+60	−40/+60	−20/+60
Internal resistance [mΩ]	20	21	17	n.r.
Size [mm]	⌀ ≈ 18.6, h ≈ 65.2
Mass [g]	46	48	47	44

, the cells’ characteristics and performance from the manufacturers’ data sheets are reported.

The tests were mostly conducted in the laboratories of FIAMM Energy Technology by using the following major equipment:

• A thermal chamber, Binder Mk115, to maintain a constant operating temperature in each experiment and to allow for testing at different temperatures;
• A four-terminal sensing cell holder, where a BioLogic CBH-4 was used for electrical tests;
• An in-house polymeric cell holder for thermal tests;
• A thermocouple array, to detect the battery surface temperature and the room temperature inside the thermal chamber, connected to a Hioki LR8450 data logger;
• A cell cycler consisting of a Rohde&Schwarz^® (Munich, Germany) HMP4040 charger with a Rigol DLC3031 (Beijing, China) load to measure the entropic contribution and the pseudo-$U_{OC}$ experiment, while for the other test a Digatron Systems UBT150-020 (Aachen, Germany) cells cycler was used.

The experimental set-up was controlled by a PC, and data were post-processed in the MATLAB and Simulink environments. Figure 4 shows a scheme of the experimental set-up.

3.2. Electrical Characterization Tests

3.2.1. Capacity Determination

The battery capacity at the beginning of life (BoL) is an important key performance indicator (KPI) for applications where a long cycle life does not drive the design of the parameters, as in the case of the target application of this work, i.e., an FSAE racing car [25,26,27].

In order to evaluate the dependence of the cell capacity on the temperature and discharge current, as in [28,29,30,31], the following testing procedure was implemented:

• Fully charge the cell to $SoC=100\%$ with (a) 1 C constant current (CC) until the voltage reaches the upper cut-off ($4.2$ $\mathrm{V}$) and (b) constant voltage (CV) until the current decreases to the rate C/20, at the reference temperature $T_{ref}$ = 25 °C.
• Set the thermal chamber to the temperature $T_i$ and wait 1 h to allow for cell temperature and voltage relaxation.
• Discharge the cell at CC with a rate $C_{r,i}$ until the voltage decreases to the lower cut-off voltage of $2.5$ $\mathrm{V}$.
• Bring the thermal chamber to the reference temperature $T_{ref}$ and wait 1 h to allow for cell temperature and voltage relaxation.
• Repeat steps 1–4 five times.

The testing procedure was run at $T_i$ = 5 °C, 25 °C, and 40 °C and at discharge currents with C-rates $C_{r,i}$ = $0.5$ C, 1 C, 3 C, and 5 C. The cell charge capacity [mAh] for each test was computed as the time integral of the current during CC discharge. To quantify the spread of the performance among different cells of the same type [32], three samples for each model were tested and each of them underwent five discharges. The capacity of the cell model was then obtained as the average of 15 such tests. In addition, the standard deviations of these tests are shown in

Table 2. Capacity of the tested cells at different C-rate discharge currents and temperatures. The shown values are the averages and deviation among three cells per type and five discharges per each cell.

	Temperature	0.5 C	1 C	3 C	5 C
	[°C]	[mAh]	[mAh]	[mAh]	[mAh]
P28A	5	2656 ± 20	2575 ± 10	2541 ± 10	2562 ± 10
	25	2747 ± 60	2685 ± 70	2620 ± 70	2606 ± 70
	40	2687 ± 30	2658 ± 20	2575 ± 20	2561 ± 30
P28B	5	2527 ± 30	2490 ± 20	2459 ± 10	2477 ± 20
	25	2720 ± 100	2670 ± 100	2581 ± 60	2567 ± 60
	40	2542 ± 30	2547 ± 20	2499 ± 30	2504 ± 80
P30B	5	2825 ± 60	2747 ± 40	2710 ± 30	2810 ± 20
	25	3041 ± 30	2943 ± 10	2915 ± 20	2908 ± 30
	40	3015 ± 40	2961 ± 20	2890 ± 10	2893 ± 10
VTC5D	5	2712 ± 50	2616 ± 20	2568 ± 50	2578 ± 50
	25	2861 ± 20	2791 ± 5	2685 ± 20	2668 ± 10
	40	2749 ± 50	2704 ± 40	2618 ± 60	2607 ± 40

. The four battery models were tested as described below.

3.2.2. OCV Measurements

Determining the dependence of $U_{oc}$ on the SoC is crucial to accurately predicting the battery voltage $V_t$. The main experimental technique for a priori OCV vs. SoC measurements is the “pseudo-$U_{oc}$ test”, also referred to as the “low-current continuous OCV measurement” and the “intermittent-current pulse test” [33,34]. Measurement data can be collected in a look-up table or used to fit mathematical functions [35]. In the present work, the OCV vs. SoC curve was obtained by applying the pseudo-$U_{oc}$ test for all the cells, which consisted of the following procedure:

• Fully charge the cell to $SoC=100\%$ with (a) 1 C CC until the voltage reaches the upper cut-off ($4.2$ $\mathrm{V}$) and (b) CV until the current decreases to a rate C/20, at the reference temperature $T_{ref}$ = 25 °C.
• Relax the cell voltage for 1 h.
• Discharge the cell with CC at a rate C/20 until the voltage decreases to the lower cut-off of $2.5$ $\mathrm{V}$.
• Charge the cell with CC at a rate C/20 until the voltage reaches the upper cut-off of  $4.2$ $\mathrm{V}$.

The cell OCV curve was obtained as the average between voltages in charging and discharging (Figure 5).

This is a simple and reliable method, which has proven to be successful in the present application. Future developments may involve the use of more complex post-processing data algorithms, aimed at identifying voltage hysteresis in OCV measurements [36], correcting partial relaxation effects during pulse tests [37], or implementing filtering techniques (e.g., Kalman filters), as in [38].

3.2.3. Gitt Characterization Tests

Impulsive current charge/discharge tests are commonly presented in the literature to determine the ECM parameters of lithium-ion batteries [19,21,39]. Such impulsive tests have different names, e.g., the galvanostatic intermittent titration technique (GITT) test. Considering the ECM described above, the test was oriented to identify the circuit parameters in charging and discharging at different operating temperatures. The testing procedure used for GITT characterization was as follows:

• Fully charge the cell ($SoC=100\%$) with (a) 1 C CC until the voltage reaches the upper cut-off ($4.2$ $\mathrm{V}$) and (b) CV until the current is reduced to a rate C/20, at the reference temperature $T_{ref}$ = 25 °C.
• Relax the cell voltage for 1 h.
• Impose a discharge 2 C current impulse lasting for ${\tau }_{imp}$ and then relax the battery voltage for 1 h.
• Repeat step 3 until the voltage reaches the lower cut-off of $2.5$ $\mathrm{V}$ and then relax the battery voltage for 1 h.
• Repeat step 3 with a charge current impulse until the voltage reaches the upper cut-off of $4.2$ $\mathrm{V}$.
• Repeat the impulsive test at 5 °C and 40 °C.

The duration of the load impulse ${\tau }_{imp}$ varied between 180 $\mathrm{s}$ when $25\%\le SoC\le 75\%$ and 72 $\mathrm{s}$ otherwise. The four cell models underwent the GITT characterization tests under the conditions described above.

Data post-processing consisted of an optimization procedure, with the goal of minimizing the error between the cell voltage measured during the experiments and that computed with ECM-based simulations. The output of the GITT characterization was a set of look-up tables defined for different temperatures and SoCs in charging and discharging. The optimization problem was developed in the MATLAB Optimization Toolbox by using the lsqnonlin solver. A finite difference approximation approach was used to implement ECM behavior. The differentiation time step corresponded to the sampling frequency of the cell voltage during experiments. To reduce the computational cost, instead of performing a single optimization operation through the entire GITT test, independent optimization operations were run for each GITT cycle (pulse and relaxation), corresponding to the given SoC, temperature, and current sign. The output parameters calculated for a given cycle were then used as guess values for the subsequent one, which resulted in a layered approach [17]. Figure 6 shows the experimental and modeled GITT test voltages, while the ECM parameter tables for the four tested cell models are reported in Appendix A.

3.3. Entropic Contribution Measurement

The entropic contribution of lithium-ion cells is traditionally determined from potentiometric and calorimetric measurements [40]. The former consist of measuring the cell OCV at different temperatures and SoCs [41]. A thermal cycle needs to be applied after the complete relaxation of the cell voltage. In addition, at each temperature of the cycle, the thermal equilibrium condition requires some time to be reached, and the larger the thermal capacity of the cell, the larger the system thermal time constant [42]. On the other hand, the calorimetric method is based on the cell heat flux measurement during charge/discharge operations: the entropic contribution is determined after separating the irreversible and reversible heat contributions in the overall measured heat flux [42]. This method can be considered superior to the potentiometric one, allowing for the quasi-continuous measurement of the cell entropic profile. On the other hand, it presents some disadvantages: many cell electrical parameters [43,44] have to be previously determined, and advanced cell-specific experimental equipment is needed, such as isothermal or accelerating rate calorimeters.

To overcome the limitations of the potentiometric and calorimetric methods, a novel $\partial U/\partial T$ determination technique based on electrothermal impedance spectroscopy (ETIS) has been developed by Schmidt et al. in [45]: a thermal transfer function is obtained to relate the surface temperature to the heat flux; then, the reversible heat flux is split from the irreversible term by Fourier analysis. This technique, used also by Geng et al. in [42], presents some drawbacks regarding the precise determination of a thermal transfer function and the spectroscopy data analysis [40].

Recently, different improved approaches have been proposed to reduce the testing time required by the potentiometric method, mainly in the form of the correction of the voltage baseline drift, as in [40,46]. Furthermore, in [11], Lin et al. proposed an improved potentiometric method based on the current positive adjustment method (PAM). In the present work, the common potentiometric method (CPM) was modified to reach the desired SoC, i.e., after a long charge (or discharge) phase, an opposite current was applied for a short time. This PAM was expected to accelerate the depolarization and reduce the voltage relaxation time (from 10–20 h for the CPM to ∼10 min for the PAM). The approach was validated by comparing the measured entropy profile of 18650 lithium-ion cylindrical cells with those obtained from the CPM; the results showed good agreement between the two, thus confirming the advantage of saving test time.

A similar approach to the PAM was used in this paper. Considering that all cells are based on similar NMC chemistries and have similar forms, sizes, and capacities, only the P30B model was tested. The testing procedure consisted of the following:

• Fully charge the cell to $SoC=100\%$ at the reference temperature $T_{ref}$ = 25 °C.
• Relax the cell voltage for 20 h.
• Apply a controlled thermal cycle (1 h at 20 °C, 1 h at 10 °C, 1 h at 30 °C, 1 h at 40 °C, and 1 h at 25 °C).
• Discharge the cell for ${\tau }_{entr}$ at a 1 C rate and then charge at a $0.1$ C rate for $2\times {\tau }_{entr}$.
• Relax the cell voltage for 1 h.
• Repeat steps 3–5 until the voltage reaches the lower cut-off of $2.5$ $\mathrm{V}$.

The value of ${\tau }_{entr}$ was varied in order to collect more data points at high and low $SoC$ values. Figure 7 shows the current profile imposed and the voltage measured at the cell terminals, zooming in on the temperature profile for $U_{OC}$ = $3.832$ $\mathrm{V}$.

During the PAM test, the battery OCV was measured at various temperatures and SoCs (Figure 8).

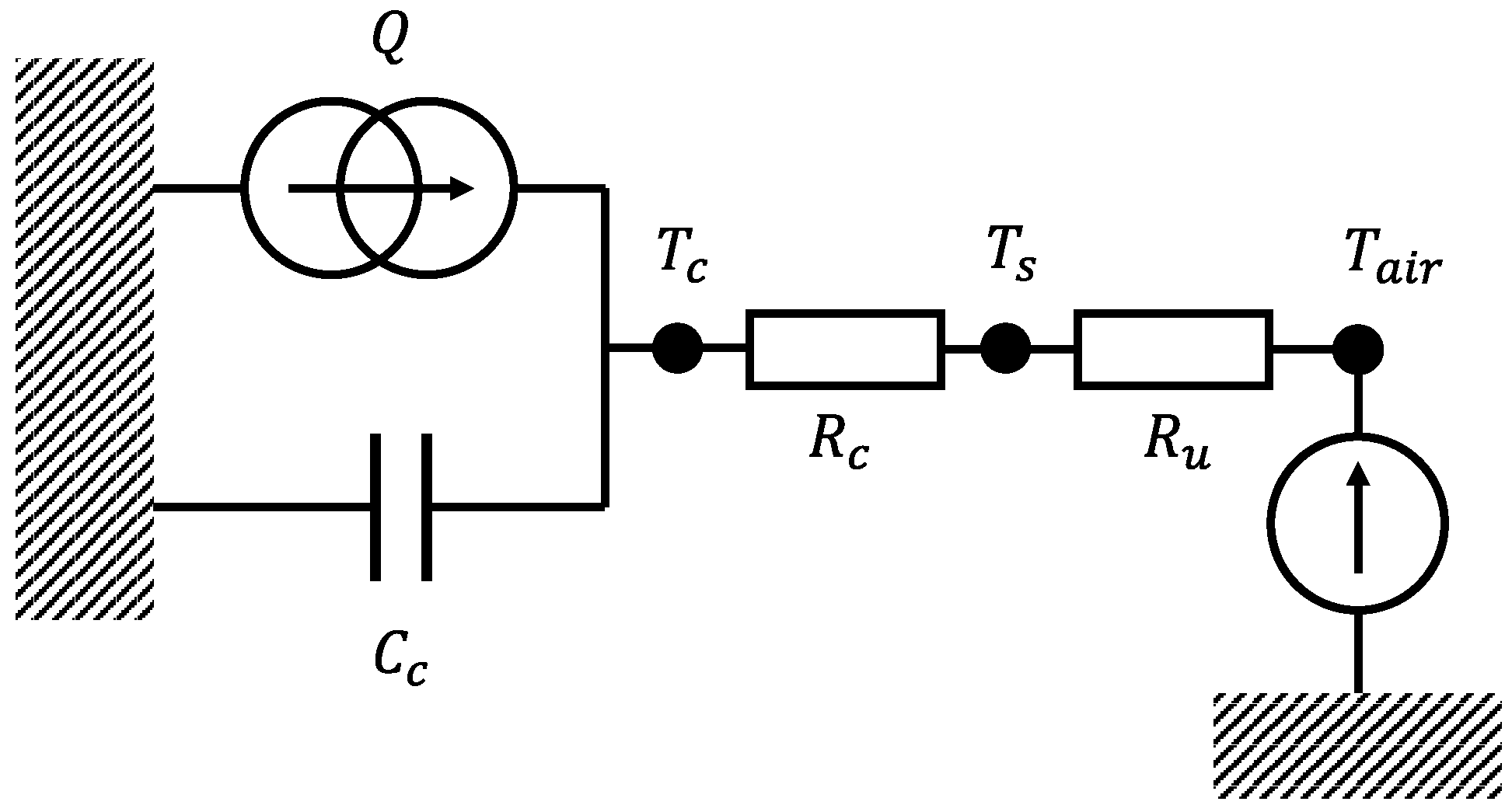
3.4. Thermal Characterization Tests

The thermal parameters involved in the thermal modeling of the lithium-ion cell can be identified in different ways. A common approach is to use calorimetric measurements to determine the battery heat capacity and the anisotropic thermal conductivity. Vertiz et al. [48] used an accelerating rate calorimeter (ARC) technique to determine the heat capacity and thermal conductivity of a lithium-ion pouch cell, coupling an electrical circuit model to a thermal circuit model. Sheng et al. [49] imposed a controlled heat flux to investigate the thermal parameters of a prismatic lithium-ion cell, whereas Cao et al. studied the heat generation characteristics through heat flux measurements of commercial 18650 cells [50]. Calorimetric measurements, though precise, require expensive equipment: this is one of the reasons why many papers on the thermal modeling of Li-ion cells cited above adopted the volume fraction method to determine the battery thermal parameters from the material properties. This is the case in [51,52], or [53], where cylindrical cells are studied by coupling an electrochemical model with a 2D thermal model.

Other works present thermal characterization procedures based on cell surface temperature measurements and obtain the internal thermal parameters through numerical optimization studies. Al-Zareer et al. [54] determined the heat capacity and the radial and axial cell thermal conductivities by measuring the cell surface temperature and implementing an optimization routine on a COMSOL Multiphysics^® 3D model for a cylindrical 18650 cell. A similar approach to identify the heat transfer coefficient and the thermal parameters for a prismatic lithium-ion cell was adopted by Samad et al. [55], who used MATLAB software and considered an array of surface temperature probes, coupling the thermal model with a two-RC-loop ECM. Different online parameterization algorithms have also been proposed, in particular for BMS applications for battery stacks, such as that described by Lin et al. [56], who implemented a simple equivalent circuit-based thermal model, or that described in [57].

Bryden et al. [58] proposed a new method based on non-invasive cell surface temperature measurements under two experimental heat transfer conditions: natural convection and forced convection. This method, used also by Akbarzadeh et al. [18] on prismatic cells, allows for fast and easy thermal characterization, and it is particularly suitable for equivalent thermal circuit models; for these reasons, it was chosen in this work.

The experimental procedure applied to the cell model consisted of the following:

• Fully charge the cell and then discharge to $SoC\approx 50\%$ at the reference temperature $T_{ref}$ = 25 °C.
• Relax the cell voltage and temperature for 1 h.
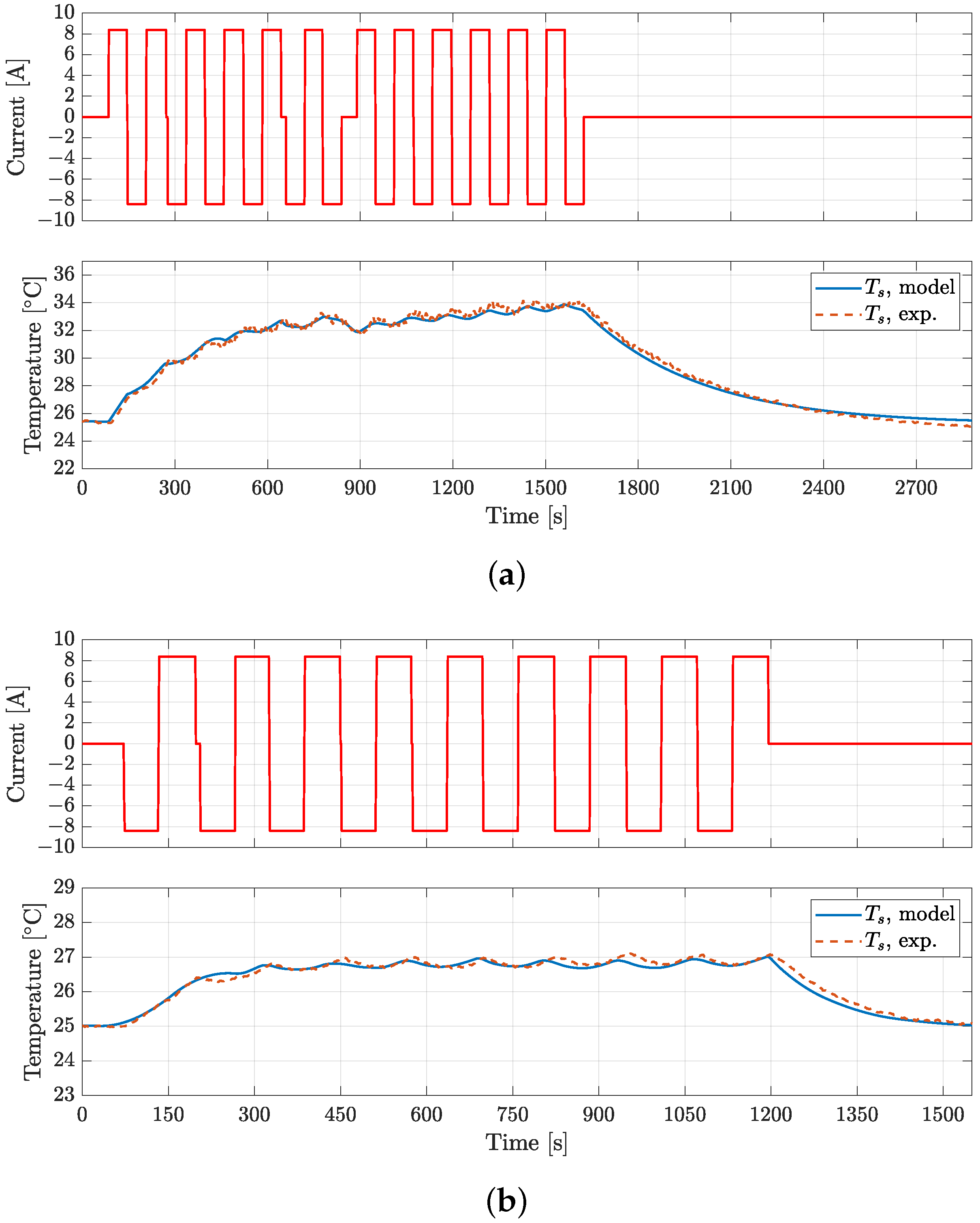
• Apply a square alternating wave load current with a period of 120 $\mathrm{s}$ and a peak-to-peak amplitude corresponding to a rate of 6 C until a steady-state thermal equilibrium is reached on the cell surface. In this way, the entropic heat contribution could be neglected (see Equation (1)).
• Repeat steps 1–3 for two heat exchange conditions:
  ($Cond1$) Low-convective heat transfer condition (the cell is placed in $CellHold1$ and exchanges heat by natural convection with the air inside the thermal chamber);
  ($Cond2$) High-convective heat transfer condition (the cell is placed in $CellHold1$ and a pair of fans cools it down, so that heat exchange is mainly driven by forced convection).

In Equation (2), $T_c$ in the first equation can be replaced, giving:

$$C_c\left(1+\frac{R_c}{R_u}\right)\frac{d{T}_s}{dt}=\frac{T_{air}-T_s}{R_u}+Q.$$

(3)

By measuring $V_t$, the time-dependent heat rate Q was calculated; once the thermal quasi-stationary equilibrium condition ($T_{s,inf}$) is reached, we can estimate a first-try value for $R_{u,0}$ as follows:

$$R_{u,0}=\frac{T_{s,\infty }-T_{air}}{Q}.$$

(4)

By considering the two different heat transfer conditions $Cond1$ and $Cond2$ and defining

$$C_p^{\prime }=C_c\left(\frac{R_c}{R_u}+1\right),$$

(5)

We can write Equation (3) as follows:

$$\begin{array}{c}\hfill \{\begin{array}{c}\hfill C_{p,1}^{\prime }=C_c\left({\displaystyle \frac{R_c}{R_{u,1}}}+1\right),\\ \hfill C_{p,2}^{\prime }=C_c\left({\displaystyle \frac{R_c}{R_{u,2}}}+1\right).\end{array}\end{array}$$

(6)

The Levenberg–Marquardt optimization algorithm was run by using the MATLAB routine lsqcurvefit; the values of $R_{u,1}$ and $R_{u,2}$ obtained from Equation (4) were considered first tries, and the final values of $C_{p,1}^{\prime }$, $R_{u,1}$ and $C_{p,2}^{\prime }$, $R_{u,2}$ were calculated by minimizing the residuals between the modeled and experimental temperature $T_s$ under the two conditions. Eventually, the algebraic solution of the system in Equation (6) yielded $C_c$ and $R_c$. Figure 9 shows the thermal characterization $Cond1$ and $Cond2$ test profiles of the P28A cell, revealing good agreement between the experimental and simulated $T_s$ profiles obtained by using the optimized thermal parameters.

The thermal model parameters obtained from the thermal characterization tests for the four tested cells are listed in

Table 3. The thermal model parameters obtained from the thermal characterization tests for the four tested cell models.

	Cc	Rc	Ru1	Ru2
	[J/K]	[K/W]	[K/W]	[K/W]
P28A	56.3	0.41	6.02	1.07
P28B	55.7	0.24	5.54	2.49
P30B	70.2	0.10	4.94	0.80
VTC5D	68.6	0.15	5.54	1.90

.

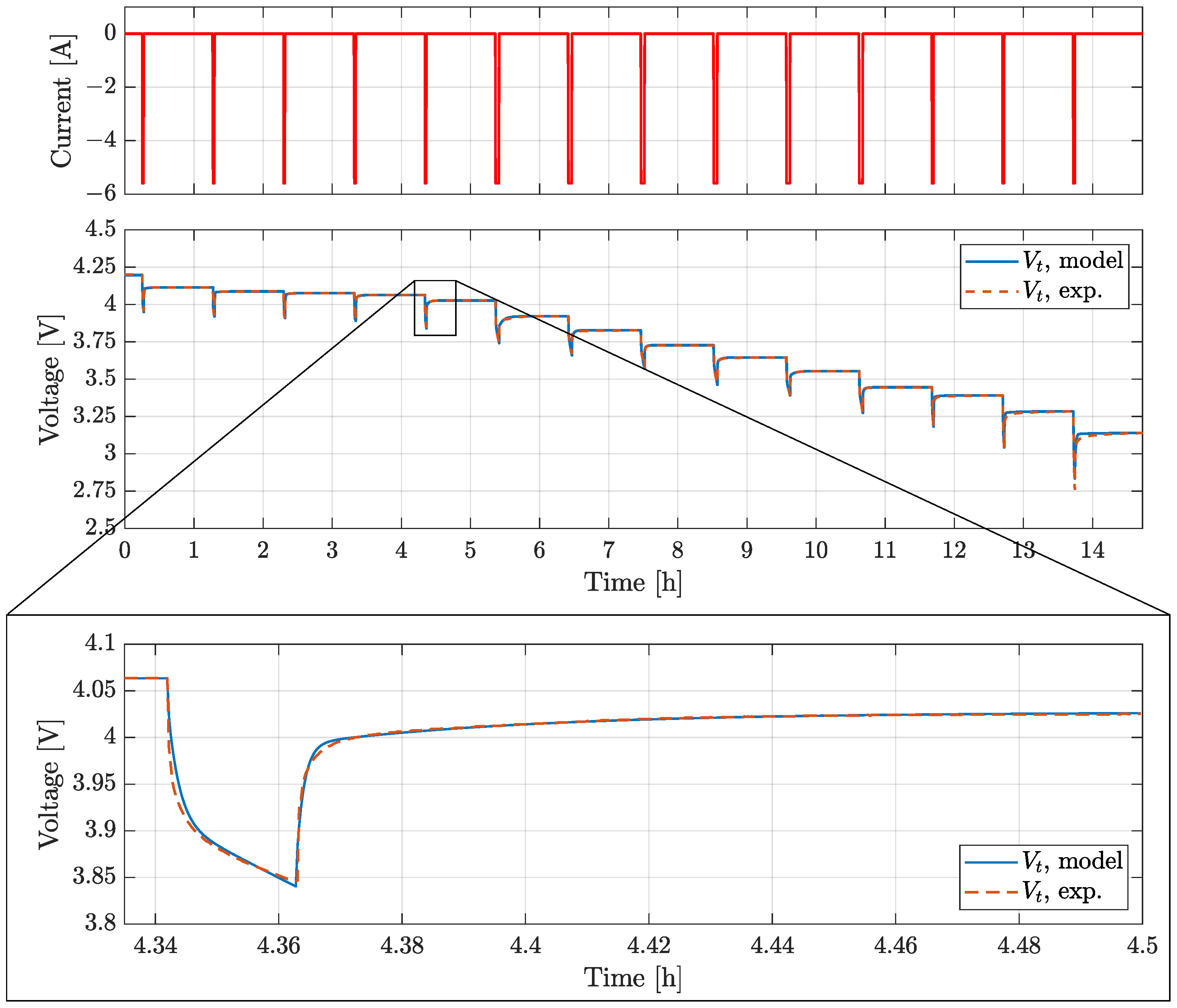
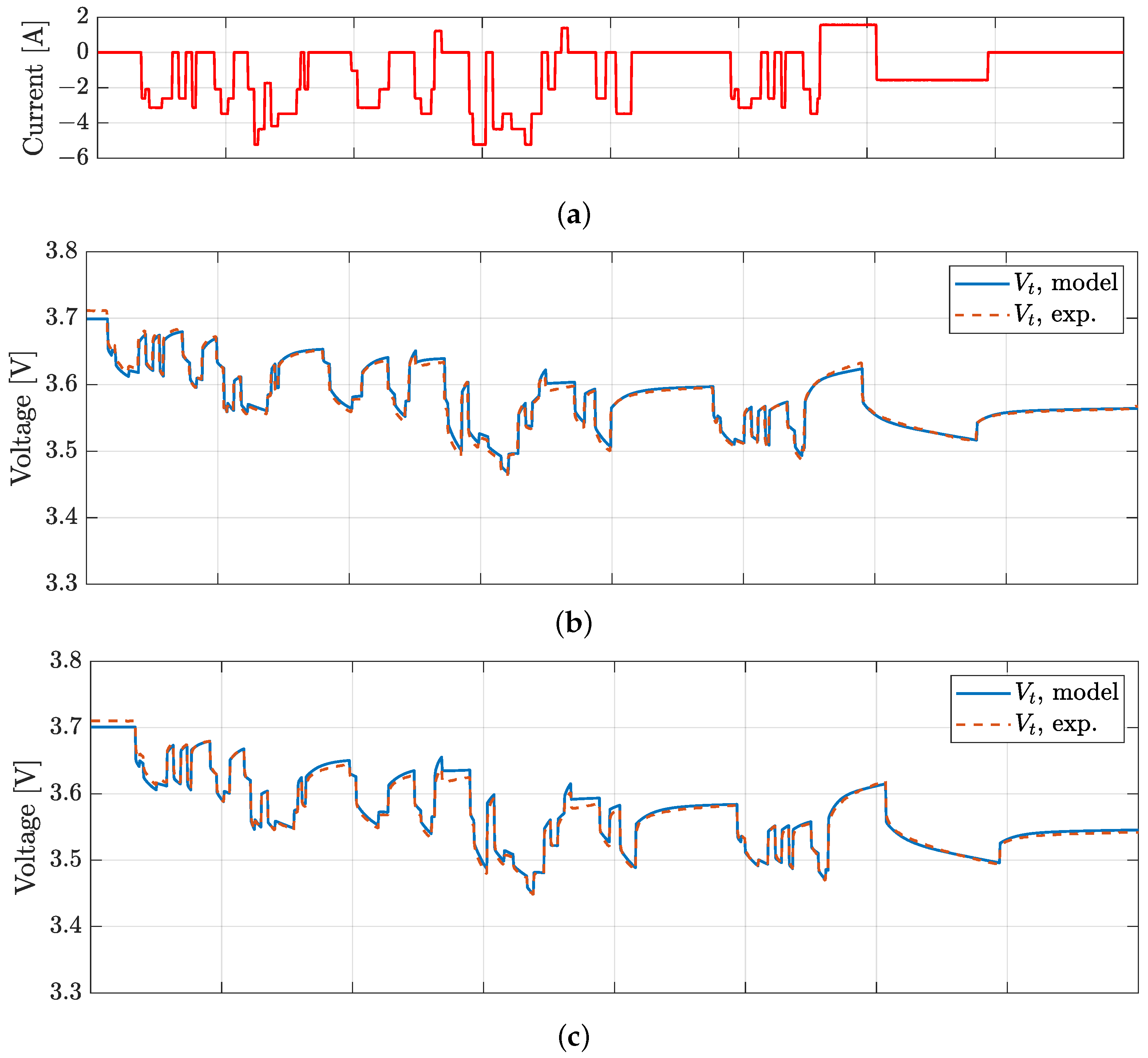
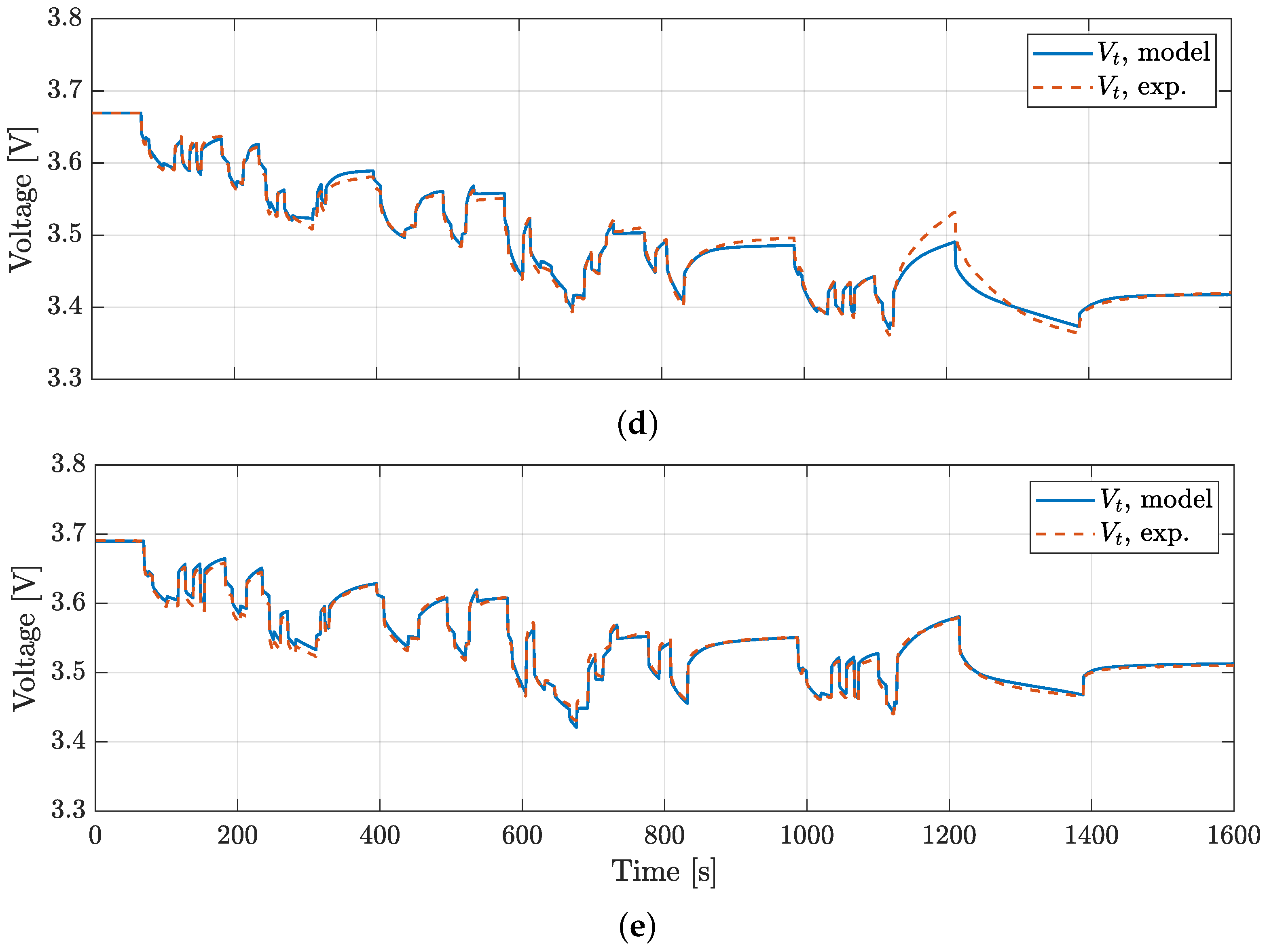
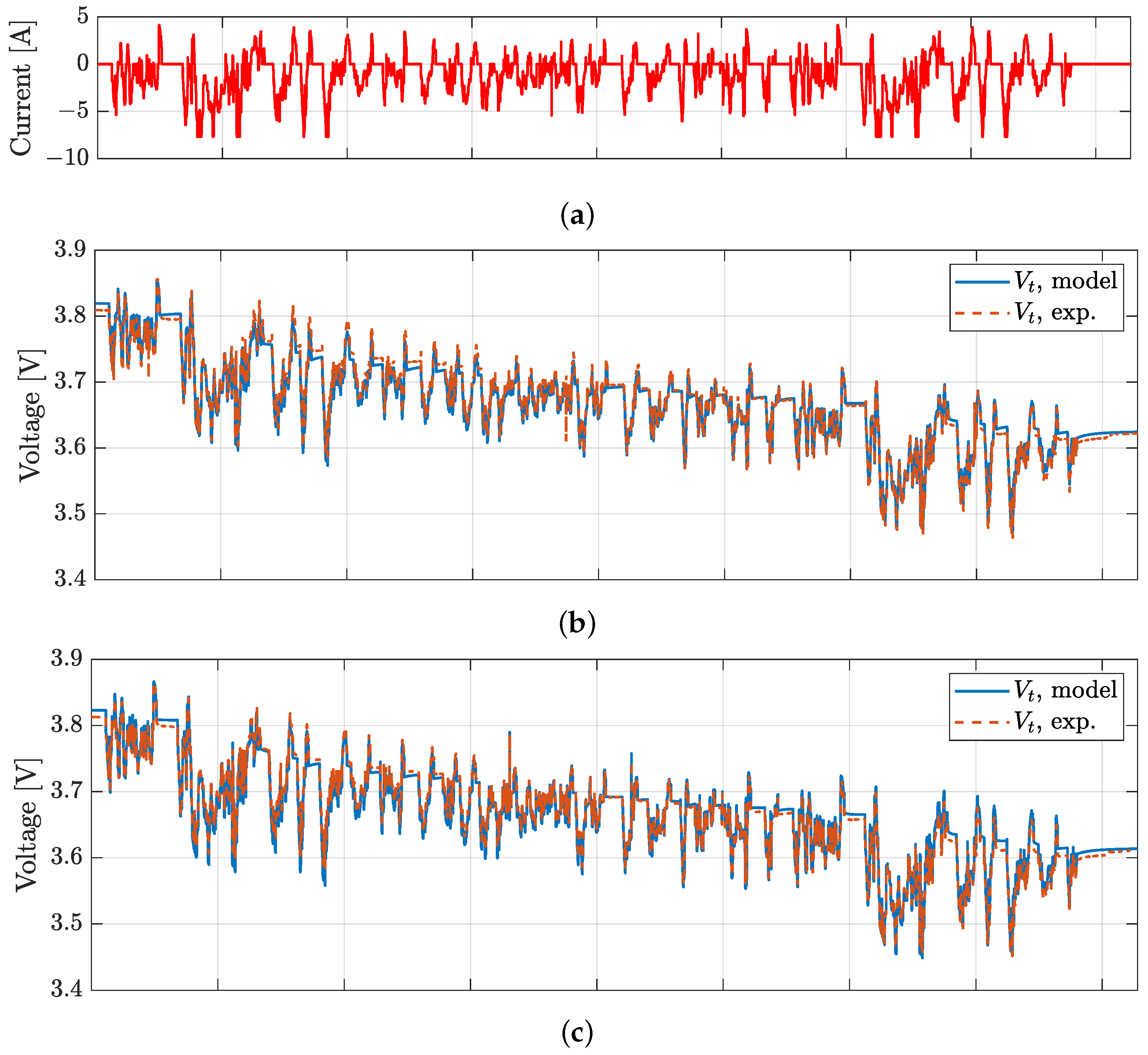
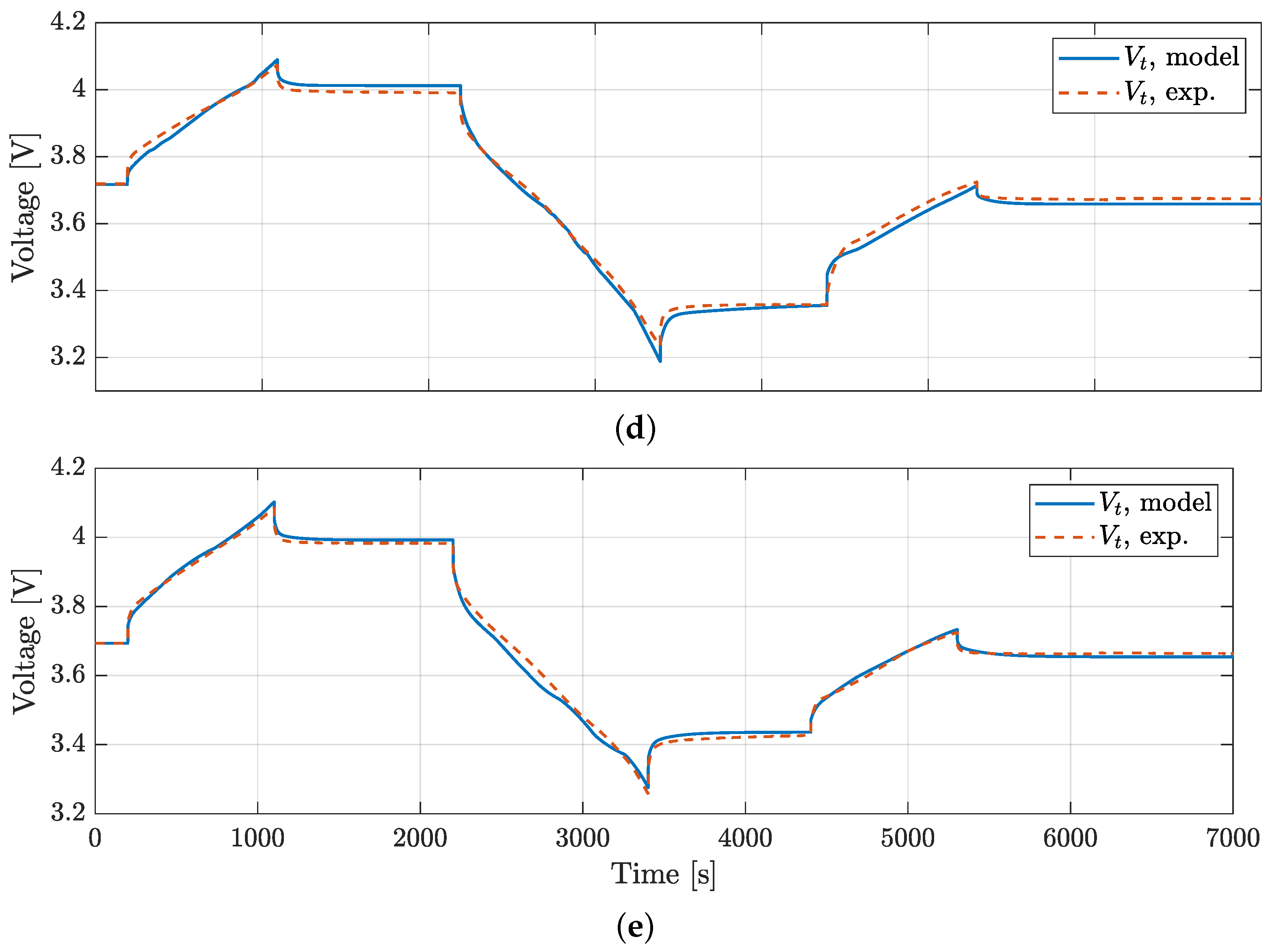
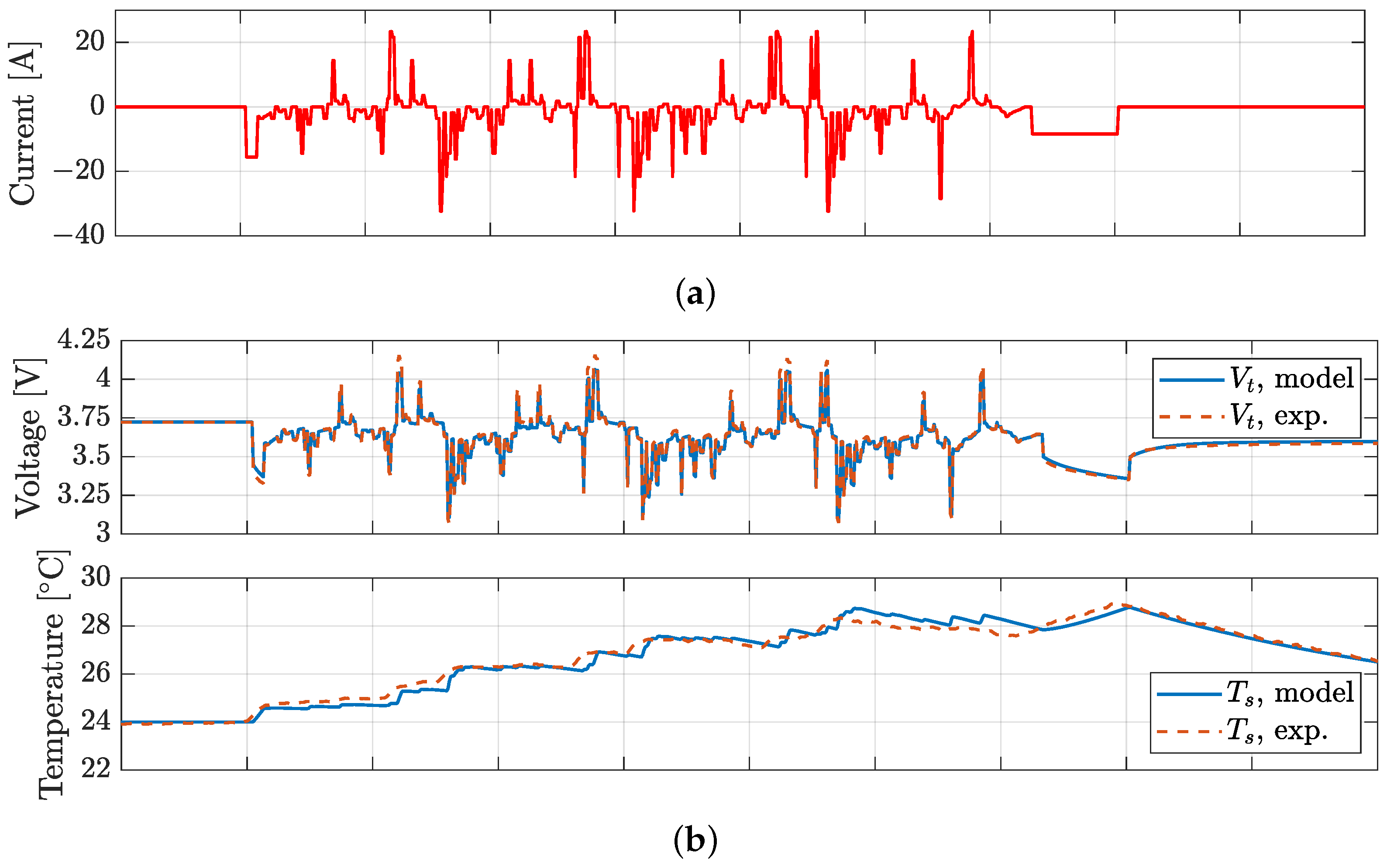
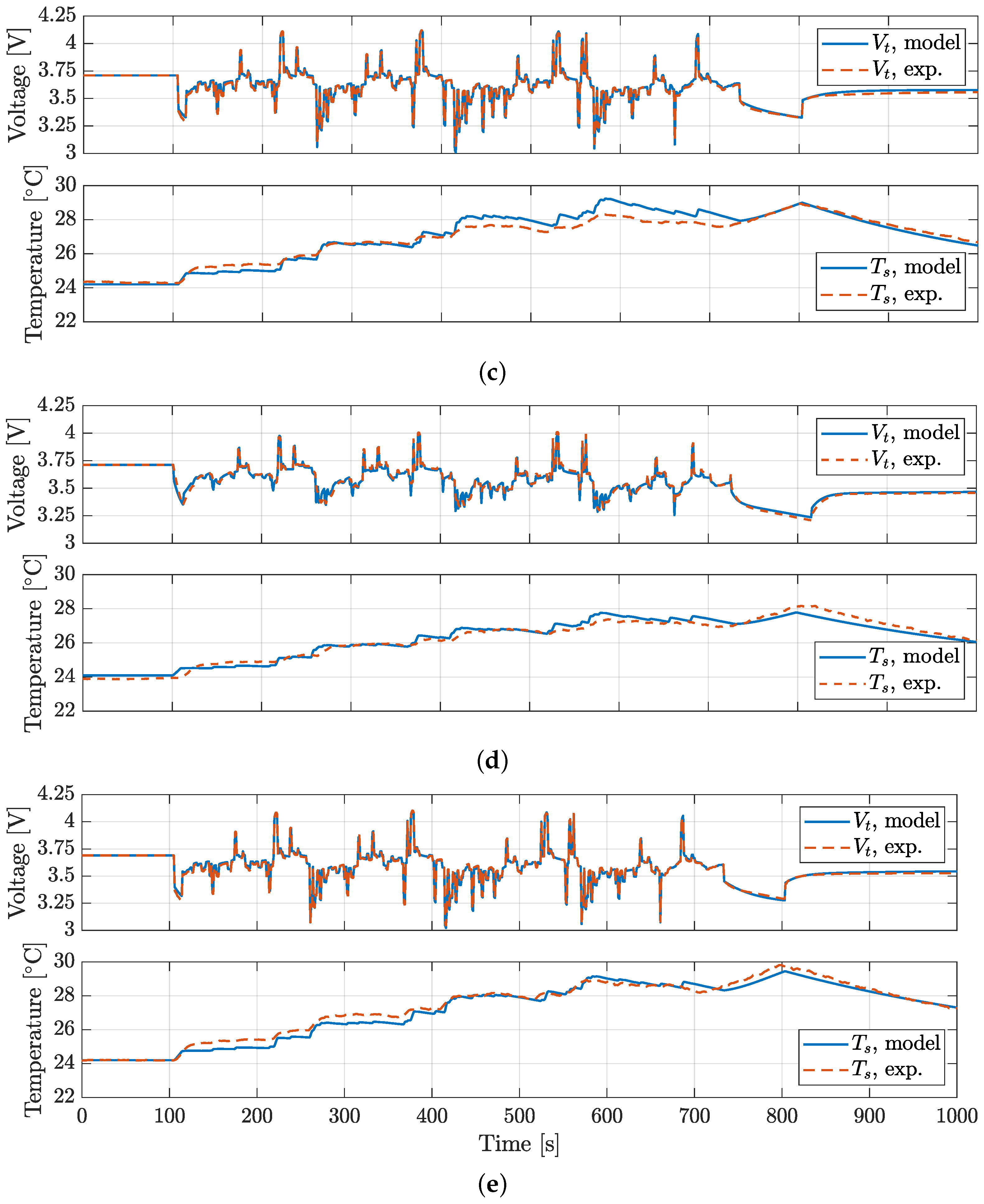
4. Model Validation

To validate the battery model, four different load profiles were considered. The first and the second were taken from common automotive sector-oriented testing profiles, the Beijing Dynamic Stress Test (BJDST) and the Federal Urban Driving Schedule (FUDS), respectively [59]. The third profile is called the Non-Dynamic Cycle (NDC), and it accounts for nonintensive electrical device loads, like smartphones or low-usage systems [19]. The fourth is the High-Power Load (HPL) profile, characterized by high-magnitude discharge current peaks (up to 10 C) [16].

The BJDST, FUDS, and NDC profiles were used to validate the model voltage prediction for the batteries considered, while the HPL was also used for the validation of the $T_s$ model prediction. Experimental data were collected by using the testing facility described above, with the thermal chamber air temperature equal to 24 °C. The validation results for the BJDST and FUDS profiles are reported in Figure 10 and Figure 11, while Figure 12 and Figure 13 account for the NDC and HPL profiles, respectively. In

Table 4. The RMSE for the validation profiles considered for the P28A, P28B, P30B, and VTC5D cells.

	BJDST	FUDS	NDC	HPL
	RMSE, Vt	RMSE, Vt	RMSE, Vt	RMSE, Vt	RMSE, Ts
	[mV]	[mV]	[mV]	[mV]	[°C]
P28A	4.4	7.3	17.7	15.4	0.21
P28B	5.7	14.7	12.9	16.5	0.30
P30B	9.8	12.1	17.7	17.8	0.20
VTC5D	5.3	8.8	13.6	15.9	0.25

, the root mean square error (RMSE) values for the various profiles tested are reported.

The results show that voltages are predicted with an RMSE lower than 20 $\mathrm{m}$$\mathrm{V}$, while $T_s$ prediction presents an RMSE lower than $0.3$ $\mathrm{K}$. It is worth noting how the ECM could be further improved. In particular, the actual Coulomb counting-based SoC estimation could be enhanced by using an optimization routine (e.g., Kalman filter). In this way, the dependence of the battery capacity on the load could be better accounted for; in the actual work, a charge/discharge $\eta$ equal to $0.9$ was considered. The P30B cell shows the largest RMSE in the voltage evolution, which could be related to the nonlinearity of the parameters with the operational current (which could call for a current-dependent estimation of the parameters of the $RC$ ECM) and also to a hysteretic behavior not considered in the model (indeed, a hysteresis term in the $V_t$ prediction could be considered, as in [19]). Moreover, the battery impedance could be nonlinear with the operational current, thus resulting in the need for a current-dependent estimation of the parameters of the $RC$ ECM. Regarding the thermal validation test, the relative error of the surface temperature prediction is lower than 5 % of the total $\Delta T_s$ experienced by the cells in operation.

5. Conclusions

Four different market-available 18650 Li-ion cells, including the Molicel P28A, P28B, and P30B and the Sony Murata VTC5D, were tested and characterized. The CC discharge performances were measured for all the cells at operating temperatures of 5 °C, 25 °C, and 40 °C and C-rates of 0.5 C, 1 C, 3 C, and 5 C. The performance spread was quantified as the standard deviation over a sample of three cells per model. The capacity tests showed that in the case of the P28A and P28B types at an air temperature of 25 °C, a 4% drop in the CC discharge capacity with respect to the nominal value appeared at 1 C and an 8% drop appeared at 5 C. Conversely, the P30B and VTC5D cells showed a smaller capacity drop at 25 °C, which varied with the discharge C-rate, being 4% at 5 C. The tests also showed that low temperatures affected the battery discharge CC capacity more than high temperatures. On the other hand, operating the batteries at high discharge C-rates at 5 °C resulted in slightly higher capacities; in fact, high discharge currents warm up the cells, providing a better performance temperature.

A second-order $RC$ ECM was characterized: first, the OCV curves were measured through a pseudo-$U_{oc}$ technique; then, the ECM parameters were extrapolated by using a MATLAB-based algorithm from GITT tests at various temperatures and SoC values. The comparisons of the values of the circuit parameters reported in

Table A1. The ECM parameters for the P28A cell model.

	Tc = 5 °C
	Discharge						Charge
SoC	Rs	R1	C1	R2	C2		Rs	R1	C1	R2	C2
	[Ω]	[Ω]	[F]	[Ω]	[F]		[Ω]	[Ω]	[F]	[Ω]	[F]
0.1	0.0271	0.0308	1173	0.0196	21,970		0.0266	0.0433	8526	0.0355	24,350
0.2	0.0263	0.0219	1412	0.0211	33,364		0.0242	0.0662	4058	0.0281	21,050
0.3	0.0264	0.0230	1573	0.0225	42,927		0.0222	0.0570	512	0.0155	20,215
0.4	0.0269	0.0216	1197	0.0154	40,665		0.0218	0.0171	886	0.0268	16,880
0.5	0.0272	0.0178	819	0.0130	33,119		0.0217	0.0132	823	0.0110	20,650
0.6	0.0273	0.0152	646	0.0190	23,145		0.0208	0.0127	941	0.0092	21,596
0.7	0.0283	0.0134	775	0.0325	15,821		0.0227	0.0148	1085	0.0135	31,539
0.8	0.0305	0.0183	959	0.0397	11,399		0.0284	0.0114	1531	0.0140	34,055
0.9	0.0313	0.0215	999	0.0180	24,522		0.0331	0.0059	2139	0.0096	22,909
	Tc = 25 °C
	Discharge						Charge
SoC	Rs	R1	C1	R2	C2		Rs	R1	C1	R2	C2
	[Ω]	[Ω]	[F]	[Ω]	[F]		[Ω]	[Ω]	[F]	[Ω]	[F]
0.1	0.0191	0.0128	2345	0.0101	21,935		0.0166	0.0098	1141	0.0110	38,210
0.2	0.0170	0.0083	1844	0.0080	19,192		0.0160	0.0092	2314	0.0109	53,291
0.3	0.0165	0.0106	2187	0.0101	29,387		0.0155	0.0069	1735	0.0099	38,424
0.4	0.0170	0.0106	1833	0.0069	36,820		0.0152	0.0068	1847	0.0068	34,442
0.5	0.0173	0.0077	1408	0.0063	30,551		0.0152	0.0093	2521	0.0082	49,947
0.6	0.0174	0.0073	1192	0.0121	35,108		0.0154	0.0084	2256	0.0075	45,617
0.7	0.0173	0.0085	1375	0.0193	24,324		0.0155	0.0073	1505	0.0046	36,110
0.8	0.0179	0.0106	1953	0.0125	19,786		0.0161	0.0110	1623	0.0052	43,433
0.9	0.0184	0.0106	1874	0.0056	90,703		0.0148	0.0144	2441	0.0116	63,415
	Tc = 40 °C
	Discharge						Charge
SoC	Rs	R1	C1	R2	C2		Rs	R1	C1	R2	C2
	[Ω]	[Ω]	[F]	[Ω]	[F]		[Ω]	[Ω]	[F]	[Ω]	[F]
0.1	0.0141	0.0169	2955	0.0086	162,380		0.0121	0.0088	1084	0.0203	40,517
0.2	0.0132	0.0094	2871	0.0052	184,930		0.0134	0.0076	2574	0.0142	78,985
0.3	0.0135	0.0092	3330	0.0045	178,230		0.0133	0.0044	1921	0.0121	34,480
0.4	0.0137	0.0101	2264	0.0033	133,110		0.0132	0.0035	1918	0.0063	21,319
0.5	0.0132	0.0082	1705	0.0031	90,442		0.0130	0.0046	2800	0.0059	24,030
0.6	0.0130	0.0068	1995	0.0054	63,078		0.0131	0.0040	2360	0.0050	20,253
0.7	0.0130	0.0094	2733	0.0079	48,266		0.0132	0.0033	2042	0.0038	17,394
0.8	0.0142	0.0085	2367	0.0051	55,187		0.0135	0.0046	2425	0.0050	16,172
0.9	0.0138	0.0074	1858	0.0044	104,600		0.0124	0.0063	2394	0.0096	15,963

,

Table A2. The ECM parameters for the P28B cell model.

	Tc = 5 °C
	Discharge						Charge
SoC	Rs	R1	C1	R2	C2		Rs	R1	C1	R2	C2
	[Ω]	[Ω]	[F]	[Ω]	[F]		[Ω]	[Ω]	[F]	[Ω]	[F]
0.1	0.0307	0.0269	1037	0.0222	16,531		0.0312	0.0194	706	0.0409	16,162
0.2	0.0273	0.0220	1333	0.0262	31,633		0.0290	0.0168	930	0.0295	15,259
0.3	0.0271	0.0227	12,08	0.0227	33,162		0.0264	0.0139	931	0.0114	19,789
0.4	0.0279	0.0197	915	0.0157	25,628		0.0235	0.0135	932	0.0114	19,789
0.5	0.0276	0.0166	657	0.0136	17,738		0.0220	0.0185	921	0.0164	28,506
0.6	0.0207	0.0143	581	0.0197	13,993		0.0206	0.0212	1121	0.0198	34,355
0.7	0.0289	0.0137	744	0.0367	12,739		0.0192	0.0175	1338	0.0114	19,324
0.8	0.0329	0.0214	911	0.0528	9585		0.0179	0.0190	1303	0.0150	17,600
0.9	0.0345	0.0230	817	0.0334	14,201		0.0166	0.0185	1206	0.0160	21,537
	Tc = 25 °C
	Discharge						Charge
SoC	Rs	R1	C1	R2	C2		Rs	R1	C1	R2	C2
	[Ω]	[Ω]	[F]	[Ω]	[F]		[Ω]	[Ω]	[F]	[Ω]	[F]
0.1	0.0178	0.0190	2365	0.0105	46,810		0.0161	0.0110	1094	0.0203	23,947
0.2	0.0161	0.0102	1757	0.0078	27,662		0.0155	0.0113	2165	0.0185	44,449
0.3	0.0159	0.0106	2445	0.0104	34,794		0.0147	0.0071	1525	0.0123	29,553
0.4	0.0162	0.0112	1950	0.0071	42,074		0.0142	0.0065	1385	0.0077	25,390
0.5	0.0163	0.0082	1328	0.0060	37,689		0.0139	0.0095	1699	0.0084	37,180
0.6	0.0164	0.0083	1039	0.0115	35,216		0.0137	0.0099	1510	0.0085	37,336
0.7	0.0171	0.0073	1779	0.0202	23,936		0.0138	0.0080	1058	0.0052	26,508
0.8	0.0177	0.0135	1339	0.0146	16,296		0.0138	0.0118	1304	0.0061	33,520
0.9	0.0181	0.0114	1615	0.0067	59,597		0.0158	0.0130	2103	0.0120	47,036
	Tc = 40 °C
	Discharge						Charge
SoC	Rs	R1	C1	R2	C2		Rs	R1	C1	R2	C2
	[Ω]	[Ω]	[F]	[Ω]	[F]		[Ω]	[Ω]	[F]	[Ω]	[F]
0.1	0.0126	0.0161	2360	0.0084	142,620		0.0120	0.0091	1243	0.0143	32,013
0.2	0.0111	0.0095	1792	0.0047	104,860		0.0116	0.0075	2534	0.0092	75,070
0.3	0.0111	0.0086	2315	0.0046	71,871		0.0116	0.0055	2529	0.0112	59,639
0.4	0.0119	0.0076	2389	0.0048	50,264		0.0112	0.0047	2021	0.0060	41,868
0.5	0.0125	0.0052	1959	0.0050	43,107		0.0106	0.0068	2819	0.0047	53,780
0.6	0.0125	0.0051	2382	0.0094	43,637		0.0100	0.0080	2985	0.0053	78,268
0.7	0.0127	0.0083	3214	0.0138	38,551		0.0110	0.0062	1864	0.0033	111,810
0.8	0.0130	0.0092	2863	0.0091	85,219		0.0114	0.0084	2512	0.0046	136,800
0.9	0.0132	0.0071	2231	0.0056	93,891		0.0116	0.0116	2404	0.0073	74,297

,

Table A3. The ECM parameters for the P30B cell model.

	Tc = 5 °C
	Discharge						Charge
SoC	Rs	R1	C1	R2	C2		Rs	R1	C1	R2	C2
	[Ω]	[Ω]	[F]	[Ω]	[F]		[Ω]	[Ω]	[F]	[Ω]	[F]
0.1	0.0238	0.0311	1356	0.0406	26,412		0.0228	0.0795	4076	0.0190	50,626
0.2	0.0189	0.0218	1160	0.0231	26,096		0.0207	0.0606	4832	0.0319	60,550
0.3	0.0176	0.0211	1146	0.0274	24,765		0.0174	0.0179	1907	0.0353	57,155
0.4	0.0175	0.0211	1011	0.0295	23,330		0.0142	0.0116	1858	0.0184	29,798
0.5	0.0177	0.0188	824	0.0202	15,980		0.0140	0.0134	1026	0.0110	19,511
0.6	0.0180	0.0135	652	0.0200	10,938		0.0137	0.0158	831	0.0128	28,351
0.7	0.0188	0.0147	742	0.0373	10,167		0.0135	0.0203	965	0.0170	38,968
0.8	0.0213	0.0236	1197	0.0512	16,595		0.0137	0.0173	938	0.0089	34,889
0.9	0.0224	0.0244	1100	0.0202	27,749		0.0145	0.0280	1012	0.0135	47,824
	Tc = 25 °C
	Discharge						Charge
SoC	Rs	R1	C1	R2	C2		Rs	R1	C1	R2	C2
	[Ω]	[Ω]	[F]	[Ω]	[F]		[Ω]	[Ω]	[F]	[Ω]	[F]
0.1	0.0170	0.0394	1760	0.0255	49,984		0.0114	0.0345	2178	0.0144	62,725
0.2	0.0118	0.0179	1731	0.0115	64,108		0.0106	0.0164	1909	0.0338	48,519
0.3	0.0110	0.0130	1302	0.0083	43,164		0.0096	0.0064	1763	0.0209	23,110
0.4	0.0105	0.0110	1239	0.0082	29,060		0.0094	0.0041	1100	0.0106	11,786
0.5	0.0116	0.0108	1862	0.0090	19,562		0.0094	0.0046	1170	0.0078	11,054
0.6	0.0119	0.0078	1297	0.0076	16,602		0.0093	0.0068	1062	0.0101	16,393
0.7	0.0120	0.0086	1273	0.0138	26,587		0.0095	0.0060	1109	0.0087	14,093
0.8	0.0127	0.0128	2017	0.0168	21,666		0.0096	0.0054	1227	0.0075	7982
0.9	0.0127	0.0125	1652	0.0069	95,862		0.0103	0.0088	1371	0.0132	10,814
	Tc = 40 °C
	Discharge						Charge
SoC	Rs	R1	C1	R2	C2		Rs	R1	C1	R2	C2
	[Ω]	[Ω]	[F]	[Ω]	[F]		[Ω]	[Ω]	[F]	[Ω]	[F]
0.1	0.0110	0.0274	6336	0.0309	57,321		0.0090	0.0160	1332	0.0651	14,153
0.2	0.0093	0.0131	3732	0.0141	105,080		0.0081	0.0077	1708	0.0662	14,516
0.3	0.0087	0.0103	2516	0.0095	124,580		0.0076	0.0037	1253	0.0245	26,619
0.4	0.0080	0.0083	1943	0.0064	130,980		0.0076	0.0045	900	0.0125	39,521
0.5	0.0084	0.0095	2198	0.0043	90,444		0.0076	0.0061	1006	0.0115	58,670
0.6	0.0092	0.0068	2204	0.0066	75,590		0.0077	0.0070	1493	0.0081	37,061
0.7	0.0093	0.0070	2610	0.0066	78,856		0.0078	0.0054	1540	0.0081	37,061
0.8	0.0095	0.0102	3046	0.0073	75,567		0.0080	0.0045	1549	0.0053	36,016
0.9	0.0095	0.0077	2187	0.0054	129,950		0.0083	0.0083	2227	0.0081	50,669

and

Table A4. The ECM parameters for the VTC5D cell model.

	Tc = 5 °C
	Discharge						Charge
SoC	Rs	R1	C1	R2	C2		Rs	R1	C1	R2	C2
	[Ω]	[Ω]	[F]	[Ω]	[F]		[Ω]	[Ω]	[F]	[Ω]	[F]
0.1	0.0265	0.0330	1125	0.0271	11,198		0.0291	0.0219	658	0.0450	8029
0.2	0.0249	0.0188	1367	0.0154	15,964		0.0266	0.0067	768	0.0324	3196
0.3	0.0238	0.0215	1650	0.0197	25,405		0.0232	0.0073	804	0.0168	5071
0.4	0.0235	0.0243	1814	0.0218	31,775		0.0216	0.0066	1080	0.0144	5541
0.5	0.0238	0.0206	1440	0.0149	30,667		0.0216	0.0096	962	0.0211	6901
0.6	0.0243	0.0173	1222	0.0151	30,607		0.0218	0.0117	647	0.0214	7393
0.7	0.0254	0.0159	1552	0.0287	26,171		0.0227	0.0121	818	0.0128	6113
0.8	0.0273	0.0259	1767	0.0387	20,423		0.0264	0.0160	1208	0.0145	8581
0.9	0.0294	0.0259	1251	0.0154	34,463		0.0402	0.0245	2300	0.0450	17,704
	Tc = 25 °C
	Discharge						Charge
SoC	Rs	R1	C1	R2	C2		Rs	R1	C1	R2	C2
	[Ω]	[Ω]	[F]	[Ω]	[F]		[Ω]	[Ω]	[F]	[Ω]	[F]
0.1	0.0227	0.0165	2772	0.0123	15,823		0.0163	0.0358	2089	0.0175	62,603
0.2	0.0176	0.0089	1832	0.0066	19,355		0.0154	0.0133	2257	0.0234	51,085
0.3	0.0158	0.0105	1741	0.0078	17,670		0.0147	0.0106	1727	0.0230	24,814
0.4	0.0151	0.0123	1760	0.0092	17,286		0.0144	0.0070	1581	0.0118	15,220
0.5	0.0156	0.0086	1208	0.0097	13,320		0.0144	0.0082	1632	0.0103	16,589
0.6	0.0160	0.0079	1198	0.0186	17,363		0.0146	0.0084	1337	0.0094	16,235
0.7	0.0160	0.0114	1898	0.0259	24,139		0.0150	0.0080	1328	0.0057	14,737
0.8	0.0167	0.0146	2295	0.0157	18,389		0.0158	0.0115	1324	0.0058	21,896
0.9	0.0174	0.0127	1965	0.0061	37,337		0.0137	0.0197	1617	0.0121	41,477
	Tc = 40 °C
	Discharge						Charge
SoC	Rs	R1	C1	R2	C2		Rs	R1	C1	R2	C2
	[Ω]	[Ω]	[F]	[Ω]	[F]		[Ω]	[Ω]	[F]	[Ω]	[F]
0.1	0.0150	0.0184	2727	0.0086	80,205		0.0116	0.0193	1153	0.0372	18,047
0.2	0.0138	0.0093	2013	0.0043	44,757		0.0117	0.0099	1311	0.0184	40,515
0.3	0.0127	0.0083	1614	0.0041	30,351		0.0120	0.0078	1806	0.0160	55,242
0.4	0.0124	0.0089	1788	0.0060	20,576		0.0123	0.0069	1619	0.0083	45,626
0.5	0.0133	0.0063	1975	0.0066	16,017		0.0122	0.0084	1929	0.0078	38,101
0.6	0.0133	0.0057	2361	0.0062	21,600		0.0123	0.0068	1826	0.0065	32,643
0.7	0.0134	0.0090	3291	0.0090	31,691		0.0127	0.0060	1701	0.0040	34,223
0.8	0.0137	0.0096	2348	0.0056	21,288		0.0131	0.0083	1671	0.0044	39,989
0.9	0.0141	0.0058	2081	0.0039	10,820		0.0116	0.0142	1904	0.0087	61,896

show that the P30B cells exhibited lower $R_s$ values; in addition, $R_s$ variations with temperature were smaller than in the other cells.

The entropic term was measured by using a PAM approach. This shortened the time needed to measure the temperature derivative of the OCV at various $SoC$ values, without the need for expensive equipment such as calorimeters or complex modeling. The results showed good agreement with the literature for NMC-based cells.

The thermal behavior of the cells was described with a thermal lumped parameter model, which was characterized by using only temperature data. The coupled model was validated against three dynamic load profiles and one non-dynamic load profile. The cell voltages were predicted with an RMSE lower than 20 mV, while the battery surface temperature prediction RMSE was lower than 0.3 K. Further developments of the ECM could use a Kalman filter to predict the battery $SoC$ over longer simulations and improve the circuit, taking into account voltage hysteresis effects.

As a final remark, the overall performances of the Molicel P28A and P28B and the Sony Murata VTC5D were fairly close; in particular, given the same current load profile, overvoltages were similar, thus giving a similar thermal behavior. On the contrary, the Molicel P30B, considering its higher nominal capacity, resulted in lower overvoltages and in a lower temperature rise on the same testing profile.