Abstract
The continuing increase in pollutant emissions requires the use of alternative power sources. This includes the use of electric or hybrid vehicles whose energy storage system is based on batteries of various types, including lithium-ion batteries. The optimum operating temperature is between 15 °C and 35 °C. Too high temperatures can lead to catastrophic phenomena such as thermal runaway. The thermal gradient within the system should not exceed 5 °C. An effective Battery Thermal Management System can mitigate this problem. This study analysed a lithium-ion battery with a bag structure. Temperature control was evaluated using a passive (low-cost) system with phase-change materials (PCMs). The material chosen was n-octadecane (paraffin) due to its thermophysical properties and market price. Four different cooling methods were analysed, including air, fins, pure PCM, and a mixed system of single cells and small battery packs. The results show that an undesirable temperature peak around 50 °C (323.15 K) can occur at hot spots. The best system for containing the temperature inside the battery pack is the PCM cooling system with fins. The optimum fin thickness is 1.5 mm. To contain the temperature inside the battery pack, the number of fins studied is 10, while the best temperature containment is achieved with n+ 1 plates, where n is the number of cells.
1. Introduction
The transport sector is one of the major emitters of pollutants and a large contributor to global warming. To reduce climate-changing emissions, the quickest solution is to improve the conversion efficiency of conventional vehicles [1,2]. Fossil-fuelled vehicles consume large amounts of fuel, and overall efficiency is limited to 40 percent or less [3]. For the combined reduction in pollutant and climate-altering emissions, the plausible solution lies in the transition to alternative fuels, such as biofuels, green hydrogen, etc. [4,5]. The use of electric vehicles could also be advantageous as an alternative system to fossil fuels and to complement other alternative propulsion systems [4,6]. For this reason, manufacturers have shown increasing interest in the development and construction of electric cars in recent decades. Despite the many advances, there are still points that can be worked on and improved, such as long charging times, limited range, and poor battery performance due to operating temperatures [7]. The most important is poor battery efficiency. When operating at high temperatures, user safety is not guaranteed. High temperatures have the most destructive effect on battery cell and module performance, as they can lead to thermal loss, fading, limited range, and safety issues [8,9,10,11,12]. Thermal runaway (TR) under stress conditions can shorten battery life. It can also create a risk of fire or explosion [12]. Mainly, three macrocategories of abuse lead to the phenomenon of TR. Mechanical abuse is by far the most complex to predict, and the Battery Management System (BMS) fails to intervene promptly [13,14]. It was also found that thermal leakage temperature varies according to the state of charge [15]. The main parameters to consider in thermal management systems for electric vehicles are battery life, battery weight, compactness, maximum battery temperature, temperature gradients within cells and modules for uniform temperature distribution, safety, range, and cost [16,17]. Better performance from a power and energy density perspective is driving the electric vehicle world to use technologies such as NMC (Nickel Manganese Cobalt) and NCA (Nickel-Cobalt-Aluminium) to produce cells. The benefits of using LFP (Lithium Iron Phosphate) cells include smaller batteries and, thus, more compact electric vehicles [18]. The ideal working temperature for lithium-ion cells is between 15 and 35 °C (288–308 K) [17]. Failure to meet this range may cause problems with the durability and safety of the cell. Even in extreme cold weather conditions (−20 °C–253.15 K), the cell will suffer problems related to improper storage [19]. However, the loss of capacity is attributed to the loss of lithium and the reduction in active material within the battery [20], while the origin of the power reduction is the increase in the cell’s internal resistance due to high temperatures [21]. Another problem arises from the non-uniformity of temperature between the cells of the battery pack and within the cell itself. The maximum acceptable temperature difference between the cells of the battery pack and the battery as a whole is 5 °C to avoid any performance problems [17,22]. The primary objective of a BTMS (Battery Thermal Management System) is to maintain the batteries at an optimal operating temperature with uniform temperature distribution throughout the cell and pack. The classification of BTMSs can be based on the location of heat removal (internal or external) and whether it is passive (use of the surrounding environment) or active (cooling with forced fluids) [23]. A comprehensive review of cooling techniques for BTMSs has been extensively studied in the literature [24,25,26,27,28,29]. A review work on the battery cooling solution proposed by Wazeer et al. pointed out that most commercial vehicles have passive or active air cooling [30]. Due to its low cost and simplicity of design, the air-cooling technique is widely used [10]. Problems arise because of the poor thermophysical properties of air [31] and the difficulty of letting the central part of the battery core cool down [10]. The thermophysical properties of liquids, such as water, provide greater cooling system efficiency than in the case of air alone [32]. These systems have the major flaw of showing a pushed control to avoid extreme temperature spikes. This can be dampened and partly limited using PCMs. PCM-based BTMSs reduce cell temperature rise due to their ability to absorb the latent heat of phase change [33]. Because of the lower complexity of phase-change management and the reduced volumes involved, solid–liquid PCMs are the most widely used. These materials can be divided into three main groups: organic (paraffin, non-paraffinic compounds such as fatty acids), inorganic (hydrated salts, metals), and their eutectic mixtures. PCMs with a high latent heat can significantly reduce temperature and temperature difference, promoting a uniform distribution within modules and individual cells [34]. The physicochemical properties of PCMs, such as thermal conductivity, latent heat, and melting temperature, have an important effect on the performance of BTMSs. Geometric parameters such as thickness, contact area, number of layers, structure, etc., are also important [35]. Extreme conditions of use and consequent safety issues require the optimisation of the properties of PCM materials [36]. It is necessary to implement thermal conductivity enhancement (TCE) methods in PCMs. To improve material performance, the addition of materials with high thermal conductivity has been considered to increase the heat transfer rate. The inclusion of fins, beads, or metal powders leads to a 60–80% increase in overall thermal conductivity [37]. Finning can increase the heat transfer area on the side with lower conductivity [38]. Thanks to optimisation procedures, thermal efficiency can be increased by up to 24% [39]. The goal is to integrate a passive thermal energy storage system with a PCM structure with electrical energy storage systems in HEVs. By removing heat, the overall efficiency of the vehicle can be improved. The main novelty of this research work concerns the use of a passive fin system with phase-change materials to control the temperature uniformity of the bag cells under normal operating conditions by working on several parameters (fin thickness, number of fins, fin spacing, C-rate). These results can be considered, starting with a single-cell study and then scaling up to battery packs of a few elements, due to issues of computational cost and geometrical expediency. This study will be developed further by simplifying the geometry of a battery pack system to observe the scale-up of a passive battery system under extreme working conditions.
2. Material and Methods
The objective of the present work is to implement an effective cooling system with PCM and finned housings for a single cell and a battery pack. The proposed model for the thermal behaviour of the battery pack was built with Ansys Fluent (USA), and validation was carried out with experimental data from the literature.
2.1. Geometry of the Model
The proposed model and the procedure for identifying the equivalent circuit parameters were applied to two Nickel Manganese Cobalt (NMC) cells with nominal voltage and capacity of 3.70 V and 59.3 Ah, respectively [40]. Table 1 and Table 2 show the geometric and electrical parameters of the pouch cell studied. The cell has a pouch structure with the same side terminals, which is a typical solution for automotive applications. The literature highlights how the capacity of tested cells varies according to temperature and discharge current [40]. The pouch cell consists of an alternating series of anode–separator–cathode assemblies protected by an aluminium casing. This case is filled with the electrolyte and sealed, leaving the positive and negative terminals exposed [31]. The current-collection tabs are placed on the same side as the active part. The temperature difference is minimal, and the discharge current at which the model must be validated is 1C, at which point the differences are less pronounced. For this reason, it was possible to consider the different tab arrangements as ineffective for successful validation [41]. The model, once validated, is tested under higher-reality conditions with a 2C discharge ratio.

Table 1.
Geometric characteristics of cells [40].

Table 2.
Electrical parameters of cells.
The goal of this research is to minimise the maximum temperature the battery can reach and to optimise the temperature distribution within the cell. These conditions are essential to maximise battery life. Initially, our study involved the analysis of a single cell subjected to different cooling systems, then the cooling system was developed for the battery pack (consisting of three cells placed in series). The phase-change material was placed in direct contact with the walls of the active part of the battery pack. Then, an aluminium layer (metal fins—thermal conductivity 160 W/mK, specific heat 903 J/kgK, density 2700 kg/m3) was added to increase the heat exchange surface between the cell and the PCM. To demonstrate the effect of increasing the exchange surface area on the thermal behaviour of the battery, it was decided to adopt a geometry that was the perfect combination of PCM and heat sink, as shown in Figure 1. The choice of size was largely arbitrary but inevitably influenced by the physical and computational limitations of the problem. To ensure good stability in solving the problem, very thin volumes do not allow proper mapping of the geometry. As can be seen in Figure 1, the plates that act as supports for the fins have been placed on the faces of the cell, leaving the narrow sides and the base of the cell free. The configuration chosen for the battery pack is a 1P3S, which is simply three batteries connected in series. This series arrangement of the cells ensures that the voltage of the entire module is equal to the sum of the nominal voltages of the individual cells. The bus bar is made of copper, while the case is made of aluminium. To avoid safety issues, a bimetallic transition plate has been installed. The geometry of the simplest case analysed concerns a scheme of three coils arranged in an equidistant series of 4 mm. All the walls have natural convection as the only cooling system.

Figure 1.
Batteries with PCM and finned housing geometry (single cell, with PCM in the external part—orange portion) on the left and battery pack geometry on the right (1P3S); the tab and connections are underlined in red, blue, and grey.
2.2. Thermophysical Properties of the Cell
The typical internal structure of a bag cell consists of alternating layers that identify the outer aluminium, the positive or negative electrode or collector, the positive or negative electrode material, and, finally, the separator. The structure is repeated throughout the development of the cell thickness, alternating the collector materials and the positive and negative electrodes (see Figure 2). The alternation of layers is not directly realisable in the geometry developed in the model; in fact, the active part of the cell is made as a single block. In this case, it is useful to assume that the thermophysical parameters of the cell are invariant with temperature since the variation in the latter over time is of the order of tens of degrees. The value of the product of density and heat capacity is calculated as follows [42]:
where Vi denotes the volume (m3), cp,i is the specific heat (J·kg−1·K−1), and ri is the density (kg·m−3) of a specific component of the battery. Contact resistance for the active part is negligible because all voids are filled by the electrolyte, and its thermal conductivity is of the same order of magnitude as that of other materials [41].
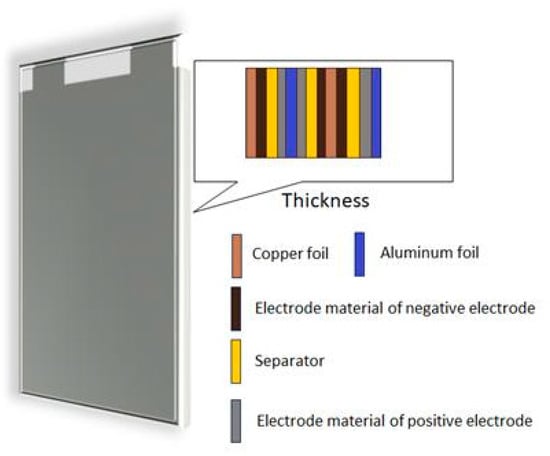
Figure 2.
Aluminium laminated battery 3.2 V/10 Ah LFP [41].
Because Li-ion batteries consist of multiple layers of different materials separated by electrolytes, the thermal conductivity coefficient of the battery is anisotropic. Heat transfer can be divided into parallel heat transfer and series heat transfer [43]. The average coefficient of thermal conductivity in parallel can be determined from Equation (2), and that in series from Equation (3) [43].
, , and are the heat conductivity of the battery materials (W·m−1·K−1) at the directions of x, y, and z, respectively. Lp, Ln, and Ls (m) are the anode slice, cathode slice, and separator slice within the battery, respectively. Since the control volume is extremely small compared to the volume of each component, the above equations work well for estimating physical properties [43]. UDS diffusivity instead of electrical conductivity is used by Ansys (Inc., Canonsburg, PA 15317, USA) in the active area to consider both materials (the collector and the electrode). Equation (4) was used to calculate the values of UDS0 and UDS1. In the equation, UDS0 is the positive side diffusivity (m2/s), σ is the electric conductivity (S·m−1), δ is the thickness, and subscripts c and e denote the collector and electrode (m), respectively. An analogue equation was used to estimate UDS1, the negative side diffusivity [44].
The pouch cell studied has dimensions of 150 × 100 × 6.67 mm in terms of W × H × T, with a weight of 237 g and a NMC chemistry [45]. Table 3 shows the main details of the pouch cell to carry out the simulation.

Table 3.
Envelope cell used for simulation.
The order of magnitude of the contact resistance is comparable to the resistance of the tab; it is an effect that cannot be ignored [46]. The rate of heat generation in the current-collecting tabs due to ohmic and electrical contact resistances, q, can be obtained from the following expression [47]:
where is the resistivity of the current-collecting tab (Ωm), is the resistivity of the electrical contact between the current-collecting tab and the lead wire connecting the battery cell and the external cycler (Ωm) (see Table 4 [48]), and is the current density concerning the cross-sectional area of the current-collecting tab (Am−2).

Table 4.
Parameters related to the heating of current-collecting tabs.
2.3. Physics of the Problem
The first step in numerical simulations is to create a thermal model for the studied batteries. To represent heat generation inside the battery, it is useful to combine electrochemical models with thermal models [19]. During the charging and discharging process, the battery generates heat. Some of this heat is dissipated to the outside and managed by cooling systems. The remaining energy is retained inside the active part [19]. The simplified formulation of the energy conservation equation is given in Equation (6), which gives the temperature distribution inside the battery [23].
The generation of heat of lithium-ion batteries includes both reversible and irreversible heat, depending on the origin of the production process. A localised heat generation equation is shown in Equation (7), which is derived from the electrochemical analysis [49].
The first term refers to the polarisation heat, the second term is the reaction heat, the third term is the joule heat, and the fourth and fifth terms refer to the ohmic losses due to the impedance to the ionic transport in the electrolyte phase.
It is also possible to follow the method proposed by Bernardi et al. [50], where the irreversible heat is calculated with the ohmic production (first term), while the second term expresses the reversible heat.
where is the open-circuit potential and V is the operating potential of the battery cell. The second term is the reversible heat or entropy generation term. The term (dU_OC/dT) is the entropy coefficient, which is a function of the density and temperature of the battery cell. The term (dU_OC/dT) changes sign in charge and discharge modes and becomes zero when there is no current.
The thermal and electric fields of the battery are solved in the CFD (Computational Fluid Dynamic) domain at the battery-cell scale using the following differential equations for a complete view [51]:
In this study, the term abuse is set to zero, meaning the conditions of abuse are avoided. The Equivalent Circuit Model (ECM) is used to analyse the electrochemical behaviour (see Figure 3 [51]).
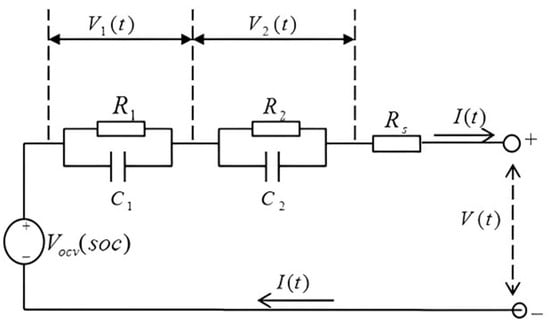
Figure 3.
Electric circuits used in the ECM model.
In the Equivalent Circuit Model (ECM), the electrical behaviour of the battery is simulated by an electrical circuit. ANSYS Fluent adopted a six-parameter ECM model, following the work of Chen [52]. In this model, the circuit consists of three resistors and two capacitors, as shown in Figure 3. The extracted nonlinear open-circuit voltage [ () (V)], series resistor () (Ω), and RC network (, , , and ) (Ω) [52] are functions of the state of charge (SOC) and discharge current. All extracted RC parameters are approximately constant between 20% and 100% SOC and change exponentially between 0% and 20% SOC due to the electrochemical reaction within the battery. One of the limitations of Chen’s model is that it is only applicable to an assigned temperature value, so the parameters can only vary as the state of charge progresses. The physical reality of the problem, however, is quite different, as changes in these parameters depend on both SOC and temperature variations [45]. Under operating conditions, cell operating temperature is the real culprit in the variation in ECM model parameters [40]. The operating range of the battery under examination is around 10 °C (DT) during a complete discharge cycle at 1C. Therefore, it was possible to make an approximation, which was to consider Chen’s model with only the variation in parameters as a function of SOC as a basis. The small parameter differences between the curves for different discharge currents indicate that these parameters are approximately independent of the discharge currents, which may simplify the model [52].
2.4. PCM Model Description
It is difficult to describe the behaviour of phase-change materials because the moving interfaces have a velocity range governed by the heat absorbed or lost [53]. The solidification process is dominated by heat conduction [39], and natural convection acts only at the beginning of the process. Consequently, after these hypotheses, the energy equation becomes the following:
where is the density (kg·m−3) of the PCM, is the thermal conductivity (W·m−1·K−1), is the enthalpy (J), and is the source term. The source term is directly derived from the battery domain in this case, and its value is calculated as discussed above. The liquid fraction of the PCM is a quantity that is calculated iteratively and represents the volume in liquid form; it can range between 0 and 1 in the mushy zone [54]. The sensible enthalpy can be expressed as follows:
where is the reference enthalpy (J) at the reference temperature Tref (K), cp is the specific heat (J·kg−1·K−1), m is the mass of the PCM, is the latent heat of the PCM (J), is the liquid fraction that occurs during the phase change between the solid and liquid states when the temperature is , and is the heat content used in (13). Thus, may be written as follows [55]:
Normal octadecane was chosen for the current study as the PCM. Its melting point is about 27.7 °C (300.85 K), making it more suitable for the current application and temperature control [31,56]. Solidus and liquidus temperatures also depend on the purity of the materials. The values considered for n-octadecane are and . During the phase transition, the PCM does not change its temperature unless the effects are due to impurities in the material itself. Such impurities affect the temperature constancy at the beginning and end of liquefaction, but with a range that varies by more than about 2 °C (275.15 K) ( different from ). Thermal conductivity and density in the mushy phase are defined as follows [57]:
The value of dynamic viscosity was obtained from the literature [58]. A piecewise polynomial function was used to implement the variation in dynamic viscosity, density, and thermal conductivity as a function of temperature. The Differential Scanning Calorimetry of commercial n-octadecane can be obtained from the work published by Abdi et al. [59].
3. Results and Discussion
3.1. Model Discussion
A summary of the main working hypotheses that led to the creation of the model is presented here:
- The boundary between the terminal and the cell itself is a “coupled” type of boundary condition that assures the continuity of the temperature across the defined boundary;
- The initial temperature is considered to be 298 K, which is equal to the ambient temperature;
- No flow field is considered for the liquid phase of the PCM;
- The contribution of thermal radiation is not considered;
- The time step was set to 0.6 s, and the number of time steps was determined based on the different C-rates until the cell was completely discharged. The convergence criterion was set with a residual threshold equal to 10−6 for all computational variables monitored;
- Heat transfer from the end surfaces to the room temperature occurs by free convection, and the heat transfer coefficient was set at 10 W/m2K [40].
The very simplified structure of the battery allows a “structured” type of mesh to be adopted. Figure 4 shows the “Mesh Independent Grid”, and from the results obtained, the total number of elements was 16,300 with 20,526 nodes. Figure 5 identifies the measurement points located on the surface of the cell.
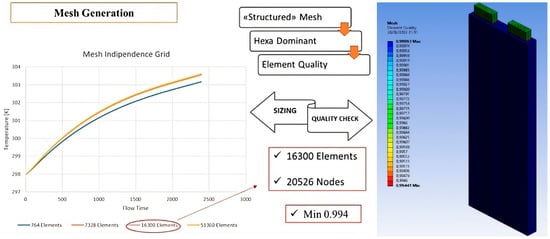
Figure 4.
Evaluation of the mesh independence grid versus temperature.

Figure 5.
Identification of measuring points.
The validation process consists of a comparison between the data obtained experimentally, contained in the study by Perez Estevez et al. [44], and those obtained from the numerical model through the CFD simulation. A pouch cell with a graphite anode and a NMC cathode was used for the experimental activity. The voltage at 100% charged state was 4.2 V, and the depth of discharge varied from 0.9 to 0.4 at a temperature of 25 °C, with the C-rate set to 1.
In this case, a comparative analysis of the temperature and voltage trends of the single cell was performed. For this purpose, the temperature trend of two characteristic points of the cell (the central part of the surface and the area adjacent to the positive tab, as shown in Figure 5) was used as a reference. For the voltage trend, the average trend of the active part of the cell was used as a reference. The average trend of the active part of the cell was used as the reference for the voltage trend. Specifically, the analysis was performed with a discharge current of 1C at a temperature of 25 °C, as shown in Figure 6 and Figure 7.
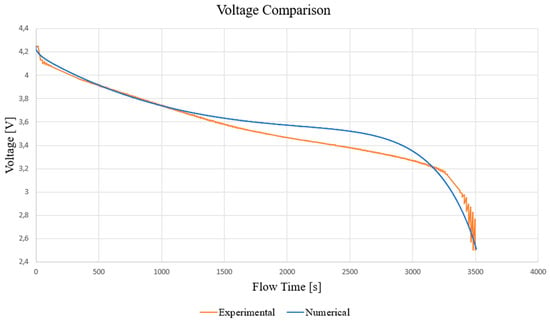
Figure 6.
Voltage comparison at 298 K and 1C rate.
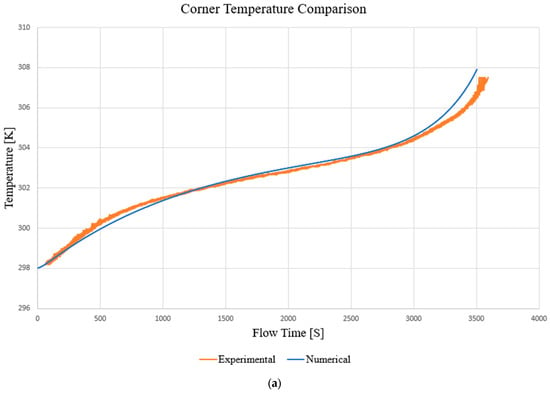
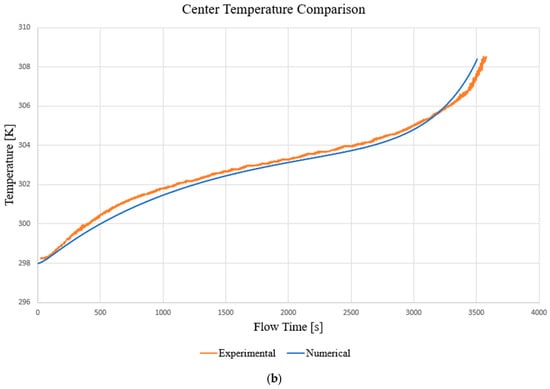
Figure 7.
Corner (a) and centre (b) temperature comparison at 298 K and 1C rate.
The Figure 6 and Figure 7 show the time course of the above quantities. Attention should be paid to the values presented in the final part of the simulation: the canonical discharge time should have been 3600 s (1C rate), but in this case, the simulations automatically stop at a time of 3520 s. The reason for this behaviour lies in the fact that, as a function of the ECM parameters of the state of charge of the battery, in the final phase of the discharge, these parameters grow exponentially, generating instability in the resolution of the characteristic equations [52].
In the phase between 3500 and 3600 s, the state of charge is between 3% and 0%, which are values to be considered categorically avoidable in real battery operation (the optimal state of charge range is between 80% and 20%). The Mean Squared Error (MSE) method is used to evaluate the performance of the model. The final value of the MSE for the battery centre temperature curve is 0.12, a value very close to the optimal value of 0. A similar approach was followed by Panchal et al. [60,61]. The points with the greatest discrepancy are those representing the initial and final parts of the simulation. The highest values of heat generation were obtained under both extreme DOD conditions [62]. Maximum heat production is generated at around 0% of the SOC. The temperature difference may be related to the determination of the set boundary conditions; in particular, the natural convection condition and its coefficient are an approximation of the reality of the problem [44]. The final MSE value for the battery voltage curve is 0.0413, a value strongly biased towards 0. This means that the curve obtained from the numerical model optimally simulates the experimental trend. The animation of the temperature contour of the cell subjected to a discharge current of 2C rate was made. Figure 8 shows the contour of the battery temperature at four significant times: (a) 15 s after the start of the discharge; (b) 102 s after the start of the simulation; (c) 300 s after the start of the simulation; and (d) 1083 s after the start of the simulation.
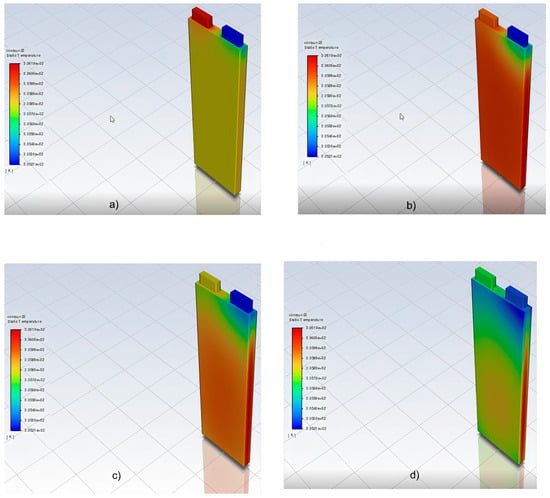
Figure 8.
Simulated temperature contour at different time steps at 298 K and 2C—(a) 450 s, (b) 900 s, (c) 1350 s, (d) 1800 s.
The thermal distribution of the cell can be seen in the Figure 8. In the initial phase of the discharge (a), the greatest concentration of heat is on the positive tab, while the “coolest” region turns out to be the negative one. Shortly after the start of the simulation (b), heat begins to spread evenly over the entire volume of the active part. The only exception is the region adjacent to the negative tab, which has an expected behaviour since contact resistances of a lower order of magnitude have been set in this region. These results are supported by He et al. during the discharge phase [63]. In the third snapshot (c), there is a loss of homogeneity in heat distribution and, hence, temperature. In the last snapshot (d), all regions of the battery assume a heat distribution very similar to that of the final configuration, obtained for a discharge time of about 1800 s. In this case, it can be appreciated that the core temperature is the highest temperature in the cell, which confirms the importance of CFD studies in investigating temperature peaks. All this leads to a sudden rise in the temperature gradient in the battery itself. In the case of a discharge current equal to the 2C rate, the maximum DT is 2.35 °C (275.5 K).
To demonstrate the ability of the proposed design to control battery temperature, numerical simulations were performed for discharge rates at 1C and 2C. A significant decrease in battery surface temperature was observed by switching from natural convection to the use of heat sinks. The core temperature for natural convection was 45.6 °C (318.75 K) (2C rate). In comparison, the temperature for a heat sink without PCM was 39.5 °C (312.65 K) due to the better surface heat transfer. It should also be noted that the two curves follow an almost identical time course, overlapping for more than two-thirds of the simulation. In the last phase, there is a natural separation of the curves given by the instability of the processes inside the cell, with SOC values tending to 0%. The second case analysed is the addition of phase-change material blocks to the cell surfaces. At about 600 s after the start of the discharge, the temperature increase slows down until 1400 s of discharge.
Such behaviour indicates that the material has begun to change state. The latent heat of the phase change “absorbs” the heat generated by the coil, preventing the coil temperature from rising. Due to the high latent heat absorption characteristics, the pure PCM module limits the core temperature below 32.9 °C (306.05 K) (see Figure 9). Unlike heat sinks, the temperature difference between the positive and negative plates is almost eliminated due to the negligible value of the contact resistance. In addition, unlike the cases of natural convection only and convection with fins, the addition of the phase-change material results in long uniformity in the Y direction of the heat distribution. The largest temperature difference occurs between the outer surface and the centre of the active part (along the Z direction of the geometry). The temperature difference achieved with heat sinks is better in absolute terms, but the heat uniformity along the Y direction is not comparable. The thickness of the PCM remains unchanged from the previously analysed case; this choice was made to better visualise the effect of the fins on the thermal behaviour of the battery and the material itself.
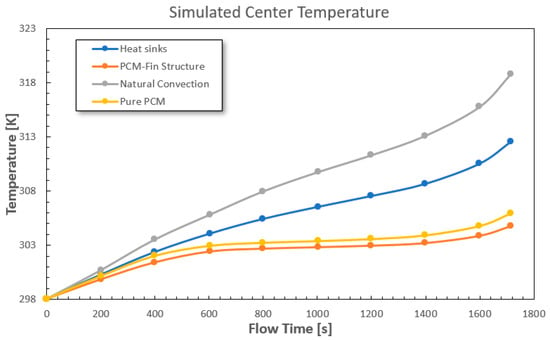
Figure 9.
Simulated centre temperature with various cooling systems—2C discharge current.
The inclusion of a finned structure led to a reduction in the temperature range. In the first part of the discharge, the increased exchange surface area in the PCM has no influence.
However, as the core temperature continued to exceed the minimum temperature of the phase transition, the rate of battery temperature increases at the same state of discharge decreased in the case of the fin structure in the PCM. The phase-transition segment in which the centre temperature increased linearly formed almost a temperature plateau in the case of the fin structure in PCM, whose temperature increase was only 1.2 °C (274.35 K). Although the introduction of the fins slightly reduces the volume of the PCM, the fins affect the thermal behaviour of the PCM by improving heat conduction and natural convection (see Table 5 and Table 6). Notably, the PCM–fin structure further improved the thermal performance of the battery by containing the temperature rise in the mid-to-late discharge process [64].

Table 5.
Summary of the performance of the various cooling systems with 1C discharge current.

Table 6.
Summary of the performance of the various cooling systems with 2C discharge current.
In the following figure (Figure 10), and using Table 5 and Table 6, it is possible to observe the maximum temperature reduction and thermal gradient. Figure 10 visually describes the comparison of different cooling systems for the single pouch cell. From the contour plot, the effectiveness of the system with the PCM and the finned housing can be seen.
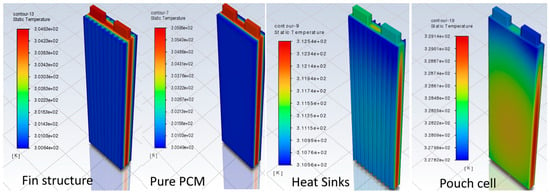
Figure 10.
Cooling system comparison (the performance for the configurations studied decreases to the right).
The purpose of inserting the fins is to increase the heat exchange surface area of the PCM to make up for the reduced thermal conductivity. The resulting useful effect reduces the battery centre temperature in the case of pure PCM. In the case of the finned housing, the phase-change onset time is reduced by about 200 s. In addition, the maximum fraction of liquid formed during discharge reaches a value of 47%, compared to 39% in the case of pure PCM.
3.2. Battery Pack
A battery pack with three pouch batteries in series was analysed by evaluating the cooling system (see Figure 11).
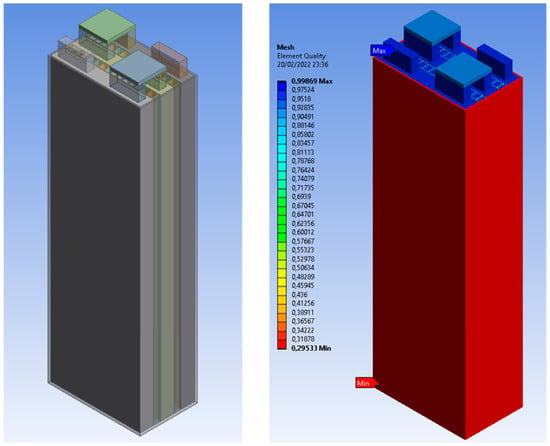
Figure 11.
Battery pack geometry (1P3S). Tab and connections are underlined in light blue and blue. The mesh and the element quality are underlined.
Results are shown for a battery pack without a cooling system, with a PCM-filled housing, and with a PCM-filled finned housing. The housing with PCM is studied by analysing the effect of PCM thickness. The finned housing is studied in terms of cooling by also considering the thickness and spacing of the fins. The main purpose is to monitor the maximum temperature and maximum temperature difference of the housing during the discharge process, as reported before. In the following figure (Figure 12), the time trend of temperature in the battery pack without cooling (natural convection) is shown. The maximum temperature value registered was 45.7 °C (318.85 K), while the maximum temperature difference was 2.5 °C (275.65 K).

Figure 12.
Battery pack temperature distribution (natural convection).
The first battery pack cooling system analysed consists of placing two layers of PCM inside the metal housing. The thickness of the two layers of PCM is 8 mm. Figure 13a shows the maximum temperature trends of the first and second cells inside the battery pack. The two trends are jarring, and this is due to the uneven distribution of the cooling system, as can be seen from the contour (see Figure 13b). All this leads to a lowering of the maximum cell temperature (34.7 °C–307.85 K) but a 28% (3.25 °C–276.4 K) increase in the temperature difference of the whole module.
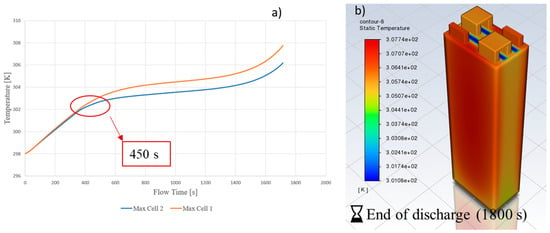
Figure 13.
Battery pack max. temperature (a), battery pack temperature distribution (b) (PCM).
Another interesting aspect to note is the maximum temperature trend of a PCM layer (see Figure 14). The first phase is pure solid, the second phase is what is called the “mushy zone”, in which there is a phase change, and the last phase is pure liquid. The phase change does not occur at a constant temperature because the PCM analysed is not free of impurities (CH3(CH2)16CH3–99%, Sigma Aldrich (St. Louis, MO, USA), CAS 593-45-3).
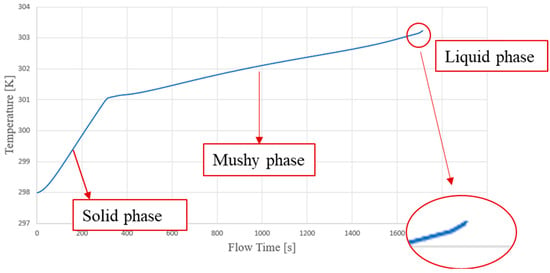
Figure 14.
Maximum temperature distribution—temporal variation.
The choice of PCM thickness is not arbitrary but conditioned by the sensitivity analysis conducted. From Figure 15, the temperature trend shows an increasingly sparse variation as the PCM thickness increases. Both the 8 and 11 mm thicknesses manage to keep the temperature below the desired range. The abatement of temperature difference tends to be unchanged as thickness increases, as confirmed by the literature [64], and the optimal thickness is 8 mm.
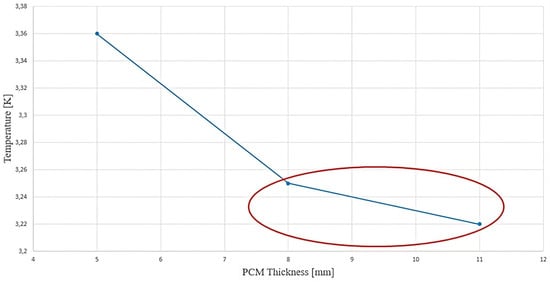
Figure 15.
Maximum temperature difference versus PCM thickness.
The second cooling method analysed is the insertion of a PCM–fin structure between the active parts of the cells.
The PCM blocks are 8 mm thick, and the fin configuration is the same as that used in the single battery analysis. Due to the high latent heat absorption characteristics, the PCM-only module limited the maximum temperature to less than 33.4 °C (306.55 K). Compared to the case without a PCM–fin structure, the temperature curve shows a maximum peak reduction of 26.9 percent, which in absolute terms corresponds to a total reduction of 12.3 °C (285.45 K). The maximum value of the liquid fraction is lower than in the case of pure PCM, but the average distribution of the liquid fraction at the end of the simulation is 14 percentage points higher in the case of the PCM–fin structure. The reason for this is the greater uniformity of heat distribution due to the presence of heat sinks (see Figure 16).
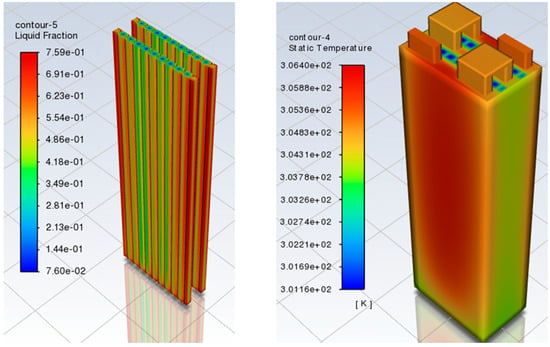
Figure 16.
Battery pack with PCM–fin: liquid fraction (left side), temperature distribution (right side).
A further sensitivity analysis concerns the thickness and number of fins. An increase in thickness with the same spacing leads to an increase in the exchange surface area and a reduction in the volume of PCM. This results in an increase in maximum temperature and maximum temperature difference (see Figure 17). The described behaviour was supported by a previous literature study [64]. With the same thickness, increasing the number of fins produces a similar effect [64]. The only difference concerns the case with 20 fins, where the excessive increase in the exchange surface generates the maximum temperature drop. The best configuration remains that with 10 fins of 1.5 mm thickness each (see Figure 17 and Figure 18).
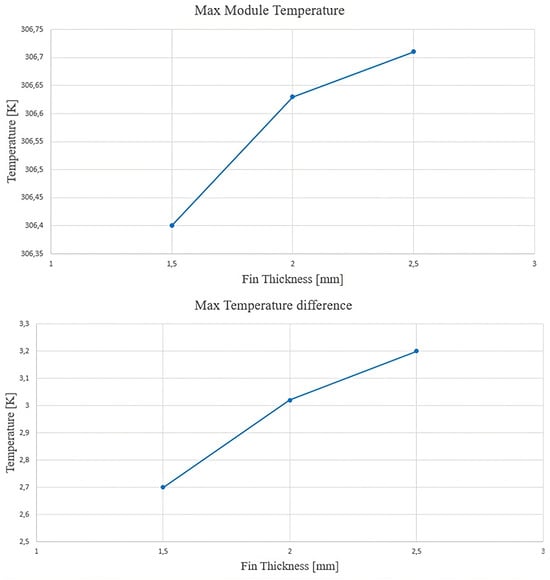
Figure 17.
Maximum temperature for the module versus fin thickness (upper part); maximum temperature difference versus fin thickness (lower part).
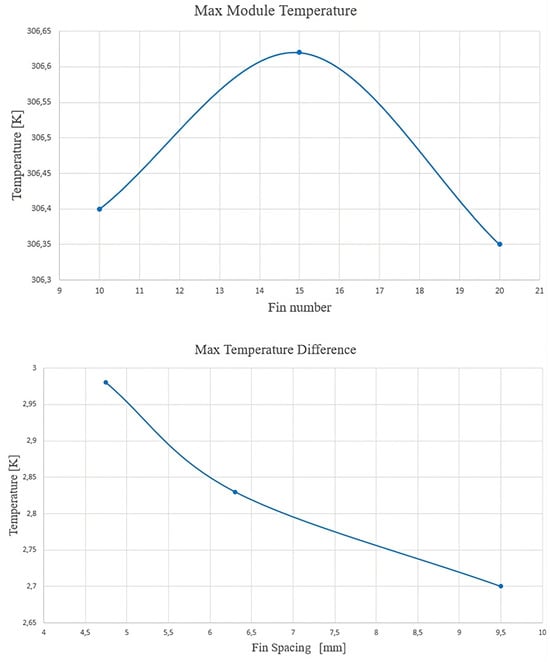
Figure 18.
Maximum temperature for fin number (upper part); maximum temperature difference versus fin spacing (lower part).
Figure 18 shows how the maximum temperature is reached with 15 fins, while the maximum temperature decreases with 10 fins. A fin spacing of 9.5 mm allows for a small temperature difference compared to the other fin spacing values considered.
3.3. Effect of the Number of Plates
Previously, the analysis was performed with n − 1 plates, where n is the number of cells involved in the stack configuration.
As discussed earlier, this approach leads to an increase in the inhomogeneity of the temperature distribution among the cells. The reason is that only one of the three batteries hits the cooling system on both sides. In this further analysis, the effect of placing n + 1 cooling plates inside the battery pack is studied. In this way, all cells are affected by the cooling system on both surfaces. The effects presented in this section concern the maximum temperature reached by the cells, the maximum value of the liquid fraction of the different PCM layers, and the direct comparison of these parameters with previous configurations. To carry out our study, a modification was made to the most efficient cooling system. The latter turned out to be the one with a PCM wing structure (10 metal fins with a thickness of 1.5 mm). Two additional cooling plates were inserted on the side surfaces of the pack. In contrast to what has been seen previously, the maximum temperature of the first cell is always lower than the central one (see Figure 19). The temperature curves coincide throughout the entire discharge time, and in the case of four cooling plates, the maximum liquid fraction of the PCM is lowered overall, which allows the paraffin to be used for much higher discharge currents.
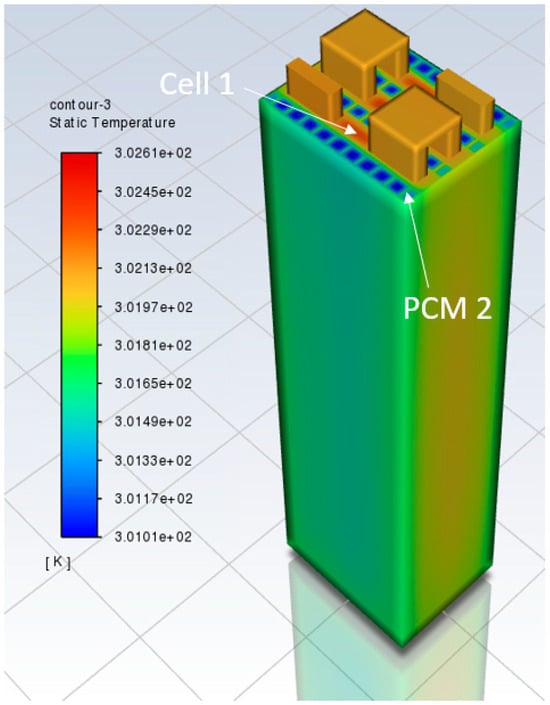
Figure 19.
Battery pack temperature contour with a 4-plate PCM–fin structure at 3600 s, 1C rate (bottom part).
As shown in Figure 20, the first observation that can be made concerns the maximum value reached by the two curves. In the case of four cooling plates, the maximum value is 15.7 percent (as previously reported), while in the case of two cooling plates, the maximum value is 35.8 percent. The layer under consideration is the same and in contact with the same cells. The reason for such a large difference (about 20 percentage points) is the different nature of the heat sources. In the case of two cooling plates, cell 1 is in contact with only one layer, which results in higher heat generation than in the case of four plates. The addition of an extra layer in contact with cell 1 significantly reduces the heat generated by the latter; this is evidenced by the fact that the maximum temperature of cell 1 is even lower than that of cell 2. A second aspect to be considered is the time of onset of the phase change: in the case with two plates, liquefaction starts about 700 s earlier than in the case with four plates. This aspect should not be underestimated, since the use of multiple layers could lead to a wider operating range, especially in cases with discharge currents above 1C and 2C rates. The largest temperature difference occurs between cell 1 and cell 2. The reason is in the physics of the cell. The reason lies in the physics of the problem, where cell 1 is subject to greater cooling. The largest temperature difference is found at the end of the discharge phase and corresponds to about 0.92 °C (274.07 K), a 26.4 percent reduction from the 1.25 °C (274.4 K) obtained in the case with only two plates. The second analysis presented concerns the 2C discharge current. All the considerations presented in the case of the 1C discharge current have the same value from a qualitative point of view. The absolute value of the temperature reached by the first cell at the end of the discharge is 31.6 °C (304.75 K), a reduction of 5.4 percent compared to the 33.4 °C (306.55 K) reached with the two-plate system alone. Cell 2 also experiences a temperature drop to 31.8 °C (304.95 K), a 1.7 percent reduction from 32.37 °C (305.52 K) in the two-plate case. In this case, unlike the 1C discharge, there is no delay in the onset of the melting of the material. The liquid fraction formed in the first layer is 45 percent (PCM layer 1), while the maximum achieved for the second layer is 34.9 percent (PCM layer 2). The greatest temperature difference occurs between cell 1 and cell 2. The reason is the physics of the material. The reason lies in the physics of the problem (cell 1 is subject to greater cooling). The maximum temperature difference is found at the end of the discharge phase and corresponds to about 2.07 °C (275.22 K), a 23.3 percent reduction from the 2.7 °C (275.85 K) obtained in the case with only two plates.
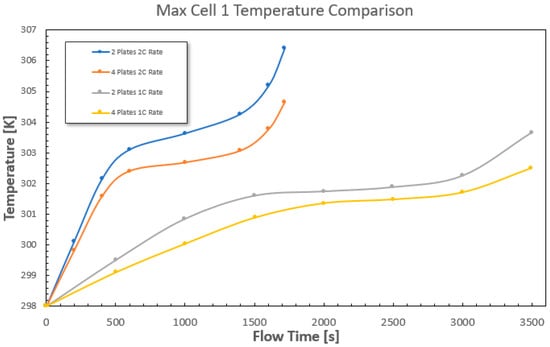
Figure 20.
Battery pack temperature of cell 1 during the discharge time—comparison between plates and C-rates.
4. Conclusions
The model built in this work was aimed at studying the passive cooling of a single LIB cell and a simplified battery pack consisting of three LIB cells, placed in series. Four different cooling methods were studied, including natural convection air, finning, pure PCM, and PCM and finning. The model was validated using experimental tests conducted by Perez Estevez et al. [44]. The purpose of the presented model is to highlight the results obtained during the discharge phase at 1C and 2C. Natural cooling with natural convection alone is insufficient, and the maximum temperature is intolerable for normal system operation, decreasing the battery’s life. The validated model showed high accuracy, except for the last 60 s of discharge (an interval difficult to predict in a real operating regime). The results obtained show a temperature peak near 40 °C (313.15 K) (for the single cell) and near 50 °C (323.15 K). An appropriate cooling strategy must be implemented. The maximum temperature and the maximum temperature difference of the cells were recorded. To optimise the BTMS, a sensitivity analysis of parameters such as PCM thickness, thickness, and distance of the cooling fins was conducted. Some concluding remarks can be made as follows:
- -
- The thickness of the fins is designed into the battery pack, reducing the maximum temperature and temperature difference and increasing the heat exchange area with the PCM. The best configuration was achieved with 10 fins of 1.5 mm thickness each.
- -
- The fin spacing and number of fins are important factors that should be carefully considered when designing the PCM–fin structure. A fin spacing of 9.5 mm results in the smallest temperature difference among the other values considered.
- -
- Adequately increasing the thickness of the PCM can improve thermal performance and is more efficient than other factors. After the PCM thickness exceeded the critical value of 11 mm, the improvement in heat dissipation efficiency was insignificant.
These values are used to dimension a passive system (PCM–fins) to control the maximum temperature of a battery pack of a few elements. Future work will focus on the parallel configuration of the battery pack, increasing the energy capacity of the system (a more realistic battery pack), and also including extreme conditions. In addition, a suitable experimental setup will be set up at the Energy Centre facilities to validate the proposed model.
Author Contributions
Conceptualization, D.P.; Methodology, P.P. and D.P.; Software, P.P.; Validation, P.P. and D.P.; Formal analysis, P.P. and D.P.; Investigation, P.P. and D.P.; Resources, D.P.; Writing—original draft, P.P. and D.P.; Writing—review & editing, D.P.; Supervision, D.P.; Project administration, D.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data will be provided on request.
Acknowledgments
This research is partially derived from the thesis activity conducted by Paciolla and supervised by Papurello [65].
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Acronyms | |
| 1P3S | three batteries connected in series |
| BMS | Battery Management System |
| BTMS | Battery Thermal Management System |
| CFD | Computational Fluid Dynamic |
| DOD | depth of discharge |
| ECM | Equivalent Circuit Model |
| HEV | Hybrid Electric Vehicle |
| LFP | Lithium Iron Phosphate |
| LIB | Lithium-Ion Battery |
| MSE | Mean Squared Error |
| NCA | lithium Nickel Cobalt Aluminium oxide |
| NMC | Nickel Manganese Cobalt |
| PCM | Phase change material |
| SOC | state of charge |
| TCE | thermal conductivity enhancement |
| TR | thermal runaway |
| UDS | User-Defined Scalar |
| Variables | |
| cp | specific heat (J·kg−1·K−1) |
| cp,i, | specific heat for the specific component (J·kg−1·K−1) |
| H | PCM enthalpy (J) |
| Href | reference enthalpy (PCM) (J) |
| i | current density (Am−2) |
| l | thermal conductivity of the liquid phase (W·m−1·K−1) |
| s | thermal conductivity of the solid phase (W·m−1·K−1) |
| L | latent heat of the PCM (J) |
| Ln | cathode slice (m) |
| Lp | anode slice (m) |
| Ls | separator slice (m) |
| m | PCM mass (kg) |
| volumic heat generation rate (W·m−3) | |
| q | heat generation rate (W·m−2) |
| r | resistivity of the current-collecting tab (Wm) |
| rc | resistivity of the electrical contact (Wm) |
| S | source term (W·m−3) |
| t | time (s) |
| T | temperature profile (K) |
| Tl | temperature of the liquid phase (PCM) (K) |
| Ts | temperature of the solid phase (PCM) (K) |
| UDS0 | diffusivity of the positive side (m2/s) |
| UDS1 | diffusivity of the negative side (m2/s) |
| Uoc | open-circuit potential (V) |
| Vi | volume of the specific component (m3) |
| V | battery operating potential (V) |
| DH | latent heat content variation: 0 for the solid phase and 1 for the liquid phase (J) |
| dc | collector thickness (m) |
| de | electrode thickness (m) |
| g | liquid fraction |
| lx | heat conductivity coefficient on the x-axis (W·m−1·K−1) |
| ly | heat conductivity coefficient on the y-axis (W·m−1·K−1) |
| lz | heat conductivity coefficient on the z-axis (W·m−1·K−1) |
| r | density (kg·m−3) |
| ri | density for the specific component (kg·m−3) |
| rl | density for the liquid phase PCM (kg·m−3) |
| rs | density for the solid phase PCM (kg·m−3) |
| sc | electric conductivity of the collector (Sm−1) |
| se | electric conductivity of the electrode (Sm−1) |
References
- Brinklow, G.; Herreros, J.M.; Rezaei, S.Z.; Doustdar, O.; Tsolakis, A.; Millington, P.; Kolpin, A. Impact of Cylinder Deactivation Strategies on Three-way Catalyst Performance in High Efficiency Low Emissions Engines. Chem. Eng. J. Adv. 2023, 14, 100481. [Google Scholar] [CrossRef]
- Avaritsioti, E. Environmental and Economic Benefits of Car Exhaust Heat Recovery. Transp. Res. Procedia 2016, 14, 1003–1012. [Google Scholar] [CrossRef]
- Zahabi, S.A.H.; Miranda-Moreno, L.; Barla, P.; Vincent, B. Fuel economy of hybrid-electric versus conventional gasoline vehicles in real-world conditions: A case study of cold cities in Quebec, Canada. Transp. Res. Part Transp. Environ. 2014, 32, 184–192. [Google Scholar] [CrossRef]
- Zhang, W.; Fang, X.; Sun, C. The alternative path for fossil oil: Electric vehicles or hydrogen fuel cell vehicles? J. Environ. Manag. 2023, 341, 118019. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, P.; Khoshnevisan, A. Dynamic simulation and lifecycle assessment of hydrogen fuel cell electric vehicles considering various hydrogen production methods. Int. J. Hydrogen Energy 2022, 47, 26758–26769. [Google Scholar] [CrossRef]
- Santos, G.; Smith, O. Electric vehicles and the energy generation mix in the UK: 2020–2050. Energy Rep. 2023, 9, 5612–5627. [Google Scholar] [CrossRef]
- Sanguesa, J.A.; Torres-Sanz, V.; Garrido, P.; Martinez, F.J.; Marquez-Barja, J.M. A Review on Electric Vehicles: Technologies and Challenges. Smart Cities 2021, 4, 372–404. [Google Scholar] [CrossRef]
- Ali, H.M. Thermal management systems for batteries in electric vehicles: A recent review. Energy Rep. 2023, 9, 5545–5564. [Google Scholar] [CrossRef]
- Kong, D.; Lv, H.; Ping, P.; Wang, G. A review of early warning methods of thermal runaway of lithium ion batteries. J. Energy Storage 2023, 64, 107073. [Google Scholar] [CrossRef]
- Mallick, S.; Gayen, D. Thermal behaviour and thermal runaway propagation in lithium-ion battery systems—A critical review. J. Energy Storage 2023, 62, 106894. [Google Scholar] [CrossRef]
- Shahid, S.; Agelin-Chaab, M. A review of thermal runaway prevention and mitigation strategies for lithium-ion batteries. Energy Convers. Manag. X 2022, 16, 100310. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, R.; Shen, Z.; Yu, Q.; Xiong, R.; Shen, W. Towards a safer lithium-ion batteries: A critical review on cause, characteristics, warning and disposal strategy for thermal runaway. Adv. Appl. Energy 2023, 11, 100146. [Google Scholar] [CrossRef]
- Christensen, P.A.; Milojevic, Z.; Wise, M.S.; Ahmeid, M.; Attidekou, P.S.; Mrozik, W.; Dickmann, N.A.; Restuccia, F.; Lambert, S.M.; Das, P.K. Thermal and mechanical abuse of electric vehicle pouch cell modules. Appl. Therm. Eng. 2021, 189, 116623. [Google Scholar] [CrossRef]
- Wang, W.; Li, Y.; Cheng, L.; Zuo, F.; Yang, S. Safety performance and failure prediction model of cylindrical lithium-ion battery. J. Power Sources 2020, 451, 227755. [Google Scholar] [CrossRef]
- Ianniciello, L.; Biwolé, P.H.; Achard, P. Electric vehicles batteries thermal management systems employing phase change materials. J. Power Sources 2018, 378, 383–403. [Google Scholar] [CrossRef]
- Pema, T. How to Choose Right Battery for Electric Two-Wheelers, Econ. Times 2023. Available online: https://economictimes.indiatimes.com/news/how-to/how-carbon-emissions-can-also-be-used-to-achieve-green-goals/articleshow/102673617.cms (accessed on 16 August 2023).
- Olabi, A.G.; Maghrabie, H.M.; Adhari, O.H.K.; Sayed, E.T.; Yousef, B.A.A.; Salameh, T.; Kamil, M.; Abdelkareem, M.A. Battery thermal management systems: Recent progress and challenges. Int. J. Thermofluids 2022, 15, 100171. [Google Scholar] [CrossRef]
- Zubi, G.; Dufo-López, R.; Carvalho, M.; Pasaoglu, G. The lithium-ion battery: State of the art and future perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Liu, H.; Wei, Z.; He, W.; Zhao, J. Thermal issues about Li-ion batteries and recent progress in battery thermal management systems: A review. Energy Convers. Manag. 2017, 150, 304–330. [Google Scholar] [CrossRef]
- Ning, G.; Haran, B.; Popov, B.N. Capacity fade study of lithium-ion batteries cycled at high discharge rates. J. Power Sources 2003, 117, 160–169. [Google Scholar] [CrossRef]
- Belt, J.R.; Ho, C.D.; Motloch, C.G.; Miller, T.J.; Duong, T.Q. A capacity and power fade study of Li-ion cells during life cycle testing. J. Power Sources 2003, 123, 241–246. [Google Scholar] [CrossRef]
- Park, C.; Jaura, A.K. Dynamic Thermal Model of Li-Ion Battery for Predictive Behavior in Hybrid and Fuel Cell Vehicles; SAE Technical Paper; SAE Internation: Warrendale, PA, USA, 2003; p. 2003-01-2286. [Google Scholar] [CrossRef]
- Chen, Y.; Evans, J.W. Thermal Analysis of Lithium-Ion Batteries. J. Electrochem. Soc. 1996, 143, 2708–2712. [Google Scholar] [CrossRef]
- Lin, J.; Liu, X.; Li, S.; Zhang, C.; Yang, S. A review on recent progress, challenges and perspective of battery thermal management system. Int. J. Heat Mass Transf. 2021, 167, 120834. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, X.; Negnevitsky, M.; Zhang, H. A review of air-cooling battery thermal management systems for electric and hybrid electric vehicles. J. Power Sources 2021, 501, 230001. [Google Scholar] [CrossRef]
- Sharma, D.K.; Prabhakar, A. A review on air cooled and air centric hybrid thermal management techniques for Li-ion battery packs in electric vehicles. J. Energy Storage 2021, 41, 102885. [Google Scholar] [CrossRef]
- Murali, G.; Sravya, G.S.N.; Jaya, J.; Vamsi, V.N. A review on hybrid thermal management of battery packs and it’s cooling performance by enhanced PCM. Renew. Sustain. Energy Rev. 2021, 150, 111513. [Google Scholar] [CrossRef]
- Murugan, M.; Saravanan, A.; Elumalai, P.V.; Murali, G.; Dhineshbabu, N.R.; Kumar, P.; Afzal, A. Thermal management system of lithium-ion battery packs for electric vehicles: An insight based on bibliometric study. J. Energy Storage 2022, 52, 104723. [Google Scholar] [CrossRef]
- Shen, Z.-G.; Chen, S.; Liu, X.; Chen, B. A review on thermal management performance enhancement of phase change materials for vehicle lithium-ion batteries. Renew. Sustain. Energy Rev. 2021, 148, 111301. [Google Scholar] [CrossRef]
- Phase Change Materials for Battery Thermal Management of Electric and Hybrid Vehicles: A Review—ScienceDirect, (n.d.). Available online: https://www.sciencedirect.com/science/article/pii/S2772427122000869 (accessed on 13 December 2023).
- Landini, S.; Leworthy, J.; O’Donovan, T.S. A Review of Phase Change Materials for the Thermal Management and Isothermalisation of Lithium-Ion Cells. J. Energy Storage 2019, 25, 100887. [Google Scholar] [CrossRef]
- Kim, J.; Oh, J.; Lee, H. Review on battery thermal management system for electric vehicles. Appl. Therm. Eng. 2019, 149, 192–212. [Google Scholar] [CrossRef]
- Maknikar, S.K.; Pawar, A.M. Application of phase change material (PCM) in battery thermal management system (BTMS): A critical review. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Choure, B.K.; Alam, T.; Kumar, R. A review on heat transfer enhancement techniques for PCM based thermal energy storage system. J. Energy Storage 2023, 72, 108161. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, X.; Yang, B.; Cai, S. A review of battery thermal management systems using liquid cooling and PCM. J. Energy Storage 2024, 76, 109836. [Google Scholar] [CrossRef]
- Chen, J.; Kang, S.; E, J.; Huang, Z.; Wei, K.; Zhang, B.; Zhu, H.; Deng, Y.; Zhang, F.; Liao, G. Effects of different phase change material thermal management strategies on the cooling performance of the power lithium ion batteries: A review. J. Power Sources 2019, 442, 227228. [Google Scholar] [CrossRef]
- Xu, Y.; He, C.; Chen, Y.; Sun, Y.; Yin, H.; Zheng, Z.-J. Experimental and numerical study on the effect of the intelligent memory metal fin on the melting and solidification process of PCM. Renew. Energy 2023, 218, 119366. [Google Scholar] [CrossRef]
- Triscari, G.; Santovito, M.; Bressan, M.; Papurello, D. Experimental and model validation of a phase change material heat exchanger integrated into a real building. Int. J. Energy Res. 2021, 45, 18222–18236. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Gagliardi, F.; Verda, V. Maximization of performance of a PCM latent heat storage system with innovative fins. Appl. Energy 2015, 137, 707–715. [Google Scholar] [CrossRef]
- Estevez, M.A.P.; Calligaro, S.; Bottesi, O.; Caligiuri, C.; Renzi, M. An electro-thermal model and its electrical parameters estimation procedure in a lithium-ion battery cell. Energy 2021, 234, 121296. [Google Scholar] [CrossRef]
- Du, S.; Jia, M.; Cheng, Y.; Tang, Y.; Zhang, H.; Ai, L.; Zhang, K.; Lai, Y. Study on the thermal behaviors of power lithium iron phosphate (LFP) aluminum-laminated battery with different tab configurations. Int. J. Therm. Sci. 2015, 89, 327–336. [Google Scholar] [CrossRef]
- Buck, W.; Rudtsch, S. Thermal Properties. In Springer Handbook of Materials Measurement Methods; Czichos, H., Saito, T., Smith, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 399–429. [Google Scholar] [CrossRef]
- Chen, S.C.; Wan, C.C.; Wang, Y.Y. Thermal analysis of lithium-ion batteries. J. Power Sources 2005, 140, 111–124. [Google Scholar] [CrossRef]
- Estevez, M.A.P.; Caligiuri, C.; Renzi, M. A CFD thermal analysis and validation of a Li-ion pouch cell under different temperatures conditions. E3S Web Conf. 2021, 238, 09003. [Google Scholar] [CrossRef]
- Lidbeck, A. Experimental Characterization of Li-Ion Battery Cells for Thermal Management in Heavy Duty Hybrid Application. 2017. Available online: https://publications.lib.chalmers.se/records/fulltext/252994/252994.pdf (accessed on 23 March 2024).
- Wu, B.; Li, Z.; Zhang, J. Thermal Design for the Pouch-Type Large-Format Lithium-Ion Batteries: I. Thermo-Electrical Modeling and Origins of Temperature Non-Uniformity. J. Electrochem. Soc. 2015, 162, A181–A191. [Google Scholar] [CrossRef]
- Yi, J.; Kim, U.S.; Shin, C.B.; Han, T.; Park, S. Three-Dimensional Thermal Modeling of a Lithium-Ion Battery Considering the Combined Effects of the Electrical and Thermal Contact Resistances between Current Collecting Tab and Lead Wire. J. Electrochem. Soc. 2013, 160, A437–A443. [Google Scholar] [CrossRef]
- Lide, D.R. Handbook of Chemistry and Physics, 84th ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Xiao, M.; Choe, S.-Y. Theoretical and experimental analysis of heat generations of a pouch type LiMn2O4/carbon high power Li-polymer battery. J. Power Sources 2013, 241, 46–55. [Google Scholar] [CrossRef]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A General Energy Balance for Battery Systems. J. Electrochem. Soc. 1985, 132, 5–12. [Google Scholar] [CrossRef]
- ANSYS Fluent Advanced Add-On Module, Software Release 17.0. 2016. Available online: https://www.scribd.com/document/344930548/ANSYS-Fluent-Advanced-Add-On-Modules (accessed on 22 March 2024).
- Chen, M.; Rincon-Mora, G.A. Accurate electrical battery model capable of predicting runtime and I-V performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Dutil, Y.; Rousse, D.R.; Salah, N.B.; Lassue, S.; Zalewski, L. A review on phase-change materials: Mathematical modeling and simulations. Renew. Sustain. Energy Rev. 2011, 15, 112–130. [Google Scholar] [CrossRef]
- Voller, V.R.; Prakash, C. A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems. Int. J. Heat Mass Transf. 1987, 30, 1709–1719. [Google Scholar] [CrossRef]
- Al-abidi, A.A.; Mat, S.B.; Sopian, K.; Sulaiman, M.Y.; Mohammed, A.T. CFD applications for latent heat thermal energy storage: A review. Renew. Sustain. Energy Rev. 2013, 20, 353–363. [Google Scholar] [CrossRef]
- Agyenim, F.; Hewitt, N.; Eames, P.; Smyth, M. A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems (LHTESS). Renew. Sustain. Energy Rev. 2010, 14, 615–628. [Google Scholar] [CrossRef]
- Khateeb, S.A.; Amiruddin, S.; Farid, M.; Selman, J.R.; Al-Hallaj, S. Thermal management of Li-ion battery with phase change material for electric scooters: Experimental validation. J. Power Sources 2005, 142, 345–353. [Google Scholar] [CrossRef]
- Caudwell, D.R.; Trusler, J.P.M.; Vesovic, V.; Wakeham, W.A. The Viscosity and Density of n-Dodecane and n-Octadecane at Pressures up to 200 MPa and Temperatures up to 473 K. Int. J. Thermophys. 2004, 25, 1339–1352. [Google Scholar] [CrossRef]
- Abdi, A.; Ignatowicz, M.; Gunasekara, S.N.; Chiu, J.N.; Martin, V. Experimental investigation of thermo-physical properties of n-octadecane and n-eicosane. Int. J. Heat Mass Transf. 2020, 161, 120285. [Google Scholar] [CrossRef]
- Panchal, S.; Dincer, I.; Agelin-Chaab, M.; Fraser, R.; Fowler, M. Experimental and theoretical investigation of temperature distributions in a prismatic lithium-ion battery. Int. J. Therm. Sci. 2016, 99, 204–212. [Google Scholar] [CrossRef]
- Panchal, S.; Dincer, I.; Agelin-Chaab, M.; Fraser, R.; Fowler, M. Thermal modeling and validation of temperature distributions in a prismatic lithium-ion battery at different discharge rates and varying boundary conditions. Appl. Therm. Eng. 2016, 96, 190–199. [Google Scholar] [CrossRef]
- Lin, C.; Wang, F.; Fan, B.; Ren, S.; Zhang, Y.; Han, L.; Liu, S.; Xu, S. Comparative study on the heat generation behavior of lithium-ion batteries with different cathode materials using accelerating rate calorimetry. Energy Procedia 2017, 142, 3369–3374. [Google Scholar] [CrossRef]
- He, T.; Zhang, T.; Wang, Z.; Cai, Q. A comprehensive numerical study on electrochemical-thermal models of a cylindrical lithium-ion battery during discharge process. Appl. Energy 2022, 313, 118797. [Google Scholar] [CrossRef]
- Ping, P.; Peng, R.; Kong, D.; Chen, G.; Wen, J. Investigation on thermal management performance of PCM-fin structure for Li-ion battery module in high-temperature environment. Energy Convers. Manag. 2018, 176, 131–146. [Google Scholar] [CrossRef]
- Paciolla, P. Enhancement of PCM Materials Using Metal Fins in a Battery Thermal Management System, Laurea, Politecnico di Torino. 2022. Available online: https://webthesis.biblio.polito.it/22462/ (accessed on 10 May 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).