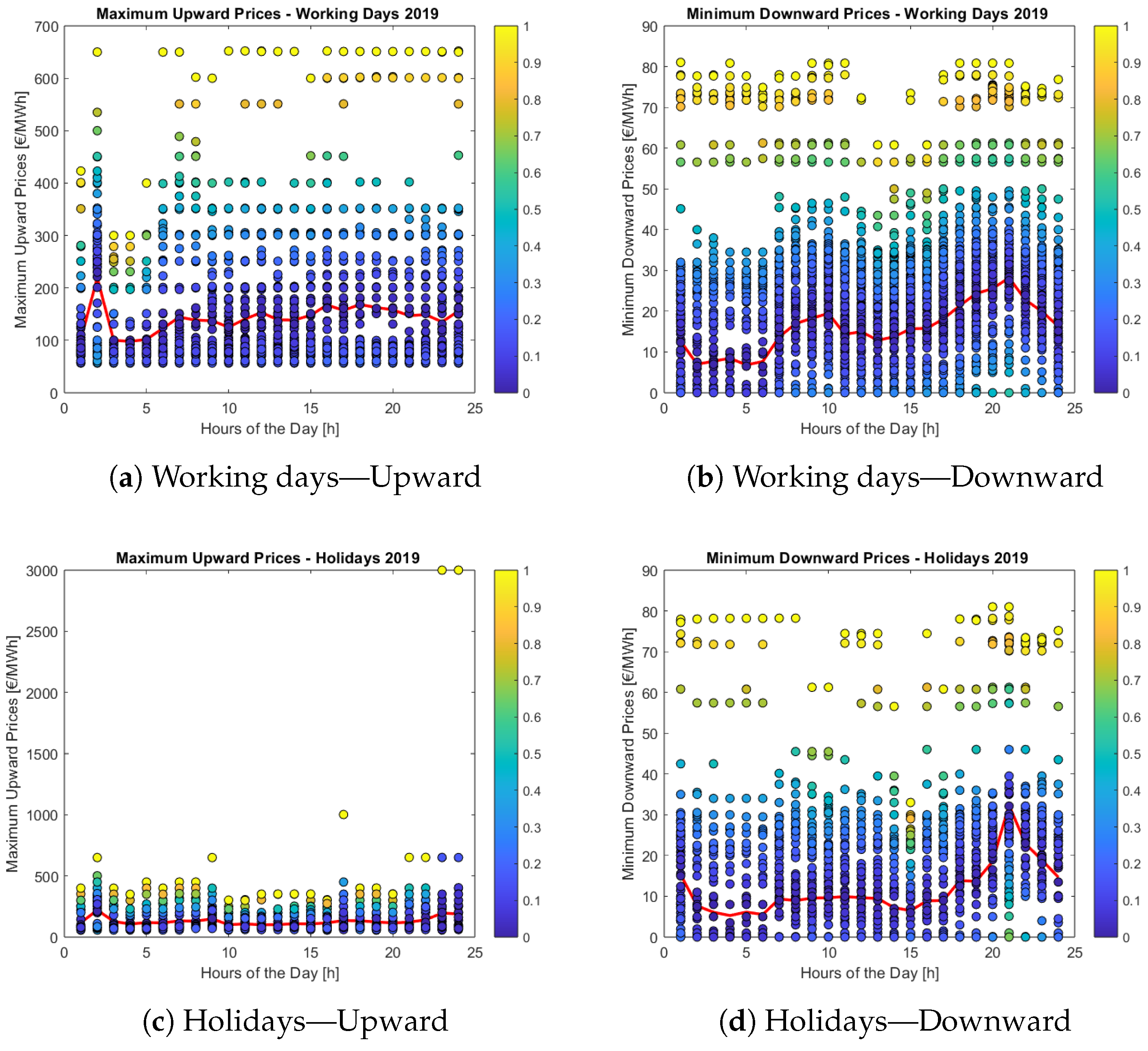
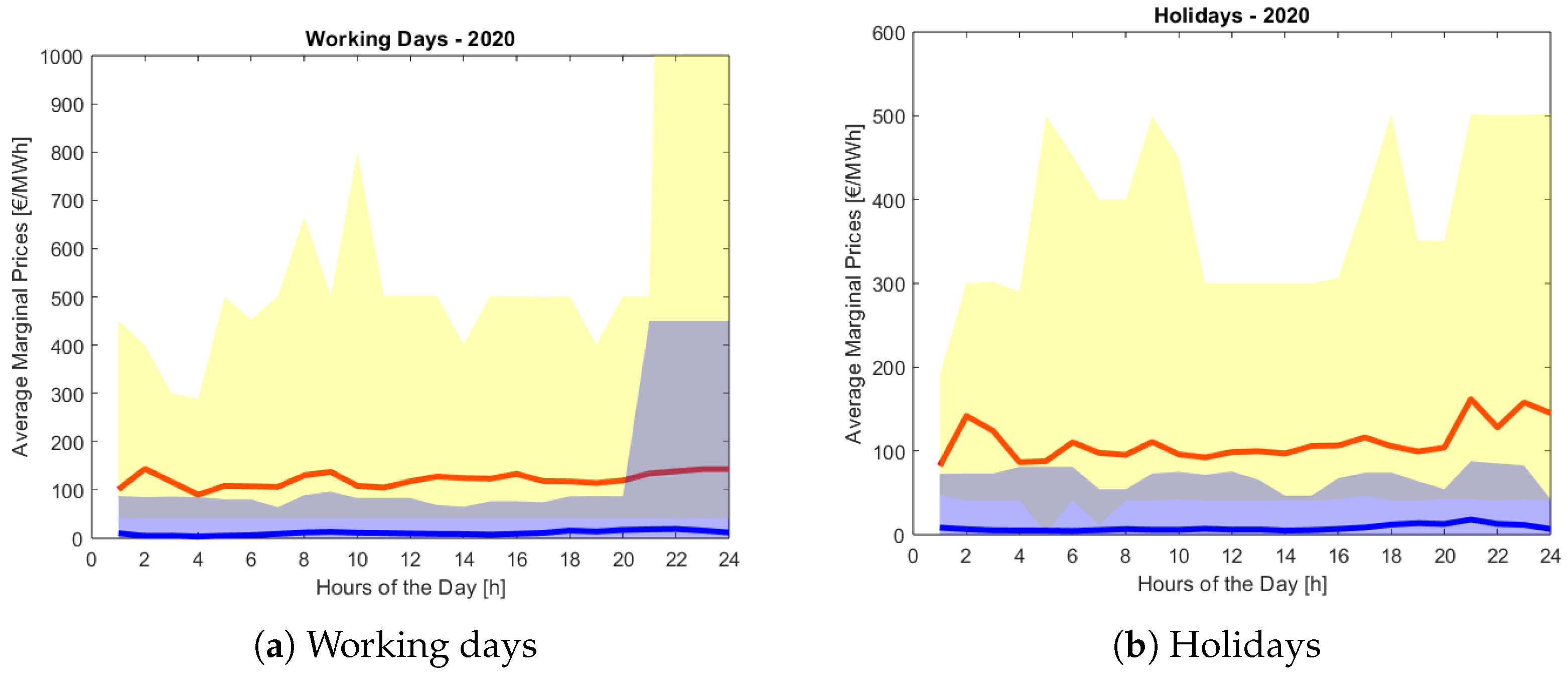
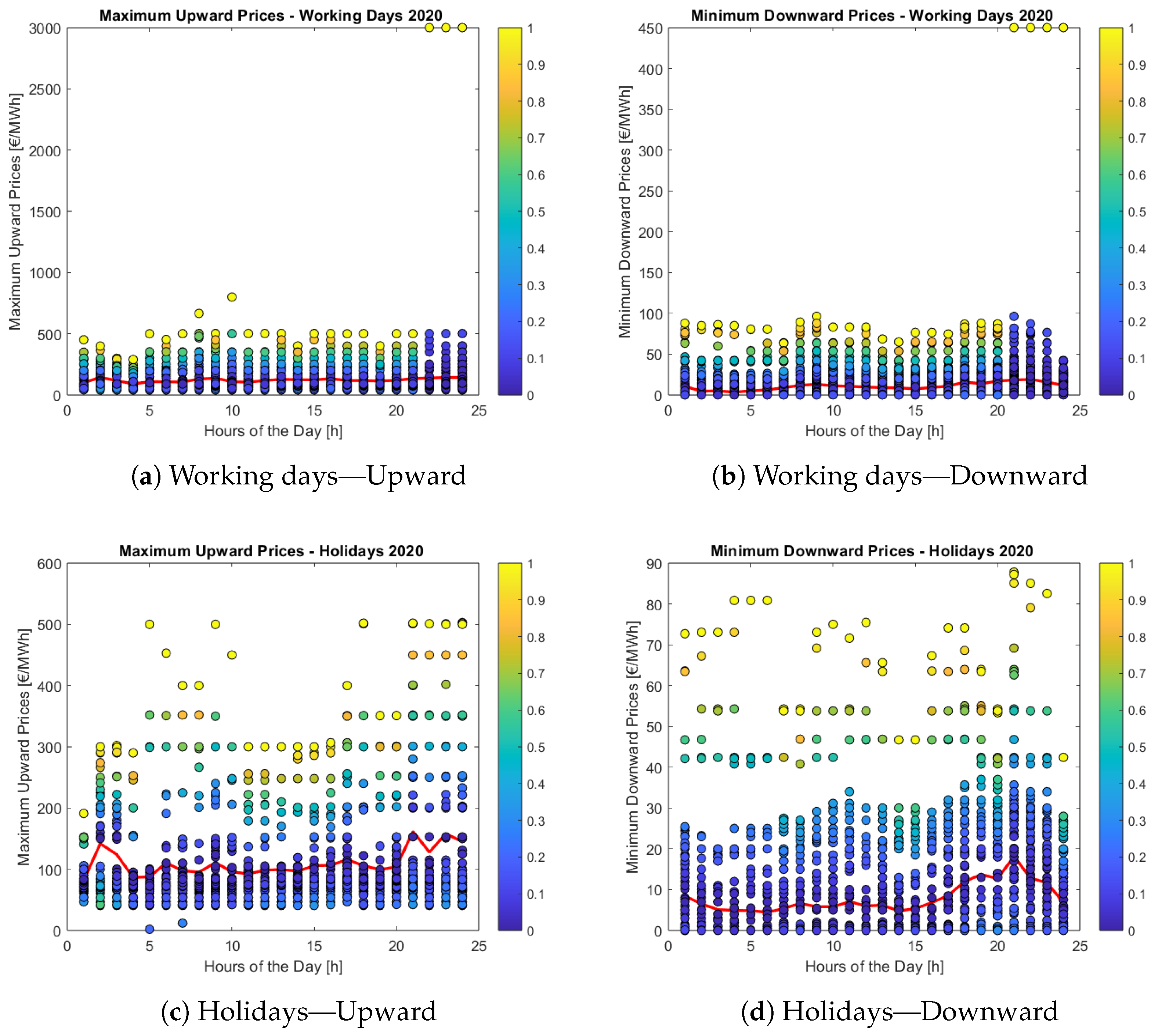
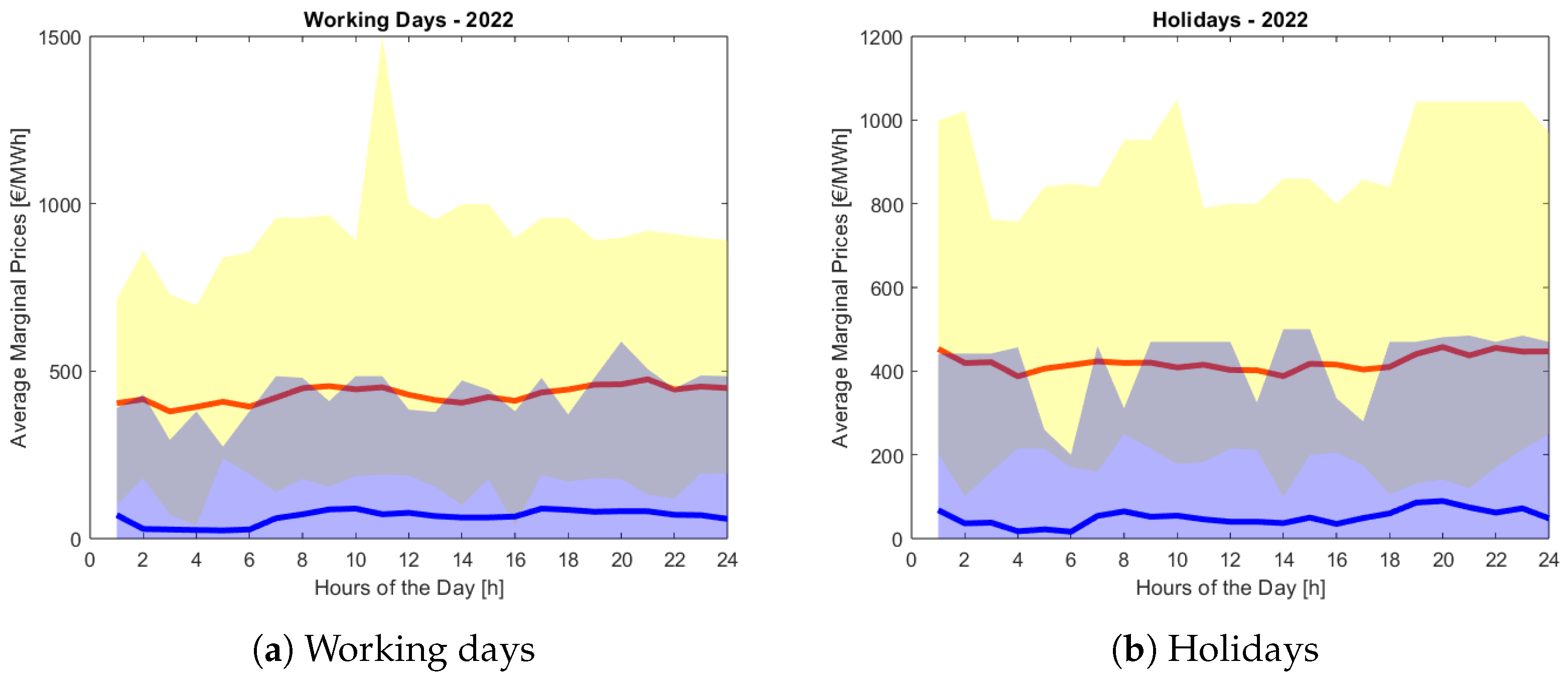
2.2.1. The Italian Electricity Market
The structure of the Italian Electricity Market, assumed as the focus of this paper, is based on Decree No. 79 of 16 March, 1999 [
17]. It is based on two different markets: The Forward Electricity Market (Mercato a Termine dell’Energia) and the Spot Electricity Market (Mercato a Pronti dell’Energia). The Forward Electricity Market is the market where energy trading is based on predetermined prices and terms for future delivery. On the other hand, the Spot Electricity Market is based on the supply and demand curves, which define the market clearing price and quantity. The Italian Spot Electricity Market can be divided into the following sessions:
The Day-Ahead Market, Mercato del Giorno Prima (MGP), is the first market session of the electricity market. It is the auction market where a large amount of energy is generally traded. This market closes at noon on the day before delivery (D-1). Demands can be satisfied by bidding in the electricity pool or through bilateral contracts.
In the Intra-day Market, Mercato Infragiornaliero (MI), the market participants are allowed to adjust their bids defined in the MGP. Opposite to MGP, less energy is usually traded in the MI. It is divided into three MI-A auction sessions and one MI-XBID continuous trading session. Additionally, the submitted supply offer and demand bids are evaluated based on the same criterion defined in the day-ahead market. However, the accepted demand bids are paid at the zonal price.
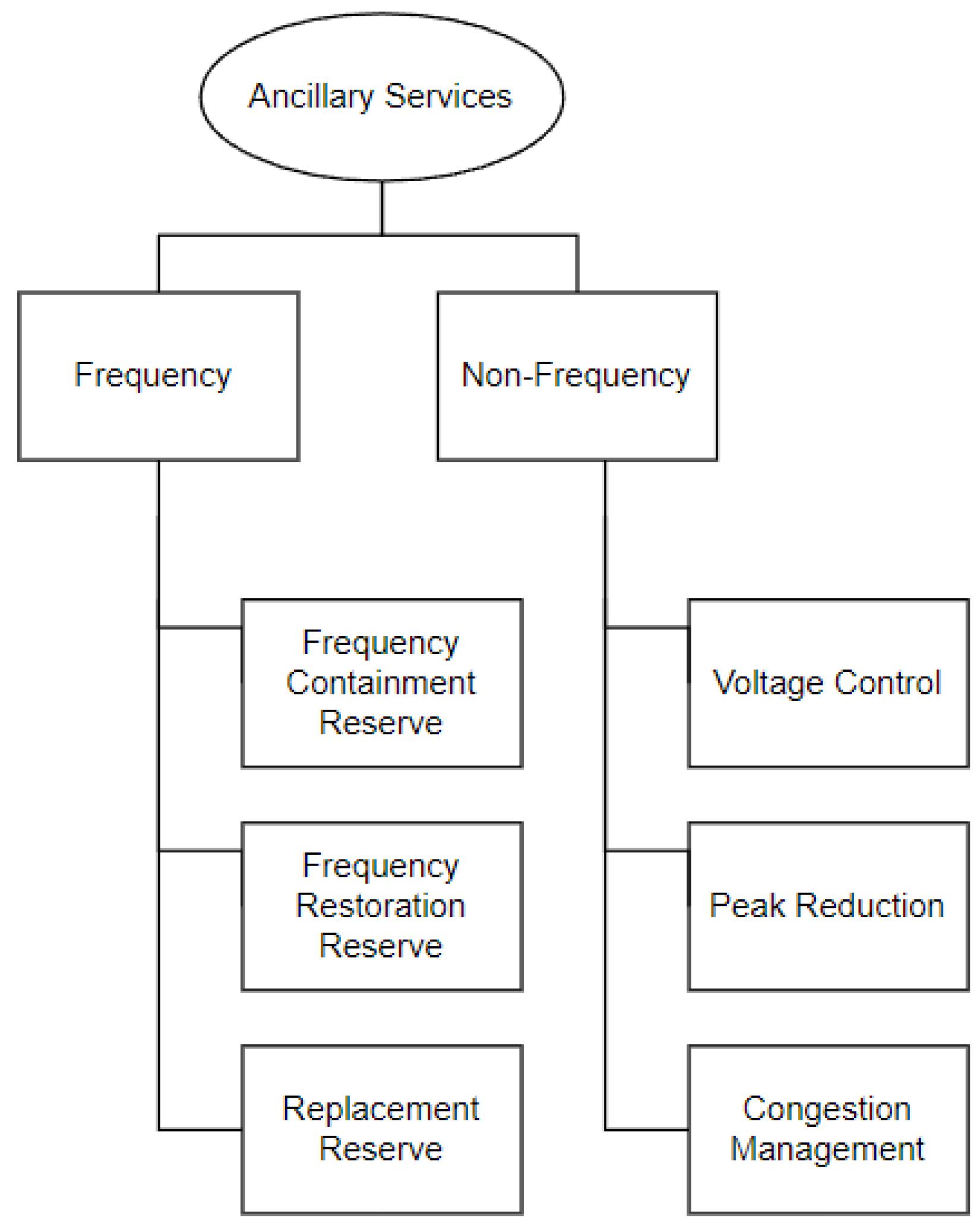
In the Ancillary Services Market, Mercato per il Servizio di Dispacciamento (MSD), the Italian Transmission System Operator (TSO), Terna S.p.A., is the only buyer. It secures the energy reserves and the resources needed to maintain the real-time balance of the grid and maintain the system’s stability and security. Moreover, it is a pay-as-bid market where accepted bids are paid at the offered price. It is noteworthy to mention that, in Italy, not all ancillary services are traded based on organized market sessions. As illustrated in
Figure 1, the services traded in the MSD can be classified as frequency and non-frequency ancillary services [
18].
The ancillary services designed to maintain the power system’s frequency and the balance between generation and demand are summarized and discussed below:
Frequency Containment Reserve: The Frequency Containment Reserve (FCR), also known as Primary Frequency Control, is the first action needed in the context of imbalances. The principles of FCR provision are defined in the grid code Annex A15 published by TERNA [
19]. In particular, this service is automatic, activated locally, fast, and aims to stabilize the frequency value in the event of load generation imbalances. This service must be activated within 30 s starting from the occurrence of the imbalance [
20]. As this service is required by the TSO of each EU member state, the reserve imposed on each state is defined according to the European Network of Transmission System Operators for Electricity (ENTSO-E) prescriptions.
Frequency Restoration Reserve: The Frequency Restoration Reserve (FRR) is divided into automatic (aFRR) and manual (mFRR). The aFRR, also known as Secondary Frequency Control (SFC), is an automatic regulation that aims to restore the frequency at the nominal value of 50 Hz. The provision of aFRR is controlled centrally based on a regulating signal received by the speed regulators of the units participating in this service [
21]. Moreover, the so-called Automatic Generation Control (AGC) is the applied control for the generators [
21]. AGC uses the area control error (ACE) as evidence of any disturbance or imbalance in the system [
22].
Replacement Reserve: The Replacement Reserve (RR) must be fully delivered within 120 min, and it is usually used to solve problems related to shifts in demand, variable injection from RES due to forecast errors, and the long faults of some generating units [
23]. The RR can be divided into upward and downward RR. The upward RR corresponds to the cases where the injection is increased or the consumptions are reduced. On the contrary, the downward reserve corresponds to increasing consumption or reducing generation. In this context, the Trans European Replacement Reserve Exchange (TERRE) project was approved by ENTSO-E in 2016 as the European platform for the exchange of balancing resources from replacement reserves [
24]. The exchange platform is based on the LIBRA solution in which the balancing energy bids are optimized and allocated to the members of the TERRE project in order to meet their needs.
To contextualize the market size, it is essential to note that within the Italian electricity markets significant volumes of energy are traded. Specifically, the volumes amount to 290 terawatt-hours (TWh) in the DAM, 26 TWh in the IM as of 2022, and 11.2 TWh in the ASM as of 2023, with 4 TWh in the ASM ex-ante and 7.2 TWh in the BM [
25,
26].
2.2.2. The Evolution of Ancillary Services Market for BESS Participation
Traditionally, the ancillary services have only been provided by conventional large-scale power plants such as coal, natural gas, nuclear, and hydro power plants [
27]. Given the increase of variable RES share and the decommissioning of fossil-fuel-based power plants, maintaining the stability and security of the power system is likely to become more challenging for the grid and regulators [
28]. Therefore, the centralized approach that has been followed in providing the ancillary services is becoming outdated, and the electricity market design should be revised to adapt to the integration of the new flexibility sources, the Distributed Energy Resources (DER) such as the BESS.
The Balancing Service Provider (BSP), as defined by [
29], is the market participant that owns units or an aggregate of units capable of providing balancing services. On the other hand, Balancing Responsible Parties (BRP) are the market participants responsible for the injection and withdrawal programs of their generating units as well as their imbalances. Imbalances are defined as the difference between the scheduled energy volume and the final one within the imbalance settlement period, a time unit within which the imbalances are calculated. Therefore, the BSP can aggregate a group of DERs for the provision of balancing services, given some terms and conditions, in a scheduling area [
29]. These DERs can include demand facilities, Energy Storage Systems (ESS), and power generation facilities.
Given the new paradigm, many countries are adapting their regulations and legislations to facilitate the integration of DER into electricity markets. Rancilio et al. discussed in [
30] the trends, features, and trade-offs of the evolution of the Ancillary Services Market to cope with the integration of DER.
In Italy, only conventional power plants with power > 10 MVA, programmable, and connected to the transmission network were allowed to provide the ancillary services as defined by the Italian Transmission System Operator (TERNA) in the Italian grid code. However, in 2017 a series of pilot projects were initiated by the Italian National Regulatory Authority (NRA), ARERA, to gradually evolve the provision of ancillary services by Non-Programmable Renewable Energy Sources (NP-RES). Different pilot projects have been activated with the purpose of investigating the possibility of Enabled Virtual Units (Unità Virtuali Abilitate: UVA) to participate in the ancillary services provision [
31]. The ancillary services allowed to be provided by DERs were limited to mFRR and RR, with a minimum bid size of 1 MW [
32]. Initially, the remuneration in the UVAM pilot project was based on a combination of energy remuneration expressed in EUR/MWh based on the energy activated in the ASM and a capacity remuneration expressed in EUR/MW based on the capacity available for the regulation [
33]. In 2021, another pilot project expanded the services that the units mentioned before are allowed to offer to include the aFRR as well. In addition, the Fast Frequency Response (FFR) was introduced as a new service to be provided with a minimum bid size of 5 MW.
2.2.3. Services Provided by BESSs and Revenue Stacking
BESSs can be aggregated with other plants and participate in the provision of grid services. They are attractive energy sources, as they are capable of offering a wide range of applications such as arbitrage, ancillary services, and the integration of intermittent RES. However, a BESS is characterized by high capital costs [
34]. One of the effective ways of maximizing the profitability of the BESS is through revenue stacking.
BESSs are widely used in different applications. These services can be categorized into power-based services and energy-based services. Power-based services require a high power for a limited amount of time, whereas energy-based services require a limited amount of power for an extended amount of time [
35].
As previously mentioned, the increasing penetration of intermittent RES ensures the necessity of designing fast and more precise frequency control. In particular, the inertia of the power system decreased due to the penetration of inverter-based energy sources affecting the robustness of the grid towards imbalances.
FFR is a possible solution for this problem. The specific requirements to provide this service can vary between countries, but generally it is based on the provision of active power within a few seconds as a response to an imbalance [
36]. In Italy, TERNA proposed
Fast Reserve (FR) as a new frequency control service in a pilot project launched in 2021. It is not traded in the ASM, but it is contracted to the energy sources for 5 years. The participating units provide power within 1 s. Currently, only energy sources with qualified power in the range of 5–25 MW are allowed to participate in this service. The provision of FR is based on a droop curve [
37]. The units participating should provide the qualified power in response to the frequency deviations in 30 s. In case the frequency deviations have not exceeded the limits set by “level #2”, the fade-out can be activated, and the unit decreases the output power gradually in 300 s. On the other hand, if the highlighted frequency limits are violated, the unit must provide the full qualified power for at least 15 min.
As highlighted previously,
FCR is the first control action taken in the context of frequency deviations. It is the process of supplying active power due to frequency fluctuations that occur due to the imbalance between generation and demand. Several studies in the literature have proven the effectiveness of BESSs in providing this service. Amin et al. [
38] compared the provision of FCR by synchronous generators and a BESS using mathematical equations of governors and turbines. The results obtained showed that BESSs can provide a faster and better response to frequency deviations than synchronous generators. In [
39], Arrigo et al. analyzed the impact of FCR provided by a BESS on the transient response of the grid. The authors confirmed in the conclusion the positive impact of the BESS on the reduction of the frequency variations, given a proper control strategy and enough installed capacity. The effectiveness of the provision of the service was evaluated based on an effectiveness index. Moreover, a comparison was conducted regarding the provision of the FCR by conventional generators and BESSs. They found that if the inertia of the network decreases, the BESSs are more effective in providing the service. Additionally, Datta analyzed, in [
40], the impact of a BESS in providing FCR to enhance the penetration of wind power plants using a model implemented in DigSILENT. It was shown that BESSs can play a vital role in reducing oscillations after disturbances and can support the penetration of RES by absorbing excess energy and providing deficit energy. Secca et al. [
41] compared the provision of FCR in three major European Countries: the Netherlands, Germany, and the UK in terms of lifetime and economics, taking into account the remuneration schemes in each country. They found that the provision of FCR by BESSs is economically viable in all the analyzed countries given the remunerations in each country. Moreover, given the remuneration schemes in the Netherlands, results showed that the Net Present Value (NPV) of BESSs providing FCR there can be 47% and 76% higher than in Germany and the UK.
However, BESSs should respect the technical requirements defined by TSOs for the provision of FCR. Therefore, it is crucial to implement SoC management strategies to ensure the availability and service continuity of BESSs. In particular, these strategies ensure that the SoC is set at a value within the maximum and minimum thresholds set by the BMS. In case of reaching the pre-defined thresholds, the BESS can be saturated, and the defined power setpoint cannot be respected. In particular, not respecting the power setpoint can lead to penalties.
Energy arbitrage involves buying electricity when prices are low and selling it when prices are high. In other words, the BESS is charged during low demand times, resulting in low prices, and discharged during high demand times, resulting in an increase in the prices. It is an energy-based service that requires the BESS to store energy for long durations [
2]. In general, energy is traded in the day-ahead market. For energy arbitrage, it is of paramount importance to forecast the future behavior of the market to maximize the amount of profits.
Ponnaganti et al. assessed in [
42] the potential revenues from the integration of energy storage systems with wind farms, taking advantage of the difference in prices in the DAM, comparing the profits generated by BESSs and the Thermal Energy Storage System (TESS). The DAM’s prices were predicted based on a feed-forward neural network forecasting algorithm. They adopted an analytical model to describe the charging and discharging processes of the BESS. The revenues generated were higher when the energy storage system is integrated with the wind farm. Additionally, they found that BESS is better than TESS in utilizing wind energy but worse in terms of operating and maintenance costs.
Penaranda et al. [
43] compared different arbitrage strategies to determine the best one that could maximize the revenues generated in the Colombian electricity market by adopting a Mixed Integer Linear Programming (MILP) optimization problem. They proved that providing energy arbitrage only could result in negative economics, represented by negative NPV. Therefore, it is better to provide other services associated with the energy arbitrage.
Given the typically high capital costs associated with BESSs, maximizing their utilization through the provision of multiple services becomes advantageous, allowing for revenue stacking and the full exploitation of the installed battery capacity. In [
44], the authors proposed the provision of a second service to generate additional revenues. The provision of several services is generally referred to as service stacking. In general, service stacking can be categorized into three different types [
45]:
Sequential Stacking: During the sequential stacking, the BESS can be used to provide multiple services sequentially. In particular, the full capacity of the BESS is dedicated to a service for a defined time stamp and then switched to another application over time.
Parallel Stacking: During parallel stacking, the capacity of the BESS is divided between different services. Moreover, the capacity allocated for each service remains constant over time.
Dynamic Stacking: During dynamic stacking, multiple services are provided simultaneously while varying the capacity allocated for each service with time. This method is considered the most flexible, but it requires a complex Energy Management System (EMS) to be implemented.
Englberger et al. [
46] compared the annual profitability of stacking methods by evaluating three scenarios of stacking services: Peak Shaving (PS) + FCR, PS + Spot Market Trading (SMT), and PS + FCR + SMT. Moreover, they compared the profitability of the dynamic and sequential strategies as a function of the inverter switching time. The study revealed that dynamic stacking has the highest profitability compared to the others in the three scenarios evaluated. Sequential stacking is more profitable than the parallel strategy, indicating that sequential switching between services is more effective than allocating fixed capacities among them.
In [
37], Rancilio et al. developed a BESS model to evaluate a techno-economic analysis of the provision of two sequentially stacked ancillary services: FR and RR. The analysis pointed out that the efficiency and the Internal Rate of Return (IRR) improved with revenue stacking.
Spiller et al. developed, in [
47], a procedure to size a hybrid system of BESSs and RES while evaluating the economic performance of the provision of multiple services. The different services evaluated were energy arbitrage, capacity market, mFRR, and FFR. The study compared different stacking scenarios by combining different services. The results obtained highlighted the importance of revenue stacking to enhance the economics of the project. In particular, it has been pointed out that the CAPEX covered and the IRR increased while stacking more services without increasing the number of Full Cycle Equivalent (FCE) performed by the BESS.
Finally, Hameed et al. [
48] investigated the participation of BESS in the Nordic ancillary markets, with a focus on business aspects by analyzing the market prices in the past six years. In particular, they simulated two services traded in the Danish market: frequency-controlled disturbance reserve (FCR-D) and frequency-controlled normal operation reserve (FCR-N). The analysis revealed an increase in profits by 2%–8% in each of the simulated years.