Abstract
Reducing greenhouse emissions can be done via the electrification of the transport industry. However, there are challenges related to the electrification such as the lifetime of vehicle batteries as well as limitations on the charging possibilities. To cope with some of these challenges, a charge scheduling method for fleets of electric vehicles is presented. Such a method assigns the charging moments (i.e., schedules) of fleets that have more vehicles than chargers. While doing the assignation, the method also maximizes the total Remaining Useful Life (RUL) of all the vehicle batteries. The method consists of two optimization algorithms. The first optimization algorithm determines charging profiles (i.e., charging current vs time) for individual vehicles. The second algorithm finds the charging schedule (i.e., the order in which vehicles are connected to a charger) that maximizes the RUL in the batteries of the entire fleet. To reduce the computational effort of predicting the battery RUL, the method uses a Machine Learning (ML) model. Such a model predicts the RUL of an individual battery while taking into account common stress factors and fabrication-related differences per battery. Simulation results show that charging a single vehicle as late as possible maximizes the RUL of that single vehicle, due to the lower battery degradation. Simulations also show that the ML model accurately predicts the RUL, while taking into account fabrication-related variability in the battery. Additionally, it was shown that this method schedules the charging moments of a fleet, leading to an increased total RUL of all the batteries in the vehicle fleet.
1. Introduction
Greenhouse gas emission mitigation is one of the major challenges of the 21st century. The negative consequences of these emissions are already visible in the environment [1]. One way of reducing these emissions is by lessening the fossil-fuels usage. Such fuels are used in multiple sectors of the economy, with the transport sector alone accounting for of its total usage via Internal Combustion Engines (ICEs) [2]. Reducing the fossil fuel usage in the transport sector would significantly contribute towards mitigating the emissions problem.
Due to climate change, alternatives are being explored in the transport sector such as switching from ICEs to Battery Electric Vehicles (BEVs) [3]. During their lifetime, the BEVs’ emissions are lower than those of ICEs [4]. However, the adoption of BEVs faces multiple challenges, such as the relatively long charging time and a shorter driving range than ICE-based vehicles [5]. This implies that BEVs cannot drive long distances as time-efficiently as their ICE-based counterparts. Adding to these challenges, the battery of BEVs continuously degrades over time, resulting in less capacity and further reducing the BEVs range [6]. Degradation is accelerated when stress factors are present in the battery cycle, such as overcharging, large depth of discharge or storing while fully charged [7]. Taking into account these stress factors is therefore crucial for the lifetime of a BEVs.
Another point of consideration is that charging increases the load on the grid. As more fleet operators are switching from ICEs to BEVs, the pressure on the grid is increasing. The consequence is that fleet operators cannot freely place charging stations for a BEV fleet. Therefore not all BEVs in a fleet can be charged simultaneously [8] and need to be scheduled by fleet operators. Additionally, the charging stations account for a significant amount of the total cost of ownership of a fleet of BEVs, which is another reason for fleet operators to limit the amount of charging stations.
A solution to this problem is to impose a charging order (i.e., a schedule) and charging scheme (i.e., a charging profile) on the fleet. The charging scheme regulates the charging power of a fleet. The charging order refers to the sequence in which vehicles are connected to the charging station, assuming there are less charging stations than vehicles.
To optimize the charging scheme and order of an fleet, the impact of the charging scheme on the RUL of the battery needs to be calculated. The battery RUL is the amount of operational time a battery has left until it reaches End of Life (EoL). EoL of a battery is commonly defined as reaching 80% of the original capacity [9,10]. Calculating the RUL is a way to quantify the effectiveness of a charging scheme and order.
An earlier version of this paper has been published [11], which optimized the charging scheme of a single vehicle as well as a fleet of vehicles, while focusing on cost effectively reducing the load on the electricity grid. This paper extends such a version by creating a ML model that predicts the degradation speed of a battery while taking into account internal variability of batteries. Such an internal variability refers to the fact that even though two seemingly identical batteries treated in exactly the same way, they can still differ in terms of degradation speed [12]. This is due fabrication-related differences. Lastly, based on this ML model, an algorithm was implemented to generate the charging order (i.e., a charging schedule) of a BEV fleet, that takes into account constraints such as the amount of charging points and common timing requirements of fleet operators (e.g., departure and arrival times).
Previous studies have focused on multiple BEVs charging challenges with a variety of objectives. Objectives such as optimizing the route of the vehicle (e.g., [13]), minimizing the electricity price (e.g., [14]), or a combination of both (e.g., [15]). However, these studies do not acknowledge the fact that charging may be limited by the amount of charging points, as well as the fact that batteries have internal variability that impacts the optimal charging for each battery.
To address this gap, this paper presents a method for scheduling the charging moments of a fleet of BEVs and determining the charging profiles. The resulting schedule and profiles maximizes the total RUL of the batteries in the vehicle fleet, while taking into account that there are fewer available charging points than vehicles. Further, the method uses a ML model to predict the fleet RUL, while taking into account the internal variability of the vehicle batteries. This method is applied to a case study of lightweight electric delivery vehicles, used for last-mile deliveries.
This paper is divided as follows. Section 2 reviews the literature and highlights the knowledge gap. Section 3 introduces the used modelling strategy for vehicle batteries and the ML algorithms. Section 4 summarizes the method presented in this paper. Section 5 formalizes the mathematical aspects of optimizing the charging profile of a BEV. Section 6 explains the data collection and training of the ML model. Section 7 formalizes the optimization problem of scheduling a fleet of vehicles. Section 8 presents the application of the method to a motivational case study. Section 9 closes the paper with conclusions.
2. Literature Review
This research focuses on two study areas. One is the scheduling of the charging of one or more BEVs, the second is the use of an ML algorithm that can predict the RUL of a vehicle. From the charging scheduling perspective, previous studies have focused on creating charging schemes while minimizing a certain objective. For example, [16] developed an optimized decentralized charging strategy, which kept account of electricity network congestion. The authors of [17] show the impact of uncontrolled charging BEVs on the electricity grid. They further elaborate on optimal charging strategies to mitigate such an impact. In [13], an optimization strategy was developed for buses, where the desired routes and fleet charging was jointly determined. The authors of [14] developed an optimal charging algorithm taking into account electricity price. A later study [15] focused on developing an algorithm for the overnight charging of buses with respect to battery degradation and electricity price. Lastly, [18] focused on optimizing the charging cost of a fleet while considering a limited number of charging points; however, they did not look into battery degradation. None of this research considers the constraint of a limited amount of charging points, while also taking into account the degradation of a battery.
From the ML perspective, studies have focused on predicting the RUL of a battery using different types of algorithms. For example, [19] showed that there are multiple ML algorithms available that are able to predict the RUL. They also showed what the advantages and disadvantages of each algorithm are. They showed that there are multiple frequently used ML algorithms for predicting the RUL. The first is the Neural Network (NN) algorithm, which is explored by [20], who showed the that NN can be a good replacement for the Kalman filter and also showed that a NN is accurate for small datasets with a large number of predictor variables. The second is the Support Vector Machine (SVM) algorithm, Ref. [21] combined this method with a particle filter method to predict the RUL. Another algorithm is the Gaussian Process Regression (GPR) algorithm, which was explored by [22], who showed that GPR can predict the RUL, but also showed the uncertainty in this prediction. Another study showed that decision tree algorithms were also able to predict the RUL based on real life drive cycles [23].
None of this earlier work takes into account the effect that the internal variability of a battery has on the RUL of that battery with a constrained amount of charging points. This research fills both the mentioned gaps by creating a method for scheduling the charging and order of charging of a fleet of electric vehicles. This research uses the ML algorithm to create a model that is able to predict the RUL while also taking into account the internal variability of a battery.
3. Theoretical Background
To optimize the charging scheme of a fleet of BEV, multiple models and algorithms are required. To capture the dynamics of the battery and its degradation, a modelling section is included. Likewise, different ML algorithms are explained and criteria for selecting the ML algorithm are explained. The used models in this section correspond to modelling techniques that can be applied to calculate battery dynamics. However, notice that other models can be substituted to represent a battery, which would not change the described method.
3.1. Battery Model
The second order Equivalent Circuit Model (ECM) shown in Figure 1a is used to model a battery cell [24]. This commonly used model is preferred as it has relatively low computational complexity and yet it provides relatively high accuracy in predicting the cell voltage. Using this ECM, the following model is derived:
where denotes the terminal cell voltage, is the open circuit voltage, cell current, R, and are resistances, and are polarization voltages over the RC tanks and and are capacitors. All magnitudes in this paper are expressed in SI units unless noted otherwise. The model parameters , , , , R and are dependent on the current direction (i.e., charging or discharging), cell temperature and State of Charge (SoC). An example of the dependency of one of these parameters on SoC and temperature is found in Figure 1b. All the other parameter dependencies are found in the previous version of this work [11].
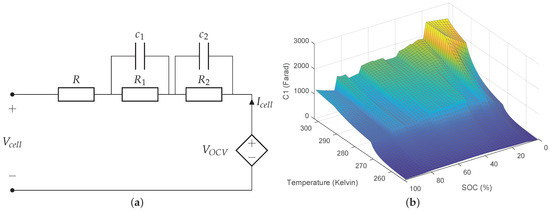
Figure 1.
Overview of the ECM model and the parameter . (a) Overview of second-order equivalent-circuit model. (b) Example of the parameter for the ECM under charging conditions.
The current and voltage at pack level is computed by scaling up the cell current and voltage, i.e.,
where I is the pack current, is the number of parallel cells in the pack, V is the pack voltage and is the number of cells in series in the pack. The SoC is calculated with coulomb counting
where Z is the SoC, is the capacity of the battery when it is fully charged in ah. Note the capacity of a fully charged battery changes due to degradation. The constant 3600 is used to convert seconds to hours, k is the discrete-time index and the length of one time step in hours.
Based on the battery model presented in this subsection, a degradation model and thermal model for batteries are introduced in the next subsections.
3.2. Degradation of Batteries
Although multiple processes cause degradation in batteries, these can be grouped in two categories: calendar ageing and cyclic ageing. The first happens over time, whether the battery is used or not. This type of ageing is mainly caused by irreversible and unintended side reactions that slowly consume the lithium in the battery [25]. Cyclic ageing happens only when the battery is used and is mainly caused by forming an unintended layer on the anode, which hinders or prevents the anode from releasing electrons, therefore reducing the capacity of the battery [26]. To capture these degradation processes, [25] proposed an empirical model which takes into account SoC, current, voltage, battery temperature and time to calculate the corresponding degradation of a cell. Such a degradation is expressed in terms of capacity loss and resistance increase. In this research, only the loss of capacitance is considered (instead of the resistance increase) as the optimizer is designed to minimize capacity loss. Including resistance increase remains an interesting research topic. This model has been validated in [25].
The calendar loss is defined by [25] as
with the average voltage over one cell, the average cell temperature in Kelvin and t the time in days. is the new capacity after t days, only taking into account the calendar aging effects. The resulting capacity ranges from 0 to 1.
Cycling aging is defined as
where
Here, is the Root Mean Square (RMS) of the cell terminal voltage, is the depth of discharge, Q is the cell charge throughput of one cycle in Ah and is the number of cycles, assuming that each cycle has the same charge depth of discharge. is the new capacity after cycles if only the cyclic aging is taken into account. Notice that the numeric parameters from Equations (4) and (5) have been determined by [25] for the degradation of a particular cell chemistry. Although these parameters would need to be updated to be applied to a different type of cell, the method which is the main contribution of this work remains the same.
The updated capacity is obtained using
where is the new capacity after a cycle has been applied.
3.3. Thermal Model
A thermal model at cell level is used to compute the cell temperature. The thermal model considers the addition of four heat flows as described and validated in [27], i.e.,
where is the reversible reaction heat, is the overpotential heat, is the heat transferred to the environment and is the heat added by a cooling system. All heat flows are expressed in watts. is the heat capacity of one cell and is the mass of one cell. The multiple heat flows are further described as:
where is the partial derivative of the open circuit voltage with respect to the cell temperature. This parameter is obtained via experiments and dependents on the SoC. is the thermal resistance between the battery surface and the environment. is the ambient temperature. Note that depends on the cooling capacity of the thermal system and the battery geometry, therefore a general definition is not included in Equation (9).
3.4. Machine Learning Strategy Selection
This research uses a ML algorithm to predict the RUL of a battery pack. RUL prediction corresponds to the estimation of a single value, which narrows the types of ML algorithms that are suited for this purpose. Ref. [28] showed that there are three main algorithms that theoretically work best on predicting a single numerical value. These are the following:
- Gaussian Process Regression (GPR): Predicts a numerical value by approximating the function that creates the value (target function) using a Gaussian distribution of functions. This algorithm considers all possible functions that pass through the observed data points and predicts the probability that each function is the correct function. The function with the highest probability is used for prediction [29].
- Support Vector Machine (SVM): Predicts a numerical value by approximating a function that stays as close as possible to the observed data. It creates margin lines around this function, which are defined by the function upper and lower bounds. The algorithm then fits as many points as possible within the functions margin lines, while keeping the margin lines as close to the function as possible. This is done by altering the fitting function. This algorithm is able to automatically exclude outliers in the data set [30].
- Decisions Tree (Tree): This algorithm builds a decision tree that checks multiple thresholds of each parameter. If the parameter is higher than the threshold, the tree advances to one path, while when its lower it chooses another path. Both paths lead to a different new threshold check of certain parameters. Reaching the end of all paths generates the output [31].
A notable exclusion is the use of a neural network. This was considered for this research, however this algorithm was shown to be very time consuming to train [32] without having a higher accuracy to the considered algorithms. This algorithm was also shown to be suitable for small datasets with a large number of predictors [20], where the used dataset has a small number of predictors and a large number of data points and [33] used a similar data set and showed that a neural network was not suitable, therefore it is not considered. Other versions of NN remain interesting solutions which are beyond the scope of this paper. The versions of the algorithms as defined by Matlab R 2022A are used. The advantage and disadvantage of each algorithm is shown in Table 1. The data that is used to train the ML algorithm in this research has only a five input parameters with a large number data points, which is explained in Section 6. GPR seems the best option, because it is efficient with smooth data with a small number of dimensions.

Table 1.
Advantages and disadvantages of each ML algorithm [29,34].
4. Methodology Overview
This work contains three steps, which are graphically explained in Figure 2. These steps are based on the battery model explained in Section 3. These steps are briefly introduced here and are explained in more detail in the next sections:
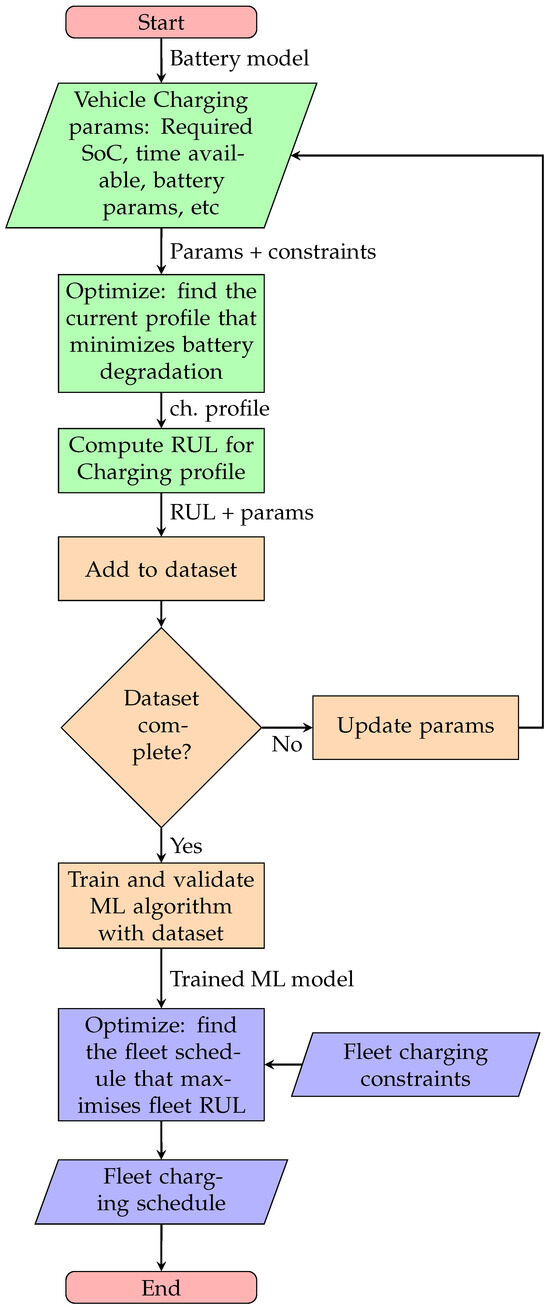
Figure 2.
Proposed methodology. From the description of Section 4, the green blocks correspond to Step 1; the orange blocks to step 2; and the blue blocks to step 3.
- Step 2: Obtain the RUL from the optimization in step 1 then train a ML model to predict the RUL based on this charging profile. This is explained in Section 6
- Step 3: Create an optimal charging schedule for charging a fleet of vehicles. This uses the ML model from the previous step to predict the RUL of a given charging profile. The optimization problem focuses on finding the optimal time slot (and associated charging profile) for charging each vehicle. This is explained in Section 7
In comparison with the earlier conference paper on which this publication is based [11], step 2 and 3 have not been published in that paper. Note that the first step could have been used directly for the third step (skipping the ML step). However, doing so would be very computationally expensive. Therefore the second step, namely the ML algorithm, is introduced, to save computational time.
5. Optimizing the Charging Profile of One Vehicle
This section explains the optimization regarding a single vehicle and the applied constraints. The charging of a BEV is optimized with respect to the degradation. The objective is to maximize the RUL (), which is determined by calculating when the battery reaches EoL. The EoL of a battery is defined as reaching 80% of the original capacity and it is assumed that the battery has no second-life value. This is common practice among researchers [9,10]. RUL is calculated with the following equation,
t is defined in Equations (4) and (6). The assumption for this formula to be valid is that t is equal to , which equates to one cycle per day. This implies that the vehicle is used during the day and charged during the night, which fits the case study as mentioned in Section 1. refers to the capacity of the battery when it was new and refers to the capacity after charging and discharging t times.
To calculate the RUL resulting from a charging scheme, the time needed to reach the EoL is simulated by applying the particular charging scheme for the entire life time of the vehicle. This implies that the vehicle starts its charging cycle every day with the same initial battery temperature and SoC. No discharge cycle is actually run in the simulation, as it cannot be controlled for electric vehicles, and of doing so it would have an uncontrolled effect on the battery ageing and battery RUL. The degradation of the battery is solely manipulated and calculated through the charging cycle.
The optimization objective maximizes the RUL of a single vehicle. This is captured by the following optimization problem:
where is the charging current profile of the vehicle, further defined by
where is the number of steps in which the total charging time is divided. Note that is a design choice: a large number of steps results in a more detailed current profile at an extra cost of computational effort. is the charging current during time slot k. The definition of implies that the current is discrete during the duration of each time slot . Also note that the optimizer can freely choose the current neglecting the common constant current and constant voltage phases of charging.
The constraints are the following:
refers to the SoC at the end of the charging period, therefore Equation (12) makes sure that the battery of each vehicle is charged to at least 97% before the end of the charging period and not more than 99%. Equation (13) is the lower bound, which prevents the current from being negative.
6. Dataset Generation and ML Algorithm Training
The ML algorithm is trained using a dataset created from the optimization explained in Section 5. The dataset is composed of a RUL for each charging profile, which is computed for several values of the following parameters:
- Initial SoC: The SoC of the battery before it starts charging.
- Initial battery temperature: The temperature of the EV battery before it starts charging.
- Initial State of Health (SoH): The SoH of the battery, before it starts charging, calculated by . Therefore a SoH of 0 refers to EoL being reached, defined as reaching 80% of the original capacity.
- Time slot for charging: The start and end time for charging the EV.
- Age of the battery: Age of the battery in days, assuming the same charging scheme over the battery life time.
With these inputs, a set of optimal charging schemes and corresponding RUL was calculated. Each parameter is randomized between the maximum and minimum value as shown in Figure 3a. Note that the constraint that each vehicle is charged to at least a SoC of 97% as shown in Equation (12), is implicit in the RUL prediction of the ML model.
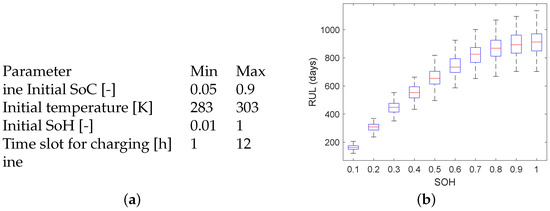
Figure 3.
Variation in RUL and input parameters. (a) Minimum and maximum value between which the data is randomized. (b) RUL variance due to the internal variability. Initial SoC = 0.1, initial battery temperature = 12, time slot length = 8 h.
As noted in Section 1, the degradation of a battery is not deterministic. Even when using the same charging scheme for two batteries, the rate of degradation might differ due to internal differences in the battery. The ML algorithm needs to be able to account for this effect. Therefore, these differences were implemented by adding variability in the degradation model. Each time that the RUL of a single-vehicle model was simulated, a new set of parameters of the degradation model (i.e., the non-integer numbers in Equations (4) and (5)) was used for each vehicle. Likewise, the initial battery SoC and temperature were kept constant during the whole lifetime. The RUL was calculated using Equation (10). To simulate the variability on the RUL, the procedure is repeated with a new set of model parameters and a new set of initial conditions for SoC and temperature.
In these simulations, all the cells in the pack are considered to have the same non-integer parameters per RUL calculation. Considering the effects of differences in cell degradation per pack (e.g., a single fast-degrading cell), remains an interesting research question. Notice that the initial cell capacity is not varied in these equations, as manufacturing-related variations in capacity are unlikely to affect the useful battery capacity, instead affecting the total capacity. Likewise, battery resistance is not varied, as these are not part of coefficients in Equations (4) and (5). Cell resistance remains an interesting parameter to analyse, as it could help to justify the variations in fabrication-related differences in battery degradation.
Varying these parameters leads the RUL ranging from 80% to 120% of its original value. This was shown by [35] to be a realistic assumption. An example of this varying RUL can be found in Figure 3b. What can be seen is that for the for SOH of 0.5 to 1 the RUL is relatively stable. This is due to the fact that the first few percentages of capacity loss are often within a relatively low amount of cycles; however, the RUL is still quite large as the later cycles reduce capacity less than the first cycles [25,36].
Additionally, to improve the accuracy of the predictions, the ML algorithm needs to have information about how long the battery has been in the degradation process. Therefore the ML algorithm is also given the actual age of the battery in days, by the time that the optimal charging scheme is used. This is the battery age at the moment of the RUL prediction. This additional input gives the ML algorithm enough information to find a relationship between the current age of the battery and the expected RUL of the battery.
This ML model was trained using Matlab’s regression learner toolbox. The three algorithms are trained and tested using a division of 20% and 80% between test and train data, respectively, using the k-fold cross-validation technique. The test and train data stem are from the same dataset.
7. Optimization of Charging Schedule of an Entire Fleet
The next step is to solve the charging order problem. The optimization objective is to maximize the total RUL of the fleet () by controlling how long each vehicle () is connected. This is written as:
with
where corresponds to whether the vehicle n is connected during time slot z. corresponds to the total number of vehicles in the fleet. The sets and denote the fleet of vehicles and the available charging slots, respectively, i.e.,
is the number of steps in which the total charging time is divided. Note that is a design choice. is predicted by the ML model and therefore is dependent on the characteristics of each vehicle. As can be seen from Equation (15), this is a binary optimization, where is the decision variable and where a 1 corresponds with the vehicle charging and a 0 with the vehicle not charging.
The constraints of the optimization problem are defined as
Equation (19) constrains the amount of vehicles that are charged simultaneously to be equal or less than the number of charging points .
Equation (20) makes sure each vehicle is connected at least the minimum amount of hours needed for the vehicle to be at least 97% full, which also implies that the vehicles SoC is at least equal to 97% after this charging period. is the minimum amount of hours needed for the vehicle n to be full, defined as,
where is the maximum charge current applicable to vehicle n. Equation (22) assumes a linear relationship between charging time and current. That is because the commonly used constant voltage phase of charging, which is used to charge the battery to 100%, is not included in this work.
Equation (21) reflects the fact that all chosen time slots should be adjacent to each other, meaning each vehicle can only be connected once during the charging period. captures the time slots when the vehicle is connected, i.e.,
In Equation (21), refers to the number of elements in . refers to taking the highest number of the vector where refers to taking the lowest number of the vector.
The optimization algorithm finds the optimal charging order (i.e., the schedule) of the fleet. This optimization is solved using the intlinprog function of Matlab R 2022A. Refs. [37,38] showed that this algorithm is suitable for solving binary problems while giving valuable results. This algorithm first relaxes the problem by solving a non-integer version of it. Then it tightens the found solution using cut generation techniques, as well as a branch and bound algorithm to find an integer solution. See [39] for information on these algorithms.
8. Simulation Results and Discussion
To illustrate the applicability of the proposed method, this section shows some simulation results on a numeric example. To do so, a realistic case study is presented. Then, the applicability of the single-vehicle optimization algorithm is shown, after which the applicability of the ML in combination with the charging order optimization algorithm is presented.
8.1. Case Study
To show the benefits of the optimization algorithm, a case study was created, which gives insights in how the algorithm works. The case study is based on lightweight electric-freight trucks used for last-mile deliveries. The BEV weighs a maximum of 3500 kg including payload. This weight makes these vehicles an attractive solution for a fleet operator, because no truck driver license is required.
The BEVs are used for deliveries throughout the day. At the end of the day, all vehicles are brought back to the same depot and can be charged overnight from 20:00 till 8:00. They can be charged with different currents, which is decided by a central coordinator, i.e., the methodology presented in in this paper.
The batteries are assumed to be Li(NiMnCo)O2 18650 lithium-ion batteries. The complete set of battery model parameters is shown in the previous work [11]. An overview of some key model parameters is shown in Table 2. The ageing model proposed by [25] is used. Notice that the chemistry used to derive the ageing-model parameters in Equations (4) and (5) corresponds to an older version of Li(NiMnCo)O2, as updated parameters were not available. This implies that the battery degradation presented on this paper follow the one of [25], with the method presented on this paper remaining the same.

Table 2.
Example of model parameters values.
The ambient temperature is assumed to be constant. The BEVs do not have active cooling/heating for their batteries (i.e., ). However, in case of vehicles with this system, this heat flow could be added as explained in [40]. The fleet size is 20 where the inputs explained in Section 7 were randomized for each vehicle. There are two charging points available.
Using the steps presented in Section 4, the optimization objective and constraints are formulated. The simulation results are presented in the next subsections.
8.2. Single-Vehicle Result
Two scenarios were considered to show the impact of the algorithm of Section 5. More scenarios and results can be found in the previous work [11]. This result assumes a single vehicle connected for 12 h, where for the fleet result the time the vehicles are connected is changed. The considered scenarios are the following:
- Greedy charging: No optimization is applied. This implies that the vehicles are charged at the moment they are connected with a charging current high enough to charge the pack in approximately 3 h.
- Optimized charging: A charging profile is derived solving the optimization objective presented in Equation (11).
The resulting charging profile per scenario can be seen in Figure 4. Note here that the assumed initial SoC is 30%, SoH is 1 and the battery of the vehicle is assumed to be the exact same between scenarios. corresponds to the starting time of 20:00, which is the moment when the BEVs are connected. The time step is taken to be 0.25 h. Such a value saves computational time, while maintaining the accuracy needed for the optimization.
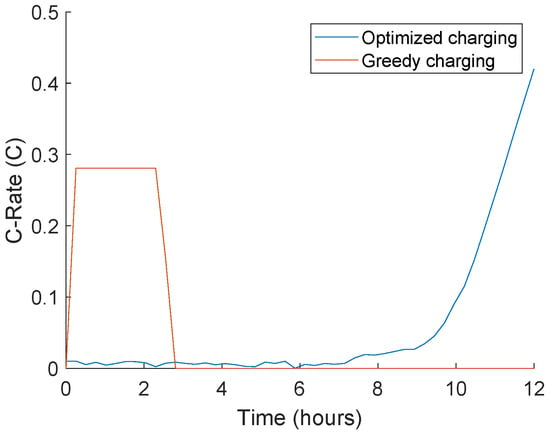
Figure 4.
Current profile comparison.
The greedy charging scenario charges the vehicle as soon as it arrives. The optimized charging charges as late as possible. This is because charging late reduces the average and RMS voltage in Equations (4) and (5). Reducing these voltages leads to less degradation. Likewise, the optimized charging scheme shows higher charging currents than the greedy scenario, at the last moments of charging, which leads to an overall lower RMS voltage, leading to lower degradation, even though C-rate is higher. This is a model-dependent effect, which might be different from other models from the literature. The RUL of the greedy scenario was 833 days, where the optimized scenario had a RUL of 1419 days, which is an increase of 71%. Notice that the greedy scenario was only created for reference, therefore it does not apply the highest possible charging current.
8.3. ML Selection for Fleet-Ordering Optimization
A dataset was obtained as explained in Section 6. The three ML algorithms explained in Section 3.4 were trained.
In Figure 5, the predictions of each trained algorithm can be found. As can be seen, the GPR has the lowest error margin, with predictions closer (and more frequent) to the actual value.
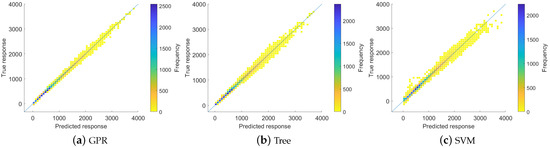
Figure 5.
Comparison true response and predicted response in RUL prediction of every ML algorithm. The line in the middle of the graph denotes the ideal response. True response is the actual value of the data point, predicted response is the value predicted by the ML algorithm.
This trend is also seen when comparing the Root Mean Square Error (RMSE) of each algorithm. GPR had a RMSE of 48.6 days. Where Tree and SVM had a RMSE of 84.1 and 95.8 days, respectively. The Tree algorithm has more outliers, but is more accurate at predicting the other points, while for SVM the opposite holds true. From the error prediction point of view, SVM performs the worst while GPR the best. The fact that GPR is the best can be explained by the fact that GPR is accurate with data sets with only a few dimensions, where the underlying relations are smooth. This is case for RUL. This means that of these three algorithms, GPR can most accurately predict RUL.
The three ML algorithms were also tested by creating new randomized inputs and comparing the predicted RUL of the ML model with the RUL of the model (expected value). These results can be found in Figure 6. In Figure 6a, the predicted RUL of each algorithm and the actual RUL can be seen, these values have been ordered based on the RUL. In Figure 6b the absolute error in the prediction can be seen. Both figures show that GPR has on average the lowest error in predicting the RUL. In Figure 6b, the frequency of each error range can be observed. As can be seen, the Tree algorithm performs poorly, as it has a some very large outliers in the error of its prediction. SVM predicts more accurately than Tree, but GPR has the most points in the lowest error range of 0–42 days. Using a GPR model to predict the RUL is 2000 times faster than the recurrently running the ageing model and the optimization algorithm created in Section 5.
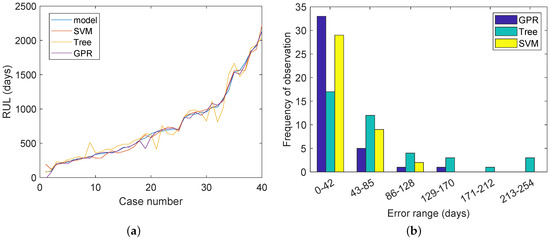
Figure 6.
Comparison of different ML predictions. (a) Predicted RUL compared to the calculated RUL from the battery model. Ordered based on their RUL. (b) Occurrences of each error range.
8.4. Optimizing Charging Order
To show the benefits of the optimization algorithm, simulations are performed with charging scenarios for a fleet of vehicles as the one described in the case study of Section 8.1. The charging scenarios are:
- Greedy charging order: The vehicles are charged as soon as possible without implementing any optimization. They are connected, based on a first come, first serve basis. This is considered common practice in the day-to-day operation of fleets.
- Optimized charging schedule: A charging order is derived by solving the optimization problem described in Section 7.
8.4.1. Fleet Scheduler Example
The optimization algorithm of Section 7 chooses a suitable start and end time of the vehicles. Time steps of 30 min were used in order to save on computational time. Note that when considering steps of 5 min, the total RUL increases by 2%. Such an increase is due to the increased decision space and the higher algorithm precision, which enables finding a lower minimum. However the computational time is six times longer than when 30 min time steps are used. After running the algorithm with several time steps, it was noticed that the computational time increased in a near-linear fashion while reducing the time steps length. Similarly, the computational time increases nearly linearly while increasing the fleet size. Time steps of 30 min were chosen, as it provides a balanced trade-off between accuracy and computational time.
The resulting charging order can be found in Figure 7. The red bar shows which vehicle is connected and charged at which time slots. As can be seen, the total RUL of the optimized charging is 2.4 times higher than the greedy charging order and optimizing this order can therefore significantly increase the lifetime of a fleet of vehicles. Important to notice is that the charging profile is selected to maximize the RUL of each vehicle given charge window i.e., a different time window produces a different optimal RUL. However, the charge windows are chosen to maximize the total fleet RUL and not the individual vehicle RUL. Therefore, a single vehicle can have a better RUL using the greedy algorithm than the optimized algorithm, due to the difference in charge window. In Figure 7c, the charging power of three vehicles is shown. What can be seen is that a longer time period in general leads to lower C-rates, where charging at the last time step leads to higher C-rates. However, also note that only vehicles with relatively high initial SoC are charged in one time slot.
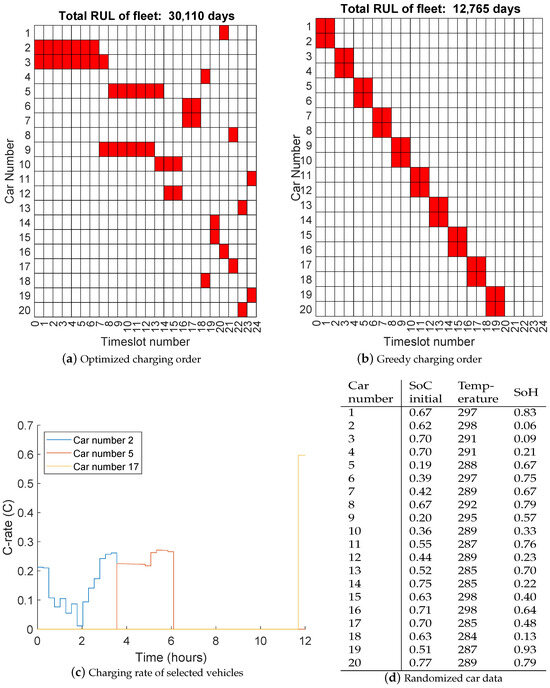
Figure 7.
Charging schedule of a 20-vehicle fleet and 2 chargers. Red squares denote vehicles connected per time slot.
8.4.2. Charging Order Analysis
In this subsection, the influence on the charging order of varying the initial value of a single vehicle parameters (i.e., SoC, SoH and temperature) is shown. To do so, the algorithm is tested on a fleet of 10 vehicles while varying a single parameter. In Figure 8, the results of the single varied parameter scenario can be seen. Each line represents the result of varying only that parameter, while the others were kept constant.
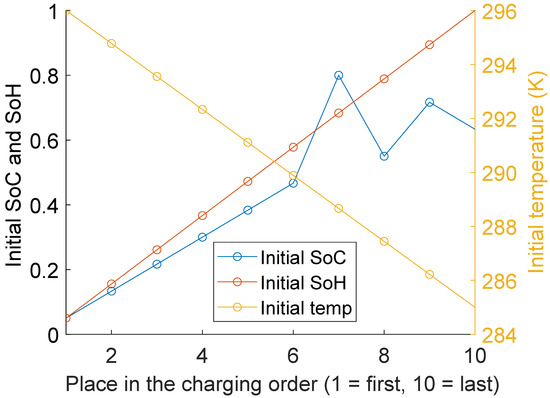
Figure 8.
Charging order of single varied input scenario for SOH, SOC and temperature.
The resulting charging order based on the initial SoH shows that the vehicle with the lowest initial SoH (i.e., an old vehicle) should be charged first and the one with the highest initial SoH should be connected last. Recall from Figure 4 that charging a vehicle soon leads to the highest degradation (see the greedy charging scheme for reference). Also consider that an old vehicle has already shorter RUL than a newer one, because it is closer to its end of life. Therefore, there is more to gain from a fleet perspective by charging the newer vehicles in the optimal scenario (as late as possible) and the older vehicles in the sub-optimal scenario (as soon as possible).
The resulting charging order based on the initial SoC of vehicles shows the same trend as the Initial SoH. First the vehicles with a low initial SoC are charged, because vehicles with a higher initial SoC the needed charge time is lower and therefore more vehicles can be charged later, which is the optimal charging pattern. Also, the optimizer has little influence on the RUL of vehicles with high SoC, because little energy needs to be transferred during the charging session. This is reflected in the alternation in charging order for vehicles with .
For the initial temperature the relationship is linear: first the vehicle with the highest initial temperature is charged and later the vehicles with a lower initial temperatures. Recall from Equation (4) that higher temperatures result in higher capacity loss due to calendar ageing (i.e., a shorter RUL). Likewise, a battery with a higher temperature cools down faster because the difference with the ambient temperature (which is assumed to be constant at 283 °K) is higher. Therefore, from a fleet perspective, it is preferable to charge the warmest battery first, as it cools down faster (than a colder battery) resulting in the least amount of total fleet degradation.
9. Conclusions
This paper presented a method for finding the charging moments (i.e., scheduling) of a fleet of electric vehicles. The method finds a schedule that maximizes the RUL of all the vehicle batteries in the fleet, while taking into variations in RUL due to fabrication-related differences in the batteries and considering that more vehicles than chargers are available.
The method is composed of three key elements: an optimization algorithm for creating a charging profile for a single vehicle; an ML model to predict the battery RUL when the charging profile is used; an optimization algorithm to schedule the charging moments of an entire fleet. The charging profile optimization is based on a modelling strategy that captures the battery dynamics and battery degradation. Such an optimization maximizes the RUL of an individual vehicle. Based on the resulting charging profile, an ML model was created to predict the battery RUL. Such an ML algorithm uses Gaussian Process Regression and is fed by repeatedly applying the optimal charging profiles of the previous step, while considering multiple values in the battery ageing parameters to account for its internal variability. Using the output of such a ML model, the second optimization calculates the charging order, while maximizing the total RUL of the fleet and taking into account common timing requirements of the fleet operator.
To show the method’s applicability, a case study is presented, where a 40-vehicle fleet needs to be charged over a period of 12 h with 5 charging points. A “greedy” charging strategy (i.e., charging as soon as the vehicle arrives to the depot) is used as a comparison baseline. Simulation results shows that in a single-vehicle charging scheme, the RUL is 71% higher when the optimal charging is used than with the baseline strategy. This was achieved by charging the battery as late as possible, as it corresponds in the least amount of ageing. Likewise, simulation results show that the ML model achieved a Root Mean Square Error (RMSE) of 48 days, over the entire lifetime of the battery. Lastly, using the ML model, the optimization algorithm that schedules the charging moments of the fleet improves the total RUL of all the batteries in the fleet by 250%, when compared to a greedy charging scenario.
Future works is currently exploring the inclusion of a grid constraint in the algorithm, where the power that can be drawn from the grid is (dynamically) influenced by the effect of external power consumers or power generators.
Author Contributions
Conceptualization, D.G.; data curation, D.G.; formal analysis, D.G. and R.M.; funding acquisition, S.W.; investigation, D.G.; methodology, D.G. and R.M.; software, D.G.; supervision, R.M., W.v.S. and S.W.; validation, D.G.; visualization, D.G.; writing—original draft, D.G. and R.M.; writing—review and editing, R.M., W.v.S. and S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research has received funding from the European Union’s Horizon 2020 research and innovation programme under grant No. 101006943, title of URBANIZED.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
Steven Wilkins is currently one of this journal’s Guest Editors. The remaining authors have no conflicts of interest to declare.
References
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M.I.; et al. Summary for Policymakers. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPPC: Rome, Italy, 2021. [Google Scholar]
- OECD. Companion to the Inventory of Support Measures for Fossil Fuels 2021; Technical Report; OECD Publishing: Paris, France, 2021. [Google Scholar]
- Sotnyk, I.; Hulak, D.; Yakushev, O.; Yakusheva, O.; Prokopenko, O.V.; Yevdokymov, A. Development of the US electric car market: Macroeconomic determinants and forecasts. Polityka Energetyczna 2020, 23, 147–164. [Google Scholar] [CrossRef]
- Smith, W.J. Can EV (Electric Vehicles) address Ireland’s CO2 emissions from transport? Energy 2010, 35, 4514–4521. [Google Scholar] [CrossRef]
- Orcioni, S.; Conti, M. EV Smart Charging with Advance Reservation Extension to the OCPP Standard. Energies 2020, 13, 3263. [Google Scholar] [CrossRef]
- Xu, B.; Oudalov, A.; Ulbig, A.; Andersson, G.; Kirschen, D.S. Modeling of lithium-ion battery degradation for cell life assessment. IEEE Trans. Smart Grid 2016, 9, 1131–1140. [Google Scholar] [CrossRef]
- Guo, J.; Yang, J.; Lin, Z.; Serrano, C.; Cortes, A.M. Impact analysis of V2G services on EV battery degradation—A review. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar]
- Gyllenswärd, M.; Jerresand, M. Electricity Network Tariff Targeting EV Chargers: A Socio-Economic Analysis; 2020; Available online: https://kth.diva-portal.org/smash/record.jsf?pid=diva2%3A1456508&dswid=4932 (accessed on 1 February 2024).
- Haram, M.H.S.M.; Lee, J.W.; Ramasamy, G.; Ngu, E.E.; Thiagarajah, S.P.; Lee, Y.H. Feasibility of utilising second life EV batteries: Applications, lifespan, economics, environmental impact, assessment, and challenges. Alex. Eng. J. 2021, 60, 4517–4536. [Google Scholar] [CrossRef]
- Canals Casals, L.; Rodríguez, M.; Corchero, C.; Carrillo, R.E. Evaluation of the end-of-life of electric vehicle batteries according to the state-of-health. World Electr. Veh. J. 2019, 10, 63. [Google Scholar] [CrossRef]
- Geerts, D.; Medina, R.; van Sark, W.; Wilkins, S. Optimal charging of electric vehicle fleets: Minimizing battery degradation and grid congestion using Battery Storage Systems. In Proceedings of the Second International Conference on Sustainable Mobility Applications, Renewables and Technology (SMART), Cassino, Italy, 23–25 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–11. [Google Scholar]
- Li, W.; Sengupta, N.; Dechent, P.; Howey, D.; Annaswamy, A.; Sauer, D.U. One-shot battery degradation trajectory prediction with deep learning. J. Power Sources 2021, 506, 230024. [Google Scholar] [CrossRef]
- Rogge, M.; Van der Hurk, E.; Larsen, A.; Sauer, D.U. Electric bus fleet size and mix problem with optimization of charging infrastructure. App. Energy 2018, 211, 282–295. [Google Scholar] [CrossRef]
- Houbbadi, A.; Trigui, R.; Pelissier, S.; Bouton, T.; Redondo-Iglesias, E. Multi-objective optimisation of the management of electric bus fleet charging. In Proceedings of the 2017 IEEE Vehicle Power and Propulsion Conference (VPPC), Belfort, France, 11–14 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Houbbadi, A.; Trigui, R.; Pelissier, S.; Redondo-Iglesias, E.; Bouton, T. Optimal scheduling to manage an electric bus fleet overnight charging. Energies 2019, 12, 2727. [Google Scholar] [CrossRef]
- Carli, R.; Dotoli, M. A distributed control algorithm for optimal charging of electric vehicle fleets with congestion management. IFAC-PapersOnLine 2018, 51, 373–378. [Google Scholar] [CrossRef]
- Lopes, J.; Peças, A.; Soares, F.J.; Almeida, P.M.R. Integration of electric vehicles in the electric power system. Proc. IEEE 2010, 99, 168–183. [Google Scholar] [CrossRef]
- Wu, J.; Su, H.; Meng, J.; Lin, M. Electric vehicle charging scheduling considering infrastructure constraints. Energy 2023, 278, 127806. [Google Scholar] [CrossRef]
- Su, C.; Chen, H. A review on prognostics approaches for remaining useful life of lithium-ion battery. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Kunming, China, 22–25 September 2017; IOP Publishing: Bristol, UK, 2017; Volume 93, pp. 1–8. [Google Scholar]
- Andre, D.; Nuhic, A.; Soczka-Guth, T.; Sauer, D.U. Comparative study of a structured neural network and an extended Kalman filter for state of health determination of lithium-ion batteries in hybrid electricvehicles. Eng. Appl. Artif. Intell. 2013, 26, 951–961. [Google Scholar] [CrossRef]
- Dong, H.; Jin, X.; Lou, Y.; Wang, C. Lithium-ion battery state of health monitoring and remaining useful life prediction based on support vector regression-particle filter. J. Power Sources 2014, 271, 114–123. [Google Scholar] [CrossRef]
- Liu, D.; Pang, J.; Zhou, J.; Peng, Y.; Pecht, M. Prognostics for state of health estimation of lithium-ion batteries based on combination Gaussian process functional regression. Microelectron. Reliab. 2013, 53, 832–839. [Google Scholar] [CrossRef]
- Liu, H.; Xiao, Q.; Jiao, Z.; Meng, J.; Mu, Y.; Hou, K.; Yu, X.; Guo, S.; Jia, H. LightGBM-Based Prediction of Remaining Useful Life for Electric Vehicle Battery under Driving Conditions. In Proceedings of the 2020 IEEE Sustainable Power and Energy Conference (iSPEC), Chengdu, China, 23–25 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 2577–2582. [Google Scholar]
- Huang, B.; Hu, M.; Chen, L.; Jin, G.; Liao, S.; Fu, C.; Wang, D.; Cao, K. A Novel Electro-Thermal Model of Lithium-Ion Batteries Using Power as the Input. Electronics 2021, 10, 2753. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Käbitz, S.; Ecker, M.; Sauer, D.U. A holistic aging model for Li (NiMnCo) O2 based 18650 lithium-ion batteries. J. Power Sources 2014, 257, 325–334. [Google Scholar] [CrossRef]
- Redondo-Iglesias, E.; Venet, P.; Pelissier, S. Calendar and cycling ageing combination of batteries in electric vehicles. Microelectron. Reliab. 2018, 88, 1212–1215. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Gao, Y.; Zhang, W.; Liu, Q.; Hu, X. Charging optimization in lithium-ion batteries based on temperature rise and charge time. Appl. Energy 2017, 194, 569–577. [Google Scholar] [CrossRef]
- Badillo, S.; Banfai, B.; Birzele, F.; Davydov, I.I.; Hutchinson, L.; Kam-Thong, T.; Siebourg-Polster, J.; Steiert, B.; Zhang, J.D. An introduction to machine learning. Clin. Pharmacol. Ther. 2020, 107, 871–885. [Google Scholar] [CrossRef]
- Wang, J. An intuitive tutorial to Gaussian processes regression. arXiv 2020, arXiv:2009.10862. [Google Scholar]
- Zhang, F.; O’Donnell, L.J. Support vector regression. In Machine Learning; Elsevier: Amsterdam, The Netherlands, 2020; pp. 123–140. [Google Scholar]
- Carrizosa, E.; Molero-Río, C.; Romero Morales, D. Mathematical optimization in classification and regression trees. Top 2021, 29, 5–33. [Google Scholar] [CrossRef]
- Antorán, J.; Allingham, J.; Hernández-Lobato, J.M. Depth uncertainty in neural networks. Adv. Neural Inf. Process. Syst. 2020, 33, 10620–10634. [Google Scholar]
- Nhu, V.H.; Shirzadi, A.; Shahabi, H.; Singh, S.K.; Al-Ansari, N.; Clague, J.J.; Jaafari, A.; Chen, W.; Miraki, S.; Dou, J.; et al. Shallow landslide susceptibility mapping: A comparison between logistic model tree, logistic regression, naïve bayes tree, artificial neural network, and support vector machine algorithms. Int. J. Environ. Res. Public Health 2020, 17, 2749. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian processes in machine learning. In Proceedings of the Summer School on Machine Learning, Canberra, Australia, 11–22 February 2002; Springer: Berlin/Heidelberg, Germany, 2003; pp. 63–71. [Google Scholar]
- Wang, Z.P.; Liu, P.; Wang, L.F. Analysis on the capacity degradation mechanism of a series lithium-ion power battery pack based on inconsistency of capacity. Chin. Phys. B 2013, 22, 088801. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, J.; Yang, Y.; Mu, L.; Wei, C.; Yu, X.; Pianetta, P.; Zhao, K.; Cloetens, P.; Lin, F.; et al. Machine-learning-revealed statistics of the particle-carbon/binder detachment in lithium-ion battery cathodes. Nat. Commun. 2020, 11, 2310. [Google Scholar] [CrossRef]
- Danna, E.; Rothberg, E.; Pape, C.L. Exploring relaxation induced neighborhoods to improve MIP solutions. Math. Prog. 2005, 102, 71–90. [Google Scholar] [CrossRef]
- Cornuéjols, G. Valid inequalities for mixed integer linear programs. Math. Program. 2008, 112, 3–44. [Google Scholar] [CrossRef]
- Kuendee, P.; Janjarassuk, U. A comparative study of mixed-integer linear programming and genetic algorithms for solving binary problems. In Proceedings of the 2018 5th International Conference on Industrial Engineering and Applications (ICIEA), Singapore, 26–28 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 284–288. [Google Scholar]
- Onda, K.; Kameyama, H.; Hanamoto, T.; Ito, K. Experimental study on heat generation behavior of small lithium-ion secondary batteries. J. Electrochem. Soc. 2003, 150, A285–A291. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).