Adaptive Integrated Thermal Management System for a Stable Driving Environment in Battery Electric Vehicles
Abstract
1. Introduction
1.1. Research Background
1.2. Research Survey
1.3. Motivation and Novelty
2. Simulations Methods
2.1. Powertrain System Model
2.1.1. High-Voltage Battery Model
2.1.2. Power Electronics Module Model
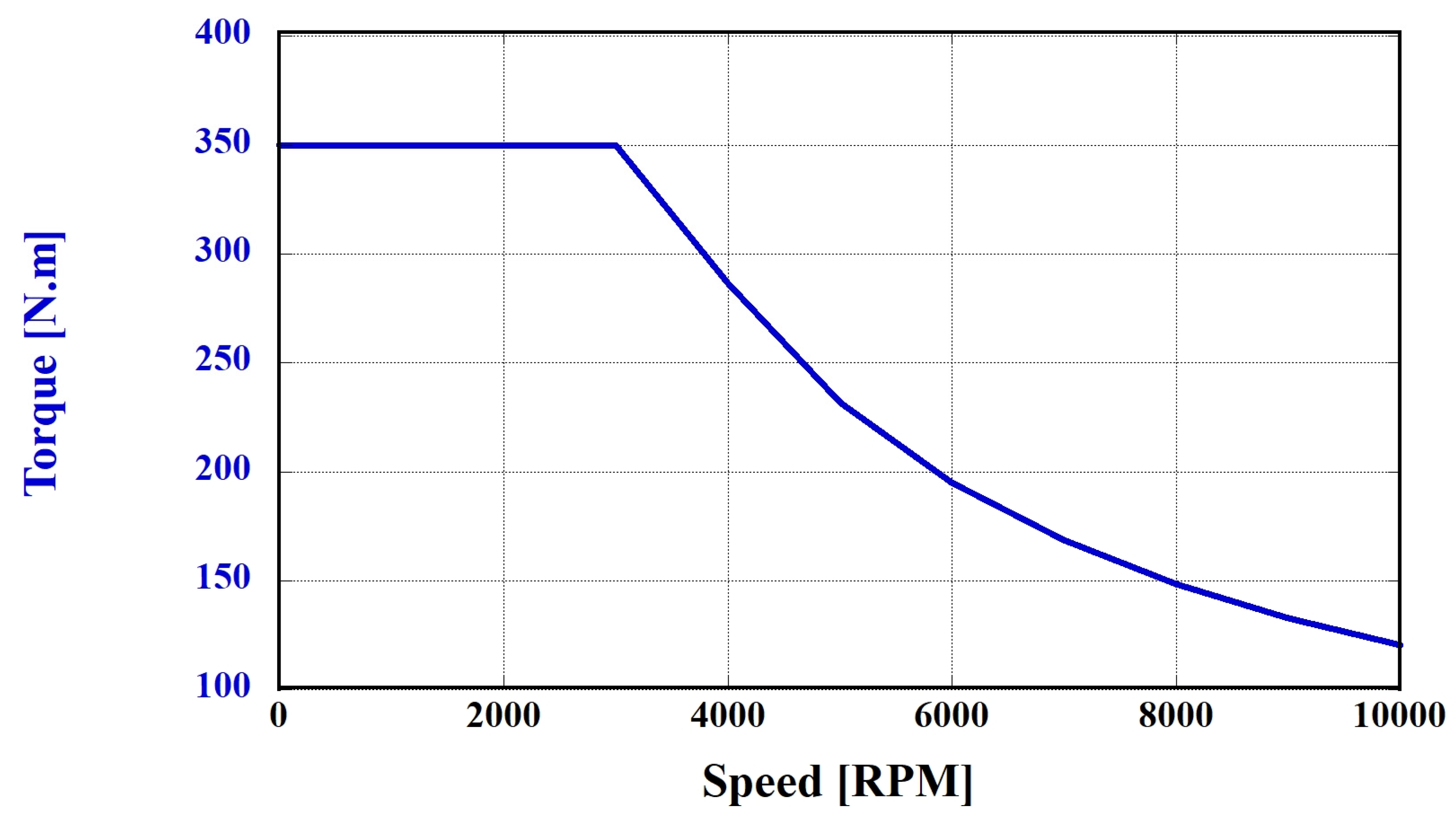
2.1.3. Reducer Model
2.1.4. Vehicle Dynamic Model
2.1.5. DC/DC Converter, Low-Voltage Battery, and Electrical Loads Model
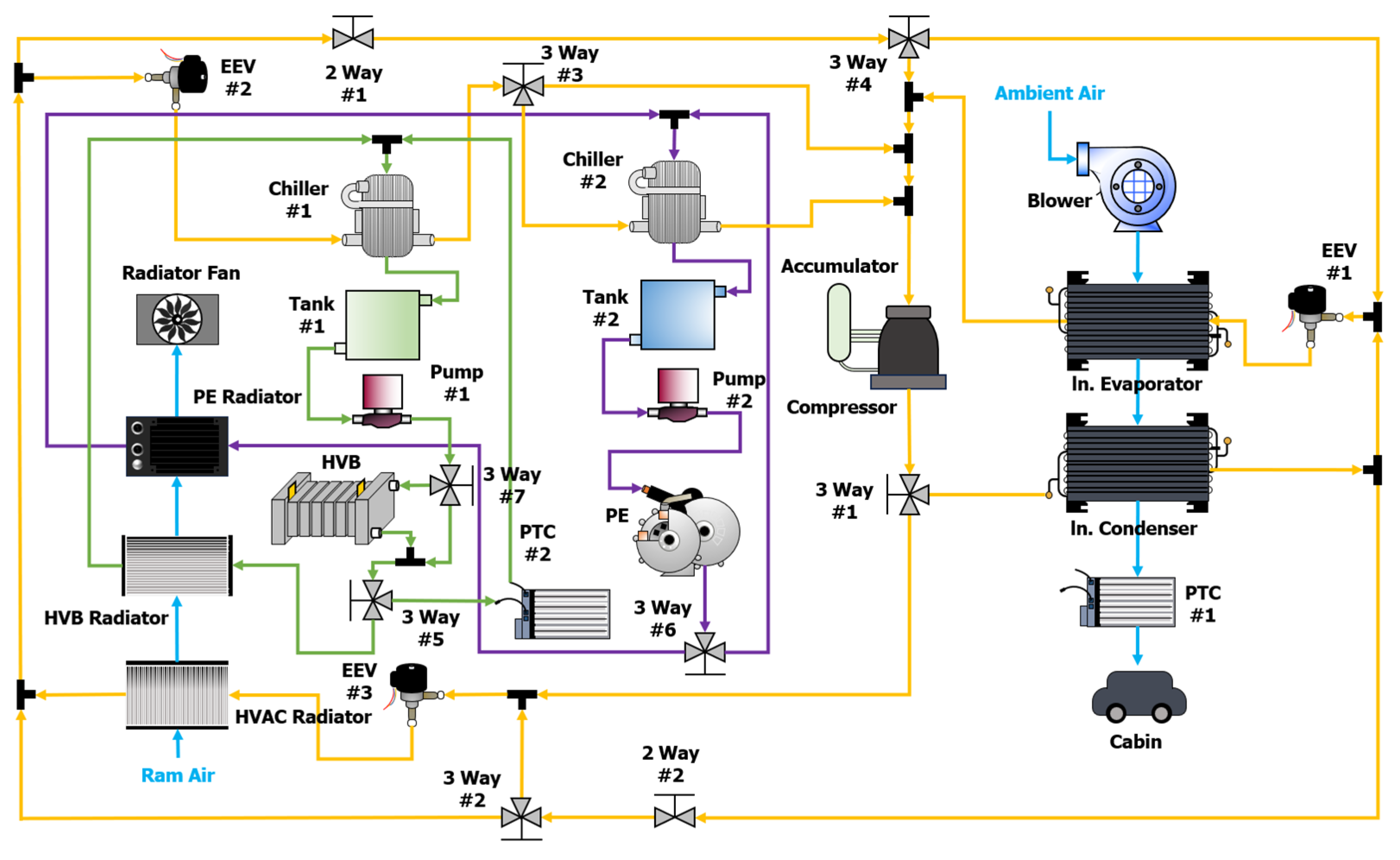
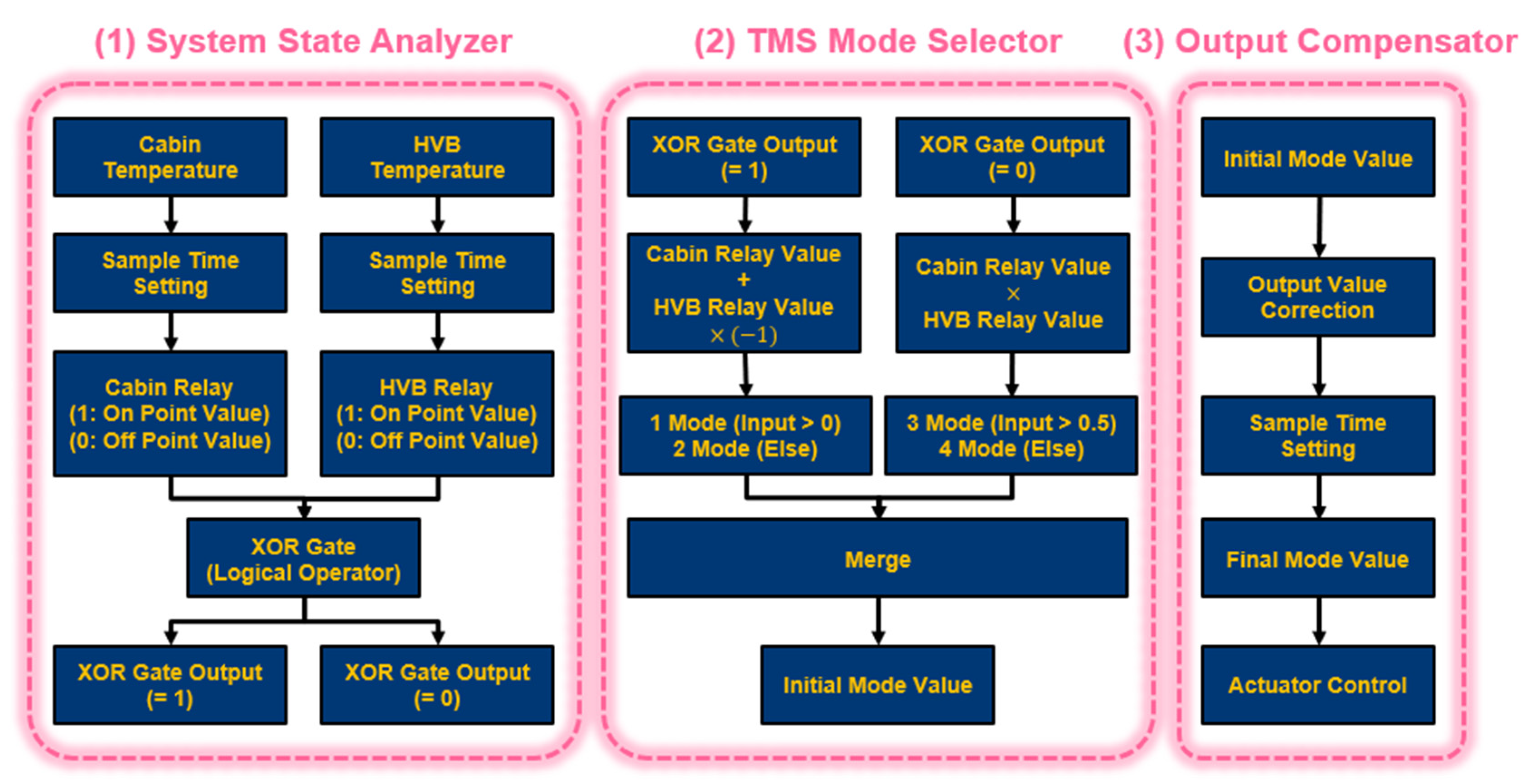
2.2. Integrated Thermal Management System Model
2.2.1. Compressor Model
2.2.2. Electric Expansion Valve Model
2.2.3. Water Pump Model
2.2.4. Chiller Model
2.2.5. Radiator, Condenser, and Evaporator Model
2.2.6. Positive Temperature Coefficient Heater
2.2.7. Ram Air and Radiator Fan Model
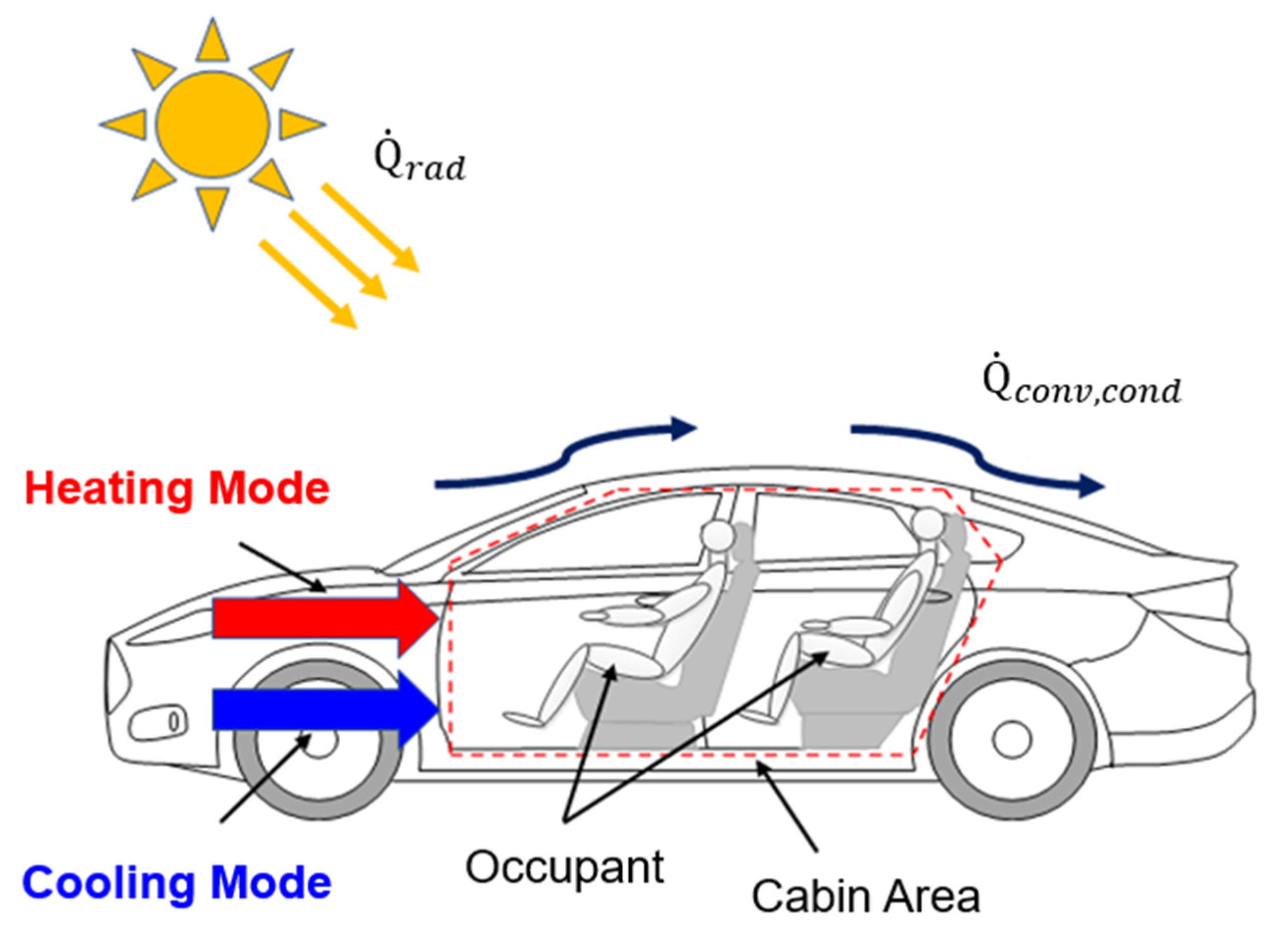
2.2.8. Cabin Model
2.2.9. HVB and PE Module Cooling Channel Model
3. Results and Discussion
3.1. Simulation Scenario
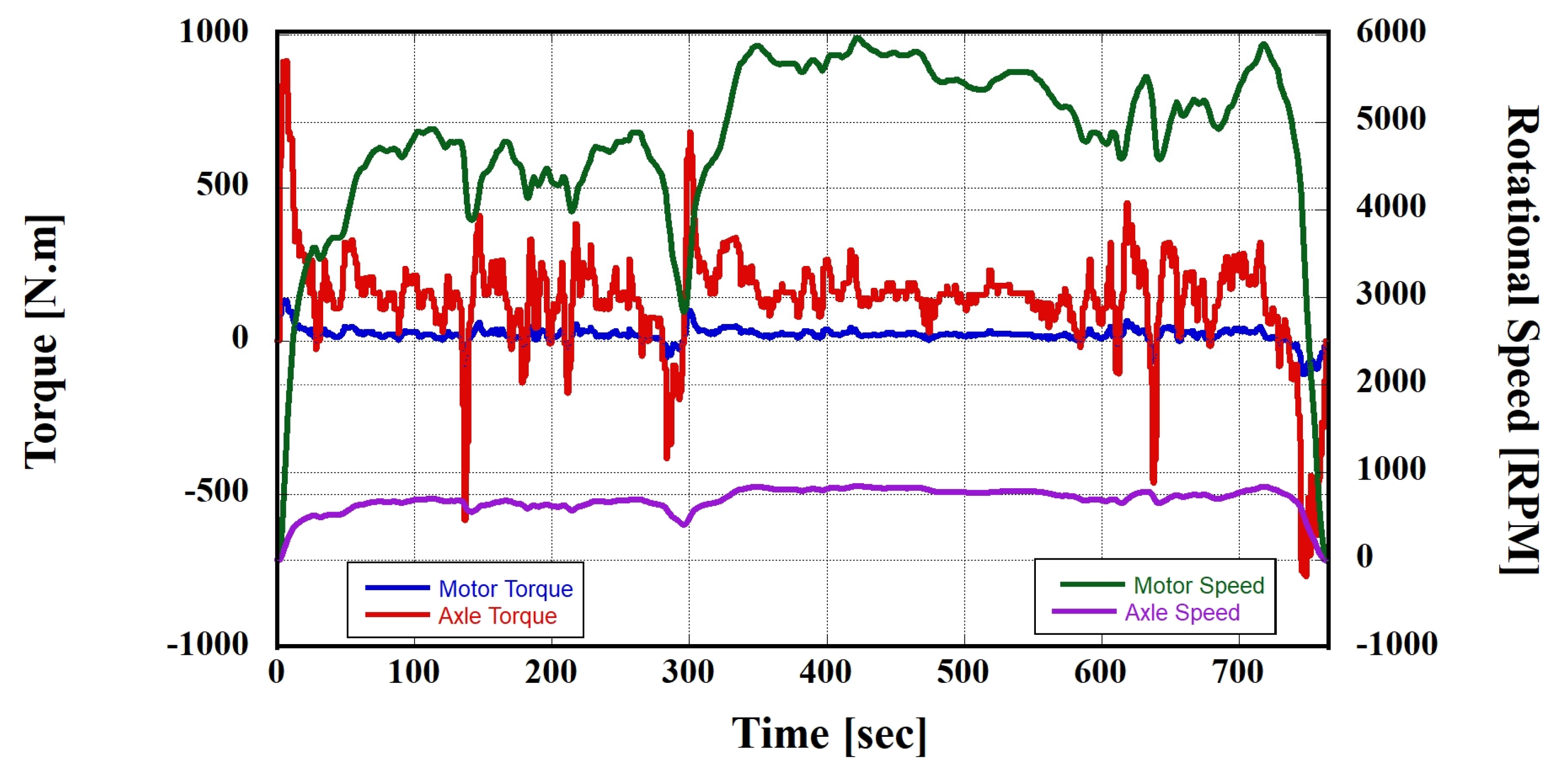
3.2. Results of the Powertrain System Model of the Battery Electric Vehicle
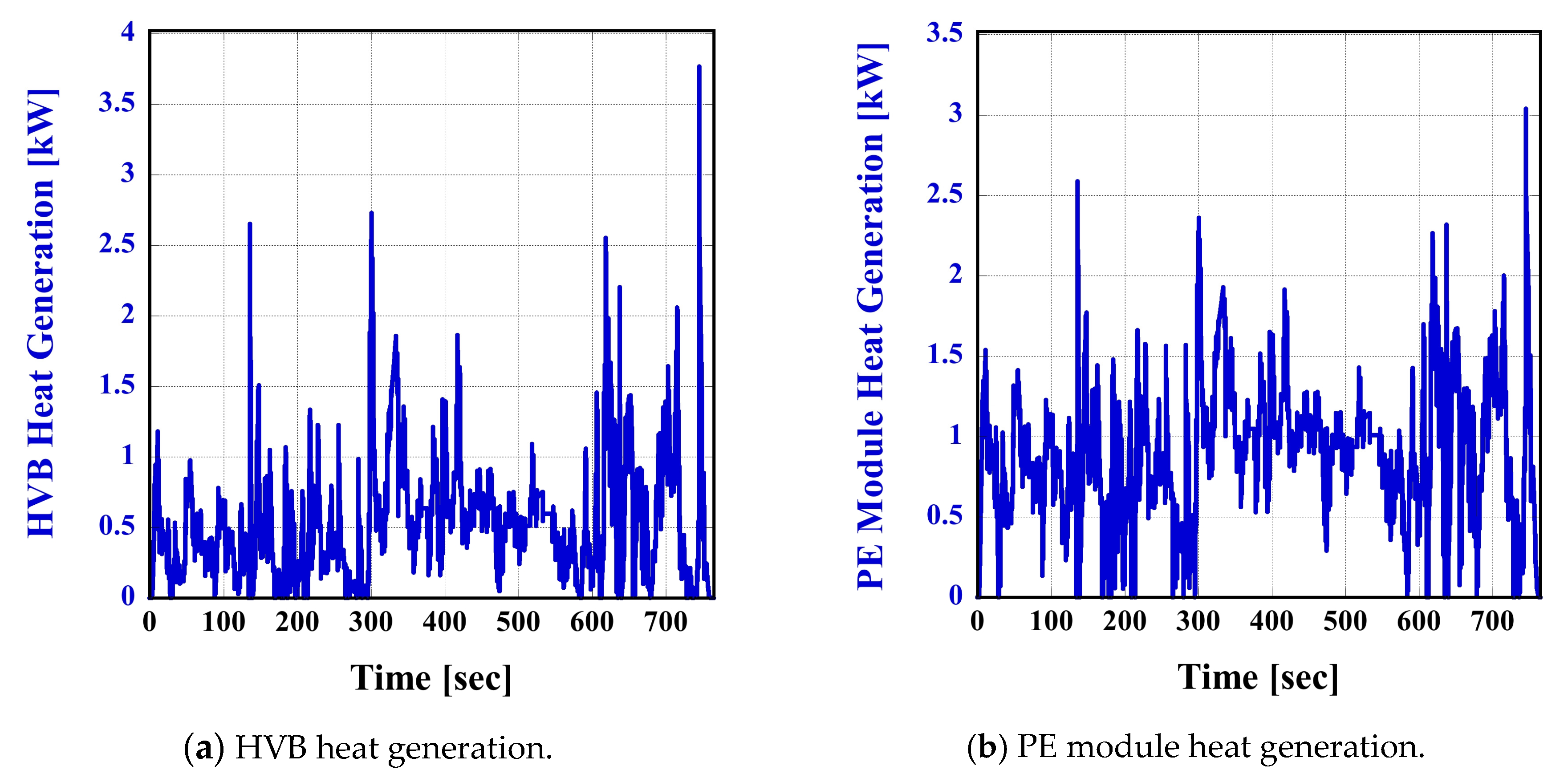
3.3. Results of the Integrated Thermal Management System Model
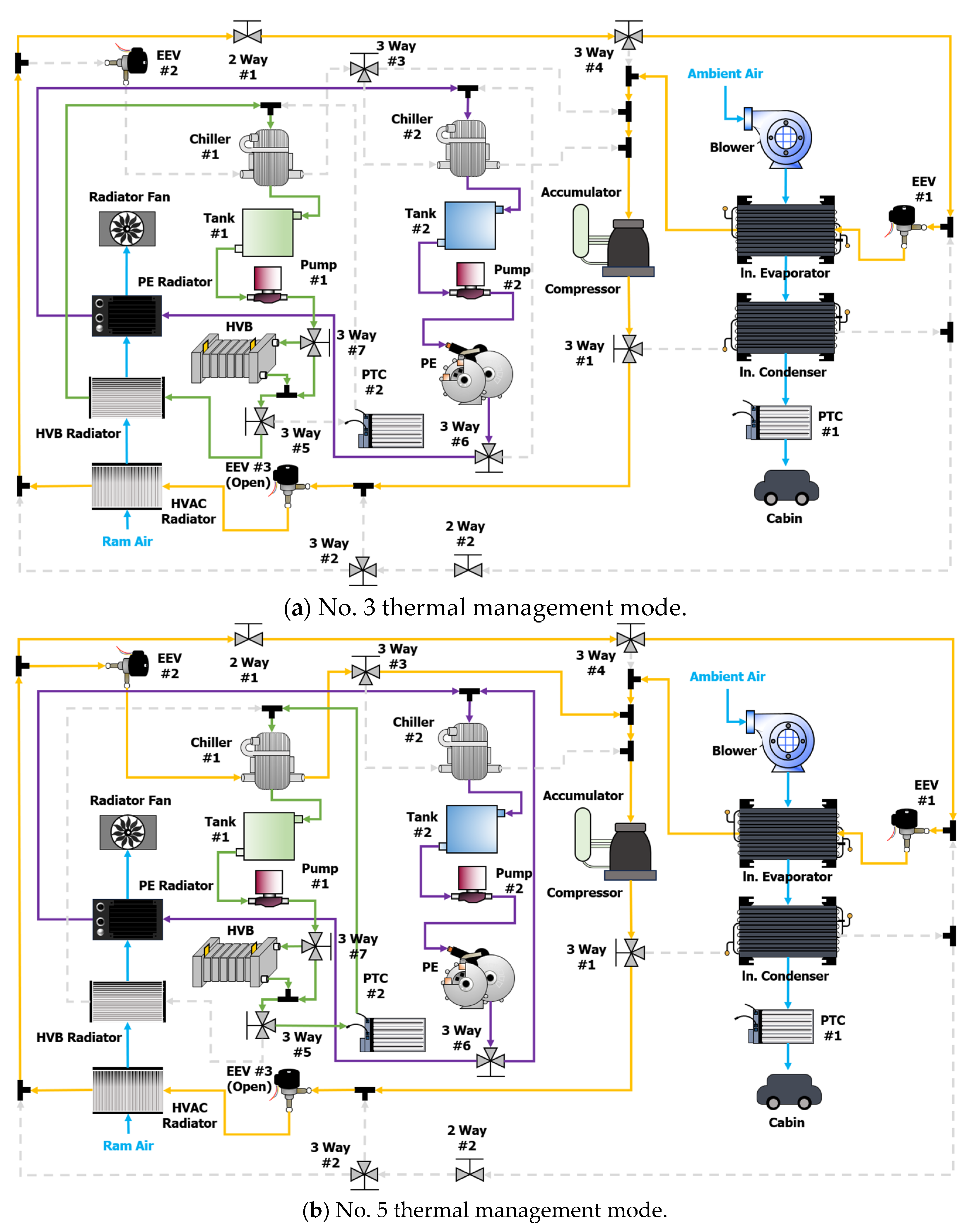
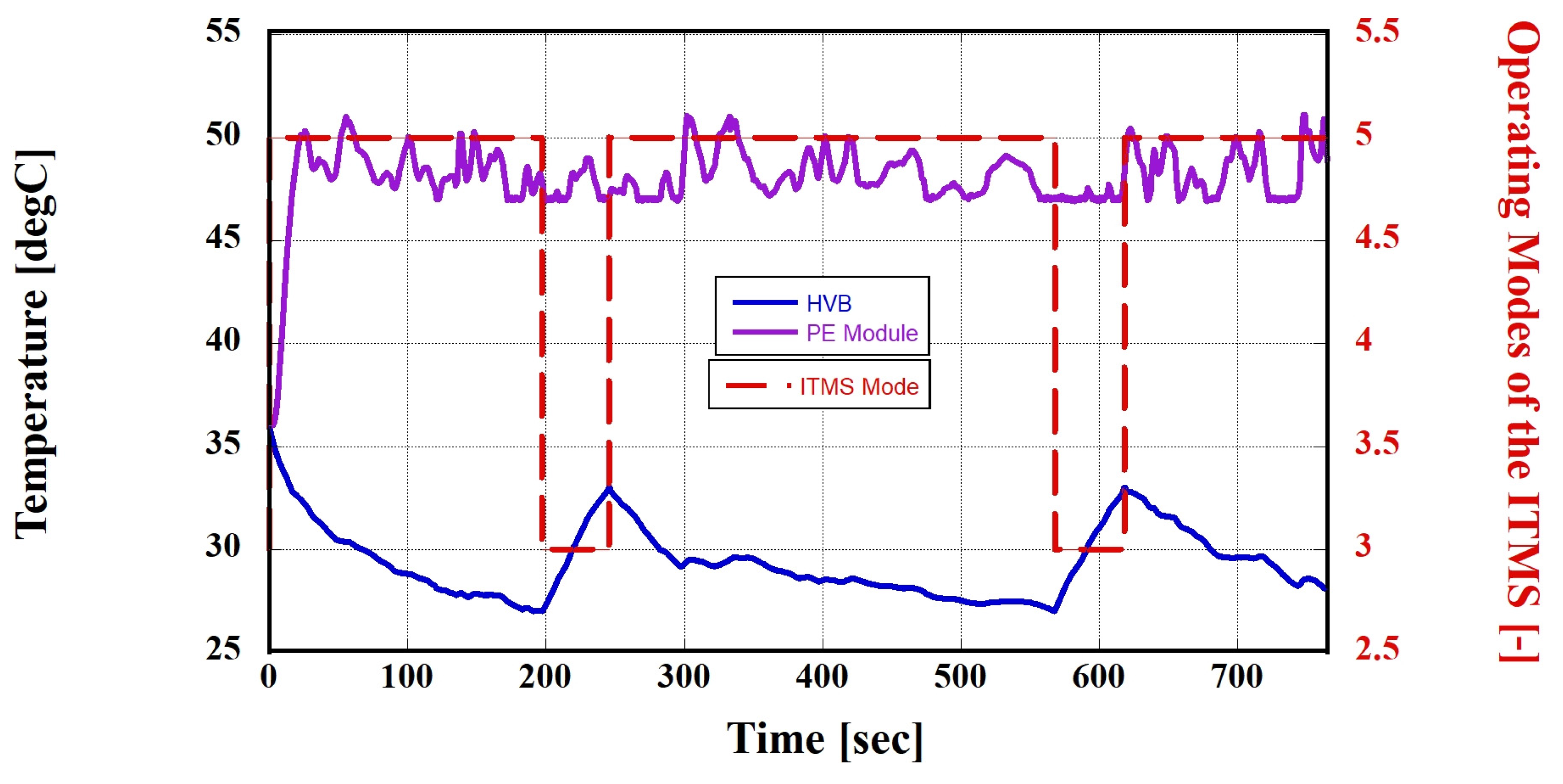
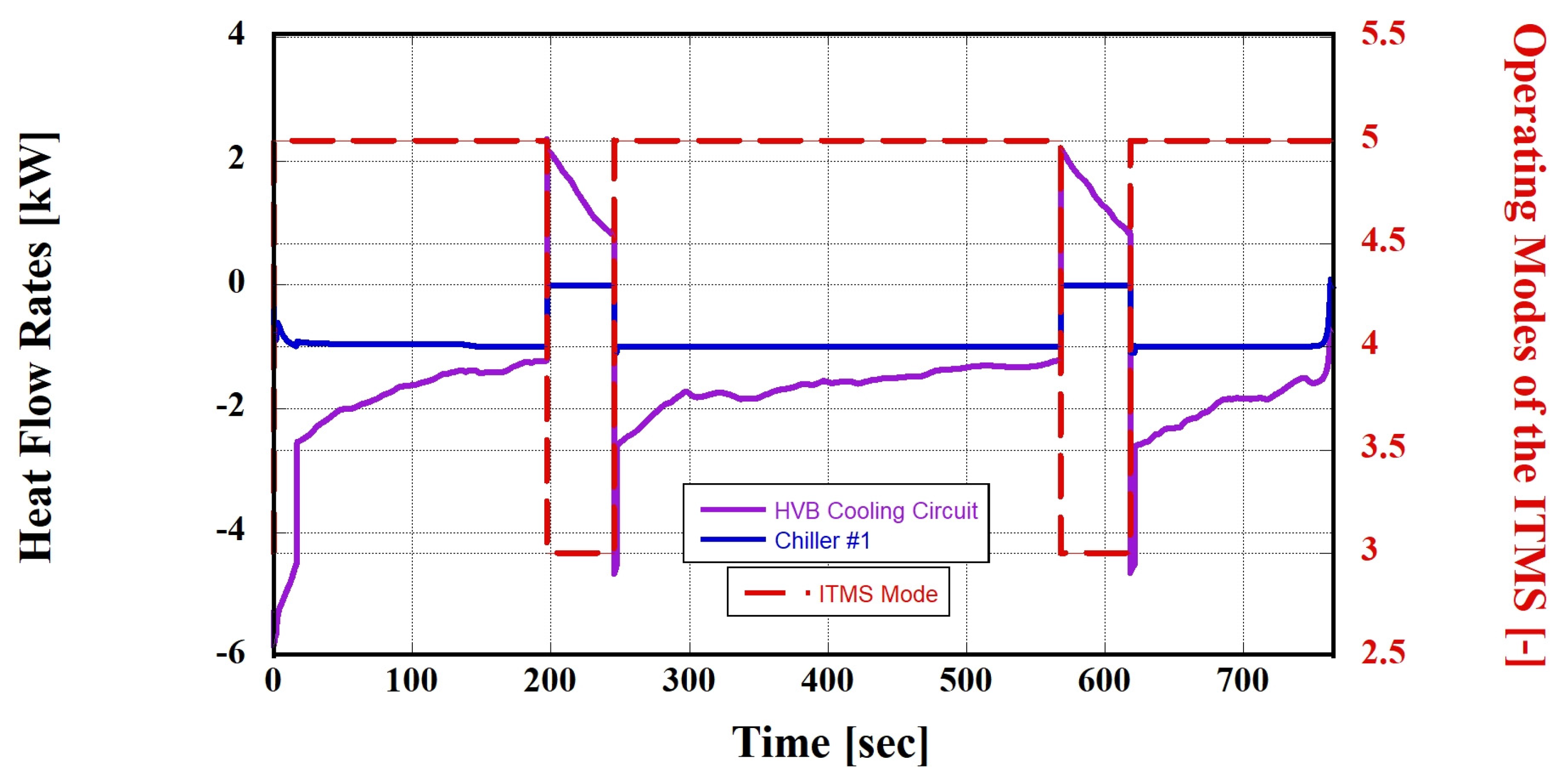
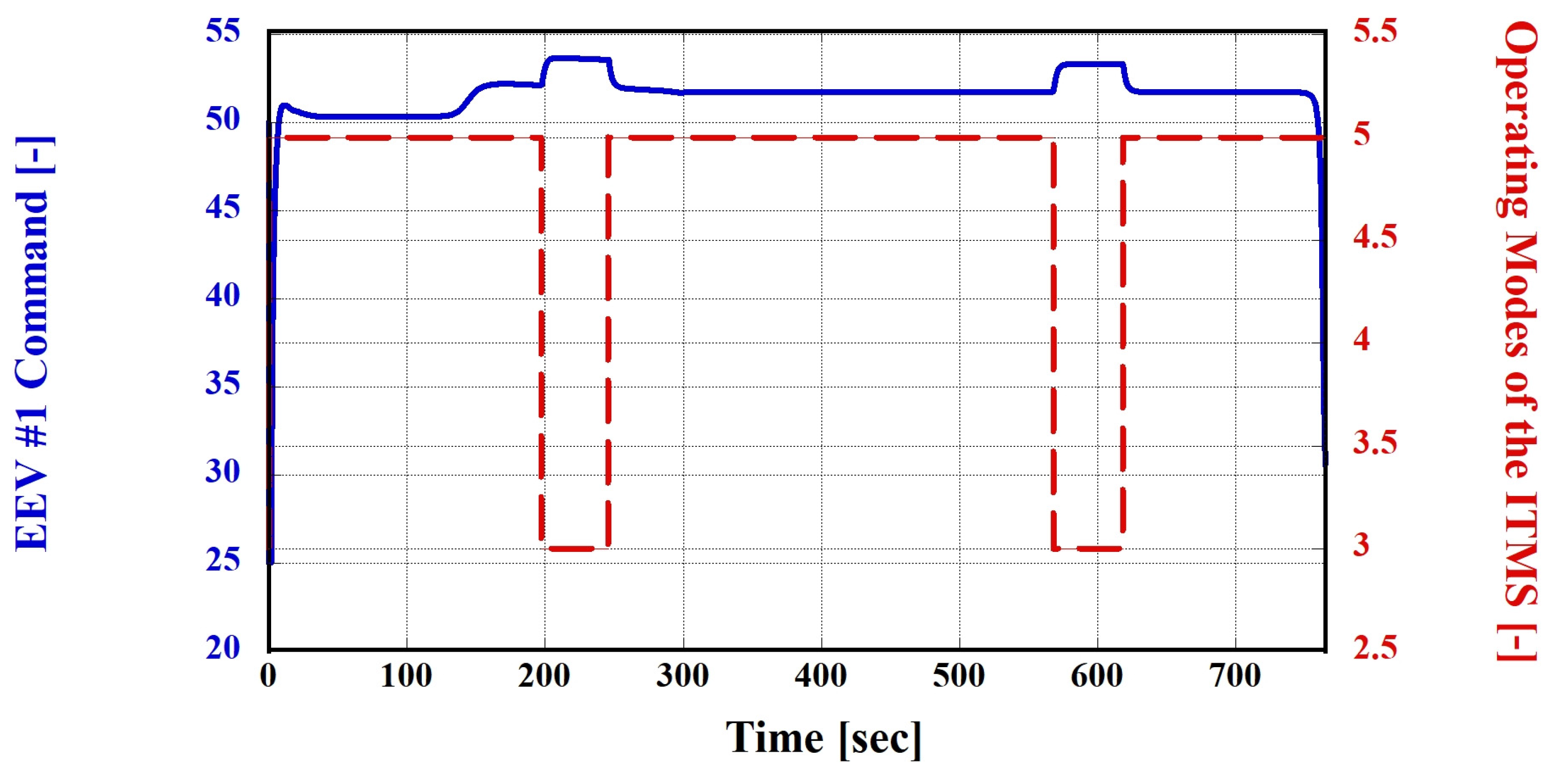
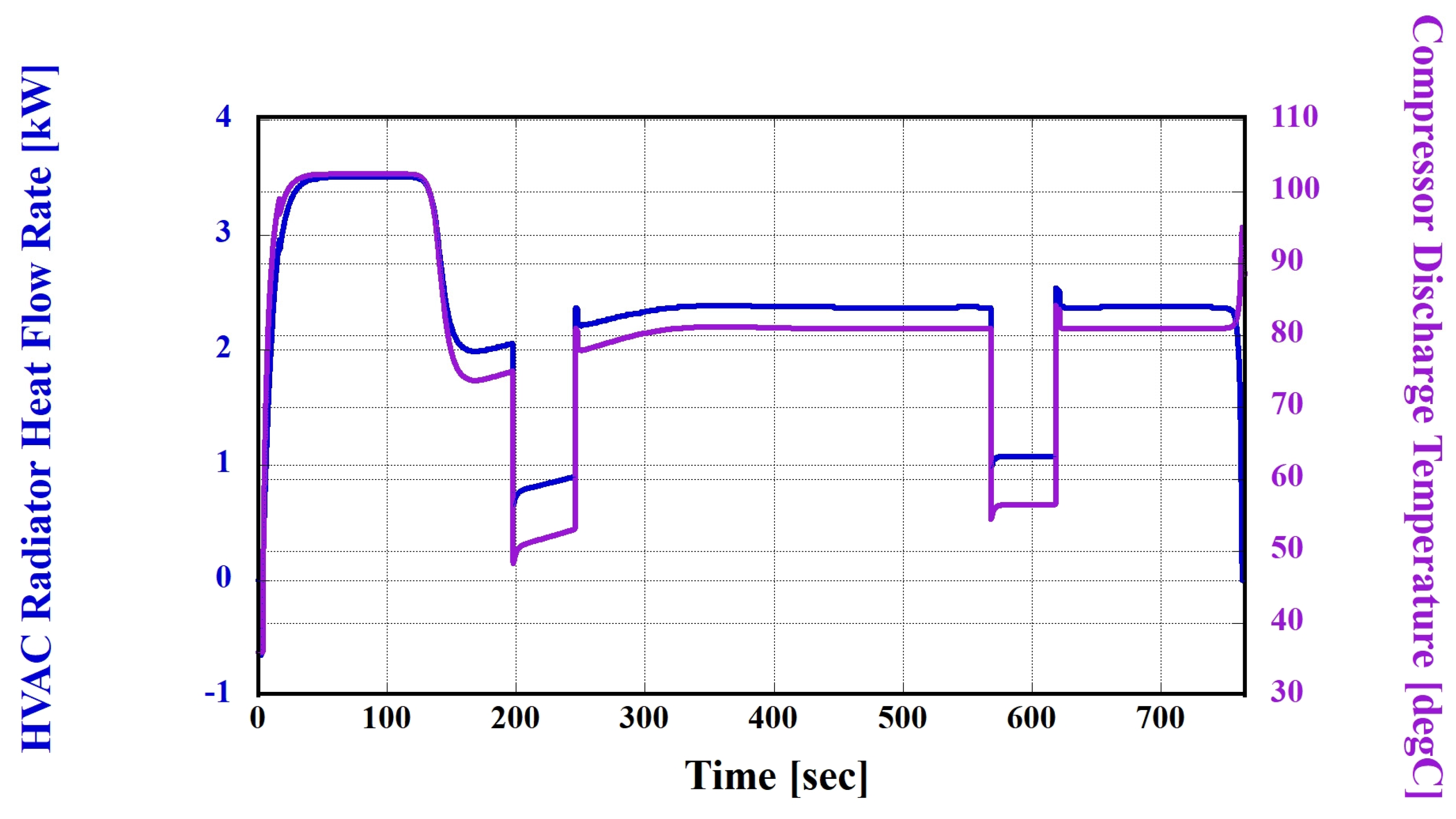
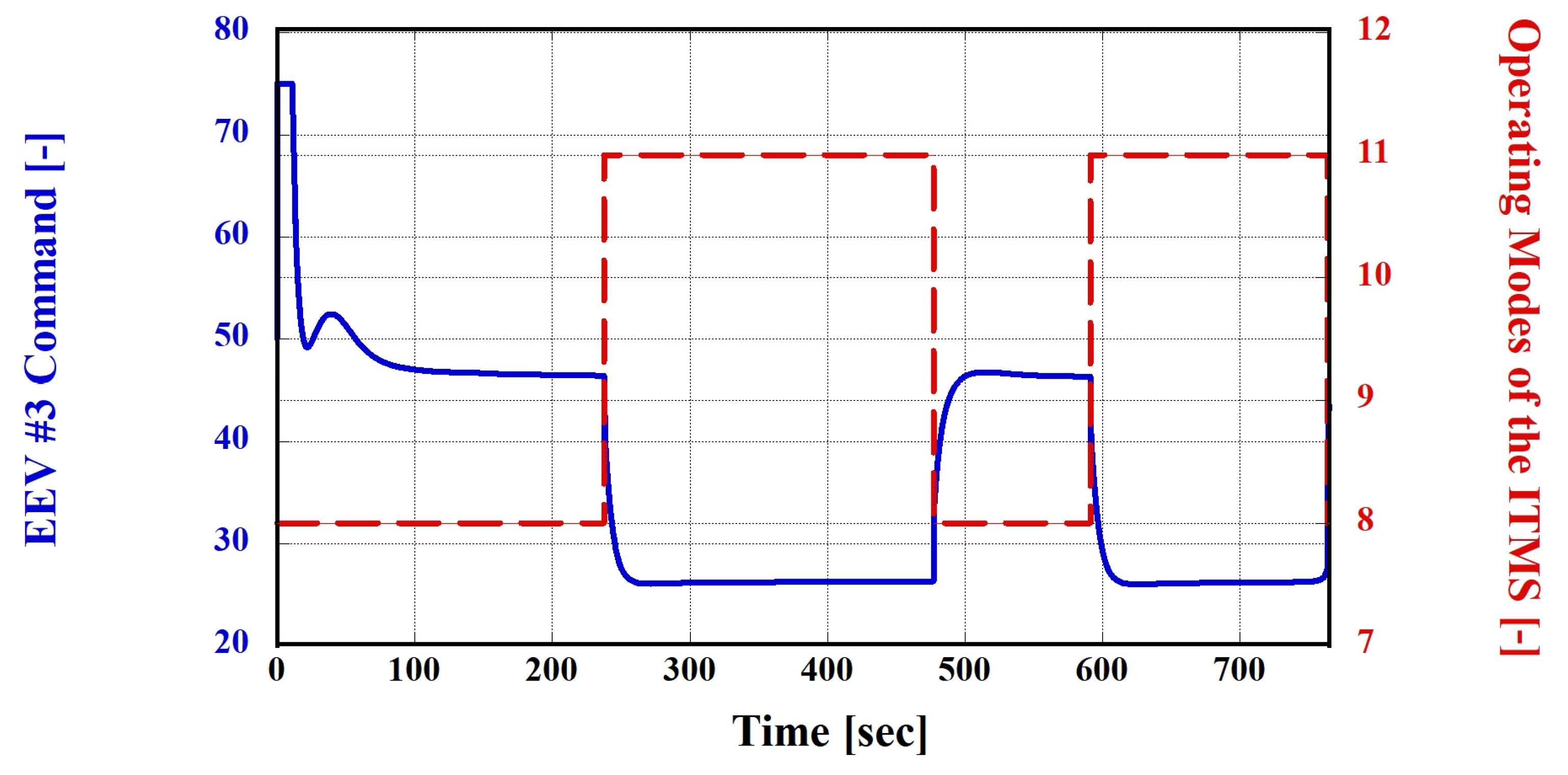
3.3.1. Simulation Case 1 (Hot Climate): Using Nos. 3 and 5 Thermal Management Modes
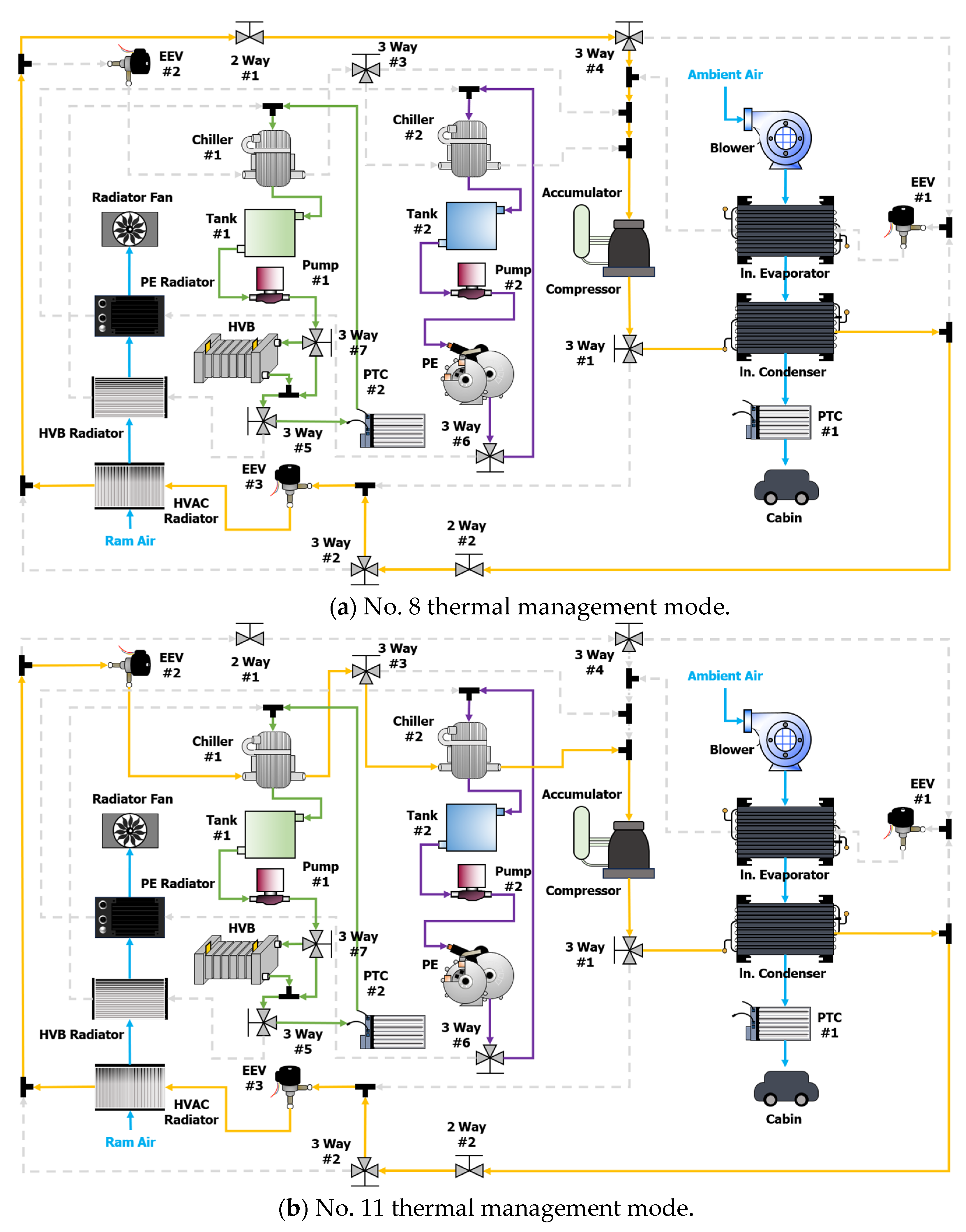
3.3.2. Simulation Case 2 (Cold Climate): Using Nos. 8 and 11 Thermal Management Modes
4. Conclusions
- The powertrain system of the BEV was modeled to calculate thermal loads as it tracks the HWFET driving cycle, and a precise thermal load was generated with a speed-tracking error of less than 0.0005%.
- Through this study, the designed and modeled ITMS based on a heat pump system for BEV was able to cool the HVB using the HVAC system under high-temperature conditions with an outside air temperature of 36 °C. Additionally, under low-temperature conditions with an outside air temperature of −10 °C, it could perform cabin heating using not only the outside air as a heat source but also waste heat from the HVB and PE module components.
- In this study, the designed and modeled heat-pump-system-based ITMS was evaluated under high-load conditions, specifically the HWFET driving cycle. It demonstrated stable thermal control for the cabin, HVB, and PE module, effectively adapting to both high-temperature conditions with an outside air temperature of 36 °C and low-temperature conditions with an outside air temperature of −10 °C.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nonobe, Y. Development of the fuel cell vehicle mirai. IEEJ Trans. Electr. Electron. Eng. 2017, 12, 5–9. [Google Scholar] [CrossRef]
- Selleri, T.; Melas, A.D.; Franzetti, J.; Ferrarese, C.; Giechaskiel, B.; Suarez-Bertoa, R. On-Road and Laboratory Emissions from Three Gasoline Plug-In Hybrid Vehicles—Part 1: Regulated and Unregulated Gaseous Pollutants and Greenhouse Gases. Energies 2022, 15, 2401. [Google Scholar] [CrossRef]
- Fuinhas, J.A.; Koengkan, M.; Leitão, N.C.; Nwani, C.; Uzuner, G.; Dehdar, F.; Relva, S.; Peyerl, D. Effect of battery electric vehicles on greenhouse gas emissions in 29 European Union countries. Sustainability 2021, 13, 13611. [Google Scholar] [CrossRef]
- Office of Energy Efficiency & Renewable Energy. FOTW #1275, 30 January 2023: Monthly Plug-in Electric Vehicle Sales in the United States Exceeded 7% of All New Light-Duty Vehicle Sales for the First Time in September 2022. 2023. Available online: https://www.energy.gov/eere/vehicles/articles/fotw-1275-january-30-2023-monthly-plug-electric-vehicle-sales-united-states (accessed on 30 January 2023).
- Falchetta, G.; Noussan, M. Electric vehicle charging network in Europe: An accessibility and deployment trends analysis. Transp. Res. D Transp. Environ. 2021, 94, 102813. [Google Scholar] [CrossRef]
- Hao, X.; Wang, H.; Lin, Z.; Ouyang, M. Seasonal effects on electric vehicle energy consumption and driving range: A case study on personal, taxi, and ridesharing vehicles. J. Clean. Prod. 2020, 249, 119403. [Google Scholar] [CrossRef]
- Lahlou, A.; Ossart, F.; Boudard, E.; Roy, F.; Bakhouya, M. Optimal management of thermal comfort and driving range in electric vehicles. Energies 2020, 13, 4471. [Google Scholar] [CrossRef]
- Park, M.H.; Kim, S.C. Heating performance characteristics of high-voltage PTC heater for an electric vehicle. Energies 2017, 10, 1494. [Google Scholar] [CrossRef]
- Zou, H.; Wang, W.; Zhang, G.; Qin, F.; Tian, C.; Yan, Y. Experimental investigation on an integrated thermal management system with heat pipe heat exchanger for electric vehicle. Energy Convers. Manag. 2016, 118, 88–95. [Google Scholar] [CrossRef]
- 2011 Nissan LEAF—Repair Manual—High Voltage Cooling System (HCO). 2015. Available online: https://ownersmanuals2.com/nissan/leaf-2011-repair-manual-high-voltage-cooling-system-hco-43099 (accessed on 1 August 2022).
- 2011 Nissan LEAF—Repair Manual—Heater & Air Condition (Section HA). 2015. Available online: https://ownersmanuals2.com/nissan/leaf-2011-repair-manual-heater-air-condition-section-ha-43101 (accessed on 1 August 2022).
- Al Faruque, M.A.; Vatanparvar, K. Modeling, analysis, and optimization of Electric Vehicle HVAC systems. In Proceedings of the 2016 21st Asia and South Pacific Design Automation Conference (ASP-DAC), Macao, China, 25–28 January 2016; pp. 423–428. [Google Scholar]
- Park, C.H.; Jee, Y.J.; Lee, D.W. Development trends of heat-pump system for electric driven vehicles. Auto J. 2011, 33, 29–35. [Google Scholar]
- Kang, H.S.; Sim, S.; Shin, Y.H. A numerical study on the light-weight design of PTC heater for an electric vehicle heating system. Energies 2018, 11, 1276. [Google Scholar] [CrossRef]
- HYUNDAI Motors. Hyundai and Kia Turn up EV Efficiency with New Heat Pump Technology. 2020. Available online: https://www.hyundai.news/eu/articles/press-releases/hyundai-and-kia-turn-up-ev-efficiency-with-new-heat-pump-technology.html (accessed on 9 June 2020).
- Xu, B.; Arjmandzadeh, Z. Parametric study on thermal management system for the range of full (Tesla Model S)/compact-size (Tesla Model 3) electric vehicles. Energy Convers. Manag. 2023, 278, 116753. [Google Scholar] [CrossRef]
- Wang, F.; Lin, Z.; Liu, L.; Wei, X.; Lin, S.; Dai, L.; Wei, Y.; Liang, C.C.; Liaw, B. Does polarization increase lead to capacity fade? J. Electrochem. Soc. 2020, 167, 090549. [Google Scholar] [CrossRef]
- Aris, A.M.; Shabani, B. An experimental study of a lithium ion cell operation at low temperature conditions. Energy Procedia 2017, 110, 128–135. [Google Scholar] [CrossRef]
- Bodenes, L.; Naturel, R.; Martinez, H.; Dedryvère, R.; Menetrier, M.; Croguennec, L.; Pérès, J.-P.; Tessier, C.; Fischer, F. Lithium secondary batteries working at very high temperature: Capacity fade and understanding of aging mechanisms. J. Power Sources 2013, 236, 265–275. [Google Scholar] [CrossRef]
- Abada, S.; Petit, M.; Lecocq, A.; Marlair, G.; Sauvant-Moynot, V.; Huet, F. Combined experimental and modeling approaches of the thermal runaway of fresh and aged lithium-ion batteries. J. Power Sources 2018, 399, 264–273. [Google Scholar] [CrossRef]
- Chen, Y.L.; Ni, J.; Shao, W.; Azzam, R. Experimental study on the influence of temperature on the mechanical properties of granite under uni-axial compression and fatigue loading. Int. J. Rock Mech. Min. Sci. 2012, 56, 62–66. [Google Scholar] [CrossRef]
- Bingyi, Z.; Wei, Z.; Fuyu, Z.; Guihong, F. Design and starting process analysis of multipolar line-start PMSM. In Proceedings of the 2007 International Conference on Electrical Machines and Systems (ICEMS), Seoul, Republic of Korea, 8–11 October 2007; pp. 1629–1634. [Google Scholar]
- Sathik, M.H.M.; Sundararajan, P.; Sasongko, F.; Pou, J.; Natarajan, S. Comparative analysis of IGBT parameters variation under different accelerated aging tests. IEEE Trans. Electron. Devices 2020, 67, 1098–1105. [Google Scholar] [CrossRef]
- Na, S.I.; Chung, Y.; Kim, M.S. Performance analysis of an electric vehicle heat pump system with a desiccant dehumidifier. Energy Convers. Manag. 2021, 236, 114083. [Google Scholar] [CrossRef]
- Miri, I.; Fotouhi, A.; Ewin, N. Electric vehicle energy consumption modelling and estimation—A case study. Int. J. Energy Res. 2021, 45, 501–520. [Google Scholar] [CrossRef]
- Hariharan, C.; Gunadevan, D.; Prakash, S.A.; Latha, K.; Raj, V.A.A.; Velraj, R. Simulation of battery energy consumption in an electric car with traction and HVAC model for a given source and destination for reducing the range anxiety of the driver. Energy 2022, 249, 123657. [Google Scholar] [CrossRef]
- Singirikonda, S.; Obulesu, Y.P. Adaptive secondary loop liquid cooling with refrigerant cabin active thermal management system for electric vehicle. J. Energy Storage 2022, 50, 104624. [Google Scholar] [CrossRef]
- Department of Climate Change, Energy, the Environment and Water. Global Warming Potential Values of Hydrofluorocarbon Refrigerants. Available online: https://www.dcceew.gov.au/environment/protection/ozone/rac/global-warming-potential-values-hfc-refrigerants (accessed on 10 October 2021).
- Vikram, S.; Vashisht, S.; Rakshit, D. Performance analysis of liquid-based battery thermal management system for Electric Vehicles during discharge under drive cycles. J. Energy Storage 2022, 55, 105737. [Google Scholar] [CrossRef]
- Zou, H.; Jiang, B.; Wang, Q.; Tian, C.; Yan, Y. Performance analysis of a heat pump air conditioning system coupling with battery cooling for electric vehicles. Energy Procedia 2014, 61, 891–894. [Google Scholar] [CrossRef]
- Park, I.; Kim, D.; Cha, H. EV car battery charge and discharge simulation verification for implementation and experiments of the bidirectional DC-DC charger. In Proceedings of the KIPE Conference, Seoul, Republic of Korea, 15 November 2013; pp. 35–36. [Google Scholar]
- Omar, N.; Van den Bossche, P.; Coosemans, T.; Van Mierlo, J. Peukert revisited—Critical appraisal and need for modification for lithium-ion batteries. Energies 2013, 6, 5625–5641. [Google Scholar] [CrossRef]
- Doerffel, D.; Sharkh, S.A. A critical review of using the Peukert equation for determining the remaining capacity of lead-acid and lithium-ion batteries. J. Power Sources 2006, 155, 395–400. [Google Scholar] [CrossRef]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A general energy balance for battery systems. J. Electrochem. Soc. 1985, 132, 5. [Google Scholar] [CrossRef]
- Zhu, L.; Xiong, F.; Chen, H.; Wei, D.; Li, G.; Ouyang, C. Thermal analysis and optimization of an EV battery pack for real applications. Int. J. Heat Mass Transf. 2020, 163, 120384. [Google Scholar] [CrossRef]
- Ahmadou Samba, A.; Omar, N.; Gualous, H.; Van den Bossche, P.; Van Mierlo, J.; Boubekeur, T.I. Development of 2D thermal battery model for Lithium-ion pouch cells. World Electr. Veh. J. 2013, 6, 629–637. [Google Scholar] [CrossRef]
- Emission Test Cycles. Available online: https://dieselnet.com/standards/cycles/hwfet.php (accessed on 1 November 2023).
- Kim, H.; Kim, D.; Shu, I.; Yi, K. Time-varying parameter adaptive vehicle speed control. IEEE Trans. Veh. Technol. 2015, 65, 581–588. [Google Scholar] [CrossRef]
- Nie, L.; Guan, J.; Lu, C.; Zheng, H.; Yin, Z. Longitudinal speed control of autonomous vehicle based on a self-adaptive PID of radial basis function neural network. IET Intell. Transp. Syst. 2018, 12, 485–494. [Google Scholar] [CrossRef]
- Xu, S.; Peng, H.; Song, Z.; Chen, K.; Tang, Y. Accurate and smooth speed control for an autonomous vehicle. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 1976–1982. [Google Scholar]









| Parameters | Value | Unit |
|---|---|---|
| 1 cell capacity | 56.85 | Ah |
| Number of parallel cells per module | 2 | EA |
| Number of serial cells per module | 6 | EA |
| Number of modules per pack | 30 | EA |
| Number of packs | 1 | EA |
| Parameters | Value | Unit |
|---|---|---|
| Vehicle mass | 1950 | kg |
| Tire rolling radius | 0.3 | m |
| Front area | 2.3 | m2 |
| Air drag coefficient | 0.31 | - |
| Gravitational acceleration | 9.81 | m/s2 |
| Operating Environment | Number | HVAC Circuit | HVB Circuit | PE Circuit |
|---|---|---|---|---|
| Hot climate | 1 | Air condition | Circulation | Circulation |
| 2 | Air condition | Radiator cooling | Circulation | |
| 3 | Air condition | Radiator cooling | Radiator cooling | |
| 4 | Air condition | Chiller cooling | Circulation | |
| 5 | Air condition | Chiller cooling | Radiator cooling | |
| 6 | Air condition | Circulation | Radiator cooling | |
| 7 | - | Radiator cooling | - | |
| Cold climate | 8 | Cabin heating | Circulation | Circulation |
| 9 | Cabin heating (Dehumidification) | Circulation | Circulation | |
| 10 | Cabin heating | Chiller cooling | Circulation | |
| 11 | Cabin heating | Chiller cooling | Chiller cooling | |
| 12 | Cabin heating (Not air absorption) | Chiller cooling | Circulation | |
| 13 | Cabin heating (Not air absorption) | Chiller cooling | Chiller cooling | |
| 14 | Cabin heating (Dehumidification) | Circulation (HVB heating) | Circulation | |
| 15 | - | Circulation (HVB heating) | - |
| Area | Parameters | Value | Unit |
|---|---|---|---|
| Glass | Convective heat transfer coefficient | 40 | W/m2.K |
| Thermal conductivity | 0.00096 | W/m.K | |
| Thickness | 0.002 | m | |
| Heat transfer area | 3.5 | m2 | |
| Doors | Convective heat transfer coefficient | 40 | W/m2.K |
| Thermal conductivity | 0.00008 | W/m.K | |
| Thickness | 0.03 | m | |
| Heat transfer area | 4 | m2 | |
| Roofs | Convective heat transfer coefficient | 40 | W/m2.K |
| Thermal conductivity | 0.0008 | W/m.K | |
| Thickness | 0.02 | m | |
| Heat transfer area | 2 | m2 | |
| Cabin | Volume | 3 | m3 |
| Solar radiation | 0.9 (Hot climate) | W/m2 | |
| 1.3 (Cold climate) | |||
| One Occupant heat source | 70 | W | |
| Simulation Conditions | Case No. 1 | Case No. 2 |
|---|---|---|
| Operating environment | Hot climate | Cold climate |
| Ambient temperature | 36 °C | −10 °C |
| Driving cycle | HWFET | HWFET |
| Simulation time | 765 s | 765 s |
| Cabin target temperature | 23 °C | 23 °C |
| HVB target temperature | 27–33 °C | 27–33 °C |
| PE module target temperature | 47–51 °C | 47–51 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bae, J.; Hyun, D.; Han, J. Adaptive Integrated Thermal Management System for a Stable Driving Environment in Battery Electric Vehicles. Batteries 2024, 10, 59. https://doi.org/10.3390/batteries10020059
Bae J, Hyun D, Han J. Adaptive Integrated Thermal Management System for a Stable Driving Environment in Battery Electric Vehicles. Batteries. 2024; 10(2):59. https://doi.org/10.3390/batteries10020059
Chicago/Turabian StyleBae, Jaehyun, Daeil Hyun, and Jaeyoung Han. 2024. "Adaptive Integrated Thermal Management System for a Stable Driving Environment in Battery Electric Vehicles" Batteries 10, no. 2: 59. https://doi.org/10.3390/batteries10020059
APA StyleBae, J., Hyun, D., & Han, J. (2024). Adaptive Integrated Thermal Management System for a Stable Driving Environment in Battery Electric Vehicles. Batteries, 10(2), 59. https://doi.org/10.3390/batteries10020059









