On the State of Usability for Lithium–Ion Batteries

Abstract

Lithium–ion batteries are well established as traction batteries for electric vehicles. This has led to a growing market for second-life batteries that can be used in applications like home energy storage systems. Moreover, the recyclability and safe handling of aged or damaged cells and packs has become more important. While there are several indicators, like state of health (SOH), state of power (SOP), or state of safety (SOS), which describe the state of a battery before its defined end of life (EOL), there is no consistent classification methodology by which to describe the usability of a cell or pack after its EOL is reached. The proposed state of usability (SOU) provides a new indicator that accounts for the usability for second life, recyclability, and possible required safety handling of a lithium–ion battery after its first intended life cycle. This work presents a decision tree method, which in turn leads to five discrete usability levels enabling a fast and rough determination of the SOU for practical use. Further, a calculation methodology for reasonable continuous regions of the SOU is proposed. Both methods are based on a literature-based rating of all of the relevant defect and aging mechanisms displayed in a risk matrix. Finally, some experimental methods that can be used for SOU determination are proposed. The developed methodology and the hands-on approach using a decision tree are well-suited for real world application in recycling companies and battery test laboratories.

1. Introduction

Nowadays, lithium–ion batteries are well established as traction batteries for electric vehicles (EVs) [1,2]. Along with this comes a growing demand for second-life applications, recycling processes and the safe handling of aged battery cells and packs.

There are several well-known indicators for the state of batteries in general and lithium–ion batteries in particular. The state of charge (SOC) indicates the remaining discharge capacity of the cell. The state of health (SOH) indicates the remaining capacity of the cell in relation to its initial capacity [3]. The state of power (SOP) describes the power performance of the battery and indicates the retrievable maximum power of the battery within a certain time span. Furthermore, a state of function (SOF) is presented in the literature and is usually defined similarly to the SOP [4,5,6]. The common range for these indicators is from 0 to 1 or 0% to 100% respectively.

All these indicators possess limited significance when it comes to the categorization of used batteries or battery packs in terms of their usability for second-life applications, their readiness for recycling or possible safety issues caused by their past usage.

Cabrera-Castillo et al. proposed the calculation of a state of safety (SOS) [7] to account for the failure probability of a cell without considering a specific operational state. The SOS can be used to prevent battery abuse and may also be applicable for other energy storage systems. However, the SOS does not provide any information about the usability of the battery for second-life applications or recycling.

This work introduces the state of usability (SOU), which enables the categorization of batteries and battery packs regarding their usability for second-life applications, recycling, and possible safety hazards. This new metric also ranges from 0 to 1, i.e., from 0% to 100%. The aim is to establish an indicator that is able to classify battery packs and cells in miscellaneous conditions. The SOU is intended to be used by automotive engineers, recycling companies and even firefighters when determining the proper handling of a battery. Recycling companies, in particular, often face the decision as to whether or not a battery is fit for recycling or second life usage. This decision has a high economic relevance for the companies and can be supported by a proper metric describing the usability state of the battery or battery system. A direct comparison between the information contained in each indicator is shown in

Table 1. Comparison of well-known indicators and SOU regarding their information content.

Feasible Information On	SOC	SOH	SOP/SOF	SOS	SOU
Current battery state	√	✗	✗	✗	✗
Degradation	✗	√	√	√	√
Safety	✗	✗	✗	√	√
Recyclability	✗	✗	✗	✗	√
Second life usability	✗	✗	✗	✗	√

.

2. Derivation of the State of Usability

The usability of a battery cell or pack can generally be divided into three sub categories [8]:

• Second life usability;
• Recyclability;
• Limited recyclability after required safe handling.

The first category includes batteries that are directly (e.g., usage of full batteries to replace damaged batteries in an identical system) or indirectly (implementing full batteries in a new system) usable for second life application. The second category includes all batteries that have reached their defined end of life (EOL) with an SOH < 80% [9] and that are, for some reason, not suited for a second life application. Possible reasons include mechanical defects and connection faults. The third category includes all batteries that are suited for recycling after proper and safe handling, i.e., batteries that are at risk of catching fire or where the safety state of the cell or pack is not directly identifiable. This also includes possible pollution of the materials, e.g., caused by a fire.

Saxena et al. [10] have investigated the influence of SOH on second life usability. In contrast with the usual definition of EOL, it has been shown that EV batteries often still satisfy the typical needs of people’s everyday driving habits. Hence, reaching the standard EOL does not necessarily disqualify batteries from second-life use. Therefore, an SOH smaller than 0.8 only limits the applicability in high energy demanding applications. The same applies for an SOP smaller than 0.8 for high power demanding applications [11].

The existing usability definitions are therefore not appropriate for the classification of aged or damaged batteries. A more detailed approach is necessary. Thus, in the following the SOU is introduced.

The state of usability of a battery indicates in which way the battery and its components may be reused or recycled after their previous usage. The aim of this work is twofold. First, a general and broad approach is presented and, second, a methodology is provided for a more precise determination of the SOU for second life applications, taking into account the strong dependence on the intended further use of the battery.

To determine the SOU, it is necessary to account for all relevant defect and aging mechanisms, including their impact as well as their likelihood. Generally the three main categories are mechanical, thermal and electric defects [9]. Figure 1 shows a risk matrix that categorizes the most common and relevant defect and aging mechanisms that are essential to identify when determining the usability of a battery. The risk matrix displays how likely the mechanism is to occur (y-axis) and how severe the impact on the cell safety is (x-axis). It contains the following mechanisms [12]:

• External
  • Sensor faults (SF)
  • Cell connection faults (CCF)
  • Cooling system faults (CSF)
• Internal:
  • Overcharge (OC)
  • Overdischarge (OD)
  • Internal short circuit (ISC)
  • External short circuit (ESC)
  • Overheating (OH)
  • Accelerated degradation (AD)
  • Thermal runaway (TR)
  • SEI growth (SEI)
  • Lithium plating (LP)
  • Electrolyte leakage (EL)
  • Open current interrupt device (CID)

Note that SEI growth is an inevitable mechanism that can be quantified by the rising internal resistance, which is the dominating degradation effect caused by the SEI growth [13]. Furthermore, mechanisms like EL, TR, or an open CID are classified as binary, and thus no continuous range is applicable. The proposed ratings for likelihood and impact for all mechanisms in Figure 1 are based on a literature review considering the related effects and possibilities of each mechanism. In the following, the terms high, moderate, and low are specified:

-

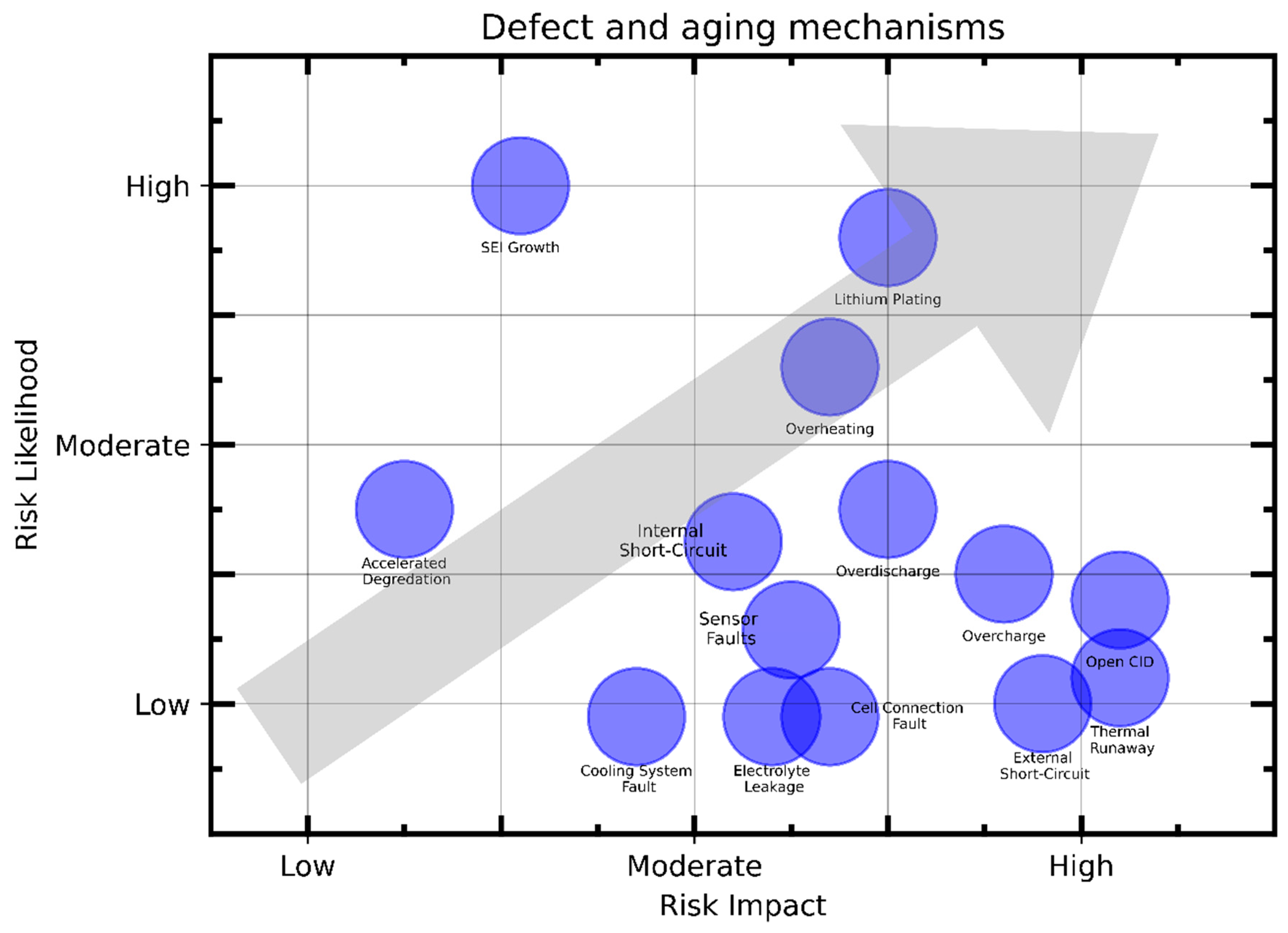
A high impact means that an occurrence leads to a cell with limited recyclability and a safety risk. This applies for mechanisms like a thermal runaway, where a contamination of the electrode active materials is inevitable or a severe overcharge that usually also leads to a thermal runaway of the cell [14,15].

-

A moderate impact means that an occurrence leads to a cell that does not require safety handling but the usability for second life may be limited to low power demanding applications. This applies for mechanisms like sensor or cooling system faults, where the single battery is usually not damaged and may be used in a newly built second life battery pack [12,16].

-

A low impact either means that the cell is usually not affected by the mechanism (e.g., cooling system faults are usually detected by the BMS and do not severely affect the single cells) or that the effect is limited and does not necessarily limit the general usability (e.g., mild capacity losses due to conditions causing accelerated degradation) [12].

-

A high likelihood means that the mechanism is inevitable or arises in almost every lithium–ion battery system, e.g., this applies for SEI growth [14] and lithium plating [13].

-

A moderate likelihood means that the mechanisms should normally not occur but may occur due to incorrect handling. For instance, this might be the case for a cell that is exposed to AD mechanisms such as high ambient temperatures [17].

-

A low likelihood means that those mechanisms are usually prevented by a battery management system (BMS) or other safety barriers like CIDs, which are usually not prone for faults [17,18,19]. This applies for overcharges, which are typically prevented by voltage control [12].

The risk of each mechanism rises with an increasing likelihood and an increasing impact. The grey arrow in Figure 1 displays this relation. A mechanism in the upper right corner contains the greatest risk (high likelihood and high impact), whereas a mechanism in the lower left corner contains the smallest risk (low likelihood and low impact).

The risk matrix and its rating of impact and likelihood of a defect or aging mechanism is used to quantify the influence on the usability of the battery cell or pack. Now, a metric is introduced, which divides the continuous range from 0–1 into five regions, and therewith roughly defines the usability of the battery cell or pack. The division is based on the practical application of the approach in the second life and recycling stream. Thereby, each region can be interpreted as a specific case for further usage or handling of the battery. Details about necessary investigations and the corresponding general handling classification can be found in [20,21]. Here, each region corresponds to a small range of the related state of usability that can be used as an indicator for a different treatment in the afterlife of the battery.

❖

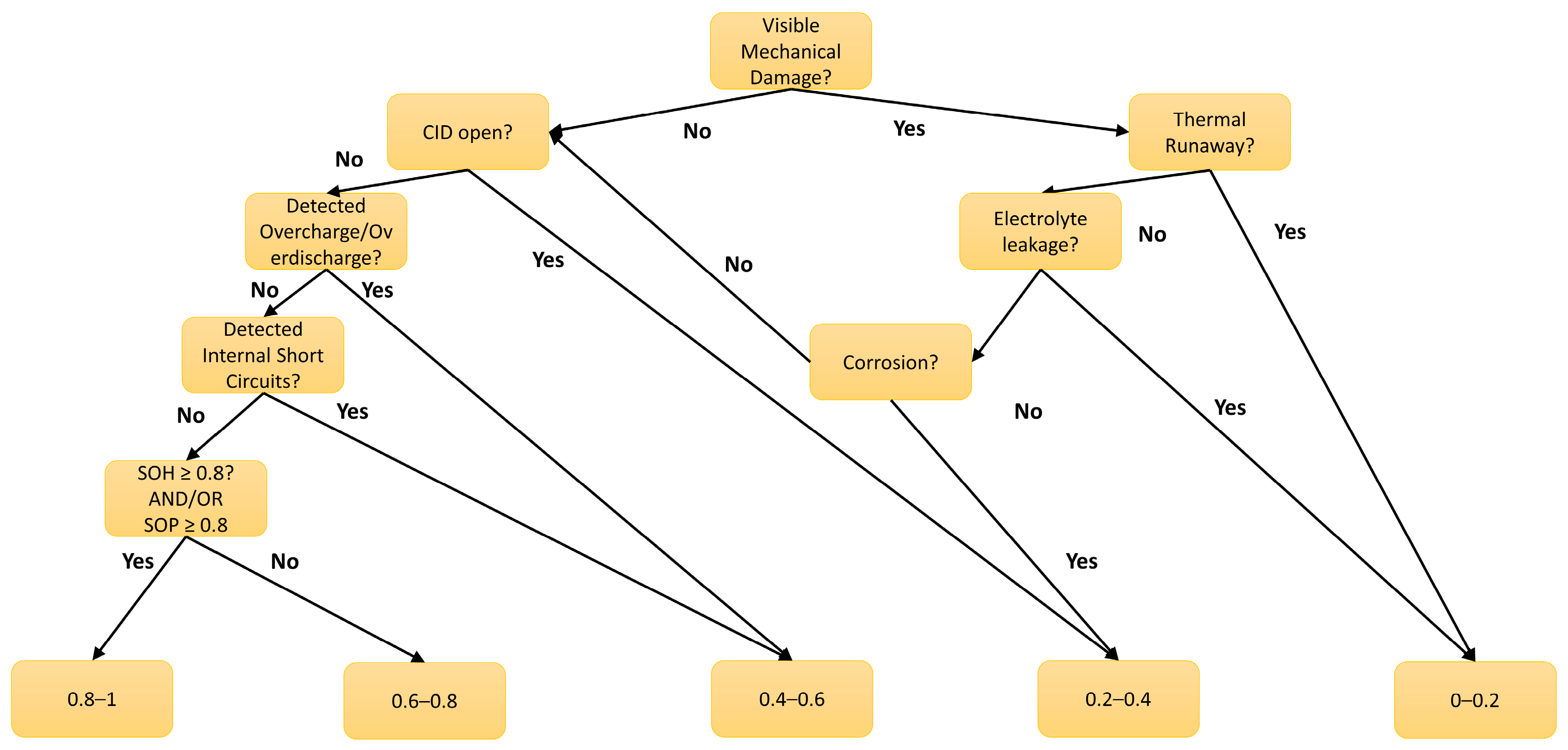
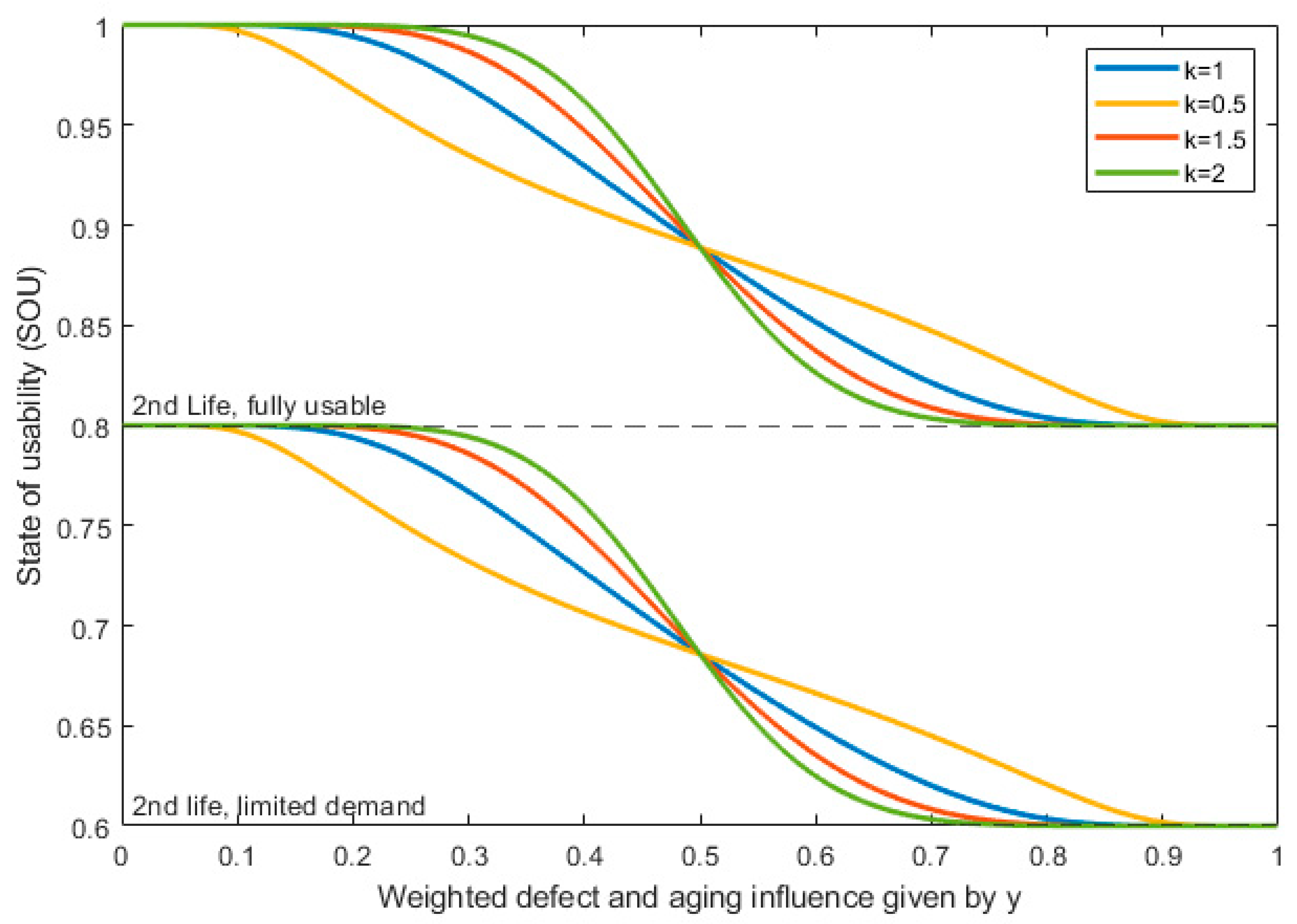
1 ≥ SOU > 0.8: Fully usable for second life applications, only mild capacity or power losses (SOH and SOP > 80%).

❖

0.8 ≥ SOU > 0.6: Usable for certain second life applications, e.g., with limited power demands.

❖

0.6 ≥ SOU > 0.4: Not usable for second life, still fully recyclable.

❖

0.4 ≥ SOU > 0.2: Limited recyclability because of unknown components or safety issues due to defects (e.g., CID is open, but cell did not catch fire), minor active material contamination or mechanical damage on the cell casing.

❖

0.2 ≥ SOU ≥ 0: Very limited recyclability, safe handling is required, severe active material contamination.

The division into five equally spaced intervals for the SOU is to be understood as a suggestion, i.e., that this can be adapted for particular use cases where specific information is at hand. In the following, the methodology regarding determination and calculation of the above classification is presented.

3. Classification Scheme

To classify the battery SOU, the following two-step methodology is proposed. This methodology is in accordance with the impact rating of the defect and aging mechanisms as shown in Figure 1. In a first step, a rough classification into the five discrete usability levels, introduced in Section 2, is carried out by employing a decision tree. For practical applications, this often yields a sufficient classification regarding appropriate further battery handling and can be performed quickly. In a second step, a calculation method is proposed that allows for a more precise determination of the SOU within the upper two usability levels.

3.1. Decision Tree

In practice, the available information about a used battery or battery pack is often limited [8]. For a fast and practical estimation of a battery’s usability, a decision tree is introduced that has five possible outcomes. These five classes are separated by the deduced treatment of the battery or system and are described above in Section 2. Figure 2 depicts the decision tree. The first step for classifying used batteries is to check for visible mechanical damage. If this is the case and either a thermal runaway or electrolyte leakage has occurred, safe handling is required. Thus, the battery is assigned the lowest class on the bottom right, corresponding to an SOU range from 0 to 0.2. When only corrosion has occurred, the recyclability of some materials may be limited but safe handling is not required. If none of the mentioned defects appear, but the CID is open and hence the flow of current is interrupted, the cell is also counted as limited recyclable. Hence, the second lowest class is assigned with an SOU range from 0.2 to 0.4. If the CID is still closed and no visible defects are detectable or only the cell casing is damaged but did not visibly affect the cell materials, the battery is fully recyclable. If no mechanical damage was detected but an overcharge or overdischarge occurred, the cell is also fully recyclable but not usable for second life applications. The same applies for detected internal short circuits. In this case, the medium class is assigned with an SOU range from 0.4 to 0.6. If none of the above damage has occurred, and depending on the desired second life application, the SOP and SOH values need to be checked. Note that effects like buckling of electrode particles lead to a decrease in SOH and SOP and are therefore not separately covered in the decision tree [22]. If the SOH and the SOP, or one of both values, are below 0.8, the battery is usable for second life applications with corresponding limited power or capacity demands. If both the SOH and the SOP are below 0.8, the battery is usable for second life applications with correspondingly limited power and capacity demands. This relates to the second highest class, with an SOU range from 0.6 to 0.8. If SOH and SOP are both greater or equal to 0.8, the battery is fully deployable in second life applications, and the highest class is assigned, with an SOU range from 0.8 to 1. The classification of the case SOH > 0.8 and SOP ≤ 0.8, (or vice versa for SOP > 0.8 and SOH ≤ 0.8), depends on the intended second life use case. For applications with low power demands (or low capacity demands), the battery can nevertheless be assigned to the highest class, since all requirements are fully met. If this does hold, the battery is assigned to the second highest class.

The choice of 0.8 as threshold for SOH and SOP is also to be understood as a suggestion based on the usual boundaries for these values and can be adapted if specific knowledge of a certain use case is at hand.

To showcase the practical applicability of the decision tree for SOU determination, two exemplary test scenarios are presented.

#1: Application as home energy storage for PV

Assunção et al. modelled the usage of used traction batteries from EVs as residential energy storage for a photovoltaic (PV) plant [11]. They showed that the power demand of a residential energy storage is far below the power demand of an EV. Hence, when assessing the SOU of a used traction battery for this application, it is mainly the SOH that is relevant when reaching full second life usability.

We assume a battery with the following indicators:

-

No visible mechanical damage.

-

CID is not open.

-

No overcharge or deep discharge.

-

No detected internal short circuits.

-

SOH = 0.85.

-

SOP = 0.72.

Following the logic of the proposed decision tree from Figure 2, with the threshold choice of 0.8 for SOH and SOP, the SOU is in the range of 0.8–1 and thus implies full second life usability for the desired use case.

#2: Usage as off-grid PV charging station

Tong et al. have proposed the application of used EV battery packs as off-grid PV powered charging stations for EVs [23]. Usually, the demanded capacity for such an application can be easily met by choosing the number of second life packs accordingly. On the other hand, for providing the possibility of fast charging for EVs, the SOP of the battery pack needs to meet certain requirements. In our exemplary use case, we assume that a minimum SOP of 0.9 is required.

We assume a battery with the following indicators:

-

No visible mechanical damage.

-

CID is not open.

-

No overcharge or deep discharge.

-

Detection of internal short circuits.

-

SOH = 0.65.

-

SOP = 0.93.

While all other indicators suggest that the battery pack is suitable for its desired application, the detection of internal short circuits leads to a medium SOU classification in the range of 0.4–0.6. Hence, the battery is fully recyclable but is not appropriate for the desired use case.

3.2. Calculation of SOU for Second Life Application

Similar to the SOS calculation by Cabrera-Castillo et al. [7] we assume a reversed proportionality between the SOU and the defect and aging mechanisms of the battery:

$$f_{usability}\left(x\right)=\frac{1}{d\left(x\right)+1}$$

(1)

where $f_{usability}$ is the function describing the SOU and $d\left(x\right)$ is a function describing the occurred defects and aging mechanisms. The vector x includes all relevant variables that represent the defect and aging states of the battery. By adjusting the denominator via $d\left(x\right)\in [0,\mathrm{\infty })$, the SOU values are located in the interval from 0 to 1.

In contrast with SOH and SOS, the introduced SOU does not only have one specific lower boundary value, like the EOL at 0.8 for SOH or the safety threshold at 0.8 for the SOS [7]. Further, because, for example, the recyclability is bound to specific criteria defined by recycling companies, the definition of $d\left(x\right)$ for calculating the SOU needs to be a piecewise-defined function to account for classification into the five discrete usability levels of Section 2. Moreover, only the first two regions between 1 and 0.8 and between 0.8 and 0.6 have a continuous physical meaning, as they are determined by SOH and SOP. Hence, for the lower three classes discrete usability values are sufficient, as they are directly related to a specific treatment of the battery.

For the high-level grouping into the five levels, the following relevant classification criteria are introduced:

-

Mechanical damage (MD) $\in \left\{0,1\right\}.$

-

Thermal runaway (TR) $\in \left\{0,1\right\}$.

-

Open CID (CID) $\in \left\{0,1\right\}$.

-

Overcharge/overdischarge (OC/OD) $\in \left\{0,1\right\}.$

-

Electrolyte leakage (EL) $\in \left\{0,1\right\}$.

-

Corrosion (CR) $\in \left\{0,1\right\}$.

-

Internal short circuits (ISC) $\in \left\{0,1\right\}.$

-

State of health (SOH) $\in \left[0,1\right]$.

-

State of power (SOP) $\in \left[0,1\right]$.

The five classes can be defined by the disjunctive normal form of the decision tree, using the binary switching variables $a_i\in \left\{0,1\right\},i=1,\dots ,5$:

$$\begin{array}{l}MD=0\wedge CID=0\wedge \left[OC=0\wedge OD=0\right]\wedge ISC=0\wedge [SOH\wedge SOH>0.8]⟶a_1=1\\ MD=0\wedge CID=0\wedge \left[OC=0\wedge OD=0\right]\wedge ISC=0\wedge \left[SOH\vee SOH\le 0.8\right]⟶a_2=1\\ \left[MD=0\wedge CID=0\wedge \left(\left[OC\vee OD=1\right]\vee ISC=1\right)\right]\\ \vee \left[MD=1\wedge EL=0\wedge CR=0\wedge CID=0\wedge \left(\left[OC\vee OD=1\right]\vee ISC=1\right)\right]⟶a_3=1\\ \left[MD=0\wedge CID=1\right]\vee \left[MD=1\wedge TR=0\wedge EL=0\wedge CR=1\right]⟶a_4=1\\ \left[MD=1\wedge TR=1\right]\vee \left[MD=1\wedge TR=0\wedge EL=1\right]⟶a_5=1\end{array}$$

When one of the five cases apply, the corresponding switching variable $a_i$ is set to one, while the remaining switching variables are set to zero. Note that the above definitions for $a_1$ and $a_2$ are quite restrictive, i.e., only batteries with SOH and SOP larger than 0.8 are assigned to the highest SOU class. In case the specific application does not require high capacity and power demands, these definitions can be adapted accordingly.

Equation (1) becomes:

$$f_{usability}\left(x;a_i\right)=\frac{1}{d\left(x;a_i\right)+1}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}d\left(x;a_i\right)={\sum }_{i=1}^5{d}_i\left(x\right)·a_i$$

(2)

where the values of the $d_i\left(x\right)$ are in the following distinct intervals or take on the following fixed values, respectively:

$$d_1\left(x\right)\in \left[0,\frac{1}{4}\right),d_2\left(x\right)\in \left[\frac{1}{4},\frac{2}{3}\right),d_3\left(x\right)=1,d_4\left(x\right)=\frac{7}{3}\mathrm{and}{d}_5\left(x\right)=9.$$

(3)

The $d_1\left(x\right)$ and $d_2\left(x\right)$ terms account for the defect mechanisms within the first two usability levels corresponding to second life applicability. The interval for the defect and aging function $d_1$ from $\left[0,\frac{1}{4}\right)$, i.e., for the highest SOU class, corresponds to the interval $f_{usability}\in \left.\left(0.8,1\right.\right]$. The interval $\left[\frac{1}{4},\frac{2}{3}\right)$ for $d_2$, corresponding to the second highest SOU class, is related to the interval $f_{usability}\in \left.\left(0.6,0.8\right.\right]$. The three fixed values for $d_3$, $d_4$ and $d_5$ correspond to the center values of the corresponding ranges for the lower three SOU classes, i.e., $d_3\left(x\right)=1$ yields $f_{usability}=0.5,d_4\left(x\right)=\frac{7}{3}$ yields $f_{usability}=0.3,$ and $d_5\left(x\right)=9$ yields the usability value of $f_{usability}=0.1.$

The vector $x\in R^n$ consists of its elements $x_i$, with $i=1,...,n$, reflecting the n considered defect and aging mechanisms. Typically, the value of an element $x_i$ is between 0 and 1, with 0 as no defect, and 1 for a full defect. Intermediate values between 0 and 1 might also be reasonable, depending on the specific mechanism. Suitable possible variables for considered defects and aging $x_i$ are, e.g., 1-SOP, 1-SOH, 1-SOS, CR, EL, ISC, MD, CID, OD, OC, or other suitable binary indicators, such as SOP < 0.7 or SOH < 0.9. To map the vector x to the corresponding intervals for the first two defect and aging functions $d_1$ and $d_2$, an additional variable y is introduced, which is a linear combination of the single defects $x_i$, i.e., a weighted average of the vector x:

$$y\left(x;b_i\right)={\sum }_{i=1}^n{x}_i·b_i,$$

(4)

with non-negative weighting factors ${1\ge b}_i\ge 0$, which sum up to one, i.e., $\sum _i{b}_i=1.$ As the values for the single $x_i$ range from 0 to 1, the same holds for the resulting range of the variable y. This weighting variable y can now be used for mapping onto the intervals specified in Equation (3). In general, different suitable shapes for $d_i\left(x\right)$ can be applied, as, e.g., inverse tangents, or sigmoid or exponential decay functions. Here, the use of properly scaled sigmoid functions are employed, which are commonly used activation functions [24]. One variant of the sigmoid function is the logistic function, with its general adapted form given by:

$$\mathrm{d}\left(\tilde{y}\right)=c+d\cdot \frac{1}{1+e^{-k\cdot \tilde{y}}}$$

(5)

with real parameters $c$ and $d$, and a scaling parameter $k>0.$ The range of $\mathrm{d}\left(\tilde{y}\right)$ is the interval $\left(c,c+d\right)$ or $\left(c+d,c\right)$, depending on the sign of $d$. For proper application of the sigmoid function in (5) a mapping from $y\in (0,1)$ to $\tilde{y}\in (-\mathrm{\infty },\mathrm{\infty })$ must be performed. Here, the simple mapping function $\tilde{y}=-\left(\frac{1}{y}+\frac{1}{y-1}\right)$ is chosen, which monotonically maps the interval $\left[0,1\right]$ to the complete real axis with $y=0.5$ corresponding to $\tilde{y}=0$, and $y\to 1$ corresponding to $\tilde{y}\to \mathrm{\infty }$. Using the sigmoid function as the basis, the specific defect functions $d_1\left(y\right)$ and $d_2\left(y\right)$ are obtained by adjusting the parameters c and d in Equation (5), such that the limits from Equation (3) are met:

$$d_1\left(y\right)=\frac{1}{4}\cdot \frac{1}{1+e^{-k\cdot \tilde{y}}}\mathrm{ }\mathrm{ },d_2\left(y\right)=\frac{1}{4}+\frac{5}{12}\mathrm{ }\cdot \frac{1}{1+e^{-k\cdot \tilde{y}}},$$

(6)

Figure 3 shows exemplary SOU plots for the two continuous regions of second life usage. Here, the sigmoid activation function was used for calculating $d_1\left(y\right)$ and $d_2\left(y\right)$. Using different scaling parameters, $k$ yields different curves. The value y = 0 on the left corresponds to a negligible defect or aging effect, with respect to all actual considered mechanisms, and thus is related to the largest SOU values of 0.8 for $d_2$ and 1 for $d_1$.

The proposed approach is now applied to test case #1 from Section 3.1. The SOH is assigned to $x_1$ and the SOP is assigned to $x_2$. Further, $x_3$ and $x_4$ are introduced as lost capacity and power as $x_3=1-\mathrm{S}\mathrm{O}\mathrm{H}$ and $x_4=1-\mathrm{S}\mathrm{O}\mathrm{P}$, respectively. The weighting factors are $b_1=0.6,b_2=0.1,b_3=0.2$, and $b_4=0.1$. This leads to $y=0.158$ and $d_1\left(\mathrm{ỹ}\right)=0.0015$. The SOU can now be calculated by:

$$f_{usability}\left(x\right)=\frac{1}{0.0015+1}\approx 99.85\%$$

This value changes with varying weightings and scaling factors depending on the specific application case.

4. Experimental SOU Determination

There are numerous well-established ways to determine the necessary indicators for the SOU. In the following, we categorize the most relevant indicators and propose some state-of-the-art determination methods. Note that for completely unknown batteries the identification of the cell chemistry may also be important for determining the listed indicators. Furthermore, a visual inspection should always be carried out in the first place in order to detect visible mechanical damage like traces of a thermal runaway or corrosion. Figure 4 depicts the basic procedure by which to obtain the SOU of an unknown battery. Each individual block in Figure 4 may contain other experimental techniques depending on the use case. The SOU estimation can be carried out using the decision tree method, the calculation method, or other heuristics.

4.1. State Estimation

To ensure that the battery is currently not in a state of overcharge or deep discharge, the determination of SOC is crucial. Ampere counting, which is the most basic approach for SOC estimation, is not suited for systems where the initial SOC is unknown and is prone to measurement errors. Hence, a better approach would be a lookup table method using either voltage measurements or impedance responses from electrochemical impedance spectroscopy (EIS) for estimating the SOC [25]. The drawback of these methods is that, usually, parameterization data from the exact same battery type is necessary for valid results. The most common and well-established method for SOC estimation in real world applications is the model-based approach, e.g., with equivalent circuit models (ECM) [26] or electrochemical models [27]. The latter ones, in particular, are also extensively used for SOH estimation, usually in combination with Kalman filters, particle filters, or state observers [28]. Similar approaches have been presented and tested for SOP estimation [29]. Furthermore, Yang et al. have presented a model-based Kalman filter approach to detect internal soft short circuits [30].

Finally, open circuit voltage (OCV) measurements, current profiles or driving cycles may be applied to the battery in order to estimate its states via model-based approaches [25].

4.2. Defect and Aging Mechanism Detection by EIS

As mentioned above, EIS can be used to determine states like SOC, SOH or SOP in lithium–ion batteries [31,32]. Moreover, the impedance response and its corresponding metrics, e.g., total harmonic distortion (THD) or distribution of relaxation time (DRT), can also be analyzed for the determination of aging and defect mechanisms in batteries and for state estimation purposes [33,34,35,36]. Furthermore, Kim and Kowal have used the THD to identify over-discharged cells in a battery pack [35]. Ongoing research in this field has led to several new analysis and measurement techniques [33].

4.3. Non-Invasive Defect Detection

On the experimental side, several non-invasive detection methods have been studied in recent years. For identifying mechanical defects like an open CID or delaminated electrode layers, methods like X-ray measurements and computer tomography (CT) have been validated as well-suited methods [37,38,39]. The detection of triggered CIDs is particularly crucial for a safe and fast diagnosis of batteries, as it indicates severe abuse or defects such as overcharge, high cell pressure, or high temperature and thus immediately leads to a low SOU classification [19].

4.4. Data-Driven Approaches

More recently, many data-driven approaches have been presented to determine battery states [25]. For example, Li et al. have applied ensemble learning for SOH estimation [3] and Beltran et al. have tested the suitability of different machine learning models for SOH estimation based on partial charge/discharge events [40]. Wang et al. have presented a fuzzy c-means clustering algorithm for SOP estimation [5]. Machine learning methods can also be used for the detection of isolation and grading faults in battery packs, as shown by Yang et al. [41].

Furthermore, data-driven approaches have been developed in combination with non-invasive experimental methods. For example, Chen et al. proposed a sorting method based on the analysis of X-ray data [42].

5. Conclusions

The state of usability methodology presented in this paper provides an approach by which to estimate the usability of used lithium–ion batteries after their initial deployment. The impact and proposed likelihood of relevant defect and aging mechanisms are rated based on state-of-the-art literature. The SOU range from 0 to 1 is separated into five different regions that are related to all basic decisions required for second life, recycling, and proper safety handling of the battery. A practical approach using a decision tree is proposed for determining the SOU based on a number of critical indicators and two exemplary test scenarios are presented. Furthermore, a calculation methodology is proposed that allows for a continuous determination of the SOU for second life applications, i.e., within the upper two SOU levels. Finally, measuring and analysis methods for determining the crucial parameters and necessary information for SOU determination are presented. The developed methodology is suited for application in various fields like battery recycling and second life assessment, battery test laboratories, and safety assessment for accident vehicles.