Impact of Mixing Shear on Polymer Binder Molecular Weight and Battery Electrode Reproducibility
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
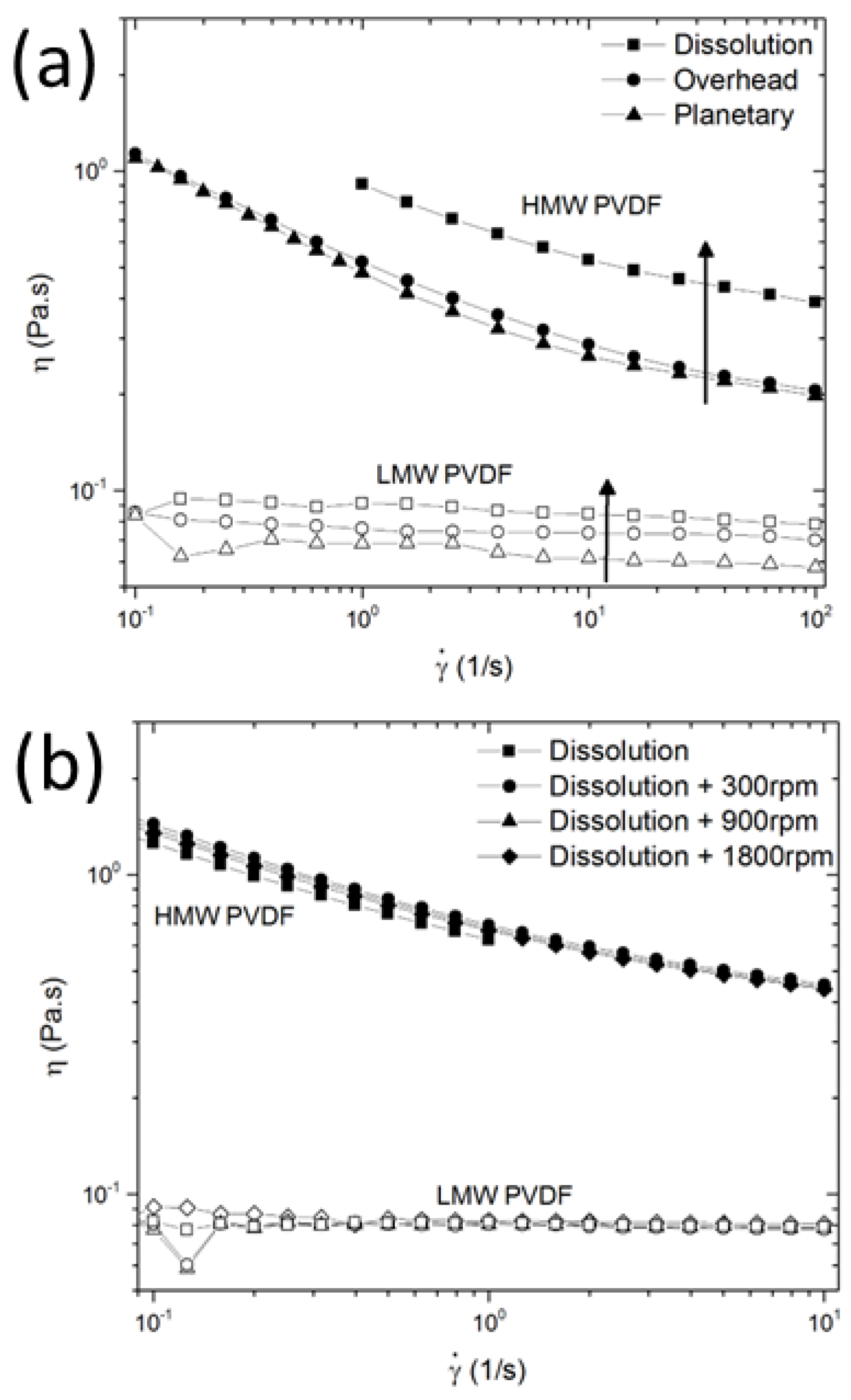
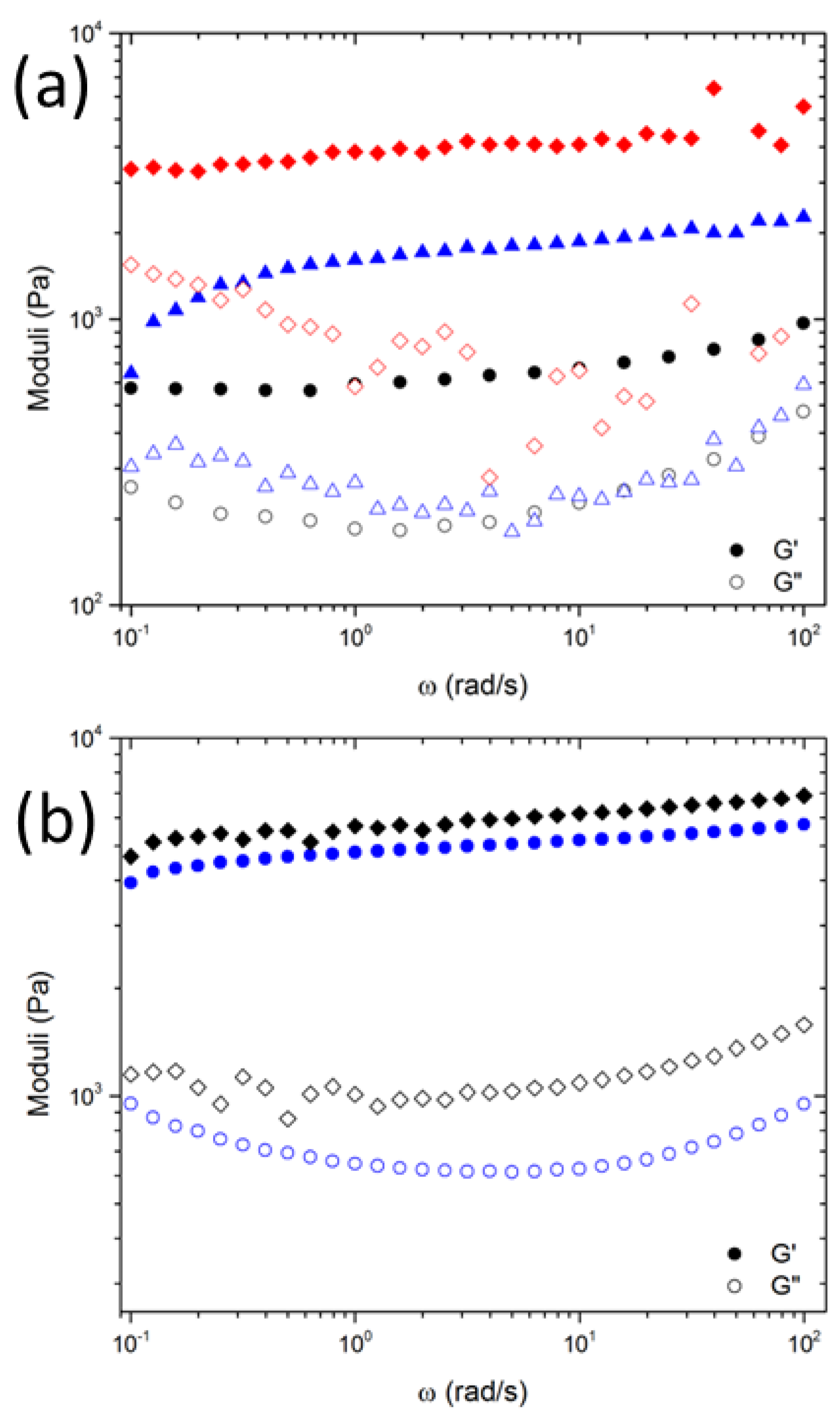
3.1. Polymer Scission during Slurry Mixing
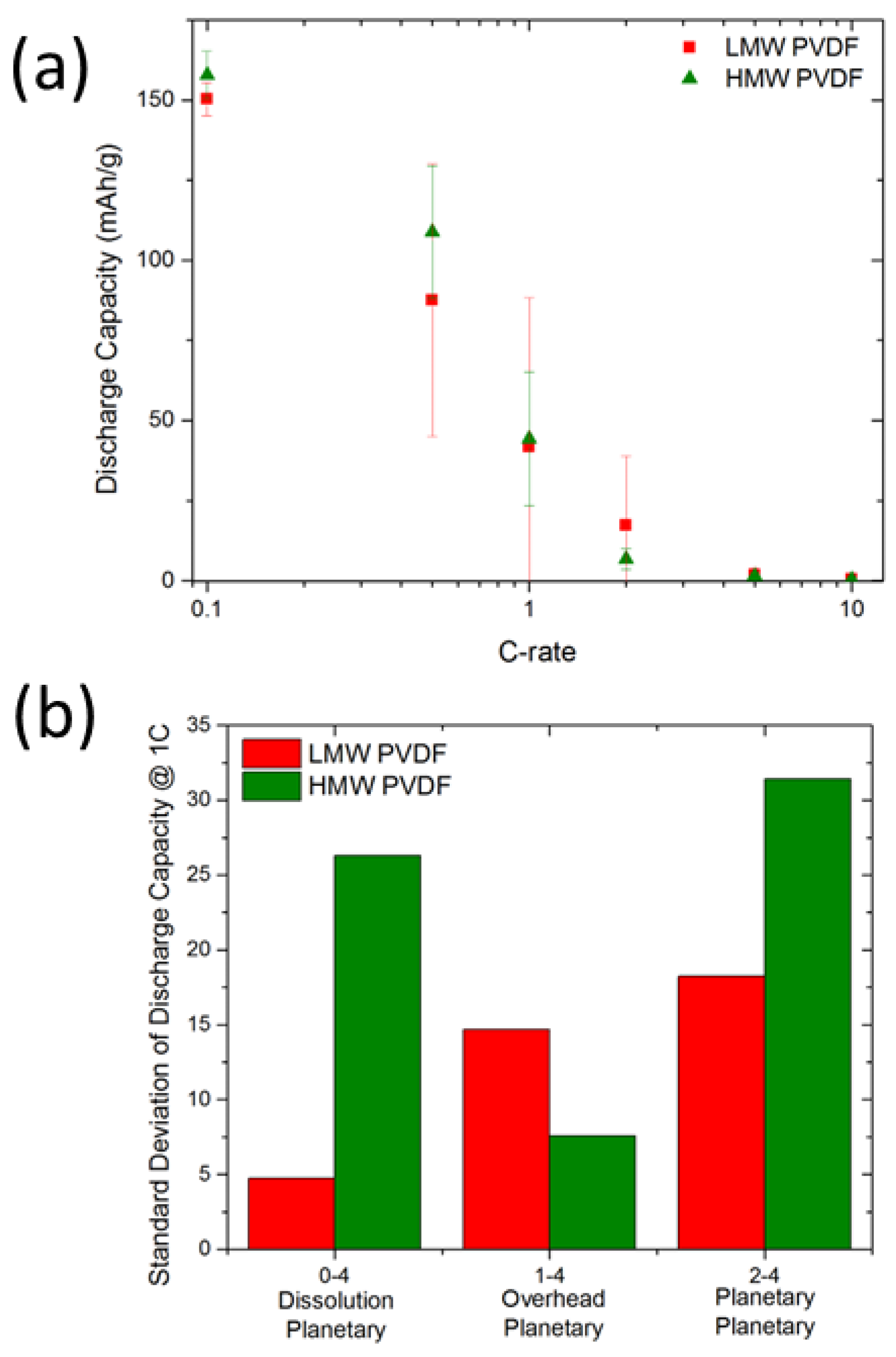
3.2. Effects of Mw on Electrode Reproducibility and Performance
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Entwistle, J.; Ge, R.; Pardikar, K.; Smith, R.; Cumming, D. Carbon Binder Domain Networks and Electrical Conductivity in Lithium-Ion Battery Electrodes: A Critical Review. Renew. Sustain. Energy Rev. 2022, 166, 112624. [Google Scholar] [CrossRef]
- Kim, K.M.; Jeon, W.S.; Chung, J.; Chang, S.H. Effect of Mixing Sequences on the Electrode Characteristics of Lithium-Ion Rechargeable Batteries. J. Power Sources 1999, 83, 108–113. [Google Scholar] [CrossRef]
- Lee, G.W.; Ryu, J.H.; Han, W.; Ahn, K.H.; Oh, S.M. Effect of Slurry Preparation Process on Electrochemical Performances of LiCoO2 Composite Electrode. J. Power Sources 2010, 195, 6049–6054. [Google Scholar] [CrossRef]
- Bockholt, H.; Indrikova, M.; Netz, A.; Golks, F.; Kwade, A. The Interaction of Consecutive Process Steps in the Manufacturing of Lithium-Ion Battery Electrodes with Regard to Structural and Electrochemical Properties. J. Power Sources 2016, 325, 140–151. [Google Scholar] [CrossRef]
- Bockholt, H.; Haselrieder, W.; Kwade, A. Intensive Dry and Wet Mixing Influencing the Structural and Electrochemical Properties of Secondary Lithium-Ion Battery Cathodes. ECS Trans. 2013, 50, 25–35. [Google Scholar] [CrossRef]
- Bockholt, H.; Haselrieder, W.; Kwade, A. Intensive Powder Mixing for Dry Dispersing of Carbon Black and Its Relevance for Lithium-Ion Battery Cathodes. Powder Technol. 2016, 297, 266–274. [Google Scholar] [CrossRef]
- Titscher, P.; von Olenhusen, A.G.; Arlt, T.; Manke, I.; Kwade, A. Evaluation of a High-Intensive Mixing Process in a Ring Shear Mixer and Its Impact on the Properties of Composite Particles for Lithium–Sulfur Battery Cathodes. Energy Technol. 2019, 7, 1801059. [Google Scholar] [CrossRef]
- Morelly, S.L.; Tang, M.H.; Alvarez, N.J. The Impotence of Non-Brownian Particles on the Gel Transition of Colloidal Suspensions. Polymers 2017, 9, 461. [Google Scholar] [CrossRef]
- Poon, W.C.K.; Pirie, A.D.; Pusey, P.N. Gelation in Colloid-Polymer Mixtures. Faraday Discuss. 1995, 101, 65–76. [Google Scholar] [CrossRef]
- Laurati, M.; Petekidis, G.; Koumakis, N.; Cardinaux, F.; Schofield, A.B.; Brader, J.M.; Fuchs, M.; Egelhaaf, S.U. Structure, Dynamics, and Rheology of Colloid-Polymer Mixtures: From Liquids to Gels. J. Chem. Phys. 2009, 130, 134907. [Google Scholar] [CrossRef]
- Zaccone, A.; Winter, H.H.; Siebenbürger, M.; Ballauff, M. Linking Self-Assembly, Rheology, and Gel Transition in Attractive Colloids. J. Rheol. 2014, 58, 1219–1244. [Google Scholar] [CrossRef]
- Saraka, R.M.; Morelly, S.L.; Tang, M.H.; Alvarez, N.J. Correlating Processing Conditions to Short- and Long-Range Order in Coating and Drying Lithium-Ion Batteries. ACS Appl. Energy Mater. 2020, 3, 11681–11689. [Google Scholar] [CrossRef]
- Serra, T.; Colomer, J.; Casamitjana, X. Aggregation and Breakup of Particles in a Shear Flow. J. Colloid Interface Sci. 1997, 187, 466–473. [Google Scholar] [CrossRef] [PubMed]
- Griessl, D.; Adam, A.; Huber, K.; Kwade, A. Effect of the Slurry Mixing Process on the Structural Properties of the Anode and the Resulting Fast-Charging Performance of the Lithium-Ion Battery Cell. J. Electrochem. Soc. 2022, 169, 020531. [Google Scholar] [CrossRef]
- Poon, W.C.K.; Haw, M.D. Mesoscopic Structure Formation in Colloidal Aggregation and Gelation. Adv. Colloid Interface Sci. 1997, 73, 71–126. [Google Scholar] [CrossRef]
- Nakken, T.; Tande, M.; Elgsaeter, A. Measurements of Polymer Induced Drag Reduction and Polymer Scission in Taylor Flow Using Standard Double-Gap Sample Holders with Axial Symmetry. J. Non-Newton. Fluid Mech. 2001, 97, 1–12. [Google Scholar] [CrossRef]
- Soares, E.J. Review of Mechanical Degradation and De-Aggregation of Drag Reducing Polymers in Turbulent Flows. J. Non-Newton. Fluid Mech. 2020, 276, 104225. [Google Scholar] [CrossRef]
- Yao, D.; Feng, J.; Wang, J.; Deng, Y.; Wang, C. Synthesis of Silicon Anode Binders with Ultra-High Content of Catechol Groups and the Effect of Molecular Weight on Battery Performance. J. Power Sources 2020, 463, 228188. [Google Scholar] [CrossRef]
- Li, J.; Armstrong, B.L.; Daniel, C.; Kiggans, J.; Wood, D.L. Optimization of Multicomponent Aqueous Suspensions of Lithium Iron Phosphate (LiFePO4) Nanoparticles and Carbon Black for Lithium-Ion Battery Cathodes. J. Colloid Interface Sci. 2013, 405, 118–124. [Google Scholar] [CrossRef]
- Lee, B.-R.; Oh, E.-S. Effect of Molecular Weight and Degree of Substitution of a Sodium-Carboxymethyl Cellulose Binder on Li4Ti5O12 Anodic Performance. J. Phys. Chem. C 2013, 117, 4404–4409. [Google Scholar] [CrossRef]
- Byun, S.; Choi, J.; Roh, Y.; Song, D.; Ryou, M.-H.; Lee, Y.M. Mechanical Robustness of Composite Electrode for Lithium Ion Battery: Insight into Entanglement & Crystallinity of Polymeric Binder. Electrochim. Acta 2020, 332, 135471. [Google Scholar] [CrossRef]
- Apachitei, G.; Hidalgo, M.; Dogaru, D.; Lain, M.; Heymer, R.; Marco, J.; Copley, M. Optimisation of Industrially Relevant Electrode Formulations for LFP Cathodes in Lithium Ion Cells. Batteries 2023, 9, 192. [Google Scholar] [CrossRef]
- Spahr, M.E.; Goers, D.; Leone, A.; Stallone, S.; Grivei, E. Development of Carbon Conductive Additives for Advanced Lithium Ion Batteries. J. Power Sources 2011, 196, 3404–3413. [Google Scholar] [CrossRef]
- Chen, Z.; Rana, D.; Matsuura, T.; Meng, D.; Lan, C.Q. Study on Structure and Vacuum Membrane Distillation Performance of PVDF Membranes: II. Influence of Molecular Weight. Chem. Eng. J. 2015, 276, 174–184. [Google Scholar] [CrossRef]
- Eberle, A.P.R.; Martys, N.; Porcar, L.; Kline, S.R.; George, W.L.; Kim, J.M.; Butler, P.D.; Wagner, N.J. Shear Viscosity and Structural Scalings in Model Adhesive Hard-Sphere Gels. Phys. Rev. E 2014, 89, 050302. [Google Scholar] [CrossRef]
- Gordon, M.B.; Kloxin, C.J.; Wagner, N.J. The Rheology and Microstructure of an Aging Thermoreversible Colloidal Gel. J. Rheol. 2016, 61, 23–34. [Google Scholar] [CrossRef]
- Hipp, J.B.; Richards, J.J.; Wagner, N.J. Structure-Property Relationships of Sheared Carbon Black Suspensions Determined by Simultaneous Rheological and Neutron Scattering Measurements. J. Rheol. 2019, 63, 423–436. [Google Scholar] [CrossRef]
- Mayer, J.K.; Almar, L.; Asylbekov, E.; Haselrieder, W.; Kwade, A.; Weber, A.; Nirschl, H. Influence of the Carbon Black Dispersing Process on the Microstructure and Performance of Li-Ion Battery Cathodes. Energy Technol. 2020, 8, 1900161. [Google Scholar] [CrossRef]
- Odell, J.; Keller, A.; Rabin, Y. Flow-Induced Scission of Isolated Macromolecules. J. Chem. Phys. 1988, 88, 4022–4028. [Google Scholar] [CrossRef]
- Vanapalli, S.A.; Ceccio, S.L.; Solomon, M.J. Universal Scaling for Polymer Chain Scission in Turbulence. Proc. Natl. Acad. Sci. USA 2006, 103, 16660–16665. [Google Scholar] [CrossRef] [PubMed]
- Kuijpers, M.W.; Iedema, P.D.; Kemmere, M.F.; Keurentjes, J.T. The Mechanism of Cavitation-Induced Polymer Scission; Experimental and Computational Verification. Polymer 2004, 45, 6461–6467. [Google Scholar] [CrossRef]
- Mehta, K.; Madras, G. Dynamics of Molecular Weight Distributions for Polymer Scission. AIChE J. 2001, 47, 2539–2547. [Google Scholar] [CrossRef]
- Tayal, A.; Khan, S.A. Degradation of a Water-Soluble Polymer: Molecular Weight Changes and Chain Scission Characteristics. Macromolecules 2000, 33, 9488–9493. [Google Scholar] [CrossRef]
- Kutringer, G.; Weill, G. Solution Properties of Poly(Vinylidene Fluoride): 1. Macromolecular Characterization of Soluble Samples. Polymer 1991, 32, 877–883. [Google Scholar] [CrossRef]
- Flory, P. Principles of Polymer Chemistry; Comell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- Morrison, F. Understanding Rheology; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Karis, T.E.; Novotny, V.J.; Johnson, R.D. Mechanical Scission of Perfluoropolyethers. J. Appl. Polym. Sci. 1993, 50, 1357–1368. [Google Scholar] [CrossRef]
- Sakaguchi, M.; Kinpara, H.; Hori, Y.; Shimada, S.; Kashiwabara, H. Ionic Products in Ground Polymer. IV. Anions in Poly(Vinylidene Fluoride). J. Polym. Sci. Part B Polym. Phys. 1988, 26, 1307–1312. [Google Scholar] [CrossRef]
- Ndour, M.; Bonnet, J.-P.; Cavalaglio, S.; Lombard, T.; Courty, M.; Aymard, L.; Przybylski, C.; Bonnet, V. The Formulation of a CMC Binder/Silicon Composite Anode for Li-Ion Batteries: From Molecular Effects of Ball Milling on Polymer Chains to Consequences on Electrochemical Performances. Mater. Adv. 2022, 3, 8522–8533. [Google Scholar] [CrossRef]
- Chartrel, T.; Ndour, M.; Bonnet, V.; Cavalaglio, S.; Aymard, L.; Dolhem, F.; Monconduit, L.; Bonnet, J.-P. Revisiting and Improving the Preparation of Silicon-Based Electrodes for Lithium-Ion Batteries: Ball Milling Impact on Poly(Acrylic Acid) Polymer Binders. Mater. Chem. Front. 2019, 3, 881–891. [Google Scholar] [CrossRef]
- Haberzettl, P.; Filipovic, N.; Vrankovic, D.; Willenbacher, N. Processing of Aqueous Graphite–Silicon Oxide Slurries and Its Impact on Rheology, Coating Behavior, Microstructure, and Cell Performance. Batteries 2023, 9, 581. [Google Scholar] [CrossRef]
- Bauer, W.; Notzel, D.; Wenzel, V.; Nirschl, H. Influence of Dry Mixing and Distribution of Conductive Additives in Cathodes for Lithium Ion Batteries. J. Power Sources 2015, 288, 359–367. [Google Scholar] [CrossRef]
- Morelly, S.L.; Alvarez, N.J.; Tang, M.H. Short-Range Contacts Govern the Performance of Industry-Relevant Battery Cathodes. J. Power Sources 2018, 387, 49–56. [Google Scholar] [CrossRef]
- Stephenson, D.E.; Hartman, E.M.; Harb, J.N.; Wheeler, D.R. Modeling of Particle-Particle Interactions in Porous Cathodes for Lithium-Ion Batteries. J. Electrochem. Soc. 2007, 154, A1146. [Google Scholar] [CrossRef]
- Albertus, P.; Christensen, J.; Newman, J. Experiments on and Modeling of Positive Electrodes with Multiple Active Materials for Lithium-Ion Batteries. J. Electrochem. Soc. 2009, 156, A606. [Google Scholar] [CrossRef]
- Burdette-Trofimov, M.K.; Armstrong, B.L.; Rogers, A.M.; Heroux, L.; Doucet, M.; Yang, G.; Phillip, N.D.; Kidder, M.K.; Veith, G.M. Understanding Binder–Silicon Interactions during Slurry Processing. J. Phys. Chem. C 2020, 124, 13479–13494. [Google Scholar] [CrossRef]
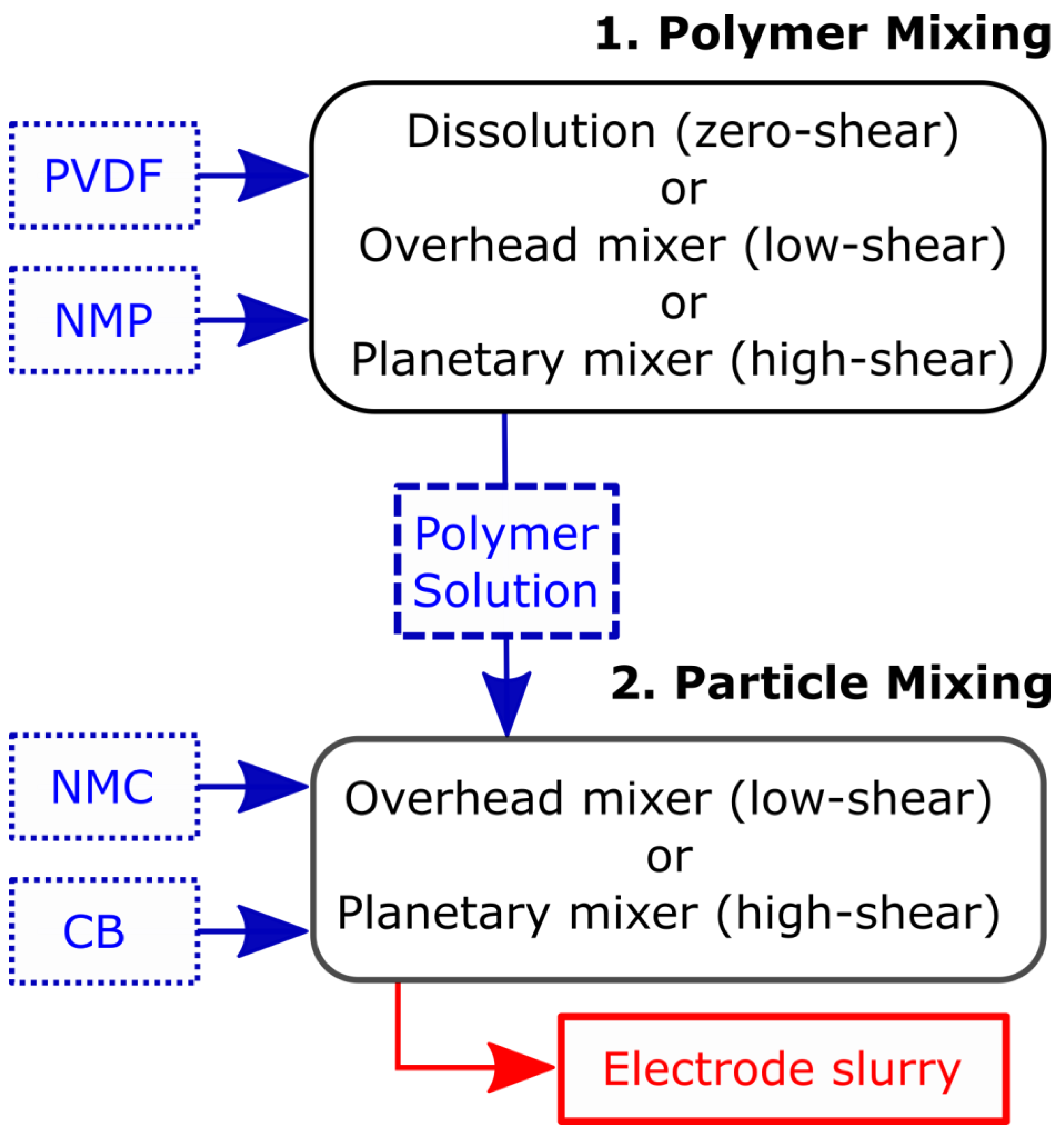
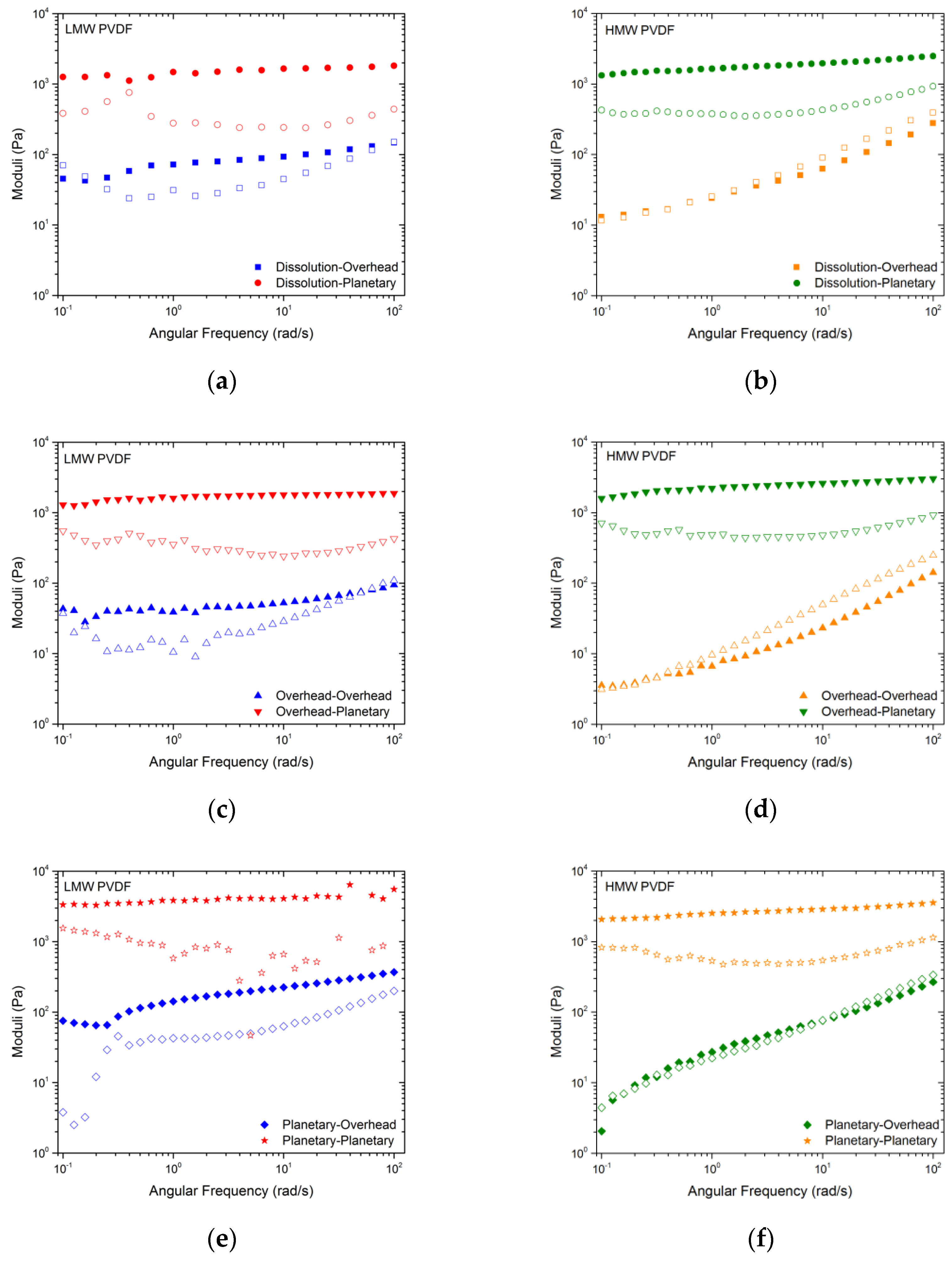

| Figure | Polymer MW | Polymer Mixing | Particle Mixing | Microstructure |
|---|---|---|---|---|
| Figure 2a | LMW | Dissolution | Overhead | Weak gel |
| LMW | Dissolution | Planetary | Strong gel | |
| Figure 2b | HMW | Dissolution | Overhead | Fluid |
| HMW | Dissolution | Planetary | Strong gel | |
| Figure 2c | LMW | Overhead | Overhead | Weak gel |
| LMW | Overhead | Planetary | Strong gel | |
| Figure 2d | HMW | Overhead | Overhead | Fluid |
| HMW | Overhead | Planetary | Strong gel | |
| Figure 2e | LMW | Planetary | Overhead | Weak gel |
| LMW | Planetary | Planetary | Strong gel | |
| Figure 2f | HMW | Planetary | Overhead | Fluid |
| HMW | Planetary | Planetary | Strong gel |
| Parameter | Component | Expected Value |
|---|---|---|
| Gravitational Peclet number | CB | |
| NMC | ||
| Polymer concentration ratio | LMW PVDF | 2 |
| HMW PVDF | 10 | |
| Attraction energy | CB & LMW PVDF | −0.5 |
| CB & HMW PVDF | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morelly, S.L.; Saraka, R.M.; Alvarez, N.J.; Tang, M. Impact of Mixing Shear on Polymer Binder Molecular Weight and Battery Electrode Reproducibility. Batteries 2024, 10, 46. https://doi.org/10.3390/batteries10020046
Morelly SL, Saraka RM, Alvarez NJ, Tang M. Impact of Mixing Shear on Polymer Binder Molecular Weight and Battery Electrode Reproducibility. Batteries. 2024; 10(2):46. https://doi.org/10.3390/batteries10020046
Chicago/Turabian StyleMorelly, Samantha L., Renee M. Saraka, Nicolas J. Alvarez, and Maureen Tang. 2024. "Impact of Mixing Shear on Polymer Binder Molecular Weight and Battery Electrode Reproducibility" Batteries 10, no. 2: 46. https://doi.org/10.3390/batteries10020046
APA StyleMorelly, S. L., Saraka, R. M., Alvarez, N. J., & Tang, M. (2024). Impact of Mixing Shear on Polymer Binder Molecular Weight and Battery Electrode Reproducibility. Batteries, 10(2), 46. https://doi.org/10.3390/batteries10020046









