Abstract
To analyze the safety behavior of electric vehicles, mechanical simulation models of their battery cells are essential. To ensure computational efficiency, the heterogeneous cell structure is represented by homogenized material models. The required parameters are calibrated against several characteristic cell experiments. As a result, it is hardly possible to describe the behavior of the individual battery components, which reduces the level of detail. In this work, a new data-driven material model is presented, which not only provides the homogenized behavior but also information about the components. For this purpose, a representative volume element (RVE) of the cell structure is created. To determine the constitutive material models of the individual components, different characterization tests are performed. A novel method for carrying out single-layer compression tests is presented for the characterization in the thickness direction. The parameterized RVE is subjected to a large number of load cases using first-order homogenization theory. This data basis is used to train an artificial neural network (ANN), which is then implemented in commercial FEA software LS-DYNA R9.3.1 and is thus available as a material model. This novel data-driven material model not only provides the stress–strain relationship, but also outputs information about the condition of the components, such as the thinning of the separator. The material model is validated against two characteristic cell experiments. A three-point-bending test and an indentation test of the cell is used for this purpose. Finally, the influence of the architecture of the neural network on the computational effort is discussed.
1. Introduction
The global demand for lithium-ion battery cells is increasing rapidly, driven by the e-mobility sector [1]. An important aspect here is the safety behavior, since damaged batteries of electric vehicles that are exposed to abusive mechanical loads have an increased risk potential [2]. This is the case, for example, in traffic accidents. To analyze the behavior of such systems, simulations [3] are used in addition to experiments [4]. An essential tool here is a finite element analysis (FEA). In addition to the mechanical [5], thermal [6], and electrochemical behavior [7], their coupled behavior (multi-physics simulations) [8,9] is also investigated. These properties are investigated in both an experiment and simulation at different levels of scales (Figure 1). These range from the investigation of the constituent parts of the individual components (micro-level), to the classic hierarchical structure (cell—module—battery pack), to the entire vehicle [10].

Figure 1.
Different scales of experiments and simulations of electric vehicles.
In addition, cells can be modeled at different levels of detail. Zhu et al. [10] categorized the modeling approaches into homogenized, detailed, and RVE models. In homogenized models, the heterogeneous structure of the cell is neglected and modeled as a unitary object [5,11,12,13,14,15,16,17,18]. The main advantage here is the computational efficiency. Due to the homogeneous consideration of the cell, fewer and larger elements can be used in the discretization. This has a positive effect on the critical time step in explicit time integration. In addition, less elements need to be calculated per time step. The challenge here is the selection of suitable constitutive material models and their parameterization. To calibrate these models, the results of experiments with the cell to be modeled are used. For example, Beaumont et al. [18] used three intrusion and two bending tests of a cell to calibrate the behavior. In a previous study, a machine learning tool was used to calibrate six parameters of a macroscopic model against three load cases [13]. A great deal of effort is put into determining characteristic load cases and testing them using precise experimental setups [19,20,21,22,23,24]. However, such an extensive test program requires a large number of already existing cells. Predicting the behavior of a cell in the development stage is not possible without producing prototypes. Moreover, no statement can be made about the deformation of the individual components.
The counterparts to macroscopic or homogenized models are detailed or mesoscopic models [10,25,26,27,28,29,30]. Here, the cell is no longer considered as a unified entity. The cell is modeled heterogeneously by representing the individual components. For the parameterization of such models, material parameters of each component are required. For this purpose, mechanical characterizations of the individual components are performed [31,32,33]. There are several hurdles in modeling. One of them is the consideration of the interaction between the individual layers. For example, Breitfuss et al. [25] created a model in which all contacts between the different layers are represented. This large number of serial contacts brings with it the problems of instability and an increased computational effort. However, a subdivision of the electrodes into active material and current collectors also leads to a large number of elements with small dimensions, which has a negative influence on the calculation time. In a previous study, the authors showed approaches on how to reduce the computational effort for a detailed modeling of the cell [27]. For this purpose, contact definitions and the subdivision between active material and current collectors are dispensed with, and a discrete element formulation for a constant time step is used. In another work, a reduced-order model of a detailed structure was generated using the separation-of-space approach to further reduce the computational effort [30]. However, the computational effort can by no means be reduced to the level of macroscopic modeling. Therefore, for now, it does not seem appropriate to use such detailed models at the higher scales such as the module or even battery pack.
In order to keep the characterization effort low and still have a parameterization based on the component properties, it is often attempted to transfer information from the lower scales. For this purpose, a representative volume element (RVE) is modeled. This RVE can be used to investigate the general structural behavior or to derive the homogenized material properties [34,35,36,37,38]. Therefore, homogenization theories are used, which describe the relationship between the scales [39,40,41]. Sahraei et al. [34] used this method to investigate the influence of component failure on cell behavior. The RVE was subjected to various load situations and a macroscopic material model was calibrated with the results. The disadvantage of this procedure is that a lot of information is lost when transferring the behavior from the RVE to the macroscopic level. This is especially true for the behavior of the individual components. In addition, the use of a constitutive material law for the description of the macroscopic behavior is a huge simplification.
A more accurate variant is the simultaneous multi-scale simulation, also known as FE2. Here, both the macroscopic problem and the underlying meso- or microscopic problems are solved simultaneously. Tikarrouchine et al. [42] used this approach to solve three-dimensional problems of composites. The main hurdle here is the transfer of information between the different scales. Unfortunately, this does not lead to an efficient solution of the problem, since in addition to the macroscopic problem, the underlying structures must also be fully calculated.
An increase in efficiency can be achieved by separating the simulations of the individual scales in time. In this way, the corresponding detailed structures are subjected to a large number of loads in advance in a training phase (offline phase). The data generated in this way can later be used in the macroscopic simulation (online phase). The relationship between the scales can be generated by data-driven formulations such as neural networks. These replace the classical constitutive surrogate material models of the overall structure. In general, there is a wide range of use cases for data-driven material modeling. Hashash et al. [43] used neural networks to describe the material behavior including yielding and plasticity. Gorji et al. [44] used recurrent neural networks (RNNs), an extension of the classical network architecture, to include memory cells to incorporate history. Tancogne-Dejean et al. [45] also used an RNN to reproduce the macroscopic behavior of the structure of a Li-ion cell. For this purpose, however, relatively large neural networks with up to 200 neurons per layer were used, which were conditioned with data from around 20,000 load cases. The high level of detail was demonstrated with several RVE load cases. An implementation and application of this RNN in commercial solvers for the simulation of entire cells or even a stack of several cells (module) appears to be very computationally intensive due to the network size. In addition, the high number of training simulations further reduces the efficiency.
The authors addressed this problem. In this paper, they show the implementation of a data-driven material model in commercial FEA software LS-DYNA R9.3.1 (ANSYS Inc., Livermore, CA, USA) and how the required training data can be reduced. In addition, the influence of the type and size of the neural network on the computational efficiency is discussed. This creates a balance between the level of detail and computational efficiency. The focus here is on load configurations of the cell in the thickness direction.
2. Materials and Methods
2.1. Cell Under Study
The lithium-ion cell used for this work is an NMC pouch cell with a mass of 0.9 kg and a capacity of 64.6 Ah. During the disassembly process, 66 separators, 33 anodes, and 32 cathodes were extracted. Dimensions of the entire cell are 354 × 101 × 11.25 mm (SOC: 0%). The properties of the individual components are listed in Table 1.

Table 1.
Information about the cell under study.
2.2. Concept
To overcome the contradiction between the level of detail and computation time, a data-driven multi-scale approach is investigated. This can be divided into five phases (See Figure 2).
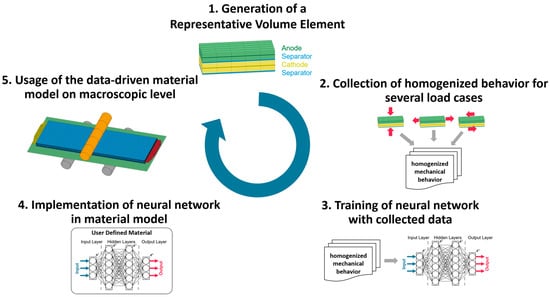
Figure 2.
Modeling concept for data-driven multi-scale approach.
- The selection and modeling of a representative volume element.
- The generation of training data in appropriate load cases (homogenized mechanical behavior).
- The training of a neural network.
- The implementation of the trained neural network in a commercial FEA solver.
- The application of the data-driven material model on a macroscopic cell level.
In the first phase, a section of the structure is selected that is representative of the structure of the entire cell. This allows the geometric pattern of the cell structure to be exploited. The small section is modeled in detail and parameterized with the material properties of the corresponding components.
This representative volume element (RVE) is homogenized to determine the overall mechanical behavior under several loading scenarios. Here, suitable simulation planning and assumptions keep the effort of the training phase low. The variables determined from this include the macroscopic behavior (stress and strain) of the RVE as well as information of the component behavior.
In the next phase, the relationship between homogenized strain and stress is reproduced by means of a neural network. Additional outputs are the component deformations, which are of interest. Here, the influence of the network architecture on the computational effort and resulting error is investigated. After the training process with a suitable algorithm, the network quantities are exported.
These quantities are used after the network is implemented in the commercial FEA solver LS-DYNA R9.3.1 as a user-defined material model. For this purpose, the calculation routine of the selected neural network is reproduced in the corresponding programming language. In addition, the required substitute material values are defined. These are necessary to calculate the time step of the explicit time integration.
After the successful implementation of the neural network, the lithium-ion cell can be modeled macroscopically. This requires additional components such as the pouch envelope and the consideration of the electrolyte. However, these are not represented by data-driven laws but by constitutive material laws. This cell model can now be validated with corresponding cell experiments. An essential advantage of this approach is its transferability. The transfer of this modeling approach from one cell to another is possible because mainly component properties are required for parameterization. This is a significant advantage over homogenized models, which are calibrated with results from cell tests. Another advantage is the macroscopic discretization of the cell. In contrast to detailed models, the dimensions of the components do not limit the minimum element dimension. By using larger elements, not only the larger time step leads to a shortening of the calculation time, but also the fact that fewer elements have to be calculated. This fact is also used in common RVE-based cell models. However, macroscopically, they are based on constitutive material laws. This means that the behavior of the RVE structure can only be reproduced to a limited extent. The data-driven approach offers the possibility of outputting component deformations as additional information.
2.3. Representative Volume Element (RVE)
In order to determine the homogeneous behavior, a suitable section (RVE) of the cell is selected. This should represent the mechanical behavior of the entire structure. By enlarging the selected area, the behavior of the RVE converges to that of the cell. However, this also increases the computational effort. Since the simulation of various load cases is planned, it is attempted to keep the area as small as possible. In the thickness direction, the selected section consists of the sequence of anode—separator—cathode—separator (Figure 2-1). This is the structure as it occurs in the real cell except for the edge areas. The commercial solver LS-DYNA R13.0 is used to simulate the RVE.
The thickness of the RVE is 0.336 mm. For the in-plane dimensions, a size of 1 × 1 mm is chosen. For the modeling of the electrodes, a distinction is made between the active material and current collector. For the discretization of the electrodes, volume elements (hexahedrons) are used. In the thickness direction, each ply of active material consists of three layers of elements while the current collector is modeled with one element in thickness. It is assumed that in the case of the electrodes, the current collectors absorb the majority of the tensile loads. The materials (aluminum and copper) are modeled with the isotropic elastic–plastic material model *MAT_PIECEWISE_LINEAR_PLASTICITY. The *MAT_CRUSHABLE_FOAM material model is used for the active materials. This is mainly intended to represent the compression behavior in the thickness direction.
The separators are discretized by a hybrid structure of solids and shells. The shell elements represent the extensive in-plane behavior. The *MAT_EXTENDED_3PARAMETER_BARLAT model is used. This is an anisotropic material model, which represents the directional dependence of the tensile behavior of the separators. The solids (one layer on both sides) only have out-of-plane mechanical properties. This requires a decoupled material model. The *MAT_MODIFIED_HONEYCOMB is used for the hexahedral elements. This is a fully decoupled material model, which offers the possibility to define only the behavior in the thickness direction and the out-of-plane shear behavior. Those elements represent the out-of-plane behavior of the separator as well as the interlaminar behavior. Coincident nodes connect the different layers of materials. This requires a homogeneous mesh width of all layers. For this, 5 × 5 elements are used in the plane. For the characterization of the different material models, tensile tests and compression tests of the components are performed. For the calibration of the interlaminar behavior, a three-point bending cell test is used.
2.4. Homogenization
The first-order homogenization theory implemented in LS-DYNA (*RVE_ANALYSIS_FEM) was used to determine the overall behavior of a heterogeneous microstructure [46]. This follows the Hill–Mandel condition [47] enhanced for finite strain formulation (Equation (1)). It describes the equilibrium of virtual work between macro- and microscales. is the space of admissible deformations of the microscale in the defined domain . is the first Piola–Kirchhoff stress tensor and is the deformation gradient.
Here, the defined structure is given the deformation with the macroscopic displacement gradient . This corresponds, as shown in Equation (2), to the gradient of the macroscopic deformation field . This is equal to the deformation gradient minus the identity tensor . Generally, is not symmetrical.
According to Equation (3), this can be divided into rigid body rotations and a stretch tensor . The stretch tensor is symmetrical. Since the rigid body rotations have no influence on the mechanical behavior of the microstructure, the following can be assumed here, .
This shows that both the deformation gradient and the macroscopic displacement gradient are symmetrical. For the three-dimensional case, both consist of six components each.
So-called control points apply the deformation of the heterogeneous structure. For three-dimensional problems, the relationships between the displacements of these additional points and the deformation gradient are listed in Table 2.

Table 2.
Relation between displacement of control points and macroscopic deformation gradient [46].
These control points can be used to apply different displacement boundary conditions to the RVE. In principle, linear as well as periodic boundary conditions are possible. The difference is shown graphically in Figure 3.
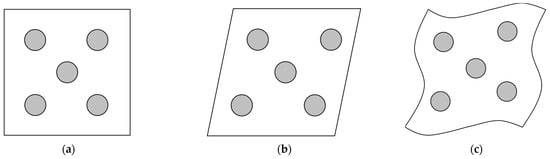
Figure 3.
(a) Initial configuration. (b) Deformed configuration with linear boundary conditions. (c) Deformed configuration with periodic boundary conditions.
From different sources, it can be seen that the boundary conditions have an influence on the result. Periodic boundary conditions are to be preferred, as they provide a more accurate result. Linear boundary conditions usually behave too stiffly. By increasing the RVE size, this deviation can be minimized [34,46,48]. However, since this has a negative effect on the calculation time, periodic boundary conditions are used.
Based on the deformation gradient , further strain formulations can be calculated, such as the true strain tensor (Equation (5)) using the Cauchy–Green deformation tensor (Equation (4)).
Based on the first Piola–Kirchhoff tensor and the deformation gradient, the Cauchy stress tensor is calculated as an additional stress formulation (Equation (6)). Here, is the determinant of .
In general, different couplings of the mechanical behavior can occur. The best-known example of this is the Poisson effect, which is a strain–strain coupling. In addition, other couplings such as strain–shear or shear–shear are also possible. However, it is assumed that in the cell structure, the couplings, with the exception of transverse contraction, are either non-existent or negligibly small. The Voigt notation is shown in Equation (7).
This has significant advantages in the training phase, as corresponding data from coupled loads must be generated. Uniaxial loads on the RVE can be used to determine which couplings of mechanical behavior are present.
The majority of the loads on a cell are monotonic load cases (no alternating tensile and compressive phases). Therefore, a modeling of corresponding effects by the elastic–plastic behavior is omitted. The same applies to the resulting path dependence of the mechanical behavior. These circumstances lead to a further reduction in the effort for generating training data.
Since a coupled mechanical behavior of the normal directions is expected, corresponding training data must be generated for this. For this purpose, a spherical region in the strain space is chosen. The required parameters for the homogenization theory are shown in Equations (8)–(10).
These are now dependent on the radius of the training space and the angles and . A step size of 10° is chosen for the angles (Equations (11) and (12)).
A maximal value of 0.3 is considered as plausible for the macroscopic displacement gradient . The resulting training space for the normal directions is shown in Figure 4.
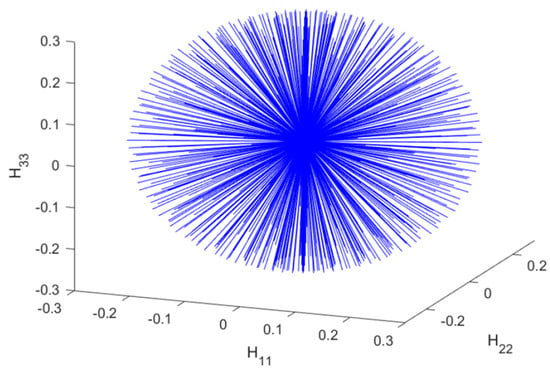
Figure 4.
Training space for normal directions.
Since no coupling is expected for the shear directions, they can be considered independently. Thus, values up to ±0.2 are assumed for the off-diagonal components of the macroscopic displacement gradient (Equation (13)).
The training phase thus consists of 614 unique deformation combinations for the behavior in normal directions and six more for the shear behavior. This already shows the advantage of the non-existent or neglected additional couplings. The simulation effort for the decoupled shear behavior is only a fraction of that for the coupled behavior in the normal direction.
All necessary simulations were carried out with implicit time integration. This makes it possible to keep the effort for generating the training data within limits despite the small element dimensions.
2.5. Artificial Neural Network
No constitutive material model is used to represent the mechanical behavior of the homogenized structure. The behavior is modeled with the help of a feed-forward neural network in its most generalized form. This consists of an input layer, several hidden layers, and a final output layer (Figure 5). Each of these layers has a number of different neurons. The number of corresponding variables determines the number of input and output layers. The number of hidden layers and their neurons is selectable. This so-called architecture has an influence on performance, computing time, and the duration of the training process.
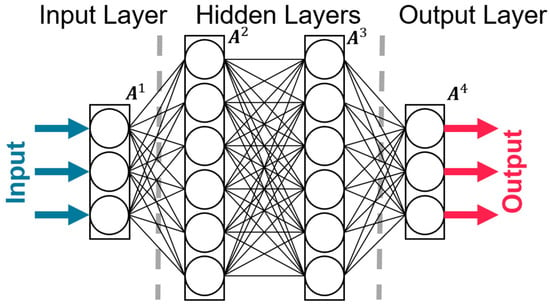
Figure 5.
Architecture of a feed-forward neural network with three inputs, three outputs, and two hidden layers with six neurons each.
At the beginning, the input variables are normalized, as the variables can differ greatly in the value range. is the normalization value of the individual input variables . The respective maximum of the absolute values of the training data is used (Equation (14)).
At the input layer (), the variables are thus normalized. are the output values of the input layer (Equation (15)).
For the subsequent hidden layers and the final output layer, the relationship applies according to Equation (16). The output of the previous layer is used as the input of the current layer . These values are multiplied by the corresponding weights and summed up before the biases are added. Finally, the activation function of the respective layer is applied. This applies to all layers except the input layer.
The hidden layer and the output layer differ only in the activation function used. For the first ones, the Tansig function is used for activation, which is shown in Equation (17).
A linear activation function without the scaling factor is used for the output layer (Equation (18)).
Finally, the results of the output layer are re-normalized to according to Equation (20). Equivalent to the input layer, the maximum absolute values of the output training data are used for this (Equation (19)).
This neural network can now be used to infer from the homogenized true strain to the homogenized Cauchy stress , as well as the essential information of the components (e.g., the compression of the different layers). For this purpose, the mean strain values in the thickness direction of the individual layers are used.
Assuming monotonic load cases without path dependence, it is possible to derive the stress state and the state variables from the current strain state (Equation (21)). Otherwise, additional input parameters would have to be used to define a prediction model for the current stress state. For example, Hashash et al. [43] used the previous stress and strain states and . The work of Gorji et al. [44] discussed the use of the previous load path, as well as the load direction and the use of other network types like recurrent neural networks (RNNs).
Since the coupled behavior is modeled in the normal direction, all three directions must be included in a single neural network (Equation (22)).
The homogenized shear behavior is represented in a decoupled manner; no joint neural network is required. As shown in Equation (23), a separate neural network is created for each of the three shear directions.
An essential condition of the behavior is the initial state. As shown in Equation (24), it must be ensured that a strain-free state leads to a stress-free state. This also applies to the information of the microstructure . Here, it is under the assumption that the strains are those of the individual components.
Due to the bias (see Equation (16)), it usually happens that this condition is not exactly fulfilled. Removing the bias values would reduce the flexibility and performance of the neural network. The deviations are—with successful training of the network—minimal, but present. As shown in Equation (25), an offset vector is subtracted from the output vector to achieve the corrected output (stress values and state values . These thereby fulfill the initial condition.
The required offset vector can be calculated via the trained neural network with a strain-free state as input (Equation (26)).
The relative errors are used for evaluation. These are calculated as shown in Equation (27) by the absolute deviations and the maximum values of the training data . A relative deviation of one percent is chosen as the limit.
Matlab R2020b software with Deep Learning Toolbox 14.1 is used for the training phase.
After importing the training data, the architecture of the network is defined. The type used is a feed-forward neural network. The influence of the network size (number of hidden layers and neurons per layer) is investigated.
Bayesian regularization backpropagation is used as a training algorithm. Here, the linear combinations of squared errors and weights are minimized [49,50].
For training, the data are divided into training and testing sets. The proportion of testing data is set at 20%, which is the most common variant for data splitting [51]. These testing sets have no influence on the training and are therefore an independent measure for the evaluation.
Various options are available as criteria for terminating the training. For example, a maximum number of training epochs, the duration of the training, the current performance (MSE), or its gradient are available. Since a high training speed is achieved due to the selected architecture, a termination criterion of 500 epochs is selected.
The quality of the training is then evaluated. The criteria available are the mean squared error, the regressions, and the error histogram. The definition of the mean square error is shown in Equation (28). Here, is the number of data points, are the observed values, and are the predicted values.
2.6. Consideration of Component Failure
So far, no failure of the component layers has been considered. However, Goodman et al. [22] showed that bending loads cause the components to fail in tension. Instabilities also lead to loss of the load capacity in compression.
In order to take this behavior into account at the macroscopic level, the damage tensor is introduced according to Equation (29). This represents the connection between the undamaged stress and the damaged stress .
Since it is assumed that the components fail under in-plane loading and that there is no failure due to lateral compression, the local damage variable is only introduced in the in-plane normal directions in accordance with Equation (30).
Since it is assumed that the current collectors of the anode and cathode have a dominant effect on the homogenized in-plane behavior and that these fail in a brittle manner, the damage progression is selected abruptly according to Equation (31). The local damage variable is zero as long as the in-plane strain according to Equation (32) is smaller than the strain limit . By checking the history via , the irreversibility of the damage can be modeled. It should be noted that the component failure is not represented by the neural network.
If this condition is not met, the value of is assigned to the local damage variable. The result is the residual load capacity of the separator layers and the active materials.
The required parameters and are determined by the comparison of the component tensile tests.
2.7. Implementation in LS-DYNA
The described relationship between homogenized strain and stress is now implemented in a commercial solver. LS-DYNA R9.3.1 is used for this purpose. In LS-DYNA, it is possible to create user-defined material models. These mainly consist of the keyword and the subroutine. The corresponding material behavior is coded in Fortran in the subroutine. After compilation, the material model can be used by means of the keyword. Table 3 lists all used input parameters that can be used in the subroutine.

Table 3.
Used input parameters for the user-defined ANN-based material in LS-DYNA [52].
Since eps (6) are only the strain increments of the time step, these must be summed up according to Equation (33). Here, is the strain increment per time step.
The stresses calculated by the ANN are written to the stress parameters sig (6). The history variables hsv (*) are used for the status variables . The required information regarding the architecture of the neural network will be inserted through the material constants cm (*). This refers mainly to the number of layers, neurons per layer, and the activation function.
The corresponding values of these parameters are defined in the keyword. It is also mandatory to define the material density , the bulk modulus , and the shear modulus . These are required for the calculation of the wave propagation speed as shown in Equation (34). Although these parameters are not required for the representation of the material behavior, they are indispensable for the time step calculation.
The density is chosen in a way that the mass of the cell model corresponds to that of the real cell. The values for the bulk modulus and the shear modulus were chosen in a way that the wave propagation speed is higher than the highest value of the components.
The verification of the data-driven material model is performed by comparing the detailed RVE with a single element, which has the data-driven material model assigned. A compression in the thickness direction up to 20% is used as the load case, since this is representative for a typical cell load. The actual values for the component compressions (z-strain) of the separators and the active materials are compared with the predicted values of the ANN model. Both simulations are carried out with explicit time integration, which also makes it possible to evaluate the increase in computational efficiency. The validation is carried out afterwards by comparing the force–displacement curve of the simulation and experiment of an indentation test of the whole cell.
2.8. Cell Model
The model of the cell can now be set up macroscopically. This has great advantages in terms of computational time, as usually fewer and larger elements are required for the discretization. The main quantities that are transferred from RVE to cell level are stresses and strains. These are dimension-independent. Thus, it is not mandatory that the macroscopic elements have the same dimensions as the selected RVE. The jelly stack of the cell is represented by 74,880 solid elements (128 × 39 × 15). The pouch foil is modeled by shell elements. The same applies to the cell tabs. Coincident nodes connect the pouch and jelly stack. The common in-plane mesh size is chosen as 2.5 × 2.5 mm. For the pouch foil, an isotropic elastic–plastic material model, *MAT_PIECEWISE_LINEAR_PLASTICITY, is used.
An airbag model represents the electrolyte inside the pouch in a very simple way. As shown in Equation (35), a linear fluid model is used. The pressure inside the pouch is denoted as , while means the bulk modulus of the electrolyte. and describe the initial and the deformed volumes enclosed by the pouch.
2.9. Experiments for Characterization and Vaildation
2.9.1. In-Plane Characterization of Components
For the determination of the in-plane behavior of the components, tensile tests are carried out on component samples. For this purpose, a cell is discharged to an SOC of 0% following a constant current–constant voltage protocol. Afterwards, the cell was opened and the various layers were extracted and strips with a width of 5 mm were cut using paper guillotine shears. To check the anisotropy of the materials, these are taken in the machine direction (MD) and transverse direction (TD). For the separator, samples were also taken in the diagonal direction (DD), as strong anisotropy was expected here. The samples are then stored in Dimethyl carbonate (DMC) as a substitute electrolyte. All tensile tests are carried out with wet samples on an RSA-G2 (DMA) device. The test length was 15 mm and the test velocity was 20 mm/min (Figure 6a). The stress–strain curve is calculated from the measured forces, displacements, and specimen geometries. To check the reproducibility, each configuration is carried out five times.

Figure 6.
Different experimental setups for characterization and validation of component and cell level: (a) In-plane characterization of components. (b) Novel out-of-plane characterization of components. (c) Three-point-bending test. (d) Indentation test with cylindrical impactor.
2.9.2. Out-of-Plane Characterization of Components
For the characterization of the out-of-plane components, samples of the components were also extracted from a cell with SOC at 0%. Since the component layers are very thin, it is the state of the art to test stacks of the same components [31,33,34]. In this work, instead of testing stacks to characterize the out-of-plane behavior, a novel method is used for single-layer compression tests. The device shown in Figure 6b comes from the paper technology sector and is used to characterize thin films in the thickness direction. This ZwickRoell compressibility device is operated with the ZwickRoell zwickiLine Z2.5 TN. The individual layers are loaded with a circular plate with a surface of 5 mm2. To rule out errors due to plate orientation, the stamp is mounted freely and its orientation adapts to the specimens. The maximum force is 200 N, which means that stresses up to 40 MPa can be achieved. The point of first contact is determined by a force level of 2 N, which represents a stress of 0.4 MPa. In order to determine the influence of the loading speed, the electrodes are compressed with a loading speed of 0.1 mm/min as well as 0.2 mm/min. Since the separator thickness is around one tenth of the electrodes, velocities of 0.02 mm/min and 0.2 mm/min are selected and so a wider velocity range is also used. To avoid chemical reactions between the electrolyte and the polished load head, the components are tested when dry. Each test configuration is carried out three times.
2.9.3. Cell Tests for Calibration and Validation
For the calibration of the behavior between the layers, as well as for validation, results of cell tests are used. For the interlaminar behavior, the results of a three-point-bending test are used, which are already shown by Schmid et al. [13]. Therefore, the cell is positioned on two cylinders (D = 30 mm) at a distance of 120 mm. Between the specimen and cylinders is a steel sheet with a thickness of 1 mm. This serves as support to achieve a defined bending load in the center and friction situation. This is induced by a third cylinder, which presses centrally on the cell with a velocity of 1 mm/s (Figure 6c). Although the cell used in this previous study had a state of charge of 100%, the results of Qu et al. [53] showed that the SOC has only a minor influence on the bending behavior of pouch cells. Furthermore, the SOC does not influence the initial slope of the force–displacement curve, which is used to calibrate the interlaminar behavior.
An indentation test is used for the validation. Here, a cylindrical impactor (D = 30 mm) presses on the cell with SOC at 0%, which lies on a flat base. To exclude the effects of boundary zones and especially the tabs, the impactor deforms a length of about 75 mm. So, none of those zones are affected. The edges of the cylinder are rounded with a radius of 5 mm (Figure 6d). The test velocity is 1 mm/s. For both test setups, the same testbench including measuring devices as described in the previous work [13] is used. Of particular interest here is the indentation depth and the resulting force up to the point of an internal short circuit. The indentation is measured with a linear glass scale with a 1 µm resolution and an accuracy of ±0.01 mm/m. For measuring the force, the load cell type K 500 kN from GTM is used. To determine the internal short circuit, the cell voltage was measured during the tests.
3. Results
3.1. In-Plane Characterization of Components
The experimental results as well as the simulation results of the component tensile tests are shown in Figure 7. As shown in Subplot 7a, the separator samples are taken in three different directions (MD, TD, and DD), resulting in three pairs of curves. These differ only slightly in their shape but much more in the failure range. For example, all samples taken in the machine direction failed in a strain range of around 35% to 50%. The samples from the transverse direction (TD) withstood a range of 45% to 70%. Those from the diagonal direction (DD) failed in a range of 52% to 62%. These also achieved the maximum stress value of around 85 MPa.
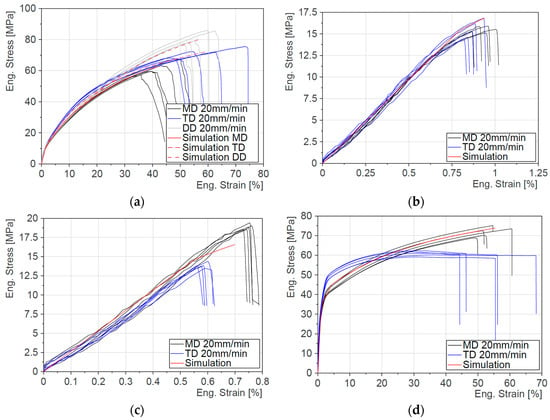
Figure 7.
Results of the tensile tests for the in-plane characterization of the components: (a) Separator. (b) Anode. (c) Cathode. (d) Pouch.
The results for the electrodes are shown in Figure 7b,c. It should be noted that the stress is related to the entire output cross-section consisting of active material and current collectors. The anode and cathode samples failed much earlier than those of the separator. For example, the anode samples fail in a range of around 0.8 to 1% strain. Maximum stresses of around 17 MPa are achieved. In contrast to the anode, there is a difference between MD and TD for the cathodes. The samples from the machine direction fail at a strain of around 0.75%, while those in TD have a failure strain of only around 0.6%.
Figure 7d shows the results of the tensile tests with pouch specimens. It is noticeable that the pairs of curves differ in their characteristics. For example, the plastic range of the samples from the machine direction is steeper than those from the transverse direction. Although the average failure strain is approximately the same, there is a wider range of failure in the TD specimens.
The material parameters of the components, which are important for the in-plane behavior, are listed in Table 4. All tensile tests were simulated with these parameters upon the mentioned values for failure strain and the results are also shown in Figure 7.

Table 4.
Material parameters for the components.
Furthermore, it is noticeable from Figure 7b,c that the failure strain of the electrodes only differs minimally. For the macroscopic representation of the component failure, the earliest detected component failure is used for , which has a value of 0.6%. The proportion of the separator on the in-plane behavior of the RVE is assumed to be around 5%, considering the component thicknesses. This results in a value of 0.95.
3.2. Out-of-Plane Characterization of Components
The results of the out-of-plane characterization are shown in Figure 8. Figure 8a shows the results of the anode. The black curves represent the behavior at the lower velocity of 0.1 mm/min while the gray curves show the results at 0.2 mm/min. There is no significant difference between the two speeds. All curves achieved their maximum compression at a load of 40 MPa in a range of 21.05 to 23.77%. The tested samples had an average thickness of 168.1 µm. In Figure 8b, the results for the cathode are shown. Again, the black curves represent the results with a test velocity of 0.1 mm/min and the gray curves are the ones with 0.2 mm/min. Comparing the results for the anode and cathode, it is visible that the cathode behaves stiffer than the anode and that the results have a wider spread since the maximum stress of 40 MPa is reached in a corridor between 5.00 and 7.31%. Also, the mean thickness of the tested components (149.6 µm) has a bigger deviation from the values listed in Table 1. The results for the separator are shown in Figure 8c. Since the separator is ten times thinner than the anode or cathode, other velocities were used. The results with 0.02 mm/min are shown in black and the gray curves show the results with a test velocity of 0.2 mm/min. Also, through a wider range of the strain rate, no influence is noticeable since all curves reach their maximum value between 36.20% and 45.25% compression. The specimen had a mean thickness of 15.5 µm. The mechanical behaviors of the components used for the simulations are shown in red.
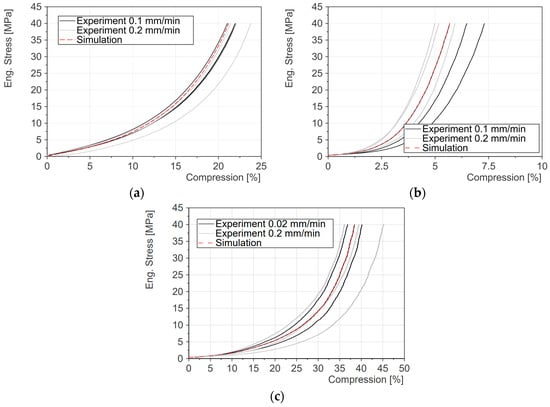
Figure 8.
Results of the compression tests for the out-of-plane characterization of the components: (a) Anode. (b) Cathode. (c) Separator.
3.3. Verification of Data-Driven Material Model
The RVE is compared with a single element for verification and to evaluate the increase in efficiency. The single element has the same dimensions as the RVE. Compression in the thickness direction is used as the load case. This increases in both cases to a compression value of 20%. The compression of the individual component elements of the detailed RVE is compared with the predicted values from the ANN. Since the deformation of the cell in the thickness direction primarily influences the separators as well as the active materials, the focus is on these components, while the current collectors are not used for verification. The results are shown in Figure 9a. The blue curves represent the z-strain of the separator elements. These reach a value of −0.6 at a compression of 20%. The deformation of the active materials is shown in black for the anode and in green for the cathode. It is noticeable that with a minimal value of −0.3, the anode is deformed more than the cathode with a z-strain of −0.11. The predicted values of the ANN are shown in red. It can be seen that there are only slight deviations between the detailed RVE and ANN single element.
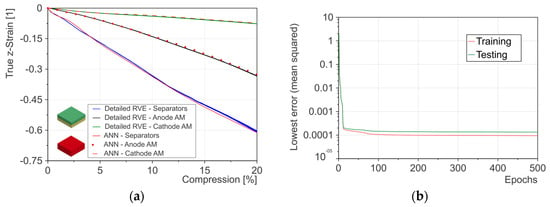
Figure 9.
(a) Comparison of component behavior detailed RVE vs. ANN single element. (b) Results of neural network training.
For the data-driven material model, a neural network configuration of two hidden layers and 20 neurons per layer is used. The result of the training and testing (for the normal stresses) is shown in Figure 9b. The red curve shows the results for the training data, while the green curve stands for the testing data. It is shown that both curves are close to each other and reach convergence with a mean squared error of less than 1 × 10−4 for training data and 1.3 × 10−4 for testing data after 500 epochs.
Since both simulations were carried out using explicit time integration, a comparison in terms of computing efficiency is possible. The initial time step of the detailed RVE is 1.65 × 10−6 ms, while that of the single element is 5.84 × 10−5 ms. Accordingly, there is a factor of 35.4 between the two scales. This can also be seen from the comparison of the calculation time. Due to the smaller time step and higher number of elements, the detailed model requires around 420 times the computing time, although the computing is distributed on 60 CPUs while the state of the single element is calculated on 1 CPU. It should be noted that the simulations of the training phase are not carried out with explicit time integration but with implicit time integration and this is much more efficient. The duration of a training simulation (detailed RVE) is in the order of magnitude of the ANN single element.
3.4. Validation Through Cell Tests
The results of the two cell tests are shown in Figure 10. The force–displacement curve of the experiment is compared with that of the simulation. There are two different configurations for the three-point-bending test in Figure 10a. First, the steel sheet was tested alone (blue curves). This was used to validate the material model and the contact situation between the cylinder and the steel plate. The corresponding simulation curve is shown in gray. The black curves represent the results of the tests in which both the steel sheet and the cell were tested. The test configurations were performed three times to check repeatability. It is noticeable that there is a prominent point at around 3 mm. Up to this point, the resulting force increases almost linearly to a value of around 0.85 kN. This part of the curve was used to calibrate the shear behavior (interlaminar behavior). Afterwards, the curve flattens out and oscillations occur. The measured cell voltage is shown as black dotted lines. No internal short circuit was detected during the tests. This cell test was simulated over the range of 10 mm displacement. The force–displacement curve from the simulation is shown in red. For the data-driven material model, again, a neural network with two hidden layers and 20 neurons per layer was used. Just like the simulation curve of the pure steel sheet, the red curve is also slightly above the level of the experiment.
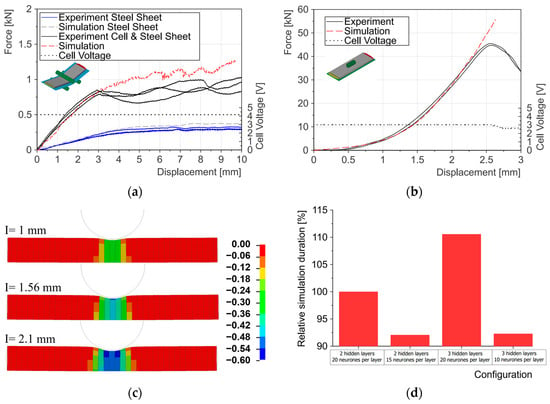
Figure 10.
Comparison of experimental and simulative force–displacement curves for (a) three-point-bending test, (b) indentation test with cylindrical impactor, and (c) predicted separator true strain for different intrusions as well as (d) comparison of relative simulation duration for different network architectures.
The results of the indentation test with the cylindrical impactor are shown in Figure 10b. The force over intrusion is used here. Also, this configuration was repeated to check the quality of the experiment. Both experimental curves are very close to each other. The curves reach their maximum of around 46 kN at an indentation of 2.55 mm. At this point, there is also a drop in the cell voltage, which indicates an internal short circuit. For the simulation, the same cell model is used as for the three-point-bending test. The force–displacement curve resulting from the simulation is shown in red.
In addition, Figure 10c shows the thinning of the separators in the form of the true strain in the thickness direction at three different intrusions, I. This shows that the ANN also predicts reasonable values in the cell simulation.
3.5. Influence of Network Size
A parameter study is carried out to analyze the influence of the size of the neural network. The results are shown in Figure 10d. This illustrates the relative simulation time of the indentation test with four different network configurations. The first configuration is used as the reference value. The number of hidden layers of the ANN is changed for the normal stresses. The first configuration consists of two hidden layers with 20 neurons each. Since this is the reference, the resulting relative simulation duration is 100%. In the second configuration, the number of neurons per hidden layer is reduced to 15. So, a relative simulation duration of 92% is reached. In the third configuration, a hidden layer was added and all of them had 20 neurons. This leads to an increase in the relative simulation duration to 110.6%. A fourth configuration is carried out with three hidden layers but 10 neurons per layer so the total number of neurons is equal to the second configuration. This configuration has a relative simulation duration of 92.3%.
4. Discussion
The results of the in-plane characterization, which are shown in Figure 7, agree with the assumptions made for the modeling. Only the assumption of an isotropic in-plane behavior for the pouch envelope is questionable, as these layers are obviously directionally dependent. However, the influence is estimated to be too small, which means that the material model does not need to be adapted.
Nevertheless, it should be emphasized that assumptions regarding isotropy, the choice of material models, and their parametrization have a fundamental influence on the accuracy of the cell model at the macro-scale. This essentially affects three aspects. Firstly, the RVE simulations based on component data are the data basis for the data-driven model for the macroscopic level. Secondly, the assumptions about component failure are also crucial for the cell behavior. Thirdly, the material model of the pouch envelope is a direct component of the cell model. An improvement in the representation of the component behavior therefore has a direct influence on the quality of the macroscopic cell model.
A new method was used to characterize the components in the thickness direction (out-of-plane). Here, individual layers were tested instead of stacks of the same components. The results, which are shown in Figure 8, indicate good reproducibility, especially for the anode and separator. Only the cathode showed an increased scattering of results. None of the components showed a significant influence of the loading speed.
The verification was carried out by comparing the detailed RVE with a single element that had the data-driven material model assigned. The results, which are shown in Figure 9a, show that the component compression was predicted with sufficient accuracy. A neural network with an architecture of two hidden layers, each with 20 neurons, was used for the data-driven material model. The results of the training are shown in Figure 9b. A distinction is made between training data (red) and testing data (green). The neural network has a mean squared error of less than 1 × 10−4 for training data and 1.3 × 10−4 for testing data after 500 epochs, which is why the model performance can be classified as sufficiently good. Since both curves have the same shape and are ending in the same range, it can be assumed that no overfitting occurs. The same data-driven model is also used for the cell model.
Since both the detailed RVE and the single element are computed with explicit time integration, the efficiency increase can be evaluated. The initial time step of the single element is 35.4 times higher than that of the detailed RVE. The computing time of the RVE is 420 times higher than that of the single element, although the computing effort is distributed over 60 CPUs and is not calculated on a single CPU like the single element.
This demonstrates that the data-driven modeling approach has advantages over state-of-the-art modeling approaches. The great advantage over conventional macroscopic approaches is that the component behavior can also be predicted with sufficient accuracy. Although detailed modeling approaches also provide this information, they are much more computationally intensive, which is not only due to the smaller critical time step, but also to the higher number of the elements to be calculated.
The validation of the data-driven material model derived from the RVE behavior was carried out by comparing the experimental and simulative force–displacement curves of two cell tests. The comparison for the three-point-bending test is shown in Figure 10a. As can be seen, there is only a slightly higher force level in the simulation than in the experiments. Therefore, the validation against the three-point-bending test can be considered as successful.
The simulation results for the indentation test with the cylindrical impactor match the experimental results very well over large areas until the failure point, as shown in Figure 10b. Only at the beginning of the intrusion is a higher force level predicted by the simulation, as well as shortly before the occurrence of the internal short circuit. After this point, the mechanical behavior is of less interest; rather, the electrical and thermal behavior is of interest, which is not the scope of this work. As already discussed, the data-driven model has the additional advantage that it can output information about the components. This is illustrated using the example of the separator deformation in Figure 10c. Here, the true strain in the thickness direction is output as a status variable, demonstrating that this is not only the case for the single element but also in the full cell simulation.
Finally, Figure 10d shows the influence of the architecture of the neural network. The relative simulation duration is compared for four different neural network architectures. However, it can be seen from the results that the network architecture has an influence on the computational time. Since configuration two and four have the same total number of neurons and similar values for the relative simulation duration, it can be assumed that the decisive factor is not the number of hidden layers, but the total number of neurons or the associated computing operations.
5. Conclusions
In this study, a data-driven multi-scale approach is presented for a lithium-ion pouch cell to simulate the mechanical behavior under abusive conditions in a time-efficient but detailed way. First, a representative volume element with in-plane dimensions of 1 × 1 mm is modeled in detail. This consists of four layers (anode—separator—cathode—separator). Material characterizations of the individual components are carried out for the parametrization of the RVE. The results of the tensile tests show that the assumptions according to isotropic behavior were reasonable. Only the pouch cover showed a more pronounced anisotropic behavior than expected. Nevertheless, the deviations were considered too small to require adjustment. The behavior under transversal pressure was also in line with the expectations and assumptions made. The macroscopic behavior of the modeled RVE is determined by applying the first-order homogenization theory. This was carried out in a spherical strain range for over 600 different directions to generate data for the normal behavior. Since a decoupled behavior for shear is assumed, only six runs were therefore necessary. The resulting data were used to train a neural network, which was available as a material model after implementation in the commercial solver. Although simplifications, such as the neglect of alternating loading and unloading phases and the direction-dependent plasticity, were made, the macroscopic behavior of the cell could be reproduced. A comparison was made with experiments at the cell level. The macroscopic consideration of component failure made it possible to reproduce the characteristic behavior under bending loads. In addition, the neural network makes it possible to predict the component-specific compressions. Although these are not considered further in this work, they represent the starting point for future developments. For example, it is conceivable to develop a short-circuit criterion using the separator compression in combination with the in-plane strain state. The application of the presented approach to other cell formats and chemistries would also be a desirable goal in order to check the generality and transferability.
The modeling approach presented here is of course subject to certain limitations. This study focuses on load cases in the thickness direction, i.e., perpendicular to the electrode surface. This constraint allows for the omission of detailed interlaminar contact representations, which, while simplifying the model, restricts its applicability to other load configurations. Notably, in-plane loading scenarios, which may induce component buckling and interlayer gap formation, fall outside the scope of this model.
In the interest of computational efficiency, path-dependent plasticity remained unconsidered. The model is limited to monotonically increasing loads and does not account for complex mixed load and unload scenarios.
In addition, no consideration is made of the strain rate effects of the components or the complex behavior of the electrolyte under dynamic loads.
These omissions represent areas for potential future refinement of the model, as the inclusion of such factors could enhance its predictive capabilities, particularly in dynamic loading environments.
The inclusion of these refinements may adversely influence the efficiency and the amount of training data needed. One promising approach to overcome these challenges is physics-informed neural networks (PINNs), which integrate known physical laws and constraints (thermodynamic consistency) directly into the neural network architecture. Physics-informed approaches have been successfully applied to nonlinear, path-dependent material behavior, including plasticity, interface cracking, and intergranular fracturing [54]. PINN can further improve the extrapolation capability and reduce the amount of training data [55].
However, it should be noted that this could result in an increase or general change in the network architecture, which has a negative effect on the computing time. This was already demonstrated by a parameter study in this paper.
Author Contributions
Conceptualization, A.S., C.E. and F.F.; Data curation, A.S.; Formal analysis, A.S.; Funding acquisition, C.E.; Investigation, A.S.; Methodology, A.S., C.E. and F.F.; Project administration, C.E. and F.F.; Software, A.S.; Supervision, C.E. and F.F.; Validation, A.S.; Visualization, A.S.; Writing—original draft, A.S.; Writing—review and editing, A.S., C.E., E.E. and F.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work originates from the research project SafeLIB. The COMET Project SafeLIB is funded within the framework of COMET—Competence Centers for Excellent Technologies (Grant agreement No. 882506) by BMK, BMDW, the Province of Upper Austria, the province of Styria, and SFG. The COMET Program is managed by FFG. The authors thank the consortium members of the SafeLIB project for supporting this work.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Acknowledgments
The authors would like to thank Zwick GmbH & Co. KG in Ulm, Germany, for providing the novel compression tests of the battery components. Additionally, they would like to thank the ZID of the Graz University of Technology for providing HPC resources. Open Access Funding by the Graz University of Technology.
Conflicts of Interest
Author Eduard Ewert was employed by the company Porsche Aktiengesellschaft. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Fleischmann, J.; Hanicke, M.; Horetsky, E.; Ibrahim, D.; Jautelat, S.; Linder, M.; Schaufuss, P.; Torscht, L.; Van de Rijt, A. Battery 2030: Resilient, Sustainable and Circular: Battery Demand Is Growing—and so Is the Need for Better Solutions Along the Value Chain; McKinsey & Company: New York, NY, USA, 2023. [Google Scholar]
- Chombo, P.V.; Laoonual, Y.; Wongwises, S. Lessons from the Electric Vehicle Crashworthiness Leading to Battery Fire. Energies 2021, 14, 4802. [Google Scholar] [CrossRef]
- Li, G.; Fu, X.; Yang, Y. Anti-vibration safety performance research of battery pack based on finite element method in electric vehicle. In Proceeding of the 36th Chinese Control Conference (CCC), Dalian, Chian, 26–28 July 2017; pp. 10281–10285. [Google Scholar] [CrossRef]
- Fasching, M.; Grollitsch, S.; Höschele, P.; Schmid, A.; Ellersdorfer, C. Investigating the mechanical in-plane characteristics of lithium-ion pouch cells under crush loads. J. Energy Storage 2024, 89, 111581. [Google Scholar] [CrossRef]
- Sahraei, E.; Campbell, J.; Wierzbicki, T. Modeling and short circuit detection of 18650 Li-ion cells under mechanical abuse conditions. J. Power Sources 2012, 220, 360–372. [Google Scholar] [CrossRef]
- Sievers, M.; Sievers, U.; Mao, S.S. Thermal modelling of new Li-ion cell design modifications. Forsch. Ingenieurwes 2010, 74, 215–231. [Google Scholar] [CrossRef][Green Version]
- Ramadesigan, V.; Northrop, P.W.C.; De, S.; Santhanagopalan, S.; Braatz, R.D.; Subramanian, V.R. Modeling and Simulation of Lithium-Ion Batteries from a Systems Engineering Perspective. J. Electrochem. Soc. 2012, 159, R31–R45. [Google Scholar] [CrossRef]
- Lin, N.; Röder, F.; Krewer, U. Multiphysics Modeling for Detailed Analysis of Multi-Layer Lithium-Ion Pouch Cells. Energies 2018, 11, 2998. [Google Scholar] [CrossRef]
- Allu, S.; Kalnaus, S.; Simunovic, S.; Nanda, J.; Turner, J.A.; Pannala, S. A three-dimensional meso-macroscopic model for Li-Ion intercalation batteries. J. Power Sources 2016, 325, 42–50. [Google Scholar] [CrossRef]
- Zhu, J.; Wierzbicki, T.; Li, W. A review of safety-focused mechanical modeling of commercial lithium-ion batteries. J. Power Sources 2018, 378, 153–168. [Google Scholar] [CrossRef]
- Zhu, L.; Xia, Y.; Liu, Y.; Ge, Y.; Wang, L.; Zhang, L. Extending a Homogenized Model for Characterizing Multidirectional Jellyroll Failure in Prismatic Lithium-Ion Batteries. Energies 2021, 14, 3444. [Google Scholar] [CrossRef]
- Xu, J.; Liu, B.; Wang, X.; Hu, D. Computational model of 18650 lithium-ion battery with coupled strain rate and SOC dependencies. Appl. Energy 2016, 172, 180–189. [Google Scholar] [CrossRef]
- Schmid, A.; Pasquale, A.; Ellersdorfer, C.; Raffler, M.; Champaney, V.; Ziane, M.; Chinesta, F.; Feist, F. Mechanical Characterization of Li-Ion Cells and the Calibration of Numerical Models Using Proper Generalized Decomposition. In Proceeding of the ASME International Mechanical Engineering Congress and Exposition, New Orleans, LA, USA, 29 October–2 November 2023; Volume 7. [Google Scholar] [CrossRef]
- Schmid, A.; Pasquale, A.; Ellersdorfer, C.; Champaney, V.; Raffler, M.; Guévelou, S.; Kizio, S.; Ziane, M.; Feist, F.; Chinesta, F. PGD based meta modelling of a lithium-ion battery for real time prediction. Front. Mater. 2023, 10, 1245347. [Google Scholar] [CrossRef]
- Raffler, M.; Sevarin, A.; Ellersdorfer, C.; Heindl, S.F.; Breitfuss, C.; Sinz, W. Finite element model approach of a cylindrical lithium ion battery cell with a focus on minimization of the computational effort and short circuit prediction. J. Power Sources 2017, 360, 605–617. [Google Scholar] [CrossRef]
- Qin, D.; Wang, P.; Wang, T.; Chen, J. Modeling and Dynamic Impact Analysis of Prismatic Lithium-Ion Battery. Sustainability 2023, 15, 8414. [Google Scholar] [CrossRef]
- Kisters, T.; Gilaki, M.; Nau, S.; Sahraei, E. Modeling of Dynamic Mechanical Response of Li-Ion cells with Homogenized Electrolyte-Solid Interactions. J. Energy Storage 2022, 49, 104069. [Google Scholar] [CrossRef]
- Beaumont, R.; Masters, I.; Das, A.; Lucas, S.; Thanikachalam, A.; Williams, D. Methodology for Developing a Macro Finite Element Model of Lithium-Ion Pouch Cells for Predicting Mechanical Behaviour under Multiple Loading Conditions. Energies 2021, 14, 1921. [Google Scholar] [CrossRef]
- Zhu, J. Standardizing mechanical tests on li-ion batteries to develop a useful cell-level model under extreme mechanical loads. J. Energy Storage 2023, 65, 107320. [Google Scholar] [CrossRef]
- Sinz, W.; Feist, F.; Gstrein, G.; Gugler, J.; Tomasch, E.; Breitfuss, C.; Luttenberger, P.; Steffan, H.; Gollob, P.; Hennige, V. Concepts for Mechanical Abuse Testing of High-Voltage Batteries; SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2012. [Google Scholar]
- Ellersdorfer, C.; Höschele, P.; Heider, E.; Kovachev, G.; Gstrein, G. Safety Assessment of High Dynamic Pre-Loaded Lithium Ion Pouch Cells. Batteries 2023, 9, 71. [Google Scholar] [CrossRef]
- Goodman, J.K.S.; Miller, J.T.; Kreuzer, S.; Forman, J.; Wi, S.; Choi, J.-M.; Oh, B.; White, K. Lithium-ion cell response to mechanical abuse: Three-point bend. J. Energy Storage 2020, 28, 101244. [Google Scholar] [CrossRef]
- Raffler, M.; Sinz, W.; Erker, S.; Brunnsteiner, B.; Ellersdorfer, C. Influence of loading rate and out of plane direction dependence on deformation and electro-mechanical failure behavior of a lithium-ion pouch cell. J. Energy Storage 2022, 56, 105906. [Google Scholar] [CrossRef]
- Kisters, T.; Sahraei, E.; Wierzbicki, T. Dynamic impact tests on lithium-ion cells. Int. J. Impact Eng. 2017, 108, 205–216. [Google Scholar] [CrossRef]
- Breitfuss, C.; Sinz, W.; Feist, F.; Gstrein, G.; Lichtenegger, B.; Knauder, C.; Ellersdorfer, C.; Moser, J.; Steffan, H.; Stadler, M.; et al. A ‘Microscopic’ Structural Mechanics FE Model of a Lithium-Ion Pouch Cell for Quasi-Static Load Cases. SAE Int. J. Passeng. Cars-Mech. Syst. 2013, 6, 1044–1054. [Google Scholar] [CrossRef]
- Schaufelberger, B.; Altes, A.; Matura, P. Modeling the Mechanical Behaviour of a Li-Ion Pouch Cell under Three-Point Bending. In Proceeding of the 13th European LS-DYNA Conference, Ulm, Germany, 5–7 October 2021. [Google Scholar]
- Schmid, A.; Ellersdorfer, C.; Raffler, M.; Karajan, N.; Feist, F. An efficient detailed layer model for prediction of separator damage in a Li-Ion pouch cell exposed to transverse compression. J. Power Sources 2023, 581, 233510. [Google Scholar] [CrossRef]
- Wang, L.; Yin, S.; Xu, J. A detailed computational model for cylindrical lithium-ion batteries under mechanical loading: From cell deformation to short-circuit onset. J. Power Sources 2019, 413, 284–292. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, J.; Cao, L.; Wu, Z.; Santhanagopalan, S. Constitutive behavior and progressive mechanical failure of electrodes in lithium-ion batteries. J. Power Sources 2017, 357, 126–137. [Google Scholar] [CrossRef]
- Schmid, A.; Pasquale, A.; Ellersdorfer, C.; Ziane, M.; Raffler, M.; Champaney, V.; Feist, F.; Chinesta, F. Application of PGD separation of space to create a reduced-order model of a lithium-ion cell structure. Front. Mater. 2023, 10, 1212400. [Google Scholar] [CrossRef]
- Cannarella, J.; Liu, X.; Leng, C.Z.; Sinko, P.D.; Gor, G.Y.; Arnold, C.B. Arnold, Mechanical Properties of a Battery Separator under Compression and Tension. J. Electrochem. Soc. 2014, 161, F3117–F3122. [Google Scholar] [CrossRef]
- Wang, L.; Yin, S.; Zhang, C.; Huan, Y.; Xu, J. Mechanical characterization and modeling for anodes and cathodes in lithium-ion batteries. J. Power Sources 2018, 392, 265–273. [Google Scholar] [CrossRef]
- Li, Z.; Chen, J.; Lan, F.; Li, Y. Constitutive Behavior and Mechanical Failure of Internal Configuration in Prismatic Lithium-Ion Batteries under Mechanical Loading. Energies 2021, 14, 1219. [Google Scholar] [CrossRef]
- Sahraei, E.; Bosco, E.; Dixon, B.; Lai, B. Microscale failure mechanisms leading to internal short circuit in Li-ion batteries under complex loading scenarios. J. Power Sources 2016, 319, 56–65. [Google Scholar] [CrossRef]
- Ali, M.Y.; Lai, W.-J.; Pan, J. Computational models for simulations of lithium-ion battery cells under constrained compression tests. J. Power Sources 2013, 242, 325–340. [Google Scholar] [CrossRef]
- Ali, M.Y.; Lai, W.-J.; Pan, J. Computational models for simulation of a lithium-ion battery module specimen under punch indentation. J. Power Sources 2015, 273, 448–459. [Google Scholar] [CrossRef]
- Budiman, B.A.; Rahardian, S.; Saputro, A.; Hidayat, A.; Nurprasetio, I.P.; Sambegoro, P. Structural integrity of lithium-ion pouch battery subjected to three-point bending. Eng. Fail. Anal. 2022, 138, 106307. [Google Scholar] [CrossRef]
- Kermani, G.; Keshavarzi, M.M.; Sahraei, E. Deformation of lithium-ion batteries under axial loading: Analytical model and Representative Volume Element. Energy Rep. 2021, 7, 2849–2861. [Google Scholar] [CrossRef]
- Geers, M.G.D.; Kouznetsova, V.G.; Brekelmans, W.A.M. Multi-scale computational homogenization: Trends and challenges. J. Comput. Appl. Math. 2010, 234, 2175–2182. [Google Scholar] [CrossRef]
- Vernerey, F.; Liu, W.K.; Moran, B. Multi-scale micromorphic theory for hierarchical materials. J. Mech. Phys. Solids 2007, 55, 2603–2651. [Google Scholar] [CrossRef]
- Schmitz, A.; Horst, P. A finite element unit-cell method for homogenised mechanical properties of heterogeneous plates. Compos. Part. A: Appl. Sci. Manuf. 2014, 61, 23–32. [Google Scholar] [CrossRef]
- Tikarrouchine, E.; Chatzigeorgiou, G.; Praud, F.; Piotrowski, B.; Chemisky, Y.; Meraghni, F. Three-dimensional FE2 method for the simulation of non-linear, rate-dependent response of composite structures. Compos. Struct. 2018, 193, 165–179. [Google Scholar] [CrossRef]
- Hashash, Y.M.A.; Jung, S.; Ghaboussi, J. Numerical implementation of a neural network based material model in finite element analysis. Int. J. Numer. Meth. Engng. 2004, 59, 989–1005. [Google Scholar] [CrossRef]
- Gorji, M.B.; Mozaffar, M.; Heidenreich, J.N.; Cao, J.; Mohr, D. On the potential of recurrent neural networks for modeling path dependent plasticity. J. Mech. Phys. Solids 2020, 143, 103972. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Gorji, M.B.; Zhu, J.; Mohr, D. Recurrent neural network modeling of the large deformation of lithium-ion battery cells. Int. J. Plast. 2021, 146, 103072. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, C.T.; Ren, B.; Liu, K.W.; Grimes, R. Multiscale Simulations of Material with Heterogeneous Structures Based on Representative Volume Element Techniques. In Proceeding of the 15th International LS-DYNA Users Conference, Detroit, MI, USA, 10 June 2018. [Google Scholar]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Livermore Software Technology (LST). LS-DYNA® Keyword User’s Manual Volume I R13; Livermore Software Technology Corporation: Livermore, CA, USA, 2021; pp. 3518–3527. [Google Scholar]
- MacKay, D.J. Bayesian Interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- The MathWorks, Inc. Documentation: Bayesian Regularization Backpropagation. Available online: https://www.mathworks.com/help/deeplearning/ref/trainbr.html (accessed on 23 September 2024).
- Joseph, V.R. Optimal ratio for data splitting. Stat. Anal. 2022, 15, 531–538. [Google Scholar] [CrossRef]
- Erhart, T. User Defined Materials in LS-DYNA; Dynamore GmbH: Stuttgart, Germany, 2015. [Google Scholar]
- Qu, Y.; Xing, B.; Wang, C.; Xia, Y. Simplified layered model of pouch cell for varied load cases: An indentation and three-point bending study. J. Energy Storage 2023, 59, 106476. [Google Scholar] [CrossRef]
- Rezaei, S.; Moeineddin, A.; Harandi, A. Learning solution of nonlinear constitutive material models using physics-informed neural networks: COMM-PINN. arXiv 2023, arXiv:2304.06044. [Google Scholar]
- Kalina, K.A.; Linden, L.; Brummund, J.; Kästner, M. FE ANN: An efficient data-driven multiscale approach based on physics-constrained neural networks and automated data mining. Comput. Mech. 2023, 71, 827–851. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).