Quantifying Lithium-Ion Battery Rate Capacity, Electrode Structuring, and Transport Phenomena Using E-I Measurements
Abstract
1. Introduction
2. Theory and Analysis Approach
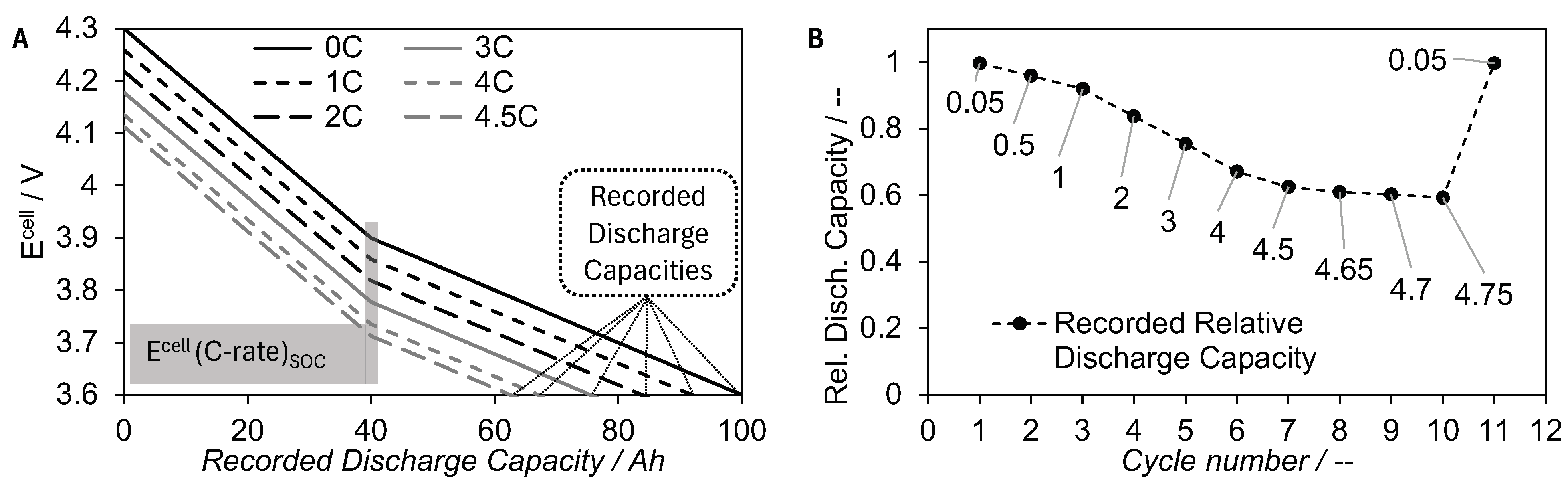
2.1. Rate Capacity Retention
2.2. Framework for Mass Transfer Coefficient Determination
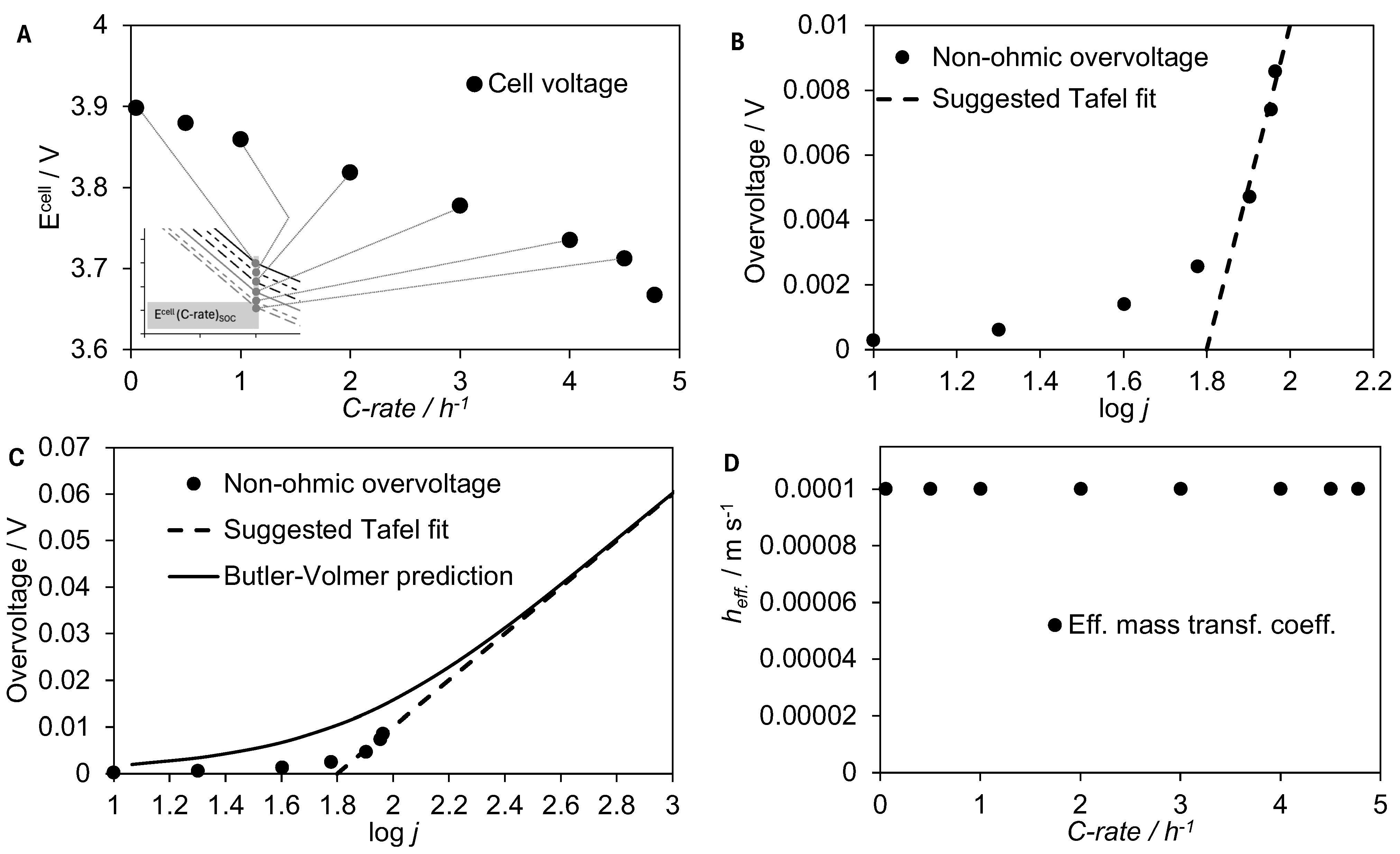
2.3. Distinguishing Non-Ohmic Overpotential Contributions
3. Experimental Section
3.1. Cathode Composition
3.2. Production Process
3.3. Characterisation
4. Results and Discussion
4.1. SEM
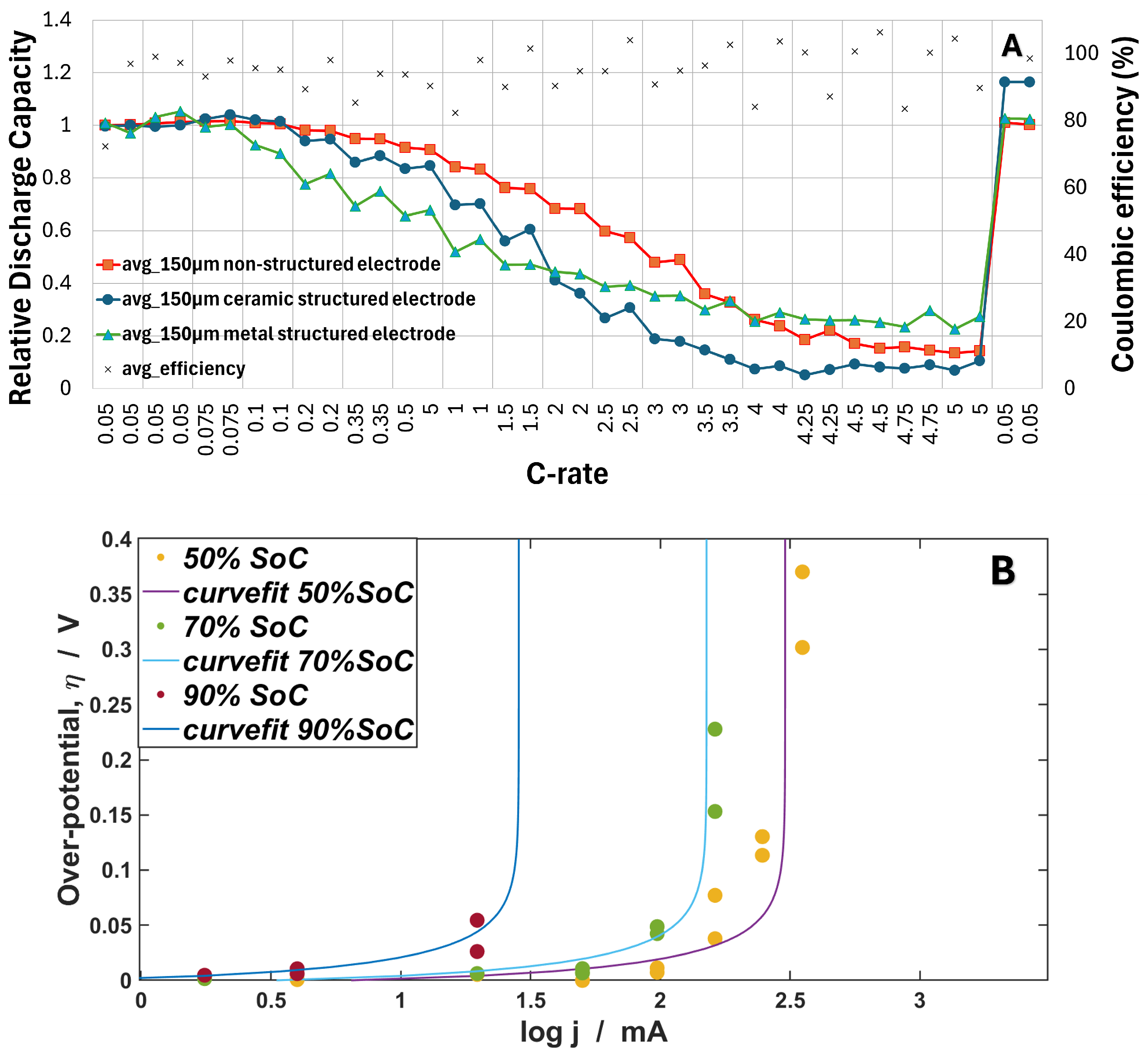
4.2. Rate Capacity Retention Analysis
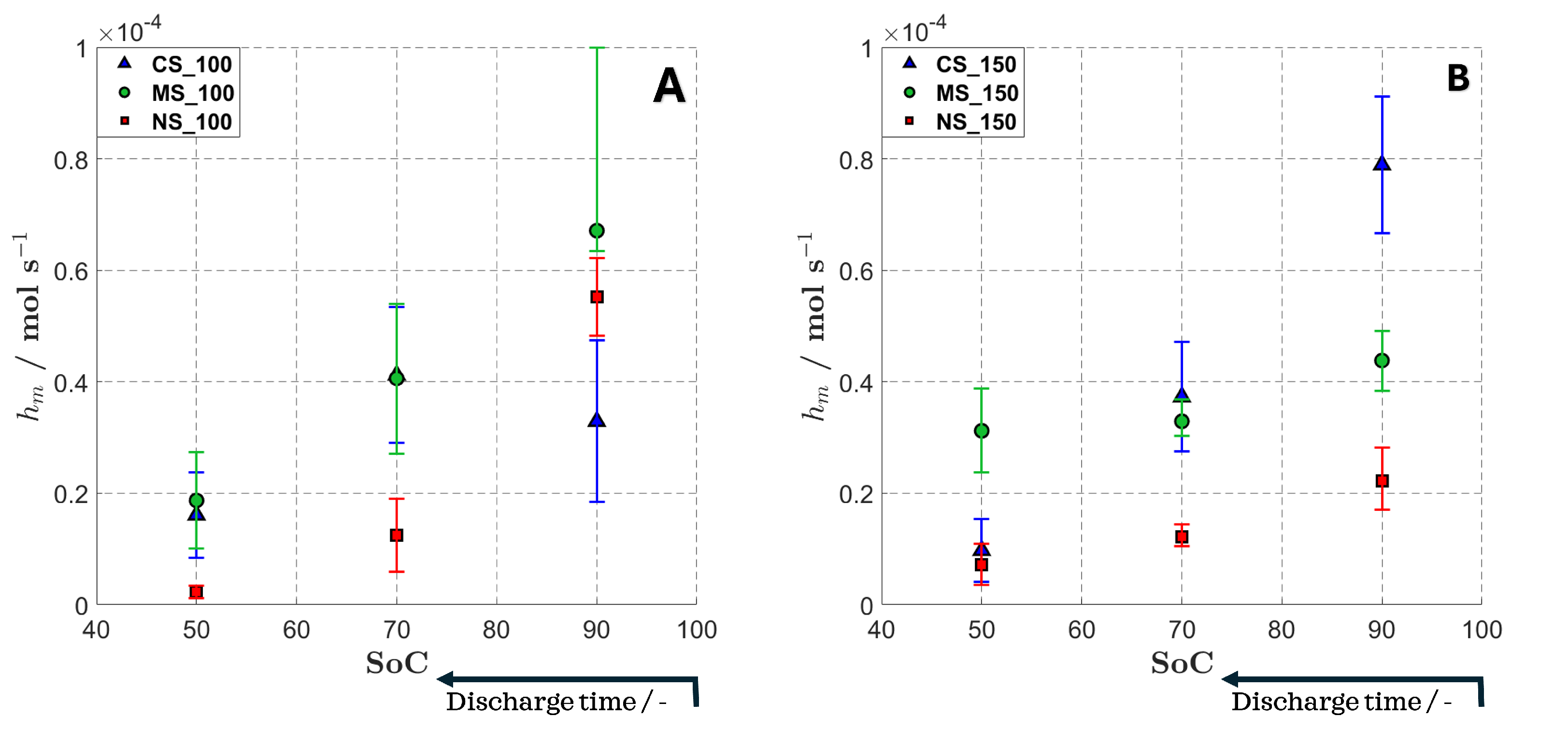
4.3. Effective Mass Transfer Coefficient Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Burheim, O. Engineering Energy Storage, 1st ed.; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Orangi, S.; Manjong, N.; Clos, D.P.; Usai, L.; Burheim, O.S.; Strømman, A.H. Historical and prospective lithium-ion battery cost trajectories from a bottom-up production modeling perspective. J. Energy Storage 2024, 76, 109800. [Google Scholar] [CrossRef]
- Orangi, S.; Manjong, N.B.; Clos, D.P.; Burheim, O.S.; Strømman, A.H. A Bottom-Up Framework to Investigate Environmental and Techno-Economic Aspects of Lithium-Ion Batteries: A Case Study of Conventional vs. Pre-Lithiated Lithium-Ion Battery Cells. J. Clean. Prod. 2024, 478, 143934. [Google Scholar] [CrossRef]
- Spitthoff, L.; Shearing, P.R.; Burheim, O.S. Temperature, Ageing and Thermal Management of Lithium-Ion Batteries. Energies 2021, 14, 1248. [Google Scholar] [CrossRef]
- Singh, M.; Kaiser, J.; Hahn, H. Thick Electrodes for High Energy Lithium Ion Batteries. J. Electrochem. Soc. 2015, 162, A1196. [Google Scholar] [CrossRef]
- Xie, W.; Zhang, Z.; Gao, X. Understanding the limitations of thick electrodes on the rate capability of high-energy density lithium-ion batteries. Electrochim. Acta 2024, 493, 144396. [Google Scholar] [CrossRef]
- Zhu, P.; Slater, P.R.; Kendrick, E. Insights into architecture, design and manufacture of electrodes for lithium-ion batteries. Mater. Des. 2022, 223, 111208. [Google Scholar] [CrossRef]
- Ye, G.; Tong, W.; Liu, X.; Song, X.; Zhou, J.; Zhou, X. An analytical method for the optimization of pore network in lithium-ion battery electrodes. Chem. Eng. Res. Des. 2019, 149, 226–234. [Google Scholar] [CrossRef]
- Li, J.; Liang, X.; Panat, R.; Park, J. Enhanced battery performance through three-dimensional structured electrodes: Experimental and modeling study. J. Electrochem. Soc. 2018, 165, A3566. [Google Scholar] [CrossRef]
- Gao, T.; Lu, W. Physical model and machine learning enabled electrolyte channel design for fast charging. J. Electrochem. Soc. 2020, 167, 110519. [Google Scholar] [CrossRef]
- Kraft, L.; Habedank, J.B.; Frank, A.; Rheinfeld, A.; Jossen, A. Modeling and simulation of pore morphology modifications using laser-structured graphite anodes in lithium-ion batteries. J. Electrochem. Soc. 2020, 167, 013506. [Google Scholar] [CrossRef]
- Chen, K.H.; Namkoong, M.J.; Goel, V.; Yang, C.; Kazemiabnavi, S.; Mortuza, S.; Kazyak, E.; Mazumder, J.; Thornton, K.; Sakamoto, J.; et al. Efficient fast-charging of lithium-ion batteries enabled by laser-patterned three-dimensional graphite anode architectures. J. Power Sources 2020, 471, 228475. [Google Scholar] [CrossRef]
- Goel, V.; Chen, K.H.; Dasgupta, N.P.; Thornton, K. Optimization of laser-patterned electrode architectures for fast charging of Li-ion batteries using simulations parameterized by machine learning. Energy Storage Mater. 2023, 57, 44–58. [Google Scholar] [CrossRef]
- Sui, C.; Li, Y.Y.; Li, X.; Higueros, G.; Wang, K.; Xie, W.; Hsu, P.C. Bio-Inspired Computational Design of Vascularized Electrodes for High-Performance Fast-Charging Batteries Optimized by Deep Learning. Adv. Energy Mater. 2022, 12, 2103044. [Google Scholar] [CrossRef]
- Miyamoto, K.; Broderick, S.; Rajan, K. Three-dimensional microbattery design via an automatic geometry generator and machine-learning-based performance simulator. Cell Rep. Phys. Sci. 2021, 2, 100504. [Google Scholar] [CrossRef]
- Wang, J.; Sun, Q.; Gao, X.; Wang, C.; Li, W.; Holness, F.B.; Zheng, M.; Li, R.; Price, A.D.; Sun, X.; et al. Toward high areal energy and power density electrode for Li-ion batteries via optimized 3D printing approach. ACS Appl. Mater. Interfaces 2018, 10, 39794–39801. [Google Scholar] [CrossRef]
- Hu, J.; Jiang, Y.; Cui, S.; Duan, Y.; Liu, T.; Guo, H.; Lin, L.; Lin, Y.; Zheng, J.; Amine, K.; et al. 3D-printed cathodes of LiMn1-xFexPO4 nanocrystals achieve both ultrahigh rate and high capacity for advanced lithium-ion battery. Adv. Energy Mater. 2016, 6, 1600856. [Google Scholar] [CrossRef]
- Plateau, T.P.; Pham, H.; Zhu, Y.; Leu, M.; Park, J. Enabling Ultrathick Electrodes via a Microcasting Process for High Energy and Power Density Lithium-Ion Batteries. Adv. Energy Mater. 2022, 12, 2201353. [Google Scholar] [CrossRef]
- Jang, D.; Suh, S.; Yoon, H.; Kim, J.; Kim, H.; Baek, J.; Kim, H.J. Enhancing rate capability of graphite anodes for lithium-ion batteries by pore-structuring. Appl. Surf. Sci. Adv. 2021, 6, 100168. [Google Scholar] [CrossRef]
- Tran, M.X.; Smyrek, P.; Park, J.; Pfleging, W.; Lee, J.K. Ultrafast-Laser Micro-Structuring of LiNi0.8Mn0.1Co0.1O2 Cathode for High-Rate Capability of Three-Dimensional Li-ion Batteries. Nanomaterials 2022, 12, 3897. [Google Scholar] [CrossRef]
- Lu, L.L.; Lu, Y.Y.; Xiao, Z.J.; Zhang, T.W.; Zhou, F.; Ma, T.; Ni, Y.; Yao, H.B.; Yu, S.H.; Cui, Y. Wood-inspired high-performance ultrathick bulk battery electrodes. Adv. Mater. 2018, 30, 1706745. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, Y.; Li, Y.; Kuang, Y.; Song, J.; Luo, W.; Wang, Y.; Yao, Y.; Pastel, G.; Xie, J.; et al. Highly conductive, lightweight, low-tortuosity carbon frameworks as ultrathick 3D current collectors. Adv. Energy Mater. 2017, 7, 1700595. [Google Scholar] [CrossRef]
- Keilhofer, J.; Schaffranka, L.W.F.; Wuttke, A.; Günter, F.J.; Hille, L.; Dorau, F.A.; Daub, R. Mechanical Structuring of Lithium-Ion Battery Electrodes Using an Embossing Roller. Energy Technol. 2023, 11, 2200869. [Google Scholar] [CrossRef]
- Bryntesen, S.N.; Finne, P.H.; Svensson, A.M.; Shearing, P.R.; Tolstik, N.; Sorokina, I.T.; Vinje, J.; Lamb, J.J.; Burheim, O.S. Structured aqueous processed lignin-based NMC cathodes for energy-dense LIBs with improved rate capability. J. Mater. Chem. A 2023, 11, 6483–6502. [Google Scholar] [CrossRef]
- Bryntesen, S.N.; Tolstorebrov, I.; Svensson, A.M.; Shearing, P.; Lamb, J.J.; Burheim, O.S. Introducing lignin as a binder material for the aqueous production of NMC111 cathodes for Li-ion batteries. Mater. Adv. 2023, 4, 523–541. [Google Scholar] [CrossRef]
- Vogt, M.; Buchholz, C.; Thiede, S.; Herrmann, C. Energy efficiency of Heating, Ventilation and Air Conditioning systems in production environments through model-predictive control schemes: The case of battery production. J. Clean. Prod. 2022, 350, 131354. [Google Scholar] [CrossRef]
- Vogt, M.; Dér, A.; Khalid, U.; Cerdas, F.; Herrmann, C. Model-based planning of technical building services and process chains for battery cell production. J. Clean. Prod. 2022, 370, 133512. [Google Scholar] [CrossRef]
- Park, J.; Hyeon, S.; Jeong, S.; Kim, H.J. Performance enhancement of Li-ion battery by laser structuring of thick electrode with low porosity. J. Ind. Eng. Chem. 2019, 70, 178–185. [Google Scholar] [CrossRef]
- Park, J.; Song, H.; Jang, I.; Lee, J.; Um, J.; Bae, S.g.; Kim, J.; Jeong, S.; Kim, H.J. Three-dimensionalization via control of laser-structuring parameters for high energy and high power lithium-ion battery under various operating conditions. J. Energy Chem. 2022, 64, 93–102. [Google Scholar] [CrossRef]
- Gebrekiros Berhe, M.; Oh, H.G.; Park, S.K.; Mondal, M.; Lee, D. Effect of laser-induced groove morphology on the wettability and performance of Lithium-ion batteries. Mater. Des. 2023, 231, 112020. [Google Scholar] [CrossRef]
- Park, D.; Lee, D. Effect of Fluence and Multi-Pass on Groove Morphology and Process Efficiency of Laser Structuring for 3D Electrodes of Lithium-Ion Batteries. Materials 2021, 14, 1283. [Google Scholar] [CrossRef]
- Jung, T.; Wang, A.A.; Monroe, C.W. Overpotential from Cosolvent Imbalance in Battery Electrolytes: LiPF6 in EMC:EC. ACS Omega 2023, 8, 21133–21144. [Google Scholar] [CrossRef]
- Kane, S.; Ulrich, R.; Harrington, A.; Stadie, N.P.; Ryan, C. Physical and chemical mechanisms that influence the electrical conductivity of lignin-derived biochar. Carbon Trends 2021, 5, 100088. [Google Scholar] [CrossRef]
- Chakar, F.S.; Ragauskas, A.J. Review of current and future softwood kraft lignin process chemistry. Ind. Crops Prod. 2004, 20, 131–141. [Google Scholar] [CrossRef]
- Thakur, V.K.; Thakur, M.K.; Raghavan, P.; Kessler, M.R. Progress in Green Polymer Composites from Lignin for Multifunctional Applications: A Review. ACS Sustain. Chem. Eng. 2014, 2, 1072–1092. [Google Scholar] [CrossRef]
- Kai, D.; Tan, M.J.; Chee, P.L.; Chua, Y.K.; Yap, Y.L.; Loh, X.J. Towards lignin-based functional materials in a sustainable world. Green Chem. 2016, 18, 1175–1200. [Google Scholar] [CrossRef]
- Doherty, W.O.S.; Mousavioun, P.; Fellows, C.M. Value-adding to cellulosic ethanol: Lignin polymers. Ind. Crops Prod. 2011, 33, 259–276. [Google Scholar] [CrossRef]
- Bresser, D.; Buchholz, D.; Moretti, A.; Varzi, A.; Passerini, S. Alternative binders for sustainable electrochemical energy storage—The transition to aqueous electrode processing and bio-derived polymers. Energy Environ. Sci. 2018, 11, 3096–3127. [Google Scholar] [CrossRef]



| Chemical | State | Function | Supplier | Density |
|---|---|---|---|---|
| NMC111 | Powder | Active material | Targray | 2.3 |
| Carbon black | Powder | Conductive additive | Imerys | 1.9 |
| Lignin | Powder | Binder | Sigma Aldrich | 1.3 |
| Distillied water | Liquid | Solvent | - | - |
| Lignin + water | Mixture | - | - | - |
| Configuration | 100 μm | 150 μm | ||||
|---|---|---|---|---|---|---|
| SOC/% | 50 | 70 | 90 | 50 | 70 | 90 |
| / mol | 0.12–0.34 | 0.59–1.90 | 4.82–6.22 | 0.35–1.09 | 1.05–1.44 | 1.71–2.82 |
| / mol | 0.89–2.38 | 2.91–5.34 | 1.84–4.74 | 0.41–1.54 | 2.75–4.71 | 6.68–9.12 |
| / mol | 1.01–2.74 | 2.71–5.41 | 6.30–9.96 | 2.37–3.88 | 3.03–3.68 | 3.84–4.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dunne, R.N.; Solberg, S.B.B.; Amiri, M.N.; Ezeigwe, E.R.; Lamb, J.J.; Burheim, O. Quantifying Lithium-Ion Battery Rate Capacity, Electrode Structuring, and Transport Phenomena Using E-I Measurements. Batteries 2024, 10, 364. https://doi.org/10.3390/batteries10100364
Dunne RN, Solberg SBB, Amiri MN, Ezeigwe ER, Lamb JJ, Burheim O. Quantifying Lithium-Ion Battery Rate Capacity, Electrode Structuring, and Transport Phenomena Using E-I Measurements. Batteries. 2024; 10(10):364. https://doi.org/10.3390/batteries10100364
Chicago/Turabian StyleDunne, Ronan N., Simon B. B. Solberg, Mahsid N. Amiri, Ejikeme Raphael Ezeigwe, Jacob J. Lamb, and Odne Burheim. 2024. "Quantifying Lithium-Ion Battery Rate Capacity, Electrode Structuring, and Transport Phenomena Using E-I Measurements" Batteries 10, no. 10: 364. https://doi.org/10.3390/batteries10100364
APA StyleDunne, R. N., Solberg, S. B. B., Amiri, M. N., Ezeigwe, E. R., Lamb, J. J., & Burheim, O. (2024). Quantifying Lithium-Ion Battery Rate Capacity, Electrode Structuring, and Transport Phenomena Using E-I Measurements. Batteries, 10(10), 364. https://doi.org/10.3390/batteries10100364










