Optimizing Energy Management and Sizing of Photovoltaic Batteries for a Household in Granada, Spain: A Novel Approach Considering Time Resolution
Abstract
:1. Introduction
2. Materials and Methods
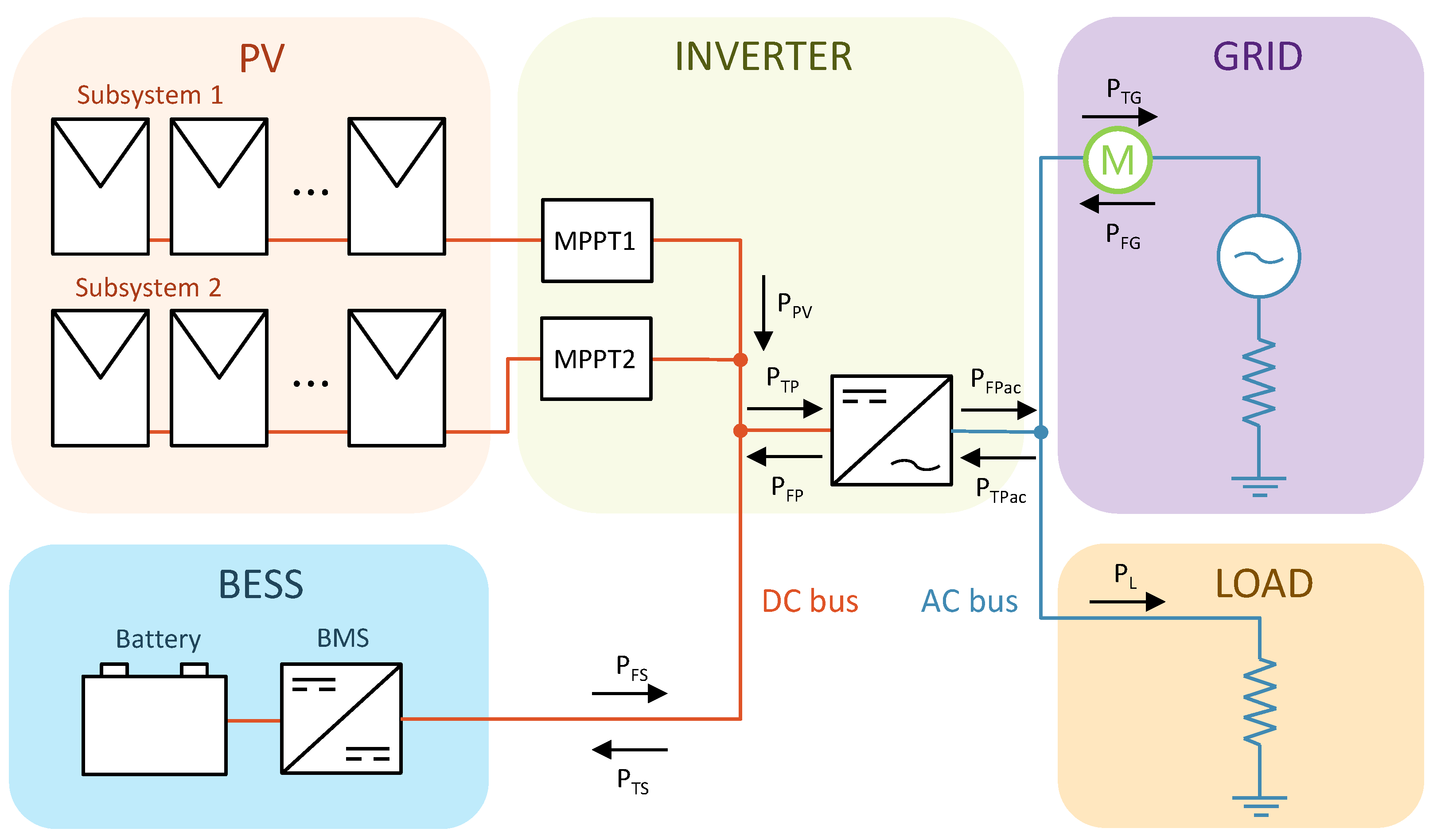
2.1. Description of the System
2.2. Monitored Data
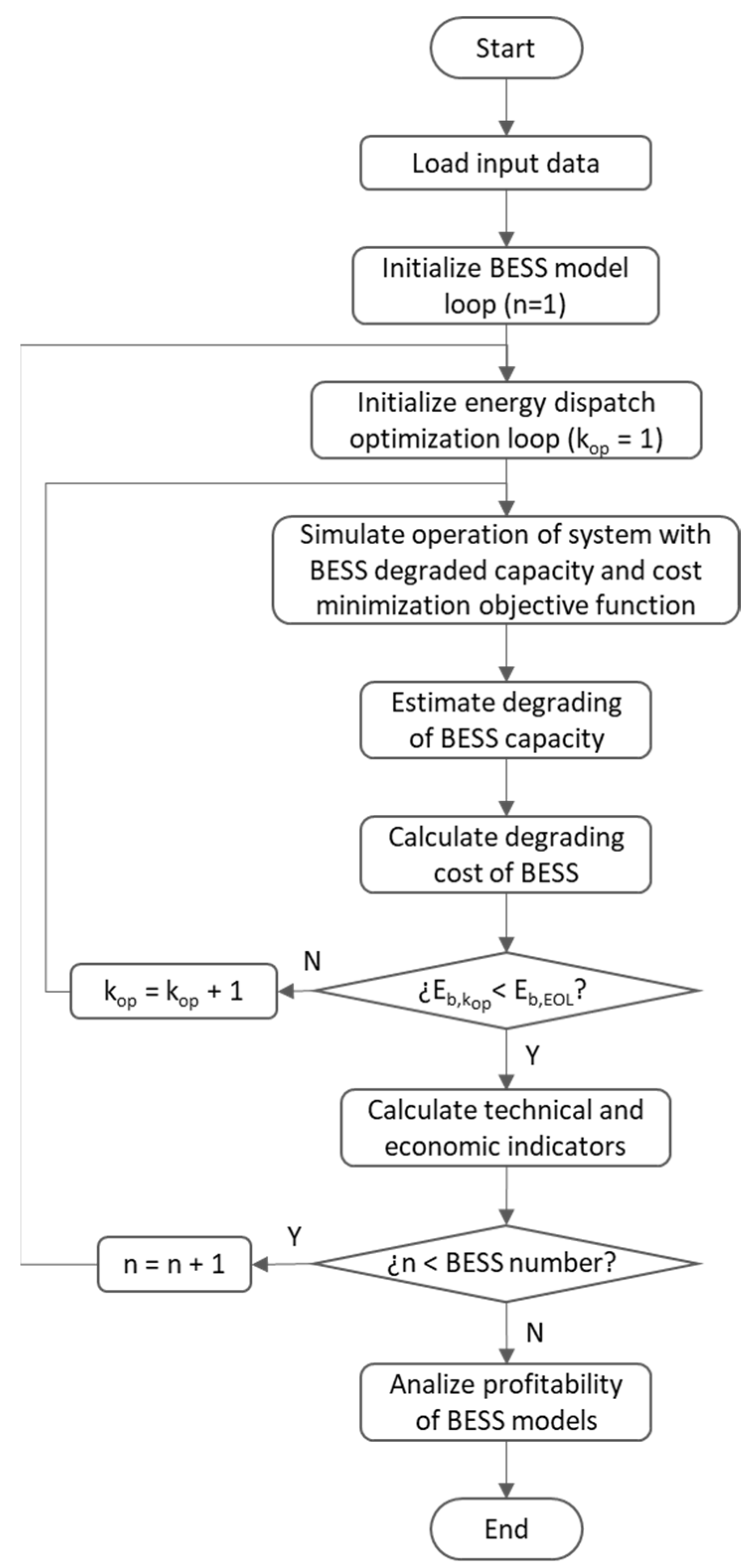
2.3. Optimization Method
2.3.1. Energy Balances
2.3.2. Restrictions
2.3.3. Objective Function
2.3.4. Technical and Economic Sizing Criteria
2.4. Case Studies
- BESS sizing with the proposed energy management method: the operation of the BESS was simulated over its lifetime with a time resolution of 5 min.
- Sensitivity analysis of temporal resolution: the lifetimes of the different BESSs were simulated with the proposed energy management method for the temporal resolutions of 5, 15, 30 and 60 min.
- Comparison of the real operation with the proposed method: a study of the real operation of the installed BESS was conducted in order to compare and evaluate the proposed method.
3. Results
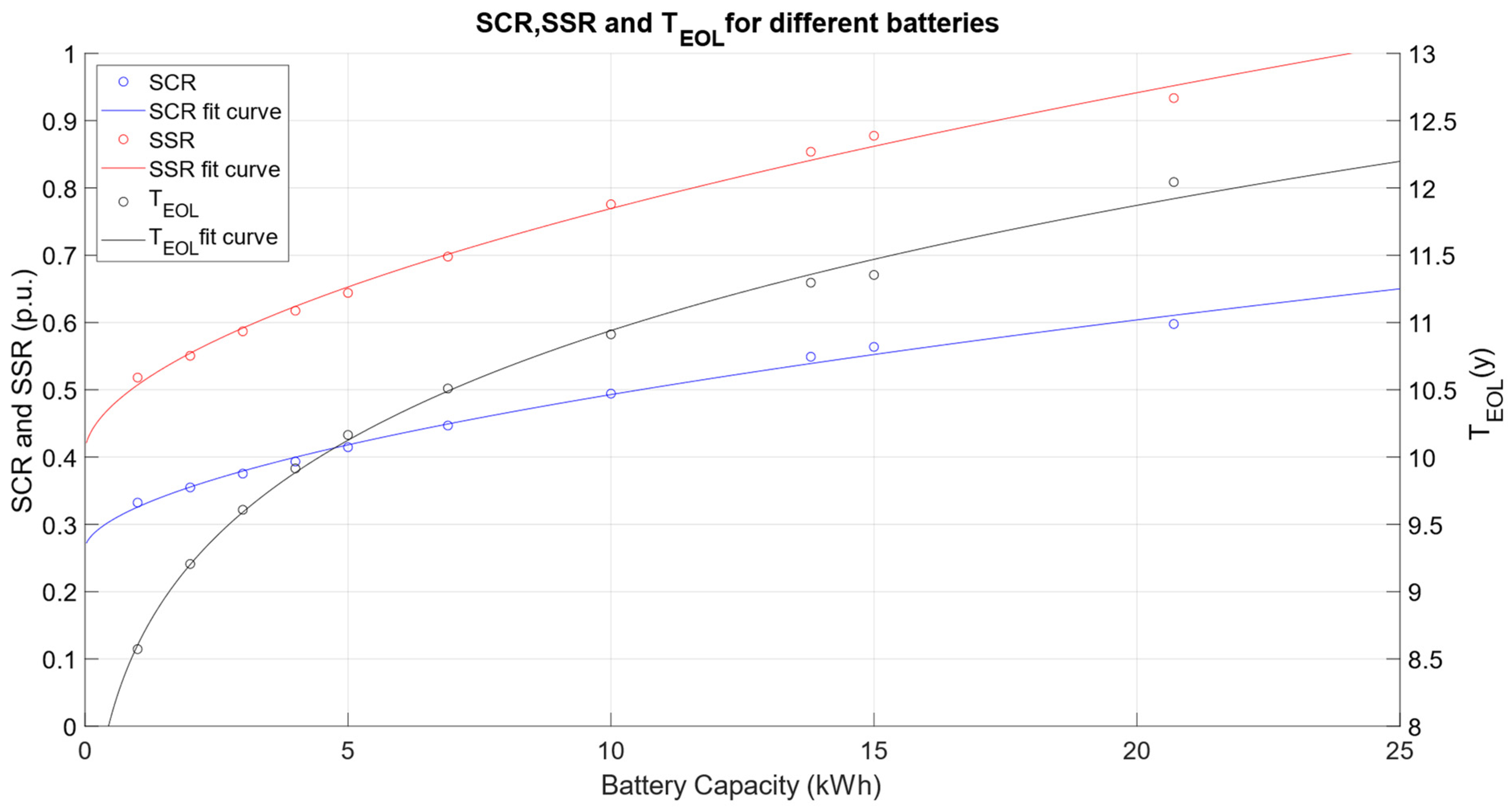
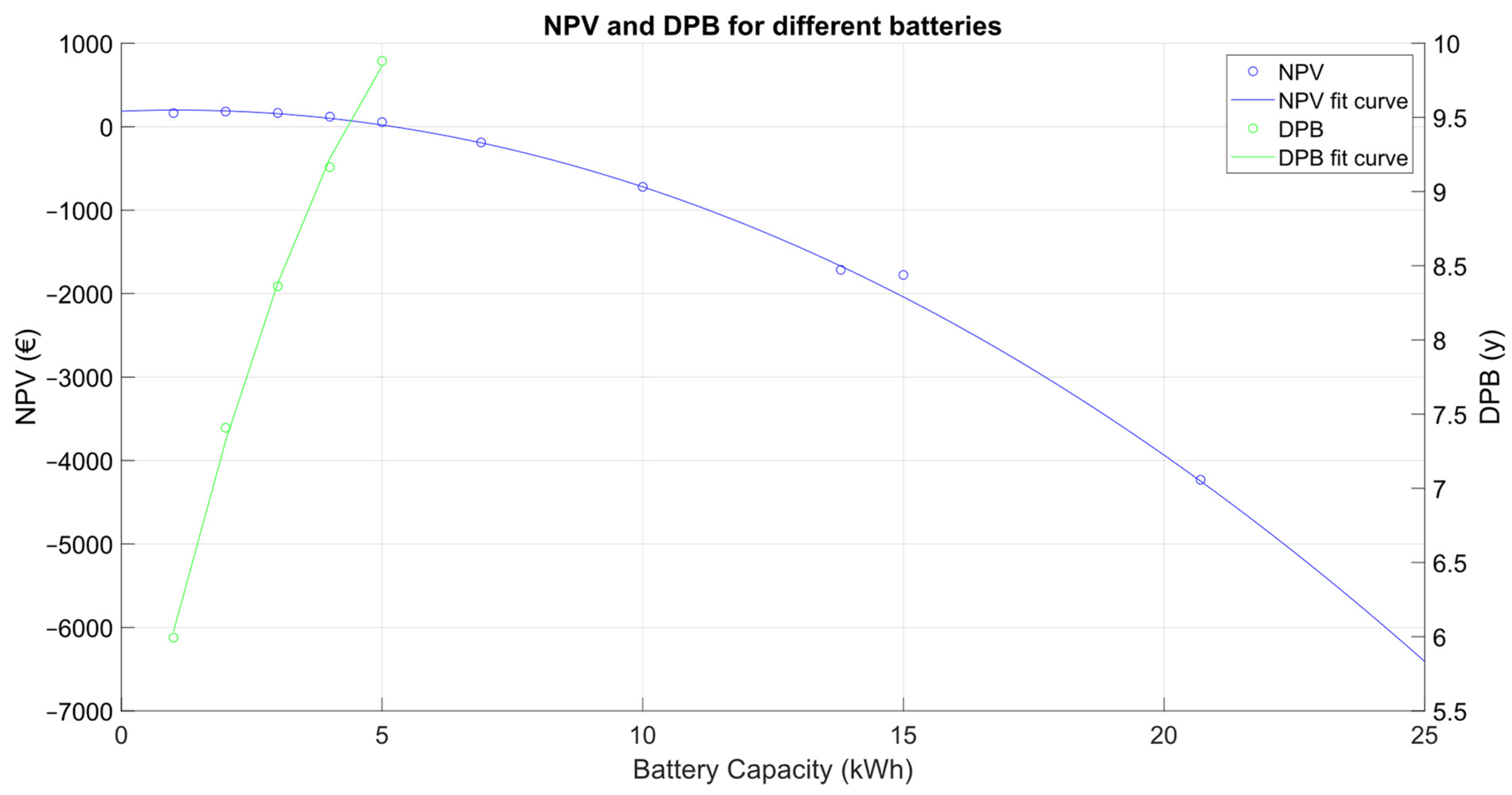
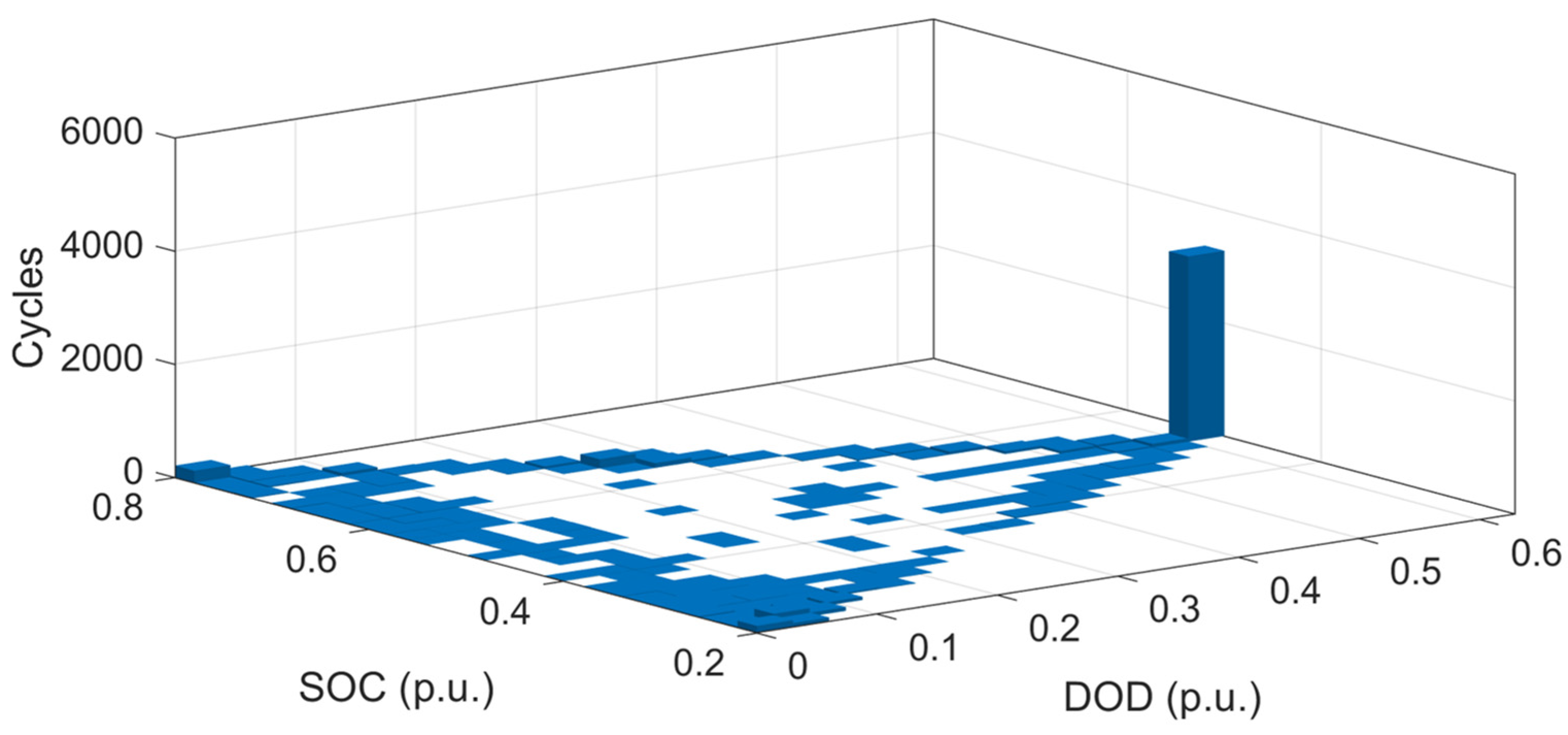
3.1. BESS Sizing with the Proposed Method
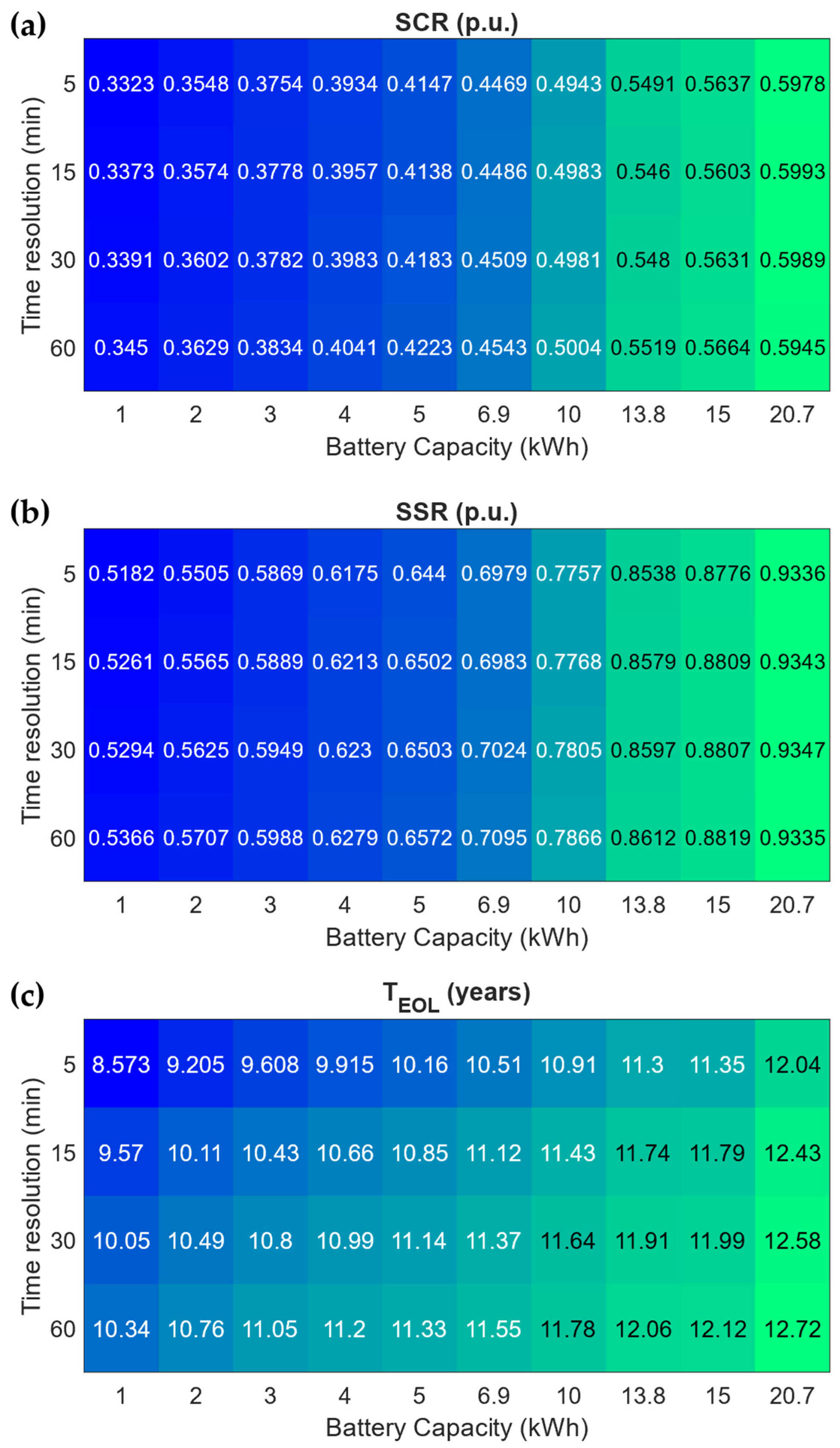
3.2. Sensitivity Analysis of Time Resolution
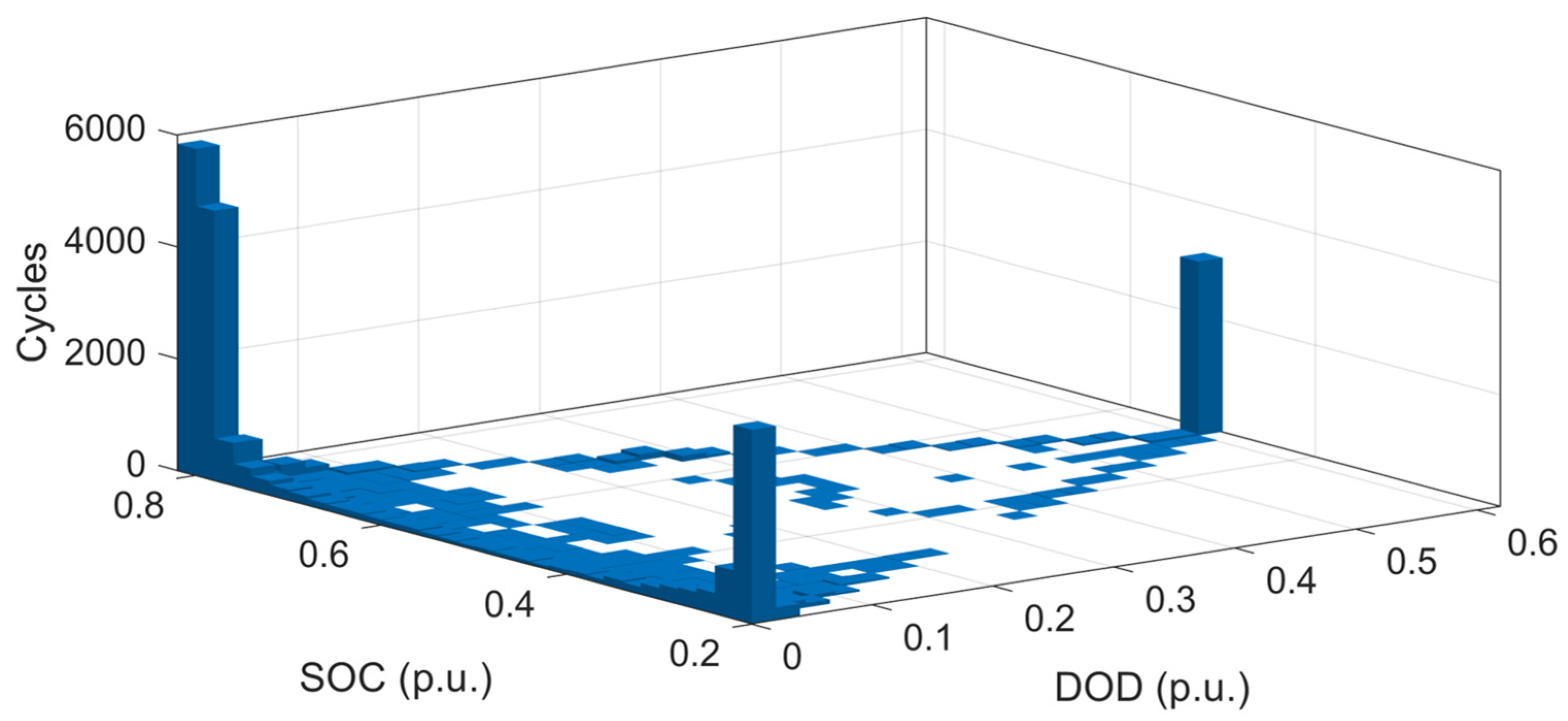
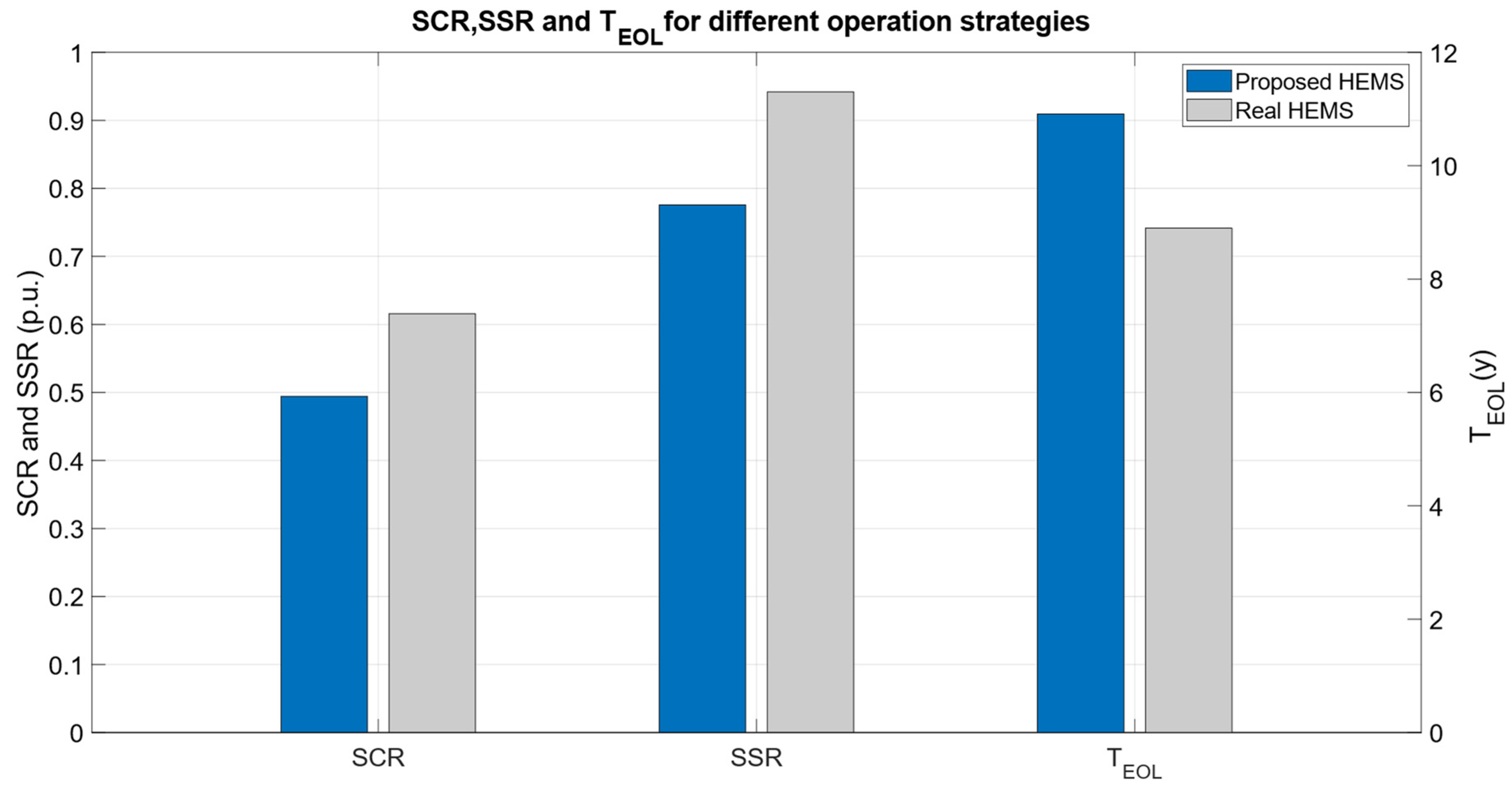
3.3. Comparison of Current Operation with the Proposed Method
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Alternating current |
| BESS | Battery energy storage system |
| BTM | Behind the meter |
| DC | Direct current |
| DCF | Discounted cash flow |
| DG | Distributed generation |
| DOD | Depth of discharge |
| DPB | Discounted payback period |
| EOL | End of Life |
| FIT | Feed-in tariff |
| FTM | Front of the meter |
| HEMS | Home energy management system |
| IRR | Internal rate of return |
| LCOE | Levelized cost of energy |
| LFP | Lithium iron phosphate |
| MILP | Mixed integer linear programming |
| MPPT | Maximum power point tracker |
| NPV | Net present value |
| PV | Solar photovoltaic |
| RES | Renewable energy systems |
| ROI | Return on investment |
| RTP | Real-time price |
| RTPV | Rooftop photovoltaic system |
| SCR | Self-consumption ratio |
| SEI | Solid-electrolyte interface |
| SOC | State of charge |
| SOH | State of health |
| SSR | Self-sufficiency ratio |
| TOU | Time-of-use |
| VAT | Value-added tax |
| VPSC | Voluntary price for small customer |
Appendix A
| Symbol | Value | Units |
|---|---|---|
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| 25 | ||
| 0.5 |
References
- Tzeiranaki, T.; Bertoldi, S.; Castellazzi, P.; Gonzalez Torres, L.; Clementi, M.; Paci, E. Energy Consumption and Energy Efficiency Trends in the EU, 2000–2020; Publications Office of the European Union: Luxembourg, 2022. [Google Scholar] [CrossRef]
- European Commission. EU Solar Energy Strategy; Publications Office of the European Union: Luxembourg, 2022; Volume 1, pp. 5–24. Available online: https://eur-lex.europa.eu/resource.html?uri=cellar:516a902d-d7a0-11ec-a95f-01aa75ed71a1.0001.02/DOC_1&format=PDF (accessed on 2 April 2024).
- UNEF. Informe Anual UNEF 2023. Available online: https://www.unef.es/es/recursos-informes?idMultimediaCategoria=18& (accessed on 10 April 2024).
- IRENA. Renewable Power Generation Costs in 2022; IRENA: Abu Dhabi, United Arab Emirates, 2023; Available online: www.irena.org/Publications/2023/Aug/Renewable-Power-Generation-Costs-in-2022 (accessed on 8 April 2024).
- Tamimi, B.; Canizares, C.; Bhattacharya, K. System Stability Impact of Large-Scale and Distributed Solar Photovoltaic Generation: The Case of Ontario, Canada. IEEE Trans. Sustain. Energy 2013, 4, 680–688. [Google Scholar] [CrossRef]
- Remon, D.; Cantarellas, A.M.; Mauricio, J.M.; Rodriguez, P. Power System Stability Analysis under Increasing Penetration of Photovoltaic Power Plants with Synchronous Power Controllers. IET Renew. Power Gener. 2017, 11, 733–741. [Google Scholar] [CrossRef]
- Análisis|ESIOS Electricidad Datos Transparencia. Available online: https://www.esios.ree.es/es/analisis (accessed on 12 June 2024).
- Hesse, H.C.; Martins, R.; Musilek, P.; Naumann, M.; Truong, C.N.; Jossen, A. Economic Optimization of Component Sizing for Residential Battery Storage Systems. Energies 2017, 10, 835. [Google Scholar] [CrossRef]
- Mulleriyawage, U.G.K.; Shen, W.; Hu, C. Battery System Selection in DC Microgrids for Residential Applications: An Australian Case Study. In Proceedings of the 14th IEEE Conference on Industrial Electronics and Applications, ICIEA, Xi’an, China, 19–21 June 2019; pp. 1926–1931. [Google Scholar] [CrossRef]
- Zhao, C.; Andersen, P.B.; Træholt, C.; Hashemi, S. Grid-Connected Battery Energy Storage System: A Review on Application and Integration. Renew. Sustain. Energy Rev. 2023, 182, 113400. [Google Scholar] [CrossRef]
- Luo, W.; Stynski, S.; Chub, A.; Franquelo, L.G.; Malinowski, M.; Vinnikov, D. Utility-Scale Energy Storage Systems: A Comprehensive Review of Their Applications, Challenges, and Future Directions. IEEE Ind. Electron. Mag. 2021, 15, 17–27. [Google Scholar] [CrossRef]
- Yasmin, R.; Amin, B.M.R.; Shah, R.; Barton, A. A Survey of Commercial and Industrial Demand Response Flexibility with Energy Storage Systems and Renewable Energy. Sustainability 2024, 16, 731. [Google Scholar] [CrossRef]
- Luthander, R.; Widén, J.; Nilsson, D.; Palm, J. Photovoltaic Self-Consumption in Buildings: A Review. Appl. Energy 2015, 142, 80–94. [Google Scholar] [CrossRef]
- Wu, X.; Tang, Z.; Stroe, D.I.; Kerekes, T. Overview and Comparative Study of Energy Management Strategies for Residential PV Systems with Battery Storage. Batteries 2022, 8, 279. [Google Scholar] [CrossRef]
- International Renewable Energy Agency. Electricity Storage and Renewables: Costs and Markets to 2030; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2017. [Google Scholar]
- Martins, R.; Hesse, H.C.; Jungbauer, J.; Vorbuchner, T.; Musilek, P. Optimal Component Sizing for Peak Shaving in Battery Energy Storage System for Industrial Applications. Energies 2018, 11, 2048. [Google Scholar] [CrossRef]
- Kuźniak, R.; Pawelec, A.; Bartosik, A.; Pawełczyk, M. Determination of the Electricity Storage Power and Capacity for Cooperation with the Microgrid Implementing the Peak Shaving Strategy in Selected Industrial Enterprises. Energies 2022, 15, 4793. [Google Scholar] [CrossRef]
- Fioriti, D.; Pellegrino, L.; Lutzemberger, G.; Micolano, E.; Poli, D. Optimal Sizing of Residential Battery Systems with Multi-Year Dynamics and a Novel Rainflow-Based Model of Storage Degradation: An Extensive Italian Case Study. Electr. Power Syst. Res. 2022, 203, 107675. [Google Scholar] [CrossRef]
- Rotella, P., Jr.; Rocha, L.C.S.; Morioka, S.N.; Bolis, I.; Chicco, G.; Mazza, A.; Janda, K. Economic Analysis of the Investments in Battery Energy Storage Systems: Review and Current Perspectives. Energies 2021, 14, 2503. [Google Scholar] [CrossRef]
- EASE. Business Case Taxonomy of Behind-the-Meter Battery Energy Storage Systems in Europe; EASE: Brussels, Belgium, 2023; Available online: https://ease-storage.eu/wp-content/uploads/2023/10/2023.10.11-Behind-the-Meter-Paper_for-distribution.pdf (accessed on 14 June 2024).
- GIZ. Guía Para El Dimensionamiento de Sistemas de Almacenamiento de Energía Con Baterías; Deutsche Gesellschaft für Internationale Zusammenarbeit: Ciudad de México, México, 2022; Available online: www.giz.de/mexico (accessed on 20 May 2024).
- Parra, D.; Patel, M.K. Effect of Tariffs on the Performance and Economic Benefits of PV-Coupled Battery Systems. Appl. Energy 2016, 164, 175–187. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, Y.; Lin, X.; Li, C.; Cai, Z.; Yang, P. Optimal Sizing of PV and Bess for a Smart Household Considering Different Price Mechanisms. IEEE Access 2018, 6, 41050–41059. [Google Scholar] [CrossRef]
- Han, B.; Zahraoui, Y.; Mubin, M.; Mekhilef, S.; Seyedmahmoudian, M.; Stojcevski, A. Home Energy Management Systems: A Review of the Concept, Architecture, and Scheduling Strategies. IEEE Access 2023, 11, 19999–20025. [Google Scholar] [CrossRef]
- Korjani, S.; Casu, F.; Damiano, A.; Pilloni, V.; Serpi, A. An Online Energy Management Tool for Sizing Integrated PV-BESS Systems for Residential Prosumers. Appl. Energy 2022, 313, 118765. [Google Scholar] [CrossRef]
- Martínez-Caballero, L.; Kot, R.; Milczarek, A.; Malinowski, M. Comparison of Energy Storage Management Techniques for a Grid-Connected PV- and Battery-Supplied Residential System. Electronics 2024, 13, 10087. [Google Scholar] [CrossRef]
- Regis, N.; Maina Muriithi, C.; Ngoo, L. Optimal Battery Sizing of a Grid-Connected Residential Photovoltaic System for Cost Minimization Using PSO Algorithm. Eng. Technol. Appplied Sci. Res. 2019, 9, 4905–4911. [Google Scholar] [CrossRef]
- Baniasadi, A.; Habibi, D.; Al-Saedi, W.; Masoum, M.A.S.; Das, C.K.; Mousavi, N. Optimal Sizing Design and Operation of Electrical and Thermal Energy Storage Systems in Smart Buildings. J. Energy Storage 2020, 28, 101186. [Google Scholar] [CrossRef]
- Faessler, B.; Jakobsen, A.B. Autonomous Operation of Stationary Battery Energy Storage Systems—Optimal Storage Design and Economic Potential. Energies 2021, 14, 1333. [Google Scholar] [CrossRef]
- Mulleriyawage, U.G.K.; Shen, W.X. Optimally Sizing of Battery Energy Storage Capacity by Operational Optimization of Residential PV-Battery Systems: An Australian Household Case Study. Renew. Energy 2020, 160, 852–864. [Google Scholar] [CrossRef]
- Yuan, T.; Mu, Y.; Wang, T.; Liu, Z.; Pirouzi, A. Using Firefly Algorithm to Optimally Size a Hybrid Renewable Energy System Constrained by Battery Degradation and Considering Uncertainties of Power Sources and Loads. Heliyon 2024, 10, e26961. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Z.; Li, B.; Liu, J.; Zhang, L. Energy Management Strategy and Optimal Battery Capacity for Flexible PV-Battery System under Time-of-Use Tariff. Renew. Energy 2022, 200, 558–570. [Google Scholar] [CrossRef]
- Bhoi, S.K.; Nayak, M.R. Optimal Scheduling of Battery Storage with Grid Tied PV Systems for Trade-off between Consumer Energy Cost and Storage Health. Microprocess. Microsyst. 2020, 79, 103274. [Google Scholar] [CrossRef]
- Zhang, N.; Leibowicz, B.D.; Hanasusanto, G.A. Optimal Residential Battery Storage Operations Using Robust Data-Driven Dynamic Programming. IEEE Trans. Smart Grid 2020, 11, 1771–1780. [Google Scholar] [CrossRef]
- Ullah, I.; Rasheed, M.B.; Alquthami, T.; Tayyaba, S. A Residential Load Scheduling with the Integration of On-Site PV and Energy Storage Systems in Micro-Grid. Sustainability 2019, 12, 184. [Google Scholar] [CrossRef]
- Gabr, A.Z.; Helal, A.A.; Abbasy, N.H. Multiobjective Optimization of Photo Voltaic Battery System Sizing for Grid-Connected Residential Prosumers under Time-of-Use Tariff Structures. IEEE Access 2021, 9, 74977–74988. [Google Scholar] [CrossRef]
- Uddin, K.; Gough, R.; Radcliffe, J.; Marco, J.; Jennings, P. Techno-Economic Analysis of the Viability of Residential Photovoltaic Systems Using Lithium-Ion Batteries for Energy Storage in the United Kingdom. Appl. Energy 2017, 206, 12–21. [Google Scholar] [CrossRef]
- Naumann, M.; Schimpe, M.; Keil, P.; Hesse, H.C.; Jossen, A. Analysis and Modeling of Calendar Aging of a Commercial LiFePO4/Graphite Cell. J. Energy Storage 2018, 17, 153–169. [Google Scholar] [CrossRef]
- Naumann, M.; Spingler, F.; Jossen, A. Analysis and Modeling of Cycle Aging of a Commercial LiFePO4/Graphite Cell. J. Power Sources 2020, 451, 7666. [Google Scholar] [CrossRef]
- Xu, B.; Oudalov, A.; Ulbig, A.; Andersson, G.; Kirschen, D.S. Modeling of Lithium-Ion Battery Degradation for Cell Life Assessment. IEEE Trans. Smart Grid 2018, 9, 8950. [Google Scholar] [CrossRef]
- Khezri, R.; Mahmoudi, A.; Aki, H. Multiobjective Long-Period Optimal Planning Model for a Grid-Connected Renewable-Battery System. IEEE Trans. Ind. Appl. 2022, 58, 5055–5067. [Google Scholar] [CrossRef]
- Collath, N.; Cornejo, M.; Engwerth, V.; Hesse, H.; Jossen, A. Increasing the Lifetime Profitability of Battery Energy Storage Systems through Aging Aware Operation. Appl. Energy 2023, 348, 121531. [Google Scholar] [CrossRef]
- Rezaeimozafar, M.; Barrett, E.; Monaghan, R.F.D.; Duffy, M. A Stochastic Method for Behind-the-Meter PV-Battery Energy Storage Systems Sizing with Degradation Minimization by Limiting Battery Cycling. J. Energy Storage 2024, 86, 111199. [Google Scholar] [CrossRef]
- Muala, A.; Bany Issa, Z.A.; Bello Bugallo, M.A.; Integrating, P.M.; Mi, C.; Gao, W.; Al Muala, Z.A.; Issa, M.A.B.; Bello Bugallo, P.M. Integrating Life Cycle Principles in Home Energy Management Systems: Optimal Load PV–Battery–Electric Vehicle Scheduling. Batteries 2024, 10, 138. [Google Scholar] [CrossRef]
- IEC 61724-1; Photovoltaic System Performance—Part 1: Monitoring. International Electrotechnical Commission: Geneva, Switzerland, 2021.
- Muñoz-Rodríguez, F.J.; Jiménez-Castillo, G.; de la Casa Hernández, J.; Aguilar Peña, J.D. A New Tool to Analysing Photovoltaic Self-Consumption Systems with Batteries. Renew. Energy 2021, 168, 1327–1343. [Google Scholar] [CrossRef]
- Downing, S.D.; Socie, D.F. Simple Rainflow Counting Algorithms. Int. J. Fatigue 1982, 4, 31–40. [Google Scholar] [CrossRef]
- Park, S.J.; Song, Y.W.; Kang, B.S.; Kim, W.J.; Choi, Y.J.; Kim, C.; Hong, Y.S. Depth of Discharge Characteristics and Control Strategy to Optimize Electric Vehicle Battery Life. J. Energy Storage 2023, 59, 106477. [Google Scholar] [CrossRef]
- Deshpande, R.D.; Uddin, K. Physics Inspired Model for Estimating ‘Cycles to Failure’ as a Function of Depth of Discharge for Lithium Ion Batteries. J. Energy Storage 2021, 33, 101932. [Google Scholar] [CrossRef]
- Mirletz, B.; Vimmerstedt, L.; Stehly, T.; Akar, S.; Stright, D.; Augustine, C.; Beiter, P.; Cohen, S.; Cole, W.; Duffy, P.; et al. Annual Technology Baseline (ATB) Cost and Performance Data for Electricity Generation Technologies; DOE Open Energy Data Initiative (OEDI): Washington, DC, USA; National Renewable Energy Laboratory (NREL): Washington, DC, USA, 2023. [Google Scholar] [CrossRef]
- Comisión Nacional de Los Mercados y La Competencia. Circular 2/2019, de 12 de Noviembre, de La Comisión Nacional de Los Mercados y La Competencia, Por La Que Se Establece La Metodología de Cálculo de La Tasa de Retribución Financiera de Las Actividades de Transporte y Distribución de Energía Eléctrica. Boletín Of. Del Estado 2019, 279, 127725–127734. Available online: https://www.cnmc.es/sites/default/files/2749227_42.pdf (accessed on 20 May 2024).




| Ref. | Sampling Period | Scheduling Optimization Objective | Optimization Time Resolution | Optimization Period |
|---|---|---|---|---|
| [23] | 60 min | Min. Operation Cost | 60 min (average daily profile by season and weather conditions) | 1 day |
| [31] | 60 min | Min. Total Cost | 60 min (average daily profile) | 365 days |
| [41] | 60 min | N/A | N/A | N/A |
| [30] | 60 min | Min. Energy Cost | 60 min | 365 days |
| [43] | 60 min | Min. Energy Cost and Investment Cost | 60 min | 365 days |
| [18] | 15 min | N/A | N/A | N/A |
| [42] | 15 min | Max. Savings and min. degradation cost | 15 min | 0.5 day |
| [44] | 1 min | Min. Operation Cost | 1 min | 365 days |
| This work | 5 min | Min. Energy Cost and Degradation cost | 5 min | 7 days |
| Equipment | Specification | Value |
|---|---|---|
| PV modules | Technology | Polycrystalline silicon |
| Max. rated power (STC 1) | 275 W | |
| Number | 27 | |
| Efficiency | 16.90% | |
| Inverter | Max. PV input power | 9 kW |
| Number of MPPTs | 2 | |
| Rated output power | 6 kW | |
| European efficiency | 97.8% | |
| BESS | Chemistry | LFP |
| Effective battery capacity | 10 kWh | |
| Max. charge/discharge power | 5 kW | |
| Max. depth of discharge (DOD) | 100% | |
| Roundtrip efficiency | 94% |
| BESS Model | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Energy Capacity (kWh) | 1 | 2 | 3 | 4 | 5 | 6.9 | 10 | 13.8 | 15 | 21.7 |
| Power Capacity (kW) | 0.5 | 1 | 1.5 | 2 | 2.5 | 3.5 | 5 | 7 | 5 | 10.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rus-Casas, C.; Gilabert-Torres, C.; Fernández-Carrasco, J.I. Optimizing Energy Management and Sizing of Photovoltaic Batteries for a Household in Granada, Spain: A Novel Approach Considering Time Resolution. Batteries 2024, 10, 358. https://doi.org/10.3390/batteries10100358
Rus-Casas C, Gilabert-Torres C, Fernández-Carrasco JI. Optimizing Energy Management and Sizing of Photovoltaic Batteries for a Household in Granada, Spain: A Novel Approach Considering Time Resolution. Batteries. 2024; 10(10):358. https://doi.org/10.3390/batteries10100358
Chicago/Turabian StyleRus-Casas, Catalina, Carlos Gilabert-Torres, and Juan Ignacio Fernández-Carrasco. 2024. "Optimizing Energy Management and Sizing of Photovoltaic Batteries for a Household in Granada, Spain: A Novel Approach Considering Time Resolution" Batteries 10, no. 10: 358. https://doi.org/10.3390/batteries10100358
APA StyleRus-Casas, C., Gilabert-Torres, C., & Fernández-Carrasco, J. I. (2024). Optimizing Energy Management and Sizing of Photovoltaic Batteries for a Household in Granada, Spain: A Novel Approach Considering Time Resolution. Batteries, 10(10), 358. https://doi.org/10.3390/batteries10100358








